Summary
Biological circuits and systems within even a single cell need to be represented by large-scale feedback networks of nonlinear, stochastic, stiff, asynchronous, non-modular coupled differential equations governing complex molecular interactions. Thus, rational drug discovery and synthetic biological design is difficult. We suggest that a four-pronged interdisciplinary approach merging biology and electronics can help: (1) The mapping of biological circuits to electronic circuits via quantitatively exact schematics; (2) The use of existing electronic circuit software for hierarchical modeling, design, and analysis with such schematics; (3) The use of cytomorphic electronic hardware for rapid stochastic simulation of circuit schematics and associated parameter discovery to fit measured biological data; (4) The use of bio-electronic reporting circuits rather than bio-optical circuits for measurement. We suggest how these approaches can be combined to automate design, modeling, analysis, simulation, and quantitative fitting of measured data from a synthetic biological operational amplifier circuit in living microbial cells.
Subject Areas: Bioelectronics, Engineering, Electrical Engineering
Graphical Abstract

Bioelectronics; Engineering; Electrical Engineering
Introduction
Biological networks are notoriously difficult to analyze and interpret because they comprise tens of thousands of biochemical pathways that are linked. Pathways that are studied in isolation seldom provide deep insights into the behaviors of larger networks because they do not account for the complex interactions between pathways. In medicine, such systems biology interactions are important for drug or drug cocktail discovery based on pathway analysis. They are necessary for predicting drug or drug cocktail efficacy, safety, side effects, mechanism and site of action, and changes in cocktail composition or dosage with changing symptoms.
Molecular interactions manifest in several forms. For example, they can include resource limitations, which couple biochemical reactions that share the same enzyme or molecule; loading or non-modular effects that change the behavior of pathways depending on their downstream and upstream connections (Cardinale and Arkin, 2012); cross-talk between pathways caused by synergistic or antagonistic effects of transcription and translation regulation (Mukherji and Van Oudenaarden, 2009; Zeng et al., 2018) or by molecules having multiple fan-out interactions with downstream targets; feedback effects from interactions that form a closed loop between upstream and downstream molecules (Ferrell, 2002). To compound these difficulties, biochemical reactions are generally non-linear and noisy () such that simplified biological models that assume linear and/or deterministic interactions are not accurate.
One solution adopted by synthetic biologists is to fit biological circuits into neat computational blocks defined by logic gates. This digital framework has seen some successes in designing small biological circuits that use a relatively small number of logic gates. For example, Ausländer et al. built a 1-bit adder in a mammalian system using over 20 logic gates distributed among 9 different cell types (Ausländer et al., 2018). So far, it has proven difficult to scale these circuits to larger networks due to issues such as resource limitations including metabolic burden, loading and non-modularity, stochastics (noise), cross-talk, and feedback (Sarpeshkar, 2014; Teo et al., 2015).
Bio-molecular reactions are analog and stochastic by nature, so a blanket solution that treats all reactions like logic gates works optimally only in special cases such as memory storage and decision-making where deterministic digital behavior is appropriate. Additionally, an analog approach offers resource (molecular copy number) and energy (ATP) advantages compared to a digital approach for many biological functions that are low precision by nature. For example, we showed in a previous paper (Sarpeshkar, 2014) that the number of molecules needed to perform 2-bit precise addition is 3 orders of magnitude lower with an analog approach compared to a digital approach. The energy advantage of the same addition is almost 4 orders of magnitude lower when using an analog approach. By adopting an analog electronic circuit framework, we can use a language that describes biological processes more naturally. We also gain an appreciation for the power, speed, and precision trade-offs exhibited by nature when she makes complex circuits and systems function under tight resource constraints of power (ATP/sec) for a given speed (1/(time taken to do the computation)) and precision (signal-to-noise ratio or bits of precision) (Sarpeshkar, 2014).
All of the problems that we have described with respect to biological circuits and systems are also exhibited in analog electronic circuits, especially in those that have resource limitations with respect to energy and power and part count. For example, analog circuit designers also need to build robust functional devices using components that are often noisy at low electron copy number and that can be subject to significant manufacturing variations. Even well-characterized components sometimes exhibit unintended behaviors when operating in the context of a larger circuit due to loading, cross-talk, and feedback. Analog circuit designers often build systems that operate within a range of robustness and performance specifications while subject to constraints of power or physical space on an integrated circuit (chip) or board. For example, medical implants that are both small and power efficient (Bradley, 2006; Sarpeshkar, 2010) use ultra-low-power electronics to operate. Such electronic design is often made possible by a deep understanding of feedback systems that circuit designers have developed and refined over the past 100 years (Sarpeshkar 2010, 2014) for linear and nonlinear circuits.
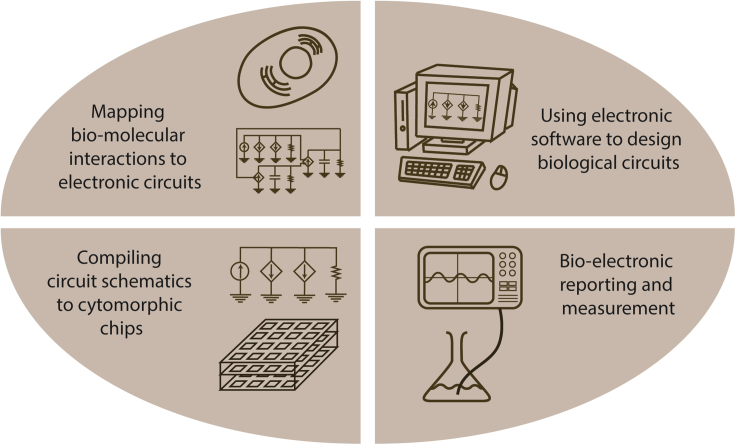
Given the many similarities between biological and electronic circuits, we posited in a previous review paper that 17 synthetic biological circuits over 20+ years could be effectively studied through the lens of analog circuits for obtaining insight into their operation at the DNA, RNA, protein, or small-molecule/metabolite levels (Teo et al., 2015). Figures S1 and S2 and associated captions summarize the key ideas in this paper for the reader's convenience. Intuitively, flow variables can be mapped to current; state variables can be mapped to voltage; relationships between these variables, whether linear or nonlinear, map to corresponding current-voltage relationships as in Figure 3. Readers interested in detailed mathematical derivations of biochemical reaction networks can also find them in chapter 24 of (Sarpeshkar 2010) with associated hardware work described in (Woo et al. 2015, 2018; Kim et al., 2018). Important relationships between energy, information, and power in cells can be found in (Sarpeshkar 2014). Here, we suggest a four-pronged interdisciplinary methodology that is capable of leveraging the full power of analog electronic circuit design for general modeling, design, analysis, rapid simulation, and electronic reporting and measurement of biological circuits as shown in Figure 1. The Results subsections of our paper are organized as follows. In Section I, we discuss how to create electronic circuit schematics that are an exact representation of mathematical equations that describe biological circuits and use the enzyme-substrate binding circuit as an example (Figures 2 and 3). In Section II, we show how existing electronic circuit software, e.g. Cadence, which has been used for the hierarchical design of billions of electronic transistor devices on modern complex integrated circuit chips for decades, can be leveraged for the design of biological circuits. To show how our method can work in concrete detail and practice, we focus on a synthetic microbial biological operational amplifier circuit as shown in Figure 4. In Section III, we discuss how custom cytomorphic integrated circuit chips can rapidly simulate many instantiations and parameters of biological circuits that have been compiled into equivalent electronic circuits and thus help with automated parameter discovery and automated data fitting of measured biological data. We show a concrete example w.r.t. to the synthetic biological operational amplifier (Figures 5, 6, and 7). In Section IV, we illustrate how bio-electronic rather than bio-optical reporting and measurement can further help with the merging of biology and electronics with respect to such automation (Figure 8). We conclude by discussing the potential impact of our work in the future. Supplemental Sections I-III provide further details that correspond to Sections II and III in the main body of the paper.
Figure 3.
Mapping of Biological Circuits to Electronic Circuits
The table illustrates how mappings of biological concentration variables, represented as voltage, and biological flux variables, represented as current, are used to create controlled (dependent) and constitutive (independent) current sources and other electronic circuit equivalents. Such electronic circuit equivalents of biological circuits represent their operation faithfully including noise, nonlinearity, dynamics, and loading effects.
Figure 1.
A Framework for Merging Biological and Electronic Circuits
The framework consists of four parts – (1) Biological circuits are represented as pictorial analog electronic circuit schematics that represent their mathematical dynamics exactly and quantitatively while preserving intuition about several circuit aspects such as feedback loops; (2) Electronic circuit software is then used for rigorous design, analysis, and simulation of these schematics; (3) The electronic circuit schematics are then compiled to and simulated on digitally programmable analog “cytomorphic” chips for rapid parameter discovery, automation, and learning including highly computationally intensive stochastic dynamics; (4) Further automation can be achieved if bioelectronic reporting and measurement is also electronic rather than optical such that the feedback loops between design, modeling, analysis, simulation, parameter discovery, fitting of data, and learning are completely electronic.
Figure 2.
Enzyme-Substrate Binding as an Analog Circuit Schematic
The enzyme-substrate binding reaction is commonly represented by a chemical equation or cartoon blocks. The rate of complex association and dissociation is written in the form of coupled ordinary differential equations (ODEs). Using mappings described in the text and illustrated in Figure 3, we construct an analog circuit equivalent of an ES binding reaction. The latter circuit represents the mathematical dynamics of the ODE exactly while providing pictorial intuition on substrate depletion loading effects in chemical reactions, the stochastics of Poisson noise in the electronic current fluxes, and multiplicative and saturation non-linearities that are present in the reaction. Thus, it is very useful for design, modeling, analysis, and simulation of complex biological systems that can be composed in a hierarchical fashion out of such circuit schematics via software.
Figure 4.
Biological Operational Amplifier
(A) In open-loop configuration, the biological operational amplifier amplifies the difference between two input concentrations of small molecules such as AHL and arabinose to create a large concentration of an output target biomolecule. When the output biomolecule is the same as the input at the negative terminal, a negative feedback loop enhances robustness to parameters, buffering, and tracking performance can be achieved.
(B) The biological operational amplifier (Bio-OpAmp) has three amplification stages. The first stage is a fast stage that generates guide RNAs based on the input concentration of AHL and arabinose. The sgRNAs bind to CRISPR dCas9, and the resulting complex inhibits either LuxI or AiiA expression in the second stage. The concentration of aTc regulates dCas9 expression, which enables control of the total strength of the inhibition. The last amplification stage is a fast stage that uses LuxI and AiiA to synthesize or degrade AHL, respectively. AHL binds to LuxR at the inverting input to close the feedback loop.
(C) To represent the production of bio-molecules in its stages of amplification, the schematic uses a circuit motif similar to the enzyme-substrate binding motif in Figure 2.
Figure 5.
Computational Pipeline to Program Cytomorphic Chips and Systems for Automating Parameter Discovery and for Learning
Using compilers that have been developed or are currently in development (Medley et al., 2020), we translate biochemical reactions in SBML or in SPICE netlists to programming bits for the cytomorphic chips that have hardware instantiations of chemical reaction circuits. To aid in such programming, MATLAB and Simulink interfaces interact with field programmable gate arrays (FPGAs) on circuit boards composed of many such cytomorphic chips. The programmable bits configure DACs, switches, and bio-molecular network connectivity on the cytomorphic chips.
Figure 6.
A Compilation of the Bio-OpAmp Circuit to an Equivalent Cytomorphic Chip Instantiation
Figures S6–S9 illustrate how to generate a cytomorphic configuration of the Bio-OpAmp in detail.
Figure 7.
Dynamics of a Bio-OpAmp as it Reaches Equilibrium
(A) Software simulation data.
(B) Cytomorphic chip simulation data. The time series illustrate the transient response of the Bio-OpAmp using normalized concentrations centered at 50 nA. Both simulations exhibit similar transient behavior including overshoots, rise time, and settling time. In the cytomorphic simulation, current levels at equilibrium deviate from 50 nA due to manufacturing variability in the chips.
Figure 8.
Biological Comparator
(A) Biological circuit cartoon representation.
(B) Transcription regulation network of biological comparator.
(C) Analog circuit schematic representation of biological comparator.
(D) Measured biological data comparing bio-electronic and optical reporting performance that is adapted from (Zeng et al., 2019).
Section I: Mapping Bio-Molecular Interactions to Electronic Circuits
Bio-molecular interactions are generally represented by cartoon illustrations and modeled by systems of ordinary differential equations (ODEs). Cartoons are great for developing intuition of simple biological systems but are often too coarse and abstract for developing deep insights. On the other hand, ODE models provide detailed mathematical descriptions of the dynamics of bio-molecular interactions; however, as system complexity scales, they are difficult to interpret meaningfully. We have developed a mapping from biology to electronics that combines the ease of interpretation of illustrations with the mathematical exactness of ODEs. It can be applied to all circuits in molecular biology at the DNA, RNA, protein, and small-molecule levels, which we have illustrated as a canonical circuit schematic in a previous review (Teo et al., 2015) and in Figure S2. To demonstrate how the general mapping works, outlined in Figure 3, we use the specific and ubiquitous example of an enzyme-substrate (ES) binding reaction shown in Figure 2.
ES binding is typically represented by a cartoon or a mass action equation as in Figure 2. The cartoon provides a quick visual description while the equations capture the underlying thermodynamics. The equations in Figure 2 show that the rate of association of E and S depends on the product of free enzyme and free substrate multiplied by a forward rate constant Kf, while the rate of dissociation depends on the concentration of bound complex with a reverse rate constant Kr. We can represent such dynamics using a circuit where a current generator, resistor, and capacitor are connected in parallel. Such a pictorial circuit representation allows biological circuit designers to identify key characteristics such as feedback and noise without performing laborious calculations: Current fluxes through the current generator and resistor represent the association and dissociation molecular fluxes, respectively. As current flows in and out of the capacitor, its voltage changes accordingly. The voltage across the capacitor in this case corresponds to the concentration of bound substrate complex. The circuit subtracts bound variables from total conserved molecular variables to create free voltage variables via the voltage subtractors, creating two parallel “use-and-lose-it” negative feedback loops that are ubiquitously present in all chemical reactions. These “free voltage variables” are multiplied to generate a current that matches the forward association flux. The overall analog schematic is one that represents biological interactions succinctly while being faithful to the underlying mathematical descriptions including noise, dynamics, robustness, and feedback (Sarpeshkar, 2010, 2014; Teo et al., 2015). Figure S1, adapted from (Teo et al., 2015), provides further details.
Figure S1 shows that even diffusion can be exactly modeled via distributed resistor-capacitor (RC) circuits. Chapter 14 in (Sarpeshkar 2010) discusses how current-mode diffusor circuits can map such distributed RC circuits to highly efficient current-mode equivalents suitable for integrated circuit implementation, e.g., on the cytomorphic chips, discussed in Section III. In practice, as shown in Figure S5 and (Woo et al. 2015, 2018), cytomorphic chips and boards are assembled with field programmable gate arrays (FPGAs) for digital programmability of network connectivity and analog parameters. Therefore, via simple attenuation and delays in digital data packets to adjacent addresses, delays and diffusion can also be easily implemented in the digital domain.
To uncover properties of a biological circuit, we can study its analog schematic equivalent using analytical tools from analog circuit design. In the case of an ES binding circuit, the Poisson noise in ES flux is effectively the sum of Poisson noise from forward and reverse current fluxes in the dependent current generator and resistor, respectively, and determines the voltage or concentration noise on the capacitor (Sarpeshkar 2010, 2014). If the substrate negative feedback loop is effectively absent due to a large concentration of substrate, the enzyme negative feedback loop with a small-signal loop gain of Kf STOT/Kr = S/KD determines the proportional tracking of ES (output) with ETOT (input) as in a simple negative feedback buffer operational amplifier circuit in electronics, generating well-known Michaelis-Menten input-output relationships. Figure 3 summarizes how mappings can be similarly created for 10 other common bio-molecular processes. The papers (Sarpeshkar, 2014; Teo et al., 2015) provide further details on the same treatment for several other well-known circuits from synthetic biology.
Section II: Using Electronic Circuit Software for Biological Circuit Design
Circuits, which convert equations to pictures, enable a big picture intuitive view of a whole system with all of the important feedback loops and interactions visibly obvious in a schematic or map. It is possible to design small circuits without such a schematic by using only mathematical equations. But, for design, analysis, and simulation of circuits and systems with hundreds to millions of state variables, pictorial intuition, model-order reduction, and hierarchy are essential. It is also important that we have the ability to rapidly switch the complexity of a model in a simulation to see if it actually matters at the timescale and for input-output relationships that are of relevant experimental biological importance in a practical application. For example, a “level 1” model with two experimentally constrained parameters may be more useful in a practical application even though the actual biology may involve significantly more parameters in an accurate “level 57” model with 1,000s of free parameters, many of which are unknown and are not experimentally constrained or relevant. Thus, certain subsystems can be well approximated with reduced-order input-output circuits: Finally, analog schematics are important for the scaling of biological circuits from simple low-level circuit motifs to circuits that can be connected and composed to create large-scale systems that are composed in a hierarchical fashion: For example, many ES reactions in cascade can form a glycolysis circuit, which itself can be a sub-circuit in a higher level glucose-to-ATP circuit. The glucose-to-ATP circuit can be a metabolic driving circuit with an effective nonlinear driving source impedance that powers other small and large subsystems within a cell. Many such subsystems can form the system of the cell.
Hierarchical and complex circuit design can be ported from electronic to biological circuit design with existing software. Over about 50 + years, analog circuit designers have developed computer-aided design software such as Cadence and circuit simulation tools such as SPICE to visualize circuits and to simulate them with ease (see Figure S3). SPICE also comes packaged with over 25 analysis tools, e.g. to perform small-signal .AC frequency analysis; to study transient .tran time-domain behavior; to study steady-state .DC input-output behavior; to see the effects of noise via .PNOISE; or to use monte-carlo simulation to study parameter sensitivity. Such tools can be leveraged rather than re-inventing the wheel from scratch. Schematic circuits at one level of a hierarchy can be connected to create a higher-level input-output circuit at the next level of hierarchy, which is represented abstractly by a circuit “symbol”. Such symbols can then be combined with each other to create higher level circuits. The process can be recursively repeated to create systems of massive complexity. The microprocessor and analog cell phone chips that we take for granted today, which often have billions of interconnected transistor devices, were designed in such a fashion. Here, we shall only provide an example of a relatively simple synthetic biological operational amplifier circuit to illustrate how electronic circuit software can be concretely used for creating biological circuit schematics. Nevertheless, it will illustrate all of the concepts. Subsequently, we shall focus on discussing how to compile, simulate, discover parameters, and fit data in an automated fashion.
Synthetic biologists have designed and ported many basic electronic circuit motifs such as logic gates (Bonnet et al., 2013; Maung and Smolke, 2008; Nielsen et al., 2016), latches (Gardner et al., 2000; Lee et al., 2016), load driver circuits (Mishra et al., 2014), oscillators (Chen et al., 2015; Elowitz and Leibier, 2000; Prindle et al., 2014), and log-linear circuits (Daniel et al., 2013) to biology. In contrast, the operational amplifier (OpAmp), which is a popular device used in analog circuits, has only just started gaining traction (Klavins, 2014). An OpAmp is often considered a fundamental building block for designing large regulatory loops in analog circuits due to its many attributes for modulating feedback robustly. It implements a simple circuit building block wherein the voltage difference of its two control inputs is amplified with a large gain and reported at its output terminal (see Figure 4 and Appendices from (Zeng et al., 2018)). When connected to companion components in a negative feedback loop, an OpAmp enables robust and precise analog computations such as weighted summation, inverting and non-inverting amplification, and integration. It performs these calculations rigorously despite being susceptible to manufacturing variations. An OpAmp's robustness to parameter variation is essential for making analog electronics that are scalable, versatile, and context independent from an input-output point of view. Therefore, by building a biological OpAmp (Bio-OpAmp) (Zeng et al., 2018), we can leverage its properties to regulate feedback in a variety of important biological processes such as homeostasis (Berridge et al., 2003; Nemazanyy et al., 2015; Wong et al., 2012), metabolic regulation (Pan et al., 2009; Sturm et al., 2010), and immune response (Fukao et al., 2002; Liu et al., 2015).
The Bio-OpAmp design shown in Figures 4A–4C is a concrete instantiation of the framework of Figure 1. It is largely inspired by a classical three-stage operational amplifier (Zeng et al., 2018). An electronic OpAmp typically has three gain stages: an initial high-bandwidth input stage, an intermediate amplification stage, and a high-bandwidth output stage. The Bio-OpAmp mimics this architecture using a combination of transcription and translation regulatory mechanisms (See Figure 4B). The first stage is a fast differential input stage that senses the difference between arabinose (non-inverting signal) and acyl homoserine lactone (AHL) (inverting signal) and generates corresponding guide RNAs (sgRNAs). The sgRNAs compete for binding with dCas9, such that when sgRNA1 binds to dCas9, it removes a potential binding site for sgRNA2 and vice versa, thereby amplifying the input signal via a “push-and-pull” mechanism. The second stage is a slow differential stage that uses bound dCas9-sgRNA complexes to downregulate AiiA and LuxI protein expression levels. Since each mRNA transcript of AiiA and LuxI is translated to multiple copies of their respective proteins, changes to sgRNA levels are amplified via this downstream increase in copy number. Translation generally happens on a slower timescale than transcription, so the second stage is slower to respond to changes. The third stage is a fast differential stage where AiiA and LuxI enzymes degrade or produce AHL, respectively. Since each enzyme can potentially catalyze multiple copies of AHL, the third stage creates yet another level of amplification. Additionally, since both enzymes catalyze production/degradation of the small molecule, they effectively combine the two inputs into a single-ended output. When the three gain stages are combined, they produce a large open-loop gain that is difficult to achieve using only a single gain stage in isolation due to biological limitations.
Further details of the Bio-OpAmp w.r.t use of electronic circuit software for biological circuit design including robustness, sensitivity to parameters, buffering capability, oscillation, and tracking performance are described in Supplemental Section I of this paper. Figures S10–S14 and Figure 7 show several details of its performance, comparing circuit software and circuit hardware instantiation on cytomorphic chips. We shall now focus on an important part of the framework of Figure 1, namely the compilation of circuit schematics to cytomorphic chips.
Section III: Compiling Circuit Schematics to Cytomorphic Chips for Fast Simulation, Parameter Discovery, and Data Fitting
While existing circuit software tools like Cadence are useful for the design of large-scale systems and the simulation of relatively small circuits like the Bio-OpAmp, the simulation of large-scale biological systems can be slow on general-purpose digital computers. In particular, stochastic stimulations of relatively low-copy-number molecular variables are slow even for systems with as few as 10 variables (Gibson and Bruck, 2000; Li and Petzold, 2010; Ramaswamy et al., 2009). Such simulations require Poisson process emulation via the Gillespie stochastic simulation algorithm (GSSA), which is extremely computationally intensive on digital computers, regardless of the software package used (MATLAB, Cadence, COPASI, ….) (Kim et al., 2018; Woo et al., 2015). They are not parallelizable due to the need to faithfully emulate asynchronous Poisson processes and create pseudo-random numbers at every time step on synchronous digital computers with fixed time steps and clocks. Stiff differential equations with diffusion and compartmentalization exacerbate such problems.
Fortunately, deterministic and stochastic simulations of large-scale bio-molecular dynamical systems can be done extremely quickly on digitally programmable highly parallel asynchronous analog cytomorphic systems (Sarpeshkar 2010; Kim et al., 2018; Woo et al., 2015, 2018). These systems have a flat simulation time even as reaction network size or the number of species scales. Some of these systems amplify natural thermal noise to achieve highly stochastic simulations or use inherent analog noise in current fluxes for moderate levels of noise (Kim et al., 2018). Their readouts and programmability are compatible with traditional digital computers such that the user can be agnostic to the details of internal chip operation, viewing such simulations as simply originating from a fast custom Bio co-processor. While there is an argument to be made for keeping model complexity low such that data can be interpreted more meaningfully, biology as a whole is moving toward understanding bigger and more complex systems. Knowledge of such systems is rapidly progressing because of advances in next-generation sequencing technology and because of the advent of big data and machine learning. Thus, it is advantageous to compile circuits to cytomorphic chips for fast simulation and then leverage cytomorphic chip simulations to train large biological networks that fit biological data. In this paper, we shall only briefly summarize how these cytomorphic chips operate. Readers interested in further details should consult past work over more than a decade (Sarpeshkar et al., 2005a; Mandal and Sarpeshkar, 2009a, 2009b; Sarpeshkar, 2010; Kim et al., 2018; Woo et al., 2015, 2018).
As described extensively in the latter papers, the same equations of Boltzmann exponential thermodynamics govern the stochastics of molecular reaction dynamics as well as current flow in subthreshold electronic transistor circuits. Thus, a mapping of the mathematical differential equations that govern interactions between molecules with log (molecular concentration) mapped to voltage and molecular flux mapped to current, respectively, lead to an efficient and exact translation of nonlinear biological circuits and systems to equivalent nonlinear electronic circuits and systems that simulate them. Such physical emulation to do fast simulation is analogous to the idea of using GHz inductor-capacitor-resistor (LCR) electronic circuits to simulate slow spring-mass-damping mechanical circuits. In the papers (Kim et al., 2018; Woo et al., 2015, 2018), the authors describe the architecture, specifications, and performance of the cytomorphic chips in detail. The authors demonstrate the ability of the chips to be digitally configured to simulate any biochemical reaction network using programmable circuit building blocks. For example, we can simulate synthesis, degradation, association, dissociation, dimerization, substitution, cascade, fan-in, fan-out, and loop networks by appropriately configuring and connecting analog circuit blocks. Figure S5 shows the key circuit building block, and Figures S6B and S6C provide specific examples of a branching network important for competitive drug binding and ES reactions, respectively. Other examples that have been described include the dynamics and stochastics of a repressilator, a p53-MDM2 cancer pathway, and glycolytic oscillations. Even for modest networks with only about 80 stochastic reactions, cytomorphic simulations exhibit a significant 700X speedup over digital COPASI simulations or 30,000x speedup over digital MATLAB simulations, while yielding identical results (Woo et al., 2015, 2018). For large-scale systems, such speedups could be greater than a million fold (Woo, 2016).
Building on such prior work, we were motivated to compile and simulate the Bio-OpAmp with cytomorphic chips. To do so, we developed a mapping between analog circuit representations useful in this particular Bio-OpAmp case and circuits on cytomorphic chips. The Bio-OpAmp uses three primary motifs: a transcription-translation motif, a fan-out motif for substrate competition, and a dependent production and degradation motif for AHL regulation. Figures S7–S9 and Supplemental Sections I and II discuss these mappings in greater detail. The circuit in Figure 4C is compiled to its cytomorphic equivalent in Figure 6 using these mappings. Specifically, we use the translation-transcription cytomorphic block from Figure S7 in OpAmp gain stages 1 and 2; we use the conductance divider cytomorphic block that models sgRNA and dCas9 binding from Figure S8 in OpAmp gain stage 1; we use the AHL production-degradation cytomorphic block from Figure S9 in OpAmp gain stage 3.
The pipeline shown in Figure 5 enables us to program the chip and run multiple simulations of the Bio-OpAmp in parallel. The pipeline can adapted to read SBML files using a compiler that was developed recently by Medley et al. (2020). It is worth noting that digital calibration can drastically improve the precision and variability of analog circuits (Sarpeshkar, 2010). Calibrating analog-to-digital converters (ADCs), digital-to-analog converters (DACs), and other analog circuits to yield high-precision, low variability analog systems has been proven in cochlear implants for deaf patients (Sarpeshkar et al, 2005a, 2005b) and in other applications (Sarpeshkar, 2010). Such calibration would be needed in actual commercial or large-scale systems. However, they do not alter the conclusions of our smaller-scale proof-of-concept demonstrations here such that we shall not focus on them.
Figures 7A and 7B show that Cadence software simulations and cytomorphic chip simulations of the Bio-OpAmp are in good agreement, illustrating how the general framework of Figure 1 can be concretely instantiated in practice. Using the pipeline of Figure 5, we programmed multiple chips to simulate the Bio-OpAmp in parallel as shown in Figure S10. Chip-to-chip variations in such simulations can be calibrated for digitally as in a past cochlear implant for the deaf, which worked on a deaf subject on the first try (Sarpeshkar, 2010; Sarpeshkar et al., 2005b).
We simulated the Bio-OpAmp in electronic circuit software and on cytomorphic chips with varying concentrations of AHL and arabinose. These simulations replicate the biological experiments in (Zeng et al., 2018) that characterize the open- and closed-loop behavior of the Bio-OpAmp: As shown in Figure S11, the steady-state AHL concentration (reported as RFP in the experiments) tracks input arabinose closely while rejecting the added disturbance input AHL in closed-loop configurations. In an open-loop configuration, output AHL exhibits non-linear input-output characteristics with input arabinose that are reminiscent of the saturation function used to describe cooperative binding. The steady-state outputs from biological data, software simulation, and cytomorphic chip implementation are in good agreement, suggesting that the schematic and cytomorphic circuit models of Figures 4 and 6 are indeed accurate.
We ran high-throughput cytomorphic simulations to perform sensitivity analysis and parameter discovery to optimize the Bio-OpAmp. For example, the open-loop gain is maximized when the dissociation constants of sgRNA1 and sgRNA2 are similar, as shown in Figure S12. This finding illustrates the importance of symmetry in all feedback systems and high-performance circuits. The closed-loop gain in Figure S13 is also in accord with predictions of such gain from small-signal analysis corresponding to Figure S4 or (Zeng et al., 2018). Figure S14 shows that the steady-state tracking error is also in accord with the overall gain of the OpAmp as predicted from feedback system theory. Chapter 5 of (Teo, 2019) provides a more detailed discussion including additional findings based on parameter discovery and machine learning. A short conference paper (Teo et al., 2019) presents a highly abbreviated version of some portions of this journal paper.
In biological systems, due to low molecular copy numbers and/or high burst noise factor, the dominant measured noise is of thermal origin, has a flat or “white” power spectral density, and obeys the Poisson statistics of uncorrelated current flow at the fundamental chemical reaction level (Chapter 7 on noise in Sarpeshkar 2010; Sarpeshkar 2014). Hence, as in the GSSA, we have mostly focused on only discussing the emulation of such Poisson noise, which is fundamental to all thermodynamic processes. However, at the system level, due to correlations, explicit feedback, filtering, self-organization, scale invariance, and “defects” in biological membranes and other biological structures, one can also see “pink noise” with a sloping power spectrum at frequencies below a certain relatively low corner frequency. Such noise is observed in electronic transistors as well due to “traps” or “mobility fluctuations” in current flow where it is often called “1/f noise” or “power-law noise”. From quantitative models of such power-law noise in devices and circuits as discussed in chapters 7, 8, 12, 13, 14, and 24 in (Sarpeshkar 2010), we can certainly also emulate such biological noise both explicitly, e.g., as the noise in the membrane, and implicitly, e.g., if it emerges in circuits due to time-scale invariance in certain systems, e.g. heartbeats and traps in transistors. Such emulations can be done in both circuit software and cytomorphic chip hardware if desired. In fact, most electronic circuit software has such 1/f noise models by default to ensure that electronic circuits perform as desired.
As discussed in chapter 19 in (Sarpeshkar 2010), emergent properties such as “stochastic resonance” wherein the detectability of a signal is improved if an optimal amount of noise helps it cross a fixed threshold can emerge in both electronics and biology and can also be easily represented and modeled. Such effects may be present in p53 in cancer networks, among the networks that we have been able to successfully model. In fact, we can even quantitatively model fundamental and system noise in any circuit including the Bio-OpAmp. However, as in several synthetic biological circuits to date, the Bio-OpAmp is implemented with relatively high copy numbers of molecules with many cells in solution. Thus, Bio-OpAmp open-loop gains were nearly always stably measured to be in the 50–100 range, both in experimental biological measurements and in quantitatively accurate models that fit such biological data (Zeng et al., 2018). While current optical reporting and measuring systems in biology, which are not prohibitively expensive, cannot easily and non-destructively measure signal and noise in a single cell easily, the more sensitive bio-electronic systems, which we describe in Section IV, may be capable of such measurements in the future. Hence, we shall discuss them now.
Section IV: Bio-Electronic Reporting and Measurement.
New synthetic regulatory network designs are increasingly driven by iterative design-built-test-learn (DBTL) cycles (Carbonell et al., 2018; Opgenorth et al., 2019). While the field has developed many logic-based tools to accelerate and simplify the circuit prototyping process, the testing and validation process is still based on making optical measurements of a fluorescent or luminescent reporter molecule produced by the circuit. Many modern methods such as fluorescent microscopy, flow cytometry, and short-read sequencing make use of fluorescent proteins for their core functions (Bentley et al., 2008; Lichtman and Conchello, 2005; Lyons and Parish, 1994). Optical biosensors are used in many canonical circuits in synthetic biology (Elowitz and Leibier, 2000; Stricker et al., 2008), and they continue to be the default mode of reporting in most biological circuits. However, despite their popularity, optical biosensors present several caveats; fluorescent proteins cause cytotoxicity when produced in large concentration (Shen et al., 2017); fluorophores undergo photobleaching when exposed to long periods of excitation (Greenbaum et al., 2000) reducing dynamic range and limiting the number of consecutive measurements; long photoexcitation causes phototoxicity by generating reactive oxygen species that damage the cell (Ganini et al., 2017). Due to these limitations, fluorescent biosensors are unsuitable for reporting certain types of behavior such as taking continuous readings in time-lapse microscopy, which may be necessary for a DBTL paradigm.
To create biosensors for a wider range of circuits, we need biosensors that can take real-time measurements, have a wide dynamic range and good sensitivity, and do not cause significant cell death. As an example, we developed a microbial fuel cell (MFC) that uses an electricigenic bacterium to generate currents based on circuit activity (Zeng et al., 2019). The fuel cell consists of a co-culture of E. coli MG1655 and S. oneidensis MR-1 that resides on the anode. A co-culture system was chosen because it exhibits greater tolerance to metabolic burden and cytotoxicity and experiences less cross-talk compared to monoculture systems (Lisa et al., 2014; Stephens et al., 2019). E. coli converts lactose in its environment to lactate with the aid of an intermediate reporting enzyme LacZα while S. oneidensis metabolizes the resulting lactate and transfers the electrons to the anode using either direct electron transfer or metabolite (e.g. flavin)-mediated electron transfer (Busalmen et al., 2008; Okamoto et al., 2013, 2014). When we measure current in the MFC, we are effectively measuring the concentration of LacZα in E. coli. To use the MFC as an electrical biosensor, we simply replace fluorescent protein genes on the plasmid with LacZα and measure electrical current instead of fluorescence intensity.
As an example of how bio-electronic reporting can be instantiated in practice, a component of the framework of Figure 1, we compared the response of a biological comparator (Figure 8) using either a fluorescent reporter or our electrical reporter. An electronic comparator is a device that compares two inputs to generate an irreversible on/off output signal depending on whether one input is higher than the other. The biological comparator reproduces the same behavior by utilizing a wide dynamic range log-linear input analog LuxR circuit first described in (Daniel et al., 2013) and a subsequent positive feedback latch circuit as shown in Figure 8B. The LuxR circuit combines an analog positive feedback loop circuit and a decoy “shunt” circuit to increase the log-linear dynamic range with respect to the input Arabinose.
To generate an irreversible digital output, the comparator of Figure 8 uses LacI to repress TetR and vice versa, thereby creating a switch-like behavior. Arabinose activates LacI expression via LuxR while an inducer with action similar to lactose (IPTG) represses LacI activity. The relative strength of the two antagonistic effects decides the final reporter output. When using a fluorescent reporter (RFP), changes to IPTG concentration did not significantly affect the threshold concentration of arabinose required to switch the comparator on. In contrast, when using a LacZα reporter, a higher IPTG concentration increases the threshold concentration of arabinose needed to flip the comparator (See (Zeng et al., 2019)). The wider dynamic range can be explained by LacZα catalyzing lactose to lactate, which serves as a mode of signal amplification, improving both the measurement as well as providing a convenient electronic output.
Concluding Remarks
We have suggested how electronic circuit design and measurement can serve to automate design, modeling, analysis, simulation, and quantitative fitting of measured data as shown in the framework of Figure 1. We have also shown how such a framework can be concretely instantiated in a synthetic biological operational amplifier circuit in living microbial cells. While this work is in a proof-of-concept and foundational stage, in the future, large-scale biological circuits and systems for drug cocktail discovery could be designed and simulated quickly for a systems biology and medical application. Alternatively, precise and robust synthetic circuits for medicine, e.g, Bio-OpAmp-like homeostasis circuits for drug dosage control can benefit from the robust and predictive power of design automation, enabling quick applications in multiple contexts rather than via tedious time-consuming experimentation. In both cases, the merging and unification of biology and electronics via unifying and hierarchical circuit motifs, accurate modeling and compilation, fast simulation for parameter discovery and learning, and bio-electronic measurement may help scale the design and understanding of biological systems. Thus, the current state, which is to do relatively simple or empirical design, could grow toward more complex and more rational design, which is highly important if medicine and bioengineering are to scale.
Limitations of the Study
We acknowledge that complex biological systems often require many unknown parameters to model, which is still an issue for us as well as for others. However, the combination of fast simulation such that a brute-force exploration of many parameters is possible via cytomorphic chips; of machine learning and data fitting associated with such exploration; the collapsing of many parameters and topologies into model-order-reduced input-output circuit equivalents and/or circuits with net feedback loop gains or gains that are dependent on the products of many parameters rather than on each as in our Bio-OpAmp; and the use of physical constraints such as energy, power, copy numbers, max. flux rates, flux balance, which are all very natural and easy and automatically entangled in circuits (Sarpeshkar, 2010, 2014) serve to make this problem not seem as daunting as it may seem. We hope that our four-pronged approach will help in this regard.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgments
We acknowledge useful discussions with Ji Zeng, Jaewook Kim, and Sung Sik Woo. This work was supported by the AFOSR under grant number FA9550-18-1-0467 and by the NIH under grant number R01 GM 123032-01 to R.S. J.T. was supported in part by funds from the A∗STAR and by funds from Dartmouth College.
Author Contributions
J.T. and R.S. designed the model and the computational framework. J.T. carried out the implementation and analyzed the data. J.T. and R.S. contributed to the writing of the manuscript. R.S. was in charge of overall direction and planning of the project.
Footnotes
Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.101688.
Supplemental Information
References
- Ausländer D., Ausländer S., Pierrat X., Hellmann L., Rachid L., Fussenegger M. Programmable full-adder computations in communicating three-dimensional cell cultures. Nat. Methods. 2018;15:57–60. doi: 10.1038/nmeth.4505. [DOI] [PubMed] [Google Scholar]
- Bentley D.R., Balasubramanian S., Swerdlow H.P., Smith G.P., Milton J., Brown C.G., Hall K.P., Evers D.J., Barnes C.L., Bignell H.R. Accurate whole human genome sequencing using reversible terminator chemistry. Nature. 2008;456:53–59. doi: 10.1038/nature07517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berridge M.J., Bootman M.D., Roderick H.L. Calcium signalling: dynamics, homeostasis and remodelling. Nat. Rev. Mol. Cell Biol. 2003;4:517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
- Bonnet J., Yin P., Ortiz M.E., Subsoontorn P., Endy D. Amplifying genetic logic gates. Science. 2013;340:599–603. doi: 10.1126/science.1232758. [DOI] [PubMed] [Google Scholar]
- Bradley P.D. An ultra low power, high performance Medical Implant Communication System (MICS) transceiver for implantable devices. IEEE 2006 Biomed. Circuits Syst. Conf. Healthc. Technol. Biocas. 2006;2006:158–161. [Google Scholar]
- Busalmen J.P., Esteve-Núñez A., Berná A., Feliu J.M. C-type cytochromes wire electricity-producing bacteria to electrodes. Angew. Chem. Int. Ed. 2008;47:4874–4877. doi: 10.1002/anie.200801310. [DOI] [PubMed] [Google Scholar]
- Carbonell P., Jervis A.J., Robinson C.J., Yan C., Dunstan M., Swainston N., Vinaixa M., Hollywood K.A., Currin A., Rattray N.J.W. An automated Design-Build-Test-Learn pipeline for enhanced microbial production of fine chemicals. Commun. Biol. 2018;1:1–10. doi: 10.1038/s42003-018-0076-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardinale S., Arkin A.P. Contextualizing context for synthetic biology - identifying causes of failure of synthetic biological systems. Biotechnol. J. 2012;7:856–866. doi: 10.1002/biot.201200085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Kim J.K., Hirning A.J., Josić K., Bennett M.R. Emergent genetic oscillations in a synthetic microbial consortium. Science. 2015;349:986–989. doi: 10.1126/science.aaa3794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel R., Rubens J.R., Sarpeshkar R., Lu T.K. Synthetic analog computation in living cells. Nature. 2013;497:619–623. doi: 10.1038/nature12148. [DOI] [PubMed] [Google Scholar]
- Elowitz M.B., Leibier S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- Ferrell J.E. Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr. Opin. Cell Biol. 2002;14:140–148. doi: 10.1016/s0955-0674(02)00314-9. [DOI] [PubMed] [Google Scholar]
- Fukao T., Tanabe M., Terauchi Y., Ota T., Matsuda S., Asano T., Kadowaki T., Takeuchi T., Koyasu S. P13K-mediated negative feedback regulation of IL-12 production in DCs. Nat. Immunol. 2002;3:875–881. doi: 10.1038/ni825. [DOI] [PubMed] [Google Scholar]
- Ganini D., Leinisch F., Kumar A., Jiang J.J., Tokar E.J., Malone C.C., Petrovich R.M., Mason R.P. Fluorescent proteins such as eGFP lead to catalytic oxidative stress in cells. Redox Biol. 2017;12:462–468. doi: 10.1016/j.redox.2017.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner T.S., Cantor C.R., Collins J.J. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- Gibson M.A., Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J. Phys. Chem. A. 2000;104:1876–1889. [Google Scholar]
- Greenbaum L., Rothmann C., Lavie R., Malik Z. Green fluorescent protein photobleaching: a model for protein damage by endogenous and exogenous singlet oxygen. Biol. Chem. 2000;381:1251–1258. doi: 10.1515/BC.2000.153. [DOI] [PubMed] [Google Scholar]
- Kim J., Woo S.S., Sarpeshkar R. Fast and precise emulation of stochastic biochemical reaction networks with amplified thermal noise in silicon chips. IEEE Trans. Biomed. Circuits Syst. 2018;12:379–389. doi: 10.1109/TBCAS.2017.2786306. [DOI] [PubMed] [Google Scholar]
- Klavins E. Lightening the load in synthetic biology. Nat. Biotechnol. 2014;32:1198–1200. doi: 10.1038/nbt.3089. [DOI] [PubMed] [Google Scholar]
- Lee J.W., Gyorgy A., Cameron D.E., Pyenson N., Choi K.R., Way J.C., Silver P.A., Del Vecchio D., Collins J.J. Creating single-copy genetic circuits. Mol. Cell. 2016;63:329–336. doi: 10.1016/j.molcel.2016.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Petzold L. Efficient parallelization of the stochastic simulation algorithm for chemically reacting systems on the graphics processing unit. Int. J. High Perform. Comput. Appl. 2010;24:107–116. [Google Scholar]
- Lichtman J.W., Conchello J.A. Fluorescence microscopy. Nat. Methods. 2005;2:910–919. doi: 10.1038/nmeth817. [DOI] [PubMed] [Google Scholar]
- Lisa G., Paul F., Polizzi K.M. Co-culture systems and technologies: taking synthetic biology to the next level. J. R. Soc. Interfaces. 2014;11:20140065. doi: 10.1098/rsif.2014.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z., Gerner M.Y., Van Panhuys N., Levine A.G., Rudensky A.Y., Germain R.N. Immune homeostasis enforced by co-localized effector and regulatory T cells. Nature. 2015;528:225–230. doi: 10.1038/nature16169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons A.B., Parish C.R. Determination of lymphocyte division by flow cytometry. J. Immunol. Methods. 1994;171:131–137. doi: 10.1016/0022-1759(94)90236-4. [DOI] [PubMed] [Google Scholar]
- Zeng J., Teo J.J.Y., Banerjee A., Chapman T.W., Kim J., Sarpeshkar R. A synthetic microbial operational amplifier. ACS Synth. Biol. 2018;7:2007–2013. doi: 10.1021/acssynbio.8b00138. [DOI] [PubMed] [Google Scholar]
- Mandal, S., and Sarpeshkar, R. (2009a). Log-domain circuit models of chemical reactions. In 2009 IEEE International Symposium on Circuits and Systems, (IEEE), pp. 2697–2700.
- Mandal, S., and Sarpeshkar, R. (2009b). Circuit models of stochastic genetic networks. In 2009 IEEE Biomedical Circuits and Systems Conference, (IEEE), pp. 109–112.
- Maung N.W., Smolke C.D. Higher-order cellular information processing with synthetic RNA devices. Science. 2008;322:456–460. doi: 10.1126/science.1160311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medley J.K., Teo J., Woo S.S., Hellerstein J., Sarpeshkar R., Sauro H.M. A compiler for biological networks on silicon chips. PLoS Comput. Biol. 2020;16:e1008063. doi: 10.1371/journal.pcbi.1008063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra D., Rivera P.M., Lin A., Del Vecchio D., Weiss R. A load driver device for engineering modularity in biological networks. Nat. Biotechnol. 2014;32:1268–1275. doi: 10.1038/nbt.3044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherji S., Van Oudenaarden A. Synthetic biology: understanding biological design from synthetic circuits. Nat. Rev. Genet. 2009;10:859–871. doi: 10.1038/nrg2697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nemazanyy I., Montagnac G., Russell R.C., Morzyglod L., Burnol A.F., Guan K.L., Pende M., Panasyuk G. Class III PI3K regulates organismal glucose homeostasis by providing negative feedback on hepatic insulin signalling. Nat. Commun. 2015;6:8283. doi: 10.1038/ncomms9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen A.A.K., Der B.S., Shin J., Vaidyanathan P., Paralanov V., Strychalski E.A., Ross D., Densmore D., Voigt C.A. Genetic circuit design automation. Science. 2016;80:352. doi: 10.1126/science.aac7341. [DOI] [PubMed] [Google Scholar]
- Okamoto A., Hashimoto K., Nealson K.H., Nakamura R. Rate enhancement of bacterial extracellular electron transport involves bound flavin semiquinones. Proc. Natl. Acad. Sci. U S A. 2013;110:7856–7861. doi: 10.1073/pnas.1220823110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamoto A., Kalathil S., Deng X., Hashimoto K., Nakamura R., Nealson K.H. Cell-secreted flavins bound to membrane cytochromes dictate electron transfer reactions to surfaces with diverse charge and pH. Sci. Rep. 2014;4:1–8. doi: 10.1038/srep05628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opgenorth P., Costello Z., Okada T., Goyal G., Chen Y., Gin J., Benites V., De Raad M., Northen T.R., Deng K. Lessons from two design-build-test-learn cycles of dodecanol production in Escherichia coli aided by machine learning. ACS Synth. Biol. 2019;8:1337–1351. doi: 10.1021/acssynbio.9b00020. [DOI] [PubMed] [Google Scholar]
- Pan D., Fujimoto M., Lopes A., Wang Y.X. Twist-1 is a PPARδ-inducible, negative-feedback regulator of PGC-1α in Brown fat metabolism. Cell. 2009;137:73–86. doi: 10.1016/j.cell.2009.01.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prindle A., Selimkhanov J., Li H., Razinkov I., Tsimring L.S., Hasty J. Rapid and tunable post-translational coupling of genetic circuits. Nature. 2014;508:387–391. doi: 10.1038/nature13238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramaswamy R., González-Segredo Ń., Sbalzarini I.F. A new class of highly efficient exact stochastic simulation algorithms for chemical reaction networks. J. Chem. Phys. 2009;130:1–14. doi: 10.1063/1.3154624. [DOI] [PubMed] [Google Scholar]
- Sarpeshkar R. Cambridge University Press; 2010. Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems. [Google Scholar]
- Sarpeshkar R. Analog synthetic biology. Philos. Trans. R. Soc. A. Math. Phys. Eng. Sci. 2014;372:20130110. doi: 10.1098/rsta.2013.0110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarpeshkar R., Salthouse C., Sit J.J., Baker M.W., Zhak S.M., Lu T.K.T., Turicchia L., Balster S. An ultra-low-power programmable analog bionic ear processor. IEEE Trans. Biomed. Eng. 2005;52:711–727. doi: 10.1109/TBME.2005.844043. [DOI] [PubMed] [Google Scholar]
- Sarpeshkar, R., Baker, M.W., Salthouse, C.D., J. Sit, Turicchia, L., and Zhak, S.M. (2005b). An analog bionic ear processor with zero-crossing detection. In International Solid-State Circuits Conference, (IEEE International Digest of Technical Papers. Solid-State Circuits Conference), pp. 78–79.
- Shen Y., Chen Y., Wu J., Shaner N.C., Campbell R.E. Engineering of mCherry variants with long Stokes shift, red-shifted fluorescence, and low cytotoxicity. PLoS One. 2017;12:1–14. doi: 10.1371/journal.pone.0171257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens K., Pozo M., Tsao C.Y., Hauk P., Bentley W.E. Bacterial co-culture with cell signaling translator and growth controller modules for autonomously regulated culture composition. Nat. Commun. 2019;10:1–11. doi: 10.1038/s41467-019-12027-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricker J., Cookson S., Bennett M.R., Mather W.H., Tsimring L.S., Hasty J. A fast, robust and tunable synthetic gene oscillator. Nature. 2008;456:516–519. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturm O.E., Orton R., Grindlay J., Birtwistle M., Vyshemirsky V., Gilbert D., Calder M., Pitt A., Kholodenko B., Kolch W. The mammalian MAPK/ERK pathway exhibits properties of a negative feedback amplifier. Sci. Signal. 2010;3:1–8. doi: 10.1126/scisignal.2001212. [DOI] [PubMed] [Google Scholar]
- Teo J.J.Y. Massachusetts Inst. Technol; 2019. Synthetic Analog Feedback Control Circuits in Living Cells. Ph.D Thesis. [Google Scholar]
- Teo J.J.Y., Woo S.S., Sarpeshkar R. Synthetic biology: a unifying view and review using analog circuits. IEEE Trans. Biomed. Circuits Syst. 2015;9:453–474. doi: 10.1109/TBCAS.2015.2461446. [DOI] [PubMed] [Google Scholar]
- Teo, J. Kim, J. Woo, S. and Sarpeshkar, R. “Bio-molecular Circuit Design with Electronic Circuit Software and Cytomorphic Chips”, Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS 2019), Nara, Japan, pp. 1–4
- Wong V.W.Y., Stange D.E., Page M.E., Buczacki S., Wabik A., Itami S., Van De Wetering M., Poulsom R., Wright N.A., Trotter M.W.B. Lrig1 controls intestinal stem-cell homeostasis by negative regulation of ErbB signalling. Nat. Cell Biol. 2012;14:401–408. doi: 10.1038/ncb2464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo S.S. Massachusetts Inst. Technol.; 2016. Fast Simulation of Stochastic Biochemical Reaction Networks on Cytomorphic Chips. PhD. Thesis. [Google Scholar]
- Woo S.S., Kim J., Sarpeshkar R. A cytomorphic chip for quantitative modeling of fundamental bio-molecular circuits. IEEE Trans. Biomed. Circuits Syst. 2015;9:527–542. doi: 10.1109/TBCAS.2015.2446431. [DOI] [PubMed] [Google Scholar]
- Woo S.S., Kim J., Sarpeshkar R. A digitally programmable cytomorphic chip for simulation of arbitrary biochemical reaction networks. IEEE Trans. Biomed. Circuits Syst. 2018;12:360–378. doi: 10.1109/TBCAS.2017.2781253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng J., Banerjee A., Kim J., Deng Y., Chapman T.W., Daniel R., Sarpeshkar R. A novel bioelectronic reporter system in living cells tested with a synthetic biological comparator. Sci. Rep. 2019;9:1–7. doi: 10.1038/s41598-019-43771-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.