Abstract
Background and purpose
Magnetic Resonance Imaging (MRI) is increasingly being used in radiotherapy (RT). However, geometric distortions are a known challenge of using MRI in RT. The aim of this study was to demonstrate feasibility of a national audit of MRI geometric distortions. This was achieved by assessing large field of view (FOV) MRI distortions on a number of scanners used clinically for RT.
Materials and methods
MRI scans of a large FOV MRI geometric distortion phantom were acquired on 11 MRI scanners that are used clinically for RT in the UK. The mean and maximum distortions and variance between scanners were reported at different distances from the isocentre.
Results
For a small FOV representing a brain (100–150 mm from isocentre) all distortions were < 2 mm except for the maximum distortion of one scanner. For a large FOV representing a head and neck/pelvis (200–250 mm from isocentre) mean distortions were < 2 mm except for one scanner, maximum distortions were > 10 mm in some cases. The variance between scanners was low and was found to increase with distance from isocentre.
Conclusions
This study demonstrated feasibility of the technique to be repeated in a country wide geometric distortion audit of all MRI scanners used clinically for RT. Recommendations were made for performing such an audit and how to derive acceptable limits of distortion in such an audit.
Keywords: Magnetic resonance imaging, Geometric distortion, Radiotherapy, Quality assurance, Audit
1. Introduction
Traditionally, computed tomography (CT) images have been used to inform radiotherapy (RT) treatment planning. Recently, interest in the use of magnetic resonance imaging (MRI) in RT has increased [1], owing to its superior soft‐tissue contrast compared with CT [2].
MRI is typically used in RT to define the tumour and/or organ at risk volumes and then registered to CT for dose calculation. However, this method is susceptible to coregistration errors [3]. For this reason, the magnetic resonance-only (MR-only) pathway for RT planning has been developed to estimate electron density information directly from MRI images [4], [5], [6]. Furthermore, MRI-guided RT using a magnetic resonance linear accelerator (MR-linac) is an emerging technology for RT treatments [7], [8].
Geometric distortion remains an inherent issue with MRI that needs to be corrected for [9], [10]. In RT planning, uncorrected geometric distortions can lead to target localisation uncertainties [11]. Geometric distortion is more significant when imaging a large field of view (FOV) such as the head and neck/pelvis, in some MR-only applications [12] and MRI-guided RT [13].
The causes of geometric distortions can be divided into two main categories: hardware-related and patient-related distortions. Patient-related distortions, such as chemical shift and magnetic susceptibility, arise due to variations in the magnetic susceptibility of different body tissues and the surrounding air [14]. The magnitude of the distortion can be affected by magnetic field strength, MRI sequence, patient anatomy, receiver bandwidth and the presence of implants [13], [15]. Hardware-related distortions occur due to magnetic field inhomogeneity and gradient-nonlinearity [15]. Gradient-nonlinearity is the main cause of geometric distortion in MRI systems [16], [17], [18]. MRI scanner gradient performance can be specified both in terms of the maximum spatial gradient strengths that can be achieved and the rate at which the gradients can be switched (the slew rate). Achieving high gradient strengths and slew rates can lead to compromises in gradient linearity [18], [19], which may compromise the scanner performance in terms of geometric accuracy.
Although manufacturers generally equip MRI scanners with algorithms that aim to correct hardware-related distortions [20], these are known not to be completely effective [1], [21] with some residual geometric distortion generally remaining. Therefore, it is important to assess the magnitude of residual geometric distortion and a number of professional bodies offer advice on performing this. According to the American Association of Physicists in Medicine (AAPM) Report 100 [22], any lengths measured in an image should be within 2% of the true value if the image is to be used for RT purposes. The American College of Radiology (ACR) [23] recommends that length measurements be within ± 2 mm of the actual measurements for their accreditation programme, although this guidance is specific to their phantom.
Gustafsson et al. [17] studied the effects of geometric distortion on RT planning for prostate patients on a 3 T MRI scanner using the same a large FOV MRI distortion phantom used in this study. The repeatability of measurements with such a phantom have also been demonstrated by Wyatt et al. [24].
The first report in the literature assessing geometric distortion in various MRI scanners was from 2012 which compared six 3 T MRI scanners in the Scottish Imaging Network a platform for scientific excellence (SINAPSE) [25]. This work assessed geometric distortion over different imaging volumes quantitatively to ensure the suitability for application such as RT treatment planning.
The objective of the work presented here was to show feasibility of a method for auditing the geometric distortion on a range of MRI scanners used for clinical RT applications and to define procedures for future audits. A secondary objective was to enhance the literature by providing typical values of geometric distortion that can be used in future audits.
2. Materials and methods
A large FOV phantom was used to measure the geometric distortion on 11 MRI scanners, listed in appendix 1, with all major vendors assessed. To preserve anonymity randomly assigned numbers (1–11) were used to refer to scanners in this study.
The large FOV MRI geometric distortion phantom used in the study was a GRADE phantom (Spectronic Medical AB, Helsingborg, Sweden). The phantom is a plastic container filled with a foam matrix with approximately 1200 spherical polyethylene glycol markers of 17 mm diameter at known locations. The MRI opaque markers are arranged in a grid with a spacing of approximately 50 mm in the central region and 30 mm in the outer region. The phantom size is 50.2 cm × 40.4 cm × 53.4 cm, and the imaging dimensions are 49 cm × 31 cm × 50 cm.
The GRADE phantom was setup on each MRI scanner to its crosshair markings using the scanner’s internal lasers. Phased array body (anterior surface) and spine (integrated into the patient couch) coils were used where possible. For two scanners, where space constraints within the bore made this impossible, the integrated body coil was used instead (see appendix 1). Two consecutive MRI scans of the phantom were acquired on each MRI scanner, with the phantom removed from the MRI scanner couch and re-setup on the MRI scanner couch in between acquisitions. This was done to ensure that the distortions measured were reproducible and due to the scanner rather than attributed to setup errors.
A 3D gradient echo (GRE) sequence recommended by the phantom manufacturer was used where possible for all scanners, as defined in Table 1. Due to scanner limitations, some acquisition parameters had to be modified in a way that would not be expected to significantly affect the geometric distortion results. Standard 3D geometric distortion correction was applied for all acquired images. The vendor’s standard automatic B0 shimming mode was used with an adjustment volume identical to the field of view.
Table 1.
MRI acquisition parameters recommended by the phantom manufacturer, and those used on each scanner. Note differences due to limitations in different scanners. Note: The dashes (–) mean the recommended parameters were used.
| Parameters recommended by phantom manufacturer | Siemens Aera, (all centers) | Prisma | Sola | Skyra | Espree | Unity | Ingenia | GE PET/MR | |
|---|---|---|---|---|---|---|---|---|---|
| Seq. | GRE | – | – | – | – | – | – | – | – |
| FoV (mm × mm) | 500 × 500 | – | – | – | – | 450 × 450 | – | 501 × 375.5 | – |
| Flip angle | 20° | – | – | – | – | – | – | – | – |
| Number of slices | 256 | – | – | – | – | – | 205 | 205 | – |
| Slice thickness (mm) | 1.95 | – | – | – | – | 1.75 | – | – | – |
| Slice gap (mm) | 0.39 | – | – | – | – | 0.35 | 0 | 0 | 0 |
| phase-encoding direction | A ≫ P | – | – | – | – | – | – | – | – |
| TR (ms) | 6.2 | – | 4.4 | 5.1 | 5 | 5 | 5 | 5 | 3.8 |
| TE (ms) | 2.18 | – | 1.58 | 1.81 | 1.78 | 2.39 | 2.5 | – | 1.3 |
| Voxel size (mm3) | 1.0 × 1.0 × 2.0 | – | – | – | – | – | – | – | – |
| Pixel BW (Hz/Pix) | 490 | – | – | 488 | – | – | – | – | – |
The software supplied with the GRADE phantom, MriPlanner (Spectronic Medical AB, Helsingborg, Sweden), was used for data analysis. The software reports the mean and maximum observed distortion (mm) at five distances from the isocentre: <100 mm, 100–150 mm, 150–200 mm, 200–250 mm, and ≥ 250 mm.
The mean and maximum reported geometric distortion was measured for each distance to isocentre, for each MRI scanner and for each of the two consecutive measurements. The mean of the mean and maximum distortion of the two consecutive results per scanner are defined throughout as meanps and maxps. For comparison purposes, the mean and standard deviation of meanps over all scanners, defined as meanmean-as and SDmean-as respectively, were calculated at each distance from the isocentre. Values that did not fall within meanmean-as ± 2SDmean-as were considered statistically significant outliers. Similarly, the mean and standard deviation of maxps over all scanners, defined as meanmax-as and SDmax-as respectively, was calculated at each distance from the isocentre. Values that did not fall within meanmax-as ± 2SDmax-as were considered statistically significant outliers. In addition, the variance (δ2) between scanners at each distance from the isocentre was calculated.
3. Results
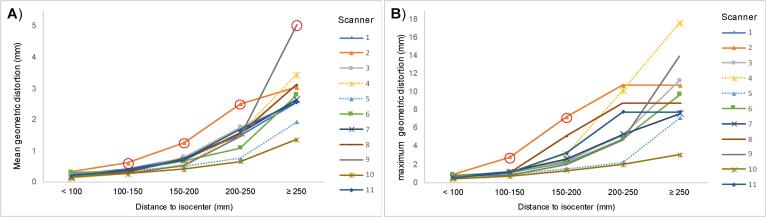
Meanps and maxps for each distance from the isocentre are shown in Fig. 1. For scanner 4 these are based on a single measurement, due to a technical error resulting in loss of data from the second measurement. Table 2 shows the mean and standard deviation over all scanners (meanps and maxps). Fig. 1 and table 2 shows that, as expected, the distortion increases when moving away from the isocentre. All of the meanps results were within the meanmean-as ± 2SDmean-as limit except those for scanners 2 and 9 (indicated by the circled points in Fig. 1). The greatest meanps geometric distortion was 5.0 mm on scanner 9, at ≥ 250 mm from the isocentre. In comparison with the other scanners, scanner 2 showed the worst performance at all distances except at ≥ 250 mm from the isocentre. This was considered significant for three measurements with geometric distortions of 0.6 mm at 100–150 mm, 1.3 mm at 150–200 mm, and mm 2.5 at 200–250 mm from isocentre. Scanner 10 showed the best performance in terms of geometric distortion at all distances, but this did not reach significance. δ2 of the geometric distortion between scanners was found to increase with distance to isocentre as shown in table 2. The general trends for the maximum reported distortion are shown in Fig. 1 and Table 2 and match those of the mean, i.e. the maximum distortion increases with distance to isocentre. The only maximum distortion measurements to be considered significant outliers were for scanner 2 at 100–150 mm and 150–200 mm from isocentre which showed maxps of 2.8 and 7.2 mm respectively.
Fig. 1.
Geometric distortion for each scanner at 5 different distances to isocentre: A) Mean geometric distortion per scanner (meanps) and B) Maximum geometric distortion per scanner (maxps). Note: The red circles indicate values that are>2 standard deviations from the mean over all scanners and hence are considered to be significantly worse/better.
Table 2.
Mean and standard deviation of meanps and maxps over all scanners (meanmean-as, SDmean-as, meanmax-as and SDmax-as) as well as δ2 between all scanners, at all distances to the isocentre.
| Distance from the isocentre (mm) | <100 | 100–150 | 150–200 | 200–250 | ≥ 250 |
|---|---|---|---|---|---|
| meanmean-as (mm) | 0.2 | 0.4 | 0.7 | 1.5 | 2.8 |
| SDmean-as (mm) | 0.1 | 0.1 | 0.2 | 0.5 | 0.9 |
| meanmax-as (mm) | 0.6 | 1.2 | 3.0 | 6.1 | 9.6 |
| SDmax-as (mm) | 0.2 | 0.6 | 1.7 | 2.9 | 3.9 |
| δ2 (mm2) | <0.01 | 0.01 | 0.05 | 0.23 | 0.78 |
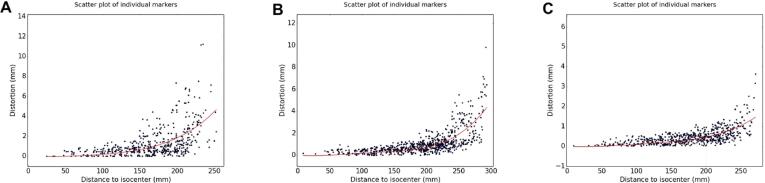
Scatterplots of the geometric distortion measured for each marker as a function of distance to isocentre for all scanners are shown in appendix 2. The only notable difference between the two consecutive measurements is evident on scanner 3 which has two erroneous points on the second measurement, however these are both at distances of > 250 mm from the isocentre. Some key examples of scatterplots have been included in Fig. 2 for scanners 2, 6, and 10 which can be considered the worst, average and best-performing scanners respectively. In scanner 10, the dots are visibly less scattered at any given distance to isocentre than they are for scanner 2.
Fig. 2.
Scatterplots for a single measurement from 3 different scanners. A) Scanner 2 which represent the worst scanner B) Scanner 6 which is an example of an average scanner C) Scanner 10 which represent the best scanner. Each scatterplot shows the distortion as a function of distance from the isocentre as measured for all markers as well as the trend line calculated using a second-degree polynomial using a least squares method.
4. Discussion
The aim of this work was to evaluate the feasibility of auditing geometric accuracy across a number of MRI scanners. Geometric distortion was evaluated in 11 clinical MRI scanners used for RT purposes using a GRADE phantom. This study found that geometric distortion increased with distance from the isocentre, as other studies have reported [21], [26], [27], [28]. For RT purposes, it has been suggested in the literature that a geometric distortion of < 2 mm is required [13], [29]. However, it is unclear whether the mean distortions or the maximum value is intended in these recommendations. This study cannot be considered as an audit study since it was not done under full audit conditions. However, it represents a first step that could serve as a basis for future audits and shows feasibility of such audits. If the results shown here were part of an audit then scanner 2 has been shown to be significantly worse in terms of geometric distortion. Therefore scanner 2 would require further investigation to assess the reason for this higher geometric distortion and if it could be reduced. In this case scanner 2 was a short, wide-bore MRI scanner so it is understandable that it has a higher main field inhomoegneity (and hence larger geometric distortion) compared to the other scanners.
For a future audit it is suggested that limits to warrant further investigation could be based on the mean distortion + 2 SD over a large number of MRI scanners. This should be done at different distances to isocentre with the distances chosen being relevant to the clinical applications of interest. Measurements should be based on mean distortions, rather than maximum distortions as maximum distortions can be effected by a single erroneous point. Geometric distortion of MRI scanners varies depending on the phantom and MRI sequence used and hence for an audit these parameters must be fixed. If a future audit used the GRADE phantom and the specific MRI sequence we have used then the limits of acceptability of such an audit could be based on meanmean-as + 2 SDmean-as for different distances to isocentre as shown in table 2.
Gustafsson et al. [17] used a GRADE phantom with a GE Discovery MR750w 3 T MR Scanner (General Electric Healthcare, Milwaukee, WI), and found mean and maximum distortions at all distances to isocentre similar to the mean values over all scanners that we have shown in Table 2.
This study did not compare differences in measured distortions that depended on whether 3D or 2D geometric disortion correction was used or not. However, Sun et al [30], reported a maximum distortion of 7.5 mm across the pelvis without the use of any correction algorithm, and that distortion decreased to 2.6 mm when 2D correction was used and to 1.7 mm when 3D correction was used. The bandwidth they used in this study was not clarified so a direct comparison between our results is not valid, however this work shows the importance of using 3D geometric distortion correction consistently during an audit.
The spherical markers in the GRADE phantom are filled with polyethylene glycol solution. For any water-based markers there might be some chemical shifts from doping agents. However, the bandwidth used was large enough to account for this. The present study did not take into account distortions that were patient/phantom induced. According to Gustafsson et al. [17], the magnetic susceptibility induced distortion of the GRADE phantom is < 0.5 mm for all radial distances of < 250 mm from the isocentre. This magnetic susceptibility induced distortion is small in comparison to the maximum distortions measured above 150 mm from the isocentre (above 2 mm) and hence can be ignored. However, in clinical use Walker et al. [14] registered CT images with MRI images obtained by a 3 T scanner and concluded that the maximum distortion was 3.8 times greater that of the distortion obtained from the phantom. Therefore, although suitable for an audit to compare MRI scanners, reliance only on phantom results is not adequate to fully assess geometric distortions within a patient [31].
This study had some limitations. Firstly, because of a technical problem, only one measurement, rather than two, was used for scanner 4. Secondly, it was not possible to include all the MRI scanners used for RT purposes in England. However, the aim of this work was to demonstrate feasibility on 11 scanners of the methodology that could be used in a country wide audit in the future. A further limitation is that the results for geometric distortion presented are only valid within the phantom for the sequence investigated. The MRI sequence was provided by the manufacturer and was optimised for the phantom and not for a patient and hence the distortions displayed are not representative of the absolute distortions that would be observed in a patient. This limitation is acceptable as the aim of this work was to rigorously compare MRI scanners in clinical use for RT planning and show feasibility for a future audit.
In conclusion, the variance in distortion between scanners was found to be low and distortion was found to increase with distance from the isocentre. This study demonstrates feasibility of the technique to be repeated in a country wide audit of all MRI scanners used clinically for RT. It is recommended in such an audit that mean geometric distortions at clinically relevant distances to isocenter be used to assess MRI scanners. Acceptance limits could be based on the observed variability across multiple scanners.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Dr Richard Speight is supported by the Sir John Fisher Foundation and Dr Richard Speight and Dr Robert Chuter are supported by a Cancer Research UK Centres Network Accelerator Award Grant (A21993) to the ART-NET consortium. Jonathan Wyatt is supported by an EIT Health award.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.phro.2020.07.004.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Schmidt M.A., Payne G.S. Radiotherapy planning using MRI. Phys Med Biol. 2015;60:R323. doi: 10.1088/0031-9155/60/22/R323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Metcalfe P., Liney G., Holloway L., Walker A., Barton M., Delaney G. The potential for an enhanced role for MRI in radiation-therapy treatment planning. Technol Cancer Res Treat. 2013;12:429–446. doi: 10.7785/tcrt.2012.500342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nyholm T., Nyberg M., Karlsson M.G., Karlsson M. Systematisation of spatial uncertainties for comparison between a MR and a CT-based radiotherapy workflow for prostate treatments. Radiation Oncol. 2009;4:54. doi: 10.1186/1748-717X-4-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dowling J.A., Sun J., Pichler P., Rivest-Hénault D., Ghose S., Richardson H. Automatic substitute computed tomography generation and contouring for magnetic resonance imaging (MRI)-alone external beam radiation therapy from standard MRI sequences. Int J Radiation Oncol Biol Phys. 2015;93:1144–1153. doi: 10.1016/j.ijrobp.2015.08.045. [DOI] [PubMed] [Google Scholar]
- 5.Siversson C., Nordström F., Nilsson T., Nyholm T., Jonsson J., Gunnlaugsson A. MRI only prostate radiotherapy planning using the statistical decomposition algorithm. Med Phys. 2015;42:6090–6097. doi: 10.1118/1.4931417. [DOI] [PubMed] [Google Scholar]
- 6.Owrangi A.M., Greer P.B., Glide-Hurst C.K. MRI-only treatment planning: benefits and challenges. Phys Med Biol. 2018;63:05TR1. doi: 10.1088/1361-6560/aaaca4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lagendijk J.J., Raaymakers B.W., Raaijmakers A.J., Overweg J., Brown K.J., Kerkhof E.M. MRI/linac integration. Radiother Oncol. 2008;86:25–29. doi: 10.1016/j.radonc.2007.10.034. [DOI] [PubMed] [Google Scholar]
- 8.Pollard J.M., Wen Z., Sadagopan R., Wang J., Ibbott G.S. The future of image-guided radiotherapy will be MR guided. Br J Radiol. 2017;90:20160667. doi: 10.1259/bjr.20160667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fransson A., Andreo P., Pötter R. Aspects of MR image distortions in radiotherapy treatment planning. Strahlenther Onkol. 2001;177:59–73. doi: 10.1007/pl00002385. [DOI] [PubMed] [Google Scholar]
- 10.Wang D., Doddrell D.M. Geometric distortion in structural magnetic resonance imaging. Curr Med Imaging. 2005;1:49–60. doi: 10.2174/1573405052953029. [DOI] [Google Scholar]
- 11.Karaiskos P., Moutsatsos A., Pappas E., Georgiou E., Roussakis A., Torrens M. A simple and efficient methodology to improve geometric accuracy in gamma knife radiation surgery: implementation in multiple brain metastases. Int J Radiation Oncol Biol Phys. 2014;90:1234–1241. doi: 10.1016/j.ijrobp.2014.08.349. [DOI] [PubMed] [Google Scholar]
- 12.Walker A., Liney G., Holloway L., Dowling J., Rivest-Henault D., Metcalfe P. Continuous table acquisition MRI for radiotherapy treatment planning: distortion assessment with a new extended 3D volumetric phantom. Med Phys. 2015;42:1982–1991. doi: 10.1118/1.4915920. [DOI] [PubMed] [Google Scholar]
- 13.Weygand J., Fuller C.D., Ibbott G.S., Mohamed A.S., Ding Y., Yang J. Spatial precision in magnetic resonance imaging–guided radiation therapy: the role of geometric distortion. Int J Radiation Oncol Biol Phys. 2016;95:1304–1316. doi: 10.1016/j.ijrobp.2016.02.059. [DOI] [PubMed] [Google Scholar]
- 14.Walker A., Metcalfe P., Liney G., Batumalai V., Dundas K., Glide-Hurst C. MRI geometric distortion: Impact on tangential whole-breast IMRT. J Appl Clin Med Phys. 2016;17:7–19. doi: 10.1120/jacmp.v17i5.6242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pappas E.P., Alshanqity M., Moutsatsos A., Lababidi H., Alsafi K., Georgiou K. MRI-related geometric distortions in stereotactic radiotherapy treatment planning: evaluation and dosimetric impact. Technol Cancer Res Treat. 2017;16:1120–1129. doi: 10.1177/1533034617735454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baldwin L.N., Wachowicz K., Thomas S.D., Rivest R., Fallone B.G. Characterization, prediction, and correction of geometric distortion in MR images. Med Phys. 2007;34:388–399. doi: 10.1118/1.2402331. [DOI] [PubMed] [Google Scholar]
- 17.Gustafsson C., Nordström F., Persson E., Brynolfsson J., Olsson L. Assessment of dosimetric impact of system specific geometric distortion in an MRI only based radiotherapy workflow for prostate. Phys Med Biol. 2017;62:2976. doi: 10.1088/1361-6560/aa5fa2. [DOI] [PubMed] [Google Scholar]
- 18.Wang D., Strugnell W., Cowin G., Doddrell D.M., Slaughter R. Geometric distortion in clinical MRI systems: Part I: evaluation using a 3D phantom. Magn Reson Imaging. 2004;22:1211–1221. doi: 10.1016/j.mri.2004.08.012. [DOI] [PubMed] [Google Scholar]
- 19.Tao S., Trzasko J., Gunter J., Weavers P., Shu Y., Huston J., III Gradient nonlinearity calibration and correction for a compact, asymmetric magnetic resonance imaging gradient system. Phys Med Biol. 2016;62:N18. doi: 10.1088/1361-6560/aa524f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fonov V.S., Janke A., Caramanos Z., Arnold D.L., Narayanan S., Pike G.B. International Workshop on Medical Imaging and Virtual Reality. Springer; 2010. Improved precision in the measurement of longitudinal global and regional volumetric changes via a novel MRI gradient distortion characterization and correction technique; pp. 324–333. [Google Scholar]
- 21.Walker A., Liney G., Metcalfe P., Holloway L. MRI distortion: considerations for MRI based radiotherapy treatment planning. Australas Phys Eng Sci Med. 2014;37:103–113. doi: 10.1007/s13246-014-0252-2. [DOI] [PubMed] [Google Scholar]
- 22.Jackson E., Bronskill M., Drost D., Och J., Pooley R., Sobol W. Acceptance testing and quality assurance procedures for magnetic resonance imaging facilities. American Association of Physicists in Medicine One Physics Ellipse College Park. 2010 [Google Scholar]
- 23.American College of Radiology. Phantom Test guidance for use of the large MRI phantom for the ACR MRI accreditation program, https://www.acraccreditation.org/-/media/ACRAccreditation/Documents/MRI/LargePhantomGuidance.pdf 2018 [accessed 15 September 2019].
- 24.Wyatt J., Hedley S., Johnstone E., Speight R., Kelly C., Henry A. Evaluating the repeatability and set-up sensitivity of a large field of view distortion phantom and software for magnetic resonance-only radiotherapy. Phys Imag Radiat Oncol. 2018;6:31–38. doi: 10.1016/j.phro.2018.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Scottish Imaging Network a platform for scientific excellence. Assessment of Geometric Distortion as part of Quality Assurance in Multicentre Magnetic Resonance Imaging Research, http://www.sinapse.ac.uk/news/report-assessing-geometric-distortion-as-part-of-qa-in-multicentre-mri 2012 [accessed 12 September 2019].
- 26.Tan E.T., Marinelli L., Slavens Z.W., King K.F., Hardy C.J. Improved correction for gradient nonlinearity effects in diffusion-weighted imaging. J Magn Reson Imaging. 2013;38:448–453. doi: 10.1002/jmri.23942. [DOI] [PubMed] [Google Scholar]
- 27.Price R.G., Kadbi M., Kim J., Balter J., Chetty I.J., Glide-Hurst C.K. Characterization and correction of gradient nonlinearity induced distortion on a 1.0 T open bore MR-SIM. Med Phys. 2015;42:5955–5960. doi: 10.1118/1.4930245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Torfeh T., Hammoud R., Perkins G., McGarry M., Aouadi S., Celik A. Characterization of 3D geometric distortion of magnetic resonance imaging scanners commissioned for radiation therapy planning. Magn Reson Imaging. 2016;34:645–653. doi: 10.1016/j.mri.2016.01.001. [DOI] [PubMed] [Google Scholar]
- 29.Kutcher G.J., Coia L., Gillin M., Hanson W.F., Leibel S., Morton R.J., Palta J.R., Purdy J.A., Reinstein L.E., Svensson G.K., Weller M., Wingfield L. Comprehensive QA for radiation oncology: report of AAPM Radiation Therapy Committee Task Group 40. Med Phys. 1994;21(4):581–618. doi: 10.1118/1.597316. [DOI] [PubMed] [Google Scholar]
- 30.Sun J., Dowling J., Pichler P., Menk F., Rivest-Henault D., Lambert J. MRI simulation: end-to-end testing for prostate radiation therapy using geometric pelvic MRI phantoms. Phys Med Biol. 2015;60:3097. doi: 10.1088/0031-9155/60/8/3097. [DOI] [PubMed] [Google Scholar]
- 31.Ranta I., Kemppainen R., Keyriläinen J., Suilamo S., Heikkinen S., Kapanen M. Quality assurance measurements of geometric accuracy for magnetic resonance imaging-based radiotherapy treatment planning. Phys Med. 2019;62:47–52. doi: 10.1016/j.ejmp.2019.04.022. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.