High spin-wave propagation length consistent with low damping in a metallic ferromagnet

Abstract

We report ultralow intrinsic magnetic damping in Co₂₅Fe₇₅ heterostructures, reaching the low 10⁻⁴ regime at room temperature. By using a broadband ferromagnetic resonance technique in out-of-plane geometry, we extracted the dynamic magnetic properties of several Co₂₅Fe_75-based heterostructures with varying ferromagnetic layer thicknesses. By measuring radiative damping and spin pumping effects, we found the intrinsic damping of a 26 nm thick sample to be α₀ ≲ 3.18 × 10⁻⁴. Furthermore, using Brillouin light scattering microscopy, we measured spin-wave propagation lengths of up to (21 ± 1) μm in a 26 nm thick Co₂₅Fe₇₅ heterostructure at room temperature, which is in excellent agreement with the measured damping.

Itinerant ferromagnets (FMs) are advantageous for spintronic and magnonic devices. They benefit from, e.g., large magnetoresistive effects and current-induced spin–orbit torques.¹ In many magnetoresistive technologies (e.g., anisotropic magnetoresistance, giant magnetoresistance, and tunnel magnetoresistance), electronic conductivity is indispensable. Moreover, due to high saturation magnetization in metallic FMs, spin-wave (SW) group velocities are in general significantly higher than those in insulating ferrimagnets.^2–5 High saturation magnetizations in general are easily detectable. Nevertheless, itinerant FMs typically have considerable magnetic damping.^6,7 This is unfavorable for many applications. For example, low damping is crucial for oscillators based on spin transfer torques and spin–orbit torques as well as for achieving large spin-wave propagation lengths (SWPLs).^8–10 The need for thin film materials with low magnetic damping has triggered the interest in the insulating ferrimagnet yttrium-iron garnet (Y₃Fe₅O₁₂, YIG).^11–13 Although for YIG, very small total (Gilbert) damping parameters on the order of α_G ≈ 10⁻⁵ and large SWPLs of a few tens of micrometers (up to ~25μm) in thin films (~20 nm) have been reported,^5,13,14 its insulating properties and requirement for crystalline growth are challenges for large scale magnonic applications.

Schoen et al. recently observed ultralow intrinsic magnetic damping in Co₂₅Fe₇₅ (CoFe) metallic thin films [α₀ = (5±1:8) × 10⁻⁴],¹⁵ and Körner et al. reported PLs of 5 μm – 8 μm in CoFe using time resolved scanning magneto-optical Kerr microscopy.⁴ This motivated our study on sputter-deposited CoFe-based thin film heterostructures. We use broadband ferromagnetic resonance (BB-FMR) spectroscopy¹⁶ in out-of-plane (OOP) geometry and Brillouin light scattering (BLS) microscopy¹⁷ and find intrinsic damping parameters in the lower 10⁻⁴ regime as well as SWPLs of more than 20 μm. The damping is therefore comparable to YIG/heavy metal (HM) heterostructures,¹⁸ and the SWPL is comparable to that of state-of-the-art YIG thin films.^5,13 Thin film CoFe is a promising candidate for all-metal magnonic devices, as it combines low magnetic damping with good electrical conductivity and large saturation magnetization, while enabling easy fabrication by room-temperature processing/deposition, no required annealing, polycrystalline structure, and scalability to the nanometer regime.

For BB-FMR, Ta(3 nm)/Al(3 nm)/Co₂₅Fe₇₅(t)/Al(3 nm)/Ta(3 nm) heterostructures with different thicknesses t of the CoFe layer were sputter deposited on a thermally oxidized Si (100) substrate at an Ar pressure of 5 × 10⁻⁶ bar at room temperature. No subsequent annealing process was performed. The CoFe layer thickness was varied in the range of 1.4 nm < t < 26 nm as determined by X-ray reflectometry.

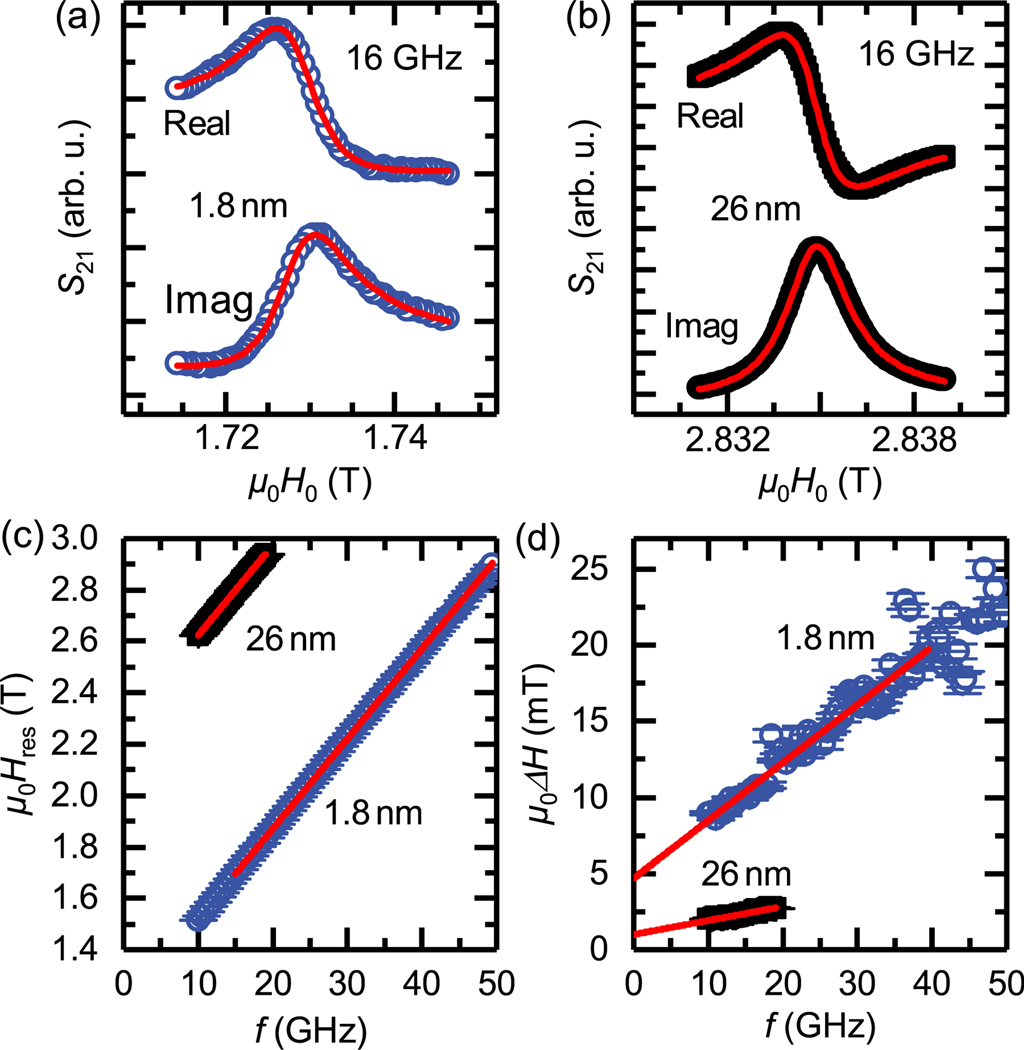
The OOP BB-FMR measurements were performed at room temperature using a vector network analyzer (VNA). This geometry was chosen to determine the intrinsic magnetic damping without further damping contributions due to magnon-magnon scattering.¹⁹ The samples were placed directly on a coplanar waveguide (CPW), with an 80 μm wide center conductor. For the measurements, the VNA frequency f was kept constant and the microwave transmission parameter S₂₁ was recorded as a function of applied magnetic field H₀ for a range of frequencies at a VNA output power of 0 dBm. A representative set of data as measured for the real and imaginary part of S₂₁ at 16GHz for samples with t = 1.8 nm and t = 26 nm is shown in Figs. 1(a) and 1(b).

FIG. 1.

(a) Measured microwave transmission S₂₁ at 16 GHz vs applied OOP magnetic field H₀ for blanket Ta(3 nm)/Al(3 nm)/Co₂₅Fe₇₅(t)/Al(3 nm)/Ta(3 nm) samples with CoFe thickness t = 1.8 nm [(a) blue symbols] and t = 26 nm [(b) black symbols], respectively. The red lines are fits of Eq. (2) to the data. The extracted resonance fields H_res and linewidths ΔH as a function of the applied microwave frequency are shown in (c) and (d), respectively. Here, the error bars (smaller than the symbol size) are extracted fit errors from (a) and (b). In (c), the red line is a fit to Eq. (3) to extract the Landé-factor g and the effective magnetization M_eff. In (d), the linewidth is plotted vs frequency. The Gilbert parameter α_G and the inhomogeneous linewidth broadening H_inh are extracted by fitting the data to Eq. (4) (red lines). The linewidth of the t = 26 nm thick sample is shown in Fig. 2(c) on an expanded scale.

The magnetic response of the thin film FM magnetized out-of-plane is given by the susceptibility χ which is obtained by solving the Landau-Lifshitz-Gilbert (LLG) equation,^15,20

$$\chi \left(H_0\right)=\frac{M_s\left(H_0-H_{\text{res}}+H_{\text{eff}}\right)}{{\left(H_0-H_{\text{res}}+H_{\text{eff}}+i\frac{\Delta H}{2}\right)}^2-H_{\text{eff}}^2}$$. (1)

Here, M_s is the saturation magnetization, H_res is the resonance field, H_eff = 2πf / (μ₀γ), with γ being the gyromagnetic ratio, and ΔH = 2(2πfα)/(γμ₀) is the full width at half maximum (FWHM) line-width of the resonance. The data in Figs. 1(a) and 1(b) are fitted to²¹

$$S_{21}\left(H_0\right)=S_{21}^0+iA\frac{\chi \left(H_0\right)}{M_{\text{s}}}=S_{21}^0\left(1+\Delta S_{21}\right)$$, (2)

where $S_{21}^0$ is the background transmission through the CPW without the magnetic resonance peak. It is determined from the fits as a complex linear background to the data $S_{21}^0\left(H_0\right)=S_{21}^a+H_0{S}_{21}^b$. Factor A is a complex-valued scaling parameter.

In the OOP geometry, the resonance condition for thin films is given by²²

$${\mu }_0{H}_{\text{res}}={\mu }_0{M}_{\text{eff}}+{\mu }_0{H}_{\text{eff}}$$, (3)

where M_eff = M_s – H_k is the effective magnetization, with the uniaxial out-of-plane anisotropy field H_k. In Fig. 1(c), we plot the determined H_res vs the frequency f. From the fit to Eq. (3) [red solid lines in Fig. 1(c)], we obtain M_eff and γ of the specific sample.

The FWHM linewidth vs frequency data shown in Fig. 1(d) are fitted to

$${\mu }_0\Delta H={\mu }_0{H}_{\text{inh}}+2\cdot \frac{2\pi f{\alpha }_{\text{G}}}{\gamma }$$. (4)

Here, H_inh is the inhomogeneous linewidth broadening and α_G is the phenomenological Gilbert damping parameter.^23,24 H_inh indicates the presence of long-range magnetic inhomogeneities, which become more relevant for thinner films but do not contribute to our α_G.

Several contributions to the measured total damping (α_G) were extracted from our data. In addition to the intrinsic damping of the magnetic material itself (α₀), spin pumping (α_sp) contributes significantly^25–27 to the total damping in our thinner heterostructures due to the adjacent HM (Ta) layers. Furthermore, we consider additional damping contributions from eddy currents (α_eddy) and radiative damping (α_rad).^15,21 Due to these contributions, the total damping (α_G = α_{0 +} α_{sp +} α_{eddy +} α_rad) depends on the FM thickness. We calculated damping due to eddy currents and measured radiative damping contributions to the total damping. The eddy current contribution is given by¹⁵ ${\alpha }_{\text{eddy}}=\gamma {\mu }_0^2{M}_{\text{s}}{t}^2/16\rho$. Here, μ₀M_s = 2.35 T (see the supplementary material) and ρ = 340 nΩ m is the estimated weighted resistivity value of the CoFe film derived from the resistivities of iron and cobalt thin films with thicknesses of around 20 nm.^28,29 With these values, we find an almost negligible eddy current contribution to the total damping. A quantitative determination analogous to Ref. 21 of the radiative damping is done by analyzing the magnitude of the measured inductance L of all samples. The quantification of this contribution is important for BB-FMR because it represents a damping by inductive power dissipation into the CPW and, hence, is not a property of the sample itself but depends on the setup. In possible applications like, e.g., magnonic waveguides or spin-Hall nano-oscillators, this contribution vanishes and the damping lowers by α_rad. With Eq. (2) in this work and Eq. (9) from Ref. 21, one obtains

$$\frac{L}{\chi }\equiv \tilde{L}=-\frac{2Z_{0}A}{M_{\text{s}}{S}_{21}^0\omega }$$. (5)

Here, Z₀ = 50 Ω is the CPW impedance. It has been shown that $\tilde{L}={\tilde{L}}_0+{\tilde{L}}_1(\omega )$, where ${\tilde{L}}_0\in ℝ$ and ${\tilde{L}}_1\in ℂ$, due to the effect of inverse spin–orbit torques.²¹ We extract L from the FMR measurements, and the dipolar inductance ${\tilde{L}}_0$ from a fit of $\tilde{L}$ vs f for each sample. The radiative damping contribution is then given as¹⁵

$${\alpha }_{\text{rad}}=\frac{1}{4}\frac{\gamma {\mu }_0{M}_{\text{s}}}{Z_0}{\tilde{L}}_0$$. (6)

This analysis allows us to determine α_rad independent of geometrical parameters of the samples or CPWs and is used to quantitatively extract the dipolar inductance without any calibration of the microwave circuit. For the thickest sample, we obtain α_rad = (4.69 ± 0:05) × 10⁻⁴, which is comparable to the previously obtained values.^15,30 The damping including the spin pumping contribution α_sp is given by

$${\alpha }_0+{\alpha }_{\text{sp}}={\alpha }_0+2\frac{\gamma \hslash g_{\text{eff}}^{\uparrow \downarrow }}{4\pi M_{\text{s}}}\frac{1}{t}$$. (7)

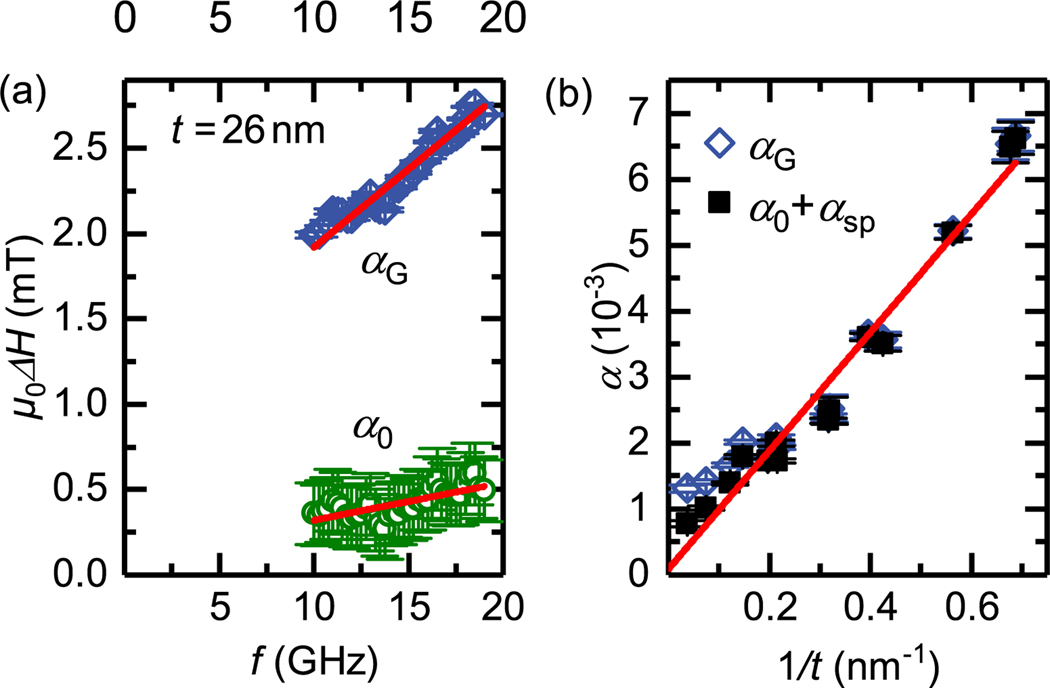
where $g_{\text{eff }}^{\uparrow \downarrow }$ is the effective spin mixing conductance.³⁰ We subtract α_rad and α_eddy from the measured total damping α_G [see Figs. 2(a) and 2(b)] and plot the remaining damping α_{0 +} α_sp as a function of 1/t in Fig. 2(b) together with the total damping α_G. From a linear fit [Eq. (7)] to α_{0 +} α_sp, we obtain g_eff and α₀. Therefore, we use M_s as above and γ/2π = 28.65 GHz/T. The fitted g_eff = (5.5 ± 0.3) × 10¹⁸ m⁻² is in agreement with literature values.¹⁵ The y-intercept indicating the extrapolated intrinsic damping yields α₀ = (0.91 ± 1.69) 10⁻⁴, and hence, the intrinsic damping is below the sensitivity of our approach. For the thickest sample t = 26 nm shown in Fig. 2(a), we obtain α₀ = (3.18 ± 0.48) 10⁻⁴ (see the supplementary material for details). Within the errors, this value lies close to the extrapolated value and is the lowest intrinsic damping for a thin film ferromagnetic metal reported so far. We attribute the slightly reduced intrinsic α₀ compared to Ref. 30 to the use of a different seed layer, which has a substantial impact on the damping of CoFe.³¹

FIG. 2.

(a) An expanded view of the linewidth vs frequency plot of the t = 26 nm sample. The total linewidth is shown by the blue diamonds, from which the total Gilbert damping parameter α_G was extracted. The green circles represent the intrinsic linewidth contribution. In (b), the total damping α_G is plotted for different thicknesses t as blue diamonds. We subtracted the contributions from radiative damping and eddy currents and show the resulting α₀ + α_sp as black squares. The red line is an unweighted fit to Eq. (7) in order to quantify the spin pumping contribution within our samples and to be able to extrapolate the intrinsic damping of CoFe within our multilayer system. For thicker samples, the available frequency range is rather small, leading to an increased uncertainty, as discussed in Ref. 32.

The low damping properties of the CoFe heterostructures, in combination with the high saturation magnetization, are expected to result in long PLs of dipolar SWs. We use microfocused BLS¹⁷ to study the SW propagation in patterned CoFe samples, which is schematically depicted in Figs. 3(a) and 3(b).

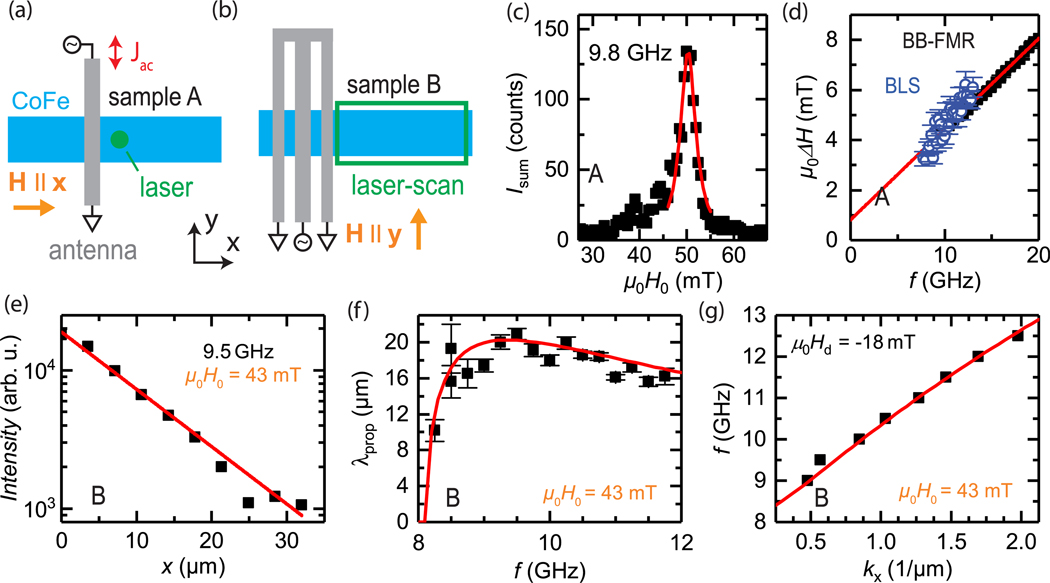
FIG. 3.

(a) and (b) Schematic top view of samples A and B, respectively. (c) Integrated BLS intensity vs field of sample A. By use of a Lorentzian fit (red line), the linewidth is extracted. In (d), we compare the BLS linewidth (open symbols) with the values obtained by in-plane BB-FMR on a blanket film (closed squares). (e) Representative dataset of sample B with f = 9.5 GHz. The BLS intensity was measured as a function of the position (x, y) in the area highlighted with the green rectangle in (b). The measured signal was then integrated in the y direction, and the exponential decay in the x direction is fitted (red curve). (f) Propagation length λ_prop for varying frequencies f. The depicted error bars are fit errors. The red curve is based on an analytical model calculation (see the text). (g) f vs k_x dispersion determined by phase-resolved μBLS. The red line is a model from Eq. (8).

For our experiments, we fabricated patterned stripes of a Pt(3 nm)/Cu(3 nm)/Co₂₅Fe₇₅(t)/Cu(3 nm)/Ta(3 nm) heterostructure using laser (sample A) and electron beam (sample B) lithography, sputter deposition, and a subsequent lift-off process. This stack sequence was used as lower in-plane damping was observed compared to the samples containing Al. Below, we present data on only two samples with a thickness of t = 5 nm and a width of w = 1.5 μm for sample A and t = 26 nm and w = 5 μm for sample B, respectively. An aluminum antenna was placed on top of the CoFe strip to drive spin dynamics via a microwave drive applied to the antenna. For sample A, we used a simple aluminum strip optimized for excitation of the uniform (FMR) mode, whereas for sample B, we used a CPW antenna optimized for an efficient excitation of SWs with wave number k ≤ 2 μm⁻¹.

In order to compare the uniform FMR-mode linewidths of the extended and patterned films, we used sample A in backward volume geometry and placed the laser spot close to the antenna, where the FMR mode is dominantly excited. We recorded BLS spectra for several magnetic fields for each frequency. The BLS intensity is integrated, and the signal sum is then plotted vs the external magnetic field in Fig. 3(c). The FWHM-linewidth ΔH is determined by fitting a Lorentzian (red line). We then compared the fitted linewidth with the measured in-plane BB-FMR linewidth of a blanket film, deposited simultaneously with the structured BLS sample. In the in-plane configuration, the total damping increases due to magnon-magnon scattering^19,33 and possible anisotropic damping.^34–37 As shown in Fig. 3(d), the linewidths μ₀ΔH determined from BB-FMR (black symbols) and BLS (blue symbols) are very similar, indicating that the damping properties are not affected by the patterning, as expected in a lift-off process with micrometer feature sizes.

In the next set of experiments, we investigate the SWPL of sample B [see Fig. 3(b)]. Here, the magnitude of the external magnetic field was fixed at μ₀H₀ = 43 mT, while the field was applied perpendicular to the CoFe strip (Damon-Eshbach geometry). The BLS intensity was recorded as a function of position (x, y) over the CoFe strip. The BLS intensity decay in the x direction (i.e., the BLS intensity averaged over the width of the strip in order to suppress mode-beating effects^38–40) is shown in Fig. 3(e) for f = 9.5GHz. The SWPL λ_prop is extracted by a fit to I = I₀ exp (−2x/λ_prop)⁴¹ and plotted vs f in Fig. 3(f). From our experiments, we extract a maximum SWPL of (21 ± 1) μm, well exceeding the previously obtained results for FeNi alloys⁴² and CoFe⁴ and very comparable to values found for YIG thin films.^5,13 The red curve is the theoretical prediction, based on the analytical Kalinikos-Slavin model detailed below and using the magnetic parameters determined by in-plane BB-FMR (μ₀M_s = 2.35 T, μ₀M_eff = 2.29 T, α_G – α_rad = 3.92 × 10⁻³, and g = 2.051) for a codeposited reference sample (see the supplementary material).

Starting with a simplified version of Kalinikos and Slavin’s SW dispersion for the modes with k_x ⊥ M,^43,44

$$\begin{array}{c}{f}_{res}=\frac{{\mu }_o\gamma }{2\pi }\sqrt{H_0+H_d+H_k+M_s\frac{1-\exp \left(-kt\right)}{kt}}\\ \times \sqrt{H_0+H_d+M_s\left(1-\frac{1-\exp -\left(-kt\right)}{kt}\right)},\end{array}$$ (8)

we calculated the group velocity υ_g = 2π∂f_res/∂k. Here,$k=\sqrt{k_{\text{x}}^2+k_{\text{y}}^2}$ is the in-plane wave vector of the traveling SW and μ₀H_k = μ₀M_eff – μ₀M_s = −60 mT is the effective interface anisotropy field. The calculation of the transversal wave vector component k_y = 0.31 μm⁻¹ due to geometrical confinement was shown to be nontrivial and is used as a fitting parameter, as in Ref. 45. The resonance linewidth is given by⁴⁶ Δω = αμ₀γ(M_eff/2 + H₀ + H_d), and the lifetime of the SW is τ = 1/Δω. Here, α = α_G – α_rad. The SWPL is λ_prop = υ_gτ. The demagnetization field in the y-direction was set to μ₀H_{d =} −18 mT, as required for matching Eq. (8) to the SW dispersion obtained by phase-resolved μBLS¹⁷ [see Fig. 3(g)]. This value for H_d is in good agreement with the demagnetization (μ₀H_d ≈ −12 mT) obtained for an ellipsoid with the axes corresponding to the CoFe-stripe dimensions.⁴⁷ We find excellent agreement between this model and our experimental data in Fig. 3(f).

In summary, our sputter-deposited Co₂₅Fe₇₅ layers exhibit a record low intrinsic damping for metallic thin film ferromagnets of α₀ ≲ 3.18 × 10⁻⁴ in OOP geometry. The damping properties of extended films are maintained for micropatterned films, and spin-wave propagation lengths are in very good agreement with the properties extracted from BB-FMR. The low magnetic damping, together with the high saturation magnetization, leads to spin-wave decay lengths of more than 20 μm at room temperature, which is the highest reported so far in itinerant magnetic systems. This property makes Co₂₅Fe₇₅ a promising material for all-metal spintronic and magnonic devices, compatible with semiconductor technology.

See the supplementary material for (I) the determination of the saturation magnetization M_s, (II) a detailed linewidth analysis of the t = 26 nm sample, and (III) IP BB-FMR data of the reference sample for optical measurements.