Spectral Phenotyping of Physiological and Anatomical Leaf Traits Related with Maize Water Status^,

Hyperspectral phenotyping has the potential to act as a surrogate for standard reference measurements of physiological and anatomical leaf traits related with water stress in maize.

Abstract

Advancements in phenotyping techniques capable of rapidly and nondestructively detecting impacts of drought on crops are necessary to meet the 21st-century challenge of food security. Here, we describe the use of hyperspectral reflectance to predict variation in physiological and anatomical leaf traits related with water status under varying water availability in six maize (Zea mays) hybrids that differ in yield stability under drought. We also assessed relationships among traits and collections of traits with yield stability. Measurements were collected in both greenhouse and field environments, with plants exposed to different levels of water stress or to natural water availability, respectively. Leaf spectral measurements were paired with a number of physiological and anatomical reference measurements, and predictive spectral models were constructed using a partial least-squares regression approach. All traits were relatively well predicted by spectroscopic models, with external validation (i.e. by applying partial least-squares regression coefficients on a dataset distinct from the one used for calibration) goodness-of-fit (R²) ranging from 0.37 to 0.89 and normalized error ranging from 12% to 21%. Correlations between reference and predicted data were statistically similar for both greenhouse and field data. Our findings highlight the capability of vegetation spectroscopy to rapidly and nondestructively identify a number of foliar functional traits affected by drought that can be used as indicators of plant water status. Although we did not detect trait coordination with yield stability in the hybrids used in this study, expanding the range of functional traits estimated by hyperspectral data can help improve trait-based breeding approaches.

One of the more influential, yet unpredictable, factors expected to change in future environments over the next 50 years will be the intensity and frequency of precipitation events (Intergovernmental Panel on Climate Change, 2014). These changes will likely have a dramatic effect on plant metabolism, growth, and production (Pryor et al., 2013; Miao et al., 2017). Over a comparable time period, global food demand is predicted to double, requiring intensification of agricultural production systems (Tilman et al., 2011). The rapid development and adoption of climate-resilient crop genotypes capable of maintaining comparable yield production under favorable and stress conditions (i.e. with high yield stability) is important to overcome this 21st-century challenge (Mickelbart et al., 2015). Advancements in phenotyping techniques capable of rapidly assessing the effects of drought on plant functional responses from a wide genetic range is necessary to understand plant traits required to maintain yield stability under predicted future environmental conditions (Araus et al., 2012; Cotrozzi et al., 2017; Miao et al., 2017).

Maize (Zea mays) represents an excellent species for developing phenotyping approaches. It is one of the most important crops globally for humans and other animals (Miao et al., 2017), and while yield has increased in absolute value in the last decades, mainly due to genetic gain and improved agronomic practices, the negative impact of drought on maize productivity has also increased due to increased frequency and intensity of drought events (Araus et al., 2012). Maize also uses more water at specific developmental stages (e.g. during flowering), making the optimal water management of this species challenging (Araus et al., 2012). Moreover, the functional responses that are associated with increased yield stability and targeted by maize breeders, such as the ability to maintain photosynthesis under stressful conditions, limit transpiration, increase water-use efficiency, and regulate osmotic adjustment (Ribaut et al., 2009) are difficult, time-consuming, and mostly destructive to measure by standard approaches (e.g. those performed by classic infrared gas analyzers, Scholander-type pressure chambers, and vapor pressure osmometers). All of these aspects make monitoring of a large number of individual plants logistically impractical.

To date, a number of foliar anatomical, physiological, and biochemical traits have been successfully quantified using vegetation spectroscopy (Asner et al., 2011; Couture et al., 2013, 2016; Serbin et al., 2015; Cotrozzi et al., 2017). The estimation of these traits from leaf reflectance relies on variations in absorption as a consequence of vibrational excitation of molecular bonds, primarily C-H, N-H, and O-H bonds at specific wavelengths in the visible (400–700 nm), near-infrared (NIR; 700–1,100 nm), and short-wave infrared (SWIR; 1,100–2,400 nm) spectral regions. Model calibrations are accomplished by pairing leaf spectral signatures with independent and reliable reference measurements. Plant traits are modeled as a function of the spectra using multivariate methods, such as partial least-squares regression (PLSR; Wold et al., 2001) or least absolute shrinkage and selection operator (Lasso; Tibshirani, 2011). Best practices suggest that these models are validated using independent samples, after which models can be used to predict the variable of interest in unknown samples on the basis of their spectral reflectance alone (Couture and Lindroth, 2012; Schweiger, 2020). Importantly, leaf reflectance measurements are rapid, taking only seconds; are nondestructive; and relatively inexpensive. Although the purchase of a spectrometer can range from hundreds to tens of thousands of U.S. dollars, the expenses to run such instruments are minimal compared with the cost and maintenance of other analytical instrumentation (e.g. high performance liquid chromotography). A spectral approach also provides the potential to assess considerably more individual plant traits in situ and in vivo over multiple time periods than standard reference measurements alone (e.g. those performed with classic ecophysiological techniques or wet chemistry). In addition, this approach can help us to monitor plant function over large geographic regions if scaled to remote sensing collections from air- or spaceborne platforms (Cotrozzi et al., 2018).

Although the use of hyperspectral reflectance (by both imaging or nonimaging sensors) is broadly regarded as a promising phenotyping approach in agriculture (Weber et al., 2012; Araus and Cairns, 2014; Serbin et al., 2015; Heckmann et al., 2017; Yendrek et al., 2017; Couture et al., 2018), the potential of this technique is still not fully realized. At present, studies aimed at understanding relationships among leaf optical properties and photosynthetic metabolism (e.g. Doughty et al., 2011; Serbin et al., 2012, 2015; Ainsworth et al., 2014; Heckmann et al., 2017; Silva-Perez et al., 2017; Yendrek et al., 2017) have estimated only a relatively small number of traits, focusing on the maximum rates of ribulose bisphosphate carboxylation (V_cmax) and electron transport (J_max). Similarly, while plant water status has been the focus of a number of studies utilizing foliar optical properties in the last decades (e.g. Hunt et al., 1987; Peñuelas et al., 1993; Gao, 1996; Ceccato et al., 2002; Sims and Gamon, 2003; Cheng et al., 2008; González-Fernández et al., 2015), these studies have primarily focused on foliar water content or changes in water content. To date, only a few studies (Rodríguez-Pérez et al., 2007; Santos and Kaye, 2009; De Bei et al., 2011; Rallo et al., 2014; Rapaport et al., 2015; Cotrozzi et al., 2017) have examined the ability of reflectance spectroscopy to estimate leaf water potential. These studies, however, have been limited to C3 species, and mostly grapevine (Vitis vinifera), which potentially presents a limitation when dealing with C4 species because of different leaf morphology, physiology, and biochemistry of the two photosynthetic types (Yendrek et al., 2017). Moreover, none of these studies have examined the ability of spectral measurements to estimate individual components of leaf water potential (e.g. osmotic potential). Maize represents a model C4 species, and reflectance spectroscopy has been used to assess the quality of maize leaves (Weber et al., 2012; Heckmann et al., 2017; Yendrek et al., 2017), seeds (Spielbauer et al., 2009), and forage (Volkers et al., 2003). To date, however, few studies have explored the capacity of spectroscopy to estimate important fresh leaf traits in maize plants under drought stress.

In this study, we tested the capability of reflectance spectroscopy to characterize physiological and anatomical responses of six maize hybrids with different sensitivities to drought, determined by previously established differences in yield stability. We collected spectral leaf signatures from maize hybrids growing under both controlled greenhouse conditions and field conditions. Our objectives in this study were to (1) develop statistical models to estimate leaf gas-exchange, greenness, water status, thickness, and stomatal density; and (2) compare the performance of models built using only greenhouse samples with models including also field samples. Further, we tested relationships among physiological and morphological responses of maize hybrids and their yield stability under drought conditions.

RESULTS

Prediction of Leaf Traits

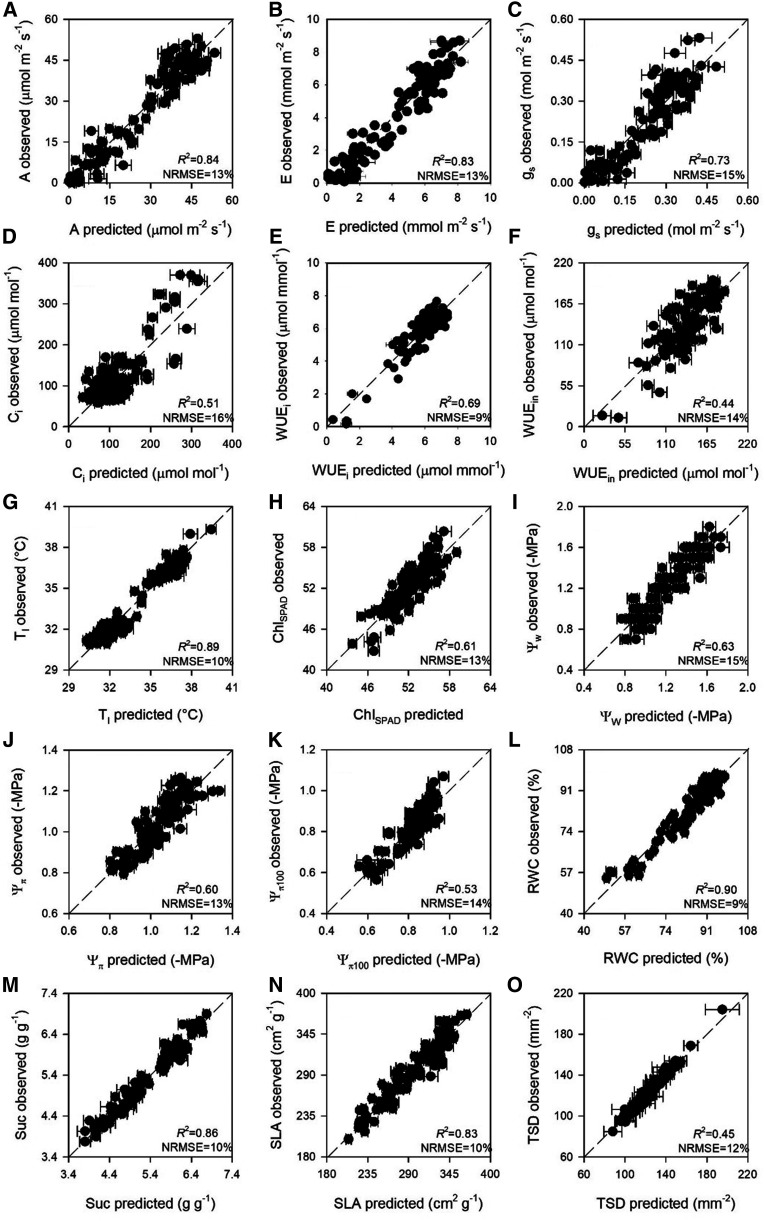
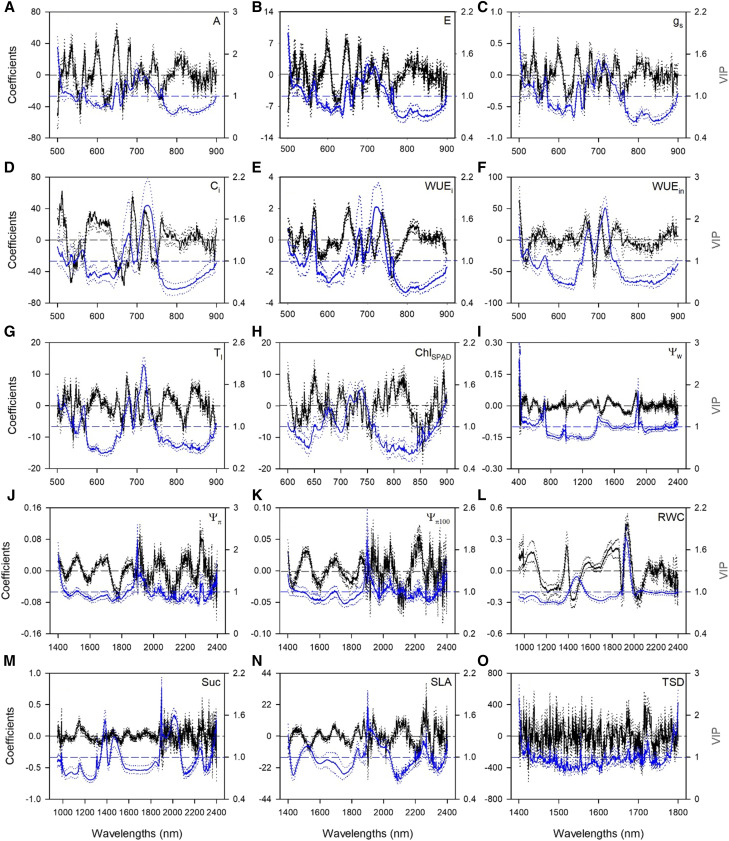
To optimize model performance, we initially examined numerous models containing different wavelength ranges, characterized by specific absorption features in known literature that are directly or indirectly related to specific traits (Supplemental Table S1). Final models for gas-exchange traits utilized the wavelength range 500 to 900 nm for net CO₂ assimilation (A), transpiration (E), stomatal conductance (g_s), intercellular CO₂ concentration (C_i), instantaneous water-use efficiency (WUE_i), intrinsic water-use efficiency (WUE_in), and leaf temperature (T_l; Supplemental Table S1). Cross-validated models accurately characterized A, E, g_s, and T_l (Fig. 1, A, B, C, and G; Table 1). Performance metrics of cross-validated modes of C_i, WUE_i, and WUE_in models were slightly lower than those of A, E, g_s, and T_l (Fig. 1, D, E, and F; Table 1). Standardized PLSR coefficients and the variable important to the projection (VIP) measures exhibited similar profiles for both sets of models. Specifically, VIP highlighted important wavelengths at ∼550 nm and from 650 to 750 nm (Fig. 2, A–G). While statistically significant (r = 0.52, P > 0.001, n = 61), the correlation between WUE_in calculated using either observed or predicted values of A and g_s was lower and the bias higher than estimation accuracy of modeling WUE_in directly (Fig. 2F).

Figure 1.

Observed versus predicted cross-validated values of assimilation (A), transpiration (B), stomatal conductance (C), intercellular CO₂ concentration (D), instantaneous water-use efficiency (E), intrinsic water-use efficiency (F), leaf temperature (G), leaf chlorophyll concentration (H), leaf water potential (I), leaf osmotic potential (J), leaf osmotic potential at full turgor (K), relative water content (L), succlence (M), specific leaf area (N), and total stomatal density (O). Error bars for predicted values represent the sd generated from the 500 simulated models. Dashed line is 1:1 relationship.

Table 1. Model performance statistics for calibration (C) and cross-validation (CV) data generated via using 500 random permutations of the data, with 80% used for calibration and 20% used for cross validation for models predicting leaf traits from maize spectra.

Averaged R², RMSE, and NRMSE. Data are shown as mean ± sd. Values in parentheses are fifth and 95th percentil confidence intervals.

Trait	R2		RMSE		Bias		NRMSE
	C	CV	C	CV	C	CV	C	CV
A (µmol CO2 m−2 s−1)	0.92 ± 0.01 (0.91–0.94)	0.84 ± 0.05 (0.74–0.91)	4.61 ± 0.23 (4.24–4.95)	6.61 ± 0.93 (5.09–8.15)	0.0 ± 0.0 (0.0 ± 0.0)	0.28 ± 1.60 (−2.43–2.95)	9	13
E (mmol water m−2 s−1)	0.92 ± 0.01 (0.91–0.93)	0.83 ± 0.05 (0.74–0.90)	0.77 ± 0.04 (0.71–0.82)	1.15 ± 0.15 (0.91–1.40)	0.0 ± 0.0 (0.0–0.0)	0.02 ± 0.27 (−0.41–0.48)	9	13
gs (mol water m−2 s−1)	0.86 ± 0.01 (0.84–0.89)	0.73 ± 0.08 (0.59–0.83)	0.05 ± 0.00 (0.05–0.06)	0.08 ± 0.01 (0.06–0.10)	0.0 ± 0.0 (0.0 ± 0.0)	0.00 ± 0.02 (−0.03–0.03)	9	15
Ci (µmol mol−1)	0.69 ± 0.03 (0.63–0.74)	0.51 ± 0.17 (0.22–0.74)	40.43 ± 1.88 (37.41–43.37)	50.06 ± 7.52 (37.50–63.03)	0.0 ± 0.0 (0.0 ± 0.0)	−0.36 ± 11.76 (−19.25–18.11)	13	16
WUEi (µmol CO2 mmol−1 water)	0.85 ± 0.03 (0.80–0.88)	0.69 ± 0.17 (0.36–0.88)	0.53 ± 0.02 (0.50–0.56)	0.69 ± 0.10 (0.55–0.86)	0.0 ± 0.0 (0.0–0.0)	0.02 ± 0.16 (−0.26–0.29)	7	9
WUEin (µmol CO2 mmol−1 water)	0.64 ± 0.04 (0.57–0.70)	0.44 ± 0.17 (0.17–0.71)	21.35 ± 0.92 (19.66–22.62)	26.57 ± 4.01 (20.41–33.38)	0.0 ± 0.0 (0.0 ± 0.0)	0.10 ± 6.11 (−10.59–9.06)	12	14
Tl (°C)	0.95 ± 0.00 (0.94–0.96)	0.89 ± 0.03 (0.82–0.93)	0.52 ± 0.02 (0.48–0.55)	0.79 ± 0.11 (0.61–0.96)	0.0 ± 0.0 (0.0 ± 0.0)	0.01 ± 0.18 (−0.31–0.27)	5	10
ChlSPAD	0.75 ± 0.02 (0.73–0.78)	0.61 ± 0.09 (0.45–0.75)	1.72 ± 0.06 (1.61–1.81)	2.22 ± 0.27 (1.74–2.63)	0.0 ± 0.0 (0.0 ± 0.0)	0.02 ± 0.53 (−0.91–0.80)	10	13
Ψw (−MPa)	0.85 ± 0.01 (0.83–0.87)	0.63 ± 0.10 (0.44–0.77)	0.10 ± 0.00 (0.10–0.11)	0.17 ± 0.02 (0.13–0.20)	0.0 ± 0.0 (0.0 ± 0.0)	0.01 ± 0.04 (−0.06–0.07)	9	15
Ψπ (−MPa)	0.79 ± 0.02 (0.77–0.82)	0.60 ± 0.11 (0.40–0.76)	0.06 ± 0.00 (0.05–0.06)	0.08 ± 0.01 (0.07–0.10)	0.0 ± 0.0 (0.0 ± 0.0)	0.00 ± 0.02 (−0.04–0.03)	13	17
Ψπ100 (−MPa)	0.77 ± 0.02 (0.74–0.81)	0.53 ± 0.14 (0.24–0.73)	0.05 ± 0.00 (0.05–0.05)	0.07 ± 0.01 (0.06–0.09)	0.0 ± 0.0 (0.0 ± 0.0)	0.00 ± 0.02 (−0.03–0.03)	10	14
RWC (%)	0.93 ± 0.01 (0.92–0.94)	0.90 ± 0.04 (0.80–0.94)	3.22 ± 0.12 (3.04–3.43)	3.83 ± 0.48 (2.92–4.62)	0.0 ± 0.0 (0.0 ± 0.0)	0.01 ± 0.93 (−1.51–1.56)	7	9
Suc (g g−1)	0.97 ± 0.01 (0.96–0.97)	0.86 ± 0.05 (0.77–0.92)	0.15 ± 0.01 (0.13–0.17)	0.32 ± 0.05 (0.25–0.40)	0.0 ± 0.0 (0.0 ± 0.0)	−0.01 ± 0.09 (−0.16–0.11)	5	10
SLA (cm2 g−1)	0.91 ± 0.01 (0.90–0.93)	0.83 ± 0.06 (0.71–0.91)	12.10 ± 0.49 (11.28–12.84)	17.21 ± 2.50 (13.17–21.11)	0.0 ± 0.0 (0.0 ± 0.0)	−0.24 ± 3.92 (−6.45–6.39)	7	10
TSD (mm−2)	0.99 ± 0.00 (0.99–1.00)	0.45 ± 0.16 (0.16–0.68)	1.42 ± 0.19 (1.10–1.71)	14.28 ± 2.16 (10.72–17.91)	0.0 ± 0.0 (0.0 ± 0.0)	0.27 ± 3.30 (−4.79–5.92)	1	12

Figure 2.

Mean (solid), fifth, and 95th percentile (dotted) of standardized coefficients (black) and VIP values (blue) by wavelengths for PLSR-models predicting assimilation (A), transpiration (B), stomatal conductance (C), intercellular CO₂ concentration (D), instantaneous water-use efficiency (E), intrinsic water-use efficiency (F), leaf temperature (G), leaf chlorophyll concentration (H), leaf water potential (I), leaf osmotic potential (J), leaf osmotic potential at full turgor (K), relative water content (L), succlence (M), specific leaf area (N), and total stomatal density (O) for detection of drought in maize.

The most optimal leaf chlorophyll concentration, quantified using a Soil Plant Analysis Development (SPAD), (Chl_SPAD) PLSR model used the 600- to 900-nm spectral region, and cross-validated models estimated chlorophyll concentration well (Fig. 1H; Table 1; Supplemental Table S1). Similar to gas-exchange traits, Chl_SPAD standardized coefficients, and VIP values were most pronounced in the 650- to 750-nm spectral region (Fig. 2H).

The best-model performance for leaf water potential (Ψ_w) was found using the spectral full range (400 to 2,400 nm), whereas best-model performance for leaf osmotic potential (Ψ_π) and leaf osmotic potential at full turgor (Ψ_π100) utilized the wavelength range 1,400 to 2,400 nm. Cross-validated models predicting Ψ_w, Ψ_π, and Ψ_π100 preformed reasonably (Fig. 1, I, J, and K; Table 1). Standardized coefficients and VIP profiles for Ψ_w were relatively flat, showing some peaks at ∼600, 1,500, and 1,900 nm, whereas Ψ_π and Ψ_π100 were more variable, with important wavelengths at ∼1,900 nm (Fig. 2, I, J, and K). Final models for relative water content (RWC) and succulence (Suc) utilized the 950- to 2,400-nm region (Supplemental Table S1). Predictive models accurately characterized RWC and Suc (Fig. 1, L and M; Table 1). Both RWC and Suc standardized coefficients and VIP values were most pronounced in the 1,350- to 1,500-nm and 1,900- to 2,100-nm spectral regions (Fig. 2, L and M). There was no relationship between the estimation of Ψ_π100 calculated using either observed or predicted values of Ψ_π and RWC (r = 0.11, P = 0.40, and n = 61). No field measurements were collected for Ψ_π100, RWC or Suc; therefore, models were developed only from greenhouse-collected data.

Specific leaf area (SLA) was accurately predicted with a PLSR model that utilized wavelengths from 1,400 to 2,400 nm (Supplemental Table S1). Cross-validated models estimated SLA very accurately (Fig. 1N; Table 1). SLA-standardized coefficients and VIP values highlighted important wavelengths at ∼1,500 nm, from 1,850 to 2,050 nm, and ∼ 2,280 nm (Fig. 2N).

The best performance for the total (sum of abaxial and adaxial surfaces) stomatal density (TSD) model was found using the wavelength range 1,400 to 1,800 nm (Supplemental Table S1) and cross-validated models yielded suboptimal estimations (Fig. 1O; Table 1;). TSD-standardized coefficients and VIP values were highly variable throughout the whole spectral range used (Fig. 2O). No field measurements were collected for TSD; therefore, models consisted only of data from the greenhouse. Best models for abaxial and adaxial stomatal density were less accurate than TSD (average R²: 0.17 and 0.10, respectively, using the 1,400- to 1,800-nm range).

Averaged fit statistics (R², root mean square error [RMSE], bias, and normalized root-mean-square error [NRMSE]) for external validations were similar to those registered for cross validation for A, E, g_s, C_i, WUE_i, WUE_in, T_l, Suc, SLA, and TSD, whereas they were slightly lower for Chl_SPAD (R²: 0.61 versus 0.44 for cross- and external validation, respectively), Ψ_w (R²: 0.63 versus 0.40), Ψ_π (R²: 0.60 versus 0.34), Ψ_π100 (R²: 0.53 versus 0.40), and RWC (R²: 0.90 versus 0.65; Table 2).

Table 2. Model performance statistics for external validation.

Averaged R², RMSE, and NRMSE (%) for external validation data generated via regression analysis using 500 random permutations of the data for models predicting leaf traits from maize spectra.

Trait	R2	RMSE	Bias	NRMSE
A (µmol CO2 m−2 s−1)	0.86	6.96	0.70	13
E (mmol water m−2 s−1)	0.89	1.39	0.33	13
gs (mol water m−2 s−1)	0.79	0.08	0.02	15
Ci (µmol mol−1)	0.52	49.54	−11.32	15
WUEi (µmol CO2 mmol−1 water)	0.76	0.77	−0.13	11
WUEin (µmol CO2 mmol−1 water)	0.55	24.54	0.97	15
Tl (°C)	0.79	1.06	0.15	18
ChlSPAD	0.44	2.99	−0.15	17
Ψw (−MPa)	0.40	0.25	0.00	20
Ψπ (−MPa)	0.34	0.10	−0.02	21
Ψπ100 (−MPa)	0.40	0.07	0.00	16
RWC (%)	0.65	6.28	0.80	15
Suc (g g−1)	0.74	0.36	−0.04	14
SLA (cm2 g−1)	0.77	19.87	−0.88	12
TSD (mm−2)	0.37	22.37	−14.87	22

Using A, Ψ_w, Ψ_π, and SLA as testing traits, the performances of models built that included field and greenhouse data or only greenhouse data were comparable for calibration and cross validation (Supplemental Table S1). For external validation, the performance of the models built using greenhouse and field samples was similar whether validations were performed using a dataset containing both greenhouse and field samples (as reported above;, Table 2) or on field samples only, with the exception of A (R²: A, 0.86 versus 0.31; Ψ_w, 0.40 versus 0.41; Ψ_π, 0.34 versus 0.34; and SLA, 0.77 versus 0.69). However, predictions generated from a data set containing only field samples were dramatically compromised if using coefficients from models built from greenhouse data only, with the exception of Ψ_π, which was slightly stronger (R²: A, 0.31 versus 0.00; Ψ_w, 0.41 versus 0.07; Ψ_π, 0.34 versus 0.46; and SLA, 0.69 versus 0.35).

For all leaf traits, modeling performance of Lasso using the full spectral range (400–2400 nm) was lower or comparable to PLSR. Using A, g_s, C_i, and Ψ_π as testing traits, the Lasso modeling performance decreased when using the smaller spectral regions from the final PLSR modeling (Supplemental Table S2).

Correlations among Leaf Traits and Leaf Traits with Spectral Indices

Similar correlations were found either using greenhouse samples only or both greenhouse and field samples together (Supplemental Tables S3 and S4). All significant and strong correlations (P < 0.05, r > 0.4) among leaf traits of greenhouse samples using reference values were confirmed by using the predicted values, except RWC with T_l and Ψ_π100, where the relationships between reference and predicted data did not hold. We found significant and strong correlations among reference and predicted field data, with the exception of some correlations related with Ψ_w and Ψ_π (Ψ_w with T_l and Ψ_π; Ψ_π with SLA). Overall, we found more and stronger correlations using predicted data than when using reference measurements (Supplemental Tables S3 and S4). Using the reference values only, few significant correlations found in the greenhouse were confirmed in the field (A with E and g_s, E with g_s, C_i with WUE_in, WUE_i with T_l, and Ψ_w and Ψ_π; Supplemental Table S3).

Using reference values, greenhouse measurements of A were positively related with the normalized differential vegetation index (NDVI) and a scaled photochemical reflection index (sPRI, r of 0.41 and 0.52, respectively, P < 0.05, n = 155), but not the normalized differential water index (NDWI, r of 0.24, P > 0.05, and n = 155). Using reference measurements collected in the field, however, A was not related with NDVI, sPRI, or NDWI (r of 0.18, −0.25, and 0.05, P > 0.05 n = 36). Greenhouse reference values of RWC, Suc, and Ψ_w were positively related to NDWI; although statistically significant, the relationships for all three variables with NDWI were weak (r of 0.22, 0.26, and 0.17, respectively; P < 0.05; n = 173 for RWC and Suc; and n = 169 for Ψ_w).

Leaf Trait Responses under Different Drought Conditions

A three-way ANOVA, including yield stability, water treatment, and stage (Table 3) revealed that Suc and SLA were generally higher (4%) in genotypes with high yield stability. No other traits were significant for yield stability (Supplemental Fig. S1). We found significant water treatment effects for all leaf traits except WUE_in, T_l, and TSD (Table 3). In general, A, E, g_s, WUE_i, Chl_SPAD, Ψ_w, and RWC decreased under mild drought (MD; −75%, −75%, −79%, −22%, −5%, −45%, and −10%, respectively), and even more under severe drought (SD; −86%, −85%, −88%, −32%, −12%, −64%, and −20%, respectively). Overall, Ψ_π and Suc decreased ∼12% and 6%, respectively, and C_i increased ∼65% under MD and SD. Ψ_π100 and SLA increased only under SD (+11% and +9%, respectively, Supplemental Fig. S1). We also found significant stage effects for all leaf traits except Ψ_w (Table 3), with A, E, g_s, WUE_i, WUE_in, Chl_SPAD, Ψ_π, RWC, Suc, and SLA generally decreasing (−39%, −30%, −35%, −38%, −25%, −2%, −5%, −12%, −24%, and −16%, respectively) and C_i, T_l, Ψ_π100, and TSD increasing (+85%, +13%, +9%, and +14%, respectively) at the later V10 developmental stage (Supplemental Fig. S1). The magnitude of response, however, varied across water treatments and was different for different genotypes.

Table 3. P values of three-way ANOVA for the effects of yield stability under drought (Ys), water treatment (W), stage (S), and their interactions on observed leaf traits of maize.

Significant values (P < 0.05) are shown in bold. df, Degrees of freedom.

Trait	df	A	E	gs	Ci	WUEi	WUEin	Tl	ChlSPAD	Ψw	Ψπ	Ψπ100	RWC	Suc	SLA	TSD
Ys	1	0.141	0.349	0.393	0.652	0.384	0.999	0.449	0.090	0.916	0.124	0.118	0.780	0.023	0.008	0.590
W	2	<0.001	<0.001	<0.001	<0.001	<0.001	0.372	0.743	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.470
S	1	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.022	0.622	0.002	<0.001	<0.001	<0.001	<0.001	<0.001
Ys×W	2	0.226	0.301	0.347	0.788	0.578	0.970	0.778	0.152	0.346	0.648	0.612	0.607	0.610	0.447	0.396
Ys×S	1	0.614	0.668	0.924	0.305	0.383	0.262	0.236	0.071	0.141	0.609	0.326	0.400	0.133	0.644	0.626
W×S	2	<0.001	<0.001	0.002	<0.001	<0.001	<0.001	0.303	0.346	0.002	0.303	<0.001	<0.001	0.690	0.300	0.154
Ys×W×S	2	0.222	0.360	0.424	0.633	0.501	0.673	0.918	<0.001	0.780	0.242	0.397	0.764	0.763	0.574	0.371

We found no significant yield stability × water treatment or yield stability × stage interactions, whereas we found significant water treatment × stage interactions for A, E, g_s, C_i, WUE_i, WUE_in, Ψ_w, Ψ_π100, and RWC (Table 3). Early in development (V6), A, E, and g_s were decreased more under SD than under MD, whereas at the later (V10) stage, the effects were similar under MD and SD. A similar behavior was observed for Ψ_w, which had the lowest values at the first developmental stage under SD. C_i and WUE_i decreased under water deprivation only at the V10, and the degree of effect of the stress was similar in both MD and SD treatments. WUE_in was increased in MD and SD plants at the first developmental stage but decreased in both treatments at the second developmental stage. Ψ_π100 increased in V10 plants under SD. The decrease of RWC was greater under SD than MD only at the V10 stage (Supplemental Fig. S1). Only Chl_SPAD showed a significant yield stability × water treatment × stage interaction. Genotypes with high yield stability maintained high Chl_SPAD values under MD at the V6, but not V10, stage (Table 3; Supplemental Fig. S1).

A second three-way ANOVA, including genotype, water treatment, and stage (Table 4), revealed specific genotype characteristics for several traits. For A, E, g_s, and Suc, PI601361 (drought-sensitive) and PI543842 (drought-tolerant) had higher values, whereas PI55936 and PI601438 (both drought-sensitive) had lower values across all water treatments. For Chl_SPAD and TSD, we found higher values in PI6011361 and PI543842 but lower values in Ames27193 (drought-tolerant) across water treatments. When averaged across water treatments, PI6011361 showed higher Ψ_π values that were statistically significantly different from those of Ames27193, PI601438, and PI55935 (drought-tolerant). Ames27193, PI601438, and PI55936 had lower SLA values than PI55935 (Supplemental Fig. S1; Supplemental Table S5). We also found significant genotype × water treatment interactions for A, E, Chl_SPAD, Ψ_w, and Ψ_π100 (Table 4). Under MD, PI6011361 and PI543842 had higher values of A, E, and Chl_SPAD than the other genotypes, whereas no genotypic differences for these traits were observed under SD. PI543842 and PI601438 had a greater decrease in Ψ_w under SD, whereas no genotypic differences were found under MD. Although genotypic differences of Ψ_π100 were found for controls with higher values in PI559936 and PI6011361 and lower values in PI601438 and Ames27193, no differences among genotypes were found under either MD or SD (Supplemental Fig. S1). Significant genotype × stage interactions were found for Chl_SPAD, Ψ_w, SLA, and TSD (Table 4). PI6011361 showed numerically the highest Chl_SPAD values at both stages of analysis, but it was significantly different from only Ames27193 at V6, while it was significantly different from PI55935, PI559936, and PI601438 at V10. At V6, Ames27193 and PI6011361 demonstrated higher Ψ_w values than PI601438, whereas no genotypic differences in Ψ_w were observed at V10. SLA was higher in PI559935 than PI559936, PI601438, and Ames27193, whereas no genotypic differences were observed at V10. No genotypic differences were observed at V6 in terms of TSD, while at V10 only PI601438 and Ames 27193 remained at the levels reported at V6 as all the other genotypes increased (Supplemental Fig. S1). A significant genotype × water treatment × stage interaction was found only for WUE_in and Chl_SPAD (Table 4, Supplemental Fig. S1). PI6011361 (drought-sensitive) and PI559936 (drought-sensitive) were the only genotypes where WUE_in remained high at V10, and specifically so under MD and SD. PI6011361 (drought-sensitive) showed an ability to maintain optimal Chl_SPAD values at V6 under water stress, whereas PI543842 (drought-tolerant) showed this response at V10. The greatest reductions in Chl_SPAD under MD were observed in Ames27193 (drought-tolerant) at V6 and in PI601438 (drought-sensitive) at V10.

Table 4. P values of three-way ANOVA for the effects of genotype (G), water treatment (W), stage (S), and their interactions on observed leaf traits of maize.

Significant values (P < 0.05) are shown in bold. df, Degrees of freedom.

Trait	df	A	E	gs	Ci	WUEi	WUEin	Tl	ChlSPAD	Ψw	Ψπ	Ψπ100	RWC	Suc	SLA	TSD
G	5	<0.001	<0.001	<0.001	0.553	0.455	0.562	0.794	<0.001	0.157	0.003	0.431	0.026	<0.001	0.001	<0.001
W	2	<0.001	<0.001	<0.001	<0.001	<0.001	0.375	0.764	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.293
S	1	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.009	0.761	0.002	<0.001	<0.001	<0.001	<0.001	<0.001
G×W	10	0.008	0.032	0.081	0.255	0.159	0.221	0.909	0.008	0.049	0.272	0.023	0.410	0.446	0.253	0.752
G×S	5	0.080	0.183	0.163	0.602	0.817	0.266	0.786	0.009	0.014	0.570	0.162	0.292	0.196	0.010	0.006
W×S	2	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.359	0.209	0.001	0.208	<0.001	<0.001	0.631	0.274	0.122
G×W×S	10	0.065	0.187	0.326	0.302	0.452	0.046	0.992	<0.001	0.071	0.428	0.657	0.980	0.149	0.322	0.842

DISCUSSION

We describe a nondestructive approach by which plant responses to water availability can be monitored using reflectance spectroscopy. By combining reflectance measurements, standard physiological and anatomical measurements and statistical modeling, we demonstrate the potential of using spectral data to estimate maize leaf traits that often change under drought stress. This documents the potential of spectroscopy to estimate a large number of drought-related leaf features in maize and also highlights the possibility to estimate water potential traits in C4 plants.

Photosynthesis is a key plant process that is affected by drought, primarily through stomatal and mesophyll limitations (Pinheiro and Chaves, 2011). Standard measurements of light- and CO₂-saturated photosynthesis, however, are logistically challenging, potentially taking 20 to 30 min per leaf, as the leaf has to acclimate to the cuvette conditions. Hyperspectral approaches present a rapid alternative to standard reference measurements and have been used previously to estimate photosynthetic activity in plants both indirectly, via xanthophyll cycling (PRI; Gamon et al., 1997; Peñuelas et al., 2011) and directly, by predicting specific traits from spectral data, mainly ribulose bisphosphate, V_cmax, and J_max (e.g. Serbin et al., 2012; Ainsworth et al., 2014, Heckmann et al., 2017; Yendrek et al., 2017).

The spectral region best predicting gas-exchange traits was 500 to 900 nm. This wavelength region contains wavelengths with pigment absorption features (Merzlyak et al., 2003) as well as the red-edge (700 to 750 nm; Mutanga and Skidmore, 2007), a spectral region strongly influenced by chlorophyll content (Filella and Peñuelas, 1994; Clevers et al., 2004; Smith et al., 2004; Zarco-Tejada et al., 2004) and plant stress condition (Smith et al., 2004; Mutanga and Skidmore, 2007; Cotrozzi et al., 2017). The importance of spectral features in this wavelength region for assessing photosynthetic processes has been reported for several plant species (e.g. Gamon et al., 1997; Merzlyak et al., 2003; Serbin et al., 2012; Yendrek et al., 2017). The similarities in wavelength ranges of importance across the different models we report highlight that changes in pigments are important for spectral detection of plant stress (Gamon et al., 1997; Merzlyak et al., 2003). Here we also show that the range of traits estimable (e.g. gas-exchange) can be expanded using spectroscopy to better understand specific physiological responses to water stress.

We found that the most important spectral region for prediction of SPAD-based chlorophyll estimates was 600 to 900 nm. Wavelengths between 700 and 750 showed the highest VIP values reported for predicting SPAD-based chlorophyll, highlighting the stronger relationship between SPAD values and the red-edge, compared with other traits.

A, E, and g_s were well predicted, followed by WUE_i and Chl_SPAD, and then by C_i and WUE_in. These outcomes suggest that physiologically processes derived from calculations of other measurements (i.e. predictions were used in calculation of processes) lost prediction accuracy, compared with processes that were directly predicted (e.g. A, E, g_s). The performance of the model predicting A was confirmed by the strong and positive relation with NDVI and sPRI, two spectral indices related to photosynthetic activity (Gamon et al., 1995, 1997). Using predicted values to calculate WUE_in (WUE_incalc), compared with predicting WUE_in directly, as a test case (WUE_incalc versus WUE_in), the prediction accuracy further decreased when using predicted values to calculate WUE_incalc (i.e. predicted A and g_s) opposed to directly predicting WUE_incalc using spectral data alone. This outcome is likely due to the propagation of error from the individual predictions in the calculations.

Interestingly, we found excellent prediction performance for T_l (R²: 0.89, for cross validation). The capability of reflectance spectroscopy to detect T_l changes has been previously reported across several C3 species exposed to variable air temperatures (e.g. Serbin 2012). The wavelength range utilized by Serbin (2012) included a much larger range (400 to 2,400 nm), contrasted with the narrower range (500 to 900 nm) we utilized. The differences between the two outcomes is likely a consequence of the different treatments utilized in the two studies: temperature opposed to water stress. The ability of photosynthetic and accessory pigments to safely dissipate excess light energy through the xanthophyll cycle (Demmig-Adams and Adams, 1996) likely contributes to the ability of spectral data to accurately predict temperature in this study. A further explanation of the discrepancy between wavelength regions from this study and those from Serbin (2012) is that it is likely due to the different photosynthetic pathways, foliar anatomical structure, and experimental treatments used. Moreover, the SWIR region is strongly sensitive to water content, given the prominent water absorption features in this spectral region (Curran, 1989), and the inclusion of different watering treatments in this study may have altered the influence of this spectral region on predicting leaf temperature, shifting focus on excess energy dissipation via shifts in pigment profiles.

Measurements of water status can be broadly divided into either the amount of leaf water or leaf energy status (Jones, 2007). Reflectance spectroscopy likely utilizes information from both approaches because vegetation reflectance is influenced by the amount of water as well as by the composition and concentration of osmolytes that affect variation in Ψ_π, and ultimately in Ψ_w (Cotrozzi et al., 2017). We found that three spectral regions best predicted the investigated water-related traits. Unexpectedly, Ψ_w, which is currently the most widely used parameter to estimate the water status of plants exposed to drought (González-Fernández et al., 2015), was best predicted using the full spectral range (400 to 2,400 nm). This is in contrast with previous findings (Santos and Kaye, 2009; De Bei et al., 2011; Cotrozzi et al., 2017) that the NIR-SWIR region best predicts Ψ_w. However, Ψ_w is the sum of a number of components, including dissolved solutes (Ψ_π), the pressure potential (Ψ_p, equal to the hydrostatic pressure), and the gravitational potential (Ψ_g, ignorable except in tall trees), and is also influenced by photosynthetic regulation (Jones, 2007). Thus, Ψ_w is the outcome of the coordination of several underlying factors, each of which can potentially interact with spectral regions differently. We feel that the inconsistency among other studies and ours in determining the best spectral region for predicting Ψ_w is likely due to the anatomical differences among C3 and C4 species, photosynthetic pathways, and the severity and range of stress investigated.

For other modeled water-status-related traits, the best predicting models were derived from the spectral region dominated by water content and outside of wavelengths commonly associated with pigments. As we expected, models of RWC and Suc, which are the measurements based on the amount of leaf water, performed better by using the whole NIR-SWIR spectral region. Agreeing with Cotrozzi et al. (2017), standardized coefficients and VIP values effectively highlighted two important water absorption features of the leaf reflectance profile (1,350 to 1,500 and 1,900 to 2,100 nm). The ability of vegetation spectroscopy to estimate RWC in maize has been previously reported, but primarily through the use of spectral indices (Schlemmer et al., 2005; Zygielbaum et al., 2009; Zhang and Zhou, 2015). While we also found statistically significant relationships among RWC, Suc, and Ψ_w with NDWI, a spectral index widely used to estimate plant water content (Gao, 1996), the relationships were weak and had substantially less explanatory power than the PLSR-predicted estimates we generated, likely due to the limited inclusion of spectral data with strong water absorption features. We found that the wavelength region that best predicted Ψ_π and Ψ_π100 was primarily the SWIR region and excluded the minor water absorption features centered at 970 nm and 1200 nm. By eliminating the NIR portion of the spectrum, we potentially amplified the contribution of osmolytes to the prediction of Ψ_π and Ψ_π100 in maize leaves. Multiple studies (Shetty and Gislum, 2011; Rubert-Nason et al., 2013; Asner and Martin, 2015; Ramirez et al., 2015; Cotrozzi et al., 2017) have reported that wavelength regions are important for predicting nonstructural carbohydrates and other foliar osmolytes using spectroscopy alignment, or they at least closely overlap with the more important wavelengths we found for optimal model prediction of Ψ_π and Ψ_π100. This finding suggests that when SWIR data are available, they can provide a more accurate representation of foliar water content than indices alone. Scaling this approach to airborne data, however, may be challenging because of the noise generated by atmospheric water in the spectral region of strong foliar water absorption.

In this study, estimation of Ψ_w was weak for severely drought-stressed plants (Ψ_w < −2.0 MPa), contrary to similar data in live oak reported by Cotrozzi et al. (2017). Given the suboptimal model performance, we encourage caution when interpreting results from a narrow range of values of Ψ_w, Ψ_π, and Ψ_π100. Regardless of this limitation, and considering that measurements of these traits with standard methods (pressure chamber and vapor pressure osmometer) have several constraints in that they are destructive, user-dependent, and point-based (Santos and Kaye, 2009; González-Fernández et al., 2015), we propose spectroscopy as a rapid and nondestructive approach to unbiasedly estimate water, increasing data collection efforts over larger spatial and temporal scales.

Leaf anatomical traits (e.g. leaf thickness and stomatal density) play a pivotal role in plant tolerance to drought (Zhao et al., 2015; Wellstein et al., 2017), yet measurements of these traits are time-consuming and destructive. By using the SWIR region, we observed a strong predictive ability for SLA (R²: 0.83 for cross validation). This outcome was comparable with outcomes reported by Yendrek et al. (2017; R²: 0.68 to 0.78) using spectral data collected from diverse inbred and hybrid lines grown at ambient and elevated ozone concentrations in the field. Standardized coefficients and VIP metrics for SLA highlighted the importance of the wavelengths related to the water content of leaves. As we expected, the weakest predictive ability among the models presented in this study was for stomatal density. For the nature of the trait, we found it difficult to estimate stomatal density from leaf reflectance, as suggested by the variability in the model coefficient and VIP weighting. Stomata are localized only on the epidermal surfaces of leaves, and while the interaction of light with the epidermis contributes to overall reflection profiles, reflectance measurements are also affected by the leaf tissue as a whole, including the palisade and cuticular layers, and this relationship likely impeded stomatal density prediction from spectral data.

An emergent outcome of this study is the advancement of conceptual approaches of chemometric modeling by examining the influence of multiple modeling approaches and different reference measurement collections on model outcomes. Comparing different modeling approaches, we found that performance of PLSR was always higher or comparable with the performance of the Lasso approach. The reason for the higher performance of PLSR than Lasso likely has to do with the trait response being modeled. Responses that contain singular relationships with spectra (e.g. predictors can converge to a few highly important wavelengths, such as pigments) can be modeled after removing a large portion of the spectrum, as done by Lasso through penalizing intercorrelated variables. We also found that Lasso lost prediction accuracy when smaller spectral ranges are used, opposed to starting with full spectrum data. Physiological processes and other phytochemical compounds may need larger portions of the spectrum for successful modeling because the necessary absorption features are contained within numerous and different spectral regions associated with the component parts of these processes. The contributions of smaller coefficients, which are included in PLSR but removed in Lasso, likely improve prediction accuracies in PLSR because they provide related information to the coefficient of absorption features that individually are suboptimal, but cumulatively contribute more than individual wavelengths alone.

Our measurements of spectral and reference measurements from both controlled and field environments revealed three outcomes. First, greenhouse-based models allowed us to capture a greater proportion of trait variation than using only field-grown plants because plants were exposed to a greater and wider range of stress conditions. Second, the prediction accuracy of models built using both greenhouse and very few field measurements was similar with predictions made using spectra on either greenhouse or field samples, as long as the trait values in field samples were within the prediction range of models built using greenhouse collections. Third, the prediction of field responses was dramatically compromised if using predictive models created from spectral data collected from greenhouse-only collections. These outcomes demonstrate that field collections are a necessary compliment to controlled environment studies if the intent is to use models for phenotyping field plant stress responses.

We found that few of the physiological and anatomical traits measured in this study were correlated with yield stability for the specific maize hybrids used in this study. Only the regulation of chlorophyll content, determined as SPAD, varied between genotypes with high or low yield stability conditions. Indeed, we commonly found that a genotype within each drought-sensitivity class (i.e. tolerant or sensitive) exhibited inconsistent physiological responses to water stress. Both drought-sensitive and drought-tolerant genotypes exhibited higher photosynthesis, transpiration rates, and Chl_SPAD under moderate drought stress, and some drought-sensitive genotypes had the lowest Ψ_w values under water stress. We found a significant three-way interaction (yield stability class by water stress by ascension) for only Chl_SPAD and intrinsic water use efficiency with two drought-sensitive genotypes able to maintain this status at optimal levels under water stress at later developmental stages. The lack of a relationship between the traits contributing to a statistically significant response and yield stability is likely due to the speed of the onset of stress and differences in water availability in the containers, compared to field conditions where yield stability was assessed. However, we found that the physiological and anatomical responses measured in the maize hybrids in response to water stress were well predicted using hyperspectral data, as almost all the statistical outputs for the correlations obtained with reference measurements were confirmed in both greenhouse and field samples. This is in agreement with those of others for spectral predictions of maize traits under differential environmental treatments (Yuan et al., 2016, Heckmann et al., 2017; Yendrek et al., 2017).

CONCLUSION

Here we demonstrate that reflectance spectroscopy provides a rapid, nondestructive approach to accurately quantify physiological and anatomical functional traits associated with water relations in maize using a single spectral measurement. Importantly, this suggests that the predictions from spectral data can be used in place of standard reference collections. Moreover, this approach can dramatically increase data collection from a larger number of individual genotypes and plants, in both controlled and field conditions, than reference measurements alone. The increase in data volume collected using hyperspectral data, coupled with similarity in the outcomes of statistical analyses used to measure responses across treatments, should promote the implementation of more complex experimental designs that can provide greater insight into the genetic, environmental, and gene-by-environment interactions that enhance and repress agricultural production. While logistical challenges (e.g. solar angle or atmospheric interference) exist, leaf-level spectroscopy can be effectively used as ground reference or training input for airborne-based platforms and scaled to field and landscape levels (Serbin et al., 2015; Meacham-Hensold et al., 2019, 2020). Our ability to detect crop stress responses may play a pivotal role in precision agriculture and advancing trait-based plant breeding.

MATERIALS AND METHODS

Plant Material and Experimental Design

Greenhouse Experiment

Experiments were conducted in the Purdue University Horticulture Plant Growth Facility (40°25′15″N, 86°54′51″W, 611 m above sea level) in West Lafayette, Indiana. The United States is the world leader in maize (Zea mays) production, and the United States Midwest represents the major maize production region of North America (Araus et al., 2012). Seeds of six maize hybrids with different yield stability responses under drought (drought-tolerant: Ames27193×PHP02, PI543842×PHP02, and PI559935×PHP02; drought-sensitive: PI559936×PHP02, PI6011361×PHP02, and PI601438×PHP02; Supplemental Table S5; M.V. Mickelbart and M.R. Tuinstra, unpublished data) were planted in a growing media containing a mixture of Fafard 52 Mix Metro-Mix 852 RSi (professional growing mix; Sun Gro Horticulture) and Turface Athletics MVP conditioner (PROFILE Products; 2:1 in volume) in 7.5-l black plastic containers. After planting, containers were regularly irrigated to field capacity with a fertilizer mix (400 μL L⁻¹) using 21-5-20 Peters Excel fertilizer (ICL Specialty Fertilizers). The greenhouse day and night mean temperatures were 26°C and 20°C, respectively; and maximum day and night relative humidity were ∼60% and ∼50%, respectively.

After a randomized block design, plants were then assigned to two different sets each composed of 15 seedlings per genotype, and sub-assigned to three different water treatments: irrigated every day to field capacity (well-watered), water withheld for 4 d (MD) before measurements, or water withheld for 9 d before measurements (SD). The water treatments were applied at two developmental stages. Both sets of plants experienced the first episode of different watering regimes, but only the V6-stage leaf of the first set of plants was measured for Stage 1. After the second round of different water treatments, the V10 leaf of the second set of plants was measured for Stage 2. On the sixth or tenth leaf (i.e. the youngest fully expanded leaves at the two stages of analysis) of each plant, we collected measurements in the following order: gas-exchange, leaf greenness, reflectance, and water potential, then leaf portions were collected for the determination of other water status traits and thickness, as well as imprinted slides for stomatal density (for a total of 180 leaf samples; Supplemental Fig. S2). These specific traits were selected because they are commonly investigated to evaluate the effects of drought on plants. All measurements were performed between 10 and 12 h.

Field Experiment

Field activities were conducted at the Agronomy Center for Research and Education of Purdue University (40°28′22″N, 86°59′37″W, 216 m above sea level), West Lafayette, Indiana. The soil type is a Chalmers silty clay loam. Average soil pH, organic matter, exchangeable P, and available K were 5.4, 2.5%, 39 lbs/acre, and 170 lbs/acre, respectively. The previous crop was soybeans (Glycine max). Tillage consisted of deep-ripping the previous fall, and field cultivation in the spring before planting. The same six hybrids used for the greenhouse experiment were planted in a 36-randomized–blocks design (12 × 3, six replications per hybrid). Each block was 5.334-m long and 3.048-m wide with four rows and 0.762-m row spacing. Each row of each block contained ∼25 plants. Planting date was June 1, 2017. All grass and broadleaf weeds in the plot areas were controlled with a pre-emergent residual herbicide Bicep II Magnum (s-metolachlor and atrazine). All maize seeds were treated in a similar manner with Acceleron (Difenoconazole, Fludioxonil, Mefenoxam, and Thiamethoxam). Force 3G (Tefluthrin) was soil-applied at planting to control corn rootworm (Diabrotica virgifera virgifera).

On July 19, 2017, measurements of gas exchange, leaf greenness, reflectance, water and osmotic potentials, and thickness were collected on the ninth leaf (the youngest fully expanded leaf) of the plant located in the center (12th plant of the second row) of each of 36 blocks (36 leaf samples, six leaves per hybrid) from 11 to 16 h, following the same procedure adopted for the greenhouse experiment. Weather data were collected from the Purdue University Indiana State Climate Office at station “ACRE-West Lafayette” (http://www.iclimate.org/). Total precipitation from June 1, 2017 to July 19, 2017 was 257.53 mm, and averaged daily, maximum, and minimum temperatures were 22.7°C, 27.6°C, and 16.3°C, respectively. No supplemental irrigation was applied.

The collection of data in both greenhouse and field environments was performed to achieve the second main goal of this study (i.e. compare the performance of models built using greenhouse-only samples with models that also included field samples) as schematized in Supplemental Figure S3. Further details are reported below.

Gas Exchange and Chlorophyll Content

Net CO₂ A, E, g_s, C_i, and T_l were determined using a LI-6400XT portable photosynthesis system equipped with a 6400-02B LED light source (Li-Cor), operating at 400-μL L⁻¹ CO₂ concentration and saturating light conditions (1,700 μmol m⁻² s⁻¹ photosynthetically active radiation). WUE_i and WUE_in were calculated as A/E and A/g_s, respectively. A SPAD 502 m (Minolta) was used to determine leaf greenness (Chl_SPAD). Three measurements per leaf were made, and the mean of these measurements was recorded.

Collection of Leaf Spectra

Full-range (350 to 2,500 nm) reflectance profiles of maize leaves were collected using a SVC-1024i spectroradiometer (Spectral Vista) with a leaf-clip and an internal halogen light source attached to a plant probe. Integration time (i.e. the length of time that the detectors are allowed to collect photons before passing the accumulated charge to the converter for processing) was set at two seconds. Measurements were made on three and five areas of the leaf adaxial surface for each greenhouse and field leaf, respectively, with one measurement per area, and all measurements were combined to produce an average leaf spectrum. The relative reflectance of each leaf was determined from the measurement of leaf radiance divided by the radiance of a white reference panel internal to the leaf clip, measured every 12 spectral collections.

Water Status and Leaf Thickness

Ψ_w was measured on the distal portion of the leaf (15 to 20 cm) that was cut with a sharp razor blade, inserted into a rubber stopper, and then placed in a Scholander-type pressure chamber (model 600; PMS Instrument), following the precautions suggested by Tiekstra et al. (2000). To determine Ψ_π, a portion of the leaf used for Ψ_w was placed in a mesh insert into a microcentrifuge tube, immersed in liquid nitrogen, and then stored at −20°C until processing. Solute concentration was determined with a vapor pressure osmometer (model no. 5500; Wescor) as reported in Stanton and Mickelbart (2014). RWC and Suc were determined on another portion of the same leaf. Following a standardized procedure (Stanton and Mickelbart, 2014), RWC was calculated as FW-DW/TW-DW, where FW, DW, and TW are fresh, dry, and turgid weights, respectively. Leaf Suc was calculated as FW/DW. The Ψ_π100 was calculated as Ψ_π × RWC.

After determination of TW, the leaf portion used for determining RWC was scanned before drying, and its leaf area was determined using the software ImageJ v.1.38 (National Institutes of Health). SLA was calculated as leaf area/DW.

Stomatal Density

A leaf surface imprint method was used to determine stomatal density (Weng et al., 2012). Abaxial and adaxial epidermal cell outlines of leaves were imprinted onto cyanoacrylate droplets that were placed onto glass slides. Images were taken under 10× magnification using an OptiPhot2 microscope (Nikon). Stomata were counted in an area of 0.474 mm². For each slide, four independent leaf areas were counted and averaged for each biological replicate. TSD was calculated as abaxial SD + adaxial SD.

Model Calibration and Validations

Using both greenhouse and field samples, we generated models to predict leaf traits from untransformed reflectance profiles using PLSR (Wold et al., 2001). When predictor variables are highly correlated, as is the case with hyperspectral data, classical regression techniques can produce unreliable coefficients and error estimates (Grossman et al., 1996). In contrast to standard regression techniques, PLSR reduces a large number of collinear predictor variables into relatively few, uncorrelated latent variables, and has become the preferred method for chemometric approaches (Bolster et al., 1996; Atzberger et al., 2010; Couture et al., 2013, 2016; Cotrozzi et al., 2018). To avoid potential overfitting the PLSR model, the number of latent variables used was based on reduction of the predicted residual sum-of-squares statistic (Chen et al., 2004) using leave-one-out cross validation. Once minimized, the final set of extracted components was combined into a linear model predicting leaf traits based on leaf spectral profiles.

Model performance was evaluated by conducting 500 randomized permutations of the data sets using 80% of the data for calibration (i.e. training) and the remaining 20% for cross validation (i.e. testing) with random resampling for each permutation. Then, for each permutation, we tracked the R², the overall error rate (RMSE), the percentage of error relative to the data range (NRMSE) and bias to assess model performance when applied to the validation data set. These randomized analyses generated a distribution of fit statistics allowing for the assessment of model stability as well as uncertainty in model predictions. We further determined the strength contribution of PLSR loadings by individual wavelengths using the VIP selection statistic. The VIP statistic evaluates the importance of individual wavelengths in explaining the variation in both the response and predictor variables, where larger weightings confer greater value upon the contribution of individual wavelengths to the predictive model (Wold et al., 2001; Chong and Jun, 2005). Using A, Ψ_w, Ψ_π, and SLA as testing traits, we also compared the performance of models built with both greenhouse and field samples and models including only greenhouse data (Supplemental Fig. S3B).

We additionally performed external validation by applying PLSR coefficients on a dataset distinct from the one used for calibration and cross validation, including again both greenhouse and field samples (∼40% of the full dataset). Five-hundred randomized permutations were conducted, and relations between predicted and observed values were tested by regression analysis. Fit statistics (R², RMSE, bias, and NRMSE) were again used to assess model estimation accuracy. Using A, Ψ_w, Ψ_π, and SLA as testing traits, we also compared the estimation efficacy for these traits in field samples between the models built with both greenhouse and field samples and models including only greenhouse data (Supplemental Fig. S3B).

Before building the final models, we developed preliminary models to identify wavelength regions associated with the trait of interest and to identify poorly predicted outliers on either the reference or target measurements. Final wavelength regions included individual wavelengths at 1-nm intervals, thus maintaining high-density spectral information in regions associated with traits, but excluding wavelengths that contribute error to the predictions likely because of lack of absorption features. Prediction residuals were used to identify potential outliers. Spectral data of outliers were further examined for errors, detectable from elevated reflectance in the visible wavelengths or spectral jumps in the NIR region that occur when the leaf clip is not fully closed. Reference data of outliers were also examined for extremes in the data distribution (Couture et al., 2013, 2016; Cotrozzi et al., 2018; Marchica et al., 2019). The same approach was followed to remove outliers from the data set used for external validations. Outliers removed accounted for 12% to 13% of the initial data.

To test another multivariate statistical approach, we also analyzed the same data sets using least absolute shrinkage and selection operator (Lasso; Tibishirani, 1996, 2011). The aim of the Lasso approach is to improve prediction accuracies by minimizing, or shrinking, coefficients to be less than a fixed, upper-bounded value and removes coefficients of intercorrelated variables by setting them to zero, providing variable selection. The same as our PLSR approach, Lasso model performance was evaluated by conducting 500 randomized permutations of the data sets using 80% of the data for calibration and the remaining 20% for cross validation; and for each permutation, we tracked R², RMSE, NRMSE, and bias statistics. The modeling approach and data analyses were performed using the “pls” (Mevik et al., 2016) and “glment” (Friedman et al., 2010) packages in R (www.r-project.org) for PLSR and Lasso, respectively.

Spectral Indices

Some widely used spectral indices thought to be related with plant health and water status were also calculated: PRI, an indicator of photosynthetic radiation use efficiency, (R₅₃₁ − R₅₇₀)/(R₅₃₁ + R₅₇₀); Gamon et al., 1997). To avoid negative values of PRI, values were scaled as sPRI = (PRI + 1)/2 as reported by Letts et al. (2008); NDVI, an indicator of leaf greenness, photosynthetic activity, and plant health (R₇₈₀ − R₅₇₀)/(R₇₈₀ + R₅₇₀); Gamon et al., 1995); and NDWI, an indicator of vegetation liquid water content, (R₈₅₇ − R₁₂₄₁)/(R₈₅₇ + R₁₂₄); Gao, 1996). R_x indicates reflectance at x nm wavelength.

Statistical Analyses

We first determined the effects of yield stability under drought, water treatment, stage, and their interactions on leaf traits of greenhouse samples, by using a three-way ANOVA following the model

Then, we similarly determined the effects of genotype, water treatment, stage, and their interaction on leaf traits of greenhouse samples, using a three-way ANOVA following the model

In these models, μ represents the mean, Ys is yield stability under drought level i, G is genotype level i, W is water treatment level j, S is stage level k, and e_ijk represents the error term.

Relationships among predicted leaf traits from greenhouse, field, or greenhouse-and-field samples were evaluated using Pearson’s correlations. Pearson’s correlations were also used to test the relations among A with NDVI, sPRI, and NDWI, as well as Ψ_w, RWC, and Suc with NDWI. For relationships among A and spectral indexes, data were separated into either greenhouse or field data; for relationships among Ψ_w, RWC, Suc, and NDWI, only greenhouse data were available. Statistical analyses (that included regression analyses for external validations of models) were performed in the program JMP 13.2 (SAS Institute). The normality of data was preliminarily tested by the Shapiro–Wilk W test. Effects with P < 0.05 were considered statistically significant.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Observed leaf traits of six hybrids of maize characterized by different yield stability under drought exposed to different water treatments at different developmental stages.

• Supplemental Figure S2. Experimental scheme of the greenhouse experiment.

• Supplemental Figure S3. Modeling-approach schematic.

• Supplemental Table S1. Metadata and performance of the preliminary PLSR-models used for the estimation of leaf traits by spectral data.

• Supplemental Table S2. Metadata and performance of the Lasso-derived models used for the estimation of leaf traits by spectral data.

• Supplemental Table S3. Pearson’s correlation matrix describing relationships among leaf traits of greenhouse and field samples by observed standard measurements.

• Supplemental Table S4. Pearson’s correlation matrix describing relationships among leaf traits of greenhouse and field samples predicted by PLSR models.

• Supplemental Table S5. Identification and description of hybrids used in this study.