Hyperspectral infrared microscopy with visible light

A microscope with correlated photons reveals infrared images via detection of visible light.

Abstract

Hyperspectral microscopy is an imaging technique that provides spectroscopic information with high spatial resolution. When applied in the relevant wavelength region, such as in the infrared (IR), it can reveal a rich spectral fingerprint across different regions of a sample. Challenges associated with low efficiency and high cost of IR light sources and detector arrays have limited its broad adoption. Here, we introduce a new approach to IR hyperspectral microscopy, where the IR spectral map is obtained with off-the-shelf components built for visible light. The method is based on the nonlinear interference of correlated photons generated via parametric down-conversion. In this proof-of-concept we demonstrate the chemical mapping of a patterned sample, where different areas have distinctive IR spectroscopic fingerprints. The method provides a wide field of view, fast readout, and negligible heat delivered to the sample, which opens prospects for its further development for applications in material and biological studies.

INTRODUCTION

The development of optical metrology techniques in infrared (IR) range is quite active due to the richness of material and molecular signatures that are observable in this spectral range (1–3). Multiple IR spectroscopic instruments are commercially available but are saddled with nonideal light sources, low-efficiency detector arrays, and high cost. This limits the application for hyperspectral IR microscopy, in particular, for dynamic studies of live cells (4, 5).

Typical light sources used for IR absorption spectroscopy are robust, low-cost thermal blackbody emitters. Although their emission band covers the detection range of IR photodetectors, these sources have limited spectral brightness. Applications requiring bright and well-collimated beams, such as wide-field hyperspectral IR microscopy, use light produced by synchrotron light sources (6) or high-power quantum cascade lasers (QCLs) (7). In recent years, the availability of tunable QCL has spawned a resurgent interest in developing new designs for combined IR-visible microscopes, which allow increase in the detection speed (in part justified by the reduced number of frequencies to acquire), high signal-to-noise ratio, and diffraction-limited spatial resolution (8). However, access to synchrotron light is limited and costly, while QCL technology has limitations in terms of cost, reliability, and spectral range/tunability.

There are limitations to light detection with wide-field IR microscopy as well. Currently, arrays of IR point detectors, referred to as focal plane arrays (FPAs), are used. These FPAs face several technical limitations such as cryogenic operation, high noise floor, nonuniform response, low pixel count, and thermal sensitivity (9). They are costly and subjected to stringent end-user controls.

Besides developing easy access and reliable IR light sources and detectors, notable efforts have also been put in improving the spatial resolution of IR spectroscopy. While the development of advanced techniques based on fluorescent probes has allowed breaking the diffraction limit in optical microscopy (10–13), the lower performances of standard IR spectroscopy, with a spatial resolution at best reaching the diffraction limit, have been one major factor preventing a broader adoption in biological studies. More recently, this limitation seems to be overcome thanks to alternative approaches, such as atomic force microscopy (AFM)–based IR spectroscopy, which uses an AFM tip to scan the surface of a sample with spatial resolution in the range of 10 nm. The local detection of the thermal expansion, as a result of the absorption of IR radiation, allows reconstructing an absorption spectrum of the sample (14). A new microscope combining optical microscopy and photothermal IR spectroscopy is one of the promising results shown recently (15). The technique uses illumination of the sample with QCL and measures the thermal expansion of a thin sample (or a tissue section) in a wide-field interferometric arrangement to improve the spatial resolution down to the diffraction limit for the visible light. The only limitation to this approach at this stage might be the lack of broadband-tunable QCLs and the preselection requirement of IR frequencies of laser sources before imaging.

To overcome the existing challenges of IR light sources and detectors, it is possible to use techniques with the detection in the visible range, where conventional complementary metal-oxide semiconductor (CMOS) and charge-coupled device (CCD) technologies are well developed. One such approach is represented by vibrational microspectroscopy techniques based on Raman scattering. However, these techniques are hampered by a relatively low cross section and a fluorescence background, which mask the Raman signal (16). Furthermore, the selection rules for Raman and absorption spectroscopy are different: A given transition may reveal itself in the absorption measurement while showing a weak Raman signal, and vice versa. Hence, the two techniques are complementary to each other.

Another possibility is using nonlinear optical phenomena to transfer the detection of the signal into the visible range. For example, a scheme based on photon up-conversion was demonstrated recently (17). However, it requires the use of an expensive optical parametric oscillator and high-end electron-multiplying CCD (EMCCD) camera. Furthermore, the technique works with a relatively intense flux of up-converted photons, which may damage fragile biological samples.

Here, we propose a measurement method to circumvent the need for IR sources and detectors in hyperspectral wide-field IR microscopy by using quantum optical phenomenon. Our method is based on the concept of the nonlinear interference of correlated photons, also known as induced coherence (18, 19). Two photons are generated in a nonlinear crystal via spontaneous parametric down-conversion (SPDC) with one photon (signal) in the visible range and the correlated photon (idler) in the IR range (20, 21). The crystal is put into an interferometer, where the interference pattern of the detected visible photons carries the information about the IR photons, which are the ones interacting with the sample. Thus, information about the properties of the sample in the IR range is inferred from the measurements of visible-range photons using standard visible light components.

The induced coherence phenomenon has been demonstrated for various applications. Among them is IR phase imaging in a transmission configuration exploiting Mach-Zehnder interferometer (22), but it was limited to a single telecom wavelength and a low spatial resolution. Spectrally tunable optical coherence tomography is also shown, but it used time-consuming point-by-point (raster) scanning. In that experimental scheme, the scan of an area of a few hundred square micrometers at a given frequency took a few hours. Such a long acquisition time does not meet the requirements for imaging live biological objects (23, 24). Multiple experiments have also been performed for IR spectroscopy (25–30), including the cascaded interferometer setup, which, however, did not have imaging capabilities.

In this work, we combine IR absorption spectroscopy and microscopy in a single measurement for the wide-field hyperspectral IR microscopy. Our concept is based on a compact Michelson interferometer configuration, which uses a single crystal, requires a minimum number of optical elements, and allows us to easily set the desired magnification by an advanced built-in imaging system. The method also uses off-the-shelf and inexpensive visible-range laser and a CMOS camera to acquire the IR images of the sample. Next, the hyperspectral microscopy is achieved by tuning the probing wavelengths in the mid-IR range, which is highly relevant to biological imaging, in particular in lipidomics, and material investigation. There are not many suitable lasers and cameras for 3 to 4 μm, yet this range presents interesting absorption features, such as methylene asymmetric stretching and methyl asymmetric stretching. These vibrational features appear in CH-rich lipids.

Here, as a proof-of-concept demonstration, we perform a spectroscopic IR imaging and retrieve the absorption map of a microfabricated sample. The sample contains a spatial pattern with different chemical composition, which is successfully retrieved by our method through interferometric imaging from 2.8 to 3.4 μm. The demonstrated method shows high spatial resolution and fast readout and holds a promise for application in mid-IR hyperspectral microspectroscopy measurements.

RESULTS

Theoretical description

In our setup, the SPDC crystal is put in an imaging Michelson interferometer, where down-converted and pump photons are split according to their frequencies (see Fig. 1). To realize a wide-field imaging configuration, we exploit the natural divergence of the SPDC photons (31, 32). We insert a three-lens system in each arm of the interferometer, which performs the Fourier transformation from a k-space into an x-space (see section S1) (33). The signal and pump photons are reflected by the reference mirror, while the idler photons are reflected by the sample. For the reflected beams, the lenses perform the inverse transformation, so that the spatial modes of the down-converted photons overlap in the crystal (34).

Fig. 1. Experimental setup.

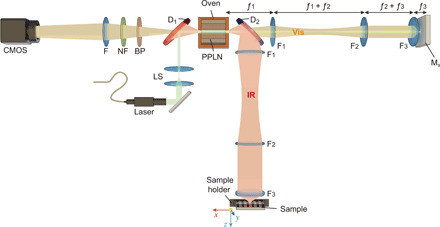
A continuous-wave laser is used as a pump for the PPLN crystal. The laser is injected into the setup by a dichroic beamsplitter D₁. The signal (visible) and idler (IR) photons are generated via SPDC and separated into different channels of the Michelson-type interferometer by the dichroic mirror D₂. The frequencies of the photons are tuned by changing the temperature of the crystal and switching among regions with different poling periods within the same crystal. The identical confocal three-lens systems F₁, F₂, and F₃ in each arm of the interferometer project the k-spectrum of down-converted photons onto the reference mirror and the sample. The pump is reflected back to the crystal and generates other SPDC photons. The state vectors of SPDC photons, generated in the forward and backward passes of the pump through the crystal, interfere. The interference pattern is measured by focusing the signal (using lens F) into a standard CMOS camera preceded by notch and bandpass filters (NF and BP). The measured interference pattern of signal photons depends on the properties of the sample probed by idler photons.

The state vectors of down-converted photons, generated in the forward and backward passes of the pump through the nonlinear crystal, interfere (see section S2). The intensity map of the signal photons, measured in the experiment, is given by (23, 34, 35)

$$I_{\mathrm{s}}\propto 1+\mid \mathrm{\mu }\mid \mid t_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}})\mid \text{cos}({\mathrm{\phi }}_{\mathrm{p}}-{\mathrm{\phi }}_{\mathrm{s}}({\mathrm{\rho }}_{k_{\mathrm{s}}})-{\mathrm{\phi }}_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}}))$$ (1)

where ρ_ks and ρ_ki are polar coordinates of signal and idler wave vectors, respectively; t_i(ρ_ki) is the amplitude transmission for idler photons through the interferometer; μ is the normalized first-order correlation function of SPDC photons (19); and φ_p,s,i are the phases of the pump, signal, and idler photons, respectively. Next, assuming that the interferometer is balanced (|μ| = 1), the visibility of the interference pattern is given by

$$V({\mathrm{\rho }}_{k_{\mathrm{s}}})=\mid t_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}})\mid$$ (2)

Thus, the transmission (absorption) map of the sample in the IR range can be inferred from the visibility of the interference pattern of the visible-range photons. In the experiment, we measure the visibility of the interference pattern by scanning the relative phase φ_i between the interferometer arms by a fine translation of the sample. We tune the frequencies of the photons by changing the temperature of the crystal and switching among regions with different poling periods (36, 37). By capturing interference patterns of signal photons at different frequencies, we perform IR spectroscopic mapping of the sample (see Materials and Methods).

IR microscopy results

First, we study the spatial resolution of our method by using a reflective chromium-coated resolution test target (1951 USAF, Thorlabs). We acquire interference patterns for signal photons at each scanning position of the relative phase φ_i (see section S3). Each pattern is acquired for 500 ms. The wavelengths of the idler and signal photons are set to 3 μm and 647 nm, respectively. Then, we obtain the visibility map from the interference patterns and retrieve the image of the resolution test target with lenses F₃ of different focal lengths (see Materials and Methods). Figure 2 shows the results obtained with f₃ = 25-mm lens. Here, four measurements are stitched together to obtain the full image of the resolution test target. Insets show fragments of the image obtained using lenses f₃ = 15 mm and f₃ = 4 mm. For lenses with focal distances f₃ = 25 mm, f₃ = 15 mm, and f₃ = 4 mm, we obtain spatial resolutions of 78, 50, and 17 μm, respectively. These values are close to the theoretical values given by eq. S3. Hence, by appropriate choice of the magnification optics in interferometer arms, we can set the spatial resolution of the method to meet the requirements of specific applications.

Fig. 2. Imaging of the resolution test target.

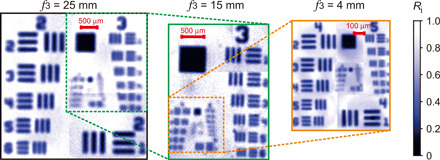
Reflectivity image of the resolution test target measured using lenses F₃ with different focal lengths f₃. The first image corresponds to the f₃ = 25 mm; the insets show results for f₃ = 15 mm and f₃ = 4 mm.

The experimental results reported next are obtained with the lens of f₃ = 15 mm, which provides sufficient resolution for the samples under test. The sample is formed by the layer of SU-8 polymer (epoxy-based negative photoresist) coated on top of a (100) silicon wafer (see Fig. 3A). The thickness of the SU-8 layer is 21 μm (see Materials and Methods). SU-8 is a photosensitive polymer, and its spectral response in the mid-IR range depends on the polymerization condition. For this experiment, we expose the photoresist film to ultraviolet (UV) light (i-line of a Hg arc lamp) through an optical mask with a spatial pattern of rectangles (exposed areas), while the surrounding area is kept nonexposed. The image of the sample under the optical microscope is shown in Fig. 3B. Since SU-8 is transparent in the visible range, the image does not show any variance in the optical properties at different areas of the sample. Note that rectangular edges of the exposed area can be seen due to slight shrinkage of the resist upon reticulation. To avoid the Fabry-Pérot effect inside the SU-8 layer, we place a 400-μm-thick calcium fluoride (CaF₂) window on top of the SU-8.

Fig. 3. Sample.

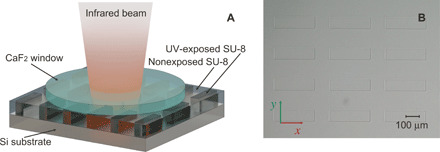
(A) Schematic of the sample. A photosensitive polymer (SU-8) is coated on the silicon substrate. The CaF₂ window is placed on top of the SU-8 polymer to avoid the Fabry-Pérot effect. Ultraviolet (UV)–exposed areas of the sample form rectangles (dark gray), which are surrounded by nonexposed SU-8. (B) Optical microscope image of the SU-8 layer through the CaF₂ window. Rectangles have 300 μm by 80 μm size and distributed in an array with 130- and 160-μm gaps in x and y directions, respectively.

We probe the sample at different wavelengths of idler photons in the range from 2.75 to 3.35 μm with a step of ~25 nm. The correlated wavelengths of detected signal photons are in the range from 663 to 632 nm. The spectral widths of the signal and idler photons are 1.91 ± 0.02 and 42.8 ± 0.5 nm, respectively (see section S4). Examples of the absorption map of the sample at four probing wavelengths are shown in Fig. 4:

Fig. 4. Hyperspectral IR microscopy.

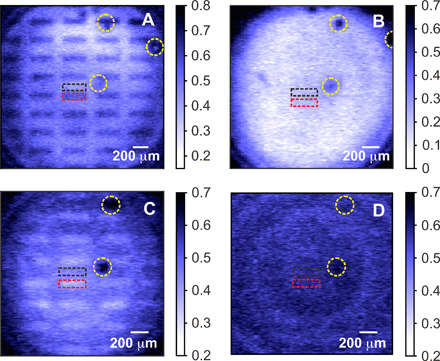
Absorption map of the sample at probe (detected) wavelength of (A) 2.87 μm (653.2 nm), (B) 3.18 μm (638.8 nm), (C) 3.32 μm (633.5 nm), and (D) 3.34 μm (632.8 nm). The contrast between the exposed (rectangles) and nonexposed areas (surroundings) is changing depending on the wavelength of the probing IR photons, due to the difference in the chemical property triggered by UV illumination. The red (black) dashed rectangles show the exposed (nonexposed) areas of SU-8 used for the absorption measurements shown in Fig. 5. The yellow dashed circles highlight the air bubbles between CaF₂ and SU-8 interface, which were used as spatial references.

1. Idler photon at 2.87 μm, signal photon at 653.2 nm. The exposed rectangles show stronger absorption than the surrounding nonexposed area (see Fig. 4A).

2. Idler photon at 3.18 μm, signal photon at 638.8 nm. Low absorption of the sample and there is no distinctive contrast between different areas of the sample (see Fig. 4B).

3. Idler photon at 3.32 μm, signal photon at 633.5 nm. The image inverts, and the exposed rectangles show weaker absorption than the nonexposed area (see Fig. 4C).

4. Idler photon at 3.34 μm, signal photon at 632.8 nm. Strong absorption of the sample and the contrast between different areas of the sample vanishes (see Fig. 4D).

The regions, indicated by yellow dashed circles, are air bubbles formed between calcium fluoride window and SU-8 interface, which are used as spatial references. We set ranges of interest within corresponding areas on the sample (black and red dashed rectangles in Fig. 4) and measure the dependence of the absorption on the wavelength of idler photons. The results are shown in Fig. 5. The dots correspond to our experimental data, and the dashed curves show the Fourier transform IR (FTIR) data obtained for reference samples (38). The FTIR data are normalized and averaged over a bandwidth of idler photons. The two datasets are in good agreement, which validates our method.

Fig. 5. Measured IR absorption spectra.

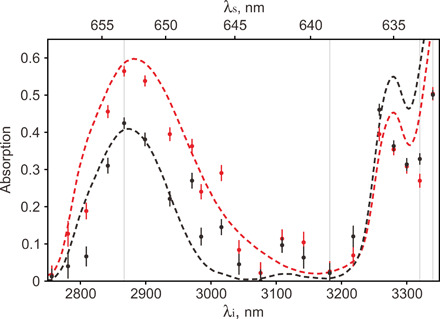
Absorption spectra of SU-8 sample exposed (red curve) and nonexposed (black curve) by UV light. Dots show the experimental results; dashed curves show the FTIR data. Vertical gray lines show the wavelengths, which correspond to images shown in Fig. 4. The bottom abscissa axis corresponds to the wavelengths of the idler probe photons, while the top abscissa axis shows the wavelengths of detected signal photons. The error bars show the SD.

The overall acquisition time for each image at a given wavelength is about 70 s. Thus, it takes about 25 min to collect 21 images in the range from 2.75 to 3.35 μm with a step of 25 nm. This measurement time compares favorably with commercially available FTIR microscopes.

The accuracy of the visibility measurements in our experiments is 0.3%, which translates to the accuracy in the measurements of the absorption within 4%. The spectral resolution in our method is defined by the bandwidth of idler photons and is equal to ~43 nm. As discussed above, the spatial resolution is defined by the parameters of the imaging system and is set at 50 μm.

DISCUSSION

We demonstrated the wide-field hyperspectral IR microscopy using off-the-shelf components designed for visible light. In our measurements, we imaged the absorption pattern of SU-8 photoresist, which was partially exposed to UV light. The wavelength of probing idler photons was tuned across the fingerprint region of the sample, while correlated signal photons were detected using a visible-light CMOS camera. The IR absorption peaks, determined by our method, are consistent with the photoinduced reaction in the sample and with conventional FTIR data.

The spectral resolution of our method is given by the spectral width of the SPDC photons, which is inversely proportional to the length of the nonlinear crystal. The 40-mm-long periodically poled lithium niobate (PPLN) crystals are available off the shelf. With such a crystal, we can (i) enhance the spectral resolution to about 11 nm, which is sufficient for bioimaging, and (ii) reduce the measurement time by at least a factor of 16 due to an increase in the flux of down-converted photons.

We demonstrated the spatial resolution of up to 17 μm with a basic three-lens system, built from off-the-shelf lenses. The resolution can be improved further by designing a specialized imaging module with the provision for compensation of optical aberrations (see eqs. S1 and S3). Our method could also benefit from resolution-enhancing methods, such as structured illumination, which is a subject of ongoing investigations.

The measurement time of our method compares favorably with standard commercial FTIR microscopy systems, which use raster scanning and cryogenically cooled detectors. Although existing FTIR microscopes cover a broader spectral range, we suggest that our method could well find its specific applications while providing benefits of low cost and decent performance. Further steps on setup optimization in terms of spectral resolution, spatial resolution, and measurement time are discussed in detail in section S5.

Our system simplifies IR wide-field imaging while adding a hyperspectral component, wide field, and phase contrast to this useful method. The combination of these three functionalities using the concept of induced coherence has not been demonstrated earlier. This scheme is highly specialized as it provides (i) high optical magnification, which can be easily changed, and (ii) a nearly perfect overlap of the spatial and temporal modes of photons, which is necessary for the observation of interference with high visibility.

The method can also be incorporated into existing optical microscopes, working as an add-on to the systems for bioimaging and material investigation. The interferometric sensitivity of our method enhances the image contrast, which can be highly appealing for biological applications. Moreover, the low intensity of the probing IR beam will allow imaging of a biospecimen without introducing any damage.

The presented range of mid-IR wavelengths can be relevant to biological imaging. In particular, lipids are a major component of cells, and FTIR has been used, for example, to evaluate the bacterial contents in human skin (39). Lipidomics is a field of studies in which IR spectroscopy is already a valuable analytical tool. Combining our instrument with microfluidics opens opportunities for its further applications in live-cell imaging. This work is in progress.

For the prospects of extending the spectral coverage of our method for the far-IR range, crystals, such as silver gallium sulfide AgGaS₂ (AGS) and gallium phosphide (GaP), can be used. They have a broad transparency range of up to ~13 μm, thus comfortably covering the fingerprint region of IR wavelengths.

Next, although the work presented here is in a reflection configuration, the method can be implemented in a transmission configuration by using alternative designs of nonlinear interferometers (22, 40, 41). The method can also be used for polarization-sensitive measurements (42). With this demonstration, a new hyperspectral IR microscopy will be unlocked for practical applications in bioimaging and material analysis. We should also mention the possibility of implementing the method in high gain (43) or stimulated (44, 45) regimes of PDC, which is an exciting topic for further investigations.

MATERIALS AND METHODS

Experimental setup

The experimental setup is shown in Fig. 1. We use a 532-nm continuous-wave laser (Laser Quantum, Torus, 80 mW) as a pump (see Fig. 1). The laser beam is reflected by a dichroic mirror D₁ (Semrock) and then sent into the PPLN crystal (1 mm by 10 mm by 10 mm) (HC Photonics) with three different poling periods of 9.84, 10.28, and 10.73 μm. The crystal is put on the oven, controlled by a temperature controller (temperature range from 40° to 200°C with the stability of ±0.1°C). The oven is mounted on a linear stage to change the poling periods. Using three different periods and temperature tuning, we generate signal photons in the range of λ_s = 663 to 632 nm and idler photons in the range of λ_i = 2.75 to 3.35 μm. The two lens system (LS) before the PPLN crystal form a collimated laser beam with a diameter of 0.8 mm, which fits into the clear aperture of a single poled region in the crystal.

The SPDC photons generated in the crystal are separated into different channels (visible and IR) by a dichroic mirror D₂ (ISP Optics). In each arm of the interferometer, three lenses (uncoated CaF₂ biconvex) are used. Lenses F₁ and F₂ have focal distances of f_1,2 = 100 mm, while lens F₃ has a focal distance of f₃ = 25, 15, or 4 mm, which gives numerical aperture = 0.02, 0.03, and 0.1, respectively, according to eq. S3 for the given pump radius of 0.4 mm. The pump and signal beams are reflected by the mirror M_s, while the sample reflects the idler beam. The sample is mounted onto a motorized XYZ translation stage (Thorlabs), which allows imaging different areas of the sample and to balance the arms of the interferometer. The sample is attached to a piezo stage (Thorlabs), which is used for fine scanning of the relative phase in the interferometer. The signal photons are filtered by a notch and a bandpass interference filter (Semrock). The interference pattern is detected by focusing (f = 150 mm) the signal SPDC photons into the silicon CMOS camera (Thorlabs, DCC1240C).

First, we balance the interferometer arms and then introduce fine phase shifts in the interferometer. At each position of the piezo stage, we capture the phase image of the sample. From the phase images, we infer the interference visibility, which is then used to calculate the absorption of the sample (see section S6). The exposure time for each image is about 500 ms. We make 140 steps to cover the full period of the interference fringe. Thus, the overall acquisition time for each image at a given wavelength is 70 s.

Sample preparation

We prepared our sample via UV lithography. Standard (100) silicon wafer with 50 mm diameter is used as a substrate, where we spin-coat an SU-8 3025 (Microchem, USA) photoresist layer with 21-μm thickness. After the soft baking (1 min at 65°C followed by 10 min at 95°C on hot plates), a periodic pattern of exposed rectangles (300 μm by 80 μm, distributed in a rectangular array with 130- and 160-μm gaps in two directions, respectively) is generated by UV exposure (i-line of a Hg arc lamp, ~200-mJ/cm² power density at 365 nm) using a mask aligner (MJB4, Suss MicroTec, DE) and a soda-lime optical mask. Then, we perform a postexposure baking (5 min at 65°C, followed by 5 min at 95°C). A change in the chemical composition of the exposed polymer occurs during the postexposure baking. The 400-μm-thick CaF₂ cylindrical window is placed on top of the photoresist during the postbake.

Spectroscopic response of the sample

In the range of probing IR wavelengths, the absorption spectrum of SU-8 is defined by the absorption of ─OH molecules and ─C─O─C─ epoxy rings. ─OH groups present a distinctive broad peak of absorption at around 2.84 μm, while the epoxy ring has an absorption peak at 3.32 μm (38). The absorption peaks assigned to ─OH molecules and ─C─O─C─ epoxy rings follow the same behavior and present the characteristic switch of the relative absorption of the exposed and nonexposed SU-8 at 2.87 and 3.32 μm (see Fig. 5). The observed dependence is correlated with the underlying chemical reaction induced by UV exposure. UV photons in the range around the i-line of the Hg arc lamp (340 to 350 nm) are absorbed by the photo-acid contained in the formulation of SU-8 photoresist (triarylsulfonium hexafluoroantimonate salts). This absorption activates the photo-acid through the formation of radical species. During the postexposure baking, the radicals lead to the opening of the epoxy rings of the SU-8 monomers, and the reaction propagates following the scheme of a classic acid-catalyzed cationic reaction that ends with the resin reticulation. This chemical process results in an increase in ─OH molecules and a decrease in epoxy ─C─O─C─ rings in the exposed areas. Thus, the chemical modification induced by UV exposure and postbaking is well reflected in our images shown in Fig. 4.

Measurement of the reflection (absorption)

Measurement of the reflectivity of the resolution test

When the reflective specimen is put in the IR arm, the amplitude transmission of the idler photons through the interferometer is determined by the amplitude reflectivity of the sample ∣t_i(ρ_ki)∣ = ∣r_i(ρ_ki)∣. Thus, from Eq. 2, the ratio of the visibility of the interference patterns with the resolution test target and with the reference gold mirror is determined as

$$\frac{V^{\text{test}}}{V^{\text{Au}}}=\frac{\mid r_{\mathrm{i}}^{\text{test}}\mid }{\mid r_{\mathrm{i}}^{\text{Au}}\mid }$$ (3)

where $r_{\mathrm{i}}^{\text{test}}$ and $r_{\mathrm{i}}^{\text{Au}}$ are the amplitude reflectivity of the resolution test target and a gold mirror, respectively. In this case, the reflectivity of the resolution test target is given by

$$R_{\mathrm{i}}^{\text{test}}={\left(\frac{V^{\text{test}}}{V^{\text{Au}}}\right)}^2{R}_{\mathrm{i}}^{\text{Au}}$$ (4)

where $R_{\mathrm{i}}^{\text{test}}\equiv {\mid r_{\mathrm{i}}^{\text{test}}\mid }^2$ and $R_i^{\text{Au}}\equiv {\mid r_{\mathrm{i}}^{\text{Au}}\mid }^2$ are the intensity reflectivity of the resolution test target and gold mirror, respectively. Note that our reference measurements with a gold reflecting mirror yield the maximum visibility values of 30 ± 0.3%, which is due to losses introduced by uncoated lenses in the three-lens system.

Measurement of the absorptivity of the sample

When the sample under study is inserted into the IR arm, the amplitude transmission of the idler photons through the interferometer is given by ∣t_i(ρ_ki)∣ = ∣τ_i(ρ_ki)∣²∣r_i(ρ_ki)∣, where τ_i(ρ_ki) is the amplitude transmission of idler photons through the sample (single pass) and r_i(ρ_ki) is the amplitude reflectivity of one of the interfaces inside the sample. The amplitude transmission coefficient of the sample ∣τ_i(ρ_ki)∣ is defined by (i) reflection from the air-CaF₂ surface $\sqrt{1-{\mid r_{\mathrm{i}}^{\text{CaF}2}\mid }^2}$, (ii) reflection from the CaF₂–SU-8 interface $\sqrt{1-{\mid r_{\mathrm{i}}^{\text{CaF}2-\text{SU}‐8}\mid }^2}$, and (iii) transmission of the idler photons through the SU-8 $\mid {\mathrm{\tau }}_{\mathrm{i}}^{\text{SU}-8}\mid$

$$\mid {\mathrm{\tau }}_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}})\mid =\sqrt{1-{\mid r_{\mathrm{i}}^{\text{CaF}2}\mid }^2}\sqrt{1-{\mid r_{\mathrm{i}}^{\text{CaF}2-\text{SU}‐8}\mid }^2}\mid {\mathrm{\tau }}_{\mathrm{i}}^{\text{SU}‐8}\mid$$ (5)

The reflection from the back surface is determined by the reflection of idler photons at the Si–SU-8 interface $\mid r_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}})\mid =\mid r_{\mathrm{i}}^{\text{Si}‐\text{SU}‐8}\mid$.

Taking into account Eq. 2, the ratio of the visibility of the interference pattern with the sample under study V^sample and the reference V^Au is given by

$$\frac{V^{\text{sample}}}{V^{\text{Au}}}=\frac{{\mid {\mathrm{\tau }}_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}})\mid }^2\mid r_{\mathrm{i}}({\mathrm{\rho }}_{k_{\mathrm{i}}})\mid }{\mid r_{\mathrm{i}}^{\text{Au}}\mid }=(1-R_{\mathrm{i}}^{\text{CaF}2})(1-R_{\mathrm{i}}^{\text{CaF}2-\text{SU}‐8})T_{\mathrm{i}}^{\text{SU}‐8}\frac{\mid r_{\mathrm{i}}^{\text{Si}‐\text{SU}‐8}\mid }{\mid r_{\mathrm{i}}^{\text{Au}}\mid }$$ (6)

where R_i ≡ ∣r_i∣² and T_i ≡ ∣τ_i∣² are the intensity reflection and transmission of the materials, respectively. The measured visibility maps with the sample are shown in section S6.

From Eq. 6, the transmission through the SU-8 photoresist is determined as

$$T_{\mathrm{i}}^{\text{SU}‐8}=\frac{V^{\text{sample}}}{V^{\text{Au}}}\frac{\mid r_{\mathrm{i}}^{\text{Au}}\mid }{\mid r_{\mathrm{i}}^{\text{Si}‐\text{SU}‐8}\mid }\frac{1}{(1-R_{\mathrm{i}}^{\text{CaF}2})(1-R_{\mathrm{i}}^{\text{CaF}2-\text{SU}‐8})}$$ (7)

Using the Fresnel equations (46) and values of the refractive indices of the sample’s components at the wavelength of 3 μm (47–49), we set the reflection from the air-CaF₂ surface at $R_{\mathrm{i}}^{\text{CaF}2}={\mid r_{\mathrm{i}}^{\text{CaF}2}\mid }^2=0.03$, the reflection from the CaF₂–SU-8 interface at $R_{\mathrm{i}}^{\text{CaF}2‐\text{SU}‐8}={\mid r_{\mathrm{i}}^{\text{CaF}2‐\text{SU}‐8}\mid }^2=0.003$, the reflection from the Si–SU-8 interface at $\mid r_{\mathrm{i}}^{\text{Si}‐\text{SU}‐8}\mid =0.371$, and the reflectivity of the gold mirror at $\mid r_{\mathrm{i}}^{\text{Au}}\mid =0.99$. Then, we determine the absorption of the SU-8 as

$$A_{\mathrm{i}}^{\text{SU}‐8}=1-T_{\mathrm{i}}^{\text{SU}‐8}=1-2.76\frac{V^m}{V^{\text{Au}}}$$ (8)

Here, we neglect the wavelength dependence of the refractive index, its small difference between exposed and nonexposed areas of SU-8, and losses in CaF₂ window.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/44/eabd0460/DC1