Abstract
Diffusion coefficient is one the most effective factors in mass transfer calculation, which plays an important role in study at the molecular scale. In this study, Material Studio software was used to simulate the diffusion coefficient of methane in water through molecular dynamics. COMPASS force field was also used for optimization of atomic structures of methane and water, and Group-Based method was applied to model to calculate both van der Waals and electrostatic forces. In addition, Universal force field was used to optimize of amorphous cell, while Ewald and Atom-Based methods were applied for modeling and calculation of van der Waals and electrostatic potential energy at constant temperatures. The simulation duration for equilibrium of amorphous cell in both state of NVT and NVE was assumed 5ps. The impact of temperature as well as concentration on diffusion coefficient were investigated and results showed that the diffusion coefficient had linear relationship with temperature and third-degree polynomial relationship with concentration. As a result, of the simulation, the diffusion coefficient function versus temperature and concentration was developed.
Keywords: Chemical engineering, Mechanical engineering, Organic chemistry, Petroleum engineering, Theoretical chemistry, Diffusion coefficient, Methane, Molecular dynamics simulation
Chemical engineering; Mechanical engineering; Organic chemistry; Petroleum engineering; Theoretical chemistry; Diffusion coefficient, Methane, Molecular dynamics simulation.
1. Introduction
The diffusion coefficient in liquids is an important parameter to discover not only the mechanism of complicated mass transfer phenomenon but also to design different types of separation columns such as distillation and adsorption column [1]. In particular, the infinite dilution diffusion coefficient of solute (component 1) in solvent (component 2) abbreviated as D12, is one of the most important transport features in velocity-controlled processes [2, 3, 4]. The diffusion coefficient for a particular chemical system can be obtained experimentally but the procedure comes at a huge cost and takes a lot of time as well. There are a number of models calculating the diffusion coefficient in liquids, neither of which has the ability to predict the diffusion coefficient of systems containing only one liquid component [5]. Most of the presented models are based on the Stokes-Einstein model [6]. In 2002, Kooijman developed a model based on Stokes-Einstein theory that reduced the error by 10% [7]. The quality of a model is measured by comparison with experimental values; the lower difference between the predicted and the experimental values, the better accuracy of the model. In recent years, due to costly prolonged procedure of experimental data acquiring and significant error of presented models, the calculation of diffusion coefficient using molecular dynamics simulation has attracted much attention. The experimental molecular diffusion coefficients in studies are slightly different from the results of simulation with molecular dynamics, which can be due to distinct in the samples and the corresponding methods [8, 9]. Kang et al. reported methane diffusion coefficient in kaolinite [10] as an example of the difference.
Gao et al. [11] used the Materials Studio software package to simulate the adsorption and diffusion of Nitrogen, Methane, Water and Carbon Dioxide into micropores of lignite in which Einstein equation was used to calculate the diffusion coefficient. In this study, the Ewald Group-basedmethod with accuracy of 0.001 kcal/mol was used to calculate the electrostatic potential, while the Atom-based summation method with the cutoff truncation of 1.25 nm used for van der Waals interactions as well.
In addition, in the study of JingHua Tan et al. [12], the diffusion and adsorption process of five gases N2, H2, CH4, CO2 and O2 in hydrogenated nitrile butadiene rubber (HNBR) and ethylene-propylene-diene rubber (EPDM) were simulated by Molecular Dynamics Simulation. The diffusion coefficients of all gases except CO2 in HNBR and EPDM molecules are related to the diameter of effective diffusion. Because of linearity, CO2the lowest diffusion coefficient. Also, the interaction between CO2 and HNBR increases the coherence between the chains due to the presence of –CN polar groups in the HNBR chains and shows a lower diffusion coefficient range than EPDM.
The dependence of molecular diffusion coefficient on mass transfer operations is often underestimated, while this factor plays an important role in the transfer study of gases into liquids. Khalifi et al. [13] investigated the effect of different concentrations of Ethane on the molecular diffusion coefficient of this gas in liquid Toluene. The results proved that there is a significant dependence on the concentration of the gas in the liquid mixture. They used the obtained data to investigate the dependence impact of molecular diffusion coefficient on concentration in mass transfer of ethane in toluene. Findings also revealed that the assumption of a constant diffusion coefficient introduces 10%–60% error in calculation of diffusional mass transfer flux in the ethane-toluene system.
The purpose of the study is to investigate the accuracy and possibility of using molecular dynamics simulation to calculate the molecular diffusion of methane in water, as well as comparing experimental and simulated results by molecular dynamics. Moreover, the impact of temperature and concentration on the molecular diffusion coefficient was investigated to find an appropriate equation.
2. Models and method
Application of computational methods using computer simulation has had a significant effect on our awareness about Nano-fluids behavior and the physical phenomena occurring on molecular scale. In addition, when it is not possible to conduct laboratory tests in some cases, computer simulations can be used instead. Molecular dynamics is one of the computer simulation techniques that is based on the interaction between atoms and molecules. It solves the Newton's equations of motion for particles using the theory of atomic motion in a period of time to measure their pathway, while the particles force field and potential energy is determined by applying atomic potential or molecular mechanics force field [14, 15, 16, 17, 18]. Also, molecular dynamics can give us a physical data set, such as diffusion coefficient, viscosity, adsorption, etc. [19, 20].
In this study, diffusion process of methane in water was simulated by Molecular Dynamics Simulation method at different temperature and concentration. Materials Studio software was used for molecular dynamics simulation to calculate the molecular diffusion coefficient of methane in water. Initially, the structure energy of water and methane molecules were optimized before production of cells, and an optimized structure was used for molecular simulation and diffusion. The COMPASS1 force field was applied for optimization of water and methane atoms. A Group-Based integration method was used to model and calculate the potential energy of van der Waals and electrostatic energy. Having formed the structure of water and methane atoms, the Universal force field was used to optimize the amorphous cells. In addition, Ewald and Atom-Based integration method were applied for modeling and calculation of the electrostatic and van der Waals energy potential at constant temperatures. In a study done by Zhaoal [21]. about the impact of system resizing by changing amorphous cell dimensions in three different size of 30, 50 and 70 , it was concluded that the dimensions had negligible effect on predicting the diffusion coefficient. One molecule of methane in 1000 molecules of water for a concentration of 0.1 wt% was used to make the amorphous cell. Besides, the cell was optimized in the temperature range of 290–500 K. In Table 1, the number of CH4 and H2O molecules and the resulting concentration is shown in each cell dimension. For example, amorphous cell dimension for weight fraction of 0.1% was assumed as 3.11 nm × 3.11 nm × 3.11 nm.
Table 1.
Characteristics of Amorphous cell.
| C (ppm) | H2O | CH4 | a×b×c (nm) |
|---|---|---|---|
| 300 | 3333 | 1 | 4.64×4.64×4.64 |
| 400 | 2500 | 1 | 4.21×4.21×4.21 |
| 500 | 2000 | 1 | 3.91×3.91×3.91 |
| 1000 | 1000 | 1 | 3.11×3.11×3.11 |
| 1500 | 677 | 1 | 2.73×2.73×2.73 |
| 2000 | 500 | 1 | 2.47×2.47×2.47 |
| 2500 | 400 | 1 | 2.29×2.29×2.29 |
In order to reach the equilibrium state, Canonical ensemble (NVT) was initially applied for 5 ps on system. Chemical potential (μ), volume (V) and temperature (T) are were considered as constant amounts during the simulation and it is assumed that the framework is in contact with a tank by infinite temperature and pressure [22, 23]. Finally, Micro-Canonical ensemble (NVE) was applied on system at temperatures of 293, 298, 303.05, 308.25, 315.75 and 320 K adjusted by Langevin thermostat for 5 ps to reach the equilibrium [24, 25]. The application of the NVE ensures that dynamic properties such as scattering coefficients are not biased by the system-wide algorithms used to generate a constant temperature set [26, 27]. To calculate the diffusion coefficient according to Eq. (1) in which there is a linear relationship between MSD and time, Mean Square Displacement abbreviated as MSD was used [28]:
| (1) |
Where is the number of dispersed atoms in system and ri(t) is the displacement vector of the i molecule at time of t. MSD diagram versus time can be drawn to calculate diffusion coefficient by plotting the best line (y = a×x + b) passes through the points. Diffusion coefficient can be obtained by Eq. (2) [29]:
| (2) |
2.1. Force field and model validation
The simulation results compared with reported experimental data by Witherspoon and Saraf [30] who measured diffusion coefficient of methane in water at 298, 305.25 and 315.74 K (Table 2). Firstly, the diffusion coefficient of methane in water was simulated at these temperatures, then, the accuracy of method was confirmed by comparison of obtained result- (cm2/s)- with experimental data- (cm2/s)- in Eq. (3).
| (3) |
Table 2.
Reported diffusion coefficient of methane in water at 298, 305.25 and 315.74 K [30].
| T(k) | (cm2/s)×105 | (cm2/s)×105 | Error (%) (MD) | (cm2/s)×105 | Error (%) (WC) |
|---|---|---|---|---|---|
| 298 | 1.880.01 | 1.90013 | -1.7 | 1.8489 | 1.65 |
| 308.25 | 2.120.03 | 2.11698 | 0.142 | 2.3786 | -12.19 |
| 315.75 | 2.41 | 2.38968 | 0.843 | 2.80776 | -16.504 |
In addition, comparison of and revealed the reported force field data and that were significant in the model and could be used to measure temperature and concentration effects.
Moreover, in order to validate the accuracy of simulation result, calculation of theoretical diffusion coefficient was implemented by Wilke-Chang equation [31]. This equation was used to calculate the diffusivity of CH4 and H2O [32]. Eq. (4) shows the Wilke-Chang equation.
| (4) |
MB: Molecular Weight of solvent B (kg/kmol)
= Viscosity of solvent B (kg/ms)
VA = Molar Volume of solute at the boiling point (m3/kmol)
= Association parameter for solvent, 2.26 for water
T = Temperature of system (K)
A comparison between experimental and simulated data, as well as theoretical results can be made from Table 2 and Figure 1. The MD simulation results are closer to experimental data.
Figure 1.
Diffusion coefficient of methane in water versus temperature with a concentration of 1000 ppm.
Figure 2 shows the line graphs for MSD versus time at four distinct temperatures of 293 K, 303.05 K, 308.25 K and 315.75 K regarding the procedure that Masiren et al. and Gautieri have already described in which line graphs of MSD versus time were used for calculation of diffusion coefficient [18, 33]. Thus, according to Figure 2, linear increase in the slope of MSD graphs versus time [34] indicates a rise in temperature as well [18]. The more temperature rises, the size of the box increases and make the atoms move faster. Zhao et al. [21] conducted a research on the diffusion of methane in supercritical water at the temperature of 673–973 K and the pressure of 250 atm. As the temperature increased, the slope of the MSD line increased and they found that the MSD graph fluctuated more at higher temperatures although there is no change in the tendency to be linear.
Figure 2.
Prediction of diffusion coefficient graph for methane in water at 293 K, 303.05 K, 308.25 K and 315.75 K.
2.2. Effect of temperature on diffusion coefficient of methane in water
One of the basic equations to determine the diffusion coefficient of gas in liquids is the Stokes-Einstein equation [35] According to which, the diffusion coefficient is directly proportional to the absolute temperature:
| (5) |
As the temperature increases, the mean kinetic energy of the gas molecules increases, which leads to a rise in the velocity of the molecules. The more speed enhances, collision between the molecules and better diffusion as a result is more likely to happen. Khane Athar et al. [36] calculated the diffusion coefficient of propane gas in heavy oil at high temperatures. In this study, the diffusion coefficient increased linearly with rise in temperature. In the heating process, the viscosity of the heavy oil reduces, which causes an enhancement on the diffusion coefficient of propane in the heavy oil based on the Stokes-Einstein equation.
In addition to a similar result reported for methane diffusion [9], Molecular motion of gas enhances by rising the temperature and causes an increase in diffusion coefficient as well [10]. Figure 3 shows the impact of temperature on diffusion coefficient of methane in water at constant concentration. It has been proved that the diffusion coefficient linearly increases at higher temperatures with regard to Eq. (6):
| (6) |
Figure 3.
Diffusion coefficient of methane in water versus temperature at constant weight percent of methane (0.1%).
Furthermore, Vasileios et al. [37] predicted the diffusion of methane into water. At a pressure of 0.1 MPa and the temperature range of 273–360 K, the diffusion coefficient increased linearly. while at pressures of 5 and 20 MPa and higher temperatures, the linear mode changed to the curved graph. Mr. Zhao et al. [21] have also achieved similar results in the temperature range of 673–973 K and pressures of 250, 265 and 280 atm.
In addition, the given Figure 4 is the illustration of diffusion coefficient of methane in water as a function of temperature at a constant pressure of 100 kPa, and there is a comparison between experimental and simulated data [30, 38, 39, 40]. In all cases, the diffusion coefficients increase with rise in temperature for liquid soluble gases [4]. Figure 4 also shows that the Universal force field provides an appropriate agreement between the experimental data and simulation results for the studied systems and conditions.
Figure 4.
Diffusion coefficient of methane in water versus temperature at constant pressure of 100 kPa.
2.3. Effect of concentration on diffusion coefficient of methane in water
Although methane concentration has complicated impact on diffusion coefficient, investigation of its reliance is a key factor for understanding the mechanism of diffusion phenomena through modeling [36]. Figure 5 indicates the influence of concentration on diffusion coefficient at constant temperature of 298 K. Having increased the concentration from 300 ppm to 1000 ppm, diffusion coefficient initially reduced while it enhanced from 1000 ppm to 2500 ppm. Therefore, diffusion coefficient of methane in water has a minimum value at 1000 ppm and this fact has been discussed in several researches [41, 42]. Moreover, Eq. (7) shows a correlation between diffusion coefficient of methane in water and concentration that follows third order in which the R2 equals to 98.53%. In addition, Eq. (7) was obtained as a result of using molecular dynamics simulation for prediction of diffusion coefficient, while Eq. (8) measures the calculated value of this parameter. Table 3 and Figure 5 show the simulation and calculated findings. Differences in R2 between Eqs. (8) and (9) are presented in Table 4 which indicates a significant similarity. The decline in both MD and Calc. lines has been attributed to a decrease in the mean leap distance, since there are more frequent collisions at higher concentrations [42]. In Darken relation, several groups were assumed responsible for the enhancement of both MD and Calc. curved lines [43, 44, 45]. This approach is based on the empirical models relating the mutual diffusion coefficients to the self-diffusion coefficients of the components with the help of the mixing rules of the Darken Due to the inconsistencies in experimental results, the dependence of diffusion on sorbate concentration is not well understood, but in general, the increase in diffusion is attributed to increase in concentration difference which is explained by Darken equation, while the decrease in diffusion is attributed to the rise in molecules collision [43, 45].
| (7) |
| (8) |
Figure 5.
Molecular dynamics simulated and calculated diffusion coefficient of methane in water at T = 298 K.
Table 3.
The Molecular Dynamics simulated and calculated for diffusion coefficient of methane in water at T = 298 K.
| C (ppm) | (cm2/s)×105 | (cm2/s)×105 |
|---|---|---|
| 300 | 2.44276 | 2.443087 |
| 400 | 2.275016 | 2.31165 |
| 500 | 2.246983 | 2.200888 |
| 1000 | 1.90013 | 1.908341 |
| 1500 | 1.92625 | 1.92325 |
| 2000 | 2.05433 | 2.071096 |
| 2500 | 2.196516 | 2.067516 |
Table 4.
Comparison of R2 for molecular dynamics simulated and calculated diffusion coefficient of methane in water.
| MD | Calc. | |
|---|---|---|
| R2 | 98.53 | 98.24624 |
| R2adj | - | 96.93092 |
| RMSD | - | 0.0081311 |
| Variance | - | 0.0010578 |
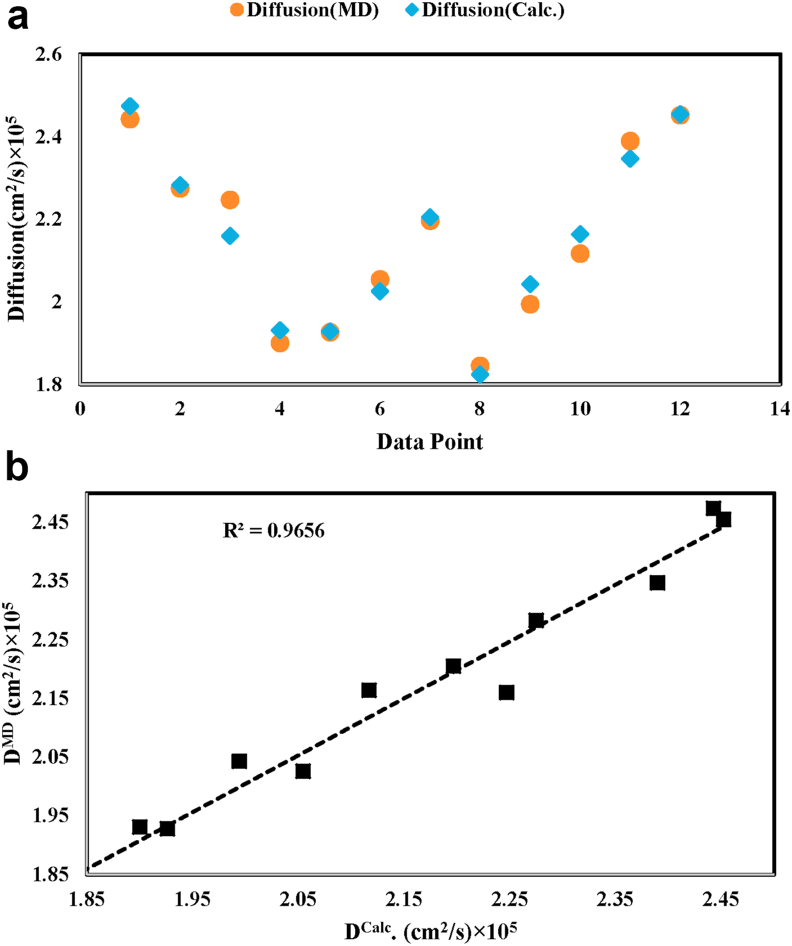
Eq. (9) was presented to predict diffusion coefficient of methane in water as a function of temperature and concentration. The obtained diffusion data from molecular dynamics simulation was adjusted by result of Eq. (9); hence, the desired coefficients were calculated by Eq. (10) as indicated in Table 5 in which result of the equation are represented. Table 6 also, shows accuracy of Eq. (10). Figure 6-a demonstrates diffusion data at constant temperature and concentration for both case of simulated by molecular dynamics and predicted by Eq. (10). Figure 6-b illustrates the molecular dynamics simulated diffusion coefficient versus predicted diffusion coefficient by Eq. (10), in which the R2 for fitted line in Figure 6-b is equal to 96.56% that shows high precision of Eq. (10).
| (9) |
| (10) |
Table 5.
Molecular dynamics simulated diffusion coefficient and predicted diffusion coefficient by Eq. (10) of methane in water for various temperature and concentration.
| T(k) | Concentration (ppm) | (cm2/s)×105 | (cm2/s)×105 |
|---|---|---|---|
| 298 | 300 | 2.44276 | 2.474 |
| 298 | 400 | 2.275016 | 2.283 |
| 298 | 500 | 2.246983 | 2.16 |
| 298 | 1000 | 1.90013 | 1.931 |
| 298 | 1500 | 1.92625 | 1.928 |
| 298 | 2000 | 2.05433 | 2.026 |
| 298 | 2500 | 2.196516 | 2.205 |
| 293 | 1000 | 1.844856 | 1.824 |
| 303.05 | 1000 | 1.99425 | 2.043 |
| 308.25 | 1000 | 2.11698 | 2.164 |
| 315.75 | 1000 | 2.38968 | 2.347 |
| 320 | 1000 | 2.452216 | 2.455 |
Table 6.
Errors of molecular dynamics simulated diffusion coefficient and predicted diffusion coefficient by Eq. (10) of methane in water for various temperature and concentration.
| Calc. | |
|---|---|
| R2 | 96.54987 |
| R2adj | 93.67477 |
| RMSD | 1.09610–7 |
| Variance | 2.88510–13 |
Figure 6.
a) diffusion coefficient acquired from molecular dynamics simulation and calculated by Eq. 10b) molecular dynamics simulated diffusion coefficient versus predicted data by Eq. (10).
3. Conclusion
In this study, the diffusion coefficient of methane in water was predicted at different temperatures and concentrations. Firstly, a comparison was made between experimental and simulation results that indicated the validity of the model and the field force model. Furthermore, the effect of temperature and concentration on the methane diffusion coefficient in water was investigated. As the temperature increases with rise in molecular motion of the gas, the diffusion coefficient also enhances. The diffusion coefficient initially decreases by increasing the concentration and it reaches to a plateau at a concentration of 1000 ppm. Then, it meets an increases. In addition, the diffusion coefficient is obtained through a function of the third order concentration. Finally, in order to predict the diffusion coefficient, a function was proposed based on the concentration and temperature, which showed an agreement with simulation results by molecular dynamics.
In overall, our primary work has focused on simulation, which acts as a bridge in another sense: between theory and experiment. We could test a theory by conducting a simulation using the same model. Additionally, the models were tested by comparing with experimental data. Moreover, the simulation's findings almost indicated same results on the computer which were difficult or takes a lot of time and money to be conducted in the laboratory.
Declarations
Author contribution statement
Hojatollah Moradi: Conceived and designed the experiments; Performed the experiments.
Hossein Bahmanyar: Analyzed and interpreted the data; Wrote the paper.
Hedayat Azizpour: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Mohammad Mohammadi: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Mahdi Akbari: Contributed reagents, materials, analysis tools or data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Footnotes
Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies.
Contributor Information
Hedayat Azizpour, Email: h.azizpour@ut.ac.ir.
Hossein Bahmanyar, Email: hbahmany@ut.ac.ir.
References
- 1.Fei W.Y., Bart H.J. Predicting diffusivities in liquids by the group contribution method. Chem. Eng. Process: Process Intensification. 2001 Nov 1;40(6):531–535. [Google Scholar]
- 2.Oliveira E.L., Silvestre A.J., Silva C.M. Review of kinetic models for supercritical fluid extraction. Chem. Eng. Res. Des. 2011 Jul 1;89(7):1104–1117. [Google Scholar]
- 3.Wankat P.C., Separations R.C. 1994. Blackie Academic & Professional. London UK. [Google Scholar]
- 4.Taylor R., Krishna R. John Wiley & Sons; 1993 Oct 22. Multicomponent Mass Transfer. [Google Scholar]
- 5.Akgerman A., Gainer J.L. Predicting gas-liquid diffusivities. J. Chem. Eng. Data. 1972 Jul;17(3):372–377. [Google Scholar]
- 6.Bosse D. 2005. Diffusion, Viscosity, and Thermodynamics in Liquid Systems. [Google Scholar]
- 7.Kooijman H.A. A modification of the Stokes− Einstein equation for diffusivities in dilute binary mixtures. Ind. Eng. Chem. Res. 2002 Jun 26;41(13):3326–3328. [Google Scholar]
- 8.Zhai Z., Wang X., Jin X., Sun L., Li J., Cao D. Adsorption and diffusion of shale gas reservoirs in modeled clay minerals at different geological depths. Energy Fuel. 2014 Dec 18;28(12):7467–7473. [Google Scholar]
- 9.Zhao Y., Feng Y., Zhang X. Molecular simulation of CO2/CH4 self-and transport diffusion coefficients in coal. Fuel. 2016 Feb 1;165:19–27. [Google Scholar]
- 10.Kang J., Zhang B., Kang T. Monte Carlo and molecular dynamic simulations of CH4 diffusion in kaolinite as functions of pressure and temperature. J. Nat. Gas Sci. Eng. 2018 Jun 1;54:65–71. [Google Scholar]
- 11.Gao D X., Hong L., Wang J., Zheng D. Molecular simulation of gas adsorption characteristics and diffusion in micropores of lignite. Fuel. 2020 Jun 1;269:117443. [Google Scholar]
- 12.Tan J P., Chen C., Liu Y., Wu J., Wu D., Zhang X., He X., She Z., He R., Zhang H. Molecular simulations of gas transport in hydrogenated nitrile butadiene rubber and ethylene–propylene–diene rubber. RSC Adv. 2020;10(21):12475–12484. doi: 10.1039/d0ra00192a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Khalifi M A., Sabet N., Zirrahi M., Hassanzadeh H., Abedi J. Concentration-dependent molecular diffusion coefficient of gaseous ethane in liquid toluene. AIChE J. 2020 Jun;66(6) [Google Scholar]
- 14.Orozco G.A., Lachet V., Mackie A.D. A molecular simulation study of aqueous solutions of amines and alkanolamines: mixture properties and structural analysis. Mol. Simulat. 2014 Jan 2;40(1-3):123–133. [Google Scholar]
- 15.Newsome D., Coppens M.O. Molecular dynamics as a tool to study heterogeneity in zeolites–Effect of Na+ cations on diffusion of CO2 and N2 in Na-ZSM-5. Chem. Eng. Sci. 2015 Jan 6;121:300–312. [Google Scholar]
- 16.Aimoli C.G., Maginn E.J., Abreu C.R. Thermodynamic properties of supercritical mixtures of carbon dioxide and methane: a molecular simulation study. J. Chem. Eng. Data. 2014 Oct 9;59(10):3041–3054. [Google Scholar]
- 17.Simond M.R., Ballerat-Busserolles K., Coxam J.Y., Pádua A.A. Molecular simulations of primary alkanolamines using an extendable force field. ChemPhysChem. 2012 Dec 7;13(17):3866–3874. doi: 10.1002/cphc.201200508. [DOI] [PubMed] [Google Scholar]
- 18.Nalaparaju A., Khurana M., Farooq S., Karimi I.A., Jiang J.W. CO2 capture in cation-exchanged metal–organic frameworks: holistic modeling from molecular simulation to process optimization. Chem. Eng. Sci. 2015 Mar 3;124:70–78. [Google Scholar]
- 19.Demontis P., Suffritti G.B. A comment on the flexibility of framework in molecular dynamics simulations of zeolites. Microporous Mesoporous Mater. 2009 Oct 1;125(1-2):160–168. [Google Scholar]
- 20.Jafari L M.M., Moradi H., Tavan Y. A theoretical and industrial study of component co-adsorption on 3A zeolite: an industrial case. Chem. Pap. 2020 Feb 1;74(2):651–661. [Google Scholar]
- 21.Zhao X D., Jin H. Correlation for self-diffusion coefficients of H2, CH4, CO, O2 and CO2 in supercritical water from molecular dynamics simulation. Appl. Therm. Eng. 2020 May 5;171:114941. [Google Scholar]
- 22.Higashi H., Tamura K. Calculation of diffusion coefficient for supercritical carbon dioxide and carbon dioxide+ naphthalene system by molecular dynamics simulation using EPM2 model. Mol. Simulat. 2010 Sep 1;36(10):772–777. [Google Scholar]
- 23.Umoren S.A., Solomon M.M. Synergistic corrosion inhibition effect of metal cations and mixtures of organic compounds: a review. J. Environ. Chem. Eng. 2017 Feb 1;5(1):246–273. [Google Scholar]
- 24.Moradi H., Azizpour H., Bahmanyar H., Mohammadi M. Molecular dynamics simulation of H2S adsorption behavior on the surface of activated carbon. Inorg. Chem. Commun. 2020 Jun 18:108048. [Google Scholar]
- 25.Masiren E.E., Harun N., Ibrahim W.H., Adam F. Effect of temperature on diffusivity of monoethanolamine (MEA) on absorption process for CO2 capture. Int. J. Eng. Technol. Sci. 2016;5(1):43–51. [Google Scholar]
- 26.Allen M.P., Tildesley D.J. Oxford University Press; New York: 1987. Computer Simulation of Liquids. [Google Scholar]
- 27.Kadoura A., Narayanan Nair A.K., Sun S. Molecular dynamics simulations of carbon dioxide, methane, and their mixture in montmorillonite clay hydrates. J. Phys. Chem. C. 2016 Jun 16;120(23):12517–12529. [Google Scholar]
- 28.Marry V., Turq P., Cartailler T., Levesque D. Microscopic simulation of structure and dynamics of water and counterions in a monohydrated montmorillonite. J. Chem. Phys. 2002 Aug 15;117(7):3454–3463. [Google Scholar]
- 29.Zeebe R.E. On the molecular diffusion coefficients of dissolved CO2, HCO3-, and CO32-and their dependence on isotopic mass. Geochem. Cosmochim. Acta. 2011 May 1;75(9):2483–2498. [Google Scholar]
- 30.Witherspoon P.A., Saraf D.N. Diffusion of methane, ethane, propane, and n-butane in water from 25 to 43. J. Phys. Chem. 1965 Nov;69(11):3752–3755. [Google Scholar]
- 31.Wilke C.R., Chang P. Correlation of diffusion coefficients in dilute solutions. AIChE J. 1955 Jun;1(2):264–270. [Google Scholar]
- 32.Gautieri A., Vesentini S., Redaelli A. How to predict diffusion of medium-sized molecules in polymer matrices. From atomistic to coarse grain simulations. J. Mol. Model. 2010 Dec 1;16(12):1845–1851. doi: 10.1007/s00894-010-0687-7. [DOI] [PubMed] [Google Scholar]
- 33.Abouelnasr M.K. 2013. A Simulation Study of Diffusion in Microporous Materials. (Doctoral dissertation, UC Berkeley) [Google Scholar]
- 34.Einstein A. Ee´ktrochem Zf. 14. 235 (1908) Ann. d. Phys. 1905;17:19. [Google Scholar]
- 35.Athar K., Doranehgard M.H., Eghbali S., Dehghanpour H. Measuring diffusion coefficients of gaseous propane in heavy oil at elevated temperatures. J. Therm. Anal. Calorim. 2020 Feb;139(4):2633–2645. [Google Scholar]
- 36.Smith J.V. Vol. 43. Mineralogical Magazine; 1980 Jun. pp. 829–830. (Barrer. Zeolites and clay Minerals as Sorbents and Molecular Sieves. London and New York). (Academic Press), 1978 viii+ 497 pp., 181 figs. Price£ 25.00. [Google Scholar]
- 37.Tiselius A. Die diffusion von Wasser in einem Zeolithkristall. Z. Phys. Chem. 1934 Feb 1;169(1):425–458. [Google Scholar]
- 38.Witherspoon P.A., Bonoli L. Correlation of diffusion coefficients for paraffin, aromatic, and cycloparaffin hydrocarbons in water. Ind. Eng. Chem. Fundam. 1969 Aug;8(3):589–591. [Google Scholar]
- 39.Gubbins K.E., Bhatia K.K., Walker R.D., Jr. Diffusion of gases in electrolytic solutions. AIChE J. 1966 May;12(3):548–552. [Google Scholar]
- 40.Lu W.J., Chou I.M., Burruss R.C., Yang M.Z. In situ study of mass transfer in aqueous solutions under high pressures via Raman spectroscopy: a new method for the determination of diffusion coefficients of methane in water near hydrate formation conditions. Appl. Spectrosc. 2006 Feb 1;60(2):122–129. doi: 10.1366/000370206776023278. [DOI] [PubMed] [Google Scholar]
- 41.Ruthven D.M., Loughlin K.F. The sorption and diffusion of n-butane in Linde 5A molecular sieve. Chem. Eng. Sci. 1971 Aug 1;26(8):1145–1154. [Google Scholar]
- 42.Kärger J., Pfeifer H., Rauscher M., Walter A. Self-diffusion of n-paraffins in NaX zeolite. J. Chem. Soc., Faraday Trans. 1: Phys. Chem. Condensed Phases. 1980;76:717–737. [Google Scholar]
- 43.Kärger J., Ruthven D.M. Diffusion in zeolites. Comparison of sorption and nuclear magnetic resonance diffusivities. J. Chem. Soc., Faraday Trans. 1: Phys. Chem. Condensed Phases. 1981;77(7):1485–1496. [Google Scholar]
- 44.Ash R., Barrer R.M. Mechanisms of surface flow. Surf. Sci. 1967 Nov 1;8(4):461–466. [Google Scholar]
- 45.Kärger J. Some remarks on the straight and cross-coefficients in irreversible thermodynamics of surface flow and on the relation between diffusion and selfdiffusion. Surf. Sci. 1973 May 1;36(2):797–801. [Google Scholar]