Consistency of variety of machine learning and statistical models in predicting clinical risks of individual patients: longitudinal cohort study using cardiovascular disease as exemplar

Abstract

Objective

To assess the consistency of machine learning and statistical techniques in predicting individual level and population level risks of cardiovascular disease and the effects of censoring on risk predictions.

Design

Longitudinal cohort study from 1 January 1998 to 31 December 2018.

Setting and participants

3.6 million patients from the Clinical Practice Research Datalink registered at 391 general practices in England with linked hospital admission and mortality records.

Main outcome measures

Model performance including discrimination, calibration, and consistency of individual risk prediction for the same patients among models with comparable model performance. 19 different prediction techniques were applied, including 12 families of machine learning models (grid searched for best models), three Cox proportional hazards models (local fitted, QRISK3, and Framingham), three parametric survival models, and one logistic model.

Results

The various models had similar population level performance (C statistics of about 0.87 and similar calibration). However, the predictions for individual risks of cardiovascular disease varied widely between and within different types of machine learning and statistical models, especially in patients with higher risks. A patient with a risk of 9.5-10.5% predicted by QRISK3 had a risk of 2.9-9.2% in a random forest and 2.4-7.2% in a neural network. The differences in predicted risks between QRISK3 and a neural network ranged between –23.2% and 0.1% (95% range). Models that ignored censoring (that is, assumed censored patients to be event free) substantially underestimated risk of cardiovascular disease. Of the 223 815 patients with a cardiovascular disease risk above 7.5% with QRISK3, 57.8% would be reclassified below 7.5% when using another model.

Conclusions

A variety of models predicted risks for the same patients very differently despite similar model performances. The logistic models and commonly used machine learning models should not be directly applied to the prediction of long term risks without considering censoring. Survival models that consider censoring and that are explainable, such as QRISK3, are preferable. The level of consistency within and between models should be routinely assessed before they are used for clinical decision making.

Introduction

Risk prediction models are used routinely in healthcare practice to identify patients at high risk and make treatment decisions, so that appropriate healthcare resources can be allocated to those patients who most need care.¹ These risk prediction models are usually built using statistical regression techniques. Examples include the Framingham risk score (developed from a US cohort with prospectively collected data)² and QRISK3 (developed from a large UK cohort using retrospective electronic health records).³ Recently, machine learning models have gained considerable popularity. The English National Health Service has invested £250m ($323m; €275m) to further embed machine learning in healthcare.⁴ A recent viewpoint article suggested that machine learning technology is about to start a revolution with the potential to transform the whole healthcare system.⁵ Several studies suggested that machine learning models could outperform statistical models in terms of calibration and discrimination.^{6 7 8 9} However, another viewpoint concerns the fact that these approaches cannot provide explainable reasons behind their predictions, potentially leading to inappropriate actions,¹⁰ and a recent review found no evidence that machine learning models had better model performance than logistic models.¹¹ However, interpretation of this review is difficult, as it included models from mostly small sample sizes and with different outcomes and predictors. Machine learning has established strengths in image recognition that could help in diagnosing diseases in healthcare,^{12 13 14 15} but censoring (patients lost to follow-up), which is common in risk prediction, does not exist in image recognition. Many commonly used machine learning models do not take into account censoring by default.¹⁶

The objective of this study was to assess the robustness and consistency of a variety of machine learning and statistical models on individual risk prediction and the effects of censoring on risk predictions. We used cardiovascular disease as an exemplar. We defined robustness of individual risk prediction as the level of consistency in the prediction of risks for individual patients with models that have comparable population level performance metrics.^{17 18 19}

Methods

Data source

We derived the study cohort from Clinical Practice Research Datalink (CPRD GOLD), which includes data from about 6.9% of the population in England.²⁰ It also has been linked to Hospital Episode Statistics, Office for National Statistics mortality records, and Townsend deprivation scores,³ to provide additional information about hospital admissions (including date and discharge diagnoses) and cause specific mortality.²⁰ CPRD includes patients’ electronic health records from general practice, capturing detailed information such as demographics (age, sex, and ethnicity), symptoms, tests, diagnoses, prescribed treatments, health related behaviours, and referrals to secondary care.²⁰ CPRD is a well established representative cohort of the UK population, and thousands of studies have used it,^{21 22} including a validation of the QRISK2 model and an analysis of machine learning.^{8 23}

Study population

This study used the same selection criteria for the study population, risk factors, and cardiovascular disease outcomes as were used for QRISK3.^{3 18} Follow-up of patients started at the date of the patient’s registration with the practice, their 25th birthday, or 1 January 1998 (whichever was latest) and ended at the date of death, incident cardiovascular disease, date of leaving the practice, or last date of data collection (whichever was earliest). The index date for measurement of cardiovascular disease risk was randomly chosen from the follow-up period to capture time relevant practice variability with a better spread of calendar time and age.²⁴ This was different from QRISK3, for which a single calendar time date was mostly used.¹⁸ The main inclusion criteria were age between 25 and 84 years, no history of cardiovascular disease, and no prescription for a statin before the index date. The outcome of interest was the 10 year risk of developing cardiovascular disease. The definition of the primary clinical outcome (cardiovascular disease) was the same as for QRISK3 (that is, coronary heart disease, ischaemic stroke, or transient ischaemic attack).³

We extracted two main cohorts from the study population—one overall cohort including all patients with at least one day of follow-up and one cohort with censored patients removed. The cohort without censoring excluded patients who were lost to follow-up before developing cardiovascular disease by year 10. The analysis of the cohort without censoring aimed to investigate the effects of ignoring censoring on patients’ individual risk predictions. This cohort mimics the methods used by some machine learning studies—that is, only patients or practices with full 10 years’ follow-up were selected.⁸

Cardiovascular disease risk factors

The cardiovascular disease risk factors at the index date included sex; age; body mass index; smoking history; total cholesterol to high density lipoprotein cholesterol ratio; systolic blood pressure and its standard deviation; history of prescribing of atypical antipsychotic drugs; blood pressure treatment or regular oral glucocorticoids; clinical history of systemic lupus erythematosus, atrial fibrillation, chronic kidney disease (stage 3, 4, or 5), erectile dysfunction, migraine, rheumatoid arthritis, severe mental illness, or type 1 or 2 diabetes mellitus; family history of angina or heart attack in a first degree relative aged under 60 years; ethnicity; and Townsend deprivation score.³ The same predictors from QRISK3³ were used for all model fitting except for Framingham,²⁵ which used fewer and different predictors.

Machine learning and Cox models

The study considered 19 models, including 12 families of machine learning, three Cox proportional hazards models (local fitted, QRISK3, and Framingham), three parametric survival models (assuming Weibull, Gaussian, and logistic distribution), and a statistical logistic model (fitted in a statistical causal-inference framework). Machine learning models included logistic model (fitted in an automated machine learning framework),²⁶ random forest,²⁷ and neural network²⁸ from R package “Caret” ²⁹; logistic model, random forest, neural network, extra-tree model,³⁰ and gradient boosting classifier³⁰ from Python package “Sklearn”³¹; and logistic model, random forest, neural network, and autoML³² from Python package “h2o.”³³ The package autoML selects a best model from a broader spectrum of candidate models.³² Details of these models are summarised in eTable 1. The study used the machine learning algorithms from different software packages, with a grid search process on hyper-parameters and cross validation, to acquire a series of high performing machine learning models; this mimics the reality that practitioners may subjectively select different packages for model fitting and end up with a different best model. The study treated the models from the same machine learning algorithm but different software packages as different model families, as the settings (hyper-parameters) of these packages to control the model fitting are often different, which might result in a different best performing model through the grid search process.

Statistical analysis

We used the Markov chain Monte Carlo method with monotone style to impute missing values 10 times for ethnicity (54.3% missing in overall cohort), body mass index (40.3%), Townsend score (0.1%), systolic blood pressure (26.9%), standard deviation of systolic blood pressure (53.9%), ratio of total cholesterol to high density lipoprotein cholesterol (65.0%), and smoking status (25.2%)¹⁸ (only these variables had missing values). We randomly split the overall cohort (which contained 10 imputations) into an overall derivation cohort (75%) and an overall testing cohort (25%). We grid searched a total of 1200 machine learning models with the highest discrimination (C statistic) on hyper-parameters with twofold cross validation estimating calibration and discrimination. They were derived from 12 model families of 100 samples with similar sample size to another machine learning study.⁸ We then estimated the individual cardiovascular disease risk predictions (averaged for missing value imputations) and model performance of all models by using the overall testing cohort. The sample splitting and model fitting process is shown in eFigure 1.

We compared distributions of risk predictions for the same individual among models. We plotted the differences of individual cardiovascular disease risk predictions between models against deciles of cardiovascular disease risk predictions for QRISK3. We produced Bland-Altman plots—a graphical method to compare two measurement techniques across the full spectrums of values.³⁴ These plotted the differences of individual risk predictions between two models against the average individual risk prediction.³⁴

We used R to fit the models from “Caret” and Python to fit models from “Sklearn” and “h2o.”^{29 30} We used SAS procedures to extract the raw data, create analysis datasets, and generate tables and graphs.³⁵

Patient and public involvement

No patients were involved in setting the research question or the outcome measures, nor were they involved in developing plans or implementation of the study. No patients were asked to advise on interpretation or writing up of results.

Results

The overall study population included 3.66 million patients from 391 general practices. The cohort without censoring was considerably smaller (0.45 million) than the overall cohort. Table 1 shows the baseline characteristics of the two study populations, which were split into derivation and validation cohorts. The average age was higher in the cohort without censoring (owing to younger patients leaving the practice as shown in eFigure 11).

Table 1.

Baseline characteristics of two study populations (patients aged 25-84 years without history of cardiovascular disease (CVD) or previous statin use). Values are numbers (percentages) unless stated otherwise

Characteristics	Overall cohort			Cohort without censoring
	Derivation cohort (n=2 746 453)	Validation cohort (n=915 479)		Derivation cohort (n=335 632)	Validation cohort (n=111 868)
CVD cases	86 769 (3.2)	28 828 (3.1)		78 826 (23.5)	26 168 (23.4)
Patients censored within 10 years	2 410 516 (87.8)	803 916 (87.8)		NA	NA
CVD risk factors
Female sex	1 406 796 (51.2)	469 098 (51.2)		173 691 (51.8)	58 169 (52.0)
Mean (SD) age, years	44.7 (15.6)	44.7 (15.7)		53.3 (16.2)	53.4 (16.2)
Mean (SD) body mass index	26.7 (5.0)	26.7 (5.0)		27.2 (4.8)	27.1 (4.8)
Mean (SD) total cholesterol/high density lipoprotein cholesterol ratio	3.9 (1.3)	3.9 (1.3)		4.1 (1.3)	4.1 (1.3)
Atypical antipsychotic drug	12 306 (0.4)	4030 (0.4)		932 (0.3)	316 (0.3)
Antihypertensive treatment	183 964 (6.7)	61 962 (6.8)		42 704 (12.7)	14 245 (12.7)
Regular steroid tablets	2059 (0.1)	694 (0.1)		289 (0.1)	100 (0.1)
History of systemic lupus erythematosus	1840 (0.1)	606 (0.1)		257 (0.1)	74 (0.1)
History of angina or heart attack in first degree relative <60 years	98 455 (3.6)	32 619 (3.6)		7950 (2.4)	2669 (2.4)
History of atrial fibrillation	20 778 (0.8)	6965 (0.8)		5213 (1.6)	1757 (1.6)
History of chronic kidney disease (stage 3, 4, or 5)	30 133 (1.1)	10 240 (1.1)		4364 (1.3)	1514 (1.4)
History of erectile dysfunction	39 651 (1.4)	13 110 (1.4)		3867 (1.2)	1287 (1.2)
History of migraines	177 439 (6.5)	59 106 (6.5)		19 629 (5.8)	6593 (5.9)
History of rheumatoid arthritis	16 167 (0.6)	5459 (0.6)		3043 (0.9)	1030 (0.9)
History of severe mental illness	219 861 (8.0)	72 832 (8.0)		32 190 (9.6)	10 673 (9.5)
History of type 1 diabetes	5899 (0.2)	2097 (0.2)		820 (0.2)	251 (0.2)
History of type 2 diabetes	35 569 (1.3)	11 826 (1.3)		8134 (2.4)	2641 (2.4)
Mean (SD) systolic blood pressure	126.9 (16.7)	126.9 (16.7)		133.1 (18.4)	133.1 (18.4)
Mean (SD) standard deviation of each individual patient’s systolic blood pressure	9.9 (5.6)	9.9 (5.6)		10.7 (5.9)	10.7 (5.9)
Ethnicity
Other ethnicity	173 271 (6.3)	58 124 (6.3)		6900 (2.1)	2273 (2.0)
White or not recorded	2 573 182 (93.7)	857 355 (93.7)		328 732 (97.9)	109 595 (98.0)
Smoking
Ex-smoker	629 500 (22.9)	209 186 (22.8)		76 060 (22.7)	25 429 (22.7)
Current smoker	806 978 (29.4)	269 717 (29.5)		94 082 (28.0)	31 335 (28.0)
Never smoker	1 309 975 (47.7)	436 576 (47.7)		165 490 (49.3)	55 104 (49.3)
Townsend deprivation
Score 1—Least deprived	600 392 (21.9)	199 937 (21.8)		86 596 (25.8)	29 156 (26.1)
Score 2	594 739 (21.7)	197 677 (21.6)		82 211 (24.5)	27 266 (24.4)
Score 3	572 903 (20.9)	191 045 (20.9)		69 897 (20.8)	23 326 (20.9)
Score 4	568 006 (20.7)	189 520 (20.7)		60 424 (18.0)	20 140 (18.0)
Score 5—Most deprived	410 413 (14.9)	137 300 (15.0)		36 504 (10.9)	11 980 (10.7)

Table 2 shows the model performance of the machine learning and statistical models. All models had very similar discrimination (C statistics of about 0.87) and calibration (Brier scores of about 0.03 in eTables 2-4 and eFigures 3-4).

Table 2.

Performance indicators of machine learning and statistical models in overall cohort

Model	Model performance*: C statistic (95% range†)	Average absolute change in model performance: % (95% range†)
Logistic (Caret)	0.879 (0.879 to 0.879)	0.00 (−0.03 to 0.04)
Random forest (Caret)	0.869 (0.867 to 0.869)	−1.20 (−1.33 to −1.10%)
Neural network (Caret)	0.878 (0.867 to 0.880)	−0.15 (−1.35 to 0.06)
Statistic logistic model	0.879 (0.879 to 0.879)	0.01 (−0.02 to 0.04)
QRISK3	0.879	Reference model
Framingham	0.865	−1.66 (−1.66 to −1.66)
Local Cox model	0.877 (0.877 to 0.878)	−0.22 (−0.28 to −0.17)
Parametric survival model (Weibull)	0.877 (0.876 to 0.877)	−0.29 (−0.35 to −0.24)
Parametric survival model (Gaussian)	0.876 (0.876 to 0.877)	−0.33 (−0.39 to −0.29)
Parametric survival model (Logistic)	0.876 (0.875 to 0.876)	−0.36 (−0.43 to −0.31)
Logistic (Sklearn)	0.879 (0.879 to 0.879)	0.00 (−0.05 to 0.03)
Random forest (Sklearn)	0.872 (0.871 to 0.873)	−0.80 (−0.89 to −0.71)
Neural network (Sklearn)	0.872 (0.832 to 0.879)	−0.85 (−5.39 to −0.03)
Gradient boosting classifier (Sklearn)	0.878 (0.877 to 0.878)	−0.17 (−0.29 to −0.08)
extra-trees (Sklearn)	0.863 (0.861 to 0.864)	−1.89 (−2.05 to −1.76)
Logistic (h2o)	0.879 (0.878 to 0.879)	−0.06 (−0.10 to −0.02)
Random forest (h2o)	0.877 (0.877 to 0.878)	−0.22 (−0.29 to −0.17)
Neural network (h2o)	0.875 (0.870 to 0.879)	−0.45 (−1.09 to −0.04)
autoML (h2o)	0.879 (0.879 to 0.880)	−0.00 (−0.07 to 0.06)

^*Model performance was calculated in binary framework. Threshold 7.5% was used to calculate precision and recall for all models.

^†95% range (2.5-97.5%) of model performance derived from 100 random samples.

Figure 1 shows the variability in individual risk predictions across the models for patients with predicted cardiovascular disease risks of 9.5-10.5% by QRISK3. Patients with a predicted cardiovascular disease risk between 9.5% and 10.5% with QRISK3 had a risk of 2.2-5.8% with logistic Caret model, 2.9-9.2% with Caret random forest, 2.4-7.2% with Caret neural network, and 3.1-9.3% with Sklearn random forest. The calibration plot (fig 2) shows that models that ignore censoring were miscalibrated (that is, predicted risks were lower than observed risks).

Fig 1.

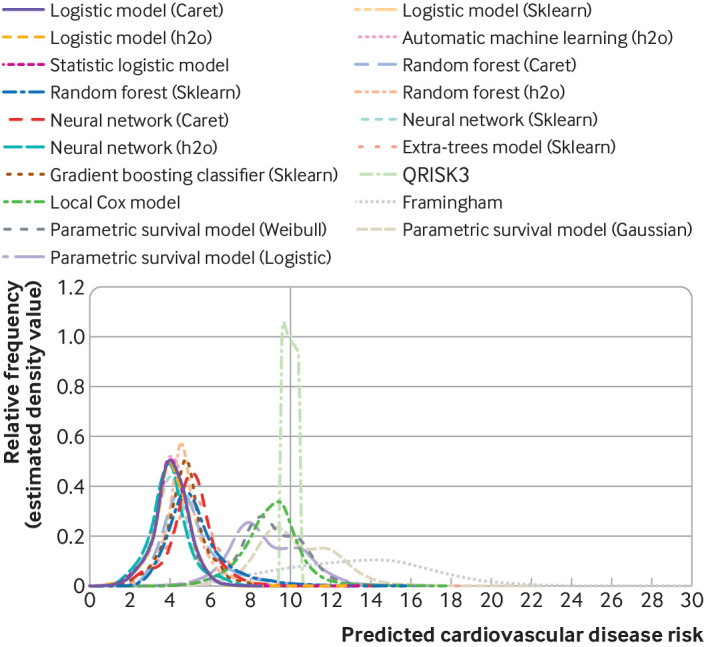
Distribution of individual risk predictions with machine learning and statistical models in overall cohort for patients with predicted cardiovascular disease risks of 9.5-10.5% in QRISK3

Fig 2.

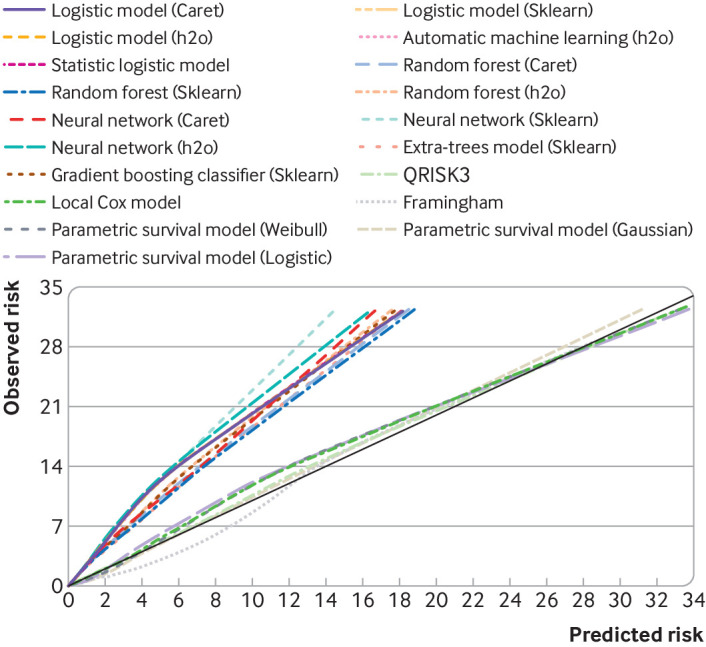
Calibration slope of machine learning models and statistical models in overall cohort in survival framework (observed events consider censoring). CVD=cardiovascular disease

Figure 3 plots the differences of individual cardiovascular disease risk predictions with the different models stratified by deciles of cardiovascular disease risk predictions of QRISK3. The largest range of inconsistencies in risk predictions was found in patients with highest predicted risks of cardiovascular disease. Low risk of cardiovascular disease was generally predicted consistently between and within models. We observed similar trends when using a different reference model (eFigure 5.2).

Fig 3.

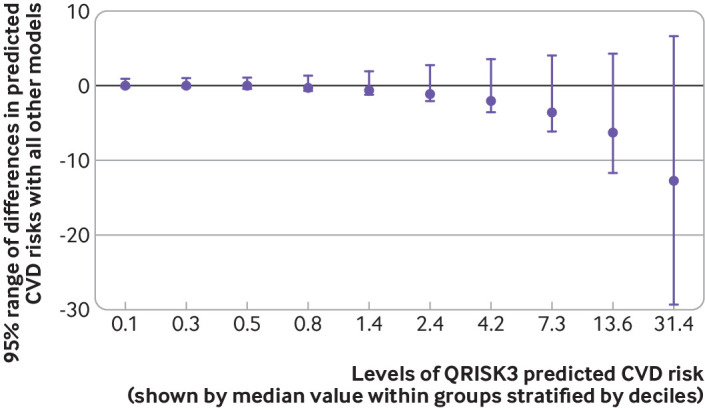
95% range of individual risk predictions with machine learning and statistical models stratified by deciles of predicted cardiovascular disease (CVD) risks with QRISK3 in overall cohort

Figure 4 shows the Bland-Altman plot of QRISK3 and neural network. We found a large inconsistency of risk predictions between models. The differences in predicted risks between QRISK3 and neural network ranged between −23.2% and 0.1% (95% range). The regression line shows similar finding to figure 3, with the largest differences in higher risk groups. More comparison between specific models can be found in eFigure 6 and eFigure 7. We found similar inconsistency of risk prediction among models when using a logistic model as reference (eFigure 2.1). The removal of censored patients changed the magnitude but not the variability of individual cardiovascular disease risk predictions (eFigure 2.2).

Fig 4.

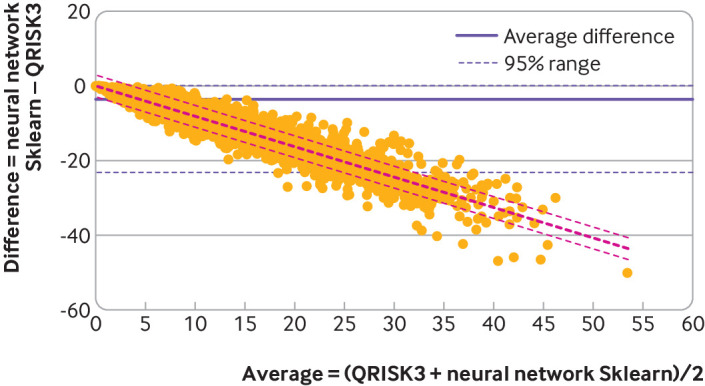
Bland-Altman analysis comparing QRISK3 with neural network model

We found substantial reclassification across a treatment threshold when using a different type of prediction model. Of 691 664 patients with a cardiovascular disease risk of 7.5% or lower, as predicted by QRISK3, 13.6% would be reclassified above 7.5% when using another model (table 3). Of the 223 815 patients with a cardiovascular disease risk above 7.5%, 57.8% would be reclassified below 7.5% when using another model. We also found high levels of reclassification with a different reference model (as shown in table 3) or a different threshold (eTable 7).

Table 3.

Reclassification of individual risk predictions with machine learning and statistical models

Model	Reclassification in overall testing cohort: No (%)*
	Reclassified*	Not reclassified
Overall cohort
QRISK3 10 year risk prediction (reference model):
≤7.5% threshold	94 186 (13.6)	597 478 (86.4)
>7.5% threshold	129 348 (57.8)	94 467 (42.2)
Logistic model (Caret) 10 year risk prediction (reference model):
≤7.5% threshold	209 221 (25.9)	597 478 (74.1)
>7.5% threshold	14 313 (13.2)	94 467 (86.8)
Cohort without censoring
QRISK3 10 year risk prediction (reference model):
≤7.5% threshold	34 607 (54.6)	28 779 (45.4)
>7.5% threshold	1248 (2.6)	47 234 (97.4)
Logistic model (Caret) 10 year risk prediction (reference model):
≤7.5% threshold	6004 (17.3)	28 779 (82.7)
>7.5% threshold	29 851 (38.7)	47 234 (61.3)

^*Patients were reclassified if they had a risk prediction in any model that crossed the threshold compared with the prediction of the reference model.

We did several sensitivity analyses with consistent findings of high levels of inconsistencies in individual risk predictions between and within models. The same machine learning algorithm with the selection of different settings (hyper-parameters) from different software packages yielded different individual cardiovascular disease risk predictions (eTable 8 and eFigure 8). The evaluation of the effects of generalisability by developing and testing models in different regions of England showed similarly high levels of inconsistencies in cardiovascular disease risk predictions (eTable 10 and eFigure 9). Changing the number of predictors did not result in lower levels of inconsistencies in cardiovascular disease risk predictions with more predictors included in the models (eTable 11 and eFigure 10),

Discussion

We found that the predictions of cardiovascular disease risks for individual patients varied widely between and within different types of machine learning and statistical models, especially in patients with higher risks (when using similar predictors). Logistic models and the machine learning models that ignored censoring substantially underestimated risk of cardiovascular disease.

Comparison with other studies

Despite claims that machine learning models can revolutionise risk prediction and potentially replace traditional statistical regression models in other areas,^{5 36 37} this study of prediction of cardiovascular disease risk found that they have similar model performance to traditional statistical methods and share similar uncertainty in individual risk predictions. Strengths of machine learning models may include their ability to automatically model non-linear associations and interactions between different risk factors.^{38 39} They may also find new data patterns.³⁰ They have the acknowledged strength of automating model building with a better performance in specific classification tasks (for example, image recognition).³⁰ However, a critical question is whether risk prediction models provide accurate and consistent risk predictions for individual patients. Previous research has found that a traditional risk prediction model such as QRISK3 has considerable uncertainty on individual risk prediction, although it has very good model performance at the population level.^{18 19} This uncertainty is related to unmeasured heterogeneity between clinical sites and modelling choices such as the inclusion of secular trends.^{18 19} Our study found that machine learning models share this uncertainty, as models with comparable population level performance yielded very different individual risk predictions. Consequently, different treatment decisions could be made by arbitrarily selecting another modelling technique.

Censoring of patients is an unavoidable problem in prediction models for long term risks, as patients frequently move away or die. However, many popular machine learning models ignore censoring, as the default framework is the analysis of a binary outcome rather than time to event survival outcome. A UK Biobank study of risk prediction for cardiovascular disease did not report how censoring was dealt with,⁷ like several other studies.^{39 40 41} Another machine learning study incorrectly excluded censored patients.⁸ Random survival forest is a machine learning model that takes account of censoring.⁴² Innovative techniques are being developed that incorporate statistical censoring approaches into the machine learning framework.^{16 43} However, to our knowledge no current software packages can handle large datasets for these methods. This study shows that directly applying popular machine learning models to data (especially for data with substantive censoring) without considering censoring will substantially bias risk predictions. The miscalibration was large compared with observed life table predictions. This is consistent with a recent study that reported loss of information due to lack of consideration of censoring with the random forest method.⁶

Models with similar C statistics gave varying estimates of individual risks for the same patients. A fundamental challenge with the C statistic is that it applies to the population level but not to individual patients.^{18 44} The C statistic measures the ability of a model to discriminate between cases and non-cases. It is a proportion of cases and non-cases that are correctly ranked by the model. This means that for a high C statistic, patients with observed events should have a higher risk than the patients without observed events.³⁸ The C statistic concerns rank of predicted probability rather than probability itself. For example, a model may predict all events with a range of probability between 50.2% and 50.3% and non-events with a probability of 50%, which would result a perfect discrimination, but the predicted probability is not clinically useful. When a large number of patients have lower risks (which is often the case for cardiovascular disease risk prediction), the C statistic becomes less informative in indicating discrimination of models, especially in patients at high risk. For example, two patients with very low risk (say 1% and 1.5%) may have similar effects on C statistic to two patients with high risk (say 10% and 20%), given that their differences in rank are the same (but the latter two are of greater clinical interest). Therefore, C statistics do not tell us whether a model discriminates specific patients at high risk correctly or consistently compared with other models. C statistics have also been shown to be insensitive to changes in the model.⁴⁴ The evaluation of consistency in individual risk predictions between models may thus be important in assessing their clinical usefulness in identifying patients at high risk.

This study considered a total of 22 predictors that had been selected by the developers of QRISK on the basis of their likely causal effect on cardiovascular disease.³ Other machine learning studies have used considerably more predictors. As an example, a study using the UK Biobank included 473 predictors in the machine learning models.⁷ A potentially unresolved question in risk prediction is what type of variables and how many of them should be included in models, as consensus and guidelines for choosing variables for risk prediction model are lacking.⁴⁵ More information incorporated into a model may increase the model performance of risk prediction at the population level. For example, the C statistic is related to both the effects of predictors and the variation of predictors among patients with and without events.⁴⁶ Including more predictors in a model may increase the C statistic merely because of greater variation of predictors. On the other hand, inclusion of non-causal predictors may lower the accuracy of the risk prediction by adding noise, increasing the risk of over-fitting, and leading to more data quality challenges.⁴⁷ Also, a very large number of predictors may limit the clinical utility of these machine learning models, as more predictors need to be measured before a prediction can be made. Further research is needed to establish whether the focus of risk prediction should be on consistently measured causal risk factors or on variables that may be recorded inconsistently between clinicians or electronic health records systems.

Guidelines for the development and validation of risk prediction models (called TRIPOD) focus on the assessment of population level performance but do not consider consistencies in individual risk predictions by prediction models with comparable population level performance.⁴⁸ Arguably, the clinical utility of risk prediction models should be based, as has been done with blood pressure devices for instance, on the consistent risk prediction (reliability) for a particular patient rather than broad population level performance.⁴⁹ If models with comparable performance provide different predictions for a patient with certain risk factors, an explanation for these discrepant predictions is needed.⁵⁰ Explainable artificial intelligence has been described as methods and techniques in the application of artificial intelligence such that the results of the solution can be understood by human experts.⁵¹ This contrasts with the concept of the “black box” in machine learning, whereby predictions cannot be explained. Arguably, a survival model that is explainable (such as QRISK3, which is based on established causal predictors) may be preferable over black box models that are high dimensional (include many predictors) but that provide inconsistent results for individual patients. Better standards are needed on how to develop and test machine learning algorithms.¹⁴

Strengths and limitations of study

The major strength of this study was that a large number of different machine learning models with varying hyper-parameters using different packages from different programming languages were fitted to a large population based primary care cohort. However, the study has several limitations. We considered only predictors from QRISK3 in order to compare models on the basis of equal information, but sensitivity analyses showed similar findings of inconsistencies in cardiovascular disease risk prediction independent of the number of predictors. Furthermore, more hyper-parameters in the machine learning models could have been considered in the grid search process. However, the fitted models already achieved reasonably high model performance, which indicates that the main hyper-parameters had been covered in the grid search process. Several machine learning algorithms were not included in this study, such as support vector machine or survival random forest, as the current software packages of these models cannot cope with large datasets.^{52 53 54 55} The Bland-Altman graph used the 95% range of differences rather than 95% confidence interval, as the differences of predicted risk (including log transformed) did not follow normal distribution (which is a required assumption to calculate the Bland-Altman 95% confidence interval). Another limitation is that this study concerned cardiovascular disease risk prediction in primary care, and findings may not be generalisable to other outcomes or settings. However, the robustness of individual risk predictions within and between models with comparable population level performance is rarely, if ever, evaluated. Our findings indicate the importance of assessing this.

Conclusions

A variety of models predicted cardiovascular disease risks for the same patients very differently despite similar model performances. Using the logistic model and commonly used machine learning models without considering censoring in survival analysis results in substantially biased risk prediction and has limited usefulness in the prediction of long term risks. The level of consistency within and between models should be assessed before they are used for clinical decision making and should be considered in TRIPOD guidelines.

What is already known on this topic

• Risk prediction models are widely used in clinical practice (such as QRISK or Framingham for cardiovascular disease)

• Multiple techniques can be used for these predictions, and recent studies claim that machine learning models can outperform models such as QRISK

What this study adds

• Nineteen different prediction techniques (including 12 machine learning models and seven statistical models) yielded similar population level performance

• However, cardiovascular disease risk predictions for the same patients varied substantially between models

• Models that ignored censoring (including commonly used machine learning models) yielded biased risk predictions

Web extra.

Extra material supplied by authors

Web appendix: Supplementary materials