Transcranial ultrafast ultrasound localization microscopy of brain vasculature in patients

Abstract

Changes in cerebral blood flow are associated with stroke, aneurysms, vascular cognitive impairment, neurodegenerative diseases and other pathologies. Brain angiograms, typically performed via computed tomography or magnetic resonance imaging, are limited to millimetre-scale resolution and are insensitive to blood-flow dynamics. Here, we show that ultrafast ultrasound localization microscopy of intravenously injected microbubbles enables transcranial imaging of deep vasculature in the adult human brain at microscopic resolution and the quantification of haemodynamic parameters. Adaptive speckle tracking to correct for micrometric brain-motion artefacts and for ultrasonic-wave aberrations induced during transcranial propagation allowed us to map the vascular network of tangled arteries, to functionally characterize blood-flow dynamics at a resolution of up to 25 μm, and to detect blood vortices in a small deep-seated aneurysm in a patient. Ultrafast ultrasound localization microscopy may facilitate the understanding of brain haemodynamics and of how vascular abnormalities in the brain are related to neurological pathologies.

Obtaining functional information of living organs non-invasively across different scales is a major challenge of medical imaging research, as diseases often start locally at the cellular level before inducing large scale observable symptoms. Brain imaging adds another layer of complexity, as the organ relies on extremely complex, multiscale and interpenetrated networks of neurons, glial cells and vessels. Assessing brain vascular morphology and function is key of course for the diagnosis and monitoring of intracranial aneurysms, stenosis or arteriovenous malformations and for the management of acute stroke. It is also of interest for neurological pathologies, such as degenerative diseases¹, as there is increasing evidence for a close interaction between cerebrovascular diseases and cognitive impairment². In humans, most of this cerebrovascular imaging is performed using expensive, ionizing and/or invasive contrast injection dependent techniques, namely computed tomography angiography (CTA) and magnetic resonance angiography (MRA). Furthermore, they are often limited to an anatomical description of the vasculature at a millimetric resolution, and without capturing the blood flow time dynamics relevant for assessing cerebrovascular function. No in vivo and non invasive imaging technique has so far been proven able to capture anatomical and functional features below the millimetric scale at the whole-brain level in humans. In this brain clinical imaging landscape, contrast-enhanced ultrasound is marginally used. It is mostly performed through transcranial acoustic bone windows (Figures 1a,b), if present, when imaging contrast of a regular Doppler examination is too low, to monitor blood flow velocities in large cerebral basal arteries in the case of spasms, stenoses, vascular malformations, dissections or after acute ischemic stroke. It is an easy-to-use, low-cost, widely available bed-side method that shows haemodynamics in real time across the brain. However, its poor spatial resolution and limited sensitivity still prevent contrast-enhanced ultrasound from being a decisive imaging modality for cerebrovascular diseases.

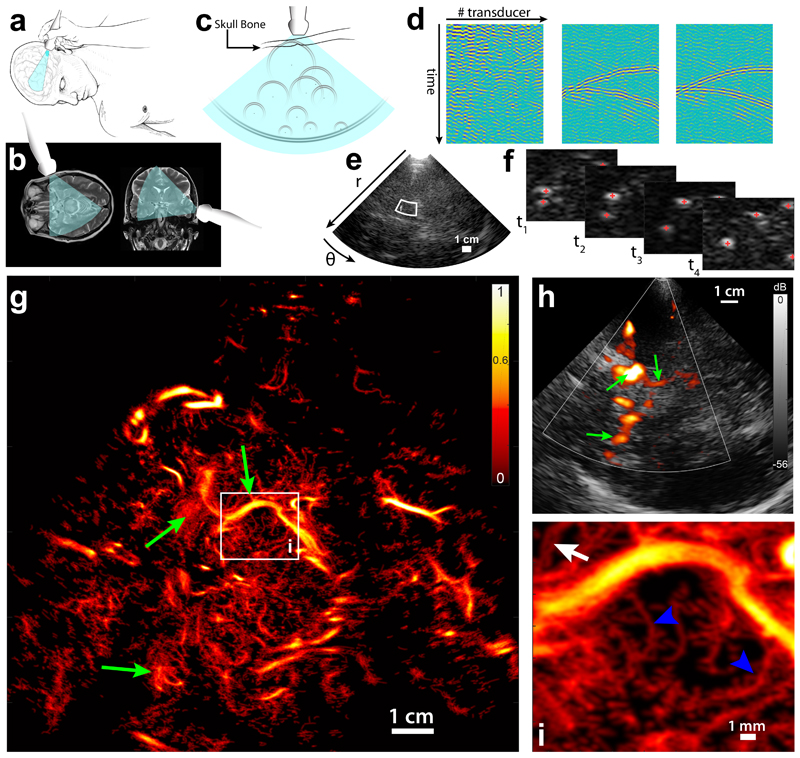
Figure 1. Transcranial Ultrasound Localization Microscopy of deep brain vessels in patients.

a. Positioning of the ultrasound transducer (Phased array XP 5-1, Supersonic Imagine) on the bone temporal window for brain imaging. b. Typical field of view in transverse and coronal brain sections. c. Diverging waves cover a wide field of view. Isolated microbubbles backscatter circular wave fronts toward the transducer array, which are distorted by the skull bone. d. Schematics of the aberration correction: (left) each transducer records the echoes backscattered from the brain, (middle) after singular value decomposition (SVD) filtering wave fronts from individual bubbles are visible and aberration law can be determined, (right) after time reversal of estimated aberration delays, bubbles echo returns to an expected hyperbola profile. e. After aberration correction, image reconstruction is performed on a polar (r,θ) grid. White box depicts zoomed area in f. f. After SVD filtering individual bubbles are localized, geometric centers are estimated and tracking of trajectories is realized. g. After the tracking of all bubbles in the field of view, a density map is reconstructed (using here 45 s of acquisition). White box depicts the zoomed panel i. Green arrows are landmarks to compare with h. Single micrograph. Scale Bar 1cm. h. Conventional Doppler image obtained in the same imaging plane as g. Green arrows are landmarks to compare with g. i. Zoom on a 15 × 17 mm area: small penetrating vessels of the mesencephalon are visible (blue arrowheads), and two very close vessels (350 μm apart) can be observed.

The recent introduction of ultrasound localization microscopy (ULM) solved the conceptual trade-off between spatial resolution and penetration depth while increasing sensitivity thanks to the joint use of ultrasound contrast agents and ultrafast imaging. ULM relies on the same kind of concept that has been the basis for the development of PALM³ (photo-activated localization microscopy) and STORM⁴ (stochastic optical reconstruction microscopy) in optics: even if an imaging modality is diffraction-limited, in the particular case of imaging an isolated object we can hypothesize that this object is at the centre of the diffraction spot. We can therefore localize it with a sub-resolution precision that depends on the signal to noise ratio of the imaging device⁵. In the case of ultrasound imaging, these isolated objects consist in diluted ultrasound contrast agents, and the method gains from imaging at the fastest rate possible⁶. ULM demonstrated the unique ability of ultrasonic waves to perform non-invasive deep microvascular imaging at the microscopic scale in rodents^5,7–9.

However, even though the ULM concept was introduced almost 10 years ago⁷, no translation of ULM imaging to the human brain has been shown so far. Indeed the application of ULM to microvascular brain imaging in humans faces major challenges, such as non-invasive brain accessibility, limited acquisition time, transcranial propagation and brain motion. Our group showed brain flow imaging in humans without contrast^10–13 using ultrafast Doppler Ultrasound, but never both transcranially and with superresolution: it was either performed in neonates through the fontanel or in adults during brain surgery (a result reproduced by Soloukey et al.¹⁴ in 2020) using an opened skull flap. Moreover, imaging without contrast agent does not allow so far to beat the diffraction limit and would result in the case of transcranial imaging to images with a resolution of the order of 1 to a few mm, 2 orders of magnitude above ULM. Imaging through the skull trans-temporally imposes the use of a small acoustic aperture because the acoustic temporal bone window rarely exceeds 20 mm in diameter, and the use of a low imaging frequency because the ultrasound attenuation coefficient in the skull is very strong, and highly increasing with frequency: it scales in f ^2.1 around 1MHz, 2.1 being the highest frequency exponent of all biological tissues¹⁵. This large ultrasound attenuation is explained by two mechanisms¹⁶: irreversible absorption in the bone and theoretically reversible diffraction effects due to the speed of sound mismatch between the brain tissue (~1500m.s⁻¹) and bone (~3000m.s⁻¹) that distorts the acoustic wave front (Figure 1c), a process called wave aberration^17,18. Finally, the influence of motion artefacts highly escalates in the micrometric resolution range and is of first importance, as ultrasound is traditionally handheld and as the brain moves inside the skull cavity.

Results

In this paper, we demonstrate transcranial deep imaging of human cerebrovascular haemodynamics at the microscopic scale by jointly solving the major challenges of spatial resolution, skull bone aberration and motion artefacts for transcranial ULM. We show that not only ULM is doable in human adults transcranially, but also that at this low ultrasound frequency, with an expected low SNR and in the presence of motion we could achieve resolutions of the order of 25 μm far beyond the typical 1 mm resolution of fUS imaging, a resolution never reached to our best knowledge by any other modality. First, we used a phased array transducer of 19.2 mm acoustic aperture, driven at a 2 MHz central frequency: this choice corresponds to a trade-off (suppl Figure 1a–b) between emitting as much as possible within the transducer’s available bandwidth (it is 1 to 5 MHz and central frequency is 3MHz, most available low frequency imaging transducers are not designed to efficiently emit ultrasound below 2 MHz), keeping the skull bone attenuation coefficient as low as possible^15,19 (10 dB/cm at 1 MHz, 40 dB/cm at 2 MHz, 60 dB/cm at 3 MHz) (suppl Figure 1a), targeting as much as possible an efficient backscatter coefficient for the contrast agent²⁰ (η = 3.5 10⁻³ cm⁻¹ at 1 MHz, η = 8.9 10⁻³ cm⁻¹ at 2 MHz. η = 1.2 10⁻² cm⁻¹ at 3 MHz), and keeping the highest possible resolution (at 2MHz, axial resolution to 0.82 mm ± 0.07 mm and lateral resolution between 1 and 5 mm, depending on the imaging depth) (suppl Figure 1c–e). Then we implemented ultrafast ultrasound imaging²¹ using unfocused diverging waves, a technique that has previously been proposed for ultrafast cardiac imaging²² and been adapted here to human brain imaging. It uses the propagation of circular waves before recording the intracranial backscattered echoes. The patient is injected with small boluses (0.2 mL) of contrast agents to attain a diluted concentration of microbubbles in the circulating blood. We chose a bolus dose that: - provided sufficient dilution for the microbubbles for individual identification, and enough concentration for an acquisition in a short time compared to what is described in the ULM literature – would allow for multiple injections in the case of probe repositioning – would remain in total lower than the maximum recommended dose of 2.4 mL²³.

The individual detection of each of these highly reflecting gas bubbles is exploited both for the correction of skull bone aberrations on the reflected wave fronts (Figure 1c, detailed in suppl. Figure 2) and for subsequent super-resolution imaging of blood vessels. The recorded raw data corresponded to a 2-dimensionnal (2D) spatio-temporal speckle pattern (schematized by Figure 1d, left), resulting from the interference of ultrasonic waves backscattered from a random set of scatterers. In these data, the tissue signal has a completely different spatial coherence signature as compared to the signal of moving microbubbles. Using a spatio-temporal singular value decomposition filter²⁴ on these data enables us to retain only the contribution of individual microbubbles (Figure 1d, middle). Therefore, assuming the acoustic sound speed to be constant in the brain, the backscattered echo of an isolated bubble will appear as a hyperbolic wave front in this particular space-time representation, with a slight aberration due to the propagation through the skull bone. The aberration law is modelled as a near-field phase screen introducing time delays on each element of the phased array^25,26. These aberration delays are determined for typically 10³ bubbles/s enabling averaging and local tuning (the same aberration law is suited for a determined area of the image thanks to the isoplanatism approximation, suppl Figure 2g), and used to correct for the aberration (Figure 1d, right, suppl. Figure 2h) before beamforming the raw data into images on a polar grid (Figure 1e). Such adaptive beamforming increases the number of microbubbles detected (increase between +5% and +13% if considering bubbles whose track length are >10 frames, can be up to +43% when considering bubbles whose track length are >30 frames, see Supplementary Figure 2j, and Supplementary Figure 2a–f for visual comparison). The stack of resulting images is then filtered using a SVD spatio-temporal filter²⁴ to keep only the microbubble signal (Supplementary Video 1), and the sub-pixel position of the microbubbles is determined using a parabolic fit of local maxima for each image (Figure 1f, Supplementary Video 1). Trajectories are obtained using a particle tracking algorithm²⁷, microbubble positions are corrected taking into account motion artefacts estimated using phase correlation of ultrafast US data (Supplementary Figure 3), before building an image out of the positions of the microbubbles in the entire field of view: trajectories are interpolated so that each pixel of the high resolution grid on the bubble trajectory is lightened up, before taking into account the uncertainty of the bubble position by convolving this “bubble presence grid” with a Gaussian kernel (whose spatial extent is function of the resolution). This produces an image whose contrast can be interpreted as proportional to the probability density function of the microbubble distribution, and which is given between 0 and 1 (Figure 1g). In a 45 s acquisition, a 2D image revealing vascular structures with unrivalled sharpness can be obtained. It shows for example very precisely part of the Willis polygon and the posterior cerebral arteries, as can generally be observed with a conventional clinical ultrasound scanner with much lower resolution (Figure 1h, green arrows). But most importantly, a very large number of small calibre vessels, such as small (Ø < 200 μm) arteries penetrating the mesencephalon, can be visualized (Figure 1i, Supplementary Video 1).

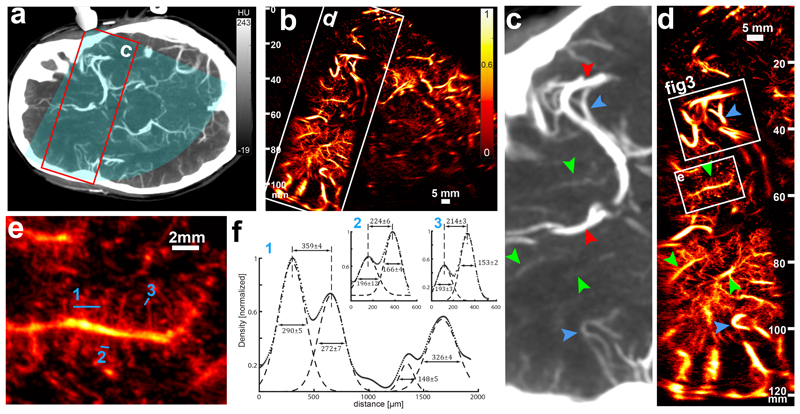
Compared with a typical clinical contrast CT imaging (Figure 2a, c), transcranial ULM (t-ULM) shows increased sensitivity and resolution (Figure 2b) at all depths (here up to 120 mm, which extend to the contralateral cortex) (Figure 2d). Note that subtle anatomical differences may appear when comparing the two images as the CT image represents a 6 mm constant thickness slab, whereas the thickness of the ultrasound image varies in space due to elevation focalization²⁸. Our images have better quality near 60-70 mm depth, as it corresponds to the elevation focus of the probe, and are degraded at large depth due to the loss of this elevation focalization, and therefore of larger out-of-plane uncertainty on the localization of the microbubbles. Attenuation is of course also a factor, but we can see in Figure 2d that sensitivity is still good at 110mm (vessels are visible) while resolution is degraded (vessels are blurry). The biggest vessels, such as the middle cerebral artery (MCA) or the anterior cerebral artery (red arrows), as well as smaller branches (blue arrows), are visible in both modalities, but many structures that are faintly captured by CT (green arrows) become clearly visible on t-ULM (Figure 2e), with at least two more degrees of vessel branching delineated (Supplementary Figure 4). At first glance, the resolution increase compared to conventional ultrasound exceeds at least one order of magnitude as neighbouring vessels that are estimated to be 214 μm apart at 60 mm depth can be evidenced from this image (Figure 2f). However, quantifying the spatial resolution by resolving two nearest small vessels is not an adapted approach as it is very unlikely to track a sufficient number of microbubbles flowing in two extremely close microvessels in the 45s acquisition time. Therefore, the proper estimation of t-ULM spatial resolution will be detailed further in the paper based on a functional rather than an anatomical definition.

Figure 2. Estimation of the ULM resolution in a standard imaging case.

a. Patient brain axial CT scan section (6mm-thick slab) depicting the ultrasonic field of view (blue overlay) and the ROI in c and d (red rectangle). b. ULM image (2 min 15 s of acquisition) obtained in the same section, with the ROI in c and d. Replicates in 2c-e are only technical. Single micrograph. Scale Bar 5 mm c. The CT scan shows the distal part of the middle cerebral artery (red arrow, top) and a segment of the anterior cerebral artery (red arrow, bottom). Very visible vessels (blue arrowheads) are also depicted as landmarks for visual comparison with ULM image d. Some structures are faintly observable (green arrowheads) d. ULM brain imaging in the same ROI (up to 120 mm depth). Blue and green arrowheads are the same landmarks than in c. Two ROIs (white boxes) are represented for further quantification in e and f and in figure 3. e. ROI (15 × 16 mm) delineating a small penetrating vessel and its radial ramifications. Numbered blue lines are used for cross section profiling in f. f. Cross sections of a wide set of vessels (1) and two pairs of close vessels (2 and 3). Dots represent the image data (see Density and Velocity display in M&M) (arbitrary unit) and dashed lines the Gaussian fit of the vessel cross sections. Inter-peak distance and full width at half maximum are given in μm with 95% confidence intervals.

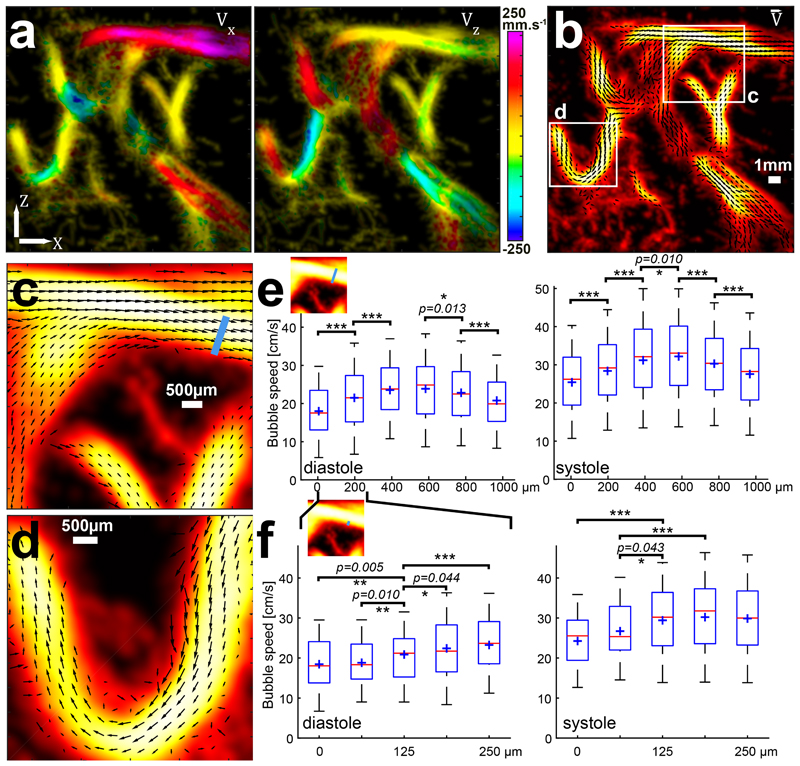
Indeed, the sub-resolution positions can be used to build an anatomic t-ULM image, but more interestingly, these positions are part of a trajectory that provides each microbubble with an instantaneous 2D speed vector (Figure 3a) and reveal the flow dynamics (Supplementary Video 2). This enables us to build vector field maps of the flow velocity inside vessels of 1 mm diameter or less (Figure 3b). In Figure 3c, one can deduct from the very sharp change of direction that we are in the presence of two overlapping but not connected vessels, while it was not obvious on the anatomical-only image. Also, Figure 3d shows a turbulent flow in the turn of the U-shaped vessel, with a large variety of flow speed magnitudes across the vessel section due to the strong change of direction. We have quantified the functional t-ULM resolution on a cross section of the vessel in Figure 3c, at 3 different scales (see Flow quantification and functional resolution estimation in the Methods). When taking bubble speeds in 188 μm wide bins along this 1 mm wide cross section it exhibits a typical parabolic blood flow profile with significant speed differences (Figure 3e). Furthermore, this cross section flow speed analysis can also be conducted at different moments in the cardiac cycle thanks to the very high temporal resolution of ultrafast imaging (see Motion detection and correction in M&M), showing an increase of the central median speed from 24.9 ± 6.2 cm/s in diastole (Figure 3e, left) to 33.1 ± 7.8 cm/s in systole (Figure 3e, right). When looking at the vessel edge where the speed gradient is the sharpest (Figure 3f), it is possible to exhibit significant differences on 62 μm wide bins both in systole and diastole, corresponding to λ/12 (equivalent to conventional axial resolution/12 and conventional lateral resolution /24 at this 38 mm depth, with a numerical aperture of 2, see suppl. Figure 1). When taking 25μm wide bins, it is still possible to exhibit significant speed differences) near the edge of the vessel but only in diastole, probably due to a more regular flow and a higher number of detected bubbles (suppl. Figure 5). The maximum achievable resolution in the experimental conditions of the present study is therefore 25μm, but might be improved with longer acquisition time or more efficient aberration corrections and motion compensation techniques.

Figure 3. ULM characterizes hemodynamics and discrimates diastolic and systolic flow.

a. X and Z component of the speed vector extracted from the bubble trajectories overlaid on the density map. Single Micrograph. Scale Bar 1mm. b. Combination of these two components enable quantitative representation of the flow vector fields inside those 1 mm wide cerebral vessels. Two ROIs are drawn for further zoom in c and d. c. A 6 × 6 mm ROI of the speed vector representation shows two superimposed vessels (top) (crossing without junction). The two bottom vessels, with lower flow speeds, are joining veins. Black arrows quantify the local flow speed (Arrow direction corresponds to the flow direction and arrow amplitude corresponds to the blood flow amplitude) d. A 5 × 5 mm ROI showing a sharp turn in an artery. The velocity profile across the vessel is very asymmetric due to the tortuosity of the vessel. e. Quantitative assessment of the velocity profile across the whole 1 mm section of the artery of c. (blue line in the thumbnail). Bubble velocities are gathered in 188 μm wide bins (λ/4≡ diffraction-limited lateral resolution/8 at this depth); red central line indicates the median; boxes, 25^th and 75^th percentile; whiskers are ± 1.26 σ corresponding to 80% coverage in the Gaussian hypothesis (blue cross represents mean value). Significant differences in the mean value have been tested with p < 0.05 (*), p < 0.01 (**) and p < 0.001 (***), Analysis of variance (ANOVA) with post hoc t-test with Bonferroni correction. This quantitative velocity assessment has been done during diastole (left panel) and systole (right panel), showing largely increased bubble speeds during systole. Mean and variance (in mm/s) and samples number (bubble positions) corresponding from left to right bins (188 μm): 180+/− 78 (N=714); 215+/− 86 (N=2162); 235+/− 83 (N=2593); 239+/− 90 (N=2081); 228+/− 83 (N=1194); 208+/− 79 (N=670) during diastole (p-values are 1.1.10⁻¹⁹, 7.0.10⁻¹⁵, 0.013 and 1.3.10⁻⁵). and 254+/− 95 (N=579); 284+/− 103 (N=1575); 312+/− 106 (N= 2619); 322+/− 100 (N=2410); 303+/− 92 (N=1206); 276+/−99 (N=547) during systole (p-values are 6,6.10⁻⁸, 2,3.10⁻¹⁶, 0.010, 3,7.10⁻⁶ and 5,7.10⁻⁶). f. The same quantitative assessment, on the extreme border of the vessel, on a 250 μm wide cross section (see thumbnail). Bins are now 62.5 μm wide (λ/12≡ diffraction-limited lateral resolution/24 at this depth) and still show significant speed differences where the speed changes are the sharpest. Mean, variance and samples number (bubble positions) correspond from left to right bins with 65 μm: 185+/− 70 (N=213); 188+/− 71 (N=301); 209+/− 76 (N=401); 225+/− 88 (N=510); 233+/− 87 (N=525) during diastole (displayed p-values are 1-3 5.10⁻³, 2-3 0.010, 3-4 0.044, 3-5 9,5.10⁻⁵) and 243+/−90 (N=173); 267+/− 88 (N=206); 294+/− 95 (N=230); 302+/− 102 (N=364); 299+/− 101 (N=528) during systole (displayed p-values are (1-3) 2.1.10⁻⁶, (2-3) 0.04, (2-4) 5.10⁻⁴, (2-5) 0.01).

In a 79-year-old patient (Supplementary Figure 6) presenting with an aneurysm on the distal part of the right MCA, t-ULM using 24 s acquisition time (Figure 4a) showed an increased sensitivity and resolution as compared to both CTA (Figure 4b) and time of flight MRA (Figure 4c). Common features, such as the communicating posterior cerebral artery and part of the Willis polygon, can be observed (blue arrows), but numerous other vessels invisible on those two major clinical modalities are unveiled, despite a very short time of acquisition. The aneurysm is very obvious under the form of an excrescence at the bifurcation of the right MCA (Figure 4a, green arrow) both in clinical images and on the t-ULM image. But beyond this, t-ULM brings an exhaustive functional comprehension of the blood flow pattern inside this aneurysm, when CT and MRI only give its anatomical description. Indeed, t-ULM reveals a small vortex inside the left part of this aneurysm whose blood flow dynamics can be characterized thanks to this 25μm resolution (Figure 4 d–f, Supplementary Video 4). The potential for such imaging is hard to predict, but it could be possible that the degree of clotting or the risk of rupture of a given aneurysm might be influenced by the local fluid mechanics and blood flow speeds reached in the aneurysm. Numerous studies try to link local flow mechanics, wall shear stress and health of the vessel wall^29–31. Therefore such unique functional information could be of clinical relevance for making the decision regarding surgical resection or coiling.

Figure 4. Clinical relevance of transcranial ULM is illustrated for a deep seated aneurysm.

a. ULM (24 s of acquisition) tilted axial brain section of a patient diagnosed with an aneurysm (green arrow) in the right MCA. Blue arrow depicts vascular landmarks visible on CT and MR images for the reader’s sake. The three white boxes correspond to the enlarged images of d–f. Representative micrograph, out of 3 images obtained. b. Maximum intensity projection of a 6 mm thick CTA slab corresponding to the ULM imaging plane. c. Maximum intensity projection of a 7 mm thick MRA slab corresponding to the ULM imaging plane. d. A 12 × 12 mm ROI on the MCA aneurysm depicting the local flow vector field. The longest arrow corresponds to a 20 cm/s speed, values above 20 cm/s are clipped. e. A 2.5 × 2.5 mm ROI on a flow vortex inside the aneurysm. f. Further zoom on an 800 × 800 μm ROI centered on the vortex, showing almost null velocity at the center. Longest arrow corresponds to a 5 cm/s speed, values above 5 cm/s are clipped g. ULM (24 s of acquisition) brain section of a patient presenting with an occlusion of the right MCA, resulting in the abnormal development of a large number of collateral arteries (white boxes). Contralateral side is visible for visual comparison. Single micrograph. h. Maximum intensity projection of a 10 mm thick CTA slab corresponding to the ULM imaging plane, where these collateral arteries are faintly observed and without functional information (flow). i. and j. ROIs (10 × 10 mm) on these collateral arteries depicting the direction and magnitude of the flow, stop points and bifurcations, enabling functional quantification. Longest arrow corresponds to a 20cm/s speed.

In a 63-year-old patient (Supplementary Figure 7) presenting with chronic cerebral hypoperfusion, right posterior cerebral artery of foetal origin and an early occlusion of the right MCA that led to the development of a complex local network of collateral arteries (Moya Moya³²-like disease), t-ULM (Figure 4g) using 24 s acquisition time largely surpasses the CTA image (Figure 4h) in terms of sensitivity (white boxes). While it is difficult to assess the functional efficiency of each of these collaterals on a CT or MR image, it becomes very easy to understand where the flow is distributed with t-ULM thanks to the capture of both flow speed and directions in all these vessels at microscopic scales (Figure 4i,j, Supplementary Video 3).

Discussion

By revealing both human cerebral vascular anatomy and flow dynamics at microscopic scales, t-ULM is very likely to become of major importance for the management of cerebrovascular diseases in the future. Its low cost, ease of use, sensitivity and quantification capabilities joined with almost two orders of magnitude improvement in terms of resolution as compared to current clinical modalities could disrupt the workflow of cerebrovascular patient management. One main limitation of this present study stands probably in the lack of real time processing for positioning the probe, this crucial positioning being performed using only the guidance of the B-Mode and conventional color Doppler. With our current ultrasound machine, raw data are saved to disk for off-line processing due to limited computation capabilities and fine tuning of image reconstruction parameters. Currently, calculations are performed on a regular computer (Intel® Xeon® CPU E5-2630 @2.40 GHz, NVidia GeForce GTX Titan X) with limited optimization (mostly Matlab® code), and typical post processing time for 1s of acquisition is: beamforming + aberration correction (8 s + 45 s + 8 s), filtering (0.5 s), localisation (45 s), bubble tracking (1 min). The two last operations are non-optimised matlab based calculations that can be heavily accelerated. In particular localization is heavily parallelizable as it is image independent, and bubble tracking can be done in parallel on image sub-patches, which would drastically reduce the calculation time as it is non-linear with the number of bubbles considered. Real time t-ULM displays (or at least partial displays) would enable to tackle less obvious cerebrovascular pathologies, such as very small aneurysms, stenoses or defects in small vessels. These aspects are only due to the computational power available on our scanner and real time displays will be achievable in the next few years.

It is difficult to infer the success rate of t-ULM based on our present study compared to color Doppler imaging³³, as we need a larger cohort. In Europe, so far, Sonovue® is routinely used in neurosonology in order to image difficult patients (absence of temporal bone window), with a good success rate, but it is difficult to foresee how the precision of t-ULM will be patient–dependent. Sonovue® has been approved in more than 40 countries, is widely used in Europe for various imaging applications. It is routinely used for transcranial ultrasound Doppler imaging in a lot of European countries such as Germany, Switzerland, Portugal or France. It has been approved in the US under the name LUMASON for echocardiographic and liver imaging applications both in adults and children, underlining its innocuousness. As transcranial color-coded ultrasound is only performed in a very few specialized medical centers in the US, SonoVue/LUMASON is not registered for this application. Nevertheless, the concept of ULM should be applicable to any other approved contrast agents (Optison, Levovist, Definity).

One important limitation of our work is the limited access provided by the temporal sutures through which sound can enter the brain. This was actually a deliberate choice to choose an ultrasonic probe and a hardware setup as close as possible to what is already available in the clinics. The obtained images show very good delineation of the central cerebro-vascular structures, but maybe with a slightly lower central frequency and deeper elevation focus we could envision good delineation of the cortical structures from the contralateral temporal window, and therefore whole brain imaging using both temporal windows. However, we could also imagine lifting the temporal access constraint by an important technological development involving much larger transcranial matrix probes working at lower frequency. By taking into account the skull bone attenuation coefficient and the backscatter coefficient of Sonovue® (suppl Figure 1a), there could be a huge advantage at developing large ultrasonic helmets working at low central frequency of 1MHz or below. Simulating the relative receive signal amplitude when using Sonovue microbubbles and propagating back and forth through 1cm of skull bone, there is a typical 50 dB difference between working at 2 MHz and 1 MHz (F.J. Fry and J.E. Barger, 1978). There will of course be a small loss of resolution, but that might be largely compensated by the much larger apertures, as the temporal window would not be a constraint anymore. Also, working on contrast agents with a peak of backscatter coefficient at lower frequency might be of interest.

3D t-ULM imaging would also be of major interest in particular for screening. There is no impediment to it as proofs of concept of 3D ULM in flow phantoms were recently published³⁴. 3D t-ULM imaging would probably reduce the examination time, operator dependence and injected doses of microbubbles, improving the workflow of the clinicians. Beyond clinical applications, the ability of t-ULM to reveal human cerebrovascular dynamics at microscopic scales will profoundly expand our fundamental understanding of brain vascular function and dysfunction.

Methods

Patient management and safety of imaging protocols

All experiments strictly complied with the ethical principles for medical research involving human subjects of the World Medical Association’s Declaration of Helsinki. One Healthy volunteer and three patients were recruited from the ambulatory consultation unit and from the stroke unit/neurovascular ward after giving informed and written consent according to the imaging protocol approved by the ethical committee of Geneva (CCER 2017-00353). The three patients presented in Fig. 1, 2 and 4 are different individuals: Patient 1 is a female patient, 27 years old, healthy volunteer (Figure 1). Patient 2 is a female patient, 25 years old, no cerebrovascular pathology targeted (Figure 2 and 3). Patient 3 is a male patient, 79 years old, aneurysm on the distal part of the right MCA (Figure 4 a–f). Patient 4 is a male patient, 63 years old, chronic cerebral hypoperfusion, right posterior cerebral artery of foetal origin and an early occlusion of the right MCA that led to the development of a complex local network of collateral arteries (Figure 4 g–j). By minimizing the dose of injected contrast agent to the minimum enabling the ultrasound localization microscopy and by minimizing the amplitudes and durations of the ultrasound exposures, the imaging sessions followed the ALARA principle. These were largely below the FDA recommendations (AUIM/NEMA 2004, Track 3) for ultrasound imaging, with a maximum mechanical index (MI) of 0.46 (FDA recommended maximum value is 1.9), a maximum derated spatial peak temporal average intensity (ISPTA) of 64.3 mW/cm² (FDA recommended maximum value is 720 mW/cm²) and a maximum thermal cranial index (TIC) of 1.99 (no recommendation but FDA regulations ask for an explanation for values above 4).

The overall aim of the study and procedures were explained to the patients before procurement of the informed and written consent. An intravenous cannula was placed in the medial cubital vein for subsequent injection of ultrasound contrast agents (SonoVue, Bracco, Italy). SonoVue® (8 microlitres/ml powder and solvent for dispersion for injection) is an ultrasound contrast agent consisting of a suspension of tiny microbubbles (most microbubbles between 2 and 9 microns) with a unique structure made of an inert gas, sulphur hexafluoride, and a phospholipid shell that provides stability and prevents microbubble coalescence. When injected intravenously, Sonovue® strongly enhances the echogenicity of blood, which results in an improved signal-to-noise ratio. It is commonly used in many European countries when the temple acoustic window does not allow good visualization of the intracranial vessels. It is quickly eliminated from the bloodstream in the lungs (EMA / 502204)³⁵ with a mean terminal half-life of 12 min. The use of second-generation contrast agents, such as SonoVue, is approved in Europe for cerebrovascular applications in humans (European medicine agency decisions EMA / 502204 / 2015 & EMEA / H / C / 000303).

Safety measurement procedures

Ultrasonic amplitudes and durations were evaluated using certified Acoustic Measurement Tank and its software (Acertara, Colorado, USA), following the provided calibration procedures. After probe alignment in the depth direction, a Z-scan was performed in the aperture’s centre to obtain the pressure profile. Raster scans were then done in three depth positions (1) Z = 0.5 cm, 2) Z = 1 cm and 3) Z = 6.5 cm), respectively, corresponding to measurements 1) in the near field at the skull location, 2) just behind the skull and 3) at the probe elevational focus. The regulation indices (Mechanical Index MI, ISPTA, and TIC) were then measured at each depth position (including measurement of the maximum peak negative pressure in the radiated ultrasonic field for MI and ISPTA calculations, and integration of the ultrasonic energy over the ultrasonic field spatial extent at each depth for TIC calculations), before using the maximum value over the three depths for each regulation index. Maximum MI was 0.465 (at 0.5 cm, value 0.202 at 6.5 cm, measured in water, will be highly mitigated by the presence of the skull (typically divided by a factor 5.6 if we consider a 15dB attenuation due to 0.5cm of skull bone)) (FDA recommendation is < 1.9) and maximum derated (−3 dB/cm) ISPTA was 64.3 mW/cm² (FDA recommendation is < 720 mW/cm²). Those values measured in water are probably much lower when imaging the patient due to skull bone attenuation. Thermal indices (TI) were also calculated and reached maximum values of 1.49 (TI soft tissue), 1.9 (TI bone) and 1.99 (TI cranial), largely below the limit of 4 recommended by the FDA (values above 4 are possible but should be explained). The TI is defined as TI=W_p/W_deg, where W_p is the relevant (attenuated) acoustic power at the depth of interest, and W_deg is the estimated power necessary to raise the tissue equilibrium temperature by 1°C according to a chosen specific tissue model.^36,37 Therefore, a TI value of 2 would correspond to a 2°C increase in equilibrium temperature assuming a worst case scenario. In our case the most important index is the cranial TI (TIC), and it largely overestimate the temperature rise as it is designed for continuous ultrasound imaging, while in our case ultrasound is on only half of the duration of the examination (1s of acquisition, 1 s of pause).

Ultrasonic sequences

Ultrasonic acquisitions were performed using an ultrafast programmable scanner (Aixplorer, Supersonic Imagine, Aix en Provence, France) and a phased array ultrasonic probe (XP 5-1, Supersonic Imagine) (central frequency 2.93 MHz, 90% bandwidth at −6 dB, pitch 0.2 mm, 96 elements). Ultrafast ultrasound imaging sequences consisted of the emission of diverging waves coming from four virtual sources regularly spaced (every 3.2 mm) placed 11.44 mm behind the transducer array (giving a 80° angular field of view). Choice of the central frequency was based on an optimization on 3 parameters whose evolution vs frequency is given in suppl Figure 1a : available transducer bandwidth (given by the transducer constructor), skull attenuation coefficient α_skull (adapted from Bamber et al¹⁵) and Sonovue® backscattering coefficient η (adapted from Schneider et al²⁰). Supplementary Figure 1 b shows in black the curve combining those parameters (BW is squared as the signal passes through the transducer at emission and at reception, α_skull is actually calculated for a total distance of skull propagation of 1 cm (0.5 cm thickness back and forth, this length actually does not influence the position of the peak), the backscatter coefficient η is taken as a square root as it comes from a power measurement and we are considering amplitude of the received signal). Supplementary figure 1 b shows in red the spectrum of the 2 MHz-2 cycle-squared electric pulse sent from the ultrasound scanner to the ultrasound transducer: it fits nicely above the black curve, we chose a slightly higher frequency in order to keep as much resolution as possible, it is a squared signal as this is the kind of signal that ultrasound pulsers are able to emit. Therefore ultrasonic pulses consisted of two cycles centred at 2 MHz, fired at the maximum pulse repetition frequency allowed by the desired imaging depth (typically 4900 Hz) by groups of four pulses (for the four sources), repeated at a “frame rate” of 800 Hz (“frame rate” means at which frequency compound frames made of the 4 different virtual sources of insonification are outputted) during 1 s. For each pulse, backscattered echoes were recorded by the transducer array, digitalized at 200% bandwidth (meaning four samples per wavelength), and stored in a so-called radiofrequency (RF) data matrix. These RF data matrices are the starting point of aberration correction and image reconstruction. This operation was repeated every 2 s, which is the fastest sequence rate achievable by our system at this point that enables to save on the enormous amount of data to disk (several Gb/s) for further processing. To summarise: for 1s, the ultrasound is on and both pulsing diverging waves at 4900Hz and acquiring data, for 1s, the ultrasound is off and saving the RF data that were just acquired to disk, and this process loops during a desired duration (45 s for patient of figure 1, 2 min 15 s for patient of figure 2 and 3, 24 s for patients of figure 4).

Aberration correction and beamforming procedures

The correction of skull bone aberrations induced during transcranial propagation can be done in a two-steps approach as already discussed ex vivo ^38–40. First, we analyse the wavefront reflected by individual microbubbles acting as point-like sources in the medium. This reflected wavefront corresponds to the exact Green’s function relating the source location to each element of the ultrasonic array and can be used to measure the skull aberration. Secondly, the time reversed version of this aberration law (corresponding to the temporal delays induced by the skull bone during the backward propagation) is introduced as a time shift correction on each element of the array before reprocessing the beamforming of the raw ultrasonic data and produce corrected ultrasonic images. SVD clutter filtering was performed on the RF data matrices to remove tissue signal and isolate wave fronts coming from individual microbubbles. Uncorrected images were reconstructed from these filtered RF matrices using delay-and-sum beamforming on a polar (r,θ) grid with classical spherical delays, and bubble positions corresponding to the isolated wave fronts were stored, along with the forward and return spherical delay laws associated with these positions. For each considered bubble, the forward delay law was used to virtually focus the filtered RF signals from the four diverging wave emissions on the bubble location, and the return delay law was then used to flatten the isolated wave front. The phase aberration profile was calculated via cross-correlation, as the remaining relative delays appeared in the wave front across the transducer elements. Measurement of the spatial coherence of the wave front was used as a metric for convergence, and only the bubble positions that encountered an increase of this coherence through this iterative process were kept until the end.

Phase aberration laws were compared over the whole image to determine isoplanatic regions within which the aberration could be considered constant (variations across bubbles < T/8). Individual bubble aberration laws were averaged within each of these regions, and corrected images were reconstructed from raw RF data using regionally-corrected delay laws in a delay-and-sum beamforming on a polar (r,θ) grid.

Motion detection and correction

Tissue motion within 1 s stack of images was estimated using cross-correlation techniques already described for ultrasonic tissue displacement or strain estimations^41,42. Briefly, estimation of the inter-frame axial displacement was obtained by multiplying the in phase-quadrature content of one pixel by the complex conjugate content of the same pixel in the subsequent frame. This was done for all pixels; a 3 × 3 pixel averaging filter was used before estimating the phase of the complex in each pixel, being proportional to the inter-frame displacement. This displacement was also used to detect the systole time point, as the tissue motion will be larger and exhibit a distinct peak during the systole. Therefore, each microbubble spatial position was accompanied by a time position relative to the systole position, enabling discrimination between systole and diastole. This will be used for further intra-cardiac cycle speed analysis. Motion between 1 s blocks was estimated as a 2-fold process: first, by calculating the affine transformation matrix between the corresponding Power Doppler images before localization processing (pre-registration) and then by computing the fine transformation matrix on density images after localization microscopy processing of those images already pre-registered. Effect of the motion correction can be appreciated on Supplementary Figure 3.

Localization microscopy data processing

Beamformed IQ data were filtered using the SVD spatio-temporal filter described by Demené et al.²⁴ (between 35 and 60 singular values were removed depending on the level of tissue motion) to remove tissue signal and keep only the signal from the moving scatterers (the microbubbles). Magnitude of the filtered IQ signal was kept and formed a stack of images depicting the individual motion of bubbles. A binary mask was built based on the vesselness filtering^43,44 (implementation available on Mathworks file exchange, ©Dirk-Jan Kroon 2009, and © Tim Jerman, 2017) of this stack of images. The vesselness filter belongs to a particular family of image processing filters optimised to improve contrast of vascular structures in 2D or in 3D, that are particularly suited for example for improvement of vascular imaging of the retina (2D) or for improvement of 3D CT angiography. They relies on the eigen decomposition of the Hessian matrix. The Hessian matrix is defined as the convolution between the image intensity (can be 3D) and the second derivative of a Gaussian kernel, therefore it approximates a 2^nd order derivative at a certain scale⁴⁵. Taking into account the relative sign and magnitude of the eigen values of this Hessian matrix within an “enhancement function” enables to identify certain types of structures (namely plate-like, tubular, blob-like). The vesselness filter is based on a certain formulation of this enhancement function, several formulations having been proposed in the past like Frangi, Sato, Li, etc⁴⁴. This type of filter is efficient in our case as bubbles moving in time will appear in a 3D matrix (space × space × time) as tubular (vessel-like) structures, and therefore will be enhanced using a vesselness filter in 3D. Both image stack and mask stack were interpolated (Fourier space based interpolation for the image stack and nearest neighbour interpolation for the binary mask) down to a radial resolution dR=λ/6 and an angular resolution of dθ=0.5°. Local maxima detection was then performed within the masked area for each 2D image of the image stack. These local maxima are locally correlated with a typical point spread function (imaging response of an isolated microbubble) modelled as a Gaussian spot of axial dimension λ and lateral (angular) dimension of arctan $\left(\frac{\lambda }{d}\right)$, and local maxima with weak correlation (< 0.6) were discarded (local spatial speckle fluctuation can generate local maxima but are not like a point spread function). Sub-pixel maxima localization was then performed using a fast local (5 × 5 pixel neighbourhood) 2^nd order polynomial fit. Maxima positions were then converted from polar to Cartesian coordinates. Tracking of the maxima positions was performed using a classical particle tracking algorithm⁴⁶ (simpletracker.m available on mathworks ©Jean-Yves Tinevez, 2019, wrapping matlab munkres algorithm implementation of ©Yi Cao 2009) with no gap filling and maximal distance linking of 1 mm (corresponding to a bubble maximum speed of 80 cm/s). Bubble tracks shorter than detected positions were removed, which was based on the idea that microbubbles should be observed in several consecutive frames, enabling us to drastically reduce the level of false bubble detection. The successive positions gathered in one track were used to compute the interframe bubble velocity vector components V_x, V_z and velocity magnitude $\parallel \overrightarrow{V}\parallel$. The successive positions were also used to compute a curvilinear abscissa along their trajectory in order to interpolate both positions and speeds at a smaller space step (0.01 mm).

Density and Velocity display

Compared to ULM maps obtained by others^46,47 in animals in very controlled conditions and non-transcranially, the data obtained in our paper were acquired in a very short time (between 24 s and 2 min 15 s) to minimize discomfort for the patient and in challenging conditions (motion, handheld probe, and skull aberrations). Therefore, we had to make the most of all the bubbles detected during the acquisition to build a vascular map as representative as possible of the underlying vasculature. Therefore, images were built based on a position map (made of very small dots in a 0.01 mm regular grid) convolved with a Gaussian kernel whose standard deviation equals the best resolution achieved in this paper (i.e., 62 μm). This visually enhances the resulting image by smoothing vessels as compared to building and imaging them directly on a 0.062 mm grid.

Velocity vector fields where obtained on a regular grid via bilinear interpolation of the irregularly distributed microbubbles vector speed. These vector fields were also spatially filtered using a Gaussian kernel (σ = 62 μm). This enables us to display the velocity components of Figure 3b and subsequent vector field images.

Flow quantification and functional resolution estimation

For quantification on cross axis speed profiles, the speeds of individual bubbles were binned along a vessel transverse section (bubbles inside 1 mm longitudinal extent), before statistical testing (ANOVA with post hoc t-test with Bonferroni correction). Bins were 188 μm, 62.5 μm (Figure 3) and 25μm (Suppl. figure 4) wide. Were retained bubbles whose trajectories were within 1 mm on either side of the cross section. Bubbles were considered in systole when within 0.3 s around the systolic peak speed and in diastole when within 0.6 s around the diastolic minimal speed. For the 188 μm bins (6 bins), speed differences were estimated on (N=92, N=224, N=271, N=223, N=138, N=100) bubble trajectories representing respectively (714, 2162, 2593, 2081, 1194, 670) bubble positions for diastole, and on (N=79, N=171, N=267, N=223, N=141, N=75) bubble trajectories representing respectively (579, 1575, 2619, 2410, 1206, 547) bubble positions for systole. For the 62.5 μm bins (5 bins), speed differences were estimated on (N=56, N=69, N=93, N=11, N=128) bubble trajectories representing respectively (213, 301, 401, 510, 525) bubble positions for diastole, and on (N=44, N=59, N=65, N=90, N=110) bubble trajectories representing respectively (173, 206, 230, 364, 528) bubble positions for systole. Finally for the 25 μm bins (5 bins), speed differences were estimated on (N=46, N=51, N=64, N=67, N=74) bubble trajectories representing respectively (150, 122, 173, 216, 233) bubble positions for diastole.

Animated flow rendering and Supplementary Video

Computed-generated imagery (CGI) animation (supplementary material) was created using the software Houdini 17.5.360 (SideFX, Toronto, Canada) to help visualizing functional information extracted from bubble positions and tracking information. Density map and velocity vector components V_x, V_z were imported into Houdini. A particle distribution was initialized with a particle density proportional to the local bubble density. Then, particle position, size, color and life duration are updated for each frame based on the velocity vector field and local density. Depending on the field of view of the highlighted area, particles were constantly emitted at a rate of 10⁴ to 10⁵ particles.s⁻¹ with a lifetime of 3 seconds. Particle size was made proportional to the measured local microbubbles density for better vizualisation, meaning that a particle passing by a region with local high density appears bigger than a particle moving through a less dense area. Color of the particles were either based on 1/ the density color map (black to red to yellow color map) or 2/ the velocity colormap (blue to green to yellow to red map).

Finally, animation was rendered using the “3D renderer Mantra” library of Houdini software after setting-up an additional dome light effect.

Clinical imaging

The clinical image of Figure 2a,c is a mean intensity projection (MIP) reconstruction from a cerebral multi detector computed tomography (MDCT) cerebral angiogram with contrast injection. The clinical image of Figure 4b and suppl Figure 6(top) are cerebral multi detector computed tomography (MDCT) with contrast injection illustrating a sacciforme aneurysm of the right M1-M2. The clinical image of Figure 4c and suppl Figure 6 (bottom) corresponds to axial and mean intensity projection (MIP) reconstructions of a time-of-flight (TOF) MR angiography of the circle of Willis illustrating the same lesion. Figure 4h and suppl Figure 7 are Time-of-flight (TOF) MR angiography of the circle of Willis. Note the Moya-moya pattern of the left middle cerebral artery M1 segment. Dominant right A1 segment and fetal origin of left PCA as normal variants.

One-sentence editorial summary.

Ultrafast ultrasound localization microscopy of intravenously injected microbubbles enables transcranial imaging of deep vasculature in the adult human brain at microscopic resolution and the quantification of haemodynamic parameters.

Data Availability

All data supporting the findings associated with the figures of this study are available upon request. Data examples are available for download in the supplementary materials of the publication from the repository website (Zenodo.org) with the identifier https://zenodo.org/record/4048550#.X6GPlVBCdPY

Code availability

Software codes for the loading of data and for the management of data will be available. Step-by-step instructions are available in a Readme pdf document to guide the user.

Data samples and codes (Matlab) regarding the most important steps of the processing routine are publicly available without restrictions from Zenodo repository website with the identifier https://zenodo.org/record/4048550#.X6GPlVBCdPY. In this data and code package, examples are provided for:

• Beamforming (image formation): we supply raw RF data and the Matlab based beamforming routine.

• Aberration correction: we supply a demo code detailing the important steps of aberration correction. Output is an aberration correction profile for different patches of the image that can be fed into the previous bullet point.

• Data Filtering: we supply the beamformed data (output of the 2 previous bullet points) and the SVD filtering and display code for visualization of the microbubbles.

• Display code: we provide super-resolution data based on the data of the previous bullet point, along with display code along with the raw data.