Subclonal reconstruction of tumors using machine learning and population genetics

Abstract

The majority of cancer genomic data are generated from bulk samples composed of mixtures of cancer subpopulations, as well as normal cells. Subclonal reconstruction approaches based on machine learning aim to separate those subpopulations in a sample and reconstruct their evolutionary history. However, current approaches are entirely data-driven and agnostic to evolutionary theory. We demonstrate that systematic errors occur in the analysis if evolution is not accounted for, and this is exacerbated by multi-sampling of the same tumor. We present a novel approach for model-based tumor subclonal reconstruction (MOBSTER) that combines machine learning with theoretical population genetics. Using public whole-genome sequencing data from 2,606 samples from different cohorts, new data and synthetic validation, we show this method is more robust and accurate than current techniques in single sample, multi-region and longitudinal data. This approach minimizes the confounding factors of non-evolutionary methods, leading to more accurate recovery of the evolutionary history of human cancers.

Introduction

Cancers change over time through a process of clonal evolution¹, inevitably resulting in intra-tumor heterogeneity². Genome sequencing of one or more bulk samples from tumors has become the most common way to study clonal evolution in human malignancies, and studies are dedicated to the identification of cancer (sub)clones³. A cancer “clone” remains a loosely defined entity, and its purest definition is “a group of cells within the tumor that share a common ancestor”. In phylogenetic terms, this would represent a monophyletic clade. However, this implies that any ancestor in the entire phylogenetic tree of a tumor can be identified as the founder of a distinct “clone”, even though it may show no biological difference from the rest of the cancer cells. This is why in the field we implicitly identify clones “of interest”, such as those that have growth/survival advantage (an ancestor under positive selection), or those that generate metastases (an ancestor that arrived and grew at a given metastatic site). The limits in the definition of a clone are important to bear in mind when attempting to recover the tumor clonal architecture.

To identify clones in bulk cancer samples, the established approach is unsupervised clustering of variant read counts⁴, with each of the resulting clusters defined as a clone. This procedure, called “subclonal reconstruction”, leverages on variant read counts and associated variant allele frequency (VAF) of somatic mutations, adjusted for copy number status and tumor purity, to identify groups of variants with similar cellular proportions. Subclonal reconstruction allows tracing the “life history” of a tumor via determination of its phylogenetic tree (sometimes called a “clone tree”)³.

Current methodologies approach subclonal reconstruction with sophisticated mixture models⁴, implemented via Dirichlet Processes^3,5,6 or Dirichlet finite mixtures⁷. These machine learning methods are entirely data-driven and are usually chosen because of their convenient statistical properties, rather than their adherence to the mechanisms of tumor evolution. They can be efficient and accurate, as long as the underlying assumptions are correct. All current subclonal reconstruction methods assume that variant read counts from bulk tumor samples present as a mixture of Binomial or Beta-Binomial mutational clusters, each one corresponding to a clone. However, these are not the only observable patterns in the data: the mutations that occur within each clone while it expands are also detectable. Given the size of the human genome, even with low mutations rates (e.g. 10^−9-nucleotide substitutions per base per division⁸), new mutations are expected at each cell division, and thus large numbers of passenger mutations inevitably accumulate within an expanding clone. The evolutionary dynamics of this passenger mutation accumulation are neutral, and give rise to a power-law distributed “tail” of ever more mutations at ever lower frequency. This has been mathematically demonstrated in theoretical population genetics^9–14 and is corroborated by genomic data at high resolution^15,16. These within-clone neutral tails have not been directly addressed by previous methods, potentially confounding the measurement of clonal heterogeneity.

Here, we reconciled data-driven machine learning approaches to clustering VAFs and corresponding Cancer Cell Fractions (CCF), with the insight given by evolutionary theory. Specifically, we combined Dirichlet mixture models with the distributions predicted by theoretical population genetics models^9–12, producing a model-based method for subclonal reconstruction called MOBSTER (MOdel Based cluSTering in cancER). MOBSTER can process mutant allelic frequencies to identify and remove neutral tails from the input data, so that machine-learning subclonal reconstruction algorithms can be applied downstream to find subclones from read counts. We also expanded MOBSTER to analyze data from multiple samples of the same tumor, collected both in space and time.

Results

Mutation, drift and selection

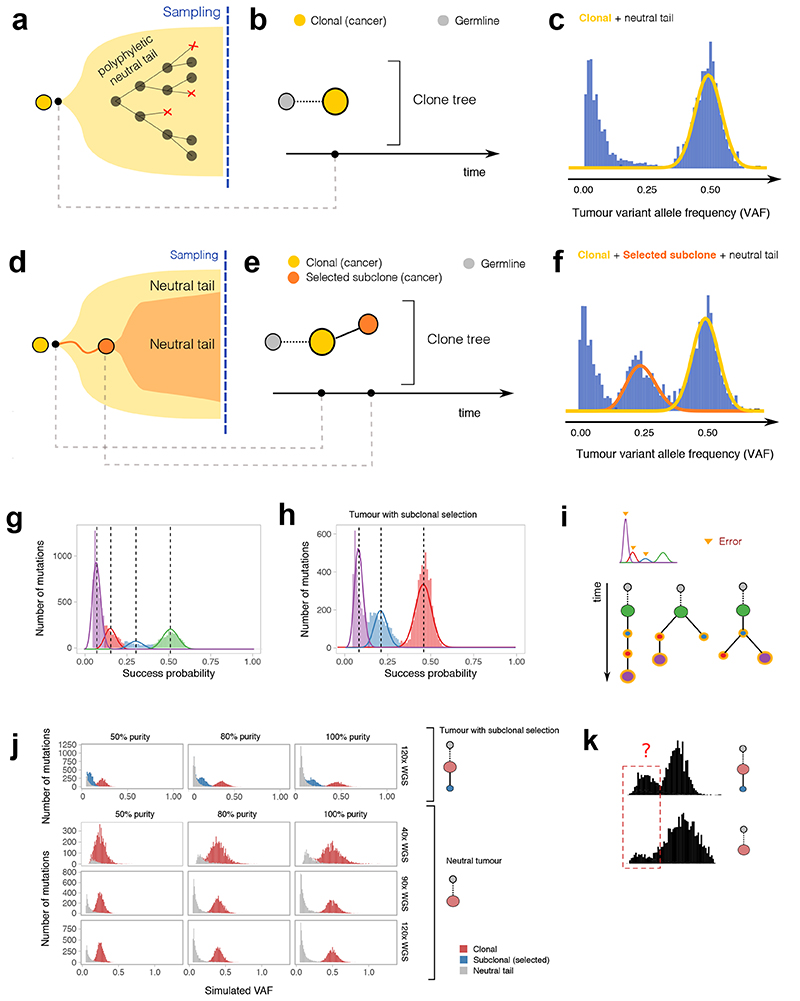
Cancers grow from a single cell, and hence neutral mutations that occur in the first few cell divisions are present at high frequency in the final population, irrespective of the action of selection. In addition, stochastic fluctuations in population size of cell lineages can also increase the frequency of mutations in the absence of selection; this is called genetic drift¹⁷. The same is true within (sub)clones: a clone originates as a single cell, and neutral mutations that occur early within the clone are found in a large proportion of the clone’s cells. Fundamental insight into the accumulation of mutations in the absence of positive selection came from the study of the Luria-Delbruck model in bacteria¹⁸. This has led to well-established population genetics theory describing the accumulation of mutations within neutrally growing populations^10,11. The same theory applies to cancer clones^9,12 and can be extended to include positive selection¹⁶. Theory states that we should expect a tail of neutral passenger mutations within a clone (Figure 1a). Neutral tails only recently became evident in cancer data with the adoption of high-depth whole genome sequencing (WGS), as lower depth sequencing (e.g. <60x) is insufficient to detect tails reliably¹⁶, and exome or panel sequencing often assay too few mutations to show a clear VAF spectrum.

Figure 1. Theoretical predictions of cancer genomic data under different evolutionary dynamics.

(a) A tumor formed by a single “functionally monoclonal” expansion follows neutral evolutionary dynamics driven only by mutation and drift. (b) The clone tree can be represented as a single “truncal” clone. (c) In diploid regions, the Variant Allele Frequency (VAF) distribution is characterized by one clonal cluster and a neutral 1/f ² tail of subclonal mutations. (d) In a tumor with one subclone under positive selection (functionally polyclonal) the evolutionary forces of mutation and drift are still at play within each clone. (e) The clone tree is represented as a truncal node giving rise to a selected subclone within it. (f) The VAF shows one extra cluster due to subclonal mutations in the subclone that have risen in frequency due to selection. (g,h) Standard subclonal deconvolution identifies clusters of neutral tail mutations that are not subclones, as they represent admixed polyphyletic lineages. (i) This causes inflated estimates of the number of clones that propagate errors and uncertainty downstream, with several incorrect phylogenetic trees fitting the data. (j) In these synthetic examples, the VAF distribution of a tumor with and without subclonal selection changes for different values of coverage and purity, affecting the ability to observe neutral tails. A neutral tail (grey) becomes difficult to detect at 40x depth. (k) The “degenerated tail” at 40x can be statistically indistinguishable from a positively selected subclonal cluster. Data at such resolution are not powered to distinguish true positive subclonal selection from neutral tail mutations.

Figure 1a shows the simplest example of a uniform ‘neutral’ tumor expansion. The corresponding clone tree has a single “truncal” node (Figure 1b). The VAF spectrum for this tumor consists of a “clonal peak” at high frequency, corresponding to the mutations that are present in all cells (i.e. in the most recent common ancestor, MRCA), and a neutral tail of mutations at lower VAF generated as the clone expands (Figure 1c). In the case where a subclone with selective advantage is present (Figure 1d,e), the data will present as two peaks at high frequency (one clonal and one subclonal) as well as a mixture of two overlapping neutral tails¹⁶ (Figure 1f). Performing subclonal reconstruction on these data assuming a generative mixture of just Binomial or Beta-Binomial distributions will detect several clusters within the neutral tail that are erroneously identified as subclones, as illustrated in two simulated cases (neutral in Figure 1g, and with one selected subclone in Figure 1h). Importantly, mutations in neutral tails are not monophyletic, and hence grouping them together into clones is erroneous even under the strictest definition of a clone. Moreover, when these incorrect clones are used downstream for phylogenetic reconstruction, the resulting trees (Figure 1i) have a very different structure from the true trees (Figure 1b,e), thus propagating errors and uncertainty in the tree construction, with many equivalent (but wrong) trees potentially fitting the same data.

Moreover, low-depth sequencing and low purity data cause neutral tails to be under-sampled and likely to be mistaken for subclones, as they lose their characteristic power-law shape. Simulated WGS data (Figure 1j) show that with low coverage or purity, the signal of a neutral tail becomes statistically difficult to distinguish from that of a selected subclonal cluster (Figure 1k). This observation indicates that sequencing depth below 90x/100x and low purity prevents reliable subclonal reconstruction. We note that patterns of noisy subclonal VAF distributions that may represent under-sampled tails (e.g. Figure 1k), are commonly observed in cancer sequencing data at depth <90x/100x.

Model-based clustering of variant allelic frequencies

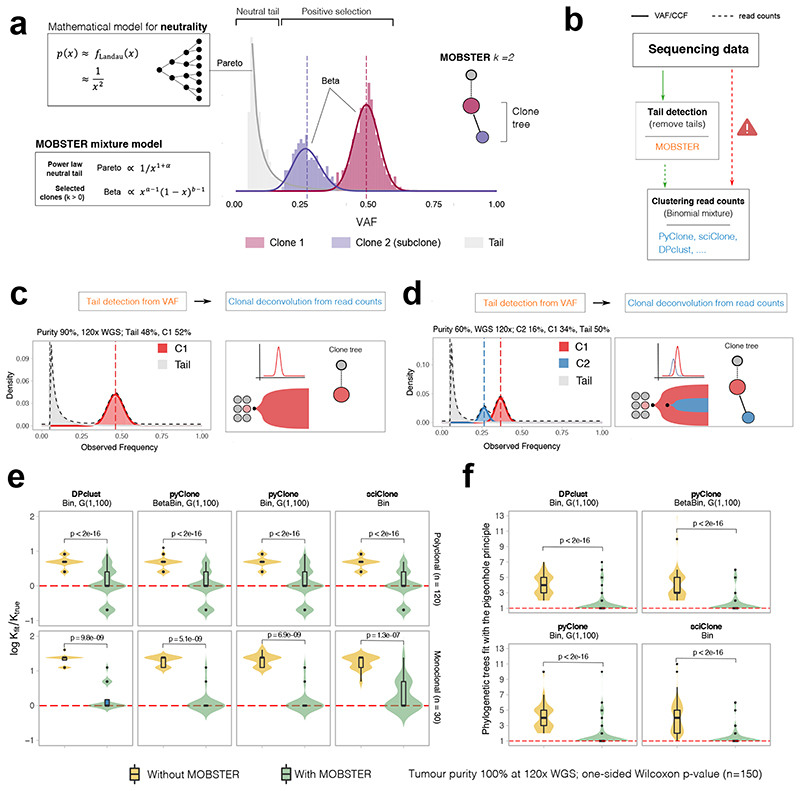
The frequency f of newly acquired passenger mutations in an expanding population follows a Landau distribution¹⁰, which at the frequency range detected by current sequencing standards can be approximated by a power law distribution X~1/f ² (Figure 2a), as we previously reported⁹. Subclonal alleles under positive selection, together with their hitchhiking passengers, will instead form clusters in the VAF distribution as they rise in frequency due to positive selection^16,19.

Figure 2. Model-based tumor subclonal reconstruction.

(a) MOBSTER combines a Pareto Type-I distribution with k Beta random variables into a univariate finite mixture with k+1 components. The Pareto captures the frequency spectrum of neutral mutations predicted by theory (Landau distribution decaying as 1/f ²), whereas Beta components detect alleles under positive selection. The histogram shows clustering assignments for a tumor with one selected subclone (k=2). (b) MOBSTER filters out neutral tail mutations, and one can cluster the rest with any tool for subclonal reconstruction using read counts. CCF, cancer cell fraction. (c, d) MOBSTER applied to the examples in Figure 1a,b detects the clusters corresponding to the true selected clones, hence recovering the correct clonal architecture. WGS, whole genome sequencing (e,f) We used synthetic 120x WGS data from n=150 simulated tumors to compare current methods with MOBSTER (plots show mean and inter quartile range IQR, upper whisker is 3rd quartile +1.5 * IQR and lower whisker is 1st quartile −1.5 * IQR). We measured how many clusters (e) and clone trees we identify (f). Tests compare Binomial mixtures from DPclust, pyClone and sciClone, and Beta-Binomial mixtures from pyClone, parameterized by concentration α > 0. DPclust and pyClone learn α from the data assuming a Gamma prior. sciClone is a variational method with hardcoded α. In (e) we report the logarithm of the ratio between the number of subclones found by MOBSTER (k _fit) and the true number of clones (k _true). Red dashed line represents k_fit = k_true. In (f) we plot the number of trees that can be fit by pigeonhole principle using the output of each tool.

We can model VAFs or fraction data via Beta distributions⁷, and model read counts with Binomial or Beta-Binomial distributions^3,5–7. In MOBSTER (Figure 2a), we model the evolutionary dynamics of a growing tumor containing subclones by combining Beta distributions (expected from subclones under selection) with a power law (expected from neutral tails). After fitting the VAF distribution, tail mutations can be removed and clustering of read counts from the remaining mutations can be performed via standard methods (Figure 2b). MOBSTER controls for tails while retaining the original variance of the data when clustering non-tail read counts downstream. Notably, MOBSTER always compares the fit of a mixture of clones with and without a neutral tail and uses a regularized model selection strategy to determine the best model fit to the data.

MOBSTER combines one Pareto Type-I random variable (a type of power-law) with k Beta random variables, resulting in a univariate finite mixture with k+1 components. The likelihood for n datapoints x_i is

$$p(D\mid \theta ,\pi )={\displaystyle \prod _{i=1}^n\left[{\pi }_{1}g\left(x_i\mid x_{*},\alpha \right)+{\displaystyle \sum _{w=2}^k{\pi }_w}h\left(x_i\mid a_{w-1},b_{w-1}\right)\right]},$$

where g and h are density functions, θ=(x_*,α,a₁,…,a_k,b₁,…,b_k) is a vector of parameters and π are mixing proportions in a standard setting with n×(k+1) latent variables. The Pareto component follows g(x|x _*,α)∝ 1/x^(1+α) for x ≥ x _*, and the Beta follows h(x|a,b)∝ x ^a-1(1−x)^b−1 in [0,1]. A derivation of MOBSTER, its relation to other approaches and technical comments are available in the Online Methods.

In the hypothetical example of a “functionally monoclonal” tumor with neutral subclonal dynamics (Figure 1a), MOBSTER fits k=1 Beta clusters of truncal mutations (present in all cancer cells) plus a neutral tail (Figure 2c). Similarly, for a tumor with one selected subclone (Figure 1d), MOBSTER fits k=2 Beta clusters and a tail (Figure 2d). When we identify and remove tail mutations from the data, subsequent clustering of read counts mutations identifies the true tumor clones and their correct clone trees (inner clone tree panels).

Synthetic validation of the method and confounding factors

We used synthetic data to validate MOBSTER and quantify the degree to which neutral tails confound subclonal deconvolution with standard methods (Supplementary Note, Supplementary Figures 1-9). We used a stochastic branching process¹⁶ to simulate the growth of n=150 tumors (Online Methods and Supplementary Data vignette “Example Subclonal Dynamics”). Out of these 150 cases, 30 tumors were neutral (as Figure 1a) and 120 contained one selected subclone (as Figure 1d). For each tumor we simulated bulk WGS at 120x median coverage and 100% purity. In every test, we always compared the fit of MOBSTER with and without a tail, retaining the best; we then recorded the predicted number of selected clones, k, and the fit precision (Supplementary Figure 3 and 4). We note that by applying further population genetics theory¹⁶ to the output of MOBSTER, we can estimate the tumor evolutionary parameters, such as the mutation rate, the time of emergence of subclones, and their selection coefficients (Supplementary Figure 5). We also carried out several other tests for the detection of low-frequency subclones admixed with tails (Supplementary Figures 6 and 7).

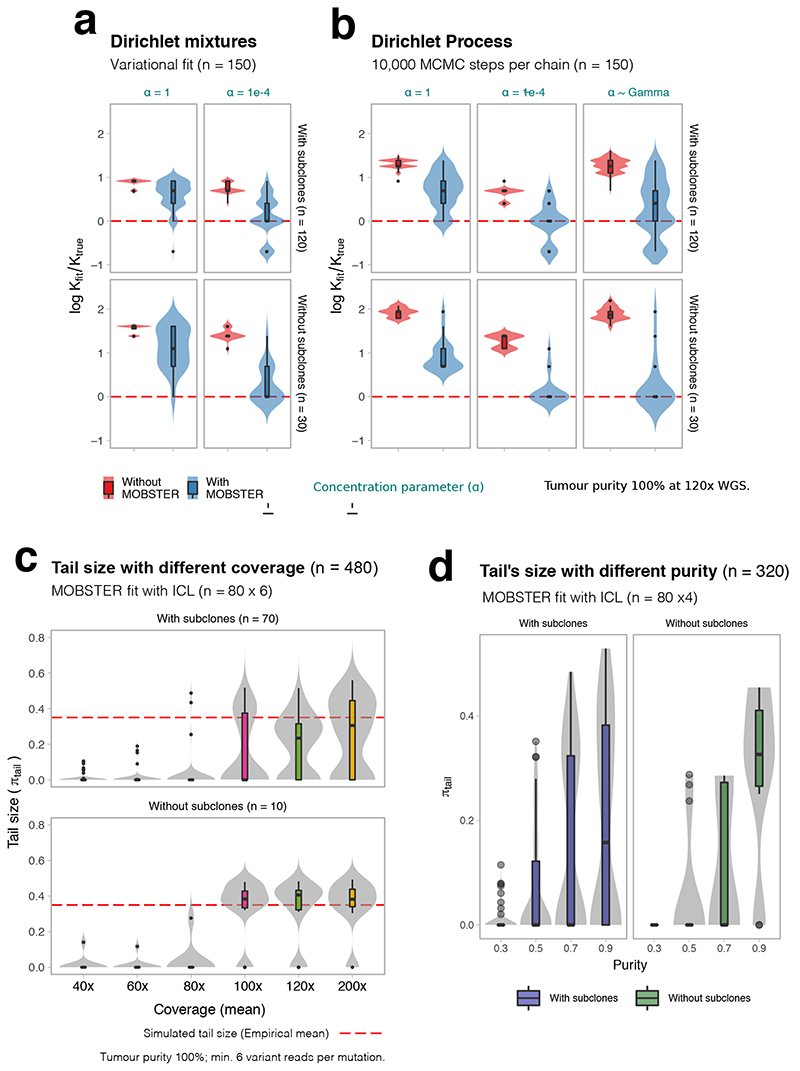
By accounting for neutral tails, MOBSTER significantly outperformed standard approaches based on both Dirichlet variational mixtures and Dirichlet Processes (Extended Data Figure 1), two statistical frameworks at the core of subclonal reconstruction tools like sciClone⁷, pyClone⁵, DPclust³ and many others. Results are consistent for various parameterizations, in particular of the concentration parameter α > 0, which determines the propensity of adding clusters to the fit³. In Figure 2e we report the error rates for the inferred number of clones (k) with DPclust, pyClone (Binomial and Beta-Binomial) and sciClone. The detection of spurious extra clusters caused high uncertainty around the clone tree, with many solutions fitting the data equally well (Figure 2f). We tested the effects of sequencing coverage and purity on tail detection, and found that ~100x coverage and high purity were required to systematically identify tails. Higher coverage is required for samples with lower purity (Extended Data Figure 1). Additional synthetic tests with complex clonal architectures confirmed the robustness of the method (Supplementary Figures 8 and 9). These analyses indicate that the previously published moderate-depth WGS studies were underpowered to detect reliable subclonal architectures, since the signal used to distinguish a tail from a subclone deteriorates with lower sequencing depth (Figure 1j). With adequate data and controlling for neutral tails, we found the correct number of clones in the large majority of tests. Not considering neutral tails led to a systematic pattern of errors that, in the worst cases, could lead to a four-fold overestimation of the number of clones.

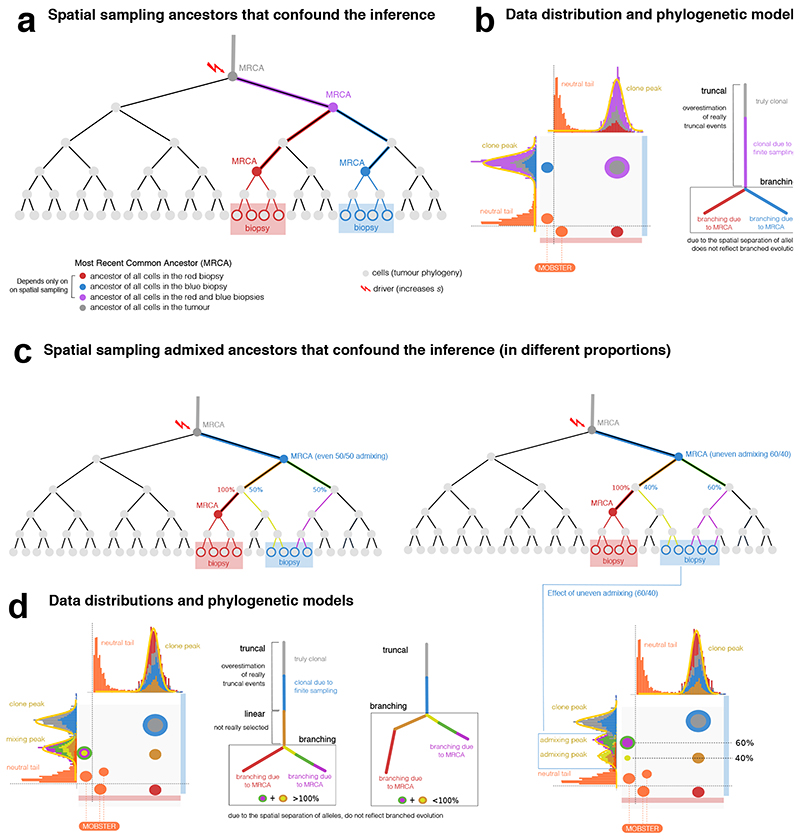
Not accounting for neutral tails also significantly impacts multi-region sequencing, as we discuss in the Supplementary Note. We found that multi-region bulk sequencing is affected by confounders that originate from the spatial effects of tumor growth and spatial sampling bias. In multi-sample analyses (Supplementary Note) we characterized a confounder termed the “hitchhikers mirage” (Extended Data Figure 2) caused by parts of neutral tails that spread in space, and that current methods mistake for selected subclones (Supplementary Figure 10). We also characterized two additional confounders due to the presence of locally sampled ancestors (Extended Data Figure 3) and admixing of multiple lineages (Extended Data Figure 4). These spatial confounders affect virtually all tumors (Supplementary Figures 11-13). Therefore, the joint use of MOBSTER and other heuristics is necessary to interpret subclonal deconvolution results from multi-region samples (Extended Data Figure 5, Supplementary Figure 14).

Analysis of genomic data from human samples

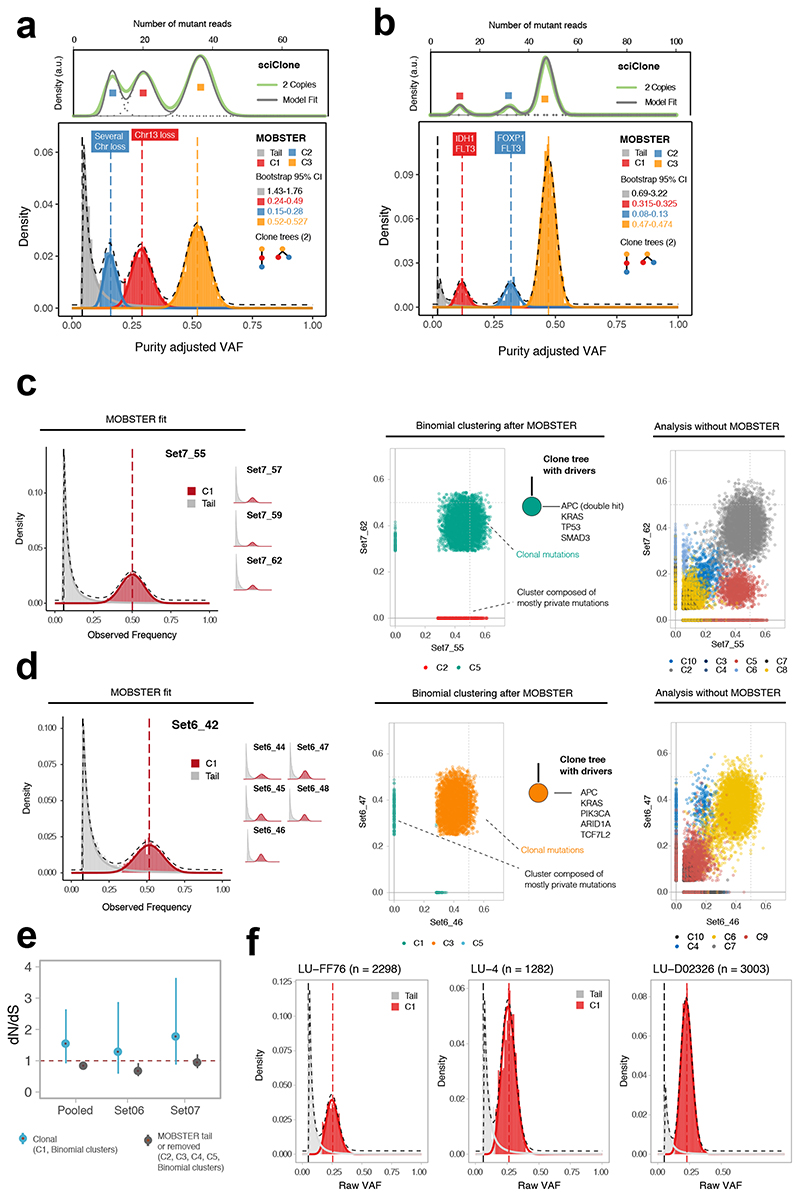
We applied MOBSTER to high coverage (>100x) WGS data available in the public domain (Supplementary Note). We first re-analyzed the breast cancer sample PD1420a sequenced at ~188x from Nik-Zainal et al.³. Compared to the original analysis, which found 3 subclones, MOBSTER fits two subclones (k=3) and places a neutral tail for the lowest frequency cluster (Figure 3a). sciClone analysis of read counts for non-tail mutations confirmed k=3 Binomial clusters (2 selected subclones). Both linear and branching phylogenies could be fit to the output, with the branching tree matching the original analysis³. The cluster that MOBSTER fits to a tail appears in multiple positions of the tumor tree in the original paper after phasing³. This is consistent with our analysis, as the tail is polyphyletic, and hence composed of a mixture of descendants of the different clones. We measured the evolutionary parameters of this tumor from the fits, finding concordant estimates with our previous work¹⁶. Mutation rate was μ=3.5 * 10⁻⁷ mutations per base per tumor doubling, subclones emerged at t=5.5 (smaller subclone) and t=10.4 (larger subclone) doublings, and had selective coefficients of s=0.3 and s=0.66 respectively.

Figure 3. Analysis of single sample and multi-region whole-genome data.

(a) Breast carcinoma ~180x WGS sample from ref³. MOBSTER identified a neutral tail plus k = 3 Beta clusters (2 subclones, consistent with two clone trees). Analysis of non-tail mutations with sciClone confirmed 2 subclones. sciClone without MOBSTER would have fit one extra clone to the tail. Non-parametric bootstrap is used to estimate the 95% bootstrap confidence intervals for the parameters. (b) Leukemia ~320x WGS sample from ref²⁰. MOBSTER found two subclones (k = 3), confirmed with sciClone, and 2 clone trees. (c) WGS data at 100x from 4 biopsies of colorectal cancer Set07. From VAF of diploid mutations we identified neutral tails and no subclonal selection; from non-tail mutations we found 5 clusters (multivariate clustering with α = 10⁻⁶, Supplementary Note). C1 is the truncal cluster; all other clusters are enriched mutations private to a biopsy, indicating ancestor effect (Supplementary Note). The clone tree depicts a neutrally expanding tumor with all drivers in the trunk. Analysis without MOBSTER would have inflated the number of subclones (right panel; Supplementary Figures 20-23). (d) WGS data at 100x from 6 biopsies of cancer Set06 also showed neutral subclonal dynamics. Without MOBSTER we would have inflated the number of selected subclones (right panel; Supplementary Figures 24-27). (e) dN/dS analysis for Set06 and Set07 comparing truncal vs subclonal mutations confirmed lack of evidence for positive selection at the subclonal level, corroborating our conclusions. (f) Three lung cancer cases from ref²⁴ sequenced at 100x WGS were consistent with neutral subclonal dynamics.

We reanalyzed the acute myeloid leukemia (AML) sample sequenced at 320x WGS by Griffith et al.²⁰. MOBSTER identifies k=3 clusters (2 subclones) and a neutral tail (Figure 3b). The two subclones were also detected by Griffith et al.²⁰, and were confirmed running sciClone after MOBSTER. However, MOBSTER simplified the clonal architecture by removing one spurious low-frequency “subclone”. This observation likely improves the interpretation of these data, possibly explaining why the tail was the only cluster without a clear subclonal driver mutation. Measured mutation rate was μ=9.9 * 10⁻¹⁰ per base per tumor doubling, subclones emerged at t = 22 and t = 27, and selection coefficients were s = 1.3 and s = 3, respectively.

We also generated new multi-region WGS data (median 100x) from spatially separated regions of two primary colorectal cancers previously analyzed at lower depth in Cross et al.²¹. In tumor Set06 we analyzed high-confidence single nucleotide variants (SNVs) in diploid segments consistent across samples, and ran a comparative analysis with and without MOBSTER (Supplementary Note). The analysis with MOBSTER did not find evidence of positive subclonal selection (Figure 3c, Supplementary Figure 15), corroborated by the lack of subclonal drivers and truncal APC, KRAS, SMAD3 and TP53 mutations, as originally reported²¹. The analysis without MOBSTER would have depicted a complex subclonal structure, with several Binomial clusters consistent with multiple clone trees (Supplementary Figure 16). The analysis of Set06 gave similar results (Figure 3d, Supplementary Figure 17). Consistent with Cross et al.²¹, the clone tree depicted a tumor with only truncal driver events in APC, KRAS, PIK3CA, ARID1A and TCF7L2, and neutral subclonal dynamics. Again, a standard analysis would have identified a complex clonal architecture with multiple subclones (Supplementary Figure 18). Mutation rates were μ=5.6 * 10⁻⁷ for Set07, and μ=4.3 * 10⁻⁷ for Set06. Notably, orthogonal dN/dS analysis that uses the ratio of non-synonymous to synonymous mutations to detect selection^22,23, confirmed the lack of evidence for positive selection at the subclonal level in those tumors (Figure 3e, Supplementary Note).

We also applied MOBSTER to n=3 non-small cell lung cancer samples sequenced at high depth (Figure 3f). These three tumors were those with the highest coverage and purity amongst a recently published cohort²⁴ (see also low-purity cases in Supplementary Figure 19).

Neutral evolution in 2,566 whole-genomes from PCAWG

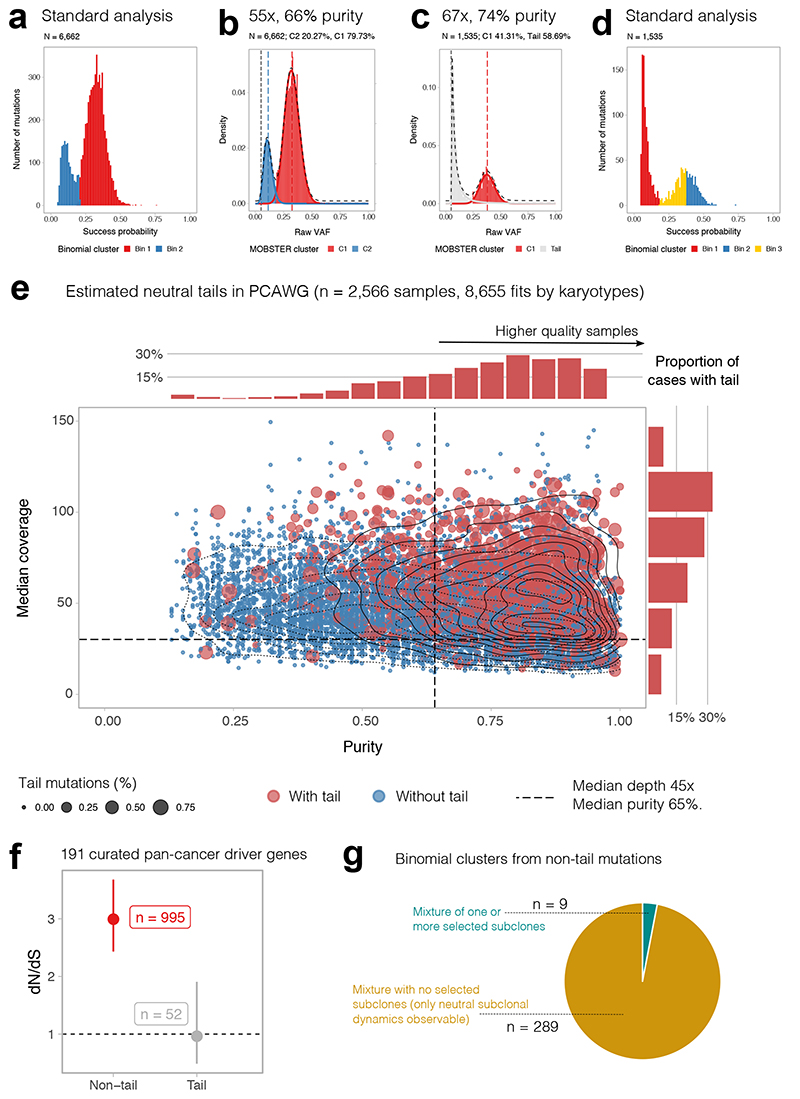
We reanalyzed with MOBSTER one of the largest available cohorts of cancer WGS data to date, collated by the Pan-Cancer Analysis of Whole Genomes (PCAWG) international consortium and recently published in a series of studies²⁵, including the evolutionary history of more than 2,600 cancers²⁶. The median depth of coverage in this dataset was 45x, with median purity of 65%. According to our power analysis, data at this resolution are not suitable for reliable subclonal reconstruction (Figure 1j, 1k and Extended Data Figure 1). Figure 4a shows a PCAWG case where a standard analysis called a selected subclone. The coverage was 55x and purity 66%, with a VAF distribution similar to the down-sampled synthetic neutral cases shown in Figure 1j. With these data, MOBSTER (Figure 4b, more cases in Supplementary Figure 20) cannot fit a neutral tail in the low-frequency portion of the VAF spectrum, and instead fits a subclone (Beta component). The ground-truth is not known, but given the resolution of the data we cannot exclude the likelihood that subclonal mutations in this sample are the result of a degenerate neutral tail (see Figure 1j,k). In cases where coverage and purity were higher, MOBSTER did identify neutral tails and resolved the remaining clonal structure (Figure 4c). As expected, standard approaches would have identified spurious clusters (Figure 4d), thus compromising the whole subclonal reconstruction.

Figure 4. Analysis of 2,566 whole-genomes from PCAWG with MOBSTER.

(a) Fit of a PCAWG²⁵ tumor with 55x coverage and 66% purity using standard methods. (b) At this data resolution, neutral tails are under-sampled (Figure 1j,k) and cannot be distinguished from selected subclones. (c) In PCAWG cases with higher coverage (67x) and purity (74%), neutral tails can be clearly detected using MOBSTER. (d) Analysis of the same tumor with standard methods would have identified multiple subclonal clusters, including a cluster of neutral tail mutations. (e) We analyzed n=2,566 PCAWG samples, plotted here for purity vs coverage. Blue dots are tumors where MOBSTER cannot fit a tail. Red cases have a neutral tail. Percentage of tail mutations determines dot size. The marginal histograms report the normalized number of cases with tail. (f) We focused on the 902 diploid cases with coverage > 30x and purity > 65% (median of the cohort) where we could fit a tail. Using a panel of 191 pan-cancer driver genes, we show that tail mutations have dN/dS~1, providing no evidence of positive selection (point estimate and Confidence Intervals from dndscv). Clonal and subclonal non-tail mutations show dN/dS> 1, consistent with positive selection. (g) If we take the 298 diploid cases with a tail containing at least 10% of the total mutational burden, we find evidence of a selected subclone only in 9 cases (3% of tumors). Similar proportions are obtained if we impose a 5% or 2% cutoff on the size of the tail. See Supplementary Figures 29-31.

We found widespread presence of neutral evolutionary patterns in PCAWG data using MOBSTER. We analyzed the VAF spectrum of 2,566 cancers (Supplementary Note). Theoretical population genetics predicts that, given enough power in the data, we should always expect to find a neutral tail, with or without selected subclones (Figure 2a). However, we consistently found neutral tails only in samples with higher coverage and purity (Figure 4e, red=cases with neutral tail, blue=cases without detectable tail), suggesting lack of power for subclonal inference in the majority of cases (Supplementary Figure 21).

To further validate the presence of neutral tail mutations in this cohort, we focused on n = 902 near-diploid cancers with >30x depth, >65% purity and where a tail was detected. From these cases we identified somatic mutations mapping to putative cancer driver genes^25,26 in neutral tails versus non-tail and performed dN/dS analysis²² (Figure 4f). This orthogonal measurement confirmed that mutations in tails were likely neutral (dN/dS~1), aside from the caveats of interpreting dN/dS values in growing tumours²⁷, whereas non-tail mutations indicated selection (dN/dS>1).

We then focused on n = 298 diploid cases that were found to have at least 10% of the total mutation burden in the tail, indicating sufficient power to detect the clonal architecture with confidence. We measured the proportion of tumors with a selected subclone, defined by 2 or more Binomial clusters detected from non-tail mutations. We found evidence of ongoing subclonal selection only in n = 9 (3% of total, Supplementary Figure 22). In the remaining n = 289 cases, neutral evolutionary dynamics at the subclonal level were the adequate description of the data (Figure 4g). Lowering the threshold for proportion of tail mutations did not change the results (5% tail = 2.7% non-neutral cases; 2% tail = 3.7% non-neutral cases).

Our analysis suggests that for the majority of PCAWG cases, the data resolution was too low to conduct robust subclonal reconstruction. Moreover, neutral tails were detectable in higher coverage and purity samples, indicating that neutral dynamics are often an adequate description of the observed subclonal heterogeneity. Standard analyses of these data therefore risk systematically mistaking neutral tails for subclonal clusters, thus inflating the complexity of the inferred subclonal architectures and producing incorrect phylogenetic trees. Our analysis using MOBSTER hence demonstrates that neutral evolutionary patterns are prevalent in PCAWG data.

Analysis of longitudinal whole-genome datasets

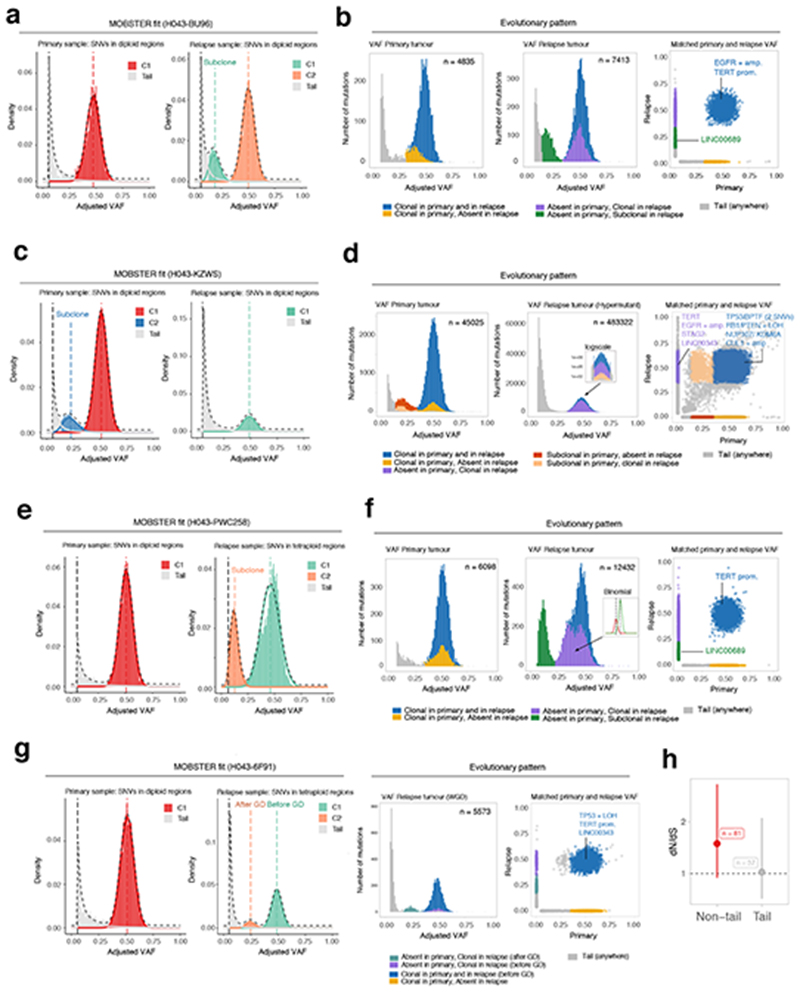
We analyzed a cohort of n = 35 matched primary-relapse glioblastoma samples from 16 patients profiled using ~100x WGS in a recent study by Körber et al. 2019²⁸. Our analysis identified 9 cases characterized only by neutral evolutionary dynamics at the subclonal level in both primary and relapse, while 7 patients had a detectable ongoing subclonal expansion (Supplementary Figure 23). We found cases where positively selected subclones were unique to the primary or the relapse (Figure 5a,b), but also cases where pre-existing subclones in the primary swept through the population in the relapse, likely due to positive selection from treatment (Figure 5c,d). In some cases, we found evidence of novel subclones at relapse (Figure 5e,f). MOBSTER also identified clusters of mutations that were due to whole-genome duplications, as in the case of a diploid primary tumor that became tetraploid at relapse (Figure 5g,h). We note that some of the confounding effects of neutral tails in multivariate analyses (Supplementary Note) were ubiquitous in these data and would have negatively impacted standard subclonal reconstruction (Supplementary Figure 23). Orthogonal analysis with dN/dS^22,23 methods suggested neutral values for tail mutations (dN/dS ~1) and positive selection for others (dN/dS >1) using a panel of glioma driver genes (Figure 5h). We note that the presence of subclones under positive selection in these data was also reported in the original study²⁸. However, using MOBSTER we obtained simplified clonal architectures, pruning some of the clusters that were due to neutral tails. Indeed, a mixture of subclonal selection and neutral evolutionary dynamics through therapy has been recently reported in a large glioblastoma study²⁹.

Figure 5. Analysis of longitudinal glioblastoma samples with MOBSTER.

(a). Patient H043−BU96 is one of n = 16 IDH-wildtype glioblastomas for which we analyzed WGS data (~100x) from pre-treatment and post-treatment longitudinal samples previously generated²⁸. (b) Analysis following MOBSTER identified subclones private to the primary (yellow) and relapse (green) tumor respectively, the latter containing a putative driver mutation in LINC00689. (c) Patient H043−KZWs MOBSTER fits. (d) Here a subclone detected in the primary went on to sweep through the relapse, which was hypermutant after temozolomide treatment (zoom-in logscale panel). (e) Patient H043−PWC258 MOBSTER fits. (f) Here the primary sample showed neutral evolutionary dynamics, whereas the relapse contained detectable subclones possibly mixing with the neutral tail. An additional high-frequency subclone was detected from a downstream analysis using Binomial clustering of read counts (purple cluster, split into 2 Binomial components). (g) MOBSTER can also be used to identify and assign clusters that are produced by whole-genome duplications, or more general aneuploid states. In such contexts, we expect to see peaks in the VAF distribution that distinguish mutations that happened before and after genome doubling. In the case of patient H043−6F91, a diploid primary tumor (neutral) became whole-genome duplicated at relapse. (h) Orthogonal dN/dS analysis (point estimate and Confidence Intervals from dndscv) of mutations in 74 putative GBM driver genes assigned to neutral tails versus non-tail provided evidence of selection only in non-tail mtuations. The full list of analyzed cases is available in Supplementary Figure 32.

Discussion

Subclonal reconstruction from cancer bulk sequencing data has paved the way to the study of cancer evolution^3,30. Measurement of subclonal architectures have also clinical relevance: subclone multiplicity and other measures of intra-tumor heterogeneity have been reported as prognostic biomarkers^31–34. Naturally therefore, there is the need to ensure that subclonal reconstruction is accurate.

Here we have presented a subclonal reconstruction method that combines data-driven machine learning with theoretical population genetics. This is in contrast to purely data-driven approaches that lack an underlying evolutionary model. Recently proposed standards for subclonal reconstruction³⁵ do not account for evolutionary dynamics, and hence this recommended best practice analysis is inherently flawed.

Moreover, we suggest that only high depth sequencing data of >90/100x is appropriate to infer subclonal architectures, and even higher depth is required for purity <75%. Subclonal reconstruction from lower depth data and lack of consideration for neutral tails risks a systematic over-calling of spurious subclones (Figure 1j,k), leading to incorrect inference of the life history of tumors. These problems affects multiple previously published studies (for example refs^3,34,36) and prohibit the inference of subclonal structures in the large majority of PCAWG cases. Various issues arise also in multi-region sequencing data, resulting from biases that are intrinsic to spatial sampling (Supplementary Note) and thus affect several previous studies that had insufficient depth of sequencing to infer metastatic spread (for example refs^37–39). These issues also lead to inflated estimates of positive subclonal selection from VAF distributions. Single-cell sequencing removes the problem of admixing of populations⁴⁰, however the underlying evolutionary dynamics described by theory remain valid for the frequency of mutations amongst the N cells sequenced⁴¹.

The major impact of MOBSTER is that it controls for neutrally evolving cancer cell subpopulations, cleaning up the signal for downstream analyses that seek to focus on “functional” intra-tumor heterogeneity. Given the wide use of clustering methods for subclonal reconstruction, MOBSTER has the potential to impact intra-tumor heterogeneity studies that use bulk sequencing, and even that analyze the distribution of clade sizes in single-cell sequencing.

We also highlight the limitations of the definition of “clone” in cancer as a monophyletic clade with a most recent common ancestor, noting that in the clinic we are not interested in all the ancestors of a given group of cancer cells, but only in those few ancestors that drive progression, metastasis or treatment resistance. Importantly, even under this looser definition of a clone, clustering neutral tails with Binomial models is incorrect and leads to the identification of false clones, mistaking the polyphyletic branching process that gives rise to neutral tails for a monophyletic lineage.

This study highlights that there are intrinsic limitations to the information on tumor evolution encoded in current data, foremost because of the systematic confounding factors caused by sampling complex three-dimensional tumors. We propose that our analysis represents a step towards a more refined approach to subclonal reconstruction in bulk cancer data, a necessity for genomic-aided precision medicine.

Online Methods

Model-based clustering of cancer subclonal populations with MOBSTER

The subclonal deconvolution problem is popular in the cancer literature³⁵. Given read counts for a list of mutations detected from bulk sequencing of multiple tumor samples, we want to detect clusters of mutations that represent cancer subpopulations admixed in our samples. The problem can be framed to include any type of somatic mutation for which we can estimate the frequency, in the data, of the somatic (i.e., alternative) allele. Usually, the mutations that are easier to call are Single Nucleotide Variants (SNVs); more complex structural variations or insertion-deletions are more challenging to determine accurate allelic frequencies. Regardless mutation types, our aim is to use determine mutations clusters that suggest cancer subpopulations (i.e., clones) under positive selection.

MOBSTER is a mixed method that combines two types of random variables to approach this problem.

The frequency spectrum and the observational process

Kessler and Levin¹⁰ have shown that, in the large population solution of the stochastic Luria-Delbrück model, the probability of having m mutants follows a fat-tail Landau distribution

$$p(m)=\frac{1}{\mu N}{f}_{\text{Landau }}\left(\frac{m}{\mu N}-\text{log}\mu N+\gamma -1\right)$$

Here N is population size, μ the average fraction of birth events and γ the Euler constant. The asymptotic behavior of f _Landau can be approximated as f _Landau(x)=1/x², which leads to the power-law approximation that has also been derived by others^12–14 as p(m) ≈ 1/m².

A generative model for this power law can be constructed with a standard Markovian stochastic birth-death process of cell division – sometimes called branching process ¹⁶. The existence of patterns of neutral evolution is thus a consolidated result from Population Genetics arguments that describe the spread of alleles in growing populations without recombination, such as cancer¹⁷. In other words, the progeny of each clone accumulates neutral passenger mutations until any of their daughter cells acquires a new mutation that undergoes selection because it triggers a new clonal expansion with increased fitness: the power-law spectrum emerges therefore by the frequencies of passengers. When a daughter cell enjoys a clonal expansion, however, the frequency of the variant alleles that accrued from the ancestor cell to the actual cell that acquired the driver, will grow. Eventually, this new subclonal expansion will become detectable if selection forces are strong compared to background (which is the clone within this cell was born). In a recursive fashion, the progeny of this new cell/ subclone will start dividing, giving rise to another power-law distributed tail of within-clone neutral dynamics. Example subclonal evolutionary dynamics are shown in the vignette “1. Example subclonal dynamics” (Supplementary Data), where we animate a subclonal expansion which shows how subclones emerge from low frequency up until they sweep, and how the allele frequency distribution changes over time.

Importantly, we want to make it clear that the power-law part of the spectrum – i.e., the tail – results from the accumulation of passenger mutations in the progeny of each clone. We note that this result – in particular the exponent 2 (shape) – refers to the total population structure of the tumor, which is accessible only in the theoretical scenario in which we can sequence all the cancer cells. Therefore, any specific finite sample that we collect and sequence, which is also contaminated by normal cells, might exhibit deviations from this theoretical distribution¹⁶. Deviations from strict exponential growth – e.g., due to spatial constrains – can also cause theoretical deviations from the exponent two^13,42. However, we use this result to create a parametric model-based approach to analyze cancer data (i.e., we fix the type of distribution, but not its parameters).

Input data and conceptualization

We work with sequencing data for the variant alleles of n somatic mutations, which we can pre-process in different ways. One option is to adjust Variant Allele Frequency (VAF) values for copy number and purity, retrieving the so-called Cancer Cell Fractions (CCF) and re-scaling them into [0, 1] by halving the CCF. With these adjusted VAF values we expect a clonal peak at roughly 50% VAF, with outliers spreading around 0.5 but well below 1; compared to CCF, these values avoid the truncation of values above 1³. Another similar option is to adjust VAF values only by copy number, obtaining the so-called Cellular Prevalence (CPs). A third option is using directly the raw VAF data; in this last scenario we can further split mutations by karyotype – i.e., the absolute copy number segments where they map to – and account for the fact that different aneuploidy states have different expected distributions (e.g., a triploid tumor is expected to have two peaks of mutations, plus a tail and possibly subclonal clusters).

On real data, we suggest to use mutations that map to copy number segments with common karyotypes (i.e., copy states), such as diploid regions (with or without loss of heterozygosity), and triploid and tetraploid segments. Mutations mapping to more complex karyotypes (e.g., highly amplified oncogenes) can always be mapped post hoc, after clustering, and should account for a small subset of the tumor’s mutational burden. We stress to use mutations in high-confident copy-number regions to carry out subclonal deconvolution; miscalled copy number states confound the inference creating artifact clusters of mutations. As a best practice, we usually attempt a first fit using diploid genomes without losses of heterozygosity (i.e., regions with one copy of the major and minor alleles), where we can identify high-confidence diploid SNVs.

Regardless the representations, a model for the frequency spectrum ρ of the observed mutations with k ≥ 1 detectable clones is a random variable that follows

$$\rho ~{\displaystyle \sum _{i=1}^k\left(Y_i+B_i\right)}$$

where

• Y _i ∝ x^-α is a power-law random variable for frequencies of neutral mutations in the progeny of clone i. The generic exponent α > 0 gives flexibility to accommodate all the confounders described above;

• B_i∈[0,1] is a Beta random variable modelling the signal of clone i. In layman terms, B_i models the “peak” in the VAF distribution due to the hitchhikers of the clone. These distributions range in [0,1], rendering them suitable to describe allelic frequencies (and also motivating why we scale CCF values to fit this range). For the sake of simplification, we assume here to work with adjusted VAF values, so that aneuploidy states (amplified, unamplified) are adjusted to form a single peak in the distribution (i.e., exactly as with CCF).

This model looks simple, and further observations are required to turn it into a mixture of standard random variables. In this formulation, the random variables for the tail and the bump of a clone are coupled to capture a joint signal. While the overall mixing proportions can be assumed to be independent, this compound random variable requires an extra level of mixing within each clone – i.e., another mixing weight to properly capture the proportions of the clone tail, and bump. We can however simplify this model accepting to track at finer detail only the clusters of each clone, which we use to identify subpopulations in the frequency spectrum (i.e., we use the clone’s peak, obtained from the cluster’s mean, to assess the phylogenetic history of the tumor).

We therefore simplify the model by noting that all tails have the same exponent α > 0, which holds if all clones have the same mutation rate. If the mutation rate does not change among subclones – i.e., when there are no hypermutant subclones – all tails are described by the same theoretical distribution, and can be represented as multiple instances of the same random variable. Thus, we group them together in a single power-law tail

$$\rho ~\left(Y+{\displaystyle \sum _{i=1}^k{B}_i}\right).$$

Here the random variables have the same meaning as above, but the clone is no longer indexed by i. This model has a key advantage over the one where each clone “emits” its own tail: the random variables are decoupled and allow a simple mixture-model formulation which we will present below.

Before concluding, we observe that given ρ, the observational model for read counts collected from NGS sequencing, is a standard binomial process n|ρ,m ~ Bin(n|m,ρ), where m is the coverage (total number of reads), and w the number of reads harboring the variant allele; ρ is then the success probability for m iid Bernoulli trials. It is important to observe that the frequency spectrum and the observational process look at the data from different perspectives: the former is a distribution on allelic frequencies, while the latter on read counts. In this observational model we can in principle use Beta-Binomial distributions to account for coverage overdispersion.

Relation to other models in the literature

The literature is rich with models that describe the above observational process and variation thereof, either with Binomial or Beta-Binomial distributions. We briefly discuss those that are more related to our framework.

Bayesian methods that employ Dirichlet Processes for infinite Binomial mixture models are a popular generalization of the observational process. These non-parametric methods can fit an unspecified number of clusters k to data, simplifying model selection procedures. pyClone⁵, DPclust³ and PhyloWGS⁶ are three popular tools for clonal deconvolution that in different ways use this framework. pyClone and DPclust implement Binomial mixtures, with the former also supporting Beta-Binomial distributions; in both cases a stick-breaking construction for Dirichlet Process priors is adopted⁴³. PhyloWGS, instead, combines Binomial distributions with a tree stick-breaking construction for the Dirichlet Process priors⁴⁴, which allows PhyloWGS to cluster jointly the input SNVs, and construct a phylogenetic tree for the detected clones.

An alternative popular approach based on finite mixture models is SciClone⁷, which supports Binomial, Beta and Gaussian mixtures. SciClone fits the models to data via Variational Inference, an information-theoretic approach to approximate the posterior distribution over the model’s parameters. SciClone is a hybrid tool, as it can cluster allelic frequencies via Beta/ Gaussian mixtures, and read counts via Binomial mixtures. We want to note that, with Beta distributions, canonical Bayesian modeling leads to intractable priors, even if the conjugate prior distribution of the Beta distribution can be found by following the principles of conjugate priors for the exponential family. For this reason, Variational Inference of Beta mixtures exploits a Gamma approximation to the prior and posterior distributions, originally derived by Mao and Li⁴⁵. In this approximation we cannot derive the so-called evidence lower bound, a standard measure to monitor convergence of a variational fitting algorithm.

These models are related to MOBSTER’s framework: they assume that ρ can be approximated by a point-process (e.g. a Dirac distribution) centered at the Beta means. The potential pitfall is clear: by applying the observational process to neutral mutations, the number of clones is overestimated. Clusters will be called from tail mutations (polyphyletic lineages), which is wrong when we look for clones under selection. We note that SciClone with Beta distributions models the allele frequency spectrum as well, however, they do not account for power-law tails of neutrally-evolving mutations.

Distributions and likelihood

MOBSTER implements a statistical model to fit n VAF values to Y, the tail, and to any one of the B_i Betas, the clones (predefined in number). From a fit, tail mutations can be removed inspecting clustering assignments, and other methods can be used to fit the observational process on the read counts of the remaining data. For this reason, MOBSTER is complementary to the tools mentioned above, as it works upstream the observational process. Nonetheless, our method provides also a preliminary indication on the possible number of subclones in the tumor: with high-quality data with low dispersions, one can expect the same number of clones to be confirmed by downstream analysis of non-tail mutations.

The fit uses a pre-specified number of k+1 components, where Y is a Pareto Type-I distribution as the power-law tail. For a scale x _* and shape α > 0, its density is

$$g\left(x\mid x_{*},\alpha \right)=\alpha x_{*}^{\alpha }\frac{1}{x^{\alpha +1}}$$

for x > x_*, and 0 otherwise. Notice that the density is 0 for values below the scale parameter, which requires a sharp cutoff on the input VAF, and that its support is [0,+∞). The model also uses k Beta distributions B ₁,…,B_k to model clonal and subclonal clusters. For a shape a > 0 and b > 0 the density of a Beta random variable is

$$h(x\mid a,b)=\frac{x^{a-1}{(1-x)}^{b-1}}{ \text{B}(a,b)}$$

where $B\left(a,b\right)={\displaystyle {\int }_0^1{x}^{a-1}{\left(1-x\right)}^{b-1}dx}$ is the beta-function. The support of this distribution is [0,1], the full frequency spectrum.

The overall model uses a Dirichlet prior on the abundance of each clone; thus MOBSTER is a Finite Dirichlet Mixture Model with both Beta and Pareto distributions. The model likelihood for a dataset X = {x _i|i=1,…,n} where we assume each x_i to be iid, is a combination of two types of densities

$$p(D\mid \theta ,\pi )={\displaystyle \prod _{i=1}^n\left[{\pi }_{1}g\left(x_i\mid x_{*},\alpha \right)+{\displaystyle \sum _{w=2}^k{\pi }_w}h\left(x_i\mid a_{w-1},b_{w-1}\right)\right]}.$$

We use θ as a shorthand to the model parameters, and π=[π₁…π_k+1] for the mixing proportions – a standard Dirichlet variable on the (k+1)-dimensional probability simplex. Notice that, just for notational convenience, we are assuming that the first model component is the Pareto random variable (the tail); we hold this setup fixed even if the model does not fit a tail (in that case we force π ₁=0). Because of this, we use the index w−1 for the parameters of the Beta distributions just to reflex that their index start from one.

Fitting MOBSTER

The formulation uses n × (k+1) latent variables z. A variational approach to fit this mixture is theoretically possible: we could use conjugate Gamma priors for the Pareto, and we would approximate the posteriors for the Beta components as in sciClone. However, we could only approximate a criterion for convergence of the fit, as mentioned above.

We fit the model parameters via Maximum Likelihood Estimation (MLE) through an adaptation of a standard Expectation-Maximization approach (EM). This alternative is faster than a Bayesian Monte Carlo strategy, at the drawback of inferring a point estimate of the parameters. The lack of an explicit measure of uncertainty in the prediction (confidence) can be mitigated using the bootstrap.

We perform these steps to fit a MOBSTER model. In the E-step, we compute the posterior estimates of the latent variables as usual, once we account for the two different distributions involved

$$z_{w,1}\left|\theta \propto {\pi }_{1}g\left(x_i\mid x_{*},\alpha \right)z_{w,i}\right|\theta \propto {\pi }_{i}h\left(x_w\mid a_i,b_i\right)$$

In both cases the normalisation constant C_w is the overall density mass for point x_w

$$C_w={\pi }_{1}g\left(x_w\mid x_{*},\alpha \right)+{\displaystyle \sum _{i=2}^k{\pi }_i}h\left(x_w\mid a_i,b_i\right).$$

In the M-step, for the Pareto tail, we begin by noting that the scale x _* of the distribution can be set to its MLE⁴⁶, which is known to be the smallest observed frequency x _*= min X. This is a constant of the data, so we have one less parameter to fit. We fit the Pareto shape α, given x _*; switching to the log-likelihood and including latent variables its MLE estimator is

$${\text{α}}_{\text{MLE}}=-\frac{{\displaystyle {\sum }_{i=1}^n{z}_{i,1}}}{{\displaystyle {\sum }_{i=1}^n{z}_{i,1}}\text{log}\left(x_{*}/x_i\right)}$$

For the Beta clones, in the M-step, the MLE estimator for the distributions has no closed form; we can resort to approximate it numerically, increasing the computational burden. We can also rely on a recent analytical result on the Moment-Matching (MM) estimator of mixtures of Betas by Schröder and Rahmann⁴⁷. MM consists in matching t empirical moments of the data X to the theoretical moments of the distribution, and solving for them. Here t = 2 (mean and variance); a Beta distribution has mean μ and variance σ given by

$$\mu =\frac{a}{a+b}\sigma =\frac{ab}{{(a+b)}^2(1+a+b)}.$$

For a Beta, conditioned on the latent variables, the MM estimator is

$${\mu }_{i_{\text{MM}}}=\frac{{\displaystyle {\sum }_{w=1}^n{z}_{w,i}{x}_w}}{n{\pi }_i}{\sigma }_{i_{\text{MM}}}=\frac{{\displaystyle {\sum }_{w=1}^n{z}_{w,i}}{\left(x_w-\mu \right)}^2}{n{\pi }_i}.$$

Given estimates for μ_i and σ_i, we can re-parametrize the Beta as

$$a_{i_{MM}}=\left(\frac{1-{\mu }_i}{{\sigma }_i}-{\mu }_i^{-1}\right){\mu }_i^2{b}_{i_{MM}}={\mu }_i\left({\mu }_i^{-1}-1\right)$$

We remark that MM is not the same as computing the MLE, which computes the zeroes of the derivative of the likelihood with respect to the parameters θ, ∂h/∂θ. Thus, the properties of standard EM do not hold when we compute updates via MM: we cannot guarantee that the likelihood increases monotonically, because we cannot employ Jensen’s inequality. It is however shown⁴⁷ that the differences between the estimators are negligible in most cases. For the sake of precision, Schröder and Rahmann propose to call a fit through the MM for Beta distributions the “iterative method of moments”, rather than EM.

In MOBSTER’s implementation we provide both a standard EM fit with numerical solution for the MLE of Beta distributions, and the faster iterative method of moments. In the former case we monitor convergence of the likelihood, as standard. In the latter we use the posterior estimates of π since the likelihood is not monotonically increasing. A theoretical property of this MM approach is that, in each step, before updating the component weights, the expectation of the estimated density equates the sample mean. In particular, this is true at a stationary point; a proof of this is in Lemma 1 of Schröder and Rahmann⁴⁷.

Initial conditions

As standard in EM approaches, we compute the fit with several random initial conditions. We provide two heuristics to compute the initial condition of the fit (Supplementary Figure 1). One is based on a peak detection heuristic applied in the frequency range [0.1,1] to VAF values binned with size 0.01. To detect k initial peaks we perform kmeans clustering of each peak’s x-coordinate, and store their centres. If there are w < k peaks to cluster, we sample k−w random values in (0,1) for the remaining peaks. We use the centers of these clusters as the mean of k Beta distributions with randomized variance sampled in [10⁻³,0.25]; we do sample variance values until the corresponding Beta parameters a and b are positive. For the tail, α is randomly sampled in the interval [0.01,5]. These values provide wide ranges of different initial distributions. An alternative method to select the initial condition of the fit is totally randomized.

Experimental results show that peak detection is a more robust initialization method; the random counterpart sometimes leads to Beta distributions with mean approaching one, a region of parameter values where the likelihood becomes less stable, leading to numerical difficulties. In many cases, we test fits with both initial conditions and retain the best one.

Clustering assignments and model selection

We do not want the fit to be biased towards tails, as we would miss low-frequency subclones that hide in the tail. Besides, simulations suggest limits to the detectability of tails, and therefore we shall not assume tail to be always present in the data. For this reason, MOBSTER can “turn off” the Pareto component of the mixture (i.e., setting π 1 = 0) and fit just k Beta. Hence, we can perform model selection for 1 ≤ k ≤ K considering both models with and without a tail. This induces a statistical competition and allows us to select the model that best explains the data, with or without a tail.

In MOBSTER we compute the negative log-likelihood NLL = −log f(X|θ,π) of the data, which we use to derive the usual AIC and BIC scores BIC = 2NLL +|Θ|log n, and AIC = 2NLL +2|Θ|.

These criteria favor simpler fits by penalizing a model for the number of its parameters |π|. A model with k Beta distributions and one tail has |π|=3k+2 parameters (k+1 for the Dirichlet mixture π, 2k for the Beta(s) and 1 for the Pareto tail). The fit without tail model has |π|=3k−1 parameters; fewer parameters reduce less the penalty, thus favoring fits without a tail.

In MOBSTER we want to drive the fit to select separate clusters, i.e., fits with few overlapping components, which we do not achieve using BIC or AIC. We achieve these separations by using instead two types of entropy terms. In one case we compute, from the latent variables, the usual entropy H(z)

$$\text{H}(z)={\displaystyle \sum _{i=1}^{k+1}{\displaystyle \sum _{j=1}^n{z}_{i,j}}}\text{log}{z}_{i,j}$$

and obtain the standard Integrative Classification Likelihood (ICL) ICL = BIC + H (z), approximated through the BIC⁴⁸. In this paper we also introduce a heuristic variation to the ICL, which we call reICL, a reduced-entropy criterion where we use the entropy of mutations that are not assigned to a tail (Supplementary Figure 1). This is defined as reICL = BIC+H(ẑ), where ẑ are the latent variables for the set of mutations {x|1 ≠ argmax z _x,.}, re-normalized. Notice that in practice ẑ is defined from the hard clustering assignments that we use to assign mutations to clusters; cluster “1” is the label to identify tail mutations.

Entropy terms in ICL and reICL help to fit separate clusters because overlapping mixture components have higher entropy, and therefore penalty. The maximum entropy distribution is the uniform one, which is when we cannot confidently assign mutations to clusters (a point seems to be equally-well explained by multiple components). By definition, ICL will push towards fits with a clear separation among tail and Beta components, while reICL will only require separation of the Beta ones. This modification to the ICL seems reasonable because the Pareto tail overlaps - by definition - to all subclonal clusters, and this leads to strong entropy penalizations with ICL. For this reason, ICL will be more stringent in calling tails than reICL, which drops a part of the entropy penalty restricting its computation to ẑ. See also Supplementary Figure 1 for a graphical explanation.

Notice that, because we are using NLL, we seek to minimize these scores. In the tests, we investigate different model-selection strategies, and choose as default score for model selection in MOBSTER reICL, which seems to provide a nice tradeoff. Between the ability to identify the Beta components, while retaining the tail structure.

Analysis of synthetic data

In the Supplementary Note and in the Supplementary Data (vignettes “Simulated single-sample data analysis” and “Simulated multi-sample data analysis”) we explain how we used branching processes to generate tumors without and with space, and present output metrics to assess precision and sensitivity of our analyses (number of clusters, confidence in the predictions, rates of false/true positives/negatives, the effect of coverage and purity and the ability to identify subclones). In the tests we used MOBSTER and other tools for subclonal deconvolution.

We found MOBSTER and the analyses built around it to be accurate, across all simulated tumors. In all cases tails improve fit quality, from a statistical point of view. This clustering problem is challenging because tails and clones overlap, confounding weak signals of subclonal selection at the low-frequency VAF. We used our performance and combinations of coverage and purity to identify minimum requirements for reliable deconvolution in non-spatial data. In general, we assessed that we can fit subclones and tails for a wide range of parameter values, but overlapping distributions complicate the inference. MOBSTER does not show biases and can identifies subclones, even when they have low VAF (Supplementary Note).

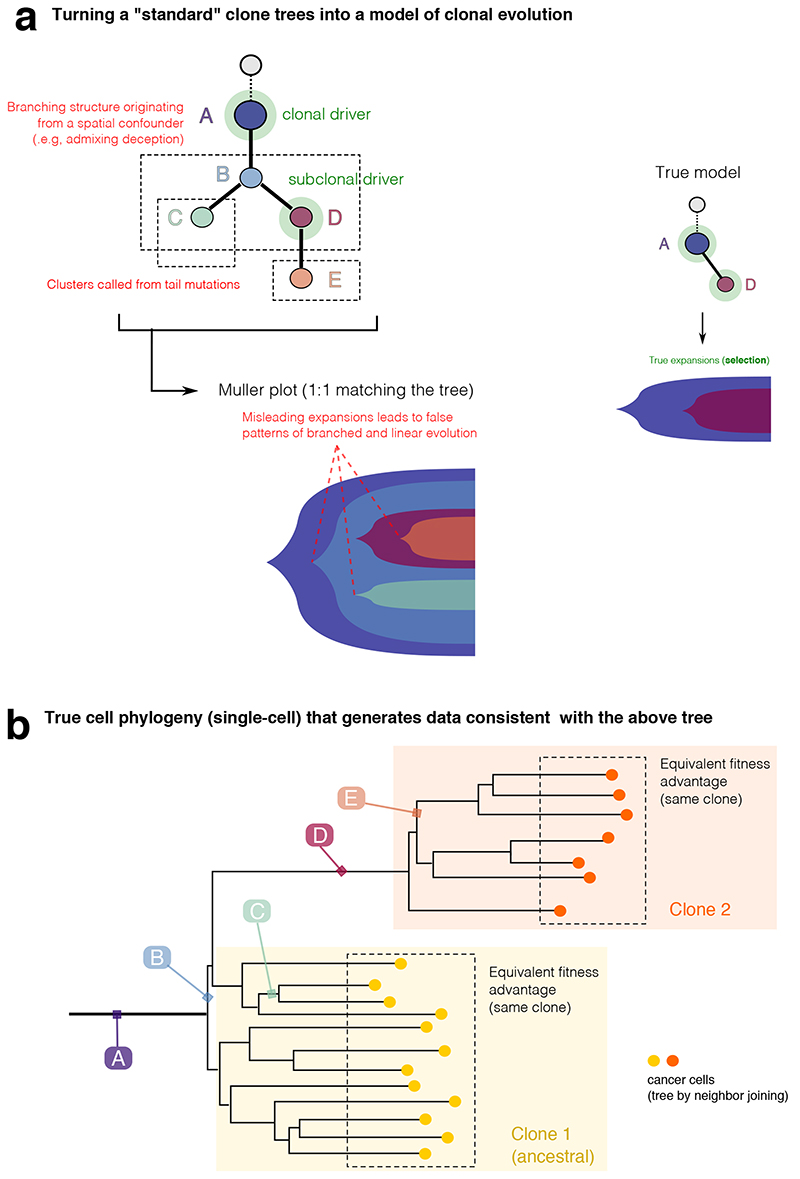
From multi-region data (Supplementary Note) of polyclonal tumors we identified three confounders that inflate the number of clones reported by a “standard” analysis. The confounders contribute Binomial clusters that cannot be directly linked to clonal evolution patterns originating from positive selection. Branching structures originating from the confounders are also misleading, and do not reflect selection-driven branched evolution. One of the confounders can be solved by MOBSTER; two require extra heuristics discussed in the Supplementary Note.

Analysis of patient derived data

The description of all the data analyzed is in the Supplementary Note, as well as in the Supplementary Data. All summary statistics for all fit samples of this paper are available in Supplementary Table 1.

Extended Data

Extended Data Fig. 1. Synthetic tests with MOBSTER.

Example MOBSTER fit of synthetic single-sample tumors (details in Supplementary Note 1). All boxplots and violins show mean and inter quartile range (IQR), upper whisker is 3rd quartile +1.5 * IQR and lower whisker is 1st quartile - 1.5 * IQR. (a,b) Subclonal reconstruction with MOBSTER, against standard methods (variational fit of a Dirichlet finite mixture, and a Markov Chain Monte Carlo sampling for a Dirichlet Process). These methodologies are at the basis of many approaches in the field. The test uses synthetic data from n = 150 simulated tumors (n = 120 with one subclone, and n = 30 without subclones), generated from a stochastic branching process. We report the logarithm of the ratio between the number of clones fit (k_fit) and the true number (k_true). Tests show different values of the concentration parameter α, which tunes the propensity to call clusters. Values (e.g., α = 10^-4 are point estimates, but we also test also a Dirichlet Process where α is learnt from the data using a Gamma prior. (c) Proportion of mutations assigned to MOBSTER’s tail changes with coverage, at fixed 100% tumor purity. We span coverage from 40x to 200x, using a subset of n = 80 tumors from the test in panels (a, b). The red dashed line is the median tail size across the test set (obtained from simulated tumor); tests suggest the coverage required to fit a tail. (d) As for coverage, we tested with n = 320 tumors (n = 80 per configuration) the ability of detecting tails as a function of purity, fixing a coverage of 120x. The average tail size is reported (number of SNVs assigned to the tail in the fit).

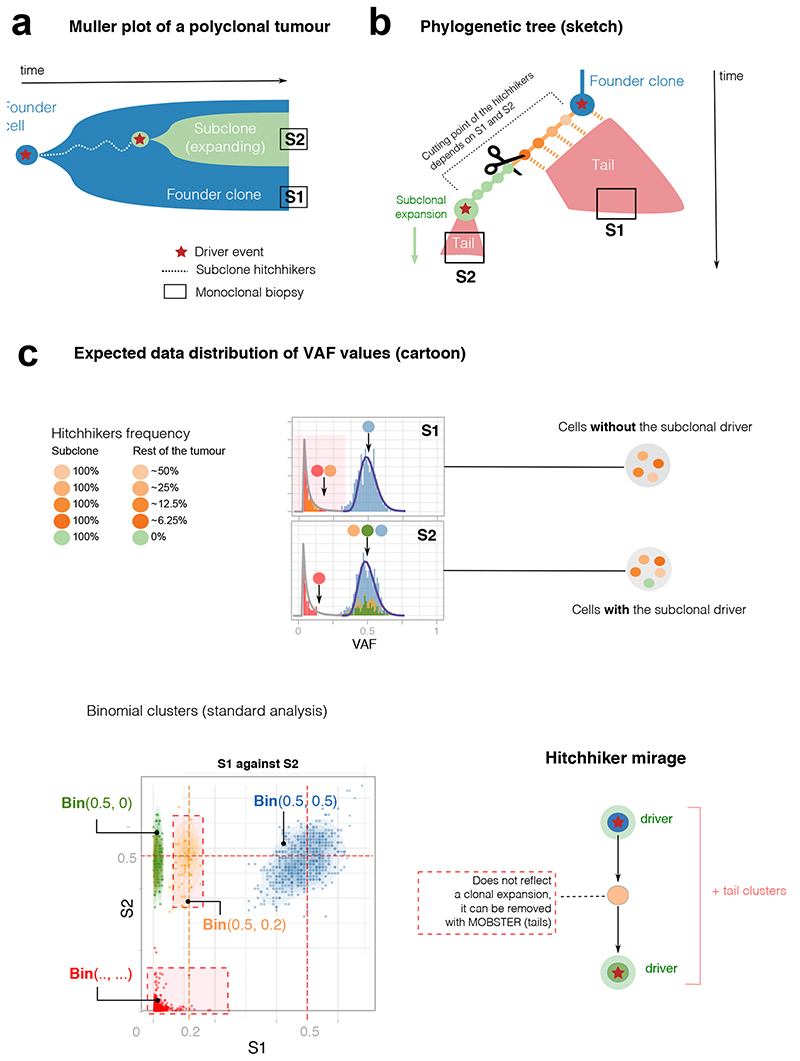
Extended Data Fig. 2. The hitchhiker mirage in multi-region sequencing data.

(a,b) Evolutionary history of a tumor with one subclone. After the first cancer cell gives rise to the tumor (blue founder clone), the population evolves neutrally accumulating passenger mutations (orange), until eventually a subclonal driver occurs triggering a new subclonal expansion (green, with its own tail). The subclonal driver, together with its passenger hitchhikers (orange) will rise in frequency with the subclonal expansion, forming a subclonal cluster in the VAF distribution. However, some early hitchhikers will also be present elsewhere in the tumor as part of the tail of the founder clone. In the example of perfect cell doubling, we expect mutations in the first doubling to be in 50% of the cells of the tumor, mutations in the second doubling to be in 25% etc. We take monoclonal biopsies S1 and S2, and find the founder clone (S1) and a subclonal sweep (S2). (c) The hitchhiker mirage (Supplementary Note 2) is a confounder determined by passengers that hitchhike to the subclonal driver in S2, but diffuse neutrally in S1 (orange). This can be seen in the S1 vs S2 VAF scatter, where the orange mutations do not travel together in the two samples, because cells in S1 do not harbor the subclonal driver (while those in S2 do). The VAF scatter shows that orange hitchhikers can generate an extra cluster with Binomial parameters 0.5/0.2 for S1/S2, on top of the green clone with different parameters (S1/S=0.5/0). Moreover, extra clusters are generated by fitting tail mutations with a Binomial mixture, further inflating the true number of clones (k = 2) and suggesting false clonal sweeps (from which the illusion of a non-existing clonal expansion). If we remove mutations assigned to a tail by MOBSTER we clean up the signal and retrieve the true clonal architecture.

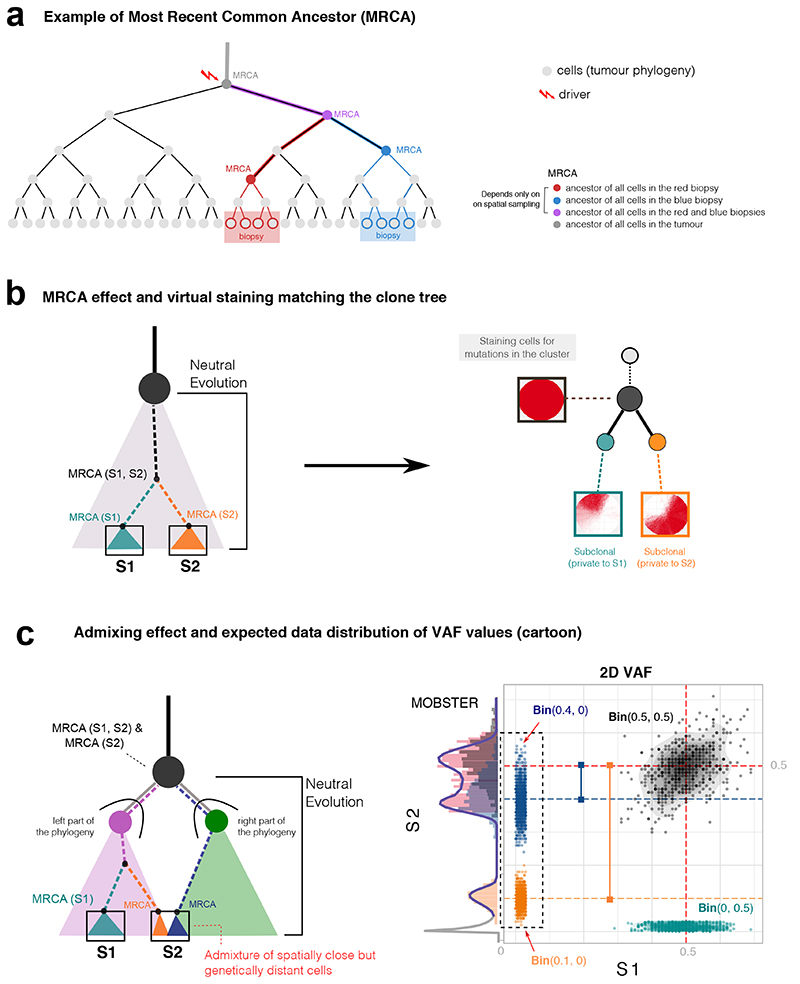
Extended Data Fig. 3. The MRCA fallacy in multi-region sequencing data.

(a) Every cell has always an ancestor, and the cell starting the tumor is the Most Recent Common Ancestor (MRCA) of the whole tumor. We never sequence that cell, we sequence some of its progeny. We can travers the phylogeny of cell divisions backward, and determine the MRCA of all biopsy cells (red and blue), or the MRCA of all biopsies (purple). (b) The ancestor effect (Supplementary Note 2) is the MRCA of cells from a spatially-localized biopsy, compared to other biopsies. Hence, mutations that are observed at high frequency in one biopsy are not necessarily due to selection. We simulate the growth of a 2D neutral tumor, and sample two biopsies (100% purity, S1 and S2). Both samples contain truncal mutations; each biopsy also contains private mutations (green and orange) that are clonal within the sample but are not due to selection. When we generate a virtual staining of all cells that harbor the mutations in a cluster, we see the separation between cells in S1 and S2, and the branched evolutionary structure in the clone tree that is not due to selection, but to spatial sampling (Extended Data Figure 4). (c) The admixing deception stems from spatial tumor intermixing, with cells that are close in space, but genetically distant in the phylogeny. In this example, whereas S1 is a bulk of closely related cells, suffering only from the ancestor fallacy, S2 contains a mixture of cell lineages from distinct parts of the tree (here split in right and left). Intermixing is bond to happen since distant parts of a phylogeny must mix somewhere in space; again, in this example, no selection is at play. From these biopsies, we find truncal (black) and private mutations in S1(green, ancestor fallacy). In S2 we find a mixture of lineages (orange and blue) peaked like subclonal clusters (here we omit neutral tails for simplicity). The orange and blue clusters deviate by an offset that is determined by the level of admixing, which is unknown a priori (see the VAF of S2 in Extended Data Figure 4).

Extended Data Fig. 4. Effects of the MRCA fallacy and the admixing deception in multi-region sequencing data.

(a) Phylogenetic tree of cellular divisions in a neutral expansion, i.e., inside a clonal expansion triggered by a driver hitting the grey cell. The tree shows the sampling of 2 biopsies (red and blue), and the MRCAs. For example, the mutational load present in the red MRCA will characterize cells in the red biopsy. (b) Data distribution and the associated phylogenetic tree show how our estimate of the true evolution of this tumor is confounded by spatial sampling. Mutations that accrue in the lineages from which the MRCAs originate, will create clusters in the data. The corresponding phylogenetic model will also show an inflated number of clonal events (purple MRCA), and branches that do not represent real selection-driven branched evolution (red and blue MRCAs). (c) Example admixing deception in the blue biopsy, where two independent lineages are represented. Admixing can be even or uneven, depending on the proportion of lineages (left versus right) in the biopsy. Remark that no subclonal selection is at play in this example. (d) If we sequence the above biopsies, we find truncal mutations (gray and blue), and a number of clusters that look like genuine subclones. The admixing effect is observed on the vertical of the blue biopsy. In the even case (50% each), the admixing generates one 50% peak for both independent lineages. According to the relation between the frequencies of the observed ancestors, we can also fit two different trees to data; notice that the branching structure presented in both of them is the result of the confounders and does not reflect actual branched evolution. In the uneven case (60% versus 40%), the two admixing peaks separate, originating 2 peaks hitting at the frequencies of 40% and 60%. This shows the pervasive effect of admixing, with up to 8 clusters in this simple scenarios.

Extended Data Fig. 5. Interpreting clone trees as clonal evolution models.

Interpreting clone trees that contain spatial confounders as clonal evolution models can be difficult. We show an example consistent with the data shown in these Extended Data Figures 2-5. (a) All the spatial confounders discussed in Supplementary Note 2 lead to additional nodes and branching structures in the estimated clone tree. These confounders need to be accounted for in a clonal deconvolution analysis, if we seek to identify waves of clonal expansions due to positive selection. The translation of clusters that originate from confounders, into clonal expansions due to selection is misleading, and the inferred clonal evolution is much more complex than the actual one. (b) For clarification, a phylogenetic tree at the single cell level of the tumor, showing that clusters B, C, E and F are arbitrary ancestors identified by the specific spatial bias of the measurement.

Data Availability

Data in Figure 3a were from Nik-Zainal et al. 2012³. Data in Figure 3b were from Griffith et al. 2015²⁰. Data in Figure 3c-e were cases from Cross et al. 2018²¹, here re-sequenced at higher sequencing depth. Sequence data from those colorectal cancer cases have been deposited at the European Genome-phenome Archive (EGA), which is hosted by the EBI and the CRG, under accession number EGAS00001003066. Further information about EGA can be found on https://ega-archive.org. Diploid SNVs and copy number calls are available in the Supplementary Data in vignette “5. Multi-region cross-sectional colorectal carcinomas”. Data in Figure 3f were from Lee et al. 2019²⁴. Data in Figure 4 are available through the PCAWG consortium²⁵. Whole-genome variant call data in Figure 5 that were not available from the original publication, were provided upon email request by Korber et al. 2019²⁸.

Code Availability

MOBSTER is available as an R package at https://github.com/sottorivalab/mobster/; future updates, as well as all vignettes and manuals are maintained at https://caravagn.github.io/mobster/. A repository with all Supplementary Data is available at https://github.com/sottorivalab/mobster_supp_data. Supplementary Data contain vignettes that show the analysis of single-sample and multi-region simulated tumors, the whole analysis of multi-region colorectal samples and single-sample lung cancers, and summary results from the PCAWG and GBM cohorts. Somatic single nucleotide variants and copy number calls used for the analysis of multi-region colorectal samples are also available as Supplementary Data. The implementation of all other R packages that we have developed are available at https://caravagn.github.io/.