Summertime increases in upper ocean stratification and mixed layer depth

Abstract

The surface mixed layer of the world ocean regulates global climate by controlling heat and carbon exchanges between the atmosphere and the oceanic interior^1–3. The mixed layer also shapes marine ecosystems by hosting most of the ocean’s primary production⁴ and providing the conduit for oxygenation of deep oceanic layers. Despite these important climatic and life-supporting roles, possible changes in the mixed layer during an era of global climate change remain uncertain. Here, we use oceanographic observations to show that from 1970-2018 the density contrast across the mixed-layer base increased and that the mixed layer itself deepened. The summertime density contrast increased by 8.9±2.7% dec^-1 (10^-6-10^-5 s^-2 dec^-1, depending on region), more than six times greater than previous estimates due to our use of a more physically-based definition of mixed layer stability following the differing dynamical regimes across the global ocean. While prior work has suggested that a thinner mixed layer should accompany a more stratified ocean^5–7, we instead find that the summertime mixed layer deepened by 2.9±0.5% dec^-1 or several meters per decade (typically 5-10m dec^-1, depending on region). A detailed mechanistic interpretation is challenging, but the concurrent stratification and deepening of the mixed layer are related to an increase in stability associated with surface warming and high latitude surface freshening^8,9, accompanied by a wind-driven intensification of upper-ocean turbulence^10,11. Our results are based on a complex dataset with incomplete coverage of a vast area; we found our results to be robust within a wide range of sensitivity analyses, but important uncertainties remain, such as sparse coverage in the early years. Nonetheless, our work calls for reconsideration of the drivers of ongoing shifts in marine primary production, and reveals stark changes in the world’s upper ocean over the past five decades.

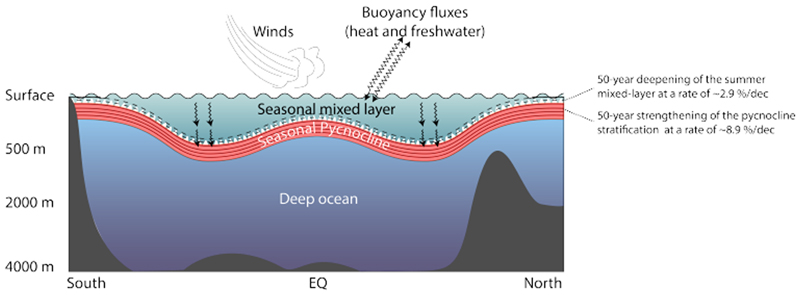
The fundamental vertical structure of the world ocean consists of three main layers: the surface mixed layer, which continually exchanges heat, freshwater, carbon and other climatically important gases with the atmosphere; the pycnocline, characterised by its pronounced stratification, i.e. an enhanced density contrast between shallower and deeper layers, which inhibits cross-layer vertical mixing; and the deep ocean, which is largely isolated from the atmosphere (Fig. 1; some regions have an additional layer between the mixed layer and pycnocline, which is termed "barrier layer" and is associated with an enhanced vertical salinity gradient¹²). Changes in the surface and pycnocline layers can have widespread consequences for climate, as they may alter the rates at which exchanges occur between the surface and the deep ocean. For example, increased pycnocline stratification will expectedly weaken surface-to-depth exchanges as enhanced density gradients decouple surface and subsurface waters, act to shoal the surface mixed layer, and result in reduced air-sea gas transfer, deep-ocean ventilation and biological productivity^3,13–15. Detecting and understanding physical changes in the ocean’s surface and pycnocline layers is thus essential to diagnose the role of the ocean in climate, and predict climate change and its ecosystem impacts. The latest Special Report on Ocean and Cryosphere in a Changing Climate from the Intergovernmental Panel on Climate Change (IPCC)¹⁶ clearly identifies this aspect of oceanic evolution as highly policy-relevant. Changes in the surface mixed layer depth and pycnocline stratification feature prominently in the Special Report’s summary for policymakers, and in multiple contexts including ocean de-oxygenation, nutrient supply to living organisms in the mixed layer, and the global energy budget.

Figure 1. The three-layer structure of the world ocean.

Schematic of an idealized meridional section across the world ocean illustrating the ocean’s three-layer structure. The upper seasonal mixed layer is stirred by a range of turbulent processes driven by wind and buoyancy forcings (see Suppl Mat. 3); the seasonal pycnocline emerges from the density contrast (i.e. stratification) between surface and deep waters, and acts as a barrier reducing communication between surface and deep waters; the deep ocean is largely insulated from the atmosphere, but climate signals propagate from and to the deep ocean through mixing across the seasonal pycnocline and / or through direct contact with the mixed layer as seasonal pycnocline stratification is eroded in winter. In this paper, we present 50-year trends in both mixed layer depth and pycnocline stratification, with impacts on upper-ocean structure and deep-ocean ventilation.

Despite its far-reaching climatic effects, the variability in the mixed layer depth and pycnocline strength have never been examined in a systematic fashion from observations. A few studies have documented changes in upper-ocean stratification, but they have done so by focusing on mixed layer depth variations at specific locations¹⁷ or on changes in stratification averaged over a fixed depth range (generally 0-200 m, 0-1000 m, or 0-2000 m) that conflates the distinct dynamical regimes of the mixed layer, pycnocline and deep ocean^8,9,18–20. For instance, stratification over 0-200 m, which has been widely used in past studies, entirely misses pycnocline changes in regions where the mixed layer is deeper than 200 m (typically at high latitudes in the Southern Ocean and North Atlantic), and can underestimate pycnocline changes where the mixed layer is shallower than 200 m (like in the tropics and the subtropical ocean), especially when the mixed layer depth also evolves in time (see Methods; Extended Data Fig. 1). As a result, we currently lack a physically consistent assessment of the climatic evolution of upper-ocean structure, and do not know whether or how this structure is being affected by global climate change. It is generally expected that, in a warming world, the mixed layer will shoal and the pycnocline stratification will increase^{20, 21}, because the ocean surface warms more rapidly than deeper layers, and oceanic freshening by enhanced ice melting and precipitation at high latitudes is surface-intensified²⁰. This expectation, however, is yet to be tested on a global scale.

Here, we confront this challenge by performing the first assessment of the multi-decadal evolution of the mixed layer and pycnocline across the world ocean. Stratification over a fixed 0-200 m layer is also computed for comparison with previous studies^8,9,18–20. We combine different sources of in situ temperature and salinity observations obtained between 1970 and 2018 (see Methods; Extended Data Fig. 2). Notably, our analysis includes observations from instrumented marine mammals, which afford robust and consistent coverage of the climatically important subpolar Southern Ocean^22,23. For each of these observations, we calculate the mixed layer depth and pycnocline strength (i.e. the squared buoyancy frequency, N², expressed in s^-2) directly below the mixed layer (see Methods), as well as the 0-200 m stratification, N2₀₀, providing us with more than 3 million estimates of each quantity distributed between 80°S and 80°N (60% in the Northern Hemisphere; 40% in the Southern Hemisphere). We then fit a linear regression model based on generalised least squares, locally around each grid point (see Methods), to produce a global, finely-resolved seasonal climatology and associated linear temporal trend estimates. Data selection is based on a rigorously tested data mapping procedure^22,24–26, temporal and spatial decorrelation scales used in the regression model are estimated from the data²⁷, and uncertainties associated with each individual observation are propagated through the model to produce standard error maps for the climatology and the associated trends (see Methods for details). Because of the large seasonal cycle that characterizes the upper ocean, all our results are presented by season, where summer (winter) refers to August-October in the Northern (Southern) Hemisphere and to January-March in the Southern (Northern) Hemisphere. The fields referred to hereafter as ''climatological fields" are seasonal means estimated for year 2000, computed from the monthly weighted local linear regression (see Methods). In regions where salinity-driven barrier layers are present between the mixed layer and the pycnocline (mostly in the tropics¹²), the variable referred to as pycnocline strength, i.e. the density gradient at the base of the density-defined mixed layer (see Methods), is actually a measure of the salinity-driven density contrast between the mixed layer and the barrier layer. Thus, in such regions, our methodology tends to underestimate density contrasts and changes associated with the pycnocline.

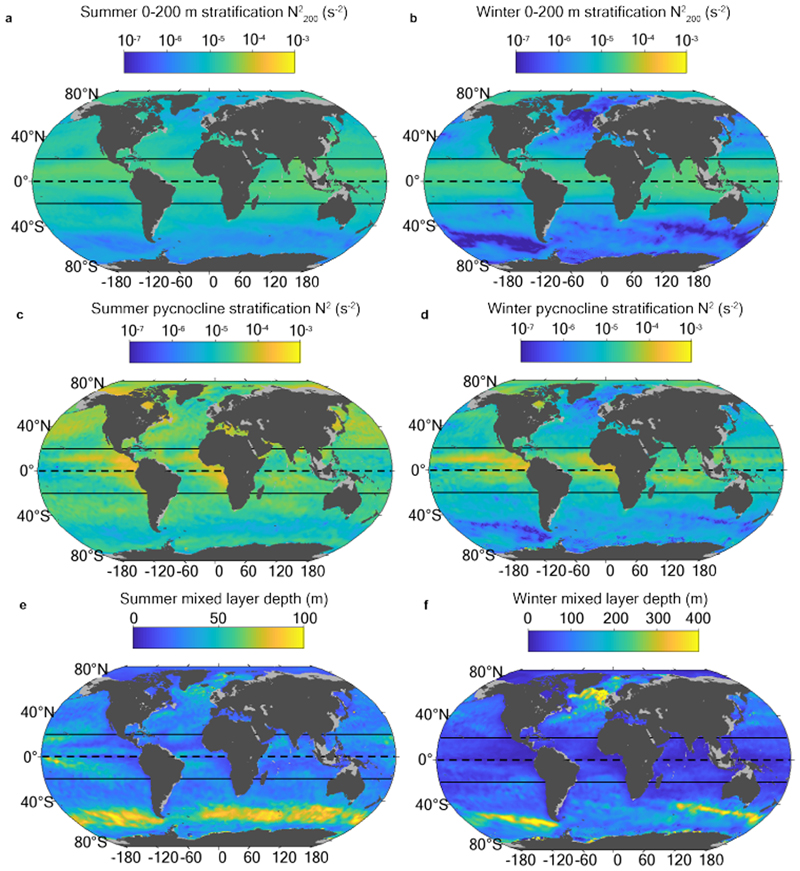
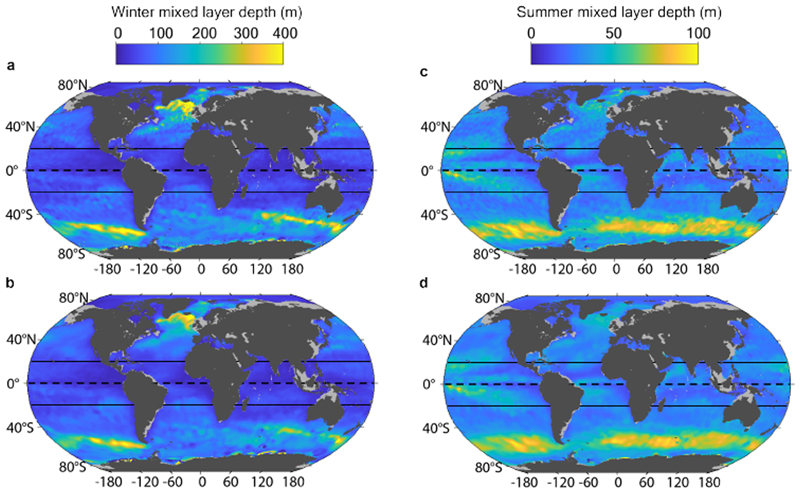
On basin and seasonal time scales, the climatological mixed layer depth generally mirrors the pycnocline stratification, with shallower mixed layers in regions of stronger pycnocline stratification, and vice versa (Fig. 2). Both the spatial pattern and seasonal evolution of the pycnocline and 0-200 m stratification are consistent, although pycnocline stratification exhibits more structure, arguably because it is associated with a dynamically consistent layer of the ocean across all regions and seasons. Pycn- ocline stratification is stronger in summer than in winter, as the mixed layer deepening induced by the wintertime intensification of upper-ocean turbulence (driven by the de-stratifying forcings of oceanic buoyancy loss, wind and waves²⁸) erodes the elevated summer stratification. Pycnocline stratification then increases from winter to summer, and the mixed layer shoals, in response to stratifying forcings (e.g., solar warming and high-latitude sea-ice melt) and relaxation of de-stratifying forcings. In summer, the deepest mixed layers are found in the Southern Ocean, co-located with the year-round intense westerly winds in this region (Fig. 2e). This summertime geographical pattern suggests that regional differences are at least partially driven by a balance between stratifying buoyancy fluxes and de-stratifying wind-driven turbulence. In winter, the deepest mixed layers occur in the subpo¬lar North Atlantic, and directly to the north of the Antarctic Circumpolar Current in the Indian and Pacific basins^22,29–31 (Fig. 2f).

Figure 2. Climatological upper-ocean stratification and mixed layer depth.

(a, c, e) Summer and (b,d,f) winter climatological map of the (a, b) 0-200 m, and (c, d) pycnocline stratification, and (e,f) mixed layer depth over the world ocean.

Seasonal pycnocline changes

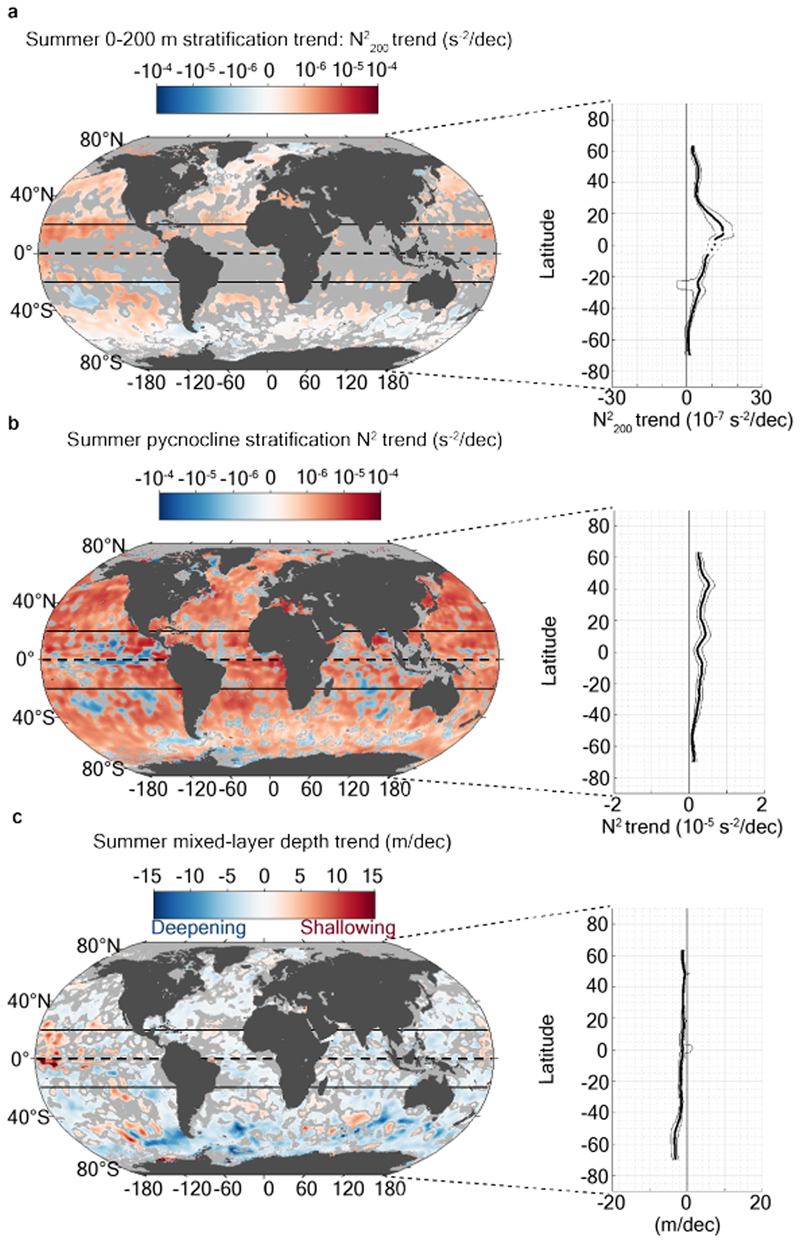
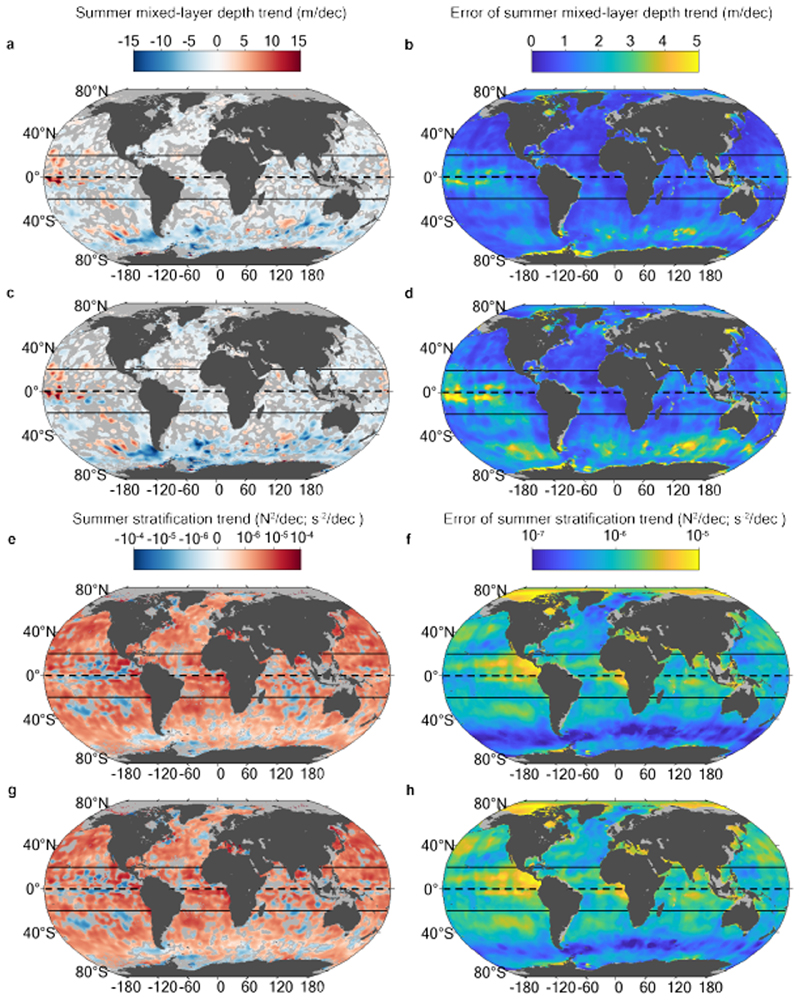
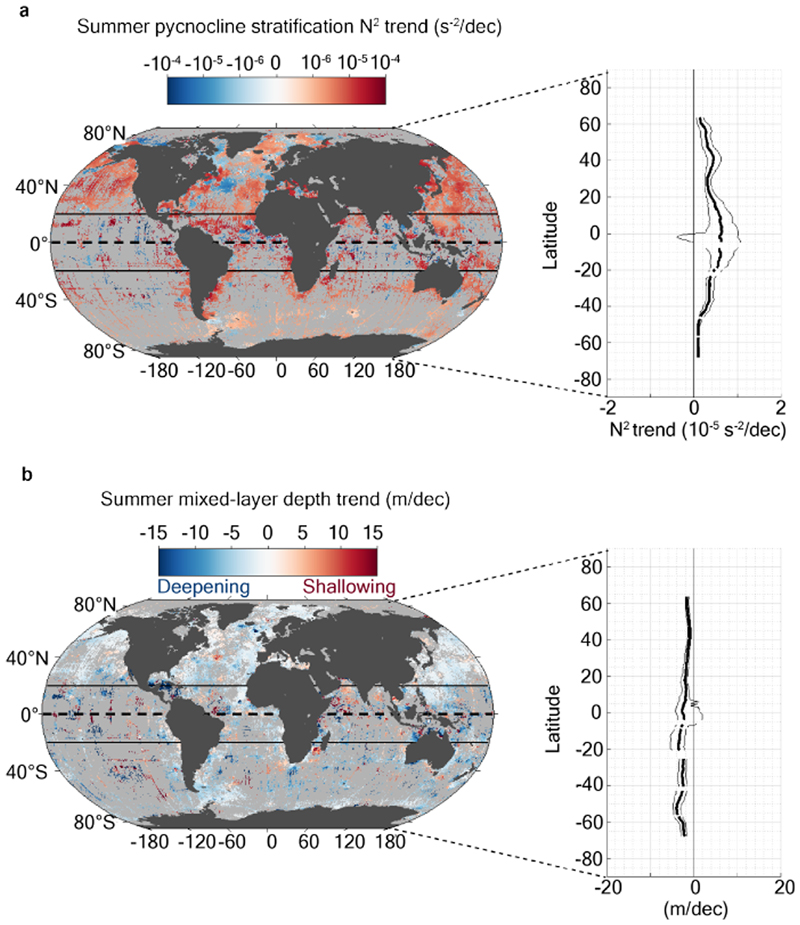
Summertime pycnocline stratification has increased worldwide across all ocean basins since 1970, at a rate ranging from 10^-6 to 10^-5 s^-2 dec^-1 (Fig. 3b). Trends display a marked regional pattern, with greater trends in the tropics (~ 10^-5 s^-2) than at high latitudes (~ 10^-6 s^-2). Consistent with pycnocline stratification, the 0-200 m stratification also shows a global increase, though at a lower rate ranging from 10^-7 to 10^-6 s^-2 dec^-1 (Fig. 3a). Overall, regions with stronger climatological stratification have experienced larger changes than regions with weaker climatological stratification. As a result, the percentage change from local climatological stratification is broadly consistent across all latitudes, and the global-mean percentage rate of change is 8.9±2.7 % dec^-1 (mean ± one standard error; Table 1). This global-mean percentage rate of change of pycnocline stratification is considerably higher than the equivalent rate of change of the 0-200 m stratification estimated here with the same methodology, which is only 1.3±0.3 % dec^-1 (Table 1). Using a dynamically consistent framework to analyse the ocean’s vertical structure thus reveals upper-ocean density contrasts increasing at a rate 6 to 7 times higher than when considering a fixed (i.e. non-dynamical) 0-200 m reference frame. The latter glaringly misrepresents the increase in upper-ocean stratification that has occurred globally over the past five decades. Notably, our estimate of 0-200 m stratification change is consistent with previous annual-mean estimates of the same variable from the IPCC Fifth Assessment Report³² (1% dec^-1); from the latest IPCC Special Report¹⁶ (0.46-0.51% dec^-1); or from more recent works using individual observational databases⁹ (0.6-1.1% dec^-1), or a range of gridded observational products⁸ (1.2±0.1% dec^-1 using the IAP product, 1.2±0.4% dec^-1 using the Ishii product, 0.7±0.5% dec^-1 using the EN4 product, 0.9±0.5% dec^-1 using the ORAS4 product, and 1.2±0.3% dec^-1 using the NCEI product; see Li et al⁸ for details on each of these products and associated references). Our diagnostics of pycnocline stratification change complement preceding views that relied on a fixed 0-200 m layer (which gives a false impression of more moderate upper-ocean change than in reality), and call for a careful revisiting of the impacts of the upper ocean’s evolution in assessments of future climate change and corresponding adaptation strategies. Although our quantification of the wintertime pycnocline stratification change is more uncertain, due to the comparatively modest number of winter observations, it does reveal a very clear strengthening of pycnocline stratification too (see Methods; Extended Data Fig. 5 and Extended Data Fig. 6).

Figure 3. 1970-2018 trends in summer upper-ocean stratification and mixed layer depth.

Map of the 1970-2018 summer (a) 0-200 m (${\text{N}}_{200}^2$ trend in s^-2 dec^-1), and (b) pycnocline stratification trend (i.e. N² trend in s^-2 dec^-1), along with zonal-median value in bold black, and 33-66 percentile in thin black. Regions with no significant trend (see Methods) are shaded in gray on the map. (c) same as panel (a,b) but for summer mixed layer trend in m dec^-1 (note that mixed layer deepening is shown as a negative trend).

Table 1. Global mean percentage change.

Table showing the global mean percentage change and the associated standard errors of the mean for ${\text{N}}_{200}^2$, N², and the mixed-layer depth (MLD). Local trend estimates at each grid point are divided by the local climatological mean value, and the global mean and standard error of the global mean are then computed. Standard error is computed by propagating the local standard error produced by the regression method (see Methods; Extended Data Fig. 4).

(% dec-1)	Choice 1	Choice 2	Mean
${\text{N}}_{200}^2$	1.5±0.2	1.1±0.3	1.3±0.3
N2	9.5±4.4	8.3±0.9	8.9±2.7
MLD	-2.6±0.1	-3.2±0.9	-2.9±0.5

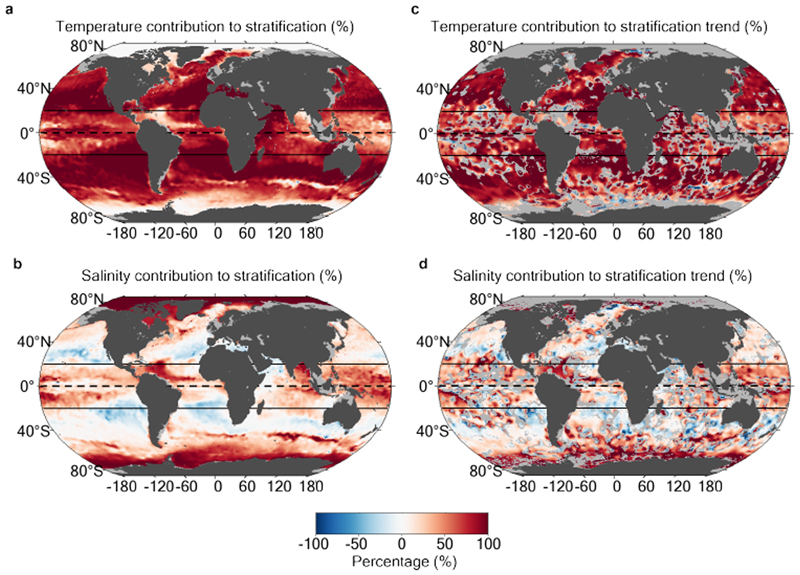
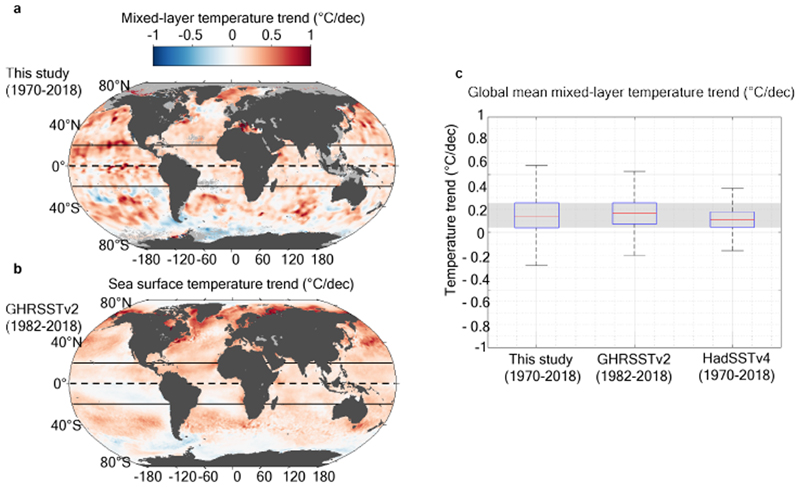
The pycnocline stratification can be linearly decomposed into contributions associated with vertical gradients in temperature and in salinity (see Methods). Over much of the world ocean, the density contrast of the pycnocline is mainly linked to the vertical temperature gradient (warmer waters overlying cooler waters; Fig. 4a); however, we note that in the tropics and at high latitudes, salinity is either dominant over or has a comparable effect to temperature. The strong control of stratification by temperature is particularly obvious in the evaporation-dominated regions of the subtropics and mid latitudes. These are characterized by high climatological upper-ocean salinity (higher than the global mean), and exhibit an unstable vertical salinity gradient (saltier waters overlying fresher waters), which the vertical temperature gradient overcompensates to attain a state of upper-ocean stability (Fig. 4a,b). In contrast, high latitudes are precipitation-dominated regions and contain very cold surface waters, such that upper-ocean stability is almost entirely established by the vertical salinity gradient (Fig. 4a,b). Interestingly, the observed change in pycnocline stratification results from an amplification of this climatological regional pattern: areas with an unstable salinity profile in the climatology have further de-stabilised in the past 50 years, and areas with a stable salinity profile in the climatology have further stabilised in the past 50 years. These changes in vertical salinity gradient are consistent with the now widely documented paradigm of a contemporary acceleration of Earth’s hydrological cycle, as a result of which fresh oceanic regions have become fresher and salty regions have become saltier^32–35. In turn, the contribution of the vertical temperature gradient to increased pycnocline stratification has consistently increased worldwide in response to global ocean surface warming²⁰. An exception is the subpolar Southern Ocean, where modest change in the vertical temperature gradient is in accord with reports of weak warming or even slight cooling having occurred in this region over recent decades^36,37 (see Extended Data Fig. 7). Viewed overall, the consistency of our results with previous assessments of changes in the Earth’s surface temperature and hydrological cycle endorses the robustness of our analytical approach. More quantitatively, our method produces estimates of mixed layer temperature change that are in accord with other widely recognised and used sea-surface temperature products (see Methods and Extended Data Fig. 7).

Figure 4. Temperature and salinity contributions to pycnocline stratification and its change.

Percentage contribution of (a) temperature and (b) salinity to the summer climatological pycnocline stratification shown in Fig. 2a. Percentage contribution of (c) temperature and (d) salinity to the summer climatological pycnocline stratification trend shown in Fig. 3a. Regions with no significant trend (see Methods) are shaded in gray in panels c and d.

Changes in mixed layer depth

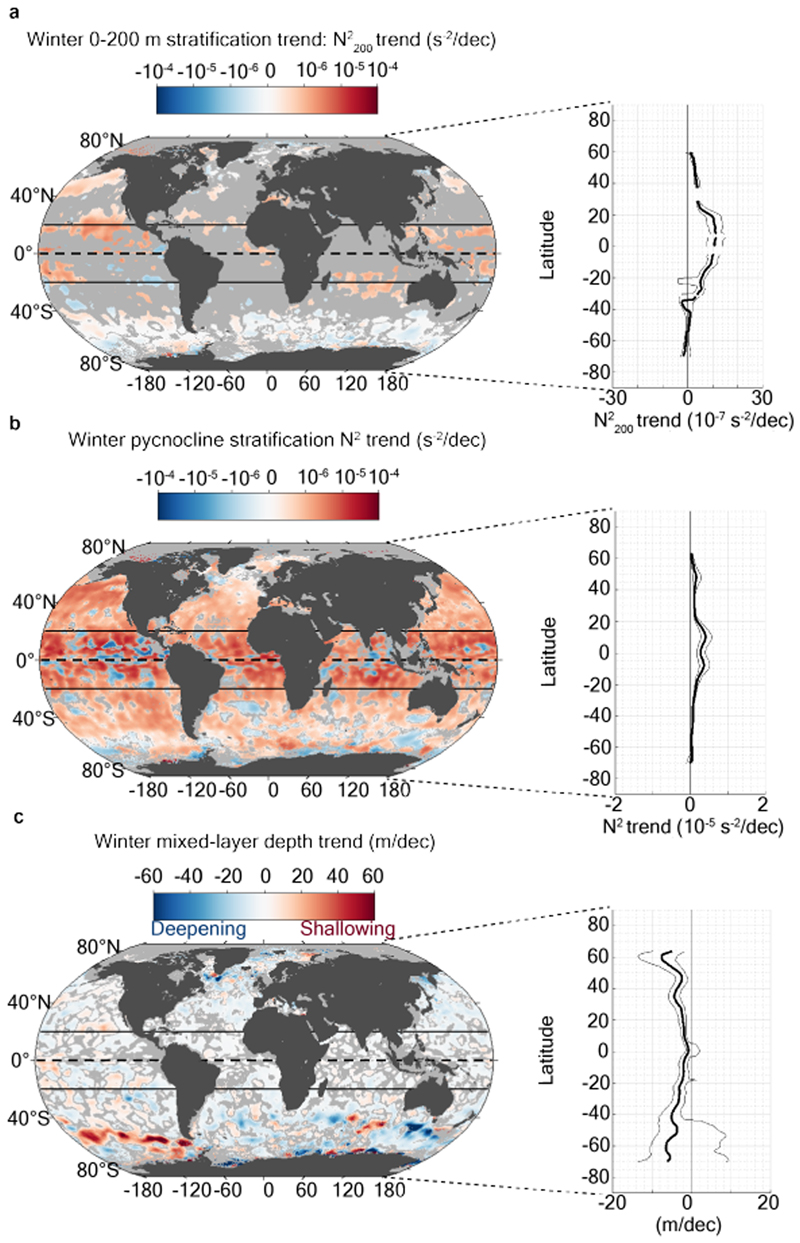
The global-scale pycnocline stratification strengthening is, in principle, well understood, as it is predicted to arise from ocean surface warming associated with recent climate change. In contrast, the evolution of the mixed layer depth might be expected to be more complex, as it is shaped by a delicate interplay between stabilising and de-stabilising forcings. To date, it has been generally assumed that there is a direct association between increasing pycnocline stratification and mixed layer shoaling^5–7. Here we show that, counter-intuitively, this commonly accepted assumption is at odds with observed changes in upper-ocean structure over the past fifty years. Our analysis reveals that the summertime strengthening of pycnocline stratification has occurred in association with a worldwide deepening (rather than shoaling) of the summer mixed layer at a rate of several meters per decade, ranging from 5-10 m dec^-1 depending on region (Fig. 3c). The multi-decadal deepening is remarkably consistent globally, with most intense deepening in the Southern Ocean, within the 40-60° S latitude band containing the deepest climatological mixed layers (Fig. 2e). Our results present some local patchiness in the Southern Ocean. Data sparseness in the Southern Ocean can be a limitation to compute local/regional trends, which can explain some this patchiness, though basin-scale diagnostics in the Southern Ocean are robust to data sparseness (see further analysis on that aspect in Supplementary Information). Overall, the global-mean percentage rate of change (percentage of the local climatogical mean) is -2.9±0.5 % dec^-1 (mean ± one standard error; Table 1; by convention negative change refers to deepening). Note that these rates of change are not artificially generated by variations in the global ocean observing system, e.g., with the launch of the Argo program in the 2000s (see Methods and Extended Data Fig. 8 and 9), and are not only due to the largest changes in the Southern Ocean (see Supplementary Information), but do reflect a widespread mixed-layer deepening. Changes in mixed layer depth, pycnocline stratification, and 0-200 m stratification are dynamically linked, and it is reassuring that all of the global-mean rates of change estimated in this study are mutually consistent (see Methods). Our diagnostics of trends in winter mixed layer depth must be treated with caution, as they are based on shorter time series and may be affected by sub-sampling of large intra-seasonal and interannual variability. Nevertheless, they concur with the summer results: there is a global-scale deepening of the winter mixed layer, though with a suggestion of regional winter shoaling in the Pacific sector of the Southern Ocean (see Methods; Extended Data Fig. 5 and Extended Data Fig. 6).

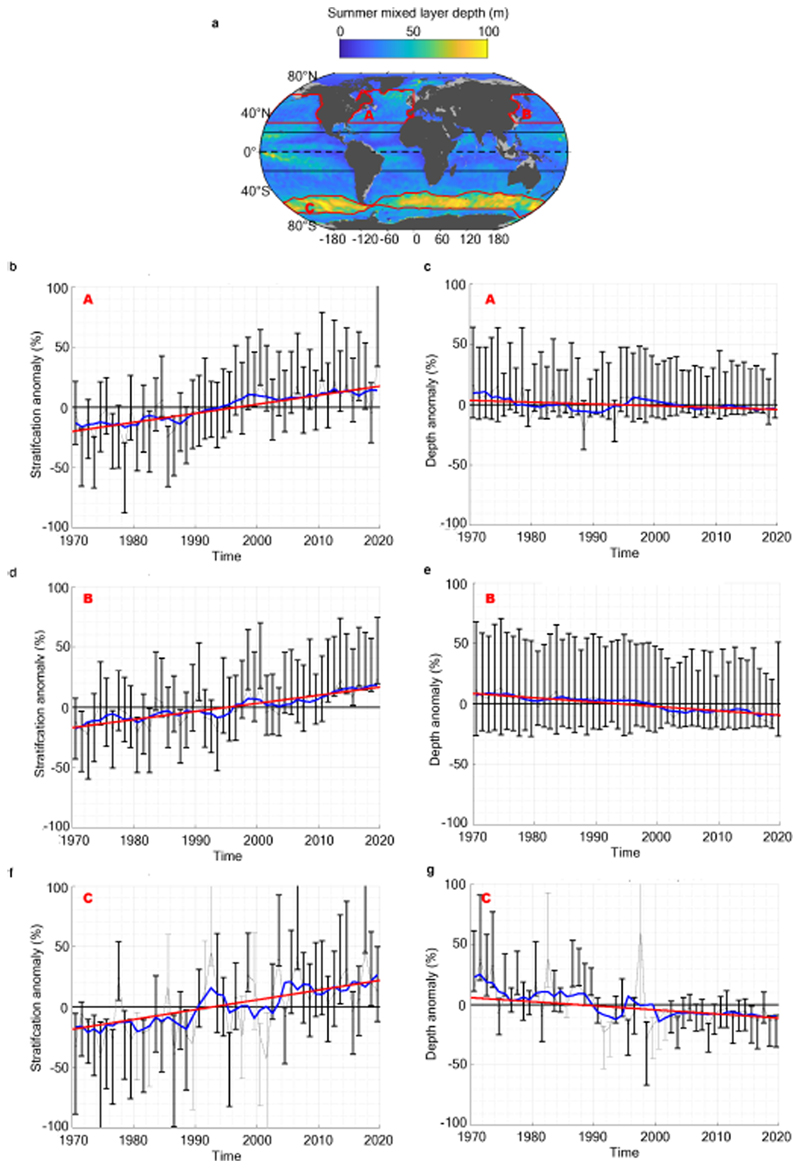
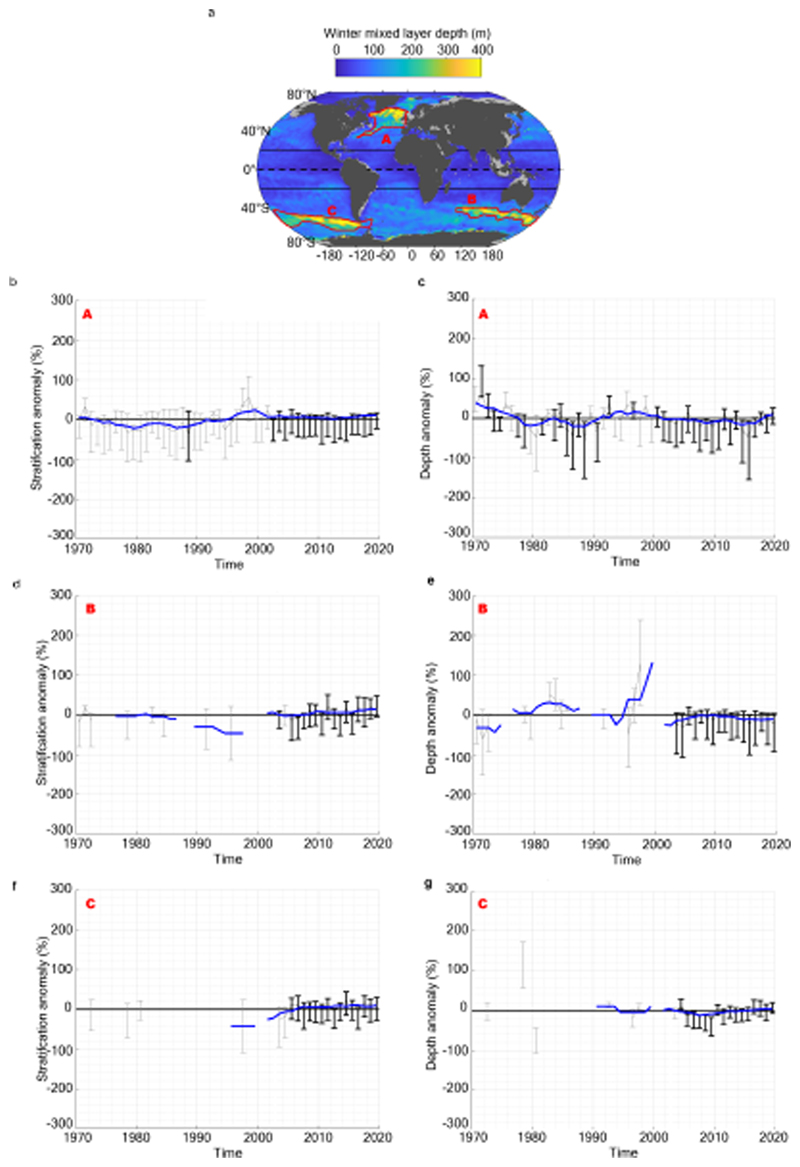
It is helpful to visually examine time series of the evolution of upper-ocean structure on regional scales, in order to increase our confidence in the observed large-scale changes. We therefore produce annual-median percentage anomaly (percentage anomaly from the local seasonal climatology) diagnostics using all available individual observations, and fit a linear regression model to the annual medians. This method has the advantage of being grounded on individual observations (by avoiding the gridding procedure) but, while it allows visualization of regional time series, it may induce regional biases due to the uneven spatio-temporal sampling, as well as averaging out the largest changes (Fig. 5). The locally-gridded linear regression trends presented above (Fig. 3) are more robust in this regard. Focusing on the North Atlantic basin between 30-60^°N, on the North Pacific basin between 30-60°N, or on the Southern Ocean in the circumpolar band containing the deepest summer mixed layers, invariably confirms our central result of a significant strengthening of pycnocline stratification occurring in tandem with a mixed layer deepening (Fig. 5). Even with this statistically less robust approach, we find basin-scale rate of change quantitatively consistent with the more robust approach presented above: increasing pycnocline stratification at a rate of 8.1±4.1% dec^-1 in the Southern Ocean, 6.7±1.5% dec^-1 in the North Atlantic, and 7.5±1.7% dec^-1 in the North Pacific; and deepening mixed-layer at rate of -3.4± 1.5% dec^-1 in the Southern Ocean (see a further analysis on the sensitivity of this trend in Supplementary Information), -1.5±0.9% dec^-1 in the North Atlantic, and -3.6±0.9% dec^-1 in the North Pacific. While a 50-year, large-scale increase in the mixed layer depth has not been previously documented, one recent study¹⁷ reported a deepening of the mixed layer at three selected sites in the North Atlantic and North Pacific between 1990 and 2015, at rates ranging from 1 to 8 meters per decade that are consistent with our results (5-10 m dec^-1).

Figure 5. Regional time series of summer pycnocline stratification and mixed layer depth anomaly.

(a) Summer climatological mixed layer depth, as in Fig. 2e, with three specific regions of interest outlined by red contours: North Atlantic (A); North Pacific (B); and Southern Ocean (C). For each of these regions, summer stratification anomaly times series and associated trends are respectively displayed in panels (b,d,f); and summer mixed layer depth anomaly times series and associated trends are respectively displayed in panels (c,e,g). Note that a negative depth anomaly refers to a deepening. Each times series panel shows: in thin gray line, the annual median percentage anomaly (from the local climatological seasonal cycle), computed for each individual observation; the errorbars refer to the 33-66 percentile range of percentage anomaly (errorbars are shown in black (gray) when more (fewer) than 50 data points are used in the annual statistics); the associated 5-year smoothed median time series is superimposed in blue; a linear trend from 1970-2018 is shown by the red line if greater than twice its standard error.

Given the increasing pycnocline stratification, the observed deepening of the mixed layer must have necessarily been driven by an intensification of surface turbulence overcoming the increased stability below the mixed layer. Surface turbulence can be generated by a range of processes, including surface buoyancy fluxes (giving rise to convective mixing), wind-driven mechanical mixing, wave breaking, wave-generated Langmuir turbulence or internal waves, and wind- or buoyancy-forced submesoscale instabilities at upper-ocean fronts^28,38,39 (see Methods). Under the current climate change, variations in surface buoyancy fluxes act to suppress turbulence by increasing the buoyancy of mixed-layer waters, as indicated by Fig. 4, so they cannot account for the observed mixed-layer deepening. Even in regions which have experienced a salinity-driven destabilisation, arguably due to an increased evaporation (blue regions in Fig. 4d), our results show that the vertical density stratification has increased (Fig. 4a), because the increase of temperature-driven stability has overcompensated the salinity-driven destabilisation (Fig. 4a). As a consequence, the body of available evidence suggests that changes in air-ice-sea heat or freshwater fluxes cannot have driven a destabilisation of the upper ocean, which would have led to a deepening mixed layer. Intensification of mechanical turbulence overcoming the increased stability is needed. Observations of such turbulence are, however, limited to a number of process-oriented studies, and there is currently no physically-consistent, observation-based data set available to assess long-term change in upper-ocean turbulence. Instead, we use scaling arguments to demonstrate that our current theoretical understanding of mixed layer physics is potentially compatible with the mixed layer deepening and increased stratification that have occurred in recent decades. This theoretical framework suggests that the mixed layer deepening documented here may plausibly have been driven by a global intensification of the wind field, including its high-frequency component, for which there is a range of emerging evidence^10,11,40 (see Methods). The influence of invigorated winds may have been exerted through one or several of: internal wave-driven turbulence linked to high-frequency winds³⁹, wave-generated Langmuir turbulence³⁸, and submesoscale instabilities at upper-ocean fronts²⁸. Note, though, that the contribution of the latter process is less clear, as submesoscales could also have a counteracting, mixed layer shoaling effect that we do not consider here^41,42 (see Methods).

Conclusions

Our findings carry important implications for our understanding of the impacts of global climate change on ocean circulation and marine ecosystems. First, we have shown that, over the last five decades, all ocean basins have experienced a significant strengthening of summer pycnocline stratification, at a rate at least 6 times higher than previously reported^16,18,19. If the turbulent energy reaching the pycnocline had remained constant, such a change in stratification would bring about a large reduction in mixing between the upper and deep oceanic layers⁴³. Weaker vertical mixing would likely result in a slowdown of deep-ocean ventilation and oxygenation⁴⁴, as well as substantially weaken upper-ocean nutrient recharge by mixing with deeper waters. Second, we have found that the surface mixed layer has deepened across much of the world ocean. This may possibly counteract the effects of a strengthened pycnocline stratification, as a deepening mixed layer would promote the upward transfer of poorly ventilated and oxygenated, and nutrient-enriched, pycnocline waters. Such mixed-layer deepening could also affect near-surface temperature and salinity changes by increasing the volume of the surface layer, hence providing a climatic feedback mechanism². Deepening of the summer mixed layer may also lead to a degradation of light conditions within the near-surface waters in which most primary producers live, thus negatively impacting the biological carbon pump^5,6,15. A final consequence of the changes in pycnocline stratification and mixed layer depth uncovered by our work is a shift in a range of fundamental dynamical properties of the ocean circulation that depend sensitively on upper-ocean stratification. These include⁴³: the first baroclinic Rossby radius of deformation⁴⁵, which is the natural horizontal scale of oceanic boundary currents, eddies and fronts; the speed of propagation of baroclinic waves across ocean basins; and the vertical structure of oceanic gyres and coastal upwelling systems. To conclude, given their many ramifications for ocean circulation and climate, our results represent a critical benchmark for the evaluation of the current generation of Earth System Models, and highlights the need to maintain a global ocean observing system which provides the necessary measurements to best inform on the scales of current changes in our oceans and help shaping relevant adaptation strategies and policies going forward.

Methods

Data sources and density

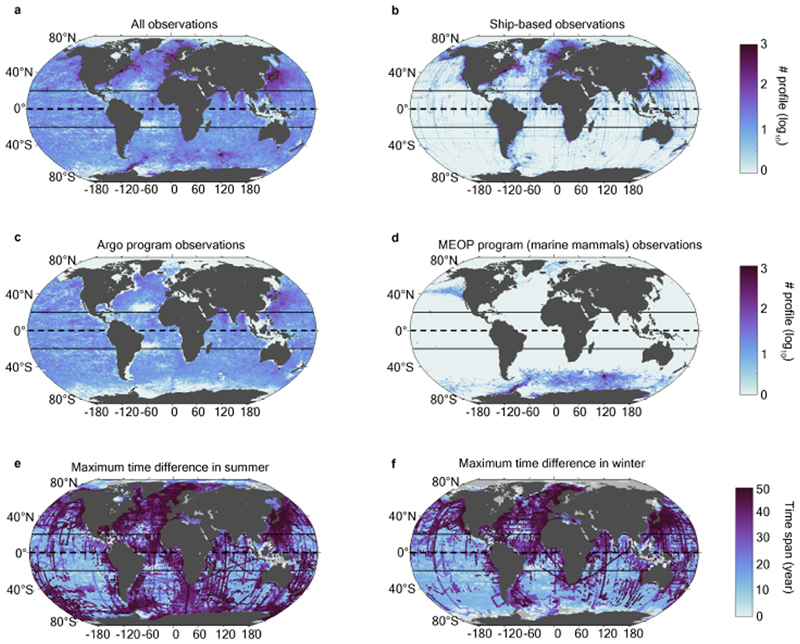
Three distinct types of observations are considered in this study in order to maximize spatial and temporal coverage. First, we use vertical conductivity-temperature-depth (CTD) profiles obtained from ship campaigns during the period 1970-2018 (Extended Data Fig. 2b). We use "high-resolution CTD" data (i.e., vertical resolution of less than 2 meters) from the NOAA World Ocean Database (https://www.nodc.noaa.gov/OC5/SELECT/dbsearch/dbsearch.html), and augment it with profiles obtained from the PANGAEA database (https://www.pangaea.de/). We only use profiles that have an "accepted profile" quality-control flag (i.e., best quality only), and that contain information on position, date, temperature and salinity. These amount to a total in excess of 1.37 million profiles (Extended Data Fig. 2b). Note that earlier observations might have been sampled by less technologically mature salinity sensors⁴⁶. However, while salinity in the 1950s or 1960s could be associated with errors on the order of 10^-2 g kg^-1, the typical salinity accuracy in the 1970s or 1980s was, although inferior to today’s, on the order of several times 10^-3 g kg^-147. This is unimportant for detecting a density shift of 0.03 kg m^-3 (see section on “Definition of mixed-layer depth and pycnocline stratification” below), which typically corresponds to a salinity change of ~ 0.04 g kg^-1. The vertical resolution of the profiles could be a more important issue to accurately describe the mixed layer, but we account for it in our uncertainty estimates (see section "Definition of mixed-layer depth and pycnocline stratification" below).

This ship-based hydrographic database⁴⁸ is complemented by float data from the Argo international program (http://www.argo.ucsd.edu/). The Argo program commenced in 2000, and has crucially increased the number of ocean observations acquired every year over the world ocea^n49,50. All publicly available profiles up to the end of 2018 were used that contained information on position, date, temperature and salinity. We only use profiles that have a quality flag “good data” (i.e., best quality only), and we use delayed time calibrated values if provided. These amount to a total in excess of 1.39 million profiles (Extended Data Fig. 2c).

Finally, we also consider profiles from marine mammal-borne sensors, obtained through the Marine Mammals Exploring the Oceans Pole to Pole program (MEOP) (http://www.meop.net/)²³. We use a calibrated data set⁵², and only consider profiles that have a quality control flag "good data" (i.e., best quality only), that are adjusted after the delayed time calibration provided by MEOP, and that contain information on position, date, temperature and salinity. These amount to a total in excess of 480,000 profiles (Extended Data Fig. 2d).

These three types of observations are complementary in space and time. Ship-based observations are concentrated along repeated hydrographic sections or near coastlines (Extended Data Fig. 2b). Ship-based observations are a key data set for our study, since they provide the longest time series. In turn, Argo float observations are more widely spread across ocean basins (Extended Data Fig. 2c) and less seasonally biased than ship-based observations. However, they are scarce in regions that are seasonally capped by sea ice, despite the recent growth of the under-ice Argo network. The instrumented marine mammal data set provides measurements in the climatically important southern subpolar region, and to a lesser extent in the subtropics and high latitudes of the Northern Hemisphere (Extended Data Fig. 2d). Overall, the combination of these three data sets affords an unprecedented cover of the world ocean from pole to pole (Extended Data Fig. 2a).

In this paper, we are interested in detecting long-term trends from this observing system. Therefore, one specific aspect that is important to our study is the long-term temporal coverage provided by the data set. A metric of this coverage is the maximum time difference between available observations in 1°x1° longitude-latitude bins over the globe. In summer, most of the world ocean exhibits a maximum time difference exceeding 40 years, with some notable exceptions in parts of the eastern tropical and southern subtropical Pacific (Extended Data Fig. 2e). In winter, the maximum time difference is mostly larger than 40 years in the Northern Hemisphere, but generally closer to 20 years in the Southern Hemisphere, with exceptions near the coasts and along repeated hydrographic sections (Extended Data Fig. 2f). This maximum time difference metric indicates that summer trends will be better constrained than winter trends, and that the suitability of available observations for the detection of multidecadal trends is geographically variable. Close attention to this heterogeneity in data abundance is necessary when interpreting global-mean statistical analyses⁵³. Here, we investigate mapped (i.e., region-specific) trends, consider trends in individual seasons, and examine regional time series, in order to overcome this issue.

Definition of mixed layer depth and pycnocline stratification

The mixed layer is defined as the oceanic surface layer in which density is nearly homogeneous with depth. A number of methods have been developed over the years to compute mixed layer depth from a given density, salinity or temperature profile^29,54,55,57. Methods based on density profiles rather than temperature profiles are usually more successful in detecting the mixed layer base^31,57,58 and have become a standard for defining the mixed-layer depth. A range of methods applicable to density profiles have been proposed, based on, e.g., a threshold density deviation from surface density, a density gradient threshold, or a piece-wise fit to the density profile. A recently developed hybrid approach proposes the use of a combination of these different methods, and appears to work well worldwide³¹. In this paper, we adopt the method based on a threshold density deviation from surface density^29,58. Specifically, we define the mixed layer depth as the depth at which the potential density referenced to the surface, σ₀, exceeds by a threshold of 0.03 kg m^-3 the density of the water at 10 m: σ₀(z = -H) = σ₀(z = -10 m)+0.03 kg m^-3, with H as the mixed layer depth. We choose this threshold because it has been shown to robustly detect the base of the mixed layer in various regions of the world^29,57,58. Further, this approach produces, overall, nearly identical diagnostics of mixed layer depth to those from more complex methods³¹. At any rate, we acknowledge this methodological sensitivity by quantifying the uncertainty in our mixed layer results as the standard deviation of the values computed from the three independent density-based procedures proposed by Holte and Talley^22,57. This approach allows us to define an overall uncertainty estimate, including uncertainties associated with temperature, pressure and conductivity sensor performance, as well as uncertainties associated with vertical resolution²². We reject all mixed layer depth estimates from density profiles for which the standard deviation between results from the three procedures is greater than 25% of the results’ mean value. If the computed standard deviation is smaller than the vertical resolution of the individual profile, the uncertainty is set to the vertical resolution, i.e. 2 m for ship-based CTD data, 10 m for Argo profiles, 20 m for instrumented marine mammal profiles. The resulting uncertainty is then propagated into the gridding method as contributing to the variance associated to each observation.

Seasonal pycnocline stratification is defined as the squared buoyancy frequency computed from the density gradient over the 15 m layer directly below the mixed layer base:

$$N^2=-\frac{g}{\rho }\frac{\partial {\sigma }_0}{\partial z}|{}_{-H\ge z\ge -H-15}\prime |$$ (1)

where σ₀ is potential density referenced to the surface, and g is the gravitational acceleration. The squared buoyancy frequency, N², is expressed in s^-2 in this manuscript following the Standard International unit convention.

The pycnocline stratification can be expressed, to a first approximation, as a linear combination of distinct temperature and salinity contributions⁴³ (See Fig. 4):

$$N^2=N_{\text{T}}{}^2+N_S{}^2,\text{with}{N}_S{}^2=g\beta \frac{\partial S}{\partial z}\left|{}_{-H\ge z\ge -H-15}\right|\text{and}{N}_{\text{T}}{}^2=-g\alpha \frac{\partial T}{\partial z}|{}_{-H\ge z\ge -H-15}\prime |$$ (2)

where β is the haline contraction coefficient and α is the thermal expansion coefficient.

Mapping method for computing climatologies and associated trends

The pycnocline stratification, mixed layer depth, and associated uncertainties are computed for each profile in our database. We then produce gridded maps of climatological mean fields and trends, calculated as local linear regressions of individual profiles around a grid point. We adopt a regular 0.5° x0.5° longitude-latitude grid. The method for computing a mean field and the associated long-term trend involves: (i) defining a spatial distance metric; (ii) selecting individual profiles that are close in space and time to a given grid point for a specific month; and (iii) producing a local generalised least-squares linear regression. These steps are described in turn in this section. We then consider the impact of the modelling choices. Associated uncertainties are discussed in the next section ("Robustness and uncertainty quantification") below.

Defining a distance metric. For each grid point, we compute the distance, Δd_i;, separating each individual observation, i, from the grid point. We use a distance that follows bathymetric contours. In the ocean, near-conservation of potential vorticity translates into water particle pathways that tend to follow bathymetric contours, constraining all quantities from surface to depth^62–64. We therefore construct a distance that follows this along-pathway constraint, using the fast marching method described in Schmidtko et al.²⁴, which is based on Dijkstra’s algorithm⁶⁶. We refer the reader to Schmidtko et al.²⁴ for more details on the fast marching method.

Data selection. For each grid point and each month of the year, a distance weight, w_i, is ascribed to each individual observation, i, with a conventional Gaussian form accounting for the along-path distance (Δd_i) and time of the year difference from the given month (Δτ_i):

$$w_i=e^{-[{\left(\frac{\Delta d_i}{L_d}\right)}^2+{\left(\frac{\Delta {\tau }_i}{L\tau }\right)}^2]},$$ (3)

with Lτ and L_d chosen as fixed length scales representing the resolution at which we wish to map our field, respectively L_τ = 1.5 months and L _d=330 km. Using this distance weight, the 300 closest data points (i.e., 300 largest values of w_i) are selected to proceed to a linear regression fit for the given grid point and month.

Local generalized least-squares regression. Based on the selected observations, we compute, for each grid point and month, a local generalized least-squares regression solving y = Xβ + ε, where y is the observed quantity (e.g., mixed layer depth, stratification, etc.), β are the unknown regression coefficients, and ε the associated errors, which are assumed to be Gaussian with mean zero and covariance matrix cov(ε) = Ω. The resulting regression depends on the choice of the design matrix X, as well as the covariance matrix Ω. In order to investigate the sensitivity of our results to these choices, we use two different covariance matrices Ω.

We choose X to regress a constant and a linear time trend term, essentially: y_i = β₀ + β₁ (t_i - t₀) + ε_i, where t_i is the time of the ith observation and t ₀ is a reference time for the climatology, set to year 2000. (Note that we also explored the sensitivity of our results to using a second choice for X to regress a constant, a linear time trend, as well as linear and quadratic spatial terms around the grid point; all results and conclusions of the paper remained virtually unchanged.) In this model, the estimate of the climatological mean for the given grid point and month is given by β₀ and the estimate of the time trend by β ₁, and the uncertainties are quantified as the standard errors of these local regression coefficients.

For the covariance matrix Ω, we use on the diagonal the local total variance ω_i composed of a large-scale "Gaussian Process" variance ϕ, a fine-scale "nugget" variance ${\sigma }_n^2$, and the variance associated with the observation uncertainty ${\sigma }_{m,i}^2$.In order to localize the least-squares fit in space and time, we also include the distance weight to the grid point, w_i, leading us to perform a weighted fit based on the effective variances

$${\tilde{\omega }}_i=\frac{{\omega }_i}{w_i}=\frac{1}{w_i}(\varphi +{\sigma }_n^2+{\sigma }_{m,i}^2).$$ (4)

The observation uncertainty ${\sigma }_{m,i}^2$ is defined above in the section on "Definition of mixed layer depth and pycnocline stratification". The "Gaussian Process" variance ϕ and the "nugget" variance ${\sigma }_n^2$ are estimated, along with spatial and temporal decorrelation scales (${\lambda }_d$ and ${\lambda }_t$, respectively), for each grid point and month of the year using a maximum likelihood estimator based on the 300 selected observations, following the locally stationary Gaussian process approach presented in Kuusela and Stein (2018)²⁷. The initial estimate of the mean field required by the Kuusela-Stein method is obtained by performing a local weighted regression with the weights w_i and the model y_i = β₀ + ε_i.

Our first choice of covariance matrix, Ω₁, is based on considering ω_i for the individual observations but assuming no covariance between the observations. With weights included, this yields effective covariance ${\tilde{\Omega }}_1=\text{diag}\left(\tilde{\omega }\right)$, i.e., a diagonal matrix with diagonal elements being ${\tilde{\omega }}_i$. Our second choice of covariance matrix entails including, in addition to the diagonal elements of Ω₁, covariances between the individual observations in the off-diagonal elements, which we compute as:

$${\omega }_{ij}=\varphi \cdot e^{-\sqrt{{\left(\frac{\Delta d_{ij}}{{\lambda }_d}\right)}^2+{\left(\frac{\Delta d_{ij}}{{\lambda }_t}\right)}^2,}}$$ (5)

with Δd_ij the spatial distance between the two observations (i, j) computed using the fast marching algorithm; Δt_ij the time difference of the acquisition of the two observations (i, j); X_d and the spatial and temporal decorrelation scales estimated from the observations as described above. The resulting covariance matrix, Ω₂, is then composed of ω_ij for the elements outside the diagonal, and of ω_ii = ω_i for the elements on the diagonal. The corresponding effective covariance ${\tilde{\Omega }}_2$ has elements

$${\tilde{\omega }}_{ij}=\frac{{\omega }_{ij}}{\sqrt{w_i\cdot w_j}}.$$ (6)

We note that using a non-Euclidean distance metric to compute $\Delta d_{ij}$ in Eqn. (5) can in principle affect the positive definiteness of Ω₂; however, we checked for this during our calculations and did not observe any issues with positive definiteness.

The generalized least-squares regression estimates β = (β₀, β₁)^T and their associated covariances, and may be written

$$\widehat{\beta }={\left({\text{X}}^T{\tilde{\Omega }}_i^{-1}\text{X}\right)}^{-1}{\text{X}}^T{\tilde{\Omega }}_i^{-1}y$$ (7)

and

$$\text{cov}\left(\widehat{\beta }\right)={\left({\text{X}}^T{\tilde{\Omega }}_i^{-1}\text{X}\right)}^{-1}{\text{X}}^T{\tilde{\Omega }}_i^{-1}\text{cov}\left(y\right){\tilde{\Omega }}_i^{-1}\text{X}{({\text{X}}^T{\tilde{\Omega }}_i^{-1}\text{X})}^{-1},$$ (8)

where i = 1,2 and cov(y) = cov(ε) is the covariance matrix Ω_i without the weight terms.

The final winter/summer maps are obtained as averages of the relevant three-monthly maps. Acknowledging that the three maps are strongly correlated, the standard error of the average is computed as the average of the individual standard errors, which serves as a conservative estimate of the desired standard error. Standard errors of percentage changes β₁ / β₀ are obtained by propagating the standard errors and covariance of both the trend β₁ and the climatological mean β₀.

Sensitivity to modeling choices. We produce two solutions based on the following local regressions:

• Choice 1 (covariance between observations): $y=\mathbf{\text{X}}\beta \text{+}\epsilon$, with cov(ε)=Ω₂

• Choice 2 (no covariance between observations): $y=\mathbf{\text{X}}\beta \text{+}\epsilon$, with cov(ε)=Ω₁

The resulting summer and winter mixed layer depth mean fields, the 1970-2018 summer mixed layer depth and pycnocline stratification trends, and the standard errors of the trends for each of the two choices are shown in Extended Data Fig. 3 and Extended Data Fig. 4. Small local differences, consistent with the anticipated behavior of the regression model, are observed between the different choices. In particular, the off-diagonal covariance elements primarily affect the uncertainties and less so the point estimates. However, the main global and regional patterns remain unchanged across the two methods, for all of the mean, trend and standard error estimates, providing great confidence in the robustness of our results. In the core of the paper, we present results from "choice 1". Global percentage changes are computed as the mean of the two models.

Robustness and uncertainty quantification

We adopt four strategies to investigate the uncertainty and robustness of our trend analysis results:

1. We estimate uncertainty for each individual observation (see "Definition of mixed layer depth and pycnocline stratifica¬tion" section above), and then propagate it through the linear regression analysis (see "Mapping method for computing climatologies and associated trends" section above) and compute the standard errors of the trends and mean fields from it. The standard error associated with the trends is shown in Extended Data Fig. 4. In this paper, we regard trends as significant if they are larger than their estimated standard error. In all figures, insignificant trends are blanked. Standard errors maps are shown in Extended Data Fig. 4.

2. We investigate the robustness of our linear regression analysis by adopting two different regression model choices and presenting the corresponding trends (see "Mapping method for computing climatologies and associated trends" section above). The impact of the regression choice is limited, and does not challenge the conclusions presented in this paper.

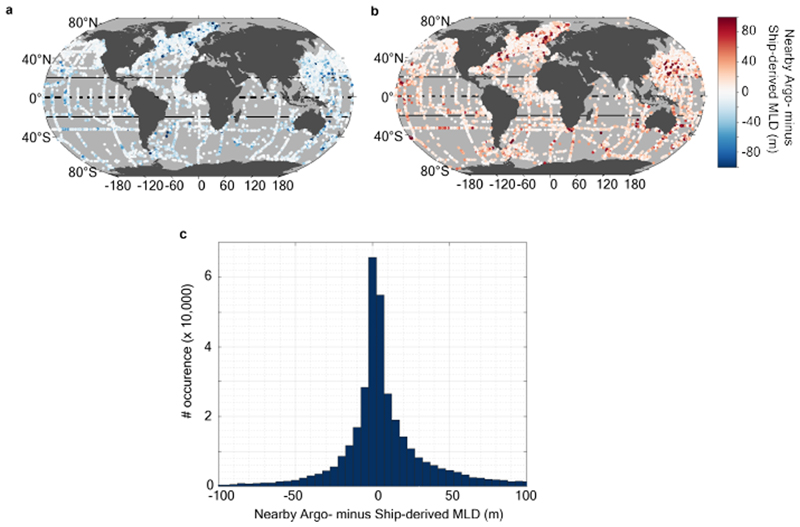
3. We investigate the potential impact of the marked variations in the global ocean observing system that have occurred over past decades, particularly as a result of the Argo and MEOP programs. In particular, Argo- and MEOP- based sensors are often less closely calibrated than ship-based sensors, as they are mostly not recovered, so could potentially be subject to e.g., a pressure bias. In comparison, pressure drift is not an issue neither for Argo or MEOP^68,69. They also have coarser vertical resolution, and while this is taken into account in our standard error quantification (see (i) above), we here seek potential systematic biases that would force a tendency (the Argo program is the most prominent source of information after year 2000). Extended Data Fig. 8 shows all mixed-layer depth estimates from closely located pairs of Argo- and ship-based profiles (sampled within 330 km and 1.5 days). We see significant differences, reflecting that mixed layer depth anomaly can be highly variable on small scales, but we find no significant bias that could produce an unphysical trend. Going further, by repeating the trend analysis using only ship-based profiles, most regions are blanked because observational coverage is limited, but in the few regions where coverage allows the recovery of long-term trends, the conclusions of this paper are endorsed (Extended Data Fig. 9). Limiting the analysis to only ship-based profiles strongly constrains the number of observations available, and therefore limits the spatial domain where we are able to recover significant trends.

4. We compare trends in mixed layer mean temperature to trends recovered from alternative sea-surface temperature (SST) datasets. SST is arguably the best observed ocean quantity historically, with numerous in situ observations since the end of the 19^th century⁷⁰, enriched by the advent of global satellite remote sensing at relatively high horizontal and temporal resolutions since 1982⁷¹. The observational coverage of SST is far from perfect, even with satellite observations, which, depending on the technology used, can be blocked by cloud cover (the longest time series from as far back as 1982, and associated trends, are impacted by cloud cover). However, SST remains one of the best observed variables, and is entirely independent from the observational database used in the present study. Extended Data Fig. 7 shows a map of the mixed layer mean temperature trends from 1970 to 2018 estimated in this study compared with other estimates derived from GHRSSTv2⁷¹ and HaddSSTv4⁷⁰. The three estimates show a very consistent picture of long-term SST trends.

While we wish to make the reader fully aware of the limitations of our analysis, each of the different approaches detailed in this section endorses our key results, and provide high confidence in the conclusions of this paper.

The upper ocean’s vertical structure

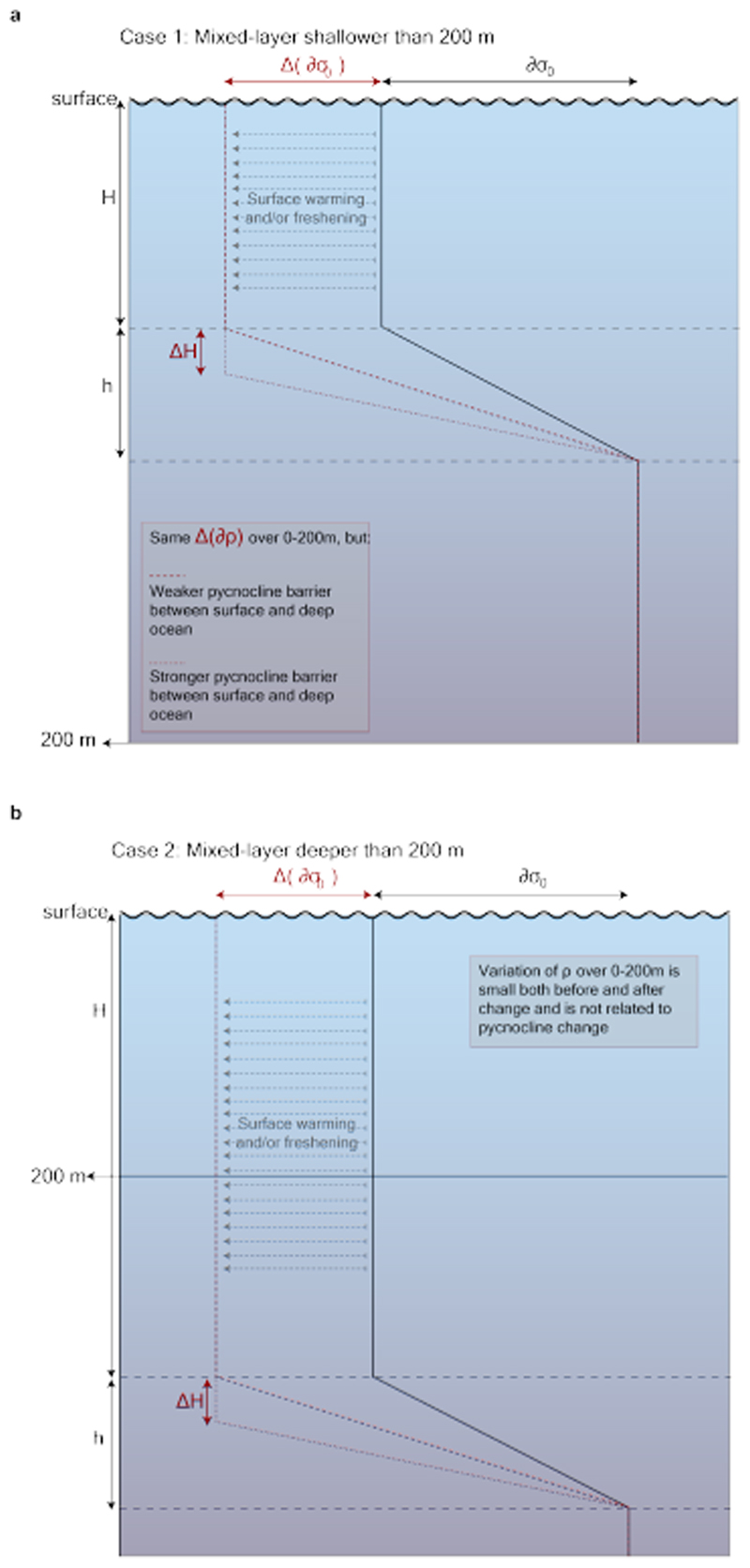
The 0-200 m layer cuts across several distinct dynamical regimes, depending on whether the mixed layer and pycnocline are shallower or deeper than 200 m, which depends on the region and season (Extended Data Fig. 1).

When the mixed layer is deeper than 200 m, the 0-200 m layer is contained entirely within the mixed layer, so stratification will be close to null (not exactly null because, by definition, there is a small density difference of 0.03 kg m^-3 between the ocean surface and the base of the mixed layer; see "Definition of mixed layer depth and pycnocline stratification" section above). In that context, change of the 0-200 m stratification would only reflect change in mixed layer depth, but would be entirely unrelated to pycnocline stratification (Extended Data Fig. 1b). When the mixed layer is shallower than 200 m, change in 0-200 m stratification is related to pycnocline stratification, but can underestimate or overestimate the actual change within the pycnocline depending on the change in mixed layer depth (Extended Data Fig. 1a). In this sense, annual and global mean estimates of 0-200 m stratification change amalgamate different dynamical regimes (mixed layer and pycnocline), which makes such diagnostics difficult or impossible to interpret. At the very least, these diagnostics cannot be interpreted as a measure of a strengthening of the pycnocline (which is one of the key metrics for impact and adaptation), as has been done in the past¹⁶.

In summer, most of the world ocean’s mixed layers are shallower than 200 m. In this season, the rate of change of the 0-200 m and pycnocline stratification can be related to the rate of change of the mixed layer depth. With some strong assumptions, the relationship can be very easily derived analytically. For instance, assuming that all stratification change is due to surface change⁹, and that the 0-200 m layer can be represented by a perfect three-layer structure with a linear density gradient in the pycnocline (Extended Data Fig. 1a), one can write:

$$\{\begin{array}{l}\overline{N_{200}^2}\propto \frac{\partial {\sigma }_0}{200}\hfill \\ \Delta N_{200}^2\propto \frac{\Delta (\partial {\sigma }_0)}{200}\hfill \\ \delta N_{200}^2=\frac{\Delta N_{200}^2}{N_{200}^2}=\delta (\partial {\sigma }_0)\hfill \end{array}$$

and:

$$\{\begin{array}{l}\overline{N_{200}^2}\propto \frac{\partial {\sigma }_0}{h}\hfill \\ \Delta N^2\propto \frac{\partial {\sigma }_0+\Delta (\partial {\sigma }_0)}{h-\Delta H}-\frac{\partial {\sigma }_0}{h}=\frac{\partial {\sigma }_0}{h}(\frac{1+\delta (\partial {\sigma }_0)}{1-\delta H}-1)\hfill \\ \delta N^2=\frac{1+\delta (\partial {\sigma }_0)}{1-\delta H}-1=\frac{1+\delta N_{200}^2}{1-\delta H}-1\hfill \end{array}$$

where the operator $\overline{(\cdot )}$ denotes a climatological mean, Δ refers to absolute change, and δ refers to change relative to the climatological mean (e.g., $\delta x=\Delta x/(\overline{x})$. We refer the reader to Extended Data Fig. 1a for the meaning of $\partial \rho ,\Delta (\partial \rho )$, h and ΔH.

In summary, a deepening of the mixed layer sharpens the density gradient in the pycnocline, which causes an increased pycnocline density gradient much larger than seen by the density change over a fixed depth range, even if the depth range encompasses the mixed layer and the pycnocline. Assuming an idealised vertical density profile as drawn in Extended Data Fig. 1a, an increase of $\delta N_{200}^2$ of 1.1-1.5 % dec^-1 associated with amixed layer deepening of 2.2-3.6% dec^-1 would translate into an increase of ~ 3-5% dec^-1 of $\delta N^2$, lower than but consistent with our estimate. Our goal is not to derive a detailed quantitative relationship between $\delta N^2,\delta N_{200}^2$, and δH, as the shape of a vertical profile of density in the ocean may deviate markedly from the idealised case drawn in Extended Data Fig. 1a, which is used to derive the relationship. In particular, the pycnocline is not a linear gradient, and there are many cases where, even in summer, the base of the pycnocline is arguably deeper than 200 m, so that the simple relationship used here would underestimate δN ².

Time series of percentage anomalies

In order to gain further confidence in our mapped trends, we examine time series of mixed layer depth and pycnocline stratification in specific regions. The goal here is to visualise time series that are independent of the statistical machinery associated with the gridding procedure. As noted above, this procedure will be biased due to uneven sampling in time and space, and will tend to average out the largest changes: the local regression model procedure is more robust in this respect. We, however, produce these alternative time series primarily for visualisation purposes. In order to minimise spatio-temporal biases linked to uneven sampling, we generate regional and yearly percentage anomaly distributions (shown as median and 33-66 percentiles, black error bars in Fig. 3b,d; Fig 5b,d; Extended Data Fig. 5; and Extended Data Fig. 6). Percentage anomaly distributions are computed from all available observations in a given region, for which we subtract from the quantity of interest its local climatological seasonal cycle, and divide the anomaly by the corresponding local seasonal climatological value.

A 1970-2018 trend and associated standard error are then quantified by applying a weighted linear regression model, which regresses the annual median values weighted by the number of observations in each year (red lines in Fig. 3b,d; Fig 5b,d; Extended Data Fig. 5; and Extended Data Fig. 6; trends are only plotted if significant). A trend is considered significant if it is greater than double its estimated standard error.

Winter mixed layer and stratification trends

Multi-decadal trends in wintertime pycnocline stratification and mixed layer depth are shown and briefly discussed here (Extended Data Fig. 5). Consistent with summertime results, pycnocline stratification in winter undergoes a substantial strengthening (at an even greater rate than in summer), while the winter mixed layer is found to deepen in most regions. There are a few exceptions to this winter deepening, though, particularly in the Pacific sector of the Southern Ocean. However, as shown by Extended Data Fig. 2, the time series of winter measurements are considerably shorter than those of summer observations, and data density is much lower in winter than in summer (not shown). Caution must therefore be exerted in interpreting the mapped winter trends. Indeed, examining detailed time series from specific regions suggests that winter trends are weakly constrained (Extended Data Fig. 6). Thus, our finding of an overall, worldwide increase in winter pycnocline stratification and mixed layer depth remains tentative, and must be validated when data availability improves in the medium-term future.

Dynamical forcing of changes in mixed layer depth

The most likely cause of the observed variations in mixed layer depth is a change in surface-forced mechanical turbulence. Turbulence in the mixed layer can be generated by a range of processes. In this section, we explore the possibility that an intensification of some of these processes might have driven the mixed layer deepening documented in this article. Such an intensification is required because the mean stratification at the base of the mixed layer has increased in recent decades, implying that turbulence must have intensified to overcome the strengthening stratification and effect a mixed layer deepening. Our analysis indicates that the mixed layer and pycnocline-averaged stratification, N ², has increased with time at a rate of ~ 6% dec^-1, based on the approximation, $N^2=\frac{N_0^3}{H}$ where H the mixed layer depth (which has increased at a typical rate of ~ 3 % dec^-1) and is the pycnocline stratification (which has increased at a typical rate of ~ 9 % dec^-1). This section considers a range of processes that might have counteracted such increased stratification to lead to a deepening of the mixed layer.

Local (1-d) processes generating turbulence in the mixed layer are forced at the ocean surface by air-sea buoyancy exchanges, waves and winds. While in principle surface buoyancy forcing can drive increased surface turbulence, under the ongoing climate change, changes in buoyancy forcing act to suppress turbulence rather than promote it, as suggested by the global increase in density stratification. Surface buoyancy forcing is therefore not considered further as a driver of increased turbulence. A range of evidence indicates that injection of turbulence by breaking waves is likely to be the dominant source of turbulence near the surface⁷⁴, but the contribution of wave breaking to turbulence at the mixed layer base is less clear; modelling results suggest that it is likely a secondary effect modulating Langmuir turbulence⁷⁵. Consequently, we have chosen to assess the role of the following processes that may have significant impacts at the mixed layer base: (i) wave-generated Langmuir turbulence⁷⁶; (ii) wind-generated high-frequency internal waves³⁹; and (iii) submesoscale frontal instabilities²⁸. We stress, however, that our theoretical understanding of mixed layer physics remains incomplete, such that it is impossible to provide a comprehensive assessment of the roles of all physical processes affecting the mixed layer. Here, we merely consider a selection of processes to demonstrate that they, individually or combined, may have potentially induced a mixed layer deepening over recent decades in a context of increasing upper-ocean stratification.

(i) Wave-generated Langmuir turbulence. The interaction of wave forcing with wind can drive Langmuir turbulence, which may reach the mixed layer base⁷⁶ and entrain pycnocline waters into the mixed layer. In order to assess the possible implication of Langmuir turbulence in mixed layer deepening, we consider a Froude number characterizing the balance between Langmuir turbulence and stratification, given by⁷⁹: $\text{Fr}=w_L/NH$, where $w_L$ is a characteristic Langmuir vertical velocity. This velocity can be expressed as³⁸: $w_L={(u_{*}^2{u}_{S0})}^{1/3}$, where $\begin{array}{l}{u}_{*}=\sqrt{\tau /\rho }\end{array}$ is the water-side friction velocity, T is the wind stress, and u_S0 is the surface Stokes drift velocity. Assuming a constant turbulent Langmuir number, La_t = (u*/u_S0)^1/2, the Langmuir vertical velocity scales as w_L « u*. Numerical experiments have shown that Langmuir-driven vertical mixing is limited once a constant Froude number is reached⁷⁹, meaning that the mixed layer depth controlled by Langmuir turbulence scales as

$$H\propto \frac{u_{*}}{N}.$$ (9)

This relation can also be derived using a Richardson number scaling based on direct surface forcing from winds and waves.

From dimensional arguments, wind stress is frequently parameterised as $\tau =C_{D\rho }{U}_{10}^2$, where U₁₀ is the 10 m wind speed. However, the non-dimensional drag coefficient, C_D, varies with U ₁₀ due to changes in sea surface roughness with wind speed. The global average of observations of this dependency is linear within statistical uncertainty over the approximate range U₁₀ < 5 ms^-1 to U₁₀ > 20 m ^-181. Since the vast majority of the wind data exhibiting increasing trends of U₁₀ falls within this range¹⁰, the scaling of wind stress with wind speed can be represented as $\tau \propto U_{10}^3$, leading to $u_{*}\propto U_{10}^{3/2}$ for the following analysis.

We now introduce δ, the percentage change in any given quantity x, so that $\delta x=\Delta x/\overline{x}$, with Δx referring to absolute change and $\overline{x}$ to a climatological mean value. Applying this scaling to Eqn. 9 gives $H\propto U_{10}^{3/2}/N$, which we can then translate into an estimate of the percentage change in mixed layer depth expected from variations in Langmuir forcing, namely $\overline{H}+\Delta H\propto {({\overline{U}}_{10}+\Delta U_{10})}^{3/2}/(\overline{N}+\Delta N)$. This can be re-written as $\overline{H}(1+\delta H)\propto ({\overline{U}}_{10}^{3/2}/\overline{N}){(1+\delta U_{10})}^{3/2}/(1+\delta N)$, and simplified to $(1+\delta H)\propto {(1+\delta U_{10})}^{3/2}/(1+\delta N)$.

Ship- and satellite-based records^10,11,83 suggest that mean open-ocean wind speeds have intensified by approximately $\delta U_{10}\sim 1-3\%{\text{dec}}^{-1}$ in recent decades (this is also endorsed by a wide range of atmospheric reanalyses⁴⁰); as discussed above, δN ~ 2.5% dec^-1 (δN² ~ 6% dec^-1). Applying the preceding scaling to these values suggests that Langmuir turbulence may have effected a deepening of the mixed layer at a rate ranging from 0-2 % dec^-1, considerably lower than, but of consistent order of magnitude with, the observed mixed layer deepening, δH ~ 3% dec^-1. Since mixed layer deepening typically occurs during strong forcing events, trends in these strong events may be more relevant than trends in mean conditions. Multi-decadal increases in 90^th percentile wind speeds have more than doubled those of the seasonal- or annual-mean wind speeds^10,11. This suggests that an intensification of wind and wave forcing may be a plausible explanation for our observed mixed layer deepening. However, there are considerable measurement and sampling uncertainties associated with both in situ and satellite observations of intermittent, strong wind forcing events, which make a more quantitative assessment difficult.

(ii) Wind-generated high-frequency internal waves. High-frequency wind forcing generates an internal wave (IW) field at the base of the mixed layer, which can then trigger a forward energy cascade to dissipation³⁹. In an idealized, high-resolution numerical experiment, Barkan et al.³⁹ demonstrated the significance of the internal wave-mediated forward cascade, by showing that the ratio between the enhanced dissipation rate and the added high-frequency wind work is 1.3, when turning on high-frequency winds. Past observations show a marked increase of high-frequency winds over recent decades that is surprisingly consistent on a global scale, although possibly larger in the Southern Hemisphere (similar to our estimated mixed layer deepening), occurring at a rate of^10,11 ~ 2% dec^-1. If we assumed that the surface ocean velocity field has not changed substantially in recent decades, we would infer an increase in the wind work associated with high-frequency winds of similar magnitude to that in the wind stress, which (see above) scales like $\tau \alpha U_{10}^3$. The wind work associated with high-frequency winds would therefore have increased at a rate of ~ 6% dec^-1. Using Barkan et al.’s relationship, we would infer an enhancement in the dissipation driven by internal waves generated by intensifying high-frequency winds at a rate 30% greater than that of the associated wind work increase. This would translate into a dissipation rate enhancement on the order of ~ 40% dec^-1.

This is a significant increase in dissipation, which we can attempt to relate to an expanding mixing depth though the Ozmidov length scale, characterizing turbulent mixing in stratified waters^86,87:

$$L_0={\epsilon }^{1/2}{(N)}^{-3/2}.$$ (10)

Based on this relationship, a ~ 40% dec^-1 increase in ε, concomitant with a 2.5% dec^-1 increase in N, would result in a deepening mixing layer on the order of 14% dec^-1, five times larger than our global mixed layer deepening (occurring at a rate of ~ 3% dec^-1). Although this scaling argument is contingent on many arbitrary approximations, it highlights a potentially efficient process to deepen the mixed layer in a stratifying ocean.

(iii) Submesoscale frontal instabilities.

There is a vast diversity of processes that can occur at submesoscales in the upper ocean, and which may deepen or shoal the mixed layer. Many studies have shown how processes linked to submesoscale frontogenesis may drive upward buoyancy fluxes that act to restratify the mixed layer^41,42,89,91. However, other submesoscale frontal processes (notably, symmetric instability) energise upper-ocean turbulence. Although the large-scale effects of symmetric instabilities in the ocean remain poorly constrained, we here quantify the change in turbulent dissipation associated with symmetric instabilities, ε_SI, that might have occurred in recent decades. Near the mixed layer base (say, at depths exceeding 3/4.H), e_SI may be quantified as²⁸:

$${\epsilon }_{SI}=\{\begin{array}{cc}\frac{1}{4}(B_e),& \text{if}{B}_e>0\\ 0,& \text{otherwise}\end{array}$$ (11)

where B_e is the wind-driven Ekman buoyancy flux. When the wind stress is directed "down" an upper-ocean front (i.e. an area of enhanced horizontal density contrast), the Ekman flow conveys waters from the dense side to the light side of the front (by "wind directed down front", we mean wind oriented along and in the same direction as the oceanic frontal jet). This triggers symmetric instability, which grows by extracting energy from the front’s vertical shear^92–94. The Ekman buoyancy flux is given by $B_e=\frac{\tau \times f}{\rho f^2}\cdot {\nabla }_{h}b$, where ∇_h b is the submesoscale horizontal buoyancy gradient on which a wind stress t acts. At any location in the ocean, there is a probability, P, of the wind stress being partially or fully directed down a submesoscale front, resulting in B_e > 0. The rate of turbulent kinetic energy dissipation associated with wind-forced symmetric instability is then: ${\epsilon }_{SI}=\frac{P}{4}{B}_e\alpha \tau {\nabla }_{h}b$. We now assume that changes in the square of the submesoscale horizontal buoyancy gradient in the mixed layer are related to those in $N_0^2$, the stratification in the pycnocline, through the 3-d, frontogenetic distortion of the vertical density gradient by mesoscale motions⁹⁵. We thus have: ${({\nabla }_{h}b)}^2\propto N_0^2$ and $\tau \propto U_{10}^3$ (see above), which we use to translate ${\epsilon }_{SI}\propto \tau {\nabla }_{h}b$ into ${\epsilon }_{SI}\propto U_{10}^3{N}_0$. Finally, it follows that the scaling for a change in ε_SI is $\delta {\epsilon }_{SI}\propto {(1+\delta U_{10})}^3(1+\delta N_0)-1$, which implies a change in mixing length scale of (Eqn. 10):

$$1+\delta L_0\propto {(\frac{1+\delta U_{10}}{1+\delta N})}^{3/2}\sqrt{1+\delta N_0}.$$ (12)

Using our best estimates of the characteristic percentage changes in the three parameters on the right hand side (δU₁₀ ~ 1-3 % dec^-1, δN₀ ~ 9 % dec^-1, δN ~ 2.5 % dec^-1), Eqn. 12 suggests an increase in the mixing length scale of ~3 % dec^-1, in broad agreement with our observations of mixed layer deepening of ~3 % dec^-1.

Summary. While these scaling arguments are associated with multiple approximations and uncertainties, they do suggest that intensifying winds (and, in the symmetric instability case, the enhanced pycnocline stratification itself) provide a plausible driver of our observed multi-decadal deepening of the mixed layers across the world ocean, concomitant with increased pycnocline stratification. Among the three mechanisms connecting winds to invigorated turbulent mixing explored here, the intensification of wind-driven high-frequency internal wave turbulence appears to provide the most plausible process for two reasons: first, because of the observed world-wide, consistent strengthening of high-frequency winds, consistent with our observed mixed layer deepening; and second, because scaling arguments suggest that it could be highly efficient at expanding the mixing depth. In contrast, while submesoscale symmetric instability may have played a significant role too, it remains unclear what the net effect of energised submesoscales would be on mixed layer depth, given the restratifying action of submesoscale frontogenetic processes. Finally, wave-driven Langmuir turbulence may have been a significant driver of mixed layer deepening too, but our scaling arguments suggest a weaker effect. We conclude that, while these scaling analyses are merely illustrative, they suggest that a global intensification of the winds may have forced a deepening of the mixed layer in the presence of increasing stratification over recent decades, and that a range of oceanic processes may have been involved. The intensification of winds in recent decades is indicated by both ship- and satellite-based record^10,11,83, as well as by reanalysis products⁴⁰. Assessing this proposition and clarifying the key mixed layer deepening mechanisms is a pressing challenge that must be addressed by follow-up investigations.

Extended Data

Extended Data Figure 1. Upper ocean vertical structure associated trends.

Schematics showing idealised density profiles in the upper ocean, for a case where mixed-layer and pycnocline are (a) shallower, and (b) deeper than 200 m. The black profile shows the typical shape of the density profile with a total density increase of ∂ρ across the pycnocline of thickness h, and a mixed-layer of thickness H. While the dashed red profiles show the density profile after a lightening of the mixed-layer, with no change of mixed-layer depth, the dotted red profiles show the density profile after a lightening of the mixed-layer, concomitant with a deepening of the mixed-layer.

Extended Data Figure 2. Geographical distribution of available observations.

Number of mixed layer estimates in 1°x1° longitude-latitude bins: (a) from all available observation sources; (b) from ship profiles; (c) from Argo profiles; (d) from instrumented marine mammal observations. Maximum time span (in years) covered by the combined data set in 1°x 1° longitude-latitude bins in (e) summer and in (f) winter.

Extended Data Figure 3. Impact of linear regression choices on mean mixed-layer.

(a,b) Winter and (c,d) summer mean mixed-layer depth computed using slightly different linear regression model: (a, c) Choice 1 (covariance between observations); and (b, d) Choice 2 (no covariance between observations). See Methods for more details.

Extended Data Figure 4. Impact of linear regression choices on summer mixed-layer depth, stratification trends, and their associated standard errors.

1970-2018 summer trend for (a,c) mixed layer depth and (e,g) summer pycnocline stratification, and their associated standard error: (b,d) standard error of mixed layer depth trend and (f,h) standard error of summer pycnocline stratification trend. Panels (a-b and e-f) show the solution computed with the linear regression model Choice 1 (covariance between observations); Panels (c-d and g-h) show the solution computed with the linear regression model Choice 2 (no covariance between observations).

Extended Data Figure 5. 1970-2018 trends in winter upper-ocean stratification and mixed layer depth.

Map of the 1970-2018 winter (a) 0-200 m ($N_{200}^2$ trend in s^-2 dec^-1), and (b) pycnocline stratification trend (i.e. N² trend in s^-2 dec^-1), along with zonal-median value in bold black, and 33-66 percentile in thin black. Regions with no significant trend (see Methods) are shaded in gray on the map. (c) same as panel (a,b) but for winter mixed layer trend in m dec^-1 (note that mixed layer deepening is shown as a negative trend).

Extended Data Figure 6. Regional time series of winter pycnocline stratification and mixed layer depth anomaly.

(a) Winter climatological mixed layer depth, same as Fig. 2f, with three specific regions of interest outlined by red contours: North Atlantic subpolar convection region (A); Southern Ocean Indian sector convection region (B); and Southern Ocean Pacific sector convection region (C). For each of these regions, winter stratification anomaly times series and associated trends are respectively displayed in panels (b,d,f); and winter mixed layer depth anomaly times series and associated trends are respectively displayed in panels (c,e,g). Note that a negative depth anomaly refers to a deepening. Each times series panel shows: in thin gray line, the annual median percentage anomaly (from the local climatological seasonal cycle), computed for each individual observation; the errorbars refer to the 33-66 percentile range of percentage anomaly (errorbars are shown in black (gray) when more (fewer) than 50 data points are used in the annual statistics); the associated 5-year smoothed median time series is superimposed in blue; a linear trend from 1970-2018 is shown by the red line if greater than twice its standard error.

Extended Data Figure 7. Comparison between mixed-layer temperature trend and sea surface temperature trends.

(a) Summer mixed-layer mean temperature trend from 1970 to 2018 as estimated in this study; (b) Summer sea surface temperature trend from 1982 to 2018 as estimated from the satellite-based product GHRSSTv2, and (c) box plot showing median (red) and interquartile range (blue box) of local summer surface temperature trend estimates from this study (mixed-layer mean temperature from 1970-2018), from the satellite-based product GHRSSTv2 (sea surface temperature from 1982-2018), and from the in situ observation reconstruction product HadSSTv4 (sea surface temperature from 1970-2018). The whiskers extend to the most extreme data points

Extended Data Figure 8. Difference between Argo- and ship-based derived mixed-layer depth.

Difference between mixed-layer depth estimates coming from nearby (sampled within 330 km and 1.5 day) Argo and ship-based observation profiles (i.e. co-located in time and space), for all instances where we derived (a) a shallower or (b) a deeper mixed-layer depth from the Argo profile than from the ship-based profile. (c) Histogram of all differences. Because Argo started in the 2bbbs, the co-located profiles cover only the years 2000-2018.

Extended Data Figure 9. 1970-2018 trends in summer pycnocline stratification and mixed layer depth when only using ship-based profiles (removing all Argo and MEOP program observations).

(a) Map of the 1970-2018 summer pycnocline stratification trend (i.e. N² trend in s^-2 dec^-1), along with zonal-median value: median in bold black, and 33-66 percentile in thin black. The red shading shows the global 33-66 percentile range of the local trend estimates. Regions with no significant trend (see Methods) are shaded in gray on the map. (c, d) same as panel (a,b) but for summer mixed layer trend in m dec^-1 (note that mixed layer deepening is shown as a negative trend).

Data and Code Availability

The code used to generate the analysis presented in the main paper and in the supplementary materials is available from https://github.com/jbsallee-ocean/GlobalMLDchange (DOI: 10.5281/zenodo.4073200). All information about source database used in the paper can be found here: https://github.com/jbsallee-ocean/GlobalMLDchange/tree/main/Databases. The resulting global maps of trends and climatological fields presented in the present study is available from: https://zenodo.org/record/4073174#.YA_jsC2S3XQ (DOI: 10.5281/zenodo.4073174)