A method for genome-wide genealogy estimation for thousands of samples

Abstract

Knowledge of genome-wide genealogies for thousands of individuals would simplify most evolutionary analyses for humans and other species, but has remained computationally infeasible. We developed a method, Relate, scaling to > 10,000 sequences while simultaneously estimating branch lengths, mutational ages, and variable historical population sizes, as well as allowing for data errors. Application to 1000 Genomes Project haplotypes produces joint genealogical histories for 26 human populations. Highly diverged lineages are present in all groups, but most frequent in Africa. Outside Africa, these mainly reflect ancient introgression from groups related to Neanderthals and Denisovans, while African signals instead reflect unknown events, unique to that continent. Our approach allows more powerful inferences of natural selection than previously possible. We identify multiple novel regions under strong positive selection, and multi-allelic traits including hair color, body mass index (BMI), and blood pressure, showing strong evidence of directional selection, varying among human groups.

Large-scale genetic variation datasets are now available for many species, including tens of thousands of humans. In principle, all information about a sample’s genetic history is captured by their underlying genealogical history, which records the historical coalescence, recombination, and mutation events producing the observed variation patterns. In practice, several key existing approaches (e.g., Refs. [1,2]) leverage an underlying coalescent model, which provides a flexible modelling framework and is the limiting behavior of a variety of finite-population models^3,4. However, coalescent-based inference is complicated by the structure of the model, and the extremely large space of probabilistically plausible sample histories conditional on observed data⁵. Other approaches^6–11 use more heuristic coalescent approximations, sometimes reducing accuracy: regardless, published existing methods scale to tens or a few hundred samples at most.

These issues have restricted the use of direct genealogy-based approaches to infer recombination, mutational ages, and natural selection to smaller datasets^1,2, while for larger datasets diverse approaches based on data summaries^12–14 or downsampling^15,16 have predominated. In humans, such tools have detected genetic structure and admixture in good agreement with independent evidence^17,18, changes in population size^15,19–21 and introgression with archaic groups, including Neanderthals²².

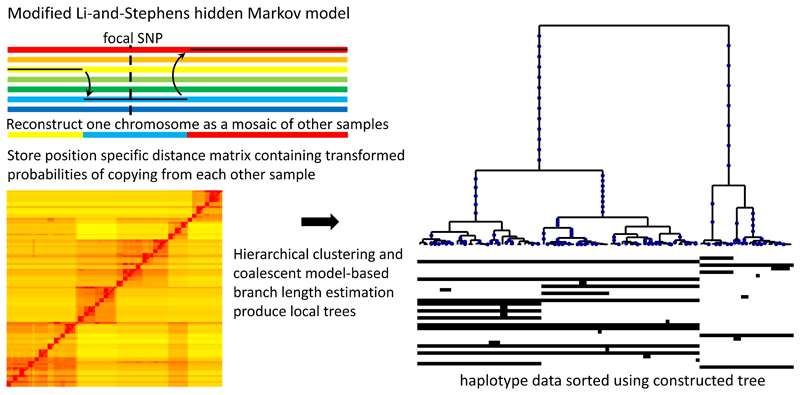
We developed a scalable method, Relate, to estimate genome-wide genealogies (Figure 1; Methods; https://myersgroup.github.io/relate/ for implementation). Relate separates two steps; firstly identifying a genealogical framework at each site in the genome, describing ancestral relationships among sequences but not their coalescence times. Secondly, these times are estimated after mutations are mapped to branches of these trees, allowing for variable population sizes simultaneously inferred from the data, to produce complete genealogies. These are then used directly for downstream inferences. Our approach approximates the coalescent model, but performs as well as or better than existing approaches in our simulations, whilst being thousands of times faster.

Figure 1. Relate method overview.

Our method applies a version of the Li-and-Stephens hidden Markov model¹⁵, modified to take ancestral and derived states into account, to calculate at a focal SNP (dotted vertical line) a position-specific distance matrix d (bottom left). Each entry d_ij of this matrix stores the rescaled loglikelihood of generating haplotype i by copying from haplotype j, which can be interpreted as the number of mutations carried by i, but not by j, locally around the focal SNP. (Methods; Supplementary Note). Our tree builder uses the resulting inferred distance matrix to coalesce haplotypes (right-hand side). After mapping mutations to their corresponding branches, we estimate branch lengths using an MCMC algorithm that employs a coalescent prior model.

We demonstrate the utility of a genealogy-based analysis by applying Relate to 4,956 haplotypes of the 1000 Genomes Project (1000GP) dataset^23,24. We estimate population sizes of all 26 populations in the dataset and their split times using cross-coalescence rates. In agreement with previous work, we identify an increase in the mutation rate of TCC to TTC around 10,000 to 20,000 years ago²⁵. The estimated genealogies contain signals of introgression between Neanderthals and modern humans in Eurasia, and between modern East and South Asians and Denisovans, alongside other signals specific to African groups. Finally, we suggest a test statistic that identifies loci under positive selection by tracking mutation frequencies through time. We demonstrate that for plausible scenarios of selection on complex traits, involving selection dispersed over many loci, this test improves power over the integrated Haplotype Score (iHS)²⁶, and identify previously unreported genomic regions under strong positive selection. We find a remarkable enrichment of SNPs identified in genome-wide association studies (GWAS) among targets of selection, and evidence of widespread directional polygenic adaptation.

Results

Overview of the Relate approach

At each genomic position, Relate first identifies a non-symmetric distance matrix whose rows estimate the relative order of coalescence events between a particular sequence and the remaining observed sequences. To do this, Relate uses the posterior probabilities output by a hidden Markov model (HMM) similar to that proposed by Li and Stephens²⁷, but leveraging knowledge of ancestral and derived status at each single nucleotide polymorphism (SNP) to improve speed and accuracy. This distance matrix is used to construct a rooted binary tree using a bespoke algorithm. Mathematical arguments demonstrate, encouragingly, that if the “infinite-sites” model is satisfied so that each observed mutation occurs exactly once, our approach is guaranteed to generate genealogies exactly producing the observed data, in the limiting cases where either there is no recombination, where the recombination rate is very large, or where all recombination occurs in intense widely spaced hotspots (Supplementary Note). Because the distance matrix is position specific, these binary trees adapt to changes in local genetic ancestry due to recombination. In practice, we save computational time by only rebuilding trees at a subset of sites along the genome (Methods, Supplementary Figures 1 and 2).

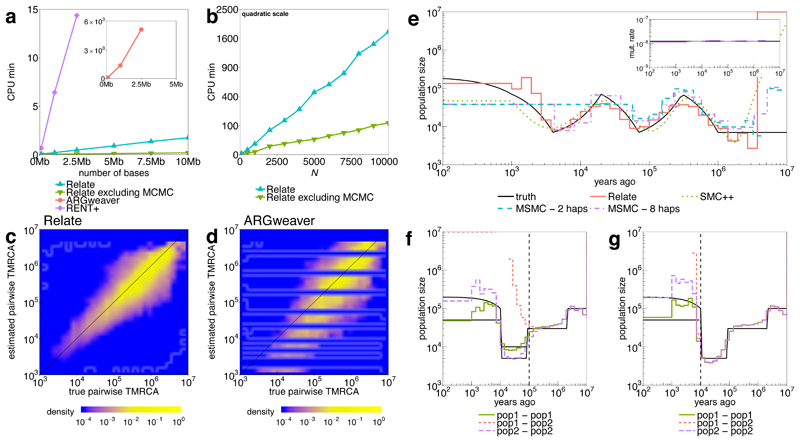
Figure 2. Simulated data.

a, Runtimes of Relate, RENT+ and ARGweaver in CPU minutes as a function of the number of bases simulated with N = 200, μ = 1.25 × 10^-8, 2N_e = 30,000, and recombination rates taken from human chromosome 1. We also show the runtime of Relate excluding the estimation of branch lengths. b, Runtime of Relate in minutes as a function of sample size N, where we simulate 2.5Mb for each data point. Other parameters are the same as in a; y-axis is on a quadratic scale. c, True TMRCAs for pairs of haplotypes (x-axis) versus those estimated by Relate (y-axis). d, As c, except showing results for ARGweaver. e, Comparison of population size estimates across methods for a simulation of 200 haplotypes, 200Mb and an oscillating population size²⁰. Relate and SMC++ estimates are based on 200 haplotypes, MSMC estimates are obtained from 2 or 8 haplotypes. Inset shows the mutation rate over time estimated by Relate. f, g, Populationspecific estimates of population size and cross-population coalescence rates for a simulation with a discrete bottleneck for two populations that separated 80,000 YBP (f; vertical dashed line), or 10,000YBP (g). TMRCA, time to most recent common ancestor.

To estimate branch lengths while allowing for changing population sizes, we first map mutations onto each genealogical tree and then apply an iterative Markov Chain Monte Carlo (MCMC) algorithm to estimate times under a coalescent prior. We simultaneously estimate a stepwise varying effective population size through time, using the genome-wide collection of estimated genealogies (Methods). Our final time estimates account for changes in population size, assuming an unstructured population. We can also explore population stratification within a sample, by leveraging estimated coalescence rates of any pair of sampled sequences. By averaging pairwise coalescence rates within and across groups, we obtain effective population size estimates for sub-populations and cross-coalescence rates between populations. As we show in the next section, this can provide accurate estimates despite the fact that our tree-builder does not account for such population stratification.

Simulations

We evaluated Relate for its speed, accuracy of inferred trees, robustness, and ability to infer evolutionary parameters, by simulating data under the coalescent with recombination using msprime²⁸. We compared performance to ARGweaver², which samples from a time-discretized approximation to the coalescent with recombination, and which we therefore expect to perform well on these simulations. Relate was >4 orders of magnitude faster than ARGweaver, for cases we were able to apply the latter, and also much faster than RENT+¹¹ (Figure 2a,b). Our approach scales linearly in sequence length and quadratically in sample size N_i, enabling genealogical inference for e.g. 10,000 human samples genome-wide using a compute cluster.

To evaluate accuracy, we compare, at each locus and for each of the $\left(\begin{array}{c}N\\ 2\end{array}\right)$ pairs of haplotypes, the estimated time to their most-recent common ancestor (TMRCA) to the truth (Figure 2c,d), observing improved performance relative to both ARGweaver and RENT+. Relate also showed improved robustness to errors in the data, identified misclassified ancestral alleles, and estimated times well in the context of varying population size (Supplementary Figure 3). Other accuracy measures yielded similar improvements (Supplementary Note). Relate identified repeat mutations and variable mutation rates, and is robust to computational rephasing of haplotypes (Supplementary Figure 4). We next compare Relate’s inferred population sizes to those from applying two leading specialist approaches, MSMC²⁰ and SMC++²¹. For multiple previously tested^20,21 scenarios including oscillating population sizes and bottlenecks similar to those observed in out-of-Africa events of modern humans, Relate obtains more accurate estimates, particularly in the recent past (Figure 2e, Supplementary Figure 3). While Relate assumes a single population when estimating branch lengths, when applied to a combined sample from two diverged populations, it still performs well in recovering their distinct population histories and estimating their split time(s) (Figure 2f,g).

Genome-wide human genealogies

We applied Relate to 2,478 1000GP individuals with diverse genetic ancestry and approximately 81 million SNPs (see Methods for data pre-processing). Computation time, using up to 300 processors, was ~4 days (Supplementary Table 1). 86% of all SNPs (>96% of SNPs at >0.2% derived-allele frequency (DAF)) map uniquely to trees, falling to 76% for CpG dinucleotides, known to possess strongly elevated mutation rates (Supplementary Figure 5). The number of different trees in a genomic subregion strongly correlates with recombination rate (r ² = 0.63) and the average tree has 3,883 SNPs mapped to it, reflecting block-like structures of human haplotypes between recombination hotspots (Supplementary Figure 5).

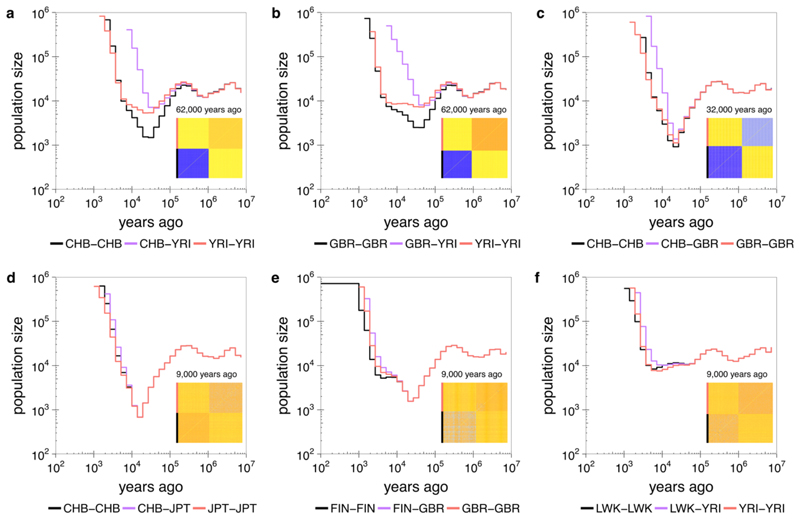
We estimated within and across-group coalescence rates for pairs of groups, by first extracting the genealogy for members of a particular subsample of interest embedded within the full genealogy, and then re-estimating coalescence rates for this genealogy. We observe a clear out-of-Africa bottleneck for Eurasian populations (CHB: Chinese in Beijing and GBR: British in England and Scotland shown), and gradual separation from African populations (YRI: Yoruba in Ibadan, Nigeria shown) already visible 200,000 years before present (YBP) and lasting to around 60,000YBP (Figure 3a,b). This is consistent with recent studies^15,29 and might reflect several out-of-Africa dispersal events. Asian (CHB shown) and European (GBR shown) populations separate more recently, with a clear and visibly more sudden separation around 30,000 YBP (Figure 3c). We also detect, and date, very recent separations <10,000 YBP, such as between CHB-JPT (JPT: Japanese in Tokyo) or FIN-GBR (FIN: Finnish in Finland) (Figure 3d,e). Finnish samples exhibit a second bottleneck, around 3000-9,000 YBP following separation from GBR^30,31, with other population-specific events in e.g. Peruvians and Gujarati individuals (Supplementary Figure 6). The Finnish bottleneck is thought to have caused enrichment of certain disease-causing gene variants, commonly classified as Finnish heritage diseases^30,31. A strong bottleneck post-dating separation from Eurasian groups is absent in African populations (LWK: Luhya in Webuye, Kenya and YRI shown, Figure 3f). All populations show a remarkable increase often to >1,000,000, in the recent past (Supplementary Figure 6), however we note possible inaccuracies due to incomplete power to detect rare variants²⁴ leading to underestimation, and computational phasing leading to overestimation (Supplementary Figure 4).

Figure 3. Population sizes and split times in 1000 GP.

Relate-based population-specific estimates of population size and cross-population coalescence rates using genome-wide genealogies for CHB and YRI (a), GBR and YRI (b), CHB and GBR (c), CHB and JPT (d), FIN and GBR (e), and LWK and YRI (f). Insets show the matrices of coalescence rates between pairs of haplotypes at the indicated time. Rows and columns are sorted by population labels of haplotypes, as indicated by the colour on the left of each matrix.

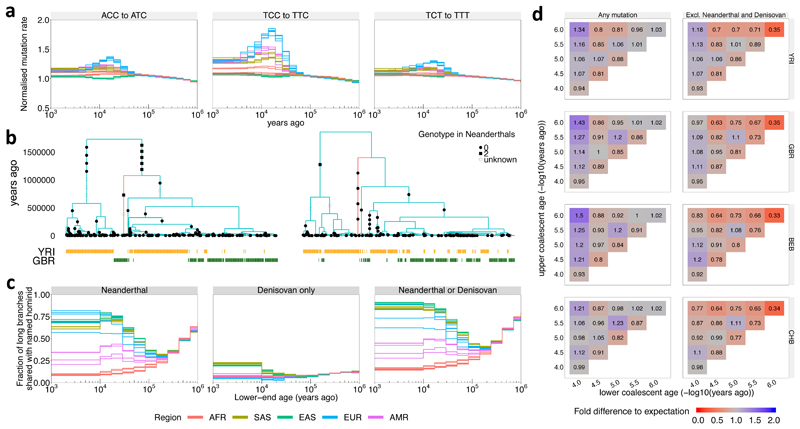
Exploring the relative mutation rate of particular mutation classes through time confirms, as reported previously²⁵, a strong elevation in the rate of trinucleotide changes including TCC->TTC in West Eurasian groups, which we date to 5,000-30,000 YBP, but infer to be weak or absent in the present day (Figure 4a). Other mutation types show more subtle temporal biases and signatures consistent with GC-biased gene conversion³² (Supplementary Figure 6). Overall, these results support accuracy of our inferred historical relationships, including the timing of a range of different historical events, identified within a single analysis framework.

Figure 4. Evolution of human mutation rates and evidence for introgression.

a, Evolution of mutation rates for three triplet mutations ACC to ATC, TCC to TTC, and TCT to TTT (see Supplementary Fig. 7 for all 96 triplet mutations, Methods for normalization). b, Marginal trees for a subregion on chromosome 14 (left) and chromosome 11 (right). The tree on the left contains a long branch with descendants only in GBR (red) consistent with Neanderthal introgression into GBR. The tree on the right contains a long branch with descendants only in YRI (red) consistent with introgression in YRI involving a hominid not closely related to Neanderthals. c, Fraction of branches with an upper-end age >1M YBP that are shared with Neanderthals (left), Denisovans and not Neanderthals (center), or Neanderthals or Denisovans (right) (Methods;). In a and c, colours encode geographic regions (AFR: Africa, EAS: East Asia, EUR: Europe, SAS: South Asia, AMR: Americas). d, Number of mutations binned by age of upper and lower coalescent event, relative to the expected number of mutations when randomising topology while fixing ages of coalescence events (Methods). Right column shows mutations not present in Neanderthal or Denisovan samples.

Neanderthal/Denisovan and unexplained introgression events

Introgression from distantly related groups in the past is expected to introduce lineages which forward in time can randomly spread in the tree, and backward in time remain distinct from other lineages, resulting in an excess of long branches associated with particular times. We identified such deep branches (>1 million years (MY) in age and with varying lower end), across human groups (Figure 4b,c). It is established that all nonAfrican human groups possess similar levels of Neanderthal introgression, and specific Asian and Australasian groups possess admixture from a group related to Denisovans^22,33. We therefore label deep branches possessing at least two derived mutations by whether at least one mutation is shared with the sequenced Denisova³³ or Neanderthal^22,34 genomes (Figure 4b shows one example of likely introgression from Neanderthals into European GBR, but not African YRI individuals). After classifying deep branches based on their lower-end times, for branches originating within the last 10,000YBP, 85-90% are shared with Neanderthal or Denisovan for most Eurasian groups (Figure 4c, Methods). Any lineages from recent introgression events will show a lower-end age younger than the time of introgression, and upper-end older than the split time of the introgressing group, so we expect branches with a younger lower-end to be most enriched with lineages that came from distantly diverged introgressing groups. This suggests that aside from groups closely related to Neanderthals and Denisovans, no strongly diverged hominid has left a major, recent impact in non-African populations studied here. An exception is IBS, which has more long branches shared with African populations (Supplementary Figure 6). In East and South Asian groups, the data suggest a very recent arrival of Denisovan DNA (mainly <15,000YBP). In non-Africans, Neanderthal sharing remains high for branches with lower-end age younger than ~30,000YBP. These dates are only lower bounds on the introgression time, and an accurate arrival date of Neanderthal DNA would require estimating a joint genealogy which requires further work. Nevertheless, they are consistent with previous estimates based on linkage disequilibrium (LD)³⁵, and of direct evidence of hybrids^35,36 around 40,000 YBP. Moreover, elevation in the sharing of quite deep haplotypes with Neanderthals steadily increases for branches with lower-end age of ~100,000 YBP towards the present, which is suggestive of introgression beginning from this time in nonAfrican individuals, although it is important to note that our date estimates for individual events might be over- or under-estimates in some cases.

In contrast to non-African groups, sharing with Neanderthal/Denisovans is lower (<20%, Figure 4c) in African populations, and declines towards the present, suggesting minimal recent interactions^22,33. This is despite the fact that African populations possess far more long branches (on average, on deep branches with lower coalescence age <30,000 YBP; 42,434 vs. 7,012 mutations occur in African vs. non-African populations). Of mutations on long branches found in Africa, 98% are Africa-specific, indicating separate events occurring in non-African and African populations (Supplementary Figure 6). Comparing YRI, GBR, BEB (Bengali in Bangladesh), and CHB to expectations under panmixia, we observe a strong excess of mutations on deep branches with lower coalescence age <40,000 YBP in all cases, which is almost entirely explained by Neanderthals/Denisovans in the non-African populations, but not in YRI (Figure 4d, Methods). In panmictic simulations with matched population size histories, we observe no such excess (Supplementary Figure 6). This evidences ancient but uncharacterised population structure within Africa, as suggested elsewhere^37,38. Figure 4b shows one example consistent with an introgression event in YRI, not involving a closely relative of Neanderthals.

Powerful tree-based approaches to study natural selection

By directly modelling how mutations arise and spread, genealogical trees offer the potential to powerfully investigate different modes of natural selection. For example, a recent method, SDS, indirectly tests for differences in tree tip branch lengths between carriers and non-carriers using the density of singletons around a focal SNP³⁹ and a tree-based analogue (trSDS) tests this directly⁴⁰. Here, we propose a class of approaches (Relate Selection Tests) based on estimating the speed of spread of a particular lineage (carrying a particular mutation), relative to other “competing” lineages, over some chosen time range. To test for selection over the entire lifetime of a mutation, we condition on the number of lineages present when it first arises, and use as a test statistic the number of present-day carriers. Assuming no population stratification, the null distribution of this statistic can be calculated analytically and is robust in principle to population size changes (Methods).

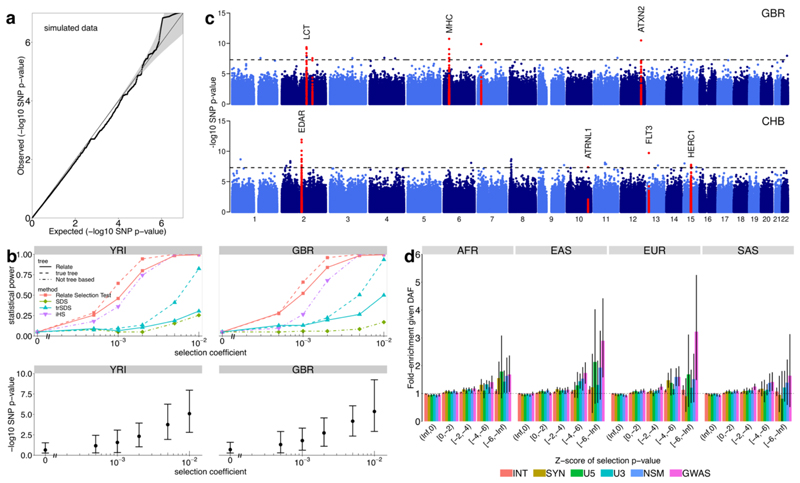
Simulated data (Figure 5a) show a close match in null no-selection scenarios of our p-values p _R to the expected uniform distribution. Across a range of selective advantages and SNP frequencies (Figure 5b, Supplementary Figure 6), our approach increases power relative to (tr)SDS, as well as iHS for weaker selection in particular. trSDS is more powerful than SDS, while applying the Relate Selection Test to true genealogical trees yields a test that is uniformly more powerful than other approaches (Figure 5b), indicating the strength of tree-based approaches. In practice, there is some decrease in power from the need to infer trees via Relate. The power increases for weak selection might be particularly beneficial for testing complex, polygenic traits, where small effect sizes at individual loci are expected to yield small selection coefficients⁴¹.

Figure 5. Natural selection.

a, QQ-plot of p-values p _R for selection evidence of SNPs. We simulated 250Mb for N = 1000 haplotypes using the recombination map of chromosome 1 and a bottleneck population size resembling that of non-African populations. b, Power simulations using N = 1000 haplotypes. We use historical population sizes estimated by Relate for YRI (left) and GBR (right). Top row shows statistical power and bottom row shows p _R with the mean indicated by circles and the 5^th and 95^th percentiles indicated by the error bars. We performed 500 simulations for the neutral case and 200 simulations for s > 0. c, Manhattan plot showing p _R of SNPs, for GBR and CHB. We highlight regions containing a SNP with p _R < 5 × 10^-8 in at least three populations (see Supplementary Table 3 for a full list), as well as the MHC region in GBR. d, Mean enrichment of functional annotation among targets of selection, conditional on allele frequency. Error bars show 95% confidence intervals estimated from 1000 iterations of a block bootstrap resampling (Methods). We group SNPs by mean regional Z-score corresponding to the log p-value for selection evidence, where a smaller Z-score indicates stronger selection evidence. SNPs are binned by partially overlapping functional annotations: intronic mutations (INT), synonymous mutations (SYN), mutations at the 5’ end and 3’ end of a gene (U5, U3), non-synonymous mutations (NSM), and GWAS hits (GWAS).

Calculating p _R for SNPs across twenty 1000GP populations (Methods) identified 35 distinct (24 novel) stringent signals genome-wide (p _R < 5 × 10^-8 in each of three or more groups) (Supplementary Table 3). These include the LCT region associated with Lactose tolerance in Europeans, and a mutation in the EDAR gene in East Asian populations^42,43, with both likely causal variants strongly associated with our most significant mutation (r ² ≥ 0.8). We also observe a previously-detected strong signal of positive selection in the MHC region in GBR⁴⁴ (Figure 5c). Among new regions, we identify selection evidence at the EDARADD gene - which interacts with the EDAR gene⁴⁵ in the formation of hair follicles, sweat glands, and teeth⁴³ - in all South Asian populations and Finns, with p_R < 10^-6 in all other European populations. In 16 of 35 regions, we identify GWAS catalogue hits (OR=6.44; p=0.01), non-synonymous mutations (OR=2.49; p=0.16), or expression quantitative trait loci (eQTLs; OR=1.74; p=0.1), in LD with the mutation with strongest selection evidence (r ² ≥ 0.8, Methods), suggesting functional effects, reaching statistical significance for the case of GWAS hits despite the small number of cases tested. Notably, 18 of the 35 regions are found only for African populations.

SNPs in functional parts of the genome are significantly enriched among targets of positive selection (Figure 5d, Methods), with strongest enrichment for GWAS hits, across all considered populations. This encouragingly supports a link between evidence of selection and SNPs with detectable influences on phenotypes at the organism level. Multiple previous studies^46–49 have attempted to test polygenic traits for evidence of directional selection, but confounding due to population stratification^50,51 is potentially problematic in practice. To leverage potential power gains, we tested whether derived mutations increasing (or decreasing) a trait show increased selection evidence relative to randomly sampled control mutations of the same frequency (one-sided Wilcoxon test; Methods). For each trait, we thin GWAS hits to account for LD and examined only SNPs showing “genome-wide significant” associations (p < 5 × 10^-8), because confounding due to population stratification is thought to occur through relatively small - but systematic - biases in effect size estimates^50,51, but is not expected, in general, to produce genome-wide significant false-positives. At each SNP, we use only the association direction, rather than its strength, to offer additional robustness to potential confounding.

If positive selection influences a trait in a certain direction, e.g. increasing, we would expect positive selection on trait-increasing and negative selection on trait-decreasing mutations. We expect our test to be sensitive mainly to the former, because selection will increase frequencies of such SNPs, and the Relate Selection Test has reduced power to identify selection at rarer markers (Figure 5b). However, for traits with a large number of hits and strong selection, it is theoretically possible to observe some selection evidence in both directions^52,53, because to avoid ascertainment effects we condition on SNP allele frequencies at traitinfluencing sites. Therefore, we additionally test for differences in present-day DAFs between trait-increasing and trait-decreasing mutations, which can provide orthogonal evidence of polygenic adaptation, aiding interpretation of results (Methods).

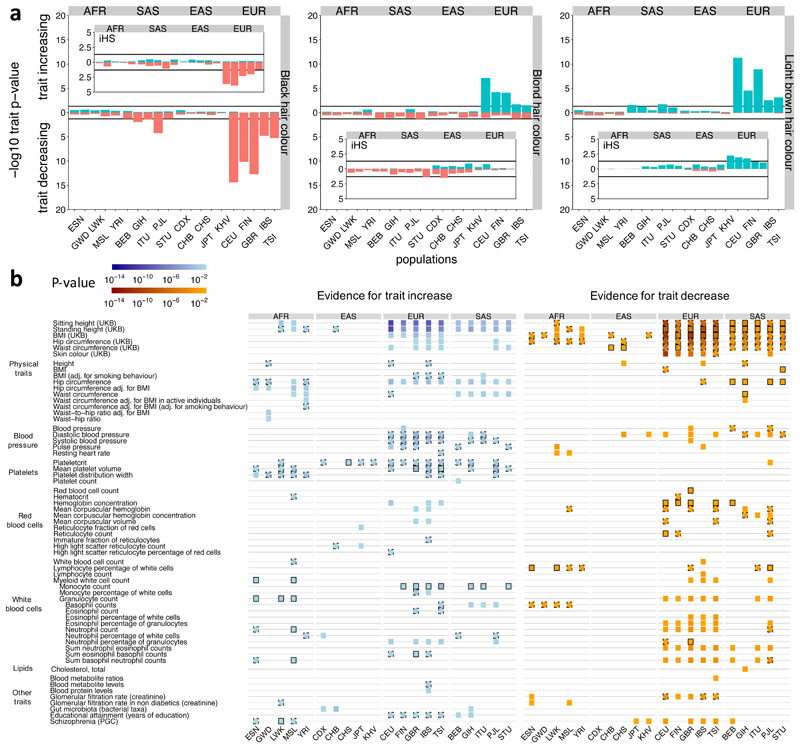
As a positive control, we applied our test to GWAS for hair colour within the UK Biobank⁵⁴ (Figure 6a). As in previous studies^49,55,56, we find a signal for SNPs associated with blonder hair color among European populations. We further observe strong selection towards light brown hair color and against black hair color, including more weakly in South Asians, but not in other groups. Testing based on iHS scores decreases significance by up to 4 orders of magnitude (Figure 6a), and some signals become non-significant. We applied the same test to test 84 traits: 6 from the UK Biobank, and 78 with at least 10 genome-wide significant GWAS catalogue association signals in each effect direction, in all populations except recently admixed groups. 61 of these (73%) showed nominal selection evidence (p<0.05) in at least one population (Figure 6b), with strong geographic clustering. The most significant signal (p = 6 × 10^-14) is for SNPs associated with decreased Body Mass Index (BMI) in CEU. The largest number of selection signals are observed for Europeans, likely because many GWAS were conducted in these groups. Interestingly, East Asians have the fewest signals and no enrichment of low p-values (Supplementary Figure 8), possibly explained by their stronger population bottleneck, which would theoretically be expected to weaken selection signals.

Figure 6. Evidence of selection on traits.

a, P-values for evidence of directional selection of black, blond, and light brown hair color (see Methods for calculation of p-values). Insets show p-values for the same test but using iHS scores instead, where iHS scores are calculated for each population separately for any variant with a minor allele frequency >5% in that population. b, Evidence for directional or bidirectional selection on multi- allelic traits. Each trait is associated with at least 10 SNPs in both effect directions in each of the considered populations. We show evidence for a trait increasing over time (left) and evidence for a trait decreasing over time (right) if p ≤ 0.05. Black boundaries indicate consistency with an additional test that tests for shifts in the DAFs (solid: p ≤ 0.05, dashed: p ≤ 0.5, Methods).

Height, BMI, and Schizophrenia have been studied previously and show a large number of association signals⁵⁷. While several studies have reported genetic differentiation between populations^58–60, evidence for selection remains controversial^{40,47–51,58,59,61} and some studies reporting recent selection on increased height in Europeans appear confounded by subtle population stratification^40,50,51. Our test finds selection evidence for both effect directions in each population for height, except in East Asians, using the UK Biobank GWAS. DAFs tend to be larger towards the height-decreasing direction. This complex picture may be a consequence of both negative and positive selection acting on height, as well as pleiotropy. SNPs impacting other traits might also impact height (Supplementary Note). We identify strong evidence of selection favouring BMI-decreasing SNPs across almost all populations, with agreement of DAF shifts, indicative of directional selection. For both traits, we detect little evidence of selection in the smaller GWAS catalogue collection. Decreased risk of Schizophrenia has evidence of selection in Europeans, and some South and East Asian populations, while African populations show selection evidence towards a risk increase.

Among other phenotypes, we see selection evidence for a variety of blood-related phenotypes, with congruent DAF signals. In Europeans and some South Asians, we detect a strong signal favoring SNPs associated with blood pressure increases, contrary to previous studies suggesting the opposite direction^55,62. We moreover find evidence in many groups for selection favouring SNPs associated with decreased hemoglobin concentration and related traits, and with increases in platelet-related traits.

Discussion

We introduced Relate, a scalable method for estimating genealogies genome-wide and demonstrated its accuracy and utility on a diverse set of applications. In many settings, Relate improved on existing state-of- the-art methods, which have previously required separate analyses: by instead obtaining inferences from the same genealogies, comparisons across different applications become straightforward. This approach is highly modular; methods developed for genealogy-based inference should be applicable regardless of the specific algorithm used for estimating marginal trees. Although we have focused on human genomes, Relate should work equally well in other recombining species.

In our 1000GP data analysis, we provide several examples whereby Relate-based trees are able to capture evolutionary processes that are themselves evolving through time: “evolution of evolution”. Temporal changes in mutation rates, population size, migration, and archaic admixture are simultaneously inferred, as are population-specific signals of natural selection. Genealogies provide a powerful, natural way to study these complex, interacting phenomena, and we believe studies of other evolutionarily and temporally dynamic processes - for example of evolution of recombination rates^63,64 - will yield new insights.

Interpretation of our findings regarding natural selection requires some care. A strength of our selection test is that it provides p-values, which are naturally calibrated, even if population sizes vary through time. In common with previous studies, we find a relatively small (<40) number of clear signals of strong, ongoing selection across multiple human populations. In contrast, we find a much larger collection of phenotypes where - based on published GWAS - there is evidence of an influence of directional selection. These traits include BMI, blood pressure, and white and red blood cell counts, and more generally, we see an enrichment of selection evidence at loci shown to associate with human phenotypes. These findings appear highly consistent with the polygenic nature of most human phenotypes - which are expected to impose very weak selection, but on a large collection of loci⁴¹. However, temporal changes in selection, overlapping genetic influences across traits, and the possibility of compensatory evolution in response to other genetic changes or the environment, are among reasons complicating the assignment of selection signals to specific phenotypes (Supplementary Note).

Relate provides age estimates for mutations and other events, and these enable us to construct statistics to understand evolutionary history, including natural selection either on individual mutations or collections of mutations. We regard the selection statistics introduced here as initial approaches along a path towards a richer inference framework, including e.g. background selection, full selective sweeps, or balancing selection. Development of methods to better understand directional migration and ancient admixture is another direction for future work. As one example, our results suggest a large impact of ancient substructure specific to African populations, as has been previously hypothesized^37,38. More generally, we hope that methods will be developed to perform statistical analyses on a set of trees generated either by Relate or other approaches. Other analyses might use estimated mutational ages obtained here directly (https://zenodo.org/record/3234689).

There are several natural extensions to Relate itself, e.g. allowing for increasing sample sizes. A recently developed method, tsinfer⁶⁵, has impressive scaling with sample size and might readily extend to even millions of samples, while Relate currently only handles at most a few tens of thousands of samples genome-wide. While tsinfer currently only infers tree topologies (as part of a full ancestral recombination graph structure), and so cannot infer tree times or model demographic histories, it would be possible to use tsinfer-based tree topologies in our framework, allowing full tree-based inference for huge sample sizes. Incorporation of ancient DNA sequences is another important direction. Such samples may have substantially higher error rates or more missing data than modern-day individuals, potentially requiring an approach that “threads” (ancient) sequences through genealogies that are initially built using modern individuals². This approach might also be useful for efficient statistical phasing and/or imputation of individuals only typed at a subset of markers.

Online Methods

Relate overview

We estimate genealogies as a sequence of rooted binary trees, where each tree captures the genealogy for a subregion of the genome. This representation serves as an approximation of an Ancestral Recombination Graph (ARG)⁴. We estimate local ancestry without global constraints on tree topology, thereby transforming genealogy reconstruction into a feasible and highly parallelizable problem.

Our approach can be divided roughly into three steps, which we detail below (also see Figure 1, Supplementary Figure 1, and Supplementary Note).

Calculating position specific distance matrices

While trees vary along the genome, our method heavily utilizes ancestry information from nearby SNPs to reconstruct the tree at a specific position. We achieve this by using a HMM similar to that first proposed by Li and Stephens²⁷ (see Supplementary Figure 2 for parameter choices). Intuitively, this HMM reconstructs a haplotype as a mosaic of other sample haplotypes along the genome (Supplementary Figure 1), allowing for mismatching in the copying process, and viewing changes in haplotype as recombination events. After applying the HMM, at a focal SNP ℓ each of the other haplotypes j therefore has some probability p_ij¿ of being copied from, to generate haplotype i. After rescaling log p_ij¿ appropriately (Supplementary Note), we obtain a position-specific distance matrix d whose entry (i,j) converges to the number of mutations derived in i and ancestral in j in the limit of no recombinations. In the presence of recombination, this d can be interpreted to store a local number of derived mutations, where more closely related haplotypes tend to have fewer mismatches over longer stretches, therefore receiving a smaller distance in this matrix.

We modified the Li-and-Stephens HMM to account for ancestral and derived states, a modification that guarantees our approach will construct the correct tree topology under the infinite-sites assumption with no recombination, while simultaneously speeding up the calculation of posterior copying probabilities.

Tree builder

The distance matrix is turned into a binary tree using a hierarchical clustering algorithm. This hierarchical clustering algorithm is motivated by the observation that each row of the distance matrix should indicate the order in which this haplotype coalesced with other haplotypes of the dataset. This can be shown mathematically in some limit conditions, such as the case with no recombination (Supplementary Note).

Our algorithm iteratively merges clades of haplotypes, corresponding to past coalescences. After merging clades, we update the distance matrix by combining the corresponding rows and columns using a weighted sum, with weights determined by the size of clades. In each step of the algorithm, we merge the pair of clades that coalesce with each other before coalescing with any other clade, as determined using rows of the distance matrix. If multiple pairs of clades satisfy this condition, we choose the pair with minimum symmetrized score in the distance matrix. If the data are consistent with a binary tree under the infinite-sites model, such a pair always exists. In practise, errors in the data, complex recombination histories, or violations of assumptions made by our model, may result in a distance matrix that is inconsistent with a binary tree. To be robust to such cases, we relax the conditions for identifying pairs of clades to coalesce.

Mapping mutations to branches and estimating branch lengths

Once tree topology is estimated as above, where possible we map mutations to the (unique) branch that has the identical descendants as the carriers of the derived allele in the data. To be robust to errors, where necessary we use an approximate rule for such mapping; however some mutations, e.g. repeat mutations or error-prone loci, may still not map to a unique branch. For these loci, we determine the smallest collection of branches, such that the data can be fully recovered. If a mutation maps to the tree only after reinterpreting the derived allele as the ancestral allele (and vice versa), we “flip” ancestral and derived alleles at this locus. For computation efficiency, to avoid having to construct a new tree at every locus we construct trees starting at the 5’ end of a region or chromosome, and move along the region constructing a new tree only when a SNP is flipped or cannot be mapped to a unique branch. Finally, after identifying equivalent branches in adjacent trees along the genome, we apply a Metropolis-Hastings type Markov Chain Monte Carlo (MCMC) algorithm to estimate branch lengths. The MCMC algorithm has a coalescent prior assuming a single panmictic population³.

Estimating coalescence rates through time

We estimate the effective population size, defined as the inverse of the coalescence rate, by applying the following iterative algorithm. We initially estimate branch lengths using a constant effective population size. We then calculate a maximum-likelihood estimate of the coalescence rates between pairs of haplotypes given the branch lengths (Supplementary Note). By averaging coalescence rates over all pairs of haplotypes and taking the inverse, we obtain a population-wide estimate of the effective population size. We then use this population size estimate to re-estimate branch lengths, which requires only the final MCMC step of the branchlength estimation. By repeating these two steps until convergence (in practice, we use only 5 iterations as this provides good performance), we obtain a self-contained algorithm for jointly estimating branch lengths and the effective population size. We can average pairwise coalescence rates in different ways to obtain rates for sub-populations and cross-coalescence rates between populations.

Estimating relative mutation rates through time

We estimate the mutation rate through time for all 96 triplet mutations (Figure 4a, Supplementary Figure 6). To estimate mutation rates for a mutation category of interest, we calculate, for each epoch, the quotient of the number of mutations in that category by the total branch length over bases at which such a mutation may have occurred. In our model, we fix the average mutation rate to a constant value through time, such that any change in average mutation rate should in theory be absorbed in our population size estimate. We therefore first eliminate any remaining temporal trends in the average mutation rate by dividing by the average mutation rate in each epoch. For each population, we then normalise the mutation rates such that the average rate over time equals 1. In simulations (Supplementary Figure 4), we show that variable mutation rates among categories can be detected by this approach, and approximately dated.

Pre-processing of the 1000 Genomes Project dataset

The 1000 Genomes Project dataset comprises 2504 individuals, from 26 populations. We obtained a phased version of the dataset (see Data availability). We next excluded multi-allelic SNPs, and we exclude one individual (two haplotypes) from each population for future applications, and analyzed the remaining 2,478 individuals (Supplementary Table 2). We use a genomic mask provided with the 1000 Genomes Project dataset (see Data availability) to exclude regions in the marked as “not passing” in the pilot mask, to remove loci with low certainty of genotypes. We also exclude any base for which the fraction of “not passing” bases within 1,000 bases to either side exceeds 0.9. To account for this filtering, we readjust the number of bases between SNPs at which we could have potentially observed a SNP. We use an estimate of the human ancestral genome (see Data availability) to identify the most likely ancestral allele for each SNP.

Identifying branches indicative of Neanderthal and Denisovan introgression

We use genome sequences of the Vindija²² and Altai³⁴ Neanderthals (NEA), and a Denisovan (DEN)³³ to identify branches indicative of Neanderthal and Denisovan introgression into non-African populations. To identify branches that remain segregated from other human lineages for a long time, we use the world-wide genealogy of 2,487 samples. To identify whether a branch is shared with NEA or DEN, at least one mutation needs to be mapped to that branch. We therefore exclude any mutation that has not been genotyped (or does not pass the genomic masks) in these ancient genomes. We further restrict our analysis to branches with at least two mutations mapped to them, as well as having an upper end that is older than 1M YBP. Of any such branches, we calculate the fraction of branches with at least one NEA or DEN mutation. In Figure 4c, we plot these fractions as functions of the lower-end age of the branch. Because the same branch may persist over multiple trees, we identify equivalent branches (Supplementary Note) and average ages of lower and upper ends across these equivalent branches. We assign a branch to a population if at least one descendant of that branch is in the population.

In Figure 4d, we observe an enrichment of branches indicative of introgression. This enrichment is identified by comparing the observed number of mutations in bins divided by upper and lower coalescence age to that expected in a panmictic history. To calculate the expected number of mutations in each bin, we fix the ages of coalescence events in each tree but randomise the topology assuming a panmictic population. The probability of upper and lower coalescence ages falling into bins s and r, conditional on the mutation arising while k lineages remain, is given by $P(r,s|k)={\Sigma }_{\mathcal{l}\ge k,h<k}{I}_{t\mathcal{l}\in r}\frac{2h}{\mathcal{l}(\mathcal{l}-1)}\frac{1}{k}$ where I denotes the indicator function. Assuming neutrality, a mutation is equally likely to have arisen anywhere on the branch it maps to. We therefore calculate the weighted average ${\Sigma }_k^N{=}_2{w}_{k}P(r,s|k)$ with weights w_k defined as the proportions of a branch while k lineages remain. Summing this over all SNPs yields the expected number of mutations with upper and lower coalescence age falling, respectively, into bins s and r. In Figure 4d, log10 age bins are defined by [− ∞, 4.25),[4.25,4.75),[4.75,5.25),[5.25,5.75),[5.75, ∞).

Tree-based statistic for detecting positive selection

Positive selection is expected to result in favourable mutations spreading rapidly in a population. One approach to capture this is via the number of lineages ultimately descending from the potentially favourable mutation(s): although we note that this is not the maximum likelihood approach, it has the benefit of making calculations straightforward. Under a null model of the standard coalescent model without selection, it is known that while k lineages remain, the joint distribution of the number of descendants of these k lineages is uniform in the partitions of N haplotypes to k lineages (see e.g., Ref. [66]). Using this property, we analytically calculate the marginal distribution that two of k lineages have more than f_Z descendants, where f_Z is the present-day DAF of the mutation. Here, we choose k to be the number of lineages remaining when the mutation of interest increased from frequency 1 to 2 (see Supplementary Note for the mathematical details).

To remove false-positive selection hits due to poorly inferred genealogies, our analysis for the 1000 Genomes Project dataset is based on a subset of all SNPs mapping to trees, and present in 3 or more copies in the dataset. Specifically, we remove SNPs failing any of the following filters: (i) the number of mutations mapping to that SNP’s tree is in the bottom 5^th percentile, or (ii) the fraction of tree branches having at least one SNP is in the bottom 5^th percentile. This excludes approximately 7% of SNPs.

Simulation of positive selection

To simulate positive natural selection, we adopt the pipeline outlined in Ref. [49]. We first simulate the trajectory of the DAF using simuPOP⁶⁷. We vary the selection coefficient between s = 0.001 and s = 0.05 and assume that the selected allele is beneficial throughout its history. We fix the present-day DAF to 0.7 (see Supplementary Figure 7 for other present-day DAFs). We then use mbs2⁶⁸ (mutation rate μ = 1.25 × 10^-8, constant recombination rate ρ = 5 × 10^-9) to simulate a region of 20 Mb, given the DAF trajectory for the central selected SNP. For each non-zero selection coefficient, we perform 200 simulations, and we perform 500 simulations for the neutral case. We assume a population size history as for our estimates for YRI and GBR, in separate simulations.

We compare to iHS, SDS, and a tree-based variant of SDS (trSDS) proposed in Ref. [40]. For iHS, SDS, and trSDS, we standardise scores using the mean and standard deviation in the neutral case, which is an idealised setting that should favour the power estimates of these methods. We then determine a critical standardized score that corresponds to a given type I error rate in the neutral case to estimate the statistical power. For Relate, we use frequency-conditioned p-values, by calculating a critical p-value that yields the desired false-positive rate in the neutral case (for the statistical power using raw p-values, see Supplementary Figure 7).

Enrichment of SNPs with functional annotation among targets of positive selection

We merge selection evidence for SNPs by region (AFR: Africans, EAS: East Asians, EUR: Europeans, SAS: South Asians) by first calculating Z-scores of the logarithm of selection p-values within populations, and then averaging these Z-scores across populations. We exclude groups expected to be highly admixed⁶⁹ (ACB, ASW, CLM, MXL, PEL, PUR (Supplementary Table 2)), because recent admixture may confound selection signals. We further exclude SNPs with a DAF <5% in the region of interest.

To assess statistical significance for the observed enrichment of GWAS hits and functional mutations in groups of SNPs showing evidence of selection, we used a block bootstrap with a block size of 1 Mb. This will account for LD at scales below this threshold. In each bootstrap iteration, we resample blocks containing SNPs with a selection Z-score within the range of interest, with replacement, and calculate the ratio of the number of SNPs with functional annotation obtained using the HaploReg database⁷⁰ (see Data availability) and the GWAS catalogue to the expected number of such SNPs, conditional on DAF. We condition on frequency, to account for the possibility that skewed frequency spectra in functional SNPs could be driving the signal.

Pre-processing of GWAS

We use SNP-trait associations documented in the GWAS catalogue⁷¹ (see Data availability) to study polygenic adaptation. We use only association signals whose GWAS p-value is smaller than 5 × 10^-8. For each trait, we also remove any duplicate SNPs.

For every combination of population, trait, and effect direction, we compile a set of approximately independent GWAS signals as follows.

For each pair of population and trait, we remove associations that are in close physical proximity and may therefore be in LD. For this, we first group SNPs into approximately independent blocks, such that any two GWAS hits in separate blocks are separated by at least 100 kb and there are no intervals larger than 100 kb with no GWAS hit inside a block. We then choose one GWAS hit from each block uniformly at random. We remove any SNP with a DAF <5%. To determine the effect direction of a SNP, we use the annotation in column “95% CI (TEXT)” combined with the indicated risk allele. We then realign the effect direction to the derived allele. We only consider SNPs for which an effect direction can be determined with this procedure. As described in the main text, we only analyze traits with at least 10 independent hits in both effect directions in all populations. This results in 76 traits and a total of 7,302 GWAS hits (before filtering for SNPs in close proximity in each population).

For Schizophrenia, we are unable to obtain an effect direction using the procedure described above. Instead, we downloaded results for a large-scale GWAS conducted by the Psychiatric Genomics Consortium⁷². We considered SNPs reaching a GWAS p-value of 5 × 10^-8 of which there were 9,138. We intersected this set of SNPs with SNPs segregating in each of the considered populations. As for the GWAS catalogue, we identified approximately independent blocks. We then chose the SNP with lowest GWAS p-value in each block, resulting in 81 to 89 hits per population.

In addition, we use GWAS conducted as part of the UK Biobank⁵⁴, focussing on highly polygenic physical traits. Our pre-processing protocol is analogous to that for schizophrenia detailed above. The number of approximately independent hits per population range from 272 hits for waist circumference to 989 hits for standing height.

Trait selection test

For every combination of population, trait, and effect direction, we test whether p-values are smaller than expected. For this test, we first sample SNPs that we use for comparison. For each SNP associated with the population, trait, and effect direction tuple of interest, we sample 20 SNPs uniformly at random with replacement from SNPs, with the same present-day DAF in the population of interest. We then use a one-sided Wilcoxon rank-sum test to test whether the p-values of SNPs associated with the tuple of interest tend to be smaller than those for the frequency-matched set of SNPs. We repeat this test 20 times and report the mean p-value of the Wilcoxon rank-sum test.

Our primary test identifies selection evidence conditional on DAF. However, shifts in DAF can themselves serve as orthogonal evidence of polygenic adaptation, complementing our inferences. Therefore, we conducted a one-sided Wilcoxon rank-sum test to test whether DAFs of SNPs associated with the effect direction with selection evidence tend to exceed those associated with the opposing effect direction, and compared to our results conditional on SNP frequency. We note that we expect to lack power to reliably detect selection with this test, given that there are typically only tens of SNPs independently associating with each trait In addition, the relationship between selection and SNP frequencies can be complex if selection strength varies through time and/or geographic locations.

Data availability

Relate-estimated coalescence rates, allele ages, and selection p-values for the 1000 Genomes Project can be downloaded from https://zenodo.org/record/3234689.

Datasets used in the current study were obtained from the following URLs:

1000 Genomes Project phased dataset, https://mathgen.stats.ox.ac.uk/impute/1000GPPhase3.html (13 Jan 2017); Genomic mask, ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502/supporting/accessible genome masks/ (20 Jul 2017); Human ancestral genome, ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase1/analysis results/supporting/ancestral alignments/ (20 Jul 2017); GWAS catalogue, https://www.ebi.ac.uk/gwas/api/search/downloads/full (9 Nov 2017); PGC GWAS study, https://www.med.unc.edu/pgc/results-and-downloads (23 Nov 2018); HaploReg, http://archive.broadinstitute.org/mammals/haploreg/data/haploregv4.020151021.vcf.gz (21 Oct 2017); GTEx eQTL https://storage.googleapis.com/gtex analysis v7/single tissue eqtl data/GTEx Analysis v7 eQTL.tar.gz (13 Jan 2019); UK Biobank GWAS summary statistics, http://www.nealelab.is/uk-biobank (4 Oct 2018); PopHumanScan, https://pophumanscan.uab.cat (13 Jan 2019)

Code availability

The software Relate can be downloaded from https://myersgroup.github.io/relate under an Academic Use Licence.

External software used in the current study were downloaded from the following URLs:

ARGweaver, https://github.com/mdrasmus/argweaver (24 Jan 2017);RENT+, https://github.com/SajadMirzaei/RentPlus (2 Oct 2017); msprime, https://github.com/tskit-dev/msprime (22 Jul 2017); msmc, https://github.com/stschiff/msmc2 (14 Oct 2017); SMC++, https://github.com/popgenmethods/smcpp (14 Oct 2017); simuPOP, http://simupop.sourceforge.net/ (27 Jun 2018); mbs, http://www.sendou.soken.ac.jp/esb/innan/InnanLab/ (27 Jun 2018); SDS, https://github.com/yairf/SDS (27 Jun 2018), selscan, https://github.com/szpiech/selscan (31 Jul 2018); hapbin, https://github.com/evotools/hapbin (11 Dec 2018)