Abstract
Altruism between close relatives can be easily explained. However, paradoxes arise when organisms divert altruism towards more-distantly-related recipients. In some social insects, workers ‘drift’ extensively between colonies and help raise less-related foreign brood, seemingly reducing inclusive fitness. Since being highlighted by W. D. Hamilton, three hypotheses (bet-hedging, indirect reciprocity, and diminishing returns to cooperation) have been proposed for this surprising behaviour. Here we show using inclusive fitness theory that bet-hedging and indirect reciprocity could only drive cooperative drifting under improbable conditions. However, diminishing returns to cooperation create a simple context in which sharing workers is adaptive. Using a longitudinal dataset comprising over a quarter of a million nest-cell observations, we quantify cooperative payoffs in the Neotropical wasp Polistes canadensis, where drifting occurs at high levels. As the worker-to-brood ratio rises in a worker’s home colony, the predicted marginal benefit of a worker for expected colony productivity diminishes. Helping on related colonies can allow effort to be focused on related brood that are more in need of care. Finally, we use simulations to show that cooperative drifting evolves under diminishing returns when dispersal is local, allowing altruists to focus their efforts on related recipients. Our results indicate the power of nonlinear fitness effects to shape social organisation, and suggest that models of eusocial evolution should be extended to include neglected social interactions within colony networks.
Altruism – sacrifice of Darwinian fitness to increase that of a recipient – is easily explained when occurring between close relatives1, through an increase in the altruist’s inclusive fitness (success at propagating copies of its genes in the population)2–4. However, paradoxical forms of altruism arise when individuals divert help from the closest relatives and towards more-distantly-related recipients5,6. This seemingly irrational behaviour appears to reduce inclusive fitness7.
Social insect colonies are often impenetrable ‘fortresses’8. However, in some (especially primitively-eusocial) species, between-colony movement (‘drifting’) by both workers6,7,9–12 and foundresses13 can be extensive. Often, opportunities for reproductive parasitism14 or nest inheritance13 provide clear direct fitness motives. In other cases, drifters lack obvious opportunities for direct fitness7,11,12, and help more-distant relatives than recipients on their home colony. In some primitively-eusocial Polistes paper wasps, the extreme extent of drifting by nonreproductive workers has become clear: in the tropics (where Polistes originated), 56% of workers within a population were detected at multiple colonies12. Drifting workers perform standard cooperative tasks12 (henceforth, ‘cooperative drifting’), creating ‘extended kin groups’11 (networks of cooperating colonies). However, despite primitively-eusocial insects being long-standing models for understanding trajectories to complex eusociality15, the driver of cooperative drifting has not been identified.
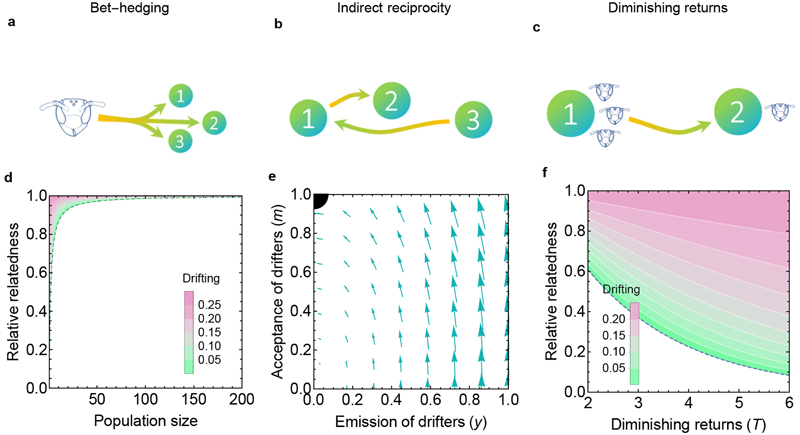
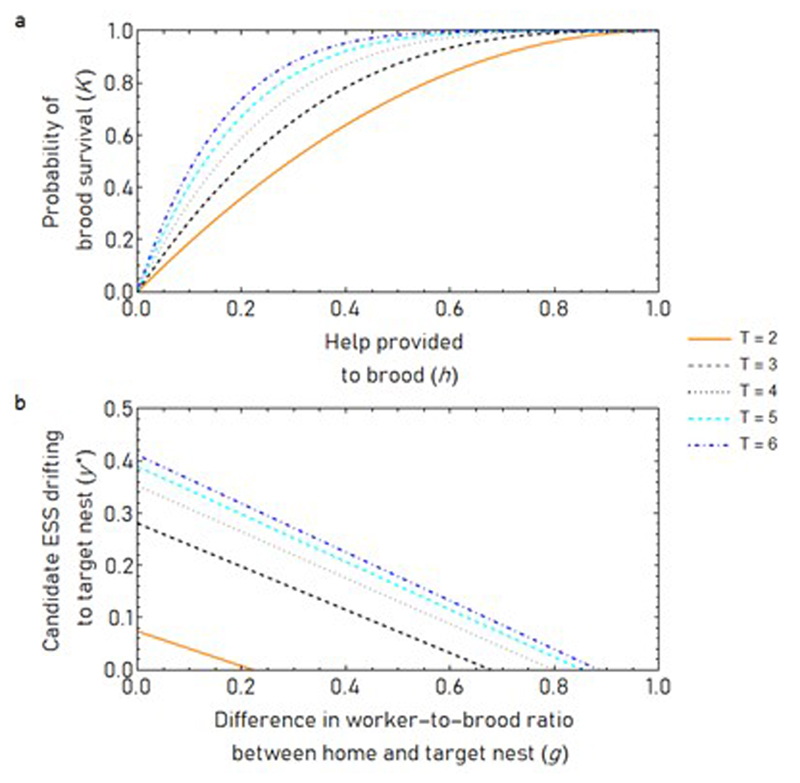
Three hypotheses have been proposed to explain the evolution of cooperative drifting by non-reproductive primitively-eusocial workers. The bet-hedging hypothesis12 suggests that helping multiple related colonies (‘1’, ‘2’, and ‘3’ in Fig. 1a) avoids the risk of investing in a single colony that could succumb to chance failure or predation. By diversifying investments, workers accept reduced expected inclusive fitness for the benefit of reduced variance in inclusive fitness. The indirect reciprocity hypothesis5 suggests that helping in partner colonies (‘2’ in Fig. 1b) leads to other workers (‘3’ in Fig. 1b) – who may be nonrelatives – helping the home colony (‘1’ in Fig. 1b). For this to be beneficial, it is assumed that help exchanged between neighbours is worth more than help from natal workers due to ‘social heterosis’: a negative relationship between relatedness and ability to improve colony productivity16. The diminishing returns hypothesis7,12 suggests that the marginal benefit provided by a worker diminishes as the number of workers tending brood increases17,18 (‘1’ in Fig. 1c), an effect first highlighted by Michener in 196419, and helping on related colonies allows effort to be redirected towards brood that are more in need of care (‘2’ in Fig. 1c). There has been no formal comparison of these hypotheses, so we begin by using inclusive fitness theory to assess the plausibility of each.
Fig. 1. Three adaptive hypotheses have been proposed for cooperative drifting.
(a) Bet-hedging. (b) Indirect reciprocity. (c) Diminishing returns. (d) Cooperative drifting is only favoured by bet-hedging (above dashed line) at extremely small population sizes and when recipients differ only slightly in relatedness to the actor. Equilibrium divestment levels shown (Methods 1). (e) Cooperative drifting cannot be explained by the indirect reciprocity hypothesis because free-riders invade (y→0, m→1). Arrows show direction of selection. Black quarter-circle is the global attractor (Methods 2). (f) Diminishing returns can select for cooperative drifting. Stronger diminishing returns and higher relatedness favour more cooperative drifting (Methods 3). Relative relatedness is d in Equation 3 of main text. For illustration, we plot equal reductions in relatedness for female and male brood . ψ=1; g=0.5; x=0.75; z=0.25.
Results
Selection for cooperative drifting
First, we show that, under normal conditions, bet-hedging12 cannot select for cooperative drifting. We derive an explicit mean-risk trade-off for bet-hedging traits for an organism maximizing its inclusive fitness3 (Methods 1):
| 1 |
subject to where the organism must choose the optimal weights (q) to place on different investments, balancing the expectation (q†µ, where † denotes transpose) and variance (q† Cq) in absolute inclusive fitness returns, for particular values of risk-aversion (v) and the correlation (ρ) between the portfolio’s return and whole-population average reproductive success . The vector µ contains the offspring production per unit invested (weighted by offspring relatedness), C is the variance–covariance matrix for the investment payoff rates, and 1 is a vector of ones. A ‘risky’ portfolio has high variance. In Methods 1, we show that the value of risk aversion (v) that maximizes inclusive fitness is the coefficient of variation in . However, under demographic stochasticity – which is generated by random colony failures – meaningful fluctuations in will only occur if the population is extremely small (Methods 1), so v≈0. Moreover, in reasonably sized populations, fluctuations in that do happen due to random colony failure occur independently of fluctuations in the portfolio’s returns, so ρ≈0. Since v≈0 (and ρ≈0), the second term of (1) is negligible, so workers should maximise only the expectation of inclusive fitness (q†µ). The same logic underpins why bet-hedging against randomly occurring clutch failure is an unlikely explanation for birds distributing eggs over multiple nests20 or parasitoids distributing eggs over multiple hosts21. In summary, the bet-hedging hypothesis for cooperative drifting is mathematically coherent (Fig. 1d) only in an extremely small population and/or in cases where drifting would lead to a very small reduction in expected inclusive fitness q†µ, circumstances that only rarely arise in the natural world. One way, for instance, is if there were near-negligible differences in relatedness towards brood on home and neighbouring colonies, but Polistes drifters face falls in relatedness12.
Second, we show that indirect reciprocity5 is unlikely to explain cooperative drifting. Using simulations, Nonacs5 has argued that drifters will automatically help only at colonies sharing indirect reciprocator alleles because these are the only colonies willing to accept them. However, there is no reason to expect pleiotropy between these two behaviours, so (unlike Ref.5) we allow the emission (y) and acceptance (m) of drifters to evolve independently in a kin-selection model (Methods 2). As in Ref.5, we find that when m is prevented from decreasing whilst y increases, drifting can evolve (Methods 2). But when this unjustified assumption is relaxed, indirect reciprocity collapses due to the invasion of free-riding: colonies willingly accept foreign workers10 (m=1) whilst none of their own workers drift (y=0) (Methods 2; Fig. 1e).
Third, we show that diminishing returns7,12 can be a simple driver of cooperative drifting (Methods 3): as the effect of helping closely-related recipients declines, diversion of altruism towards more-distantly-related recipients can satisfy Hamilton’s rule (increase in benefit b more than compensates for the decrease in relatedness r). In a kin-selection model using the framework of Davies et al.22, we let the probability of brood surviving to maturity (K) be determined by a simple diminishing returns function: , where is help received from workers. Higher values of T result in stronger diminishing returns. Help (h) received by each brood depends on the worker-to-brood ratio in their colony, which may vary stochastically between and within colonies through time. For simplicity, we consider neighbouring colonies with equal brood numbers, lying at different points on a line of possible worker-to-brood ratios. Worker-to-brood ratios greater than ψ=1 occur only on colonies in terminal decline, so we focus on . Drifting reduces a worker’s relatedness to the brood it cares for to the (nonzero) proportions and for female and male brood respectively, relative to raising siblings at home. When a home colony has worker-to-brood ratio ψ, selection favours a small increase in drifting (y) to a colony with a proportion g of the home colony’s workforce when the improvement in indirect fitness from escaping diminishing returns (left-hand side) compensates for reductions in recipient relatedness (right-hand side):
| 2 |
where x is the proportion of females that are behaviourally sterile (not reproductive) and z is the proportion of offspring that are male, so x(1−z) is the proportion of offspring that are workers.
To find candidate evolutionarily stable strategies (ESS) for drifting level y, we set equal the left and right sides of Inequality 2 and rearrange for y. Letting consanguinity to male and female brood be devalued by the same amount , the ESS drifting level y*) occurs at:
| 3 |
Given the possibility to drift to related colonies at sufficiently steeper points on an inclusive-fitness-returns curve, workers should tolerate a reduction in recipient relatedness (Methods 3; Fig. 1f; Extended Data 1, 2). The ESS drifting level y* increases whenever a gap in worker payoff increases between two related colonies: y* increases with higher T (Fig. 1f), higher ψ and lower g, and for scenarios in which there is a larger workforce (lower z and higher x). For example, a worker may be twice as related to brood on its home colony as to brood on a partner colony (). Assume the home colony (with ψ=1) has twice as many workers as the partner colony (). With diminishing returns factor of T=4, three-quarters of females developing as non-reproductive workers (), and a sex ratio of 3:1 female eggs to male eggs (), the expected equilibrium level of cooperative drifting from the home colony would be for 13.2% of worker effort to be divested to the less-related partner colony (y*=0.132). As workers drift and group sizes consequently change, the marginal payoff of staying on the home colony rises and the marginal payoff of helping on the partner colony falls until y=y*, where any further drifting would reduce inclusive fitness.
Diminishing payoffs in the wild
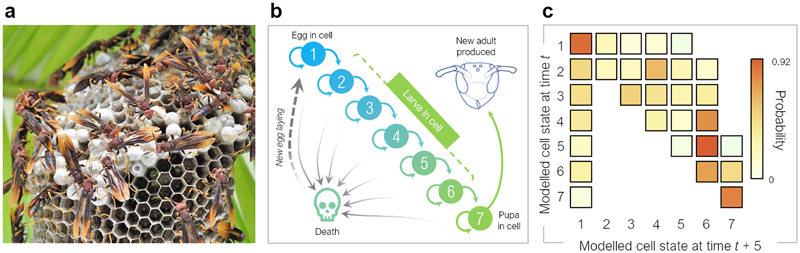
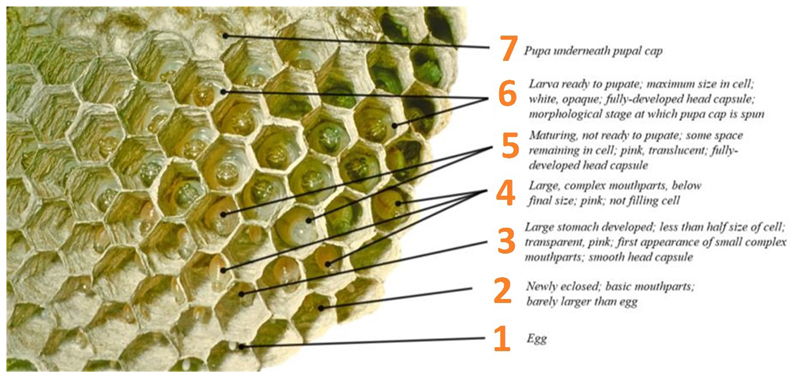
To investigate plausible ranges within which diminishing returns to cooperation may exist, we used longitudinal field tracking of brood development and worker numbers in a Neotropical paper wasp. Polistes canadensis is a model species in which cooperative drifting is common and can reduce relatedness to recipient brood considerably (e.g., r=0.56 at home vs r=0.19 on partner colonies)12. Colonies typically consist of a single queen and behaviourally nonreproductive daughter workers and non-nestmate drifters12. As workers emerge, colonies can grow in group size from fewer than 10 females to up to 200 females. In dominance hierarchies below the queen, a small number of high-ranking wasps have an opportunity to inherit the nest on the death of the resident queen23; most subordinates perform helping behaviours (including foraging, nest hygiene, brood inspection, nest building, and nest defense)12,24,25. The lack of a covering nest envelope allows clear observation of individual brood (Fig. 2a) and the opportunity to document whole-colony development through time26.
Fig. 2. Brood development in the Neotropical paper wasp Polistes canadensis.
(a) P. canadensis colonies allow easy observation of individual brood cells. Photograph: PK. (b) Wasp development involves states from egg (state 1) through larvae (2 to 6) to pupa 7 and finally a new adult (definitions of states in Extended Data 3). This can be represented using a Markov model. (c) Baseline transition probabilities between developmental states using an intercepts-only model (Methods 4). In using developmental rates to produce a measure of colony productivity as a function of worker behaviour, we set transitions to death as transitions back to egg (state 1), in order to exclude confounding effects from between-queen variation in egg-laying rates.
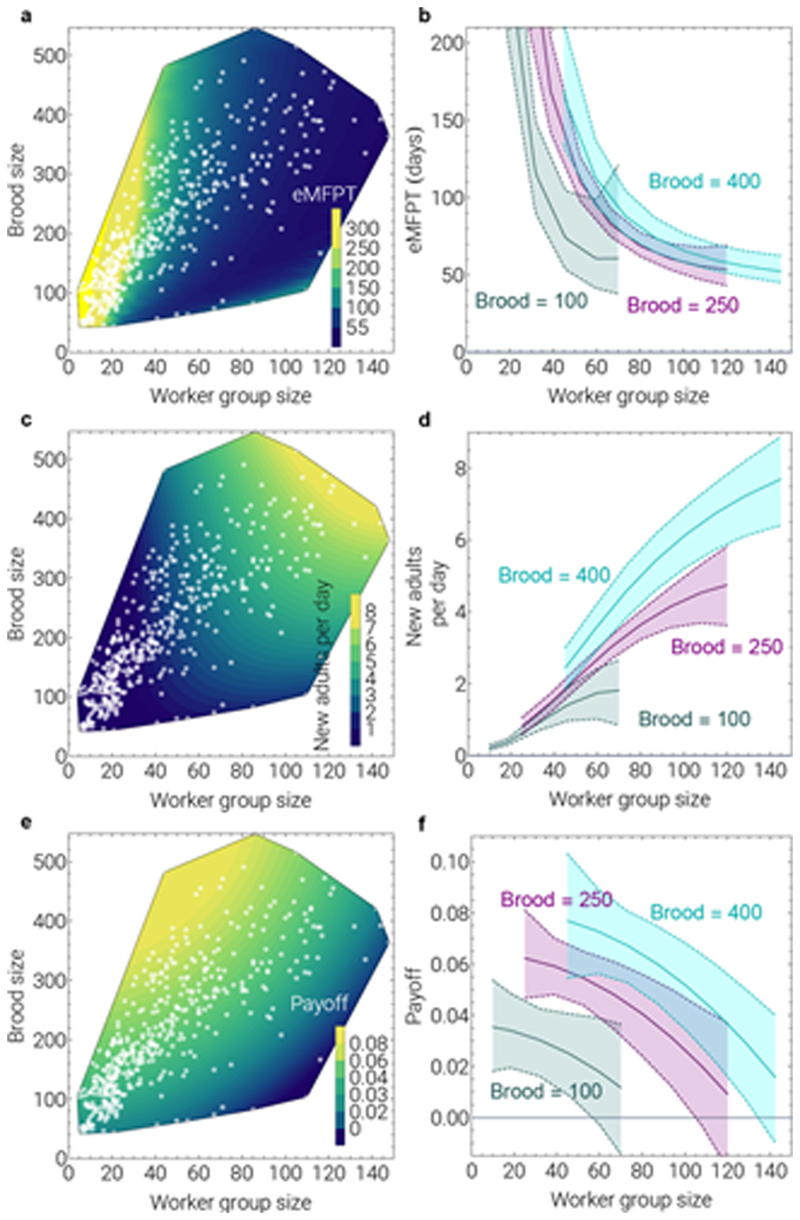
We aimed to assess how a colony’s success at producing new adults is associated with numbers of workers and brood on the colony. Across 56 days, we made over a quarter-of-a-million observations of more than 20,000 individually tracked brood cells on 91 wild post-worker-emergence colonies in Panamá. The stage of brood development in every cell in each colony was recorded repeatedly (Methods 4; Extended Data 3) and treated as a state in a Markov model (Fig. 2b,c). The number of adults on the nest at night (when all workers are present) was counted at intervals over the observation period. This resulted in a dataset of 123,116 state-transitions involving live brood on 85 colonies in 471 colony-observations for which worker number can be predicted by interpolation through the night censuses (Methods 4). To investigate the extent to which there may be variation in payoffs within networks of colonies, we asked how the number of workers correlated with colony success at different points of larval development.
Using between-colony variation in the number of workers and worker-to-brood ratio, whilst controlling for within-colony variation and colony state (using the extent of brood-cell emptiness as a proxy), a Bayesian hierarchical model predicts that colonies with higher worker-to-brood ratios and worker numbers are associated with higher brood development pace and lower brood death. The Markov model predicts that the expected time for a single egg-containing brood cell to produce an adult successfully in colonies with different worker and brood numbers (‘expected mean first passage time’, eMFPT) declines as more workers tend the brood (Fig. 3a,b; Extended Data 4). Multiplying 1/eMFPT by brood number estimates the expected number of new adults that can be produced per day (whole-colony productivity), which is highest in colonies with many workers and many brood (Fig. 3c,d). The slope of whole-colony productivity with respect to worker number (Fig. 3e,f) then provides a prediction of the marginal increase in the daily number of brood successfully raised associated with each additional worker (i.e., plausibility values for the payoff rate). The ‘payoff’ in Fig. 3e,f represents an empirical estimate of the benefit b in Hamilton’s rule from working on a colony of the given size. An investment in a partner colony 2 is in the inclusive-fitness interest of a worker from a home colony 1 if .
Fig. 3. Brood-rearing rates in Polistes canadensis.
(a) Expected number of days for an idealised brood cell successfully to produce an adult (‘expected mean first passage time’, eMFPT) predicted by between-colony effects. Brood size denotes number of prepupal brood (states 1-6). Worker group size denotes interpolated group size using night-time censuses. White dots denote colony observations. To illustrate predictions in the main parameter space, we generated the prediction of eMFPT for 1,000 simulated colonies inside the convex hull set by those colony observations with up to 150 workers and over 40 brood (only 10 colony observations, from six colonies, in the dataset of 471 colony observations used to generate the model, lie outside this range). (b) 95% credible intervals corresponding to a. (c) Predicted whole-colony productivity (daily expected number of new adults, given the eMFPT values) is highest in colonies with many workers and many brood. (d) 95% credible intervals corresponding to c. (e) Slope of predicted whole-colony productivity with respect to worker group size, representing predicted effect of adding a new worker (the ‘payoff’ provided to the recipients), an empirical estimate of the potential benefit b in Hamilton’s rule. (f) 95% credible intervals corresponding to e. See Methods 4.
The difference in the predicted payoff from the model suggests that – within the main parameter space occupied by colonies – workers are more valuable (lighter colours in Fig. 3e) at colonies with a relatively ‘understaffed’ workforce faced with large brood-rearing challenges than at colonies with fewer brood to rear. Future models that consider within-colony dynamics may further explain finer-scale variation in brood development rates (see Extended Data 5–8; SI Table S3). However, the prediction of variation in plausible payoff rates between colonies with different workforce sizes suggests a context in which workers can increase indirect fitness by helping at less-closely-related colonies.
Scales of competition
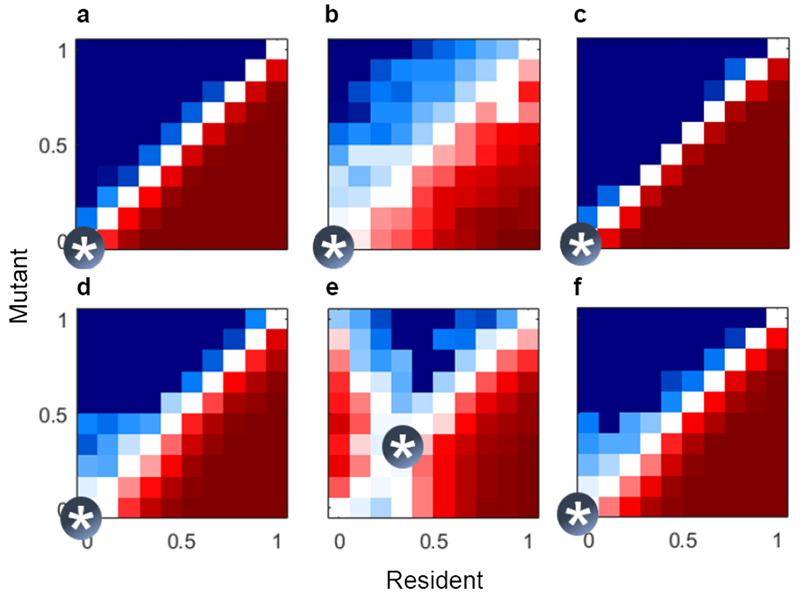
To explore the demographic conditions that can sustain cooperative drifting, we use agent-based haplodiploid simulations (Methods 5) of a large population of monogynous colonies distributed over a square lattice (where each colony has eight neighbours in a ‘Moore neighbourhood’). To model simple colony growth, we assume a ‘unit’ is a group of workers (e.g., 10 workers), and let colonies produce a new unit every three time-steps (e.g., 3 weeks) until reaching a maximum of 10 units. We assume a saturated environment in which each square on the lattice is occupied by one colony. At each time-step, a randomly chosen 10% of colonies die and are replaced. The foundress of the replacement colony is drawn either from lottery competition among the local eight colonies in the Moore neighbourhood (when female philopatry is assumed) or globally from the whole population (when female philopatry is relaxed). Males compete globally for mating with females in lottery competition. The number of reproductively-destined offspring that colonies produce is a diminishing-returns function of the helper effort h on the colony, as above. Colonies with more helpers therefore produce more reproductively-destined females and males, and so have a greater chance in competition for nest sites and mating, respectively. We evolve units’ propensity to drift for workers on colonies with more than five units, and show the results of competition by introducing mutant alleles to resident populations at an initial frequency of 5%. After 1,000 time-steps, we record the mutant frequency and plot the average change in frequency over three replicate simulations (Methods 5).
Under linear returns, drifting does not invade, regardless of demography (Fig. 4a-c). We then consider moderate diminishing returns (T=3) under three conditions: female philopatry and altruism directed at local colonies in the Moore neighbourhood (Fig. 4d); female philopatry and altruism directed at partner colonies whose queens are parents or daughters of their own queen (Fig. 4e); and female global dispersal with altruism directed at local colonies in the Moore neighbourhood (Fig. 4f). (Female global dispersal with altruism directed at the genealogically-close partner colonies is not considered, because global female dispersal makes these pairings vanishingly rare.) Cooperative drifting can invade only when we allow female philopatry and kin-directed altruism (Fig. 4e): under this scenario, neighbouring nests develop genealogical links (spatial kin structure), and – when drifters are shared preferentially within these links – cooperative drifting occurs at a more local scale than the spatial scale of competition. Polistes wasps often form colony clusters within wider aggregations of tens to hundreds of colonies11,12,27, a context in which cooperative drifting can evolve by spatial selection under diminishing returns.
Fig. 4. Evolution of cooperative drifting in a spatially explicit social haplodiploid simulation.
Results of competition from agent-based simulations of the invasion of drifting. Red denotes mutants invading from a starting frequency (pinitial) of 5% of the population; blue denotes mutants declining. White denotes negligible change in frequency. Convergence-stable strategies are marked by asterisks. Conditions were (a-c) no diminishing returns, T = 1, and (d-f) moderate diminishing returns, T = 3; (a, d) female philopatry and altruism directed at local colonies in the Moore neighbourhood, (b, e) female philopatry and altruism directed at partner colonies with queens who are parents or daughters of their own queen, (c, f) global female dispersal with altruism directed at local colonies in the Moore neighbourhood. Nonlinear returns drive inter-colony cooperation only under both local female dispersal and kin-directed altruism (panel e).
Discussion
Established accounts of the evolution of eusociality assume actors must choose either to stay as helpers or leave as reproductives8,28. Our results suggest that diminishing returns may drive altruists to diversify their help across recipients: workers in some primitively-eusocial societies may increase inclusive fitness by providing altruism to recipients beyond their home colony. Under positive kinship, spatial kin clustering, and diminishing returns17,29, worker investments can evolve to become diffusible public goods.
Our model predicts the conditions under which we expect cooperative drifting to have evolved (Equation 2, Fig. 1f). Intuitively, drifting is more likely when there are stronger diminishing returns (higher T), a larger difference in workforce between nests (smaller g), increased total workforce (higher ψ), and a greater capacity to target kin (higher and ). For simplicity in Equation 2, we assume that all colonies have the same sex ratio, but between-colony sex-ratio variation suggests an additional factor: a colony producing mainly brothers has a reduced worker relatedness to the brood, at which point switching colony may be rational for a worker. In short, drifting offers a simple route to boost inclusive fitness when neighbouring colonies differ in parameters that determine the value of a worker. Differences in worker and brood number arise easily among P. canadensis colonies (Fig. 3a), which are subject to several sources of stochasticity. These include fluctuations in worker number due to the high attrition rate of foraging workers12, frequent loss of brood to parasitoids, presumed loss of brood due to disease (based on workers’ hygienic removal of larvae), episodes of queen replacement, and so on. Fluctuations in brood cohort size translate into fluctuations in workforce size once the brood pupate.
Since Michener19 highlighted diminishing returns in hymenopteran societies in 1964, a number of studies across ants, bees, and wasps have revealed declines in per-capita productivity with rising group size (e.g.18,30–33). This so-called ‘reproductivity effect’ has not proved universal (e.g.34–36), but its frequent occurrence leads to ‘Michener’s paradox’: why do apparently partly-redundant helpers exist26,30? Previous tests of the reproductivity effect have used snapshots of per-capita productivity. By contrast, we provide a prediction of plausible ranges for the payoffs of cooperation in a primitively-eusocial insect using colony dynamics. Diminishing returns exist, but – through cooperative drifting – workers can mitigate redundancy arising from stochastic variation in worker-to-brood ratios between colonies.
The extent of drifting across primitively-eusocial insects remains to be explored5,12. However, the relatively high levels of drifting observed in Neotropical species such as P. canadensis contrast with, for example, the European wasp P. dominula, which also forms dense colony aggregations13 but shows high aggression towards neighbours. This difference in social organization may be due to differences in the intensity of diminishing returns (e.g., due to food availability or parasite density). Higher stochastic predation of workers in some species may undermine workers’ abilities to track need across nests. Alternatively, drifting may be more likely in the tropics: unlike temperate species in which foundresses establish nests synchronously in the spring, tropical species often establish nests throughout the year25, and so nests may be more likely to differ in worker-to-brood ratio. Tropical species may also experience less uncertainty in neighbour relatedness, since nests are more commonly founded by local dispersal from parent nests (simulated in Fig. 4e), although kin spatial structure can be reestablished in temperate species by natal philopatry of spring foundresses37. Direct comparisons between species with and without cooperative drifting are needed.
Cooperative drifting has also emerged among complex eusocial species. Ant ‘supercolonies’ exist when nests with multiple queens (polygyny) exchange workers (polydomy)6,38. Supercoloniality results in remarkably low-relatedness cooperation, and remains a theoretical challenge. The evolution of supercoloniality is likely to involve informational constraints preventing nepotism6, although some positive relatedness may be maintained by cryptic kin structure39. Our results are relevant here: the initial drivers of low-relatedness cooperation are unlikely to have been either bet-hedging by risk-spreading at the expense of the expectation of inclusive fitness (Equation 1; Fig. 1d) or the reciprocity scenario proposed by Ref.5 (Fig. 1e). In principle, diminishing returns may initially have favoured partial diversion of altruism to more-distantly-related colonies. However, supercoloniality and primitively-eusocial cooperative drifting are not completely analogous. Supercoloniality may have been a relatively small step for ants that had already evolved high within-colony polygyny – and consequently reduced relatedness40 – for other reasons. Unlike primitively-eusocial wasps, the first step to explaining cooperative drifting in ants is explaining polygyny41.
Manipulating colony networks by adjusting worker-to-brood ratio (ψ) may offer tests of whether wasps make strategic adjustments to investments (y). Empirical studies are needed to identify whether host workers discern cooperative drifters and adjust acceptance thresholds (m) adaptively42,43 according to need. Future theoretical work could assess the tension between selfish and cooperative drifting in determining the acceptance of foreign workers. Wasps with high resource-holding potential may exploit the relaxation of nest boundaries to drift for direct fitness (e.g., joining dominance hierarchies on multiple nests to maximise chance of nest inheritance). Models of the mechanisms individual workers might use to distribute their effort would be useful, potentially inspired by resource-use models in foraging theory44.
Nonlinear payoffs exert strong effects on social evolution: diminishing returns can limit the tragedy of the commons45, promote polymorphic equilibria46, and increase sharing in reproductive skew games47. However, the extent to which diminishing returns shape investment patterns remains little quantified – despite clear theoretical predictions. A tempting explanation for divestment across recipients is that actors help different recipients in proportion to relatedness (an idea known as the ‘proportional altruism’ model48). This argument commits the ‘gamblers’ fallacy’49: instead, it is always best to invest in the single recipient who carries the highest inclusive fitness returns at any one time50. To explain altruism towards more-distant relatives, in the 1980s Altmann49, Weigel17, and Schulman and Rubenstein29 highlighted diminishing returns to investment by a single individual. Here, we have considered diminishing returns to investment by multiple individuals. In both cases, diminishing returns provide a simple explanation for helping multiple recipients, which awaits empirical study in many species. Our results indicate the power of nonlinear fitness effects to shape social organisation, and suggest that models of eusocial evolution should be extended to include neglected social interactions within colony networks.
Author contributions. PK, SS, and ANR planned field data collection, and PK and PB collected field data. PK and ADH conducted modelling. PK, NJW, and ANR conducted statistical analysis, and PK, SS, and ANR interpreted the results. PK drafted the manuscript and all authors contributed to its development.
Methods
Tables of notation and supplementary detail on models are available in the Supplementary Information, and supplementary figures are provided in the Extended Data.
1. Bet-hedging
We consider when an inclusive fitness maximising actor should divide its investments between separate recipients to minimise the risk that its investments will be lost12. Notation is summarized in Table S1 (see Supplementary Information). Following Grafen3, we start with the Price equation under uncertainty and treat the target of selection as an individual maximand. The expected change in allele frequency due to selection – where average reproductive success for the population is , and Ii is absolute inclusive fitness – is equal to the covariance over individuals i between the expectation of relative inclusive fitness and the individual’s genotype Gi
| 1.1 |
where expectations are taken across possible states of the population that may occur. The absolute inclusive fitness is the sum of all effects bijt of actor i on the absolute fitness of recipient j (including the actor itself) across each role t (i.e., ). For derivation of Equation 1.1, see the first term on the right-hand side of Eq. 6 in Grafen3. Under fitness additivity and frequency-independence, the quantity is considered to represent a maximand of organismal behaviour3: it is a target of selection (as it covaries with genotype) that is under the control of the actor since Ii is composed of the effects of the actor’s behaviours.
The expectation of a ratio of random variables can be approximated by the Taylor series expansion. The Taylor series is an acceptable approximation when does not rise to greater that 51. We expand the maximand to the second order as follows:
| 1.2 |
where denotes standard deviation over the states , and ρ denotes the correlation between Ii and . The division by does not affect the optimal decision, and so we focus on the terms in the brackets.
To make more explicit the quantity under a focal organism’s control, we can describe as q the vector of investment weights (the proportions of its total resource) that the individual chooses to place on different investments that affect the reproductive success of itself and other individuals. The expectation of the focal individual’s absolute inclusive fitness ( is given by , where is the vector of expected inclusive fitness payoffs from the different potential options (the expectation over the different states ). By convention, † denotes transpose. Likewise, the standard deviation of a focal individual’s absolute inclusive fitness appearing in Equation 1.2 () is given by , where C is the variance-covariance matrix of the payoffs over the states , and gives the variance (over the states ) of the individual’s absolute inclusive fitness.
The aim for the organism can then be expressed using the following maximand (echoing financial portfolios52):
| 1.3 |
where the sum of q is one. The coefficient of variation in population average reproductive success (v) is not affected by the organism’s choice of q. Whereas in economics, individuals have subjective risk aversions, ‘risk aversion’ in biology is imposed by the environment: a higher v makes individuals more averse to having an inclusive fitness investment portfolio that has correlated fluctuations with population average reproductive success. An environment can have high v or low v, and this is imposed on the organism. The bet-hedging hypothesis implies that an optimisation trade-off exists within q, balancing the expectation and the variance in inclusive fitness profit (measured in the absolute number of offspring-equivalents produced).
Equation 1.4 highlights that variance in inclusive fitness () only matters when the level of stochasticity v (i.e., the coefficient of variation in population average reproductive success ) and the correlation ρ are non-negligible. This is generally only true when there is environmental stochasticity that makes a genotype’s total reproductive success fluctuate in a correlated fashion between environmental states. For instance, there may be some distinct environmental states when one type of colony does worse, such as big colonies fail when there is a drought. However, this would require a genotype starting from a position of overinvesting workers in one type of colony, such that it may then be able to reduce its variance by diverting some effort towards a different type of colony that doesn’t fail in that environmental state.
The bet-hedging hypothesis proposed by Sumner et al.12 is based on hedging against individual risks to colonies: demographic stochasticity. In general, demographic stochasticity can only generate meaningful fluctuations in when population (or deme) size is very small53,54. Next, we illustrate the effect of population size, which we then plot in Fig. 1d of the main text.
To illustrate the bet-hedging hypothesis in a specific example, we switch to a neighbour-modulated perspective55. Notation is summarised in Table S2. We focus on the effects experienced by recipients due to the actions of related actors. Thus, instead of focusing on the expected relative inclusive fitness of an actor i, we focus on the expected relative fitness of a recipient j. The Taylor approximation allows us to write the condition for selection of a trait of interest in a population undergoing pure demographic stochasticity as:
| 1.4 |
since and under pure demographic stochasticity56
We consider the following scenario. Workers invest in colony reproductive success (where w j is the reproductive success of the colony’s queen) with linear returns w j=An j, where n j is the number of workers helping at queen j’s colony and A is a constant. After this investment period, queens are exposed to random catastrophe (such as a predation of the nest) with independent probability θ which reduces their reproductive success to a proportion k of its value. Workers must decide during the investment period whether to invest solely in their home colony, where the queen is the closest related queen, or divest some of their investment to neighbour colonies.
We assume that there are two sizes of colony with equal numbers of brood: colony type 1 and colony type 2. Type 1 and type 2 colonies have a high (n 1) and low (n 2, where 0 < n 2 < n 1) number of workers, respectively. For each genotype we let half the colonies be type 1 and half be type 2, and pair each type 1 colony with a type 2 colony. For simplicity, we assume a haploid asexual population (i.e., workers share their queen’s allele for the trait of interest). We ask whether workers on a type 1 colony should divest part of their investments to a type 2 colony in order to hedge against the risk of their investments on the home nest being lost to random colony failure. If workers divest from a type 1 colony, they are paired with a foreign queen on a type 2 colony identical at the focal locus with probability α or a random queen (who may or may not be identical at the focal locus) on a type 2 colony with probability 1−α. A mutant worker from a type 1 colony with divestment level y will expend a proportion y of its effort on the neighbouring type 2 colony and a proportion 1−y on its own colony. We assume a population monomorphic for a resident strategy .
The absolute fitness w 2 of a queen on an n 2 colony carrying a mutant allele y if no catastrophe occurs is:
| 1.5 |
where P is the frequency of mutant allele in the population. The absolute fitness w 1 of a queen on an n 1 colony carrying the mutant allele is as follows if no catastrophe occurs:
| 1.6 |
There are then four outcomes for any given queen:
| Starts with few workers (n 2) | Starts with many workers (n 1) | |
|---|---|---|
| No catastrophe occurs | w 2 | w 1 |
| Catastrophe occurs | kw 2 | kw 1 |
The probability of each outcome is:
| Starts with few workers (n 2) | Starts with many workers (n 1) | |
|---|---|---|
| No catastrophe occurs | ||
| Catastrophe occurs |
Accordingly, the variance of w over population states ω is:
| 1.7 |
where:
| 1.8 |
To ask if a small increase in the level of altruism divested to relatives () can invade, we evaluate the derivative of the approximation of expected relative fitness (which covaries with genetic value in Equation 1.5). We set this to equal to zero to find the candidate equilibria y*:
| 1.9 |
As y* is too complex to give intuition, we plot y* for a range of population sizes (N) and differences in relatedness between the home and partner colony in Fig. 1d of the main text (i.e., when ‘relative relatedness’ is one, there is no difference between a worker’s relatedness to the home colony and the partner colony). The region in which divestment to multiple relatives is favoured is very narrow.
2. Indirect reciprocity
In this section and the diminishing returns section below, we apply the Taylor-Frank method55 to a haplodiploid population, using the framework of Davies et al.22, where x is level of altruistic sterility, z is the sex ratio (proportion male), y is probability of drifting, and m is probability of accepting incoming drifters. An overview and further detail is given in Section 2 of the Supplementary Information, with notation in Table S1 and the consanguinity values for haplodiploids in Table S2.
We model the indirect reciprocity hypothesis for drifting between unrelated colonies proposed by Ref.5 in a haplodiploid population. Ref.5 argues that a colony’s ‘willingness to accept drifters’ (m) is an honest signal of its cooperative willingness to emit drifters, allowing the evolution of drifting in the absence of genealogical kinship. We follow Nonacs5 in letting m be the ‘tag’ used passively to determine whether to drift to a target colony: if the colony will let the worker in, it enters. Accordingly, we look for evolutionarily stable strategy, y* and m*.
We randomly match each colony with a local unrelated recipient colony. Capital letters denote the mean value of the trait in a social group. We assume that the probability with which females develop as sterile helpers is the same on all colonies (x). The following events occur:
Of helper females on a focal (‘home’) colony, a proportion Y f will be emitted to a recipient colony as drifters (i.e., Y f is the mean value of the drifting trait in the home colony). Of these, a proportion M r are on average accepted (since M r is the average level of willingness to accept drifters among members of the recipient colony that receives drifters from the focal colony). Any workers that attempt to drift but are rejected by the neighbour colony return to their home colony and work there.
Of helper females on a donor colony to the ‘home’ colony, a proportion Y d will be emitted to the home colony as drifters. Of these, a proportion M f are accepted.
To include ‘social heterosis’, we let help have the effect u on an unrelated partner colony and the effect a on the home colony. When u>a, workers can make a bigger contribution on an unrelated partner colony (having unrelated genotypes in the workforce amplifies productivity). When u<a, workers can make a bigger contribution on their own home colony (having unrelated genotypes in the workforce impairs productivity).
Brood developing on the home colony receive h units of help:
| 2.1 |
In this section, we assume linear returns to cooperation, such that K=h, where K is a brood member’s probability of successfully developing and h is the help received during its development (see Supplementary Information for table of notation).
In Case A, we show that the result of Ref.5 can be recovered in the improbable scenario where workers that accept incoming drifters are unable to stop themselves from drifting in turn. In Case B, we show that cooperative drifting does not invade when this constraint is removed.
2.1. Case A: Constrained pleiotropy between emission and acceptance of drifters
Here, we force m and y into pleiotropy, so that an increase in the trait value of one is accompanied by an increase in the trait value of the other. We assume , , and , where β is a constant (β>0). Substituted into Equation 2.1:
| 2.2 |
In the Supplementary Information, we provide the background to the relative fitness functions. The relative fitness of both male and female brood is:
| 2.3 |
In the absence of kinship between colonies (as assumed by Ref.5), selection favours a small increase in drifting y when it increases the fitness of the home brood (sisters and brothers on the home colony), which occurs when:
| 2.4 |
where is the class reproductive value for females, which for haplodiploids is 2/3, and is the class reproductive value for males, which for haplodiploids is 1/3. The terms p sis and p bro are haplodiploid consanguinities to sisters and brothers, respectively, which are 3/8 and 1/4. Evaluating with both Y f and Y r at the population average drifting level , the effect on the fitness of female and male brood in the home nest due to a small increase in drifting by workers from the home nest is:
| 2.5 |
Substituting the relevant consanguinities (p sis and p bro) and Equation 2.5 into the condition for selection on drifting (Equation 2.4) gives:
| 2.6 |
Since has a positive real value, drifting is favoured in this scenario if:
| 2.7 |
Accordingly, cooperative drifting can invade under the hypothesis proposed by Ref.5 when increasing the emission of drifters (y>0) to non-relatives is the unavoidable price of increasing the acceptance of drifters (m>0) from non-relatives. Due to a constraint forcing pleiotropy between the traits (β), it is worth paying the price of losing home workers when the incoming non-relatives increase the colony’s productivity more than home workers (through social heterosis, u>a).
2.2. Case B: Absence of pleiotropy between emission and acceptance of drifters
We now remove the assumption of pleiotropy, so that m and y are treated independently. Again assuming that drifters would be unrelated to brood they care for on partner nests as in Ref.5, the condition for selection to favour a small increase in drifting is the same as Equation 2.4. The relative fitness of male and female brood is now:
| 2.8 |
Evaluating again with both Y f and Y r at the population average drifting level , and with M f and M r at the population average acceptance level , the effect on the fitness of female and male brood in the home nest due to a small increase in drifting by workers on the home nest is:
| 2.9 |
As long as a recipient colony does not reject incoming drifters (), a small increase in drifting by workers leads to a loss in relative fitness for their sibling brood. Again substituting the relevant consanguinities (p sis and p bro) and Equation 2.9 into the condition for selection on drifting (Equation 2.4) gives:
| 2.10 |
Since has a positive real value, drifting is favoured if:
| 2.11 |
That is, if home workers are actively deleterious to the home colony’s productivity. Thus if workers provide any benefit to their home colony (a>0), they should not be emitted as drifters to unrelated colonies.
Selection favours an increase in acceptance (m) of any incoming drifters from other colonies when:
| 2.12 |
A small increase by workers in acceptance to the home nest of incoming drifters increases the relative fitness of their brother and sister brood on the home nest:
| 2.13 |
Substituting Equation 2.13 into Equation 2.12 gives the condition for an increase in acceptance (m):
| 2.14 |
Assuming incoming drifters would contribute positively to productivity (u>0), has a positive real value, and acceptance is favoured if:
| 2.15 |
Selection favours acceptance (m>0) whenever drifters are being emitted by other colonies (). Whilst selection favours the minimisation of drifting to unrelated colonies in all circumstances in which workers are helpful (Equation 2.15), it favours maximum acceptance m of foreign cooperative drifters (i.e., free-riding) (Equation 2.11). Accordingly, willingness to accept drifters (higher m) is not an honest signal of willingness to emit drifters (higher y). In the absence of complex and implausible social insect colony versions of the stabilising mechanisms known to sustain indirect reciprocity (including between-colony monitoring of whole-colony reputation, uncheatable physical greenbeards, or punishment of free-riding colonies by cooperative colonies), the proposed effect of indirect reciprocity5 cannot drive drifting. We plot the direction of selection in Fig. 1e of the main text.
Finally, we note that in principle ‘social heterosis’ (u>a) between related nests could drive drifting by kin selection, rather than by indirect reciprocity: a large benefit that could be provided to distant kin would compensate for their more distant relatedness, and so satisfy Hamilton’s rule. However, this would require acutely strong social heterosis at levels unknown in any social insect: high synergies between genotypes would need to ensure that halving relatedness to recipients would more than double the benefit a worker can provide.
3. Diminishing returns
We consider a situation in which colonies differ in their worker-to-brood ratio ψ, in the range 0<ψ≤1. For simplicity, we consider neighbour colonies with equal absolute brood numbers. Variation in worker-to-brood ratio can arise for any reason. For instance, Polistes canadensis colonies show considerable variation in worker number for a given brood size (as shown in the horizontal range of the scatter-points of Fig. 3 in the main text), often through chance worker mortality (estimated at 7% per day12). We ask when workers on a home colony with ψ should invest in a partner colony that has a proportion g<1 of worker-to-brood ratio of the home colony. The diminishing returns hypothesis predicts that workers should not invest in other colonies, despite ψ variation, when the returns from cooperation are linear: the increment in the payoffs of altruism is the same regardless of ψ. When there are diminishing returns to cooperation, however, a worker on a home colony with high ψ may experience weaker indirect fitness returns on its home colony than on a neighbour colony.
We assume that ψ variation between colonies occurs unpredictably from the perspective of an individual. Accordingly, wasps are blind to their colony type when deciding whether to pursue altruistic sterility (worker phenotype) or reproduction. Let the sex ratio (z) and proportion of females that are sterile altruists (x) be common to all nests. We assume that the partner colony will emit no drifters and ask what the equilibrium level of drifting will be from the home colony to the partner colony. The average level of drifting y from the home colony to the partner colony is Y. Both y and Y are evaluated at population average value .
We consider the extent of drifting that should evolve between two types of nest (‘1’ and ‘2’), which differ in their worker-to-brood ratio (ψ). Using the framework of Davies et al.22 (described in the Supplementary Information), we let the absolute fitnesses of focal female brood on the home type 1 colony (subscript ‘1’) and the partner type 2 colony (subscript ‘2’) respectively be:
| 3.1 |
| 3.2 |
The rate of producing reproductives on a home colony of type s is (see Supplementary Information for details). The total help received by brood on each colony type is:
| 3.3 |
| 3.4 |
The population average levels of help on colonies of each type in the population:
| 3.5 |
| 3.6 |
The population average relative fitnesses on each nest type, for both male and female brood, assuming colony types 1 and 2 are equally frequent in the population, are (Supplementary Information):
| 3.7 |
| 3.8 |
where is the population average value of K s for colonies of type s.
As above (Equation 2.4), let be the class reproductive value for females (2/3). Let be the class reproductive value for males (1/3). Selection favours an increase in cooperative drifting from nest type 1 to nest type 2 (y) when the net effect on all potentially-affected parties (sisters, brothers, partner-colony female brood, and partner-colony male brood) leads to an expected increase in the success of a mutant allele for drifting (we assume no effect on self fitness, since drifters are already committed to being behaviourally-sterile helpers):
| 3.9 |
with traits evaluated at their population average values (), and where is the devaluation in consanguinity to female brood on the partner colony (relative to sisters on the home colony) and is the devaluation in consanguinity to male brood on the partner colony (relative to brothers on the home colony). Although we are focusing on scenarios in which a worker’s consanguinity to brood is lower on the partner colony than on the home colony, and hence ‘devalued’ (, <1), there can also be scenarios in which a worker is more consanguineous with brood on the partner colony, which may only apply to one sex. For instance, nephews are more consanguineous to a female than brothers are (p nephew= 3/8 but p bro=1/4). If the partner-colony male brood are nephews, would be greater than 1. If the partner-colony female brood are nieces, remains below 1 (since p niece=3/16 but p sis=3/8).
A small increase in drifting (Y) by workers from the home type 1 nest leads to a loss of relative fitness for the workers’ sibling brood on their home nest:
| 3.10 |
A small increase in drifting (Y) by workers from the home type 1 nest leads to an increase in relative fitness for the related brood on the partner type 2 nest to which they drift:
| 3.11 |
Substituting Equations 3.10 and 3.11 into Inequality 3.9, and dividing both sides by , gives the condition for selection to favour a small increase in drifting:
| 3.12 |
which is Inequality 2 in the main text.
To find candidate evolutionarily stable strategies (ESS) for drifting (y*), we set the left and right sides of Inequality 3.12 equal to one another, and rearrange for y. The ESS level of drifting is given by:
| 3.13 |
which is Equation 3 in the main text (where, for simplicity, we assume that consanguinity to male and female brood is devalued by the same proportion;==d). Higher levels of relatedness (higher and ) and stronger diminishing returns (higher T) select for higher levels of drifting y(*) at equilibrium (Extended Data 1). We plot the equilibria at illustrative values in Fig. 2f of the main text. In Extended Data 2, we plot the candidate equilibria at different values of sex ratio z and female helping x.
4. Polistes canadensis payoffs
To obtain empirical measures of productivity in Polistes canadensis, we tracked a cohort of developing brood on 91 free-living post-emergence colonies over a 56-day period (from 14th June to 8th August 2016). Colonies were clustered in six aggregations on the north coast of Panamá (15.2 ± 7.7 colonies per aggregation, mean ± S.D.). Five aggregations were in clearings between lowland tropical forest and the Panama Canal (former US Army Base Fort Sherman, San Lorenzo National Park, Colón Province) and one aggregation was in a clearing in a mangrove swamp (Galeta Point, Colón Province). We use an observational approach to quantify productivity. Key parameters of brood-rearing can be quantified effectively in unmanipulated colonies, including natural rates of stochastic failure, predation, parasitism, queen turnover, workforce fluctuations, and male production. Associations between brood transition rates and workforce size are correlational, and so we view our results as plausible ranges within which causal effects can exist.
To measure the impact of workers at different developmental states, we split brood into stereotypical categories in a sequence. Each category, and its notation, is listed in Extended Data 3. We examined each brood cell at 5-day intervals, using a ladder to access colonies and a flashlight to illuminate each cell. A small number of observations were made on the following morning due to issues with field site access. The current classification of the brood cell was dictated to a second observer, who recorded it on a hexagonal grid of the nest. Accordingly, brood classification was done by a single observer blind to the previous state of the cell.
We censused adult group size by recording total adult numbers at night (8 pm–11 pm, 6–7 censuses per colony across the monitoring period). We used a red light (which wasps are unable to see) to avoid disturbance. Nests that were difficult to observe were counted multiply on a given night and averages taken. A small number of males emerged and stayed on nests. Adult males observed in daylight surveys during the brood counts on 5-day intervals were used to interpolate male number through time; otherwise, males were assumed to be absent. Female number (henceforth, ‘group size’) during each 5-day interval was defined as interpolated total number of adults minus interpolated male number. We assumed that any changes in group size between night-censuses occur gradually without sudden jumps, to avoid imposing artificial step changes in the model. We therefore estimated group size during each interval as the mean (across 5 days) of the fitted group sizes generate by a cubic spline interpolation through the night-censuses. For 5-day brood-observation intervals in which the first night census occurred within 1 day of the beginning of the interval, we allowed a limited extrapolation of 1 day in order to approximate mean group size over the 5-day interval. All intervals that would require any other extrapolation of group size were excluded from the analysis below in which group size is used as a predictor. To obtain estimates of the payoff rates, we fit a Markov model (shown in Fig. 3) to the brood development data, asking how colony productivity changes in association with different worker and brood numbers.
4.1. Statistical methods
The (relatedness-weighted) marginal effect of a worker on the development time of a larva is an incomplete measure of indirect fitness payoff. This is because Polistes nests experience considerable individual brood death12, which returns the cell to the start of the developmental process (once the queen has redeposited an egg). A worker’s major contribution might be to prevent inefficiency by minimising the rate of brood death. To accommodate both effects, we therefore analysed brood development as a Markov model, where the target parameter for inference is the expected time for a brood cell to produce a new adult (‘time to absorption’ of the Markov model57). The cell may cycle through repeat deaths before finally producing an adult. We treated the Markov transition matrix as a function of the predictor variables worker number, worker-to-brood ratio, brood-cell emptiness, and interactions. To estimate the transition matrix, we used Bayesian mixed models with colony as a random effect. Using the resulting estimate of the ‘time to absorption’ for P. canadensis colonies of different worker and brood sizes, we then obtained the predicted colony productivity rate, defined as the expected number of new adults produced per unit time. Because we are interested in the marginal effect of each additional worker on brood production, we took as an estimate of Hamiltonian benefit B the partial derivative of this rate with respect to worker number, evaluated at the point in demographic parameter space characterising any focal colony.
In principle, workers absconding due to a colony entering the declining phase and productivity falling might generate the appearance of a decline in worker number causing a decline in productivity, whilst in reality the decline in productivity caused the decline in worker number. To mitigate this as far as is possible, we include brood-cell emptiness as a measure of colony state and allow for its interactions.
Because (1) brood states are categorical and (2) longitudinal data were collected in discrete time steps, we give a multinomial likelihood for the number of transitions observed from each development state i into each state j, which provides information on the probability of a brood transition from developmental state i to state j. We model the number of transitions (defined over a 5-day interval) where the self-transition provides the reference category () and all other transitions are described by log-linear functions of the predictors x p in the vector x (i.e., ):
| 4.1 |
The predictors include random effects for colony ID (defined below, Equation 4.3). The transitions are the entries in the following matrix:
State 1 is egg, states 2-6 are larval states, state 7 is pupa, state 8 is adult (successful pupation), and state 9 is death during development. The final two rows, adulthood (8) and death (9), are absorbing.
The model is solved in discrete time because brood were observed at intervals. Accordingly, brood are free to transition from one state to a state further downstream than the next step in the sequence; they have passed through the transitional states during the 5-day window. Some transitions are not biologically possible during a 5-day window (such as 1 to 6 or 3 to 7), so are not permitted in the Markov transition matrix (represented by a dash). We present two models with increasing complexity. ‘Model 1’ focuses on the baseline transition rates (i.e., intercepts and random effects only) for the complete dataset of observed transitions between live-brood-containing cells, which allows us to estimate the baseline productivity rate of P. canadensis colonies (Fig. 2c of the main text).
Next, we present an indicator-variable-selection model (‘Model 2’) to identify the marginal change in productivity associated with each additional worker at different points in the parameter space typifying P. canadensis colonies. We exclude all colony-observations lying outside of the night-census range, and a small number of colony observations with fewer than 10 (2-to-6 state) larvae. These steps focus the payoff model onto a core dataset of 471 colony observations on 85 colonies, comprising 123,116 observed brood transitions (from the total dataset of 168,811 observed brood transitions on 1,027 colony observations on 91 colonies). The model parameters were estimated using a Bayesian approach computed using Markov chain Monte Carlo (MCMC) simulation in JAGS (using rJAGS58 in R). We confirmed MCMC convergence using potential scale reduction factors (PSRF; ) for five chains (1.1 for the large majority of parameters). After an adaptation phase of 5,000 iterations and a burn-in of 1,000 iterations, we sampled parameter slope values for 15,000 iterations with a thinning of 4. For the posterior predictive model (described below) to generate the inference about payoff rates using simulated input values for colony worker and brood numbers, we continued running MCMC sampling for a further 10,000 iterations with a thinning of 10.
4.2. Within and between effects
We use a ‘within-between’ formulation59, which follows the ‘de-meaning’ procedure suggested by Mundlak60. We split each time-varying predictor (i.e., predictors whose values can differ between different colony-observations within the same colony) into a ‘between-colony’ component and a ‘within-colony’ component. The between-colony component is the mean value of the relevant predictor for the focal colony C (across its colony-observations). The within-colony component is the deviation from this mean in any one colony-observation.
We denote the slope dealing with a between-colony component with the subscript ‘b’ (e.g., ) and the slope dealing with a within-colony component with the subscript ‘w’ (e.g., ). We also permit xworkers to interact with the two other predictors: denotes an interaction between xempty and xworkers, and denotes an interaction between xratio and xworkers. We allow these interactions at both the between-colony and within-colony levels. The random intercept for the transition i→j for colony C is . Thus, the fully saturated model for the transition from state i to state j (subject to pruning of variables during the indicator-variable-selection process detailed in the next section) is:
| 4.3 |
The random effect of colony ID is:
| 4.4 |
where the precision τ is drawn from a gamma distribution:
| 4.5 |
4.3. Model averaging
In an indicator-variable-selection procedure, we construct the saturated model (Equation 4.3), and introduce a series of binary indicator variables that ‘switch on’ or ‘switch off’ each predictor throughout MCMC61. The duration of MCMC time with each coefficient switched on is proportional to the coefficient’s marginal likelihood of contribution. For each predictor p’s regression slope β(ij,p) (within the vector β(ij,p) in Equation 4.1), we can therefore annex a binary coefficient g(ij,p) that switches between 0 and 1, and then track the mean of the posterior distribution for g(ij,p). The closer this mean is to 1, the more frequently the corresponding regression slope β(ij,p) is retained in the model.
For the random effects, we used independent Bernoulli priors for g(ij,p) to allow the MCMC sampler to turn the specific random effect on or off directly. For other predictors, we used a product of the independent priors for g(ij,p) and β(ij,p) 62:
| 4.6 |
Following Ref.62, we used normal priors for the conditional distribution of β(ij,p) given g(ij,p). β(ij,p) is indistinguishable from zero when g(ij,p) switches the predictor off. We model the indicators as Bernoulli random variables with a 50:50 prior (g(ij,p) ~ Bernoulli(0.5)), representing our starting point of indifference between either including or dropping the slope β(ij,p). For interactions, we set a prior of Bernouilli(0.2). To accommodate the within-between formulation, we apply the indicator variables to the whole fixed effect predictor: the predictor cannot be turned on for one component (e.g., the between-colony component) and switched off for the other component (e.g., the within-colony component).
The effects on the transition probabilities whose 95% credible intervals do not overlap zero are shown in Extended Data 3.
4.4. Model checking: residual deviance
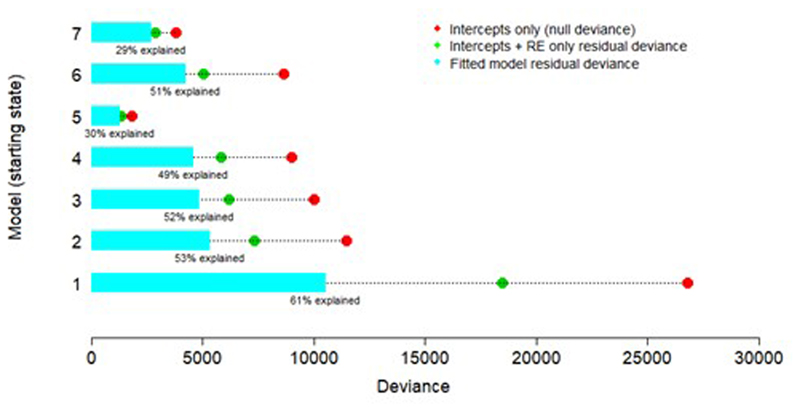
The residual deviances Di for each multinomial model corresponding to the seven initial states i are given by summing over the residual deviance contributions for each colony-observation k, where Ekij is the observed number of transitions from state i to state j for colony-observation k and is the corresponding expected number of transitions from the fitted model63:
| 4.7 |
The deviance explained by the fixed effects is presented in Extended Data Fig. S6.
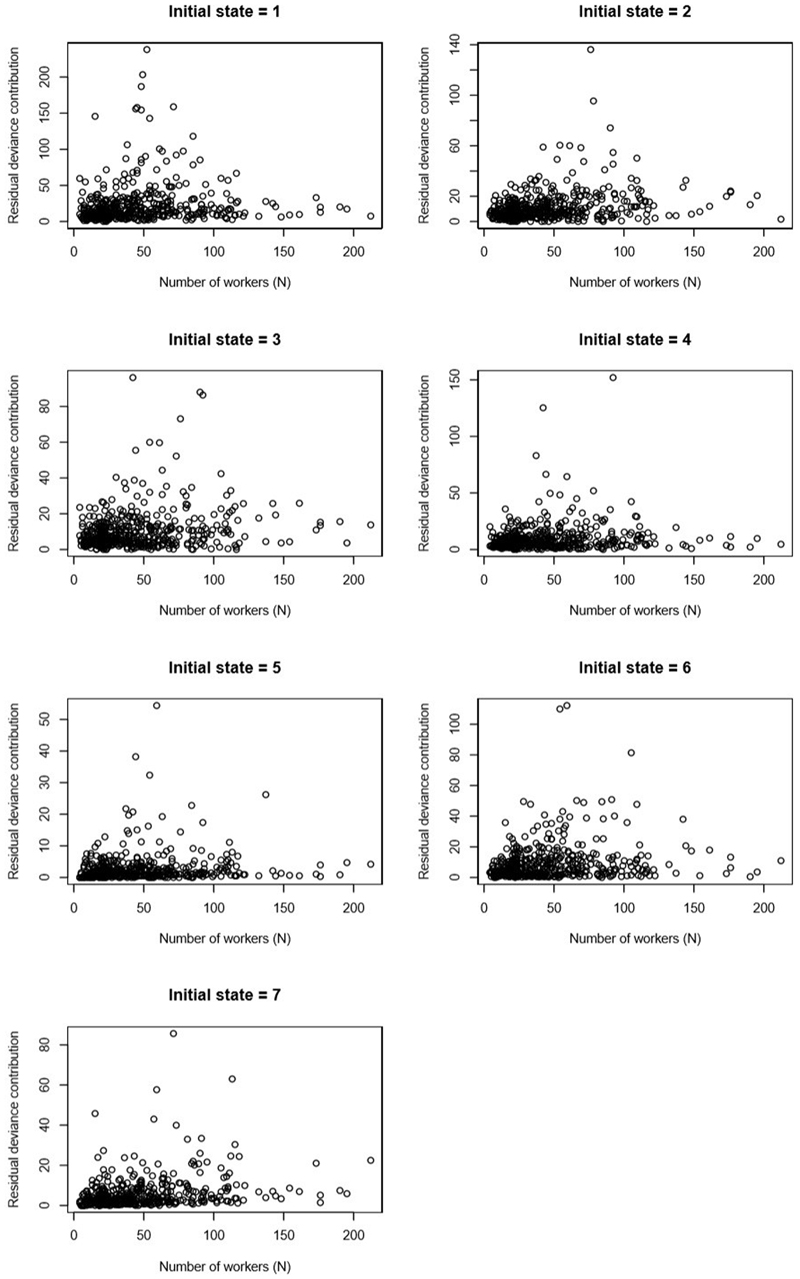
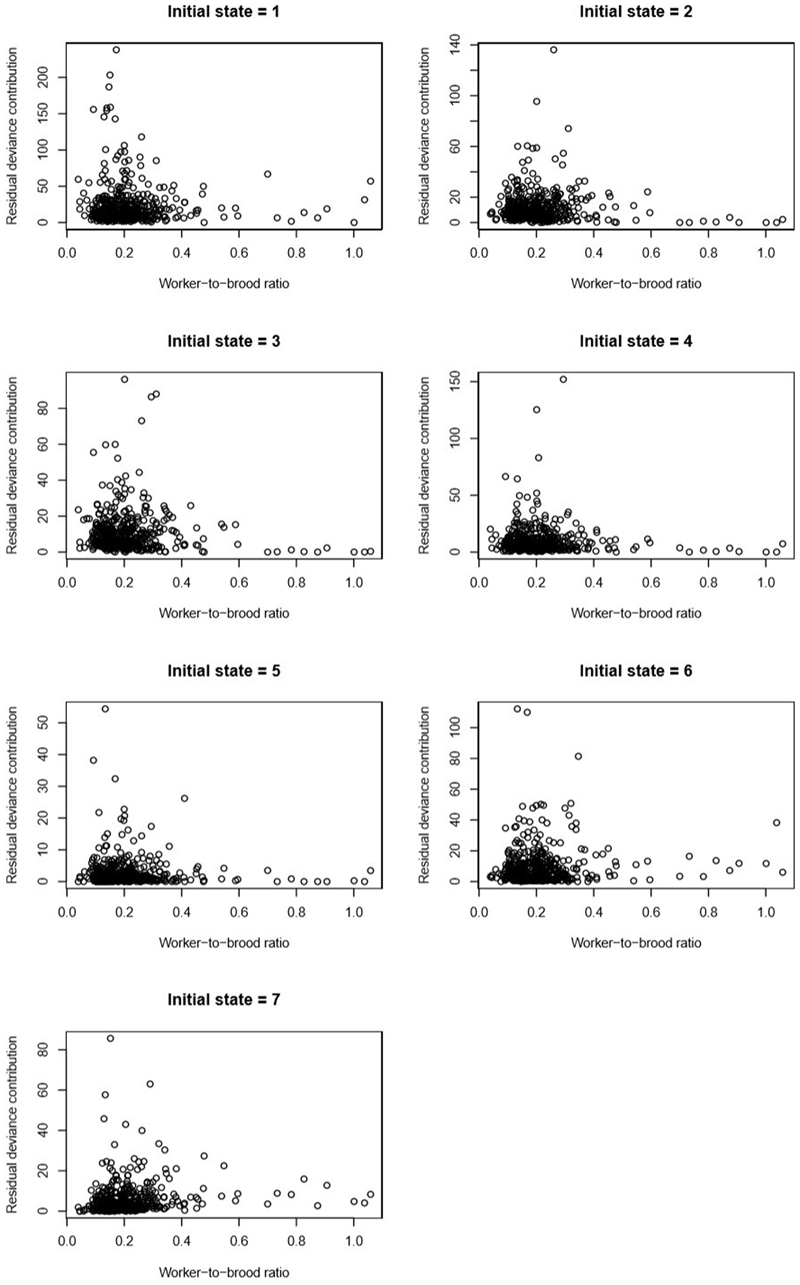
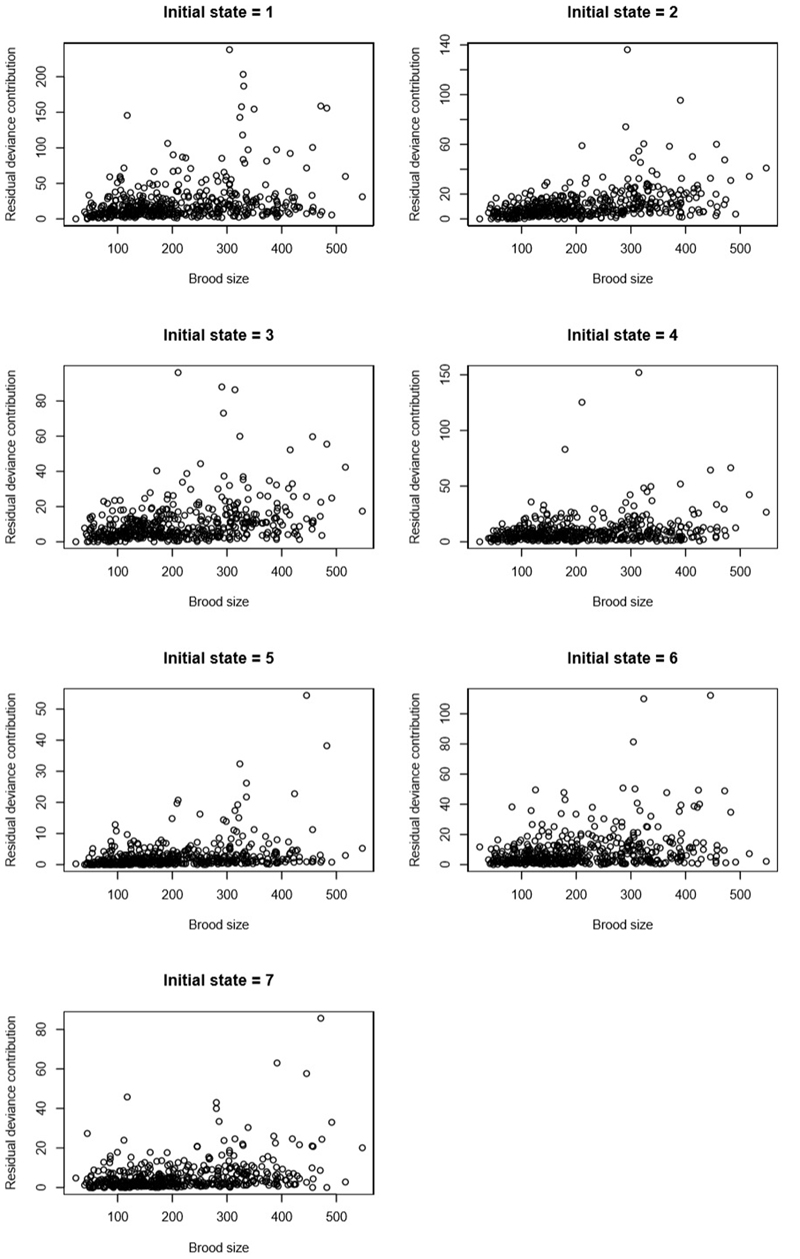
In Extended Data 6–8, we plot residual deviance contributions for each colony-observation against predictors. There is no evidence of structure in the plots: most colony-observations fit relatively well, but some colony-observations exhibit very high deviance. In Supplementary Information Table S3, we provide the mean residual deviances for each of the seven starting state models (residual deviances divided by 471ni, where ni is the number of states into which a cell can transition from starting state i, and 471 is the number of colony-observations. The models for starting states 1 and 6 have high mean residual deviances. Inspection of potential outlier colony-observations (colony-observations with unusually high residual deviance contributions) suggests that these high residual deviances may be partly reflective of episodes of unusually high mortality on colonies, with substantial death of large larvae (starting state 6) and substantial cannibalism of eggs (starting state 1). Future models focusing on predictors of severe mortality episodes and other on-colony dynamics may be required to reduce residual deviance in these scenarios.
4.5. Expected time to adulthood
To calculate the worker effect on the transition matrix, controlling for oviposition rate, we submit all estimated transition-to-death probabilities () to the prediction matrices as transitions to new eggs. This isolates the potential effect of workers (as opposed to the egg-layer) to obtain per-cell efficiency without the confounding effect of variation between queens in the rate at which replacement eggs are laid following the death of larvae.
The expected time to absorption (‘expected mean first passage time’ in Fig. 3a of the main text), in which a brood cell transitions from egg to adulthood () via intermediate states, can be obtained using the linear algebra for a discrete Markov process via the ‘fundamental matrix’ method of Kemeny and Snell57. Following Grinstead & Snell64, we obtain the fundamental matrix N by inverting the matrix It−Q, where It is the identity matrix for the transient states and Q is a square matrix of transition probabilities between each transient brood state with length equal to the number of transient states (i.e., all states apart from adulthood and death). Accordingly:
| 4.8 |
We solve for N for each of the recorded iterations in MCMC separately, in order to sample the posterior predictive distribution using simulated colonies across the parameter space of worker and brood number, with the number of empty cells set to the population-average value. The element n(i,j) in N is the frequency with which the brood cell is expected to visit state j given a current state i. The vector t of times to absorption (using the values at any one recorded iteration of MCMC) is then:
| 4.9 |
where 1 is a column vector of 1s. The ith element of t is the duration (in step numbers) from state i to successful production of a new adult.
To obtain the It−Q matrix within MCMC, we employ the between-colony effects, which provide a measure of the quantities of interest (workforce size and worker-to-brood ratio) that abstracts away extraneous between-colony variation (in the random intercepts terms ?_(ij,C)) and within-colony variation that is likely to be confounded by colony ageing (in the within-colony effects). We then derive the predicted whole-colony rate of brood production by converting the per-cell time to absorption to a productivity rate per unit time and scaling this rate by the brood cohort size on each colony (using the total number of eggs to large larvae, states 1–6, a measure of cohort size).
In the main text, we plot the expected mean first passage time in Fig. 3a and the estimated whole-colony productivity in Fig. 3c.
4.6. Indirect fitness payoff calculation
Extracting predictions at the population mean level of cell emptiness (Extended Data 9), we plot the posterior predictive distribution for whole-colony productivity using the 1,000 simulated points (in Mathematica). That is, to extract the shape of the posterior predictive distribution, we fit the smooth interpolation to 1,000 closely-packed samples monitored in MCMC.
The diminishing returns hypothesis predicts that a worker can maximise inclusive fitness by shifting from a home colony 1 with worker-to-brood ratio ψ1 and brood number t1 (where she is related to the brood by r1) to a partner colony 2 with worker-to-brood ratio ψ2 and brood number t2 (where she is related to the brood by r2):
| 4.10 |
where she has a larger effect on the production rate w of offspring-equivalents by changing ψ2 on 2 than she would have by changing ψ1 on 1. The end result of the Markov model is a model of these partial derivatives (estimates of the payoffs driving the benefit term in Hamilton’s rule) for colonies of different worker numbers and brood numbers (Fig. 3e in the main text).
5. Individual-based simulation
To simulate the spatial invasion of cooperative drifting under nonlinear returns to cooperation, we consider the evolution of a decision rule in a haplodiploid population on a square lattice in a spatially explicit individual-based simulation. Nodes represent colony sites. Each colony has a single monogamous reproductive pair of a diploid queen and haploid drone. We simulate a death–birth updating process: each time-step, 10% of nodes are selected, and their resident colonies die. A new colony at each updating node is then founded by a new queen drawn from within the dispersal range for females, with probabilities proportional to the payoffs of each of the surrounding eight colonies. We consider two discrete conditions for the female dispersal range: (1) female philopatry (local dispersal within the Moore neighbourhood [the surrounding eight nodes]); and (2) global female dispersal (dispersal from any distance on the lattice with equal probability).
Drones are selected from anywhere in the lattice37, with probabilities proportional to the queen’s fitness at each colony on the lattice. Colonies produce female workers as they age: every three time-steps, they gain a unit of workers, until reaching a maximum number of units (set to 10 in the main text results; Fig. 4). Queen fitness w (production of reproductively destined brood) is determined by:
| 5.1 |
where h is the total worker effort received by the colony rescaled between 0 (no workers) and 1 (maximum number of workers possible). We consider two discrete conditions for diminishing returns: no diminishing returns (T=1) and moderate diminishing returns (T=3).
Each worker has a finite amount of help to distribute. We consider selection on a single locus y, which is the probability of drifting by workers on colonies above a threshold worker number (5 in Fig. 4). Drifter help is distributed at random within each worker’s local helping window. We consider two discrete conditions for the size of the helping window: (1) workers help indiscriminately within the local Moore neighbourhood; (2) workers restrict the helping window only to colonies with immediate genealogical ties to the home colony (defined as the parent colony from which the mother queen came or a daughter colony on which a sister is queen).
Main Text Fig. 4 summarises the role of local cooperation.
Additional information
Additional detail on methods is provided in the Supplementary Information, and statistical and simulation code is provided in the electronic material. Additional figures are provided in Extended Data.
Extended Data
Extended Data Figure 1. Diminishing returns can allow the invasion of cooperative drifting.
(a)The parameter captures the level of diminishing returns in the model. (b)Candidate equilibrium levels of drifting predicted by Equation 3 of the main text, for illustrative values: d =0.5, x =0.75, φ =1, z = 0.25
Extended Data Figure 2. Candidate equilibrium drifting levels from a colony with φ 1 =1.
We assume a monomorphic sex ratio z̄ and level of female helping x̄ common to all colonies. Diminishing returns become more likely drivers of cooperative drifting as the level of helping rises (top left corner). m̄ = 1, φ 1 =1, d♀ = d♂ = 0.5.
Extended Data Figure 3. Repeat observations (n = 257,867) were made of all brood cells on 91 post-emergence colonies over a 56-day period, recording eight developmental states, empty cells, and death due to parasitism (sarcophagid flies and ichneumonid wasps).
Brood pass through a clear developmental sequence of changing size, colour, and mouthpart complexity, which allows categorisation of larvae into stereotyped morphological categories on their transition from egg to pupa. Photograph of P. canadensis nest: J. Pickering (1976) © www.discoverlife.org.
Extended Data Figure 4. Main effects on the probability of transitions in the Markov model of wasp development.
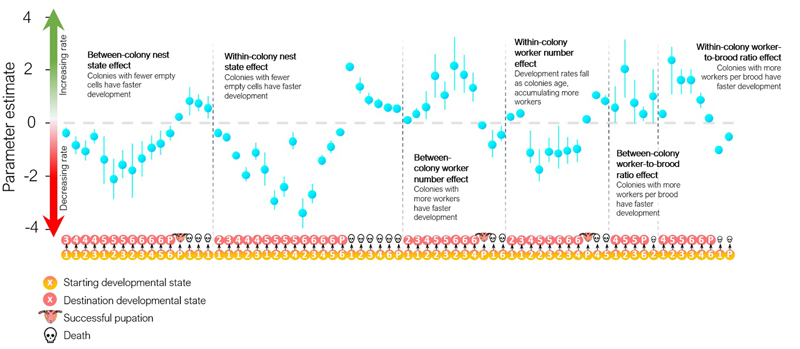
Transitions corresponding to steps through the Markov model states (represented in Fig. 2b of the main text) are shown along the horizontal axis. For instance, the first transition on the left is 1?3, and the effect is negative (below the dashed line): accordingly, the model fits a negative association (at a between-colony level) between nest emptiness (‘nest state effect’) and the probability that an individual egg (state 1) transitions to larval state 3 in a 5-day interval.Only main effects whose 95% credible intervals do not overlap zero are shown. In the main text, we focus on whether increased worker number and/or worker-to-brood ratio is associated with higher productivity. When considering between-colony variation (‘between-colony worker number effect’ in the figure), worker number increases brood development pace and reduces brood death. Higher worker-to-brood ratios (‘between-colony worker-to-brood ratio effect’ in the figure) increase brood developmental pace.
Extended Data Figure 5. Posterior mean of the total residual deviance.
Deviance explained is the posterior mean of the total residual deviance of the fitted model as a percentage of the null posterior mean residual deviance (for an intercepts-only model). There are seven models, corresponding to the seven starting states.
Extended Data Figure 6.
Residual deviance contributions by each 5-day colony-observation, plotted against the predictor 'worker number' (x workers).
Extended Data Figure 7.
Residual deviance contributions by each 5-day colony-observation, plotted against the predictor 'worker-to-brood ratio' (x ratio).
Extended Data Figure 8.
Residual deviance contributions by each 5-day colony-observation, plotted against the predictor 'brood number' (x brood).
Extended Data Figure 9.
Predictions for between-colony effects plotted in Fig. 3 in the main text take the mean proportion emptiness across colony-observations (dashed red line).
Supplementary Material
Acknowledgements
We thank Christina Riehl, Petri Rautiala, and an anonymous reviewer for constructive reviews during peer review. PK was funded by a Smithsonian Tropical Research Institute (STRI) Short-Term Fellowship (hosted by Dr William Wcislo), the National Geographic Society (GEF-NE 145-15), and a European Research Council Grant to ANR (award no. 682253). SS was funded by the Natural Environmental Research Council (NE/M012913/2). ADH was funded by the Natural Environment Research Council (NE/L011921/1). ANR was funded by a European Research Council Consolidator Grant (award no. 682253). Simulations were run on the University of Bristol’s high-performance computing facility, BlueCrystal. B. Wharam and A. C. Chadwick assisted with data entry.We are very grateful for the support of the Panamanian authorities for this project; data were collected in accordance with Panamanian law under a Ministerio del Ambiente research permit (SE/A-46-16) and Ministerio de Economia y Finanzas authorisation for field site access (024-2016).
Footnotes
Competing interest statement.
The authors declare no competing interests.
Data availability
The transitions data for P. canadensis is available as supplementary information.
Code availability
The statistical code and individual-based simulation code are both available as supplementary information.
References
- 1.Gardner A, West SA, Wild G. The genetical theory of kin selection. J Evol Biol. 2011;24:1020–1043. doi: 10.1111/j.1420-9101.2011.02236.x. [DOI] [PubMed] [Google Scholar]
- 2.Gardner A. The purpose of adaptation. Interface Focus. 2017;7 doi: 10.1098/rsfs.2017.0005. 20170005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Grafen A. Optimization of inclusive fitness. J Theor Biol. 2006;238:541–563. doi: 10.1016/j.jtbi.2005.06.009. [DOI] [PubMed] [Google Scholar]
- 4.Bourke AFG. The validity and value of inclusive fitness theory. Proc R Soc B Biol Sci. 2011;278:3313–3320. doi: 10.1098/rspb.2011.1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nonacs P. Go high or go low? Adaptive evolution of high and low relatedness societies in social Hymenoptera. Front Ecol Evol. 2017;5:87. [Google Scholar]
- 6.Helanterä H, Strassmann JE, Carrillo J, Queller DC. Unicolonial ants: where do they come from, what are they and where are they going? Trends Ecol Evol. 2009;24:341–349. doi: 10.1016/j.tree.2009.01.013. [DOI] [PubMed] [Google Scholar]
- 7.Hamilton WD. The genetical evolution of social behaviour. II. J Theor Biol. 1964;7:17–52. doi: 10.1016/0022-5193(64)90039-6. [DOI] [PubMed] [Google Scholar]
- 8.Queller DC, Strassmann JE. The many selves of social insects. Science. 2002;296:311–313. doi: 10.1126/science.1070671. [DOI] [PubMed] [Google Scholar]
- 9.Tsuchida K, Itô Y. Internidal drifting and dominance behaviour in Polistes jadwigae Dalla Torre workers (Hymenoptera: Vespidae) J Ethol. 1987;5:83–85. [Google Scholar]
- 10.Page R, Post D, Metcalf R. Satellite nests, early males, and plasticity of reproductive behavior in a paper wasp. Am Nat. 1989;134:731–748. [Google Scholar]
- 11.Pickering J. PhD Thesis. Harvard University; Cambridge, Massachusetts: 1980. Sex ratio, social behaviour, and ecology in Polistes (Hymenoptera, Vespidae), Pachysomoides (Hymenoptera, Ichneumonidae) and Plasmodium (Protozoa, Haemosporida) [Google Scholar]
- 12.Sumner S, Lucas E, Barker J, Isaac N. Radio-tagging technology reveals extreme nest-drifting behavior in a eusocial insect. Curr Biol. 2007;17:140–145. doi: 10.1016/j.cub.2006.11.064. [DOI] [PubMed] [Google Scholar]
- 13.Grinsted L, Field J. Market forces influence helping behaviour in cooperatively breeding paper wasps. Nat Commun. 2017;8:1–8. doi: 10.1038/ncomms13750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beekman M, Oldroyd BP. When workers disunite: intraspecific parasitism by eusocial bees. Annu Rev Entomol. 2008;53:19–37. doi: 10.1146/annurev.ento.53.103106.093515. [DOI] [PubMed] [Google Scholar]
- 15.Gadagkar R. Origin and evolution of eusociality: a perspective from studying primitively eusocial wasps. J Genet. 1990;69:113–125. [Google Scholar]
- 16.Nonacs P, Kapheim KM. Social heterosis and the maintenance of genetic diversity. J Evol Biol. 2007;20:2253–2265. doi: 10.1111/j.1420-9101.2007.01418.x. [DOI] [PubMed] [Google Scholar]
- 17.Weigel RM. The distribution of altruism among kin: a mathematical model. Am Nat. 1981;118:191–201. [Google Scholar]
- 18.Grinsted L, Field J. Predictors of nest growth: diminishing returns for subordinates in the paper wasp Polistes dominula. Behav Ecol Sociobiol. 2018;72 doi: 10.1007/s00265-018-2502-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Michener C. Reproductive efficiency in relation to colony size in Hymenopterous societies. Insectes Soc. 1964;11:317–341. [Google Scholar]
- 20.Bulmer MG. Risk avoidance and nesting strategies. J Theor Biol. 1984;106:529–535. [Google Scholar]
- 21.Hopper K, Rosenheim J, Prout T, Oppenheim S. Within-generation bet hedging: a seductive explanation? Oikos. 2003:219–222. [Google Scholar]
- 22.Davies NG, Ross L, Gardner A. The ecology of sex explains patterns of helping in arthropod societies. Ecol Lett. 2016;19:862–872. doi: 10.1111/ele.12621. [DOI] [PubMed] [Google Scholar]
- 23.Sumner S, Kelstrup H, Fanelli D. Reproductive constraints, direct fitness and indirect fitness benefits explain helping behaviour in the primitively eusocial wasp. Polistes canadensis Proc R Soc B. 2010;277:1721–1728. doi: 10.1098/rspb.2009.2289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ferreira PG, et al. Transcriptome analyses of primitively eusocial wasps reveal novel insights into the evolution of sociality and the origin of alternative phenotypes. Genome Biol. 2013;14:R20. doi: 10.1186/gb-2013-14-2-r20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Southon RJ, et al. High indirect fitness benefits for helpers across the nesting cycle in the tropical paper wasp Polistes canadensis. Mol Ecol. 2019:1–6. doi: 10.1111/mec.15137. [DOI] [PubMed] [Google Scholar]
- 26.Wenzel JW, Pickering J. Cooperative foraging, productivity, and the central limit theorem. Proc Natl Acad Sci. 1991;88:36–38. doi: 10.1073/pnas.88.1.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lengronne T, et al. Little effect of seasonal constraints on population genetic structure in eusocial paper wasps. Ecol Evol. 2012;2:2610–2619. doi: 10.1002/ece3.366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Davies NG, Gardner A. Monogamy promotes altruistic sterility in insect societies. R Soc Open Sci. 2018;5 doi: 10.1098/rsos.172190. 172190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schulman SR, Rubenstein DI. Kinship, need, and the distribution of altruism. Am Nat. 1983;121:776–788. [Google Scholar]
- 30.Kramer BH, Scharf I, Foitzik S. The role of per-capita productivity in the evolution of small colony sizes in ants. Behav Ecol Sociobiol. 2014;68:41–53. [Google Scholar]
- 31.Tindo M, Kenne M, Dejean A. Advantages of multiple foundress colonies in Belonogaster juncea juncea L.: greater survival and increased productivity. Ecol Entomol. 2008;33:293–297. [Google Scholar]
- 32.Naug D, Wenzel J. Constraints on foraging success due to resource ecology limit colony productivity in social insects. Behav Ecol Sociobiol. 2006;60:62–68. [Google Scholar]
- 33.Clouse R. Some effects of group size on the output of beginning nests of Mischocyttarus mexicanus (Hymenoptera: Vespidae) Florida Entomol. 2001;84:418–425. [Google Scholar]
- 34.Smith AR, Wcislo WT, O'Donnell S. Survival and productivity benefits to social nesting in the sweat bee Megalopta genalis (Hymenoptera: Halictidae) Behav Ecol Sociobiol. 2007;61:1111–1120. [Google Scholar]
- 35.Bouwma AM, Nordheim EV, Jeanne RL. Per-capita productivity in a social wasp: no evidence for a negative effect of colony size. Insectes Soc. 2006;53:412–419. [Google Scholar]
- 36.Shreeves G, Field J. Group size and direct fitness in social queues. Am Nat. 2002;159:81–95. doi: 10.1086/324125. [DOI] [PubMed] [Google Scholar]
- 37.Parsons PJ, Grinsted L, Field J. Partner choice correlates with fine scale kin structuring in the paper wasp Polistes dominula. PLoS One. 2019;14:1–17. doi: 10.1371/journal.pone.0221701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Helanterä H. Supercolonies of Ants. Encycl Soc Insects. 2020:1–3. doi: 10.1007/978-3-319-90306-4_121-1. [DOI] [Google Scholar]
- 39.Holzer B, Keller L, Chapuisat M. Genetic clusters and sex-biased gene flow in a unicolonial Formica ant. BMC Evol Biol. 2009;9:1–11. doi: 10.1186/1471-2148-9-69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Boomsma JJ, Huszár DB, Pedersen JS. The evolution of multiqueen breeding in eusocial lineages with permanent physically differentiated castes. Anim Behav. 2014;92:241–252. [Google Scholar]
- 41.Keller L. Social life: the paradox of multiple-queen colonies. Trends in Ecology & Evolution. 1995;10:355–360. doi: 10.1016/s0169-5347(00)89133-8. [DOI] [PubMed] [Google Scholar]
- 42.Mora-Kepfer F. Context-dependent acceptance of non-nestmates in a primitively eusocial insect. Behav Ecol Sociobiol. 2013;68:363–371. [Google Scholar]
- 43.Couvillon MJ, et al. En garde: rapid shifts in honeybee, Apis mellifera, guarding behaviour are triggered by onslaught of conspecific intruders. Anim Behav. 2008;76:1653–1658. [Google Scholar]
- 44.McNamara J. Optimal patch use in a stochastic environment. Theor Popul Biol. 1982;21:269–288. [Google Scholar]
- 45.Foster KR. Diminishing returns in social evolution: The not-so-tragic commons. J Evol Biol. 2004;17:1058–1072. doi: 10.1111/j.1420-9101.2004.00747.x. [DOI] [PubMed] [Google Scholar]
- 46.Sibly RM, Curnow RN. Selfishness and altruism can coexist when help is subject to diminishing returns. Heredity (Edinb) 2011;107:167–173. doi: 10.1038/hdy.2011.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cant MA. A tale of two theories: Parent-offspring conflict and reproductive skew. Anim Behav. 2006;71:255–263. [Google Scholar]
- 48.Dugatkin LA. The Altruism Equation: Seven Scientists Search for the Origins of Goodness. Princeton University Press; 2006. [Google Scholar]
- 49.Altmann S. Altruistic behaviour: the fallacy of kin deployment. Anim Behav. 1979;27:958–962. [Google Scholar]
- 50.Dawkins R. Twelve misunderstandings of kin selection. Z Tierpsychol. 1979;51:184–200. [Google Scholar]
- 51.Rice SH. The expected value of the ratio of correlated random variables. 2015 Available at: http://www.faculty.biol.ttu.edu/rice/ratio-derive.pdf.
- 52.Zivot E. Introduction to Computational Finance and Financial Econometrics, Econ. Vol. 424 University of Washington; 2011. Portfolio theory with matrix algebra. [Google Scholar]
- 53.Shpak M. Evolution of variance in offspring number: The effects of population size and migration. Theory Biosci. 2005;124:65–85. doi: 10.1016/j.thbio.2005.05.003. [DOI] [PubMed] [Google Scholar]
- 54.Starrfelt J, Kokko H. Bet-hedging - a triple trade-off between means, variances and correlations. Biol Rev. 2012;87:742–755. doi: 10.1111/j.1469-185X.2012.00225.x. [DOI] [PubMed] [Google Scholar]
- 55.Taylor P, Frank S. How to make a kin selection model. J Theor Biol. 1996;180:27–37. doi: 10.1006/jtbi.1996.0075. [DOI] [PubMed] [Google Scholar]
- 56.Rice SH. A stochastic version of the Price equation reveals the interplay of deterministic and stochastic processes in evolution. BMC Evol Biol. 2008;8:262. doi: 10.1186/1471-2148-8-262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kemeny JG, Snell J. Finite Markov Chains. Vol. 40 Springer-Verlag; 1983. [Google Scholar]
- 58.Plummer M. Package rjags. update. 2003 [Google Scholar]
- 59.Bell A, Fairbrother M, Jones K. Fixed and random effects models: making an informed choice. Qual Quant. 2019;53:1051–1074. [Google Scholar]
- 60.Mundlak Y. On the pooling of time series and cross section data. Econometrica. 1978;46:69–85. [Google Scholar]
- 61.Hooten MB, Hobbs NT. A guide to Bayesian model selection for ecologists. Ecol Monogr. 2015;85:3–28. [Google Scholar]
- 62.Ntzoufras I. Gibbs variable selection using BUGS. J Stat Softw. 2002;7:1–19. [Google Scholar]
- 63.Dias S, Sutton AJ, Ades AE, Welton NJ. Evidence synthesis for decision making 2: A generalized linear modeling framework for pairwise and network meta-analysis of randomized controlled trials. Med Decis Mak. 2013;33:607–617. doi: 10.1177/0272989X12458724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Grinstead CM, Snell JL. Introduction to Probability. American Mathematical Society; 2006. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The transitions data for P. canadensis is available as supplementary information.
The statistical code and individual-based simulation code are both available as supplementary information.