Spontaneous phase-coupling within cortico-cortical networks: How time counts for brain-state-dependent stimulation

The two primary motor cortices (M1) interact via functional connectivity during resting state and motor activity [1]. Focal transcranial magnetic stimulation (TMS) of one M1 results in inhibition of the TMS response of the contralateral M1. This short-interval interhemispheric inhibition (SIHI) is a measure of M1-M1 effective connectivity [2]. The “communication through coherence” theory [3] predicts that alignment of excitation/inhibition periods through synchronization of oscillatory phases in two nodes of a neural network will directly determine the level of effective connectivity between them. Accordingly, SIHI is strongest at instants of time when both M1 are synchronized in a high-excitability state (i.e., the negative peak of the ongoing sensorimotor μ-oscillation) [4]. Moreover, spike-timing-dependent plasticity models [5] predict that induction of plasticity of the M1-M1 pathway (or any other pathway) will be most effective if the two nodes are stimulated consistently whenever synchronized in the high-excitability state.

One important unaddressed question is how long synchronicity states (i.e., a particular phase angle between oscillations of nodes in a network) typically last for. This directly relates to the time-resolution of brain network connectivity estimation, where the length of the analysis time window needs to be shorter than the dwell time of a synchronicity state [6]. This question is fundamental for further development of network-state-dependent stimulation, e.g., the EEG-informed multilocus TMS technology [4]. Adapting TMS to the temporal dynamics of the targeted network will provide better control over the effects of TMS on excitability and plasticity and, thus, maximize efficacy of neurostimulation-based treatment.

Here we addressed this question by examining the dwell time of spontaneous phase-coupling of the μ-oscillations between the two M1 during resting state. Data used for this analysis were taken from 10-min resting-state EEG recordings performed on right-handed healthy adults with no history of neurological or psychiatric pathologies. The study was approved by the ethics committee of the medical faculty of the University of Tübingen (protocol 716/2014B02) and all participants provided written informed consent.

EEG data were selected based on the following criteria : ( 1 ) Spectral signal-to-noise ratio peak within the μ-frequency band (8–13 Hz) > 12 dB in the Hjorth-style Laplacian spatially filtered EEG centered on C4 (with surrounding electrodes FC2, FC6, CP2, CP6) for the right hemisphere, and C3 (surrounding electrodes FC1, FC5, CP1, CP5) for the left hemisphere; (2) absence of noise contamination exceeding a defined threshold within the EEG channels used for Hjorth-style filtering (see Supplementary Material); (3) no more than four non-consecutive noise-contaminated time periods of unconstrained length excluded from the data (see Supplementary Material); (4) μ-rhythm peak frequency interhemispheric difference < 1 Hz. Criteria (1)–(3) were introduced to ensure high reliability of oscillatory phase estimation as well as temporal continuity of the analysed signals. Criterion (4) ensured that the signals from both hemispheres were filtered to and analysed on the same frequency. Out of 23 screened subjects, data from 7 subjects (6 female, 1 male; mean age ± SD: 24.7 ± 3.5 years) met these requirements. The data of one of those subjects was excluded because the distribution of interhemispheric phase differences was skewed towards zero, suggesting that volume conduction had affected signal extraction. Therefore, the data from 6 subjects were finally included in this analysis.

Eyes-open resting-state EEG was recorded at a sampling rate of 5 kHz using a 24-bit biosignal amplifier in DC mode (NeurOne, Bittium, Finland) and a 64-channel cap with Ag/AgCl sintered ring electrodes (EasyCap, Germany), placed according to the International 10–20 system. EEG signal preprocessing and analysis were carried out in MATLAB (The Mathworks, R2020a) using the Field-trip toolbox [7] and custom scripts. Recordings were truncated to a similar length (8.5–9.5 min). EEG data was preprocessed according to a standardized pipeline (for details, see Supplementary Material). Signals from EEG channels corresponding to right and left Ml regions (C4 and C3 electrodes, respectively) were analysed after Hjorth-style surface Laplacian transformation. Individual μ-peaks within the 8–13 Hz frequency band were calculated for both C4-Hjorth and C3-Hjorth signals. The mean frequency of the two (μ-peaks was chosen as a target frequency for further analysis. The signals were zero-phase filtered with a 6th-order Butterworth filter to a 6-Hz-wide band, centered at the individual target frequency. Analytic signals were calculated from the filtered data using the Hilbert transform, followed by determining the phase difference between the two analytic signals, which was calculated by dividing the two analytic signals and taking the angle.

In the next step, the phase difference between the two signals at each time instant was compared to the phase differences between the two signals in increasingly more distant samples following and preceding this time instant, until these comparisons exceeded a predefined limit of ±π/4. The dwell time (i.e., the duration of a phase-coupling period) was then defined as the period during which a phase difference deviation of ≤ π/4 around any time instant persisted between the two signals (see Supplementary Material). We set this limit in accord with previous multi-unit activity and local field potential recordings in cat visual cortex that demonstrated optimal mutual influence between two recording sites over a phase range of approximately ±π/4 centered on the mean phase relation [8].

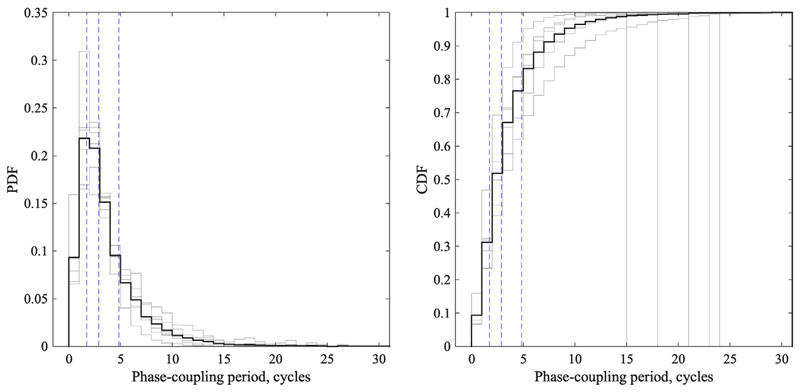
Across subjects, the most frequent dwell time of spontaneous phase-coupling between the two M1 was 1.6 cycles, while 95% of dwell times were in the range between 0.5 and 12 cycles of the μ-oscillation (i.e., approx. 50–1200 ms, Fig.1). Phase-coupling at any random time instant had a length of ≤3 cycles and ≤5 cycles with 50% and 75% probability, respectively (Fig. 1). These results indicate that synchronization of oscillatory activity in the two M1 operates at a fast time scale to enable dynamic interhemispheric communication [9], Therefore, real-time phase estimation based on a sliding window of 500 ms (i.e., approximately 5 cycles for μ-oscillations) [4,10] matches a substantial fraction (approximately 25%) of the dwell times of rapidly fluctuating M1-M1 connectivity states. In this context of short-lived phase synchronization states, it remains to be determined if other (shorter or longer) analysis times will result in higher accuracy of connectivity estimation [6,11]. Importantly, the strict exclusion criteria and small sample size of the present analysis need to be taken into consideration when interpreting and extrapolating these results onto the general population.

Fig. 1.

Mean probability density function (PDF) and cumulative distribution function (CDF) estimates of phase-coupling periods in the interhemispheric M1-M1 network, pooled from all subjects (n = 6, thick black curves). PDF describes the probability for a random sample to be part of a phase-coupling period of length n. CDF describes the probability that a random sample is part of a phase-coupling period less or equal to n. The individual data are shown as thin grey curves. Phase-coupling periods are indicated as number of cycles at the individual μ-peak frequency. Vertical dashed blue lines indicate 0.25, 0.5, and 0.75 quartiles of the distribution.

In conclusion, our results indicate that synchronization of phase over few cycles of the ongoing oscillations within two nodes of a resting interhemispheric motor network, rather than time-extended phase-coupling, appears to be a valid target for realtime estimation of spontaneously occurring and rapidly changing connectivity. Choosing the appropriate time resolution of connectivity analysis within a given brain network is critical for the development of network-state-dependent brain stimulation. An unaddressed but essential question is the functional role of the observed spontaneous synchronizations, which could represent either effective connectivity or random phase-alignment. While our previous work provided evidence for effective connectivity [4], further investigation is clearly needed to determine origins of the observed short-lived phase-couplings, as well as their possible differential effect on plasticity induction.