Ultrasound-Guided Wireless Tubular Robotic Anchoring System

Abstract

Untethered miniature robots have significant poten-tial and promise in diverse minimally invasive medical applications inside the human body. For drug delivery and physical contra-ception applications inside tubular structures, it is desirable to have a miniature anchoring robot with self-locking mechanism at a target tubular region. Moreover, the behavior of this robot should be tracked and feedback-controlled by a medical imaging-based system. While such a system is unavailable, we report a reversible untethered anchoring robot design based on remote magnetic actuation. The current robot prototype’s dimension is 7.5 mm in diameter, 17.8 mm in length, and made of soft polyurethane elastomer, photopolymer, and two tiny permanent magnets. Its relaxation and anchoring states can be maintained in a stable manner without supplying any control and actuation input. To control the robot’s locomotion, we implement a two-dimensional (2D) ultrasound imaging-based tracking and control system, which automatically sweeps locally and updates the robot’s position. With such a system, we demonstrate that the robot can be controlled to follow a pre-defined 1D path with the maximal position error of 0.53 ± 0.05 mm inside a tubular phantom, where the reversible anchoring could be achieved under the monitoring of ultrasound imaging.

I. Introduction

UNTETHERED miniature robots offer the capability of accessing complex, difficult-to-reach, and narrow areas inside our body to perform minimally invasive medical operations [1]–[5]. Diagnostic, therapeutic, surgical, and sample collection tasks inside tubular structures, such as gastrointestinal (GI) tract using these robots have been investigated recently [6]. For medical operations, such as drug delivery in an intestinal infection or cancer site and effective physical contraception in the Fallopian tube, untethered medical robots need to stay at the desired locations for a controlled duration, where self-locking mechanism is required to maintain the robot’s anchoring state without external control input [6].

In order to fulfill the above requirements, motor-driven systems with a transmission mechanism [7]–[10] have been proposed. However, they are hard to scale down below 10 mm. For the intestinal tract, the tubular dimensions range from 2.5 cm to 6.5 cm in diameter [6], [11]. For narrower tubular structures such as the Fallopian tube in the female birth system, the diameter of the lumen can be as small as 1 mm [12] in diameter, where these mechanisms are hard to be adopted. To miniaturize such devices, magnetic interactions have been used to remove complex on-board components [13]–[17]. Specifically, there are two design approaches for the existing tubular anchoring systems. The first approach adopts the magnetic interaction of inner permanent magnets to actuatethe anchoring mechanism [14], [15]. Thenext one uses a single inner magnet as the power source to actuate the transmission mechanism under an external magnetic field [17]. However, a self-locking mechanism to maintain the anchoring state is not available.

Next, such robots should be tracked and controlled with reliable medical imaging feedback for safe and precise operations. Ultrasound imaging modality is very promising for such purpose for milliscale medical robots [18], [19] since it can provide real-time images in 2D or 3D, it is safe with no ionization radiation, compact, and cost-effective. Also, it has high tissue penetration depth and possibly sub-millimeter scale high-resolution imaging capability in lower penetration depths (i.e., higher imaging frequencies). For the tracking of medical robots, active elements can be embedded inside robots to inform therobot states using acoustic waves [20], [21].Tofurtherreduce the size and tethering of such robots, active elements should be removed. In this case, external ultrasound acts as the only source to detect and track the robot by using either 2D or 3D scanning. Previous works have shown this applicability through the proper imaging process to extract the motion information of miniature medical robots [22]–[24]. Moreover, for real medical scenarios, the ultrasound transducers are integrated into flexible motion systems such as robotic arms [25]–[27] or X-Y stages [28]. In [25]–[27], the authors adopt two robotic arms, one with a magnet as the robot actuation tool, and the other one with an ultrasound transducer as the imaging tool. In these works, the movement of the imaging plane depends on the assumption that the plane is intersected with the robot for each control step. No relevant tracking Solutions have been discussed if the robot has not arrived at the desired location due to the complex interaction with the surrounding tissues. On the other hand, the solution discussed in [28] provides a promising idea. The robot’s position measurement can be actively updated and tracked by sweeping the probe in the operational area and analyzing the pixel distribution of the imaging. However, the range of sweeping is fixed and not adaptive, making this approach inefficient for real application scenarios, especially when the working range is enlarged.

To solve the first challenge of lacking a self-locking mech-anism to maintain the anchoring state, we propose a reversible anchoring robot for tubular structures, where the two states of the robot can be maintained/locked without supplying any control and actuation input. This design is inspired by the magnetically actuated Sarrus linkage mechanism from [13], [29]. Next, we show that the proposed design could be generalized to different tubular dimensions. Moreover, we implement a robot tracking approach based on the local sweeping of the ultrasound imaging plane, inspired by [28]. The position measurement of the robot is updated based on the distribution of pixel value sums of the ultrasound images along with its sweeping direction. A robotic arm is integrated in order to improve the flexibility of robot tracking compared with the previous work [28]. Moreover, a 2D robot position control system based on this tracking approach is implemented. We demonstrate that the robot can be controlled by the system to follow the desired 1D path inside a small intestine phantom. The reversible anchoring under the ultrasound imaging monitoring is also shown.

II. Design and Fabrication

Here, we first make a unified definition of different coordinate frames used in the paper. x_o-, y_o-, z_o-axes define the global coordinate frame, and it is attached at the initial position of the robot during locomotion. x_m-, y_m-, z_m-axes represent the coordinate frame attached to the locomotion manipulation magnet. x_r-, y_r-, z_r-axes define the anchoring robot-attached coordinate frame, which is in its center. x_arm-, y_arm-, z_arm-axes define the robotic arm frame attached at its base. x_i-, y_i-, z_i-axes define the frame attached at the end of the ultrasound transducer and used to represent the imaging plane. Moreover, we use the superscript to represent the base frame and use the subscript to represent the agent. For example, $x_{\text{r}}^{\text{o}}$ represents the robot’s position along the x-axis in the global frame. Note that this superscript and subscript definition does not apply to forces in this paper, which would be explained separately. In the following contents, actuation refers to the enabling of the relaxation state and the anchoring state; manipulation and control relate to the robot locomotion while at the relaxation state.

A. Anchoring Robot Design

The robot is composed of an external linkage structure, and two inner permanent magnets, inspired by [13], [29], as shown in Fig. 1a. The external linkage structure has two shells to hold cubic magnets and a four-legged Sarrus linkage. The two inner magnets are with the same magnetization direction. The design parameters are labeled in Fig. 1, and the corresponding values for a prototype are summarized in Table I. This simple yet effective structure has no sliding frictions among inner components during deformation. Also, it ensures the co-axial movement of two magnets when the whole structure expands. These two advantages make it a desirable choice for designing magnetically actuated anchoring devices.

Fig. 1.

Design of the proposed soft magnetic anchoring robot module. a. CAD model (i) and photo (ii) of a representative prototype. The robot is composed of two inner magnets and an external four-legged Sarrus linkage. b. Half-section CAD view of the robot with labeled design parameters.

Table I. Design Parameters of a Robot Prototype.

Parameters	Value
Diameter at the relaxation state, D (mm)	7.5
lHeight of the inner cubic magnets center, h m (mm)	3.7
Height of the shells, h s (mm)	6.25
Height of the leg connection slots, h t (mm)	1.9
Dimension of the leg connection slots, lt (mm)	3.2
Length of the linkage leg, l g (mm)	15
Side length of the inner cubic magnets, l c (mm)	3
Young’s modulus of the material, E c (MPa)	11.66
Diameter of the circular hinge, ϕc(mm)	0.65
Minimal thickness of the circular hinge, t c (mm)	0.25
Width of a single leg, b C (mm)	3

B. Robot Fabrication

The anchoring robot is fabricated with both 3D printing and molding techniques, similar to the one used in [13], [29]. The shells of the external frame are 3D-printed directly (VeroClear & Objet260 Connex3, Stratasys Ltd.). Then the inner magnets are inserted to shells. The linkage legs, which are 3D-printed first, are then used as a mold to fabricate the final parts. Currently, we use water white clear urethane liquid rubber Clear Flex™ 95 (Smooth-On, Inc.), as the material for legs in the robot prototype. The fabricated legs and shells are glued together using LOCTITE 401 (Henkel Corporation).

III. Modeling of Robot Actuation

In this section, we first elaborate and model the actuation method. We demonstrate that both states can be maintained stably without any control input, and the switch between two states can be actuated. The stability here refers to the relations between the inner magnetic force F _mag and the elastic restoration force F _res from the linkage structure when the actuation magnets are moved away. If |F _mag| is 20% larger than |F _res|, a stable anchoring state can be maintained. If |F _res| is 20% larger than |F _mag|, a stable relaxation state can be kept. Next, we further discuss the applicability of this design in real application scenarios.

For the simplicity of modeling, we assume that the friction in the tubular structure and the reaction force when the robot anchors to the tubular structure are negligible, compared with F _mag and F _res. Moreover, we assume that the robot body is well confined in the tubular structure, and cannot flip around the z_r-axis (Fig. 2). In the discussion about using the design in real applications, this constraint would be relaxed.

Fig. 2.

Actuation method of the robot for reaching to the relaxation or anchoring state. a. Diagram of the actuation method. The anchoring state is actuated by the approaching of actuation magnets with the reverse magnetization direction as the robot’s inner magnets’. The sequence of the state transition is i → ii → iii. The relaxation state is actuated by the one with the same magnetization direction. The sequence of the state transition is iii → iv → i. b. Experimental demonstration photos of two states in a soft plastic tube. In real application scenarios, multiple robots (modules) should be connected in serial to enhance the anchoring state, if necessary.

The nomenclature for different magnetic forces is explained here. The total magnetic force applied to an inner magnet is ${\mathit{\text{F}}}_{\text{mag}}={\mathit{\text{F}}}_{\text{mag}}^{\text{in}}+{\mathit{\text{F}}}_{\text{mag}}^{\text{ext}}$, where ${\mathit{\text{F}}}_{\text{mag}}^{\text{in}}$ denotes the component of attractive force when no actuation magnets are around, and ${\mathit{\text{F}}}_{\text{mag}}^{\text{ext}}$ denotes the component from the approaching of actuation magnets. Specifically, ${\mathit{\text{F}}}_{\text{mag}}^{\text{ext,s}}$ represents the force added by actuation magnets with the same magnetization direction as the inner magnets’, and ${\mathit{\text{F}}}_{\text{mag}}^{\text{ext},\text{r}}$ represents the one from the actuation magnets with the reverse magnetization direction. Therefore, ${\mathit{\text{F}}}_{\text{mag}}^{\text{r}}$ and ${\mathit{\text{F}}}_{\text{mag}}^{\text{s}}$ are used to describe the total magnetic force for two cases, respectively. Without special notation, the following F _mag refers to the one applied on the left-hand side inner magnet, and it is positive if towards x_r-axis (Fig. 2), negative if reverse.

A. Stability of the Relaxation and the Anchoring States

When no actuation magnets are around, since the minimal distance between the two 3 mm-long cubic inner magnets (Nd-FeB, N45, Supermagnete, Webcraft GmbH) is 5 mm, the error associated with the dipole model approximation is less than 5% according to [30]. Based on this approximation, ${\mathit{\text{F}}}_{\text{mag}}^{\text{in}}$ between the two co-axial cubic magnets, assuming no current flowing in the workspace, can be given by dipole approximation as [31]

$$\mathit{\text{F}}\begin{array}{c}\text{in}\\ \text{mag}\end{array}=\frac{3{\mu }_0|{\mathit{\text{m}}}_c|}{4\pi |{\mathit{\text{r}}}_c{|}^4}[{\widehat{\mathit{\text{m}}}}_c\widehat{\mathit{\text{r}}}\begin{array}{c}T\\ c\end{array}+{\widehat{\mathit{\text{r}}}}_c\widehat{\mathit{\text{m}}}\begin{array}{c}T\\ c\end{array}-(5{\widehat{\mathit{\text{r}}}}_c\widehat{\mathit{\text{r}}}\begin{array}{c}T\\ c\end{array}-I)({\widehat{\mathit{\text{m}}}}_c.{\widehat{\mathit{\text{r}}}}_c)]{\mathit{\text{m}}}_c,$$ (1)

where m_c is the the magnetic moment of the magnet, ${\widehat{\mathit{\text{m}}}}_c$ is a unit vector such that ${\mathit{\text{m}}}_c=|{\mathit{\text{m}}}_c|{\widehat{\mathit{\text{m}}}}_c,{\mu }_0=4\pi \times {10}^{-7}$ Tm/A is the permeability of free space, I is the 3 x 3 identity matrix, r_c is the vector from the center of right-hand side magnet to the left-hand side one, and $\widehat{r}$ _c is a unit vector in that direction. The deformation of the robot along the axial direction can then be expressed as:

$$\Delta L=l_{\text{m},\text{max}}-|r_c|\in [0,l_{\text{m},\text{max}}-l_{\text{m},\text{min}}],$$ (2)

where l _m,max is the largest distance between the center of two inner magnets, and l _m,max = L – 2h_m = l_g + 2(h_t – h_m). l _m,min is the smallest distance between two inner magnets, when the shells are in contact and l _m,min = 2(h _s – h _m). Based on Equation 1, the attractive force between two inner magnets along with the deformation can be calculated.

To model the restoration force provided by the four-legged Sarrus linkage, the dimensionless rotational stiffness of each hinge (12 in total) can be calculated by [32]:

$$K_c=\frac{1}{E_c{b}_c{t}_c^2}\frac{|M|}{\Delta \theta },$$ (3)

where E _c is the Young’s modulus of the elastomeric material, b _c is the width of a single leg, t _c is the minimal thickness of the circular hinge, M is the moment on the hinges, and Δθ is the rotation angle of the hinge due to the deformation. Since all the hinges are circular flexure hinges in current design and using the values from Table I, the dimensionless rotational stiffness is K _c = 0.0687, which is computed by the empirical fitting model in [32]. When compression force is applied to the linkage from the magnetic force, moments are induced on hinges. This results in shape deformation and F _res. The deformation of the linkage and the restoration force can be expressed as [29]:

$$\Delta L=l_g(1-\cos \Delta \theta )$$ (4)

$$|{\mathit{\text{F}}}_{\text{res}}|=\frac{2(|M_1|+|M_2|)}{l_{\text{g}}\text{sin}\Delta \theta }=\frac{32K_{\text{c}}{E}_{\text{c}}{b}_{\text{c}}{t}_{\text{c}}^2\Delta \theta }{l_{\text{g}}\text{sin}\Delta \theta },$$ (5)

where |M ₁| = |M ₂|, |M ₁| is the sum of moments applied on the hinges close to the ends of the robot, and |M ₂| is the sum of moments on the middle hinges. All the forces and moments are labeled in Fig. 2. Using the parameter values in Table I and Equation 1-5, |${\mathit{\text{F}}}_{\text{mag}}^{\text{in}}$| and |F _res| along with the deformation are calculated. The robot’s two states are stable and can be locked, since |F _res(ΔL = 0)| > |${\mathit{\text{F}}}_{\text{mag}}^{\text{in}}$(ΔL = 0)|, and ${\mathit{\text{F}}}_{\text{mag}}^{\text{in}}$(ΔL = 5)| > |F _res(ΔL = 5)|, respectively (unit: mm).

B. Actuation of the Transition Between Two Stable States

The approaching of actuation magnets would affect |F _mag| and enable the state switch. For the anchoring state (Figs. 2 and 3), two cubic magnets (10 mm side length, NdFeB, N42, Supermagnete, Webcraft GmbH) with reverse magnetization move to the robot along y_r-axis from 40 mm away. |F ^r _mag| continuously increases due to the increased magnetic flux density gradient ▽B towards each other of two inner magnets. When it exceeds |F _res|, the robot starts to deform, and then two magnets shells are in contact with each other. When the actuation magnets are moved away, |F _mag| decreases. Since it is still larger than |F _res|, the anchoring state can be maintained in a stable manner. The variation of |F _mag| and |F _res| along these steps are shown in Fig. 3a, where |F _mag| is computed using the finite element simulation in COMSOL Multiphysics 5.3a. The actuation of the relaxation state can be realized through the approaching of actuation magnets with the same magnetization direction (Figs. 2 and 3). With the actuation magnets moving closer, $|{\mathit{\text{F}}}_{\text{mag}}^{\text{s}}|$ continuously decreases due to the increased ▽B pointing away from each other of the two inner magnets. Beyond the critical point where $|{\mathit{\text{F}}}_{\text{mag}}^{\text{s}}|$ is smaller than |F _res|, the robot can then recover back to the relaxation state. After the magnets are taken away, the relaxation state can be maintained since |F _mag| is smaller than |F _res|.

Fig. 3.

Variation of the total inner magnetic force Fmg during the actuation of two robot states. a. Actuation of the anchoring state. The sequence of the state transition is A → B → C → D, where the diagrams of the robot’s configurations are shown aside. $|{\mathit{\text{F}}}_{\text{mag}}^{\text{in}}(\Delta L=5)|>|{\mathit{\text{F}}}_{\text{res}}(\Delta L=5)|$ ensures that the anchoring state can be maintained stably without any control input. b. Actuation of the relaxation state. The transition sequence is D → E → F → A. $|{\mathit{\text{F}}}_{\text{mag}}^{\text{in}}(\Delta L=0)|<|{\mathit{\text{F}}}_{\text{res}}(\Delta L=0)|$ ensures that the relaxation state can be maintained stably (unit: mm).

C. Actuation Towards Real Application Scenarios

In reality, the robot (a single module) introduced above can be challenging to be applied in tubular structures. For example, when the robot structure expands, there are only four points of beams anchoring into the wall. Therefore the robot is prone to rotate/flip around z_r-axis when forces, such as the tubular peristaltic forces [6], are applied. To deal with such issue, we further propose a serial configuration of multiple robots (modules) connected (Fig. 2b). Using this serial configuration, such undesirable rotation can be avoided, and there are more contact points against the inner wall of the tube, enhancing the anchoring effect.

Moreover, multiple symmetrically patterned magnets can be used to actuate the state-transition switch. In the current prototype, we use one pair of symmetrically patterned magnets. According to dipole approximation [31], the magnetic force applied on the inner magnets is linear with the pairs of actuation magnets. More pairs could provide more actuation force, and in this way, these actuation magnets do not have to be this close to the tubular structure, which is more applicable in real medical scenarios.

D. Applicable Tubular Range of the Current Design

From the above analysis, the desired l_g should satisfy the following relations to achieve two stable states that can be actuated:

$$|{\mathit{\text{F}}}_{\text{mag}}^{\text{in}}(\Delta L=0)|<|{\mathit{\text{F}}}_{\text{res}}(\Delta L=0)|$$ (6)

$$|{\mathit{\text{F}}}_{\text{mag}}^{\text{in}}(\Delta L=l_{\text{gap}})|>|{\mathit{\text{F}}}_{\text{res}}(\Delta L=l_{\text{gap}})|$$ (7)

$$|{\mathit{\text{F}}}_{\text{mag}}^{\text{r}}(\Delta S=S_{\max },\Delta L=0|>|{\mathit{\text{F}}}_{\text{res}}(\Delta L=0)|,$$ (8)

$$|{\mathit{\text{F}}}_{\text{mag}}^{\text{r}}(\Delta S=S_{\max },\Delta L=l_{\text{gap}}|<|{\mathit{\text{F}}}_{\text{res}}(\Delta L=l_{\text{gap}})|,$$ (9)

where $\Delta L\in [0,l_{gap}],\Delta S\in [0,S_{\text{max}}]$. Equation 6 and 7 ensure that two states can be maintained in a stable manner; 8 and 9 ensure that the switch of the state can be actuated. The corresponding values are calculated for the leg length $l_g\in (2(h_s-h_t),20]$. The computed design regions for leg length that satisfies the relations 6-9 is $l_g\in [9,15.1]$. This range corresponds to the available tubular dimension $D_{\text{blk}}\in [9,20]$ for anchoring (unit:mm).

E. Scaling Analysis for Smaller Tubular Dimensions

Here we carry out a simple scaling analysis to show the design can be possibly further miniaturized. For cuboidal magnets, the relationship between the contact force and the magnet dimension is given as [33]: $|{\mathit{\text{F}}}_{\text{mag}}|\propto l_{\text{c}}^2$. Meanwhile, when the overall size of the robot scales down, $l_c\propto l_g\propto b_c\propto t_c$ Based on Equation 5, it can then be expressed as: $|{\mathit{\text{F}}}_{\text{res}}|\propto l_{\text{c}}^2$. Therefore, when both the magnetic force and restoration force decrease with $l_{\text{c}}^2$, it is possible to design a smaller robot, based on the current design approach, towards narrower tubular structures.

IV. Ultrasound Imaging-Based Tracking and Control System

In this section, we start by introducing the locomotion manipulation approach for the robot. Then we explain the details of the robot position tracking approach based on local sweeping. The 2D closed-loop position control algorithm based on the above methods is followed. The hardware components of the current system to realize the above functions are introduced lastly. Note that, we implement the control system on the x_oy_o plane of the global coordinate frame currently. The complete approach, however, can be generalized to 3D space directly. Moreover, as discussed in Section III.C, for real application cases, multiple robot modules can be connected into a serial configuration. In the following, we focus on the tracking and control of a single module since a similar method can be generalized to the configuration with multiple modules.

A. Locomotion Manipulation

To manipulate the robot to the desired locations inside tubular structures when it is at the relaxation state, we use magnetic force and torque to enable the locomotion using the 4-degrees of freedom (4-DoF) motion of a cubic magnet (Fig. 4a). Besides the in-plane movement $x_{\text{m}}^{\text{o}}$ and $y_{\text{m}}^{\text{o}}$, the magnet could continuously rotate along the x_m-axis, with the frequency denoted by w_m and also rotates around the z_m-axis with the angle denoted by ${\theta }_{\text{m}}^{\text{o}}$. The manipulation magnet is positioned 25-30 mm away from the center of the robot. Its rotation axis, x_m-axis, is parallel to the central axis, x_r-axis, of the robot. When the magnet manipulates, the robot could rotate and also translate inside the tube. This is due to the coupled effects from the magnetic force, torque, and the constraint posed by the inner tube wall, as shown in Fig. 4b. A simplified linear model describing the robot state can be represented in a matrix form as:

$$\left[\begin{array}{l}{x}_{\text{rp}}^{\text{o}}\hfill \\ y_{\text{rp}}^0\hfill \\ {\theta }_{\text{rp}}^{\text{o}}\hfill \end{array}\right]=\left[\begin{array}{llll}1\hfill & 0\hfill & 0\hfill & a\hfill \\ 0\hfill & 1\hfill & 0\hfill & b\hfill \\ 0\hfill & 0\hfill & 1\hfill & c\hfill \end{array}\right]\left[\begin{array}{l}{x}_{\text{m}}^{\text{o}}\hfill \\ y_{\text{m}}^{\text{o}}\hfill \\ {\theta }_{\text{m}}^{\text{o}}\hfill \\ {\omega }_{\text{m}}^{\text{o}}\hfill \end{array}\right]+\vartheta ,$$ (10)

where $[x_{\text{m}}^{\text{o}},y_{\text{m}}^{\text{o}},{\theta }_{\text{m}}^{\text{o}},{\omega }_{\text{m}}]$ denotes the control input from the manipulation magnet, $[x_{\text{rp}}^{\text{o}},y_{\text{rp}}^{\text{o}},{\theta }_{\text{rp}}^{\text{o}},]$ indicates the predicted state of the robot in the global coordinate frame, a, b, c are lumen and magnet-distance dependent parameters, which are experimentally estimated, and v is the vector of the Gaussian process noise. Here we rely on the fact the robot’s inertia and stiction are negligible [34].

Fig. 4.

Principle of 2D locomotion manipulation and robot position tracking based on local sweeping. a. Isometric view of the locomotion by the manipulation magnet with 4-DoF motion capability. A, B, C refer to the cross section views of three example imaging planes. b. Time sequence demonstration of locomotion. c. Details of the tracking approach. i. Cross section views of A, B, and C. ii. Distribution of pixel value sums along with the sweeping. The sums achieve highest at the locations of two shells.

B. Position Tracking Approach Based on Local Sweeping

We implement a 2D robot position tracking approach based on local sweeping inspired by [28]. For each control step k, the imaging plane is positioned to the predicted location of the robot $\left(x_{\text{rp}}^{\text{o}}\left(k\right),y_{\text{rp}}^{\text{o}}\left(k\right)\right)$ and the plane is controlled to be perpendicular to the robot orientation, where ${\theta }_{\text{i}}^{\text{o}}\left(k\right)={\theta }_{\text{rp}}^{\text{o}}\left(k\right).$ Next, the plane starts to sweep around this location symmetrically along ${\theta }_{\text{rp}}^{\text{o}}\left(k\right).$ During sweeping, the pixel value sums S _pix,k(t) and the corresponding plane locations $\left(x_{\text{i,k}}^{\text{o}}\left(t\right),y_{\text{i,k}}^{\text{o}}\left(k\right)\right)$ are recorded. Because the anchoring robot (a single module) has two solid shells at two ends and hallow leg structure in the middle, it results in that S _pix is higher at the two ends along with the sweeping, as shown in plane A and C of Fig. 4. Therefore we assume the pixel value sums around the locations of two shells obey two Gaussians distributions, and we could use distribution moments to extract the locations of two shells. We divide the collected data into two components, $\left(x_{\text{i},\text{kl}}^{\text{o}},y_{\text{i},\text{kl}}^{\text{o}},S_{\text{pix,kl}}\right)$ and $\left(x_{\text{i,kh}}^{\text{o}},y_{\text{i,kh}}^{\text{o}},S_{\text{pix,kh}}\right)$ based on $\left(x_{\text{rp}}^{\text{o}}\left(k\right),y_{\text{rp}}^{\text{o}}\left(k\right)\right).$ The location of one shell along x_o-axis can then be computed as:

$${\mu }_{x,1}=\frac{{\displaystyle {\sum }_{t=1}^n{x}_{\text{i},\text{kl}}^{\text{o}}\left(t\right)S_{\text{pix},\text{kl}}\left(t\right)}}{{\displaystyle {\sum }_{t=1}^n{S}_{\text{pix},\text{kl}}\left(t\right)}}.$$ (11)

Similar equations apply to u_x,2 and y_o-axis.The updated robot position measurement $\left(x_{\text{rm}}^{\text{o}},x_{\text{rm}}^{\text{o}}\right)$ can then be calculated as the mean of the above values, for example, $x_{\text{rm}}^{\text{o}}=0.5\left(u_{x,1}+u_{x,2}\right).$ Moreover, the measurement model is defined as:

$$\left[\begin{array}{l}{x}_{\text{rm}}^{\text{o}}\\ y_{\text{rm}}^{\text{o}}\\ {\theta }_{\text{rm}}^{\text{o}}\end{array}\right]=\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{l}{x}_{\text{r}}^{\text{o}}\\ y_{\text{r}}^{\text{o}}\\ {\theta }_{\text{r}}^{\text{o}}\end{array}\right]+w,$$ (12)

Where the orientation measurement ${\theta }_{\text{rm}}^{\text{o}}$ could be acquired from the motion command ${\theta }_{\text{m}}^{\text{o}}$, w is the vector of Gaussian measurement noise. Since both the process model and the measurement model are linear with Gaussian noise, the Kalman filter (KF) is one of the best state estimators we can use [35]. Using KF, together with Equation 10 through 12, the robot pose can be estimated.

C. Closed-Loop Position Control

Using the above manipulation and tracking approach, we implement a 2D closed-loop control system enabling the robot locomotion, which can be divided into the locomotion control part and the imaging part. We assume that the path for the robot to follow is known before the operation. The first published position command is subscribed by the state estimator, the robotic arm controller, and the robot manipulator. The robot manipulator moves to the desired via-point. The imaging plane is then positioned to sweep around this via-point to update the robot position estimation, which is compared with the control input from the motion commander to decide the next step. The control policy is that if the distance between the estimated position and the desired position is smaller than 1 cm, the robot manipulator moves to the next via-point. If not, it stays at the current via-point while keeping the rotation rate of the magnet, then the position estimation is repeated. The overall control system design is showed in Fig. 5, and the communication framework is enabled by the Robot Operating System (ROS). The control algorithm is also summaried in Algorithm 1. In real tubular structures such as the small intestine, the complex interaction between the robot and the inner wall would pose a significant drag on the robot, and make its step-out frequency very low. In consideration of this, the complete system is adjusted to be slow on purpose to ensure robust performance. With the imaging update frequency available up to 30 Hz, the control frequency can still be increased given the case-by-case application requirements.

Fig. 5.

Block diagram of the 2D robotic ultrasound imaging-based tracking and control system. ${\sigma }_x\text{and}{\sigma }_y$ indicate the sweeping range around the predicted positions of the robot; $(x_{\text{rm}}^{\text{o}},x_{\text{rm}}^{\text{o}})$ represents the measurement of the robot position from the local sweeping approach; $({\widehat{x}}_{\text{r}}^{\text{o}},{\widehat{y}}_{\text{r}}^{\text{o}})$ represents the estimation of the robot position.

D. Hardware Components

The system has three components: imaging part, manipulation part, and computation part (Fig. 6). The imaging part has a preclinical ultrasound imaging platform, a 2D linear array trans-ducer (Vevo 3100 & MX550, FUJIFILM VisualSonics, Inc.), and a 7 DoF robotic arm (Franka Emika GmbH). The robot manipulation part has an X-Y stage (AxiDraw V3, Evil Mad Science), two servo motors (Parallax Inc.), and a cubic magnet (10 mm side length, Supermagnete, Webcraft GmbH). For the computation part, we use a high-level PC with the real-time kernel (Core i7-8650 CPU) and a low-level PC with the generic kernel (Xeon CPU). The acquired 2D US images are transferred to the low-level PC by a video grabber (DVI2USB 3.0, Epiphan Systems Inc.).

Fig. 6. Photos of the system hardware setup with the coordinate systems. The system includes the imaging part, the robot manipulation part, and the computation part.

Algorithm 1: 2D Position Control Based on Local Sweeping of Ultrasound Imaging Plane.

1:     Inputs

2:     Path ${\left(x_{\text{m}}^{\text{o}}\left(k\right),y_{\text{m}}^{\text{o}}\left(k\right),{\theta }_{\text{m}}^{\text{o}}\left(k\right)\right)}_{k=1:N}\to N$ via-points

3:     Frequency ${\omega }_m\to$ rate of the manipulation magnet

4:     Initialization:

5:     while $k<N$ do

6:       Send motion command $\left(x_{\text{m}}^{\text{o}}\left(k\right),y_{\text{m}}^{\text{o}}\left(k\right),{\theta }_{\text{m}}^{\text{o}}\left(k\right),{\omega }_m\right)$

7:       $x_{\text{i,k}}^{\text{o}}\left(0\right)=x_{\text{rp}}^{\text{o}}\left(k\right),y_{\text{i,k}}^{\text{o}}\left(0\right)=y_{\text{rp}}^{\text{o}}\left(k\right),{\theta }_{\text{i,k}}^{\text{o}}\left(0\right)={\theta }_{\text{rp}}^{\text{o}}\left(k\right)$

8:       for t = 1 to n do

9:           Collect $\left(x_{\text{i,k}}^{\text{o}}\left(t\right),y_{\text{i,k}}^{\text{o}}\left(t\right),S_{\text{pix},\text{k}}\left(t\right)\right)$

10:       end for

11:       Divide data based on $\left(x_{\text{rp}}^{\text{o}}\left(k\right),y_{\text{rp}}^{\text{o}}\left(k\right)\right)$ into two groups

12:       Update estimation $\left({\widehat{x}}_{\text{r}}^{\text{o}}\left(k\right),{\widehat{y}}_{\text{r}}^{\text{o}}\left(k\right),{\widehat{\theta }}_{\text{r}}^{\text{o}}\left(k\right)\right)$

13:       if $\sqrt{{\left(x_{\text{m}}^{\text{o}}\left(k\right)-{\widehat{x}}_{\text{r}}^{\text{o}}\left(k\right)\right)}^2+{\left(y_{\text{m}}^{\text{o}}\left(k\right)-{\widehat{y}}_{\text{r}}^{\text{o}}\left(k\right)\right)}^2}$ < a then

14:         $k=k+1\to$ move to the next via-point

15:       else

16:         $k=k\to$ stay at the current via-point keeping ${\omega }_m$

17:       end if

18:     end while

V. Experiments

In this section, we show the details in experimental demon-strations of 2D closed-loop locomotion control and the reversible anchoring monitoring. For ultrasound imaging settings, B-modeis used, and the acquisition dimension is 14 mm by 12.08 mm. The experiments are carried out in a latex-made tubular phantomwith 10 cm length, which is used to simulate a section of the small intestine. Latex is a common tissue-mimicking material (TMM) since it resembles in mechanical properties, such as hardness and modulus, to biological tissues [36]. Moreover, the diameter of the cross-section of the lumen is around 16 mm, which is within the same range of the real small intestine when it is not dilated (< 25 mm for adults [11]). To transmit the ultrasound beam for scanning, we immerse the phantom in room-temperature water. In reality, the gel applied on the skin surface and tissues around the small intestine would assist the transmission of these acous-tic beams. Note that for the locomotion control, currently, we evaluate on a single robot module. For the reversible anchoring monitoring, we use a serial configuration with two modules.

A. Closed-Loop Locomotion Control

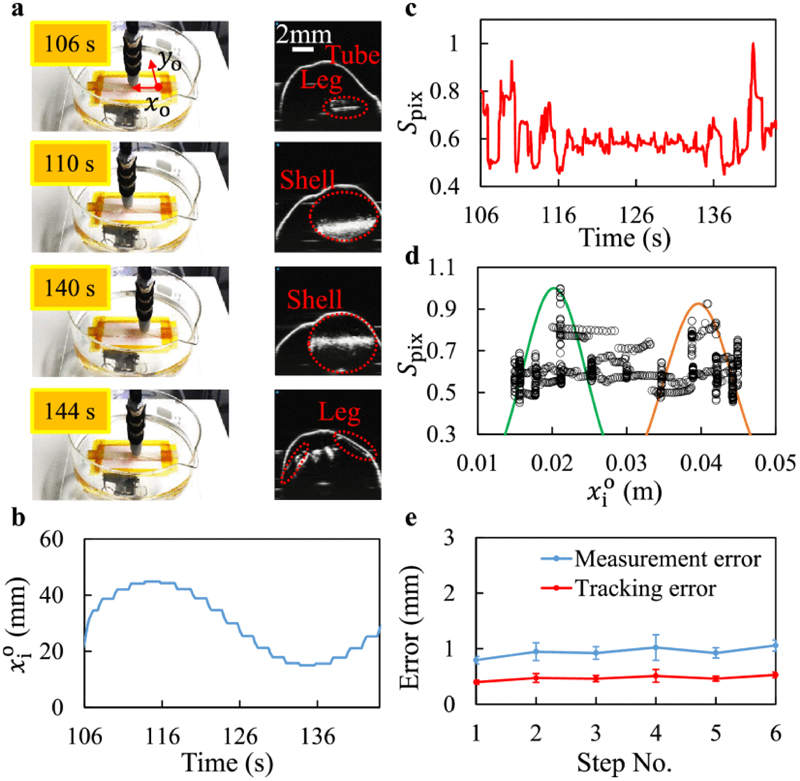
A straight path of 6 cm with six via-points (1 cm as a step) along the xo-axis is used to evaluate the control system. The control parameters are set as: ${\theta }_{\text{m}}^{\text{o}}=0,w_m=60rpm,{\sigma }_x=1.5cm,{\sigma }_y=0$. For each control step, after the manipulator moves to a pre-defined via-point, the ultrasound imaging plane is Fig. 8. Monitoring of the reversible anchoring from the cross-section view using 2D ultrasound imaging. Legs of the anchoring robot are labeled to indicate the configuration differences between the relaxation state and the anchoring state. a-c. Actuation of the anchoring state. c-e. Actuation of the relaxation state. positioned actively by the arm to sweep around the predicted position of the robot to update the position measurement. The details of the third via-point of an experiment trial are shown in Fig. 7a-d. The positions of the imaging plane along the x _o-axis from 106 s to 144 s is shown in Fig. 7b. The pixel value sums along this period are shown in Fig. 7c. At 110 s and 140 s, the sums are clearly higher. These positions correspond to the locations of the shells, as shown in Fig. 7a. After the sweeping, the imaging plane positions and the corresponding pixel value sums are all recorded, as shown in Fig. 7d. Based on the tracking approach explained in Section IV.B, the robot position measurement is updated. This value is fed back for further operations of the control system. The whole procedure takes less than 4 min. We run the tests for three trials, and the errors of each via-point are summarized in Fig. 7e. The measurement error is defined as the absolute divergence of the position measurement away from the real position of the robot. The tracking error is defined as the absolute difference between the filtered position estimation and the real position. The maximal error posted by the measurement is smaller than 1.5 mm, which is minor (less than 10%) compared to the robot’s body length. These quantitative results show the robustness of our policy based on the current test conditions.

Fig. 8.

Monitoring of the reversible anchoring from the cross-section view using 2D ultrasound imaging. Legs of the anchoring robot are labeled to indicate the configuration differences between the relaxation state and the anchoring state. a-c. Actuation of the anchoring state. c-e. Actuation of the relaxation state.

Fig. 7.

Experimental details of the 2D closed-loop locomotion control system. a-d. Results from a via-point during robot locomotion. a. Camera view and ultrasound imaging of the cross-sections at four steps during the sweeping around a via-point. b. Positions of the imaging plane along the $x_{°}-\text{axis}$ during sweeping. c. Variation of pixel value sums (normalized) during sweeping. d. Relation between the imaging plane positions and the normalized pixel sums from the collected points. Gaussian distributions are used to compute the updated measurement of robot position. e. Measurement and the tracking errors of six via-points along the 1D pre-defined path (points are the means of n = 3 trials; error bars are standard deviations from the means).

B. Reversible Anchoring Monitoring

Once the robot is controlled to arrive at the desired location, the reversible anchoring can be enabled using the method shown in Section III. Here we use a serial configuration of two robots (modules) to show the process of reversible anchoring. The state transition under 2D ultrasound monitoring is shown in Fig. 8. During the anchoring state, the tubular structure is expanded, where the diameter is increased by 25%. To quantify the anchoring effects, we use an external setup with a load cell (GSO-1K, Transducer Techniques) to measure the maximum static friction when the configuration relaxes and anchors. The results show that, during the relaxation state, the force is 290 ± 58 mN, while the force is increased more than twice to 715 ± 69 mN during the anchoring state (larger than the reported axial peristaltic force 450 mN [14]). Therefore, the robot design has proven effective in resisting peristaltic forces. In real applications, more modules can be used in the serial configuration to enhance further the anchoring effect based on the case-by-case requirements. The 3D-mode of the ultrasound machine is used to visualize better the configuration differences between the two states (Fig. 9).

Fig. 9.

Two states visualized by 3D ultrasound imaging. a-b. Front and side views of the relaxation state inside a tubular phantom. c-d. Two corresponding 3D ultrasound views of the anchoring state.

VI. Conclusion and Discussion

To improve the applicability of untethered miniature robots towards medical operations in tubular structures, this work introduces a robotic system with a reversible anchoring robot design and a 2D ultrasound imaging-based tracking and control method. The relaxation and anchoring states of the proposed robot can be maintained stably without control input, which has not been achieved in previous small-scale anchoring robots based on magnetic interaction [14], [15], [17]. How the current design could be generalized to different tubular dimensions has also been discussed. Moreover, a robot position tracking approach based on the local sweeping of the ultrasound imaging is evaluated and has proven effective. Due to the flexibility of this tracking approach, it is expected to be more robust in real medical scenarios than the previous non-sweeping tracking approach [25]–[27], when the interaction between the untethered robot and the surrounding tissue is complex and hard to predict. A 2D closed-loop position control system is also implemented to realize the robot locomotion in a tubular phantom with the maximal position tracking error of 0.53 ± 0.05 mm.

Several points need to be addressed in the future works to enable the application of the system in the real biomedical field. First, the system should be thoroughly evaluated under more real biologically relevant conditions using better tissue-mimicking phantoms. Second, more complete dynamics are required in consideration of the complex interactions in real tubular structures. Third, the flexibility of the manipulation system should be enhanced by another robotic arm as a manipulation tool. Finally, other functional parts, such as drug delivery or biopsy tool, can be added to the current robot design to enhance its medical functionality further.

Supplementary Material

Movie 1

This article has supplementary downloadable material available at https://ieeexplore.ieee.org, provided by the authors.