Ultrafast control of magnetic interactions via light-driven phonons

Abstract

Resonant ultrafast excitation of infrared-active phonons is a powerful technique to control the electronic properties of materials, leading to remarkable phenomena such as light-induced enhancement of superconductivity^1,2, switching of ferroelectric polarization^3,4 and ultrafast insulator to metal transitions⁵. Here we show that light-driven phonons can be utilized to coherently manipulate macroscopic magnetic states. Intense mid-infrared electric field pulses, tuned to resonance with a phonon mode of the archetypical antiferromagnet DyFeO₃, induce ultrafast and long-living changes of the fundamental exchange interaction between rare-earth orbitals and transition metal spins. Non-thermal lattice control of the magnetic exchange, defining the very stability of the macroscopic magnetic state, allows us to perform picosecond coherent switching between competing antiferromagnetic and weakly ferromagnetic spin orders. Our discovery emphasizes the potential of resonant phonon excitation for the manipulation of ferroic order on ultrafast timescales⁶.

The ability to control macroscopic states of matter by light on the fastest possible timescale crucially relies on finding efficient routes to manipulate the various microscopic interactions defining the very stability of the cooperative state⁷. In magnetism, these interactions either involve the electrons of only one magnetic ion, e.g. single-ion magnetic anisotropy^8,9, or rely on a mutual interaction between pairs of magnetic ions, e.g. exchange coupling¹⁰. Despite the intrinsic differences, both of these interactions originate from the same electrostatic Coulomb repulsion strongly sensitive to the lattice symmetry and the electronic overlap. Terahertz control of magnetism is a thriving field, but its main focus until now has been limited either to the direct excitation of spins by the magnetic field component of the single-cycle terahertz pulse¹¹ or to resonant pumping of the electronic degrees of freedom^9,12. Resonant pumping of infrared-active phonons with multi-terahertz pulses in the mid-infrared spectral (MIR) range has emerged as a low-energy route to drive large-amplitude net structural distortions. These coherent lattice distortions, emerging on the timescale of several picoseconds, modulate the spatial overlap of the electronic wave functions and have been shown to transiently melt charge¹³ and orbital ordering¹⁴, drive metal-insulator phase transitions⁵ and even enhance superconducting correlations in high-T _C cuprates^1,2. Although pioneering experiments have demonstrated that driving optical phonons can also affect magnetism^15–18, no coherent switching of the spin orientation or coherent light-induced magnetic symmetry breaking has been shown so far. Here we investigate phonon-induced magnetism (phonomagnetism) in dysprosium orthoferrite (DyFeO₃), a material where a strong exchange interaction between the spin of the transition metal (TM) ion and the orbital momentum of the rare-earth (RE) ion leads to a distinctive first-order spin-reorientation phase transition accompanied by a change of the magnetic symmetry from the antiferromagnetic (AFM) to the weakly ferromagnetic (WFM)¹⁹. We show that a sub-ps pulse of an intense multi-terahertz electric field, tuned in resonance with a phonon mode (see Fig. 1a), drives a coherent spin-reorientation, developing long-living WFM order within a half-cycle of the spin precession. Phonon-induced magnetism emerges via a non-equilibrium metastable state (see Fig. 1b), inaccessible not only via a thermodynamic transformation but also via optical pumping of the high-energy electronic transitions. We experimentally and theoretically demonstrate that phonomagnetism originates from phonon-induced lattice distortions leading to ultrafast modification of the RE-TM exchange interaction.

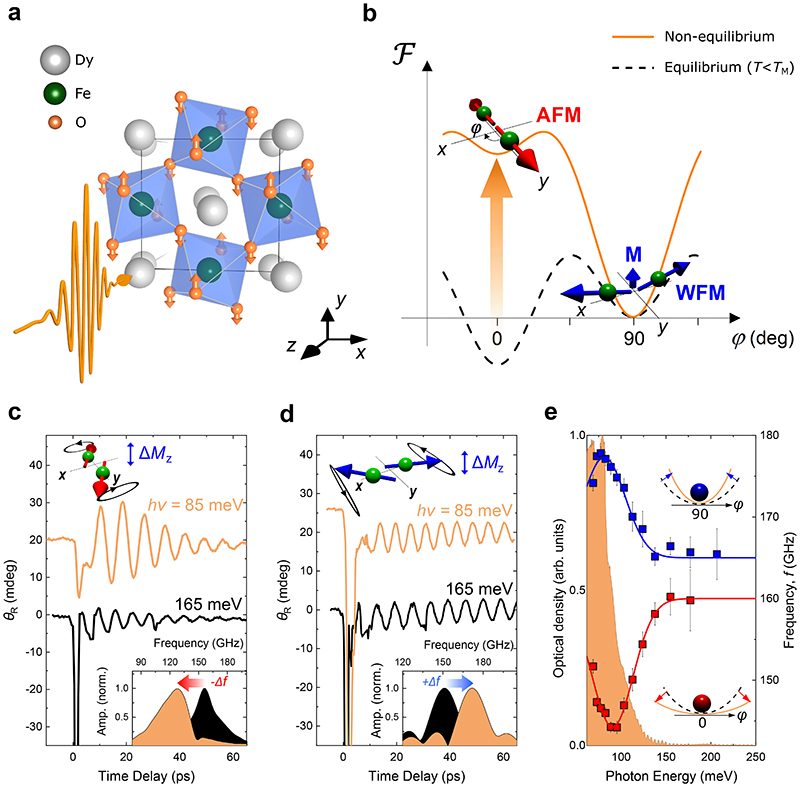
Fig. 1. Phonon-driven reconfiguration of the magnetic potential in DyFeO₃.

(a) The eigenmode of the laser-excited B_u phonon mode; orange arrows indicate the atomic motion of the oxygen ions. (b) The magnetic potential Ƒ as a function of the angle φ the spins form with the y-axis before (dashed black) and after (solid orange) phonon excitation. For simplicity the potential is shown only for T<T _M. The red and blue arrows depict the spin configurations corresponding to the antiferromagnetic (AFM) and weakly ferromagnetic (WFM) magnetic phases. The orange arrow highlights the destabilization of the AFM ground state together with the reduction of the potential barrier separating the phases. (c,d) Time-resolved transient rotation of the probe polarization plane θ _R after light excitation with photon energy of 85 meV (orange traces) and 165 meV (black traces) performed in the AFM (b) and WFM (c) phases. The bottom insets show the normalized amplitude spectra of the soft mode oscillations. The top insets are schematics of the corresponding spin precessions, with the resulting oscillating magnetic component ΔM _z. (e) Central frequency of the excited soft mode as a function of the photon energy of the pump pulse in the two magnetic phases. The solid lines serve as a guide to the eye. The background, shaded, curve shows the sample’s optical density. The insets schematically indicate changes in the local curvature of the magnetic potential.

The magnetic insulator DyFeO₃ crystallizes in a perovskite orthorhombic structure and exhibits antiferromagnetic spin order set by the Fe-Fe isotropic exchange interaction. Although the singlet state of the Fe³⁺ ion (⁶ S ground state) results in negligible single-ion magnetic anisotropy, its anisotropic exchange interaction with the large angular momentum of the dysprosium (⁶ H _15/2 ground state) mediates the strong coupling of the iron spins to the crystal lattice, thereby setting up the magneto-crystalline anisotropy¹⁹. The thermal population of the two lowest Dy³⁺ Kramers doublets (energy gap ΔE=6.4 meV) changes the orbital state of the RE. This change defines the virtue and symmetry of the Fe-Dy exchange coupling, leading to a spontaneous first-order spin reorientation transition. During this transition, at the Morin temperature T _M =51 K, the direction of the magnetic easy-axis for the iron spins changes abruptly between the y- and x-crystal axis. The reorientation is accompanied by a change in magnetic symmetry, from a collinear AFM, to a canted WFM state characterized by the emergence of a net magnetization M.

The spin-reorientation is described by the magnetic potential Ƒ which depends on the temperature and the angle φ the spins form with the y-axis (see Supplementary Note 2). In a broad temperature range this potential function features two characteristic minima at 0° and 90° (see Fig. 1b) signalling two ordered states. The height of the potential barrier separating the two competing states, as well as their relative energy, is controlled by the strength of the Fe-Dy exchange. This interaction is not only sensitive to the temperature but also to changes in the crystal environment, both via direct modulation of the Fe-Dy electronic overlap and via structurally-driven changes in the orbital state of the RE 4f multiplet^9,20. In our study we consider light-induced oscillations of atoms driven far from their equilibrium positions in order to control the strength of the Fe-Dy exchange^21,22 and to realize lattice control of the spin arrangement on the ultrafast timescale.

In our experiments we investigate spin dynamics in single crystals of z-cut DyFeO₃ (see Methods). The phonon excitation is provided by an intense (electric field in excess of 10 MV/cm), phase locked mid-infrared impulsive source (250 fs, 1 kHz), tunable in a broad photon energy range from 65 to 250 meV (16-60 THz). This energy range covers the highest frequency infrared-active TO phonon mode (B_u) centered at 70 meV and associated with periodic stretching of the Fe-O bonds, see Fig. 1a and Supplementary Figures 2,9. The ensuing spin dynamics are measured, in a conventional pump-probe scheme, by tracking the polarization rotation θ _R, imprinted by the magneto-optical Faraday effect, on co-propagating near-infrared (IR) probe pulses at the photon energy of 1.55 eV. In our experimental geometry, the Faraday rotation probes the magnetization dynamics along the normal direction. Importantly, the frequency f of the antiferromagnetic spin precession mode (the soft mode of the Morin phase transition), informs us on the local curvature of the magnetic potential, according to the relation $f^2\propto {\left.\frac{{\partial }^{2}F}{\partial {\phi }^2}\right|}_{\phi ={\phi }_0}$, both in the AFM (φ ₀ = 0°) and WFM (φ ₀ = 90°) phases, similarly to Refs. ^23,24, see also Supplementary Note 3.

Figure 1c and 1d show light-induced dynamics of the Faraday signal in the AFM and WFM phases revealing coherent oscillations, corresponding to spin precession around their respective equilibria. These dynamics are induced by pump pulses tuned in resonance with the lattice vibrational mode (85 meV). As a control experiment, we excite magnon oscillations via impulsive stimulated Raman scattering (ISRS)²⁵ using pulses tuned away from lattice or electronic resonances (165 meV). We note that the frequencies of the magnon oscillations excited by ISRS coincide exactly with the tabulated values reported in the literature^24,26 and therefore serve as in-situ probe of the curvature of the potential Ƒ at equilibrium.

A comparison of the Fourier spectra (insets in Fig. 1c and 1d) reveals that the frequency of the spin precession excited by pulses in resonance with the lattice mode is shifted as compared to the equilibrium value. The sign of the shift Δf depends on the initial magnetic configuration, being red in the AFM phase and blue in the WFM phases. To underscore the resonant character of the frequency shift we tune the photon energy of the pump pulse across the phonon resonance and extract the central frequency of the spin oscillations (Fig. 1e). The data acquired in both magnetic phases show that the onset of the frequency-shift follows closely the spectrum of the linear absorption of the B_u phonon mode, revealing a correlation between light-driven phonon and spin dynamics. These observations contain important information on the effects of the phonon-pumping on the magnetic potential. The red shift indicates a flattening of the potential energy in vicinity of the AFM minimum (φ = 0°), which may lead to a phase instability. The blue shift observed in the WFM phase points at an increased curvature of the potential and enhanced phase stability in vicinity of the WFM minimum (φ = 90°).

Time-resolved Fourier analysis indicates that the oscillations are chirped and the change in frequency occurs already within a half-cycle of the first spin oscillation, defining an upper bound for the phonon-driven changes in the magnetic potential of about 5 ps, see Fig. 2. This time is an order of magnitude shorter than the one reported in Ref. ²⁴, where the heat-driven dynamics of the magnetic potential were governed by the interaction of incoherent acoustic phonons with the Dy³⁺ electrons. Thus, the observed ultrafast response excludes heat-driven spin-lattice relaxation as the origin of the initial kinetics. Remarkably, the change in frequency persists for a time τ >100 ps exceeding the precession period by nearly an order of magnitude. We also note that the absolute value of τ closely follows the characteristic equilibrium decay time of the spin precession (see inset Fig. 2).

Fig. 2. Ultrafast dynamics of the soft mode frequency.

(Top panel) Trace of the spin precession dynamics after resonant phonon excitation (hν=85 meV) in the weakly ferromagnetic (WFM) phase. The solid lines are sine fits to extract a time varying frequency f. (Bottom panel) The resulting dynamics of the frequency f as measured in the AFM (red, T=43 K) and WFM (blue, T=57 K) phases. The solid lines are guides to the eye. The triangular markers at t < 0 correspond to reference measurements performed at a pump photon energy of 165 meV. Inset: Relaxation time τ of the frequency across the Morin temperature T _M (orange markers) imposed on the decay time of the spin precession (black markers).

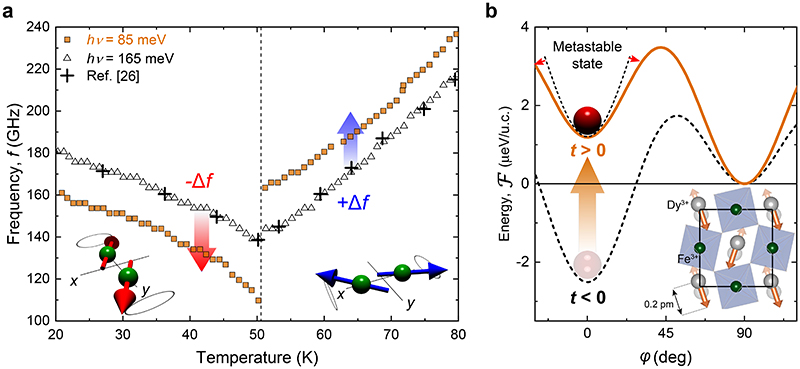
As shown in Fig. 3a, measurements of the frequency of the magnetic mode at equilibrium as a function of temperature reveal a cusp-like evolution in proximity to T _M, in excellent agreement with Ref. 26. In contrast, the frequency of the magnons launched via resonant phonon excitation is characterized by a split-up of the magnon branches at T _M leading to a pronounced discontinuity of more than 50 GHz (see Fig. 3a). The discontinuity leads to the emergence of magnetic responses at frequencies well below the minimum value attainable at equilibrium (140 GHz). Although the heat-capacity of DyFeO₃ changes by a factor of 20 between 10 and 60 K²⁷, the magnitude of the observed frequency change is nearly temperature-independent in the range 10 – 100 K, providing another indication that a non-thermal process is at play. From the analysis of the temperature dependence of the magnon frequencies, we map out the magnetic potential Ƒ (see Supplementary Note 3) before (t < 0) and after (t > 0) laser excitation, see Figure 3b. Importantly, phonon-pumping significantly increases the energy of the AFM state, simultaneously lowering the potential barrier, such that close to T _M the AFM phase may lose its stability (see also Supplementary Fig. 6).

Fig. 3. Out-of-equilibrium metastable magnetic state.

(a) Frequency of the spin precession as a function of the temperature across the Morin phase transition for different photon energies of the pump excitation. (b) Reconstructed magnetic potential Ƒ before (t < 0) (dashed black) and after (t > 0) (solid orange) the phonon-pumping. The position of the red ball represents the energy state of the system. Inset: The eigenmode of the A_g lattice distortion being considered as a driving force for the dynamics of the magnetic potential. The orange arrows depict the motions of the Dy³⁺ ions, antipolar in the adjacent layers.

We note that the frequency difference between the excited phonon (17 THz) and the magnon (0.2 THz) rules out direct phonon-magnon coupling. To describe our experimental findings, we propose a simple phenomenological model that indicates that all the changes of the magnetic potential can be explained by a renormalization of a single value parametrizing the strength of the Fe-Dy exchange by about 5 μeV/u.c. (see Supplementary Note 3 and Supplementary Fig. 6). In order to identify the microscopic pathways that connect the light-driven optical phonons with the transient changes in the Fe-Dy exchange, we use density functional theory (DFT) calculations (see Methods and Supplementary Note 5). The computations suggest the presence of a transient coherent lattice distortion in response to resonant pumping of the B_u mode. This distortion has the same lifetime as the infrared-active mode (~1 ps) and emerges as a consequence of an anharmonic interaction of different phonon modes, generally known as Ionic Raman Scattering or nonlinear phononics²⁸, which rectifies and transfers the large-amplitude excitation of the B_u polar mode into a finite time distortion along the coordinate of a coupled, Raman-active A_g phonon mode (see inset Fig. 3b and Supplementary Fig. 9). This lattice distortion involves antipolar motions of the heavy Dy³⁺ ions reaching values of about 0.2 pm for the pump fluences employed in our experiment (see Supplementary Note 5 and Supplementary Fig. 10). The DFT results also show that such displacements can alter the Fe-Dy exchange integral by about 1-2 μeV/u.c., consistent with the estimation of the phenomenological model (see Supplementary Fig. 11). The long-living effect of the distortion on the Fe-Dy exchange is presumably governed by the spin-lattice interaction, also defining lifetime of the spin precession, see inset Fig. 2.

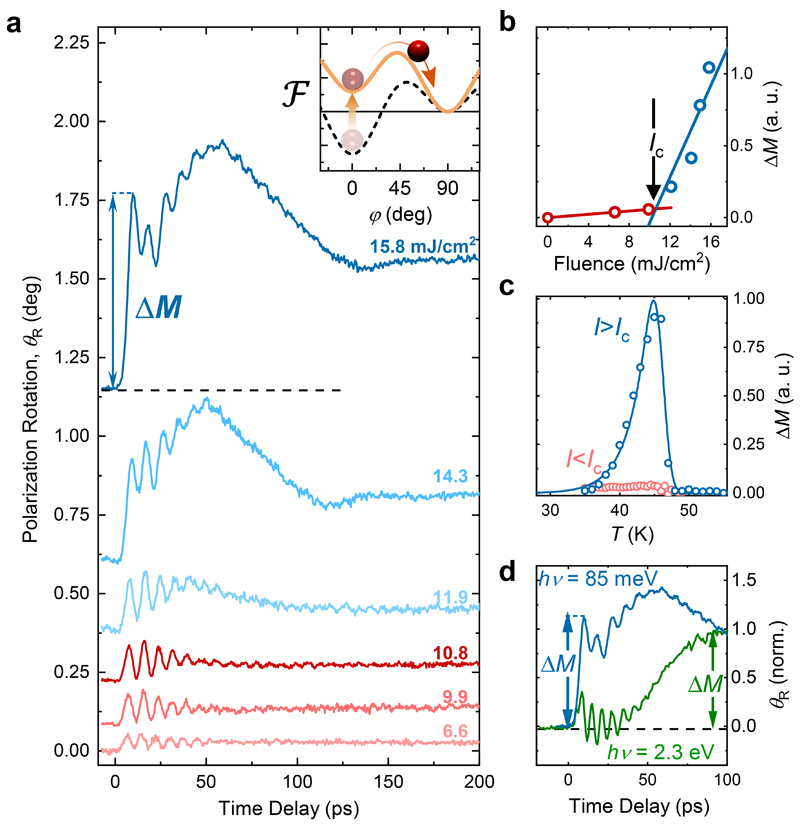
To demonstrate the potential of the phonomagnetism for ultrafast control of magnetic states we carried out phonomagnetic modifications of the RE-TM exchange interaction in proximity to T _M. Two distinct regimes of the magnetization dynamics are observed above and below a critical fluence I _c=10 mJ/cm² (see Fig. 4a,b). For fluences below I _c the pump drives a nearly harmonic response of spins mainly influencing its amplitude and frequency. However, upon exceeding the value of I _c, the course of the magnetization dynamics changes dramatically. A long-lived (>250 ps) offset, odd parity with respect to the sign of the applied field, develops within nearly a half-period of the spin precession (<5 ps), marking the coherent emergence of a transient magnetization ΔM. As the temperature is varied, it becomes apparent that the induced magnetization peaks nearly at T _M and completely vanishes for T > T _M (see Fig. 4c). The presence of a well-defined fluence threshold, as well as the observation of the phonon-induced macroscopic magnetization inherent to the WFM phase, are clear signatures that phonon pumping drives the coherent reorientation of spins accompanied by a change in the magnetic symmetry.

Fig. 4. Ultrafast phonon-induced magnetic phase transition.

(a) Time-resolved dynamics of the polarization rotation θ _R at T = 45K for various fluences of the pump. Each trace is obtained by subtracting individual traces obtained for opposite polarities of the external magnetic field to highlight magnetic components of the dynamics. Inset: Schematics of the ballistic reorientation in the altered magnetic potential Ƒ. (b) Amplitude of the transient magnetization ΔM as a function of the pump fluence I. (c) ΔM as a function of the sample temperature for fluences I above (blue curve) and below (red curve) the threshold I _c. (d) A direct comparison of the dynamics of the magnetization initiated by a pump pulse with above-bandgap photon energy (2.3 eV) and in resonance with the phonon mode (85 meV). a.u., arbitrary units.

In Fig. 4d we compare the spin-reorientation transition obtained in DyFeO₃ via conventional ultrafast heating (excitation with photon energy 2.3 eV, above the material’s band gap) with the phonomagnetism discussed here (see also Supplementary Note 6 and Supplementary Fig. 12). We note that ultrafast heating leads to the development of a net magnetization on a time scale of 100 ps, consistent with the spin-lattice relaxation time²⁴. In contrast, the phonomagnetic route develops light-induced magnetism within a half cycle of the spin precession, below 5 ps, indicating its coherent character.

By resonantly pumping infrared-active phonons with strong-field ultrashort multi-terahertz pulses of light, we have investigated a new route to reshape magnetic potentials and initiate ultrafast coherent magnetic phase transitions. Using a phenomenological description and first-principles calculations, we have demonstrated that the mechanism is based on a phonon-driven change of the exchange interaction between the rare-earth and transition metal ions. We anticipate that a similar mechanism will be active in other magnetic materials featuring anisotropic exchange interactions such as rare-earth based compounds (manganites, vanadates, and orthochromites) and type-II multiferroics²⁹. Our findings fill the gap between manipulation of magnetism with single-cycle terahertz pulses^9,11 and ultrashort pulses at optical frequencies⁶, highlighting new avenues for the manipulation of ferroic order on ultrafast timescales and providing a new platform for magnonics and antiferromagnetic spintronics³⁰.

Methods

Sample and experimental setup

We used a monocrystalline, 63-μm-thick DyFeO₃ sample grown by floating-zone melting. The sample is cut perpendicularly to the z-crystallographic axis in the form of a thin slab. The sample was kept in a dry-cycle cryostat (Montana Instruments) which allowed to cool it down to 10 K, far below T _M. Static bias fields up to B _ext = 700 mT from an electromagnet were applied within the (xz)-plane of the crystal at an angle of about 70° relative to the z-axis to provide a single domain magnetic state of the sample.

The intense pump pulses with wavelengths in the mid-infrared (MIR) spectral range used in this experiment, were generated via difference frequency generation (DFG) in a GaSe crystal using the output beams of two commercially available, independently tunable optical parametric amplifiers (OPAs) integrated into a single housing (Light Conversion, TOPAS-Twins). The OPAs were pumped by a commercially available amplified Ti:Sapphire laser system (Coherent, Astrella) delivering pulses at a 1 kHz repetition rate with a duration of 100 fs and a photon energy of 1.55 eV (λ=0.8 μm). The OPAs were seeded by the same white light generated in a sapphire crystal, which ensures separately tunable, but phase-locked output pulses³¹ with photon energies in the range 0.45-1.1 eV (λ=2.7-1.1 μm). As a result, when the pulses are mixed in the GaSe crystal, the generated MIR pulses are carrier envelope phase (CEP) stable³², linearly polarized and their energy lies in the range from 65-250 meV (λ=19-5 μm) with an average pulse duration of around 250 fs. The scheme of the setup for generation of the MIR pulses (MIR converter) is shown in Supplementary Fig. 1.

To generate pump pulses in the visible spectrum with a photon energy larger than the electronic band gap, we used a β-barium borate (BBO) single crystal to double or triple the photon energy of a single OPA output. This provided tunable excitation pulses with energies in the range of 0.9 - 3.3 eV (see Supplementary Fig. 1).

In the experiments, the mid-infrared pulses were focused onto the sample surface to a spot with a diameter of about 150 μm, using an off-axis parabolic mirror. The pump-induced dynamics were measured in a transmission geometry. The polarization rotation θ _R of the linearly polarized probe pulse, imprinted by the magneto-optical Faraday effect, was measured with the help of a polarization bridge (Wollaston prism) and a pair of balanced Si photodetectors.

The loss function of the sample in the MIR spectral range was measured using a Nicolet 6700 Fourier transform infrared (FTIR) spectrometer. The optical absorption in the visible spectral range was measured using a halogen lamp and an Ocean Optics spectrometer.

DFT Calculations

We simulated the Pnma phase of DyFeO₃ through density functional theory (DFT)^33,34 and its projected augmented wave (PAW)³⁵ flavour as implemented in the ABINIT package^36–38. The PAW atomic potentials used for Fe and O were downloaded from the GBRV pseudopotential library³⁹ with 3s, 3p, 3d, 4s and 2s, 2p considered as valence states for Fe and O respectively. For Dy we used the PAW atomic potential from M. Topsakal et al.⁴⁰ where the valence states are 4f, 5s, 5p and 6s (with f electrons in the valence). We used the PBEsol GGA functional⁴¹ for the exchange correlation interaction and Hubbard corrections⁴² on both Fe and Dy of respectively 4 and 7 eV have been used to have the closest possible properties with respect to experiments (lattice constants). All the calculations were done with a 6x6x4 mesh of k-points for the reciprocal space and a cut-off energy on the plane wave expansion of 36 Hartree and 72 Hartree for the second finer grid inside the PAW spheres. To calculate the phonons, the frozen phonon technique has been used through the phonopy software⁴³

Data availability

All data presented in this work are publicly available with identifier (DOI) 10.5281/zenodo.4338556

Code availability

The TB2J code for calculating exchange interactions is freely available under the BSD 2 clause license and can be found at https://github.com/mailhexu/TB2J/.

The Abinit code for DFT calculations is an open source code with GNU General Public License and is freely available at https://www.abinit.org/.