Evaluating Reinforcement Learning Agents for Anatomical Landmark Detection

Abstract

Automatic detection of anatomical landmarks is an important step for a wide range of applications in medical image analysis. Manual annotation of landmarks is a tedious task and prone to observer errors. In this paper, we evaluate novel deep reinforcement learning (RL) strategies to train agents that can precisely and robustly localize target landmarks in medical scans. An artificial RL agent learns to identify the optimal path to the landmark by interacting with an environment, in our case 3D images. Furthermore, we investigate the use of fixed- and multiscale search strategies with novel hierarchical action steps in a coarse-to-fine manner. Several deep Q-network (DQN) architectures are evaluated for detecting multiple landmarks using three different medical imaging datasets: fetal head ultrasound (US), adult brain and cardiac magnetic resonance imaging (MRI). The performance of our agents surpasses state-of-the-art supervised and RL methods. Our experiments also show that multi-scale search strategies perform significantly better than fixed-scale agents in images with large field of view and noisy background such as in cardiac MRI. Moreover, the novel hierarchical steps can significantly speed up the searching process by a factor of 4 − 5 times.

1. Introduction

Accurate detection of anatomical landmarks from medical images is an essential step for many image analysis and interpretation methods. For instance, the localization of the anterior commissure (AC) and posterior commissure (PC) points in brain images is required to obtain the optimal view of the mid-sagittal plane. This can be used as an initial step for image registration (Ardekani et al., 1997) or for the identification of pathological anatomy (Stegmann et al., 2005). Another example is the automated localization of standard views such as 2- and 4-chamber views in cardiac MRI examinations. This usually requires automatic landmark detection (Le et al., 2017; Lu et al., 2011) as a key step. Such view planning is important for consistent evaluation of different patients using standardized biometric measurements (Alansary et al., 2018). Landmark localization can also be used to initialize deformable models and atlas-based approaches for the evaluation of cardiac ventricular health (Bai et al., 2013). Furthermore, in fetal imaging, anatomical landmarks are used for estimating qualitative scores of fetal biometric measurements, such as: fetal growth rate, gestational age, and to identify abnormalities (Rahmatullah et al., 2012). They are also required in order to identify standardized views such as transventricular and transcerebellar planes, which are commonly used in clinical practice for fetal health screening (Li et al., 2018).

Since manual landmark annotation is time consuming and error prone, automatic methods were developed to tackle this problem. The design of such methods is challenging due to variable organ morphology, orientation, pathology, and image quality. Inspired by (Ghesu et al., 2016), we formulate the landmark detection problem as a sequential decision making process of a goal-oriented agent, navigating in an environment (the acquired image) towards a target landmark. At each time step, the agent decides which direction it has to proceed towards an optimal path to the target landmark. We use reinforcement learning (RL) to learn an approximation of the optimal solution of this sequential decision making process. One of the main advantages of applying RL to the landmark detection problem is the ability to learn simultaneously both a search strategy and the appearance of the object of interest as a unified behavioral task for an artificial agent. This approach does not require hand-crafted features and can be trained end-to-end. RL has the power to perform in a partial field-of-view or with incomplete data, which can be useful for real-time applications.

The main contributions of this work can be summarized as follows: (I) We propose and demonstrate use cases of several different deep Q-network (DQN) based models for anatomical landmark localization. (II) We investigate a fixed-and multi-scale search strategy for the optimal path with novel hierarchical action steps for agent based landmark localization frameworks. (III) We extensively evaluate the performance of the proposed agents by running multiple experiments on different MRI and US images in Section 5, outperforming state-of-the-art. (IV) We publish the first open source code of RL agents for a medical imaging task, which can accelerate significantly the potential application of RL to medical imaging.

2. Related work

Typical landmark localization methods can be categorized into three approaches: registration, appearance-based and image-based. The first category depends on robust rigid or non-rigid image registration techniques to match corresponding points of interest between target and reference images (Potesil et al., 2010; Rueckert et al., 2003). Appearance-based methods rely on spatial priors that capture the location of different landmarks by learning an appearance model (Milborrow & Nicolls, 2014; Potesil et al., 2015; Zhou et al., 2009). Image-based methods learn a set of image features located around the anatomical landmarks (Betke et al., 2003).

In the literature, most of the published works have adopted machine learning algorithms for landmark detection by learning a combined appearance and image based model. For example, Criminisi et al. (2013); Han et al. (2014) proposed a regression forest-based landmark detection approach to locate organs in full-body CT scans and Brain MRI, which uses Haar-like appearance features. Despite being fast and robust, this approach achieves less accurate localization results for larger organ structures. Gauriau et al. (2015) extended the work of (Criminisi et al., 2013) by incorporating statistical shape priors derived from segmentation masks with cascaded regression. Oktay et al. (2017) used a stratificationbased training model for a decision forest, where the latent variables within the stratified trees are probabilistic. Štern et al. (2016); Urschler et al. (2018) proposed a unified random forest framework combining appearance information with geometrical distribution of landmark points. These methods achieve robust results for locally similar structures by learning particular hand-crafted features, extracted from training data. However, the design of such features requires prior knowledge about the points of interest.

With the success of deep learning in different image-based applications, Zheng et al. (2015) proposed a two-stage approach for landmark detection using convolutional neural networks (CNNs). The first stage comprises of a shallow network with one hidden layer that is used to extract a number of 3D point candidates using a sliding window. This is followed by a deeper network, which is applied on image patches extracted around the selected points. Zhang et al. (2017) proposed a similar approach utilizing two CNNs to learn 3D displacements to a common template, which is followed by another convolutional layer for predicting the coordinates of multiple landmarks jointly. The first network is trained using image patches, whereas the second network shares the same weights from the first network with extra layers. The second network is trained using the whole image instead of patches to learn global information on top of the local information learned by the first network. Payer et al. (2016) adopted a CNN to model spatial configurations to detect multiple landmarks. The first block of their architecture generates local appearance heatmaps for individual landmark locations. Subsequently, the relative position of a single point with respect to the rest of the landmarks is learned through another convolutional kernel. The final heatmap combines both local appearance and spatial configuration between all landmarks. In order to capture global as well as local information, Andermatt et al. (2017) presented a method based on multi-dimensional gated recurrent units combining two recurrent neural networks. The first network detects a candidate region around the point of interest followed by a second network for more accurate localization. All previous methods rely on learning the search strategy and localization in two stages. This may increase the possibility that the second stage misclassifying multiple candidates from the output of the first stage as positive.

Ghesu et al. (2016) adopted a deep RL-agent to navigate in a 3D image with fixed step actions for automatic landmark detection. The artificial agent tries to learn the optimal path from any location to the target point by maximizing the accumulated rewards of taking sequential action steps. Xu et al. (2017), inspired by (Ghesu et al., 2016), proposed a supervised method for action classification using image partitioning. Their model learns to extract an action map for each pixel of the input image across the whole image into directional classes towards the target point. They use a fully convolutional network (FCN) with a large receptive field to capture rich contextual information from the whole image. Their method achieves better results than using an RL agent, however, it is restricted to 2D or small sized 3D images due to the computational complexity of 3D CNNs. In order to overcome this additional computational cost, Li et al. (2018); Noothout et al. (2018) presented a patch-based iterative CNN to detect individual or multiple landmarks simultaneously. Furthermore, Ghesu et al. (2017, 2019) extended their RL-based landmark detection approach to exploit multi-scale image representations.

3. Background

Machine learning enables automatic methods to learn from data to either make a decision or take an action. Broadly, machine learning algorithms can be classified into three main categories: unsupervised, supervised and reinforcement learning. Unsupervised learning methods rely on exploring and inferring hidden structures from unlabelled data. In a supervised manner, the learning is done from a training set of labeled examples provided by an expert. RL involves learning by interaction with an environment, which allows artificial agents to learn complex tasks that may require several steps to reach a solution (Sutton & Barto, 1998). RL has been applied to several medical imaging applications such as landmark detection (Ghesu et al., 2017, 2016, 2019), tissue localization (Maicas et al., 2017) and segmentation (Sahba et al., 2006; Shokri & Tizhoosh, 2003), image registration (Krebs et al., 2017; Liao et al., 2017), and view planning (Alansary et al., 2018), see Figure 1. In this section, we will give a brief overview of the theory behind RL followed by the application of deep learning to approximate a solution for the RL problem.

Figure 1. Previously published RL works with application to medical imaging analysis.

3.1. Reinforcement Learning

Inspired by behavioral psychology, RL can be defined as a computational approach for learning by interacting with an environment so as to maximize cumulative reward signals (Sutton & Barto, 1998). A learning agent interacts with an environment E at every state s. A single decision is made to choose an action a from a set of multiple discrete actions A. Each valid action choice results in an associated scalar reward, defining the reward signal, R. This sequential decision making can be formulated as a Markov decision process (MDP), where each s_t and a_t are conditionally independent of all previous states and actions holding the Markov assumption. The main goal is to learn an optimal policy that maximizes not only the immediate reward but also subsequent future rewards. The optimal function can be computed directly given the whole MDP using dynamic programming. However, in many applications (including in medical imaging) the MDP is usually incomplete, where the agent cannot directly observe all states. RL approximates the optimal function iteratively by sampling states and actions from the MDP, and learning from experience. There are several algorithms to solve an RL problem such as certainty equivalence, temporal difference (TD) and Q-learning. Because of the recent success of employing Q-learning in medical imaging applications (Alansary et al., 2018; Ghesu et al., 2017, 2016, 2019; Krebs et al., 2017; Liao et al., 2017; Maicas et al., 2017; Sahba et al., 2006), we adopt the common strategy of Q-learning-based methods as a solution for the RL problem formulation of landmark detection.

3.1.1. Q-Learning

Learning an optimal RL policy is defined as learning to map a given state to an action by maximizing the sum of numerical rewards r seen over the agent’s lifetime. The optimal action-selection policy can be identified by learning a state-action value function Q(s,a) (Watkins & Dayan, 1992), which measures the quality of taking a certain action a_t in a given state s_t The Q-function is defined as the expected value of the accumulated discounted future rewards $E\left[r_{t+1}+\gamma r_{t+2}+\cdots +{\gamma }^{n-1}{r}_{t+n}\mid s,a\right]$ γ ∈[0,1] is a discount factor that is used to weight future rewards accordingly. It can represent the uncertainty in the agent’s environment by providing a probability of living to see the next state. This value function can be unrolled recursively (using the Bellman Equation Bellman (2013)) and can thus be solved iteratively:

$$Q_{i+1}(s,a)=E\left[r+\gamma \underset{a^{\prime }}{\max }{Q}_i\left(s^{\prime },a^{\prime }\right)\right],$$ (1)

where s’ and a’ are the next state and action. We can find the optimal action for each state by solving Equation 1. The optimal action will have the highest long-term reward Q*(s, a).

3.1.2. Deep Q-Learning

The advent of deep learning has fuelled the current highly active RL research field. Mnih et al. (2015) proposed using a deep CNN to approximate Q(s, a) ≈ Q(s, a; ω), where ω represents the network parameters. This is known as deep Q-network (DQN), and achieved human-level performance in a suite of Atari games. Approximating the Q-value function in this manner allows the network to learn from large data sets using mini-batches. A naïve implementation of DQN suffers from instability and divergence issues because of: (i) the correlation between sequential samples, (ii) rapid changes in Q-values and the distribution of the data, and (iii) unknown reward and Q-values range that may cause large and unstable gradients during backpropagation. This can be tackled (Mnih et al., 2015) by using a target Q(ω⁻) network that is periodically updated with the current Q(ω) every n iterations, where ω⁻ represents the frozen weights of the target network. Freezing the target network during training stabilizes rapid policy changes. To avoid the problem of successive data sampling, an experience replay memory (D) (Lin, 1993) can be used to store transitions of [s, a, r, s’] and randomly sampling mini-batches for training. The approximation of best parameters ω* can be learned end-to-end using stochastic gradient descent (SGD) of the derivative of the DQN loss function $\frac{\delta L(\omega )}{\delta \omega }$, where:

$$L_{DQN}(\omega )=E_{s,r,a,s^{\prime }\sim D}\left[{\left(r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime };{\omega }^{-}\right)-Q(s,a;\omega )\right)}^2\right].$$ (2)

In order to prevent Q-values from becoming too large, also to ensure that gradients are well-conditioned, rewards r are clipped between [−1,+1]. This trick works for most of the applications in practice, however, it may have the drawback of not differentiating between small and large rewards. We outline below two recent state-of-the-art improvements to the standard DQN, and evaluate them experimentally in Section 5.

3.1.3. Double DQN (DDQN)

In noisy stochastic environments, DQN (Mnih et al., 2015) sometimes significantly overestimates the values of actions (Hasselt, 2010). This is caused by a bias introduced from using the maximum action value as an approximation for the maximum expected value. The max operator, max Q(s’,a’; ω⁻), uses the same values to select and evaluate an action resulting in selecting overestimated (overoptimistic) values. Hasselt (2010); Van Hasselt et al. (2016) proposed a solution, a double DQN (DDQN), to mitigate bias by decoupling the selected action from the target network. Thus, the current network is used for the action selection resulting in a modified loss function:

$$L_{DDQN}(\omega )=E_{s,r,a,s^{\prime }\sim D}\left[{\left(r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },Q\left(s^{\prime },a;\omega \right);{\omega }^{-}\right)-Q(s,a;\omega )\right)}^2\right].$$ (3)

DDQN improves the stability of learning and may translate to the ability to learn more complex tasks. The results of DDQN (Van Hasselt et al., 2016) illustrate reduction in the observed overestimation and better performance than DQN (Mnih et al., 2015) on several Atari games.

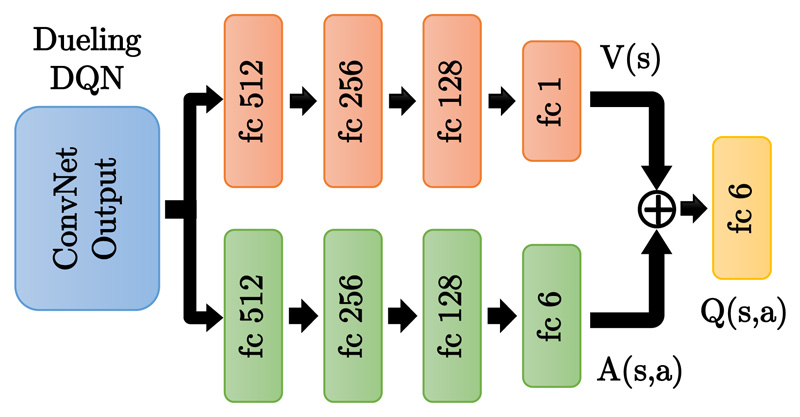
3.1.4. Duel DQN

Q-values correspond to the quality of taking a certain action given a certain state Q(s, a). Wang et al. (2015) proposed to decompose this action-state value function into two more fundamental notions of value. The first is an actionindependent value function V(s), which provides an estimate for the value of each state without having to learn the effect of each action. The second is an action-dependent advantage function A(s,a), which calculates potential benefits of each action. Intuitively, the Q-function learns separately how good a certain state is and how much better taking a certain action would be compared to the others. The new combined dueling DQN function is defined as:

$$Q(s,a)=A(s,a)+V(s).$$ (4)

This can be implemented by splitting the fully connected layers in the DQN architecture to compute the advantage and state value functions separately, then combining them back into a single Q-function only at the final layer with no extra supervision, see Fig. 2. Duel DQN can achieve more robust estimates of the state value by decoupling it from specific actions. s is more explicitly modelled, which yields higher performance in general. Duel DQN (Wang et al., 2015) shows better results than the previous baselines of DQN (Mnih et al., 2015) and DDQN (Van Hasselt et al., 2016) on several Atari games. In summary, duel DQN and DDQN introduced vast improvements in performance compared to DQN, yet it does not necessarily result in better performance in all environments.

Figure 2. Duel DQN architecture, which splits the fully connected (FC) layers into two paths: the state value V(s) and action advantage A(s,a) functions.

4. Reinforcement Learning for Landmark Detection

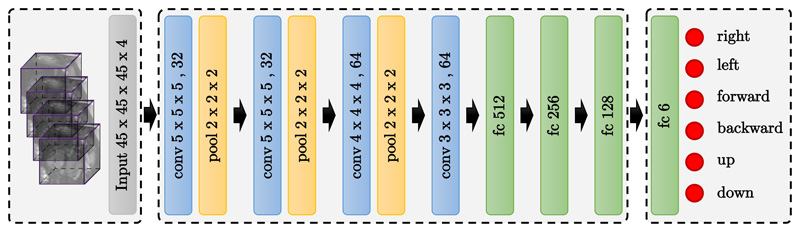
In this work, inspired by (Ghesu et al., 2016), we formulate the problem of landmark detection as an MDP, where an artificial agent learns to make a sequence of decisions towards the target landmark. In this setup, the input image defines the environment E, in which the agent navigates using a set of actions. The main goal of the agent is to find an anatomical landmark. In this section, we explain the main elements of the MDP that includes a set of actions A, a set of states S, and a reward function R. During testing, the agent does not receive any rewards and does not update the model either, it just follows the learned policy. Figure 4 shows the proposed CNN architecture for landmark detection, where the output of the CNN results in a Q-value for each action. The best action is selected based on the highest Q-value.

Figure 4.

Schematic illustration of the proposed DQN-based network architecture for anatomical landmark detection. The input are volumetric samples along the 3D trajectory of the region centered around the current location of the agent. The output is the approximated Q-value for the six possible actions. The agent will pick the action with the highest Q-value. This is done sequentially until the agent finds the target landmark.

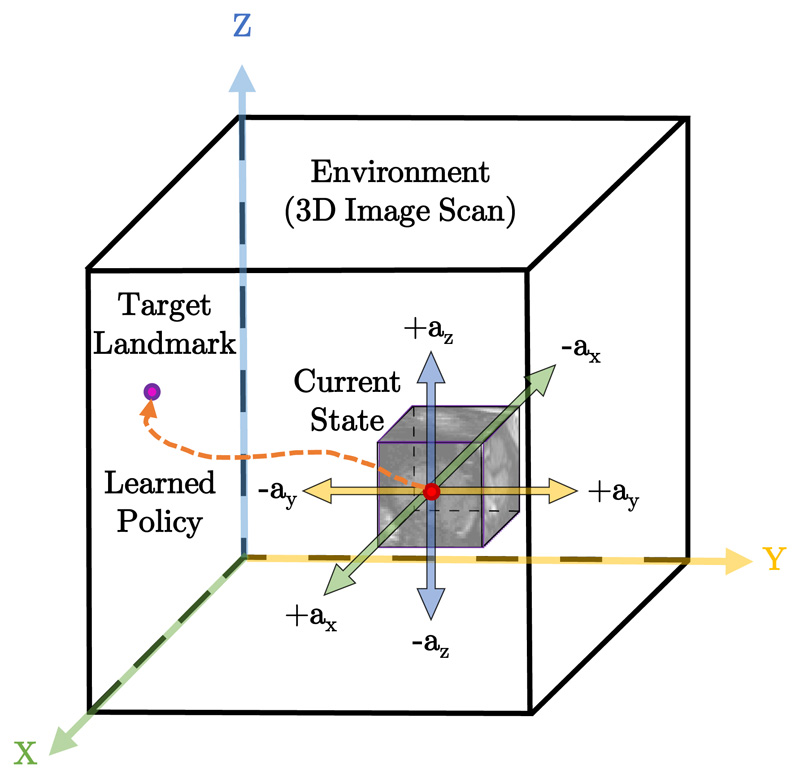
4.0.1. Navigation actions

The agent interacts with E by taking movement action steps a ∈ A that imply a change in the current point of interest location. The set of actions A is composed of six actions, {±a_x, ±a_y, ±a_z}, in the positive or negative direction of x, y or z. For instance, taking a +a_x action means that the agent will move a fixed step size in the positive x-direction. Figure 3 shows a schematic visualization of these navigation actions in a 3D scan.

Figure 3.

Schematic diagram of the proposed RL agent interacting with the 3D image environment E. At each step the agent takes an action towards the target landmark. These sequential actions forms a learned policy forming a path between the starting point and the target landmark.

4.0.2. States

Our Environment E is represented by a 3D image, where each state s defines a 3D Region of Interest (ROI) centered around the target landmark. A frame history buffer is used to capture the last 4 action steps (ROIs) taken by the agent in its search for the landmark. This stabilizes the search trajectories and prevents the agent from getting stuck in repeated cycles.

4.0.3. Reward function

Designing good empirical reward functions R is often difficult as RL agents can easily overfit the specified reward, and thereby produce undesirable or unexpected results. For our problem, the difficulty arises from designing a reward that encourages the agent to move towards the target plane while still being learnable. Thus, R should be proportional to the improvement that the agent makes to detect a landmark after selecting a particular action. Here, similar to (Ghesu et al., 2016), we define the reward function R = D(P_i−1,P_t)−D(P_i,P_t), where D represents the Euclidean distance between two points. We further denote P¿ as the current predicted landmark’s position at step i, with P_t the target ground truth landmark’s location. The difference between the two Euclidean distances, the previous step and current step, signifies whether the agent is moving closer to or further away from the desired target location.

4.0.4. Terminal state

The final state is reached when there are no further transition states for the agent to take. This means that the agent has found the target landmark P_t. We define the terminal state during training when the distance between the current point of interest and the target landmark are less than or equal to 1mm. Finding a terminal state during testing is more challenging, due to the absence of the landmark’s true location. One solution is to define a new trigger action that terminates the sequence of the current search when the target state is reached (Caicedo & Lazebnik, 2015; Maicas et al., 2017). Although this modifies the environment by marking the region that is centered around the correct location of the target landmark, it increases the complexity of the task to be learned by increasing the action space size. It also introduces a new parameter, maximum number of interactions, which needs to be set manually. It may also slow down the testing time in cases where the terminal action is not triggered. Riedmiller (1998) found that the agent shows strong oscillating behavior around the terminal state. We adopt the oscillation property to terminate the search process during testing without defining an explicit terminal state. In contrast to (Ghesu et al., 2016), we choose the terminating state based on the corresponding lower Q-value. We find that Q-values are lower when the agent is closer to the target point and higher when it is far. Intuitively, by awarding higher Q-values, DQN encourages the agent to take any action from states that are far away from the target landmark, and conversely for closer states.

4.0.5. Multi-scale agent

In images with large field of view, noisy background can deteriorate the performance of the agent for finding the target landmark. In order to capture spatial relations within a global neighborhood, we adopt a multi-scale search strategy (Ghesu et al., 2017, 2019) in a coarse-to-fine fashion with novel hierarchical action steps. The environment E samples a fixed size image-grid with initial spacing (S_x,S_y,S_z) mm around the current location P_o, and the agent searches for the target landmark with initial large action steps. Once the target point is found, E samples the new image-grid with smaller spacing, as well as the agent uses smaller action steps. Coarser levels in the hierarchy provide additional guidance to the optimization process by enabling the agent to see more structural information. Finer scales, on the other hand, provide more precise adjustments for the final estimation of the plane. Similarly, larger action steps speed convergence towards the target plane, while smaller steps fine tune the final estimation of plane parameters. The same DQN is shared between all levels in the hierarchy.

5. Experiments and results

The performance of different RL agents for anatomical landmark detection is evaluated on three different US and MR datasets. We evaluate fixed- and multiscale search strategies by sampling with different spacing values. During testing, we fix the initial selected points for all models for a fair comparison between different variants of the proposed method. We select 19 different starting points distributed in the whole image for every testing subject in order to report more robust results. We measure the accuracy based on the Euclidean distance error between detected and target landmarks. Finally, we run extensive comparison between different DQN-based architecture, namely DQN, DDQN, Duel DQN, and Duel DDQN.

Experiments

During training, a random point is sampled from a region with size 80% of the whole image dimensions around the center. An ROI of size 45x45x45 voxels is sampled around the selected point. The agent follows an e-greedy exploration strategy, where at every step it selects an action uniformly at random with probability (1 − ϵ). Every trial to find the target landmark is called an episode. Here we use 1500 frames to limit the maximum number of frames per episode. During testing, the agent follows the learned policy by selecting the action with highest Q-value at each step.

Comparison with state-of-the-art

We evaluate the performance of our agents against recent published works based on similar fixed-scale (Ghesu et al., 2016) and multi-scale (Ghesu et al., 2019) RL agents, and fully-supervised deep CNNs (Li et al., 2018) for the detection of the cavum septum pellucidum point in 3D fetal US head scans.

The method from Li et al. (2018) is based on repeatedly passing patches to a CNN until the estimated point position converges to the true landmark location with full supervision, called patch-based iterative network (PIN). We re-implemented the method in (Ghesu et al., 2016, 2019) as reported in their papers, while the code from (Li et al., 2018) is publicly available ¹. For this experiment, we use 72 fetal head ultrasound scans, divided into 21 training and 51 testing images, as detailed in Experiment 5.1. The performance of our multi-scale agents improve upon the state-of-the-art methods as shown in Table 1.

Table 1.

Comparison with stat-of-the-art RL (Ghesu et al., 2016, 2019) and supervised (Li et al., 2018) for detecting the cavum septum pellucidum point in fetal ultrasound images. Distance errors are in mm. Bold text shows the highest achieved localization accuracy for each landmark

A. State-of-the-art Results
RL Fixed-scale (Ghesu et al., 2016)	RL Multi-scale (Ghesu et al., 2019)	Supervised PIN Single-Landmark (Li et al., 2018)	Supervised PIN Multiple-Landmarks (Li et al., 2018)
7.37 ± 5.86	6.51 ± 5.41	5.47 ± 4.23	5.50 ± 2.79

B. Our Results
	DQN	DDQN	Duel DQN	Duel DDQN
Fixed-Scale	4.95 ± 3.09	5.01 ± 2.48	6.29 ± 3.95	5.12 ± 3.15
Multi-Scale	3.66 ± 2.11	4.02 ± 2.20	4.17±2.62	4.02 ± 1.55

5.1. Experiment-I: Fetal head ultrasound

Finding the target landmarks in such images is a challenging task because of ultrasound artifacts such as shadowing, mirror images, refraction, and fetal motion. We use three levels for the multi-scale agent with spacing values from 3mm to 1mm, decreasing by one at each level. Hierarchical action steps are chosen from 9 to 1 steps per iteration, dividing by 3 at each level of the hierarchy.

Dataset

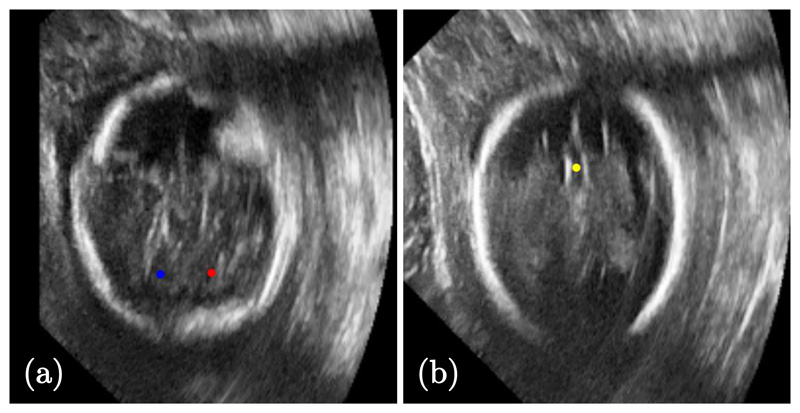
72 fetal head US scans ² are randomly divided into 21 and 51 images for training and testing. We choose three landmarks, the right and left cerebellum and cavum septum pellucidum, that define the transcerebellar (TC) plane, commonly used for fetal sonographic screening examination, see Fig. 5. The selected landmarks were manually annotated by clinical experts using three orthogonal views. All images were roughly aligned to the same orientation and re-sampled to isotropic 0.5mm spacing.

Figure 5. Sample 2D images from fetal head ultrasound showing the target landmarks:

(a) right (red) and left (blue) cerebellum, and (b) cavum septum pellucidum (yellow) points.

Results

Table 2 shows the comparative results of the performance of different agents. In general, all methods share similar performance including speed and accuracy. However, Duel DQN achieves the best accuracy detecting the right and left cerebellum points, while DQN performs the best for finding the cavum septum pellucidum point. Additionally, the multi-scale strategy improves the performance of the agents and increase pace to the target point thanks to the hierarchical action steps.

Table 2.

Comparison of different DQN-based agents using fixed-scale (FS) and multi-scale (MS) search strategies for the detection of right cerebellum (RC) and left cerebellum (LC), and cavum septum pellucidum (CSP) landmarks in fetal US images. Distance errors are in mm. Bold text shows the highest achieved localization accuracy for each landmark.

Method	Right Cerebellum (RC)		Left Cerebellum (LC)		Cavum Septum Pellucidum (CSP)
	FS	MS	FS	MS	sFS	MS
DQN	4.17 ± 2.32	3.37 ± 1.54	2.78 ± 2.01	3.25 ± 1.59	4.95 ± 3.09	3.66 ± 2.11
DDQN	3.44 ± 2.31	3.41 ± 1.54	2.85 ± 1.52	2.95 ± 1.00	5.01 ± 2.84	4.02 ± 2.20
Duel DQN	2.37 ± 0.86	3.57 ± 2.23	2.73 ± 1.38	2.79 ± 1.24	6.29 ± 3.95	4.17 ± 2.62
Duel DDQN	3.85 ± 2.78	3.05 ± 1.51	3.27 ± 1.89	3.50 ± 1.70	5.12 ± 3.15	4.02 ± 1.55

5.2. Experiment-II: Cardiac MRI

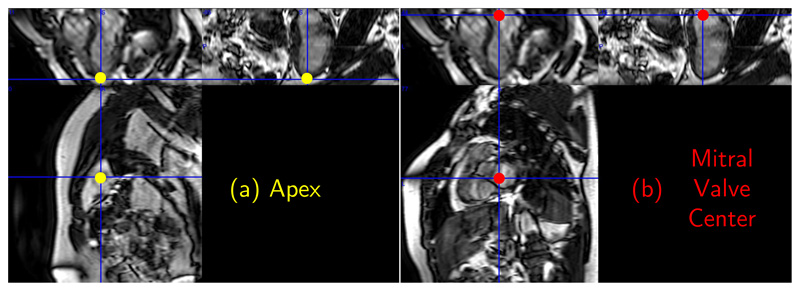
We select two landmarks, apex and centre of mitral valve, commonly used for defining the short axis view during image acquisitions, see Fig. 6. They are also used to assist automatic segmentation methods by defining starting and ending slices in the acquired cardiac stack of 2D image sequence.

Figure 6. A 2D cardiac MR-image showing the apex and center of the mitral valve points.

Dataset

455 short-axis cardiac MR images of resolution 1.25 × 1.25 × 2 mm obtained from the UK Digital Heart Project (de Marvao et al., 2014), randomly divided into 364 and 91 images for training and testing, respectively. All cardiac images are re-sampled to isotropic 1mm spacing. The ground truth landmarks are manually annotated by two experts. The localization errors are reported in terms of mean of Euclidean distance between the detected landmark position and the corresponding ground truth.

Results

Table 3 shows that Duel DQN agents perform the best for detecting the apex (AP), while all agents performs similarly for detecting the mitral valve center (MV). Multi-scale agents achieve a slight decrease in the detection error compared to inter-observer errors. They also significantly improve upon stratified decision forests (Oktay et al., 2017) and our fixed-scale agents, which is reasonable in cardiac imaging because of the bigger field of view and noisy background. We use the same dataset from (Oktay et al., 2017), but not the same setup of their experiments, and compare with the results reported in their paper.

Table 3.

A comparison between inter-observer errors, stratified decision forests (Oktay et al., 2017), and different agents using fixed-scale (FS) and multi-scale (MS) search strategies for the detection of apex and center of mitral valve landmarks in cardiac MR images. Distance errors are in mm. Bold text shows the highest achieved localization accuracy for each landmark.

Method	Apex (AP)		Mitral Valve (MV)
Inter-observer Errors	5.79 ± 3.28		5.30±2.98
Decision Forests (Oktay et al., 2017)	6.74 ± 4.12		6.32 ± 3.95
Proposed RL Agents	FS	MS	FS	MS
DQN	7.49 ± 4.05	4.47±2.63	8.33 ± 4.70	5.73±4.16
DDQN	8.13 ± 5.60	4.53±2.78	8.82 ± 4.80	5.20±2.82
Duel DQN	7.17±4.21	4.42 ± 2.67	8.82 ± 4.80	5.76 ± 3.89
Duel DDQN	7.59 ± 4.17	5.43±3.37	8.63±4.58	5.28±2.61

5.3. Experiment-III: Brain MRI

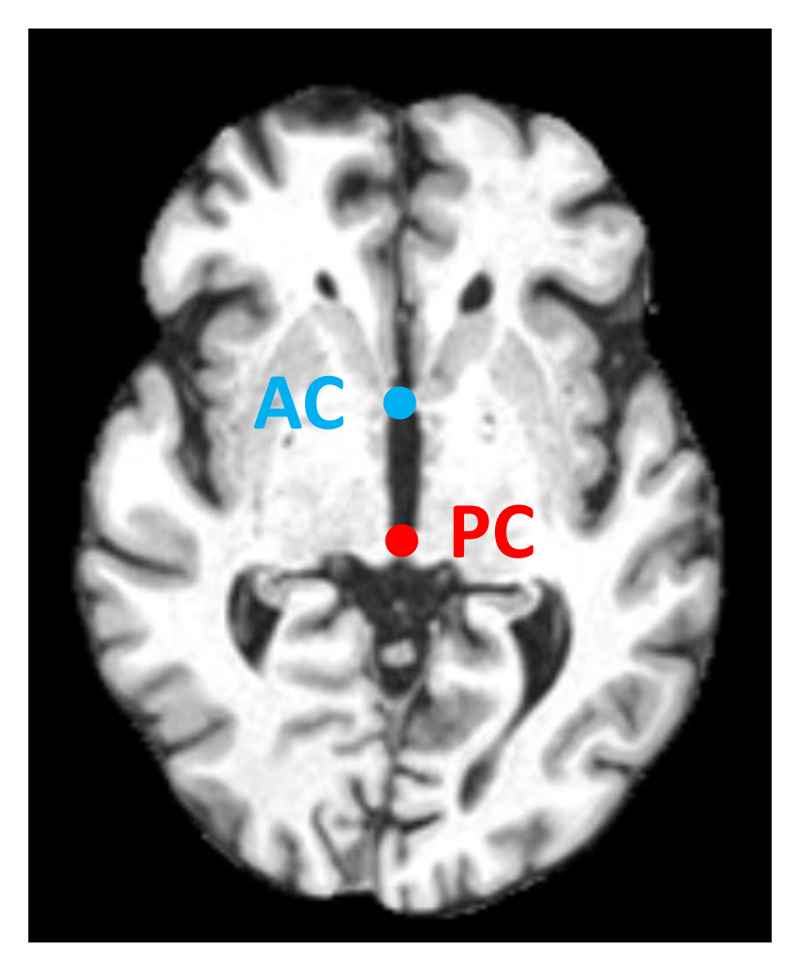
In this experiment, we select two landmarks: anterior and posterior commissure points, commonly used by the neuroimaging community to define the axial plane during image acquisition, see Fig. 7.

Figure 7. The anterior commissure (AC) and posterior commissure (PC) points in brain MRI.

Dataset

832 isotropic 1mm MR scans were obtained from the ADNI database (Mueller et al., 2005), randomly divided into 728 and 104 images for training and testing, respectively. All brain images were skull stripped and affinely registered to the same space. For both the training and testing datasets the selected landmarks were manually annotated by an expert observer using three orthogonal views.

Results

Similar to the fetal US experiment, Table 4 shows that the best performing agent varies for each landmark. However, the multi-scale strategy improves the performance of fixed-scale agents.

Table 4.

Performance of different agents using fixed-scale (FS) and multi-scale (MS) search strategies for the detection of anterior and posterior commissure landmarks in brain MR images. Distance errors are in mm. Bold text shows the highest achieved localization accuracy for each landmark.

Method	Anterior Commissure (AC)		Posterior Commissure (PC)
	FS	MS	FS	MS
DQN	3.04 ± 1.70	2.46 ± 1.44	2.03 ± 0.97	2.05 ± 1.14
DDQN	2.62 ± 1.24	2.61 ± 1.64	3.31 ± 1.2	1.86 ± 1.07
Duel DQN	3.04 ± 1.28	2.4 ± 1.42	3.6 ± 1.46	2.15 ± 1.24
Duel DDQN	2.97 ± 1.23	2.01 ± 1.29	2.04 ± 1.04	2.27 ± 1.22

Table 5 shows a list of the results from the literature for detecting the AC and PC landmarks on different datasets. These results are the same as reported from their published papers. All of these methods rely on some prior information using a pre-defined 2D plane that contain the target landmarks, region interest, or spatial prior probabilities. While the proposed method does not require any prior information and the agent is capable of finding the target landmark using any randomly initialized point.

Table 5.

General comparison with previously published works for the detection of AC and PC points. These are the results reported on the datasets used in the source papers. Note that all the other methods required some prior information either by finding the landmarks in the mid-sagittal plane only, or using spatial priors and region of interest. While the proposed method does not require any prior information, and it is also applied to the largest dataset.

Method	Mean Error (mm)		Data Size	Priors
	AC	PC
Verard et al. (1997)	0.41 ± 0.21	0.35 ± 0.32	30	Mid-sagittal plane
Prakash et al. (2006) - expert I	1.20 ± 1.30	1.10 ± 1.30	71	Mid-sagittal plane
Prakash et al. (2006) - expert II	1.20 ± 1.00	1.10 ± 1.20	71	Mid-sagittal plane
Ardekani & Bachman (2009) - NKI	0.90 ± 1.60	0.90 ± 1.80	48	Initialisation point
Ardekani & Bachman (2009) - IXI	1.10 ± 2.20	0.90 ± 1.80	84	Initialisation point
Guerrero et al. (2011)	0.45 ± 0.22	0.46 ± 0.20	200	Spatial prior probabilities
Guerrero et al. (2012)	0.67 ± 0.59	0.64±0.31	200	Spatial prior probabilities
Liu & Dawant (2015)	0.55 ± 0.30	0.56 ± 0.28	100	Region of interest
Proposed RL Agents	1.86 ± 1.07	2.01 ± 1.29	832	-

The trained RL agents have no access to any information about their position inside the image (e.g. x, y and z coordinates). These agents see only the intensity values within the current region of interest. Table 6 shows the mean and standard deviation of the Euclidean distances for each landmark to their mean point. The adult brain dataset were pre-aligned to the same coordinates resulting in mean distances around 2 pixels. While, the fetal and cardiac datasets result in larger distances around 35 and 48 mm.

Table 6. The average Euclidean distances of each landmark to their mean location in pixels.

Fetal Brain US			Cardiac MRI		Adult Brain MRI
RC	LC	CSP	AP	MV	AC	PC
35.45 ± 15.65	34.90 ± 15.27	35.83 ± 17.19	48.20 ± 10.04	47.12 ± 11.57	2.07 ± 1.08	1.95 ± 0.98

5.4. Implementation

Training times are around 24-48 hours for individual landmarks using an NVIDIA GTX 1080Ti GPU. Our experiments show that the agent is capable of finding the target landmark in less than 1 second for any random initialization. During inference, the agent finds the target location using sequential steps, where each step takes around 0.5-1 milliseconds. In our implementation we use a batch size of 48, experience replay memory of size 1e5, activation function PReLU for convolutional layers and leakyReLU for fully connected layers, ADAM optimizer, Y = 0.9, and e = 0.9 — 0.1. Hyper-parameters values were selected by evaluating the model during first few steps of training. Figure 4 shows the architecture of the proposed DQN. The source code of our implementation is publicly available³. More visualizations are on the github repository showing different animated visual examples of trained agents searching for the target landmarks.

6. Conclusion and discussion

In this paper, we have proposed different reinforcement learning agents based on DQN architectures for automatic landmark detection in medical images. These RL-agents are capable of automatically finding landmarks, by moving towards the target sequentially step-by-step, without any priors. However, starting points initialized randomly in the background (air) can result in a failure to detect the target landmark. To tackle such cases, we have proposed a schema with hierarchical step values. Agents can initially move with big action steps, and are scaled down afterwards in order to accurately localize the final landmark location. Alternatively, multiple agents can be initialized randomly at different locations, with the final target landmark calculated as the mean or median of the localized points.

Despite RL being a difficult problem, that needs a careful formulation of its elements such as states, rewards and actions, our extensive evaluations demonstrate high detection accuracy on three different datasets: fetal head ultrasound, adult brain and cardiac MRI. Finding the optimal DQN architecture for achieving the best performance is environment-dependant, whereas selecting the best DQN architecture differs for each landmark. This is one of the limitations of RL research; as shown by the varying results of performance on Atari games played by different architectures.

We have also exploited fixed- and multi-scale optimal path search strategies. The results show that multi-scale search significantly improve the performance in images with large fields of view and/or noisy backgrounds such as cardiac MRI. Moreover, hierarchical action steps significantly speed up the searching process by a factor of 4 − 5 times by using larger steps, as well as smaller steps, to fine-tune the final location.

Future work

We will investigate approaches using intrinsic geometry instead of intensity patterns for the RL environment to improve performance. Multi-landmarks detection is another interesting application to be explored using either multiple competitive and/or collaborative agents. One of the challenges that may hinder the design of such a multi-agent system is the required computational resources. As every agent may need an independent model for every specific landmark. It will be interesting to explore methods that allow such agents to communicate, e.g. by sharing their learned knowledge. Another future direction will be to investigate involving human experts for teaching the artificial agents actively. Where the agents learn from not only their self-play experience, but also from trained operators through interaction.