Flexible modulation of sequence generation in the entorhinal-hippocampal system

Abstract

Exploration, consolidation, and planning depend on the generation of sequential state representations. However, these algorithms require disparate forms of sampling dynamics for optimal performance. We theorize how the brain should adapt internally generated sequences for particular cognitive functions and propose a neural mechanism by which this may be accomplished within the entorhinal-hippocampal circuit. Specifically, we demonstrate that the systematic modulation along the MEC dorsoventral axis of grid population input into hippocampus facilitates a flexible generative process which can interpolate between qualitatively distinct regimes of sequential hippocampal reactivations. By relating the emergent hippocampal activity patterns drawn from our model to empirical data, we explain and reconcile a diversity of recently observed, but apparently unrelated, phenomena such as generative cycling, diffusive hippocampal reactivations, and jumping trajectory events.

1. Introduction

The entorhinal-hippocampal circuit (EHC) is thought to contribute to a diverse range of cognitive functions^1,2. An important motif within this circuit is the sequential non-local reactivation of hippocampal place codes^3,4. The archetypal instantiation of this functionality is “replay”, which refers to a temporally compressed representation of a previously experienced trajectory embedded within hippocampal sharp-wave ripples (SWRs)⁵. Initially observed during sleep, replay is thought to subserve long-term memory consolidation in neocortical networks⁶. More recently, sequential non-local hippocampal reactivations have been observed that do not fit with this classical definition of replay⁷. While rodents quietly rest, ensemble place cell activity appears to random walk through a cognitive map of a familiar environment instead of veridically replaying a rodent’s physical traversals⁸. In the awake immobile state, SWR-related trajectory events encode novel goal-directed routes⁹. During active movement, an alternative form of sequential non-local reactivation may also occur. Theta sequences, which typically phase precess through local positions, may sweep ahead to remote locations along potential paths available to the rodent^10–12.

Spanning these diverse forms of sequential hippocampal representation, we consider a unified algorithmic theme conceptualizing hippocampus as a sequence generator¹³, contributing sample trajectories drawn from cognitive maps to computations being executed downstream in cortex. Establishing neocortical memory traces via synaptic plasticity may be characterized as a learning process extracting information from experiential replay during sleep¹⁴. Hypothetical environment trajectories, encoded in SWRs or theta sequences, may be thought of as samples of possible future behaviors which are input into a planning algorithm for the purposes of optimizing exploration and prospective decision-making^15,16. We suggest that this generalized perspective imposes a substantial computational obligation on the EHC as a generative sampling system since the performance of algorithms can vary substantially depending on the statistical and dynamical structure of the input samples¹⁷. This motivates our computational hypothesis that hippocampal sequence generation is systematically modulated in order to optimize the resulting sampling regime for the current cognitive objective. Since previous computational EHC models have tended to focus on relatively specific applications such as localization^18–20 or vector-based navigation²¹, the necessity to modulate sequence generation between cognitive algorithms is not addressed. Therefore, the broader computational viewpoint taken here raises unique theoretical questions such as what alternative modes of hippocampal sequence generation are to be expected, by what neural mechanism can such distinctive dynamics be systematically regulated, and how can this be efficiently achieved for large relational spaces (e.g., graphs) which may be non-spatial in nature²².

We develop an algorithmic framework and associated neural mechanism by which distinct dynamical modes of sequence generation may be parsimoniously realized in a pathway between grid cells in medial entorhinal cortex (MEC) and place cells in the CA1 subregion of hippocampus (HC)². The critical technical innovation is the characterization of grid cells as encoding infinitesimal generators of hippocampal sequence generation. A generator is a mathematical object that specifies how a system evolves in continuous time^23,24. Conceptualizing hippocampal sequence generation as a dynamical system operating over a cognitive map, generators then determine the probabilities with which a given position will be reactivated at any time. We propose that MEC grid cells encode generators in a decomposed format. This enables a simple neural mechanism to flexibly interpolate hippocampal sequence generation between qualitatively and quantitatively distinctive regimes from random walks with Lévy jumps to generative cycling (Fig. 1A-E). In a phenomenological linear network model of hippocampal sequence generation, we demonstrate the systematic modulation of grid cells arrayed dorsoventrally as a function of spatial scale in the MEC layer and the consequential effects on place cell activity. In simulating this model, we show that our theory reconciles a diversity of empirical observations in sequential hippocampal reactivations.

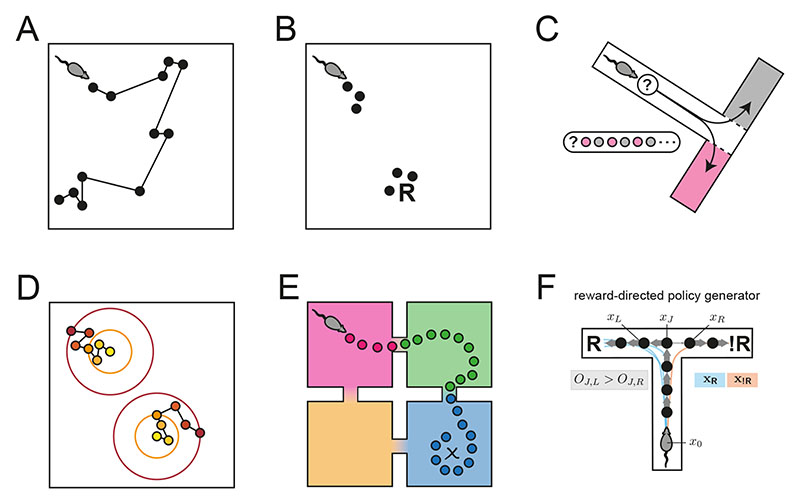
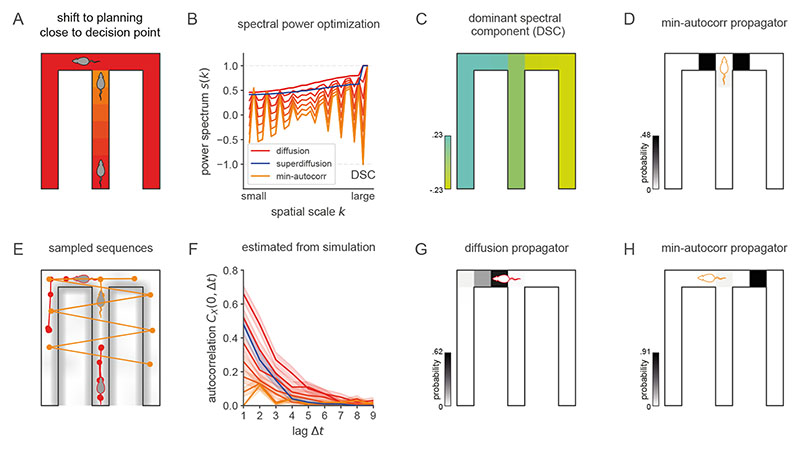
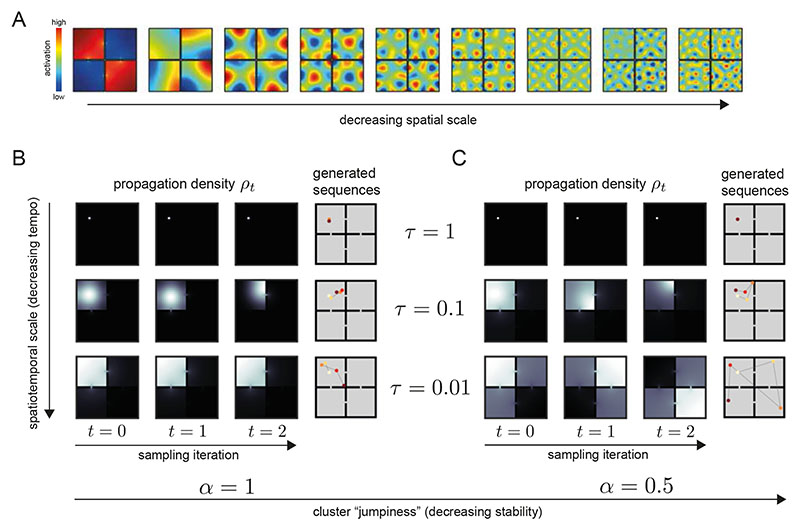
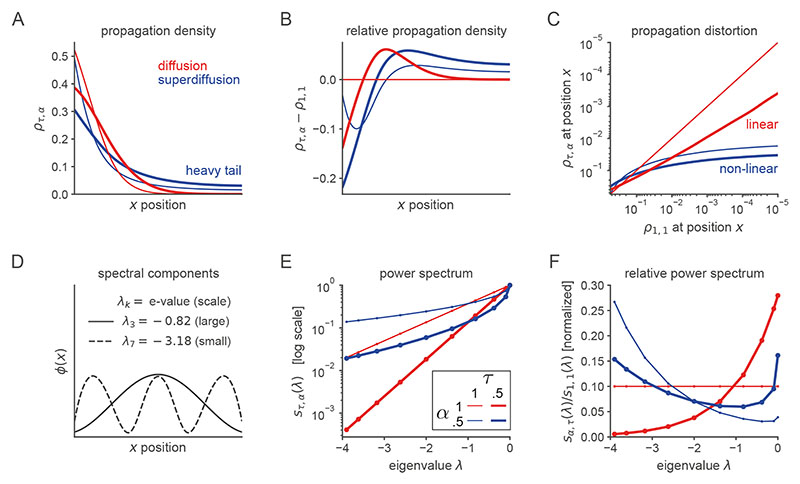
Figure 1. In different neurophysiological, behavioral, and cognitive states, distinct modes of sequence generation are active in the entorhinal-hippocampal system.

Drawing on the empirical and computational literatures, we depict several modes of sequence generation supported by our model in a rodent experiment paradigm. Each circle corresponds to a hippocampal place representation, and connecting lines indicate a place activation sequence. A. The exploration patterns of animals³⁵ and humans⁴⁸, as well as hippocampal place trajectories³⁶, interleave large “jumps” between environment positions with local steps consistent with search efficiency optimization. This distinctive regime of sequence generation is referred to as superdiffusive. B. Motivationally salient locations are over-represented in hippocampal activity as reflected in place activations at the reward location (R)^9,11. C. Generative cycling refers to the alternating representation of future possibilities in the hippocampal code which occurs during prospective decision-making¹². Here, the rodent evaluates the candidate behavioral trajectories of turning right (pink) or left (grey) at the junction. D. Diffusive random-walk trajectories are observed in hippocampal reactivations during rest⁸. Colors indicate the successive time steps at which each position is expected to be sampled along each trajectory (from yellow to red). Diffusion implies that, on average, each sampled positions will be spatially displaced from the previous by a similar distance. E. In hierarchical reinforcement learning and human decision-making⁴⁹, environments may be processed across multiple spatiotemporal scales, e.g., using room abstractions in this four-room world. F. In this T-maze task, where a rodent seeks reward R to the left (avoiding the right turn leading to no reward !R), the behavioral policy of the rodent is encoded in the generator O which biases sequence generation to the left x_L at the junction x_J. Sequence generation of hypothetical behavioral trajectories x_R is then biased towards the reward.

2. Results

2.1. Spectral modulation in an entorhinal-hippocampal network model of sequence generation

How might sequences of positions in an environment or, more generally, states of an internal world model be simulated within the brain? This question can be posed formally within a generative probabilistic framework as how to sample state sequences x = (x ₀, x ₁, …, x_t) from a probability distribution p(x) defined over state-space 𝒳. A typical example considered in this study is the sequence distribution p(x) based on the hypothetical decision-making policy of a rodent in an experimental task (Fig. 1F) as this will allow us to relate sequences generated by our model to the sequential non-local reactivations encoded in hippocampal place cells. We consider the state-space 𝒳 to be discrete as this allows us to study both continuous spatial domains (via discretization) and inherently discrete spaces (e.g. graphs) in a common formalism based on matrix-vector products. When studying discretized continuous state-spaces, we interpolate discrete probability distributions where appropriate. Analogous techniques in purely continuous domains replace matrix-vector products with integral transforms²⁴. Therefore, our model may in principle be applied across a wide range of cognitive maps, relational spaces, mental models, or intuitive physics models^22,25.

An internal simulation is initialized based on a distribution p(x ₀) over states at an initial time t = 0. We compactly denote this distribution over initial states as ρ ₀ = p(x ₀). How can this initial distribution (for example, a rodent’s initial position in an experiment) be combined with dynamics information (the rodent’s behavioral policy) in order to compute the state distribution ρ_t = p(x_t) at an arbitrary timepoint t in the future (where the rodent will be)? To answer this question, we need to understand how the state distribution ρ evolves in time. This is characterized by its time derivative $\dot{\rho }=\frac{\text{d}\rho }{\text{d}t}$. Assuming that the dynamics depend only on the current state and that they do not change over time, the evolution of a state distribution ρ is determined by a master equation

$$\tau \dot{\rho }=\rho O$$ (1)

where O is a matrix known as an infinitesimal generator ^23,26. The generator O encodes stochastic transitions between states at short timescales (see Section B.2 of the Supplementary Math Note (SMN) for details). For example, in a T-maze, an entry in O could encode the local bias for a left turn at a critical junction leading to reward acquisition (Fig. 1F). The tempo parameter τ modulates the speed of the simulated evolution. The master equation (Eqn. 1) implies that a dynamical system is economically encoded in an initial state distribution ρ ₀ and a generator O since the distribution ρ_t of possible states of the system at any time t can be retrieved from this information.

The master equation (Eqn. 1) has an analytic solution:

$${\rho }_{\Delta t}={\rho }_0{e}^{{\tau }^{-1}\Delta tO}.$$ (2)

Given an initial state distribution ρ ₀, the propagator e ^τ−1ΔtO is a time-dependent matrix which evolves ρ ₀ through the time interval Δ_t to ρ _Δt by propagating the initial state probability mass ρ ₀ across the state-space under the dynamics specified by O. Fixing Δt = 1, the propagator P_τ = e ^τ−1O can be applied iteratively to generate state distributions on successive time steps as ρ _t+1 = ρ _t e ^τ−-O. State sequences characterizing the simulated evolution of the system can therefore be generated by recursively applying this time-step propagator P_τ and sampling

$$x_t~1_{x_{t-1}}{P}_{\tau }$$ (3)

where 1_x is a one-hot vector indicating that state x is active with probability one. This will result in state sequences x that accurately reflect the generative distribution of sequences p(x) defined by the generator O and initialization ρ ₀ (Section B.8, SMN).

Directly computing the propagator $P_{\tau }={\displaystyle {\sum }_{n=0}^{\infty }{\left(n!\right)}^{-1}{\left({\tau }^{-1}O\right)}^n}$ is challenging since it requires an infinite sum of matrix powers. In Section B.3 SMN, we show that P_τ can be computed efficiently using a generator eigendecomposition O = GΛW as

$$P_{\tau }=G{e}^{{\tau }^{-1}\Lambda }W.$$ (4)

Furthermore, the facility to freely modulate the tempo τ of propagation is a highly desirable property. This would enable coarse hierarchical sequence generation to be run expeditiously rather than at the true rate of evolution of the external world or, if time allows, an internal simulation could be slowed down for a more fine-grained analysis^27–29. We show that, given this representation (Eqn. 4), the tempo τ can be efficiently manipulated via a computational mechanism which we refer to as spectral modulation. Since Λ is the diagonal matrix of O-eigenvalues, its exponentiation is trivially accomplished by exponentiating the eigenvalues separately along the diagonal ${\left[e^{{\tau }^{-1}\Lambda }\right]}_{kk}=e^{{\tau }^{-1}{\lambda }_k}$. Multiplication by G projects a state distribution ρ_t on to the generator eigenvectors ϕ_k = [G] _·k which we refer to as the spectral components of the propagator. Note that we employ this term as a broad reference for generator eigenvectors or components of alternative generator decompositions, potentially constrained by other considerations such as non-negativity, which facilitate spectral modulation (see Section A.1 SMN). In this spectral representation, time shifts simply correspond to rescaling according to the power spectrum

$$s_{\tau }\left(\lambda \right)=e^{{\tau }^{-1}}\lambda .$$ (5)

Each spectral component ϕ_k is scaled by s_τ (λ_k) based on its eigenvalue λ_k. Finally, W projects the spectral representation of the future state distribution ρ _t+1 back onto the state-space 𝒳. This spectral format factorizes time and position within an environment such that a linear readout can generate a propagator for any timescale.

We apply the spectral propagator (Eqn. 4) recursively to generate state sequences according to

$$x_{t+1}~1_{x_t}GSW$$ (6)

where S = e ^τ−1Λ is the power spectrum matrix. This generator-based model of sequence generation can be minimally realized in a linear feedback network model of EHC (Figure 2A) in which the activity profiles of the network units are qualitatively consistent with those of grid cells in medial entorhinal cortex (MEC) and place cells in hippocampus (HC). Specifically, we equate the spectral components ϕ_k (columns of G) with grid cells topographically organized by spatial scale along the dorsoventral axis of MEC (Figure 2B)³⁰. The linear readout W from the MEC layer to the hippocampal layer embeds the the future state distribution ρ_t in a predictive place code²⁸. See Section A (SMN) for further considerations regarding biological plausibility and connections to other EHC models.

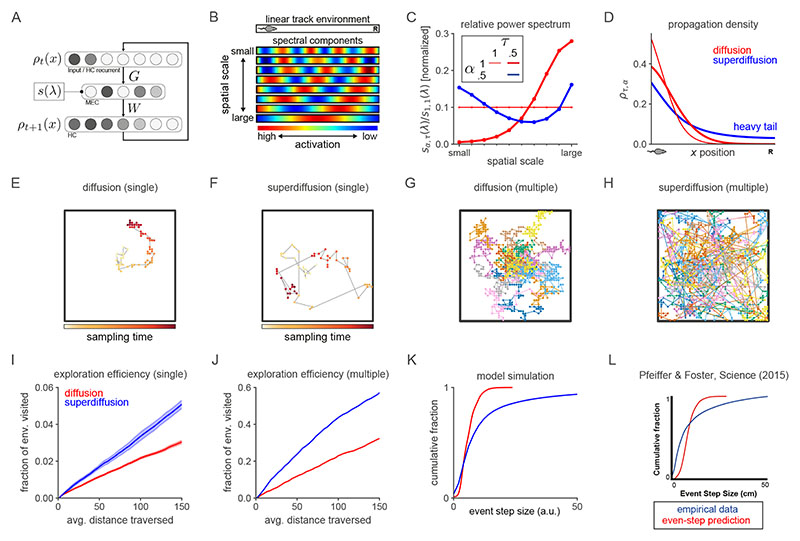
Figure 2. Spectral modulation of grid cell activity alters the statistical structure of hippocampal sequence generation.

A. Abstract entorhinal-hippocampal circuit model. ρ_t and ρ _t+1 are the propagation distributions over environment position at time-steps t and t + 1 respectively. The weight matrices G and W are identified with the generator decomposition O = GΛW. s(λ) is the power spectrum expressed as a function of the generator eigenvalue λ associated with each unit (i.e., spectral component) in the MEC layer. B. Firing maps of units in the MEC layer which exhibit periodic tuning across a range of spatial scales reminiscent of grid cells. Spectral components are equivalently ordered by their eigenvector numbers k and generator eigenvalue magnitudes |λ_k| from large to small scale. C. Characteristic changes in the power spectrum associated with the diffusive and superdiffusive regimes are highlighted by the corresponding power ratios relative to a baseline. τ-modulated diffusion (α = 1, τ = 0.5, thick red line) results from a downweighting (upweighting) of small-scale (large-scale) spectral components while a-modulated superdiffusion (α = 0.5, τ =1, thick blue line) upweights both small- and large-scale components but suppresses at medium scales. D. Diffusive (α = 1, red lines) versus superdiffusive (α = 0.5, blue line) propagation densities ρ_τ,α = 1 _x0 GS_τ,αW in a linear track environment where x ₀ corresponds to the location of the rodent. By modulating the tempo τ = 0.5, diffusive propagation can sample over larger distances (thick red line) compared to the baseline diffusion (τ = 1). However, only superdiffusive propagation facilitates an extraordinary jump to the reward (R). Note that these continuous propagation densities have been interpolated from the discrete propagation vectors output by our model. Further technical details are presented in Fig. E5. E-F. Single diffusive (panel E) and superdiffusive (panel F) sequences in an open box environment. The color code from yellow to red reflects the sampling iteration (from the initial sample to the final). Sequences are initialized at the centre of the environment. G-H. Multiple diffusive (panel G) and superdiffusive (panel H) sequences each distinguished by color. I. Mean and standard error of exploration efficiency for individual trajectory simulations (n = 20). J. Parallelized exploration efficiency across all the trajectories in panels G, H. K. Cumulative histogram of step sizes for diffusive trajectories (red) and superdiffusive trajectories (blue). An event refers to the successive representation of two different locations. Step size is measured by Euclidean distance. Therefore the x-axis reflects the Euclidean distance between successively sampled locations during sequence generation. L. Statistical analyses of hippocampal recordings in Ref. [36] indicated that hippocampal trajectory events were superdiffusive since the distribution of step sizes between state activations (blue) was heavy-tailed. This qualitatively matched the simulated cumulative histogram for superdiffusions in panel K in contrast to the prediction (red) based on simulated sequences composed of states separated by equal step sizes. In our model, the latter corresponds to diffusive sequence generation with τ varied to match the velocities exhibited by the recorded trajectory events.

The critical mechanism of spectral modulation, which sets the tempo of propagation, is the systematic regulation of MEC grid cell output as a function of spatial scale according to the power spectrum s. At the implementation level, we hypothesize that spectral modulation may be accomplished via gain control or grid rescaling according to top-down cortical input. An example of the latter would be if a small-scale grid firing map is enlarged to a medium scale in order to increase MEC power at medium scales and reduce MEC power at small scales. Notably, grid modules appear to have the capacity to rescale independently³⁰, do so as a function of experience and presumed cognitive processing³¹, and cause a consistent rescaling of place fields in hippocampus when the grid scale is perturbed³². More generally, several empirical results support the critical contribution of entorhinal input towards the coherent temporal organization of hippocampal activity^33,34. Indeed, beyond tempo control set by τ, we study several other parametric and non-parametric classes of power spectra with highly distinctive causal effects on hippocampal sequence generation. Each of these EHC settings will be motivated as an optimized operational mode for a particular cognitive process.

2.2. Foraging in an open environment

Consider a rodent foraging in a large open environment. Without cues indicating where food may be located, its exploration process must search each location. How might it generate the next environment position to inspect? Approaches to this problem range in terms of computational complexity from serial visitations minimizing repetitions (imposing increasingly burdensome memory and planning costs) to random sampling (requiring no memory). Though generators could be adaptively designed to implement sophisticated forms of uncertainty-driven exploration (e.g., based on Gaussian processes), here we focus on maximizing the efficiency of random sampling in the low-complexity limit. Assuming a random walk generator O ^rw (implying the rodent has no information as to where food may be located), we study the effect of spectrally modulating tempo in generating the next position to visit. If the rodent repeatedly samples target states at large spatial scales (τ → 0) then it will repeatedly traverse the environment expending too much energy. In contrast, a small-scale search pattern (τ ≫ 0) will lead to the rodent oversampling within a limited area and taking too long to fully explore the environment. Defining exploration efficiency as the fraction of the environment visited per cumulative distance traversed, neither tempo regime delivers a satisfactory return.

This ubiquitous conundrum has been extensively studied in the foraging literature, leading to the Lévy flight foraging hypothesis³⁵. Theoretical analysis and simulations have shown that exploration efficiency is maximized by interleaving jumps (i.e., sampling successive positions separated by a large distance) with local search patterns. Effectively, this strikes an balance between local searches (τ ≫ 0) and global re-orientations to new positions in an environment (τ → 0). It is proposed that these distinctive search dynamics are naturally selected for in animals across a wide variety of ecological niches due to their universally advantageous properties and draws its name from the Lévy distribution which characterizes the distribution of possible next positions in a Euclidean space³⁵. This is a heavy-tailed distribution and therefore in addition to a high probability of sampling a nearby position, it has a small probability of generating a large jump to a more distal region.

We show that analogous heavy-tailed propagation distributions can be accessed in our model via an alternative form of spectral modulation, thus providing a mechanistic account regarding how such sampling may be accomplished in the EHC. Based on mathematical considerations (Section C.1 SMN), we introduce the stability parameter a which determines the entorhinal power spectrum s_{τ α} according to

$$s_{\tau ,\alpha }\left(\lambda \right)=e^{-{\tau }^{-1}{\left|\lambda \right|}^{\alpha }}.$$ (7)

For α = 1, the power spectrum is unchanged, s _τ,1 = s_τ (compare Eqn. 5, Fig. 2C). This results in random walks which correspond to diffusions in continuous spaces therefore we refer to the α = 1 regime as diffusive (Section B.6, SMN). Setting α < 1, the linear readout from the MEC layer in our circuit model reflects a propagator with probability mass smoothly redistributed to remote positions from the nearby positions (Fig. 2D). Sequence generation with α < 1 is referred to as superdiffusive (Section 5.3, Methods). Although both superdiffusive and diffusive sequence generation are ultimately truncated by the limited extent of an environment, they are differentially sensitive to the possible range of spatiotemporal scales. Intuitively, stability modulation results in a scale-invariant sampling process since sampling can occur at any spatiotemporal scale simultaneously on each iteration. In contrast, τ specifies a limited range of spatiotemporal scales and therefore tempo modulation can never lead to scale-invariance. This implies that α-modulation and τ-modulation have fundamentally distinct effects on the statistical structure of sequence generation (Fig. E1).

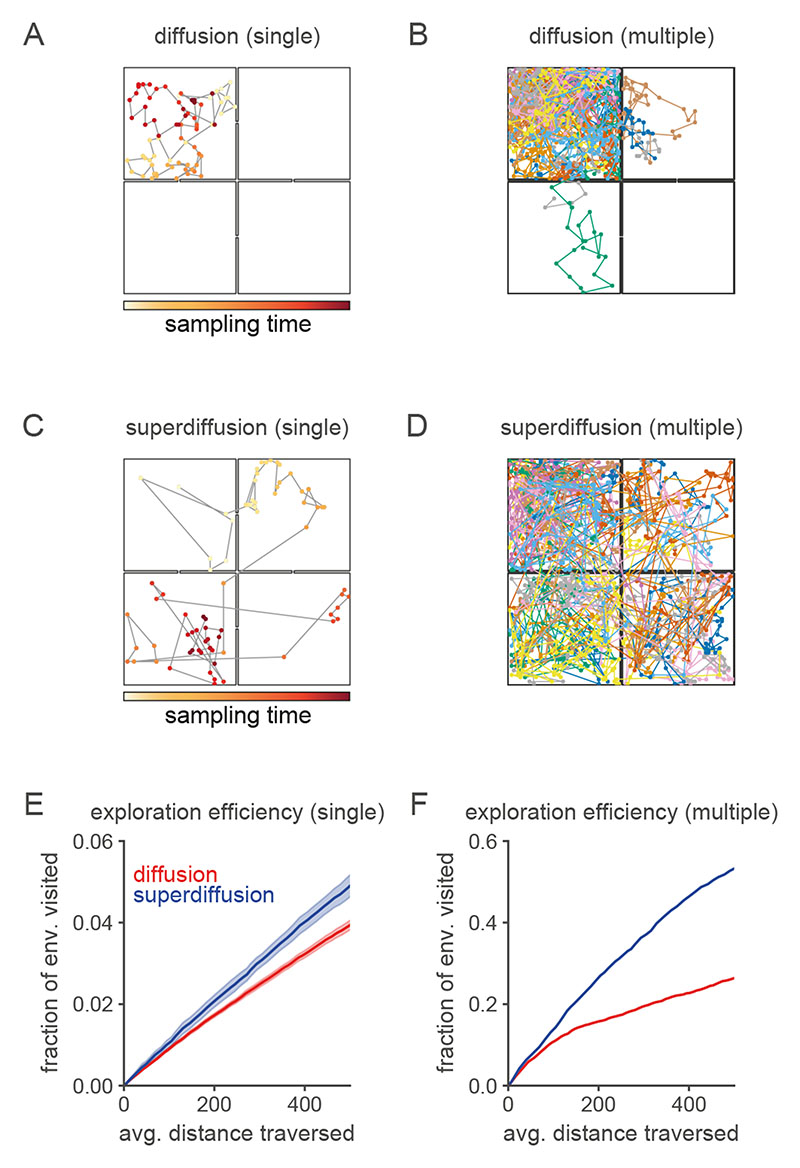
We compared diffusive (α = 1, Fig. 2E) and superdiffusive (α = 0.5, Fig. 2F) sampling in an open box environment typically used in rodent foraging experiments^8,36 postulating that EHC generates candidate exploratory trajectories which the rodent subsequently pursues physically. Whereas diffusive behavioral trajectories failed to fully explore all areas in the simulated window of time (Fig. 2G), superdiffusive trajectories visited positions in an approximately homogeneous distribution across the entire arena (Fig. 2H), thus highlighting the flexibility with which superdiffusions adapt to an arbitrary environment scale. With respect to the standard measure of exploration efficiency, superdiffusions explored significantly more positions in the open environment as a function of distance traversed than diffusions (Fig. 2I,J). This is also the case for structured state-spaces, such as compartmentalized environments with obstacles (Fig. E2). Consistent with our theoretical arguments and simulations, superdiffusive sequential activation of hippocampal place cells (Fig. 2K,L) and superdiffusive rodent behavioral trajectories have been observed^8,36 in foraging experiments where rodents are required to explore environments with essentially random distributions of food locations.

2.3. Goal-directed trajectory events with heterogeneous jumps

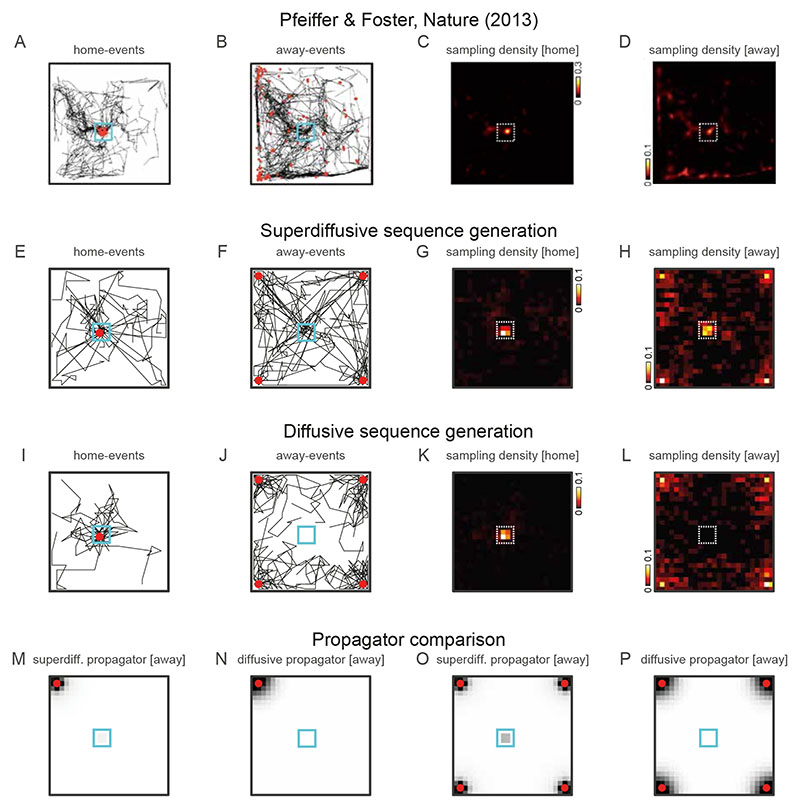
We relate our model operating in the superdiffusive regime to heterogeneous sequences of hippocampal representations exhibiting jump transitions to motivationally salient locations^9,11. In the first experiment we simulated, SWR-related place cell activity in the CA1 subregion of dorsal hippocampus was recorded from rats engaged in random foraging and spatial memory tasks in alternation⁹. In the spatial memory task, a single reward location in the open square arena was repeatedly baited and thus the rat could remember this predictable “Home” location and engage in goal-directed navigation in order to acquire the reward. The application of neural decoding analyses revealed the rapid sequential encoding of positions across the environment while the rats were task-engaged but immobile (Fig. 3A-D). This study provided evidence that the hippocampus encodes novel goal-directed paths to memorized locations which were significantly over-represented in the generated trajectories (“away-events”, Fig. 3B,D). We simulated the generation of trajectory events in this experiment with our model in order to demonstrate the novel computational mechanism by which a memorized location may be stored in a generator representation and remotely activated exclusively in the superdiffusive regime. We subtly manipulated a random-walk generator O leveraging a distinguishing feature of the generator-propagator formalism, namely the ability to independently modify the spatial and temporal statistics of sequence generation in a spatially localized manner (Section B.10, SMN). Specifically, we controlled the remote activation of the rewarded Home location by scaling the generator transition rates at home states according to v ⁻¹ O_h., where h indexes home states $x_h\in 𝒳$ and v is a scalar specifying their motivational value (Section 5.1.3, Methods). Initializing the rodent’s position away from the Home location and activating superdiffusive sequence generation in our EHC model (Fig. 3E-H) results in trajectory events reflecting random walks with biased jumps to the rewarded location (Fig. 3F,H). Using the same generator in the diffusive regime (Fig. 3I-L) does not over-represent the Home location (Fig. 3J,L). Comparing propagators between sequence generation regimes explains this remote activation as the localized increase in sampling probability exclusively at the Home location in the superdiffusive regime (Fig. 3M-P).

Figure 3. Simulating the over-representation of remote, motivationally salient, locations.

A-D [first row]. Empirical data from Ref. [9]. E-H [second row]. Superdiffusion simulations. I-L [third row]. Diffusion simulations. M-P [fourth row]. Propagators for away events in superdiffusive and diffusive regimes. These are plotted for single location initializations (panels M and N) and for multiple location initializations (panels O and P). A, E, I [first column]. Empirical and simulated trajectory events (black lines) while rodent was located (red circles) at the home location (blue square). B, F, J [second column]. Empirical and simulated trajectory events while rodent was located away from home. C, G, K [third column]. Estimated sampling density for home-events (home location indicated by dotted white square). D, H, L [fourth column]. Estimated sampling density for away-events. This set of panels contains the key comparison. Note that only superdiffusive away-events (panel H) but not diffusive away-events (panel L) remotely over-representation the home location consistent with data (panel D). In our generator model, this is explained by the remote propagation probabilities which are exclusively observed in the superdiffusive regime (panels M and O). Diffusive propagators with sufficiently low tempos (thereby sampling over large spatial scales) can jump from away locations to the home location. The critical distinction is that superdiffusive propagation does not require de-localization to a large spatial scale in order to jump to the home location. Superdiffusions can uncover motivationally salient locations stored locally within the generator regardless of spatial distance.

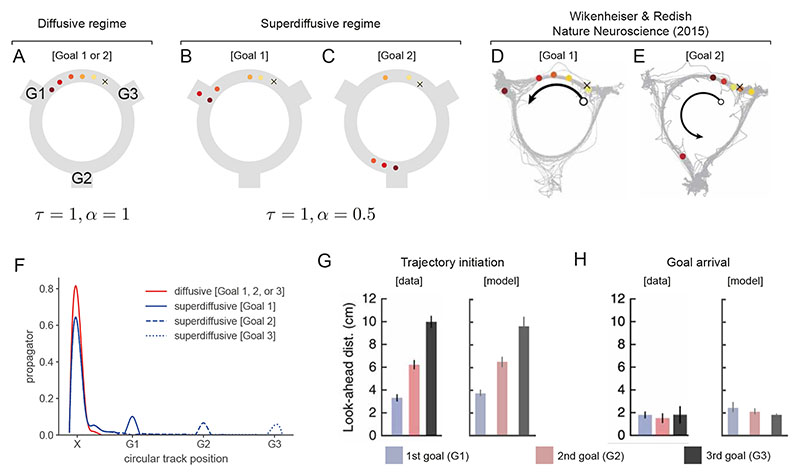
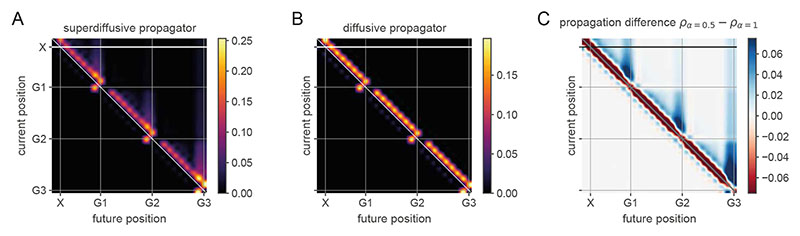
In another study of multi-goal foraging in a circular track environment¹¹, it was observed that theta sequences exhibited a strong dependency on the currently targeted goal. As the rodent initialized their behavioral trajectory, theta sequences exhibited a non-local, non-diffusive pattern of activation. Place cells near the goal destination were frequently active along with place cells near the rat’s actual position within individual cycles. We constructed a generator O which encoded a goal-directed policy of clockwise movement around this circular track, with turn-offs to the three goal locations located at the intervals G1, G2, and G3. Assuming that the rodent is located at the start position, we generated sequences in the diffusive (α = 1, Fig. 4A) and superdiffusive (α = 0.5, Fig. 4B,C) regimes. We observed that the latter had a strong tendency to generate jumps to goal locations interleaved with local roll-outs as observed empirically (Fig. 4D,E). This effect emerges from the fact that remote goal locations are over-represented in superdiffusive propagation (Fig. 4F). Taking the distance around the track to the furthest encoded location as the look-ahead distance, the distributions of look-aheads scaled with the distance to the target goal as recorded in theta sequences (Fig. 4G). After placing the rodent at locations along the circular track before each of the goal turn-offs, and without changing any parameters, the sequences exhibited short-range look-aheads which did not scale with the distance to the targeted goal (Fig. 4H).

Figure 4. Theta sequences generated during a goal-directed foraging paradigm exhibited non-local transitions in place coding.

Within individual theta cycles, sequences of place representations in hippocampus emanated from the current position of the rodent (X) and proceeded anti-clockwise around the track with characteristic jumps to one of three goal locations where food was available (labeled G1, G2, G3)¹¹. Each circle corresponds to a decoded location and the color indicates the temporal order within the sequence (from yellow to red). A. Diffusive sequence generation (a = 1) typically proceeds with localized sequential place activations regardless of the target goal location. B-C. Shifting to the superdiffusive regime (α = 0.5), sequence generation activated local place representations as well as remote goal locations (goal 1 in panel B and goal 2 in panel C) but not intervening locations. D-E. Empirically observed patterns of place activation in theta sequences. Superdiffusive goal-directed sequence generation matches the key qualitative features with goal-directed sequences representing local positions near the animal as well as jumps to goal locations which were over-represented within theta sequences. F. Diffusive propagator and the superdiffusive propagators from the initial X location are plotted. The jumps-to-goals are explained by the unique bumps in the superdiffusive propagators at the remote goal locations. G. The same stability parameter (α = 0.5) generated non-local, goal-jumping trajectories ([model]) with varying look-ahead distances as observed in hippocampal theta sequences ([data], Ref. [11]). Bar heights equal the mean across theta sequences ([data]) or simulated sequences ([model]) and error bars reflect the standard error (n = 50 simulated trajectories). H. Near the goal locations, look-ahead distances were the same across goals since superdiffusive sequence generation is attracted to goals and thus automatically alters the look-ahead distance.

These effects emerge from the specific combination of superdiffusive sequence generation and a goal-sensitive generator. In the linear track (Fig. 2B-D) and open box (Fig. 2E-H) simulations where random walk generators were used, it was shown that the superdiffusive regime engenders spatially extended jumps between states. Due to the metric correspondence between space and time (set by a specific velocity), this can be equivalently stated as superdiffusions generating large jumps through time¹³. That is, superdiffusive sequence generation interleaves state transitions over short time-scales (resulting in small spatial steps) with state transitions over long time-scales (resulting in large jumps). Since a goal-directed policy results in goal locations being over-represented in the stationary distribution of internal simulations, the probability of sampling such states in a superdiffusion is relatively high. Therefore, as observed in Fig. 4F, superdiffusive propagation specifically over-weights the goal locations (regardless of the current position of the rodent, Fig. E3).

2.4. Generative cycling emerges from minimally autocorrelated sampling

A critical element of many planning algorithms is prospectively evaluating possible future trajectories. In order to accomplish this, model-based simulations are often employed such as in Monte Carlo Tree Search³⁷. These methods rely on sampling sequences of states in a state-space, retrieving rewards associated to those states, and computing Monte Carlo estimates of choice-relevant objectives. For example, an agent can produce an estimate $\widehat{r}$ of the average reward expected to be accrued based on sampled states (x ₁, …, x_N) and a reward function r(x) as

$$𝔼\left[r\right]\approx \widehat{r}=\frac{1}{N}{\displaystyle \sum _{i=1}^{N}r\left(x_i\right)}$$ (8)

and then input such estimates into an action selection algorithm. Sequentially sampling states from a propagator, retrieving the associated rewards, and estimating the expected average reward via Eqn. 8 forms a Markov chain Monte Carlo (MCMC) algorithm in the service of planning (see Section C.4, SMN).

The quality of an MCMC estimator (Eqn. 8) is quantified by its sample variance ${𝕍}_{\text{dyn}}\left[\widehat{r}\right]$ which reports how variable the estimate will be across different sample sequences¹⁷. A major source of sample variance in MCMC, which also afflicts the generator model in both the diffusive and superdiffusive regimes, is generative autocorrelations. Technically, the sample variance is proportional to the integrated autocorrelation time Δt _ac (Eqn. 68, SMN):

$$\Delta t_{\text{ac}}={\displaystyle \sum _{t=0}^{\infty }{C}_X\left(t\right)}$$ (9)

where C_X(t) is the autocorrelation function of the state variable X at step t. Intuitively, Δt _ac is the average number of iterations that a sampling algorithm requires in order to generate a single independent sample. Although samples may be generated on each iteration t = 1, 2, 3, we can expect new independent samples to be generated on iterations t = Δt _ac, 2Δt _ac, 3Δt _ac. Standard practice in MCMC estimation, such as with the Metropolis-Hastings algorithm, is to simply discard autocorrelated samples (see Section C.4.1 SMN for further details). This brings into focus a sharp trade-off between sampling time and estimation accuracy, which necessarily burdens any cognitive function dependent on Monte Carlo estimation¹⁵.

We show that a fundamentally different solution to the autocorrelation problem of MCMC estimation is available for generator-based sampling. The need to dispose of correlated samples may be obviated by directly optimizing the power spectrum in order to minimize autocorrelations in the emitted sequences. The resulting sequences are then composed of approximately independent samples, thus facilitating rapid online simulation, estimation, and responsive action loops. Technically, we show that the integrated autocorrelation time Δt _ac of the state variable X can be expressed analytically in terms of the power spectrum s(k) (where k indexes the spectral components), and the constraints necessary to ensure that the resulting propagator is valid are linear (Section C.5 SMN). Therefore, the minimally autocorrelated power spectrum s _mac(k) can be identified using standard optimization routines. We hypothesized that minimally autocorrelated sequence generation should result in a sampling process which methodically shifts between the most salient points of divergence under dynamical evolution of the system. As a counterpoint, consider the genesis of autocorrelations in diffusive sequences (Fig. 2E, G). In diffusions, nearby states tend to be closely associated within the sampling dynamics due to overlapping propagation distributions. Therefore there tend to be relatively likely paths back to previously visited states leading to a large integrated autocorrelation time Δt _ac. A minimally autocorrelated sequence generation can avoid this pitfall by restructuring its propagation dynamics in order to successively sample states which do not admit likely paths between them.

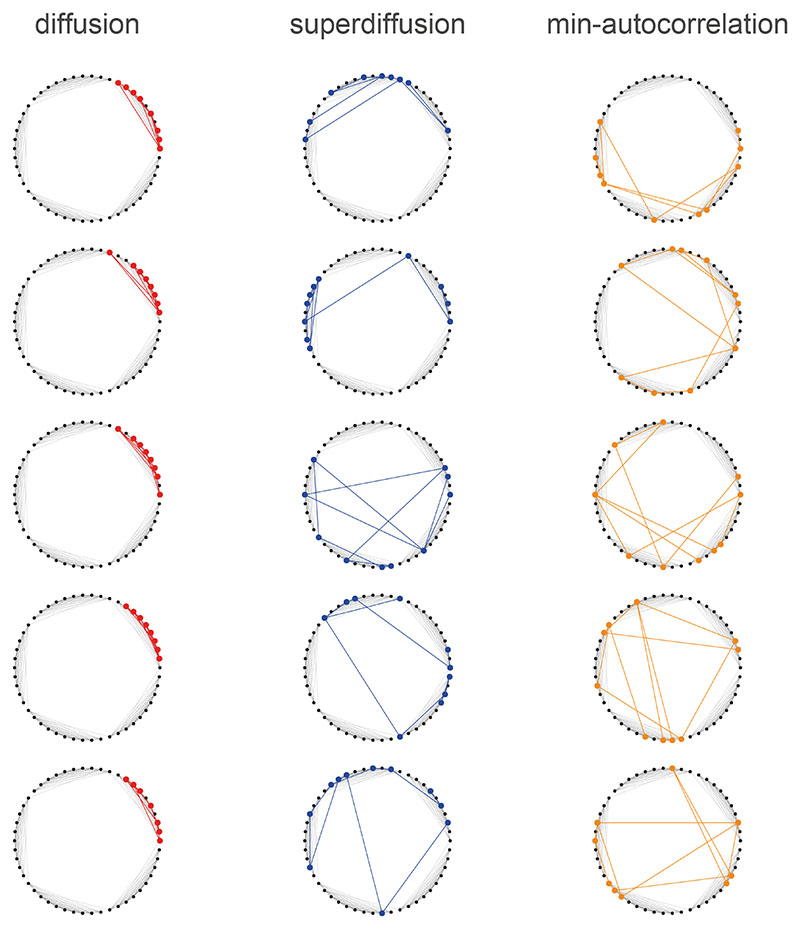
We studied this computational hypothesis in the context of a spatial alternation task where a rodent was required to make a binary decision at a junction leading to a reward or not¹². Alternating representations of hypothetical future trajectories were identified at several levels of neural organization in dorsal HC while the rats approached the critical junction (but not after the junction turn). In particular, place cells encoding the left and right arms fired in an alternating fashion within the theta band. Assuming that the rodent would initiate planning as it approached the junction where it is required to make a decision, we assumed that hippocampal sequence generation would shift to a regime of minimally autocorrelated sampling (Fig. 5A). The power spectrum s _mac which minimized the integrated autocorrelation time (Eqn. 9) bore a strikingly dissimilar profile to the parametrically modulated power spectra s_{α τ} (Fig. 5B). The most notable distinction was the emergence of counterweighted spectral components across spatial scales. The heaviest negative weighting applied to the spectral component encoding a high-level hierarchical decomposition of the environment which we refer to as the dominant spectral component (DSC, Fig. 5C).

Figure 5. Generative cycling emerges from minimally autocorrelated sequence generation.

A. Spatial alternation task environment from Ref. [12]. We assumed that the well-trained rodent had a decision-making policy composed of moving to the junction, making a binary decision, and then running to the food port at the end of an arm. On approaching the junction where the critical choice is made, we modeled hippocampal sequence generation as shifting from a localized diffusive regime (red) to minimally autocorrelating sampling (orange). B. The minimal autocorrelation (orange), diffusive (red), and superdiffusive (blue) power spectra are plotted. Intermediate colors between red and orange reflect intermediate spectra between purely diffusive and minimally-autocorrelating. Under autocorrelation minimization, we observed that for each positively weighted spectral component, s _mac negatively weighted another spectral component of a similar scale. In the EHC, this corresponds to the up- and down-regulation of MEC input into HC in alternation across grid scales. In the generator model, negative spectral modulation drives a generative repulsion depending on the structure of the associated spectral component. The dominant spectral component (DSC) is that which undergoes the largest spectral modulation from diffusion to min-autocorrelation. C. The dominant spectral component reflects a hierarchical decomposition of the state-space into the three arms of the maze. D. At the junction, the minimal autocorrelation propagator splits its propagation density evenly between the two arms in a similar fashion to diffusive propagation. E. While diffusive sequences sweep ahead of the animal in the maze (initialized at the start position and just after a left turn), minimal autocorrelation sequences cycle back and forth between the two arms. F. Estimated autocorrelation C_X(0, Δt) as a function of the time interval Δt. Via spectral optimization, the sample autocorrelations were smoothly reduced at all time intervals from pure diffusion to the minimal autocorrelation regime as predicted. Shaded error bands represent SEM (n = 100). G. Just after the turn, the diffusion propagator sweeps ahead of the sampled rodent position. H. Just after the turn, the minimal-autocorrelation propagator switches the sequence generation process to the other arm.

Despite the fact that the minimally autocorrelating propagator (Fig. 5D) samples states in both arms at the junction similar to a diffusive propagator, minimally autocorrelated sequence generation subsequently deviated radically from diffusion. Sequences generated under minimally autocorrelated spectral modulation (orange, Fig. 5E) were strongly reminiscent of the reported generative cycling phenomenon in that successive state samples were repeatedly drawn from the opposing arm in the maze¹². These stood in stark contrast to diffusive sequences generated both before and after the junction (red, Fig. 5E). Diffusively propagating into one of the arms means that it is relatively likely that a sequence will remain in that arm for a long time thus increasing the generative autocorrelation. This would imply that the rodent’s internal simulation does not have sufficient diversity (in particular it has not sampled the other arm) in order to make an informed decision. As predicted, estimated autocorrelations (Fig. 5F) were significantly lower in generatively cycling sequences (orange) compared to the diffusive (red) or superdiffusive (blue) regimes. In contrast to diffusive propagation (Fig. 5G), minimally autocorrelated sampling leverages the hierarchical structure of the environment in order to generate sequences that efficiently sample across dynamically divergent components of the environment based on repulsive propagation (Fig. 5H).

2.5. Diffusive hippocampal reactivations for structure consolidation

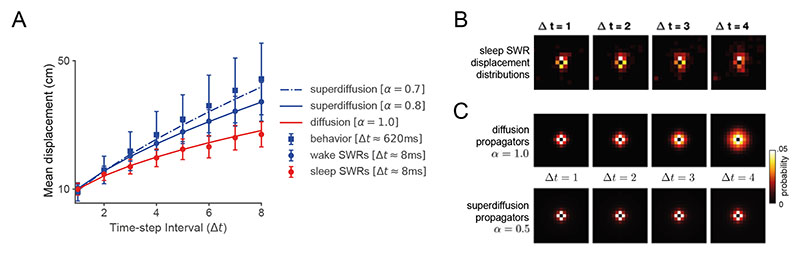
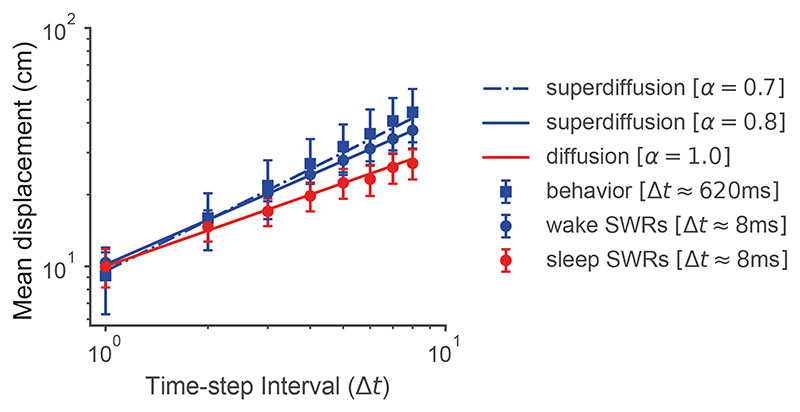
In contrast to the superdiffusive sequences observed during random and goal-directed foraging, offline hippocampal reactivations exhibit a diffusive operational mode during rest⁸. In an experiment where rats foraged for randomly dropped food pellets, spatial trajectories were decoded from SWRs during a post-exploration rest period (“sleep SWRs”) as well as during immobile pauses in active exploration (“wake SWRs”). The SWR sequence generation regime is statistically identified by estimating the mean displacement function (MD) md(t) = 〈‖x_t – x ₀‖〉 from the decoded position sequences x = (x ₀, …, x_t) (Section 5.3, Methods). On a log-log plot, the MDs of diffusions and superdiffusions are linearly related to time with different slopes α ⁻¹ determined by stability²⁴. By studying the slope of estimated MDs, it can therefore be concluded that while wake SWRs were superdiffusive (α < 1, consistent with rodent movements), sleep SWRs encoded random walks (α = 1). Furthermore, sleep SWRs were recorded over a range of velocities as parametrized by tempo τ in our model (with τ decreasing as velocity increases). Notably, SWR trajectory velocity was uniquely related to fast gamma power suggesting that it may vary as a function of MEC input^8,38. We reconcile these two SWR modes within our model from two perspectives. Mechanistically, we show that spectral modulation can interpolate between the distinct statistical regimes of SWRs associated with sleep versus wake by fitting the empirical MD measurements as a function of stability α (Fig. 6A) and that the empirical sleep SWRs step distributions (Fig. 6B) are well-approximated by diffusive propagators (Fig. 6C).

Figure 6. Spatial trajectories encoded in sharp-wave ripples exhibit distinct stability modulation between wake and sleep phases.

A. Blue dots and red dots correspond to the recorded mean displacements (MDs) of spatial trajectories decoded from sharp-wave ripples (SWRs) in the wake phase and sleep phase respectively⁸. There was a difference between the MD slopes (see Section 5.3 Methods) indicating that wake SWRs were generated in the superdiffusive regime (α = 0.8, blue line is the predicted MD curve) while sleep SWRs were diffusive (α = 1, red line is the predicted MD curve). Each of these distinct sampling regimes can be generated by subtly varying the power spectrum s_{τ α} applied to a common underlying environment representation. Note that the physical trajectories of the rodents (“behavior”, blue square markers) were superdiffusive (α = 0.7) consistent with the idea that SWRs may supply candidate exploratory trajectories. This graph is log-log plotted in Fig. E6 where the linearity of mean displacement as a function of time can be observed. Error bars +/- SEM. B. Propagators estimated from reactivated hippocampal trajectories⁸. These resemble those predicted in the diffusive regime but not the superdiffusive regime which lack the increasingly wide spreading activation surrounding the initial position in the center (see panel C). C. Propagators as a function of time interval Δt in the diffusive and superdiffusive regimes.

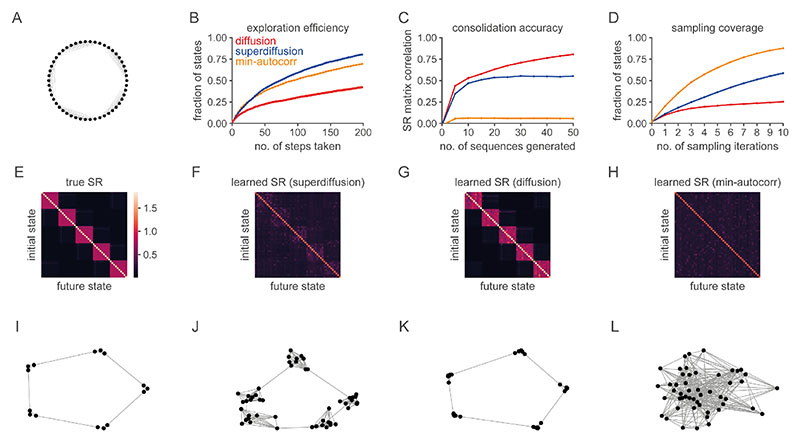
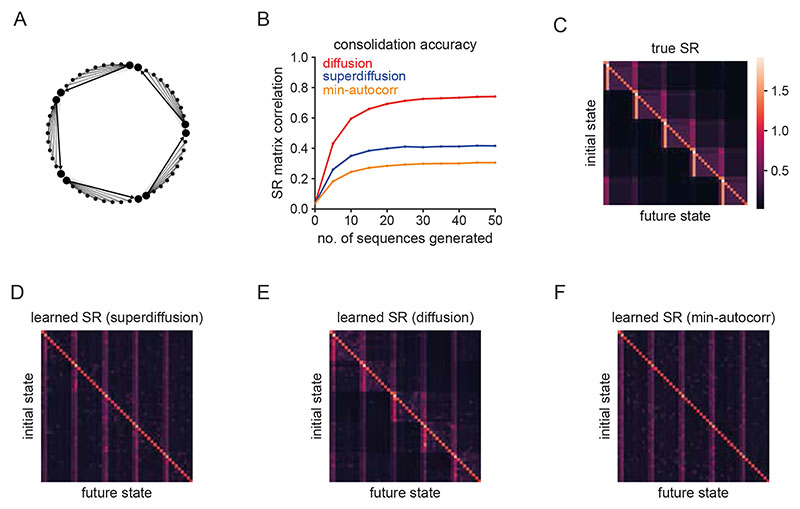
Furthermore, in support of our computational hypothesis that the statistical dynamics of sequential hippocampal reactivations are flexibly altered between exploration or planning in the wake state and memory consolidation during rest, we studied performance metrics for exploration, learning, and Monte Carlo estimation algorithms based on the sequence generation of input state sequences (Fig. 7A-D). We simulated a learning process whereby an environment representation, formalized as the successor representation (SR), is acquired through error-driven learning based on state sequences^28,39. The SR is a predictive state representation whereby the representation of each state encodes the rate at which other states will be visited in the future (Section C.2 SMN). While superdiffusions provide better exploration efficiency (Fig. 7B), and minimally-autocorrelated sampling exhibits the best sampling coverage (Fig. 7D), both are conspicuously inferior in terms of the SR consolidation accuracy (Fig. 7C). Diffusive sequence generation resulted in the best learned approximation to the random walk SR (Fig. 7E-L). Note that this result can be understood theoretically as diffusions embody fundamental spatial biases in their statistical structure (Section 5.1.7, Methods). Though we focused on consolidating the random-walk SR as reflecting a homogeneous predictive map in the absence of salient states such as rewards or landmarks, diffusive sequence generation is also relatively optimized for consolidating directed predictive maps (Fig. E4).

Figure 7. The performance of cognitive algorithms depends on the sampling regime.

A. We consider a random walk generator on a “ring of cliques” state-space⁵⁰ and compare three different sampling regimes (diffusion, superdiffusion, and minimally autocorrelated sampling) with respect to three distinct objectives which quantify the degree to which the sequences generated are optimized for exploration (panel B), learning (panel C), and sampling-based estimation (panel D) respectively. B. Exploration efficiency is defined as the fraction of states explored in an environment relative to the cumulative distance traversed. A steeper slope indicates that more states are explored for less travel distance. With respect to clustered state-spaces (panel A), the characteristic heavy-tail of the superdiffusive propagator implies that occasionally the next state sampled will be drawn from an alternative clique of states unlike diffusion which tends to remain within a single clique (Fig. E7). Minimally autocorrelated sampling is relatively inefficient since it repeatedly samples states across cliques in order to avoid the likelihood of re-sampling nearby states and thus is penalized heavily for traversal distance. C. Consolidation accuracy is the matrix correlation between the learned and true successor representations (SRs). This is plotted as a function of the number of sequences generated. Diffusive replay facilitates the most accurate structure learning of the underlying state-space. D. Sampling coverage is the fraction of states sampled across multiple sequences as a function of the number of sampling iterations. Minimally autocorrelated sampling excels since it is far less likely to resample states within and across sequences. E. The true successor representation matrix for the environment. F-H. The learned successor representations for superdiffusive, diffusive, minimally autocorrelated sequence generation respectively. I-L. Two-dimensional spectral embeddings of the true (panel I) and learned (panels J-L) SRs. The diffusive regime (panel K) successively recapitulates the geometric structure of the true SR (panel I) being composed of five well-spaced cliques of states. In contrast, the SR learned from superdiffusive replay (panel J) does not separate the cliques as clearly due to Lévy jumps leading to the erroneous consolidation of illusory long-range transitions. Minimally autocorrelated sequence generation (panel L) corrupts the spatial structure of the state-space.

2.6. Dysregulated entorhinal input degrades spatiotemporal consistency of hippocampal activity

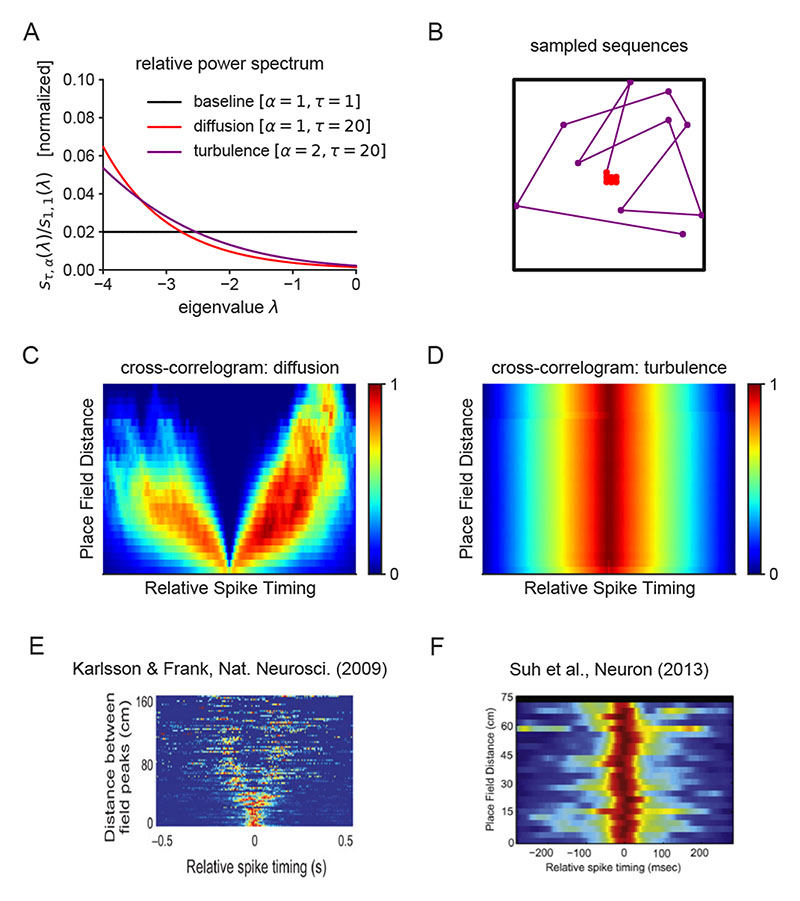
In order to flexibly shift between different regimes of sequence generation, our model requires that the spectral modulation of MEC activity be coherently balanced across grid modules. Dysregulated entorhinal activity may imbalance spectral modulation, thereby disrupting the spatiotemporal structure of hippocampal representations. In particular, spectral modulation with stability α > 1 defines a pathological regime of sequence generation which we refer to as turbulence. Despite seemingly minor differences in the power spectra from diffusion α = 1 to turbulence α = 2 (Fig. 8A), the sequences generated differ greatly. Turbulent sequences are highly irregular and fail to reflect the structure of the underlying space (Fig. 8B). In simulation, increasingly turbulent sampling propagates approximately uniformly across states independent of the initial position and propagators may even fail to preserve the state probability density. We suggest that the erroneous modulation of grid cell activity may therefore contribute to psychopathologies in cognitive processes dependent on coherent sampling from internal representations.

Figure 8. Dysregulated spectral modulation cause pathological forms of hippocampal reactivations.

A. An imbalance in the entorhinal power spectrum (purple line) results in turbulent sequence generation. B. As demonstrated in an open box environment, the resulting trajectories essentially sample randomly and thus are inconsistent with the spatiotemporal structure of the environment. C-D. Propagator cross-correlograms organized as a function of place field distance in the diffusion (panel C) and turbulent (panel D) regimes. E. The same analysis of electrophysiological recordings in rodent hippocampus (panel from Ref. [41]) revealed the characteristic V structure as in the structurally-consistent diffusion regime (panel C). Intuitively, the V-structure reflects the fact that it takes time for the process to diffuse over space as a function of the distance between locations. F. In a genetic mouse model of schizophrenia⁴⁰, the time interval between place cell activations in mutant mice did not reflect the spatial distance between the corresponding place fields, and the resulting cross-correlograms resembled those computed in the turbulent regime (panel D).

In particular, a core positive symptom of schizophrenia is conceptual disorganization. Identifying conceptual representations with nodes in an internal semantic network, this formal thought disorder is indicative of a progressive degradation of the relational structure between nodes during sequence generation consistent with that observed in the generator model as EHC dynamics is shifted deeper into the turbulent regime. The resultant disorder in the hippocampal layer of our model is reminiscent of that observed in mouse models of schizophrenia⁴⁰. In one study, electrophysiological recordings of neural activity in the CA1 hippocampal subregion of forebrain-specific calcineurin knockout (KO) mice were acquired as the mice freely explored⁴⁰. Such KO mice had previously been shown to exhibit several behavioral abnormalities reminiscent of those diagnosed in schizophrenia such as impairments in working memory and latent inhibition. The knockout of plasticity-mediating calcineurin leads to a shift towards potentiation and we sought to highlight a possible mechanism by which the resulting over-excitability may disrupt hippocampal SWRs through the lens of our theory. In particular, we model the effect of calcineurin knockout as an imbalance in the spectral regulation of entorhinal input into hippocampus. Notably, the relationship between the temporal displacement of spikes between distinct cells given the spatial displacement of their place fields was abolished under calcineurin knockout⁴⁰. This is the key quality of turbulent sequence generation. We made a direct quantitative comparison based on a spiking cross-correlation analysis⁴¹. In the diffusive regime, the cross-correlations between place cells as a function of the distance between their place fields embodies the expected relationship between spatial and temporal displacements across the population code whereby place cells at a greater distance from one another tend to activate after larger time intervals (Fig. 8C). Performing the same analysis with the same grid code but with a turbulent spectral modulation returns qualitatively distinct results (Fig. 8D) in which the cross-correlation is essentially independent of place field distance consistent with a complete loss of sensitivity to the underlying spatial structure in sequence generation. While the former reflects the characteristic “V” pattern observed in healthy hippocampal activity (Fig. 8E), the latter replicates the key characteristic of disordered hippocampal sequences recorded from this mouse model of schizophrenia⁴⁰ (Fig. 8F).

3. Discussion

Sequential hippocampal reactivations traversing cognitive maps are viewed as a potential neural substrate of internal simulation at the systems level^5,13,42. We have sought to address some of the apparent variability in the structure and statistics of sequence generation in the EHC^{8,9,11,12,36,40,41}. Our contributions are three-fold. A principled motivation for activating distinct sequence generation regimes depending on the current cognitive process was established through simulation and technical arguments. A linear feedback network model of EHC was proposed which implements the novel technique of spectrally modulating sequence generation. This provides a mechanistic account of how random walk processes may be smoothly interpolated with superdiffusive foraging patterns and minimally autocorrelated sampling. Applications of this model across a variety of environment geometries, behavioral states, and cognitive functions were shown to explain variations in the spatiotemporal structure of hippocampal sequence generation and behavior across a number of experiments.

An open computational question is how might the optimal sequence generation regime for a particular cognitive algorithm and environmental scenario be identified within the brain. We suggest that this arbitration problem is subsumed within the framework of computational rationality which seeks to understand how the parameters of resource-limited algorithms may be optimized⁴³. Previous analyses within this broad remit have focused on optimizing the distribution from which samples are drawn during decision-making⁴⁴ or how state sequence propagation should be initialized and directed for reinforcement learning¹⁶. Generators may be custom designed to embed such desirable algorithmic features within sequence generation.

Our neural network model is designed to provide conceptual clarity regarding how entorhinal spectral modulation may explain variations in hippocampal sequence generation. An integration of other anatomical and functional features of the broader entorhinal-hippocampal system into this model is warranted. Inspiration may be drawn from continuous attractor network models of theta sequences and replay⁴⁵ and MEC electrophysiological recordings which have gleaned evidence that MEC input plays a causal role in refining the temporal organization of hippocampal activity^33,34. Our simulations are based on sampling from the propagated state distribution on each network iteration assuming a noisy readout to the hippocampal code. Possible extensions of this model include the sampling of multiple steps, or sub-sequences, on each iteration which may be regulated by intra-hippocampal processing between CA3 and CA1^7,34. Indeed, a more comprehensive generalization of our model would also operationalize the spectral modulation mechanism along the trisynaptic pathway based on the projections from MEC layer II⁴⁶. With respect to theta-gamma coupling^38,47, sequence generation may be embedded within gamma oscillations alternating between hetero-associative and auto-associative intra-hippocampal dynamics³⁶.

The causal relationship between the power spectrum of MEC activity and the statistical dynamics of hippocampal sequence generation is a core prediction of our model that has not been directly tested to our knowledge. In particular, spectral modulation between diffusive sequence generation (associated with learning and consolidation during rest) and superdiffusive dynamics (expected during active exploration and goal-directed behavior) specifies distinct profiles of total grid population activity along the MEC dorsoventral axis potentially underpinned by variations in neural gain and grid rescaling. Furthermore, minimally autocorrelated hippocampal sequence generation (appropriate for sampling-based planning and inference) specifies novel non-parametric spectral motifs which may be identifiable experimentally.

5. Methods

5.1. Simulation details

5.1.1. Linear track simulation, Fig. 2

Propagator simulations were based on a generator defining random walks on a discretized linear track state-space composed of ten states. Propagation densities were interpolated between states. The (τ, α)-modulated power spectrum s_τ,α(λ) is defined as

$$s_{\tau ,\alpha }\left(\lambda \right)=e^{-{\tau }^{-1}{\left|\lambda \right|}^{\alpha }}$$ (10)

and the relative (τ, α)-modulated power spectrum r_τ,α(λ) is then

$$r_{\tau ,\alpha }\left(\lambda \right)=\frac{s_{\tau ,\alpha }\left(\lambda \right)}{s_{1,1}\left(\lambda \right)}$$ (11)

The latter is normalized for each propagator to facilitate comparisons across propagators

$${\overline{r}}_{\tau ,\alpha }\left(\lambda \right)=\frac{r_{\tau ,\alpha }\left(\lambda \right)}{{\displaystyle {\sum }_k{r}_{\tau ,\alpha }\left({\lambda }_k\right)}}$$ (12)

This measures the fraction of the total power spectrum accounted for by each spectral component relative to the baseline (τ = 1, α = 1).

5.1.2. Pfeiffer & Foster, Science (2015), Fig. 2

A square enclosure containing no obstacles was represented by a 50 × 50 lattice of states. The stability parameter was set to α = 1 and α = 0.5 for diffusive and superdiffusive exploration respectively. The tempo parameter was set to τ = 1 in both cases. The simulation results reflect 20 sequences composed of 75 samples each. Superdiffusive exploration was more efficient than diffusive across a range of parameter values and changes in the size of the environment. The performance advantage of superdiffusion diminished as the environment size was reduced as all states became locally accessible to diffusive exploration and global re-positioning rendered unnecessary. In panel 2k, the step size was computed using the Euclidean distance between states embedded within an ambient continuous space.

5.1.3. Pfeiffer & Foster, Nature (2013), Fig. 3

The square arena containing no obstacles was discretely represented by a 25 × 25 lattice of states. The random walk generator O ^rw (Section B.5, SMN) on this graph was modified to embed the rewarded Home location by scaling the generator transition rates at home states according to

$$O_{h\cdot }\leftarrow v^{-1}{O}_{h\cdot }$$ (13)

where h indexes home states $x_h\in 𝒳$ and v is a scalar quantity specifying the motivational value of home states. This leverages a unique property of the generator formalism whereby the temporal localization of states can be controlled independently of spatial structure (Section B.10, SMN).

In our simulations, the stability parameter was set to α = 1 and α = 0.5 for diffusive and superdiffusive sequence generation respectively. The tempo parameter was set to τ = 5 in both cases and the motivational value parameter v = 100. Trajectory events were simulated via sequence generation emanating from a home location (“home-events”) and four away locations (“away-events”). The home location was specified as four adjacent states close to the center of the environment and the four away locations were placed in each corner. Twenty home-events and ten away-events per away location, each composed of ten samples, were generated. Sampling density was estimated from these trajectory events as the number of samples of each state divided by the total number of samples. This function was computed for each combination of condition (home and away) and sampling regime (diffusive and superdiffusive). The results were robust to variations in simulation parameters and the number of trajectory events.

5.1.4. Wikenheiser & Redish, Nature Neuroscience (2015), Fig. 4

The circular track was discretized into 24 states with 3 further states connected at regular intervals on the outside of the circle serving as the goal locations. Consistent with the behaviors acquired by the rats during task training, the generator employed reflected a goal-directed behavioral bias in favour of anti-clockwise movement around the track and turn-offs to goal locations. For sequence generation targeting a particular goal, the generator reflected a bias towards staying at the goal location once it was reached in order to reflect the time taken for the reward to be delivered, consummatory behaviors, and trial termination. In the multi-goal scenario (Fig. E3), the generator transition structure facilitated a return to the main track after goal arrival thus enabling multiple goal locations to be visited. Simulations of theta sequences (for both the individual sequence plots and look-ahead estimations) were composed of five iterations in order to match the number of decoded positions in the figure panels from Ref. [11]. As usual, stabilities α = 1 and α = 0.5 were used for diffusive and superdiffusive sequence generation respectively with τ = 1 in both. Look-ahead distances were computed as the distance from the initial position to the furthest sampled position. The initial position was the start location marked by an X in the “Trajectory Initiation” simulations (Fig. 4G). In the “Goal Arrival” simulations, the initial position for a particular targeted goal was located in the center of the preceding track segment. The mean and standard error of the lookahead distances were estimated from 50 samples (an arbitrary number ensuring a stable estimate). The spatial scale (i.e., the numeric distance between two adjacent states) was set in order to roughly match that of the circular track employed in the experiments¹¹.

5.1.5. Kay et al., Cell (2020), Fig. 5

We assumed that the rodent’s decision-making policy reflected a directed run to the junction, a random choice to turn left or right, followed by a directed run to the end of the maze arm (where a reward might be available). A small transition rate opposing the directed transitions was added in order to ensure reversible and aperiodic propagation dynamics and numerically stable analyses. We initialized the spectrum in the diffusion regime and applied standard minimization routines (scipy.minimize) in order to solve the constrained optimization problem (Eqn. 84). We minimized the integrated autocorrelation time summed over nine lags. Autocorrelations were estimated from 100 generated sequences of 20 iterations each.

Note that the planning objective (Eqn. 8) is based on the average-reward, infinite-horizon formulation of Markov decision process⁵¹. This facilitates a simpler exposition and a more direct analogy to Markov chain Monte Carlo methods. For episodic and discounted MDPs, a similar but more complicated analysis may be pursued. In this case, the expected cumulative reward forms the value function objective requiring Monte Carlo estimation over sampled sequences. This may be accomplished via MCMC over the joint distribution over states across time points or else by applying Sequential Monte Carlo methods. Importantly, the integrated autocorrelation time Δt _ac remains the key objective for sampling optimization since it is also reflected in the sample variance of the expected cumulative reward value function estimator.

5.1.6. Stella et al., Neuron (2019), Fig. 6

We hypothesized that, though the rodents’ physical experiences conformed to superdiffusive trajectories, the EHC recapitulated the environment experiences in the form of diffusive trajectories in order to facilitate accurate spatial consolidation, reconsolidation, and maintenance processes during sleep. This is because diffusive replay embodies fundamental inductive biases regarding space, namely that space has a smooth, localized, and isotropic structure. In contrast, superdiffusive trajectories are superior for foraging as shown in simulation (Fig. 7) and theoretical studies³⁵. Therefore, we also conjectured that, in contrast to sleep SWRs, SWRs occuring during immobile periods interleaved with active foraging (i.e., “wake SWRs”) may reflect non-local, superdiffusive spatial trajectories in order to leverage a cognitive map of the environment in support of exploration. In particular, a superdiffusive sequence of positions may be generated during pauses, which the rodent can then follow physically in order to search for the food pellets.

Although rodents were familiar with the foraging environment at the time of the electrophysiological recordings and thus only a modest amount of new information may be required to be consolidated, theoretical and computational studies have shown that off-line replay is crucial to maintaining precise storage and retrieval mechanisms for previously learned information¹⁴. This need is particularly pressing in order to avoid interference due to ongoing cortical plasticity as well as the consolidation of new information such as that drawn from experiences in novel environments as is the case in the protocol of the current experiment. Furthermore, from a spatial cognition perspective, off-line replay may contribute towards “map refinement”⁸. That is, increasing the accuracy and resolution, and reducing any residual uncertainty, with respect to the structure of cognitive maps that may already be consolidated to a degree.

In order to show that our model supports the switching of the desired hippocampal sampling regime between diffusion for consolidation to superdiffusion for exploration based on monosynaptic input into the CA1 region, we modeled the mean displacement curves of generated sequences under diffusion and superdiffusion. These curves were plotted as a function of the time interval Δt and compared to the empirical mean displacements for sleep and wake SWRs respectively (Fig. 6A). The mean displacement curves of sequence generation under the generator model were analytically computed (Eqn. 17, Section 5.3, Methods) as a function of the stability parameters α and diffusion constants K estimated in Ref. [8]. This is in Fig. 6A). In order to focus on stability modulation, which specifically distinguishes between diffusion and superdiffusion, we averaged the empirical data over trajectory velocities (which is parametrized by the τ parameter in our model). In addition to SWR trajectories, we also plot the mean displacement curve for the median velocity behavioral trajectories (see “behavior” Fig. 6A). The spatial scale parameter σ was set to 4 in order to approximately match the ratio between the spatial (y-axis) and temporal (x-axis) scales. This parameter can be thought of as defining what constitutes a centimetre in our simulation and does not affect the relative slopes in mean displacement.

5.1.7. Sampling optimization, Fig. 7

A “ring-of-cliques” state-space with five cliques composed of ten states each was studied (Fig. 7A). The definitive feature of this state-space is that it exhibits a community structure. Within each clique, states are densely connected, however only sparse connections are available between cliques. Rings of cliques are commonly studied in the field of social psychology as a proxy for social networks, and it is known that human structure learning is sensitive to such community architectures⁵⁰. Propagators were based on the random walk generator on this state-space. The power spectrum was parametrized such that the propagator shape was approximately equalized across conditions. This was accomplished by equating the modal probability (i.e., the “height”) of the propagator distributions. In particular, the stability parameter was set to α = 1 for diffusion and α = 0.3 for superdiffusion. These settings were paired with tempo parameters of τ = 20.7 and τ = 3.1 respectively. The integrated autocorrelation time over nine lags was minimized for the min-autocorrelation propagator. See Fig. E7 for a visualization of sample sequences.

For exploration, a single sequence of 100 samples was generated and interpolated into a complete behavioral trajectory. For SR consolidation, sequences of 50 states were generated. The learned SRs (panels F-H) reflect the estimated SR after 500 sequences. For sampling, 10 sequences of 10 states each was generated (resulting in 100 states sampled in total). These are conceptualized as chains running in parallel as is commonly implemented in MCMC algorithms and thus the sampling coverage was computed by integrating over the 10 sequences generated. For exploration and sampling, all sequences were initialized at a fixed state presumed to correspond to the position of the agent in the environment while, for learning, sequences were randomly initialized according to the stationary distribution as if randomly sampling from memory during sleep. All curves reflect the mean and standard error over 50 simulations.

The performance rank order across generative regimes for each measure was robust with respect to variations in τ and α, the number of sequences and sampling iterations, and the parametrization of the environment (i.e., changes to the number of cliques or the number of states per clique). With regards to the latter, it seemed that the graph diameter was an important factor in determining the gain in exploration efficiency for the superdiffusive regime relative to the min-autocorrelation regime (Fig. 7B). The graph diameter measures the minimum distance the agent must travel in the worst case scenario. In the ring-of-cliques model, the graph diameter scales with the number of cliques. As the graph diameter increased and, consequently, large non-local “jumps” were more heavily penalized for distance, superdiffusions tended to excel. Therefore, one would expect that superdiffusive dynamics may be less important in small-world networks which are characterized by connectivity structures admitting a short path between almost all pairs of nodes. Such networks are inconsistent with Euclidean spaces but are notably over-represented in social and transport networks. We also observed that running multiple chains in parallel increased the min-autocorrelator performance in sampling coverage relative to superdiffusions (Fig. 7D). This suggests that, consistent with MCMC intuitions, there is a cumulative effect of sampling diversity when autocorrelations are minimized. That is, the evolution of each chain increasingly diverges from other chains over sampling iterations. More formally, the sample cross-correlation across chains is low due to the generative minimum autocorrelation property.

The structure consolidation results can be understood theoretically. Diffusion is a random process with zero drift and finite scale (measured as propagation variance as a function of time). Therefore it encapsulates inductive biases regarding spatial structure, respectively that space is isotropic and has a scale that distinguishes between local and global structure. Moreover, from an information-theoretical point of view, it is the simplest such random process, being the unique maximum entropy process with these properties⁵². This implies that diffusive sequences implicitly encode isotropy and scale, and nothing else. In contrast, the distinguishing feature of superdiffusive Lévy flight processes in unbounded Euclidean spaces is the infinite variance of its heavy-tailed propagation distribution²⁴. This means that extraordinarily large jumps may be generated and so the downstream learning process is unable to distinguish between local structure (learned from individual small jumps within short time periods) and global structure (learned from the accumulation of many small jumps over a period of time).

5.1.8. Karlsson & Frank, Nature Neuroscience (2009) and Suh et al., Neuron (2013), Fig. 8

The diffusion and turbulence regimes were parametrized by α = 1 and α = 2 respectively with τ set to 20 in both cases. In a linear track environment, 100 state sequences with 100 steps were generated in each of these stochastic regimes. The average spiking activity of each place cell (each encoding a distinct state) was taken to be the output propagator density. The Euclidean distance between states (assuming the underlying graph is embedded in an ambient continuous space) was taken to be the distance between place fields. The relative spike timings were offsets in the number of steps within the generated sequences. Given these modeling assumptions, we computed normalized cross-correlograms of place cell activity as a function of the distance between place fields⁴¹. The key qualitative distinction between the cross-correlograms was robustly observed regardless of modifications to the other model parameters (e.g., r, number of sequences, number of steps).

In Fig. 8E, we present a cross-correlogram of SWRs recorded in healthy mice which clearly shows the predicted V-structure consisted with a systematic relationship between temporal and spatial displacements during sequence generation. This plot comes from another reference Ref. [41]. Note that, in Ref. [40], the cross-correlogram for the littermate controls is also presented (see Fig. 4C ⁴⁰) but the V-structure is less clear (presumably, due to fewer SWRs and a smaller environment). Therefore, we include the V-structure from the prototypical analyses in Ref. [41] since it is easier to interpret on viewing for the first time.

5.2. Evaluating sequence generation across exploration, learning, and planning

The central computational motivation in conceptualizing MEC as a modulator of hippocampal sequence generation is that distinct cognitive algorithms have fundamentally different requirements as to the statistical and dynamical structure of the input sequences received from EHC. In order to establish this empirically, we evaluated sequences generated with respect to metrics sensitive to the performance of exploration, learning, and sampling-based planning algorithms. The three metrics are exploration efficiency, consolidation accuracy, and sampling coverage, and are defined in the following three sub-sections.

5.2.1. Exploration efficiency

In order to evaluate how appropriate a generative sampling regime is for exploration, we quantified exploration efficiency as the fraction of environment states or positions visited relative to the cumulative distance traversed. This definition is a simple adaptation to graph structures of the standard definition commonly studied in the foraging literature⁵³. Exploration efficiency is plotted as a function of the number of states sampled in Fig. 7B for diffusive, superdiffusive, and minimally autocorrelated sequence generation. Note that, if the generator model samples successive non-adjacent states, then it is assumed that the agent visits all states along the shortest path between the sampled states as if physically traversing the environment. In a discrete state-space, the distance is taken to be the number of steps taken while in a continuous domain, it is the Euclidean distance between positions.

Propagators may repeatedly sample the same state on multiple iterations leading to a period of immobility for the agent. We assume that the cost of remaining in a state is zero since the agent has not traversed any distance. However, re-sampling the same state adds to the total time cost of exploration, which can be defined as the total time taken for sampling subsequent states and moving to those states. Assuming that hippocampal state sampling is embedded within theta¹¹ or slow-gamma³⁶ cycles, the rate at which new states are sampled is on the order of centiseconds. In contrast, a rodent requires time periods on the order of seconds to move between positions sampled in a typical open box environment. Thus, the contribution of sampling time to total exploration time is neglible and is therefore not reflected in the exploration efficiency measure. Note that, in this regard, the definition of exploration efficiency contrasts sharply with the sampling coverage measure which specifically penalizes for time and not distance.

5.2.2. Consolidation accuracy

We quantify how well a structural representation of an environment (in particular, a successor representation³⁹) can be learned from replayed state sequences. As a measure of consolidation accuracy, we utilize the Spearman correlation between the true and learned state-space successor representations as a function of the number of sequences generated. This measure is plotted as a function of the number of sequences generated in Fig. 7C for each modulatory regime. Before learning commences, the prior successor representation is taken to be that generated by a fully-connected graph. This implies that the future expected rate of occupancy is completely homogeneous across initial and successor states a priori. The SR is learned via a standard temporal difference learning rule^28,39.

5.2.3. Sampling coverage

An important objective in sample-based inference (e.g., in planning³⁷ and reinforcement learning⁵⁴) is to generate a diversity of sampled states as quickly as possible as this leads to robust and rapid estimators. Sampling coverage is defined as the fraction of environment states or positions visited relative to the number of sampling iterations (Fig. 7D). Note that, unlike the exploration efficiency measure, sampling coverage does not penalize for the distance traversed between states, as it is presumed to reflect an internal sampling mechanism which is completed prior to any contingent behavior. The sampling coverage measure specifically penalizes for repeatedly sampling the same state since the fraction of states sampled remains the same despite the number of sampling iterations increasing. Both exploration efficiency and sampling coverage are sensitive to the fraction of states visited or sampled respectively. The major distinction between the two is that the former isolates the cost of distance traversed by the agent, while the latter penalizes the time taken to generate the sequence.

5.3. Mean squared displacement and mean displacement as diagnostic measures of the sequence generation regime

Mean squared displacement (MSD) msd(t) = 〈|d(t)|²〉 is a measure of the scaling law of a stochastic process and can be estimated from trajectory samples^8,24. It is a time-dependent function which characterizes the relationship between the spatial and temporal displacements. Intuitively, for any time period t, msd(t) measures how far away from the initial state at t = 0 that sequence generation is expected to sample as a function of time. Given a trajectory x = (x ₀, …, x_t) in Euclidean spaces, the measure of spatial displacement is taken to be the squared Euclidean distance d(t) with respect to the initial state:

$$d\left(t\right)=\Vert x_t-x_0\Vert =\sqrt{{\displaystyle \sum _{i=1}^D{\left(x_{t,i}-x_{0,i}\right)}^2}}$$ (14)

where x_t,i is the i-th position coordinate of the process at time t and D the dimensionality of the state-space. It can be shown analytically²⁴ that, for diffusive-type processes, MSD scales according to

$$\text{msd}\left(t\right)=\langle d{\left(t\right)}^2\rangle \propto K{\left({\tau }^{-1}t\right)}^{{\alpha }^{-1}}.$$ (15)

In log-space

$$\text{log}\langle d{\left(t\right)}^2\rangle \propto \text{log}K+{\alpha }^{-1}\text{log}\left({\tau }^{-1}t\right)$$ (16)

and so the intercept on a log-log plot is the log of the diffusion constant K (which sets the rate of diffusion independent of τ and α modulation) and the slope is the inverse of the stability parameter α. If the slope of the MSD graph equals 1 then the process is a diffusion. A slope greater than 1 indicates supralinear displacements and therefore the process is known as a superdiffusion (α < 1). This is the genesis of the term superdiffusion. Therefore, the stability regime of sequence generation can be inferred from sample trajectories by estimating msd(t). The key implication of a supralinear MSD is that a superdiffusion is expected to sample further away from its origin over time compared to diffusion. When computing msd(t) for sequences generated by our model, we consider the Euclidean distance d induced by embedding the state-space within an ambient Euclidean space.

The mean displacement (MD) is analyzed in Fig. 6 and Ref. [8]. This is similar to the MSD formula but without squaring the distance function:

$$\text{md}\left(t\right)=\langle d\left(t\right)\rangle \propto K{\left({\tau }^{-1}t\right)}^{{\left(2\alpha \right)}^{-1}}$$ (17)

therefore in log-space, we have

$$\text{log}\text{md}\left(t\right)\propto \text{log}K+{\left(2\alpha \right)}^{-1}\text{log}\left({\tau }^{-1}t\right).$$ (18)

Statistical Analyses

No statistical analyses were conducted for this study.

Extended Data

Figure E1. Sequence generation in an inhomogeneous environment with tempo τ and stability α modulation.

A. Spectral components of the four-room grid world are presented as a function of spatial scale. Generator eigenvectors coincide with the eigenvectors of the corresponding SR. Therefore, many examples of generator eigenvectors may be observed in Ref. [28]. B. As the tempo parameter τ is reduced (with the stability parameter held at α = 1), the power spectrum s_τ,α(λ) reweights the spectral components leading to changes in the spatial scale of the propagation densities ρ_t. C. The generated sequences vary in the extent of their spatiotemporal traversal of the environment.

Figure E2. Exploration efficiency in a structured environment.

The exploration simulation in Fig. 2 is repeated here but for an environment decomposed into four areas connected by bottlenecks. Each area consisted of 50 × 50 states. Simulation parameters were unchanged from Fig. 2 (see Section 5.1.2, Methods). E. Error bands +/- s.e.m. for n = 20 trajectories.

Figure E3. Propagator analysis across all possible current and future positions for the circular track task.

A-B. We plot the superdiffusive (panel A, α = 0.5) and diffusive propagators (panel B, α = 1) for the circular track task¹¹ for all current positions (y-axis) with all goals activated. The y-axis (x-axis) indexes the current (future) position. Each row reports the probability of each position being sampled given the current position (the row index). C. The difference in diffusive and superdiffusive propagators is plotted. For example, the row corresponding to the initial X position (marked by the thick black line), shows that the local activations are less likely (red) under superdiffusions compared to diffusion (though they are still possible) while remote goal locations specifically are more likely (blue).

Figure E4. Diffusions are optimized for consolidating directed transition structures.

Three regimes of sequence generation are compared in terms of consolidating a directed policy on the same graph used in Fig. 7 where the policy was assumed to be undirected (i.e. a random walk). A. The directed policy is dominated by high probability anti-clockwise transitions (heavy black arrows) between the clique bottleneck states (highlighted by increased size). Within each clique, transitions to the bottleneck state facilitating an anti-clockwise transition to the next clique are relatively likely to occur. B. The same rank order as in Fig. 7C is observed with the diffusive regime leading to the most accurate consolidation of the directed policy successor representation (SR). C. The true directed policy SR. D, E, F. The SRs learned via superdiffusion, diffusion, and minimally autocorrelated sampling respectively. Note that the superdiffusive and minimal autocorrelation regimes identify the the dominant anti-clockwise transition structure but fail to reflect the clustering of states based on their clique membership. This simulation indicates that the diffusive regime is optimal for consolidation regardless of whether the target transition structure corresponds to a random walk or not.

Figure E5. Detailed analyses of spectrally modulated propagation in the linear track environment.

A. Copy of Fig. 2D for context and comparative visualization. B. The propagation distributions in panel A are re-expressed as the difference with respect to the baseline (τ = 1, α =1). C. Each propagation density is plotted against the baseline propagation density (τ = 1, α = 1) on log scales. Note that only superdiffusion results in a non-linear warping of the propagation density. This non-linearity underpins the heavy-tail in the propagation density. D. Small-scale (dashed line) and large-scale (full line) spectral components (i.e., generator eigenvectors) are plotted as a function of linear track position. Eigenvalues take a maximum value of 0 and are ordered according to the spatial scale of the corresponding spectral component. For example, eigenvalues close to zero correspond to large-scale spectral components with the spatial scale of the corresponding spectral component decreasing with the eigenvalue which are always less than or equal to zero. Therefore, the scale of a spectral component ϕ_k decreases as the absolute value |λ_k| of its corresponding eigenvalue λ_k increases. E. Spectral power is plotted as a function of eigenvalue on a log scale. As the tempo τ decreases towards zero, the spatiotemporal horizon increases and the propagation density converges on the stationary state distribution. This corresponds to all spectral components with non-zero eigenvalues decaying to zero. Note that diffusion linearly changes the slope of the power spectrum while superdiffusion imposes a non-linear reweighting. This effect underpins the nonlinear time warping in the propagation densities in panel C. F. The characteristic modulation of the power spectrum under diffusion and superdiffusion is demonstrated by the relative power spectrum $\frac{s_{\tau ,\alpha }\left(\lambda \right)}{s_{1,1}\left(\lambda \right)}$ computed as the power ratio with respect to the baseline propagator. Note that the long-range diffusion propagator (α = 1, τ = 0.5, thick red line) downweights small-scale components and upweights large-scale components while superdiffusion (α = 0.5, τ = 1, thick blue line) relatively upweights both small- and large-scale components but suppresses at medium scales. This enables a superdiffusive propagator to jump to remote positions without traversing intermediate locations.

Figure E6. Mean displacement scales linearly on a log-log plot.

The data and simulations from Fig. 6 are plotted on a logarithmic scales demonstrating the linear relationship between mean spatial displacement and time intervals. Mean displacement (MD) measures the ratio between the spatial displacement and time interval of sequence generation and can be used to infer whether a generative sampling process is operating in a diffusive or superdiffusive regime based on sampled sequences. In particular, the MD function has a slope proportional to α ⁻¹ with respect to the time interval Δt (see Section 5.3 Methods). Error bars +/- s.e.m..

Figure E7. Sampled sequences exhibit distinctive patterns across spectral modulation regimes.

Each column shows five sample sequences generated in one of the three sampling regimes studied in Fig. 7. Note that diffusions (left column) tend to remain within a single clique. Superdiffusions (middle column) interleave local diffusions with occasional jumps to other cliques. Jumps are observed as lines crossing the center of the ring which do not conform to any transition step in the underlying state-space structure (grey lines). Minimally autocorrelating propagators (right column) repeatedly generate large jumps between cliques.

Data Availability

No data was acquired for this study.

Code Availability

Simulation code was written using open source packages in the Python 3 programming environment and can be found at https://github.com/dmcnamee/FlexModEHC.