Skip to main content
NCBI home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2021 Jun 21.
Published in final edited form as: Neuroscience. 2016 Nov 30;343:55–65. doi: 10.1016/j.neuroscience.2016.11.031

Development Of Neural Population Activity Toward Self-Organized Criticality

Yuichiro Yada a,b,c, Takeshi Mita a,b, Akihiro Sanada a,b, Ryuichi Yano a,b, Ryohei Kanzaki a,b, Douglas J Bakkum d, Andreas Hierlemann d, Hirokazu Takahashi a,b,*
PMCID: PMC7611021  EMSID: EMS127762  PMID: 27915209

Abstract

Self-organized criticality (SoC), a spontaneous dynamic state established and maintained in networks of moderate complexity, is a universal characteristic of neural systems. Such systems produce cascades of spontaneous activity that are typically characterized by power-law distributions and rich, stable spatiotemporal patterns (i.e., neuronal avalanches). Since the dynamics of the critical state confer advantages in information processing within neuronal networks, it is of great interest to determine how criticality emerges during development. One possible mechanism is developmental, and includes axonal elongation during synaptogenesis and subsequent synaptic pruning in combination with the maturation of GABAergic inhibition (i.e., the integration then fragmentation process). Because experimental evidence for this mechanism remains inconclusive, we studied the developmental variation of neuronal avalanches in dissociated cortical neurons using high-density complementary metal-oxide semiconductor (CMOS) microelectrode arrays (MEAs). The spontaneous activities of nine cultures were monitored using CMOS MEAs from 4 to 30 days in vitro (DIV) at single-cell spatial resolution. While cells were immature, cultures demonstrated random-like patterns of activity and an exponential avalanche size distribution; this distribution was followed by a bimodal distribution, and finally a power-law-like distribution. The bimodal distribution was associated with a large-scale avalanche with a homogeneous spatiotemporal pattern, while the sub-sequent power-law distribution was associated with diverse patterns. These results suggest that the SoC emerges through a two-step process: the integration process accompanying the characteristic large-scale avalanche and the fragmentation process associated with diverse middle-size avalanches.

Keywords: dissociated culture, self-organized criticality, neuronal avalanche, microelectrode array

Introduction

Emerging universally in neural systems, self-organized criticality (SoC) is a state in which moderate complexity dominates the dynamics of a system (Beggs and Plenz, 2003; Mazzoni et al., 2007; Pasquale et al., 2008; Petermann et al., 2009; Friedman et al., 2012). Maintained by a fine balance of neural excitation and inhibition (Massobrio et al., 2015), networks in such critical states exhibit characteristic cascades of spontaneous activity, which feature power-law size distributions (Beggs and Plenz, 2003) and are expressed with a rich repertoire of spatiotemporal patterns (i.e., neuronal avalanches) (Beggs and Plenz, 2004). The potential benefits of SoC in neural systems suggest that it has a functional role in neural computation, putatively maximizing information transmission (Beggs and Plenz, 2003), the number of stable patterns (Haldeman and Beggs, 2005; Chen et al., 2010), information capacity (Shew et al., 2011), and the range of usable inputs in a neural system (Shew et al., 2009). How SoC emerges in a brain network has therefore generated intense interest, with researches focusing on adaptation processes induced by synaptic plasticity (Levina et al., 2007; Millman et al., 2010; Shew et al., 2015) and neuronal development (Pasquale et al., 2008; Stewart and Plenz, 2008; Tetzlaff et al., 2010; Pu et al., 2013).

Synaptic wiring and rewiring during development (i.e., axonal elongation and synaptic pruning) and the maturation of GABAergic inhibition (Bourgeois and Rakic, 1993; Chechik et al., 1998; Wu et al., 2012) have been linked to the emergence of the critical state (Tetzlaff et al., 2010). However, the relationship between the avalanche distribution and the variability of spatiotemporal patterns, which presumably reflects alterations in network organization, remains elusive. Moreover, previous studies have focused predominantly on neural systems after two or three weeks of in vitro development (Pasquale et al., 2008; Tetzlaff et al., 2010). Synchronized bursts can be observed starting less than a week in vitro (Kamioka et al., 1996; Wagenaar et al., 2006); however, since juvenile cultures demonstrate reduced activity compared to their mature counterparts, recordings from neurons in juvenile cultures were deemed unreliable (Tetzlaff et al., 2010). Therefore, experimental evidence for the emergence of neuronal avalanches during the early developmental stages is still lacking.

The recent development of high-density complementary metal-oxide semiconductor (CMOS) microelectrode arrays (MEAs) (Berdondini et al., 2009; Frey et al., 2010; Müller et al., 2015) may be able to overcome this issue. CMOS MEAs feature a densely-packed grid of recording electrodes that provide single-cell spatial resolution. This enables the detection of enough active neurons to capture the activity of an immature network, whereas conventional MEAs with more widely spaced electrodes may miss many of the neurons residing between electrodes. The CMOS MEA’s sub-millisecond temporal resolution, combined with its single-cell spatial resolution, may adequately depict the precise dynamics of neuronal activities from early development through more mature periods.

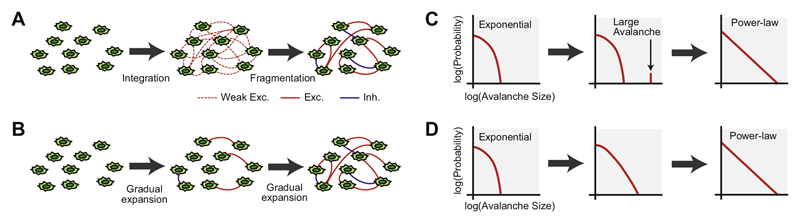
In the present study, the developmental variation of neuronal avalanches was investigated via a high-density CMOS MEA, using cortical cultures derived from an early developmental period. Initially, each neuron has few connections with others and exhibits mutually independent activity; therefore, the avalanche size should be described by an exponential distribution. As the complex neural circuit structure develops, including fine excitatory–inhibitory balance, the critical state may emerge. Such a state is characterized by an avalanche size distributed according to the power-law distribution. Between these states, there could be a hypothetical state that would feature weak but dense excitatory connections, produce characteristic large-scale synchronization, and whose connections would then be fragmented during development (Tetzlaff et al., 2010; Le Magueresse and Monyer, 2013) (Fig. 1A; integration-the n-fragmentation); alternatively, neurons could gradually expand their connections during development of the SoC (Fig. 1B; gradual expansion). In the integration- then-fragmentation model, the avalanche size distribution could capture the characteristic large-scale synchronization as specific, large avalanches that are significantly larger than the typical avalanche sizes (Fig. 1C). In the gradual-expansion model, on the other hand, the avalanche size distribution would exhibit gradual transformation from the exponential distribution to the power-law distribution (Fig. 1D). To investigate which, if either, of these hypotheses is more accurate in describing the emergence of SoC, we analyzed avalanche size distribution and spatiotemporal correlation of synchronized burst patterns over a range of days in vitro (DIV).

Fig. 1. Schematic illustration of possible models of development.

Fig. 1

Open in a new tab

(A and B) illustrate variation of network structures. (C and D) show variation of avalanche size distributions corresponding to (A and B), respectively.

Experimental Procedures

Cell culture

All experiments were conducted with the approval of local ethics committee of the University of Tokyo. This study was carried out in strict accordance with “Guiding Principles for the Care and Use of Animals in the Field of Physiological Science” published by the Japanese Physiological Society. The experimental protocol was approved by the Committee on the Ethics of Animal Experiments at the Research Center for Advanced Science and Technology, the University of Tokyo (Permit Number: RAC130106).

The cell culture protocol used in the present experiment followed that previously described (Müller et al., 2012; Bakkum et al., 2013) with slight modifications. The CMOS MEA (Frey et al., 2010) used in the present study was provided by Bio Engineering Laboratory (BEL), ETH Zurich. The CMOS MEA surface was coated with 20- μl drop of 0.05% polyethylenimine (Sigma– Aldrich, United States) and 20- μl drop of 0.02 mg/ml laminin (Sigma–Aldrich). Cortical tissue was obtained from E18 Wistar rats (CLEA Japan, Japan), dissected, and dissociated with 0.25% trypsin–EDTA (Life Technologies, United States). The dissociated cortical cells, approximately 30,000–50,000 cells per dish, were plated on the CMOS MEAs. The cells were maintained for 24 h in a cell culture incubator with plating media consisting of 850 μl of NeuroBasal (Life Technologies) supplemented with 10% horse serum (HyClone, United States), 2% B27 (Life Technologies), and 0.5 mM GlutaMAX (Life Technologies). The atmosphere of the incubator was maintained at 36.5 °C and 5% CO2 humidified condition. A day after plating, half of the media was exchanged for cell culture media consisting of 850 μl of Dulbecco’s Modified Eagle’s Medium (DMEM; Life Technologies) supplemented with 10% horse serum, 0.5 mM GlutaMax, and 1 mM sodium pyruvate (Life Technologies) and maintained in the incubator. Half of the media was exchanged with new media twice a week for the remainder of the study period.

Electrophysiological recording

The CMOS MEA features 11,011 electrodes in a 2.0-mm x 1.8-mm area, wherein signals can be simultaneously recorded from up to 126 arbitrary electrodes with a 20-kHz sampling rate. The size of the electrode is 8.2 μm x 5.8 μm. The on-chip circuit amplified (x960) and bandpass filtered (200–3.7 kHz) the obtained signals (Bakkum et al., 2013).

Nine cultures were used for experimental analysis, each from 4 to 30 days in vitro (DIV). Prior to each session of avalanche recording, 1 min of spontaneous activity was sequentially recorded at whole electrodes. Spikes were detected at each electrode and the mean amplitude of spikes was stored. Next, the amplitude at the interspace between the electrodes was interpolated and a spatial map of action potential amplitude was obtained. The spatial map was then spatially filtered using a Gaussian kernel. Local minima were detected from the smoothed map, and the electrodes closest to 126 or fewer of the most negative local minima were selected for subsequent avalanche recording. The spontaneous activity of a cortical culture was subsequently recorded for 30 min using the selected electrodes to capture avalanche distribution. The signal from each electrode was recorded and the time at which that spike was detected was stored.

In total, 77 recordings were performed. Custom-made software (BEL, ETH Zurich, Switzerland) based on MEAbench (Wagenaar et al., 2005) was used to manage recording. A LimAda algorithm (Wagenaar et al., 2005) with a threshold set to 5.0 was adopted for spike detection. Spike sorting was not performed in this experiment. All recordings were performed in the incubator.

Avalanche definition

A neuronal avalanche and its detection have been previously described (Tetzlaff et al., 2010). Briefly, spike times detected at all recording electrodes were combined into a single-spike train, and defined as an “array-wide spike” train. Then, if the time interval of such an arraywide spike was less than Dt, those spikes were determined to belong to the same avalanche. If no spike existed within Dt of a spike occurrence, the spike formed a “size one” avalanche. Therefore, each spike is included in one of the avalanches. Dt was decided according to the activity time-scale of each culture: the mean inter-spike interval (mISI) of array-wide spikes was used as Dt (Pasquale et al., 2008; Tetzlaff et al., 2010) on each recording day.

Characterization of avalanche distribution

To characterize the developmental variation of neuronal avalanches, several characteristics were defined with regard to avalanche size distribution. This included the probability of a certain size avalanche occurring, wherein the size of an avalanche was defined by the number of spikes belonging to it (Tetzlaff et al., 2010). The Kolmogorov–Smirnov (KS) test between an empirical distribution and a hypothesized distribution, parameters of which are estimated by maximum likelihood estimation, was adopted to characterize distributions (Clauset et al., 2009; Klaus et al., 2011). Briefly, the power-law distribution was formulated as

Pα(s)={csα(smin⩽s⩽smax)0(otherwise)

where s is the size of avalanche, exponent a is the slope parameter, and c is the normalized constant that satisfies ∑​smaxs=sminPα(s)=1. Similarly, the exponential distribution was formulated as

Pλ(s)={ce−λs(smin⩽s⩽smax)0(otherwise)

where k is the parameter of the distribution and c is the normalized constant that satisfies ∑​smaxs=sminPλ(s)=1. In this study, the size range parameter was set to s min = 1 and s max was set to the number of recording electrodes (Klaus et al., 2011), which was typically 126. The parameter a was estimated by maximizing the log-likelihood function logLα(α∣x)=∑​ni=1logPα(xi) where x=[x 1,x 2,...,x n,] are empirically observed avalanche sizes. The parameter k was then estimated similarly. The log-likelihood ratio (LLR) for the power-law distribution and the exponential distribution was defined as

LLR=logLα(α^∣x)−logLλ(λ^∣x)

where α^ and λ^ are maximum likelihood estimates of the distribution parameters. The KS statistic for the powerlaw distribution is defined against the empirical cumulative distribution Cemp(s) as

KSstatpower(x∣α)=maxs|Cemp(s)−Cα(s)|

where Cα(s) is the cumulative distribution of s that obeys the power-law distribution. In practice, empirically observed distributions commonly deviate from the power-law distribution at small values of s (Clauset et al., 2009). Thus, the KS statistic excluding size 1, which is defined as

KSstatpower(x∣α)=maxs≥2|Cemp(s)−Cα(s)|

was used to represent the goodness-of-fit of the empirical distribution to the power-law distribution. The goodness-of-fit to the exponential distribution was evaluated by the KS statistic, defined as

KSstatexponential(x∣λ)=maxs|Cemp(s)−Cλ(s)|,

where Cλ(s) is the cumulative distribution of s that obeys the exponential distribution.

In the distribution of avalanche sizes, a gap sometimes existed between small-scale avalanches and the other larger-scale avalanches. The largest gap in avalanche sizes was defined as G. A large G value corresponded to the emergence of large-scale avalanches with a singular spatiotemporal activity pattern deviating from both the exponential distribution and the power-law distribution. The large-scale avalanches led to a bimodal distribution, where the characteristic large-scale avalanches form a distinct peak and so-called tonic spikes not involved in the large-scale avalanches form another peak.

Avalanche size distributions were classified according to the features defined above. If a value of G was larger than a threshold defined as the third quartile of G values from all data, the distribution was classified as a bimodal distribution. Otherwise, the avalanche size distributions were analyzed for their fit to power-law distributions or exponential distributions. If the LLR was positive and KSstatpower was significantly small (<0.05), the distribution was classified as a power-law distribution, and if the LLR was negative and KSstatexponential was significantly small (<0.05), the distribution was classified as an exponential distribution.

The avalanche size distributions were also characterized with features obtained by linear regression. The coefficient of determination for the regression line, which hypothesizes a linear relationship in log–log scale between avalanche size and the probability of its occurrence, was defined as powerR 2. Additionally, a coefficient of determination for the regression line that hypothesized a linear relationship between avalanche size and log probability was defined as expR2. The regression line was calculated using a least-squares fitted model. If there is a gap in the avalanche size distribution, the regression line was fitted to the observed sizes that are smaller than the gap. A large value for powerR 2 or expR 2 indicated that the avalanche distribution was well characterized by either the power-law distribution or exponential distribution, respectively.

Pharmacology

To demonstrate that cell cultures fire independently during the early developmental stages, avalanches in juvenile cultures were recorded and compared with those in mature cultures supplied with synaptic blockers. Three mature cultures (at 44, 54 and 69 DIV) were treated with DL-2-amino-5-phosphonovaleric acid (AP5; Sigma–Aldrich), 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; Sigma–Aldrich), and bicuculline (Sigma– Aldrich). Half the media was replaced with blocker-supplemented cell culture media so that after the replacement, the media contained 30 μM AP5, 10 μM CNQX, and 30 μM bicuculline (Jiang and North, 1991).

Fano factor

The Fano factor was calculated to evaluate whether array-wide spike trains in the earliest developmental periods obeyed the Poisson process. Array-wide spikes of cultures were binned with mISI. The Fano factor was defined as

F=σ2μ

where μ was the mean array-wide spikes per mISI and σ2 was the variance of array-wide spikes per mISI. If the number of array-wide spikes per mISI obeyed the Poisson process, F = 1.

Spatiotemporal pattern analysis

The spatiotemporal patterns of neuronal avalanches were analyzed to investigate the relationship between avalanche distribution and spatiotemporal activity. In this analysis, we focused on synchronized bursts in a neuronal culture, which are likely to have a stable repertoire of spatiotemporal patterns (Segev et al., 2004; Yada et al., 2016). The synchronized burst was defined here as an avalanche that contained more than 252 (twice of the number of recording channels) spikes. To visualize the structure of these patterns, synchronized bursts were sorted by a hierarchical clustering algorithm according to the pairwise spatiotemporal activity correlation (Beggs and Plenz, 2004; Madhavan et al., 2007) with slight modifications. Spikes belonging to each synchronized burst were binned with a three-time mISI sliding time bin with a time step equivalent to the mISI at all recording electrodes. Next, the spatiotemporal pattern of each synchronized burst was represented by a matrix. To calculate correlations between different-sized synchronized bursts, a correlation was defined as the maximum peak in a cross correlation function of a matrix pair.

Results

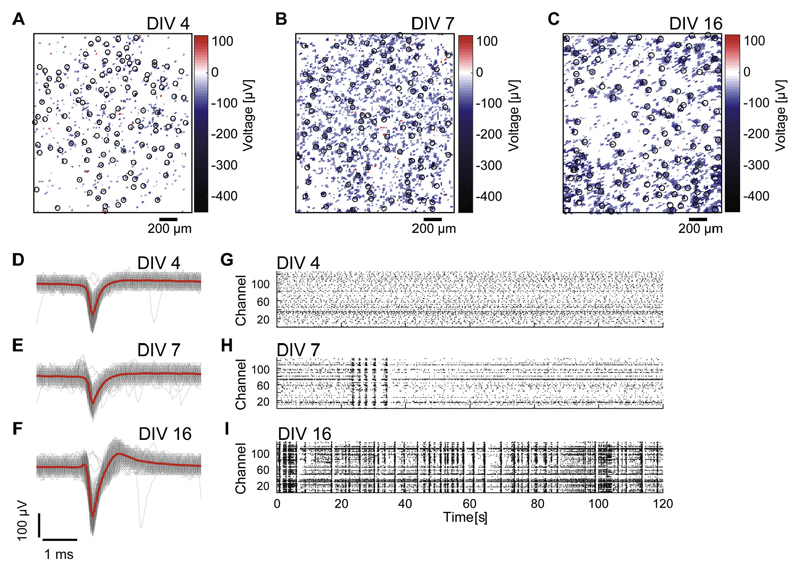
The spontaneous activities of 77 trials from 9 dissociated cortical cultures [mean ± standard deviation (SD): 8.6 ± 3.0 trials for each culture] were monitored beginning in early-stage development, and overall from 4 to 30 DIV. Spontaneous activity was recorded for 30 min in every session. Fig. 2(A–C) shows spatial maps of the action potential amplitudes recorded throughout a CMOS MEA, and Fig. 2(D–F) shows examples of mean spike waveforms. Despite the sparse activity at this very early period of development, the CMOS MEA was able to capture action potentials due to its high spatiotemporal resolution. Fig. 2(G–I) present 120-s examples of spontaneous activities from a 30-min recording in a representative culture at 4, 7, and 16 DIV, respectively. Cultures demonstrated seemingly random firing activity in the earliest stages of development, followed by synchronized bursting activity, and finally complex synchronized firing patterns (Kamioka et al., 1996).

Fig. 2. Spontaneous activity of dissociated cortical cultures at different developmental stages.

Fig. 2

Open in a new tab

(A–C) show spatial maps of action potential amplitude obtained using high-density complementary metal-oxide semiconductor microelectrode arrays (CMOS MEAs). CMOS MEAs from the same culture at 4 days in vitro (DIV) (A), 7 DIV (B), and 16 DIV (C). Black (and green) circles indicate designated recording sites. (D–F) show examples of mean spike waveforms (red lines) detected at the green circles in (A–C), respectively. The gray lines depict all traces of spike waveforms. Raster plots of 120 s of spontaneous spiking activity out of 30 min of recorded data are shown in G–I. Activities were recorded from the same dissociated cortical culture shown in (A–C) at 4 DIV (G), 7 DIV (H), and 16 DIV (I). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

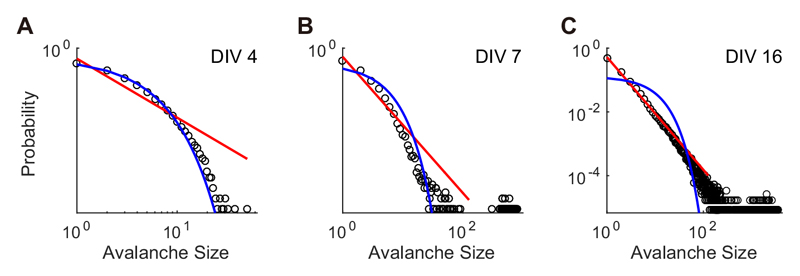
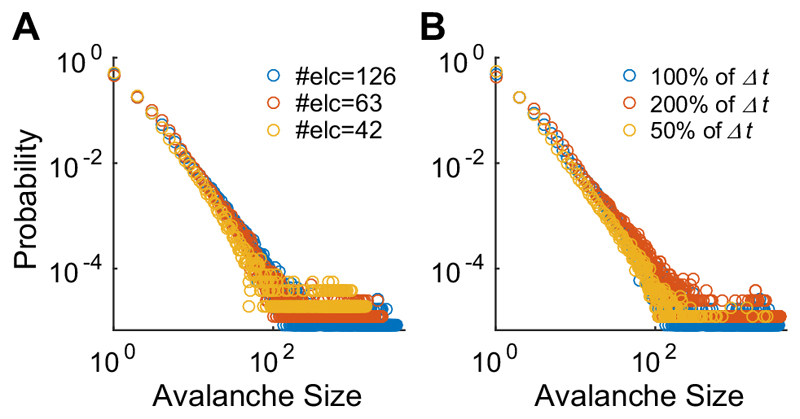
Neuronal avalanches were identified from array-wide spikes recorded during spontaneous activity. Fig. 3(A– C) displays the distribution of the avalanche size at a log–log scale from the same culture using the DIVs shown in Fig. 2 (4, 7, and 16 DIV). The lines are hypothesized distributions fitted to the empirical data using maximum likelihood estimation (red, power-law;blue, exponential). In the earliest developmental period (4 DIV), neuronal avalanches demonstrated an exponential distribution (KSstatexponential = 0.024 < 0.05: significance level, Fig. 3A). At 7 DIV, the culture exhibited a bimodal distribution characterized by a gap and large G value (0.53, Fig. 3B), which was then replaced by a powerlaw distribution at 16 DIV (KSstatpower*=0.021 <0.05: significance level, Fig. 3C). To verify the temporal and spatial scale-free features of the power-law distribution, avalanche size was computed with different parameters. Fig. 4 shows the avalanche size distribution of the same culture at the same DIV (i.e., 16 DIV) shown in Fig. 3C but including different numbers of electrodes (Fig. 4A) and the different time-bins (Fig. 4B). For the different electrode configurations described in Fig. 4A, one half (63) or one third (42) of the total electrodes that recorded the most negative mean spike amplitudes were selected. Fig. 4 (A, B) illustrates that the avalanche size distribution follows the power-law distribution regardless of the number of electrodes or the size of the time bins, as reported in previous studies (Beggs and Plenz, 2003; Petermann et al., 2009; Tetzlaff et al., 2010).

Fig. 3. Avalanche size distributions obtained from the culture shown in Fig. 2.

Fig. 3

Open in a new tab

This figure shows data from 4 DIV (A), 7 DIV (B), and 16 DIV (C), respectively. The red lines represent power-law distribution fitted to the empirical distributions, where the parameters were estimated by maximum likelihood estimation (MLE). The blue lines are fitted exponential distribution estimated by MLE (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.).

Fig. 4. Avalanche size distributions in different configurations.

Fig. 4

Open in a new tab

(A) shows avalanche size distributions from the same culture at the same DIV (i.e., 16 DIV) shown in Fig. 3C for different number of electrodes and (B) shows the avalanche size distributions for different sizes of the time bin.

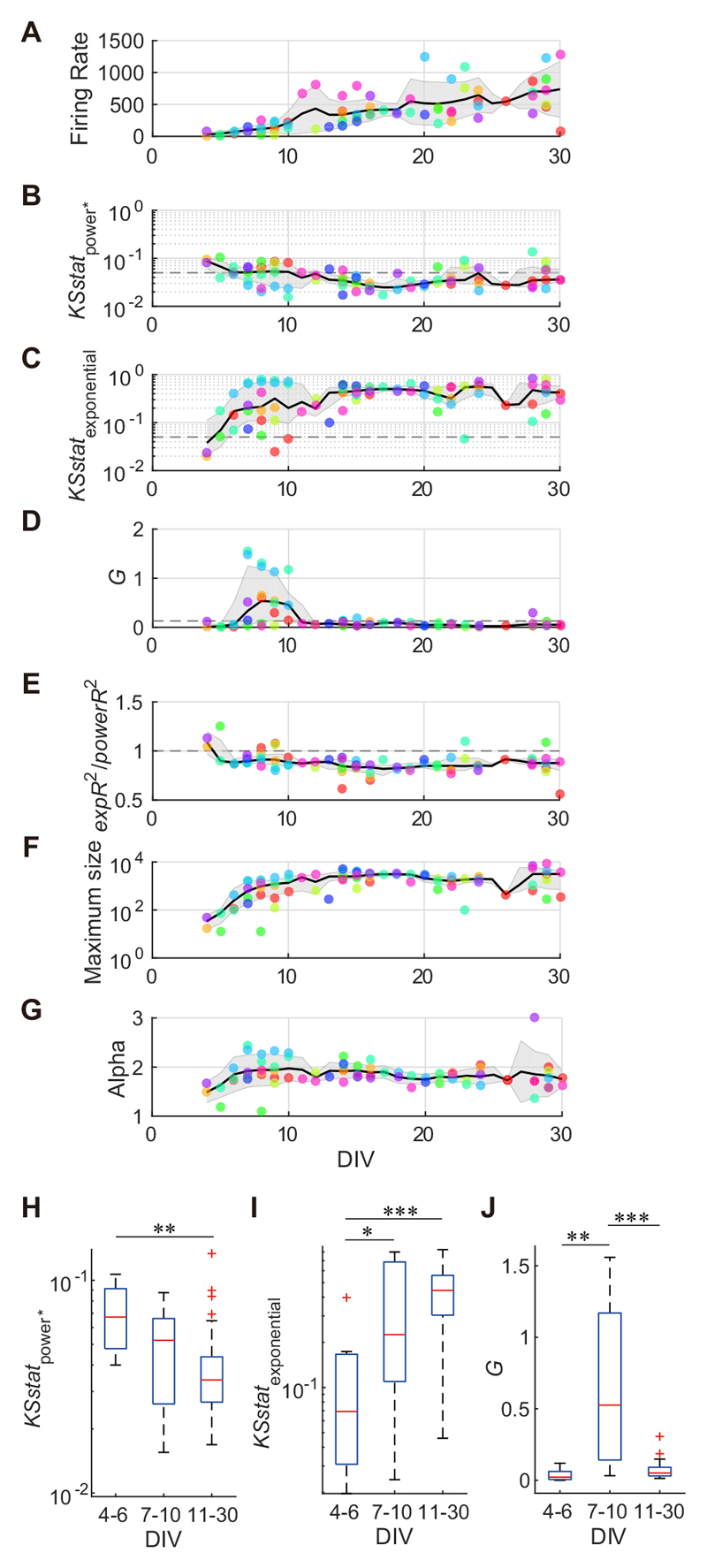
Fig. 5 illustrates the developmental variations among population activity for each of the nine cultures. Fig. 5 (A–G) displays developmental variation among arraywide firing rates, size-1-excluding KS statistics for the power-law distribution, KS statistics for the exponential distribution, G values, the ratio of expR2 to powerR2, the maximum avalanche sizes, and the exponent of powerlaw distribution (alpha), respectively. The array-wide firing rate, which was defined as the mean number of array-wide spikes occurring each second, increased gradually during development, though diversified further after 20 DIV (Fig. 5A). KSstatpower was relatively high during 4–6 DIV, and then typically decreased to below 0.05 after 11 DIV (Fig. 5B and H, Kruskal–Wallis test, p = 0.0057 < 0.01 ; followed by Mann–Whitney U-tests, 4–6 DIV vs. 11–30 DIV, p = 0.0016 < 0.01). KSstatexponential at 4–6 DIV was significantly lower than that at 7–10 DIV and 11–30 DIV, and then gradually increased (Fig. 5C and I, Kruskal–Wallis test, p = 0.0037 < 0.01 ; followed by Mann–Whitney U-tests, 4–6 DIV vs. 7–10 DIV, p = 0.028 < 0.05; 4–6 DIV vs. 11–30 DIV, p = 4.5 x 10 4 < 0.001). This suggests that avalanche sizes in the early developmental period follow an exponential distribution, and then after maturation follow a power-law distribution. In addition, the ratio of expR 2 to powerR 2, which was computed by the leastsquare linear regression analysis, supported this view. A relatively high expR 2/ powerR 2 ratio was detected for five cultures (>1) at 4–10 DIV, which then decreased to below 1 (Fig. 5E). The cultures on the first recording day (<10 DIV, mean ± SD: 6.0 ± 1.7) exhibited a significantly larger expR 2/powerR 2 ratio as compared to the expR2/powerR2 ratio of cultures at 11 or more DIVs (median: 0.92 vs. 0.86; p = 0.0043, Mann–Whitney U test). In addition, seven cultures demonstrated a larger G value (median: 0.53) than the threshold (i.e., 0.13) at 7–10 DIV (Fig. 5D). Generally, cultures at this time point exhibited a significantly larger G value compared to those of cultures at 4–6 DIV and 11 or more DIVs (Fig. 5J, Kruskal–Wallis test, p = 3.2 x 10-6<0.001; followed by Mann–Whitney U-tests, 7–10 DIV vs. 4–6 DIV, p = 0.0012<0.01; 7–10 DIV vs. 11–30 DIV, p = 3.6 x 10 -6<0.001), indicating a bimodal avalanche size distribution. The time course of the maximum avalanche size in the log scale increased until 10 DIV and stabilized at approximately 2.5 x 103 (±1.6 x 103 SD;>10 DIV) (Fig. 5F). This time period (10 DIV) coincides with a reduction in G value (>0.13). In cultures that obeyed a power-law distribution after 28 DIV, the exponent of the power-law distribution (alpha) was –1.83 ± 0.45 (mean ± SD) (Fig. 5G), which was slightly higher than the alpha in a previous study of neuronal avalanches (i.e., -1.5) (Beggs and Plenz, 2003).

Fig. 5. The developmental variation of avalanche distribution features over time.

Fig. 5

Open in a new tab

A–G illustrate the developmental variation of arraywide firing rates (A), the Kolmogorov–Smirnov (KS) statistic for power-law distribution where size 1 avalanches were excluded (B), the KS statistic for exponential distribution (C), G values (D), the ratio of expR2 to powerR2 (E), the maximum avalanche sizes (F), and the alpha exponent (G), respectively. Plotted points of the same color indicate features from the same culture on a different DIV. Black lines indicate a moving average (A, G: mean; B, C, D, E, F: median) and gray shades indicate errors (A, G: SD; B, C, D, E, F: first and third quartiles) for each feature, including the day before and after. H–J show comparison of avalanche distribution features (for B–D, respectively) between developmental periods (4–6 DIV, 7–10 DIV and 11–30 DIV). *p < 0.05, **p < 0.01, ***p < 0.001; Mann–Whitney U-test.

In the present experiments, each recording was performed with a different configuration of electrodes that determined the spatial resolution of recording (see Experimental Procedures). The configuration might be biased depending on developmental period, and thereby affect the results. We thus examined the average distance between selected recording electrodes at each session, and found no significant difference among 4–6 DIV, 7–10 DIV, and 11–30 DIV (Kruskal–Wallis test, p = 0.38 > 0.05). Therefore, the spatial resolutions of recording were comparable among recording sessions at different DIVs.

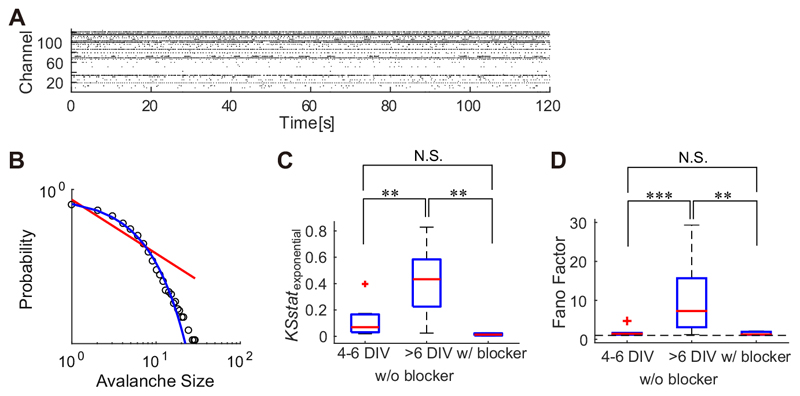
To determine whether the exponential-like avalanche distribution that has been observed between 4 and 6 DIV was produced by the independent activity of neurons during an immature stage of development, the activity of the cultures at 4–6 DIV was compared to that of mature cultures (43–69 DIV) supplemented with synaptic blockers CNQX, AP5, and bicuculline. Fig. 6A displays the spontaneous activity of a representative blocker-supplemented culture. The avalanche size distributions of the blocker-supplemented cultures showed an exponential-like distribution (Fig. 6B) similar to that of immature cultures (4–6 DIV). KSstatexponential in blocker-supplemented cultures is statistically not different from KSstatexponential in cultures at 4–6 DIV (p = 0.067 > 0.05, Mann–Whitney U- test). Cultures at > 6 DIV had significantly larger KSstatexponential compared to both blocker- supplemented cultures (p = 0.0040 < 0.01, Mann–Whitney U-test) and younger cultures (4–6 DIV; p = 0.0010 < 0.01, Mann– Whitney U-test) (Fig. 6C). To evaluate whether the spiking activities of the cultures could be modeled with the Poisson processes, which implies uncorrelated firing of neurons, the Fano factor was calculated (Fig. 6D). Cultures at 4–6 DIV and those supplemented with synaptic blockers exhibited relatively small Fano factor values (≃ 1), which indicates that spikes are generated with a Poisson-like process. Fano factors for the spontaneous activity of cultures at 4–6 DIV did not differ from those of synaptic-blocker supplemented cultures (p = 0.83 > 0.05, Mann–Whitney U-test). As compared to these cultures, cultures aged >6 DIV exhibited significantly larger Fano factors (Mann–Whitney U-test: >6 DIV vs. 4–6 DIV, p = 2.7 x 10–4 < 0.001; >6 DIV vs. w/ blocker, p = 7.3 x 10–3 < 0.01).

Fig. 6. Poisson-like spiking activity in cortical cultures with synaptic blockers.

Fig. 6

Open in a new tab

(A) illustrates a raster plot of spontaneous activity in a culture supplemented with CNQX/AP5 and bicuculline. (B) shows the avalanche size distribution of a culture supplemented with synaptic blockers. (C and D) illustrate the KS statistics for exponential distribution (C) and Fano factors (D) from cultures at 4–6 DIV, cultures older than 6 DIV, and from cultures supplemented with synaptic blockers. The horizontal dashed line in D indicates a point where the Fano factor equals one. **p < 0.01, ***p < 0.001; Mann–Whitney U-test.

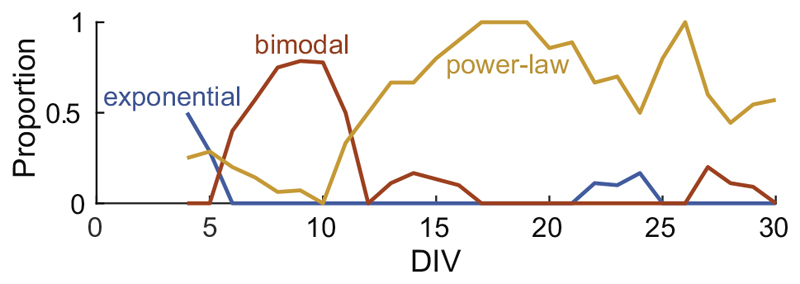
According to the classification rule as described in Experimental Procedures, Fig. 7 illustrates the proportion of a particular type of an avalanche distribution on each DIV. For smoothing the data, the proportion of each day was calculated including the day before and after. Dissociated cortical neurons sequentially exhibited an exponential distribution (≈4 DIV), bimodal distribution (≈7–10 DIV), and power-law distribution (>10 DIV).

Fig. 7.

Fig. 7

Open in a new tab

The changing proportion of avalanche distribution over time. This figure displays the proportion of each avalanche distribution type occurring at a specific time point. The details for distribution type classification are described in the Experimental Procedures. The proportions of each day include the day before and after.

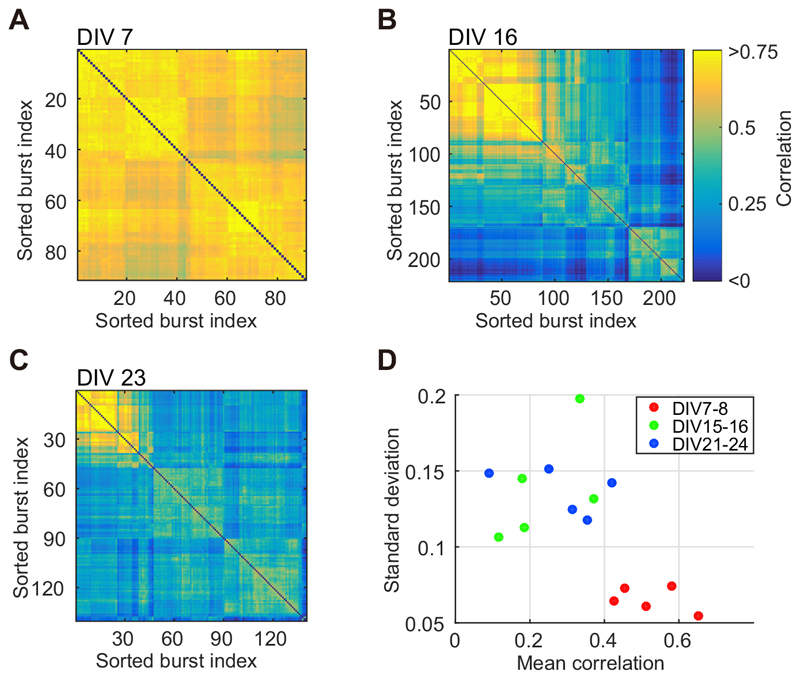
Developmental variation in the avalanche size distribution was associated with a broader variety of spatiotemporal patterns in the present study. Fig. 8A–C provides a representation of spatiotemporal patterns during early development and beyond. Synchronized bursts were the focus of this analysis, wherein only avalanches larger than 252 spikes were used. Spatiotemporal patterns of synchronized bursts were sorted to gather similar bursts using a hierarchical clustering algorithm (Beggs and Plenz, 2004). Fig. 8A illustrates a correlation matrix of spatiotemporal patterns obtained from a culture at 7 DIV, during which the culture featured a high G value (i.e., 1.55). The synchronized bursts in the correlation matrix are shown in order (sorted burst index). The majority of the matrix elements were highly correlated, wherein the minimum pair-wise correlation was 0.464. However, at 16 DIV (Fig. 8B) and 23 DIV (Fig. 8C), correlation matrices were inhomogeneous for the same culture (minimum pair correlation: 16 DIV, -0.053; 23 DIV, 0.010), indicating the emergence of multiple spatiotemporal patterns in synchronized bursts. To assess the variety of spatiotemporal patterns, the large avalanches in cultures were characterized according to the mean value and SD of their pair correlation. Fig. 8D illustrates the mean values and SDs calculated from five cultures that exhibited high G(> 0.39 = 0.13 x 3) values during 7–8 DIV. The spatiotemporal patterns of synchronized bursts at 7–8 DIV demonstrated a relatively high mean correlation and smaller SD, while those at 15–16 DIV and 21–24 DIV featured a low mean correlation and larger SD. Such findings suggest that cultures at 7–8 DIV featured large-scale avalanches displaying similar spatiotemporal patterns, while more mature cultures (>14 DIV) featured avalanches characterized by a power-law distribution and accompanied by diverse, middle-size spatiotemporal patterns.

Fig. 8. Developmental variations in spatiotemporal patterns.

Fig. 8

Open in a new tab

(A–C) displays the correlation matrices for spatiotemporal patterns in large avalanches, i.e., synchronized bursts. Each matrix was obtained from a culture at 7 DIV (A), 16 DIV (B), and 23 DIV (C), respectively. (D) illustrates the mean correlation and standard deviation of spatiotemporal pattern correlations calculated from five cultures that exhibited high G value (G > 0.39 = 0.13 x 3) during 7–8 DIV.

Discussion

The aim of present study was to investigate the early developmental process of neuronal activity as it relates to the emergence of SoC, the state at which neuronal avalanches obey a power-law distribution. The high-density CMOS MEAs measured spontaneous activities in dissociated cortical cultures from 4 to 30 DIV, the period during which SoC was established. We found that, during the early development, the avalanche size distribution was characterized initially by an exponential distribution (4–6 DIV), then a bimodal distribution (7–10 DIV), and finally a power-law distribution (>10 DIV). The large-scale avalanches with monotonic spatiotemporal activity were observed in the period of bimodal avalanche size distribution, while diverse patterns of spatiotemporal activity emerged in the period of power-law distribution.

To the best of our knowledge, this is the first report that captures developmental variations in avalanche distribution during early stage development; this new capability was made possible in part by the availability of high-density CMOS MEA technology (Frey et al., 2010). The CMOS MEA used in the present study featured a center-to-center electrode pitch of 18.0 μm, which was able to capture neural signals of interest from distributed neurons in culture at subcellular resolution (Bakkum et al., 2013). This high-resolution recording confers a great advantage over conventional MEAs, which have a typical inter-electrode spacing of a few 100 μm.

This relatively broad spacing can miss a significant number of neuronal activities – those which are distant from the recording sites (Tetzlaff et al., 2010). Particularly during early stage development, when action potential signals are small and neural processes are still immature, conventional MEAs may fail to characterize their activities properly (Tetzlaff et al., 2010). Furthermore, neuronal networks continuously modify their structure and organization through neuronal migration (Segev et al., 2003; Lledo et al., 2006), axonal elongation, and the relocation of axonal initial segments (Grubb and Burrone, 2010; Grubb et al., 2011). These structural alterations during development may also have a critical impact on neural measurement when studied with the coarse grid of a conventional MEA. Thus, high-resolution recording is a prerequisite of a stable sampling of neuronal network activity throughout development.

In our analysis, the slope of the power-law-like avalanche distribution, alpha, was –1.83 ± 0.45 (mean ± SD; ≥28 DIV). In the original report by Beggs and Plenz (2003), alpha was –1.5 in corticalslices, which successfully accounts for the theoretical branching process model. This value was validated by several additional reports (Mazzoni et al., 2007; Gireesh and Plenz, 2008; Pasquale et al., 2008). Nevertheless, alpha in dissociated neurons may not always match the typical value of –1.5 (Tetzlaff et al., 2010; Pu et al., 2013; Massobrio et al., 2015). In addition, the timescale of the temporal binning, (i.e., △t), often affects the value of exponents (Beggs and Plenz, 2003). The present study used an adaptive timescale as previously reported (Tetzlaff et al., 2010), which may explain the slightly large absolute exponent value. As shown in Fig. 4 and demonstrated in previous studies, a longer timescale produces a shallower slope for the distribution. In addition, if the maximum avalanche size does not significantly differ during maturation and development, an increase in the frequency of medium-size avalanches, along with a corresponding decrease in smaller-sized avalanches, may produce a shallower slope in the power-law distribution.

Prior to 7 DIV, the Fano factor of neural activity was approximately 1, which is a sign of random-like spiking activity (Fig. 6D). Similar random-like activity was observed in mature cultures with synaptic blockers. Previously, in dissociated cortical cultures, no evidence of synaptic connections was detected at 3 DIV, while synapse formation was confirmed at 7 DIV (Ichikawa etal., 1993; Muramoto etal., 1993). Accordingly, synapto- genesis in dissociated cortical cultures may occur between 4 and 6 DIV, which is consistent with the findings of the present study. Axonal elongation and synaptogen- esis trigger the initiation of synchronized activity and an increase in maximum avalanche size. Such activity indicates the integration of dissociated neurons into a united network.

In cultures at 7–10 DIV, stereotypically large avalanches were detected, resulting in the emergence of a bimodal avalanche size distribution during this period. Bimodal avalanche size distributions have been previously observed in dissociated cultures dosed with GABAergic antagonists (Mazzoni et al., 2007; Pasquale et al., 2008). These results indicate that a bimodal distribution may be triggered by excitatory network activity, possibly due to a disinhibitory effect mediated by changes in GABAergic inhibition. Supporting this theory, the reversal potential for chloride ions is relatively high, and GABA-mediated inputs typically induce depolarization in immature neurons (Bourgeois and Rakic, 1993; Chechik et al., 1998; Ben-Ari, 2001, 2002; Wu et al., 2012; Le Magueresse and Monyer, 2013). In rat hippocampal dissociated cultures, GABA-mediated depolarization was observed in all neurons at 4 to 6 DIV, but was, in most cases, no longer detectable after 13 DIV (Ganguly et al., 2001). This pattern of GABAergic activity is consistent with the transition from an exponential distribution to a bimodal distribution, and finally to a power-law distribution, as observed here.

Thus, the present study provides support for the influence of GABAergic activity on the maximum avalanche size. The maximum avalanche size stabilized from ≈10 DIV after the period characterized by the bimodal distribution (7–8 DIV). During early development, GABA-mediated giant depolarizing potentials occur that facilitate the wiring of immature neurons (Sipila, 2005; Le Magueresse and Monyer, 2013). Furthermore, the saturation toward a maximum avalanche size observed at ≈10 DIV suggests that a sufficient number of neurons had been incorporated into the network to trigger a developmental phase transition from network formation to synaptic elimination, in which GABA also plays an important role (Baho and Di Cristo, 2012; Le Magueresse and Monyer, 2013).

The diversification of spatiotemporal patterns may also support a role for GABA-driven network alterations. Large avalanches having a characteristic spatiotemporal pattern can be detected at 7–8 DIV if the neurons are homogeneously coupled and if synaptic transmission predominantly produces an excitatory effect. Therefore, the shift in excitatory to inhibitory GABAergic transmission following 7–8 DIV may induce spatiotemporal pattern variations through one of two possible mechanisms: (i) inhibitory transmission aborts excitatory transmission patterns, altering spatiotemporal activity, or (ii) synaptic elimination caused by GABA- mediated inhibition, which produces a network with a complex inhomogeneous structure that subsequently generates diverse spatiotemporal patterns. The bimodal avalanche distribution caused by the blockade of GABA receptors apparently supports the former; however, the interaction of neurochemical and structural methods of network fragmentation may enable neuronal networks to achieve the SoC.

In summary, in the present study, the developmental variation of neuronal avalanches was investigated in dissociated cortical neurons using high-density CMOS MEAs. The findings demonstrated that neuronal activity could be identified at 4 DIV. In addition, during the initial stages, we observed an exponential avalanche size distribution, suggesting that activity was randomly generated. Avalanche size then transitioned from an exponential distribution to a bimodal distribution in subsequent periods (≈7–10 DIV), and finally to a powerlaw distribution. In addition to variations in avalanche size distribution, the diversity of the spatiotemporal patterns was altered. Cultures that featured an obvious bimodal distribution exhibited a characteristic repeating spatiotemporal pattern, while cultures at 2–3 weeks in vitro featured a variety of patterns. These results suggest that the SoC emerges through a two-step process; the integration process accompanying the characteristic large avalanche, and the fragmentation process associated with diverse middle-size avalanches.

Acknowledgments

This work was partially supported by the Japan Society for the Promotion of Science (JSPS) through a Grant-in-Aid for Scientific Research [grant number: 26630089, 16K14191]; Grant-in-Aid for JSPS Fellows [grant number: 26-10399]; the Asahi Glass Foundation, Tokyo; and Kayamori Foundation of Informational Science Advancement, Nagoya. Financial support through the European Union, ERC Advanced Grants [grant number: 267351 “NeuroCMOS”] is also acknowledged.

YY, RK and HT designed the research. YY, TM, AS and RY performed the experiments. YY and AS analyzed the data. TM, DJB

Abbreviations

CMOS

complementary metal-oxide semiconductor

DIV

days in vitro

KS

Kolmogorov–Smirnov

LLR

log-likelihood ratio

MEA

microelectrode array

mISI

mean inter-spike interval

SoC

self-organized criticality

References

  1. Baho E, Di Cristo G. Neural activity and neurotransmission regulate the maturation of the innervation field of cortical GABAergic interneurons in an age-dependent manner. J Neurosci. 2012;32:911–918. doi: 10.1523/JNEUROSCI.4352-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bakkum DJ, Frey U, Radivojevic M, Russell TL, Müller J, Fiscella M, Takahashi H, Hierlemann A. Tracking axonal action potential propagation on a high-density microelectrode array across hundreds of sites. Nat Commun. 2013;4:2181. doi: 10.1038/ncomms3181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Beggs JM, Plenz D. Neuronal avalanches in neocortical circuits. J Neurosci. 2003;23:11167–11177. doi: 10.1523/JNEUROSCI.23-35-11167.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beggs JM, Plenz D. Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J Neurosci. 2004;24:5216–5229. doi: 10.1523/JNEUROSCI.0540-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ben-Ari Y. Developing networks play a similar melody. Trends Neurosci. 2001;24:353–360. doi: 10.1016/s0166-2236(00)01813-0. [DOI] [PubMed] [Google Scholar]
  6. Ben-Ari Y. Excitatory actions of gaba during development: the nature of the nurture. Nat Rev Neurosci. 2002;3:728–739. doi: 10.1038/nrn920. [DOI] [PubMed] [Google Scholar]
  7. Berdondini L, Imfeld K, Maccione A, Tedesco M, Neukom S, Koudelka-Hep M, Martinoia S. Active pixel sensor array for high spatio-temporal resolution electrophysiological recordings from single cell to large scale neuronal networks. Lab Chip. 2009;9:2644–2651. doi: 10.1039/b907394a. [DOI] [PubMed] [Google Scholar]
  8. Bourgeois JP, Rakic P. Changes of synaptic density in the primary visual cortex of the macaque monkey from fetal to adult stage. J Neurosci. 1993;13:2801–2820. doi: 10.1523/JNEUROSCI.13-07-02801.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chechik G, Meilijson I, Ruppin E. Synaptic pruning in development: a computational account. Neural Comput. 1998;10:1759–1777. doi: 10.1162/089976698300017124. [DOI] [PubMed] [Google Scholar]
  10. Chen W, Hobbs JP, Tang A, Beggs JM. A few strong connections: optimizing information retention in neuronal avalanches. BMC Neurosci. 2010;11:3. doi: 10.1186/1471-2202-11-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Clauset A, Shalizi CR, Newman MEJ. Power-law distributions in empirical data. SIAM Rev. 2009;51:661–703. [Google Scholar]
  12. Frey U, Sedivy J, Heer F, Pedron R, Ballini M, Mueller J, Bakkum D, Hafizovic S, Faraci FD, Greve F, Kirstein K-U, Hierlemann A. Switch-matrix-based high-density microelectrode array in CMOS technology. IEEE J Solid State Circuits. 2010;45:467–482. [Google Scholar]
  13. Friedman N, Ito S, Brinkman BAW, Shimono M, DeVille REL, Dahmen KA, Beggs JM, Butler TC. Universal critical dynamics in high resolution neuronal avalanche data. Phys Rev Lett. 2012;108:208102. doi: 10.1103/PhysRevLett.108.208102. [DOI] [PubMed] [Google Scholar]
  14. Ganguly K, Schinder AF, Wong ST, Poo M. GABA itself promotes the developmental switch of neuronal GABAergic responses from excitation to inhibition. Cell. 2001;105:521–532. doi: 10.1016/s0092-8674(01)00341-5. [DOI] [PubMed] [Google Scholar]
  15. Gireesh, Plenz D. Neuronal avalanches organize as nested theta-and beta/gamma-oscillations during development of cortical layer 2/3. Proc Natl Acad Sci U S A. 2008;105:7576–7581. doi: 10.1073/pnas.0800537105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Grubb MS, Burrone J. Activity-dependent relocation of the axon initial segment fine-tunes neuronal excitability. Nature. 2010;465:1070–1074. doi: 10.1038/nature09160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Grubb MS, Shu Y, Kuba H, Rasband MN, Wimmer VC, Bender KJ. Short-and long-term plasticity at the axon initial segment. J Neurosci. 2011;31:16049–16055. doi: 10.1523/JNEUROSCI.4064-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Haldeman C, Beggs JM. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett. 2005;94:058101. doi: 10.1103/PhysRevLett.94.058101. [DOI] [PubMed] [Google Scholar]
  19. Ichikawa M, Muramoto K, Kobayashi K, Kawahara M, Kuroda Y. Formation and maturation of synapses in primary cultures of rat cerebral cortical cells: an electron microscopic study. Neurosci Res. 1993;16:95–103. doi: 10.1016/0168-0102(93)90076-3. [DOI] [PubMed] [Google Scholar]
  20. Jiang ZG, North RA. Membrane properties and synaptic responses of rat striatal neurones in vitro. J Physiol. 1991;443:533–553. doi: 10.1113/jphysiol.1991.sp018850. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kamioka H, Maeda E, Jimbo Y, Robinson HPC, Kawana A. Spontaneous periodic synchronized bursting during formation of mature patterns of connections in cortical cultures. Neurosci Lett. 1996;206:109–112. doi: 10.1016/s0304-3940(96)12448-4. [DOI] [PubMed] [Google Scholar]
  22. Klaus A, Yu S, Plenz D. Statistical analyses support power law distributions found in neuronal avalanches. PLoS One. 2011;6:e19779. doi: 10.1371/journal.pone.0019779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Le Magueresse C, Monyer H. GABAergic interneurons shape the functional maturation of the cortex. Neuron. 2013;77:388–405. doi: 10.1016/j.neuron.2013.01.011. [DOI] [PubMed] [Google Scholar]
  24. Levina A, Herrmann JM, Geisel T. Dynamical synapses causing self-organized criticality in neural networks. Nat Phys. 2007;3:857–860. [Google Scholar]
  25. Lledo P-M, Alonso M, Grubb MS. Adult neurogenesis and functional plasticity in neuronal circuits. Nat Rev Neurosci. 2006;7:179–193. doi: 10.1038/nrn1867. [DOI] [PubMed] [Google Scholar]
  26. Madhavan R, Chao ZC, Potter SM. Plasticity of recurring spatiotemporal activity patterns in cortical networks. Phys Biol. 2007;4:181–193. doi: 10.1088/1478-3975/4/3/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Massobrio P, Pasquale V, Martinoia S. Self-organized criticality in cortical assemblies occurs in concurrent scale-free and small-world networks. Sci Rep. 2015;5:10578. doi: 10.1038/srep10578. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mazzoni A, Broccard FD, Garcia-Perez E, Bonifazi P, Ruaro ME, Torre V. On the dynamics of the spontaneous activity in neuronal networks. PLoS One. 2007;2:e439. doi: 10.1371/journal.pone.0000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Millman D, Mihalas S, Kirkwood A, Niebur E. Self-organized criticality occurs in non-conservative neuronal networks during / ‘up/’ states. Nat Phys. 2010;6:801–805. doi: 10.1038/nphys1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Muramoto K, Ichikawa M, Kawahara M, Kobayashi K, Kuroda Y. Frequency of synchronous oscillations of neuronal activity increases during development and is correlated to the number of synapses in cultured cortical neuron networks. Neurosci Lett. 1993;163:163–165. doi: 10.1016/0304-3940(93)90372-r. [DOI] [PubMed] [Google Scholar]
  31. Muüller J, Bakkum DJ, Hierlemann A. Sub-millisecond closed-loop feedback stimulation between arbitrary sets of individual neurons. Front Neural Circuits. 2012;6:121. doi: 10.3389/fncir.2012.00121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Muüller J, Ballini M, Livi P, Chen Y, Radivojevic M, Shadmani A, Viswam V, Jones IL, Fiscella M, Diggelmann R, Stettler A. High-resolution CMOS MEA platform to study neurons at subcellular, cellular, and network levels. Lab Chip. 2015;15:2767–2780. doi: 10.1039/c5lc00133a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pasquale V, Massobrio P, Bologna LL, Chiappalone M, Martinoia S. Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience. 2008;153:1354–1369. doi: 10.1016/j.neuroscience.2008.03.050. [DOI] [PubMed] [Google Scholar]
  34. Petermann T, Thiagarajan TC, Lebedev MA, Nicolelis MAL, Chialvo DR, Plenz D. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc Natl Acad Sci USA. 2009;106:15921–15926. doi: 10.1073/pnas.0904089106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pu J, Gong H, Li X, Luo Q. Developing neuronal networks: selforganized criticality predicts the future. Sci Rep. 2013;3:1081. doi: 10.1038/srep01081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Segev R, Baruchi I, Hulata E, Ben-Jacob E. Hidden neuronal correlations in cultured networks. Phys Rev Lett. 2004;92:118102. doi: 10.1103/PhysRevLett.92.118102. [DOI] [PubMed] [Google Scholar]
  37. Segev R, Benveniste M, Shapira Y, Ben-Jacob E. Formation of electrically active clusterized neural networks. Phys Rev Lett. 2003;90:168101. doi: 10.1103/PhysRevLett.90.168101. [DOI] [PubMed] [Google Scholar]
  38. Shew WL, Clawson WP, Pobst J, Karimipanah Y, Wright NC, Wessel R. Adaptation to sensory input tunes visual cortex to criticality. Nat Phys. 2015;11:659–663. [Google Scholar]
  39. Shew WL, Yang H, Petermann T, Roy R, Plenz D. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J Neurosci. 2009;29:15595–15600. doi: 10.1523/JNEUROSCI.3864-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Shew WL, Yang H, Yu S, Roy R, Plenz D. Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J Neurosci. 2011;31:55–63. doi: 10.1523/JNEUROSCI.4637-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sipila ST. Depolarizing GABA acts on intrinsically bursting pyramidal neurons to drive giant depolarizing potentials in the immature hippocampus. J Neurosci. 2005;25:5280–5289. doi: 10.1523/JNEUROSCI.0378-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Stewart CV, Plenz D. Homeostasis of neuronal avalanches during postnatal cortex development in vitro. J Neurosci Methods. 2008;169:405–416. doi: 10.1016/j.jneumeth.2007.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tetzlaff C, Okujeni S, Egert U, Wörgötter F, Butz M. Selforganized criticality in developing neuronal networks. PLoS Comput Biol. 2010;6:e1001013. doi: 10.1371/journal.pcbi.1001013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wagenaar D, DeMarse TB, Potter SM. MeaBench: A toolset for multi-electrode data acquisition and on-line analysis. Proc 2nd Int IEEE EMBS Conf. Neural Eng. Conf. 2005, March 2005; 2005. pp. 518–521. [Google Scholar]
  45. Wagenaar DA, Pine J, Potter SM. An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 2006;7:11. doi: 10.1186/1471-2202-7-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wu X, Fu Y, Knott G, Lu J, Di Cristo G, Huang ZJ. GABA signaling promotes synapse elimination and axon pruning in developing cortical inhibitory interneurons. J Neurosci. 2012;32:331–343. doi: 10.1523/JNEUROSCI.3189-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yada Y, Kanzaki R, Takahashi H. State-dependent propagation of neuronal sub-population in spontaneous synchronized bursts. Front Syst Neurosci. 2016;10:28. doi: 10.3389/fnsys.2016.00028. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES