Nonlinearity arising from noncooperative transcription factor binding enhances negative feedback and promotes genetic oscillations

Abstract

We study the effects of multiple binding sites in the promoter of a genetic oscillator. We evaluate the regulatory function of a promoter with multiple binding sites in the absence of cooperative binding, and consider different hypotheses for how the number of bound repressors affects transcription rate. Effective Hill exponents of the resulting regulatory functions reveal an increase in the nonlinearity of the feedback with the number of binding sites. We identify optimal configurations that maximize the nonlinearity of the feedback. We use a generic model of a biochemical oscillator to show that this increased nonlinearity is reflected in enhanced oscillations, with larger amplitudes over wider oscillatory ranges. Although the study is motivated by genetic oscillations in the zebrafish segmentation clock, our findings may reveal a general principle for gene regulation.

Cells can generate temporal patterns of activity by means of genetic oscillations [1, 2]. Genetic oscillations are biochemical oscillations in the levels of gene products [3–14]. They can be produced by negative feedback regulation of gene expression, in which a gene product inhibits it’s own production directly or indirectly [15]. Such autoinhibition is often performed by transcriptional repressors, proteins or protein complexes that bind the promoter of a gene and inhibit the transcription of new mRNA molecules [16, 17], Fig. 1. A theoretical description of biochemical oscillations requires a delayed negative feedback, together with sufficient nonlinearity, and a balance of the timescales of the different processes involved [18]. Delays may occur naturally in transcriptional regulation, since the assembly of gene products involves intermediate steps [16, 19, 20]. Nonlinearity refers to the presence of nonlinear terms in the equations describing the dynamics. Such nonlinear terms may occur in the equations due to the presence of cooperative biochemical processes, where cooperativity is understood as a phenomenon in which several components act together to orchestrate some collective behavior [21]. Although some processes giving rise to nonlinear terms are known, in general it is still an open question how nonlinearity is built into genetic oscillators.

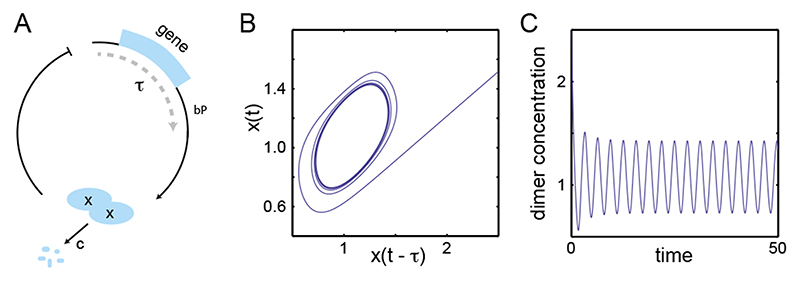
Figure 1. Delayed autoinhibition can produce genetic oscillations.

(A) The gene (light blue box) is transcribed and translated into gene products x, with a delay τ. In this example gene products form dimers that act as transcriptional repressors, inhibiting transcription of the gene (blunted arrow), and decay at a rate c. (B) and (C) Numerical solutions of Eq. (9) describing the oscillator in A. (B) Phase space: monomer concentration x(t) vs. the delayed concentration x(t — τ) settle to a limit cycle. (C) Dimer concentration oscillates as a function of time. Parameters in B, C: bP = 2, τ = 1, c =1, x₀ = 1, N =12, M = 6.

A compelling model system for genetic oscillations is the vertebrate segmentation clock [22–25]. This is a tissue level pattern generator that controls the formation of vertebrate segments during embryonic development [25, 26]. The spatiotemporal patterns generated by the segmentation clock are thought to be initiated a genetic oscillator at the single cell level [7, 9, 10, 27–29]. In this genetic oscillator, negative feedback is provided by genes of the Her family, which code proteins that form dimers and can act as transcriptional repressors [30–34]. The time taken from transcription, translation and splicing may introduce the necessary feedback delays in zebrafish and mouse [19, 34–37]. One source of nonlinearity in the segmentation clock oscillator is the dimerization of gene products that bind the promoter of cyclic genes [32]. However, this may be insufficient to generate the observed oscillations in the levels of gene products. One way to increase nonlinearity would be cooperative binding of repressors to regulatory binding sites at the promoter [21, 38, 39]. Cooperative binding to multiple binding sites can make the negative feedback steeper [40]. A similar effect occurs with ultrasensitivity in phosphorylation cascades [41]. The presence of clusters of binding sites for transcription factors may be a common motif in gene regulation [42], and cooperativity in transcription factor binding has been reported for some systems [43].

In zebrafish, multiple binding sites for Her dimers have been identified in the promoter region of Her1, Her7, and other genes of the Notch pathway [32, 44, 45]. However, there is no evidence for cooperative binding of transcriptional regulators in the case of the zebrafish segmentation clock. Therefore, although cooperative binding is not ruled out, this lack of evidence raises the general question of what contribution could be expected from the multiple binding sites reported in the promoter of segmentation clock cyclic genes. Here we use theory to study how multiple binding sites affect nonlinearity and biochemical oscillations in a generic description of a genetic oscillator.

A promoter with multiple binding sites

We first evaluate the regulatory function of a promoter that contains N binding sites for a transcriptional repressor, see Fig 2. We consider transcriptional repressors although the results in this section are more general and would apply to other types of transcription factors. We focus on a single transcriptional repressor for simplicity, and assume that all binding sites are identical. That is, binding and unbinding of repressors to the different sites occurs at the same rates for all sites. Moreover, we assume that there is no cooperativity in repressor binding. This means that binding and unbinding rates are not affected by the presence of bound factors to any of the other sites.

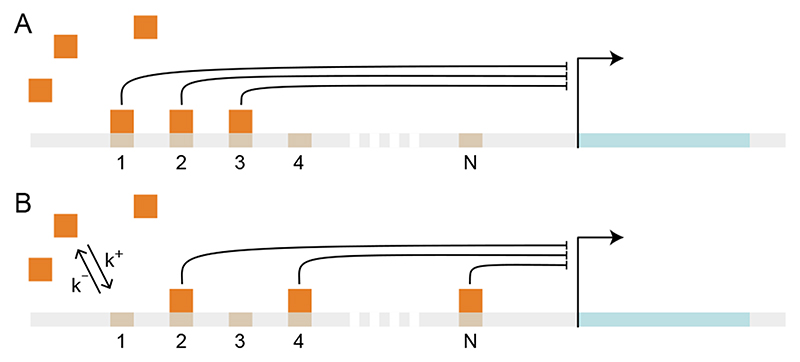
Figure 2. Schematic representation of a promoter with multiple binding sites, numbered from 1 to N.

Transcriptional repressors (orange squares) bind and unbind from binding sites (numbered platforms) at the promoter of a gene (light blue stretch). (A) and (B) illustrate two equivalent configurations of the promoter, with identical number of bound transcriptional repressors having the same inhibiting strength.

The state P_i of the promoter at any time can be characterized by the number i of bound factors, which goes from 0 to N. With a rate k⁺, a free repressor binds to an empty site at the promoter, which steps from state P_i to state P_i+1; with a rate k^-, a bound repressor falls off the promoter, which steps from state P_i to state P_i-1.

$${𝒫}_0\underset{k^{-}}{\stackrel{k^{+}}{\rightleftharpoons }}\cdots \rightleftharpoons {𝒫}_{i-1}\underset{k^{-}}{\stackrel{k^{+}}{\rightleftharpoons }}{𝒫}_i\underset{k^{-}}{\stackrel{k^{+}}{\rightleftharpoons }}{𝒫}_{i+1}\rightleftharpoons \cdots \underset{k^{-}}{\stackrel{k^{+}}{\rightleftharpoons }}{𝒫}_N$$ (1)

Denoting by P_i the promoter occupation probabilities which describe the fraction of time that the promoter spends at state P_i in the thermodynamic limit [46], the kinetics of binding and unbinding of transcriptional repressors to the binding sites is given by the set of ordinary differential equations

$$\begin{array}{l}{\dot{P}}_0=-k^{+}Nx{P}_0+k^{-}{P}_1\hfill \\ ⋮\hfill \\ \begin{array}{l}{\dot{P}}_i=-k^{+}(N-i)x{P}_i-k^{-}i{P}_i\hfill \\ +k^{+}(N-i+1)x{P}_{i-1}+k^{-}(i+1)P_{i+1}\hfill \end{array}\hfill \\ ⋮\hfill \\ {\dot{P}}_N=-k^{-}N{P}_N+k^{+}x{P}_{N-1}\hfill \end{array}$$ (2)

together with the conservation law

$$P={\displaystyle \sum _{i=0}^N{P}_i},$$ (3)

where x is the repressor concentration and P is proportional to the number of gene copies.

We assume here that binding and unbinding of repressors to the promoter occurs much faster than other processes like transcription, translation, transport and decay of molecules. This means that the promoter occupation probabilities quickly reach equilibrium with a given concentration of transcriptional repressors [46, 47]. This situation is described by P _i = 0 for all i in Eq. (2), and the resulting algebraic equations can be solved by induction to obtain

$$P_i=\left(\begin{array}{c}N\\ i\end{array}\right){\left(\frac{x}{x_0}\right)}^i{P}_0,$$ (4)

where x₀ = k^-/k⁺ is the equilibrium constant for binding of factors. Using the constraint Eq. (3) we express P₀ in terms of P

$$P_0=P{\left(1+\frac{x}{x_0}\right)}^{-N}.$$ (5)

Eq. (4) and Eq. (5) describe the equilibrium occupation of the promoter in terms of the concentration x of the transcriptional repressor.

Abrupt inhibition

In the previous section we evaluated the kinetics of noncooperative binding to a promoter with multiple binding sites. How does the presence of bound transcriptional repressors affect the transcription rate of the gene downstream of the promoter? In general,the strength of inhibition will depend on the number of bound repressors, and the regulatory function f(x) will have the form

$$f(x)={{\displaystyle \sum }}^{}_{i=0}^N{a}_i{P}_i,$$ (6)

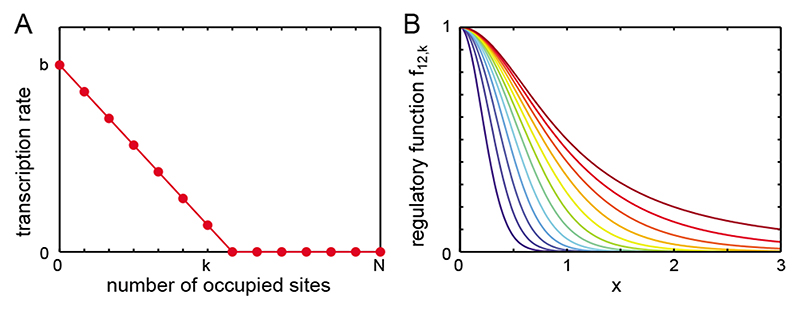
where a₀ = b is the basal transcription rate in the absence of bound repressors and α_i is the transcription rate in the presence of i bound repressors. Here we assume for simplicity that transcription proceeds at its basal rate b while there are M or less sites occupied by the repressors, and drops to zero when the number of occupied sites is larger than M, see Fig. 3; we shall consider an alternative scenario below. In this situation Eq. (6) becomes

$$f\left(x\right)=b{\displaystyle \sum _{i=0}^M{P}_i}.$$ (7)

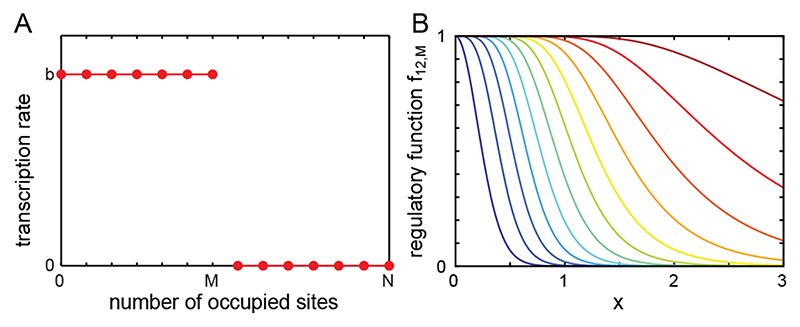
Figure 3. Abrupt inhibition.

Full inhibition occurs when more than M sites are bound by transcriptional repressors. (A) Transcription rate as a function of the number of bound transcritonal repressors. (B) Normalized regulatory function Eq. (8) as a function of repressor concentration x, with N =12 and M = 0,..., 11 (dark blue to dark red).

Using Eq. (4) and Eq. (5) the resulting regulatory function for a promoter with N binding sites is

$$f_{N,M}\left(x\right)=bP{\left(1+\frac{x}{x0}\right)}^{-N}{\displaystyle \sum _{i=0}^M\left(\begin{array}{l}\begin{array}{l}N\hfill \\ i\hfill \end{array}\hfill \end{array}\right){\left(\begin{array}{l}\frac{x}{x0}\hfill \end{array}\right)}^i}.$$ (8)

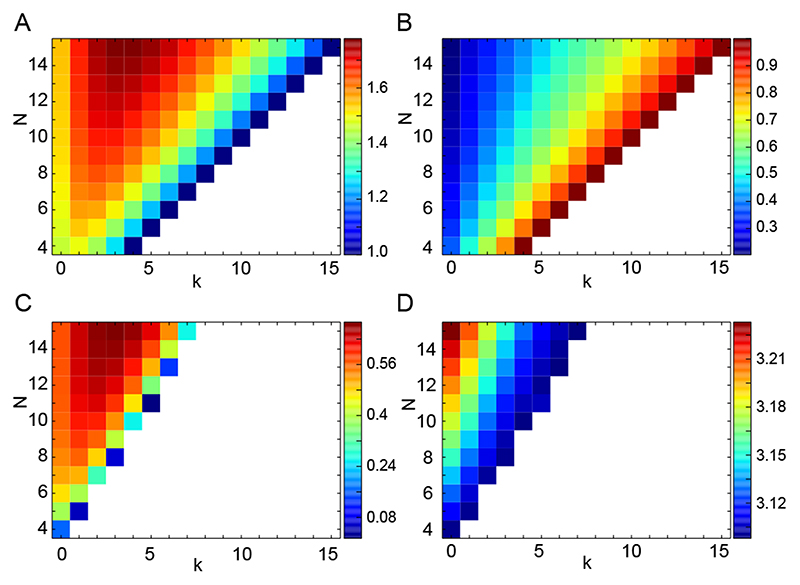
The zebrafish segmentation clock may be an interesting system to evaluate these results. In the her1/her7 locus of zebrafish, an estimated number of about 12 binding sites has been reported [32, 45]. The regulatory functions resulting from Eq. (8) for N = 12 are displayed in Fig. 3B. Although it is clear that inhibition of the promoter for a given level of repressors shifts to the right as M increases, it is less obvious how the value of M affects the steepness —that is the nonlinearity— of the negative feedback. We use Hill functions to parametrize the regulatory functions Eq. (8) in a more transparent form, see Appendix. Hill functions are parametrized by a Hill coefficient h characterizing the steepness of the curve, and an inhibition threshold K that describes the concentration of repressors that halves the production rate. We fit Hill functions to f_N,M and obtain an effective Hill coefficient h and effective inhibition threshold K, for each value of N and M, Fig. 4A,B. Increasing the number of binding sites N while keeping M fixed can increase the Hill coefficient. For fixed N, increasing M changes the Hill coefficient in a nonmonotonic way: there is an optimal value of M that maximizes the Hill coefficient and therefore nonlinearity. The effective inhibition threshold K changes in a simpler form, increasing both with N and M. In conclusion, multiple binding sites can effectively increase the nonlinearity of the feedback via the regulatory function.

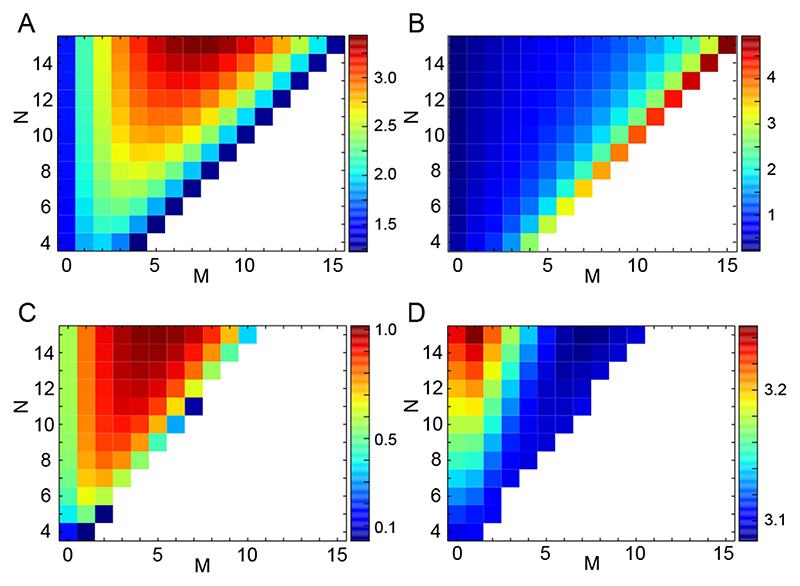
Figure 4. Multiple binding sites can increase nonlinearity and enhance oscillations.

(A) and (B) Effective Hill parameters for the regulatory function f_N,_M, Eq. (8), with b P = 1 and x₀ = 1. (A) Effective Hill coefficient h. (B) Effective inhibition threshold K. (C) and (D) Oscillations described by Eq. (9) with b P = 2, τ = 1, c =1 and x₀ = 1. (C) Amplitude of oscillations. (D) Period of oscillations. In C and D the white region represents the nonoscillatory regime, in which the system settles to a fixed point. Color bar labels indicate values in each panel.

As discussed above, nonlinearity is an essential ingredient in a theory of biochemical oscillations [18]. We therefore ask how multiple binding sites in the promoter affect a biochemical oscillator. We use the regulatory function Eq. (8) in a generic model for genetic oscillations. We consider a gene that encodes a protein that forms dimers, and these dimers can bind to multiple binding sites at the promoter to inhibit transcription, Fig. 1A. We introduce an explicit delay τ to account for transcription, translation, splicing, and other processes involved in the assembly of the gene product and its dimerization. We assume that dimerization is a fast reaction, with a separation of timescales from other processes. Therefore at any time the dimer concentration can be approximated by that of the monomers squared. The dynamics of the product concentration x(t) is given by

$$\frac{dx}{dt}=bP\frac{{{\displaystyle \sum }}^{}_M^{i=0}\left(\begin{array}{c}N\\ i\end{array}\right){\left(\frac{x(t-\tau )}{x_0}\right)}^{2i}}{{\left(1+{\left(\frac{x(t-\tau )}{x_0}\right)}^2\right)}^N}-cx(t)$$ (9)

where b is the basal production rate, c is the decay rate of products, P relates to the number of gene copies, τ is the total delay for product assembly, and x₀ is the product concentration that halves the basal transcription rate. The regulatory function Eq. (8) is parametrized by N and M. This genetic oscillator is a reduction of the models proposed by Lewis [19], and other authors [48, 49]. It describes the protein concentration, but does not include the mRNA; the duration of transcription and translation are both included in the delay τ. Furthermore, it does not describe effects present in theories that include more than one regulator [32, 50, 51], but here it suffices to illustrate the effects of multiple binding sites in a simpler context.

We integrate Eq. (9) numerically and evaluate the resulting dynamics by calculating the amplitude and period of oscillations. In all numerical simulations we use the function dde23 from MATLAB [52]. Scanning the values of N and M, we determine whether the system oscillates in steady state: when the difference in the maxima over the last ten cycles falls below 0.01 the simulation is stopped and we record the output.

The amplitude of oscillations grows with the number of binding sites N, Fig. 4C. The range where the system oscillates grows with the number of binding sites N. The amplitude is nonmonotonic in M: for a fixed number of binding sites N, there is an optimal value for M that maximizes the amplitude of oscillations, Fig.4C. The period of oscillations grows with N and decreases with M. These results show how the change in nonlinearity observed in the regulatory functions is reflected in the oscillations as the number of binding sites change.

Gradual inhibition

There is strong evidence for the products of some cyclic genes of the zebrafish segmentation clock binding their own promoters and acting as transcriptional repressors [23, 27, 32, 33, 35, 44]. However, we do not have detailed knowledge of how these transcriptional repressors affect transcription rates when bound to the promoters of cyclic genes. There is evidence from transcriptional analysis of the Hes1 gene in mouse indicating that inhibition is gradual [30]. While the wildtype Hes1 promoter containing all three N Box elements that are bound by Hes1 proteins showed a 30fold inhibition of transcription in the presence of Hes1, mutations in one, two, and three of the N Box elements showed impaired inhibition with 14-, 7-, and 2-fold inhibition respectively [30].

Motivated by these results, we consider here a scenario where additional bound repressors gradually reduce transcription rate until it drops to zero, Fig. 5A. For simplicity we assume that transcription rate drops linearly as a function of bound repressors, from a basal rate b, to zero for k + 1 occupied sites

$$a_i=\{\begin{array}{l}b(1-i/(k+1))\hfill \\ 0\hfill \end{array}\begin{array}{l}\text{if}i\le k+1\hfill \\ \text{if}i>k+1,\hfill \end{array}$$ (10)

see Fig. 5A. Using this gradual inhibition in Eq. (6) together with Eq. (4) and (5) we obtain regulatory functions f_N,_k (x)

$$f_{N,M}\left(x\right)=bP{\left(1+\frac{x}{x0}\right)}^{-N}{\displaystyle \sum _{i=0}^{K+1}\left(\begin{array}{l}1-\frac{i}{K+1}\hfill \end{array}\right)\left(\begin{array}{l}\begin{array}{l}N\hfill \\ i\hfill \end{array}\hfill \end{array}\right){\left(\begin{array}{l}\frac{x}{x0}\hfill \end{array}\right)}^i},$$ (11)

see Fig. 5B. As in the previous case it is clear that the effective inhibition threshold shifts to the right as k increases, but it is not so clear if the steepness of the regulatory function changes, and how. Performing fits to Hill functions, we find that the nonmonotonic behavior of the effective Hill exponent h is observed again as k increases, Fig. 6A,B. Oscillations are similarly affected by noncooperative binding with gradual inhibition, Fig. 6C,D. These results show that the prediction of an optimal value for the number of bound repressors that fully inhibits the promoter, is robust with respect to the details of how multiple bound repressors reduce the transcription rate.

Figure 5. Gradual inhibition. Binding of multiple transcriptional repressors gradually inhibits transcription.

(A) Transcription rate as a function of the number of bound transcriptional repressors. Transcription occurs at the basal rate b in the absence of bound repressors, and decreases linearly to zero for more than k bound repressors. (B) Normalized regulatory function Eq. (11) as a function of repressor concentration x, with N = 12 and k = 0,..., 11 (dark blue to dark red).

Figure 6. Multiple binding sites can increase nonlinearity and enhance oscillations in the presence of gradual inhibition.

(A) and (B) Effective Hill parameters for the regulatory function f_N,_k, Eq. (11), with bP = 1 and x₀ = 1. (A) Effective Hill coefficient h. (B) Effective inhibition threshold K. (C) and (D) Oscillations obtained using regulatory functions Eq. (11) with b P = 2, τ = 1, c = 1 and x _o = 1. (C) Amplitude of oscillations. (D) Period of oscillations. In C and D the white region represents the nonoscillatory regime, in which the system settles to a fixed point. Color bar labels indicate values in each panel.

Discussion

We studied the effects of multiple noncooperative binding sites in the promoter of a genetic oscillator. We evaluated the behavior of a promoter with multiple binding sites when binding of transcriptional repressors is noncooperative, Fig. 2. We considered two different hypotheses for how bound transcriptional repressors affect transcription rates, Figs. 3 and 5. In both cases, we calculated how the number of binding sites and the number of bound repressors required to produce full inhibition, affect the nonlinearity of regulatory functions. We showed that there is an optimal value of the number of repressors needed to fully inhibit transcription that maximizes nonlinearity, Figs. 4AB and 6AB. This increased nonlinearity is reflected in the behavior of a genetic oscillator controlled by such regulatory functions, Figs. 4CD and 6CD.

Cooperative binding is a well known means to increase the nonlinearity of a biological dynamical system [21, 39]. Here we show that the nonlinearity of a regulatory function can be increased by multiple binding sites, even if binding is noncooperative. This idea may have application in other biological control systems as well. Using the same formulation as we did here, one can also describe nonlinearity in the transcriptional activation of gene expression, thereby creating effective on-switches in developmental and physiological regulatory networks. A similar effect has been reported in a theoretical study of enzymes with multiple phosphorylation sites [53–55]. It was found that nonessential phosphorylation sites give rise to an increase in effective Hill coefficients, enhancing ultrasensitivity in signal transduction [55].

Previous work on the segmentation clock addressed the case of three binding sites [40], motivated by experimental observations of the Hes7 mouse promoter [31]. The authors assumed that a single bound dimer inhibits transcription completely, corresponding to the particular case M = 1 of the theory developed here. They considered both noncooperative and cooperative binding, and showed that cooperativity increases the effective Hill coefficient as expected. In a follow-up [56], the authors addressed the case of Hes1 regulation based on the report of four binding sites in the Hes1 mouse promoter [30]. Again assuming that a single bound dimer inhibits transcription completely, they used the data from the transcriptional analysis of the Hes1 gene to estimate an effective Hill coefficient for the Mouse Hes1 oscillator, obtaining an upper bound of about 3. More recently, the effect of two binding sites as compared to a single binding site was discussed together with differential decay of the monomers [57].

Our theory predicts how changing the number of binding sites N, and the number M of bound repressors that produce full inhibition, affects a single cell oscillator. Although an experiment that changes the value of M may currently be challenging in a cellular system, the number of binding sites N is more amenable to experimental manipulation. For example, binding sites could be mutated [30], or deleted from the promoter, or they could be interfered with using genome editing strategies such as TALEN [58] or CRISPR [59] to alter or delete specific binding sites. To assess the effects of these perturbations in experiments may also pose some challenges. Dropping the number of binding sites from N = 12 to N = 6 introduces a period change of about 2.5%, while amplitude halves over the same range, Fig. 4C,D. Experiments will require at least such precision to reliably detect changes.

Our results suggest a possible evolutionary mechanism to increase nonlinearity in gene regulatory systems. In this mechanism, point mutations in the promoter that increase the number of binding sites for transcription factors may increase the steepness of regulatory functions. If the resulting steeper regulation performs some function better, such mutations would have a good chance to be conserved by natural selection. In the case of the segmentation clock, the amplitude of oscillations could increase with the number of binding sites, possibly reducing the signal to noise ratio. Furthermore, the range for oscillations would be wider, making the oscillatory regime less sensitive to slow extrinsic fluctuations of parameter values. Remarkably, it may happen that after an increase in N, an increase in M also raises nonlinearity, see Fig. 4A. This means that weaker repressors would result in better oscillations. This evolutionary mechanism would provide a simple way to gradually increase the nonlinearity of a feedback or other regulatory function.

The theory for the zebrafish regulatory function could be refined using the experimentally measured relative affinities of the binding sites at the herl and her7 promoters [32]. Apart from the effects reported here, the number of binding sites may have additional roles. For example, it could serve as a buffer for fluctuations in gene expression [20, 60–64], augmenting the precision of genetic oscillations. This will be the topic of future work.