LiftPose3D, a deep learning-based approach for transforming 2D to 3D pose in laboratory animals

Abstract

Markerless 3D pose estimation has become an indispensable tool for kinematic studies of laboratory animals. Most current methods recover 3D pose by multi-view triangulation of deep network-based 2D pose estimates. However, triangulation requires multiple, synchronized cameras and elaborate calibration protocols that hinder its widespread adoption in laboratory studies. Here we describe LiftPose3D, a deep network-based method that overcomes these barriers by reconstructing 3D poses from a single 2D camera view. We illustrate LiftPose3D’s versatility by applying it to multiple experimental systems using flies, mice, rats, and macaque monkeys and in circumstances where 3D triangulation is impractical or impossible. Our framework achieves accurate lifting for stereotyped and non-stereotyped behaviors from different camera angles. Thus, LiftPose3D permits high-quality 3D pose estimation in the absence of complex camera arrays, tedious calibration procedures, and despite occluded body parts in freely behaving animals.

1. Introduction

To identify how actions arise from neural circuit dynamics, one must first make accurate measurements of behavior in laboratory experiments. Recent innovations in 3-dimensional (3D) pose estimation promise to accelerate the discovery of these neural control principles. 3D pose estimation is typically accomplished by triangulating 2-dimensional (2D) poses acquired using multiple, synchronized cameras and deep learning-based tracking algorithms [1–9]. Notably, triangulation requires that every tracked keypoint (body landmark) be visible from at least two synchronized cameras [10] and that each camera is calibrated. These requirements are often difficult to meet in space-constrained experimental systems that also house sensory stimulation devices [11–13], or when imaging untethered, freely behaving animals like fur-covered rodents [14] for whom keypoints can sometimes be occluded.

Because of these challenges, most animal studies have favored 2D pose estimation using one camera [1, 2, 6, 15–17]. Nevertheless, 3D poses are desirable because they eliminate a problematic camera-angle dependence that can arise during behavioral analyses [3]. Research on human pose estimation has long been interested in “lifting” 2D poses by regressing them to a library of 3D poses [18–21] but only recently have achieved high accuracy using deep learning [22–34]. These techniques have not been adapted to the study of animals due to the relative lack of large and diverse training datasets.

Here, we introduce LiftPose3D, a tool for 3D pose estimation of tethered and freely behaving laboratory animals from a single camera view. Our method builds on a recent neural network architecture designed to lift human poses [30]. We develop data transformations and network training augmentation methods that enable accurate 3D pose estimation across a wide range of animals, camera angles, experimental systems, and behaviors using relatively little data. We find that (i) a library of 3D poses can be used to train our network to lift 2D poses from one camera, with minimal constraints on camera hardware and positioning and, consequently, no calibration, (ii) by aligning animal poses, our network can overcome occlusions and outliers in ground truth data, and (iii) pretrained networks can generalize across experimental setups using linear domain adaptation.

2. Results

2.1. Predicting 3D pose with fewer cameras at arbitrary positions

Rather than taking independent 2D keypoints as inputs, as for triangulation-based 3D pose estimation, LiftPose3D uses a deep-neural network to regress an ensmeble of 2D keypoints viewed from a camera—the 2D pose—to a ground truth library of 3D poses. Considering all keypoints simultaneously allows the network to learn geometric relationships intrinsic to animal poses.

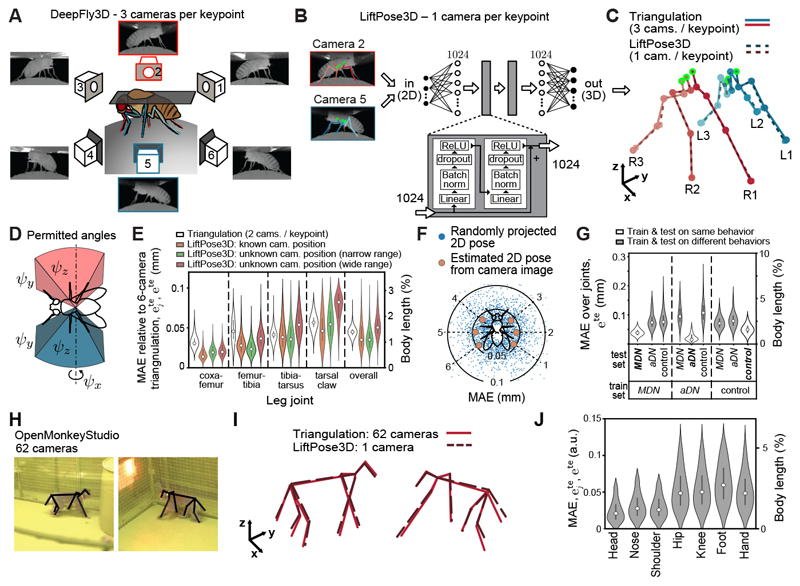
First, we illustrate how this approach can reduce the number of cameras needed for 3D pose estimation on a tethered adult Drosophila dataset [3]. Here, 15 keypoints are visible from three synchronized cameras on each side of the animal (Figure 1A). These keypoints were annotated and triangulated using DeepFly3D [3]. Using this dataset as a 3D pose library we aimed to train a LiftPose3D network that lifts half-body 2D poses from any side camera without knowing the camera’s orientation. First, we ensured that the output of LiftPose3D was translation invariant by predicting the keypoints of the respective legs relative to six ”root” immobile thorax-coxa joints (green circles, Figure 1B). Second, to avoid the network having to learn perspective distortion, we assumed that the focal length (intrinsic matrix) of the camera and the animal-to-camera distance were known, or that one of them is large enough to assume weak perspective effects. In the latter case, we normalized 2D input poses by their Frobenius norm during both training and testing. Third, to facilitate lifting from any angle, we assumed that camera extrinsic matrices, which could be obtained by calibration, might also be unknown. Instead, we parametrized them by Euler angles ψ_z, ψ_y, ψ_x representing ordered rotations around the z, y and x axes of a coordinate system centered around the fly (Figure 1D). During training, we took as inputs 2D poses (from 3D poses randomly projected to virtual camera planes, rather than 2D pose estimates), and as outputs 3D poses triangulated from three cameras. To measure lifting accuracy, we tested the network on software-annotated 2D poses (Figure 1B) from two independent animals and computed the mean absolute error (MAE), $e_j^{\text{te}}$, for each joint j as well as the MAE across all joints $e^{\text{te}}=(1/n){\displaystyle {\sum }_j{e}_j^{\text{te}}}$ relative to triangulated 3D poses.

Figure 1. LiftPose3D predicts 3D pose with fewer cameras and flexible camera positioning.

A Ground truth 3D poses of tethered Drosophila are triangulated using six camera views (3 cameras per keypoint). B LiftPose3D predicts 3D poses using deep network-derived 2D poses from only two cameras (red and blue, 1 camera per keypoint). The coordinates are considered relative to a set of root joints (green). The inputs are scaled up and passed twice through the main processing unit (gray rectangle) comprising batch norm, dropout and ReLU wrapped by a skip connection. C The output, 3D half-body poses (blue/red), are compared with triangulated 3D poses. Limbs are labeled by left (L)/right (R) and front (1), mid (2), or hind (3) positions. D LiftPose3D can be trained using virtual camera projections of 3D poses to lift from cameras within the angles ψ_z, ψ_y, ψ_x (representing ordered yaw, roll, pitch rotations). E Error of 3D poses relative to triangulation using three cameras per keypoint. We compare triangulation error using 2 cameras per keypoint (white), test error for a network trained with known camera parameters (orange) and two angle-invariant networks with narrow (green, ψ_z = ±10°, ψ_y = ±5°, ψ_x = ±5° with respect to a known camera orientation), or wide ranges (red, ψ_z = ±180°, ψ_y = ±5°, ψ_x = ±5°). F Error of lifted 3D poses at different virtual camera orientations of the wide-range lifter network and a network with known camera parameters. Blue dots represent lifting errors for a given projected 2D pose. Orange circles represent averages over the test dataset for a given camera. G Error of estimated 3D poses for a network trained and tested on different combinations behavioral data including optogenetically-induced backward walking (MDN, left), antennal grooming (aDN, middle), or spontaneous, unstimulated behaviors (control, right). H Two representative images from the OpenMonkeyStudio dataset. 2D poses are superimposed (black). I 3D poses obtained by triangulating up to 62 cameras (red lines), or using a single camera and LiftPose3D (dashed black lines). J Absolute errors for different body parts with respect to total body length. Violin plots represent Gaussian kernel density estimates with bandwidth 0.5, truncated at the 99th percentile and superimposed with the median (gray dot), 25th, and 50th percentiles (black line).

We found that LiftPose3D could predict 3D poses using only one camera per side (Figure 1C). When the virtual projections during training were performed using known intrinsic and extrinsic matrices, the network’s accuracy was at least as good as triangulation using two cameras per keypoint (Figure 1E, white). Surprisingly, the accuracy did not suffer when the network was trained (i) using virtual 2D projections around an approximate camera location (Figure 1E, green, narrow range) rather than with known instrinsic matrices, and (ii) using normalized 2D poses rather than with known intrinsic matrices. Accuracy remained excellent when virtual projections extended to all possible angles around the meridian (Figure 1E, red, wide-range). Lifting could be performed for optogenetically-induced backward walking (Video 1), antennal grooming (Video 2), and spontaneous, irregular limb movements (Video 3). Because the network predicts joint coordinates with respect to thoracic root joints, the MAE was larger for distal joints that move within a larger kinematic volume. By contrast, the error for triangulation depended only on the accuracy of 2D annotations because it treats each keypoint independently. We also assessed camera-angle dependence for our wide angle-range network by lifting virtual 2D poses projected onto the meridian of the unit sphere, or 2D poses captured from each of the six cameras (Figure 1F). The test MAE was low (< 0.05 mm) and had no camera-angle dependence. Because we make no assumptions about camera placement when training our angle-invariant networks, these pretrained networks might also be used to predict accurate 3D poses for tethered Drosophila recorded in other laboratories.

We next explored how the similarity between animal behaviors used for training and testing might influence lifting accuracy. Our tethered Drosophila dataset contained optogenetically-induced antennal grooming (aDN), and backward walking (MDN), as well as spontaneous behaviors like forward walking (control). We trained a network using poses from only one behavior (not including rest frames) and evaluated it on all three behaviors while keeping the amount of training data fixed (2.5 × 10⁴ poses). As expected, the MAE was higher when test data included untrained behaviors than when test data included trained behaviors (Figure 1G). Furthermore, training on all three behaviors led to comparable or lower MAE (Figure 1E, orange) than training and testing on one single behavior (Figure 1G). Thus, higher training data diversity improves lifting accuracy.

To illustrate the advantage of using lifted 3D poses versus 2D poses in downstream analyses, we derived joint angles during forward walking from lifted 3D poses and from 2D poses projected from 3D poses in the ventral plane (Extended Data Figure 1, green). Joint angles derived from lifted and triangulated 3D poses were in close agreement. On the other hand, we found spurious dynamics in the distal joints when viewed from a projected plane, likely due to rotations upstream in the kinematic chain (proximal joints) that cause movements of the whole leg. Thus, 3D poses predicted by LiftPose3D can help to decouple underlying physical degrees-of-freedom.

We also tested LiftPose3D in freely behaving animals where the effective camera angle dynamically changes, and in animals without exoskeletons whose neighboring keypoints are less constrained. Specifically, we considered freely behaving macaque monkeys [4] where 3D poses were triangulated using 2D poses from 62 synchronized cameras (Figure 1H). After training LiftPose3D with only 6’571 3D poses, we could lift 3D poses from test images with diverse animal poses (Video 4), acquired from any camera (Figure 1I), and with relatively low body length-normalized MAE (Figure 1J).

Taken together, these results demonstrate that, using simple data preprocessing and a relatively small but diverse training dataset, LiftPose3D can reduce the number of cameras required to perform accurate 3D pose estimation.

2.2. Predicting 3D pose despite occluded keypoints

In freely behaving animals, keypoints are often missing from certain camera angles due to self-occlusions and, therefore, only partial 3D ground truth can be obtained by triangulation. We asked how the global nature of lifting—all keypoints are lifted simultaneously—might be leveraged to reconstruct information lost by occlusions, allowing one to predict full 3D poses.

To address this question, we built an experimental system similar to others used for flies and mice [14, 35, 36] that consisted of a transparent enclosure coupled to a right-angle prism mirror and with a camera beneath to record ventral and side views of a freely behaving fly (Figure 2A). Due to the right-angle prism and the long focal length camera (i.e., negligible perspective effects), the ventral and side views are orthographic projections of the true 3D pose. Triangulation thus consisted of estimating the z-axis depth of keypoints from the side view. Although keypoints closer to the prism were simultaneously visible in both views and could be triangulated, other joints had only ventral 2D information. We therefore aligned flies in the same reference frame in the ventral view (Figure 2B), turning lifting into a regression problem similar to that for tethered animals. During training we took ventral view 2D poses as inputs, but penalized only those keypoints with complete 3D information. By also aligning these data, we found that the network could implicitly augment unseen coordinates by learning geometric relationships between keypoints. The network could predict 3D positions for every joint at test time, including those occluded in the side view (Figure 2D and Video 5). Notably, owing to the high spatial resolution of this setup, the accuracy, based on available triangulation-derived 3D positions (Figure 2E), was better than that obtained for tethered flies triangulated using four cameras (Figure 1E). Thus, LiftPose3D can estimate 3D poses from 2D images in cases where keypoints are occluded and cannot be triangulated.

Figure 2. LiftPose3D performs 3D pose estimation on freely behaving animals with occluded keypoints.

ADrosophila behaving freely within a narrow, transparent enclosure. Using a right-angle prism mirror, ventral (top) and side (bottom) views are recorded with one camera. Afterwards, 2D poses are annotated (colored lines). Ventral 2D poses (green box) are used to lift 3D poses. B Keypoints near the prism mirror (red and blue) can be tracked in both views and triangulated. Other keypoints (gray) are only visible ventrally and thus have no 3D ground truth. Unilateral ground truth for both sides are obtained by registering the orientation and position of ventral images of the fly. C Training data consist of full ventral 2D poses and their corresponding partial 3D poses. D Following training, LiftPose3D can predict 3D poses for new ventral view 2D poses. E Joint-wise and overall absolute errors of the network’s 3D pose predictions for freely behaving Drosophila. F A similar data preprocessing approach is used to lift ventral view 2D poses of mice (green boxes) walking within a narrow enclosure and tracked using LocoMouse software. LocoMouse ground truth (blue and red) and LiftPose3D (orange) pose trajectories are shown for the right forepaw (top) and hindpaw (bottom) during one walking epoch. Arrowheads indicate where LiftPose3D lifting of the ventral view can be used to correct LocoMouse side view tracking errors (red). Asterisks indicate where inaccuracies in the LocoMouse ventral view ground truth (red) disrupt LiftPose3D’s side view predictions (orange). G Absolute errors of LiftPose3D and LocoMouse side view predictions for six keypoints with respect to manually-annotated ground truth data. H Camera image from the CAPTURE dataset superimposed with the annotated 2D pose (left). LiftPose3D uses this 2D pose to recover the full 3D pose (right). I LiftPose3D can be trained to lift 3D poses of a freely moving rat with occluded keypoints (open circles). J Histograms of the measured lengths of the spinal segment for two different animals reveal large animal-to-animal skeletal variations. K Error distribution over all keypoints for the CAPTURE dataset.

These results suggested an opportunity to apply lifting to potentially correct inaccurate 3D poses obtained using other tracking approaches. To test this, we used a dataset consisting of freely behaving mice traversing a narrow corridor [14] and tracked using the LocoMouse software from ventral and side views [14]. We triangulated and aligned incomplete 3D ground truth poses as we did for Drosophila and then trained a LiftPose3D network using ventral 2D poses as inputs. Predictions were in good agreement with the LocoMouse’s side view tracking (Figure 2E and Video 6) and could recover expected cycloid-like kinematics between strides (Figure 2F). Remarkably, LiftPose3D predictions could also correct poorly labeled or missing side-view poses (Figure 2F, bottom, white arrowheads). However, lifting accuracy depended on the fidelity of input 2D poses: incorrect ventral 2D poses generated false side view predictions (Figure 2F, bottom, white asterisks). These errors were always localized to the joint-of-interest and were relatively infrequent. Overall, LiftPose3D and LocoMouse performed similarly compared with manual human annotation (Figure 2G) demonstrating that LiftPose3D can be used to test the consistency of ground truth datasets.

To assess how well spatial relationships learned by LiftPose3D could generalize to animals with more complex behaviors and larger variations in body proportions, we next considered the CAPTURE dataset of six cameras recording freely behaving rats within a circular arena [37] (Figure 2H, left). Animal poses were intermittently self-occluded during a variety of complex behaviors (Figure 2I). Therefore, to allow the network to learn the skeletal geometry, we aligned animals in the camera-coordinate frame and replaced missing input data with zeros. Furthermore, to make the network robust to bone length variability within and across animals (Figure 2J) we assumed that bone lengths were normally distributed and generated, for each triangulated 3D pose, rescaled 3D poses by sampling from bone-length distributions while preserving joint angles. Then, we obtained corresponding 2D poses via a virtual projection within the Euler angle range of ±10° with respect to the known camera locations (to augment the range of camera-to-animal angles). Finally, we normalized 2D poses by their Frobenius norm, as before, assuming a large enough camera-to-animal distance.

To show that the network generalizes across new experimental setups, we used two experiments from this dataset (i.e., two animals and two camera arrangements) for training and tested with a third experiment (a different animal, camera focal length, and animal-to-camera distance). By replacing low confidence or missing coordinates with zeros, LiftPose3D could accurately predict the nonzero coordinates (Figure 2H, K and Video 7). Thus, this is a viable way to correct for erroneous input keypoints and makes our network directly applicable to other rat movement studies.

2.3. Lifting diverse experimental data without 3D ground truth

Although our angle-invariant networks for lifting 3D poses in tethered flies (Figure 1D-F) and freely behaving rats (Figure 2H-K) can already be used in similar experimental systems without the need for additional training data, small variations resulting from camera distortions or postural differences may limit the accuracy of lifted poses. Therefore, we explored how domain adaptation might enable pretrained networks to lift poses in new experimental systems despite small postural variations.

We assessed the possibility of domain adaptation by training a network in domain A—tethered flies—and predicting 3D poses in domain B—freely-moving flies (Figure 3A). To do so, we identified two linear transformations d ₂ and d ₃. d ₂ is used to map 2D poses from domain B as inputs to the pre-trained network in domain A, while $d_3^{-1}$ is used to transform lifted 3D poses back to domain B. These linear transformations were found as best-fit mappings from every pose in a training dataset B’ to their k nearest neighbors A’ (Figure 3B). They are expected to generalize as long as the poses in domain A are rich enough to cover the pose repertoire in domain B and are sufficiently similar between domains. We found by 10-fold cross-validation that the error associated with the transformations converged after less than 500 poses (Figure 3C). The final lifted poses were also in good agreement with the triangulated poses in domain B (Figure 3D) having accuracies comparable to a network lifting purely in domain A (Figure 3E, compare dark with light gray).

Figure 3. A pretrained LiftPose3D network predicts 3D poses for diverse data and when triangulation is impossible.

A Linear domain adaptation between domain A (fly on a spherical treadmill) and domain B (fly on a flat surface). 2D poses in B are mapped to A by a linear transformation d ₂ then lifted with a network trained only on domain A poses. After lifting, the 3D poses are mapped back to B by another linear transformation d ₃. B A typical 2D pose in domain B mapped into domain A by the best-fit linear transformation d ₂ between poses in B and their nearest neighbors in A. C Error between mapped pose and k nearest neighbor poses for d ₂, d ₃ against the number of poses used to train them (k =1 for d ₂ and k = 2 for d ₃). D Lifted 3D pose following domain adapation of a ventral domain B 2D pose and lifting with a network trained on domain A data. The prediction is superimposed with the incomplete ground truth 3D pose in domain B. E Lifting error following domain adaptation of domain B poses compared with lifting error in the domain A with no domain adaptation. F Freely behaving flies were recorded from below using a low-resolution camera. Following body tracking, the region-of-interest containing the fly was cropped and registered. 2D pose estimation was then performed for 24 visible joints. G 2D poses are adapted to the prism-mirror domain. These are then lifted to 3D poses using a network pre-trained with prism-mirror data and coarse-grained to match the lower resolution 2D images in the new experimental system. H These 3D poses permit the analysis of claw movements in an otherwise unobserved x – z plane (bottom). I Freely behaving fly recorded from below using one high-resolution camera. 2D pose estimation was performed for all 30 joints. Following tracking, a region-of-interest containing the fly was cropped and registered. The same LiftPose3D network trained in panel B—but without coarse-graining—was used to predict J 3D poses and K unobserved claw movements in the x – z plane (bottom).

To demonstrate the full potential of linear domain adaptation, we next lifted Drosophila 2D poses from a single ventral camera. This experimental system is common due to its simplicity, low cost, and increased throughput and has been used to study C. elegans [38], larval zebrafish [39], larval Drosophila [40], adult Drosophila [41], and mice [42]. Because depth sensors [43, 44] cannot resolve small laboratory animals, 3D pose estimation from a single 2D view remains unsolved, but has the potential to enrich behavioral datasets and improve downstream analysis.

We developed an experimental system with a square-shaped arena in which multiple freely-behaving flies were recorded ventrally using a single camera (Figure 3F, left) at four-fold lower spatial resolution (26 px mm⁻¹) than in our prism-mirror system. We pretrained a network using prism-mirror training data for keypoints present in both datasets and then augmented these data using a Gaussian noise term with standard deviation of ~ 4. We adapted annotated 2D poses into the network’s domain before lifting (Figure 3B). We found that the network could predict physiologically realistic 3D poses in this new dataset using only ventral 2D poses (Figure 3G and Video 8). This is remarkable because ventrally-viewed swing and stance phases are difficult to distinguish, particularly at lower resolution. During walking, 2D tracking of the tarsal claws traced out stereotypical trajectories in the x-y plane (Figure 3H, top) [45] and circular movements in the unmeasured x-z plane (Figure 3H, bottom) whose amplitudes were consistent with real kinematic measurements during forward walking [46].

Another exciting possibility offered by LiftPose3D is to ’resurrect’ previously published 2D pose data for new 3D kinematic analyses. We applied our network that was trained on prism-mirror data to lift published video data of a fly walking through a capsule-shaped arena [16] (Figure 3I). Using a similar processing pipeline as before (Figure 3B,F,G), including registration and domain adaptation but not noise perturbations (the target data were of similarly high resolution as the training data), LiftPose3D could predict 3D poses from this dataset (Figure 3J). We again observed physiologically realistic cyclical movements of the pretarsi during forward walking (Figure 3K, bottom; Video 9). These data illustrate that linear domain-adaptation and LiftPose3D can be combined to lift 3D poses from previously published 2D video data for which 3D triangulation would be otherwise impossible.

2.4. Drosophila LiftPose3D station

These domain adaptation results suggested that one could make 3D pose acquisition cheaper and more accessible by designing a “Drosophila LiftPose3D station”—an inexpensive (~$150) open-source hardware system including a 3D printed rig supporting a rectangular arena (Extended Data Figure 3, Supplementary Note 1). A common hardware solution like this overcomes potential variability across different experimental systems that arise from camera distortions and perspective effects. Using pre-trained DeepLabCut and LiftPose3D networks we found that one can effectively lift Drosophila 3D poses with this system (Video 10). We envision that a similar low-cost approach might, in the future, also be taken to facilitate cross-laboratory 3D lifting of mouse 2D poses from a single camera.

3. Discussion

Here we have introduced LiftPose3D, a deep learning-based tool that dramatically simplifies 3D pose estimation across a wide variety of laboratory contexts. LiftPose3D can take as inputs 2D poses from any of a variety of annotation softwares [2, 3]. Through input data preprocessing, training augmentation, and domain adaptation one can train a lifting network [30] with several orders of magnitude less data as well as incomplete or innacurate ground truth poses. LiftPose3D is invariant to camera hardware and positioning, making it possible to use the same networks across laboratories and experimental systems. We provide an intuitive Python notebook that serves as an interface for data preprocessing, network training, 3D predictions, and data visualization.

Several factors must be considered when optimizing LiftPose3D for new experimental systems. First, because predicting depth from a 2D projection depends on comparing the lengths of body parts, input poses must be sufficiently well-resolved to discriminate between 3D poses with similar 2D projections. Second, prediction accuracy depends on training data diversity: previously untrained behaviors may not be as accurately lifted. Further work may improve LiftPose3D by constraining 3D poses using body priors [47–51] and temporal information [31].

Using our domain adaptation methodology, networks with the largest and most diverse training data, like those for the tethered fly, may be sufficiently robust to accurately lift 2D to 3D pose in other laboratories. In the future, similarly robust lifting networks might be generated for other animals through a cross-laboratory aggregation of diverse 3D pose ground truth datasets. In summary, LiftPose3D can accelerate 3D pose estimation in laboratory research by reducing the need for complex and expensive synchronized multi-camera systems, and arduous calibration procedures. This, enables the acquisition of rich behavioral data and can accelerate our understanding of the neuromechanical control of behavior.

10. Materials and Methods

10.1. Theoretical basis for LiftPose3D

LiftPose3D aims to estimate the 3D pose X = (X ₁, …, X _n), i.e., an ensemble of keypoints, by learning a nonlinear mapping between triangulated ground truth 3D poses and corresponding 2D poses x _c = (x _c,1, …, x _c,n). Formally, this operation is encoded in a lifting function f mapping a 2D pose from any camera c to their corresponding 3D pose in camera-centered coordinates, Y _c = f(x _c), and a camera transformation ϕ_c, encoding a rotation and translation operation (see Eq. (2)), mapping from camera-centered coordinates to world coordinates $\mathbf{\text{X}}={\varphi }_c^{-1}({\mathbf{\text{Y}}}_c)$. The lifting function f can be approximated using a deep neural network F(x_c; Θ), where Θ represents the network weights controlling the behavior of F. In a specific application, Θ are trained by minimizing the discrepancy between 3D poses predicted by lifting from any camera and ground truth 3D poses,

$${\mathcal{\text{J}}}_1(\Theta )≔{\displaystyle \sum _c{\displaystyle \sum _{j=1}^n{\chi }_{V_c}(j){\Vert {(F({\text{x}}_c;\Theta ))}_j-{\mathbf{\text{Y}}}_{c,j}\Vert }_2^2},}$$ (1)

where ${\chi }_{V_c}(j)$ is an indicator function of the set V_c of visible points from camera c. For F(x_c; Θ), we adapted a network architecture from [57] composed of fully connected layers regularized by batch-norm and dropout [58] and linked with skip connections (Figure 1B). This network was developed to perform human-pose estimation following training on approximately 10⁶ fully annotated 2D-3D human pose pairs for many different behaviors. We demonstrate that training augmentation methods allow this network to (i) work with a vastly smaller training dataset (between 10³-10⁴ poses acquired automatically using 2D pose estimation approaches [52, 59]), (ii) predict 3D poses from a single camera view at arbitrary angles, (iii) be trained with only partially annotated ground truth 3D poses suffering from occlusions, and (iv) generalize a single pretrained network across experimental systems and domains by linear domain adaptation.

Note that our approach implicitly assumes that the network learns two operations: lifting the 2D pose x_c to camera-centered 3D coordinates Y_c by predicting the depth component of the pose, and learning perspective effects encoded in the animal-to-camera distance and the intrinsic camera matrix (see Eqs. (2)–(5)). Notably, the intrinsic camera matrix is camera-specific, suggesting that a trained network can only lift poses from cameras used during training and that application to new settings with strong perspective effects (short focal lengths) may require camera calibration. We show that this is not necessarily the case and that one can generalize pre-trained networks to new settings by weakening perspective effects. This can be accomplished by either using a large focal length camera, or by increasing the animal-to-camera distance and normalizing the scale of 2D poses. We demonstrate that a weak perspective assumption can, in many practical scenarios, enable lifting 2D poses from different cameras without calibration. These contributions enable 3D pose estimation in otherwise inaccessible experimental scenarios.

10.2. Obtaining 3D pose ground truth data by triangulation

Triangulated 3D positions served as ground truth data for assessing the accuracy of LiftPose3D. If a keypoint j of interest is visible from at least two cameras, with corresponding 2D coordinates ${\mathbf{\text{x}}}_{c,j}\in {ℝ}^2$ in camera c and camera parameters (extrinsic and intrinsic matrices), then its 3D coordinates ${\mathbf{\text{X}}}_j\in {ℝ}^3$ in a global world reference frame can be obtained by triangulation. Let us express ${\mathbf{\text{X}}}_j=(x_j^1,x_j^2,x_j^3)$ in homogeneous coordinates as ${\widehat{\mathbf{\text{X}}}}_j=(x_j^1,x_j^2,x_j^3,1)$. The projection from the 3D points in the global coordinate system to 2D points in a local coordinate system centered on camera c is performed by the function ${\pi }_c:{ℝ}^4\to {ℝ}^3$ defined as ${\widehat{\mathbf{\text{x}}}}_{c,j}={\pi }_c({\widehat{\mathbf{\text{X}}}}_j)$. This function can be expressed as a composition π_c = proj_1,2 ∘ ϕ_c of an affine transformation ${\varphi }_c:{ℝ}^4\to {ℝ}^4$ from global coordinates to camera-centered coordinates and a projection ${\text{proj}}_{1,2}:{ℝ}^4\to {ℝ}^3$ to the first two coordinates. Both functions can be parametrized using the pinhole camera model [61]. On the one hand, we have

$${\varphi }_c({\mathbf{\text{X}}}_j)≔{\mathbf{\text{C}}}_c{\widehat{\mathbf{\text{X}}}}_j^T={\widehat{\mathbf{\text{Y}}}}_{c,j},$$ (2)

where C_c is the extrinsic camera matrix corresponding to the ϕ_c and can be written as

where ${\mathbf{\text{R}}}_c\in {ℝ}^{3\times 3}$ is a matrix corresponding to rotation around the origin and ${\mathbf{\text{T}}}_c\in {ℝ}^3$ is a translation vector representing the distance of the origin of the world coordinate system to the camera center. Likewise, the projection function can be expressed as

$${\text{proj}}_{1,2}{\widehat{\mathbf{\text{Y}}}}_{c,j}≔{\mathbf{\text{K}}\widehat{\mathbf{\text{Y}}}}_{c,j}={\widehat{\mathbf{\text{x}}}}_{c,j},$$ (4)

where K is the intrinsic camera transformation

$$\mathbf{\text{K}}=\left(\begin{array}{cccc}{f}_x& 0& c_x& 0\\ 0& f_y& c_y& 0\\ 0& 0& 1& 0\end{array}\right),$$ (5)

where f_x, f_y denote the focal lengths and c_x, c_y denote the image center. The coordinates projected to the camera plane can be obtained by converting back to Euclidean coordinates ${\mathbf{\text{x}}}_{c,j}=({\widehat{\mathbf{\text{x}}}}_{c,j}^1/{\widehat{\mathbf{\text{x}}}}_{c,j}^3,{\widehat{\mathbf{\text{x}}}}_{c,j}^2/{\widehat{\mathbf{\text{x}}}}_{c,j}^3)$.

Triangulation of the coordinate X _j of joint j with respect to π_c is obtained by minimizing the reprojection error, that is, the discrepancy between the 2D camera coordinate, x _c,j, and the 3D coordinate projected to the camera frame, π_c(X _j). Let V_c be the set of visible joints from camera c. The reprojection error for joint j is taken to be

$$e_{\text{RP}}(j;\{{\pi }_c\})={\displaystyle \sum _c{\chi }_{V_c}(j){\Vert {\mathbf{\text{x}}}_{c,j}-{\pi }_c({\mathbf{\text{X}}}_j)\Vert }_2^2},$$ (6)

where χ_Vc (·) is the indicator function of set V_c of visible keypoints from camera c. The camera projection functions π_c are initially unknown. To avoid having to use a calibration grid, we jointly minimize with respect to the 3D location of all joints and to the camera parameters, a procedure known as bundle adjustment [61]. Given a set of 2D observations, we seek

$$\underset{{\pi }_{c,}{\mathbf{\text{X}}}_j}{\text{min}}{\displaystyle \sum _j{e}_{\text{RP}}(j;\{{\pi }_c\})}.$$ (7)

using a second-order optimization method. For further details, we refer the interested reader to [3].

10.3. LiftPose3D network architecture and optimization

The core LiftPose3D network architecture is similar to the one of [57] and is depicted in Figure 1B. Its main module includes two linear layers of dimension 1024 rectified linear units (ReLU [62]), dropout [58] and residual connections [63]. The inputs and outputs of each block are connected during each forward pass using a skip connection. The model contains 4 × 10⁶ trainable parameters, which are optimized by stochastic gradient descent using the Adam optimizer [64]. We also perform batch normalization [65].

In all cases, the parameters were set using Kaiming initialization [63] and the optimizer was run until convergence—typically within 30 epochs—with the following training hyperparameters: Batch-size of 64 and an initial learning rate of 10^–3 that was dropped by 4% every 5000 steps. We implemented our network in PyTorch on a desktop workstation running on an Intel Core i9-7900X CPU with 32 GB of DDR4 RAM, and a GeForce RTX 2080 Ti Dual O11G GPU. Training time was less than 10 minutes for all cases studied.

10.4. Weak perspective augmentation

To project 2D poses from 3D poses, one needs to know the camera transformation ϕ_c (Eq. (2)), encoded by the extrinsic matix C _c (Eq. (3)) and the projection function projļ ₂ (Eq. (4)), encoded by the intrinsic matrix K (Eq. (5)). In the previous section, we described how to deal with the case when C _c is unknown. In addition, K may also be unknown a priori at test time. Alternatively, one may want to use one of our pre-trained networks on a novel dataset without having to match the camera positioning (focal length, camera-to-animal distance) used to collect the training data. In this case, one may still be able to predict the 3D pose in a fixed camera-centered coordinate frame by assuming that either the camera-to-animal distance or the focal length are large enough to neglect perspective effects and by normalizing the scale of 2D poses. Following Ref. [60], we chose the Frobenius norm to perform normalization on the input 2D poses x_c,j/‖x_c,j‖_F, which is the diagonal distance of the smallest bounding box around the 2D pose. Note, that if the 2D poses are obtained via projections, one may use the unit intrinsic matrix Eq. (5) with f_x = f_y and c_x = c_y = 0 before performing normalization. Here, using c_x = c_y =0 assumes that the 2D poses are centered, which in each of our examples is achieved by considering coordinates relative to root joints placed at the origin. Importantly, the 2D poses must be normalized both at training and test times.

10.5. Camera-angle augmentation

The object-to-camera orientation is encoded by the extrinsic matrix C _c of Eq. (3). When it is unavailable, one can still use our framework by taking 3D poses from the ground truth library and, during training, performing virtual 2D projections around the approximate camera location or for all possible angles. To this end, we assume that the rotation matrix R is unknown, but that the intrinsic matrix K and the object-to-camera distance d are known such that we may take T = (0,0, d)^T. When K or d are also unknown, or dynamically changing, one can make the weak-perspective assumption as described in the next section. Then, instead of training the LiftPose3D network with pairs of 3D poses and 2D poses at fixed angles, we perform random 2D projections of the 3D pose to obtain virtual camera planes whose centers c_x, c_y lie on the sphere of radius d. To define the projections we require a parametric representation of the rotations. Rotating a point in 3D space can be achieved using three consecutive rotations around the three Cartesian coordinate axes x, y, z commonly referred to as Euler angles and denoted by ψ_x, ψ_y, and ψ_y. The rotation matrix can then be written as

$$\begin{array}{ll}\mathbf{\text{R}}={\mathbf{\text{R}}}_{xyz}\hfill & ={\mathbf{\text{R}}}_x({\psi }_x){\mathbf{\text{R}}}_y({\psi }_y){\mathbf{\text{R}}}_z({\psi }_z)\hfill \\ \hfill & =\left(\begin{array}{ccc}1& 0& 0\\ 0& \text{cos}{\psi }_x& -\text{sin}{\psi }_x\\ 0& \text{sin}{\psi }_x& \text{cos}{\psi }_x\end{array}\right)\left(\begin{array}{ccc}\text{cos}{\psi }_y& 0& \text{sin}{\psi }_y\\ 0& 1& 0\\ -\text{sin}{\psi }_y& 0& \text{cos}{\psi }_y\end{array}\right)\left(\begin{array}{ccc}\text{cos}{\psi }_z& -\text{sin}{\psi }_z& 0\\ \text{sin}{\psi }_z& \text{cos}{\psi }_z& 0\\ 0& 0& 1\end{array}\right)\hfill \end{array}.$$ (8)

Given Eq. (2)–(5) we may then define a random projection ${\widehat{\mathbf{\text{x}}}}_j$ on the sphere of radius d of a keypoint with homogeneous coordinate ${\widehat{\mathbf{\text{X}}}}_j$ as

where T = (0, 0, d)^T. Likewise, the 3D pose in camera coordinates can be expressed as

Before training, we fix d, f_x, f_y, c_y, c_y and define intervals for the Euler angle rotations. We then obtain the mean and standard deviation in each dimension for both 2D and 3D poses in the training dataset by performing random projections within these angle ranges. The obtained means and standard deviations are then used to normalize both the training and test datasets.

10.6. Linear domain adaptation

Here we describe the process of adapting a network trained on data from experiment A to lift 2D poses in experiment B. Domain adaptation is also useful if the camera parameters or the distance from the camera are not known and the weak perspective assumption cannot be invoked. Before performing domain adaptation, we first estimate 2D poses from ventral images in domain B, as before. This allowed us to circumvent the difficulties arising from differences in appearance and illumination that are present in the more general image domain adaptation problem [?, 66]. Thus, adapting poses became a purely geometric problem of adjusting proportions and postural differences across domains.

The basis for domain adaptation is to first find a function d ₂ : B|₂ → A|₂, where A|₂ and B|₂ are restrictions of 3D poses in the two domains, to the corresponding 2n-dimensional spaces of 2D poses. This function maps poses in domain B to domain A and makes them compatible inputs for the network trained on poses in domain A. In the scenario that 3D data is available in domain B, we can also find a function d ₃ : B → A where A and B are 3n-dimensional spaces of 3D poses in the two experimental domains. After 3D poses have been obtained in domain A, we map these poses back to domain B by inverting this function.

We now describe how to obtain the functions d ₂ and d ₃, which we denote collectively as d. To find d, we assume that poses in domain B can be obtained by small perturbations of poses in domain A. This allows us to set up a matching between the two domains by finding nearest neighbor 2D poses in domain A for each 2D pose in domain B, ${\mathbf{\text{x}}}_i^B=({\mathbf{\text{x}}}_{i,1}^B,\dots ,{\mathbf{\text{x}}}_{i,n}^B)$. We use 2D rather than 3D poses to find a match because 3D poses may not always be available in domain B. Moreover, the nearest poses in 3D space will necessarily be among the nearest poses in 2D space. Specifically, for each ${\mathbf{\text{x}}}_i^B$, we find a set of k nearest poses in domain A, ${\{\mathcal{\text{N}}{({\mathbf{\text{x}}}_i^B)}_j\}}_{j=1}^k$ such that ${\Vert \mathcal{\text{N}}{({\mathbf{\text{x}}}_i^B)}_j-{\mathbf{\text{x}}}_i^B\Vert }_2<{\Vert \mathcal{\text{N}}{({\mathbf{\text{x}}}_i^B)}_{j+1}-{\mathbf{\text{x}}}_i^B\Vert }_2$. We then use these poses to learn a linear mapping ${\mathbf{\text{W}}}_{BA}\in {ℝ}^{2n\times 2n}$ from domain B to A, where n is the number of keypoints, as before. We can find this linear mapping by first defining a set of p training poses in domain B, ${\mathbf{\text{x}}}_{\text{tr}}^B={\mathbf{\text{x}}}_1^B,\dots {\mathbf{\text{x}}}_p^B$ and writing ${\mathbf{\text{W}}}_{BA}{\mathbf{\text{x}}}_{\text{tr}}^B={\mathbf{\text{x}}}_{\text{tr}}^A$, where ${\mathbf{\text{x}}}_{\text{tr}}^B\in {ℝ}^{dn\times kp}$ and ${\mathbf{\text{x}}}_{\text{tr}}^A\in {ℝ}^{dn\times kp}$ with d = 2 or 3 are matrices defined according to

$$\begin{array}{l}{\mathbf{\text{W}}}_{BA}\left(\underset{k}{\underbrace{\begin{array}{ccc}|& & |\\ {\mathbf{\text{x}}}_1^B& \cdots & {\mathbf{\text{x}}}_1^B\\ |& & |\end{array}}}\cdots \underset{k}{\underbrace{\begin{array}{ccc}|& & |\\ {\mathbf{\text{x}}}_p^B& \cdots & {\mathbf{\text{x}}}_p^B\\ |& & |\end{array}}}\right)=\hfill \\ \left(\mathcal{\text{N}}\underset{k}{\underbrace{\begin{array}{ccc}|& & |\\ {({\mathbf{\text{x}}}_1^B)}_1& \cdots & \mathcal{\text{N}}{({\mathbf{\text{x}}}_1^B)}_k\\ |& & |\end{array}}}\cdots \mathcal{\text{N}}\underset{k}{\underbrace{\begin{array}{ccc}|& & |\\ {({\mathbf{\text{x}}}_p^B)}_1& \cdots & \mathcal{\text{N}}{({\mathbf{\text{x}}}_p^B)}_k\\ |& & |\end{array}}}\right).\hfill \end{array}$$ (11)

Transposing this linear equation yields the linear problem ${({\mathbf{\text{x}}}_{\text{tr}}^B)}^T{\mathbf{\text{W}}}_{BA}^T={({\mathbf{\text{x}}}_{\text{tr}}^A)}^T$. Given that the p training poses are different, ${\mathbf{\text{x}}}_{\text{tr}}^B$ has linearly independent columns and this problem is overdetermined as long as kp > dn. Thus, by least-squares minimization, we obtain ${\mathbf{\text{W}}}_{BA}^T={({({\mathbf{\text{x}}}_{\text{tr}}^B)}^T{\mathbf{\text{x}}}_{\text{tr}}^B)}^{-1}{({\mathbf{\text{x}}}_{\text{tr}}^B)}^T{({\mathbf{\text{x}}}_{\text{tr}}^A)}^T$.

10.7. Experimental systems and conditions

All adult Drosophila melanogaster experiments were performed on female flies raised at 25°C on a 12 h light/dark cycle at 2-3 days post-eclosion (dpe). Before each experiment, wild-type (PR) animals were anaesthetized using CO₂ or in ice-cooled vials and left to acclimate for 10 min. DeepFly3D tethered fly data were taken from [52]. OpenMonkeyStudio macaque data were taken from [53]. LocoMouse mouse data were taken from [54]. CAPTURE rat data were taken from [55]. FlyLimbTracker freely-behaving fly data were taken from [56]. See these publications for detailed experimental procedures. For more information on the datasets including the number of keypoints, poses, animals, resolution, framerate we refer the reader to Table 1.

Table 1. List of datasets used.

Dataset	Views (#)	Lifted keypoints (#)	3D poses (# train/test)	Resolution (px/mm)	Framerate (Hz)	Animals (# train/test)	Source
DeepFly3D (spherical treadmill)	6	24	3.56 × 105/1.98 × 104	117	100	6/2	[3]
OpenMonkeyStudio	62	12	6’581/710	0.15	30	5/1	[4]
Fly in a prism-mirror setup	2	24	8’362/3’416	112	100	3/1	this paper
LocoMouse	2	6	28’840/10’814	2.5	400	30/4	[14]
CAPTURE	6	20	1.58 × 105/5.17 × 104	1	300	3/1	[37]
Fly in a rounded square arena	1	18	n.a.	26	80	n.a./1	this paper
Fly in a pill-shaped arena	1	18	n.a.	203	200	n.a./1	[16]
Drosophila LiftPose3D station	1	18	n.a.	56	80	n.a./1	this paper

10.7.1. Freely behaving Drosophila recorded from two high-resolution views using one camera and a right-angle prism mirror

We constructed a transparent arena coupled to a right-angle prism mirror [35, 69]. The enclosed arena consists of three vertically stacked layers of 1/16” thick acrylic sheets laser-cut to be 15 mm long, 3 mm wide, and 1.6 mm high. The arena ceiling and walls were coated with Sigmacote (Sigma-Aldrich, Merck, Darmstadt, Germany) to discourage animals from climbing onto the walls and ceilings. One side of the enclosure was physically coupled to a right-angled prism (Thorlabs PS915). The arena and prism were placed on a kinematic mounting platform (Thorlabs KM100B/M), permitting their 3D adjustment with respect to a camera (Basler acA1920-150um) outfitted with a lens (Computar MLM3X-MP, Cary, NC USA). Data were acquired using the Basler Pylon software (pylon Application 1.2.0.8206, pylon Viewer 6.2.0.8206). The camera was oriented vertically upwards below the arena to provide two views of the fly: a direct ventral view, and an indirect, prism mirror-reflected side view. The arena was illuminated by four Infrared LEDs (Thorlabs, fibre-coupled LED M850F2 with driver LEDD1B T-Cube and collimator F810SMA-780): two from above and two from below. To elicit locomotor activity, the platform was acoustically and mechanically stimulated using a mobile phone speaker. Flies were then allowed to behave freely, without optogenetic stimulation.

10.7.2. Freely behaving Drosophila recorded from one ventral view at low-resolution

We constructed a square arena consisting of three vertically stacked layers of 1/16” thick acrylic sheets laser-cut to be 30 mm long, 30 mm wide, and 1.6 mm high. This arena can house multiple flies at once, increasing throughput at the expense of spatial resolution (26 px mm^–1). Before each experiment the arena ceiling was coated with 10 uL Sigmacote (Sigma-Aldrich, Merck, Darmstadt, Germany) to discourage animals from climbing onto the ceiling. A camera (pco.panda 4.2 M-USB-PCO, Gloor Instruments, Switzerland, with a Milvus 2/100M ZF.2 lens, Zeiss, Switzerland) was oriented with respect to a 45 ° mirror below the arena to capture a ventral view of the fly. An 850 nm infrared LED ring light (CCS Inc. LDR2-74IR2-850-LA) was placed above the arena to provide illumination. Although the experiment contained optogenetically elicited behaviors interspersed with periods of spontaneous behavior, here we focused only on spontaneously generated forward walking.

The positions and orientations of individual flies were tracked using custom software including a modified version of Tracktor [70]. Using these data, a 138 × 138 px image was cropped around each fly and registered for subsequent analyses.

10.8. 2D pose estimation

DeepFly3D 2D poses were taken from [52]. OpenMonkeyStudio 2D poses were taken from [53]. CAPTURE 2D poses were taken from [55]. LocoMouse 2D poses were taken from [54]. See these publications for detailed 2D pose estimation procedures. In the prism-mirror setup, we split the data acquired from a single camera into ventral and side view images. We hand-annotated the location of all 30 leg joints (five joints per leg) on 640 images from the ventral view and up to 15 visible unilateral joints on 640 images of the side view. We used these manual annotations to train two separate DeepLabCut [59] 2D pose estimation networks (root-mean-squared errors for training and testing were 0.02 mm and 0.04 mm for ventral and side views, respectively). We ignored frames in which flies were climbing the enclosure walls (thus exhibiting large yaw and roll orientation angles). We also removed keypoints with < 0.95 DeepLabCut confidence and higher than 10 px mismatch along the x-coordinate of ventral and side views. FlyLimbTracker data [56] was manually annotated. Images acquired in the new low-resolution ventral view setup were annotated using DeepLabCut [59] trained on 160 hand-annotated images. Due to the low resolution of images, the coxa-femur joints were not distinguishable. Therefore, we treated the thorax-coxa and coxa-femur joints as a single entity.

10.9. Training the LiftPose3D network

An important step in constructing LiftPose3D training data is to choose r root joints (see the specific use cases below for how these root joints were selected), and a target set corresponding to each root joint. The location of joints in the target set are predicted relative to the root joint to ensure translation invariance of the 2D poses.

The training dataset consisted of input-output pose pairs $({\mathbf{\text{x}}}_c^{\text{tr}},{\mathbf{\text{X}}}^{\text{tr}})$ with dimensionality equal to the number of keypoints visible from a given camera c minus the number of root joints r, namely ${\mathbf{\text{x}}}_c^{\text{tr}}\in {ℝ}^{2(|V_c|-r)}$ and ${\mathbf{\text{X}}}^{\text{tr}}\in {ℝ}^{3(|V_c|-r)}$. Then, the training data was standardized with respect to the mean and standard deviation of a given keypoint across all poses.

10.9.1. Tethered Drosophila melanogaster

Of the 38 original keypoints in Ref. [52], here we focused on the 30 leg joints. Specifically, for each leg we estimated 3D position for the thorax-coxa, coxa-femur, femur-tibia, and tibia-tarsus joints and the tarsal tips (claws). Thus, the training data consisted of input-output coordinate pairs for 24 joints (30 minus six thorax-coxa root joints) from all cameras. The training convergence is shown on Extended Data Figure 2A).

10.9.2. Freely behaving macaque monkeys

The OpenMonkeyStudio dataset [53] consists of images of freely behaving macaque monkeys inside a 2.45 × 2.45 × 2.75 m arena in which 62 cameras are equidistant horizontally at two heights along the arena perimeter. We extracted all five available experiments (7, 9, 9a, 9b and 11) for training and testing. Since 2D pose annotations were not available for all cameras, we augmented this dataset during training by projecting triangulated 3D poses onto cameras lacking 2D annotation using the provided camera matrix. We removed fisheye lens-related distortions of 2D poses using the provided radial distortion parameters. We normalized each 2D pose to unit length, by dividing it by its Euclidean norm as well as the 3D pose with respect to bone lengths to reduce the large scale variability of the OpenMonkeyStudio annotations (animals ranged between 5.5 and 12 kg). We set the neck as the root joint during training. We compare our absolute errors to the total body length, calculated as the sum of the mean lengths of the nose-neck, neck-hip, hip-knee, knee-foot joints pairs. Over multiple epochs, we observed rapid convergence of our trained network (Extended Data Figure 2B).

10.9.3. Freely behaving mice and Drosophila recorded from two views using a right-angle mirror

Freely behaving mouse data [54] consisted of recordings of animals traversing a 66.5 cm long, 4.5 cm wide, and 20 cm high glass corridor. A 45° mirror was used to obtain both ventral and side views with a single camera beneath the corridor. 2D keypoint positions were previously tracked using the LocoMouse software [54]. We considered six major keypoints—the four paws, the proximal tail, and the nose. Keypoint positions were taken relative to a virtual root keypoint placed on the ground midway between the nose and the tail. The networks were trained on partial ground truth data following pose alignment, as described in the main text. The networks for Drosophila and mouse training data converged within 30 and 10 training epochs (Extended Data Figure 2C,D).

10.9.4. Freely behaving rat in a naturalistic enclosure

The CAPTURE dataset contains recordings of freely behaving rats in a 2-foot diameter cylindrical enclosure video recorded using six cameras. Motion capture markers on the animal were tracked using a commercial motion capture acquisition program [55] to obtain 2D poses. Out of 20 possible joints, we limited our scope to the 15 joints that were not redundant and provided most of the information about the animal’s pose. The dataset includes 4 experiments recording 3 rats from two different camera setups. Before using LiftPose3D, we removed the distortion from 2D poses using radial distortion parameters provided by the authors. The CAPTURE dataset has many missing 3D pose instances which we handle by not computing the loss corresponding to these keypoints during back-propagation. We selected the neck joint as the single root joint and predicted all of the other joints with respect to this root joint. We observed that LiftPose3D converged within 15 training epochs (Extended Data Figure 2E).

10.9.5. Freely behaving adult Drosophila melanogaster recorded from one ventral camera view

For both the newly acquired low-resolution and previously published high-resolution [56] images of freely behaving flies taken using one ventral view camera, we trained a LiftPose3D network on partial ground truth data acquired from the prism mirror system. For the high-resolution data, we considered the thorax-coxa joints as roots. For the low resolution data, the coxa-femur joints were imperceptible. Therefore, the thorax-coxa joints were selected as roots. The training dataset consisted of coordinate pairs $({\mathbf{\text{x}}}_{\text{ventral}}^{\text{tr}}+\eta ,{\mathbf{\text{z}}}_{\text{side}}^{\text{tr}})$ where ${\mathbf{\text{x}}}_{\text{ventral}}^{\text{tr}}$, ${\mathbf{\text{z}}}_{\text{side}}^{\text{tr}}$ were chosen to represent the annotated ventral coordinates and z-axis depth for the visible joints, as before. Meanwhile, η was a zero-mean Gaussian noise term with a joint-independent standard deviation of 4 px. The role of this noise term was to account for the keypoint position degeneracy inherent in the transformation from high-resolution prism training data to lower-resolution testing data. For the high resolution dataset this noise term was set to zero.

10.10. Comparing joint angles derived from lifted 3D and 2D poses

To illustrate the benefits of using lifted 3D coordinates versus 2D coordinates for kinematic analyis, we derived the joint angles obtained from 3D coordinates along with projected 2D coordinates. Consider the (2D or 3D) coordinates of three consecutive joints in the kinematic chain of one leg with coordinates u, v, w. Then, vectors s₁ = u – v and s₂ = u – w describe adjacent bones. Their enclosed angle is found by the cosine rule, cos^–1(s₁ · s₂/(‖s₁‖ ‖s₂‖)). Due to the uncertainty of 2D and 3D pose estimation, we assumed that keypoint coordinates are Gaussian distributed around the estimated coordinate. As a proxy for the variance we took the variation of bone lengths ||s₁|| and ||s₂|| because they are expected to remain approximately constant owing to the low mechanical compliance of the fly’s exoskeleton (with the exception of the flexible tarsal segments). This allowed us to predict 3D joint angles by Monte Carlo sampling (using 5 × 10³ samples), drawing one sample from each of three distributions and then computing the corresponding joint angle by the cosine rule.

The joint angles derived from lifted and triangulated 3D poses were in close agreement (Extended Data Figure 1, red and blue). The errors were low when comparing angle estimate variances to the amount of joint rotation during locomotor cycles. This shows that that our network learned and preserved body proportions—a remarkable fact given the absence of any skeletal constraints, or temporal information. Furthermore, when comparing the joint angles derived from 3D and 2D poses, we found that the predicted coxa-femur 3D joint angles, β, in the front and hindlegs were of larger amplitude than β’, derived from projected 2D poses. This is expected since the action of these joints has a large out-of-plane component relative to the x-y plane during walking. In the front leg, the predicted tibia-tarsus 3D joint angles, ω, were of smaller amplitude than ω’. Indeed, rotations upstream in the kinematic chain (proximal joints) cause the movement of the whole leg, introducing spurious dynamics in the distal joints when viewed from a projected plane. These results illustrate that 3D poses predicted by LiftPose3D can decouple the underlying physical degrees-of-freedom and avoid spurious correlations introduced by 2D projected joint angles.

Extended Data

Extended data figure 1. Joint angles resulting from lifting compared with 3D triangulated ground truth and 2D projections.

Joint angles α, β, γ, and ω for the front, mid, and hind left legs during forward walking. Shown are angles computed from 3D triangulation using DeepFly3D (blue), LiftPose3D predictions (red), and ventral 2D projections α′, β′, γ′, and ω′ (green). The mean (solid lines) and standard deviation of joint error distributions (transparency) are shown. Joint angles were computed by Monte Carlo sampling and errors were computed using fluctuations in bone lengths.

Extended data figure 2. Training and test loss convergence of the LiftPose3D network when applied to a variety of datasets.

Shown are the absolute test errors of LiftPose3D for all joints as a function of optimization epoch. Note that the test error is sometimes lower than the training error because we do not apply dropout at test time. A Two-camera data of Drosophila on a spherical treadmill (each color denotes a different pair of diametrically opposed cameras). B OpenMonkeyStudio dataset (each color denotes a different training run). C Single-camera data of Drosophila behaving freely in the right-angle prism mirror system. D LocoMouse dataset. E CAPTURE dataset.

Extended data figure 3. Drosophila LiftPose3D station.

A CAD drawing of the LiftPose3D station indicating major components (color-coded). B Photo of the LiftPose3D station. C Electronic circuit for building the illumination module on a pre-fabricated prototyping board. Electronic components and additional wiring are color-coded. D Printed circuit board provided as an alternative to a pre-fabricated board for constructing the illumination module.

Supplementary Material

Video 1. 3D poses lifted for tethered Drosophila walking backwards as viewed from two side cameras.

Videos obtained from cameras 2 (top-left) and 5 (bottom-left). DeepFly3D-derived 2D poses are superimposed. Orange circle indicates optogenetic stimulation of MDNs to elicit backward walking. (right) 3D poses obtained by triangulating six camera views using DeepFly3D (solid lines), or lifted using LiftPose3D and two camera views (dashed lines).

Video 2. 3D poses lifted for tethered Drosophila grooming as viewed from two side cameras.

Videos obtained from cameras 2 (top-left) and 5 (bottom-left). DeepFly3D-derived 2D poses are superimposed. Orange circle indicates optogenetic stimulation of aDNs to elicit antennal grooming. (right) 3D poses obtained by triangulating six camera views using DeepFly3D (solid lines), or lifted using LiftPose3D and two camera views (dashed lines).

Video 3. 3D poses lifted for tethered Drosophila behaving spontaneously with irregular limb movements as viewed from two side cameras.

Videos obtained from cameras 2 (top-left) and 5 (bottom-left). DeepFly3D-derived 2D poses are superimposed. (right) 3D poses obtained by triangulating six camera views using DeepFly3D (solid lines), or lifted using LiftPose3D and two camera views (dashed lines).

Video 4. 3D poses lifted for previously published OpenMonkeyStudio data of a freely moving macaque.

(left) Single image drawn randomly from one of 62 cameras. (middle) Ground truth 3D poses based on triangulation of 2D poses from up to 62 cameras (solid lines), or lifting from a single camera view using LiftPose3D (dashed lines). (right) Error distribution across the 62 cameras for a given pose. Camera locations (circles) are color-coded by error. Gray circles denote cameras for which an image was not available. Green circle denotes the camera from which the image was acquired.

Video 5. 3D poses lifted for freely behaving Drosophila when triangulation is only partially possible.

Single camera images of the ventral (top-left) and side (bottom-left) views. DeepLabCut-derived 2D poses are superimposed. (right) 3D poses obtained by triangulating partially available multi-view 2D poses (solid lines), or by lifting the ventral 2D pose using LiftPose3D (dashed lines).

Video 6. 3D poses lifted for previously published freely behaving mouse data when triangulation is only partially possible.

Side (top-left) and ventral (bottom-left) views of a freely walking mouse. Superimposed are keypoints on the paws, mouth, and proximal tail tracked using the LocoMouse software (blue circles). Using only the ventral view 2D pose, a trained LiftPose3D network can accurately track keypoints in the side view (orange circles).

Video 7. 3D poses lifted for previously published freely behaving rat data with self-occlusions.

(left) Ground truth 3D poses triangulated from six cameras (solid lines) superimposed with LiftPose3D’s predictions using 2D poses from one camera (dashed lines). (right) Images from one camera with 2D poses acquired using CAPTURE are superimposed.

Video 8. 3D poses lifted for low-resolution videos of freely behaving flies when triangulation is impossible.

(top) Three freely behaving Drosophila in a rounded square arena and recorded ventrally using a single low-resolution camera. Of these, fly 0 is tracked, cropped, and rotated leftward. Superimposed are 2D poses for 24 visible joints. (bottom) 3D poses lifted from ventral view 2D poses (x − y plane) permit analysis of leg kinematics in the otherwise unobserved x − z plane.

Video 9. 3D poses lifted for previously published ventral view videos of freely behaving flies when triangulation is impossible.

(top) Video of a freely behaving fly within a pill-shaped arena and recorded ventrally using a single high-resolution camera. (bottom-left) Following tracking, a region-of-interest containing the fly was cropped and rotated to maintain a leftward orientation. Superimposed are 2D poses estimated for 24 visible joints. (bottom-middle) 3D poses obtained by lifting ventral view 2D poses. (bottom-right) 3D poses lifted from ventral view 2D poses (top) permit analysis of leg kinematics in the otherwise unobserved x − z plane (bottom).

Video 10. 3D poses lifted for data from the Drosophila LiftPose3D station.

(left) Video of a freely behaving fly in the LiftPose3D station arena. (middle) Cropped video around the centroid of the tracked fly, registered, and superimposed with 2D pose predictions. (right) Lifted 3D poses obtained using ventral 2D poses.

10.11. Code availability

LiftPose3D code can be installed as a pip package, see https://pypi.org/project/liftpose/, or downloaded at https://github.com/NeLy-EPFL/LiftPose3D.

Custom software to acquire images using the LiftPose3D station is also available at https://github.com/NeLy-EPFL/LiftPose3D.

10.12. Data availability

The experimental data collected for this study can be downloaded at: https://doi.org/10.7910/DVN/KHFAEI