Transport of ellipsoid fibers in oscillatory shear flows: Implications for aerosol deposition in deep airways

Abstract

It is widely acknowledged that inhaled fibers, e.g. air pollutants and anthropogenic particulate matter, hold the ability to deposit deep into the lungs reaching the distal pulmonary acinar airways as a result of their aerodynamic properties; these particles tend to align with the flow and thus stay longer airborne relative to their spherical counterpart, due to higher drag forces that resist sedimentation. Together with a high surface-to-volume ratio, such characteristics may render non-spherical particles, and fibers in particular, potentially attractive airborne carriers for drug delivery. Until present, however, our understanding of the dynamics of inhaled aerosols in the distal regions of the lungs has been mostly limited to spherical particles. In an effort to unravel the fate of non-spherical aerosols in the pulmonary depths, we explore through numerical simulations the kinematics of ellipsoid-shaped fibers in a toy model of a straight pipe as a first step towards understanding particle dynamics in more intricate acinar geometries. Transient translational and rotational motions of micronsized ellipsoid particles are simulated as a function of aspect ratio (AR) for laminar oscillatory shear flows mimicking various inhalation maneuvers under the influence of aerodynamic (i.e. drag and lift) and gravitational forces. We quantify transport and deposition metrics for such fibers, including residence time and penetration depth, compared with spherical particles of equivalent mass. Our findings underscore how deposition depth is largely independent of AR under oscillatory conditions, in contrast with previous works where AR was found to influence deposition depth under steady inspiratory flow. Overall, our efforts underline the importance of modeling oscillatory breathing when predicting fiber deposition in the distal lungs, as they are inhaled and exhaled during a full inspiratory cycle. Such physical insight helps further explore the potential of fiber particles as attractive carriers for deep airway targeting.

1. Introduction

Understanding the dynamics of non-spherical particle suspensions is of interest in many areas both industrial and pharmaceutical, including but not limited to polymer suspensions, fiber composite processes, and pulp and papermaking industry (Champion et al., 2007; Njobuenwu and Fairweather, 2015; Tornberg and Shelley, 2004; Zhang et al., 2005). In the specific context of physiology and the vascular system in particular, it has been previously shown that geometry affects the transport and biodistribution of particles; this includes for example, the strength of adhesion and the internalization rate at the cellular level (Decuzzi et al., 2009). The importance of particle geometry is also noted in the field of aerosol inhalation – an area in which we base the bulk of our emphasis in the present study. Whether natural or anthropogenic (e.g. biomass burning), the majority of inhalable airborne particles are intrinsically non-spherical (Kleinstreuer and Feng, 2013). These include for example soot, asbestos fibers, glass wool and carbon nanotubes. The dynamics of inhaled fibers under various respiratory flows have been vastly investigated (Chen et al., 2016; Chen and Yu, 1991; Högberg et al., 2010; Qi et al., 2015; Tian et al., 2012) both through numerical (Marchioli et al., 2010; Tornberg and Shelley, 2004) and experimental (Qi et al., 2013; Shapiro and Goldenberg, 1993) studies. It was found that fibers tend to align with flow streamlines and when inhaled into the pulmonary system, these remain longer airborne as they somewhat act more closely as passive tracers of the flow (T. Mossman et al., 2011) and thus may deposit deeper into the lungs when compared to spherical particles of equivalent mass (Wang et al., 2005). These unique dynamical behaviors may carry adverse or favorable health outcomes, either as therapeutic aerosols (Chen et al., 2015; Heslinga et al., 2009) or pollutants (Zheng et al., 2016). On the one hand such dynamics, together with a higher surface-to-volume ratio, render anisotropic particles (e.g. fibers) potentially attractive for systemic drug delivery to the alveolar regions; this has been highlighted for example in the various methods available to produce such drug carriers (Champion et al., 2007) and leverage their targeting ability (Mellal et al., 2015). Concurrently, these same attributes may render fibrous particles particularly hazardous. Yang et al. (2016) recently explored the carcinogenetic effects of elongated nephrite particles and showed an association between exposure and increased risk of respiratory and digestive cancers, where ~20% of deposited particles were located in the deep alveolar regions. In the absence of mucociliary clearance, the acinar depths have a lower particle clearance ability compared with conductive airways such that the penetration of large anisotropic particles can often cause inflammation, fibrosis, and even lung cancer (Hamra et al., 2014; Pascolo et al., 2013). Furthermore, the interaction of long fibers (i.e. 10–50 μm) with alveolar tissue may cause alveolar macrophages to perform frustrated phagocytosis and provoke malignant processes as advanced by Sturm (2011).

While our understanding of the health outcomes resulting from fiber deposition on airway tissues has tremendously improved (Boulanger et al., 2014; Donaldson et al., 1989), there remains a gap in our prediction of their transport dynamics leading to deposition in the distal pulmonary regions in the first place. To date, the vast majority of studies exploring non-spherical aerosol transport has been limited to flow phenomena pertinent to the upper airways. Such efforts have been driven mostly by in vitro deposition studies in physical airway models or computational simulations (e.g. computational fluid dynamics). In vitro studies include that of Myojo (1987) who investigated deposition patterns of fibers in single bifurcating tubes and Marijnlssen et al. (1991) who measured nylon fiber deposition in a single bifurcation airway model. More recently, Tian et al. (2012) investigated in experiments and simulations the dynamics of fibers (14–24 μm long) in a circular duct and found that flow shear rate, fiber aspect ratio (AR) and particle-to-fluid density ratio significantly affect the transport and deposition of ellipsoidal fibers. In parallel, in silico studies have extensively complemented the elucidation of the physics of fibrous particle transport. For example, Feng and Kleinstreuer (2013) and Tian and Ahmadi (2013) performed steady flow simulations of micro-fibers of different AR in models of upper airway trees. Their results support that as AR increases deposition efficiency decreases such that fibers will penetrate deeper into the distal lung regions. Further work on the influence of unsteady unidirectional flows on fibers (i.e. 0.01–2.5 μm), where gravitational settling, Brownian motion and interception in a straight channel were considered, concluded that deposition efficiency depends on the time point from which particles are released during the inspiratory cycle (Högberg et al., 2012).

Beyond such progress and available in vivo histological data (Donaldson et al., 1989; Mitchell et al., 2007), a quantification of the transport processes of fibers in the distal pulmonary regions where unsteady oscillatory laminar airflows dominate (Sznitman, 2013) still lacks. Theoretical, numerical and experimental investigations have explored the oscillatory nature of respiratory flows in the context of spheres only. For example, Kojic and Tsuda (2004) investigated analytically the deposition patterns of micron-sized spherical particles under oscillatory flow in a pipe and concluded that gravitational deposition in small airways cannot be approximated by classical solutions based on a steady flow; oscillatory breathing phenomena must be accounted. More recently, Hofemeier and Sznitman (2015) simulated respiratory flows under breathing conditions in models of acinar airway networks and revealed the importance of intrinsic particle dynamics (i.e. diffusion, sedimentation) as a function of particle diameter in determining deposition outcomes of spheres. In parallel, Fishler et al. (2015) designed and fabricated a true-scale microfluidic acinar airway tree model incorporating alveolated ducts that expand and contract in a breathing-like fashion. By comparing the deposition patterns of spherical aerosols to computational results in an identical geometry they provided for the first time an experimental validation for simulation predictions inside a model acinus.

Motivated by ongoing questions on the transport and fate of non-spherical aerosols in the airway depths, we have conducted numerical simulations in a “toy model” of a straight pipe to quantify the unsteady kinematics of airborne fibers under oscillatory breathing. This specific geometry is chosen as a first step towards understanding particle dynamics in more complicated acinar geometries. Here, transient translational and rotational motions of ellipsoid particles are resolved under various oscillatory shear flow configurations (i.e. Womersley velocity profile), representative of distal pulmonary airways. We analyze the dynamics of micron-sized fibers of constant mass (i.e. equivalent to a sphere of 2 μm) for a wide range of aspect ratios AR (i.e. spanning 1 to 30) under the combined influence of aerodynamic drag, lift and gravitational forces. Our findings underline the mutual interplay arising between ellipsoid fibers dynamics and the oscillatory nature of the flow. Strikingly, our simulations reveal that deposition depth is independent of AR under oscillatory conditions, in contrast with previous works where AR was found to influence penetration depth under steady inspiratory unidirectional flow. Overall, our modeling efforts represent a stepping stone towards understanding more realistically the fate of inhaled fibers in the pulmonary depths and their potential as attractive carriers for targeted systemic delivery.

2. Numerical Methods

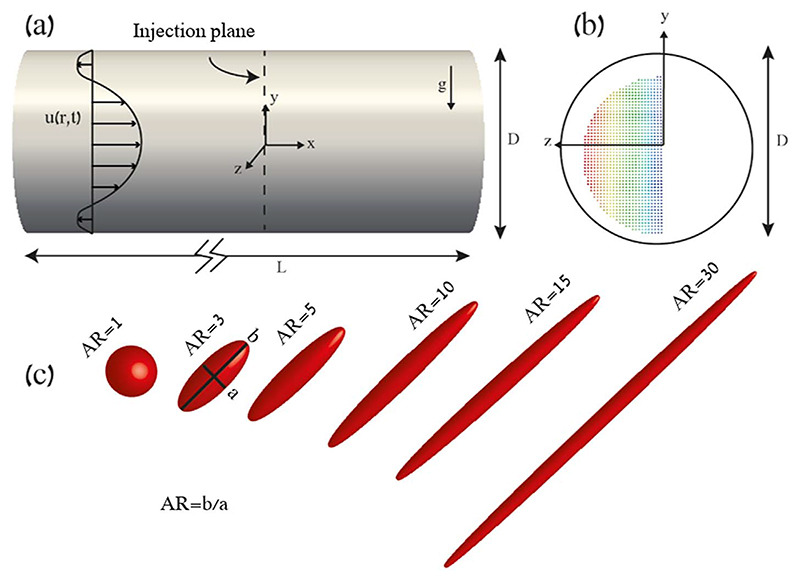
Here, we present numerical simulations of ellipsoid-shaped fibers of different AR, in a simple anatomically-inspired distal airway model. Following pulmonary acinar morphometry (Haefeli-Bleuer and Weibel, 1988), we approximate such deep respiratory bronchioles with a toy model of a circular duct of ~500 μm diameter, as depicted in Fig. 1a–b.

Fig. 1. Numerical setup of the ‘toy model’ for particle simulations of ellipsoids (i.e. fibers).

(a) Schematic of the setup: a tube of length L and diameter D is considered (with L > > D). The injection plane represents the initial location of the particles (t = 0). The Womersley velocity profile is denoted as u(r,t). Note the direction of gravity in the negative y-direction. (b) Cross-sectional view of the tube with the initial location of the particles at t = 0. Color coding of particles (from blue to red) indicates their initial position in the y–z plane. (c) Rendering of ellipsoid particles of fixed volume with varying aspect ratio (AR). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Respiratory oscillatory flows are mainly governed by two non-dimensional numbers: the Womersley number ($Wo=D\sqrt{\omega /\nu }$), capturing the importance of unsteady acceleration through the ratio of the oscillation frequency to viscous effects, and the Reynolds number (Re = UD/ν), capturing the importance of inertia through the ratio of inertial forces to viscous forces. Here, D represents the distal airway diameter, ω is the angular breathing frequency with ω = 2πf (f is the breathing frequency), ν is the fluid’s (i.e. air) kinematic viscosity, and U is a characteristic scale of the fluid velocity (i.e. peak velocity). Within the frame of our toy model, airflow is assumed to be described by a fully-developed, one-dimensional oscillatory flow profile u(r,t) according to the general Womersley solution (Womersley, 1955), valid throughout the domain including the inlet and outlet. The pressure gradients from which the Womersley solution arise are defined as a transient sinusoidal pressure gradient wave with an amplitude chosen to match physiological values of Re, where the peak Reynolds number in terminal bronchioles at the entrance of the acinus is assumed to reach about Re = 0.3 (Hofemeier and Sznitman, 2015). Air inhaled into the distal lungs is assumed to be incompressible, Newtonian and isothermal (Sznitman, 2013). For completeness and in order to shed light on the dynamics of such fibers under oscillatory laminar flows at higher Re, higher pressure gradients are simulated as well such that Re = 0.3, 1, 3, 30 and 300; note that these higher Re values do not capture per se physiological flows of the distal airways only but may also be relevant for flows in the cardiovascular system (Bluestein et al., 1996), although baseline patterns are pulsatile rather than sinusoidal. For the wall boundary conditions, a no-slip condition is implemented on the domain walls. Breathing maneuvers are described by sinusoidal flow with three different oscillation frequencies mimicking slow breathing (with f = 0.25 Hz and Wo = 0.16), normal breathing (with f = 0.33 Hz and Wo = 0.19) and heavy breathing (with f = 1 Hz and Wo = 0.33). For Wo ² ≪ 0.1, we anticipate the influence of the unsteadiness to be weak such that velocity profiles are nearly quasi-steady. Nevertheless, for Wo = 0.33 changes in the boundary layer begin to appear.

Ellipsoid-shaped fibers with a density of 1000 kg/m³ and an equivalent mass (i.e. volume) of a 2 μm sphere were simulated. We have explicitly chosen such size (i.e. 2 μm) as these particles are known to have the ability to deposit in the acinar regions (Sznitman, 2013). Concurrently, for such particle diameters Brownian motion may be safely neglected (Hofemeier and Sznitman, 2015); a transport mechanism mostly relevant for submicron particles that lies beyond the scope of the present study. The aspect ratio of our simulated fibers spans AR ≈ 1 (representing a sphere) to 30, equivalent to elongated rods (see Fig. 1c). Specifically, our algorithm is based on modeling the dynamics of ellipsoids (see Appendix) such that we chose AR = 1.002 to closely approximate a sphere; solving explicitly for AR = 1 would lead otherwise to a singularity. Our results for AR = 1.002 are nevertheless within 0.1% of analytical predictions for spheres.

For micron-sized airborne particles in the absence of electrostatic forces, transport dynamics are hence foremost governed by viscous drag, aerodynamic lift and gravity (in the negative y-direction; see Fig. 1a). Namely, we implement an Euler-Lagrangian model where a discrete element method (DEM) based on the Euler Rotational Equation Method (EL–ER) is used to solve the spatial-temporal forces and corresponding torques operating on the fiber according to its orientation relative to the flow, as recently described (Kleinstreuer and Feng, 2013). Drag forces as well as lift forces are modified in time and space according to the particle orientation and the surrounding velocity gradients of the flow field. Thus, Euler’s rotation equations combined with the translation equations are solved to achieve proper particle tracking (see Appendix for details). Six groups representing different ARs, each containing 1000 particles, are introduced as a uniform Cartesian mesh along half of the x = 0 line (due to symmetry) in an effort to capture the detailed kinematics and ensuing statistics for particles emanating from any representative location on the cross section (see Fig. 1b). Particles are initially positioned orthogonal to the streamwise flow direction; we assume that initiating the particles parallel to the flow yields no sensitive change in transport and deposition outcomes, since particles orthogonal to the flow are subjected to high moments that lead to fast alignment with the flow (Feng and Kleinstreuer, 2013). In particular, we investigate the deposition characteristics of fibers (relative to equivalent spheres) including deposition efficiency, residence time and dispersion. The DEM algorithm is implemented within a commercial solver (Ansys Fluent) as a user-defined function (UDF). As an analytical flow field is implemented, the flow solver is not necessary in the present study. Rather, our DEM strategy is intended for ease of implementation in view of future studies.

A thorough numerical validation study was first performed against the works of (Feng and Kleinstreuer, 2013; Tian et al., 2012) by simulating trajectories of a single particle with AR = 14 (matching published values) in a circular duct with D = 500 μm and L = 700 μm under unidirectional Poiseuille flow and the influence of gravity, where the initial position of the particle and the characteristic Re were identically matched. Differences in results (not included for brevity) are < 0.5% of those of Feng and Kleinstreuer (2013); Tian et al. (2012).

3. Results and Discussion

Previous works have examined the transport of fibers under unidirectional flow, either steady (Chen and Yu, 1991; Feng and Kleinstreuer, 2013; Tian et al., 2012) or more rarely unsteady (Högberg et al., 2012). Here, we present the dynamics and deposition of such particles immersed in oscillatory shear flow. Our numerical campaign focuses on fibers, characterized by six values of AR (Fig. 1c) undergoing different oscillatory flow conditions, captured by a combination of five distinct Re and three Wo values. To gain some initial insight, we begin by giving a qualitative overview of the dynamics of such fibers. Namely, to showcase representative motions of the studied cases simulations for Re = 0.3 and Wo = 0.16 are presented in Fig. 2 at the specific time instants t = T/4, 2T and 4T. Supplementary Material (SM) Video 1 is available to the reader for renderings of the resulting particle dynamics.

Fig. 2.

Time lapse sequence of particle locations under oscillatory shear flow shown at representative Re = 0.3 and Wo = 0.16. Instantaneous positions of airborne (blue) and deposited (red) particles are shown at three representative time instants, i.e. t = T/4 (left column), 2T (mid column) and 4T (right column). Three representative values of AR are illustrated: AR = 1 (top row), 5 (mid row) and 30 (bottom row). Shown in each tube is a cross section of the y–z plane (see Fig. 1b). See SM Videos 1 for dynamic renderings of the resulting particle dynamics. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We first note that fibers with AR = 5 (middle row) and 30 (bottom row) tend to align with the flow streamlines and rotate around the z-axis, either during flow reversals or when subjected to high shear rates close to the wall. Such general trends agree with Qi et al. (2015), where the absolute mean angular velocity of fibers increases significantly as they get closer to the region of highest shear, i.e. far from the main axis of the tube. Of interest, similar results were also found in an experimental study related to the papermaking industry (Carlsson, 2009), where it was shown that far from the wall most fibers were oriented close to the flow direction. Closer to the wall, within less than half a fiber length, the orientation distribution first shifted towards being more isotropic and in the very proximity of the wall the fibers were nearly oriented perpendicular to the flow direction, and thereby aligned with the vorticity axis. In parallel, we qualitatively observe that as AR increases the terminal velocity decreases as particles appear to deposit at slower rates. At T/4 (Fig. 2, first column), particles are positioned in a parabolic shape that reflects the quasi-steady velocity profile. As the fibers continuously fall in the negative y-direction, aerosols in the upper half of the tube approach faster streamlines near the tube centerline. In contrast, airborne particles in the lower half gradually approach the bottom walls and are thus subjected to slower streamlines. After two cycles (Fig. 2, second column), particles align along a diagonal line that results from sedimentation under gravity. Qualitatively, during each flow reversal one may observe wave-like deposition patterns underlining each cycle (i.e. sand ribbons; Fig. 2, second and third column). Focusing our attention on the cross section of the y-z plane, fiber rotation leads to some degree of radial and tangential mixing; a phenomenon recently described by Njobuenwu and Fairweather (2014), where ellipsoids and disks of various sizes were simulated in a channel flow, revealing higher dispersion of fibers orthogonal to the streamwise flow direction compared to spheres.

3.1. Single Particle Dynamics

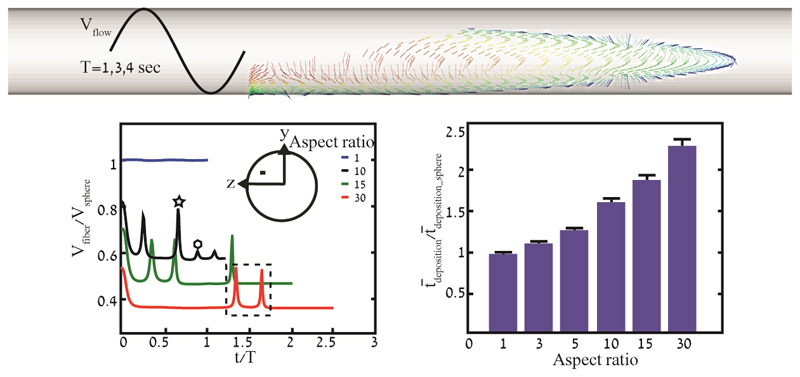
Next, we proceed to analyze quantitatively the transport problem from the perspective of single particle dynamics. Dynamics of fibers (AR = 1, 10, 15 and 30) were examined by monitoring settling velocities and trajectories under oscillatory flow. The case of Re = 0.3 and Wo = 0.095 is arbitrarily chosen for representative dynamics; trends for the other cases are found to be similar and not shown here for brevity. Individual particles originate from a chosen initial position (Fig. 3a, inset), i.e. x = 0,y = 85 μm and z = 173 μm, and oscillate at least 1 full breathing cycle until deposition. This specific initial position was selected because it deviates from the symmetry plane, but also as particles beginning from this location cross the x-z plane in less than one breathing cycle. The settling velocity (V), normalized by the mean settling velocity of an equivalent sphere (V_sphere), is presented in Fig. 3a. In general, higher drag forces in the – y direction resulting from a larger surface area relative to spherical particles resist gravity such that terminal velocities are reduced with increasing AR. This observation is rather counterintuitive from our intuition at larger scales (Re ~10⁴) where a fiber would fall faster than a sphere due to lower drag with increasing aspect ratio. As the particles rotate and are momentarily vertically aligned parallel to gravity (– y), the drag force decreases such that settling velocity increase (see dashed box in Fig. 3a and b). Similar motions for ellipsoidal particles have been previously reported under steady flow conditions (Feng and Kleinstreuer, 2013).

Fig. 3.

Unsteady particle dynamics under oscillatory shear flow at Re = 0.3 and Wo = 0.095. Four representative values of AR are exemplified, i.e. AR = 1 (blue), 10 (black), 15 (green) and 30 (red). Particles originate at a fixed chosen initial position, i.e., and experience at least 1 full oscillatory cycle. (a) Time evolution (until deposition) of the settling velocity normalized by the mean settling velocity of an equivalent sphere. The area highlighted (i.e. dashed box) captures unsteady fluctuations in the settling velocity of the particle as a result of the particle flipping (as shown in (b)). Inset: initial location of the particle in the cross-sectional z–y plane. (b) Corresponding trajectories of the selected particles in the x–y plane normalized by the tube diameter. The area highlighted (i.e. dashed box) showcases the instantaneous orientation of a particle during flipping. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

High and low peaks in the velocity plot (Fig. 3a) represent respectively full particle flips and partial flips during flow reversal, while the amplitude of the peaks (relative to a fiber’s baseline terminal velocity) depends on the maximum angle the particle reaches relative to the streamwise flow direction (x). The maximal angle achieved when particles are parallel to gravity (– y) is 90° (Fig. 3a, star), whereas any smaller angle represents rotations < 90° (Fig. 3a, polygon). For example, the maximal peak in the velocity plot at AR = 10 captures the orientation of the fiber perpendicular to gravity and is ~ 37% higher than the baseline velocity. Overall, in both orientations (i.e. parallel and orthogonal to the streamwise flow), the drag force of a fiber is higher than that of a sphere; thus, spheres will always deposit faster (Fig. 3a). Namely, the settling velocity of fibers is analytically a function of ‘K⁻¹’ (see Appendix), that reflects the resistance tensor of the fibers and more specifically the geometry (AR) and orientation of the fiber at each time step.

Examples of trajectories of the selected particles in the x-y plane normalized by the tube diameter (Fig. 3b) qualitatively emphasize how much longer aerosolized particles of high AR are compared to spheres as they experience more breathing cycles before depositing. In the area highlighted (Fig. 3b, dashed box), instantaneous renderings of the particle orientations and their corresponding flipping motion are presented. In addition, the small yet finite amount of radial and tangential mixing observed earlier (Fig. 2) leads particles to deposit at different spanwise locations in the y-z cross section (see different final y/D values in Fig. 3b), where we recall that all the particles trajectories shown in Fig. 3 originated from the same initial point.

3.2. Deposition Patterns and Residence Time

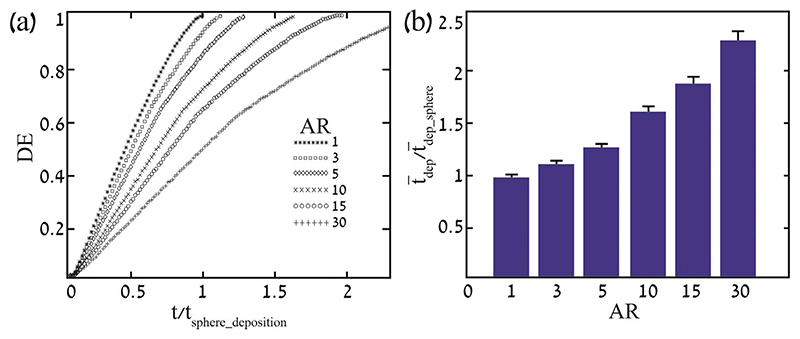
Next, we present particle statistics for deposition efficiency and residence time (i.e. time to deposition) in Fig. 4. Deposition efficiency (DE) of fibers with AR = 1, 3, 5, 10, 15 and 30, as a function of time normalized by the maximum residence time for a sphere (t_sphere ~4 s) underline how fibers tend to stay longer airborne in the domain as AR increases (Fig. 4a). This results from higher drag forces that resist gravity and inhibit sedimentation rates. As shown in Fig. 4b, the average residence time of fibers ($\overline{t}$ _dep) normalized by that of spheres ($\overline{t}$ _{dep_sphere}) increases with ’K’ that again reflects the resistance tensor (see Appendix). Our results corroborate with the lower deposition efficiency of fibers previously discussed in the works of (Feng and Kleinstreuer, 2013; Su and Cheng, 2006). Furthermore, we note that as AR increases the standard error SE (Fig. 4b) in the normalized average deposition time increases from 0.03 to 0.09, emphasizing that more elongated particles give rise to higher variance in the time till deposition, although relative to the average residence time SE is limited within a small range (i.e. 3.2%–3.8%). Not surprisingly, we also note that the narrow span of dimensionless oscillating frequencies investigated (Wo = 0.16 to 0.33) does not give rise to significant differences in the resulting residence times of the particles.

Fig. 4. Deposition statistics for the particle ensembles.

(a) Deposition efficiency (DE) as a function of time for particles of different AR. Deposition time is normalized by the maximum residence time for a sphere (i.e. 4 s). (b) Mean normalized deposition time versus AR. Error bars represent resulting standard error (SE) for different Womersley numbers. Deposition time is normalized by the mean residence time for spheres (i.e. 1.8 s).

Turning our attention to the final deposition sites (SM, Video 1), these appear to be largely independent of AR although fibers stay longer airborne. Indeed, they are inhaled and exhaled to the same depths and maintain identical deposition patterns. While previous studies (Chen et al., 2016; Feng and Kleinstreuer, 2013; Kleinstreuer and Feng, 2013; Mossman et al., 2011) have shown that as AR increases fibers are able to penetrate deeper, here we emphasize the significance of the oscillatory characteristic of the flow and how fundamentally it affects deposition as particles are potentially washed in and out of the lung depths. With regards to the different ventilation frequencies, spherical particles and ellipsoid fibers travel deeper into the duct as frequency decreases, assuming the inhaled volume is also decreased. Concurrently, dispersion in deposition tends to grow such that particles deposit over a wider space; this is shown in SM Video 2 where we showcase a fiber of AR = 5 under different Wo conditions.

As anticipated for laminar flows, an increase in Re results in a larger deposition depth (directly proportional to Re), whereas no effect on residence time was found (not shown for brevity). Xu et al. (2009) studied numerically and experimentally the deposition of spherical particles in a single bifurcation tube under oscillatory conditions and concluded that both oscillation frequency and flow rate affect deposition. Kojic and Tsuda (2004) concluded that the effects of oscillatory flow must be taken into account in the analysis of gravitational deposition for small airways, when the sedimentation time of spherical particles becomes non-negligible compared to the carrier flow oscillatory time, in analogy to this study.

To summarize our findings, the parameters that reflect flow properties (i.e. Re and Wo) affect indiscriminately particle deposition sites, whether spheres or ellipsoids, independent of AR. The likely explanation lies in the short relaxation time of such particles (i.e. Stokes number is in the range of ~ 10 ^–3) that would cause particles of all AR to follow streamlines as ideal tracers in the absence of gravity. On the other hand, the parameter that reflects the particle geometry (i.e. AR) affects strongly residence time since the drag force orthogonal to the streamwise flow direction changes significantly with AR.

3.3. Limitations and Outlook

We briefly comment on some of the limitations in the present study. Although the investigated geometry was selected to capture generic features representative of the distal airway dimensions where flow characteristics were chosen to match physiological breathing conditions, we recall that our “toy model” represents a mere straight tube and as such holds broader ramifications in describing fiber transport. Anatomically, however, the pulmonary acinar regions (i.e. starting from respiratory bronchioles) comprise intricate bifurcating networks spanning multiple generations where alveoli densely populate the acinar ducts (Haefeli-Bleuer and Weibel, 1988; Weibel et al., 2005). As discussed in recent CFD studies simulating the fate of spherical particles in acinar networks undergoing wall motion (Hofemeier and Sznitman, 2015, 2016), aerosols undergo complex transport dynamics upon entering alveolar cavities that reflect the mechanistic coupling between alveolar flow topologies and intrinsic particle motion (e.g. sedimentation); a phenomenon that was also experimentally observed and quantified in vitro (Fishler et al., 2015). An important limitation of our model lies in the single-generation airway. In reality, airborne particles are anticipated to travel in and out through multiple generations within a single breath. In turn, the simulated path lengths of aerosols within realistic alveolar networks are likely to be longer; we thus anticipate that gravity (and diffusion for sub-micron particles) will result in larger dispersion. Nevertheless, how local transport dynamics are precisely modified for inhaled fibers remains still widely unexplored. Such knowledge will ultimately help improve our understanding of the local deposition patterns anticipated in the alveolar regions and how long fibers (e.g. asbestos) have the ability to lodge within alveoli (Pascolo et al., 2013).

Our DEM model assumes that fibers deposit as the center of mass of the particle contacts the airway wall. While such limitation has little influence on the deposition outcomes in a simple straight pipe, interception constitutes in reality one of the leading mechanisms for fiber deposition (i.e. fibers deposit by intersecting their ends with the airway walls). Previously, this mechanism has been shown to be particularly significant in the upper respiratory tract where flows of high velocity encounter large directional changes due to the 3D bifurcating nature of the airway tree (Balásházy et al., 1990). In the distal acinar regions, we anticipate that such mechanisms may nevertheless be prevalent due to the presence of alveolar structures. Indeed, the oscillatory nature of respiratory flows operating in sub-millimeter acinar structures raises the opportunity for fibers to align with flow streamlines and sediment slower (Fig. 3), until depositing during flow reversal (Fig. 2) and eventually intercepting airway walls.

Finally, there has been increasing interest in predicting the outcomes of inhaling nano-scale fibers, including carbon nanotubes, where deposition is strongly influenced by Brownian motion (Högberg et al., 2012). Within the scope of the present study we have limited our efforts to micron-sized ellipsoid fibers in the absence of diffusion. Since oscillatory flows undergo a short transition period near flow reversal where convective velocities are close to and cross zero, the role of such transport mechanism will be more accentuated when simulating realistic breathing conditions. Taken together, the aforementioned points underscore a number of avenues remaining to extensively map and quantitatively assess the potential of ellipsoid-shaped fibers as attractive drug carriers for inhalation therapy.

4. Conclusions

We have explored in numerical simulations the dynamics and deposition of micron-sized ellipsoid fibers when subjected to oscillatory shear flow. Fibers of different AR (i.e. 1–30) were simulated for a range of laminar flow velocities (Re) and low oscillation frequencies (Wo) in a straight tube mimicking distal pulmonary airways undergoing various breathing maneuvers. Overall, we show how the residence time of fibers increases with AR due to larger viscous drag forces in the spanwise direction that resist sedimentation. As Re increases and Wo decreases, ellipsoid fibers of all AR are observed to deposit deeper. Unlike previous studies that have focused on unidirectional flows, fibers however do not penetrate deeper compared to spheres but remain longer airborne. Hence, although fibers have the potential to penetrate deeper into the lungs during inhalation, they are also more prone to be subsequently exhaled. Therefore, higher overall deposition of fibers in deeper airways may not be equally true for all particle sizes. These findings emphasize the importance of considering the oscillatory characteristics of breathing when studying deposition of fibers in the distal regions of the lungs.

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.ejps.2017.09.023.