Endpoints for randomized controlled clinical trials for COVID-19 treatments

Abstract

Background

Endpoint choice for randomized controlled trials of treatments for novel coronavirus-induced disease (COVID-19) is complex. Trials must start rapidly to identify treatments that can be used as part of the outbreak response, in the midst of considerable uncertainty and limited information. COVID-19 presentation is heterogeneous, ranging from mild disease that improves within days to critical disease that can last weeks to over a month and can end in death. While improvement in mortality would provide unquestionable evidence about the clinical significance of a treatment, sample sizes for a study evaluating mortality are large and may be impractical, particularly given a multitude of putative therapies to evaluate. Furthermore, patient states in between “cure” and “death” represent meaningful distinctions. Clinical severity scores have been proposed as an alternative. However, the appropriate summary measure for severity scores has been the subject of debate, particularly given the variable time course of COVID-19. Outcomes measured at fixed time points, such as a comparison of severity scores between treatment and control at day 14, may risk missing the time of clinical benefit. An end-point such as time to improvement (or recovery) avoids the timing problem. However, some have argued that power losses will result from reducing the ordinal scale to a binary state of “recovered” versus “not recovered.”

Methods

We evaluate statistical power for possible trial endpoints for COVID-19 treatment trials using simulation models and data from two recent COVID-19 treatment trials.

Results

Power for fixed time-point methods depends heavily on the time selected for evaluation. Time-to-event approaches have reasonable statistical power, even when compared with a fixed time-point method evaluated at the optimal time.

Discussion

Time-to-event analysis methods have advantages in the COVID-19 setting, unless the optimal time for evaluating treatment effect is known in advance. Even when the optimal time is known, a time-to-event approach may increase power for interim analyses.

Introduction

Designing clinical trials for treatments for novel infectious disease brings many challenges, especially during a rapidly evolving pandemic. A new disease brings uncertainties arising from an imperfect understanding about the illness, little information about putative treatments, and complexities in measuring relevant patient outcomes. A pandemic adds an overloaded medical system with limited resources for research, heightened pressure to find effective treatments quickly, and unpredictability about potential case numbers. Studies need to start quickly for enrollments to track the epidemic curve. However, early on, information about endpoints may be lacking. This means trial design should be appropriately flexible to respond to new information, but without compromising scientific rigor.

COVID-19 has a heterogeneous presentation and clinical course, ranging from asymptomatic to critical disease (Table 1).¹ While most infected patients present with asymptomatic or mild disease, some develop severe or critical illness that can result in acute respiratory distress syndrome and death. The most common symptoms are fever, dry cough, dyspnea, chest pain, fatigue, and myalgia, while less common symptoms are headache, dizziness, abdominal pain, diarrhea, nausea, and vomiting. Most patients present with signs of bilateral pneumonia.² Neurologic symptoms including taste and smell disorders have been reported, with rare case reports of severe central nervous system affections.³ Thrombotic complications in critically ill patients have also been observed.⁴ Importantly, some COVID-19 patients recover quickly with limited (or no) complications, while patients suffering from severe disease may take 6–8 weeks (or longer) for full recovery.⁵ This broad range of disease severity makes finding a common endpoint for all COVID-19 trials impractical. Endpoints for a study population representing a broad spectrum of disease may be different than those for a study with a narrow spectrum of disease.

Table 1. NIAID disease severity categories and WHO ordinal scale.

NIAID disease severity categories	WHO ordinal scale
Asymptomatic/presymptomatic infection : Individuals who test positive for SARS-CoV-2 but have no symptoms	0- Uninfected, no clinical or virological evidence of infection
Mildillness : Individuals who have any of various signs and symptoms (e.g. fever, cough, sore throat, malaise, headache, muscle pain) without shortness of breath, dyspnea, or abnormal imaging	1- Ambulatory, no limitation on activities
Moderateillness : Individuals who have evidence of lower respiratory disease by clinical assessment or imaging and a saturation of oxygen (SaO2) >93% on room air at sea level	2- Ambulatory, limitation on activities
Severeillness : Individuals who have respiratory frequency >30 breaths per minute, SaO2 ≤ 93% on room air at sea level, ratio of arterial partial pressure of oxygen to fraction of inspired oxygen (PaO2/FiO2) <300, or lung infiltrates >50%	3- Hospitalized, mild disease, no oxygen therapy
Criticalillness : Individuals who have respiratory failure, septic shock, and/or multiple organ dysfunction	4- Hospitalized, mild disease, oxygen by mask, or nasal prongs
	5- Hospitalized, severe disease, noninvasive ventilation or high-flow oxygen
	6- Hospitalized, severe disease, intubation, and mechanical ventilation
	7- Hospitalized, severe disease, ventilation, and additional organ support—pressors, RRT, ECMO
	8- Death

NIAID: National Institute of Allergy and Infectious Diseases; WHO: World Health Organization; SARS-CoV-2: severe acute respiratory syndrome coronavirus 2; RRT: renal replacement therapy; ECMO: extracorporeal membrane oxygenation.

We describe key considerations for selecting endpoints for COVID-19 treatment trials. We evaluate endpoints according to clinical relevance, ease, and reliability of measurement, interpretability of its associated statistical analysis, and statistical efficiency. We discuss the differences between fixed time-point endpoints and those that naturally incorporate changes over time. We evaluate the statistical efficiency of multiple approaches with simulation models, as well as using data from two published COVID-19 randomized trials.^6,7

Methods

Endpoint selection

Treatments for COVID-19 are intended to be curative, with the goal that the patient will survive and ultimately return to normal function. This contrasts with a disease such as stroke in which the goal of a treatment may be to reduce stroke-induced impairments that occur across a spectrum.⁸ Likewise, a benefit on mortality would be strong evidence of an effect, but deaths are relatively rare. A study powered for mortality benefit would require a large sample size. For example, a sample size of around 2000 is needed (for a two-arm study) to detect a hazard ratio (for death) of 0.65 with 85% power and a type I error rate of 5% with a 10% mortality rate. Lower mortality rates require even larger studies. In a setting with multiple putative therapies, studies powered for mortality will restrict the number of therapies evaluated, which may slow provision of effective treatments to support the outbreak response.

Furthermore, multiple clinical states in between “death” and “cure” represent meaningful patient states. The World Health Organization (WHO) proposed an ordinal scale ranging from death to full health, with states in between corresponding to the need for hospitalization, oxygen support (including type of support needed), and need for additional medical support (Table 1).⁹ These states are important markers of how a patient feels and of disease progression (or improvement). Mechanical ventilation (intubation) marks a considerable worsening, as intubated patients often require treatment with sedatives and even paralytics to address patient discomfort and maximize therapy. Intubation is also associated with a host of complications leading to additional mortality and morbidity, such as ventilator-associated pneumonia,¹⁰ gastrointestinal (GI) bleeding,¹¹ and severe physical deconditioning. In a case series of 5700 COVID-19 patients in New York, considerable numbers of patients remained intubated during the entire study.¹² Shortening the duration in a state like intubation or avoiding intubation altogether is of direct clinical benefit.

Timing of endpoint evaluation is another important consideration. A treatment effect that occurs early but dissipates over time may not be clinically meaningful. A treatment effect may be missed if evaluation is too early, before an intervention has had time for an effect. Timing of measurement is therefore crucial and can be particularly challenging in a novel disease with substantial heterogeneity. Time-to-event endpoints do not require specifying a fixed time (just the observation interval) and are more robust in this regard. We note that longitudinal models of other endpoints are possible, such as a mixed-effects proportional odds model,¹³ but are not commonly used.

Table 2 describes multiple endpoints considered for COVID-19, largely from the perspective of a definitive (Phase 3) trial. Endpoints for earlier phase studies may focus on evaluating mechanism (e.g. targeting a specific pathway) or evaluating activity so that “go/no-go” decisions for further evaluation in larger trials can be made. Endpoints are evaluated according to ease of measurement, reproducibility, whether they are clinically meaningful, and their ability to capture multiple clinical states and the time-course of disease.

Table 2.

Possible endpoints for trials in COVID-19, corresponding target population, categorization of whether the endpoint is clinically meaningful, captures the diverse nature of disease, easy to measure, and reproducible.

Endpoint	Example	Population	Clinically meaningful	Multiple disease states	Time element	Easily measurable	Reproducibility	Additional comments
Binary outcomes Mortality	Death by 28	Moderate Severe Critical	+	○	○	+	+	+ Most relevant in severe/critical disease − May miss other meaningful improvements in patient status − Requires large sample size
Recovery(discharge, discharge-eligible)	Recovered by day 28	Moderate Severe	+	○	○	+	○	− May require long observation times in higher severity populations − Deaths require special consideration
Respiratory failure	ECMO or mechanical ventilation	Moderate Severe	+	○	○	+	○	− Depends on resources − Deaths require special consideration
Hospitalization	Admission within 28 days	Mild	+	−	○	+	○	− Depends on resources − Does not capture improvement − Deaths require special consideration
ICU admission	Admission within 28 days	Moderate	+	−	○	+	○	− Depends on resources − Does not capture improvement − Deaths require special consideration
Ordinal outcomes Ordinal disease severity scale	WHO scale at a fixed day	Moderate Severe	+	+	−	○	○	− Depends on resources − Defining clinical benefit less straightforward
Time-to-event outcomes Time to recovery	Time to discharge or eligible for discharge	Moderate Severe	+	○	+	+	○	− Depends on resources − Potential for “relapse” (sustained improvement removes this concern) − Deaths require special consideration
Time to 1- or 2-point improvement in ordinal scale1	Time to 2-point improvement }in WHO ordinal scale	Moderate Severe Critical	+	○	+	○	+	− Changes in categories must be meaningful and should be considered equally important − Potential for “relapse” (sustained improvement removes this concern)
Time to intubation or death		Moderate Severe	+	-	+	+	○
Continuous outcomes National Early Warning Score (NEWS score)		Moderate Severe	○	+	○	−	+	+ Familiar measure − Not disease-specific and hence not as sensitive to certain aspects of COVID − Deaths need special consideration
Viral load/viral clearance		Mild Moderate Severe Critical	−	○	○	−	−	− Difficult to reliably measure − Relation to clinical outcomes not well established − Deaths need special consideration
Oxygen, SpO2/FiO2 or paO2/FiO2	Daily SpO2/FiO2 until discharge, death or 28 days	Mild Moderate	○	○	○	−	+	− Relation to clinical outcomes not well established − Modified by oxygen supplementation − SpO2/FiO2 not well-validated − paO2/FiO2 only broadly available for ICU patients + Deaths need special consideration
Duration of a specific ordinal state	Hopitalization days; mechanical ventilation days	Severe Critical	○	−	○	+	○	+ Captures dimension meaningful to health system + Depends on the resources available + Deaths need special consideration
FLU-PRO	Change from baseline to day 14	Mild Moderate Critical	○	+	−	○	○	+ Captures aspects important to patients − Deaths need special consideration − Not validated for COVID-19
SOFA score	Change from baseline to day 14	Severe Critical	○	+	−	○	+	+ Captures disease severity and incorporates most relevant organ systems − Familiar for ICU setting − Not validated for COVID-19 and not disease-specific − Deaths need special consideration

COVID-19: coronavirus-induced disease; ECMO: extracorporeal membrane oxygenation; WHO: World Health Organization; ICU: intensive care unit; FLU-PRO: InFLUenza patient-reported outcome; SOFA score: sequential organ failure assessment score.

“ + “ indicates good performance; “−“ indicates poor performance on this characteristic; neutral is denoted by “○.”

Meaningfulness and reproducibility can be distorted when states are influenced by external factors, as may happen when patient numbers exceed hospital capacity. For example, ordinal categories become less meaningful when mechanical ventilators are not available and patients who would normally be in this category are shifted to others (or when guidelines recommending early intubation are followed more rigorously in some centers than others). Furthermore, noninvasive ventilators or high-flow oxygen devices may not be utilized in settings where personal protection equipment is limited (or in the absence of negative pressure rooms) due to concerns about healthcare worker infection from viral aerosolization. Similarly, hospitals exceeding capacity may discharge patients early due to demand for beds. Additional concerns have been raised that one-unit changes in the ordinal scale are not equally important. For example, extubation may represent a more meaningful improvement than being moved from high-flow oxygen to standard, low-flow oxygen. Both improvements have implications on health system resources; however, from the patient view, they may not be equal.

Endpoints used in other diseases have been considered. For example, the National Early Warning Score (NEWS2)¹⁴ captures clinical deterioration in patients, but is not specific to COVID-19 and might not be sensitive enough for this disease. Other measures, such as sequential organ failure assessment (SOFA),¹⁵ are well validated but are specific to intensive care unit (ICU) patients. Patients who require intensive care have a high mortality of approximately 30%–60%.^16–18

Multiple laboratory parameters are associated with deterioration of clinical status, including surrogates for organ injury and markers of systemic inflammation, such as, markers of cardiac injury (troponin T), elevated liver transaminases, creatinine levels, procalcitonin levels, D-Dimer concentrations, fibrinogen,¹⁹ lactate dehydrogenase,²⁰ and lymphopenia.²¹ Elevations in C-reactive protein (CRP) and ferritin, further reflective of high levels of systemic inflammation, are also associated with severe disease, consistent with the observed hyperinflammatory syndrome that appears to occur in a subset of patients.²¹ While tracking these parameters is important to better understand COVID-19, they do not directly measure how a patient functions or feels and may not correlate with the clinical outcome. In supplementary Table S1, we provide examples of endpoint choices for several COVID clinical trials.

Statistical considerations

To evaluate statistical considerations in more depth, we focus on four outcomes: time to death, time to recovery/improvement, ordinal scale at a fixed time point, and ordinal scale averaged across time points. We note that, with time-to-improvement/recovery models, the competing event of death requires special handling. Patients who die during follow-up should not be censored at time of death, as that assumes their recovery time would be like all who remain alive and unrecovered at that time. To state the obvious, once dead, a patient cannot recover. A death must be set to an infinite recovery time, so that at the end of follow-up, the patient is counted as “not recovered.” We achieve the same objective by censoring deaths at the last observation day. Therefore, patients censored on the last observation day reflect two different states: death and failure to recover by day 28. Standard survival analysis methods can then be applied, but the “hazard” ratio refers to the instantaneous risk of a good outcome. Hence, we use the term “recovery rate ratio” (or “improvement rate ratio”). We note that, with administrative censoring from staggered entry before day 28, this approach corresponds to the Fine–Gray approach to competing risks.²² With staggered entry, Fine–Gray censors deaths at the time they would have been censored had they not died (i.e. time of administrative censoring).

Discretizing a continuous variable is commonly thought to result in a loss of efficiency.^23,24 Similarly, reductions in efficiency may occur when an ordinal scale is discretized into a binary endpoint and others have emphasized power advantages of a proportional odds model.^25,26 Graubard and Korn²⁷ note that rank-based methods (such as the proportional odds model) may have lower power when the marginal sums are not nearly uniform, compared with methods that use preassigned numeric values (scores) for categories of the ordinal scale. Nonetheless, collapsing information can sometimes increase power. For example, if the distribution of a continuous endpoint is skewed or has wide tails, rank-based methods, or even dichotomizing and using a test of proportions, can be more powerful than a t-test. Relatedly, if assignment to some ordinal categories is haphazard, methods that collapse categories can provide more power. Dichotomizing can also be useful when there is a clear cut-point beyond which negative sequelae of a disease manifest, such as with hemoglobin A1c or fasting glucose in diabetes. Table S2 provides a description of many statistical analysis options.

The endpoints considered are difficult to compare theoretically with respect to power. For example, time to recovery dichotomizes an ordinal scale into “recovered” and “not recovered,” so one might assume there should be a loss in power associated with using this approach. However, time to recovery incorporates health states on multiple days instead of just one, which can increase power. For instance, if the proportional odds model is evaluated so early that no one has recovered (or so late that everyone has recovered), power for the proportional odds model on that day will be very low. Using an analysis that incorporates the average ordinal score over multiple days solves that problem, but its power gain is not as great as one might imagine because measurements on the same individual on different days are likely to be highly correlated. Furthermore, a between-arm difference in an average score may also be more difficult to interpret. For example, what does an average improvement of 0.4 units on an ordinal scale mean?

We also note that time-to-event analysis is advantageous from the perspective of interim analyses, as data from all patients with any amount of follow-up time are included. This contrasts with a fixed time-point analysis, which only includes observations from patients who have made it to the prescribed follow-up milestone (e.g. all 14 days). In rapidly enrolling trials, time-to-event analysis may improve power to evaluate early efficacy (or harm) of treatments, and hence increase the speed at which treatment recommendations can be made.

Evaluation of statistical efficiency and interpretability of methods

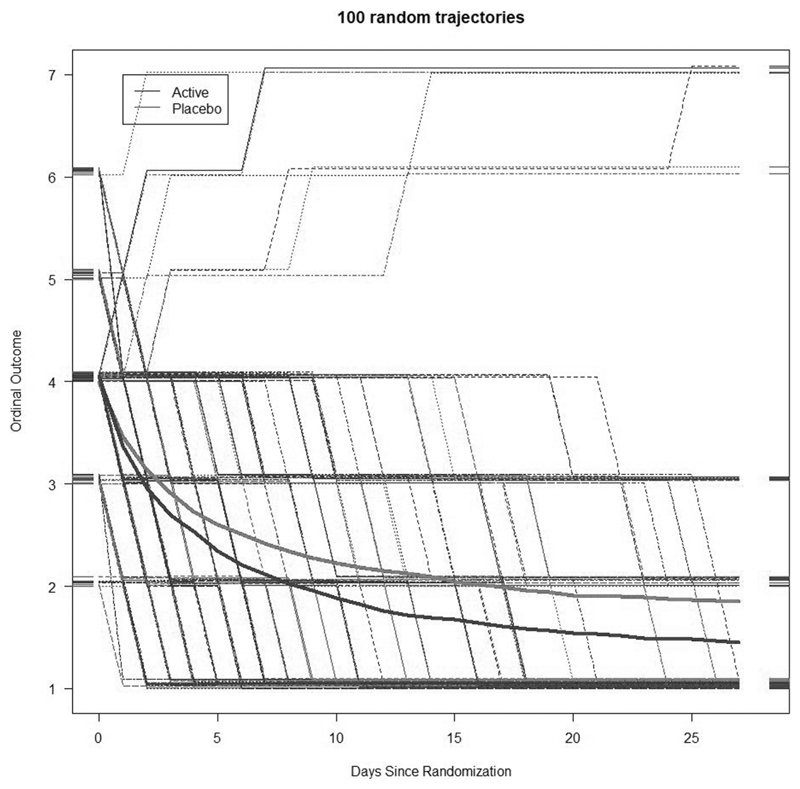
Power is compared using two simulation methods and applications to two published studies of COVID treatments. For the simulation studies, ordinal trajectories were generated according to a random line, θ_0i + θ_1i log (d) for person i, where d is the day since randomization. For day d, the ordinal score for that day was given as floor [θ_0i + θ_1i log (d)], where the notation floor [x] indicates the integer part of x. Death (score = 7) and recovery (score = 1) were considered absorbing states (i.e. values above 7 or below 1 were set to 7 and 1, respectively). One can visualize the trajectory as a subject deterministically sliding up or down their own “line of destiny” over 28 days and reporting their integer value each day. Loosely, 10% (5%) of placebo (active) patients were destined to die (having a large value of θ_1i) within the 28-day observation period. The remaining subjects were destined to recover (with negative value of θ_1i). Multiple parameter values for generating θ_0i and θ_1i were considered until trajectories roughly reflected our understanding of COVID-19 disease progression. Figure 1 depicts results for the reference scenario. Each setting was simulated 1000 times, with 800 subjects total, equal randomization to the two arms, and 28 days of follow-up. We evaluated the proportional odds model at different days, a Wilcoxon rank-sum test on the mean ordinal score (1–7) up to day 28, a test of proportions on day 28 mortality, and Cox models for time to (1) recovery, (2) a 2-point improvement, and (3) death. One possible criticism of the above simulations is that the proportional odds assumption may not hold. A second set of simulations compared methods under the proportional odds assumption. The technical details and results are given in the supplemental appendix.

Figure 1.

Ordinal outcome values by day of study from 100 simulated trajectories from the reference scenario. The smooth lines represent the average trajectories, while the bent lines represent the observed scores for individual patients.

Patient-level data from two published studies were obtained to compare methods. The Adaptive COVID-19 Treatment Trial stage 1 (ACTT-1) randomized 1062 patients to remdesivir or placebo and followed patients for 28 days.⁶ The primary outcome was time to recovery, although ordinal scales were also assessed. Due to a surge in enrollments, the study exceeded its target sample size of 400 recoveries, reaching 482 by the time of the planned DSMB interim analysis. Data were taken from a preliminary report from a 28 April 2020 data freeze (before results were made public and before actively enrolled patients were offered crossover treatment). Data cleaning for this data snapshot are ongoing, and the results presented here are intended to inform trial design. We compare empirical power for various methods with repeated random sampling of 50, 150, and 300 per arm. For each sample size, we replicated random sampling 100,000 times. In addition, we present multiple analyses applied to the LOTUS study of lopinavir/ritonavir by Cao et al.⁷ This study was stopped prior to reaching the preplanned sample size. We present analyses with the original data (199 patients) as well as with hypothetical augmented data corresponding to 398 patients.

Results

Simulation studies

Power comparisons for simulations are shown in Table 3. For the reference scenario, the proportional odds model has increasingly better power for later days, with the highest power at day 28. Empirical power for both time to (2-point) improvement and time to recovery is somewhat lower than that for the proportional odds model at the optimal time. Empirical power for mortality is notably lower than for other methods, which is no surprise due to the low event rate and modest effect. We explored four perturbations from this reference scenario to more fully assess performance. The perturbations were (1) lagged treatment effect, (2) faster recovery, (3) faster mortality, and (4) effect solely on mortality (Table S4). Under the lagged effect scenario, power for the proportional odds model decreases at days 7 and 14 but is similar on day 28 (compared with the reference scenario). This underscores the fragility in getting the day right with the proportional odds model. The faster recovery scenario has similar relative behavior to the reference scenario though power is uniformly increased. The faster mortality scenario has power like the reference scenario. These two perturbations show some robustness of the conclusions of the reference scenario. The last row in Table 3 provides scenarios with differences between arms from mortality only. Here, mortality has the highest power, as expected. More deaths on placebo necessarily implies more recoveries on treatment, which is why power for both time to improvement and time to recovery is around 30%.

Table 3. Simulated power for different analysis methods under various scenarios for simulations (type 1 error rate = 5%).

Scenario	Proportional odds				Mean score	Time to event			Proportion
	Day 1	Day 7	Day 14	Day 28		Time to 2-point improvement	Time to recovery	Time to death	28-day mortality
Reference	0.05	0.76	0.85	0.88	0.80	0.81	0.82	0.63	0.58
Lagged treatment effect	0.05	0.05	0.76	0.86	0.66	0.82	0.78	0.58	0.73
Faster recoveries	0.05	0.86	0.93	0.93	0.87	0.87	0.89	0.65	0.59
Higher mortality rate	0.05	0.76	0.85	0.88	0.80	0.81	0.82	0.75	0.71
Mortality differences only	0.05	0.23	0.26	0.32	0.24	0.31	0.28	0.51	0.46

Simulation studies under models that enforce the proportional odds assumption are provided in Table S3 and Figure S1. The results from these simulations are similar. Namely, when the fixed time point is chosen well, the proportional odds model performs well but suffers a loss of power if the time point is chosen poorly.

Applications to published COVID-19 treatment studies

Table 4 shows estimates, p values and empirical power from various methods applied to the ACTT-1 study data. At the time of the data snapshot, the following proportion of subjects had ordinal score data available: 91%, day 7; 89%, day 14; 74%, day 21; and 70%, day 28. On the observed data, the proportional odds model estimates decrease over time (opposite the simulation results above), with estimates of 1.62, 1.50, 1.42, and 1.34 for days 7, 14, 21, and 28, respectively. The odds ratio of 1.50 at day 14 indicates a 50% increase in the odds of a one-category improvement for remdesivir relative to control (at day 14). The test of mean difference between arms at days 7, 14, 21, and 28 gives estimates of 0.56, 0.62, 0.53, and 0.41 for days 7, 14, 21, and 28, respectively. The average difference at day 14 indicates an average improvement of 0.62 on the ordinal scale for remdesivir relative to placebo. The mean difference of the time-average (days 7, 14, 21, and 28) was 0.56. The time-to-recovery and time-to-(1- and 2-point) improvement analyses give estimates of 1.32, 1.29, and 1.28, respectively. The recovery rate ratio of 1.32 indicates a 32% faster (instantaneous) rate of recovery with remdesivir (relative to placebo). The hazard ratio (for mortality) of 0.70 indicates a lower hazard of death in the remdesivir group.

Table 4.

Evaluation of methods applied to ACTT-1 study data: observed data and simulated sample sizes of 50, 150, and 300 per group. Subsets of data were replicated 100,000 times.

	Day	Observed data (n = 1059)			Empirical power from simulations
		Estimates	95% CI	p value	50 per group	150 per group	300 per group
Proportional odds model	3	1.49	(1.16, 1.82)	0.001	0.16	0.39	0.77
	5	1.54	(1.23, 1.93)	<0.001	0.20	0.52	0.91
	7	1.62	(1.29, 2.04)	<0.001	0.24	0.62	0.97
	10	1.61	(1.26, 2.04)	<0.001	0.21	0.55	0.94
	14	1.50	(1.18, 1.92)	0.001	0.16	0.41	0.79
	21	1.42	(1.09, 1.85)	0.009	0.11	0.25	0.50
	28	1.34	(0.99, 1.82)	0.063	0.07	0.13	0.19
Mean difference (t-test)	3	0.28	(0.11, 0.46)	0.002	0.15	0.37	0.74
	5	0.45	(0.22, 0.68)	<0.001	0.20	0.52	0.91
	7	0.56	(0.29, 0.83)	<0.001	0.22	0.59	0.95
	10	0.58	(0.28, 0.88)	<0.001	0.20	0.53	0.91
	14	0.62	(0.27, 0.96)	<0.001	0.17	0.46	0.85
	21	0.53	(0.18, 0.87)	0.003	0.13	0.33	0.67
	28	0.41	(0.07, 0.74)	0.017	0.09	0.20	0.40
	All-days average	0.55	(0.31, 0.79)	<0.001	0.27	0.69	0.98
Time to event (log rank)	Recovery rate ratio	1.32	(1.12, 1.55)	<0.001	0.18	0.48	0.87
	Improvement rate ratio (1-point)	1.29	(1.11, 1.49)	<0.001	0.19	0.51	0.90
	Improvement rate ratio (2-point)	1.28	(1.10, 1.50)	0.001	0.17	0.44	0.84
	Hazard ratio (death)	0.70	(0.47, 1.04)	0.073	0.07	0.12	0.18

Table 4 also shows empirical power (proportion of statistically significant p values < 0.05 out of the 100,000 simulations) for sample sizes of 50, 150, and 300 per group. Power is greatest at day 7 using the proportional odds model, with rejection rates of 24%, 62%, and 97% for sample sizes of 50, 150, and 300 per group. Results for the t-test were similar, with rejection rates of 22%, 59%, and 95% for the three samples sizes. Rejection rates for the proportional odds model and t-test evaluated at day 14 were lower for all sample sizes (day 14 proportional odds rejection rates: 16%, 41%, and 79%; day 14 t-test rejection rates: 17%, 46%, and 85%, respectively, for sample sizes of 50, 150, and 300 per group). By day 28, empirical power was lower, although the t-test rejection rates were higher than for the proportional odds (proportional odds rejection rates: 7%, 13%, and 19%; t-test rejection rates: 9%, 20%, and 40%, respectively, for sample sizes of 50, 150, and 300 per group). The lower number of observations at the later time point explains some of the loss in power, although not entirely. The proportion with observations at days 7 and 14 was similar (91% vs 89%), and the power reductions were considerable (62% vs 41% for the proportional odds model at days 7 and 14, respectively, with 150 per group).

Rejection rates for the recovery rate ratio were 18%, 48%, and 87%, respectively, for sample sizes of 50, 150, and 300. Results for the time to improvements were 19%, 51%, and 90% (one-point improvement) and were 17%, 44%, and 84% (two-point improvement) for sample sizes of 50, 150, and 300 per group, respectively. Rejection rates for the hazard ratio for mortality were 7%, 12%, and 18%, for the three sample sizes considered, consistent with the low power for mortality in this setting.

Table S3 in the appendix shows results from the LOTUS study of lopinavir/ritonavir. In the observed and augmented data analysis, none of the days the proportional odds was estimated were statistically significant, while with the augmented data, the time to a two-point improvement indicated a 31% faster rate of improvement with p < 0.05.

Discussion

One important challenge with COVID-19 is disease heterogeneity. An endpoint of cure or death would be the strongest clinical evidence of treatment effect. Trials using these endpoints may take an unfeasibly long time and preclude evaluation of other candidate treatments. The WHO ordinal scale reflects meaningful patient states. However, distinctions between categories may depend on limited resources (such ventilators or high-flow oxygen devices). Furthermore, local differences in standard of care (including different guidelines recommending early intubation and/or limiting noninvasive oxygen treatments) may affect the results in multicenter trials. Ideally, such guidelines would be unified within clinical trials, but dogmatic restrictions could limit enrollments. A placebo-controlled trial will reduce the potential for subjectivity to influence changes made to a patient’s status.

Studies need to be launched quickly in order to inform the response, at a time when little information about the disease may be available. Planning for additional trial flexibility, without compromising scientific rigor, is important.²⁸ Changes made to endpoints based on results external to the trial (and prior to reviewing data) are acceptable.²⁹ In the ACTT-1 trial, the initial primary endpoint was the proportional odds model at day 14, based on early WHO guidance that recommended an analysis of ordinal scale at a fixed time point. At the time, many thought the clinical course was more like influenza illness, with recoveries occurring over 2 weeks. However, in late February, it became apparent that the course of illness was more prolonged than previously thought. Consequently, follow-up was extended to 28 days. Simulation results revealed the fragility of a fixed time-point analysis and highlighted the advantages of a time-to-recovery endpoint. The protocol was amended accordingly.

While both simulations and our examples show that power is comparable between a fixed time-point analysis and a time-to-event analysis if the timing of the former is chosen well, marked power losses are apparent when this is not the case. In addition, we believe that time-to-improvement/recovery analysis is easier to interpret. We also note that improvement in time to improvement/recovery is not only of relevance to the patient, as an indicator of faster improvement in clinical status, but also to a health system at maximum capacity. While a mortality improvement would have provided stronger evidence about treatment efficacy, initial estimates indicated a sample size of about 2000 would be needed. This was deemed impractical given the goal to evaluate multiple therapeutic candidates.

The time-to-event analysis offers other advantages such as that for interim analyses; all data collected up until the data freeze were included, which can be important in an outbreak setting with rapid study enrollment. The PALM Ebola virus disease treatment trial provides one example.³⁰ In PALM, the primary endpoint was 28-day mortality. Due to rapid enrollment, there was a striking discrepancy between the number enrolled and the number with 28 days of follow-up. At the 9 August 2019 Data and Safety Monitoring Board meeting, 673 patients (of the 725 target) were enrolled but only 376 had 28-day follow-up; the study had enrolled 93% of its targeted sample size, but information (for the mortality proportion at day) was only 52%. A time-to-event analysis would have included data on all participants (for their observed time), and information would have been 65%–70% at this analysis.

In our evaluations of the ACTT-1 data, day 7 had the highest power. However, evidence of an effect this early would likely not have been convincing for a definitive trial. A day-7 evaluation may be more appropriate for Phase 2 trials. An alternative to the time-to-event approach would have been to specify multiple outcomes (e.g. ordinal scale at days 7, 14, 21, and 28), with multiplicity adjustments. This was considered but concerns were raised about interpretation and the need to focus on an important measure of clinical benefit.

Regardless of the primary endpoint chosen, collection of core outcome measures will ensure comparability across studies and will be important for subsequent efforts to synthesize data from different trials.³¹