Payoff-based learning best explains the rate of decline in cooperation across 237 public-goods games

Abstract

What motivates human behaviour in social dilemmas? The results of public goods games are commonly interpreted as showing that humans are altruistically motivated to benefit others. However, there is a competing ‘confused learners’ hypothesis: that individuals start the game either uncertain or mistaken (confused), and then learn from experience how to improve their payoff (payoff-based learning). We: (1) show that these competing hypotheses can be differentiated by how they predict contributions should decline over time; and (2) use meta-data from 237 published public-goods games to test between these competing hypotheses. We find, as predicted by the confused learners hypothesis, that contributions declined faster when individuals have more influence over their own payoffs. This prediction arises because more influence leads to a greater correlation between contributions and payoffs, facilitating learning. Our results suggest that humans, in general, are not altruistically motivated to benefit others, but instead learn to help themselves.

Humans often face opportunities to improve group welfare but at an individual cost (‘social dilemmas’) ^1,2. For example, an individual may act to pay more taxes, practice social distancing during a pandemic, and/or reduce their carbon footprint ^3,4. Human behavior in such situations is often studied experimentally with the public-goods game ^5–7.

In the linear public-goods game, individuals can contribute financially to a group fund, which multiplies all contributions by M. The total product is then shared out equally between the N group members, providing each individual a return of M/N per unit contributed, termed the marginal per capita return (MPCR). Consequently, whenever the multiplier is smaller than the group size (M<N), the group does best if everyone contributes fully (cooperates), but individuals maximize their financial gain by not contributing. The results from hundreds of linear public goods experiments have consistently shown two patterns: (1) behaviour varies, but initial contributions average just below half (40-50%); and (2) average contributions decline as individuals repeat the game ⁸.

One potential explanation for these patterns is that most individuals are altruistically motivated to contribute, but are also averse to unfair outcomes (‘inequity aversion’) ^9–15. This preference for fair outcomes causes them to limit their altruism to match, or just undercut, what they expect others will contribute, leading to intermediate contributions (‘conditional cooperation’) ^16–18. Then, as these conditional cooperators encounter non-cooperators, who do not contribute as much, they resent the greater payoff those non-cooperators receive ^10,12,14. This causes the conditional cooperators to revise their overly optimistic expectations about their group mates, and reduce their level of contribution. The inequity aversion interpretation is based on the assumption that we can “safely assume that the players understood the game” ^9,17.

However, an alternative explanation for the data from linear public-goods games is that not all players completely understood the game, and that many were instead ‘confused learners’. This hypothesis, almost as old as the public goods game itself, posits that many individuals initially contribute because they are either uncertain or mistaken about the costs of contributing (‘confused’)^19–21. Then as the game is repeated, individuals gradually learn from how their own contribution influences their own payoff, to contribute less, leading to a gradual reduction in contributions.^8,19–28

As well as explaining the typical results from linear public-goods games, the ‘confused learners’ hypothesis can also explain data that contradict the inequity aversion hypothesis. Specifically, that: (1) individuals make similar contributions when they are playing public goods games with computers, or do not know they are playing with humans, and hence cannot be motivated by concerns for others^{22,25,27,29–31}; (2) variation in behaviour across individuals can be explained by how well they understand the game ²⁷; (3) individuals do not contribute fully (100%) in games where the multiplier is greater than the group size (M>N) and so 100% contributions would maximize the payoff for both themselves and others (MPCR>1) ^25,32–34.

Nonetheless, debate remains regarding the relative importance of altruistic inequity aversion and confused learning^{17,19,22,24,27,30,35}. While initial studies estimated around 50% of participants were confused^19–22, more recent studies of conditional cooperation, using the strategy method to control for beliefs about others, have concluded that only 4-10% of participants were confused^16,17. It has even been suggested that the role of confusion and mistakes in explaining behaviour in public gods games can be rejected ¹².

Distinguishing between these competing hypotheses is important for both understanding cooperation in humans, and determining how government policies can potentially ‘nudge’ people to behaviour more cooperatively. If individuals are altruistic but adverse to inequity, then cooperation could be nudged by emphasizing the altruistic aspect of cooperation, and by cultivating optimistic beliefs about how much others cooperate ^11,36–38. In contrast, if people are generally self-interested, cooperation would be better managed through incentives and emphasizing how and when cooperation is in an individual’s self-interest.

We used meta-data from standard linear public goods games to test between the competing hypotheses of inequity aversion and confused learners. We could test between these hypotheses because they make different predictions for how contributions will decline. The inequity aversion hypothesis predicts that “The speed of convergence depends on the actual composition of the group”, and not parameters of the game such as group size (N) ^16,17. In contrast, we show here, through simulations and an economic experiment, that the confused learners hypothesis predicts that the rate of decline will depend upon both group size (N) and the return from the public good (MPCR) ³⁹. Specifically, that when either is decreased, individuals can more reliably see the consequences of their behaviour, and so learn more quickly to contribute less. We then compare the power of these learning predictions, and a range of prosocial predictions, for explaining the variation in the rate of decline in contributions across 237 standard public goods games involving 17,940 participants.

Results

Learning and Game Parameters

We first examined, from a theoretical perspective, how the different parameters of the standard public goods game would affect the extent to which players can learn from their own payoffs. Payoff-based learning requires a reliable correlation between behaviour and payoffs. In the standard game, when the multiplier is less than the group size (M < N), players need to learn that contributing a unit will always have a cost of -1 and a personal benefit of +M/N (+MPCR), leading to a net return of (-1+MPCR).

However, the effect of this net return can be hidden by the benefits one receives from one’s groupmates that swamp the true cost. This ‘swamping’ will reduce the correlation between contributions and payoffs, impeding payoff-based learning (Figure 1). Put simply, when one can receive more benefits from others, the less likely it is that increasing one’s contribution will subsequently lead to a lower payoff. Therefore, to estimate how this swamping, and thus the correlation between contributions and payoffs is likely to vary across settings, we calculated the proportion of an individual’s range of potential payoffs that were under their own influence. We did this for each unique N*MPCR combination we found in the literature (47 combinations where MPCR < 1, and five combinations where MPCR > 1, Supplementary Figure 1). This measure does not depend on any assumptions about behaviour.

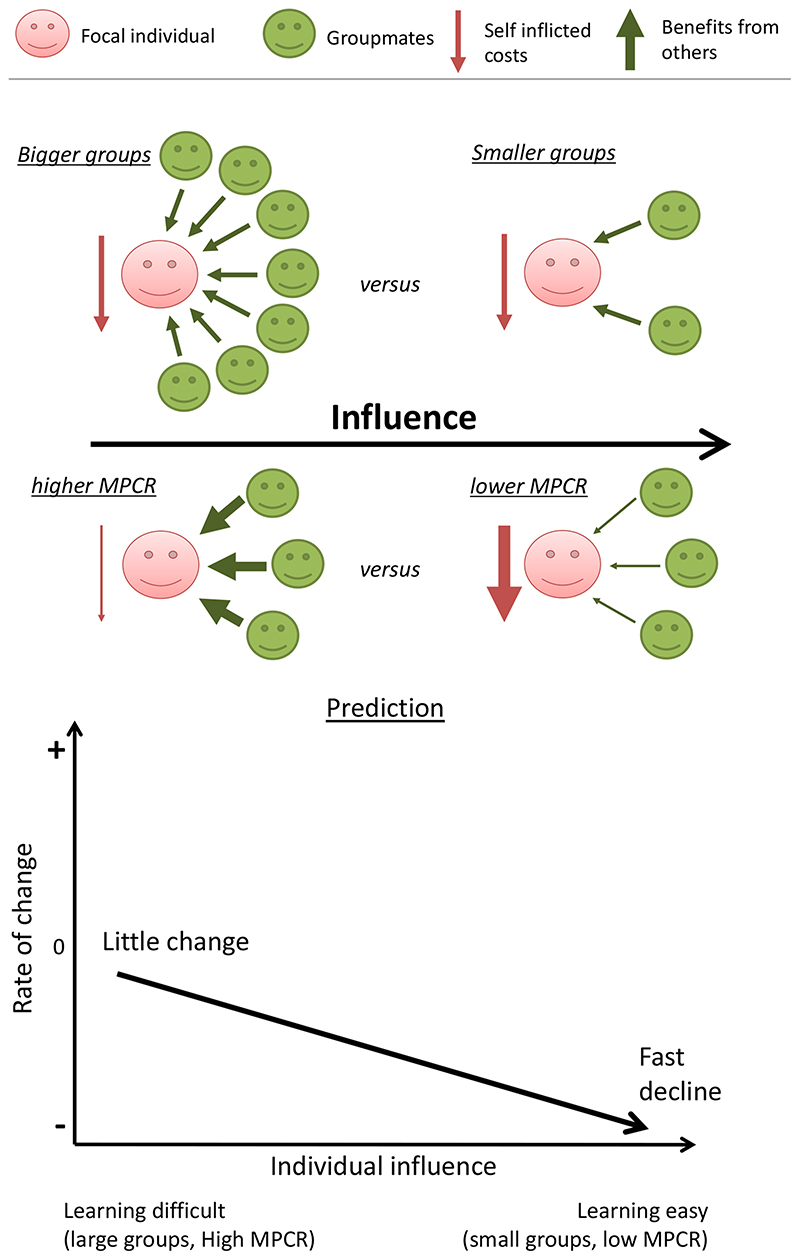
Figure 1. The confused learners hypothesis.

We hypothesized that when individuals have more influence over their own potential payoffs in the public-goods game, they will more easily learn that contributing decreases their payoff. Consequently, payoff-based learning will be easier, and thus contributions (cooperation) will decline faster. Individuals will have more influence when either groups are smaller (lower N) or the return from contributing is lower (lower MPCR). When groups are large, the benefits (green arrows) a focal individual (red) receives from her groupmates (green) can swamp out the costs she inflicts upon herself (indicated by the size of the red arrow). Likewise, when the MPCR is high, the increased benefits an individual receives (thicker green arrows), are more likely to obscure the reduced cost of contributing (thinner red arrow), and vice versa. In this cartoon, a focal player’s influence can be thought of as the ratio between the thickness of her red arrow and the sum thickness of all the arrows (red and green).

Normalizing the endowment to 1, the degree of influence over potential payoffs can be calculated as follows:

Maximum possible costs (self-inflicted) = |1-MPCR|

Maximum possible benefits (from groupmates) = maximum benefit an individual can give you, times the number of groupmates = MPCR*(N-1)

Range of potential payoffs = maximum possible costs + maximum possible benefits = (|1-MPCR|) + (MPCR*(N-1))

$$\text{Influence}(\text{i})=\text{proportion}\text{of}\text{potential}\text{payoff}\text{range}\text{under}\text{own}\text{control}=(|1\text{-MPCR}|)/((|1\text{-MPCR}|)+(\text{MPCR}*(\text{N-}1)))$$ (1)

Equation (1) shows that in a standard game, where contributions are not favoured (MPCR < 1), the degree of influence an individual has over her own range of potential payoffs (i)increases as either the return from contributing (MPCR), or the group size (N) decrease (Supplementary Figure 2). Consequently, we make the qualitative prediction that payoff-based learning will be easier, and thus the decline in contributions will be faster, when either the return from contributing (MPCR), or the group size (N) are lower.

More specifically, we predict that the rate of decline across games will positively covary with our calculated degree of influence (i) (Table 1). We make this prediction because we hypothesize that greater influence will lead to a stronger correlation between contributions and payoffs. In the next section, we test this assumption with a simulation.

Table 1.

A companion to Figure 4, outlining the competing hypotheses we test and their predictions for the rate of decline in contributions. MPCR = return from contributing (Marginal Per Capita Return); N = group size; M = experimenter’s multiplier of contributions.

Hypothesis	Sub-hypothesis	Predictions for the rate of decline in contributions
Confused learners: try to improve their own payoff		‘Qualitative’: increases to MPCR, and/or N, will each slow the decline.
		‘Influence’: faster decline when an individual has more influence (i) over her own range of potential payoffs, as calculated in text by eq. 1.
		‘Simulated’: Faster decline when there is a greater expected correlation between contributions and payoffs, as estimated in our simulations.
Inequity averse cooperators: try to avoid unfair outcomes in…	Contributions (absolute)	Neither N or MPCR or M will affect the rate of decline.
	Contributions (proportional)	Neither N or MPCR or M will affect the rate of decline.
	Payoffs (absolute)	Neither N or MPCR or M will affect the rate of decline.
	Payoffs (proportional)	Larger M will slow decline.
Patient cooperators: try harder (keep contributing) to preserve the public good when relatively more…	Collective group benefit	Larger M will slow decline.
	Individuals benefit	Larger N will slow decline.
	Benefit per individual	Larger MPCR will slow decline.
	Sum total benefits to others	More total benefits to groupmates (MPCR*(N-1)) will slow decline.
Unspecified cooperators: maximize an unknown utility function		Decline depends on best P-hacked permutation of N, MPCR and Round.

Simulating the learning environment

We used a simulation to test the robustness of our above prediction. Specifically, that a larger influence (i), as measured by equation 1, will lead to a stronger correlation between an individual’s contributions, and her payoff. Equation 1 provides a possible lower bound on the correlation between contributions and payoffs, because all groupmates will not necessarily contribute fully or zero.

We varied 11contributions of a focal player from 0-100% at 10% intervals in a public goods game where the other members of the group played randomly. Our aim was not to model human behaviour, but to measure the difficulty of the learning environment depending on both group size (N) and the return from the public good (MPCR). We repeated the process 10,000 times for each unique N*MPCR combination, to measure the average expected correlation for each combination (Methods).

Consistent with our prediction, we found that when players had more influence over their own payoffs, which was when either groups (N) or the return from contributing (MPCR) were smaller, there was a stronger correlation (more negative) between their contributions and their payoffs (Linear model, mean correlation~influence: F_1.45 = 126, P < 0.001, unstandardized coefficient B = -1.9, 95% Confidence Intervals = -1.6, -2.2, Rsq_adj = 0.73; Supplementary Figure 3). This result confirms that more influence leads to a greater expected correlation between contributions and payoffs, which we predict will facilitate payoff-based learning. We test this prediction experimentally in the next section.

Learning the game in a black box

We then experimentally tested how varying influence (i), through changing either the group size (N) or the return from contributing (MPCR), affected the ability of real players to learn the game. We made individuals play a public-goods game, but without knowing that they were in a public goods game ²⁵. Players were given the option to repeatedly input virtual money into a virtual ‘black box’ (‘contribute’), and see their payoff each round, but did not know the payoff function, nor that their payoffs were being affected by the ‘contributions’ of other players. Thus, in this asocial control, we forced the players to start ‘confused’, and the only way they could improve their payoff was by trial and error (payoff-based learning).

An advantage of this black box design is that it measures the speed of payoff-based learning, and how a population of confused learners will behave in different public goods games. This provides an alternative null hypothesis instead of the traditional model of perfectly rational players that maximize a (self-interested) utility function (Homo economicus) ⁴⁰. We varied both group size (N=3 or 12) and the return from contributing (MPCR =0.4 or 0.8) across three treatments - this led to the degree of influence an individual had over her own payoff ranging from 0.11 to 0.43 (11-43%).

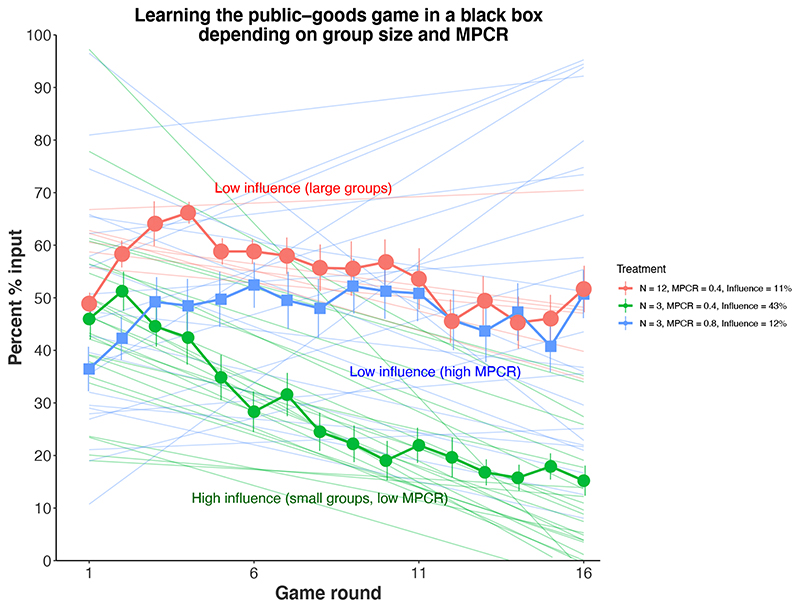
We found that when players had more influence over their own payoff that this led to a faster decline in contributions (Linear mixed model on 54 group means per round: Influence*Round, F_1.54 = 25.3, P < 0.001, B = -7.36, 95% Confidence Intervals = -4.49, -10.23, Figure 2). Comparing among the black boxes, the fastest decline was in the smaller groups with a lower return from contributing (N=3 & MPCR=0.4, influence = 43%), where contributions declined from 46% to 15% over the 16 rounds (Linear mixed model: Treatment*Round, F_2,54 = 13.8, P < 0.001). In contrast, when influence was low, either because groups were larger (N=12, influence = 12%), or because the return from contributing was larger (MPCR = 0.8, influence = 11%), contributions finished at just over 50%, indicative of no learning on average (Figure 2).

Figure 2. Payoff-based learning in a black box public-goods game.

The figure shows how well individuals can learn to contribute 0 when they unknowingly played a public-goods game. Despite being grouped together, individuals instead interacted with a ‘black box’ that converted their input into an output, unknowingly based on all the group-members’ inputs. We used three treatments that varied in their group size (N) and return from contributing (MPCR), and thus the amount of influence (i) each individual had over their own payoffs. Markers show the mean ‘contribution’ and standard errors estimated from the group means for each round of the game: blue squares, N = 12, MPCR = 0.4, i = 0.11; Magenta discs, N = 3, MPCR = 0.8, i = 0.12; green triangles, N = 3, MPCR = 0.4, i = 0.43. Thin colored lines show the separately estimated linear regression for each independent group. Contributions declined faster when individual had more influence (i) over their own range of potential payoffs, which was when they were in small groups with a low return from contributing (green) (Linear mixed model: Influence*Round: F_1,124.0 = 46.1, P < 0.001; N = 216 players, 72 players per treatment, between-participant design).

In addition, our experiment replicated the result from our simulation, that more influence led to stronger correlations between individual contributions and payoffs (Linear mixed effects model controlling for group: t_1,52 = -7.0, P < 0.001, B = -1.69, 95% Confidence Intervals = -2.17, -1.20, N = 211 individuals across 54 groups, final round contributions excluded, five individuals excluded because they made constant contributions so no correlation could be calculated, Supplementary Results, Supplementary Figure 4). Overall, our results confirm that payoff-based learning in public goods games is cognitively feasible, but impeded in larger groups (larger N) or when the return of contributing is increased (higher MPCR). This appears to be because these factors reduce a player’s influence over her payoffs, and thus reduce the correlation between her actions and payoffs, making learning unreliable.

Learning can explain variation across public-goods games

We then tested if payoff-based learning could explain variation in the rate of decline in contributions across 237 standard public-goods games. These games came from 129 studies, using 17,940 participants in 47 unique N*MPCR combinations. On average, across these games: (1) the initial contribution was 49% (95% CI: 47.2, 51.0%); and (2) contributions then declined by 2.4 percentage points per round (95% Confidence Intervals = -2.64, -2.20; F_1,127.3 = 458.5, P < 0.001).

Comparing across games, we found that the rate at which contributions declined varied, as predicted by the confused learners hypothesis. Specifically, experiments with smaller groups or smaller returns from contributing showed faster declines in contributions (Linear mixed effects model, Group size*Round: F_1,74.9 = 10.8, P = 0.002, B = 0.11, 95% Confidence Intervals = 0.04, 0.18; MPCR*Round: F_1,171.8 = 34.2, P < 0.001, B = 0.26, 95% Confidence Intervals = 0.17, 0.35; Supplementary Table 1). This analysis controlled for both the probability of future interactions ^41–45 and how much information individuals received about the behaviour and payoffs of others during the game ^25,44.

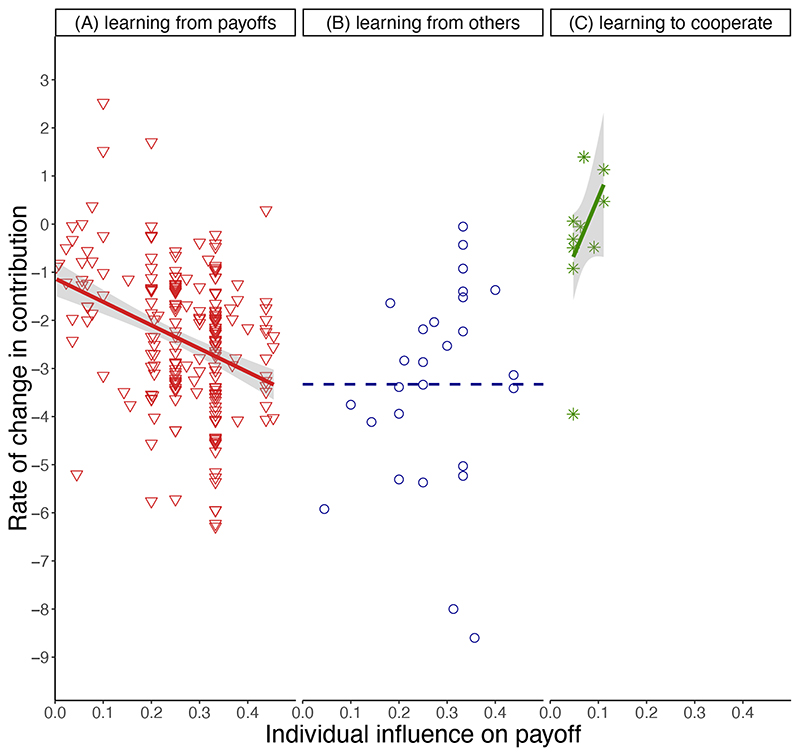
We then carried out further regression analyses, to test the robustness of our conclusions. First, we took the degree of influence (i) for each of the 47 unique N*MPCR combinations and substituted it into the model in place of the colinear variables N and MPCR. We found that influence (i) significantly predicted the rate of decline across studies (Linear mixed effects model with control covariates, Influence*Round: F_1,209.4 = 43.2, P < 0.001, B = -0.44, 95% Confidence Intervals = -0.58, -0.31, Fig. 3a). Furthermore, influence (i) provided a superior statistical model to using N and MPCR (Supplementary Table 2). This suggests that the significance of influence (i) was not just due to it correlating with both of its constituents N and MPCR.

Figure 3. abc. Influence (i) explains variation in the rate at which contributions change.

Each data point shows the percentage point change in contributions per round in: public goods games where (A) players could only see their own payoff (MPCR <1, N = 210 games), or; (B) they could also see the individual payoffs and actions of their groupmates (MPCR <1, N = 27); or (C) public delight games (MPCR >1; green, N = 10). In (A), contributions declined more quickly when individuals had more influence over their own potential range of payoffs (Linear mixed effects model with control covariates, Influence*Round: F_1,209.4 = 43.2, P < 0.001, B = -0.44, 95% Confidence Intervals = -0.58, -0.31); in (B), where individuals could learn by observing the perfect correlation between contributions and payoffs among their groupmates, the degree of influence was not significant (Influence*Round, F_1,40.2 = 3.1, P = 0.086, B = 2.5, 95% Confidence Intervals = -0.38, 5.45); in (C) the rate of change was more positive when individuals had more influence (Linear mixed model, Influence*Round: F_1,14.4 = 8.7, P = 0.010, B = 8.9, 95% Confidence Intervals = 2.44,15.39), meaning that in both types of games (public good and public delight), the rate of change was greater, and individuals were quicker to approach income-maximizing behaviour, when they had more influence over their own range of potential payoffs. Solid lines = significant regression estimate, Shaded areas represent 95% confidence intervals. Dashed line = intercept only model as regression was non-significant. This figure is for visualization purposes and does not account for the effects of covariates.

Our next regression analyses tested how well our simulation results were able to explain the variation in the rate at which contributions decline across the 237 different public goods games. Our new explanatory variable, in place of influence (i), was the average correlation between individual contributions and payoffs that we found in our simulations for each of the 47 unique N*MPCR combination (‘simulated correlations’). We found that our simulated correlations significantly explained variation in the rate at which contributions declined (Simulations*Round: F_1,569.4 = 60.1, P < 0.001, B = 2.47, 95% Confidence Intervals = 1.84, 3.09, Supplementary Fig. 5a). In addition, our simulated correlations provided a superior statistical model compared to our model which used influence (i) as an explanatory variable (Supplementary Table 2, model 3 versus 2). The greater explanatory power of our simulated correlations makes sense because our calculation of influence (i) is a proxy for the correlation between contributions and payoffs, which we more specifically estimated in our simulations.

Learning from others

If players can observe among others that contributing less leads to a greater payoff, then they may learn more quickly, regardless of how difficult it is to learn from their own payoffs. In this case, the importance of influence over own payoffs will be diminished when players are shown the contributions and payoffs of their groupmates, which will always show a perfectly negative correlation. In contrast, the inequity aversion hypothesis makes the opposite prediction, because the theory assumes that players are calculating the payoffs of their groupmates, or more simply, just responding to differences in contributions ^9,17. Consequently, if this is true, then being informed about the payoffs of others should make no difference to behaviour.

We tested between these hypotheses by including an interaction term in our regression between the degree of influence (i) and whether information on the payoffs of groupmates was shown or not to players in the public goods games. We found a significant interaction between the level of information shown and the degree of influence (i) (Information*Influence*Round: F_1.336.6 = 17.5, P < 0.001, Supplementary Table 3, model 3). Specifically, in support of the confused learners hypothesis, the coefficient for the rate of decline when groupmates’ payoffs were not shown was significantly more negative than when groupmates’ payoffs were shown (estimated difference in coefficients when groupmates’ payoffs not shown = -4.9, 95% Confidence Intervals = -2.61, -7.26, Supplementary Results). This is consistent with the degree of influence (i) being more important for learning when the payoffs of groupmates are not shown.

The same qualitative result holds for when we use the simulated correlations instead of influence (i) as an explanatory variable (Supplementary Figure 5b). From the figure one can see that when the contributions and payoffs of groupmates are shown, the estimated rate of decline is equivalent to playing a game with an estimated correlation of -1. This makes sense because the observable correlation between contributions and payoffs among groupmates is always perfectly negative (-1). In summary, a difficult environment for trial-and- error learning does not matter when players can reliably learn by observing and comparing among others. This can also explain why, in general, contributions decline faster/sooner when the payoffs of groupmates are shown, a result also inconsistent with players having perfect understanding of the game (Supplementary Table 3).

Learning to cooperate

The confused learners hypothesis can also explain data from experiments where the personal benefit of contributing outweighed the costs (when MPCR > 1). In such ‘public-delight’ games, there is no social dilemma because the behaviour that maximizes both individual and group level payoffs is to contribute 100%. We analyzed 10 public delight games involving a total of 255 participants.

We found that, on average, in public delight games, individuals began by contributing intermediate amounts (weighted samples mean ±SD = 66.1% ±10.7%). This pattern is consistent with confusion or ‘spiteful’ motives, but not altruistic motives, where 100% contributions would have been favoured ⁴⁶. In addition, as predicted by the confused learners hypothesis, when influence was greater, the rate of change was more positive (Figure 3c; Linear mixed model, Influence*Round: F_1,14.4 = 8.7, P = 0.010, B = 8.9, 95% Confidence Intervals = 2.44, 15.39). This same qualitative result held when using our simulated correlations to explain variation in the rate of change (Supplementary Results; Supplementary Figure 5c). This significant effect is despite the fact that influence is very low across all public delight games, varying from only 4.8-11.1%, and therefore the learning environment is generally difficult, leading to small rates of aggregate change.

The pattern in public delight games is analogous to that found in public goods games. In both public good and public delight games, individuals began by not maximizing their income, but were quicker to approach income-maximizing behaviour when they had more influence over their own payoffs (Fig. 3a. Supplementary Fig. 5a). Public delight games can be thought of as a ‘control treatment’, but where the payoff maximizing contribution is 100%, not 0%.

Testing alternative, prosocial, hypotheses

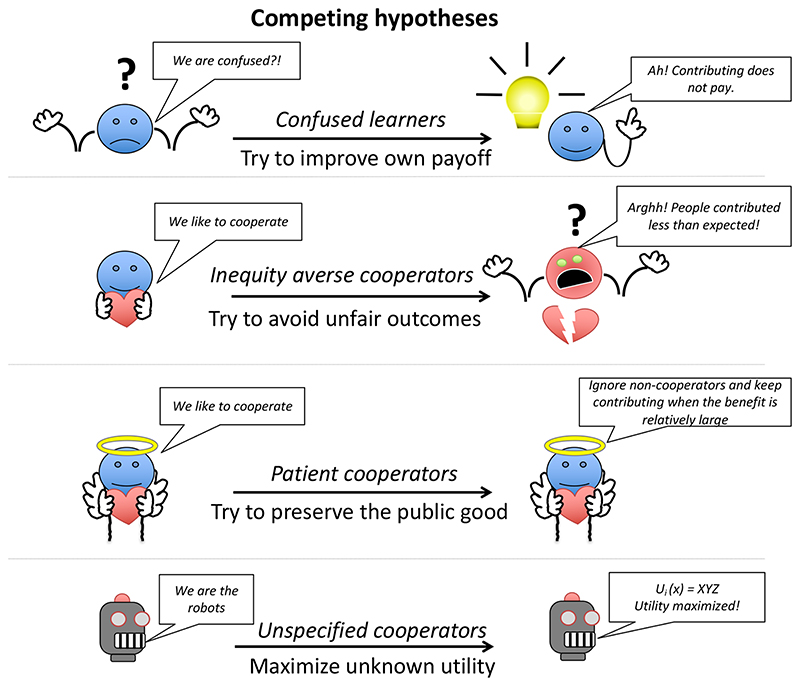
We also tested the relative ability of a range of possible ‘prosocial’ hypotheses to explain variation in the rate of decline in contributions across all 237 public goods games. These prosocial hypotheses assume that altruists respond to the costs and benefits within their group in some way, and that the frequency of different types of players (conditional cooperators and non cooperators) does not depend on N or MPCR⁴⁷. We made this assumption because otherwise the idea of stable social types would be essentially meaningless²⁸, and require estimating the frequency of types for each separate social dilemma in the real world. We statistically modelled three classes of hypotheses (Methods, Table 1, Figure 4):

• (1)Altruistic preference for fair outcomes (inequity aversion). In this hypothesis, contributions will decline faster when there is more unfairness. Fairness can be measured in either absolute or proportional differences in either contributions or payoffs (inequity averse cooperators, fairness defined in various ways, Methods);
• (2)Altruistic preference for preserving public goods when contributions are more beneficial. This hypothesis assumes players are more motivated to maintain their cooperation, and show more patience towards non-cooperators, when contributing provides more benefits. This means contributions will decline less quickly when there are more benefits. We tested four different conceptions of benefit (patient cooperators, benefit defined in various ways; Methods); and
• (3)To really challenge the learning hypothesis, we attempted to simply ‘p-hack’ a statistically superior model. We did this by comparing the information criterion scores for all 14 possible permutations of N, MPCR and Round, and then picking the best one (Supplementary Table 4) ^48,49. This hypothesis assumes individuals execute their preferences perfectly (like ‘robots’), in line with some unspecified utility function, and makes no a priori predictions (unspecified cooperators, Methods).

Figure 4. Competing hypotheses.

The competing hypotheses we test for explaining variation in the rate of decline. See text and Table 1 for detail.

We found that none of the prosocial hypotheses came close to outcompeting our confused learners hypothesis (Supplementary Table 2). This result did not depend qualitatively upon whether we included the control covariates or not and was robust to various forms of alternative analyses (Supplementary Table 5).

Our p-hacked permutation test provided further support for the confused learners hypothesis. The best prosocial model to emerge was a p-hacked permutation test containing both N*round and MPCR*round in the model (Supplementary Table 2). The best permutation model was therefore one which recapitulated the predictions of the confused learners hypothesis, and one which was confirmed in our black box experiment, where payoff based learning drove changes in behaviour.

Discussion

We found, across 237 linear public goods games, that the rate at which contributions declined could be explained by how much influence individuals had over their own range of potential payoffs (Figure 3a, Supplementary Table 2). Mean contributions declined faster when individuals had more influence, which was when groups were smaller (smaller N), and/or the return from contributing was smaller (smaller MPCR) (Figure 1, Supplementary Figure 2). When individuals have more influence over their own payoffs, we showed they can better learn how to increase their payoffs (Figure 2). This is because in the public goods game, more influence leads to a more reliable correlation between an individual’s contributions and her payoffs (Supplementary Figures 3 & 4). Consequently, it appears to be the strength of the correlation between a player’s contributions and her payoffs which is driving the decline in contributions across public-goods games (Supplementary Figure 5a). When individuals could more easily learn that contributing was costly, their contributions declined at a faster rate.

These results suggest that individuals largely act as self-interested confused learners in linear public goods games. Specifically, that individuals: (1) focus upon their own payoff; (2) start with some imperfect (confused) idea of how to maximise their own payoff; (3) learn from experience, how their contribution affects their payoff; (4) decrease their contributions, as they learn that this increases their payoff. Therefore, policies aimed at encouraging long run cooperation should still include a focus on incentives, highlighting how and when cooperation can be beneficial, rather than relying on perceptions of fairness, which may often be self-serving.

Some limitations of our study are that our comparative regressions relied on aggregate data, and not individual level data, from previous studies. However, previous experiments have shown the confused learners hypothesis can also explain individual variation in behaviour in public goods games ^{16–18,27,30}. Our literature search may also have missed some publications and does not include any studies published later than 2017, although there is no reason to suspect that this could bias the results with regards to this study’s hypotheses. Finally, we do not attempt to evaluate potential cross-cultural differences in how people play economic games ^50,51, nor the potential effects of varying the exchange rate between the laboratory currency and real-world currencies (the ‘stake’ size) ^52–54. It may be that some cultures rely more on learning by copying others rather than from payoffs, and that larger stakes make people less prone to mistakes.

Our results emphasise the need for care when interpreting the results of economic games ^55,56. For example, apparently stable contributions in a cooperative game could signal a level of norm-compliance, or merely that individuals are struggling to learn how to maximize their payoff. Likewise, studies testing how ‘cooperators’ behave when grouped together risk confounding social preferences with changes to the payoff mazimizing equilibrium, and thus how individuals learn about payoffs ^57–61.

A behavioural approach when measuring social preferences, with control treatments and appropriate null hypotheses, can be used to distinguish between alternate hypotheses. This is safer than simply inferring motivations from the financial consequences of decisions. We are not arguing that there is no possibility for altruistic preferences such as fairness, just that the overinterpretation of experiments has led to their importance being overstated.

To conclude, the results of public goods games may be especially relevant to explaining how people behave in the ‘real’ world when encountering new social situations. Perhaps much of modern life is at least partially like a black box, where individuals cannot perfectly determine the effects of their actions upon society, nor how others are affecting them. Instead, when faced with unfamiliar situations, individuals may respond intuitively, and then use trial and error learning to determine when to cooperate^62–64.

Methods

All statistical tests were two-tailed. Our research complies with all relevant ethical regulations. For the black box experiment, our pre-registered experimental design was approved by the ethics committee of the Centre for Experimental Social Science (CESS) at Nuffield College, University of Oxford, Oxford (submitted on December 14^th, 2018, and approved on January 22^nd, 2019, see supplementary files). CESS staff obtained written consent from each participant before the start of the experiment.

Simulating the learning environment

The simulation and the corresponding results figure was conducted in R using the ggplot2 package ^65,66. The simulation code and the necessary data file can be found in the supplementary information. For each unique N*MPCR combination, a focal player made 11 proportional contributions, from 0 to 1 at 0.1 intervals, and each individual in her group would separately make a corresponding decision on the same scale but at random (drawn from a uniform distribution). We then calculated the Pearson’s R correlation between the focal player’s contributions and her payoffs (N = 11). We then repeated this process for 10,000 focal individuals and recorded the overall mean Pearson’s R correlation for each N*MPCR combination. The statistical analyses were a linear model between the mean correlation for each N*MPCR combination and its corresponding degree of influence (lm function in R). Data distribution was assumed to be normal but this was not formally tested. We re-ran the whole set of simulations 10 times to check the consistency of the results (Supplementary Table 6).

Learning the game in a black box

Participants and Sessions

All sessions were conducted in February 2019 at the Centre for Experimental Social Science (CESS) at Nuffield College, University of Oxford, Oxford, and lasted around 45 minutes. CESS recruited the participants using the Online Recruitment System for Economic Experiments (ORSEE) ⁶⁷. The decisions and responses of the participants were anonymous, as were their earnings and payments, which were administered by the CESS administrators, who were not directly involved in the experiments. Participants were required to sign a consent form, were free to leave at any time and received a show-up fee of £5. We gave each participant a total endowment of £7.20, and average earnings from the experiment were £13.41 (ranging from £9.30 to £17.20), to which the show-up fee of £5 was added. We conducted 18 sessions each with 12 voluntary participants for a total of 216 participants who participated in one session each (129 self-reported females, 83 males, and 4 who declined to answer; all ages unknown but the participants were mostly students so probably aged 18-25; no participants were excluded).

Instructions and Different Treatments

Our experiment was conducted in z-Tree ⁶⁸ and utilized the same code, with some minor modifications, as our previous experiment with the black box paradigm ²⁵. The experimental files and data are available in the supplementary information. We told participants at the start of the experiment that they would play with three separate black boxes. Each participant played all three treatments, in a counter-balanced order (we used all six permutations three times each, with random participant allocation to each treatment order), in order to approximately equalize average payoffs across different sessions. Participants were incentivized directly for each decision in each treatment. However, we only used the data from the first black box from each session to avoid learning from the first treatment affecting the results from subsequent treatments. The experimenter was aware of the treatment order, therefore data collection and analysis were not performed blind to the conditions of the experiments.

Each participant was given instructions explaining that it was necessary to “decide on how many of your 20 coins to input into a virtual ‘black box’. This ‘black box’ performs a mathematical function that converts the number of ‘coins’ inputted into a number of ‘coins’ to be outputted. The mathematical function contains two components, one constant, deterministic, component which acts upon your input, and one ‘chance’ component. You will play with this ‘black box’ for many rounds (more on this later), and the mathematical function will not change, but the chance component means that if you put the same amount of coins into the ‘black box’ over successive rounds, you will not necessarily get the same output each time”. Although we did not fully inform participants that their inputs would benefit other players, we did not lie to them, and the CESS ethical committee, which forbids deception in economic experiments, approved the experiment (a full copy of the instructions are in the Supplementary Methods).

Group composition was constant for each treatment. Participants were endowed with 20 monetary units (‘virtual coins’) each round for 16 rounds for each black box. After each decision, participants saw a message saying “Calculating…” while they waited for all 12 participants to make their input. After each round, we reminded participants of their ‘input’ and the ‘output’ they received and their resulting net payoff. After the experiment we checked the participants had not perceived the experiment as a social one by asking them “In a few words, please tell us what, if anything, you think the experiment was about?” Of 216 participants, only five at most (2%) mentioned anything that could be construed as social. In contrast, the majority of participants (123 of 216, 57%) literally wrote that they thought the experiment was researching ‘risk’, ‘gambling’ or ‘investing’ (all responses are available in the Supplementary Spreadsheet on Questionnaire Responses on purpose of experiment).

Statistical Analyses

Our data are available in the supplementary information. No statistical methods were used to pre-determine sample sizes but our sample size was similar to those reported in previous publications ^25,58. We analysed the mean inputs for each group per round depending on treatment or the degree of influence using linear mixed effects models in IBM SPSS Statistics. Random intercepts and slopes were fitted for each group, and the residuals from the repeated decisions were modelled with an auto-regressive covariance (AR1) structure. We measured the Pearson R correlation between individual inputs and payoffs separately for each participant in IBM SPSS Statistics. We then tested the relationship between these correlations and the degree of influence individuals had over their own payoffs in R, fitting a random intercept for each group (using lme function and ggplot2 package) ^65,66.

Learning can explain variation across public-goods games

Literature search

We searched for relevant studies in three ways. First, we searched the “Web Of Knowledge” database. In May 2014, we searched with the phrases “public good* game*”, and “voluntary contribution mechanism”. In October 2017 we searched for additional articles between 2014-2017 inclusive, with the phrase “public good* game*”, refined by TOPIC: “experiment” AND “voluntary contribution mechanism”, and with the phrase “repeated public good* game*” refined by TOPIC: “experiment”. Second, we searched for suitable papers cited in three reviews on social dilemmas ^6,69,70. Third, we looked for other papers cited in the papers that we had found.

We were only interested in versions of the repeated linear public goods game that allowed individual players to make anonymous, voluntary contributions from 0-100%. In addition, we required that studies reported the group size, the marginal per capita return and/or the multiplier, so that we could calculate the degree of influence individuals had over their own payoffs. Studies had to give all players the same endowment, the same decision, and the same costs and benefits (symmetric games). The costs and benefits also had to be constant and could not change from round to round (no legacy effects) or depending on the actions of the players (no threshold provision points). The game had to be repeated for at least five rounds and group formation was forbidden to be on the basis of individual performance in either the game or in a prior task. Also there could be no extra actions in the game such as punishment, reward or communication. This meant that we were often taking the results from control/baseline treatments, especially in more recent publications.

Articles (studies) often contributed multiple sets of data, some independent for the purposes of our analyses and some not. Data were coded according to the study they came from, and within each study the data were coded as belonging or not to the same treatment. Data from the same treatment were not coded as independent unless they came from a different location, however we do not include a variable to encode geographical location in our analyses. Some studies, more typically older studies, presented data from separate groups playing the same treatment. In these cases, the data were collected as presented but coded as belonging to both the same study, and the same treatment, and thus the same ‘independent-case’. Thus, for data from the same study to be classified as coming from different independent-cases then they had to differ in either experimental design or location.

Overall, we collected 324 sets of data from 130 studies using 18,195 players (Supplementary Methods - Literature Search, and Supplementary Figure 6). We identified 247 independent-cases among these 324 sets of data (because different groups or sessions playing the same treatment in the same location were coded as belonging to the same independent-case). The 247 independent-cases spanned 52 unique N*MPCR combinations, with N ranging from 2 to 100 and MPCR ranging from 0.02 to 1.6. Excluding cases where the MPCR > 1 leaves 237 independent-cases spanning 47 unique N*MPCR combinations, with N ranging from 2 to 100 and MPCR ranging from 0.02 to 0.8, and using 17,940 participants across 129 studies.

We classified 20 studies as having various data suitability issues (regarding the purposes of this study). Three studies did not provide data for each round, instead choosing to aggregate them across rounds or omit intervening rounds, and one study did not make it clear if players were told their payoff or not. Four studies were lab-in-the-field experiments. Thirteen studies did not present data from fully naïve participants: ten studies had participants play two treatments, in counter-balanced order, then presented the amalgamated data of the naïve and non-naïve participants (one of these studies also did not provide data for each round); and three studies mentioned that their participants had played a public goods game before in a prior experiment. We include these studies as we reasoned the players might not necessarily recognize it is the same game or may have reason to believe that something will be different (hence the additional experiment). However, the inclusion/exclusion of these data from 20 studies does not change the qualitative results (Supplementary Table 5).

Data extraction and analyses

Our data are available in the supplementary information. Our dependent/response variable was the mean percentage contribution, to one decimal place, per round. When studies presented their data in graphical form we extracted the average level of contribution with WebPlotDigitizer ⁷¹. We ran hierarchical linear mixed models (LMM) that modeled the repeated effects of multiple rounds of play within each treatment within each study. We compared all models on the bases of their mean Information Criterion score, specifically the mean of four scores available in IBM SPSS Statistics: Akaike’s information criterion (AIC); Hurvich and Tsai’s criterion (AICC); Bozdogan’s criterion (CAIC), and Schwarz’s Bayesian criterion (BIC).

In order to reduce the temptation to ‘p-hack’ our results we first fitted the appropriate repeated/random effects model using Restricted Maximum Likelihood (REML) to evaluate competing models that differed only in their repeated/random effects (not fixed effects of interest) (Supplementary Table 7)⁷². This test of multiple competing random effects models allowed us to settle on one model structure before fitting and comparing our fixed effects of interest. The final model had random effects for both the intercept (average contribution) and slope (contributions over time) for each study and independent case (treatment) within each study. The final model also weighted the residuals by the number of participants contributing to each data point. We then used Maximum Likelihood (ML) to evaluate competing models that differed only in their fixed effects.

We also included, where possible, theoretically important control covariates in our main analyses (Supplementary Tables 8 and 9). Specifically, we include four variables: (1) a continuous variable specifying the total number of rounds; (2) a binary variable specifying if the players were told or not which round was the final round; (3) a three level variable specifying if the group composition was kept constant, randomly shuffled, or perfectly rearranged to prevent repeated interactions (Stranger); and (4) a four level nested variable encoding whether players were informed after each round of the individual contributions and payoffs of their groupmates (Ei), or just individual contributions of their groupmates (Ci), or just the group average contribution (SumC), or just their own payoff (own E) and no direct information about the contributions of groupmates. In cases where no information on the covariates was available, we imputed the value to be the same as the modal value. Specifically, when the MPCR < 1, we had to assume that in 19 cases players did indeed know when they were playing the final round, and in 13 cases that players were provided with information on the group average contribution only (Supplementary Table 9). We repeated our analyses without the imputed values, and also without the covariates, and the results stayed qualitatively the same (Supplementary Table 5).

Testing alternative, prosocial, explanations

Here we assume individuals initially contribute out of altruistic motivation rather than confusion. We tested three classes of prosocial models (Table 1, Figure 4). First, we considered conditional cooperation and inequity aversion. In the public good game, all group members receive the same return from public good, therefore absolute differences in payoffs are caused solely by how much of their endowment different players retain rather than contribute. Therefore, if players are concerned with minimizing absolute differences in either ‘effort’ (contributions), or payoffs, then they will simply attempt to match contributions and the rate of decline will be invariant with regards towards the group size (N) and the return from contributing (MPCR). Likewise, if players are concerned with proportional differences in ‘effort’, then again differences will be unaffected by either N or MPCR. However, if conditional cooperators are concerned with proportional rather than absolute differences in payoffs, they could react less strongly (less anger/ envy) to the same absolute payoff differences when the mean payoffs are larger ³⁹. Such proportional inequity aversion would predict that contributions decline more slowly when the experimenter’s multiplier (M) is increased. This is because, as M increases, the public good gets larger, and the mean payoffs increase (for a given level of contributions), meaning that the size of absolute differences in payoffs decreases with respect to the mean payoffs.

Secondly, we considered the possibility that many individuals are more motivated to maintain their cooperation, and show more patience towards non-cooperators, when contributing provides more benefits (Preserve the Public Good - PTPG). The definition of benefit could take various forms, for example players may be more motivated to maintain their cooperation over time when (1) there is more collective group benefit (hypothesizing a slower decline when the multiplier M is increased, note this is same model as proportional inequity aversion); or when (2) more individuals benefit (slower decline when group size N increased); or when (3) there is more benefit per individual (slower decline when MPCR increased); or when (4) there are more sum total benefits to others (slower decline when MPCR*(N-1) increased).

Thirdly, we attempted to ‘p-hack’ a superior performing model based on the idea that rational altruists will play perfectly, ‘like robots’, in line with some unspecified utility function (Unspecified) ^48,49. We did this by testing all 14 possible permutations of the main effects N, MPCR and Round, and any possible interactions (with the constraint that the main effects of all interactions were included). Some of these permutations are redundant in that they are described already above. We made no hypotheses here but merely selected among these models, on the basis of their mean information criterion score, to test if any outperform our learning model (Supplementary Table 4).

Data availability

Figures 2 and 3, and supplementary figures 3-5 have associated raw data. Data available from the Dryad Digital Repository: (https://doi.org/10.5061/dryad.fn2z34tsv)73. There are no restrictions on data availability.

Code availability

The R code for the simulation study is included in the Dryad Digital Repository: (https://doi.org/10.5061/dryad.fn2z34tsv)73.