A guide to performing Polygenic Risk Score analyses

Abstract

The application of polygenic risk scores (PRS) has become routine across biomedical research. Among a range of applications, PRS are exploited to assess shared aetiology between phenotypes, to evaluate the clinical utility of genetic data for common disease, and as part of experimental studies in which, for example, experiments are performed on individuals, or their biological samples (e.g. tissues, cells), at the tails of the PRS distribution and contrasted. As GWAS sample sizes increase and PRS become more powerful, they are set to play a key role in research and personalised medicine. However, despite the growing application and importance of PRS, there are limited guidelines for performing PRS analyses, which can lead to inconsistency between studies and misinterpretation of results. Here we provide detailed guidelines for performing polygenic risk score analyses. We discuss different methods for the calculation of PRS, outline standard quality control steps, provide an introductory online tutorial, highlight common misconceptions relating to PRS results, offer recommendations for best-practice and discuss future challenges.

Genome-wide association studies (GWAS) have identified a large number of genetic variants, typically single nucleotide polymorphisms (SNP), associated with a wide range of complex traits [1–3]. However, the majority of these variants have a small effect and typically correspond to a small fraction of truly associated variants, meaning that they have limited predictive power [4–6]. Using a linear mixed model in the Genome-wide Complex Trait Analysis software (GCTA) [7], Yang et al (2010) demonstrated that much of the heritability of height can be explained by evaluating the effects of all SNPs simultaneously [4]. Subsequently, statistical techniques such as LD score regression (LDSC) [8,9] and the polygenic risk score (PRS) method [5,10] have also aggregated the effects of variants across the genome to estimate heritability, to infer genetic overlap between traits and to predict phenotypes based on genetic profile [5,6,8–10].

While GCTA, LDSC and PRS can all be exploited to infer heritability and shared aetiology among complex traits, PRS is the only approach that provides an estimate of genetic propensity to a trait at the individual level. In the standard approach [5,11–14], polygenic risk scores are calculated by computing the sum of risk alleles corresponding to a phenotype of interest in each individual, weighted by the effect size estimate of the most powerful GWAS on the phenotype. Studies have shown that substantially greater predictive power can usually be achieved by using PRS rather than a small number of genome-wide significant SNPs [11,15,16]. As an individual-level proxy of genetic liability to a trait, PRS are suitable for a range of applications. For example, as well as identifying shared aetiology among traits, PRS have been used to test for genome-wide gene*environment and gene*gene interactions [15,17], to perform Mendelian Randomisation studies to infer causal relationships, and for patient stratification and sub-phenotyping [15,16,18]. Thus, while polygenic scores represent individual genetic predictions of phenotypes, prediction is often not the end objective, rather these predictions are then typically used for interrogating hypotheses via association testing.

Despite the popularity of PRS, there are minimal guidelines [12] on how best to perform and interpret PRS analyses. Here we provide a guide to performing polygenic risk score analysis, outlining the standard quality control steps required, options for PRS calculation and testing, and interpretation of results. We also outline some of the challenges in PRS analyses and highlight common misconceptions in their interpretation. We will not perform a comparison of the power of different PRS methods nor provide an overview of PRS applications, since these are available elsewhere [12,14,19,20]. Instead we focus this article on the issues relevant to PRS analyses irrespective of method used or application, so that researchers have a starting point and reference guide for performing polygenic score analyses. Accompanying this article is an online tutorial for guiding users through the steps of a standard PRS analysis, with example data and scripts provided.

1. Introduction to Polygenic Risk Scores

We define polygenic risk scores, or polygenic scores, as a single value estimate of an individual’s common genetic liability to a phenotype, calculated as a sum of their genome-wide genotypes, weighted by corresponding genotype effect size estimates (or Z-scores) derived from summary statistic GWAS data. These effect size estimates may be scaled or shrunk, as discussed in Section 3. The use of summary statistic data for the genotype effect size estimates distinguishes polygenic scores from phenotypic prediction approaches that exploit individual-level data only. In the latter, genotype effect sizes are typically estimated in joint models of multiple variants and prediction performed simultaneously, using approaches such as best linear unbiased prediction (BLUP) [21,22] or least absolute shrinkage and selection operator (LASSO) [23,24]. While we note that such methods may offer great promise in performing powerful prediction within large individual-level data sets [24], we limit our focus to polygenic scores specifically, which we believe are likely to have enduring application due to: (i) data sharing restrictions limiting full access to individual-level data, (ii) heterogeneity across cohorts reducing the motivation to pool individual-level data, (iii) the best sources of individual-level data – large population cohorts, such as the UK Biobank [25] – having relatively few individuals with specific diseases compared to dedicated case/control studies, which have not usually provided individual-level data, (iv) the desire to test specific hypotheses on richly phenotyped small-scale local data sets, leveraging powerful summary statistics.

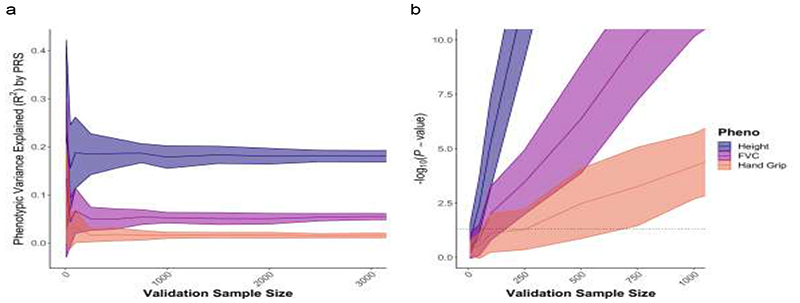
Therefore, PRS analyses can be characterized by the two input data sets that they require: (i) base (GWAS) data: summary statistics (e.g. betas, P-values) of genotype-phenotype associations at genetic variants (hereafter SNPs) genome-wide, and (ii) target data: genotypes and phenotype(s) in individuals of the target sample. If the effects of the SNPs were estimated from the GWAS without error, then the PRS could predict the phenotype of individuals in the target data with variance explained equal to the “SNP-heritability” (h_snp²) of the trait [26]. However, due to error in the effect size estimates and inevitable differences in the base and target samples, the predictive power of PRS are typically substantially lower than h_snp² (see Figure 6a) but will tend towards h_snp² as GWAS sample sizes increase.

Figure 6.

Examples of performance of PRS analyses on real data by validation sample size, according to (a) phenotypic variance explained (R²), (b) association P-value. UK Biobank data on Height (estimated heritability h² = 0.49 [8]), Forced Volume Capacity (FVC) (estimated heritability h ² = 0.23 [8]), Hand Grip (estimated heritability h² = 0.11 [8]), were randomly split into two sets of 100,000 individuals and used as base and target data, while the remaining sample was used as validation data of varying sample sizes, from 50 individuals to 3000 individuals. Each analysis was repeated 40 times with independently selected validation samples. While these results correspond to performance in validation data, the association P-values should reflect empirical P-values estimated from target data (as described in Section 4.7).

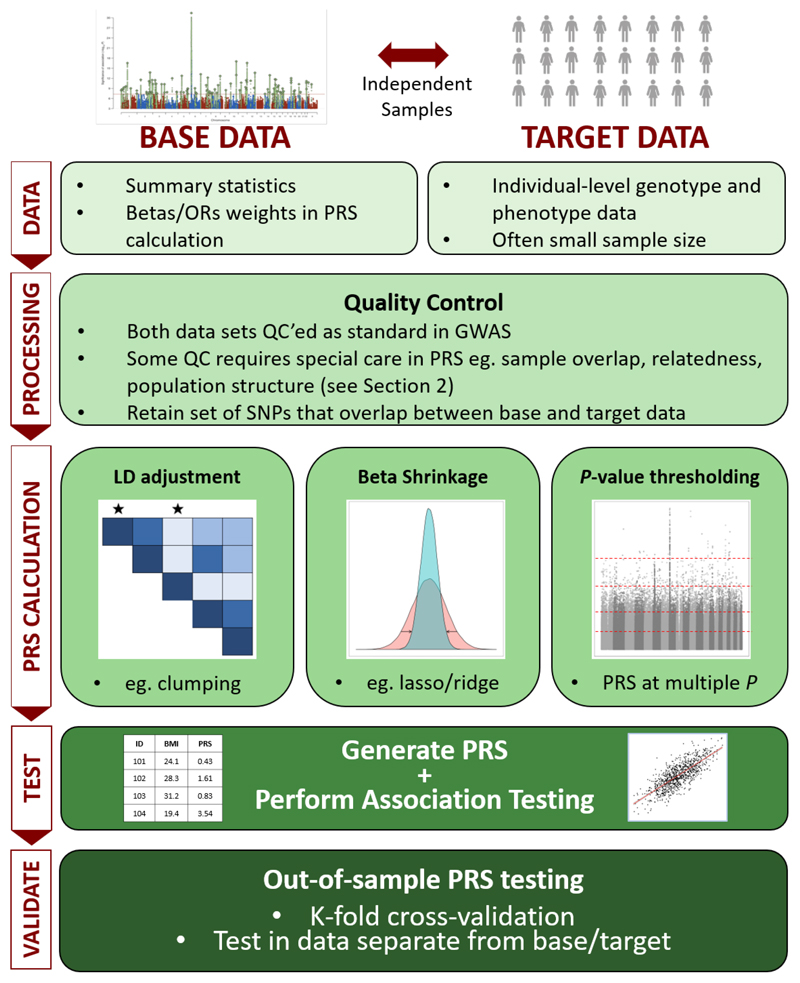
Important challenges in the construction of PRS are the selection of SNPs for inclusion in the score and what, if any, shrinkage to apply to the GWAS effect size estimates (see Section 3.1). If such parameters are already known, then PRS can be computed directly on the target individual(s). However, when parameters for generating an optimal PRS are unknown, then the target sample can be used for model training, allowing optimisation of model parameters. How to perform this parameter optimisation without producing overfit PRS is discussed in Section 4.6. Figure 1 summarises the fundamental features of a PRS analysis and reflects the structure of this guide. Having defined PRS according to the base and target data that they exploit, in the next section we outline recommended quality control (QC) of both data sets.

Figure 1.

The Polygenic Risk Score (PRS) analysis process. PRS can be defined by their use of base and target data, as in Section 1. Quality control of both data sets is described in Section 2, while the different approaches to calculating PRS – e.g. LD adjustment via clumping, beta shrinkage using lasso regression, P-value thresholding – is summarised in Section 3. Issues relating to exploiting PRS for association analyses to test hypotheses, including interpretation of results and avoidance of overfitting to the data, are detailed in Section 4.

2. Quality Control of Base and Target data

The power and validity of PRS analyses are dependent on the quality of the base and target data. Therefore, both data sets must undergo quality control (QC) to the high standards implemented in GWAS studies (see [27–29]), while numerous QC issues specific to PRS analyses need special attention. Particular care should be taken over these QC procedures since certain errors will aggregate across SNPs when PRS are computed. Below, we outline these QC measures, which should act as a QC checklist for PRS analyses. Researchers can practice performing these QC steps in our online tutorial: https://choishingwan.github.io/PRS-Tutorial/.

QC relevant to base data only

Heritability check

A critical factor in the accuracy and predictive power of PRS is the power of the base (GWAS) data [5], and so to avoid reaching misleading conclusions from the application of PRS we recommend only performing PRS analyses that use GWAS data with a chip-heritability estimate h _snp ² > 0.05. If an h _snp ² estimate has not been reported for these data, then we suggest using a software for estimating h _snp ² from GWAS summary statistics, such as LD Score regression [8] or SumHer [30].

Effect allele

Some GWAS results files do not make clear which allele is the effect allele and which is the non-effect allele. If the incorrect assumption is made in computing the PRS, then the effect of the PRS in the target data will be in the wrong direction. Therefore, to prevent the generation of spurious results, the identity of the effect allele from the base GWAS data must be obtained.

QC relevant to target data only

Sample size

We recommend performing PRS analyses that involve association testing on target sample sizes of at least 100 individuals (or effective sample sizes [31] over 100 for case/control data) and caution against analyses that utilise base data with low h _snp ² and small target sample size. This is to minimize the generation of misleading results due to the less stringent quality control feasible on small samples, potentially inaccurate adjustments (e.g. from population structure adjustments and LD calculations), and from underpowered association tests (see Section 4.7).

QC relevant to base and target data

Standard GWAS QC

Researchers should follow established guideline, e.g. [27–29] – we recommend [28] – to perform standard GWAS QC on the base and target data. Since the option of performing QC on the base GWAS data will typically be unavailable, researchers should ensure that high quality QC was performed on the GWAS data that they utilize. We recommend the following QC criteria for standard analyses: genotyping rate > 0.99, sample missingness < 0.02, heterozygosity P > 1x10^-6, minor allele frequency (MAF) > 1%, imputation ‘info score’ > 0.8. If both the base and target data are very large then SNPs with MAF < 1% may be included, in which case we recommend a minor allele count > 100 in both base and target data to ensure the integrity of normality assumptions implicit in association testing and linkage disequilibrium (LD) calculation. Future work will be required to integrate the effects of extremely rare and common variants and to establish whether their joint effects are typically additive [32]. PLINK is a useful software for performing these, and other, QC procedures [33,34].

File transfer

Since most base GWAS data are downloaded online, and base/target data transferred internally, one should ensure that files have not been corrupted during transfer (e.g. using md5sum [35]). PRS calculation errors are often due to corrupt files.

Genome Build

Ensure that the base and target data SNPs have genomic positions assigned on the same genome build [36]. LiftOver [37] is an excellent tool for standardizing genome build across different data sets.

Ambiguous SNPs

If the base and target data were generated using different genotyping chips and the chromosome strand (+/-) for either is unknown, then it is not possible to match ambiguous SNPs (i.e. those with complementary alleles, either C/G or A/T) across the data sets, because it will be unknown whether the base and target data are referring to the same allele or not. While allele frequencies can be used to infer which alleles match [38], we recommend removing all ambiguous SNPs since the allele frequencies provided in base GWAS are often those from resources such as the 1000G project, and so aligning alleles according to their frequency could lead to systematic biases in PRS analyses.

Mismatching genotypes [Strand mismatch]

When there is a non-ambiguous mismatch in allele coding between the data sets, such as A/C in the base and G/T in the target data, then this can be resolved by ‘flipping’ the alleles in the target data to their complementary alleles. Most polygenic score software perform this flipping automatically.

Duplicate SNPs

Ensure that there are no duplicated SNPs in either the base or target data since this can cause polygenic score software to crash or produce errors unless the software used specifically checks for duplicated SNPs.

Sex chromosomes

It is standard in GWAS QC to remove individuals for which there is a difference between reported sex and that indicated by the sex chromosomes. While this could be due to a difference in sex and gender identity, it may instead reflect mislabeling of samples or misreporting and thus correspond to unreliable data. A sex check can be performed in PLINK [33], in which individuals are called as females [males] if their X chromosome homozygosity estimate is < 0.2 [> 0.8]. In addition to this check, if the aim of an analysis is to model autosomal genetics only, then we recommend that all X and Y chromosome SNPs are removed from the base and target data to eliminate the possibility of non-autosomal sex effects influencing results. However, proper modelling of the sex chromosomes should improve the predictive power of PRS [39] and so may be performed in practice. However, given the different options for modelling of the sex chromosomes [40], reporting of analyses that incorporate the sex chromosomes should highlight how the modelling assumptions may have influenced results.

Sample overlap

Sample overlap between the base and target data can result in substantial inflation of the association between the PRS and the trait tested in the target data [41] and so must be eliminated. The level of inflation is proportional to the fraction of the target sample that overlaps the base sample [41], and so the problem is not resolved by using large base data. Ideally overlapping samples are removed from the base data and the base GWAS is recalculated, since this allows calculation of polygenic scores in all target individuals and, if the base is larger than the target, leads to greater power for association testing than removing the overlapping samples from the target data. A practical solution that is often applied in consortium meta-analysis settings is to generate leave-one-out meta-analysis GWAS results [42], whereby each contributing study is excluded from the meta-analysis in turn. This allows each study to be subsequently used as independent target data. Alternatively, leave-one-out meta-analysis results can be calculated analytically by rearranging the meta-analysis formula [43], but this requires availability of the contributing study-level GWAS and the meta-analysis results without subsequent adjustments, such as ‘genomic control’ [44]. We expect a correction in scenarios of partial or unknown sample overlap, when these solutions are unavailable, to be an objective of future methods development; until then, we recommend that any risk of overlap is minimised through judicious use of target samples, and if overlap is still possible then inflation in results cannot be ruled out.

Relatedness

A high degree of relatedness among individuals between the base and target data can also generate inflation of the association between the PRS and target phenotype. While population structure produces a correlation between genetics and environmental risk factors that requires a broad solution (see Section 3.4), the problem is exacerbated with inclusion of very close relatives since they may share the same household environment as well. Thus, if genetic data from the relevant base data samples can be accessed, then any closely related individuals (e.g. 1^st/2^nd degree relatives) across base and target samples should be removed to eliminate this risk. If this is not an option, then every effort should be made to select base and target data that are unlikely to contain highly related individuals. However, statistical power can be compromised in analysing base and target samples from different populations, as discussed in Section 3.4, and so ideally base and target samples are as similar as possible without risking inclusion of overlapping or highly related samples.

3. The Calculation of Polygenic Risk Scores

Once quality control has been performed on the base and target data, and the data files are formatted appropriately, then the next step is to calculate polygenic risk scores for all individuals in the target sample. There are several options in terms of how PRS are calculated. GWAS are performed on finite samples drawn from particular subsets of the human population, and so the SNP effect size estimates are some combination of true effect and stochastic variation – producing ‘winner’s curse’ among the top-ranking associations – and the estimated effects may not generalise well to different populations (Section 3.4). The aggregation of SNP effects across the genome is also complicated by the correlation among SNPs – ‘Linkage Disequilibrium’ (LD). Thus, key factors in the development of methods for calculating PRS are: (i) the potential adjustment of GWAS estimated effect sizes via e.g. shrinkage and incorporation of their uncertainty, (ii) the tailoring of PRS to target populations, and (iii) the task of dealing with LD. We discuss these issues below, and also those relating to the units that PRS values take, the prediction of traits different from the base trait, and multi-trait PRS approaches. Each of these issues should be considered when calculating PRS irrespective of setting or subsequent application. While some of these steps are automated in specific PRS software, it is important to be aware of the underlying issues to aid understanding and interpretation.

3.1. Shrinkage of GWAS effect size estimates

Given that SNP effects are estimated with uncertainty and since not all SNPs influence the trait under study, the use of unadjusted effect size estimates of all SNPs could generate poorly estimated PRS with high standard error. To address this, two broad shrinkage strategies have been adopted: (i) shrinkage of the effect estimates of all SNPs via standard or tailored statistical techniques, and (ii) use of P-value selection thresholds as inclusion criteria for SNPs into the score.

• (i)PRS methods that perform shrinkage of all SNPs [19,20,45,46] generally exploit commonly used statistical shrinkage/regularisation techniques, such as LASSO or ridge regression [19], or Bayesian approaches that perform shrinkage via prior distribution specification [20,45,46]. Under different approaches or parameter settings, varying degrees of shrinkage can be achieved: some force most effect estimates to zero or close to zero, some mostly shrink small effects, while others shrink the largest effects most. The most appropriate shrinkage to apply is dependent on the underlying mixture of null and true effect size distributions, which are likely a complex mixture of distributions that vary by trait. Since the optimal shrinkage parameters are unknown a priori, PRS prediction is typically optimised across a range of (tuning) parameters (for overfitting issues relating to this, see Section 4.4), which in the case of LDpred, for example, includes a parameter for the fraction of causal variants [45].
• (ii)In the P-value selection threshold approach [11,13], only those SNPs with a GWAS association P-value below a certain threshold (e.g. P < 1x10^-5) are included in the calculation of the PRS, while all other SNPs are excluded. This approach effectively shrinks all excluded SNPs to an effect size estimate of zero and performs no shrinkage on the effect size estimates of those SNPs included. Since the optimal P-value threshold is unknown a priori, PRS are calculated over a range of thresholds, association with the target trait tested for each, and the prediction optimised accordingly (see Section 4.4). This process is analogous to tuning parameter optimisation in the formal shrinkage methods. An alternative way to view this approach is as a parsimonious variable selection method, effectively performing forward selection ordered by GWAS P-value, involving block-updates of variables (SNPs), with size dependent on the increment between P-value thresholds. Thus the ‘optimal threshold’ selected is defined as such only within the context of this forward selection process; a PRS computed from another subset of the SNPs could be more predictive of the target trait, but the number of subsets of SNPs that could be selected is too large to feasibly test given that GWAS are based on millions of SNPs.

3.2. Controlling for Linkage Disequilibrium

The association tests in GWAS are typically performed one-SNP-at-a-time, which, combined with the strong correlation structure across the genome, makes identifying the independent genetic effects (or best proxies of these if not genotyped/imputed) extremely challenging. While conditioning on the effects of multiple SNPs simultaneously [47] provides better estimates of the independent effects, this requires access to raw data on all samples and so researchers generally need to use standard GWAS (one-SNP-at-a-time) summary statistics to compute polygenic scores. There are two main options for approximating the PRS that would have been generated from full conditional GWAS: (1) SNPs are clumped (i.e. thinned, prioritising associated SNPs) so that the retained SNPs are largely independent of each other and thus their effects can be summed, assuming additivity, (2) all SNPs are included and the linkage disequilibrium (LD) between them is accounted for. In the ‘standard approach’ to PRS calculation, option (1) is combined with P-value thresholding and called the C+T (clumping + thresholding) method, while option (2) is generally favoured in methods that implement traditional shrinkage methods [19,20,45,46]. The comparable performance of the standard approach to more sophisticated methods [14,19,20] may be due to the clumping process capturing conditionally independent effects well; note that, clumping does not merely thin SNPs by LD at random (like pruning) but preferentially selects SNPs most associated with the trait under study, and retains multiple SNPs in the same genomic region if there are multiple independent effects there: clumping does not simply retain only the most associated SNP in a region. A criticism of clumping, however, is that researchers typically select an arbitrarily chosen correlation threshold [41] for the removal of SNPs in LD, and so while no strategy is without arbitrary features, this may be an area for future development of the standard approach.

Both clumping and LD modelling require estimation of LD between SNPs. Assuming that LD values derived from the base data are unavailable, then those from a closely matched reference sample, such as from the 1000G data [47], should be used to approximate these. If there are no reference samples well-matched to the population composition of the base data, then the target data can be used to estimate LD instead. However, if base and target samples are drawn from different populations then the PRS results may differ substantively from those that would have been obtained had LD been computed in the base data itself.

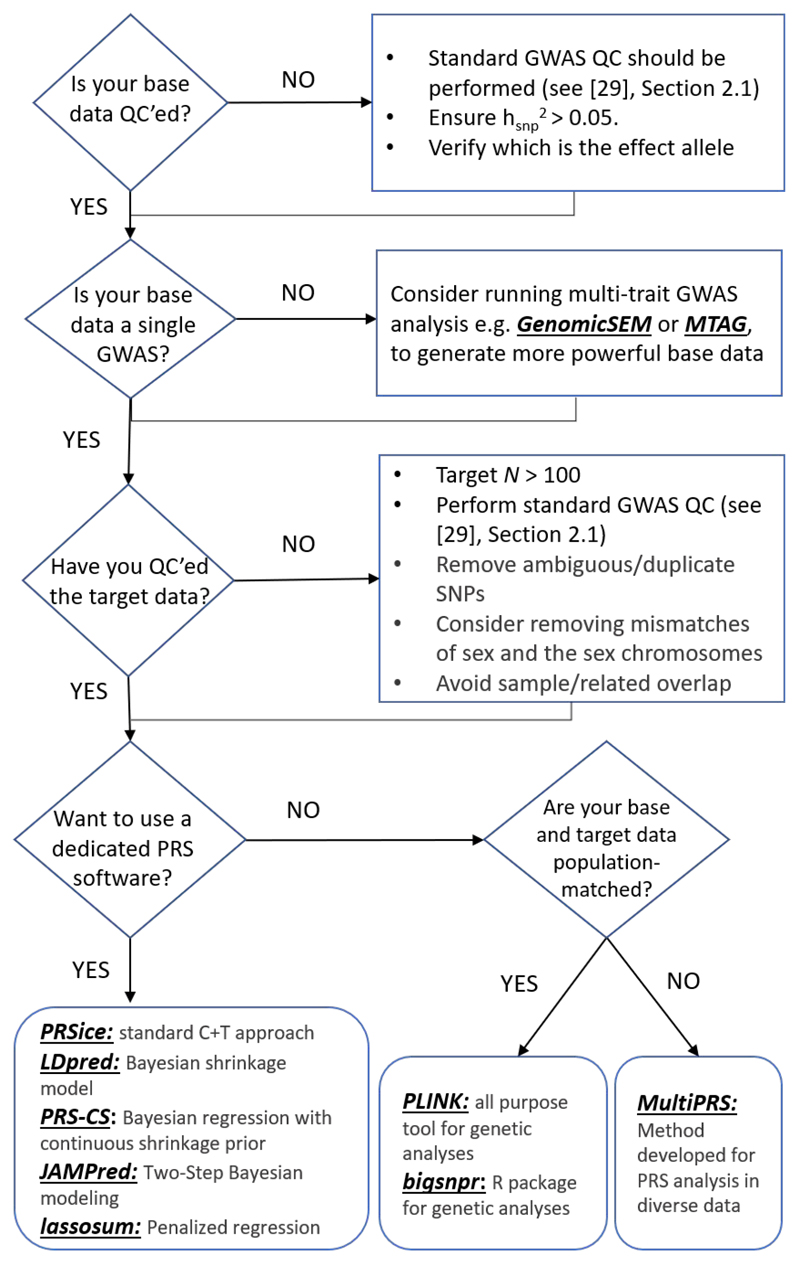
Figure 2 illustrates a PRS analysis pipeline, highlighting QC steps and some of the main software programs presently available to users as options, which may be selected according to scientific question, data and user preference. In our tutorial that accompanies this article https://choishingwan.github.io/PRS-Tutorial/, readers can perform PRS analyses on example data using several of these programs to become familiar with the process.

Figure 2.

Shown is a flow chart of suggested analytical steps that can be followed to perform quality control and select software for PRS analyses. GenomicSEM [48] and MTAG [49] are software allow for joint analysis of summary statistics from GWAS of different complex traits and can help to boost power; Common PRS software include (but not limited to): PRSice [13,14], LDpred [45], PRS-CS [20], JAMPred [46], and lassosum [19]; PLINK [33,34] and bigsnpr [50] can be used to for the implementation of custom pipelines; and MultiPRS [51] is a method to perform PRS analyses on admixed population.

3.3. PRS units

When calculating PRS, the units of the GWAS effect sizes determine the units of the PRS; e.g. if calculating a height PRS using effect sizes from a height GWAS that are reported in centimetres (cm), then the resulting PRS will also be in units of cm. PRS may then be standardised, dividing by the number of SNPs to ensure a similar scale irrespective of number of SNPs included, or standardised to a standard normal distribution. However, the latter discards information that may wish to be retained, since the absolute values of the PRS may be useful in detecting problems with the calculation of the PRS or the sample (see Section 4.5), identifying outliers, comparing or combining PRS across different samples, or even detecting the effects of natural selection.

If the trait was log-transformed, standardised or inverse normalised prior to GWAS, then the reported effect sizes will reflect this. Log-transformed effect sizes can be back-transformed, via ‘exponentiating’, to obtain effect sizes in the measured units, but typically the data required to back-transform normalised data (in Z-score units) are unavailable. In this case PRS should be calculated based on Z-score effect size estimates and the resulting scores will be in Z-score (ie. standard deviation) units. When PRS are calculated using effect sizes in units of the trait then an implicit assumption is that the absolute effect of risk alleles is equal in the base and target populations, while when computed in Z-score units the assumption is that the effect sizes are equal in terms of their impact as a fraction of trait variance.

In calculating PRS on a binary (case/control) phenotype, the effect sizes used as weights are typically reported as log Odds Ratios (log(ORs)). Assuming that relative risks on a disease accumulate on a multiplicative rather than additive scale [52], then PRS should be computed as a summation of log(OR)-weighted genotypes. It is important to know which logarithmic scale was used, since the PRS will take the same units and so will be required to enable transformation back to an OR scale.

3.4. Population structure and the generalisability of PRS

Population structure is the principal source of confounding in GWAS (post-QC). Briefly, structure in mating patterns in a population generates structure in genetic variation, correlated most strongly with geographic location, and environmental risk factors can be similarly structured. This creates the potential for associations between many genetic variants and the tested trait that are confounded by e.g. location [53,54]. Uncorrected, this can lead to inflated estimates of PRS prediction because the PRS then also acts as a marker for local environmental risk factors. PRS prediction can be inflated further by a household effect, whereby the genetics of an individual are correlated with their household environment when created by parents (or siblings) with shared genetic tendencies (e.g. of diet, books, exercise) [55,56]. A key difference between these sources of PRS inflation is that the genetic variants leading to inflation via local environment are typically non-causal of the outcome, being incidentally associated with the environment, whereas those creating the household effect are causal. Stringent adjustment of effects via principal components (PCs) [53] or the use of mixed models [57] within the base and target samples can minimize inflation due to population structure. Family designs, utilizing e.g. sibling [56] or adoptee data [58], provide a convenient way of separating out the influence of an individual’s genetics from those of the household effect [55] and population structure on PRS-trait associations.

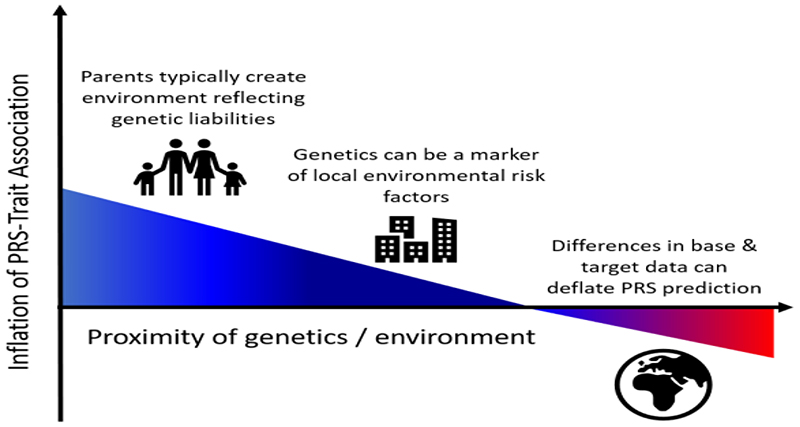
In contrast, PRS computed in individuals from a target sample that differs substantially from the base sample (e.g. by location, age, socio-economic position) can suffer from deflation [59–62], due to differences in e.g. genotype effect sizes, allele frequencies, linkage disequilibrium or environment between the two samples. This may be especially true for traits underlain by strong genetic*environment correlations or interactions. Given the potential implications for disparity in healthcare caused by PRS that only perform well in a subset of the human population, we expect the issue of the generalizability of PRS to be an active area of methods development in the coming years [51,61]. Figure 3 illustrates some of the major sources of bias in PRS-trait associations, highlighting the potential inflation caused by similarity of genetics and the environment and the likely deflation caused by dissimilarity of genetics and the environment.

Figure 3.

Illustration of major sources of inflation/deflation of PRS-trait associations. If the target data differs markedly from the base data in terms of allele frequencies, linkage disequilibrium, the environment, selection pressures etc, then the PRS-trait association will likely be deflated relative to had the target sample been well-matched to the base data (note that relative inflation is possible here if the trait has greater heritability in the target sample than the base sample [62]). Correlation between population structure of genetics and the environment can inflate PRS-trait associations unless fully controlled for. This inflation can be exacerbated by a household effect in which parents produce an environment reflecting their genetic tendencies [56], known as passive gene*environment correlation [63]. This figure illustrates in simple form some of the broad major influences on PRS-trait associations and their typical effects; it is not intended to capture the many nuances and exceptions involved or other important effects such as evocative or active genetic-environment correlations [63].

3.5. Predicting Different Traits and exploiting multiple PRS

While PRS are often analysed in scenarios in which the base and target phenotype are the same, many published studies involve a target phenotype different from that on which the PRS is based. These analyses fall into three main categories: (i) optimising target trait prediction using a different but similar (or ‘proxy’) base trait: if there is no large GWAS on the target trait, or it is underpowered compared to a similar trait, then prediction may be improved using a different base trait (e.g. education years to predict cognitive performance [64,65]), (ii) optimising target trait prediction by exploiting multiple PRS based on a range of different traits in a joint model [48,66,67], or (iii) testing for evidence of shared aetiology between base and target trait [68,69]. Applications (i) and (ii) are straightforward in their aetiology-agnostic aim of optimising prediction, achieved by exploiting the fact that a PRS based on one trait is predictive of genetically correlated traits, and that a PRS computed from any base trait is sub-optimal due to the finite size of any GWAS. A common concern in using multiple PRS as predictors is that the PRS are computed from the same SNPs and are thus inherently correlated. However, this is true of any epidemiological prediction model, since predictors typically comprise multiple shared risk factors. Therefore, when a large number of PRS (> 10) are included as predictors in a joint model then the risk of overfitting and multicollinearity should be minimised as in standard prediction modelling, such as by applying shrinkage techniques (as in [67]) or using a random effects term to model their correlation (as in [66]).

Application (iii) is inherently more complex than (i) and (ii) because there are different ways of defining and assessing ‘shared aetiology’ [70]. Shared aetiology may be due to so-called horizontal pleiotropy (separate direct effects) or vertical pleiotropy (downstream effect) [70] and there are several quantities that can be estimated – genetic correlation [9], genetic contribution to phenotypic covariance (co-heritability) [72,73], or a trait-specific measure (e.g. where the denominator relates to the genetic variance of only one of the traits).

While there is active method development in these areas [48,66,67] at present, the majority of PRS studies use exactly the same approach to PRS analysis whether or not the base and target phenotypes differ. However, this is rather unsatisfactory because of the non-uniform genetic sharing between different traits. In PRS analysis, the effect sizes and P-values are estimated using the base phenotype, independent of the target phenotype. Thus, a SNP with high effect size and significance in the base GWAS may have no effect on the target phenotype. The standard approach could be adapted so that SNPs are prioritized for inclusion in the PRS according to joint effects on the base and target traits and modifications of other PRS approaches will likely be developed in future, each tailored to specific scientific questions.

4. Interpretation and Presentation of Results

Once PRS have been calculated, selecting from the options described in Section 3, typically a regression is then performed in the target sample, with the PRS as a predictor of the target trait, and covariates included as appropriate. In this section we consider how results from PRS analyses are measured and plotted, how to avoid overfitting, the predictive power and accuracy of PRS, and the interpretation of results in terms of genetic associations and the potential clinical utility of PRS.

4.1. Association and goodness-of-fit metrics

A typical PRS study involves testing evidence for an association between a PRS and a trait(s) in the target data and evaluating its potential effect. The association between PRS and outcome can be measured with standard association or goodness-of-fit metrics, such as the P-value to test a null hypothesis of no association, phenotypic variance explained (R²), effect size estimate (beta or OR) per unit of PRS or between specific strata e.g. high vs low risk individuals (see Sections 4.2, 4.3), and with measures of discrimination in disease prediction, such as area under the curve (AUC) or area under the precision recall curve (AUPRC). The association between the PRS and the target trait is usually tested in a linear (continuous trait) or logistic (binary trait) regression, adjusting for covariates e.g., PCs, sex, age. When covariates are included in the model then measures such as the incremental R² (increase in R² with addition of PRS to model), which isolate the explanatory power of the PRS, should be reported. The incremental R² is necessarily greater than zero within sample and can only be accurately estimated out-of-sample (Section 4.6). The inclusion of covariates that are predictors of the outcome should increase statistical power and lead to more accurate estimates of PRS effects in linear regression settings but in certain scenarios can reduce power in logistic regression settings [74]. Therefore, we recommend sensitivity analyses with and without other predictors when testing binary outcomes.

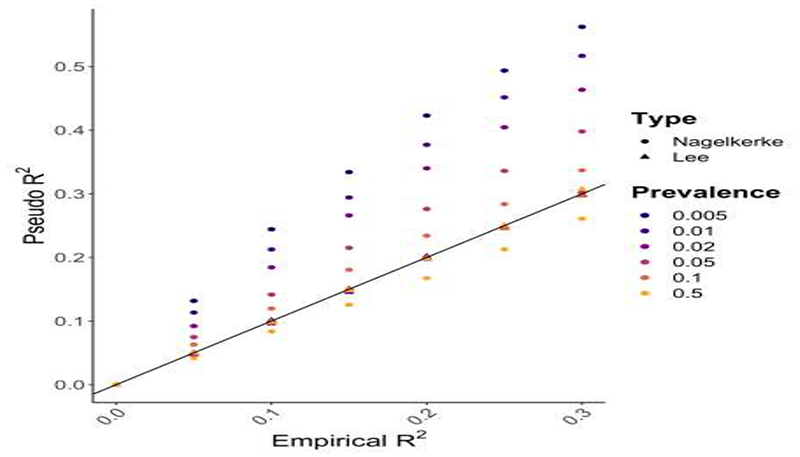
While variance explained (R²) is a well-defined concept for continuous trait outcomes, only conceptual proxies of this measure (“pseudo-R²”) are available for case/control outcomes. A range of pseudo-R² metrics are used in epidemiology [75,76], with Nagelkerke R² perhaps the most popular. However, Nagelkerke R² and similar metrics produce biased estimates of the phenotypic variance on the liability scale when the case/control ratio is not equal to the disease prevalence [75]. Intuitively, the R² on the liability scale here estimates the proportion of variance explained by the PRS of a hypothetical normally distributed latent variable that underlies and causes case/control status [75,77]. Heritability is typically estimated on the liability scale for case/control phenotypes [12,75,77]. Lee et al [75] developed a pseudo-R² metric that accounts for case/control ratio and is measured on the liability scale. Under simulation we demonstrate that this metric indeed controls for case/control ratios that do not reflect disease prevalence, while Nagelkerke R² can be highly biased (Figure 4). Thus, we recommend use of the Lee R² when the disease prevalence can be well approximated and, if not, the Lee R² should be estimated for a range of realistic prevalences to provide a credible interval of R² values. Note that if the cases in a study are milder or more severe than typical cases, then the estimated pseudo-R² (including the Lee R²) will be deflated or inflated, respectively.

Figure 4.

Results from a simulation study comparing Nagelkerke pseudo-R² with the pseudo-R² proposed by Lee et al [75] that incorporates adjustment for the sample case/control ratio. In the simulation, 2,000,000 samples were simulated to have a normally distributed phenotype, generated by a normally distributed predictor (e.g. a PRS) explaining a varying fraction of phenotypic variance, with a residual error term to model all other effects. Case/control status was then simulated under the liability threshold model according to a specified prevalence. 5,000 cases and 5,000 controls were then randomly selected from the population, and the R² of the original continuous data (Empirical R²), estimated by linear regression, was compared to both the Nagelkerke R² (discs) and the Lee R² (triangles) based on the corresponding case/control data by logistic regression.

4.2. Graphical representations of results: bar and quantile plots

When the standard C+T approach is used, the results of PRS association tests are sometimes displayed as a bar plot, where each bar corresponds to the result from testing a PRS comprising SNPs with GWAS P-value exceeding a given threshold. Typically, a small number of bars are shown, reflecting results at round-figure P-value thresholds (5e-8, 1e-5, 1e-3, 0.01, 0.05, 0.1, 0.2, 0.3 etc). If ‘high-resolution’ scoring [13] is performed then a bar representing the most predictive PRS may be included. Usually the Y-axis corresponds to the phenotypic variance explained by the PRS (R² or pseudo-R²) and the value over each bar (or its colour) provides the P-value of association between the PRS and target trait. See examples of bar plots in [78–81]. It is important to note that the P-value threshold of the most predictive PRS is a function of the effect size distribution, the power of the base (GWAS) and target data, the genetic architecture of the trait, and the fraction of causal variants, and so should not be interpreted merely as reflecting the fraction of causal variants. For instance, if the GWAS data are relatively underpowered then the optimal threshold is more likely to be P = 1 (all SNPs) even if a small fraction of SNPs are causal (see [5] for details).

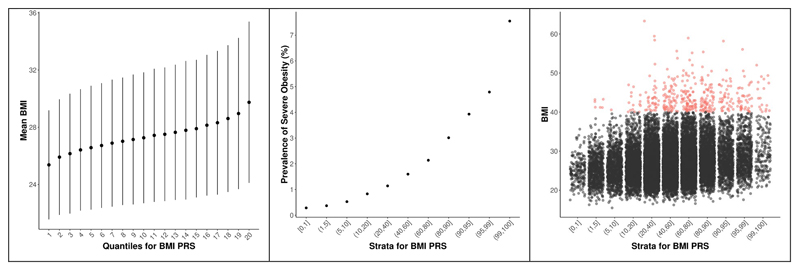
While metrics such as the AUC and R² can provide sample-wide summaries of the predictive power of a PRS, it can be useful to inspect how trait values vary with increasing PRS or to gauge the elevated disease risk among individuals with the highest PRS. This can be easily visualized using a quantile plot (Figure 5a). Quantile or strata plots in PRS studies are usually constructed as follows [18,82–84]. The target sample is first separated into strata of increasing PRS. For instance, 20 equally sized quantiles, each comprising 5% of the PRS sample distribution (Figure 5a), or unequal strata, usually used to highlight individuals with extreme PRS (Figure 5b). The phenotype values of each stratum are then either plotted directly as means or prevalences (as in Figure 5a, 5b) or are compared to those of a reference stratum (usually the median stratum or the remaining strata combined) one-by-one, with strata status as predictor of target phenotype (reference stratum coded 0, test stratum coded 1) in a regression. Performing a regression allows covariates to be adjusted for and will mean that the Y-axis takes values of beta (continuous trait) or odds ratio (binary trait).

Figure 5.

Three different ways of representing the same data. The data correspond to Body Mass Index (BMI) PRS calculated in 388,155 individuals in the UK Biobank data, derived using GIANT BMI GWAS as base data. (a) is a quantile plot with 20 quantiles of increasing BMI PRS Vs mean BMI (Y-axis), (b) is a strata plot with unequal strata of increasing BMI PRS Vs prevalence (%) of severe obesity (BMI > 40), (c) is a strata plot with the same strata as in (b), but here each individual’s BMI value is shown on the Y-axis. Lateral spread within each stratum is to make individual points visible and red points correspond to individuals with severe obesity. Qualitatively similar patterns should be expected for PRS corresponding to all reasonably heritable continuous or binary traits, with strength of patterns dependent on the predictive power of the PRS (here the PRS explains ~5% of BMI). BMI here could be considered analogous to the liability underlying a disease in the liability threshold model, and in this way plot (c) may be helpful in imagining the uncertainty in the true liability that underlies a PRS value for a disease.

Quantile plots corresponding to the effect of a PRS on a normally distributed target trait should reflect the S-shape of the probit function (Figure 5a). This is because the trait values are more spread out between quantiles at the tails of a normal distribution. Thus, plotting quantiles of PRS vs (absolute) effect on trait shows increasingly larger jumps up/down the Y-axis from the median to the extreme upper/lower quantiles. When unequal strata are plotted, with the smallest strata at the tails, then this effect appears stronger. When the target outcome is disease status and prevalence or odds ratio are plotted on the Y-axis, then the shape is expected to be different: here the shape is asymmetrical, showing a marked inflection at the upper end (Figure 5b), reflecting cases being enriched at the upper end only. Thus, inflections of risk at the tails of the PRS distribution [82,83] should be interpreted according to these expectations and not as interesting in themselves.

4.3. Interpretation for clinical utility

There is intense interest in the potential clinical utility of PRS – to improve diagnoses, to select optimal treatment, and in particular as part of preventative medicine [85–89]. Preventative medicine typically either seeks to shift entire trait distributions (e.g. to reduce population-wide BMI or salt intake) or to target high-risk individuals (e.g. screening according to age or multiple factors). The efficacy of each strategy in reducing disease burden is dependent on numerous statistical, behavioural and economic factors, discussed elsewhere [90,91]. If targeting high-risk individuals is evaluated as worthwhile for a given disease, then whether PRS can aid the subsequent stratified medicine approach taken should be considered. PRS has some attractive features as a clinical predictor, including being cheap, being available from birth and only requiring a single measure during life-time (although effects can vary by age [88]). Also, while PRS must be partially correlated with traditional risk factors given the heritability of most risk factors, PRS must also offer orthogonal information, in particular compared to family history, which does (might need two sentences for this, expanding on the family PRS issue – correlated but also independent) not differentiate between siblings despite their substantial variance in genetic risk. However, PRS often have small predictive power and so their potential utility has drawn scepticism [92–94] and generated active debate.

We use Figure 5, and BMI as an example, to illustrate in simple form some of the pertinent issues to the debate. The base data are the BMI summary statistics generated by the GIANT Consortium [1] while the target data are from the UK Biobank [25]: in these data, the PRS for BMI explains approximately 5% of the variation in BMI in the target data, which is typical for BMI and relatively high as a PRS in contemporary data. Figure 5b shows the prevalence of severe obesity across the strata, and in contrast to the moderate increase in mean BMI across quantiles (Figure 5a), shows a steep increase in obesity prevalence rates in the upper tail. The comparatively high risk in the most extreme strata, for obesity and other major diseases, has been used as an argument for the clinical utility of PRS [82,83]. However, Figure 5c highlights potential limitations. While the upper strata do have an elevated prevalence rate, the uncertainty in all individual predictions is extremely large, such that individuals should avoid interpretation of their PRS (unless considerably more powerful). Furthermore, most obese individuals have a normal or low PRS, highlighting a drawback of focusing on ‘high risk’ individuals when there is still substantial unexplained phenotypic variation. Finally, while the prevalence rates in the top 1% stratum (7.5%) are markedly higher than in the 2% – 5% stratum (4.8%), there are more individuals with severe obesity in the latter (likewise other stratum), and many are close to the obesity threshold, and so focusing on prevalence rates (or risk/odds ratios) could be misleading in terms of impact on public health, especially if the effects of BMI are continuous. Rigorous cost-benefit analyses to evaluate how estimated increases in predictive power offered by PRS are likely to translate into improvements in public health compared to alternative strategies, for different diseases, are critically needed. Until then, the debate on the topic is likely to remain largely semantic and huge investments in funds could be misguided unless robust evidence is followed.

4.4. Interpretation of genetic associations

PRS for many traits are presently such weak proxies of true genetic liability that the phenotypic variance that they explain is often very small (R² < 0.01). Association test results of PRS with very small estimated effects should be treated with caution given the possibility that they may have been generated by subtle uncorrected confounding. However, if the results are shown to be robust to confounding (see Section 3.4) then the effect size is not important if the aim is only to establish whether an association exists, which may provide aetiological insight.

Pleiotropy is ubiquitous in the genome [70,71], with potentially some shared genetic aetiology between the vast majority of phenotypes. This is likely due to the complex, highly interrelated biological and environmental network among human traits. For instance, a genetic predisposition to higher cognitive performance must, on average, lead to greater educational performance and higher socio-economic position [95]; higher socio-economic position is associated with the vast majority of diseases, and thus a component of the genetic aetiology of most diseases will be the genetics of cognition. This genetic component is likely extremely small for most diseases, but with sufficient sample size will generate significant genetic associations between cognition and many diseases (vertical pleiotropy), as well as between diseases (horizontal pleiotropy). Similar examples could be provided for genetic liabilities to addiction, risk-taking, confidence, depression, metabolism, immunity etc and the myriad of traits and diseases that they have downstream effects on. While this helps to explain both the high levels of pleiotropy and polygenicity observed in genomic data, it also warrants caution in interpretation of genetic overlap between phenotypes because an unconsidered or unknown shared sub-component of genetic risk may have driven the observed association. However, despite this complexity, important mechanistic insight can be provided by testing whether the shared aetiology between a pair of traits is due to horizontal or vertical pleiotropy [70], which is the focus of Mendelian Randomisation methods [96,97]. To this end, PRS may be useful in establishing the relative strength of genetic associations among a range of traits [43,98] and act as a step towards identifying casual mechanism [99].

4.5. PRS distribution

The central limit theorem dictates that if a PRS is based on a sum of independent variables (here SNPs) with identical distributions, then the PRS of a sample should approximate the normal (Gaussian) distribution. This is true even if the PRS has extremely low predictive accuracy, since the sum of random numbers are approximately normally distributed, and so a normally distributed PRS in a sample should not be considered as validation of the accuracy of a PRS or of the liability threshold model. However, strong violations of these assumptions, such as the use of many correlated SNPs or a sample of heterogenous ancestry (thus SNPs with markedly different genotype distributions), can lead to non-normal PRS distributions. Thus, inspection of PRS distributions may highlight calculation errors or problems of population stratification in the target sample not adequately controlled for.

4.6. Overfitting in PRS association testing

A common concern in PRS studies that adopt the standard (C+T) approach is whether the use of the most predictive PRS – based on testing at many P-value thresholds – overfits to the target data and thus produces inflated results and false conclusions. While such caution is to be encouraged in general, potential overfitting is a normal part of prediction modelling, relevant to the other PRS approaches (Figure 2), and there are well-established strategies for optimising power while avoiding overfitting [100]. One strategy that we do not recommend is to perform no optimisation of parameters – e.g. selecting a single arbitrary P-value threshold (such as P < x10^-8 or P = 1) – because this may lead to serious underfitting, which itself can lead to false conclusions.

The gold-standard strategy for guarding against generating overfit prediction models and results is to perform out-of-sample prediction. First, parameters are optimised using a training sample and then the optimised model is tested in a test or validation data set to assess performance. In the PRS setting involving base and target data sets, it would be a misconception to believe that out-of-sample prediction has already been performed because polygenic scoring involves two different data sets, when in fact the training is performed on the target data set, meaning that a third data set is required for out-of-sample prediction. The leave-one-out strategy often adopted in meta-analysis consortia (Section 2) is also at risk of overfitting if parameter optimisation and testing are both performed in the data set left out. In the absence of an independent data set, the target sample can be subdivided into training and validation data sets, and this process can be repeated with different partitions of the sample, e.g. performing 10-fold cross-validation [67,101,102], to obtain more robust model estimates. However, a true out-of-sample, and thus not overfit, assessment of performance can only be achieved via final testing on a sample entirely separate from data used in training.

Without validation data or when the size of the target data makes cross-validation underpowered, an alternative is to generate empirical P-values corresponding to the optimised PRS prediction of the target trait, via permutation [14]. While the PRS itself may be overfit, if the objective of the PRS study is association testing of a hypothesis – e.g. H0: schizophrenia and rheumatoid arthritis have shared genetic aetiology – rather than for prediction per se, then generating empirical P-values offers a powerful way to achieve this while maintaining appropriate type 1 error [14]. It is also even possible to generate optimised parameters for PRS when no target data are available [19].

4.7. Power and accuracy of PRS: target sample sizes required

In one of the key PRS papers published to date, Dudbridge 2013 [5] investigated the expected power and predictive accuracy of PRS according to derived formulae based on standard quantitative genetics models [103]. Dudbridge demonstrated that highly significant results observed in PRS association studies were consistent with expectations given the base and target sample sizes used, thus not necessarily due to confounding or bias, and calculated that several published studies with null results were likely underpowered. Dudbridge also showed that the power of PRS association testing is optimised using equal-sized base and target sample sizes, while individual-level predictive accuracy is optimised by maximising base sample size. To complement these theoretical expectations, we performed PRS analyses in the UK Biobank, testing traits with high (Height), medium (Forced Volume Capacity; FVC) and low (Hand Grip Strength) heritability. Sampling randomly from the UK Biobank, we generated a base GWAS of size 100k individuals, a target sample size of 100k for parameter optimisation, and a range of validation sample sizes from 50 to 3000. We performed PRS association tests using the standard C+T method in the validation data, predicting the same trait as used in the base GWAS, and repeating the validation sampling 40 times to estimate the variability in the results. Figure 6a displays the trait variance explained in the validation data across the range of sample sizes in the three target traits. Figure 6b displays the P-values from association testing of the PRS and each of the corresponding target traits. Since testing is performed in validation data, these results are reflective of the predictive power in PRS analyses in target data only if the parameters involved in PRS estimation (here the P-value threshold for inclusion) have been optimised; otherwise, these results are overestimates. While these results provide only an approximate indication of the performance of PRS analyses, researchers often wish to obtain some idea of whether their own data are sufficiently powered for future analyses or if they should acquire more data.

Conclusions

As GWAS sample sizes increase, polygenic scores are likely to play a central role in the future of biomedical research and personalised medicine. However, the efficacy of their use will depend on the continued development of methods that exploit them, their proper analysis and appropriate interpretation, and an understanding of their strengths and limitations.