Abstract
Detecting genetic variants associated with traits (quantitative trait loci, QTL) requires genotyped study individuals. Here we describe BaseQTL, a Bayesian method that exploits allele-specific expression to map molecular QTL from sequencing reads (eQTL for gene expression) even when no genotypes are available. When used with genotypes to map eQTL, BaseQTL has lower error rates and increased power compared with existing QTL mapping methods. Running without genotypes limits how many tests can be performed, but due to the proximity of QTL variants to gene bodies, the 2.8% of variants within a 100 kB window that could be tested contained 26% of eQTL detectable with genotypes. eQTL effect estimates were invariably consistent between analyses performed with and without genotypes. Often, sequencing data may be generated in the absence of genotypes on patients and controls in differential expression studies, and we identified an apparent psoriasis-specific eQTL for GSTP1 in one such dataset, providing new insights into disease-dependent gene regulation.
Genome-wide association studies (GWAS) have identified thousands of genetic variants associated with human disease, but their individual mechanisms remain largely unknown. The majority of variants are located outside coding regions, and are presumed to have regulatory function1. Direct regulatory effects result when the genetic variant and the target gene are located on the same chromosome, typically less than 1 MB apart, and the genetic variant affects only the expression of the gene copy on its same chromosome. These variants are referred to as cis-quantitative trait loci (cis-QTLs), for example, cis-eQTL for those which regulate gene expression. Although most gene proximal variants act in cis, some proximal variants may affect gene expression indirectly, commonly referred to as trans-eQTL. Most trans-eQTL are distant from their regulated gene.
Large studies have been established to map regulatory variants across a diverse range of tissues. Nonetheless, multiple studies have failed to enumerate more than a minority of genes regulated by disease-associated variants2–4. This is probably due to the highly context-specific effects of genetic variants on gene expression5,6 and that most eQTL studies so far have focused on healthy individuals and bulk tissues7. Gene expression data from specific cell types in disease contexts appear to be more informative for interpreting disease-associated variants8,9, but such datasets have often been generated in the context of biomarker studies or in efforts to understand the disease process rather than the genetics of gene expression. Therefore, such datasets are commonly small (<100 samples), may be designed to compare the same tissue in different contexts (for example, disease activity) and/or may have no genotype data available.
Standard eQTL studies estimate average fold change in expression according to allelic dose by comparing expression between genotyped individuals. eQTL methods are typically embedded within broader statistical analysis environments, so that custom analyses comparing fold-change estimates between sample contexts can be explored. The power to detect cis-eQTLs can be improved by approaches that additionally exploit imbalance in gene expression between chromosome pairs within heterozygous individuals, so-called allele-specific expression (ASE). However, ASE software is generally limited to detecting eQTLs, so it is difficult to extend to related questions such as comparing effects between conditions. Furthermore, to the best of our knowledge, all ASE methods so far also require study subjects to be genotyped.
Here we propose BaseQTL, for ASE analysis. By adopting a Bayesian approach, we can incorporate information from existing large eQTL studies, which allows us to shrink extreme fold-change estimates and improve accuracy in a way analogous to moderation of variance estimates in differential expression analyses10. We embed this within a standard Hamiltonian Monte Carlo environment11, allowing researchers to develop flexible analytic approaches appropriate to their data. The phase (assignment of alleles to one or other chromosomes within an individual) of regulatory single nucleotide polymorphisms (SNPs) and the genic SNPs at which allelic imbalance is measured is unknown, and standard ASE methods either infer phase from the individuals within each study or assume phase is known. Using a Bayesian approach, we also exploit external reference genotype panel data to improve phasing accuracy. Our model treats phase as latent (unknown), and we extend this latent structure to also treat candidate regulatory SNP (cis-SNP) genotypes as unknown, allowing us to analyze studies without separate genotype data.
As we are targeting sample sizes <100, we selected a subset of lymphoblastic cell line samples from Geuvadis12 for which genotypes and RNA-sequencing (RNA-seq) data are publicly available (86 samples labeled GBR and EUR). These samples form part of a larger analysis that we use as a gold standard to compare BaseQTL against standard eQTL and ASE methods when run with genotypes, and to compare the results of BaseQTL run with genotypes either available or masked.
We then used our method to call eQTLs in a publicly available RNA-seq data from 94 psoriasis and 82 normal skin samples13. The ability to call eQTLs in existing patient RNA-seq datasets, even when no genotypes are available, may help us better understand the mechanism underlying established GWAS signals for complex diseases.
Results
Basic model to detect cis-eQTL
To detect cis-QTL using RNA-seq data, standard methods test the association between a genotyped variant within a specific distance of a genome feature (gene, chromatin immunoprecipitation peak and so on) and the total count of short reads mapped to the feature. ASE models additionally exploit the knowledge that if the cis-SNP was associated with expression, we would expect this to result in imbalanced expression between the two chromosomes in individuals heterozygous at the cis-SNP. Phase-aware cis-QTL methods such as RASQUAL (Robust Allele Specific QUAntitation and quality controL)14, WASP15 or TReCASE (Total Read Counts Allele Specific Expression)16,17 substantially improve the power of sequencing-based QTL mapping by jointly modeling the differences in total read counts mapping to the feature between individuals, and the allelic imbalance at phased heterozygous SNPs located in the feature (fSNPs) within individuals, as functions of the genotype at the candidate cis-SNP (Fig. 1a). RASQUAL models total gene read counts with a negative binomial distribution, WASP with a beta negative binomial distribution and TReCASE with a Poisson–negative binomial mixture. For allelespecific signals, RASQUAL, WASP and TReCASE all use a beta binomial model, with some differences, compared in ref. 14. We begin by describing the TReCASE model16,17, which expresses the likelihood as a product of between- and within-individual components, and on which we base our approach.
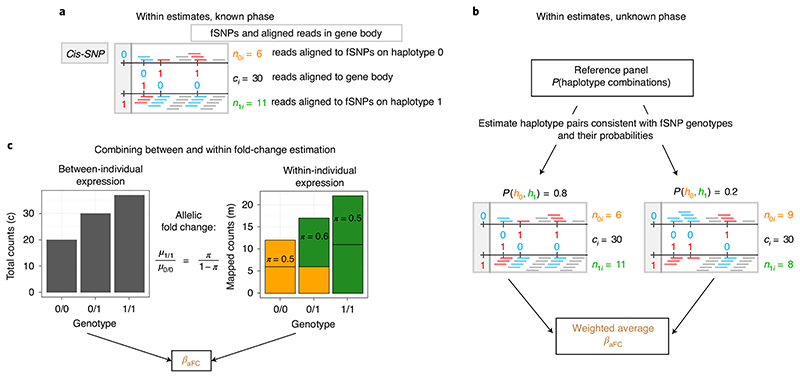
Fig. 1. Schematic representation of BaseQTL.
RnA-seq reads overlapping the reference or the alternative allele for a SNP are depicted in blue or red, respectively; gray reads do not overlap SNPs. a, Illustration of the data observed for a ‘true’ haplotype pair formed by a cis-SNP and three fSNPs within a gene in a heterozygous individual for the cis-SNP. ASe is measured as the proportion of reads mapping fSNPs within the haplotype carrying the cis-SNP alternative allele . The total counts mapped to the gene are indicated by ci. b, Model extension to account for unknown phase by assuming that β aFC follows a mixture distribution conditional on phase, which is treated as a latent variable. Phase probabilities are estimated from a large external reference panel conditional on the observed fSNP genotypes. c, In the joint model combining between-individual (left) and within-individual (right) variation, π is related to μ 0/0 and μ 1/1, which correspond to the expected total reads in homozygous individuals for the reference or alternative allele, respectively. The model estimates .
Here we summarize the key features, and assess each extension using a modest sample of RNA-seq lymphoblastoid cell lines from European individuals (GBR) generated by the Geuvadis project, for which genotypes are available12. We wanted to anticipate the scale of real-world datasets where sample sizes <100 are common and aimed to select the 91 samples with EUR ancestry and GBR code from the 1000 Genomes Project phase 3. Of those, 86 were deposited on ArrayExpress (E-GEUV-1) and were used in our analysis (Supplementary Data 1). To limit computational load, we restricted our analysis to all 264 expressed genes on chromosome 22 and cis-SNPs within 0.5 MB of each gene, thinned to r 2 < 0.9. All steps required to produce the inputs for BaseQTL along with the filtering steps and thresholds are detailed in Supplementary Section 3.
Accommodating unknown phase
With short-read data, phase cannot be known with certainty and our first extension was to treat phase as a discrete latent variable. The initial TReCASE model has previously been updated17 to assume that only the haplotypes formed by the fSNPs are observed, treating as latent the phase between the cis-SNP and the known haplotypes of the fSNPs, using a mixture model with likelihood maximized through an expectation maximization algorithm. TreCASE estimates haplotype probabilities on the basis of the ASE sample data. We employed a different strategy. We replaced the within-individual component of the initial TReCASE likelihood by a sum of beta binomial contributions conditional on haplotype phase, weighted by their respective probabilities conditional on the unphased genotypes at the fSNPs and cis-SNPs (Fig. 1b and Methods). We estimate these probabilities from 5,008 phased haplotypes from the cosmopolitan 1000 Genomes Project phase 3 reference panel to identify possible phased haplotype pairs and estimate their relative probabilities. To reduce computational burden, we do not update these estimates, and thus ignore any information about haplotype frequencies that exist in the ASE sample data, in favor of the probably more accurate estimates in the larger reference data. Consistent with previous reports that cosmopolitan reference haplotype panels are preferred18, we found that our method is generally robust to perturbations in the reference panel but, when mismatches between samples and reference panel are extreme, there is loss of power rather than any increase in false positives (Supplementary Table 1).
Modeling reference sequence mapping bias
Reference sequence mapping bias—the tendency of reads to map more easily to the reference sequence allele—can cause allelic imbalance to be overestimated in favor of the reference allele, and hence false-positive ASE results15,19–21. As expected, raw estimates of allelic imbalance in our Geuvadis data subset were indeed skewed towards over-representation of the reference allele (Fig. 2b and Supplementary Fig. 2c).
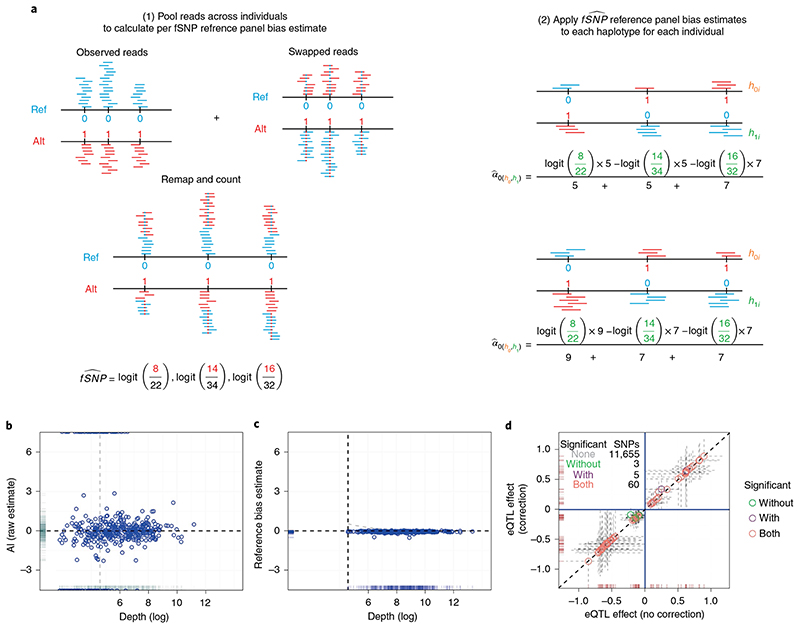
Fig. 2. Reference mapping bias correction.
a, Schematic representation of BaseQTL correction for reference panel bias. For each read that maps to an fSNP, we create a new read in which the allele of the fSNP is swapped (represented as a blue dot in a red read (alt–> ref) or a red dot in a blue read (ref->alt). The pooled reads, which have a 50:50 ratio of reads carrying the reference (ref) or alternative (alt) alleles at each fSNP, are remapped, and the number of reads mapping to each allele stored. b, For each fSNP we calculated the proportion of reads overlapping the alternative allele across all heterozygous individuals, which we refer to as the raw estimate of allelic imbalance. The plot shows logit-transformed raw estimates for AI (y axis) against depth (x axis) for each fSNP. The horizontal line indicates no allelic imbalance, the gray vertical line is displayed to ease comparison with c. c, Same as b but the y axis corresponds to the logit allelic imbalance (AI) estimates obtained as described in a. The vertical line indicates the read threshold selected for including estimates for inference (100 reads across all samples). d, each symbol corresponds to a gene–SNP association comparing the eQTL estimates (log2 allelic fold change) obtained with or without applying our reference bias panel correction.
Previous approaches to mitigate this phenomenon remove reads with evidence of mapping bias, while recognizing that discarding data is expected to reduce power15. Instead of discarding reads, we model bias explicitly using a random intercept per fSNP. We modified the procedure used by WASP15. WASP identifies reads that overlap known fSNPs. For each such read, a new pseudo read is generated in which the observed allele in the read is swapped to the unobserved allele and the pseudo read is remapped. If a pseudo read fails to map to the original location, the original read is discarded. In our approach, we create pseudo reads in a similar manner as WASP (Fig. 2a). The union of these observed and pseudo reads have exactly equal representation of reference and alternative alleles for each fSNP by design; any inequality in their realignment must reflect mapping biases.
We re-aligned this union of reads, and found estimated allelic imbalances showed similar skew towards the reference allele, but with much greater consistency between SNPs (Fig. 2c). This is due to leveraging many more reads compared with raw estimates (twice the total mapped reads compared with the subset of reads mapped to heterozygous individuals) as well as removing random noise due to true ASE (Figs. 1a and 2b,c). We used these estimates of allelic imbalance in these union of reads to define the parameters of a prior distribution for the random intercept, and found that adjusting for estimated reference mapping bias this way resulted in a small attenuation of eQTL effect estimates, with log fold changes on average 0.3% smaller (Fig. 2d).
Benchmarking of BaseQTL against standard methods
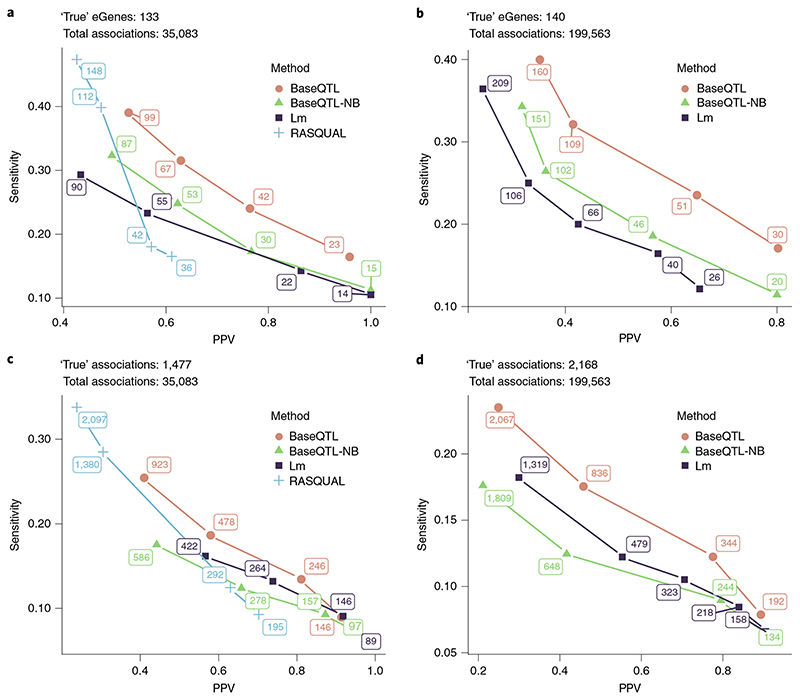
We validated BaseQTL against two other methods: standard linear regression, widely used in eQTL analysis, and RASQUAL14, representative of methods that jointly model between- and within-individual variation in a frequentist framework (Methods). BaseQTL shrinks eQTL effects via a prior distribution (Methods and Supplementary Section 2). We also ran BaseQTL modeling between-individual variation only to distinguish the effect of the prior from the ASE modeling. For the same gene–SNP associations within 100 kB (35,083 over 259 genes of which 133 were eGenes in the gold standard), BaseQTL outperformed both other methods (Fig. 3a,c) achieving the highest positive predictive value (PPV) and sensitivity trade-off. For example, calling significant associations in BaseQTL using a 99% credible interval we identified 23 eGenes, of which 22 were also called in the gold standard. Expanding the cis-window to 0.5 MB allowed us to test 199,563 gene–SNP associations over 264 genes, showing a similar trend with BaseQTL outperforming the linear model (Fig. 3b,d).
Fig. 3. Benchmarking BaseQTL with observed genotypes.
Analysis was performed with BaseQTL, BaseQTL modeling between-individual signals only (BaseQTL negative binomial (BaseQTL-nB)), a linear model (Lm) and when possible with RASQUAL using a subsample of 86 individuals from the Geuvadis project on genes expressed on chromosome 22. We used a published analysis of 462 individuals from Geuvadis dataset as a gold standard. For each method, significant eQTLs were called for a range of significance thresholds. Then, at each significance threshold, the PPV (the proportion of ‘true’ discoveries relative to all discoveries made by a method) and sensitivity (the proportion of ‘true’ discoveries made by a method relative to the ‘true’ positives in the gold standard) were calculated. eGenes correspond to genes with at least one significant association. For BaseQTL, significance thresholds correspond to different sizes of the posterior credible interval (99%, 95%, 90% and 85%) and we estimated an expected FDR given model assumptions (Methods). For the frequentist methods, we selected a range of FDR that matched the number of discoveries made by BaseQTL (Methods) to compare all methods along a similar range of sensitivity and PPV. Here the expected FDR and the PPV are quantities not mathematically related, as the FDR corresponds to the expected proportion of false discoveries estimated using the discovery data. The number of significant associations or eGenes are shown at each point. a,c, We analyzed 35,083 cis-SNPs within 100 kB of 259 genes (a), of which 1,477 (133 eGenes) (c) were significant in the gold standard. The expected FDRs for all methods were 0.1%, 1%, 5% and 10%. b,d, As in a and c except that a cis-window of 0.5 MB within 264 genes was used covering 199,563 gene–SNP associations (b) of which 2,168 (140 eGenes) (d) were significant in the gold standard. RASQUAL was excluded from the analysis as 54 genes failed to run. The expected FDRs for the Bayesian methods were as in a and c and for the linear model 5%, 10%, 20%, 30% and 50%.
From now on, we refer to significant associations as those for which 0 was excluded from the posterior 99% credible interval, which corresponded to the highest PPV for BaseQTL in Fig. 3. Overall, using BaseQTL on chromosome 22 (264 genes), we detected 192 eQTLs associated with 30 genes. Of those, 172 (90%) were replicated in the analysis of our gold-standard Geuvadis dataset corresponding to 24 eGenes (80%).
Detecting cis-eQTLs in datasets with no genotypes
We called fSNP genotypes by mapping feature reads to the reference genome and extended our latent model structure to treat the genotype at the candidate cis-SNP as latent, inferred probabilistically from the fSNP genotypes at the same time as haplotypes (Fig. 1b and Methods).
Genotyping error could have a major impact if not adequately controlled. Homozygous fSNPs miscalled heterozygous may lead to false positives because those mis-typed fSNPs will show strong allelic imbalance. We took multiple approaches to controlling genotyping errors (Methods). Of the 498 fSNPs called in the 86 samples by DNA-seq (42,828 calls), we were able to call 17,268 genotypes over 279 fSNPs with a 0.7% mismatch error (Supplementary Figs. 1 and 2, Supplementary Table 2 and Methods). While small, the mismatch rate is slightly higher than the error rate reported for shortread DNA sequencing, 0.1% to 0.6%, depending on the platform and the depth of coverage8.
We assessed the impact of using RNA-seq to call fSNPs by running BaseQTL with hidden genotypes for the cis-SNPs and the same fSNPs genotyped by either RNA-seq (RNA-fSNP) or by DNA-seq (DNA-fSNP). Estimated effects were strongly correlated (ρ = 0.89, Supplementary Fig. 3a), and all the eGenes detected with RNA-fSNPs were also called using DNA-fSNPs. We expect loss of power due to missing calls, but overall these results indicate that our method is robust to genotyping errors from RNA-seq.
Next, we examined the effect of cis-SNP imputation by running BaseQTL with ‘observed’ genotypes (measured by DNA-seq) for fSNPs and with observed or ‘hidden’ genotypes (inferred from RNA-seq) for the cis-SNP. We use a standard measure to assess imputation quality (Methods) and limited the analysis to cis-SNPs with imputation r 2 ≥ 0.5. The imputation of the cis-SNP produces more variability on the eQTL effects than genotype errors on the fSNPs (Supplementary Fig. 3b). We also assessed the effect of the quality of imputation on power by simulating typical scenarios for the magnitude of the true eQTL effect, a small sample size and common allele frequencies for the cis-SNP and fSNPs. As expected, without genotypes, power can decrease by nearly 100% when imputation quality is very low, and recovers with increasing imputation quality score (Methods and Supplementary Fig. 16).
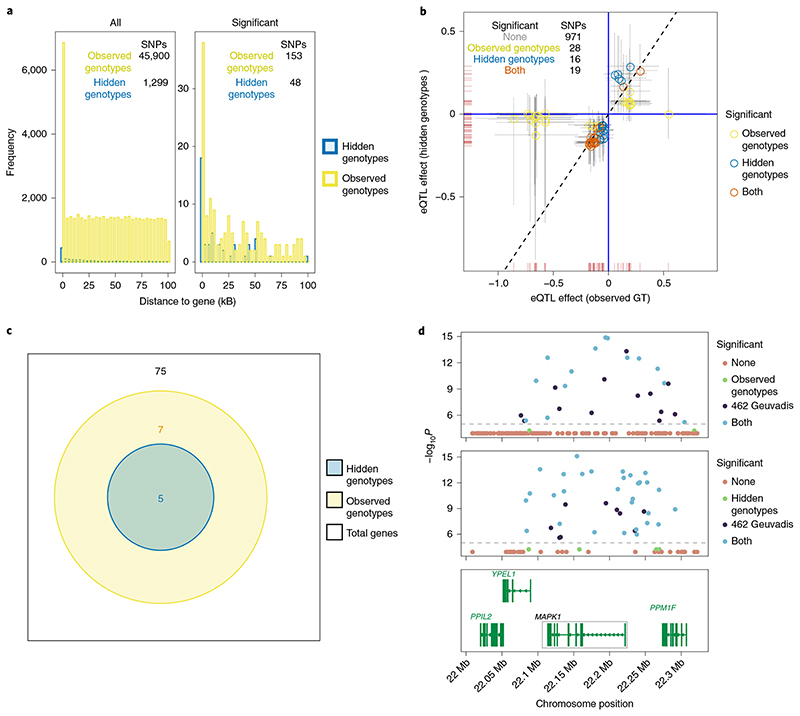
Finally, we conducted parallel analyses by BaseQTL either with DNA-seq genotypes or RNA-seq only. Of the 264 genes on chromosome 22 tested with observed genotypes, we were able to impute genotypes for 75 (28%). We selected a smaller cis-window than before (100 kb) because our method for hidden genotypes strongly relies on accurate haplotype phasing, which decreases with distance. Thus, within 100 kb, we were able to assess only 1,299 gene–SNP associations with hidden genotypes compared with 45,000 with observed genotypes (2.8%). However, both testable gene–SNP pairs with hidden genotypes and significant associations seen with observed genotypes tended to be closer to genes (Fig. 4a), in line with previous reports22, so that the proportion of significant associations discovered with hidden genotypes (48 significant out of 1,299 (3%)) was tenfold that with observed genotypes (153 significant out of 45,000 (0.3%)).
Fig. 4. eQTL effects estimated with BaseQTL with observed or hidden genotypes.
Only cis-SNPs with imputation score ≥0.5 were tested. a, For each cis-SNP, the distance to the gene was calculated as the closest to the start or end of the gene or 0 if within the gene. The left panel shows the cis-SNPs tested with hidden hidden genotypes (blue) or observed genotypes (yellow), whereas the right panel shows significant eQTLs. b, each symbol corresponds to a gene–SNP association tested with observed or hidden genotypes, respectively. For simplicity, only significant associations in at least one condition are shown, with the inset table summarizing all associations tested. Dashed lines show 99% credible intervals. c, Venn diagram showing the number of significant eGenes tested with or without genotypes. d, example of a signal detected from 462 Geuvadis individuals analyzed by linear model captured with 86 samples and observed genotypes (top) or hidden genotypes (middle) using BaseQTL. In each plot, each symbol corresponds to a MAPK1 cis-SNP within a 100 KB window. The x axis indicates the cís-SNP position and the y axis corresponds to the –log10 P reported for the 462 samples in Geuvadis. Points are colored by significance. Associations not reported in the analysis of 462 individuals in the Geuvadis study were considered not significant. To ease visualization, no significant associations in both datasets (‘none’) are plotted with a P value of 10-4 and those only called significant by BaseQTL with a P value of 5×10-5. Using a linear model on the 86 samples tested by BaseQTL would have detected no significant results (minimum P= 0.001). The bottom panel shows the genes within the cis-window for MAPK1.
On some occasions, for a given gene, the selection of cis-SNPs run with hidden genotypes and with observed genotypes may differ due to the different selection criteria in each method (Fig. 4b and Supplementary Section 3). To maximize the number of comparisons, when a tagging SNP was not originally run in one or other condition, we ran it additionally to ease comparison. Thus, we compared the same 1,034 gene–SNP associations with or without genotypes over 75 genes. The direction of the estimates for the eQTL effect was invariably consistent with hidden or observed genotypes (correlation 0.3, Fig. 4b). With hidden genotypes, we detected 5 eGenes, a subset of the 12 with observed genotypes (Fig. 4c). We also checked whether the significant associations detected with hidden genotypes were reported in our gold-standard Geuvadis dataset23. The power to detect eQTL effects without genotypes was 13% (35 significant associations both in the gold standard and with hidden genotypes out of 264 significant in the gold standard). To specifically assess the effect of missing genotypes on power, we compared the same gene–SNP associations with and without genotypes (as shown in Fig. 4b) and then calculated power relative to the Geuvadis eQTL analysis of the 462 samples. Of the common associations tested in both conditions, 215 were significant in the gold standard, 45 with genotypes and 25 with missing genotypes, which corresponds to 20% power with genotypes and 12% without. In this case, the smaller sample size has a stronger effect in power compared with the lack of genotypes. Moreover, we found 73% of the significant gene–SNP associations (35/48) detected with hidden genotypes (3/5 eGenes) were also significant in the gold standard. However, of the two genes not found in the gold standard, for APOL2 only one significant association out of 28 was detected with hidden genotypes and for NDUFA6 the same cis-SNP, rs55816780, is an eQTL in larger studies (>2,000 individuals) in blood24, which may reflect gain of power from ASE. An example of an eQTL signal that was successfully captured with no previous knowledge of genotypes is shown in Fig. 4d. Imputation quality score had only limited influence on the PPV (Supplementary Fig. 4). However, we report results with an imputation quality score of at least 0.5 as a good trade-off between minimizing the chance of false positives and the number of associations tested.
Novel skin eQTL in psoriatic and normal skin
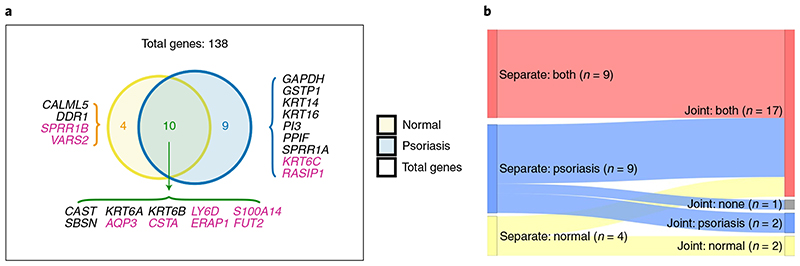
Finally, we used our method to find eQTLs in a publicly available RNA-seq dataset of 94 psoriasis skin samples and 82 controls13. To maximize discoveries relevant to psoriasis, we selected genes upregulated in psoriasis versus normal skin (51 genes13 and Methods), and/or within 100 kB of a psoriasis GWAS hit25 (380 genes). From the 429 unique selected genes, we were able to test ASE for 138, with 118 tested in both skin types, 16 in psoriasis only and 4 in normal skin only. We found significant eQTLs for 21 genes: 8 in both conditions, 9 in psoriasis and 4 in normal skin only (Fig. 5a). Associations across 10 genes for the same SNPs were previously described in healthy skin26 or were previously reported eQTLs in psoriasis27 (Fig. 5a and Supplementary Data 2), including ERAP1, FUT2 and RASIP1, which have eQTLs that are psoriasis GWAS hits (rs30187 for ERAP1, rs492602 for FUT2 and RASIP1)25,26 (rs469758 and rs281379 proxies with r 2 = 1.0 and 0.8, respectively).
Fig. 5. eQTLs in skin.
a, Of 23 eGenes detected in analysis of either normal or psoriatic skin, 10 were significant in both. For genes in pink, the same gene–SNP associations were also significant in GTex for healthy skin (GTex analysis V7). Moreover, associations for ERAP1 and FUT2 have been observed in a previous study of eQTLs in psoriasis28. b, Sankey plot comparing results from running psoriasis and normal skin samples in separate models or jointly modeling eQTL effects. All the genes shown in a were run with the joint model except for CSTA, which was excluded because only one cis-SNP was tested with normal skin and the significant signal observed in psoriasis could not be assessed in control samples (Supplementary Data 2). All 9 genes for which we observed signals in both tissues when run independently remained significant in both conditions with the joint model, and for 8 of the 13 genes with apparent condition-specific effects, the joint model favored a shared signal. Note that one psoriasis-specific gene in the individual models (SPRR1A) was no longer significant in the joint model (indicated as ‘none’).
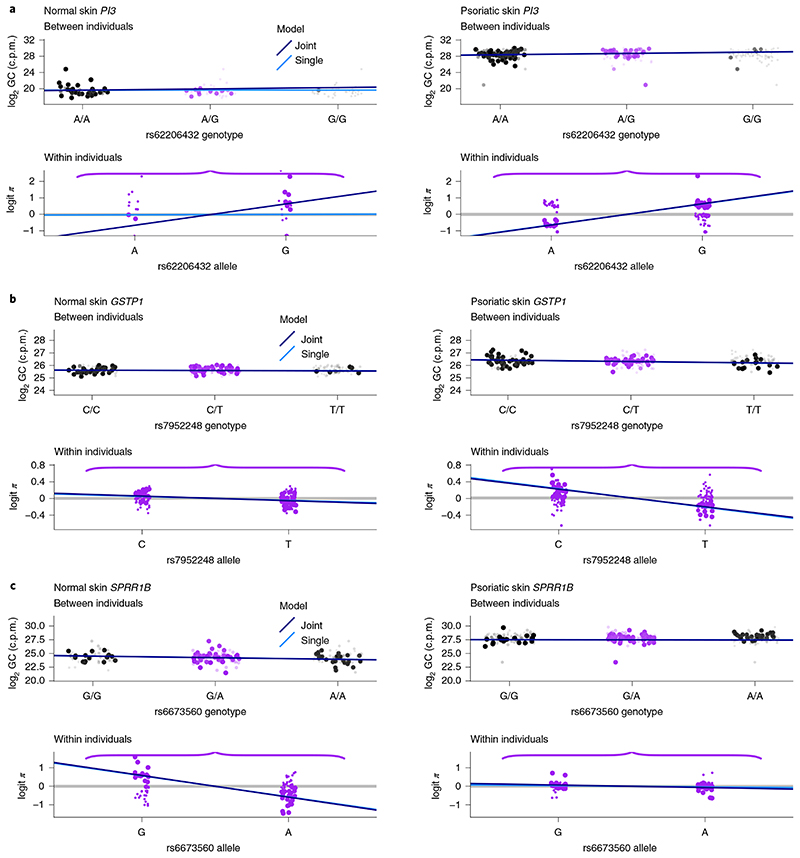
We exploited the flexibility available through using a standard statistical modeling language to jointly model eQTL effects in normal and psoriasis tissues to determine whether apparent psoriatic-specific effects reflected a lack of power in normal skin samples or were truly specific to psoriasis tissue (Methods). We considered the 23 genes that were run in both skin types with significant associations at least in one (Fig. 5a). Our joint model estimates two parameters: β a, which corresponds to the addition of the coefficients for the allelic fold change in each skin and β d, which corresponds to their difference (Methods). We are particularly interested in β d for assessing whether there is a difference in effects across conditions. We set our prior for β d that expects half of true eQTL signals to be shared in both tissues and half tissue specific (Methods). All of the eGenes with common signals across skin types assessed with separate models were also shared with the joint model (Fig. 5b). For the nine psoriasis eGenes we detected with independent models, only two were specific for psoriatic skin in the joint model, GSTP1 and KRT14, while eQTLs for SPRR1A were no longer significant (Fig. 5b). The six genes not found to be specific may reflect shared effects missed in the single models, or a lack of power in the joint model when expression is low in one tissue. PI3 encodes an antiproteinase and antimicrobial molecule highly upregulated in psoriasis13,28,29. We detected an eQTL for PI3 in psoriasis when we ran separate models but the low expression in normal skin meant the joint model could not convincingly reject a common effect in both skin types (Fig. 6a). GSTP1, which appears specific for psoriasis skin, is moderately upregulated in psoriasis (fold change 1.7), so the psoriasis-specific effect is unlikely to reflect lack of power on control samples (Fig. 6b). Of the four eGenes identified in normal skin only when running in separate models, the joint model confirmed specific signals in healthy skin for SPRR1B (Fig. 6c) and DDR1 (Fig. 5b). The SPRR1B eQTL was also found in healthy skin samples from the Genotype-Tissue Expression portal (GTEx). Its strong upregulation in psoriasis (fold change 12) is therefore likely to be driven by an eQTL-independent mechanism. Plots for each gene can be found in Supplementary Figs. 5–10 and summary results from the joint model can be found in Supplementary Data 2. We noted that for SBSN, the between-individual signal did not visually match the effect of the within-individual signal (Supplementary Fig. 10). Further examination of the ASE signal (Supplementary Fig. 11) shows that the two fSNPs have very different profiles, which would correspond with a spliceQTL at this variant reported in normal skin in GTEx.
Fig. 6. Disentangling condition-specific eQTLs.
eQTL estimates obtained from the joint or single models in normal (left) or psoriasis (right) skin. For each skin type, we plotted the eQTL effect illustrating the two components of our likelihood: between-individual (top) and within-individual (bottom) variation. Between-individual plots show the genotype of the cis-SNP (x axis) against the total gene counts per million reads, adjusted by GC content (Methods) in log2 scale (y axis). As genotypes are unobserved, for each individual we estimated the probability of each genotype and each point corresponds to the indicated genotype with the size and transparency indicating the probability. To represent within-individual variation only heterozygotes are considered. The y axis corresponds to the logit of the proportion of aggregated reads across fSNPs mapping the haplotype containing the alternative allele of the eQTL (as represented in Fig. 1). The light and dark blue lines correspond to the mean effect obtained with the single or joint model, respectively. a, PI3. b, GSTP1. c, SPRR1B.
Discussion
BaseQTL can extract meaningful genetic signals from datasets of small sample size even without genotypes. However, it is computationally intensive; therefore, it is particularly suited for targeted genomic regions to identify eQTL or condition-specific eQTLs. If genotypes are available, and for genome-wide scans, users may prefer to use a faster method such as TreCASE first and then run BaseQTL in a targeted manner.
Though we expect most of the eQTLs in close proximity to the gene body to act in cis, there may be a minority acting in trans. Trans-eQTLs will be appropriately modeled by the between-individual component of the model, with the ASE component biasing the eQTL estimate towards the null. Users interested in investigating this type of regulation can select to run BaseQTL using the between-individual variation only. We do not have a test to determine whether the effect is likely to be cis or trans, but a difference in posterior estimates from the two models would be suggestive of this.
When BaseQTL was applied to skin data, some of the signals we detected both in normal and psoriasis skin, although not reported in normal skin, have been reported in blood24 (CAST, GAPDH), T cells30 (PPIF) or adipose tissue (KRT16, GTEx), composed of adipocytes, myeloid and lymphoid cells, among other cell types. Moreover, the specific psoriasis signal we observed for GSTP1 is strongly significant in blood31 and neutrophils30 GSTP1 being highly expressed in monocytes, dendritic cells and peripheral blood mononuclear cells as a whole (https://www.proteinatlas.org/ENSG00000084207-GSTP1/tissue). Psoriatic skin is characterized by the proliferation of activated keratinocytes and infiltration of lymphocytes and myeloid cells32. The fact that some of the eQTLs we observed were replicated in larger studies of blood but not in GTEx for normal skin could reflect gain of power from ASE modeling in our method, infiltration of immune cells driving psoriasis signals or a combination of both. Modeling allele-specific signals may also detect genetic variants associated with splicing events, if fSNPs are concentrated in particular exons. This is probably the case for SBSN, for which the signal we detected has been reported as splicing-QTL in normal skin (GTEx).
The flexibility offered by embedding our method within standard statistical software allowed us to disentangle condition-specific effects. Overall, although our eQTL search targeted psoriasisspecific effects through its gene selection, joint modeling did not generally support condition-specific effects identified by running psoriatic and normal skin samples separately, in agreement with recent studies showing substantial eQTL sharing among related cell types or tissues9,33. We expect our method will facilitate discovery of cell type and disease-dependent eQTLs hidden in a wealth of RNA-seq data to unravel molecular mechanisms that contribute to disease.
methods
RNA-seq preprocessing
For the psoriasis and normal skin RNA-seq data, quality control using FASTQC indicated a high number of reads with Ns (strings of nucleotides for which the read processing software was not able to call a base), which were filtered out using Prinseq34. All samples were aligned to the human genome assembly GRCh37 using STAR35 (Supplementary Section 3), but three of the normal samples failed alignment due to some reads starting with an unrecognized character. Those samples were excluded from downstream analysis. We calculated gene expression abundance by overlapping reads to an union of annotated Ensembl exons, excluding reads overlapping different genes as we did not have strand information.
Calling genotypes from RNA-seq
For calling SNPs, we fed the aligned files into bcftools version 8 using the ‘mpileup’ and ‘call’ commands36 selecting uniquely mapping reads with a quality score of at least 20. We kept variants with read depth at least 10 that were also reported in the 1000 Genomes Project phase 3 (haplotypes from 2,504 individuals in NCBI build 37 (hg19) coordinates from mathgen.stats.ox.ac.uk/impute/1000GP_Phase3.html downloaded on 26 January 2018), with minor allelic frequency at least 0.05 in European individuals (Supplementary Section 3).
We assessed genotype errors in the fSNPs by comparing the genotype frequency of each fSNP in the samples relative to samples of same ethnicity in the reference panel by Fisher’s exact test. We report the P value for each fSNP as part of BaseQTL outputs.
Mitigating genotype errors
To minimize genotype errors, we performed the following steps. First, we called variants using a base quality threshold above 20 and limiting the analysis to uniquely mapped reads. Second, we filtered out called variants not annotated in the external reference panel (1000 Genomes Project phase 3). Third, we excluded variants according to a depth threshold. Ideally, we would be calling genotypes for the same fSNPs that were used for inference with observed genotypes, which were 498 fSNPs across 86 samples, adding to 42,828 calls. We have chosen to limit RNA-seq calls to those fSNPs with depth higher than 10 reads, as this value provided a good trade-off between error rate and missing calls (Supplementary Fig. 1a). Fourth, we excluded fSNPs with different rates of heterozygosity across study samples compared with European samples from the 1000 Genomes Project when performing a Fisher exact test (Methods). We selected a P value of 0.01 as a good compromise to exclude fSNPs with a high proportion of errors (Supplementary Fig. 1b). Using this threshold, we excluded 2 fSNPs with 33 errors out of 82 with 4 missing calls and 8 out of 20 with 66 missing calls. Last, we looked at whether fSNPs with a higher number of missing calls across samples were associated with higher error rates. This was not the case (Supplementary Fig. 2a), so we did not exclude fSNPs based on the number of missing calls.
Effect of imputation quality on the power of BaseQTL without genotypes
In this section, we simulate some scenarios to provide some concrete examples of the differences in power for BaseQTL when genotypes are or are not available. The code describing the simulations is available at https://gitlab.com/evigorito/baseqtl_paper.
We considered a cis-SNP and 3 fSNPs and we simulated 20,000 haplotypes (details below) for a population of 10,000 individuals. From this population, we sampled with replacement 2,000 haplotypes, which constituted our reference panel. In addition, we sampled with replacement 200 haplotypes from the population, which corresponded to our study sample of 100 individuals.
Simulation of haplotypes
Haplotypes are a combination of correlated binary variables. We simulated unordered haplotypes (H*) from a multivariate normal distribution (N) with mean μ and variance σ2 using the R package ‘mvtnorm’ assuming:
H* ≈ N(μ, σ 2)
For scenarios with equal effector allele frequency (EAF):
μ = (–0.5, –0.5, –0.5, –0.5)
for different EAF:
μ = (–0.1, –0.8, –0.2, –0.4)
To simulate different linkage disequilibrium (LD) scenarios, we varied the between-variable covariance as follows: LD 1, 0.6; LD 2, 0.7, LD3, 0.8; LD 4, 0.9; LD 5, 1.0.
Finally, we defined haplotypes by transforming the sampled values to 1, if positive, and 0 otherwise. This resulted in average allele frequencies ranging between 0.30 and 0.46 (Supplementary Table 3). For each of these choices of allele frequencies, we considered five scenarios of LD across SNPs (labeled LD 1–5). The squared correlation across SNPs for each of these scenarios is presented in Supplementary Tables 4–13. This allowed us to achieve a wide range of imputation quality scores for the cis-SNP.
Simulation of the eQTL effect
For the simulation of the effect size, we consider three true eQTL effects of 0.60, 0.65 and 0.70 allelic fold change (π), which in logit scale (β aFC) corresponds to 0.41, 0.62 and 0.55. For each individual (i) in the study sample (100 in total), we simulated total counts (ci) conditional on the genotype (Gi) for the cis-SNP assuming a negative binomial (NB) distribution with the expected mean in individuals homozygous for the reference allele of the cis-SNP set to 500 and overdispersion to 20. g(β aFC, Gi) models the genetic effect:
Then, to simulate ASE, we only co nsider heterozygous fSNPs. If h 1 is the haplotype carrying the alternative allele of the cis-SNP and t 1f the total number of reads overlapping fSNP f, we modeled the number of reads overlapping the allele of fSNP f in phase with the alternative allele with the cis-SNP with a beta binomial (BB) distribution as follows:
We set the number of total reads overlapping each fSNP as 1/10 of the total gene counts and the overdispersion parameter of the beta binomial distribution to 5.
Assessing power
For each condition (2 different sets of allele frequencies, 5 LD scenarios and 3 effect sizes), we simulated a study sample of 100 individuals and estimated the eQTL effect using BaseQTL with genotypes. We repeated this process 100 times and calculated power as the proportion of simulations for which the eQTL effect was significant based on the null value excluded from the 99% posterior credible interval. To assess the effect of imputation quality on power, we masked the genotype for the cis-SNP and ran BaseQTL without genotypes and calculated power in the same way as for observed genotypes (Supplementary Fig. 16). Without genotypes, power can decrease by nearly 100% when imputation quality is very low, and recovers with increasing imputation quality score.
Quantifying the number of reads overlapping heterozygous fSNPs
We adapted phASER37 to count the number of reads overlapping heterozygous fSNP in each sample. We followed the guidelines for ASE quantification suggested by Castel et al.37, by restricting the analysis to uniquely mapped reads with base quality for fSNPs ≥10 (Supplementary Section 3). We first used the ‘phaser.py’ command that counts reads overlapping SNPs. Phaser requires phased genotypes as input, so we used SHAPEIT238 using the 1000 Genomes Project phase 3 reference panel of haplotypes. Next, we adapted phASER function ‘phaser_gene_ae.py’ so that reads overlapping two or more heterozygous variants are only counted once. Last, as no strand information was available from RNA-seq, we only considered fSNPs uniquely mapped to one gene.
Statistical model
Our model maps QTLs for genetic variants (cis-SNPs) within a chosen distance of a feature (gene, isoform, ChIP peak). For each feature, we consider all SNPs within it (fSNPs) together with one potential regulatory SNP (cis-SNP). We jointly modeled the total read counts mapping the feature and the allelic imbalance between the chromosome pair carrying the cis-SNP and the fSNPs. Here we describe our model in full building from the basic model, which follows TrecASE17 adapted to account for reference panel bias then expanding by allowing phasing uncertainty and unobserved genotypes in a Bayesian framework.
Basic model for known phase and genotypes
We begin by summarizing our implementation of the TRecASE17 model with observed genotypes and fixed phasing (Fig. 1a). The likelihood can be decomposed into a product of contributions from between-individual (L between) and within-individual (Lwithin) likelihoods.
Let ci be the total read counts at the specific feature for individual i (i = 1,…,N), Gi the number of alternative alleles at the cis-SNP (0, 1, 2) and xi a vector of p covariates. We used the same parametrization as in TRecASE. We modeled total gene counts ci by a negative binomial distribution (f NB) with mean μi and and dispersion parameter Φ, to allow for overdispersion of RNA-seq reads:
where γ 0 corresponds to the intercept term, γj to the regression parameter for covariate j and g(β aFC, Gi) models the genetic effect and β aFC corresponds to the expected log allelic fold change of individuals homozygous for the alternative allele to those homozygous for the reference allele for the tested cis-SNP, as defined by the TReCASE17 model:
To model ASE, we assume initially that we observe for each individual i their complete haplotypes formed by the cis-SNP and fSNPs. We distinguish these as (h 0i, h 1i) according to the haplotype carrying the reference and alternative alleles at the cis-SNP, respectively, for individuals heterozygous at the cis-SNP, or arbitrarily for homozygous individuals. We count reads mapping to each haplotype by aggregating the counts across heterozygous fSNPs, according to their phase, in each individual. We denote mi as the aggregated counts mapping h 0i and h 1i. Of mi ≤ ci reads that overlap at least one heterozygous fSNP, we denote by n 1i the number that map to h 1i. We model n 1i|mi by a beta binomial distribution with π being the expected proportion of ASE and θ the overdispersion parameter as follows:
| (1) |
where α 0i is a random intercept parameter which depends on (h 0i, h 1i) (although we drop the dependence in the notation above for simplicity). α 0i is used to adjust for reference sequence mapping bias and would be 0 in the absence of bias. Homozygous individuals for the cis-SNP-carrying heterozygous fSNPs contribute information for estimating the overdispersion parameter θ. The within-individual likelihood can therefore be expressed as:
We put uninformative priors on the standard regression parameters and describe informative priors for α 0i and β aFC in the sections below. This basic model is described in Supplementary Fig. 13.
Extension 1 for modeling phasing uncertainty
We now relax the assumption that (h 0i, h 1i) are observed and known. We denote by Fi the unphased genotypes across the fSNPs for individual i, and by Gi their genotype at the cis-SNP.
We account for phasing uncertainty by averaging over the likelihood of n 1i|(h 0i, h 1i) over all Mi possible pairs of , weighted by a simple maximum likelihood estimate of estimated from the 1000 Genomes Project phase 3 reference panel. Note that n 1i, the number reads that overlap at least one heterozygous fSNP and map to h 1i, also varies with haplotype configuration. Thus, the likelihood contribution becomes
This ‘known genotypes’ model is described in Supplementary Fig. 14.
Extension 2 for unknown cis-SNP genotypes
We use the same idea to consider Gi latent, deriving the haplotype pair probabilities conditional only on the observed Fi, since Gi is directly specified by any haplotype pair.
but we also need to adjust
We use a standard measure of imputation quality (r 2) (ref. 39). Gi ∈ {0, 1, 2} and P(Gi = k|Fi) is the probability obtained by imputation that the genotype of the ith individual is k. The expected allele dosage for individual i is E(Gi) = P(Gi = 1|Fi) + 2P(Gi = 2|Fi) and the information metric is defined as
with G RP the genotype for the cis-SNP in the reference panel. We report this value in the summary output.
This ‘unknown genotypes’ model is described in Supplementary Fig. 15.
Extension 3 for jointly modeling different conditions in unpaired samples
We describe this in context of our application to psoriatic and normal skin, but the same method applies to compare unpaired data from any two conditions or cell types. We can write the between-individual component of independent models for normal (N) and psoriasis (P) skin as:
with the suffixes N and P indicating normal and psoriasis skin, respectively. We can jointly model total gene counts from normal and psoriasis skin as follows:
with the addition of the log allelic fold change:
the difference of the log allelic fold change:
and:
Rather than the more usual treatment contrasts, using zero/one dummy variables, we use sum-to-zero contrasts for the group variable. Mathematically, the models are identical, there is only a change in interpretation of the resulting coefficients. As a difference in conditions is our primary focus, the sum-to-zero contrast will directly assess whether there is any condition difference (regardless of direction/sign and interactions).
Prior specifications
Modeling reference mapping bias and prior on α 0i. Let be K the number of fSNPs for a given feature. To estimate expected reference panel bias at each fSNPk, we pooled observed and pseudo reads across all individuals. Let rk and tk be the number of reads re-aligned to the alternative allele and the total number of re-aligned reads, respectively. Thus, is the proportion of reads mapping to the alternative allele. On rare occasions, we observed higher than 0.5. Often when this happened, two or more SNPs were close to each other and shared overlapping reads with some alleles being reference and other alternative in the original read. We apply a binomial test assessing whether the bias estimate is significantly higher than 0.5 and discard those fSNPs with P < 0.01 because this pattern was not observed in the distribution of bias estimated from the observed reads only.
For any given gene, when β aFC = 0, then logit(πi) = α 0i (equation (1)). Note that the effect of any bias in our likelihood will depend on how the alternative allele at the fSNPs are phased with the alternative allele at the cis-SNP. Let , and define
We assume that log(α0i|(h0i,h1i)) is normally distributed, with expected value a weighted average of ãk over the fSNPs in the gene.
where sik is the number of reads in sample i overlapping fSNP k, and variance
We denote by E α the set of .
This is then an informative prior for α 0i that captures both local sequence effects and variable coverage between individuals and between SNPs, derived from observed data and its counterfactual alternative.
Informative prior on βaFC
We also use a data-derived prior on β aFC, building on information amassed from large eQTL studies. We used estimates of eQTL effects from cis-SNPs in GTEx, assuming true eQTL effects, νk at each SNPk, come from a mix of Gaussian distributions
where and that estimated eQTL effects are unbiased, that is where is the standard error of the eQTL effect for SNP/gene pair k, . We took a sample of 8 × 105, 4 × 105 and 7 × 104 values (summary statistics provided by GTEx, calculated using linear models) for unlinked SNPs within 1 Mb, 500 kB or 100 kB of the target gene’s transcription start site. Unlinked SNPs were selected genome wide by distance thinning, with a median distance between consecutive SNPs of 40 kB. We estimated by Metropolis–Hastings (Supplementary Table 14), and the code to run this analysis is available at https://github.com/chr1swallace/fitmix. The parameters identified by the model are shown in Supplementary Table 14).
Informative priors on β aFCA and β aFCD
We can express the prior for β aFC as:
When jointly modeling normal (N) and psoriasis (P) skin, we have:
β aFCA and β aFCD are independent by construction, so that
The priors for β aFCA and β aFCD can be expressed as a mixture of normal distributions with the components reported in Supplementary Table 15.
We assumed that probability of observing an eQTL effect in one tissue only would be similar to observing a shared eQTL given that the tissues are closely related.
Running linear model RASQUAL and BaseQTL
We ran the linear model in R using the ‘lm’ function regressing the logarithm of total gene counts on genotypes.
For RASQUAL, we created a VCF file with allele-specific counts using the tools provided in https://github.com/kauralasoo/rasqual/. We run RASQUAL with normal settings or the permutating test.
BaseQTL inputs were prepared as detailed above and at https://gitlab.com/evigorito/baseqtl_pipeline.
All three models were adjusted by GC-corrected library size as implemented in the library rasqualTools.
Calculation of false discovery rate (FDR)
For the linear model, we adjusted raw P values for multiple testing using the R function ‘p.adjust’ with method ‘BH’. The adjusted P values were then used to define significant associations at selected thresholds.
For RASQUAL, we used the method provided by RASQUAL14 itself, namely to generate a single P value from permuted data, and defining
where P perm corresponds to the permutation P values, P to observed data P values and α the significance threshold.
For BaseQTL, we calculated as described in ref. 40. Briefly, they define FDR as:
where δi is an indicator for rejecting the ith eQTL comparison, D = ∑δi corresponds to the number of rejections and ri ∈ {0, 1} denotes the unknown truth for a SNP being (1) or not (0) a cis-eQTL. While ri is unknown, we can calculate vi = P(ri = 1|data) from our posterior samples by calculating the proportion of times that 0 was excluded from credible intervals of specific size (α′ = 85%, 90%, 95% and 99%). (To do this with a manageable number of samples, we used normal approximations to the marginal posterior distribution of the eQTL effect). Under those conditions using a cis-window of 0.5 MB or 0.1 MB we observed the following :
The estimated FDR for each decision rule is presented in Supplementary Table 16.
Benchmarking BaseQTL against standard methods
We compared BaseQTL against two other methods: standard linear regression and RASQUAL14. For the same gene–SNP associations, we compared eQTL calls against a ‘gold standard’ analysis of 462 Geuvadis23 individuals. For each method, we calculated the ‘sensitivity’ (proportion of gold-standard hits detected by each method) and the empirical PPV for eQTLs or eGenes (genes with at least one significant eQTL) across a range of significance thresholds. We selected the 86 samples (Supplementary Data 1) and genes expressed in chromosome 22 but decreased the cis-window to 100 kB as 54/264 genes could not be run by RASQUAL within a 0.5 MB window. Using the smaller cis-window, only five genes failed with RASQUAL. For each method, significant eQTLs were called for a range of significance thresholds. Then, at each significance threshold, the PPV (the proportion of ‘true’ discoveries relative to all discoveries made by a method) and sensitivity (the proportion of ‘true’ discoveries made by a method relative to the ‘true’ positives in the gold standard) were calculated. ‘True’ discoveries correspond to eQTL with the same direction of effect and significant both in the gold standard and method. eGenes correspond to genes with at least one significant association. For BaseQTL, significance thresholds were selected based on different sizes of the posterior credible interval (99%, 95%, 90% and 85%). To relate these thresholds to the frequentist methods, we estimated an expected FDR given model assumptions. Then, for the frequentist methods, we selected a range of FDR estimated through the Benjamini–Hochberg procedure that matched the number of discoveries made by BaseQTL to be able to compare all methods along a similar range of sensitivity and PPV. The empirical PPV also allows us to calculate an empirical FDR, and, under the assumption that everything not detected at 1% FDR in the gold standard is truly false, suggests that the estimated FDR for every method is optimistic, with RASQUAL the most optimistic and the linear model the least. Although this over-optimism is itself likely to be overstated (for example, because not all true signals will achieve 1% FDR in the gold-standard reference), this highlights that the BaseQTL FDR is estimated assuming the model is correct. For all methods, the theoretical FDR underestimated the empirical FDR highlighting the importance of comparing method’s performance empirically.
Definition of significant associations using BaseQTL
We defined significant associations as those for which 0 was excluded from the 99% credible intervals of the posterior distribution, unless otherwise stated. This threshold was a good compromise between positive predictive value and sensitivity (Fig. 3).
Supplementary Material
Acknowledgements
This work was co-funded by the Wellcome Trust (WT107881), the MRC (MC_ UU_00002/2, MC_UU_00002/4, MC_UU_00002/13, MR/R013926/1 (to the CLUSTER Consortium)) and the NIHR Cambridge Biomedical Research Centre (BRC-1215-20014). S.R.W. was supported by the NIHR Cambridge Biomedical Research Centre. The views expressed are those of the author(s) and not necessarily those of the NIHR or the Department of Health and Social Care. This research was funded in whole, or in part, by the Wellcome Trust (WT107881). For the purpose of open access, the author has applied a CC BY public copyright licence to any author accepted manuscript version arising from this submission.
Footnotes
Author contributions
C.W. conceived of the project. E.V., C.W. and S.R.W. developed the model. E.V. wrote the software and performed analyses. W.-Y.L. and C.S. performed analyses and implemented the software. P.D.W.K. and S.R.W. contributed to the design of statistical analysis. E.V. and C.W. wrote the manuscript with input from all authors. C.W. directed the project.
Competing interests
The authors declare no competing interests.
Peer review information Nature Computational Science thanks Eric Gamazon, Wei Sun and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Handling editor: Ananya Rastogi, in collaboration with the Nature Computational Science team.
Reprints and permissions information is available at www.nature.com/reprints.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Data availability
Geuvadis samples were accessed from E-GEUV-1, ftp://ftp.sra.ebi.ac.uk/vol1/fastq, on 16 April 2017 or 23 January 2018 as indicated in Supplementary Table 1. Psoriasis and normal skin samples were accessed from E-GEOD-54456, ftp://ftp.sra.ebi.ac.uk/vol1/fastq, on 2 November 2018. GTEx associations for skin, blood and lymphoblastic cell lines corresponding to Analysis V7 were downloaded from https://gtexportal.org/home/datasets on 21 June 2019. Differentially regulated genes between psoriasis and normal skin were downloaded from https://ars.els-cdn.com/content/image/1-s2.0-S0022202X15368834-mmc2.xls on the 21 November 2018. We downloaded RNA-seq data from 86 Geuvadis samples with EUR ancestry (GBR code) from ArrayExpress (E-GEUV-1, Supplementary Table 1). We also analyzed 94 and 90 RNA-seq normal and psoriasis skin samples13 obtained from ArrayExpress (E-GEOD-54456). For the analysis of psoriasis eQTL we selected 51 upregulated genes in psoriasis versus normal skin (P ≤ 10-6 corresponding to family-wise error rate <0.025) and with a median expression of at least 500 RPKM in psoriasis samples (data extracted from https://ars.els-cdn.com/content/image/1-s2.0-S0022202X15368834-mmc2.xls 13, and/or within 100 kB of a psoriasis GWAS hit 25 (380 genes). Datasets to reproduce figures in this paper were uploaded into Zenodo 41.
Code availability
The source code and documentation for BaseQTL are available at https://gitlab.com/evigorito/baseqtl. We also provide a pipeline to process RNA fastq files and genotypes, if available, to prepare for running BaseQTL at https://gitlab.com/evigorito/baseqtl_pipeline (Supplementary Fig. 12 and Supplementary Section 3). The code to reproduce the figures is available at https://gitlab.com/evigorito/baseqtl_paper. The three repositories have been uploaded to Zenodo41.
References
- 1.Maurano MT, et al. Systematic localization of common disease-associated variation in regulatory DNA. Science. 2012;337:1190–1195. doi: 10.1126/science.1222794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chun S, et al. Limited statistical evidence for shared genetic effects of eQTLs and autoimmune-disease-associated loci in three major immune-cell types. Nat Genet. 2017;49:600–605. doi: 10.1038/ng.3795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Guo H, et al. Integration of disease association and eQTL data using a Bayesian colocalisation approach highlights six candidate causal genes in immune-mediated diseases. Hum Mol Genet. 2015;24:3305–3313. doi: 10.1093/hmg/ddv077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huang H, et al. Fine-mapping inflammatory bowel disease loci to singlevariant resolution. Nature. 2017;547:173–178. doi: 10.1038/nature22969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhernakova DV, et al. Identification of context-dependent expression quantitative trait loci in whole blood. Nat Genet. 2017;49:139–145. doi: 10.1038/ng.3737. [DOI] [PubMed] [Google Scholar]
- 6.Fairfax BP, et al. Innate immune activity conditions the effect of regulatory variants upon monocyte gene expression. Science. 2014;343:1246949. doi: 10.1126/science.1246949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gamazon ER, et al. Using an atlas of gene regulation across 44 human tissues to inform complex disease- and trait-associated variation. Nat Genet. 2018;50:956–967. doi: 10.1038/s41588-018-0154-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wall JD, et al. Estimating genotype error rates from high-coverage next-generation sequence data. Genome Res. 2014;24:1734–1739. doi: 10.1101/gr.168393.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Peters JE, et al. Insight into genotype-phenotype associations through eQTL mapping in multiple cell types in health and immune-mediated disease. PLoS Genet. 2016;12:e1005908. doi: 10.1371/journal.pgen.1005908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Love MI, Huber W, Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15:550. doi: 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Carpenter B, et al. Stan: a probabilistic programming language. J Stat Softw. 2017;76:1–32. doi: 10.18637/jss.v076.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lappalainen T, et al. Transcriptome and genome sequencing uncovers functional variation in humans. Nature. 2013;501:506–511. doi: 10.1038/nature12531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li B, et al. Transcriptome analysis of psoriasis in a large case-control sample: RNA-seq provides insights into disease mechanisms. J Invest Dermatol. 2014;134:1828–1838. doi: 10.1038/jid.2014.28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kumasaka N, Knights AJ, Gaffney DJ. Fine-mapping cellular QTLs with RASQUAL and ATAC-seq. Nat Genet. 2016;48:206–213. doi: 10.1038/ng.3467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.van de Geijn B, McVicker G, Gilad Y, Pritchard JK. WASP: allelespecific software for robust molecular quantitative trait locus discovery. Nat Methods. 2015;12:1061–1063. doi: 10.1038/nmeth.3582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sun W. A statistical framework for eQTL mapping using RNA-seq data. Biometrics. 2012;68:1–11. doi: 10.1111/j.1541-0420.2011.01654.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hu Y-J, Sun W, Tzeng J-Y, Perou CM. Proper use of allele-specific expression improves statistical power for cis-eQTL mapping with RNA-seq data. J Am Stat Assoc. 2015;110:962–974. doi: 10.1080/01621459.2015.1038449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Howie B, Marchini J, Stephens M. Genotype imputation with thousands of genomes. G3. 2011;1:457–470. doi: 10.1534/g3.111.001198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Degner JF, et al. Effect of read-mapping biases on detecting allele-specific expression from RNA-sequencing data. Bioinformatics. 2009;25:3207–3212. doi: 10.1093/bioinformatics/btp579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liu Z, et al. Comparing computational methods for identification of allele-specific expression based on next generation sequencing data. Genet Epidemiol. 2014;38:591–598. doi: 10.1002/gepi.21846. [DOI] [PubMed] [Google Scholar]
- 21.Castel SE, Levy-Moonshine A, Mohammadi P, Banks E, Lappalainen T. Tools and best practices for data processing in allelic expression analysis. Genome Biol. 2015;16:195. doi: 10.1186/s13059-015-0762-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stranger BE, et al. Population genomics of human gene expression. Nat Genet. 2007;39:1217–1224. doi: 10.1038/ng2142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brown AA, et al. Predicting causal variants affecting expression by using whole-genome sequencing and RNA-seq from multiple human tissues. Nat Genet. 2017;49:1747+. doi: 10.1038/ng.3979. [DOI] [PubMed] [Google Scholar]
- 24.Võsa U, et al. Unraveling the polygenic architecture of complex traits using blood eQTL meta-analysis. bioRxiv. 2018 doi: 10.1101/447367. [DOI] [Google Scholar]
- 25.Tsoi LC, et al. Large scale meta-analysis characterizes genetic architecture for common psoriasis associated variants. Nat Commun. 2017;8:15382. doi: 10.1038/ncomms15382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Aguet F, et al. Genetic effects on gene expression across human tissues. Nature. 2017;550:204–213. doi: 10.1038/nature24277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ding J, et al. Gene expression in skin and lymphoblastoid cells: refined statistical method reveals extensive overlap incis-eQTL signals. Am J Hum Genet. 2010;87:779–789. doi: 10.1016/j.ajhg.2010.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gudjonsson JE, et al. Assessment of the psoriatic transcriptome in a large sample: additional regulated genes and comparisons with in vitro models. J Invest Dermatol. 2010;130:1829–1840. doi: 10.1038/jid.2010.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schalkwijk J, Chang A, Janssen P, De Jongh GJ, Mier PD. Skin-derived antileucoproteases (SKALPs): characterization of two new elastase inhibitors from psoriatic epidermis. Br J Dermatol. 1990;122:631–641. doi: 10.1111/j.1365-2133.1990.tb07285.x. [DOI] [PubMed] [Google Scholar]
- 30.Chen L, et al. Genetic drivers of epigenetic and transcriptional variation in human immune cells. Cell. 2016;167:1398–1414. doi: 10.1016/j.cell.2016.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Joehanes R, et al. Integrated genome-wide analysis of expression quantitative trait loci aids interpretation of genomic association studies. Genome Biol. 2017;18:16. doi: 10.1186/s13059-016-1142-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nestle FO, Kaplan DH, Barker J. Psoriasis. N Engl J Med. 2009;361:496–509. doi: 10.1056/NEJMra0804595. [DOI] [PubMed] [Google Scholar]
- 33.Urbut SM, Wang G, Carbonetto P, Stephens M. Flexible statistical methods for estimating and testing effects in genomic studies with multiple conditions. Nat Genet. 2019;51:187–195. doi: 10.1038/s41588-018-0268-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schmieder R, Edwards R. Quality control and preprocessing of metagenomic datasets. Bioinformatics. 2011;27:863–864. doi: 10.1093/bioinformatics/btr026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dobin A, Gingeras TR. Mapping RNA-seq reads with STAR. Curr Protoc Bioinformatics. 2015;51:11.14.1-11.14.19. doi: 10.1002/0471250953.bi1114s51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics. 2011;27:2987–2993. doi: 10.1093/bioinformatics/btr509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Castel SE, Mohammadi P, Chung WK, Shen Y, Lappalainen T. Rare variant phasing and haplotypic expression from RNA sequencing with phASER. Nat Commun. 2016;7:12817. doi: 10.1038/ncomms12817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Delaneau O, Marchini J, Zagury J-F. A linear complexity phasing method for thousands of genomes. Nat Methods. 2011;9:179–181. doi: 10.1038/nmeth.1785. [DOI] [PubMed] [Google Scholar]
- 39.Marchini J, Howie B. Genotype imputation for genome-wide association studies. Nat Rev Genet. 2010;11:499–511. doi: 10.1038/nrg2796. [DOI] [PubMed] [Google Scholar]
- 40.Muller P, Parmigiani G, Rice K. FDR and Bayesian Multiple Comparisons Rules Working Paper. Johns Hopkins University, Department of Biostatistics; 2006. [Google Scholar]
- 41.Vigorito E, et al. Dataset to reproduce BaseQTL figures. Zenodo. 2021 doi: 10.5281/zenodo.4759202. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Geuvadis samples were accessed from E-GEUV-1, ftp://ftp.sra.ebi.ac.uk/vol1/fastq, on 16 April 2017 or 23 January 2018 as indicated in Supplementary Table 1. Psoriasis and normal skin samples were accessed from E-GEOD-54456, ftp://ftp.sra.ebi.ac.uk/vol1/fastq, on 2 November 2018. GTEx associations for skin, blood and lymphoblastic cell lines corresponding to Analysis V7 were downloaded from https://gtexportal.org/home/datasets on 21 June 2019. Differentially regulated genes between psoriasis and normal skin were downloaded from https://ars.els-cdn.com/content/image/1-s2.0-S0022202X15368834-mmc2.xls on the 21 November 2018. We downloaded RNA-seq data from 86 Geuvadis samples with EUR ancestry (GBR code) from ArrayExpress (E-GEUV-1, Supplementary Table 1). We also analyzed 94 and 90 RNA-seq normal and psoriasis skin samples13 obtained from ArrayExpress (E-GEOD-54456). For the analysis of psoriasis eQTL we selected 51 upregulated genes in psoriasis versus normal skin (P ≤ 10-6 corresponding to family-wise error rate <0.025) and with a median expression of at least 500 RPKM in psoriasis samples (data extracted from https://ars.els-cdn.com/content/image/1-s2.0-S0022202X15368834-mmc2.xls 13, and/or within 100 kB of a psoriasis GWAS hit 25 (380 genes). Datasets to reproduce figures in this paper were uploaded into Zenodo 41.
The source code and documentation for BaseQTL are available at https://gitlab.com/evigorito/baseqtl. We also provide a pipeline to process RNA fastq files and genotypes, if available, to prepare for running BaseQTL at https://gitlab.com/evigorito/baseqtl_pipeline (Supplementary Fig. 12 and Supplementary Section 3). The code to reproduce the figures is available at https://gitlab.com/evigorito/baseqtl_paper. The three repositories have been uploaded to Zenodo41.