Propensity scores using missingness pattern information: a practical guide

Abstract

Electronic health records are a valuable data source for investigating health-related questions, and propensity score analysis has become an increasingly popular approach to address confounding bias in such investigations. However, because electronic health records are typically routinely recorded as part of standard clinical care, there are often missing values, particularly for potential confounders. In ourmotivating study—using electronic health records to investigate the effect of renin-angiotensin system blockers on the risk of acute kidney injury—two key confounders, ethnicity and chronic kidney disease stage, have 59% and 53% missing data, respectively. The missingness pattern approach (MPA), a variant of the missing indicator approach, has been proposed as a method for handling partially observed confounders in propensity score analysis. In the MPA, propensity scores are estimated separately for each missingness pattern present in the data. Although the assumptions underlying the validity of the MPA are stated in the literature, it can be difficult in practice to assess their plausibility. In this article, we explore the MPA’s underlying assumptions by using causal diagrams to assess their plausibility in a range of simple scenarios, drawing general conclusions about situations in which they are likely to be violated. We present a framework providing practical guidance for assessingwhether the MPA’s assumptions are plausible in a particular setting and thus deciding when the MPA is appropriate. We apply our framework to our motivating study, showing that the MPA’s underlying assumptions appear reasonable, and we demonstrate the application of MPA to this study.

1. Introduction

Observational data are an important source of information for investigating the effect of treatments or interventions on health outcomes. In observational data, confounding is often an issue, as characteristics of treated patients can systematically differ from those of untreated patients. Propensity score methods aim to take account of confounding by achieving balance of patient characteristics across the treatment groups being compared. ¹ However, observational studiesmay suffer fromlarge amounts of missing data, which can lead to biased treatment effect estimates if the missing data are not handled appropriately. ² We focus on scenarios where the outcome and treatment of interest are fully observed, but data are missing on potential confounders. This is a common occurrence, for example, in studies using electronic health record data and insurance claims data, where prescriptions and diagnoses tend to be well recorded but potential confounders, such as smoking status, may be less well recorded. ³

The “missingness pattern” approach (MPA) is a way of handling missing confounder data, which has been proposed in propensity score analysis. ^4,5 It accounts for missing data by incorporating information about which confounders are missing into the estimation of the propensity score itself. ^4,5 Despite being easy to implement, the MPA has not been widely used in practice. This might be explained by the lack of guidance about its use in the literature. In particular, while the assumptions required for the validity of the MPA have been described formally in terms of conditional independence, ^4–6 how these mathematical statements relate to real clinical scenarios remains unclear. Our aim is, therefore, to investigate the assumptions underlying the MPA in order to provide practical guidance for researchers about how to identify whether these assumptions hold in a given clinical scenario.

We start by introducing our motivating example that investigates the association between renin-angiotensin system drugs and risk of acute kidney injury in Section 2. We review propensity score methods for complete data (Section 3) and approaches to handle missing confounder data in propensity score analysis, with a particular focus on the MPA and the related missing indicator approach (Section 4). We discuss the plausibility of the assumptions underlying the MPA in Section 5. We use causal diagrams to evaluate the assumptions in Section 6 and present a framework giving practical guidance for assessing these assumptions in Section 7. We illustrate our results on our motivating example (Section 8) and conclude with a discussion (Section 9).

2. Motivating Example

We consider data from a cohort study using electronic health records to investigate the association between use of angiotensin-converting enzyme inhibitors or angiotensin receptor blockers (ACEI/ARBs) and risk of acute kidney injury (AKI) in new users of antihypertensive drugs. ⁷

Datawere obtained from theUK Clinical Practice ResearchDatalink linked to the Hospital Episode Statistics database for adults who were new users of antihypertensive drugs between 1997 and 2014. Follow-up began at the first prescription of any of the antihypertensive drugs: ACEI/ARBs, beta-blockers, calcium channel blockers, or diuretics. Our treatment of interest is ACEI/ARB prescription at the start of follow-up, and the outcome is AKI within 5 years. Potential confounders considered are: gender, age, ethnicity, prescription of other antihypertensive drugs at start of follow-up, and status of chronic comorbidities at start of follow-up, including chronic kidney disease (CKD) stage. Table 1 shows the baseline characteristics of the cohort. Of the 570 586 patients included in the cohort, 159 389 (27.9%) were prescribed an ACEI/ARB. Many characteristics are not balanced across the treatment groups, indicating potential for confounding. Propensity score analysis is a popular method for taking account of confounding in analysis of electronic health records. However, two potential confounders have missing data: ethnicity (59.0% missing) and baseline CKD stage (52.9% missing). Only 121 527 (21%) of patients have complete data for both variables.

Table 1. Patient characteristics by prescription of ACEI/ARBs.

		Prescribed ACEI/ARB
Baseline		Yes (n (%))		No (n (%))
Characteristic		(Total = 159 389)		(Total = 411 197)
Age (years)	18 to 42	16 616	(10.4%)	94 265	(22.9%)
	43 to 53	39 541	(24.8%)	77 224	(18.8%)
	54 to 62	36 325	(22.8%)	77 985	(19.0%)
	63 to 71	30 667	(19.2%)	75 141	(18.3%)
	≥ 72	36 240	(22.7%)	86 582	(21.1%)
Sex	Female	62 652	(39.3%)	236 296	(57.5%)
Chronic Kidney Disease Stage	≤ Stage 2	88 826	(55.7%)	146 825	(35.7%)
	Stage 3a	10 535	(6.6%)	15 489	(3.8%)
	Stage 3b	2728	(1.7%)	3127	(0.8%)
	Stage 4	457	(0.3%)	551	(0.1%)
	Missing	56 843	(35.7%)	245 205	(59.6%)
Ethnicity	White	63 791	(40.0%)	153 747	(37.4%)
	South Asian	3072	(1.9%)	4734	(1.2%)
	Black	1065	(0.7%)	3905	(0.9%)
	Mixed	237	(0.1%)	681	(0.2%)
	Other	814	(0.5%)	1623	(0.4%)
	Missing	90 410	(56.7%)	246 507	(59.9%)
Comorbidities:
Diabetes Mellitus	Yes	44 727	(28.1%)	38 714	(9.4%)
Ischaemic heart disease	Yes	42 214	(26.5%)	76 013	(18.5%)
Arrhythmia	Yes	17 494	(11.0%)	39 094	(9.5%)
Cardiac failure	Yes	18 647	(11.7%)	13 074	(3.2%)
Hypertension	Yes	124 340	(78.0%)	240 135	(58.4%)
Other antihypertensives:
Beta-blocker	Yes	14 666	(9.2%)	205 156	(49.9%)
Calcium channel blocker	Yes	3501	(2.2%)	91 912	(22.4%)
Diuretic	Yes	21 950	(13.8%)	129 582	(31.5%)

Abbreviations: ACEI/ARBs, angiotensin-converting enzyme inhibitors or angiotensin receptor blockers. Diuretic: Thiazide diuretics, loop diuretics, or potassium sparing diuretics.

3. Propensity Score Methods For Complete Data

3.1. Notation and assumptions

Suppose we have a group of n patients, each with a row vector X_i of p confounders: X_i = (X_i1 , …, X_ip )^⊤, where X_ij is the value of confounder j for patient i (i = 1, …, n and j = 1, …, p). Throughout the article, we will assume that in the full data (ie, with no missing confounder data), the X_i are sufficient to control for confounding. ⁸ In this article, we restrict our attention to a binary treatment (or exposure) and a binary outcome. Patient i receives either treatment Z_i = 1 or control Z_i = 0. Each patient has two potential outcomes: Y_i (1) denotes the outcome that would have been observed for patient i if they had received treatment, and Y_i (0) denotes the outcome value that would have been observed if patient i had received control. ⁹ Y_i denotes the outcome value that was actually observed. Henceforth, we omit the i and j subscripts where unambiguous. Our estimand is the average treatment effect (ATE): E[Y(1) − Y(0)]. ^10,11 While the odds ratio suffers from noncollapsibility, the risk ratio does not and provides an alternative relative measure; results in this article follow similarly for this estimand.

To estimate the treatment effect, wemake four standard assumptions: consistency, no interference, strongly ignorable treatment assignment (SITA), and positivity. Consistency states that, for a patient who receives a particular treatment level z, their observed outcome Y is the corresponding potential outcome Y(z), irrespective of the way in which they were assigned to that treatment level. ¹² Under the assumption of no interference, the treatment received by one patient does not affect the potential outcomes of another patient. ^1,13,14 SITA implies that there are no unmeasured confounders and can be expressed as: ^1,15

$$\text{SITA}:Z\perp (Y(1),Y(0))\mid X,$$ (1)

where ⊥ denotes independence. Finally, positivity states that, given their individual characteristics, all patients have a nonzero probability of receiving either treatment or control. ^15,16 Throughout this article, we assume these four assumptions hold for the complete data.

The propensity score e(x) is the probability of receiving treatment, conditional on observed confounders X: ¹

$$e_i\left(x_i\right)=P(Z_i=1\mid X_i=x_i),$$

for patient i (i = 1, …, n)with a vector of confounder values X_i = X_i . Under the four assumptions described above, Rosenbaum and Rubin ¹ showed that at each value of the propensity score, the confounders X are balanced across treatment groups.

Typically, propensity scores are unknown and must be estimated from the data, often as the predictions, ê_i , from a logistic regression of treatment allocation on potential confounders. ¹⁷ We use inverse probability of treatment weighting (IPTW), which creates weights from the estimated propensity scores to construct “pseudo-populations” ¹⁸ in which the distribution of observed confounders are balanced across treatment groups, resulting in the following estimator: ¹⁷

$$\widehat{ATE}=\left(\frac{{{\displaystyle \sum }}_{i=1}^n\frac{Y_1{Z}_1}{{\widehat{e}}_i}}{{{\displaystyle \sum }}_{i=1}^n\frac{Z_i}{{\widehat{e}}_t}}\right)-\left(\frac{{{\displaystyle \sum }}_{i=1}^n\frac{Y_Y\left(1-Z_1\right)}{\left(1-{\widehat{e}}_i\right)}}{{{\displaystyle \sum }}_{i=1}^n\frac{\left(1-Z_1\right)}{\left(1-{\widehat{e}}_i\right)}}\right).$$ (2)

4. Propensity Score Methods With Missing Confounder Data

In practice, observational studies can suffer from large amounts of missing data, potentially leading to both loss of efficiency and biased estimates. ¹⁹ The magnitude of bias will depend on the extent to which the probability of missing confounder data is related to outcome and exposure. ¹⁹ The most common classification of missingness mechanisms is Rubin’s taxonomy, in which data are missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR). ^19,20 Under an MCAR mechanism, the probability of being missing does not depend on the observed or missing data.Missing data are MAR when the probability of being missing depends on observed data values but, given these, does not depend on missing values. If the probability of being missing depends on the unobserved values of data, then data are MNAR.

The simplest way of handling missing confounder data in propensity score analysis is a complete records (or complete case) analysis, which restricts the analyses to patients with full data on all variables. ² This approach provides unbiased estimates of the conditional ATE as long as missingness does not depend on both the treatment and the outcome. ²

The missing indicator approach is another simplemethod. For partially observed categorical confounders,a ”missing” category is added before including the confounder in the propensity score model. For continuous confounders, missing values are set to a particular value, say 0, and both the confounder and a missing indicator (a variable indicating whether that variable is observed or not) are included in the propensity score model. Applied to standard outcome regression models, this approach induces bias in a number of scenarios; ^21,22 whether this is the case in the propensity score context has been questioned. ²³

Multiple imputation is a popular alternative, involving imputing (ie, filling in) missing covariates with plausible values several times, by drawing fromthe predictive distribution of the missing covariates given observed data, to create a number of “complete” imputed datasets. The full analysis (estimation of the propensity score then estimation of the treatment effect) is performed separately in each imputed dataset. The results are then combined using Rubin’s rules to obtain an overall estimate of the treatment effect and standard error. ^19,24 Guidelines regarding optimal use of multiple imputation in conjunction with propensity score analysis have been proposed. ²⁵ Standard implementations of multiple imputation require data to be MAR. ^19,26

4.1. The missingness pattern approach

The MPA ^4,5 accounts for missing confounder data by separating patients into subgroups according to the possible combinations of confounders being observed or missing, ie, the missingness patterns, and fitting a different propensity score model to each pattern.

Let R_ij be a missing indicator indicating whether the confounder j (j = 1, …, p) for patient i (i = 1, …, n) is observed (R_ij = 1) or not (R_ij = 0). This allows us to partition the values X_ij (i = 1, …, n; j = 1, …, p) into two sets: the set of values that are observed, X _obs, and the set of values that are missing, X_mis :

$$X=\left\{X_{\text{obs}},X_{\text{mis}}\right\}\text{where}{X}_{\text{obs}}=\left\{X_{ij}\mid R_{ij}=1\right\}\text{and}{X}_{\text{mis}}=\left\{X_{ij}\mid R_{ij}=0\right\}.$$ (3)

We will use R_i = (R_i1 , …, R_ip ) to refer to the vector of missing indicators for patient i, omitting the subscript i where unambiguous.

The generalized propensity score, e*(x), is defined as the probability of receiving treatment, conditional on both the observed confounder information and the missingness pattern: e*(x) = P(Z = 1| X _obs, R). This can be estimated by using a different propensity score model for each missingness pattern, including only the confounders observed in that pattern. For example, in a study with treatment and outcome both fully observed and a single partially observed confounder X, there are two missingness patterns: X is either observed or missing. For patients with X observed, the propensity score model would include X, while the propensity score model for patients with X missing would include only a constant term. The generalised propensity score can then be used in the same way as the standard propensity score, ⁴ for example, by substituting in Equation (2) to estimate the ATE.

4.1.1. Assumptions of the MPA

Three assumptions under which the MPA leads to valid inference are given by Mattei. ⁶ We present slightlyweaker versions of these assumptions, under which the MPA still gives a consistent estimator of the ATE (proof in Supplementary Material: Section A). The first assumption is an extension of the SITA assumption (Equation (1)), which we call the missingness SITA (mSITA) assumption due to its similarities with the SITA assumption (Equation (1)):

$$\text{mSITA}:Z\perp Y(z)\mid X,R\text{for}z=0,1.$$ (4)

A key difference with Equation (1) is the inclusion of information about the missingness pattern, represented by R,in the conditioning set. We assume that SITA holds in the full data, thus this assumption states that additionally conditioning on R does not introduce bias.

We call the two further assumptions: ⁶ the conditionally independent treatment (CIT) assumption and the conditionally independent outcomes (CIO) assumption.

$$\text{CIT}:Z\perp X_{\text{mis}}\mid X_{\text{obs}},R$$ (5a)

$$\text{CIO}:Y(z)\perp X_{\text{mis}}\mid X_{\text{obs}},R\text{for}z=0,1.$$ (5b)

If mSITA holds, and either CIT or CIO holds, then the MPA provides a consistent estimate of the treatment effect. We loosely term these the “MPA’s assumptions.”

We note that the assumptions underlying the MPA are different to Rubin’s taxonomy of missing data ^24,27 in the sense that classifying data according to Rubin’s taxonomy does not provide any information as to whether the MPA’s assumptions would hold. Rather, the MPA’s assumptions require the associations between variables to differ across missingness patterns. It is possible for the MPA’s assumptions to hold when data are MNAR; conversely data being MCAR does not guarantee the MPA’s assumptions will hold.

How to assess the plausibility of the MPA’s assumptions—and thus the validity of the MPA itself—in a particular setting remains unclear.

4.1.2. Connections with the missing indicator approach

With a single partially observed confounder, the missing indicator approach can be shown to be equivalent to the MPA (Supplementary Material: Section B). Thus, the missing indicator approach will provide a consistent estimator of the ATE if mSITA and either CIT or CIO holds.

In a more complex scenario with one partially observed and one fully observed confounder, the missing indicator approach is a simplified version of the MPA, additionally imposing the assumption that the association between the fully observed confounder and treatment is the same whether or not the other confounder is observed (Supplementary Material: Section B). Therefore, the missing indicator approach relies on the same assumptions as the MPA and additionally requires no effect modification of the fully observed confounder(s) by the missingness patterns.

5. Plausibility of the Cit and Cio Assumptions

The MPA provides valid inference if either CIT or CIO holds (Equation (5)), in addition to the mSITA assumption. The plausibility of these assumptions in real-life settings will, therefore, determine how useful the MPA is as a missing data approach.

We have assumed that in the full data X is a confounder, and so is associated with both treatment and outcome. TheCIT assumption requires that the confounder-treatment relationship is absent in the subset of patients with X unmeasured, while the CIO assumption requires that the confounder-outcome relationship is absent in patients with X unmeasured. Thus, if either the CIT or CIO assumption holds, X does not confound the relationship between treatment and outcome when it is missing (ie, X is not associated with both treatment and outcome in the subset of patients missing X). Informally, we refer to this property as X being a confounder only when it is observed.

The key point to consider is that the CIT and CIO assumptions are not about the missingness mechanisms that drive the missing data, as much as which relationships between variables exist in the subgroup of patients with missing confounder values.

5.1. The CIT assumption: an illustrative example

Consider a simplified version of our motivating example, investigating the effect of prescribing ACEI/ARBs on the risk of AKI.

Underlying kidney function prior to ACEI/ARB prescription is a likely confounder: kidney function is a known risk factor for AKI and is likely to influence whether ACEI/ARBs are prescribed. Kidney function is classified into the stage of CKD, via a serum creatinine blood test. Where a clinician ordered a kidney function test prior to the prescribing decision, it is reasonable to assume that the information regarding CKD stage contributed to that decision. Where CKD stage was unavailable to the clinician, arguably it is unlikely to have influenced the prescribing decision.

In this simplified example, underlyingCKDstage is always a risk factor for the outcome but is plausibly only associated with treatment allocation when it is measured. Thus, CIT holds; baseline CKD stage is only a confounder when it is observed.

5.2. The CIO assumption: an illustrative example

Suppose we were interested in estimating the effect of exposure to farming in early life on subsequent development of asthma. Childhood exposures to domestic allergens, for example, dust mites, are potential confounders. Such domestic allergens may be measured by health visitors. Suppose that the relationship between dust mites and asthma has a threshold effect, that is, an association is seen only once a certain concentration of dust mites is present.

Since health visitors do not collect information for the purposes of research, they might plausibly record information more thoroughly for households where there were concerns about the child’s environment. Missing data for dust mites would, therefore, be more likely to occur in households with little evidence of dust mites, and less likely in households with a high concentration.

In this example, concentration of dust mites may be associated with subsequent asthma only in households where dust mite concentration was recorded. In this case, CIO holds; dust mite concentration is a confounder only when measured.

6. Detecting and Dealing with Violations of the MPA’S Assumptions

The mSITA, CIT, and CIO assumptions are statements of conditional independence. In this section, we describe how causal diagrams can be used to assess conditional independence statements. We demonstrate the use of causal diagrams in a simple scenario in order to draw some general conclusions about situations in which the MPA’s assumptions are likely to be violated.

6.1. Causal diagrams

Causal diagrams, or directed acyclic graphs, are a useful tool for assessing conditional independencies under an assumed causal structure. Because the assumptions of the MPA involve the potential, rather than observed, outcomes, we turn to a specific type of causal diagram: single world intervention templates (SWITs). ²⁸

SWITs are standard directed acyclic graphs that have been adapted to show potential, instead of observed, outcomes. This involves “splitting” the treatment node into two halves; the first represents the observed treatment Z, and the second represents an “intervened-on value,” z. Determinants of observed treatment affect the first half (ie, incoming arrows go into the Z half), and effects of treatment are determined by the second (ie, outcoming arrows leave from the z half). A consequence of this splitting is that variables affected by treatment now become potential rather than observed variables.

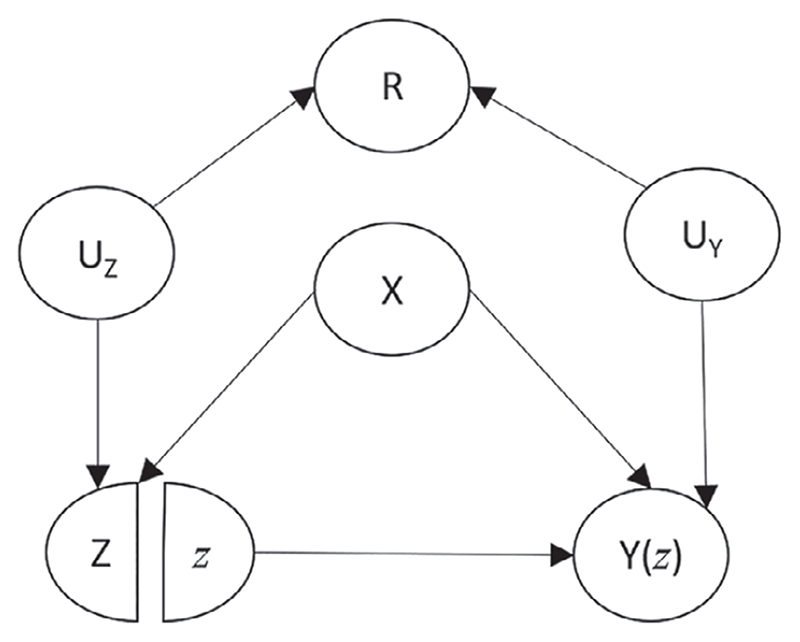
Figure 1 shows a simple SWIT representing a typical confounding scenario where the confounder X has a causal effect on the treatment and the outcome. Additionally, this graph encodes the assumption that the missing indicator R (ie, whether or not the confounder is missing) is associated with the treatment and the outcome, via shared common causes in both cases (denoted U_Z and U_Y , respectively). In Figure 1, the outcome is affected by treatment so this SWIT includes the potential outcome Y(z) rather than the observed outcome Y.

Figure 1.

A single world intervention template showing a scenario in which the mSITA assumption is violated. X: confounder. Z: treatment. Y(z): potential outcome resulting from intervening to set Z equal to a particular value z. R: missing indicator (=1 if X observed, =0 if X is missing). U_Z : unobserved common cause between R and Z. U_Y : unobserved common cause between R and Y(z)

6.2. Assessing the MPA’s assumptions using causal diagrams

6.2.1. Assessing the mSITA assumption

Suppose Figure 1 depicts the true underlying causal structure which gave rise to our study data. With a single partially observed confounder, the mSITA assumption states that Z ⊥ Y(z)| X, R. By applying d-separation to Figure 1 (as described in Supplementary Material: Section C), we find that the path from Z to Y(z) through R is open after conditioning on X and R, thus Z is not conditionally independent of Y(z) given X and R; mSITA is violated in this scenario.

For more complex causal diagrams, it may help to use software such as Dagitty to assess which conditional independencies hold. ²⁹ R code that uses Dagitty to check the MPA’s assumptions for the scenario shown in Figure 1 can be found in Supplementary Material: Section F.

6.2.2. Assessing the CIT/CIO assumptions

The CIT and CIO assumptions state that Z ⊥ X _mis| X _obs, R, and Y(z) ⊥ X _mis| X _obs, R, respectively. With a single confounder X, these assumptions are trivially true in the subgroup of patients with X observed (because X _mis is empty given R = 1). In the subgroup of patients with X missing, the assumptions become: Z ⊥ X| R = 0, and Y(z) ⊥ X| R = 0, respectively.

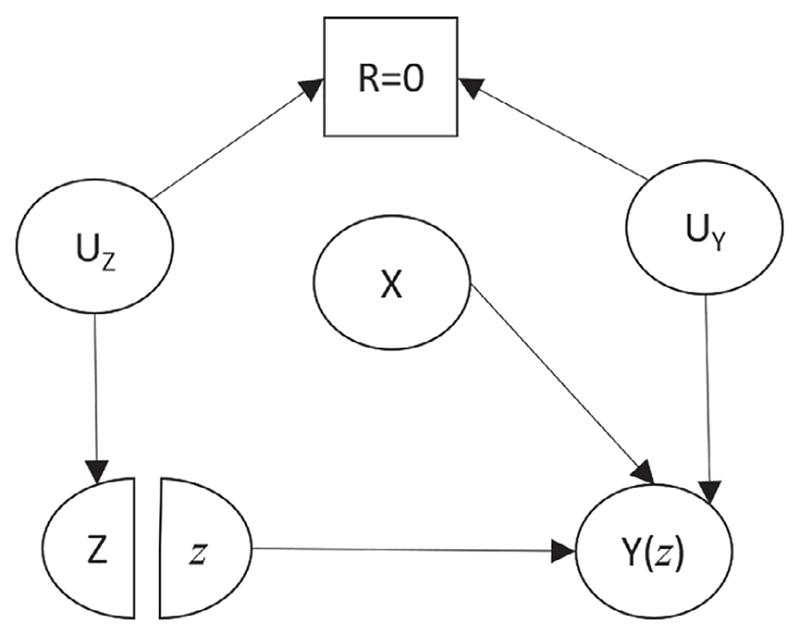
A minimum condition for CIT or CIO to be satisfied is that X cannot be a confounder when it is missing. Thus, for either of these assumptions to hold, there must be grounds for believing that the causal relationships that generate confounding bias in the full data are different in the subgroupwith missing confounder values (compared to the subgroup with observed confounder values). For example, in Figure 1, if we believe that all the arrows shown exist in the subgroup with missing confounder values, then both CIT and CIO would be violated. In contrast, suppose we believe that this diagram depicted the correct situation with full data, but we believe that the arrow from the confounder to treatment did not exist when X was missing. In this case, Figure 2 would depict the underlying causal structure for the subgroup with X unmeasured.

Figure 2.

A single world intervention template modified (from Figure 1) to assess the CIT and CIO assumptions. The square box around R denotes the restriction of our attention to the subgroup R = 0. X: confounder. Z: treatment. Y(z): potential outcome resulting from intervening to set Z equal to a particular value z. R: missing indicator (=1 if X observed, =0 if X is missing). U_Z : unobserved common cause between R and Z. U_Y : unobserved common cause between R and Y(z)

In Figure 2, the only path connecting Z and X passes through Y(z), a collider on the path; thus applying the d-separation rule shows that Z and X are conditionally independent (in the subgroup with R = 0). Here, CIT holds. Because there is a direct arrow from X to Y(z), however, CIO does not hold.

6.3. Key violations of the MPA’s assumptions

In this section, we use causal diagrams to explore when the MPA’s assumptions are violated in a range of simple settings.

Scenarios considered

We consider scenarios where the outcome Y and treatment Z are fully observed. Initially, we focus on simple scenarios with a single partially observed confounder, X. Subsequently we extend this to consider scenarios with an additional, fully observed confounder, C. We consider all combinations of the scenarios discussed below, omitting those which give rise to cycles (ie, we do not allow scenarios where a variable has a causal effect on itself).

Relationships between the confounder, treatment, and outcome

We consider causal structures where the relationships between the confounder X and the treatment and outcome are either a direct causal relationship (eg, X causes treatment) or via shared unmeasured common causes (eg, a third factor causes both X and treatment). The relationship between the confounder and the treatment is allowed to differ depending on whether the confounder is observed or missing; specifically, this relationship is allowed to be absent when R = 0. Similarly, the presence or absence of the relationship between the confounder and outcome is allowed to depend on R. This allows for X to be a confounder only when observed, as discussed in the previous section.

Missingness mechanisms

For each of the confounder, treatment, and outcome, we considered: no relationship with the missing indicator, a causal effect on the missing indicator, the missing indicator has a causal effect on the variable, or an unobserved common cause with the missing indicator (allowing scenarios where one or more variables have both a direct causal relationship and a common cause with the missing indicator).

When a variable has a causal effect on the outcome, we assume that this effect operates on the potential outcome rather than the observed (eg, X causes Y(z) rather than X causing Y). Conversely, in the case where outcome is a cause of missingness, we have chosen to allow the observed outcome to cause missingness (Y causes R) rather than the potential outcome, since this is arguably more plausible in real data.

Assessment of assumptions

In each setting, we draw the appropriate causal diagram and assess the assumptions by applying d-separation to the causal diagram overall and to the modified causal diagram restricted to the subgroup with X missing.

In some scenarios, a slightly more complex route must be taken to assess the conditional independencies involved in the MPA’s assumptions. If the treatment or outcome is a cause of missingness, then the relevant SWIT contains R(z),the “potential” missingness after intervening on treatment, rather than the observed pattern of missingness. Thus, we can no longer use this graph to assess the relevant assumptions. In these cases, we turn to twin networks ^30,31 (Supplementary Material: Section D).

6.3.1. Key violations of the mSITA assumption

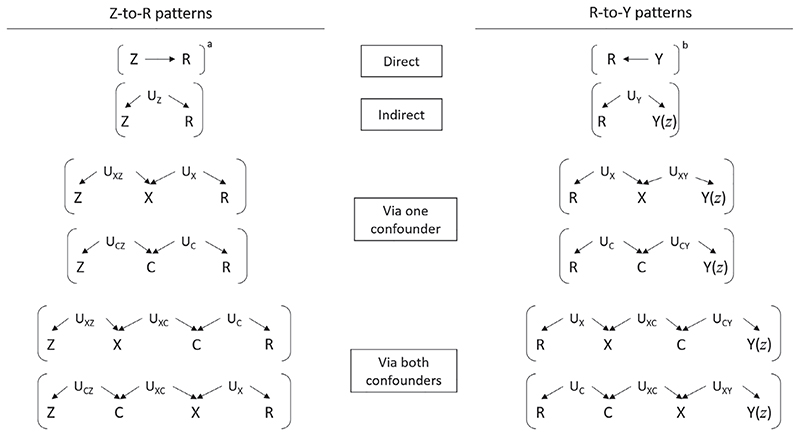
In the scenarios we considered, most violations of mSITA occurred via collider bias on R. In order for this type of violation to occur, there needs to be a path from Z to R and a path from Y(z) to R, each ending with arrows pointing toward R. These violations operate via a cause of R. We let U_X represent common causes of missingness and the confounder, U_Z represent common causes of missingness and the treatment, and U_Y represent common causes of missingness and the outcome.

The different “Z-to-R” and “R-to-Y” patterns that could occur are summarised in Figure 3. If one (or more) of each of these two patterns occurs, then mSITA will be violated. For example, Figure 1 shows the violation that arises when both the indirect “Z-to-R” pattern and the indirect “R-to-Y” pattern occur (both patterns in the second row of Figure 3).

Figure 3.

Summary of violations of the mSITA assumption. If one of the “Z-to-R” patterns and one of the “R-to-Y” patterns occurs in the causal diagram representing the study in question then the mSITA assumption will be violated. ^a Also a violation if this occurs with additional “R-to-Y patterns” shown in Supplementary Material: Section E. ^b Sufficient condition on its own, without a “Z-to-R pattern.” X: partially observed confounder. C: fully observed confounder. Z: treatment. Y(z): potential outcome resulting from intervening to set Z equal to a particular value z. Y: observed outcome. R: missing indicator (=1 if X observed, =0 if X is missing). U_st : unobserved common cause between two variables s and t. U_s : unobserved common cause between R and another variable s

A key result in Figure 3 is that when treatment and missingness are associated via shared common causes, and outcome and missingness are associated via (different) shared common causes, then mSITA is violated (as shown in Figure 1). So the MPA cannot be used in scenarios where there are unmeasured determinants of confounder missingness, which are also associated with the treatment and the potential outcomes.

Another important result in Figure 3 is that if the outcome has a causal effect on confounder missingness, that is, if Y → R, thenmSITA is violated without the need for any “Z-to-R” patterns. So the MPA cannot be used in scenarios where outcome affects whether or not confounder values are missing. For instance, in our AKI example, suppose that more efforts were made to track down historical laboratory measures of eGFR for patients who were diagnosed with AKI, then this would immediately violate mSITA.

A third important result is that when treatment causes missingness, and missingness in turn has a causal effect on the potential outcomes, mSITA is violated (see footnote a in Figure 3), although whether this is likely to occur in practice is unclear.

6.3.2. Handling violations of the mSITA assumption

All violations ofmSITA, other than those involving the treatment or the outcome causing missingness of the confounder, operate via a cause of R. Suppose itwere possible tomeasure all such factors that determinewhether or not the confounder is measured (although this may be difficult in practice). We could define a new set of confounders $\tilde{X}=\left\{X,U_X,U_Z,U_Y\right\}$ (or, where there is an additional fully observed confounder C, $\tilde{X}=\left\{X,C,U_X,U_C,U_Z,U_Y\right\}$ . Including this new set of confounders in the propensity score model, and thus the conditioning set for mSITA, removes the violation of this assumption. In most cases, measuring a subset of these variables will suffice. For example, in Figure 1, if U_Z could be measured and included in the propensity score model, the mSITA assumption would become: Z ⊥ Y(z)| X, R, U_Z , which is satisfied in Figure 1.

6.3.3. Key violations of the CIT and CIO assumptions

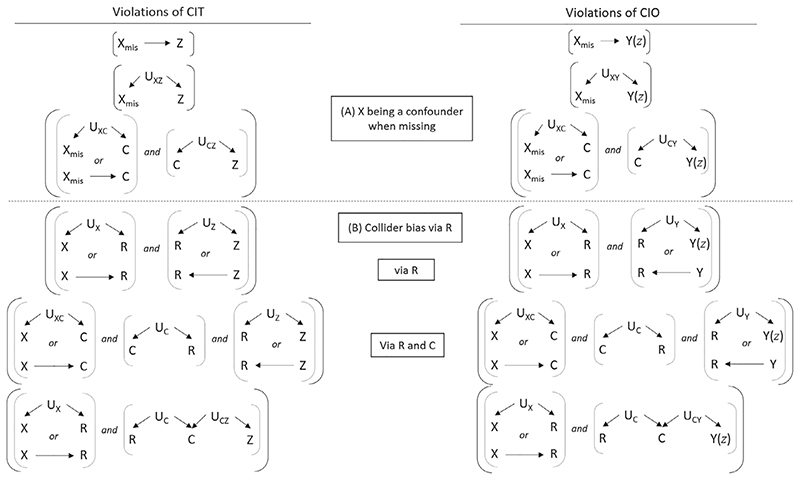
Figure 4 summarizes the possible violations of CIT and CIO, which fall into two broad groups: (A) violations related to X being a confounder when it is missing, and (B) violations due to collider bias via R.

Figure 4.

Summary of violations of the conditionally independent treatment (CIT) and conditionally independent outcomes (CIO) assumptions. If one or more of the six sets of conditions on the left hand side appear in the relevant causal diagram (modified to reflect relationships in the subgroup with X unobserved, that is, restricted to R = 0), then CIT is violated. Similarly, if any of the six sets of conditions on the right hand side occur then CIO is violated. Additional violations involving Y → R and Z → R can be found in Supplementary Material: Section E. X: partially observed confounder. C: fully observed confounder. Z: treatment. Y(z): potential outcome resulting from intervening to set Z equal to a particular value z. Y: observed outcome. R: missing indicator (=1 if X observed, =0 if X is missing). U_st : unobserved common cause between two variables s and t. U_s : unobserved common cause between R and another variable s

Since mSITA is always violated if outcome causes missingness, some CIT/CIO violations involving Y → R are shown only in Supplementary Material: Section E, along with a few additional violations involving Z → R.

Group (A) violations in Figure 4 relate to X being a confounder only when observed, in the sense that if one of the CIT group (A) violations or one of the CIO group (A) violations held, X would be a confounder when missing. For these violations, X has been replaced by X _mis to emphasise the fact that we need to focus on relationships that exist in the subgroup of patients with a missing confounder value when assessing this assumption.

In contrast, Group (B) violations relate to collider bias induced by conditioning on R.

6.3.4. Handling violations of the CIT and CIO assumptions

As with violations of the mSITA assumption, many of the violations of the CIT and CIO assumptions—specifically those belonging to Group (B)—can be removed by measuring and conditioning on causes of R. However, if either (a) both the confounder and the treatment cause the missingness, or (b) both the confounder and outcome cause the missingness, then CIT or CIO are violated, respectively; no conditioning can remove these violations.

7. Practical Guide to Assessing the Msita, Cit, and Cio Assumptions

In order to decide if the MPA’s assumptions hold in a particular clinical setting, the first and the most important step is to assess whether it is plausible for the partially observed confounder to be a confounder only when observed.

Second, key scenarios in which the MPA’s assumptions do not hold, as identified in the previous section, should be carefully considered using substantive knowledge to ensure these do not apply in the setting at hand. These are: (I) outcome affects missingness of the confounder; (II) outcome and missingness have shared unmeasured common causes, and treatment and missingness have shared unmeasured common causes; or (III) the confounder and treatment both affect missingness of the confounder and the confounder is associated with outcome in the subgroup with X missing.

Third, a causal diagram should be constructed, reflecting what is believed to be the underlying clinical structure. As with any causal diagram, any variable—measured or unmeasured—which may have a causal effect on two or more variables in the causal diagrammust also be included. Missing indicators for the partially observed confounders should be included in the causal diagram at this stage. When there are multiple partially observed confounders, the causal diagram will include one missing indicator per partially observed confounder.

Fourth, the causal diagram should be converted into a SWIT or a twin network, as appropriate. Once the SWIT or twin network has been created, d-separation can be applied to determine whether mSITA holds.

To assess CIT and CIO, the SWIT or twin network should be modified to reflect the relationship thought to be absent in the subgroup of patients with missing confounder values (ie, remove arrows to reflect the assumption that the confounder is only a confounder when observed). In this modified diagram, the d-separation rule can be again applied to assess CIT and CIO.

Supplementary Material: Section F provides R code to assess the mSITA, CIT, and CIO assumptions for Figure 1 and for the causal diagram associated with our more complex motivating example.

When there are multiple partially observed confounders, we advise constructing modified diagrams for each missingness pattern with missing values and then applying the d-separation rule to each diagram to assess the CIT and CIO assumptions for that particular missingness pattern. An assumption holds only if it holds for each missingness pattern.

7.1. Assessing the validity of the assumptions in the motivating example

7.1.1. Confounders only when observed

For the MPA’s assumptions to hold in the motivating example, we have to believe that the two partially missing confounders—ethnicity and baseline CKD stage—act as confounders only when observed. If baseline CKD stage is not available, this unobserved information cannot be used to determine the General Practitioner’s treatment decision whether or not to prescribe ACEI/ARBs. In practice, CKD stage may be recorded in a part of the patient record that the General Practitioner is aware of but researchers using CPRD data cannot access (eg, letters from secondary care). However, this is likely to reflect advanced CKD for only a small proportion of the whole study population. So, in general, it seems plausible that baseline CKD stage affects the clinician’s prescribing decision only when recorded.

The National Institute for Health and Care Excellence antihypertensive prescribing guidelines (which include ACEI/ARBs) offer different recommendations depending on ethnicity. ³² So, it is plausible that, if a clinician chooses to prescribe or not prescribe an ACEI/ARB based on an individual’s ethnicity, they would ensure that the individual’s ethnicity was recorded.

Therefore, the CIT assumption may be reasonable for this scenario. Conversely,both baseline CKD stage and ethnicity are risk factors for AKI, whether measured or not. Thus, the CIO assumption is not plausible here.

7.1.2. Checking plausibility of key violations

We also need grounds to believe that the three key scenarios listed above do not apply in this setting. Scenarios (I) and (III) rely on either outcome or treatment affecting missingness of the confounders. As CKD stage was defined at baseline, missingness of baseline CKD stage precedes treatment and, as a result, outcome. It also seems plausible that missingness of ethnicity occurs prior to treatment and outcome. Hence, we believe that these scenarios do not apply here.

Scenario (II) is when outcome and missingness have shared unmeasured common causes, and treatment and missingness have shared unmeasured common causes. Baseline CKD stage ismore likely to be recorded for patients expected to have a higher risk of kidney disease due to age or chronic comorbidities (eg, hypertension, diabetes) or due to other signs that the patient has poor kidney function (ie, CKD itself may affect the chance of the clinician measuring CKD stage). While these risk factors are associated with missingness and treatment or outcome, they are already captured in the electronic health records.

With respect to ethnicity, patients who are hospitalised are more likely to have ethnicity recorded (due to linkage of primary and secondary care data). Missingness of ethnicity may be caused by service-level factors such as level of administrative support at the time patients are admitted to hospital. It seems unlikely that these factors are also determinants of treatments previously prescribed in primary care or whether patients develop acute illnesses that require admission to hospital. Since we believe that any relevant common causes are measured, scenario (II) does not apply in our setting.

After considering the three key scenarios mentioned above, in which the MPA’s assumptions do not hold, we have found that these do not seem plausible in our motivating example. Having ruled out these violations, we proceed to the next step of our framework: to develop a causal diagram.

7.1.3. Developing a causal diagram

Figure 5 shows the SWIT developed for this example. This causal diagram encodes the investigators’ assumptions that age, sex, and ethnicity each affect both treatment and outcome. Age and sex affect the risk of developing diabetes, CKD, ischaemic heart disease, cardiac failure, arrhythmia, and hypertension. Note that the treatment node, representing prescription of ACEI/ARBs, has been split into two: “Ace” and “ace,” with the former representing the observed treatment and the latter representing the intervened-on treatment. Thus, patient factors affect “Ace” but not “ace,” and only “ace” affects subsequent AKI.

Figure 5.

A single world intervention template for the motivating example. Eth: Ethnicity. Ckd: Baseline chronic kidney disease. Hyp: Hypertension. Diab: Diabetes mellitus. Arr: Arrhythmia. Car: Cardiac failure. Ihd: Ischaemic heart disease. Ace: Prescription of ACE/ARBs (treatment). ace: intervened-on version of exposure. Aki: Acute kidney injury (outcome). Rckd: Missingness of Ckd. Reth: Missingness of Eth. Hosp: Hospitalisation. Slf: Service-level factors. U: unmeasured factor

7.1.4. Assessing the mSITA assumption

The mSITA assumption, for the motivating example, says that: Z ⊥ Y(z)| R _ckd, R _eth, Ckd, Eth, V, where Z represents ACEI/ARB prescription; Y(z) is the potential outcome (AKI status that would be observed if the patient were prescribed level z of ACEI/ARB); V represents the confounders age, sex, diabetes, ischaemic heart disease, cardiac failure, arrhythmia, and hypertension; R _eth and R _ckd are missing indicators for ethnicity and baseline CKD stage; and Ckd and Eth are the confounders baseline CKD stage and ethnicity, respectively.

The d-separation rule can be applied to the SWIT in Figure 5, to assess whether this conditional independence holds under the causal assumptions encoded in the diagram (example code in Supplementary Material: Section F.2). In this case, the conditional independence statement is true; mSITA holds under the assumed causal diagram.

7.1.5. Assessing the CIT and CIO assumptions

We have already established that the CIO assumption does not hold in our motivating example. The CIT assumption states that:

$$\begin{array}{l}Z\perp (\text{Ckd},\text{Eth})\mid R_{\text{ckd}}=0,R_{\text{eth}}=0,V,\\ Z\perp Ckd\mid R_{\text{ckd}}=0,R_{\text{eth}}=1,\text{Eth},V,\\ Z\perp \text{Eth}\mid R_{\text{ckd}}=1,R_{\text{eth}}=0,\text{Ckd},V.\end{array}$$

To assess the first of these, we create a modified version of Figure 5 which omits the arrows that we do not think exist when both ethnicity and baseline CKD stage are missing. So we remove the arrow frombaseline CKD stage to ACEI/ARB prescription, and we remove the arrow from ethnicity to ACEI/ARB prescription.

We then assess whether, after conditioning on the two missing indicators and the fully observed confounders, the treatment is independent of both ethnicity and baseline CKD stage, by applying the d-separation rule for each partially observed confounder. In this case, the conditional independence holds (example code in Supplementary Material: Section F.2).

This process is repeated in the two subgroups where only one of ethnicity and baseline CKD stage is recorded, assessing the second and third independence statements above in the appropriately modified causal diagrams. In each case, the relevant conditional independence holds. Thus, under the assumed causal diagram, CIT holds.

If our causal diagram correctly represents the causal structure giving rise to our study data, both mSITA and CIT hold. Under these two assumptions, the MPA will provide consistent estimates of the ATE.

8. Motivating Example: Applying the MPA

8.1. Methods: ACEI/ARBs and AKI

We estimated the effect of prescription of ACEI/ARBs on the incidence of AKI within 5 years of follow-up as a risk difference, first with no adjustment for confounding, and then by using IPTW. For IPTW, we estimated propensity scores using logistic regression to model ACEI/ARB prescription as a function of the covariates: age, sex, baseline CKD stage, ethnicity, diabetes mellitus, ischaemic heart disease, arrhythmia, cardiac failure, and hypertension (including an interaction between age and ischaemic heart disease, and an interaction between age and hypertension). We applied nonparametric bootstrapping (500 replications of the combined process of propensity score estimation and treatment effect estimation) to obtain Normal approximation 95% confidence intervals.

To deal with missing data in baseline CKD stage and ethnicity, we applied complete records analysis, the MPA, the missing indicator approach, and multiple imputation. For the MPA, the propensity scores were estimated separately in the four subgroups corresponding to whether or not baseline CKD stage and ethnicity were measured. For the missing indicator approach, we added “missing” categories to each of baseline CKD stage and ethnicity. Formultiple imputation, 10 imputed datasetswere created using chained equations. The imputation model included AKI incidencewithin 5 years, ACEI/ARB prescription and all covariates and interactions included in the propensity score model. In each imputed dataset, propensity scoreswere estimated and IPTWwas used to obtain treatment effect estimates, whichwere then pooled using Rubin’s rules. ²⁵ To assess covariate balance, standardized differences ¹⁰ were calculated in the original sample and after IPTW with each analysis method used.

8.2. Results and discussion: ACEI/ARBs and AKI

The complete records analysis included 121 527 patients with full data. All other missing data methods included all 570 586 patients. Using any of the analysis methods with IPTW removes most of the imbalance present in the original dataset (Table S1 in Supplementary Material: Section G).

Estimates of the effect of ACEI/ARBs on AKI are shown in Table 2. All missing data methods greatly reduce the crude estimate of effect, with complete records analysis providing the smallest estimate and multiple imputation providing the estimate closest to the crude analysis. the MPA and missing indicator approach produce almost identical results, estimating that patients prescribed ACEI/ARBs had six additional cases of AKI within 5 years, per 1000 people, with a 95% confidence interval of (5, 7), compared to patients who were not prescribed ACEI/ARBs.

Table 2. Estimated effects of ACEI/ARBs on AKI using IPTW to account for confounding.

Confounder adjustment	Missing data method	Risk difference (per 1000 people)	Normal-based bootstrap 95% CI
Crude	None	13.30	(12.52, 14.08)
IPTW	Complete records analysis	4.60	(2.76, 6.45)
IPTW	Missingness pattern approach	5.96	(5.10, 6.82)
IPTW	Missing indicator approach	5.93	(5.01, 6.85)
IPTW	Multiple imputation	6.17	(5.27, 7.07) a

^aNot bootstrapped; obtained by using Rubin’s rules across 10 imputed datasets.

Abbreviations: ACEI/ARBs, angiotensin-converting enzyme inhibitors or angiotensin receptor blockers; IPTW, inverse probability of treatment weighting.

We expect the MPA estimate to be consistent since—as discussed—the mSITA and CIT assumptions appear plausible here. Conversely, theMAR assumption underlying our application ofmultiple imputation is questionable. Baseline CKD stage is more likely to be recorded for patients with a lower level of kidney function (eg, if they are ill or have more risk factors for kidney disease that have led to testing) ³³ and therefore baseline CKD stage may be MNAR. However, since factors related to a lower level of kidney function are likely already captured in the observed data, the departure from the MAR assumption may be small. This may explain why multiple imputation and the MPA provide fairly similar estimates in this example, with multiple imputation giving an estimate closer to the crude estimate. Alternatively, having similar results may be due to misspecification of the parametric models or because ethnicity and baseline CKD stage may not be strong confounders.

In terms of precision, the complete records analysis has a very wide confidence interval, in contrast to the other missing data methods that all produce much narrower confidence intervals. This loss in precision, due to the exclusion of a large portion of the data, is recovered by the MPA, the missing indicator approach and multiple imputation.

9. Discussion

Wehave explored the three assumptions under which the MPA to dealing with missing counfounders in propensity score analysis provides valid inference. We have described how d-separation can be applied to a causal diagram to assess the MPA’s assumptions in a given setting and provided a framework and detailed example to allow researchers to ensure the appropriateness of this method in practice.

The key assumption required by the MPA is that the confounder acts as a confounder only when observed. Thus, for the MPA to be an appropriate method to use, we must believe that the relationships between treatment, outcome, and confounder are different in the subgroup with the confounder unmeasured. While this assumption will be plausible only in specific scenarios, one setting where it may have broad applicability is in the area of electronic health record research. In such studies, missing confounder information reflects information that the clinician did not have when making prescribing decisions, thus the assumption that the missing values did not affect prescribing may well be reasonable.

If this key assumption is thought to be satisfied, careful consideration is required to ensure that the remaining assumptions of the MPA are satisfied. In particular, the assumptions do not hold in the following scenarios: (i)where the outcome affects missingness of the confounder; (ii) where outcome and missingness have shared unmeasured common causes, and treatment and missingness have shared unmeasured common causes; and (iii) where a partially-missing confounder and treatment both affect missingness of the confounder and the confounder is thought to be associated with outcome whether or not it is measured. We note that the scenario where the outcome affects the missingness of the confounder also gives biased estimates of the treatment effect when using complete records analysis; ² multiple imputation can be used to deal with such scenarios if data are MAR.

We also found that many violations of the MPA’s assumptions can be dealt with by recording, and including in the analysis, auxiliary variables that are predictors of confounder missingness. Thus, although measuring such variables may be difficult in practice, careful consideration of the process by which data become missing is essential.

Our results demonstrate that classification of the missingness mechanism according to Rubin’s taxonomy does not provide information as to whether the MPA’s assumptions will hold. Unlike most missing data methods, for example, data being MCAR does not guarantee that the assumptions of the MPA are satisfied: the underlying relationships between the partially missing confounder and either the treatment or outcome (or both) would need to differ according to whether or not the confounder was missing. Also, if a confounder is MNAR, but the confounder does not confound the treatment-outcome relationship when missing, the MPA’s assumptions may hold.

The missing indicator approach is a popular and easy method to deal with missing confounder data. ^21,34 However, it is believed to be an “ad hoc” method ³⁴ that produces biased results. ²¹ Although the missing indicator approach is indeed biased under standard MAR assumptions, ²¹ our results show that in the propensity score context, the missing indicator approach is a simplified version of the MPA, and hence requires the same assumptions for valid results, along with additional assumptions about interaction terms in the propensity score model. Our work, therefore, allows researchers to use the missing indicator approach in a principled way.

There are several advantages to using the MPA, or the simpler missing indicator approach, when dealing with partially observed confounders in propensity score analysis. First, the method itself is simple to comprehend and easy to implement. Second, in contrast to complete records analysis, the MPA retains all patients in the analysis. Third, the MPA may be appropriate in some situations where multiple imputation is not, as the MPA does not require the MAR assumption to hold.

A limitation of the MPA is that we require sufficient sample size in each missingness pattern in order to be able to estimate propensity scores. This is of particular concern when there are many missingness patterns, a scenario to which the MPA is not currently easily extendable. Qu and Lipkovich ³⁵ suggested a pattern pooling algorithm to ensure sufficient sample size when estimating propensity scores when there are a large number of missingness patterns. Further work is needed to explore the performance of their algorithm in a range of scenarios. An extension to the MPA was proposed by D’Agostino et al. ²³ They suggested that in each missingness pattern, propensity scores should be estimated in the wider group of all subjects with observed data for the relevant confounders, retaining estimated propensity scores only for those who actually observed that particular pattern. Further work is required to compare this extension with the original MPA, and to investigate how to account for the correlation induced by this method.

In scenarios with a large number of confounders, causal diagrams may be prohibitively complex to construct. An alternative strategy could be to perform sensitivity analyses to assess the extent of the violation that would be required to change the study’s conclusions. However, further work is required to determine how best to implement such sensitivity analyses.

We note that the MPA assumptions are independent of the propensity score method used. In this article, we have chosen to use the IPTW method; however, other propensity score methods—including matching, subclassification, or covariate adjustment on the propensity score—could also be used under the same set of assumptions. Various alternative approaches outside the propensity score framework could also be used. One example that may provide valid inference while relaxing parametric modeling assumption is matching based on the Mahalanobis distance. ^36,37 Although further investigation is required to explore this alternative method, we expect that Mahalanobis matching within missingness patterns would be similar to the MPA, thus relying on the same assumptions. We also expect that Mahalanobis matching after inclusion of missing indicators may require additional assumptions, similar to the missing indicator approach requiring additional simplifying assumptions compared to the MPA.

We have concentrated on scenarios where treatment and outcome are both fully observed. A hybrid method, combining the MPA and multiple imputation, was proposed by Qu and Lipkovich, ³⁵ and studied by Seaman and White. ³⁸

the MPA is simple and easy to implement and may be useful in settings where other missing confounder data methods are not appropriate. We believe that this approach will be particularly useful in areas using routinely collected data, particularly electronic health record research. We have produced practical guidance for researchers to decide whether the underlying assumptions of the MPA are plausibly satisfied in a particular clinical setting.