The TREES Toolbox—Probing the Basis of Axonal and Dendritic Branching

It has now been 100 years since Ramon y Cajal described the remarkable diversity of neuronal branching. Only recently, however, have a number of rigorous formalisms emerged providing an accurate quantitative description of axonal and dendritic morphologies. We have launched a freely distributed open-source software package, the TREES toolbox, written in Matlab (Mathworks, Natick, MA), in order to help to pool together the resources offered by a wide variety of novel approaches to studying dendritic and axonal branching that have recently become available. This package introduces a simple general description of neuronal morphology as a graph and provides the basic tools to edit, visualize and analyze neuronal trees in the basis of this description. We then implement our own approach, assuming that neuronal branching can largely be expressed by local optimization of total wiring and conduction distances. We provide the corresponding modular extendable tools to automatically reconstruct neuronal branching from microscopy image stacks and to generate synthetic branched structures. The package is complemented by an extensive user interface to facilitate the generation, visualization and editing of neuronal tree structures. The TREES toolbox is structured to make it easy for other groups to integrate their own code in order to implement their own specific applications.

Accurate predictions of computation in single neurons are nowadays well known to require detailed morphological representations. Tools for compartmental modelling such as NEURON, ¹ Genesis ² and neuroConstruct ³ have recently facilitated the modelling of small and large neural circuits involving detailed compartmental models of the neurons. Also, a new trend highlighting the importance of morphology for better understanding of network connectivity adds to the appeal of acquiring morphologies in their full level of detail. ⁴ However, obtaining the morphologies of all neurons present in one network currently remains an insurmountable hurdle. On the other hand, a number of computational methods have recently emerged to face this challenge. The corresponding approaches can broadly be divided into two groups:

1. Strategies for faithful reconstruction of dendrites and axons directly from the experimental preparation. ⁵

2. Approaches for dealing with the more general understanding of neuronal branching and the generation of synthetic morphologies indistinguishable from their biological counterparts, thereby reproducing branching statistics and their variability observed in nature. ⁶

Both approaches are complementary and can each be subdivided into characteristic sequential steps: neuronal reconstruction typically can be decomposed into a sequence of image enhancement, skeletonization, tracing and post-processing, while the generation of synthetic branching structures involves a sequence of analyzing branching statistics, a growth process and several steps of postprocessing concerning pruning, diameter corrections and more. Constructing synthetic dendrites depends heavily on statistics obtained from original reconstructions, while reconstruction algorithms can perform better when they incorporate general knowledge about morphology. The sequential character of these methods and their interdependence provide an excellent starting point for a more collaborative approach linking these neighbouring lines of research.

Specific functions for extracting statistics from trees, editing them and visualizing them are among the most elementary steps that are used throughout all approaches. With the TREES toolbox we have assembled a software package which contains most of these ubiquitous procedures, described in code that is simple and flexible in its usage. The software package is written in Matlab (Math-works, Natick, MA), the most widely used scientific programming language. This should allow these functions to be easily combined in order to generate highly sophisticated yet comprehensible code.

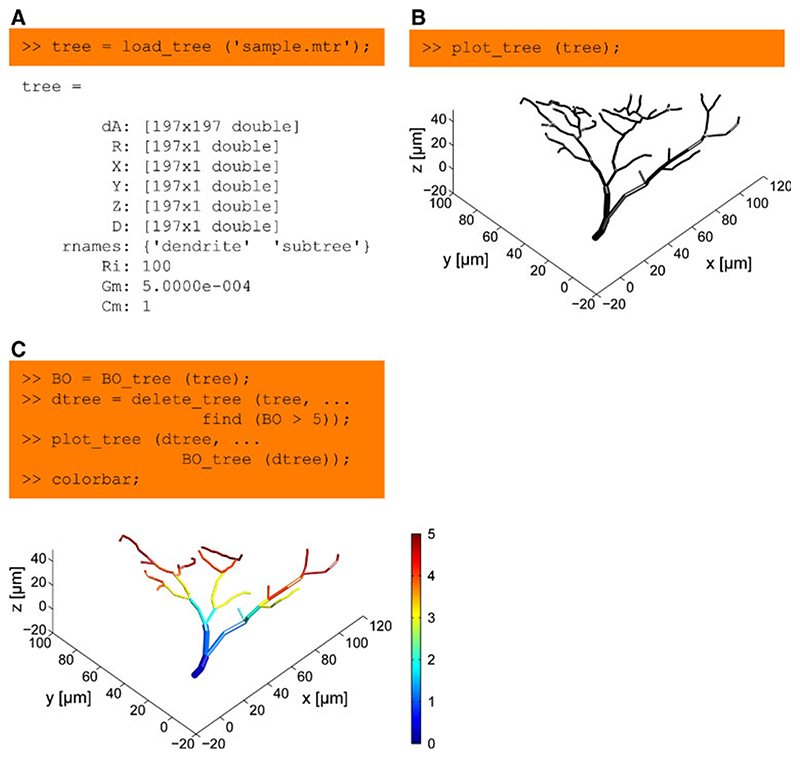
Most functions of the TREES toolbox take as a first input argument a representation of a neuron’s morphology as a tree, a simple structure with only few entries easily accessible from the command line or any Matlab script (Fig. 1a). We provide a few lines of code in Fig. 1 (see caption for further details) to demonstrate the use of the visualization function plot_tree (Fig. 1b), and both a branching statistics function BO tree and an editing function delete_tree (Fig. 1c).

Fig. 1. Basic handling of a dendritic tree using the TREES toolbox.

a A tree is represented as a structure with: a directed adjacency matrix dA attributing a parent to each node in the tree; a set of vertical vectors, such as X, Y and Z coordinates and diameter values D, each assigning a value to every node in the tree; an array rnames containing sub-region names; arbitrary optional quantities such as the global electrotonic properties Ri, Gm and Cm, specific axial resistance, membrane conductance and membrane capacitance respectively. b Most functions in the TREES toolbox take a tree as their first argument. This is the case for example for the function plot_tree, which allows a 3D interactive visualization of the sample tree loaded in (a). c Statistics and tree edit functions are generally simple and easy to use. Here the branch order (BO) values of the tree are obtained using BO_tree and all nodes with BO larger than 5 are deleted using delete_tree. The remaining tree is visualized and BO values are mapped in pseudo-colour onto the tree using the optional second argument of the function plot_tree. Axis labels were added for clarity

The TREES toolbox contains separate topology-related functions (e.g. branch order or topological path length) or metric-related functions (e.g. segment length or branch density) to obtain simple branching parameters. Together with more general meta-functions (for example to sum up any quantity along the paths of a tree) these complement each other to allow the implementation of a wide variety of traditional measures available within one line of code. The TREES toolbox enables editing at the level of single or groups of nodes but also at the level of entire trees or groups of trees within a network. Deleting or inserting groups of nodes is straightforward but also more sophisticated functions are available such as concatenation, morphing, resampling, smoothing, and many others. These all are implemented each in their own dedicated Matlab function. Any set of branching statistics or electrotonic properties can be visualized in a multitude of different ways, mapped as colours, as morphometric transforms, in density plots or different contours and tree surrounding hulls. These visualization functions output simple Matlab graphic handles whose properties can be directly accessed at the command line or by a user in an interactive way. Also simple movies can be created in the scripting environment of the TREES toolbox. More sophisticated movies can be designed by exporting to Blender (http://www.blender.org/) or to the Persistence of Vision Raytracer, POV-Ray (http://www.povray.org/). Corresponding export functions are available via the.x3d format to Blender and for raytracing to POV-Ray with a number of features such as the preservation of a viewpoint from Matlab and a choice of various layouts. OpenGL (http://www.opengl.org/) rendering of cylinder-based neuronal tree models is directly available in the Matlab environment of the TREES toolbox.

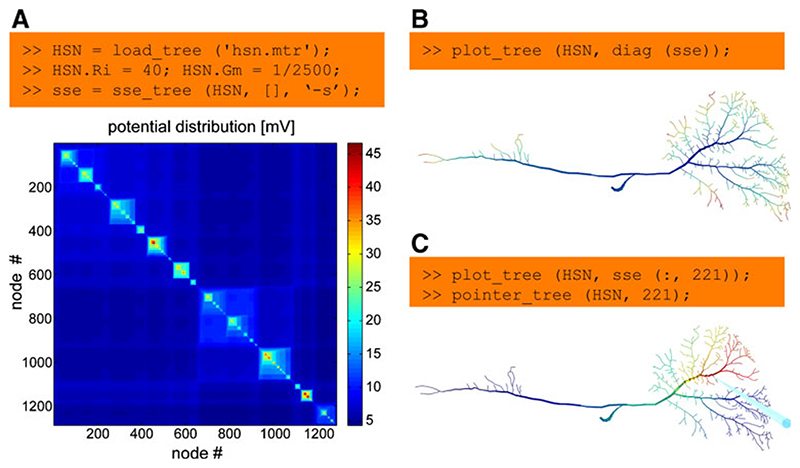
To design a compartmental model and simulate current propagation in a branched structure, steady-state electrotonic features such as local input resistances, current transfer or steady-state synaptic integration can be studied directly using the TREES toolbox in an interactive manner. This can for example be done using the sse_tree function (Fig. 2a). This function computes the electrotonic signature ⁷ which is a matrix containing the current transfer from any node to any other node. Local input resistances can therefore be read out in the diagonal of this matrix (Fig. 2b). The impact of a current injection in one specific location on local voltages throughout the cell can be obtained from a single column out of the sse matrix (Fig. 2c). Changes in electrotonic properties can also be observed in real time while editing the morphology of a tree in the user interface. For more sophisticated electrotonic analysis, morphology and passive membrane properties of trees or groups of trees can be exported to Neuron with a set of dedicated functions.

Fig. 2. Studying the electrotonic properties of a neuron.

a A sample morphology of an insect interneuron, the HSN cell, is loaded into the Matlab workspace. Specific axial resistance and membrane conductance are defined. Finally the electrotonic signature is calculated using the function sse_tree (run time: 100 ms) and displayed. This matrix shows the current transfer from any node to any other. b Measuring the potential at the same node at which the current was injected returns the local input resistance. It can therefore be read out in the diagonal of the electrotonic signature (diag (sse)). These values are mapped as false colours onto the segments of the morphology using the plot_tree function. c The potential spread as a result of injecting current into one node is obtained simply from a column in the electrotonic signature. The location of current injection is indicated by a blue pointer

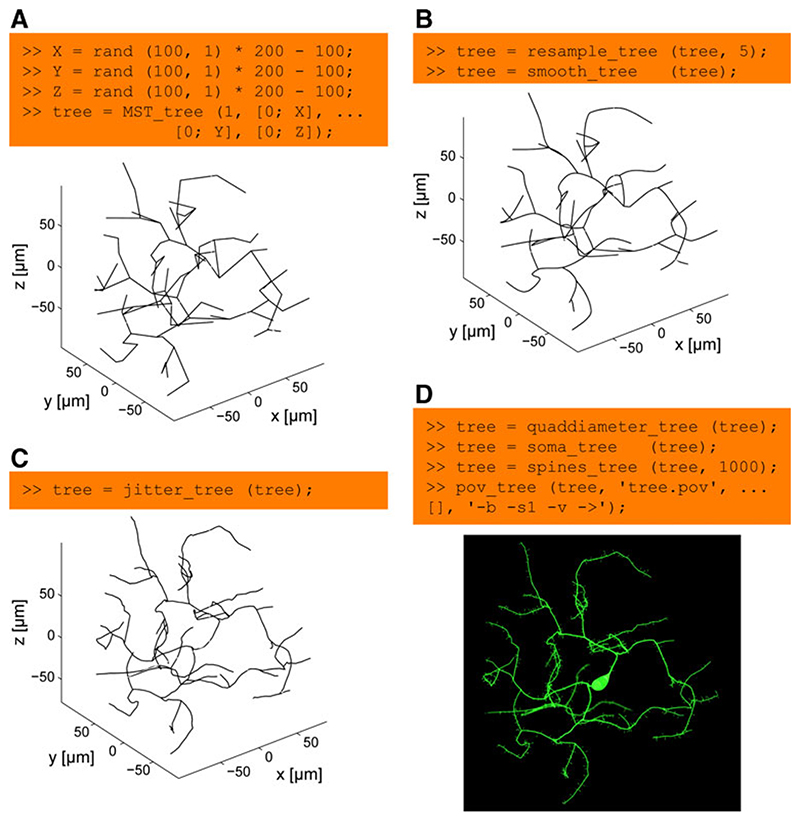
In our own approach, synthetic neuronal trees are generated using optimized graphs. ⁸ The ease of use and the modularity of the construction process is demonstrated in Fig. 3 (see caption for the full details). In our approach, nodes are connected to minimize cable length and path distances along the tree towards the root. Figure 3a depicts the corresponding code and resulting tree when connecting nodes distributed on random locations (as a simplification instead of using more realistic synaptic target locations). In the next step nodes are redistributed on the tree to lay more densely along the branches and the paths along the tree are subsequently smoothed (Fig. 3b). Adding spatial noise is just another line of code (Fig. 3c). In a few final steps, diameter values are mapped onto the nodes, spine-like structures are added and the resulting tree structure is directly sent to be rendered by POV-Ray (Fig. 3d).

Fig. 3. The modular process of generating synthetic neuronal trees.

a 100 points at random locations in the range between -100 and 100 μm are connected to a root in (0, 0, 0) using the extended minimum spanning tree algorithm implemented in MST_tree. This step is quick: run time of 50 ms on a standard computer. b The resulting tree is resampled using resample_tree to produce densely distributed nodes along the tree at 5 μm intervals. This allows the node locations to be altered to smooth the tree structure with smooth_tree (run time: 200 ms). c And, subsequently, to add biologically realistic spatial noise with jitter_tree. This step can take a bit longer (run time: 1 s in this case). d In a last step, a diameter taper is mapped onto the tree structure using quaddiameter_tree, a soma-like diameter protuberance is mapped onto the root of the tree using soma_tree and spines_tree distributes spine structures randomly along the tree. Finally, the morphology is sent in one command (pov_tree) to the POV-Ray renderer for visualization. Note that this entire process is modular and each step can be replaced by alternative algorithms. The artificial neuron generated in this figure does not reproduce a particular real counterpart since the target points were simply chosen randomly within a 200×200×200 μm cube. Axis labels were added for clarity

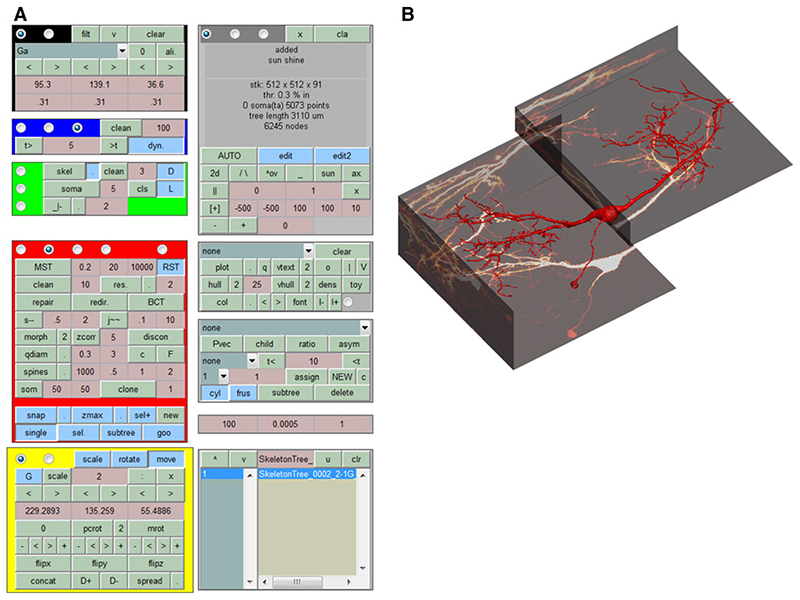
A similar modular and extendable approach is applicable to automated reconstruction from microscopy image stacks. There, image processing tools are first required to extract carrier points of the morphology. These are then connected and processed in similar ways as for the generation of synthetic neuronal trees. This flexible version of a modular algorithm should allow everybody in the community to append their own code. The ultimate goal is a method developed by the community to obtain multiple cylinder-based neuronal tree reconstructions from multiple tiled image stacks in a fully automated way. However, since fully automated reconstruction is still out of our reach for most preparations, the corresponding tool in the TREES toolbox is embedded in an extensive but well documented user interface (Fig. 4) which allows for complementary manual reconstructions of neuronal tree models from tiled image stacks. The user interface also allows the user to browse through directories of trees, edit them, and explore their properties. It is particularly useful for exploring the possibilities of the TREES toolbox before employing the corresponding functions in the command line interaction. Also, with the import and export functions within the user interface, the NEURON model and the POV-Ray rendering are just one click away.

Fig. 4.

The TREES toolbox CONTROL CENTER, an extensive user interface. A complex but extensive (and well documented) graphical user interface allows to manually interact with the construction stages of a neuronal tree. Image stacks can be visualized and trees can be traced or cloned. Individual trees and groups of trees can be visualized and edited in a variety of different ways, manually and semi-automatically. The user interface is also useful for exploring the functions provided with the TREES toolbox. a Control panels of the user interface. b Screenshot of the axis when a sample reconstruction of a neuron in the medial superior olive and the corresponding fluorescent image stacks (courtesy of Philipp Rautenberg. Rautenberg PL, Grothe B, Felmy F (2009) Quantification of the three-dimensional morphology of coincidence detector neurons in the medial superior olive of gerbils during late postnatal development. J Comp Neurol 517:385−396.) containing the morphological information were loaded in the user interface

The TREES toolbox is currently composed of 22,000 lines of commented Matlab code distributed over 120 functions. We invite users to incorporate any extensions and/or related code which they will develop. We hope that other groups can easily add to the TREES toolbox their own code for their own specific applications. The code is therefore freely distributed. The contributor’s name will be mentioned in the header of the function when integrated in the toolbox and in the toolbox documentation. To make contributions more attractive, the core function of a new method to either generate artificial neurons or reconstruct neuronal morphology from image stacks could be called “lastnameofcon-tributor_tree” to acknowledge the author’s involvement.

Information Sharing Statement

The TREES toolbox including an extensive website and documentation are freely available as open-source at http://www.treestoolbox.org. We encourage users of the toolbox software to recommend the toolbox to their peers but also to funding and award agencies.