Alternative stable states of the forest mycobiome are maintained through positive feedbacks

Abstract

Most trees on Earth forms a symbiosis with either arbuscular mycorrhizal or ectomycorrhizal fungi. By forming common mycorrhizal networks, actively modifying the soil environment, and other ecological mechanisms - these contrasting symbioses may generate positive feedbacks that favor their own mycorrhizal strategy (i.e. the con-mycorrhizal strategy) at the expense of the alternative strategy. Positive con-mycorrhizal feedbacks set the stage for alternative stable states of forests and their fungi, where the presence of different forest mycorrhizal strategies is determined not only by external environmental conditions but also mycorrhiza-mediated feedbacks embedded within the forest ecosystem. Here we test this hypothesis using thousands of U.S. forest inventory sites to show arbuscular and ectomycorrhizal tree recruitment and survival exhibit positive con-mycorrhizal density dependence. Data-driven simulations show these positive feedbacks are sufficient in magnitude to generate and maintain alternative stable states of the forest mycobiome. Given the links between forest mycorrhizal strategy and carbon sequestration potential, the presence of mycorrhizal-mediated alternative stable states affects how we forecast forest composition, carbon sequestration and terrestrial climate feedbacks.

Introduction

Most trees on Earth form belowground networks with symbiotic mycorrhizal fungi, which in turn can connect different tree stems and species within a forest ¹ . Yet, the vast majority of tree species can only form one of two predominant functional types of mycorrhizal symbiosis, arbuscular mycorrhizal or ectomycorrhizal (AM or EM), each of which may set in motion processes that favor the establishment and persistence of one mycorrhizal network over the other. For example, common mycorrhizal networks may facilitate resource transfers which favor the recruitment and survival of their own mycorrhizal strategy (the con-mycorrhizal strategy) at the expense of the alternative strategy ^2–5 . Furthermore, once established, AM and EM forests may engineer soil nutrient cycling conditions, further reinforcing positive con-mycorrhizal feedbacks to favor their own mycorrhizal strategy ^6–9 . Additionally, establishment of either strategy can lead to an accumulation of con-mycorrhizal spores and mycelium, which may further strengthen positive feedbacks, as could potentially other yet to be discovered ecological phenomena. If such positive feedbacks exist across a wide range of forests they may, in time, generate alternative stable states of forested biomes, mediated by interactions between trees and the forest fungal microbiome ¹⁰ . As a result, forest mycorrhizal type may act as a filter on forest biodiversity, restricting community membership as a function of mycorrhizal compatibility, which may be further reinforced by soil nutrient cycle feedbacks, compatible symbiont density, and more. Given the links between forest mycorrhizal status and carbon sequestration potential ^11–13 , the presence of mycorrhiza-mediated alternate stable states would affect how we forecast forest composition and emergent ecosystem carbon balance.

The potential for positive feedbacks to drive alternative stable states in AM and EM symbioses at continental scale was originally hypothesized three decades ago, yet empirically testing this hypothesis at large spatial scale remains a challenge ¹⁴ . Recent work lends support to this idea, showing mixed mycorrhizal forests are far rarer than expected by chance ¹⁵ . While this co-occurrence pattern is consistent with the presence of alternative mycorrhizal stable states, there remain numerous other possible explanations for this pattern ¹⁶ , including environmental filtering and dispersal limitation ^17,18 , which can also lead to the clumping of similar species ^18,19 . Demonstrating that patterns in AM vs. EM forests reflect mycorrhizal-induced alternative stable states requires evidence that (i) bimodality exists in the frequency distribution of forest mycorrhizal types, (ii) positive community feedbacks in time could give rise to alternative stable states, and (iii) observed feedbacks are strong enough to generate and maintain alternative stable states in the face of environmental heterogeneity and demographic stochasticity ²⁰ . Importantly, each of these criteria must consider and account for many potential non-linear controls of the environment on tree species’ demographic rates and spatial distributions, as well as signatures of dispersal limitation in recruitment dynamics ^11,18 . These challenges have prevented previous work from disentangling the effects of mycorrhizal community feedbacks from environmental filtering and dispersal limitation. As a result, the generality of potential mycorrhizal feedbacks in shaping forest distributions at large spatial scales remains unknown.

Results

Clear bi-modality in forest mycorrhizal strategies

Here we use long-term forest inventory data across the United States to show AM vs. EM forests likely coexist at a landscape scale as alternative stable states, and that these findings cannot be explained by confounding with the environment or dispersal limitation. First, we identify clear bimodality in AM vs. EM tree relative abundances, with two distinct frequency peaks at 100% AM and 100% EM dominance across the Eastern U.S. (Fig 1a-b). Importantly, this signature persists even after controlling for environmental filtering by accounting for over 200 potential environmental drivers of tree species composition (Fig 1c). This was accomplished by fitting statistical models to forest mycorrhizal composition data, accounting for linear and non-linear community-environment relationships, and then adjusting relative abundance values to remove observed environmental signatures (see Methods; Additional visualization of how each environmental driver influences the balance of AM vs. EM tree species can be found at https://hooge104.shinyapps.io/alt_stable_states_env_conditions/).

Fig 1. Bi-modality of mycorrhizal forests across the Eastern U.S.

(A) the spatial distribution of 6,965 forest inventory sites used in this analysis. Colors represent the relative abundance of ectomycorrhizal trees within a plot (purple = 100% ectomycorrhizal; green = 100% arbuscular mycorrhizal). (B) Histogram of the relative abundance of ectomycorrhizal trees by basal area across North America. Values of 1 reflect forests with 100% ectomycorrhizal dominance and no arbuscular mycorrhizal trees, while values of 0 reflect forests with 100% arbuscular mycorrhizal dominance and no ectomycorrhizal trees. (C) The same data as presented in panel B, after removing environmental signals using statistical models.

The bimodal distribution of forest types is consistent with the presence of alternative stable states fundamentally structuring the distribution of forest symbioses across North America, similar to previous analyses ¹⁵ . Importantly, however, we also find that this bimodal distribution remains after removing the signal of environmental filtering on the distribution of AM vs. EM forests (Fig 1c), demonstrating that this pattern cannot be explained solely by differing habitat preferences between AM and EM trees. Additional analysis showed stand age (a proxy for successional stage) had a very small effect on AM vs. EM balance, and could not explain the observed bimodal distribution (Extended Data Figure 1).

Positive feedbacks in mycorrhizal recruitment and survival

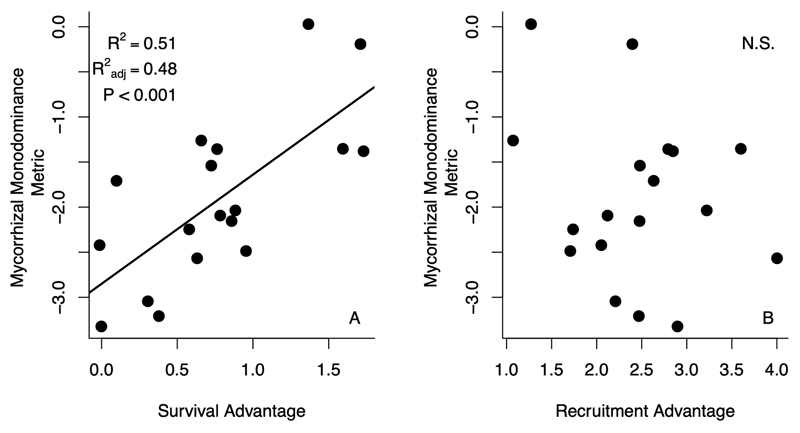
To examine the potential role of positive feedbacks in driving this observed bimodality within the forest mycorrhizal system over time, we analyzed tree recruitment and mortality across 6,965 repeatedly measured forest inventory plots. Our analysis revealed strong positive con-mycorrhizal feedbacks across the Eastern U.S.A. (Fig 2). After controlling for tree size, environmental factors, and stand conditions, an individual EM tree is more likely to die in an AM forest than an individual AM tree, and AM trees are more likely to die in EM forests than EM trees (Fig 2A). Recruitment patterns were similar to mortality, with con-mycorrhizal relative abundance having a positive effect on con-mycorrhizal recruitment. Holding all else constant, EM tree recruitment is greater than AM recruitment in EM forests, and vice versa (Fig 2C). These findings were robust to spatially subsetting the data set across geographically defined ecoregions (Extended Data Figure 2). Furthermore, finer-scale spatial-subsetting and refitting of models revealed the strength of con-mycorrhizal survival advantage was a strong predictor of the degree of mycorrhizal mono-dominance at the sub-regional level (Extended Data Figure 3). In other words, the larger the benefit of con-mycorrhizal neighbors for tree survival, the more bimodal the distribution of AM vs EM trees within a sub-region. Finally, while we observed spatial autocorrelation in raw recruitment observations, consistent with dispersal limitation that could drive clumping of individual species and therefore mycorrhizal types, final statistical models were able to capture and account for this autocorrelation, and therefore separate local community feedbacks from the potential influence of dispersal limitation (Extended Data Figure 4).

Fig 2. Positive con-mycorrhizal feedbacks observed in tree recruitment and survival.

(A) survival probability of an individual arbuscular mycorrhizal (AM) tree (green) or ectomycorrhizal (EM) tree (purple) within a forest stand where all other trees are either arbuscular or ectomycorrhizal. Plotted values are estimates based on the full model, holding environmental conditions and stand structure constant, and drawn from the model 95% confidence interval. (B) Difference in survival probability of individual tree species under EM relative to AM conditions. Differences are calculated on the logit-linear scale of the model. Positive values indicate an individual of a given tree species is more likely to survive within an EM dominated forest, and negative values indicate an individual is more likely to survive within an AM forest. Error bars represent the 95% confidence interval of the difference in means. (C) Recruitment rate of new arbuscular and ectomycorrhizal trees into a forest already dominated by arbuscular or ectomycorrhizal trees. Plotted values are estimates based on the full model, holding environmental conditions and stand structure constant, and drawn from the model 95% confidence interval. (D) Difference in recruitment rates of individual tree species under EM relative to AM conditions. Differences are calculated on the log-linear scale of the model. Positive values indicate an individual of a given tree species is more likely to recruit within an EM dominated forest, and negative values indicate an individual is more likely to recruit within an AM forest. Error bars represent the 95% confidence interval of the difference in means.

The observed patterns of recruitment and mortality were also apparent at the species level. Among the 22 most abundant AM and EM tree species, individual tree species are more likely to recruit and survive if their neighbors are of the same mycorrhizal type, a pattern that appears to be independent of hardwood vs. coniferous life history and the basal area of conspecific trees (Fig 2B, D). Individual AM trees also grew more slowly around EM neighbors, yet no tree species grew faster in EM relative to AM conditions (Extended Data Figure 5). We suspect feedbacks in recruitment and mortality feedbacks are stronger than growth, as resource transfers via common mycorrhizal networks and other feedbacks may be critically important during seedling establishment and mortality-inducing stress events ³ . The observed patterns of recruitment and mortality potentially represent positive feedbacks that could generate and maintain bimodality of AM vs. EM forest states. However, these patterns are also influenced by environmental drivers and demographic stochasticity. Strong evidence for positive con-mycorrhizal feedbacks requires that these effects are large enough to generate and maintain bimodality in the face of environmental heterogeneity, demographic stochasticity, and changes in forest structure over time.

Simulation shows observed positive feedbacks necessary and sufficient to maintain alternative stable states, and generate hysteresis across environmental gradients

To test if positive con-mycorrhizal feedbacks in recruitment and mortality observed over a short time-scale are strong enough to generate and maintain alternative mycorrhizal stable states over longer time-scales, we ran a series of demographic simulations, driven by empirically fitted statistical models of growth, recruitment and mortality. We initialized 1,000 forest plots with varying AM vs. EM composition and allowed them to grow for 200 years. We incorporated environmental heterogeneity by drawing plot-scale environmental conditions randomly from observed values across forests used to fit statistical models. We ran two sets of simulations, both of which used the same empirical demographic models of growth, mortality and recruitment described above, but the “null” model excluded con-mycorrhizal predictors.

We found simulations driven by demographic models fit without con-mycorrhizal predictors could not generate a bimodal distribution of AM vs. EM forests, while simulations driven by models fit with con-mycorrhizal predictors recovered the observed bimodal distribution of AM vs. EM forests (Fig 3). These findings suggest that observed con-mycorrhizal recruitment and mortality feedbacks are both necessary and sufficient in magnitude to generate and maintain alternative mycorrhizal stable states of the forest biome in the face of environmental heterogeneity, demographic stochasticity, and changes in forest structure over time. We note simulation results are more bimodal than observed empirical patterns, and this likely reflects our choice of initial conditions – most forests in simulations are ~200 years old, and all started from either an AM or EM dominated state (which gave our null simulation the best chance of reproducing bimodality and therefore disproving our hypothesis). Relaxing these assumptions may improve the match between the simulation and empirical data.

Fig 3. Simulating forest feedbacks.

Histogram represents the relative abundance of EM trees within 1,000 simulated forests plots after 100 years. Colors represent the relative abundance of ectomycorrhizal trees within a plot (purple = 100% ectomycorrhizal; green = 100% arbuscular mycorrhizal). (A) Outcome of null demographic simulations, driven by growth, recruitment and mortality models fit without con-mycorrhizal density predictors. Very few plots are dominated by all AM or all EM trees. (B) Outcome of demographic simulations driven by growth, recruitment and mortality models fit with con-mycorrhizal density predictors. Plots dominated by AM or EM trees are the most common frequency categories.

The presence of alternative mycorrhizal stable states may fundamentally change temporal predictions of forest mycorrhizal composition over environmental gradients. If alternative stable states are present, then forest mycorrhizal transitions should exhibit hysteresis in response to N pollution, an environmental change driver known to shift forests from EM to AM states ²⁰ . If positive feedbacks are strong, then the relative abundance of AM vs. EM trees in a forest will depend on not just the environment, but also the initial distribution of these forest types (Fig 4A vs. 4B). To understand the potential magnitude of hysteresis in forest mycorrhizal transitions under N pollution, we ran a second set of simulations, growing forests across a N deposition gradient, initializing 1,000 regenerating forests at the beginning of the simulation as either mostly EM dominated (80% of stands initialized with only EM trees, the remainder AM) or mostly AM dominated (80% of stands initialized with only AM trees, the remainder EM). Forest simulations were run for 400 years to minimize the influence of demographic lags on model outcomes. Remarkably, our simulations accurately reproduced the known relationship between a decline in EM forest dominance and N deposition ²¹ . Furthermore, we observed substantial hysteresis across the N deposition gradient, where the relative abundance of EM trees across all forest plots strongly depended on the initial community state of the simulation (Fig 4C). For the same environmental conditions, the relative abundance of EM trees was much greater if the set of forest plots were initially dominated by EM trees than if they were initially dominated by AM trees. Null simulations show the magnitude of observed hysteresis cannot be explained in the absence of mycorrhizal feedbacks (Extended Data Figure 6). While we have focused on N deposition here, as it is directly linked to one potential mechanism of positive feedback and can be easily incorporated into your model framework, this finding likely extends to other global change drivers that affect AM vs. EM dominance in forests, particularly fire frequency.

Fig 4. Hysteresis in mycorrhizal strategies across a nitrogen deposition gradient.

(A) Environmental filtering predicts the relative abundance of AM vs. EM trees across a landscape as a function of nitrogen deposition should be driven by environmental filtering, and independent of the initial distribution of AM vs. EM forests. (B) If alternative stable states are present then the relative abundance of AM vs. EM trees should exhibit hysteresis in response to N deposition. The relative abundance depends not only on environmental conditions but also the initial community state of the forest (initially AM or EM dominated). (C) Results of two sets of demographic simulations where 80% regenerating forests started in an EM dominated state (purple line) or an AM dominated state (green line). Shaded regions represent the 95% bootstrap confidence interval of the mean relative abundance of EM trees across each set of forest simulations.

Discussion

Researchers have long suspected that contrasting forest mycorrhizal strategies may generate feedbacks that reinforce the establishment and persistence of con-mycorrhizal strategies among trees ¹⁴ . However, only recently has sufficient data accrued to understand forest mycorrhizal composition and turnover at massive spatial scale, allowing us to empirically test this hypothesis. Here we show the distribution of AM vs. EM trees is bimodal across the Eastern US, likely maintained by strong positive recruitment and survival feedbacks within AM and EM forests, consistent with the presence of alternative mycorrhizal stable states. Our findings are consistent with foundational work on alternative ecosystem stable states of eastern hemlock (EM associated) and sugar maple (AM associated) forests in northern Michigan, U.S.A. ^22,23 . Findings from this previous work are likely to be a specific example of a more general and widespread phenomenon. Given the prominent role of mycorrhizal fungi in shaping the biogeochemistry of their ecosystems ^12,13 , it is unsurprising that mycorrhizal feedbacks extend across multiple tree species and larger spatial scales. Indeed, previous work on common mycorrhizal networks has shown positive associations between con-mycorrhizal, but not hetero-mycorrhizal tree species ^2,4,5 . We hypothesize that both N-cycle feedbacks and common mycorrhizal networks within mycorrhizal types may act in concert to mediate positive feedbacks that generate and maintain alternative mycorrhizal stable states.

We focus on the potential roles of common mycorrhizal networks and soil nutrient cycle feedbacks, as there is substantial empirical evidence from many different studies to support these positive feedback mechanisms ^1,3,7 , yet other mechanisms remain plausible. For example, forests dominated by a particular mycorrhizal strategy may harbor a greater abundance of compatible mycorrhizal mutualists, or may be more likely to harbor exceptionally beneficial mutualists, both of which could also explain observed positive feedbacks, as could other yet-to-be discovered ecological phenomena. Regardless of the particular mechanism, the importance of positive con-mycorrhizal feedbacks demonstrated here calls for more intensive empirical study to decompose the relative importance of different positive feedback mechanisms that give rise to alternative mycorrhizal stable states. Identifying the dominant drivers will likely affect how we understand and manage these fundamentally different symbiont strategies.

It is important to recognize that the presence of con-mycorrhizal feedbacks does not negate the role of environmental filtering in structuring the distribution of AM vs. EM forest symbioses at broad spatial scales ^11,21 . In particular, climate is a strong predictor of AM vs. EM dominance within our study region ²⁴ . However, within a continental-scale envelope of environmental conditions, prediction of AM vs. EM forests can only be made probabilistically, due to the presence of strong positive con-mycorrhizal feedbacks, which give rise to priority effects and alternative stable states ¹⁰ . This is analogous to how high vs. low rainfall is linked to the presence of savannah vs. forest, but, at intermediate rainfall, alternative stable states of forest vs. savannah emerge due to positive feedbacks linked to fire ²⁵ . It is also likely that different environmental drivers modulate the strength of con-mycorrhizal feedbacks, which may further explain environmental dependencies, and should be a focus of future work. Nevertheless, our findings help provide mechanism behind sharp transitions in the spatial distribution of AM vs. EM ecosystem types observed at global scale ¹¹ . Past analysis of the global distribution of mycorrhizal strategies reveals clear bimodality at the plot scale ¹⁵ , suggesting the feedbacks observed here may extend beyond North America, consistent with positive mycorrhizal feedbacks observed in this study and within forest plots outside of North America ^2,26 . Our analysis has also lumped incredible taxonomic and functional diversity of both plants and fungi into AM vs. EM functional groups. We recognize different tree species and different mycorrhizal fungi have diverse and complex ecological strategies ¹⁴ and that these strategies may modify the strength of con-mycorrhizal density dependence and its environmental sensitivity (Fig 2). We see exploring this diversity as the next frontier in understanding how the predominant form of tree mycorrhizal symbiosis shapes the biogeography and function of the forest macrosystem.

Alternative stable states of terrestrial ecosystems have long been hypothesized but rarely demonstrated, in part because the empirical evidence needed is notoriously difficult to obtain at sufficient spatial and temporal scales ^20,25 . This is particularly true for belowground microbial systems where it is exceptionally difficult to isolate the drivers of community change. Here we present multiple lines of evidence, each relying on independent analytical approaches, to provide strong inference for the presence of alternative mycorrhizal stable states within the temperate forests of eastern North America. These alternative stable states likely arise from a combination of divergent plant traits ²⁷ , interactions between mycorrhizal fungi and free-living soil microbial communities at the molecular scale ^28,29 , common mycorrhizal networks ^2,4,5 , and potentially additional plant and microbial mechanisms. This combination of plant and microbial feedbacks then ripples through the ecosystem to affect the patterning of forest mycorrhizal symbioses across the continent. By highlighting how the soil microbiome shapes the functioning and responsiveness of entire forests, this work demonstrates the emerging importance of the forest microbiome for understanding the biogeography and function of the forest macrosystem. Given the striking differences in carbon cycling and storage between AM and EM-dominated systems ^12,13 , the presence of alternative mycorrhizal stable states requires a rethinking of how forest composition and function vary across time and space, as well as the implications of these predictions for the global carbon cycle and in turn potential future states of the Earth.

Materials and Methods

Data collection for the United States (US) Forest Service Forest Inventory Analysis Database

All data used in this set of analyses comes from the US Forest Service’s Forest Inventory and Analysis database, version 7 ³⁰ . We further subsetted to sites within the Eastern US where re-measurement intervals are standardized, which facilitated fitting of demographic models and demographic simulations, as done in previous analyses ²⁴ (Fig 1). FIA plots are comprised of four spatially dinstict sub-plots, and so “plot-level” data should be considered a sub-sampling of the larger area. These data have proven valuable for detecting species interactions in other analyses ³¹ , and are therefore well suited to test hypotheses regarding mycorrhizal interactions. We only considered sites where all subplots were in a forested condition and excluded plantations as well as any sites with evidence of active management or harvesting. We also excluded any sites where >50% of trees died between re-census intervals, as these frequently represented sites experiencing major invasive pest outbreaks. Trees were assigned AM or EM association as in previous analyses ²¹ . Once mycorrhizal associations were assigned, we further subsetted the data set to sites where >90% of basal area was associated with either AM or EM associated trees. Therefore, a plot with 50% EM basal area and 50% AM basal area would be included in this analysis, however any plot with >10% mixed mycorrhizal, arbutoid, ericoid or non-mycorrhizal basal area would be excluded. This filter excluded 15% of all forested sites. Further investigation showed 2/3 of excluded sites (i.e. 10 of the 15%) were due to a high abundance of Populus, a well-known dual AM-EM tree genus. The remainder of exclusions were primarily driven by trees where mycorrhizal strategy was unknown. Our final dataset included 6,965 unique forest sites, re-censused at a ~5-year interval, with complete environmental covariates, comprised of 200,363 trees.

Environmental covariates

To control for potential environmental filtering we extracted information on 204 environmental variables that could be related to forest and mycorrhizal ecology. These environmental variables captured variation in climatic, soil nutrient, soil chemical, soil physical and vegetative indices, radiation and topographic variables and anthropogenic influence (Supplementary Data File 1). We explicitly did not include the soil chemical factors %C, %N, C:N or soil pH, as these are all hypothesized mechanisms by which tree species modify the soil environment to generate alternative stable states. All covariate map layers were resampled and re-projected to a unified pixel grid in EPSG:4326 (WGS84) at 30 arcsec resolution (approximately 1 km² at the equator). Layers with a higher original pixel resolution were down sampled using a mean aggregation method; layers with a lower original resolution were resampled using simple up sampling (that is, without interpolation) to align with the higher resolution grid ³² . To reduce predictor dimensionality we performed principle component analysis on all environmental predictors, and included the first ten principle components which captured ~83% of the variation in the original 204 environmental drivers. These ten environmental predictors were included in all statistical models of tree growth, recruitment and survival, as well as the relative abundance of EM trees within a plot.

In addition to the above environmental variables, we also included a metric of historic N deposition loading. By including this in addition to the above ten environmental principle components, we could ask questions about the direct effect of N deposition, independent of these other environmental factors. 15 year mean annual wet and dry N deposition was assigned at 0.25° resolution ³³ . We summed wet and dry N deposition to estimate total N deposition. Previous work has shown 15 and 30-year wet N deposition data are strongly correlated, and are representative of historical patterns of N deposition loading across the United States ²¹ .

The FIA does not report site coordinates with exact precision, and this affects the accuracy of our environmental drivers. Plot locations are limited in accuracy to ~800m, and then 20% of observations are randomly swapped at the county level. Because variation in environmental factors are much larger across counties than within, this limited spatial precision will increase parameter uncertainty associated with these environmental drivers, but does not prevent us from detecting large-scale patterns, the goal of this analysis ²¹ .

Testing for bimodality in the contemporary distribution of AM and EM forests

Alternative stable state theory predicts that, within some envelope of environmental conditions, ecosystem types should exhibit a bimodal distribution ^10,20 . However, if exogenous environmental conditions that also affect the abundance of AM vs. EM trees within a forest are also bimodal or affect the distribution of trees in non-linear ways, this may generate bimodality in the distribution of AM vs. EM forests. To control for this potential confounding, we fit generalized additive models to EM relative abundance to determine the effect of environmental drivers on the distribution of EM vs. AM relative abundance. Models were fit using a binomial error distribution and a logit link function via the gam() function within the mgcv package for R statistical software ^34,35 . Relative abundances were modeled as a function of the ten environmental principle components described above, and nitrogen deposition. County was included as a random effect to account for potential residual spatial autocorrelation. All predictors, except for county level random effects, were fit as independent spline terms with a maximum number of potential “knots” set to 5 to account for potential non-linearities, while avoiding over-fitting. Splines were fit using a penalized thin-plate spline regression method ³⁴ . Once the model was fit, we removed environmental signatures from transformed relative abundance values by subtracting fitted model values from observed values, and then adding the mean value of each environmental predictor transformed by its associated spline function. These values were then re-projected onto the original (0,1) scale via an anti-logit transformation. We tested for bimodality of both the raw and environmentally-detrended distributions using a two-tailed Hartigan’s Dip Test for statistical unimodality ³⁶ .

Testing for demographic neighborhood effects that would reinforce AM vs. EM dominated states

Changes in the overall relative abundance of AM vs. EM trees in a forest are fundamentally driven by differences in AM vs. EM forest demographic processes of growth, recruitment and mortality (or survival). We modeled each of these processes as a function of environmental factors, individual tree and stand characteristics (tree size, stand stem density and stand basal area), and the relative abundance of EM trees in the forest (our con-mycorrhizal predictor), to quantify the influence of con-mycorrhizal density dependence. Once models were fit, we held environmental, individual and stand characteristics constant and used the model to understand the sign and magnitude of con-mycorrhizal neighborhood effects. This allowed us to answer questions like, is an AM tree less likely to die in an AM forest than an EM tree? Or, does an EM tree grow more in an EM forest relative to an AM tree?

Modeling tree growth

Tree growth was modeled at the individual tree level across the most recent 5-year time interval for each forest site using a generalized additive model (gam) within the mgcv package ³⁴ for R statistical software ³⁵ . We fit separate models for AM and EM associated trees. Within each model, current tree diameter was modeled as a function of an individual tree’s previous diameter, total plot basal area, stem density within a plot, all environmental covariates, and the relative abundance of EM trees within a plot (i.e. the con-mycorrhizal predictor) ²¹ . County was included as a random effect to account for potential residual spatial autocorrelation. All predictors, except for county level random effects, were fit as independent spline terms with a maximum number of potential “knots” set to 5 to account for potential non-linearities, while avoiding over-fitting, using a penalized thin-plate spline regression method ³⁴ .

Modeling tree recruitment

Recruitment of AM and EM trees were modeled separately at the plot level across the most recent 5-year time interval for each forest site within the GAM framework using a Poisson distribution implemented within the mgcv package ³⁴ for R statistical software ³⁵ . Recruits are defined as all individuals in the current census greater than 12.7cm diameter which were not present in the previous census. Recruitment of AM or EM trees was modeled as a function of plot basal area, stem density, basal area of con-mycorrhizal trees, all environmental covariates, and the relative abundance of EM trees within a plot (i.e. the con-mycorrhizal predictor). The basal area of con-mycorrhizal trees within the plot was included as a term in addition to the con-mycorrhizal predictor to account for the fact that recruitment generally increases with the abundance of a focal species or functional group within a given site, i.e., the apple does not fall far from the tree ³⁷ . County was included as a random effect to account for potential residual spatial autocorrelation. All predictors, except for county level random effects, were fit as independent spline terms with a maximum number of potential “knots” set to 5 to account for potential non-linearities, while avoiding overfitting, using a penalized thin-plate spline regression method ³⁴ .

In recruitment models, both con-mycorrhizal basal area and con-mycorrhizal relative abundance are included, and these predictors are correlated. However, additional analysis shows this correlation does not prevent including both these predictors in the same statistical model, based on investigation of variance inflation factors (VIFs) and correlation coefficients (R² = 0.44-0.6, VIFs 1.8-2.5, Extended Data Figure 7, panels A-B), therefore, it is possible to include both predictors in the same model ³⁸ . To further address the potential influence of collinearity between con-mycorrhizal basal area and con-mycorrhizal relative abundance on our ability to separate their effects on recruitment, we performed a power analysis. We subsampled our dataset at different levels of sampling effort (preserving the correlation between con-mycorrhizal basal area and relative abundance), and then prescribed effects of con-mycorrhizal basal area and con-mycorrhizal relative abundance on ectomycorrhizal tree recruitment. We show this correlation does not prevent an unbiased estimate of the con-mycorrhizal relative abundance effect, and the sampling effort used in this analysis (>6,000 forest inventory plots) is sufficient to meaningfully constrain the uncertainty of this parameter estimate (Extended Data Figure 7, panel C).

Modeling tree mortality (survival)

Tree mortality probability was modeled at the individual level across the most recent 5-year census interval within the GAM framework using a binomial distribution implemented within the mgcv package ³⁴ for R statistical software ³⁵ . We fit separate models for AM and EM associated trees. Within each model, tree mortality probability was modeled as a function of an individual tree’s previous diameter, total plot basal area, stem density within a plot, all environmental covariates, and the relative abundance of EM trees within a plot (i.e. the con-mycorrhizal predictor). All predictors were fit as independent spline terms with a maximum number of potential “knots” set to 5 to account for potential non-linearities, while avoiding over-fitting, using a penalized thin-plate spline regression method ³⁴ . County was included as a random effect to account for potential residual spatial autocorrelation. Results are visualized as survival probability (1 – mortality probability).

Species level growth, recruitment and mortality models

We fit growth, recruitment and mortality models as above, but at the species level for the 11 most abundant AM and 11 most abundant EM tree species, based on the number of individual stems within the dataset. Models structures and covariates were identical, save for recruitment, where con-mycorrhizal basal area was replaced with the basal area of the particular species being modeled within a plot (i.e. conspecific basal area).

Ecoregion level growth, recruitment and mortality models

The study region considered here contains multiple ecological sub-regions with distinct combinations of tree species and potentially unique interactions between AM and EM associated trees at the functional group level. To understand if our findings across the Eastern U.S. generalized to ecological sub-regions, we refit growth, recruitment and mortality probability models as above to five regional subsets of the dataset. Regional subsets were chosen using EPA level 2 ecoregions that contained at least 1,000 unique forest inventory plots ³⁹ .

Exploring plot and species level random effects

In our full analysis of tree growth and mortality we would ideally account non-independence of individuals within survey plots as a random effect within statistical models. However, because of computational limitations, we could only include the larger spatial unit of county as a random effect in our analysis. To evaluate the potential influence of this decision, we fit models of mortality to a sub-region of the data, the Atlantic Highlands EPA ecoregion, with either county-level or plot-level random effects, and then evaluated how the choice plot vs. county random effect influenced the effect on ectomycorrhizal tree relative abundance of ectomycorrhizal tree mortality probability. The effect of ectomycorrhizal tree relative abundance on ectomycorrhizal tree mortality probability was nearly indistinguishable among models, with highly overlapping 95% confidence interval Extended Data Figure 8 A-C). Therefore, we concluded the coarser spatial random effect of county was sufficient to account for spatial non-independence within our analysis.

Similarly, different tree species can vary in growth and mortality rates and this may similarly bias our estimates of the role of mycorrhizal strategy. To investigate the relative importance of species effects in our overall analysis, we refit models to a sub-region of the data, the Atlantic Highlands EPA ecoregion, with or without species level random effects, and then evaluated how the choice plot vs. county random effect influenced the effect on ectomycorrhizal tree relative abundance of ectomycorrhizal tree mortality probability. The effect of ectomycorrhizal tree relative abundance on ectomycorrhizal tree mortality probability was nearly indistinguishable among models, with highly overlapping 95% confidence interval Extended Data Figure 8 D-F). Therefore, we concluded species level random effects were not necessary to understand the continental drivers of positive con-mycorrhizal feedbacks in demographic processes.

Testing Relationship Between Mycorrhizal Dominance and Con-Mycorrhizal Feedbacks

To test how observed con-mycorrhizal feedbacks may explain variation in the degree of mycorrhizal monodominance (i.e. the prevalence of forest stands comprised of only AM or only EM trees), we repeated our analyses of tree recruitment and survival across 18 hexagonal subregions of our study area, each of which contained at least 150 forest inventory plots. Using these models, we first calculated a metric of AM and EM recruitment and survival advantage – how much more likely a tree is to recruit or survive when surrounded by its same mycorrhizal strategy, compared to when it is surrounded by the alternative mycorrhizal strategy. Specifically, this was calculated by varying the relative abundance of con-mycorrhizal basal area between 0 and 1, while holding all other covariates at their means, and then subtracting one score from the other on the original linear scale. We then averaged survival and advantage scores across AM and EM groups. Second, within each subregion, we calculated the proportion of plots where only one mycorrhizal type was present by summing the number of plots with >99% basal area of only AM or only EM trees, and then dividing by the total number of plots in the study region. This number was then logit-transformed prior to analysis to meet the assumptions of linear regression. Finally, we regressed mycorrhizal monodominance scores against average recruitment or survival advantage within a study region using ordinary least squares regression via the lm function within R statistical software ³⁵ .

Demographic Simulation 1: Testing if demographic neighborhood effects are sufficient to maintain alternative stable states

Positive con-mycorrhizal effects in and of themselves are not sufficient to generate and maintain alternative stable states. Positive con-mycorrhizal effects must be sufficient in magnitude to maintain alternative stables within a dynamic forest, in the face of environmental heterogeneity, demographic stochasticity and changes in stand structure through time. To test if observed con-mycorrhizal effects were sufficient in magnitude to maintain alternative mycorrhizal stable states, we ran a series of demographic simulations driven by empirically fitted demographic models of growth, recruitment and mortality. Simulations are initialized with 1,000 forest plots comprised of 20 trees at 12.7cm DBH (the smallest tree measured in FIA surveys) within a plot area identical to that of the FIA, and then run for 200 years. We incorporated stand replacing disturbance at a probability of 0.36% per year. This number was derived based on the overall North American stand replacing disturbance probability of 0.9% a year, and then reducing this number by 60% to exclude stand replacement associated with human harvest ⁴⁰ . When stands were cleared, stem density was reset to 20 trees per plot. Regenerating trees were assigned EM vs. AM status using the stands prior relative abundance of EM trees as the probability each new regenerating tree being EM vs. AM. We incorporated environmental heterogeneity by assigning each plot a set of environmental covariates drawn randomly from the combinations of environmental covariates observed across the forest plots used to fit demographic models. We first asked if empirically fitted demographic models are sufficient to generate bimodality of AM vs. EM dominated forests after 200 years. We then ran a second simulation, driven by a second set of “null” demographic models which were fit without con-mycorrhizal predictors (the relative abundance EM trees within a plot) to ask if demographic lags or other aspects of our demographic models or simulation could generate bimodality of AM vs. EM forests without any feedback mechanism. Half of all forest plots in each simulation were initialized with all AM trees, and the other half with all EM trees. This gave our null simulation the best chance to recapitulate bimodality of AM vs. EM forests due to demographic lags and therefore disprove our hypothesis.

Demographic Simulation 2: Testing for hysteresis in AM vs. EM forest dominance across gradients of N pollution

Hysteresis in community transitions across environmental gradients is a hallmark of alternative stable states ²⁰ . We ran two sets of demographic simulations described above, across a gradient of N deposition rates from 1 to 14 kg N ha^-1 yr^-1. In the first set of simulations 800 of 1,000 forest plots were initialized at 100% EM dominance (the remainder initialized as AM), and in the second set of simulations all 800 of 1,000 forest plots were initialized at 100% AM dominance (the remainder initialized as EM). Simulations were run forward for 400 years to minimize the influence of demographic lags on simulation outcomes. We visualize the relative abundance of EM trees across all plots at the end of the simulation as a function of N deposition.

Extended Data

Extended Data Fig 1.

Extended Data Fig 2.

Extended Data Fig 3.

Extended Data Fig 4.

Extended Data Fig 5.

Extended Data Fig 6.

Extended Data Fig 7.

Extended Data Fig 8.

Data and Availability

All forest data used in this analysis are available from the FIA data mart (https://apps.fs.usda.gov/fia/datamart/). All environmental covariate data sources are publicly available, and detailed in Supplementary Data File 1.

Code Availability

All code used to work up raw data to analysis ready products, analyze data and generate figures can be found at https://github.com/colinaverill/altSS_forest_mycorrhizas ⁴¹ .