Reconstructing vascular homeostasis by growth-based prestretch and optimal fiber deposition

Abstract

Computational modeling of cardiovascular biomechanics should generally start from a homeostatic state. This is particularly relevant for image-based modeling, where the reference configuration is the loaded in vivo state obtained from imaging. This state includes residual stress of the vascular constituents, as well as anisotropy from the spatially varying orientation of collagen and smooth muscle fibers. Estimation of the residual stress and fiber orientation fields is a formidable challenge in realistic applications. To help address this challenge, we herein develop a growth based algorithm to recover a residual stress distribution in vascular domains such that the stress state in the loaded configuration is equal to a prescribed homeostatic stress distribution at physiologic pressure. A stress-driven fiber deposition process is included in the framework, which defines the distribution of the fiber alignments in the vascular homeostatic state based on a minimization procedure. Numerical simulations are conducted to test this two-stage homeostasis generation algorithm in both idealized and non-idealized geometries, yielding results that agree favorably with prior numerical and experimental data.

1. Introduction

Mathematical modeling of the mechanical behavior of vascular tissue requires consideration of many important factors. While the mechanical characterization and constituent models of arterial tissue have been well developed, a challenging factor is the consideration of residual stress in the material in vivo. This residual stress determines the overall stress state of the material in the loaded in vivo configuration, as well as vascular homeostasis, which represents the preferred mechanical configuration in which vascular constituents operate [26]. Thus, while proper constituent models are necessary to capture the detailed mechanical behavior of vascular tissue, the inclusion of residual stress is also an essential factor for predicting biomechanical behavior in vivo and vascular remodeling [39].

Another important factor in modeling arterial tissue is the consideration of fiber orientation. Arteries are generally composed of three layers (intima, media, and adventitia) and the major mechanical constituents are elastin, collagen, and smooth muscle fibers [43]. Elastin is effective under small strain, while collagen bears the majority of loading when deformation is large [58], and smooth muscle fibers provide additional and vasoactive support [27]. To model these components, different constitutive relations have been proposed, including Fung-type models [11] and formulations proposed by Holzapfel et al. [36]. Notably, the arterial wall is often considered to be a two-layer fiber-reinforced material. A non-collagenous ground matrix, including elastin, is typically described as an isotropic neo-Hookean material [17]. The collagen and smooth muscle impart anisotropic behavior and are often described by a Fung-type response [36, 7]. To characterize the deformation of the various constituents, a constrained mixture model [44, 13] is often employed, particularly in vascular growth and remodeling studies [20, 71, 68]. Fiber orientations have traditionally been prescribed from statistical analyses of histological data [37] and rule-based approaches [4], with more recent works [28, 41] considering the dispersion of fiber orientation. Nonetheless, prescription of fiber orientation is nontrivial in realistic branched vascular models.

The in vivo stress state of vascular tissue relies critically on residual stress and fiber orientation. Namely, the homeostatic state is hypothesized to be defined by relatively uniform stress distribution in the transmural direction of each layer in the vessel wall, and that non-uniform residual stress helps to maintain this condition [26]. In idealized cylindrical vascular geometries, the residual stress field is often specified based on an opening angle [2], however, this approach is often inadequate in realistic vascular geometries. Pierce et al. [57] prescribed residual stress by specifying the deformation gradient to map the stress-free configuration to the actual mixture configuration of the vessel wall. Bellini et al. [7] incorporated a prestretch ratio into the total deformation to model the effect of residual stresses and showed that the stress distribution tends to be more uniform when residual stress is included. Holzapfel et al. investigated the 3D behavior of the residual stress experimentally [42] and developed a theoretical framework to incorporate residual stress in different vascular layers [39]. Previous works have often required parameter information that can be difficult to obtain or is of challenging applicability when realistic geometries are considered. Likewise, the residual stress distribution is rarely considered when the vascular homeostatic state needs to be reconstructed in non-idealized geometries, see, e.g., [51, 53]. To the best of our knowledge, this is the first time that a residual stress field is reconstructed in general vascular geometries with anomalies such as bifurcations.

We propose a two-stage approach to the reconstruction of the vascular homeostatic state. The first stage aims to generate an appropriate residual stress level for a given configuration of the vessel, and the second stage aims to generate optimal fiber alignments based on the stress field. Inspired by kinematic G&R models [59], [61], and [62], we introduce a prestretch tensor, obtained through an iterative process to match a prescribed homeostatic stress distribution at physiologic pressure. The deposition angle of the collagen fibers is then defined by the solution of an optimization problem, which enables the vessel to sustain the stress with minimal amount of biomass, while stochasticity is incorporated into this process to account for fiber dispersion. We propose supervised learning to predict the pre-stretch in vascular bifurcations or other geometric anomalies, where theory-based methods struggle due to topological singularities. Based on this overall framework, the numerical stability of the generation of the residual stress field and fiber directions is improved for realistic vascular geometries. Beyond addressing the vascular homeostatic state reconstruction problem, the method proposed here provides a starting point for general biomechanical analyses, such as vascular tissue mechanics or fluid-structure interaction simulations, where residual stress and proper fiber alignment set the stage for the mechanical response of the tissue.

2. Methods

2.1. Constrained mixture model

The vessel wall is considered a constrained mixture [44] of collagen, elastin, and smooth muscle fibers, where all constituents deform as a continuum. The turnover of collagen and smooth muscle fibers is a process of degradation of existing material and production of new material, described mathematically as

$$M^k\left(t\right)=M^k\left(0\right)Q^k\left(t\right)+{\int }_0^t{m}^k\left(\tau \right)q^k\left(t-\tau \right)\text{d}\tau \text{,}$$ (1)

where k denotes different collagen or smooth muscle fiber families; M ^k(t) is the local mass density of constituent k in the reference configuration κ ₀; and m^k (t) is the corresponding mass production rate. Q^k (t) is the remaining fraction of the initial mass for constituent k at time t, and q^k (t − τ) is the remaining fraction at time t for the constituents produced at time τ. In contrast to collagen and smooth muscle fibers, functional elastin is assumed to be only produced during early development. Therefore, the time evolution of the mass density for elastin is given by

$$M^e\left(t\right)=M^e\left(0\right)Q^e\left(t\right),$$ (2)

where M ^e(0) is the initial mass density for elastin, and Q^e (t) is the remaining fraction of the initial mass.

Following Holzapfel et al. [36], elastin fibers are modeled as an incompressible isotropic neo-Hookean material and the constitutive relation is given by the strain energy function per unit mass

$$W^e\left(\mathbf{\text{C}}\right)=\frac{c_1}{2}\left(I_1\left(\mathbf{\text{C}}\right)-3\right),$$ (3)

where c ₁ > 0 is a stress-like material parameter and I ₁(C) = tr(C) is the first invariant of the right Cauchy-Green deformation tensor C defined with respect to the reference configuration κ ₀. Collagen and smooth muscle fibers are modeled as anisotropic Fung-type materials with a constitutive relation for each family that is given by the strain energy function per unit mass

$$W^k\left(\mathbf{C}\right)=\frac{c_2}{4c_3}\left\{\text{exp}\left[c_3{\left(I^k\left({\mathbf{\text{C}},\mathbf{\text{E}}}_{\text{f}}^k\right)-1\right)}^2\right]-1\right\},$$ (4)

where $I^k\left({\mathbf{\text{C}},\mathbf{\text{E}}}_{\text{f}}^k\right):={\mathbf{\text{C}}:\mathbf{\text{E}}}_{\text{f}}^k\otimes {\mathbf{\text{E}}}_{\text{f}}^k$ is the fiber invariant corresponding to the square of the stretch λ^k of fiber family k; ${\mathbf{\text{E}}}_{\text{f}}^k$ is the fiber direction in the reference configuration κ ₀.

Based on the mixture rule [44], the total strain energy of the constrained mixture is

$$\begin{array}{l}w\left(\mathbf{\text{C}},t\right)=M^e\left(0\right)Q^e\left(t\right)W^e\left(\mathbf{\text{C}},t\right)\\ +{\displaystyle \sum _k{M}^k\left(0\right)Q^k\left(t\right)W^k\left(\mathbf{\text{C}},t\right)}\\ +{\displaystyle \sum _k{\int }_0^t{m}^k}\left(\tau \right)q^k\left(t-\tau \right)W^k\left(\mathbf{\text{C}},t,\tau \right)\text{d}\tau \\ ≔w^e\left(\mathbf{\text{C}},t\right)+{\displaystyle \sum _k{w}^k}\left(\mathbf{\text{C}},t\right).\end{array}$$ (5)

The strain-energy function for collagen and smooth muscle fibers, W^k (C, t, τ), depends on both the current time t and the time that the fibers are produced τ, which also determines the natural configurations for the fibers.

To incorporate the nearly incompressible behavior of vascular tissue, a standard decomposition [24, 36] of the strain energy was used

$$w(\mathbf{\text{C}},t)=U(J)+w(\overline{\mathbf{\text{C}}},t),$$ (6)

$w(\overline{\mathbf{\text{C}}})$ is termed the isochoric component and

$$\overline{\mathbf{\text{C}}}=J^{-2/3}\mathbf{\text{C}}.$$ (7)

The volumetric component U(J) is given by

$$U(J)=\frac{\kappa }{2}{(J-1)}^2,$$ (8)

with κ the bulk modulus and J the determinant of the deformation gradient tensor. By way of Eq. (8), changes to M^k affect both the referential and spatial density of fibers in the tissue; this has to be taken into account when setting initial values for the mass densities in Eq. (5).

Note that the multiplicative decomposition of the deformation gradient [24] leading to Eqs. (6, 7) may lead to locking effects and nonphysical results, even for isotropic hyperelastic models [18, 33]. This problem can be mitigated by using more advanced finite elements [48, 67], augmented Lagrangian methods [31], or – in the case of fiber-reinforced materials – decompositions without the multiplicative split in the anisotropic contribution [60, 35, 33]. The underlying approach presented herein, i.e., the reconstruction of the vascular homeostatic state, does not inherently depend on the particular decomposition and the finite element used. To keep the formulation as general and concise as possible we use the approach as presented above; the particular choice of the numerical method is beyond the scope of this paper.

Once the total strain energy of the mixture is formulated, the deformation of the vessel wall can be obtained by applying the virtual work principle

$$\delta I={\displaystyle {\int }_{{\text{Ω}}_0}\delta w\text{d}V}+{\displaystyle {\int }_{\partial {\text{Ω}}_t}\mathit{\text{P}}{\mathbf{\text{n}}}_t}\cdot \delta x\text{d}a=0,$$ (9)

where δI is the virtual work; Ω₀ is the vessel tissue in the reference configuration; ∂Ω _t is the inner surface of vessel in the current configuration; P is the transmural blood pressure; n _t is the outward normal; and δx is the virtual displacement. This variational equation for momentum balance can then be discretized (i.e., by finite element analysis) and numerically solved to compute stress or strain.

2.2. Residual stress field generation

2.2.1. Basic methodology

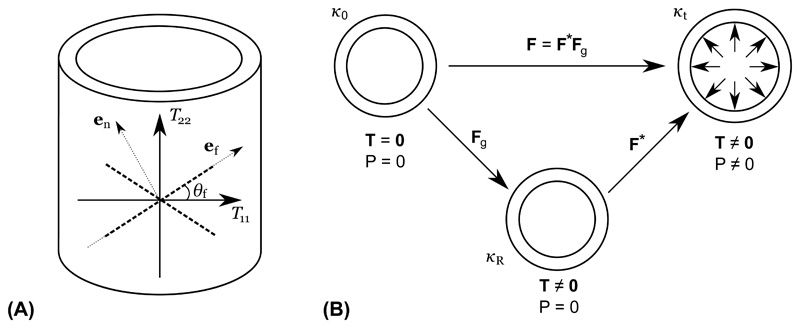
We derive residual stress implicitly through a “growth tensor” F _g that maps the unstressed reference configuration κ ₀ of the vessel to the unloaded (unpressurized) configuration with residual stress κ _R, see Figure 1(B). This approach is similar to prior works [59] and [61] that have used a similar F _g to broadly describe deformation due to growth and remodeling in development. Tensor F* in Figure 1(B) describes additional deformation due to loading, i.e., pressurization by pressure P. Thus, the total deformation F with respect to the reference configuration κ ₀ is given by

$${\mathbf{\text{F}}=\mathbf{\text{F}}}^{*}{\mathbf{\text{F}}}_{\text{g}},$$ (10)

where the growth tensor F _g is determined by the growth stretch ratios in local (r, θ, z)-directions

$${\mathbf{\text{F}}}_{\text{g}}=\text{diag}\left({\lambda }_{\text{gr}},{\lambda }_{\text{g}\theta },{\lambda }_{\text{gz}}\right).$$ (11)

If the growth stretch ratios are known (see §2.2.2 below), the elastic deformation gradient tensor F* and right Cauchy-Green deformation tensor can be written as

$${\mathbf{\text{F}}}^{*}{=\mathbf{\text{FF}}}_{\text{g}}^{-1},{\mathbf{\text{C}}}^{*}{=\mathbf{\text{F}}}_{\text{g}}^{-T}{\mathbf{\text{CF}}}_{\text{g}}^{-1},$$ (12)

and substituted into Eq. (5) to yield the total strain energy of the constrained mixture

$$w\left({\mathbf{\text{C}}}^{*},t\right)=w^e\left({\mathbf{\text{C}}}^{*},t\right)+{\displaystyle \sum _k{w}^k}\left({\mathbf{\text{C}}}^{*},t\right).$$ (13)

Figure 1.

(A) T ₁₁ and T ₂₂ are the two principal stress directions of the Cauchy stress tensor T; θ _f is the deposition angle of fiber family e _f; and e _n the fiber normal direction. (B) Relation between different configurations. κ ₀ is the unstressed reference configuration (T = 0); κ _R is the configuration with residual stress incorporated; κ_t is the current configuration with external pressure imposed.

Note, if the strain energy in Eq. (13) is decomposed via Eq. (6), near-incompressiblity is imposed by

$$U\left(J\right)=\frac{\kappa }{2}{\left(J^{*}-1\right)}^2,$$ (14)

where J* = det(F*). In general, for processes involving growth and remodeling (especially for development), constant volume should not be assumed. However it is a reasonable assumption here since the contribution from F _g, which captures the main volumetric change, is excluded.

2.2.2. Growth stretch ratios

Above we assume the growth stretch ratios are known. Here we discuss how these can be computed. The basic premise is residual stress (and hence growth stretch ratios) tend to help homogenize the stress state in the loaded configuration, thus helping to define a homeostatic stress state. While the concept of homeostatic stress is fundamental to vascular biomechanics, there is no consensus on its exactness. It has been shown that residual stress homogenizes circumferential stress in the radial direction, but it remains unclear whether homeostatic stress varies spatially. Therefore, for generality we assume that there exists a (known) homeostatic stress distribution σ _h and that the growth stretch ratios homogenize circumferential stress in the radial direction. In §2.2.3, we discuss computation of σ _h; however, the method here can be applied for any desired homeostatic stress distribution.

In solving the variational equations for momentum balance, the growth stretch ratios are updated to produce a desired homeostatic stress distribution σ _h. Namely, following [61] and [62], the growth stretch ratios are updated according to the following evolution equations

$$\frac{{\dot{\lambda }}_{\text{g}\theta }}{{\lambda }_{\text{g}\theta }}=\frac{1}{{\tau }_{\theta }}\left(\frac{{\sigma }_{\theta }\left(t\right)}{{\sigma }_{\text{h}}}-1\right),{\dot{\lambda }}_{\text{gr}}=0,{\dot{\lambda }}_{\text{gz}}=0,$$ (15)

where τ_θ is a time constant controlling how fast the growth stretch evolves and σ_θ (t) is the circumferential component of the Cauchy stress tensor, see also later in Section 2.3. Thus, the momentum equations are coupled with these evolution equations and solved in a staggered procedure until convergence of the stretch ratios (and, based on Eq. (15), circumferential stress). The algorithm for this iterative procedure can be found in Algorithm 1a. Note, radial stress is governed primarily by the boundary conditions at the inner and outer surfaces, not residual stress [45]. It is also small in comparison to the circumferential stress, which has been shown experimentally [52] and computationally [36, 46, 10]. Additionally, the axial stress component is mainly determined by the boundary condition and geometry of the vessel. Therefore, only convergence of circumferential stress is considered in Eq. (15). More details can be found in [63, 62, 43, 47].

We note that the computation of the prestretch distribution is first based on treating the collagen fibers as isotropic, the constitutive relation of which is given by the dispersion model [28]

$$\begin{array}{l}{W}^k\left(\mathbf{\text{C}}\right)=\frac{c_2}{4c_3}\{\text{exp}\left[c_3{\left(I_{*}^k-1\right)}^2\right]-1\},\\ I_{*}^k:=\left({\omega }_{\text{d}}\mathbf{\text{I}}+\left(1-3{\omega }_{\text{d}}\right){\mathbf{\text{E}}}_{\text{f}}^k\otimes {\mathbf{\text{E}}}_{\text{f}}^k\right):\mathbf{\text{C}}\end{array}$$ (16)

with the dispersion parameter ω _d equal to $\frac{1}{3}$ . This is because prestretch is mainly caused by unbalanced growth during the early development when the vascular material is more isotropic [66]. Once the proper amount of pre-stretch is incorporated, the isotropic collagen fiber network is then replaced by anisotropic fibers by setting the dispersion parameter ω _d = 0 (which recovers the original anisotropic constitutive relation Eq. (4)) and deposited in the optimal directions as defined below in §2.3. This replacement of isotropic constituents with anisotropic fibers will result in a deviation of the circumferential stress from the preset homeostatic stress. Our observation is that this this stress deviation is small. More generally, however, this deviation can be corrected for by adjusting the the homeostatic stress defined in Section 2.2.3.

2.2.3. Defining a homeostatic stress distribution

The method above can be applied for any homeostatic stress σ _h. Fung [26] demonstrated that residual stress tends to make the stress distribution uniform primarily in the transmural direction. Hence, we aim to formulate a target homeostatic stress distribution σ _h(x) that is uniform in the transmural direction, but may vary in the circumferential and axial directions according to the local geometry. This can be formulated through the steady-state solution of the following diffusion equation defined in the vessel wall domain Ω₀ as

$$\begin{array}{l}\frac{\partial }{\partial t}{\sigma }_{\text{h}}\left(x,t\right)=D{\nabla }^2{\sigma }_{\text{h}}\left(x,t\right),\text{for}x\in {\Omega }_0,t\in \left[0,T\right]\\ {\sigma }_{\text{h}}=g\left(x\right),\text{for}x\text{on}{\Gamma }_{\text{inner}},\\ \mathbf{\text{n}}\cdot \nabla {\sigma }_{\text{h}}=0,\text{for}x\text{on}{\Gamma }_{\text{outer}},\end{array}$$ (17)

where D is a virtual diffusion constant, and Γ_inner and Γ_outer denote the inner and outer wall of the vessel, respectively. Following [6] and [22], the stress distribution g(x) can be obtained from a passive nonlinear elasticity membrane problem with constitutive relations Eqs. (3) and (4), and is effectively used here to assign the variation of stress in the circumferential and axial directions. Other approaches to generate g(x) are possible. Eq. (17) is solved until steady state, which yields a stress distribution that is uniform in the transmural direction, and defines the target homeostatic stress under normal blood pressure.

Although the steady version of Eq. (17) could alternatively be used to obtain the steady state solution, we retain the unsteady version for generality since, as shown in § 3, the unsteady formulation enables the ability to generate a quasi-uniform stress distribution in the transmural direction by controlling the simulation ending time T. This quasi-uniform distribution is generally in better agreement with expectations of transmural stress, particularly when considering deviations of blood pressure from the mean arterial pressure (see e.g., Figure 7 in [7]).

2.2.4. Estimating residual stresses near bifurcations and boundaries

Generating the stretch ratios λ _gr, λ _gθ , λ _gz is based on an iterative algorithm that couples the structural mechanics (momentum) equations (9) with the evolution equations (15). The iterative method can struggle to converge in bifurcation regions where the irregular geometry may cause stress to deviate significantly from the target homeostatic value. Nonetheless, the overall theoretical framework provides a governing connection to guide how geometric and mechanical factors determine the growth stretch ratio. Therefore, the convergence of this method otherwise throughout the model may be used indirectly to guide specification at locations where the problem becomes poorly conditioned. Thus, instead of explicitly defining the growth stretch ratios at bifurcations or boundaries (or potentially other geometric anomalies), we exclude computational nodes close to these geometrical features, compute the growth stretch ratios in the rest of the domain according to the formulations above, and use that data along with supervised learning to estimate the growth stretch ratios at the excluded locations.

For the supervised learning process, random forest regression was chosen based on its general accuracy and robustness against overfitting [25]. In order to take both mechanical and geometric factors into account, the initial local stress σ ₀(x_i ) and the local curvature tensor R(x_i ) are used as the prediction features, while local growth stretch ratio λ _g(x_i ) is the training label.

The data pair (σ ₀(x_i ), R(x_i ); λ _g(x_i )) associated with each location x_i in the vascular geometry contributes to one data point in the overall training data sets. The mapping

$$\mathcal{M}:\left({\sigma }_0\left(x_i\right),\mathbf{\text{R}}\left(x_i\right)\right)\mapsto {\lambda }_{\text{g}}\left(x_i\right)$$ (18)

is obtained by constructing a random forest regressor. In random forest regression, the prediction of λ _g(x) is determined by the average of B individual regression trees characterized by their parameters Θ _b

$${\widehat{f}}_{\text{rf}}^B\left({\sigma }_0\left(x\right),\mathbf{\text{R}}\left(x\right)\right)=\frac{1}{B}{\displaystyle \sum _{b=1}^B{T}_b\left({\sigma }_0\left(x\right),\mathbf{\text{R}}\left(x\right)|{\Theta }_b\right).}$$ (19)

Each individual tree T_b (•) is constructed based on randomly sampled features and bootstrapped data sets, and the optimal tree parameters are obtained by minimizing the least square error

$${\Theta }_b^{*}=\text{arg}\underset{{\Theta }_b}{\text{min}}{\displaystyle \sum _{i=1}^N{\left({\lambda }_{\text{g}}\left(x_i\right)-T_b\left({\sigma }_0\left(x_i\right),\mathbf{\text{R}}\left(x_i\right){|\Theta }_b\right)\right)}^2.}$$ (20)

Once ${\Theta }_b^{*}$ is obtained in the training process, given a new input (σ ₀(x _new), R(x _new)), the growth stretch ratio λ _g at the new location x _new can be computed as

$$\begin{array}{l}{\lambda }_{\text{g}}\left(x_{\text{new}}\right)={\widehat{f}}_{\text{rf}}^B\left({\sigma }_0\left(x_{\text{new}}\right),\mathbf{\text{R}}\left(x_{\text{new}}\right)\right)\\ =\frac{1}{B}{\displaystyle \sum _{b=1}^B{T}_b\left({\sigma }_0\left(x_{\text{new}}\right),\mathbf{\text{R}}\left(x_{\text{new}}\right)|{\Theta }_b^{*}\right)}.\end{array}$$ (21)

We used the random forest regression implementation available from the Python package Scikit-learn [55].

To compute the local curvature tensors R(x_i ) we define a local coordinate system consisting of the radial, circumferential, and axial direction. For non-ideal, anatomically-relevant geometries this local coordinate system is defined using a Laplace–Dirichlet rule-based algorithm as described in [4]. We then use the local radial directions to define the local normal direction of the tangential surface at a given point in the geometry. Then the curvature can be calculated from the gradient of the local normal vector.

2.3. Optimal stochastic fiber deposition

After the residual stress field is generated, stress-driven fiber deposition is incorporated to capture the fiber alignment in the homeostatic state. In most prior studies, collagen fibers are deposited in predefined directions [22], and all subsequently produced collagen fibers are deposited to align with the existing corresponding collagen families. In this work, we assume fibers can be freely deposited in orientations based on the stress state at the time of deposition. Inspired by Cyron and Humphrey [14], the deposition angle is given by the solution of an optimization problem. Although the stress state is in fact triaxial for the 3D vascular geometry, the radial component of stress is much smaller compared to the axial and circumferential component. Therefore, for simplicity, we assume the vessel is under a biaxial stress condition (see Figure 1A) with T ₁₁ and T ₂₂ as the two largest eigenvalues of the Cauchy stress tensor T (we use T to denote the full Cauchy stress tensor and σ to denote scalar quantities derived from T), which is given by

$$\mathbf{\text{T}}=\frac{2}{J}\mathbf{\text{F}}\frac{\partial \omega }{\partial \mathbf{\text{C}}}{\mathbf{\text{F}}}^T.$$ (22)

2.3.1. Derivation of the optimal directions for newly produced collagen fibers

Note that in this section we derive the optimal directions for newly produced collagen fibers based on theoretical considerations. Only the final result, Eq. (28), is used in the algorithm, hence, no default values are given for parameters introduced below. We denote by σ _f,max the maximum stress that fibers can sustain when the fiber mass density is equal to some baseline value M ₀. The maximum stress is assumed proportional to the fiber mass density. Thus, for any arbitrary fiber density M _f, the maximum stress that fibers can sustain is ${\sigma }_{\text{f},\text{max}}\frac{M_f}{M_0},$ and the contribution of the fiber family to the local stress tensor is

$${\mathbf{\text{T}}}_{\text{f}}:={\sigma }_{\text{f},\text{max}}\frac{M_f}{M_0}{\mathbf{\text{e}}}_{\text{f}}\otimes {\mathbf{\text{e}}}_{\text{f}}.$$ (23)

Here, e _f = [cos θ _f, sin θ _f] ^T is the fiber direction represented in the local coordinate system defined by the circumferential and axial directions and θ _f is the fiber deposition angle (see Figure 1A). Note that the circumferential and axial directions and the deposition angle θ _f are all defined in the current configuration κ_t. Further, the local circumferential and axial directions are computed as the eigenvectors corresponding to the two largest eigenvalues T ₁₁ and T ₂₂ of the local Cauchy stress tensor T [16]. The projections of the fiber stress tensor T _f in the circumferential and axial directions are

$$T_{\text{f},\text{circ}}=[1,0]{\mathbf{T}}_{\text{f}}{[1,0]}^T={\sigma }_{\text{f},\text{max}}\frac{M_{\text{f}}}{M_0}{\text{cos}}^2{\theta }_{\text{f}},$$ (24)

$$T_{\text{f},\text{axial}}=[0,1]{\mathbf{\text{T}}}_{\text{f}}{[0,1]}^T={\sigma }_{\text{f},\text{max}}\frac{M_{\text{f}}}{M_0}{\text{sin}}^2{\theta }_{\text{f}}.$$ (25)

Assuming the body tends to minimize the mass needed for vascular fibers, while maintaining the ability to sustain circumferential and axial loading, the optimization problem to determine the deposition angle θ _f is given by

$$\begin{array}{l}\underset{M_{\text{f}},{\theta }_{\text{f}}}{\text{min}}{M}_{\text{f}}\text{such}\text{that}\\ {\sigma }_{\text{f},\text{max}}\frac{M_{\text{f}}}{M_0}\text{cos}{}^2{\theta }_{\text{f}}\ge T_{11},\\ {\sigma }_{\text{f},\text{max}}\frac{M_{\text{f}}}{M_0}\text{sin}{}^2{\theta }_{\text{f}}\ge T_{22}.\end{array}$$ (26)

The solution of Eq. (26) is

$$M_{\text{f}}^{*}=\frac{T_{11}+T_{22}}{{\sigma }_{\text{f,max}}}{M}_0,$$ (27)

$${\theta }_{\text{f}}^{*}=\pm \text{arctan}\sqrt{\frac{T_{22}}{T_{11}}},$$ (28)

which defines the optimal directions for newly produced collagen fibers. As T ₁₁ and T ₂₂ may change with time, ${\theta }_{\text{f}}^{*}$ is generally not constant. The “±” sign in Equation (28) corresponds to the two collagen families. It is worth noting that the optimal angle ${\theta }_{\text{f}}^{*}$ depends on the fiber mass density M _f indirectly via T ₁₁ and T ₂₂.

2.3.2. Stochasticity of fiber deposition

It has been observed that fiber deposition exhibits a stress-dependent stochasticity [23]. We assume that the deposition angle follows a Gaussian distribution

$${\theta }_{\text{f}}^k~\mathcal{N}\left({\theta }_{\text{f}}^{*,k},{\displaystyle \sum \left({\sigma }_{\text{f}}^{*,k}\right)}\right),$$ (29)

with mean value ${\theta }_{\text{f}}^{*}.$ The variance Σ(σ _f) is defined as a function of the fiber stress σ _f

$${\displaystyle \sum \left({\sigma }_{\text{f}}^{*,k}\right)}={\displaystyle {\sum }_0\frac{{\sigma }_{\text{scale}}}{{\sigma }_{\text{f}}^{*,k}}}$$ (30)

where σ _scale is a scale parameter for vessel wall stress, and Σ₀ is the nominal value of the variance. To avoid numerical instabilities when ${\sigma }_{\text{f}}^{*,k}$ is very small, a small positive number ϵ is added to the denominator of Equation (30). The stress in the new fiber direction is given by the projection of the Cauchy stress tensor onto the fiber direction

$${\sigma }_{\text{f}}^{*,k}=\mathbf{\text{T}}:{\mathbf{\text{e}}}_{\text{f}}^{*,k}\otimes {\mathbf{\text{e}}}_{\text{f}}^{*,k}.$$ (31)

${\displaystyle \sum \left({\sigma }_{\text{f}}^{*,k}\right)}$ is designed to be a decreasing function of the stress projection in the fiber direction ${\sigma }_f^{*,k}$ so that fibers are aligned more coherently when ${\sigma }_{\text{f}}^{*,k}$ is higher [23]. Note that the optimal deposition direction ${\mathbf{\text{e}}}_{\text{f}}^{*,k}$ and the actual fiber deposition direction ${\mathbf{\text{e}}}_f^k$ are defined respectively as

$${\mathbf{\text{e}}}_{\text{f}}^{*,k}={\left[\text{cos}{\theta }_{\text{f}}^{*,k},\text{sin}{\theta }_{\text{f}}^{*,k}\right]}^{\top },$$ (32)

$${\mathbf{\text{e}}}_{\text{f}}={\left[\text{cos}{\theta }_{\text{f}},\text{sin}{\theta }_{\text{f}}\right]}^{\top }.$$ (33)

2.3.3. Total strain energy function

Once the fiber deposition directions ${\mathbf{\text{e}}}_{\text{f}}^k$ at the time τ are determined in the deformed configuration κ _τ , the fiber direction in configuration κ_R can be computed as

$${\mathbf{\text{E}}}_{\text{f}}^k\left(\tau \right)=\frac{F^{*}{\left(\tau \right)}^{-1}{\mathbf{\text{e}}}_{\text{f}}^k\left(\tau \right)}{\parallel F^{*}{\left(\tau \right)}^{-1}{\mathbf{\text{e}}}_{\text{f}}^k\left(\tau \right)\parallel },$$ (34)

and the invariant of this fiber at a later time t is

$$I^k\left({\mathbf{\text{C}}}^{*}\left(t\right),{\mathbf{\text{E}}}_{\text{f}}^k\right):={\mathbf{\text{C}}}^{*}\left(t\right):{\mathbf{\text{E}}}_{\text{f}}^k\left(\tau \right)\otimes {\mathbf{\text{E}}}_{\text{f}}^k\left(\tau \right).$$ (35)

Substituting the fiber invariants into Eq. (4) yields the strain energy for the collagen fiber

$$W^k\left({\mathbf{\text{C}}}^{*}\left(t\right),{\mathbf{\text{E}}}_{\text{f}}^k\left(\tau \right)\right)=\frac{c_2}{4_{c3}}\left\{\text{exp}\left[c_3{\left(I^k\left({\mathbf{\text{C}}}^{*}\left(t\right),{\mathbf{\text{E}}}_{\text{f}}^k\left(\tau \right)\right)-1\right)}^2\right]-1\right\},$$ (36)

and therefore the total strain energy for fiber family k can be computed based on Eq. (5) as

$$\begin{array}{l}{w}^k({\mathbf{\text{C}}}^{\ast },t)={\displaystyle {\int }_{-\infty }^t{m}^k}(\tau )q^k(t-\tau )W^k({\mathbf{\text{C}}}^{\ast }(t),{\mathbf{\text{E}}}_{\text{f}}^k(\tau ))\text{d}\tau \\ ={\displaystyle {\int }_{t-t_{\text{l}s}}^t{m}^k}(\tau )q^k(t-\tau )W^k({\mathbf{\text{C}}}^{\ast }(t),{\mathbf{\text{E}}}_{\text{f}}^k(\tau ))\text{d}\tau \\ \approx {\displaystyle \sum _{i=0}^N{m}^k}({\tau }_i)q^k(t-{\tau }_i)W^k({\mathbf{\text{C}}}^{\ast }(t),{\mathbf{\text{E}}}_f^k({\tau }_i))\Delta \tau ,\end{array}$$ (37)

where t _ls is the lifespan of the fibers. N is the number of discretization intervals for computing the time integral. Note that, for each time slice Δτ = τ _i+1 – τ_i , the strain energy of the fiber produced at τ_i depends on the deposition angle at that time θ _f(τ_i ). In Eq. (37) q^k (t – τ_i ) is the remaining fraction at time t for the constituents produced at time τ_i ; we choose

$$q^k(t)=\{\begin{array}{l}0\text{for}t>t_{\text{ls}},\\ 1\text{for}t<t_{\text{nd}},\\ \frac{1}{2}\text{cos}\left[\frac{\text{π}}{t_{\text{ls}}-t_{\text{nd}}}\left(t-t_{\text{nd}}\right)\right]+\frac{1}{2}\text{otherwise,}\end{array}$$ (38)

with t _nd < t _ls a given period of time where there is no decay of the constituent.

We further assume that during our iterative procedure the amount of functional elastin is not changing, hence, we set Q^e (t) = 1 in Eq. (2).

This gives us the total strain energy of the constrained mixture

$$w({\mathbf{\text{C}}}^{\ast },t)=M^e(0)W^e({\mathbf{\text{C}}}^{\ast },t)+{\displaystyle \sum _k{w}^k({\mathbf{\text{C}}}^{\ast },t),}$$ (39)

for the current moment t. Finally, the balance equation (9) is solved with respect to the reference configuration κ _R which gives us the stress distribution for the current iteration step. This is used to compute the new optimal fiber deposition angle for the next iteration step.

In Eq. (39) we chose k = 10, as, e.g., suggested in [65]. That means that 10 fiber cohorts are bearing the load at the current iteration step; in addition to the elastin part that is always present. As the function q_k decays to zero, the amount of load that is taken up by the disappearing old collagen is negligible. Further, due to the stochasticity of fiber deposition, Section 2.3.2, we used a maximum number of iterations n _max = 50 to end this iterative procedure; rather than a designated convergence criterion.

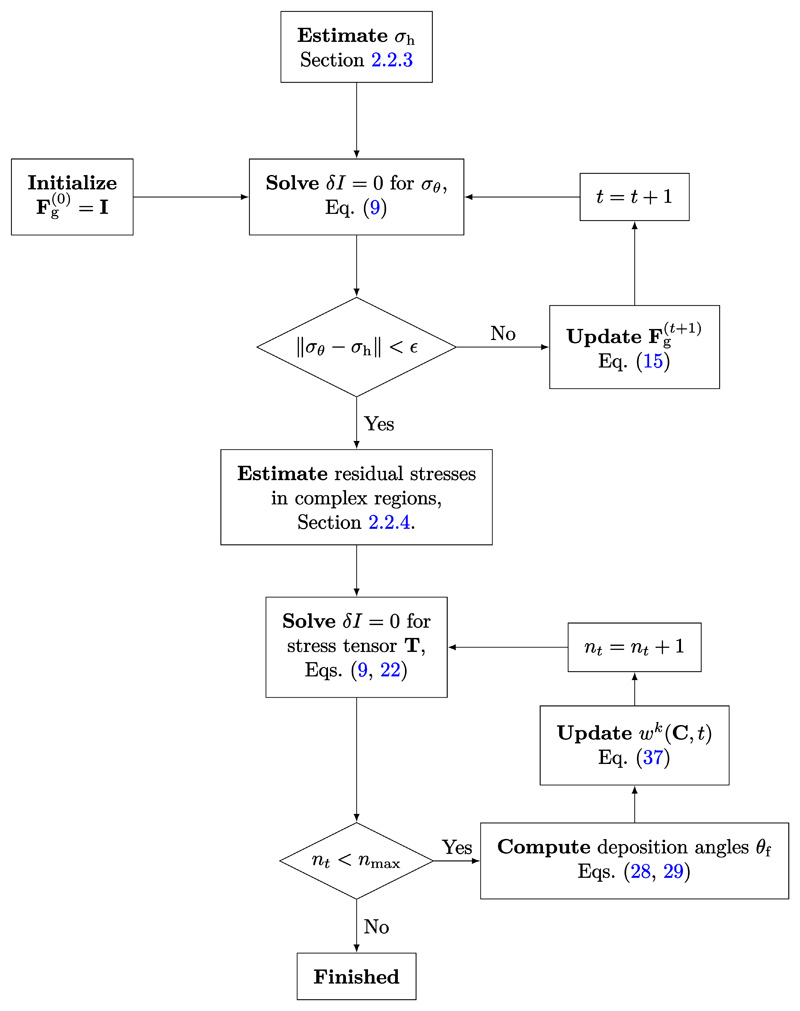
A summary of the general algorithm for applying the above method is described in Algorithm 1a and 1b and in Figure 2.

Figure 2. Detailed schematic for the algorithm to generate the vascular homeostatic state.

Algorithm 1a. Generate residual stress field by incorporating proper amount of growth prestretch.

  1: Initialize growth prestretch

$${\mathbf{\text{F}}}_{\text{g}}^{\left(0\right)}=\mathbf{\text{I}},\text{i}.\text{e}.,{\text{λ}}_{{\text{g}}^{\theta }}^{\left(0\right)}=1,{\text{λ}}_{\text{gr}}^{\left(\text{0}\right)}=1,{\text{λ}}_{\text{gz}}^{\left(0\right)}=1.$$

  2: Estimate homeostatic stress target distribution, σ _h, see Section 2.2.3.

  3: Restrict computational domain to cylindrical regions.

  4: Set tolerance ϵ and maximal number of iterations t _max.

  5: for t < t _max do

  6:       Solve the balance equation (9)

$$\delta I={\displaystyle {\int }_{{\kappa }_0}\delta w\text{d}V}+{\displaystyle {\int }_{\partial {\kappa }_t}P{\mathbf{\text{n}}}_t}\cdot \delta x\text{d}a=0,$$

             to obtain current stress ${\sigma }_{\theta }^{(t)}.$

  7:       if $\Vert {\sigma }_{\theta }^{\left(t\right)}-{\sigma }_{\text{h}}\Vert <ϵ$ then

  8:            break                ⊳Current stress converged to homeostatic stress.

  9:       end if

            Update growth tensor ${\mathbf{\text{F}}}_g^{(t+1)}$ by solving Eq. (15) for the updated prestretch ratios:

$${\text{λ}}_{{\text{g}}^{\theta }}^{\left(t+1\right)}={\text{λ}}_{{\text{g}}^{\theta }}^{\left(t\right)}+\frac{\Delta t}{{\tau }_{\theta }}\left(\frac{{\sigma }_{\theta }^{\left(t\right)}}{{\sigma }_{\text{h}}}-1\right){\text{λ}}_{{\text{g}}^{\theta }}^{\left(t\right)},{\text{λ}}_{\text{gr}}^{\left(t+1\right)}=1,{\text{λ}}_{\text{gz}}^{\left(t+1\right)}=1.$$

11:       t = t + 1

12: end for

13: Estimate residual stresses near bifurcations and boundaries using data from cylindrical regions, see Section 2.2.4.

Algorithm 1b. Generate fiber deposition angles and incorporate fibers into the vascular mixture.

1: Set maximal number of iterations n_max = 50.

2: for n_t < n_max do

3:       Solve the balance equation (9)

$$\delta I={\displaystyle {\int }_{\kappa \text{R}}\delta w\text{d}V+{\displaystyle {\int }_{\partial {\kappa }_t}P{\mathbf{\text{n}}}_t}}\cdot \delta x\text{d}a=0,$$

            using (39) to obtain current stress tensor T, and then compute two principal stress components T ₁₁ and T ₂₂.

4:         Compute the optimal deposition angle using Eq. (28)

$${\theta }_{\text{f}}^{*}=\pm \arctan \sqrt{\frac{T_{22}}{T_{11}}}.$$

5:         Generate the actual deposition angles based on the distribution introduced in Eq. (29)

$${\theta }_{\text{f}}\sim \mathcal{N}\left({\theta }_{\text{f}}^{*},\sum \left({\sigma }_{\text{f}}\right)\right).$$

6:         Modify the strain energy function, Eq. (37), to incorporate the new fibers

$$w^k\left(\mathbf{\text{C}},t\right)={\displaystyle \sum _{i=0}^N{m}^k\left({\tau }_i\right)}{q}^k\left(t-{\tau }_i\right)W^k\left(\mathbf{\text{C}},{\theta }_{\text{f}}\left({\tau }_i\right),t\right)\Delta \tau ,$$

            where

$$t=n_t*\Delta \tau ,{\tau }_i\in \left\{t-t_{ls},t-t_{ls}+\Delta \tau ,t-t_{ls}+2\Delta \tau ,\dots ,t-\Delta \tau ,t\right\}$$

7:         n_t = n_t + 1

8: end for

3. Results

The framework proposed above was implemented to first generate a residual stress field based on the evolution equations (15) and then to iteratively generate collagen fiber directions based on the optimality conditions (28) along with deposition randomness (29). The code was developed in Python, and the finite element solution was implemented using FEniCS [50]. All computations were performed using linear tetrahedral elements with an average edge size smaller than 0.7 mm. The constitutive material parameters were taken from literature [29], [71], and [21] and are summarized in Tab. 1 along with the other parameters used for the simulations.

Table 1.

Parameters used in the numerical experiments. Note that all time constants are normalized with respect to the lifespan of the fibers.

Used for	Parameter
Material model	c 1 = 688 Pa/kg	c 2 = 917 Pa/kg	c 3 = 25 [−]
Eqs. (3, 4, 8)	κ = 5 × 106 Pa
Residual stress field	Cylinder: σ h = 150 kPa
generation	Patient-specific model, nominal blood pressure: P = 100 mmHg
Eqs. (15, 17)	D = 1.0	τθ = 2.0
Fiber deposition	Σ0 = 0.5	σ scale = 200 kPa	ϵ = 0.001
Eqs. (30, 37, 39)	t ls = 1	t nd = 0.2	N = 20
	k = 10

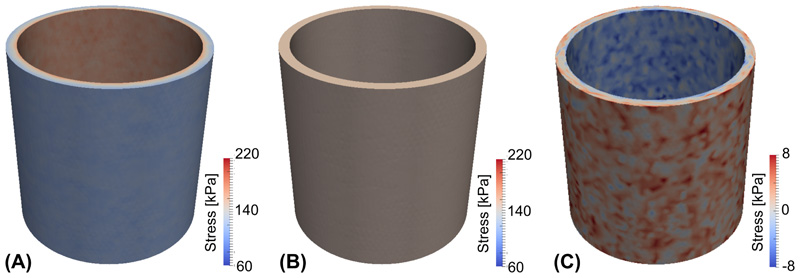
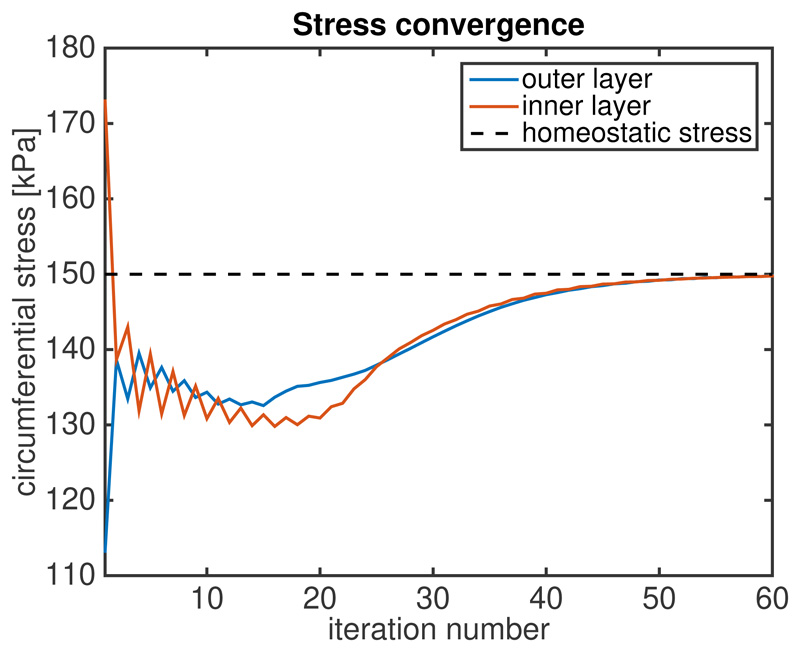
Figure 3 illustrates the results of the algorithm applied to an idealized cylindrical vessel. Panel (A) shows the circumferential stress distribution for a passive inflation with a pressure of 100 mmHg in which the material properties are assumed to be constant throughout the vessel wall and no residual stress is incorporated. As expected the resulting circumferential stress is nonuniform along the transmural direction. Panel B displays the circumferential stress distribution after prestretch is incorporated by the stretch evolution equation (15) using a prescribed homeostatic stress σ _h = 150 kPa. The convergence of the stress to the homeostatic value over the iterations of the algorithm is plotted in Figure 4.

Figure 3.

Circumferential stress distribution (A) of a standard passive inflation simulation; (B) with residual stress incorporated. (C) Residual stress distribution.

Figure 4. Convergence of circumferential stress to homeostatic value after prestretch is incorporated.

Once prestretch is generated, the residual stress distribution can be obtained by releasing the internal pressure and removing the tethering boundary conditions. Figure 3C shows the residual stress distribution after a virtual pressure release. It is noteworthy that the circumferential stress in the inner layer is negative – the tissue is under compression – and the stress in the outer layer is positive – the tissue is under extension – which is consistent with prior published results [2]. Qualitatively the pattern of the stress distribution also matches with experimental results on rabbit arteries [12]. The randomness of the stress distribution is mainly due to the stochasticity of the fiber deposition. Note that for this virtual pressure release experiment, a small axial stretch is needed to achieve numerical stability. Namely, this applied axial stretch makes the inner layer of the vessel less prone to buckling while under compression. While this can be done for an idealized cylinder geometry by applying a small displacement to one of the free ends, this is not a trivial task for more general vascular geometries and results may become unreliable (cf. [40] and [49]), which was confirmed for the patient-specific geometry presented below.

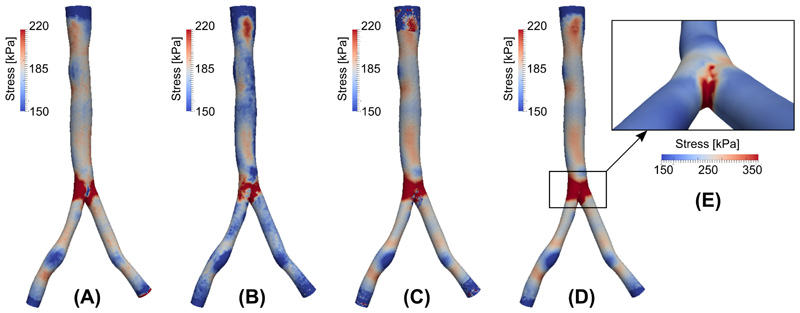
Numerical simulations were carried out for a patient-specific (image-based) aortic bifurcation geometry. The image data was obtained from the Vascular Model Repository (http://vascularmodel.com), and a membrane model was constructed using SimVascular [64]. A 3D volumetric mesh was generated using Gmsh [30], and the local thickness of vessel wall is set to 10% of the local radius (obtained from maximum inscribed sphere). A homeostatic stress distribution σ _h(x) was generated by solving Eq. (17) with g(x) set to be the solution of a passive inflation membrane problem at mean arterial pressure of 100 mmHg. Figure 5A displays the steady-state σ _h(x), which serves as the target stress distribution for the residual stress generation process. For comparison, Figure 5B displays the stress distribution of a passive inflation with a pressure of 100 mmHg with no residual stress incorporated. As an intermediate step, Figure 5C displays the stress distribution when residual stress generation is applied only to the cylindrical portions of the domain-namely nodes near the inlet, outlet, and bifurcation are excluded. The prestretch distribution at the excluded nodes were then predicted by a random forest regressor trained via the data from the remainder of the simulation domain. The resulting final stress distribution is shown in 5D, which qualitatively and quantitatively matches the nominal target stress distribution shown in Figure 5A. To better visualize the stress distribution near the bifurcation and the effectiveness of the prediction by the random forest regressor, a rescaled and zoomed-in view is provided in Figure 5E. It can be seen that higher stress is concentrated along the bifurcation ridge, consistent with previously published results [56]. We also note that the homeostatic stress values outside of the bifurcation ridge vary within the range of 150–220 kPa, which is consistent with the range 150–300 kPa given in Cyron and Humphrey [15].

Figure 5.

(A) Nominal homeostatic stress distribution. (B) Stress distribution from standard passive inflation. (C) Stress distribution after incorporation of residual stress. (D) Stress distribution after residual stress and machine learning repair. (E) Stress distribution near bifurcation (note change in color scale).

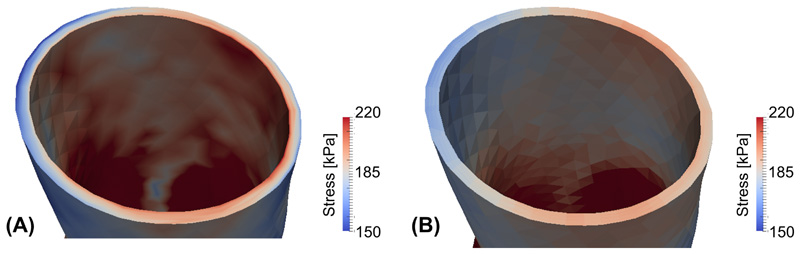
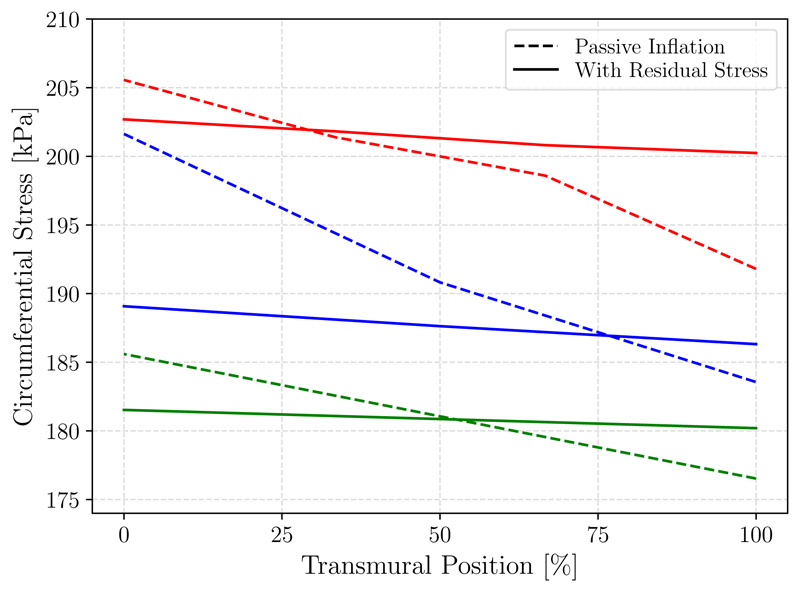
To evaluate the stress distribution along the transmural direction cross-sectional views are provided in Figure 6, with panel (A) corresponding to the simulation without residual stress and panel (B) corresponding to the simulation with residual stress incorporated. Additionally, a line plot of circumferential stresses along the transmural direction is shown in Figure 7, further demonstrating that stress becomes more uniform along the transmural direction when prestretch is included, (and becomes generally more homogenized in other directions although this is not imposed).

Figure 6.

Circumferential stress distribution in the patient-specific geometry for (A) a standard passive inflation and (B) with residual stress incorporated.

Figure 7.

Transmural circumferential stress distribution from the inner (0%) to outer (100%) wall in the patient-specific geometry for a standard passive inflation (dashes lines) and with residual stress incorporated (solid lines). Plotted are stresses along transmural lines at 3 arbitrary locations: one in each of the cylindrical regions, with the main branch in red.

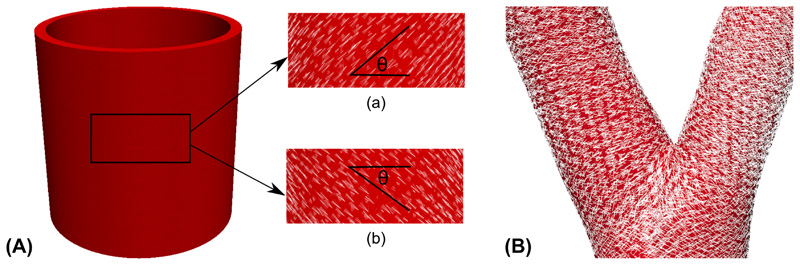
Figure 8 shows the two helical fiber directions generated by the optimal fiber deposition algorithm for both idealized and patient-specific geometries. It can be seen that in the two cases the mean directions and dispersion of the helical fibers are consistent with the previous experimental observations and numerical simulations [54, 38]. Figure 8B also shows the fiber directions in the bifurcation region of the patient-specific geometry, which is qualitatively consistent with the results in [34].

Figure 8.

(A) Fiber directions in both helical directions for the cylinder geometry; (B) Fiber directions for the patient-specific geometry near the vascular bifurcation.

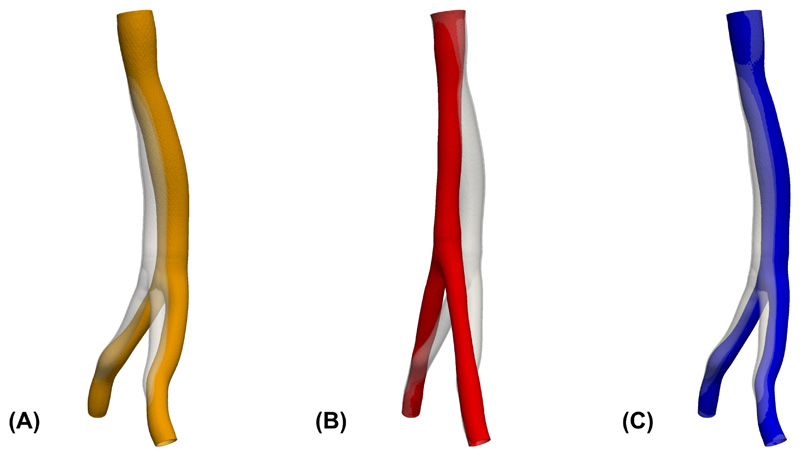
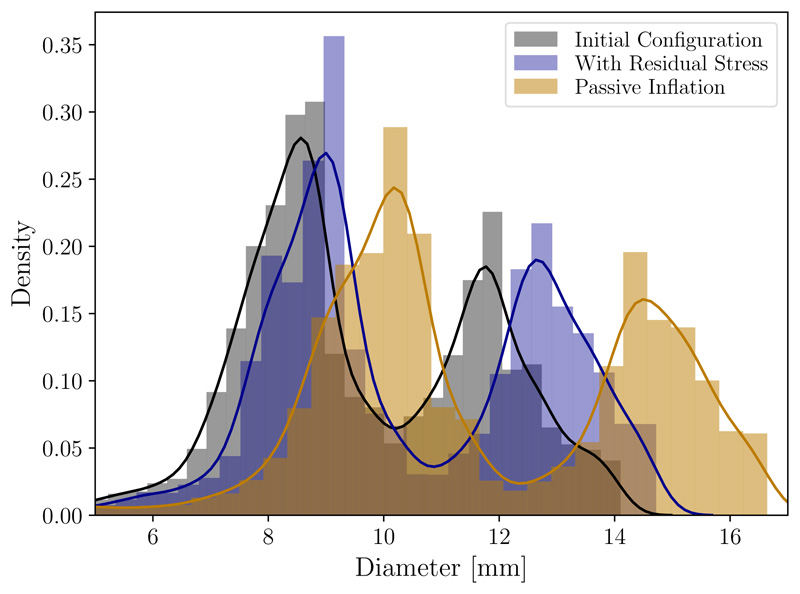
Since in most practical applications the vascular geometry is derived from in vivo imaging, it is important to consider how the generation of residual stress affects the final loaded configuration. Comparison of the loaded, pre-stretched geometry to the original image-based geometry is shown in Figure 9C, which indicates that the proposed algorithm changes the shape of the geometry to relatively smaller degree. By comparison, an inflation that does not consider residual stress results in a more curved and displaced loaded configuration as shown in Figure 9A. Also for comparison, we considered the case of prescribing a uniform homeostatic stress distribution, which as shown in Figure 9B tends to undesirably straighten the artery; indeed such configuration would be expected to achieve more uniform stress. Additionally, we compared the vessel diameter of the original image-based geometry with the diameter resulting from a passive inflation experiment and the diameter of the vessel with residual stress included, see Figure 10. Diameters for this density plot were computed using VMTK [3] as the diameters of the maximal inscribed spheres along the centerline of the geometries. These results demonstrate that inclusion of residual stress demonstrate clear improvement. While passive inflation leads to an increase of the diameter by around 2 mm to 3 mm, the diameter distribution of the vessel with residual stress generated by the proposed algorithm is generally within 1 mm of the original geometry. Although not controlled for here, adjusting the value of the desired homeostatic stress distribution σ _h(x), see Section 2.2.3, could be used to better impose matching of the inflated geometry with that from the image.

Figure 9.

Comparison of the original geometry taken from imaging (transparent gray) with the displacement field of (A) an inflation experiment without the application of the residual stress; (B) an inflation experiment with residual stress generated from the uniform homeostatic stress distribution; (C) an inflation with residual stress generated from the residual stress distribution that is uniform only in transmural direction.

Figure 10.

Density plot and histogram of diameters measured in the original geometry taken from imaging (black) in comparison with the displacement field of an passive inflation experiment (yellow, see Figure 9A) and an inflation with residual stress (blue, see Figure 9C). Diameters were computed as the diameters of the maximal inscribed spheres along the centerline of the geometries.

4. Discussion

A computational framework to generate the vascular homeostatic state has been proposed, which includes the generation of appropriate prestretch distribution and the specification of physiological vascular fiber deposition directions. A benefit of this framework is that in order to generate the residual stress distribution only a homeostatic stress value (or distribution) needs to be specified. In particular, the specification of the natural configurations of the different constituents and the mechanobiological mechanisms that form the residual stress distribution are not explicitly required and the effects of the residual stress distribution can be incorporated into a growth tensor F _g. This greatly facilitates a more practically feasible determination and generation of the residual stress distribution needed to achieve a homeostatic stress condition for the pressurized in vivo state for a particular vascular model geometry. While the approach for generating the residual stress and fiber distribution through a growth tensor is inspired by classical G&R theories [44, 13, 32], it should not be confused with trying to reproduce the actual G&R process (but rather focuses on the end result of deriving an appropriate loaded and pre-stressed homeostatic state).

A unique feature of this work is the combination of the constrained mixture model with an optimal fiber deposition process. In the classical constrained mixture model of G&R, fibers are deposited in predefined fiber family directions, with new fibers aligned in the same direction as the existing fiber family directions. In this work, fibers are deposited based on a physiologically-motivated angle that depends on the current local stress state, instead of predefined directions. And since the local stress may vary over the iterative deposition process, the deposition angle of newly produced fibers also varies. This iterative process, along with stress dependent stochasticity introduced in Eq. (29), results in fiber dispersion, which has been well documented in human arteries, see, e.g., [54]. While prior works [28] have accounted for fiber dispersion using a set dispersion parameter κ_d , the method herein leads to dispersion as a result of a stress-driven process. Also while prior work [34] has suggested a nominal deposition angle of the form tan ${\theta }_{\text{f}}^{*}=\frac{T_{22}}{T_{11}},$ the physiologically-motivated optimal deposition angle employed herein suggest an alternative square root relation of the form $\text{tan}{\theta }_{\text{f}}^{*}=\sqrt{T_{22}/T_{11}}$ consistent with the results in [14].

For cylindrical regions, the prestretch distribution can be readily computed using iterative methods, as have been applied previously, e.g, [7], [2], and [57]. However, this method is often unstable when applied to more complex geometries, particularly since topological features (e.g. bifurcations) cause irregular stress distribution that can significantly deviate from the presumed homeostatic distribution. Thus, instead of being directly computed, the prestretch in such regions can be predicted based on local geometric and mechanical properties from surrounding regions using machine learning. Namely, a random forest regressor was used to learn the physical principles based mapping from mechanical and geometric factors to the growth stretch ratio. This provided a way to deal with realistic applications where geometric complexities are difficult to handle numerically using strictly theory-based methods, while maintaining specification based on a governing theory. As with most machine learning, the mapping is not necessarily guaranteed to satisfy a theoretical (fiber-deposition) principle, it is rather trained from the principle. However, it is possible to mathematically constraints inference problems to satisfy deterministic constraints [69].

While prior work has proposed the inclusion of residual stresses on a fully three-dimensional patient-specific geometry [1], this approach results in a largely deformed loaded configuration, whereas the method proposed here results in relatively minor distortion of the loaded configuration when compared to the image-derived configuration (see Figure 9C). We note that the distortion that does persist could be due in part to the lack of external tissue support from surrounding organs, which is missing in our model. Additionally, although not explored herein, patient-specific calibration of simulation parameters could be incorporated in the residual stress generation procedure such that, as an additional constraint, the final loaded configuration matches as closely as possible with the image-based geometry. This is a reasonable addition since model parameters are generic and often fitted from ex-vivo experimental data. Also, compared to [8] where the authors presented a backward displacement method to generate prestrech for a patient-specific geometry, our approach additionally incorporates stress homogenization and a more physiological material model including the generation of fiber directions.

Although prior studies have assumed that there is a unique homeostatic stress value [20, 5, 68], there is sparse experimental data confirming this. The seminal work of Fung [26], indicates that stress tends to be homogenized in the transmural direction, and hence the approach presented herein assumes only homogenization of homeostatic stress in the transmural direction. Using a constant homeostatic stress value results in unphysiologic model deformation as shown in Figure 9(B). Nonetheless, the algorithm presented herein can accommodate any desired homeostatic stress distribution. For example, a presumed constant value can be taken from literature [6, 70], or obtained from additional computations, such as using the stress distribution from an equivalent membrane problem as proposed herein, or computed as the mean stress throughout the geometry from a passive inflation simulation. Likewise, while this method was applied to reconstruct the nominal, healthy homeostatic state, it could potentially be applied to specify a residual stress distribution and fiber alignment in diseased vessels through appropriate change to model parameters.

We note here several limitations of this work: First, the numerical robustness of the generation process should be further verified with a larger number of patient specific geometries. Second, the vessel wall in our study was modeled as a single effective layer while in reality the blood vessels consists of multiple layers that are mechanically relevant. However, this framework can be readily extended to a multi-layer setting (i.e., explicitly modeling the media and adventitia) with corresponding parameters specified for each layer. Third, the influence of external tissue support has been neglected. As noted above, inclusion of external support may be useful to improve matching the loaded, pre-stressed configuration with the image-based configuration. And forth, the in-vivo tension in axial direction is not accounted for in the computation of growth stretch ratios, while several publications, e.g., [9, 19], indicate that tensional homeostasis in axial direction may play a significant role.

5. Conclusions

A framework was presented to reconstruct the vascular homeostatic state by developing a method to compute the residual stress distribution and fiber directions. The residual stress is implicitly incorporated by iteratively computing a growth prestretch based on a prescribed homeostatic stress distribution. Vascular fiber directions are further incorporated based on the solution of a physiologically-motivated optimization problem. The methodology was applied to an idealized cylindrical geometry and a patient-specific aortic bifurcation geometry. Simulation results for residual stress distribution and fiber alignment match with numerical and experimental results in prior works. In contrast to previous studies the proposed framework is not limited by geometrical restrictions such as bifurcations making it more applicable to patient-specific modeling scenarios.