Drought self-propagation in drylands due to land–atmosphere feedbacks

Abstract

Reduced evaporation due to dry soils can affect the land surface energy balance, with implications for local and downwind precipitation. When evaporation is constrained by soil moisture, the atmospheric supply of water is depleted, and this deficit may propagate in time and space. This mechanism could theoretically result in the self-propagation of droughts, but the extent to which this process occurs is unknown. Here we isolate the influence of soil moisture drought on downwind precipitation using Lagrangian moisture tracking constrained by observations from the 40 largest recent droughts worldwide. We show that dryland droughts are particularly prone to self-propagating, because evaporation tends to respond strongly to enhanced soil water stress. In drylands precipitation can decline by more than 15% due to upwind drought in during a single event, and up to 30% during individual months. In light of projected widespread reductions in water availability, this feedback may further exacerbate future droughts.

Drought has decidedly impacted human history, and is estimated to affect about 55 million people worldwide every year ¹ . Its frequency, duration and magnitude are projected to increase in many regions around the globe ^2,3 , yet climate model projections remain uncertain ^3,4 . Unusual and prolonged precipitation shortages, or meteorological drought, spread through the soil, aquifers, rivers and lakes as agricultural and hydrological drought ^5,6 , and thereby prompt a wide array of societal, economic and ecological consequences ⁷ . Precipitation requires air saturation and involves complex microphysics ⁸ , usually achieved by cooling air to its dew point through convection, frontal or orographic lifting, and other dynamical mechanisms ⁹ . Thus, in the context of meteorological drought, precipitation variability is regarded as dominated by atmospheric circulation and thermodynamics, which in turn are often forced externally by, for instance, remote sea surface temperature changes ^9,10 . Local soil moisture deficits have also been shown to promote precipitation deficits, particularly in transitional regimes between humid and arid climates ^11,12 . In these regional hotspots, soil moisture exerts a control on the surface energy partitioning, and hence on moist convection ^12,13 . The initiation and intensification of convective storms has been linked to both local soil moisture and mesoscale soil moisture heterogeneities ^14–16 , which may also affect organized convection several hundred kilometres downwind ¹⁷ . In short, reduced evaporation due to soil water limitations affects the local atmosphere, and may thereby trigger distant modulations of dynamical saturation-achieving mechanisms, resulting in complex and tenuous soil moisture–precipitation coupling ¹⁸ . But desiccating soils have more obvious, potentially even farther-reaching impacts: a decline in evaporation implies a reduced water supply to the atmosphere.

Droughts are thus hypothesized to self-propagate ¹⁹ as soil moisture drought may cause water vapor deficits that cascade downwind, and hence favour remote drought conditions. The feedback chain thus consists of the translation of soil dryness into atmospheric water vapor deficits via reduced evaporation, and the conversion of water vapor into downwind precipitation (or lack thereof). During droughts, the conversion of water vapor into precipitation is frequently altered by anomalous large-scale atmospheric circulation and other dynamical mechanisms ²⁰ , which tend to vary more in space and time than water vapor, hence the latter frequently does not correlate well to observed precipitation ²¹ . Nonetheless, the link between (total column) water vapor and precipitation clearly emerges in the tropics ²² , throughout China ²³ and even in Eurasian boreal forests ²¹ . For instance, it has already been suggested that enhanced evaporation through irrigation increases both water vapor and precipitation downwind, in the United States ²⁴ , India ²⁵ and Africa ²⁶ . Recently, reduced evaporation in all upwind land areas was estimated to account for 62% of the total precipitation shortages during the 2012 North American drought ²⁷ . Meanwhile, terrestrial moisture deficits only resulted in rainfall decreases of ~6% during southeastern Australian droughts ²⁸ . While these studies suggested that remote evaporation affects downwind droughts to varying extents, they provided no evidence of selfpropagation. To study the latter, only the impact of a single, spatiotemporally coherent drought on its own downwind propagation should be considered ¹⁹ , rather than the impact of all terrestrial sources as in previous studies ^27,28 . At least three criteria are required for soil (moisture) stress to impact the further propagation of drought: (i) upwind soils must become dry enough for evaporation to be water-limited, (ii) the winds must blow towards other land regions still unaffected by the drought, and (iii), downwind water vapor deficits must cause precipitation shortages. Here, we examine drought self-propagation using a combination of reanalysis, satellite observations and modelling techniques, focusing on the 40 largest soil droughts worldwide from 1980 to 2016 (see Methods).

Effect of upwind soil drought on downwind water vapor

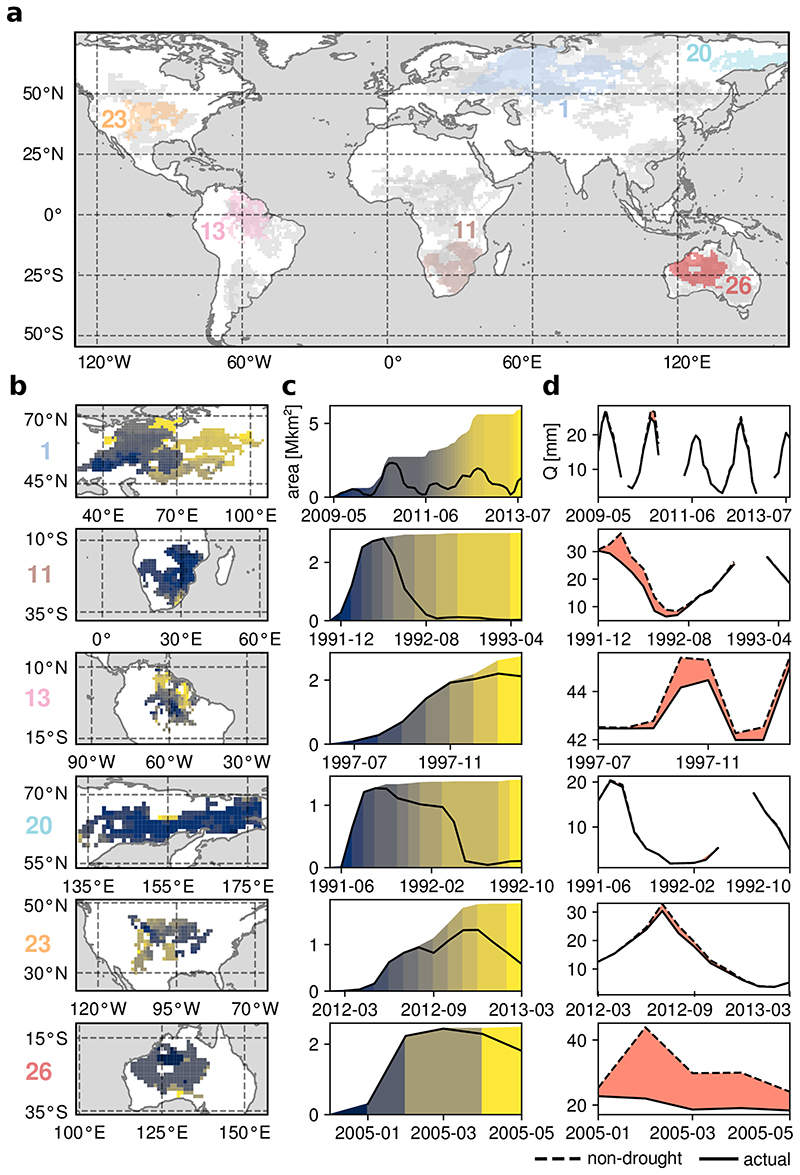
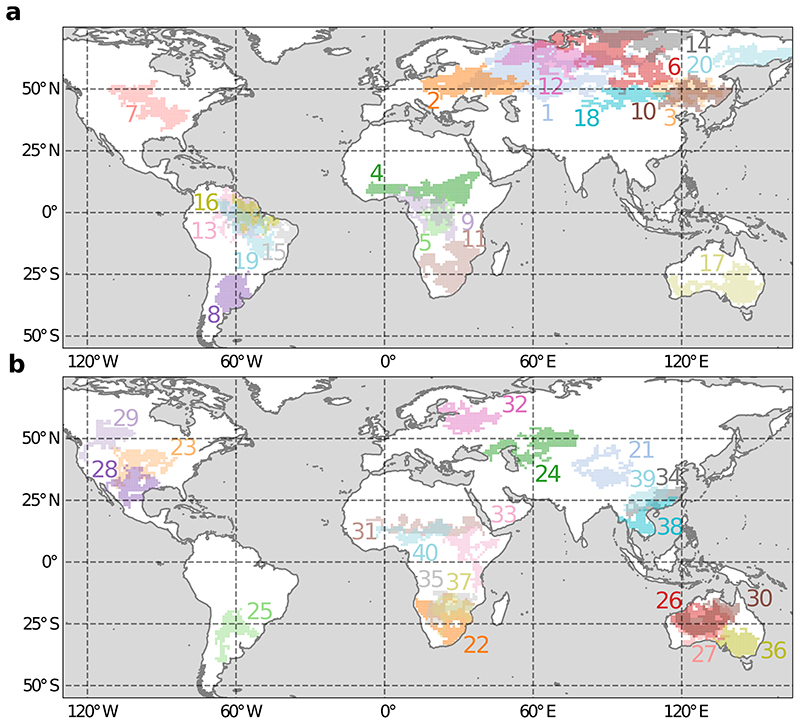
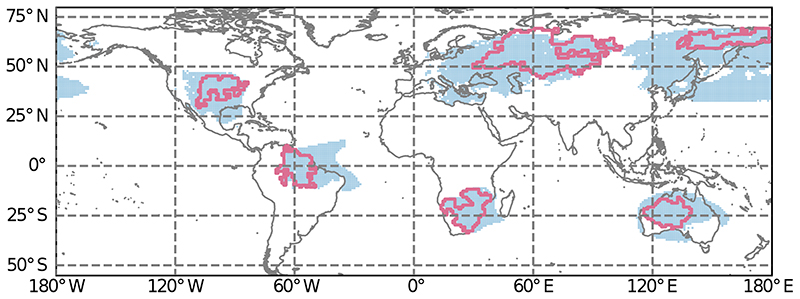
Soil drought events are selected using monthly root-zone soil moisture anomalies and a novel mathematical morphing approach (see Methods), resulting in dynamic and coherent events in space and time (see Fig. 1a and ED-Fig. 1 for an overview of all 40 droughts examined in this study). For these events, we analyse the impact of upwind drought (source) on downwind areas (target), and if the soils in the latter become subject to drought conditions. The link between source and target is established with a Lagrangian atmospheric trajectory model driven by reanalysis data: the water vapor residing in newly-affected drought areas is traced back in time, thereby revealing its evaporative sources (see Methods). Throughout the evolution of each drought event, water vapor tracking is performed for all pixels where propagation occurs in the same month (propagation step). Taking soil memory into account, the water vapor content — and ultimately precipitation — during the three months leading to the soil drought propagation is considered. The 40 largest droughts are analysed and ranked according to their spatiotemporal extent (see Supplementary Table 1). Fig. 1b–c focuses on six exemplary events that portray a range of climatic conditions: Western Russia and Kazakhstan (2009–2013, rank 1), Southern Africa (1991–1993, rank 11), Amazonia (1997–1998, rank 13) and Eastern Russia (1991–1992, rank 20), central Northern America (2012–2013, rank 23), and northwestern to central Australia (2005, rank 26). To understand the impact of upwind drought on downwind water vapor content, the latter is visualized in Fig. 1d. For all events shown here, except the Amazonian event, the propagation (coloured polygons) stagnates at least once during the drought evolution, which means that no new neighbouring areas became subject to drought conditions, yet the drought persisted (Fig. 1c). This is particularly evident for the largest event on record (Russia and Kazakhstan 2009–2013), for which the drought area (black line) decreases to nearly zero multiple times in (boreal) winter prior to further propagation during summer.

Fig. 1. Impact of upwind soil drought on downwind column water vapor.

a, An overview of the 40 largest soil droughts in recent history, with six selected events shown in colour. Any pixel of a certain colour is part of the same spatiotemporally coherent drought, but the timing of drought onset and offset varies per pixel. The ranking of each drought in terms of total extent (space and time) is provided by numbers of matching colours. b–c, Drought propagation in space for six selected events (b), with polygons of matching colour in the time series (c) indicating the cumulative area under soil drought after each of these ‘propagation steps’, as well as the actual area subject to soil drought at the time of propagation (black line). d, The actual water vapor (Q) in the areas that are newly affected by soil drought, that is, where the drought propagates to (solid black line). Ensemble-mean ‘non-drought’ water vapor, calculated for climatological soil stress in upwind drought-stricken areas using existing potential evaporation and circulation (dashed black line; see Methods). The difference (red shading) thus indicates the downwind reduction in water vapor solely due to upwind soil drought for the given atmospheric conditions and circulation.

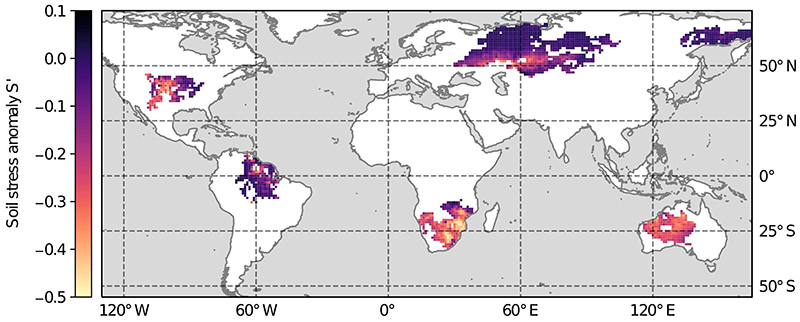
Next, we discern the impact of upwind anomalous soil moisture stress on downwind water vapor. This impact is isolated from the influence of circulation and potential evaporation using a Reynolds decomposition (see Methods), enabling an estimate of downwind water vapor if there had been no upwind drought (dashed lines in Fig. 1d). Note that this estimate of downwind water vapor does not consider changes in circulation patterns that may emerge due to the upwind soil stress ^14,29 . In the case of both Russian droughts, our estimate of non-drought downwind water vapor is nearly identical to the actual amount (Fig. 1d). By contrast, upwind soil moisture stress causes a severe reduction in downwind water vapor for both the Southern African and Australian events (red areas in Fig. 1d). Thus, at least two of the aforementioned criteria for drought self-propagation are met there: dry winds originating in already drought-stricken areas blow toward land regions the drought has not reached yet. Our analysis indicates that certain areas are more prone to be influenced by upwind drought than others: except for the regions affected by the Amazonian and Eastern Russian events, the climatological water vapor sources encompass primarily large land areas (ED-Fig. 2). What paves the way for water vapor deficits caused by upwind drought, however, is a strong reliance on proximate terrestrial evaporative sources, as is the case particularly for the Southern African drought footprint. Another crucial factor is whether upwind drought limits the atmospheric moistening in the first place: for example, evaporation is not severely water-limited in Eastern Russia, even when soils are dry relative to their own climatological expectation. On the contrary, during the drought events in Southern Africa and Australia, soil moisture was low enough to diminish evaporation rates by at least one third with respect to the climatological mean (ED-Fig. 3).

From downwind water vapor to downwind precipitation

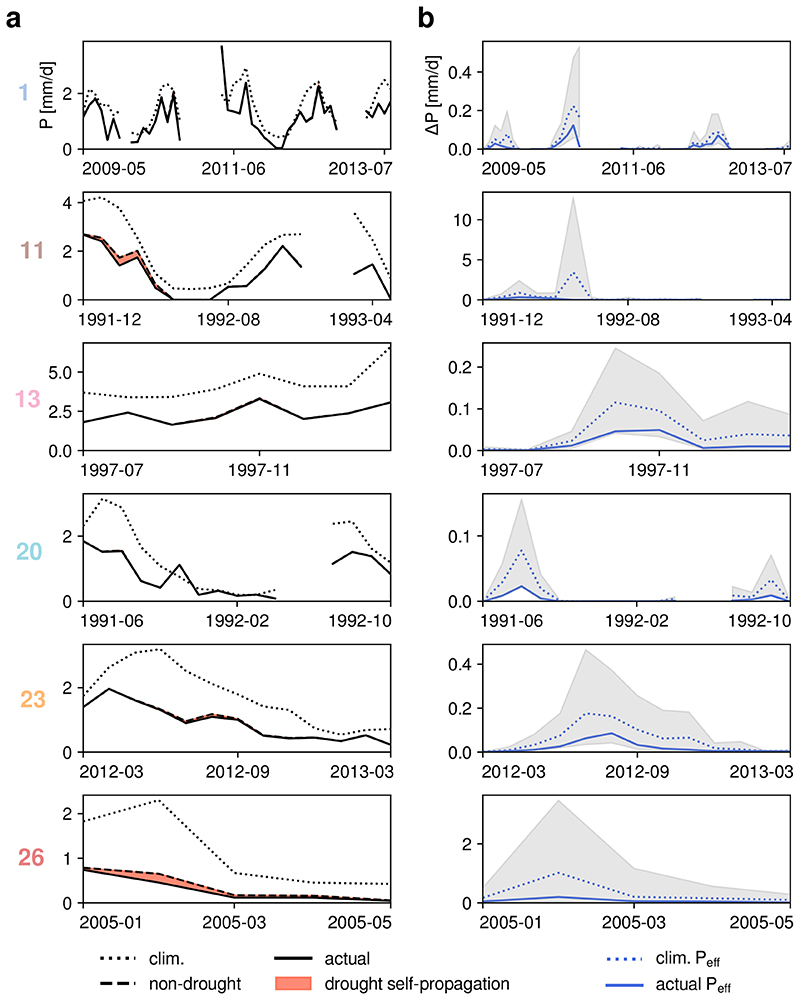
To quantify the impact of the upwind soil drought on downwind precipitation reduction, we conceptually define precipitation as the product of water vapor and precipitation efficiency (see Methods). Based on the actual precipitation efficiency during the drought events, given by the degree to which water vapor was converted into precipitation according to observations and reanalysis data, we estimate the consequences of drought-induced reductions in water vapor on precipitation (ΔP). Thus, rather than directly equating anomalous moisture transport to precipitation reductions, as for example in ref. ²⁷ , we consider the atmosphere’s propensity to convert water vapor into precipitation. To visualize the influence of this assumption, four different estimates of ΔP are shown in Fig. 2b, which correspond to the actual precipitation efficiency (blue line), the climatological one (dotted blue line), as well as the minimum and maximum efficiency (grey shading) encountered on record for the respective propagation areas. The estimate based on actual precipitation efficiency is frequently close, or even identical to the minimum estimate (Fig. 2d), implying an unusually unfavourable tendency to convert water vapor into precipitation during droughts. This suggests that all these events are mainly enabled by unusually low precipitation efficiency, whose causes are not investigated here but are often rooted in anomalous convective potential or large-scale winds ⁹ . Still, drought-induced reductions in water vapor content further contribute to these events and facilitate their spatial propagation, even though these modulations are less relevant than they would be in an atmosphere capable of condensing and precipitating water more efficiently.

Fig. 2. Upwind soil droughts propagation to downwind precipitation deficits.

a, For the same six events as in Fig. 1b–d, the climatological and actual precipitation are shown (dotted and solid black lines). The extra water vapor for non-drought conditions in Fig. 1d is converted to precipitation based on the actual precipitation efficiency (dashed black line; see main text and Methods), shown as the ensemble mean. The difference between non-drought and actual precipitation is an estimate of the drought self-propagation effect (red shading). b, Since this difference in precipitation (ΔP) depends not only on the amount of extra water evaporating at climatological soil moisture stress, but also on the conversion of water vapor to precipitation, the values corresponding to the actual precipitation efficiency employed for Fig. 2a, the climatological mean, maximum and minimum precipitation efficiency are shown (solid and dashed blue lines, upper and lower bounds of hatched grey shading), again averaged over the entire ensemble of simulations.

Due to this low precipitation efficiency, for the 1997–1998 Amazonian event and despite upwind soil drought reducing downwind water vapor (Fig. 1d), this anomaly in water vapor did not propagate in terms of precipitation (Fig. 2a). According to our estimate, drought self-propagation decreased precipitation by less than 1% during this Amazonian drought. For the 1991–1992 drought in Eastern Russia, the effects on precipitation (Fig. 2a) are minor (<1%), as already suggested by the largely unchanged water vapor content (Fig. 1d), whereas the North American and Western Russian events (Fig. 2a) are slightly more affected, with about 3% and 2%, respectively. Soil drought is known to modulate convection through enhanced sensible heating, and hence precipitation efficiency, but the uncertainty of modelling experiments is still large ^15,30,31 , and more research is needed, especially beyond the local scale ³² . We thus highlight that the atmosphere was not efficient at generating precipitation during all events (see Fig. 2b), and note the potential contribution from soil drought to the reduction in precipitation efficiency, but only consider the effect of soil drought via reductions in moisture supply in our definition of self-propagation. Regardless, as evidenced by the events in Southern Africa and Australia (Fig. 2a), pronounced alterations to the water vapor content further downwind, enabled by upwind drought, may severely affect the amount of precipitation: we estimate that 9 and 18% less precipitation occurred solely due to drought self-propagation, respectively.

Drought self-propagation worldwide

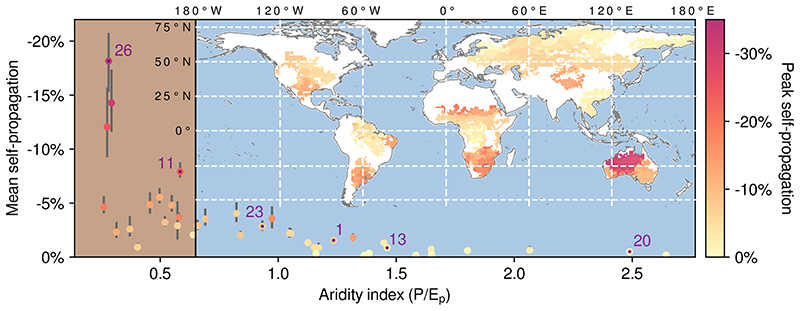
To provide a more complete global picture, the 40 largest soil drought events in the past four decades are investigated. In Fig. 3, their estimated drought self-propagation effect is visualized in space, expressed as the ratio between the ΔP induced by upwind drought and the precipitation that would have occurred without drought self-propagation (see red areas and dashed lines in Fig. 2a). As evidenced by Fig. 1a, multiple drought events occurred in Australia and Southern Africa (Supplementary Table S1). The majority of these events are associated with the most pronounced drought self-propagation among the 40 events analysed here. The map in Fig. 3 depicts a clear gradient between water- and energy-limited regimes ³³ , since strong self-propagation is confined to transitional or purely water-driven areas, whereas droughts in energy-driven regions show weaker self-propagation. The 2009–2013 drought in Western Russia and Kazakhstan — by far the longest event identified in the analysis — is a clear example of that behaviour. However, during the peak of the 2010 Russian mega-heatwave in August 2010 ³⁴ , precipitation was reduced by roughly 7% due to drought self-propagation (Figs. 1d & 2a). Similarly, the 2012–2013 drought in central North America features notable self-propagation during boreal summer, concurring with a hot extreme in the region. Therefore, even in energy-limited regions, short-duration compound dry–hot events can be associated with self-propagation.

Fig. 3. Droughts self-propagation in drylands.

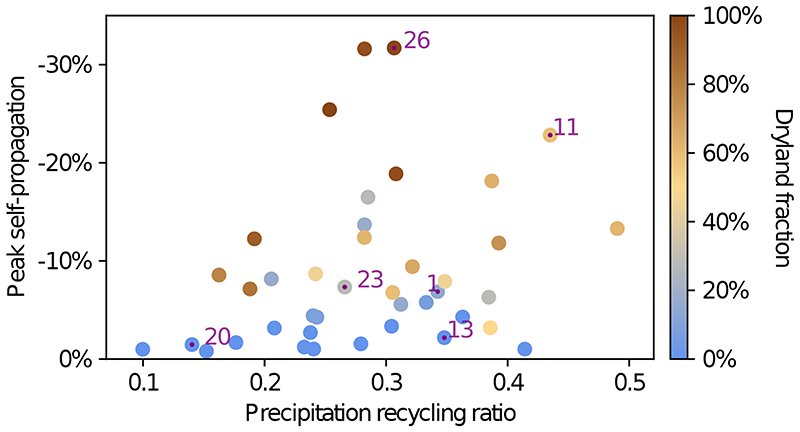
The map illustrates the monthly maximum (or ‘peak’) drought self-propagation, expressed as the ratio between the change in precipitation induced by drought self-propagation (ΔP) and the precipitation expectation without upwind drought. If several events overlap in space, their average is visualized. Only the ensemble mean is shown. The graph illustrates the mean drought self-propagation per event (including all propagation steps) as a function of the climatological aridity index (the ratio of annual mean precipitation over potential evaporation). Marker colours indicate the (monthly) peak self-propagation. Vertical grey lines represent the uncertainty range, given by the respective ensemble minima and maxima. The transition to drylands at P/Ep=0.65 (the ratio of precipitation and potential evaporation; ref. ³⁶ ) is marked by a vertical black line and a change in background colour (from blue to brown). The six events highlighted in Figs. 1 and 2 are labelled and marked with purple dots.

Revisiting the three necessary conditions for drought self-propagation — water-limited evaporation, circulation to other land regions, and conversion of water vapor into precipitation (conceptualized as precipitation efficiency here) — we point out that the characteristics of the morphed droughts also influence our results. In particular, strong self-propagation was only sustained throughout drought evolution for events that reach a large spatial extent in a short time, frequently associated with the concept of ‘flash droughts’, rather than those with a multiannual sequence of slow expansion and decay. Therefore, to reduce the sensitivity of our results with respect to event duration, the map in Fig. 3 displays the monthly peak drought self-propagation for each event (see Methods). While the peak self-propagation remains low in the tropics and also the high northern latitudes, precipitation reductions of 15% and more are identified in several regions, such as the Gran Chaco and Pampas in South America, the Sahel, Southern Africa and Australia. While our analysis shows that moisture recycling affects these results — with a higher climatological precipitation recycling ratio of a drought’s footprint generally being associated with stronger self-propagation (ED-Fig. 4) — it also indicates that water scarcity is a key factor that determines the tendency of droughts to self-propagate. To further condense our findings, the graph in Fig. 3 depicts the peak (colours) and the event-mean (y-axis) drought self-propagation for all 40 droughts, expressed as a function of aridity index (x-axis). The latter serves as a proxy for water limitation and is calculated as annual mean precipitation (P) divided by potential evaporation (E_p). In terms of peak self-propagation, events in drylands (aridity index of less than 0.65 ³⁶ ) are associated with an average precipitation reduction of nearly 16%, whereas the remaining events have a corresponding decline of less than 5% on average. Several droughts in drylands reach peak reductions beyond 20%, and even up to 32%, while events taking place elsewhere usually culminate at clearly less than 10%. Therefore, droughts occurring in more arid climates tend to display more intense drought self-propagation. In fact, none of the droughts in regions not classified as dryland exceeds a mean self-propagation of 5%, and the six strongest events with respect to both peak and mean drought self-propagation all occurred in drylands.

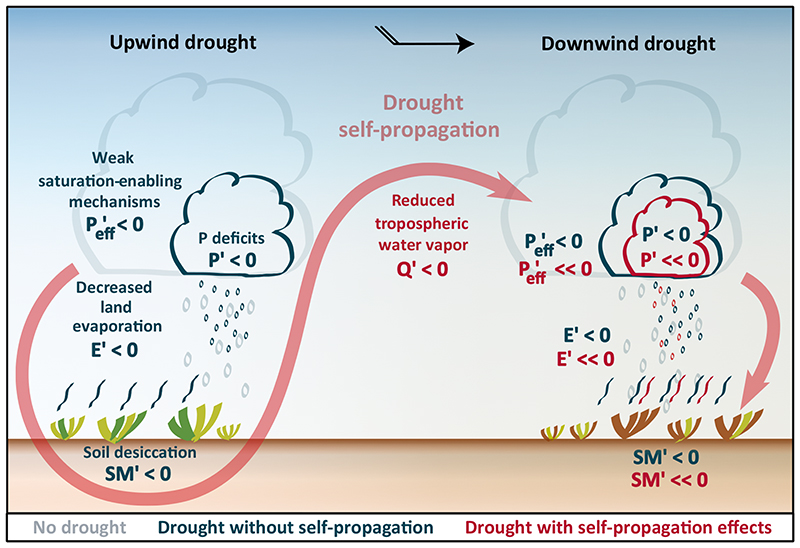
Our main findings are summarised in Fig. 4. While precipitation deficits are mostly associated with anomalously low precipitation efficiency, drought self-propagation via reduced atmospheric moistening is an important process in drylands. In such regions, potential evaporation is high and actual evaporation is frequently water-limited, since precipitation shortages cause anomalous soil stress. Only then can the negative soil moisture anomalies propagate downwind as water vapor deficits; a necessary — but not sufficient — criterion for drought self-propagation as defined here. Our results suggest that a strong dependence on self-supplied moisture facilitates this feedback; for example, the largest drought in Australia analysed here (rank 17), situated in the south and southeast of the continent, portrayed less self-propagation than the events closer to the northwest (see Fig. 3), where water vapor usually travels shorter distances between evaporation and precipitation ²⁰ . All the events characterized by a strong self-propagation take place in subtropical regions where evaporation is locally recycled all year-round ²⁰ and particularly during dry years ³⁷ . Furthermore, the convective nature of precipitation in tropical and subtropical drylands ³⁸ allows for a secondary feedback: for a given convergence and ascent, more water vapor in the vicinity strengthens updrafts through enhanced convective heating, which may invigorate convergence and enable a positive feedback loop ^39,40 .

Fig. 4. Upwind drought in drylands.

Meteorological drought is frequently triggered by weaker-than-usual dynamical saturation-enabling mechanisms (conceptualized as low precipitation efficiency; P_eff’<0), which in turn may respond to a remote forcing, such as anomalous sea surface temperatures. Once that happens, limited precipitation (P’<0) causes soil desiccation (SM’<0) and soil stress, exacerbated by the high potential evaporation due to clear skies and elevated temperatures. Then, evaporation becomes (more) water-limited (E’<0). The reduction in near-surface air moistening — extending across the troposphere via vertical mixing — causes a reduction in water vapor being exported downwind (Q’<0). Therefore, further downwind, for the same precipitation efficiency, even less precipitation is expected (P’<0), contributing to downwind drought onset (SM’<0, E’<0). Moreover, since water vapor is known to enhance uplift, additional reductions are possible for convective precipitation (P_eff’, P’, SM’, E’ << 0).

Consequently, a reduction in tropospheric water vapor may contribute to low precipitation efficiencies during droughts where precipitation is mainly convective (Fig. 4).

Our findings point to a direct connection between aridity and the ability of droughts to fuel themselves. In recent years, projections regarding the ‘dry gets drier, wet gets wetter’ paradigm ⁴¹ , and the expansion of aridity and drought affected areas, have been fiercely debated ^36,42 . Many wet areas are expected to become drier, and regions already characterized by pronounced dry and wet seasons will likely experience more variable precipitation ⁴³ . There is a consensus that increased atmospheric water demand acts to accelerate evaporation in most regions ^43,44 , resulting in an intensification of the dry season in many extratropical regions ⁴⁵ . Meanwhile, terrestrial surface relative humidity is already declining, reflecting decreases in soil moisture and thus increasingly water-limited evaporation ⁴⁶ , which underlines the exacerbating role of land–atmosphere interactions in a more arid world due to climate change ⁴⁷ . For drylands, soil moisture–atmosphere feedbacks have recently been shown to partially attenuate declines in water availability (P–E) through enhanced moisture transport from other land areas and particularly oceans ^48,49 , and a widespread conversion from temperate into subtropical drylands is projected ⁵⁰ . Together, a less stable precipitation supply in regions that already crucially depend on seasonal rainfall, and an increasing potential for rapidly desiccating soils, might increase the potential of droughts for self-propagating as we progress into the future.

Methods

Workflow and overview

The methodological steps performed for this analysis consist of (1.) drought definition and propagation, (2.) water vapor tracking from drought-propagation regions, (3.) disentangling the impact of already existing soil drought on downwind water vapor and precipitation, and (4.) conversion of water vapor (reductions) to precipitation (deficits). An overview of these steps is provided in SFig. 1.

Drought definition and propagation

This study investigates the meteorological propagation of soil drought based on root-zone soil moisture data. The latter are obtained at monthly and 0.25° horizontal resolution from the Global Land Evaporation Amsterdam Model (GLEAM) v3.5a (refs. ^51,52 ), a semi-empirical model heavily constrained by satellite and reanalysis data. Whereas many drought definitions are applied independently per pixel (or grid cell), more holistic approaches have been proposed that consider droughts as spatiotemporally connected events ⁵³ . We employ a recently suggested method that uses mathematical morphology to characterize drought events ⁵⁴ . This approach requires binary input — maps that solely distinguish between drought and no drought conditions at each pixel. We obtain this input by thresholding all timeseries of deseasonalized monthly root-zone soil moisture anomalies with the respective 10^th percentile. Then, ‘morphing’ is performed through a series of erosion and dilation operations (see Figs. 2–4 in ref. ⁵⁴ ) in the predefined spatiotemporal neighbourhood of each drought pixel, for which a 3 x 3 x 3-box is used here, i.e., 3 months and 3 x 0.25° in each horizontal direction. Since the Lagrangian moisture source identification is performed on a 1.0 x 1.0° grid, the resulting ‘morphed’ drought events are regridded, requiring that at least 75% of the 0.25° sub-pixels (i.e., 12 out of 16) are subject to soil drought conditions. Lastly, all unique drought events in space and time are identified and ranked, and the 40 largest ones by the product of area and duration are selected for analysis. The timings of drought onset and recovery are defined by the earliest appearance and complete disappearance of morphed drought pixels belonging to each event.

Each of the 40 largest drought events in space and time is represented as a series of ‘propagation steps’ at monthly temporal resolution. As soon as a pixel becomes part of an existing soil drought (via expansion), or a new drought event is triggered, the change is considered ‘propagation’ and may only occur once for each event (see SFig. 2). That is, even if a certain pixel initially belongs to a (spatially large) drought event, then recovers temporarily while the drought persists elsewhere, and finally merges with the same drought event again, only the first drought occurrence is considered as the propagation step. Note that due to the morphing technique and subsequent identification of unique droughts in spacetime, multiple seemingly separate droughts in space can belong to a singular event, granted that they concatenate spatially at some point in time prior to recovery. We emphasize here the distinction between the areas where droughts propagate, considered as ‘targets’ of water vapor, and upwind areas or ‘sources’. Specifically, we focus on the downwind impact of ‘sources’ situated within the respective drought area prior to drought propagation.

Water vapor tracking

We estimate the origins of tropospheric water vapor with a Lagrangian backward analysis. Since the drought morphing approach employed here does not, for example, constrain drought evolution to the dry or wet season, propagation can occur year-round for some of the selected drought events. To this end, the air residing over all of the 40 selected drought areas is first tracked back in time for at most 15 days during the entire analysis period (1980–2016). This is done separately for each temporally coherent propagation step per drought, so that a corresponding (evaporative) moisture source region for every month is obtained. To address the hypothesis of drought self-propagation, we only examine the moisture transport prior and up to propagation, but not afterwards. For our analysis, the moisture sources of the respective month of propagation as well as of the two antecedent months are evaluated, taking the memory of soil moisture — upon which the drought definition is based here — into account. Thus, for each propagation step, water vapor residing above the respective area is tracked backward during the month of propagation and the two antecedent months (3 months in total). In order to estimate the effect of soils already affected by drought on downwind water vapor (and hence drought self-propagation), the source regions are split into ‘drought’ and ‘elsewhere’ (see SFig. 3a); only land areas already subject to (the same) drought event are considered for the former, whereas the latter is defined as the remaining terrestrial as well as all oceanic sources. This differentiation is based on the state of the morphed drought, which may vary from month to month (SFig. 3a).

Moisture tracking is performed using a modified version of the framework first presented by ref. ⁵⁵ , following refs. ^56,57 . This process-based approach evaluates air parcel property changes along trajectories, which are affected by mixing, surface fluxes and phase changes. Air parcels are a conceptualization of coherent air masses, but mixing processes still occur — particularly within the (well-mixed) atmospheric boundary layer (ABL; e.g., ref. ⁵⁸ ). Specific humidity in the ABL, either in the absence of large-scale advection or, arguably, from a Lagrangian perspective, is largely controlled by surface evaporation and entrainment (e.g., refs. ^59,60 ). Since entrainment of free tropospheric air usually dries the ABL ^61–63 , increases in specific humidity along air parcel trajectories within the ABL may be assumed to reflect surface evaporation (as in, e.g., refs. ^55,56 ). Our Lagrangian atmospheric model is FLEXPART v.9.01 (refs. ^64,65 ) driven with ERA-Interim data ⁶⁶ , consisting of both analyses and forecasts at 3-hourly temporal resolution; only the moisture budgets of 6-hourly reanalysis steps are evaluated. Note that FLEXPART does not assume that the entire troposphere is well-mixed nor does it consist of a single or two vertical layers ^67–69 , instead relying on 3D-winds and a convective scheme ⁷⁰ . In this study, we employ FLEXPART to estimate the origins of tropospheric moisture over all propagation areas (i.e., all pixels at a certain month that meet the criteria for ‘propagation’ as described above). Note that this is different compared to many other drought studies, for which a static drought region is employed to track moisture back in time (e.g., refs. ^28,71,72 , and many others).

To determine the origin of water vapor residing over the expanding drought areas, the following steps are performed: (1) all air parcels within the troposphere are selected, (2) backward-trajectories are constructed, (3) moisture changes along these trajectories are evaluated to infer evaporative moisture sources, which are then (4) cast onto a regular 1.0 x 1.0° grid (see SFig. 3b). Only sources of tropospheric moisture are identified in step 1; tropopause heights are calculated based on a 2 potential vorticity units (PVU) threshold in the version of FLEXPART employed here ⁶⁵ , a common approach in atmospheric dynamics research (e.g., refs. ^73–75 ). As near-surface PV values can sometimes exceed this threshold, this may rarely result in unrealistically low tropopause heights. It is thus ensured that all air parcels within the first 5 km above the surface are always tracked back in time. Backward trajectories in step 2 are restricted to a maximum of 15 days as a compromise between trajectory accuracy ^{55,56,76–78} and consideration of the long, thin tail in the probability density function of the atmospheric lifetime of water vapor over long time spans ⁷⁹ . To assess the uncertainty involved in the choice of maximum trajectory length, an ensemble analysis also employing 5 and 10 days as the upper limit, following ref. ⁷⁸ , is performed. Evaporative sources (3) are detected through increasing specific humidity of air parcels in the vicinity of the ABL (see ref. ⁷⁸ ), without any additional thresholds. Any water vapor losses en route, for example due to intermittent precipitation, are considered through linear scaling of evaporative source contributions with the subsequent evolution of specific humidity ⁵⁵ .

Both evaporative sources as well as the target water vapor are bias-corrected on a daily and also a monthly basis for each pixel ⁷⁸ . The use of two different timescales when bias-correcting our estimates for both evaporation and water vapor serves to extend the uncertainty analysis to an ensemble consisting of 3 x 2 x 2 = 12 members per event. For the source correction, we employ evaporation from GLEAM v3.5a over land and from OAFlux ⁸⁰ over oceans, with 1980–1984 of the latter consisting of CDF-matched ERA-Interim evaporation ⁶⁶ , and ERA-Interim vertically integrated water vapor ⁶⁶ for the target bias-correction. Since the majority of water vapor resides in the lower troposphere (e.g., ref ⁸¹ ), and the stratosphere contains only about 0.03% (ref. ⁷⁹ ), any errors introduced by employing vertically integrated (rather than tropospheric) water vapor above the tropopause are negligible.

Disentangling effect of upwind drought on downwind water vapor

Enabled by the water vapor tracking framework, for every analysis day, a (linearly discounted) evaporative contribution ΔQ from each source pixel (i) and backward day (t) to the mean water vapor residing over a specific drought propagation pixel can be calculated. This is performed separately for each receptor pixel, that is, for all 1 x 1° areas where the respective drought propagates. The total water vapor Q of a receptor pixel is then given by the sum over all n source pixels, and over each backward day with contributions (at most 15 days into the past), that is,

$$Q={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{t=-15}^0\delta Q_{i,t}}}$$ (1)

To disentangle the impact of upwind soil drought (source) on downwind water vapor (receptor), the evaporative contribution of any source pixel to the water vapor residing over any drought propagation pixel is conceptualized as the product of circulation (α) and upwind evaporation (E):

$$\delta Q_{i=t}={\alpha }_{i=t}{E}_{i,t}$$ (2)

With our water vapor tracking framework that extracts information from air parcel trajectories, we obtain estimates (δQ_i,t ) on how much each source pixel contributes to downwind tropospheric water vapor. We introduce a circulation component α_i,t = δQ_i,t/E_i,t to describe the fraction of water vapor previously evaporating in a certain (source) region being transported to where the drought propagates (receptor). As such, α represents the complete source–receptor relationship between any evaporative source location and the downwind receptor region. It contains information on both the prevailing large-scale winds advecting air parcels in the Lagrangian framework, and on any moisture losses occurring en route, e.g. due to intermittent precipitation. α is a fraction ranging between 0 and 1, with the former implying that none of the evaporation from the source region is advected to the receptor region. On the contrary, α = 1 indicates that (i) all air parcels that gain water vapor from evaporation in the source region arrive in the receptor region, and (ii) that none of this advected water vapour is lost en route (for example, through rainfall). A value of α = 1 thus usually only occurs if source and receptor are neighbouring pixels, and typically decreases with increasing distance from the receptor region. Using this definition, we obtain how much evaporation in a source region (E) contributes to the water vapor content of the air parcels residing above this source region, and how much of this evaporation actually arrives in the receptor region (α). Furthermore, the evaporation component is conceptualized as the product of potential evaporation and soil stress to target the effect of soil drought. E_p is obtained from GLEAM v3.5a, as is actual evaporation (E) also used for water vapor tracking, so that the soil moisture stress S is calculated as

$$S_{i,t}=\frac{E_{i,t}}{E_{p\left(i,t\right)}}$$ (3)

Introducing the soil moisture stress S as such allows us to disentangle the impact of soil moisture from the prevailing meteorological conditions — captured by E_p — on evaporation, and hence ultimately tropospheric water vapor. Therefore, the evaporative contribution δQ_i,t from a single source pixel (i) and a given backward day (t) to the daily mean water vapor residing over a specific drought propagation pixel can be expressed as the product of circulation α, potential evaporation (E_p ) and soil stress S,

$$\delta Q_{i,t}={\alpha }_{i,t}{E}_{p\left(i,t\right)}{S}_{i,t}$$ (4)

Note that for aesthetic reasons, the (i,t) notation is omitted from now on, but the following equations are still expressed for an individual source pixel and backward day (and a given receptor pixel and analysis day).

Applying a Reynolds decomposition results in

$$\delta Q=\overline{\left(\alpha E_{p}S\right)}(\alpha E_{p}S{)}^{\prime }=\overline{\alpha }\overline{E_p}\overline{S}+\overline{\alpha }{E}_p{}^{\prime }\overline{S}+{\alpha }^{\prime }\overline{E_p}\overline{S}+{\alpha }^{\prime }{E}_p{}^{\prime }\overline{S}+\overline{\alpha }\overline{E_p}S\prime +\overline{\alpha }\prime E_p\prime S\prime +\alpha \prime \overline{E_p}S\prime +\alpha \prime E_p\prime S\prime$$ (5)

The first four terms, summarized as $\alpha E_p\overline{S}$ , express how much water vapor a source pixel would have contributed to the selected receptor pixel if soils experienced climatological stress $\left(S=\overline{S}\right)$ , whereas the last four terms, summarized as αE_pS’, describe the difference of transported water vapor from source to receptor due to anomalous soil stress S’ for the given circulation and potential evaporation. Such a decomposition enables the estimation of water vapor contributions from all drought source pixels to the drought propagation area if soils had not experienced unusual soil stress (S’ = 0). This is performed separately for all combinations of source and receptor pixels, and for each one, the effect of drought self-propagation is defined as

$$\delta Q_{self-propagation}=\alpha E_{p}S-\alpha E_p\overline{S}=\alpha E_{p}S\prime$$ (6)

Aggregating SQ_{seif-propagation} for each drought propagation step, that is, over all source pixels (i) and backward days (t), and additionally over all days prior to and during propagation of the respective receptor pixel (3 months), yields the estimated impact of soil drought on water vapor (red areas in Fig. 1d). The theoretical nature of this estimate is remarked, as actual (or observed) circulation and potential evaporation are employed, but also climatological soil moisture stress. In reality, a reduction in soil stress in the drought area may alter the large-scale circulation pattern ^14,29 and thereby affect potential evaporation, yet this is not investigated here.

Conversion of water vapor to precipitation

The conversion of water vapor to precipitation is enabled by various saturation-enabling, often referred to as ‘dynamical’, mechanisms. Desiccating soils are capable of affecting both water vapor and these dynamical mechanisms via water and energy fluxes (e.g., refs. ^{11,12,82–87} ). Yet, to date, moisture tracking studies have focused only on climatological moisture sources of precipitation and how they change during drought (e.g., refs. ^88–90 ). Here, a conceptual approach is employed, in which daily precipitation is considered to be the product of water vapor (Q) and precipitation efficiency (P_eff ) (e.g., refs. ^21,91 ):

$$P_{actual}=Q_{actual}\cdot P_{eff,actual}$$ (7)

P_eff can be thought of as the conceptualization of dynamical mechanisms that achieve saturation, converting water vapor into precipitation, whereas Q provides the input for this conversion. Water vapor (again from ERA-Interim) and precipitation (from MSWEP v2.2; refs. ^92,93 ) during the drought are employed to calculate the actual precipitation efficiency, per receptor pixel and day. Using this conceptualization, we estimate the daily precipitation deficits due to drought self-propagation:

$$\Delta P_{self-propagation}=\Delta Q_{self-propagation}\cdot P_{eff,actual}$$ (8)

This procedure is repeated for the climatological, as well as the maximum and minimum daily P_eff encountered from 1980–2016 for each drought event, to visualize an upper and lower bound as to how much additional precipitation might have occurred if drought-stricken soils were not anomalously stressed or the atmosphere had been more efficient at converting water vapor into precipitation (Fig. 2b). The minimum and maximum P_eff of each day and pixel are obtained from the year in which the respective monthly mean P_eff is lowest and highest. Using estimates of ΔP_{self–propagation} , we can estimate how much precipitation would have occurred in the absence of self-propagation:

$$P_{non-drought}=P_{actual}+\Delta P_{self-propagation}$$ (9)

To obtain the event-mean drought self-propagation (Fig. 3), the daily estimates of ΔP_{self–propagation} (equation 8) are first aggregated per month and drought propagation area, and then divided by analogously aggregated P_{non–drought} (equation 9). The resulting fractions express the precipitation deficits that are estimated to occur due to self-propagation (red areas in Fig. 2a). Then, an area-weighted average of ΔP_{self–propagation} across all propagation steps is calculated, and related to P_{non–droug ht} (dashed line in Fig. 2a) to estimate the mean effect of drought self-propagation for each event (Fig. 3). The peak drought self-propagation (Fig. 3) is given by the month during which the ratio of ΔP_{self–propagation} and P_{non–droug ht} culminates. To enhance the comparability across events, only propagation steps corresponding to a total receptor area of at least 100’000 km² are considered for the peak effects. All quantities are expressed as the mean of the ensemble, unless noted otherwise. Uncertainty bars in Fig. 3 are constructed using the minimum and maximum estimates of the ensemble.

Note that with this approach, a linear dependency of precipitation on water vapor content is assumed, which is not in line with some observational evidence — precipitation originating from deep convection is portrayed by an exponential relationship with column water vapor ⁹⁴ . Nevertheless, as upwind droughts tend to only moderately alter the overall column water vapor, we also only need to assume piecewise linearity rather than across the entire range from low to high water vapor. Moreover, we point out that the relationship between water vapor and precipitation is also important at synoptic scales: precipitation of cyclones is proportional to their intensity and tropospheric water vapor, and the latter is a particularly useful predictor for extratropical cyclone precipitation ⁹⁵ .

Extended Data

Extended Data Fig. 1. All drought events used for analysis.

Analogous to Fig. 1a, yet using colors for all 40 events; for aesthetic reasons, a shows the 20 largest droughts, gauged by both their spatial extent and duration. b visualizes the remaining events, ranked 21-40.

Extended Data Fig. 2. Main climatological source regions of water vapor for the six highlighted droughts.

Source regions of tropospheric water vapor (light blue) over the respective drought areas (pink contours), covering 70% of the total water vapor; for the period 1980-2016. The extent of the respective main source region can be compared across events to gauge the dependence on proximate or more remote evaporation.

Extended Data Fig. 3. Soil stress S during the six highlighted droughts.

S, given by the ratio of E over E_p , is expressed as anomalies with respect to the climatological mean. This is calculated per pixel and using only months for which drought conditions were present according to the morphed droughts—in other words, the climatology is obtained analogously to the drought values, for the same months (or seasons), but based on 1980–2016. Brighter colors imply more soil stress (lower S) and thus more severely water-limited evaporation.

Extended Data Fig. 4. Peak drought self-propagation as a function of the climatological precipitation recycling ratio.

Similar to Fig. 3, but displaying the peak self-propagation on the y-axis, while the fraction of the respective drought pixels being classified as dryland (P/E_p<0.65) is visualized by the color of each marker.

Data availability

The FLEXPART model can be downloaded via https://www.flexpart.eu/. ERA-Interim data were obtained from http://apps.ecmwf.int/datasets. GLEAM data are available through https://www.gleam.eu/. MSWEP data are accessible through http://www.gloh2o.org/. The FLEXPART simulation employed here was performed by R. Nieto, A. Drumond and L. Gimeno, and is not publicly accessible. Due to the large data volumes, post-processed FLEXPART data are available upon request from the corresponding author, and sample data are publicly accessible through Zenodo on https://doi.org/10.5281/zenodo.5839819, together with the complete drought event data used for analysis and event-aggregated results. The source data of Figs. 1–3 are also provided.

Code availability

The code used for analysis is publicly available through Zenodo on https://doi.org/10.5281/zenodo.5840791.