Abstract
We present interoperability as a guiding framework for statistical modelling to assist policy makers asking multiple questions using diverse datasets in the face of an evolving pandemic response. Interoperability provides an important set of principles for future pandemic preparedness, through the joint design and deployment of adaptable systems of statistical models for disease surveillance using probabilistic reasoning. We illustrate this through case studies for inferring and characterising spatial-temporal prevalence and reproduction numbers of SARS-CoV-2 infections in England.
Key words and phrases: Bayesian graphical models, COVID-19, Evidence synthesis, Interoperability, Modularization, Multi-source inference
1. Background and Key Principles of Interoperability
Faced with the coronavirus disease 2019 (COVID-19) pandemic that posed an urgent and overwhelming threat to global population health, policy makers worldwide sought to muster reactive and proactive analytic capabilities in order to track the evolution of the pandemic in real time, and to investigate potential control strategies. In the United Kingdom, governmental health data analytic capabilities were strengthened in the midst of the pandemic with the creation in May 2020 of the Joint Biosecurity Centre (JBC), whose mission is to provide evidence-based, objective analysis, assessment and advice so as to inform the response of local and national decision-making bodies to current and future epidemics. Early on, the JBC established links with external academic or institutional groups, and in particular the health programme (lead Chris Holmes) and the digital technology project within the defence and security programme (lead Mark Briers) of The Alan Turing Institute (herein Turing).
In parallel, institutions such as the Royal Society and the Royal Statistical Society (RSS) established task force groups to contribute their collective expertise to the UK government and public bodies. The RSS Covid-19 Task Force [1] was created in April 2020. Besides intervening on statistical issues, co-chairs and members of its steering group were mindful of ensuring coordination and avoiding duplication with other initiatives. Under the leadership of Chris Holmes (Turing and RSS Covid-19 Task Force) and with the support of Sylvia Richardson (RSS president elect, co-chair of the RSS Covid-19 Task Force) and Peter Diggle (steering group of RSS Covid-19 Task Force), a partnership to provide additional capacity to JBC was established between Turing and the RSS. This resulted in the creation in October 2020 of the “Statistical Modelling and Machine Learning Laboratory” (the Lab) within JBC. The Turing-RSS Lab's aims are to work within the JBC to provide additional capacity through independent, open-science research based on rigorous statistical modelling and inference directed at JBC priority areas. In October 2021, the United Kingdom Health Security Agency (UKHSA) was created, which incorporated the JBC, and the Lab's partnership then became a partnership with UKHSA.
Established against the background of a fast moving pandemic, this partnership brought into focus a number of interesting challenges to conventional statistical practice arising, in particular, from the need to model real-time, messy data from diverse sources, in order to efficiently address rapidly evolving public health demands. The dynamic nature of the pandemic and the resulting public health priorities led to frequent changes in the specific questions being asked of the data, with focus often shifting unpredictably and suddenly. This challenged conventional statistical analysis protocols that target specific research questions, as these would take too long to deliver, and carry an associated risk of redundancy. Instead, it was necessary to develop robust, easy-to-update and reuseable modules which could be integrated into arbitrarily complex models to provide analyses useful for decision-making.
We will often use the terminology “model” alongside the distinct but related terminology “module/modular/modularity”, so it is useful to compare and contrast these concepts at the outset:
Model. “A statistical model is a probability distribution constructed to enable inferences to be drawn or decisions made from data” [2]. A model can be comprised of one or more modules.
Module. A module is a model component or, more precisely, a joint probability distribution linking some or all of: observed data, latent (unobserved) parameters or random effects, and user-specified hyperparameters.
Of course the distinction between model and module is not strict, as a simple model may also be a module of a more complex model. Rather than trying to be pedantic with the above definitions, we are simply aiming to convey the spirit and sense of the vocabulary we use throughout the paper.
Our practice and strategic thinking led us to develop a set of inter-connected health protection models, and to articulate the principle of “interoperability” as an important statistical concept and goal for future disease surveillance systems.1 In this article, we discuss the emerging principles of interoperability of statistical models that we have operationalised since 2021, and we illustrate these on case studies carried out in the Lab. Interoperability can be usefully, and loosely, characterised as “an operational statistical and computational data-driven framework based on modularized inference designed to provide timely analyses and future preparedness for decision making on related questions relevant to a common process”. At its core, interoperability is driven by the need to optimally fulfil the following complementary principles:
P.1 Shared latent quantities. When building models to answer different questions, harmonize the models' essential elements by incorporating common key latent quantities, e.g. disease prevalence;
P.2 Modularity. Use modular statistical approaches, such as Bayesian graphical models, as a foundation for inference and computations to ensure both modelling agility and principled propagation of uncertainty;
P.3 Structural robustness. When one or more modules or data sources are considered potentially unsound, consider specifying robust model structures, in which the failure or misspecification of one module has a limited impact on other modules; aim for transparent and appropriate sharing of information across diverse data modules, paying particular attention to possibility of conflict between data sources;2
P.4 Dynamic model validation. Identify opportunities for ongoing dynamic assessment of model performance, ideally that can be applied to multiple models sharing latent quantities and/or addressing similar questions;
P.5 Composability.3 Strive for efficient transfer of results of analyses between different computational tools, with the freedom to implement each module of analysis primarily in its most convenient software package;
P.6 Probabilistic programming. Fit models using modular, efficient, high-level probabilistic programming languages, allowing flexible and fast implementation of complex methods and nimble repurposing of scripts as new data and questions arise;
P.7 Data pipelines. Maintain version-controlled data streams synchronised across a system of models and modules, accompanied by vigilant quality control, for example through global visualization of data inputs and results;
P.8 Reproducibility. Ensure the generation of stable reproducible results via an open-source code base, coupled with tight control on code and data versioning.
There are obvious connections between these objectives. The key desirability of modularity informed our choice of Bayesian inference methods and Bayesian graphical models as the core statistical framework. We have heavily relied on the known flexibility of Bayesian hierarchical models (BHMs) with latent (Gaussian) process components to deliver predictive and/or explanatory inferences whilst accommodating complex data structures and measurement processes and enabling principled data synthesis (for examples, see [3] and the introductory chapter of [4]). Recent work on Markov melding [5] and statistical learning while cutting or restricting information flow between modules [6, 7, 8, 9,10] is particularly relevant to anchor and operationalize our goals.
2. Introduction to Interoperability as a Strategic Goal, Informed by Current Approaches to Disease Surveillance
Integrated infectious disease surveillance has unusual characteristics from a statistical analysis perspective. Multiple research questions on disparate outcomes are targeted towards better understanding of a common underlying process, e.g. of the disease spread and its evolution in time and space. Asking multiple questions of a single process opens up a spectrum of modelling approaches. At one extreme, different models using potentially partially overlapping data could be built independently to estimate common latent characteristics of the disease under consideration. At the other extreme, we can look to build a single universal joint model covering every facet of the disease process that is theoretically able to answer any question. Our conjecture is that, in the face of the constraints and operational challenges outlined above, there is an optimal middle ground in which we develop models and analysis plans and couple them according to the guiding principles of interoperability.
2.1. Building separate models for common key latent quantities
Many flavours of epidemic models have been developed for tracking COVID-19 disease transmission ranging from agent-based simulation models to age-structured compartmental models or discretized semi-mechanistic models using renewal equations [11, 12]. It is not our purpose to give a comprehensive review of these but simply to take stock of the rich diversity of modelling approaches and data sources chosen by different teams to inform the calibration or estimation of epidemic parameters. In the UK, a number of academic modelling groups have been actively participating in the expert advisory panel Scientific Pandemic Influenza Group on Modelling (SPI-M), a subgroup of Scientific Advisory Group for Emergencies (SAGE), which has advised the UK government from the start of the pandemic. The adopted collegiate mode of working of SPI-M has fostered the development of a set of distinct models for estimating key epidemic quantities and producing short-term forecasts. Besides the differences between the modelling approaches, the choice of primary data sources and the ways to embed this information into the modelling framework may also differ, creating an ensemble of models with complex connections. This parallel model development step is then followed by a meta-analysis of the estimates of the key epidemic parameters at regular intervals, and the synthesized results are communicated to the public, as well as used by policy makers [13].
Such a strategy has the benefit of structural robustness for inference on latent quantities, such as the much quoted effective reproduction number, here denoted , aimed at protecting against misspecification of one or more of the models in the ensemble, as well as countering undue influence of artefacts connected to particular data sources. But it also raises unresolved statistical issues on how best to formulate criteria for including suitable models in the ensemble, and how to weight a set of inter-connected models in the final estimate. The UK government website lists ten academic groups producing models which contribute to an ensemble [13], and pooled estimates are computed via a random effects meta-analysis in which all models are given equal weight [14]. From a statistical perspective, using weights based on some measure of short-term predictive performance for each model would be a natural alternative, but would be potentially challenging to operationalize, as it requires all models to produce comparable predictive outputs; see [15] for a discussion of forecast evaluation metrics. Hence, meta-analysing results from an ensemble of models, while attractively operationally simple, results in overall estimates with unclear statistical properties, due to models using the same or overlapping inputs, and uncertainty not being fully propagated.
2.2. Building a full joint model
At the other end of the spectrum, one could strive to develop a single “uber-model” which contains all latent quantities of interest and a comprehensive set of data sources. The corresponding full joint posterior distribution of all the parameters of interest could then be derived simultaneously, using the paradigm of Bayesian graphical models. While theoretically optimal (provided the model is well specified) a full joint model is particularly challenging in a fast moving epidemic situation because it requires expansion, adaptation and revision each time a new piece of information needs to be integrated, whether it is new data source (e.g. presence of SARS-CoV-2 in geo-localised wastewater data) or a new policy or intervention influencing the structure of the model (e.g. vaccination) and the behaviour of people (e.g. mobility).
Such increasing model complexity is accompanied by a heightened risk of misspecification and conflict between sources of information. This makes it hard to understand how different data sources are balanced in their contribution to the overall results, and difficult to track the influence of the assumptions made on how information is shared [16], for example across space and time. Moreover, inevitable errors and quirks that occur in real time epidemiological data can result in contamination of inference whereby misspecification in one part of the model adversely affects analysis in another part. This may be hard to diagnose and correct for. Computationally, fitting a full joint model typically requires intricate and dedicated programming, though this can be mitigated if full modularity is embedded in the programming language; in Section 3.6 we will discuss such computational strategies with particular reference to the Turing.jl language [17], one of the probabilistic programming languages we are using in the Lab. Building a full joint model is also likely to be computationally demanding as data accrues and the associated number of model parameters increases, requiring frequent fine tuning of inference algorithms.
In spite of these implementational challenges, full joint modelling has been applied successfully in a number of inferential contexts during this pandemic. For example, the University of Cambridge Medical Research Council Biostatistics Unit (BSU) and Public Health England (PHE) model uses a deterministic age-structured compartmental model [18], data on daily COVID-19 confirmed deaths, and published information on the risk of dying and the time from infection to death, as primary sources from which they estimate the number of new severe acute respiratory syndrome coronavirus 2 (SARS-COV-2) infections over time. Starting in the early months of 2020 from a pre-existing flu transmission model, the BSU-PHE model has continually been adapted and complexified. In its December 2021 release, the model accounts for the ongoing immunisation programme and latest estimates of vaccine efficacy, differential susceptibility to infection in each adult age group, and incorporates estimates of community prevalence from the Office of National Statistics COVID-19 Infection Survey [19, 20].
2.3. Interoperability of models – the middle ground
Between building separate models and building a single full joint model, the Lab experience of the COVID-19 pandemic has motivated us to adopt a strategy of interoperability of models for disease surveillance. Our overarching goal is to ensure adaptability of models and modules so they can be repurposed as needed, while maintaining a consistent treatment of uncertainty, and ensuring our approach is as robust to misspecification as possible. We see interoperability as a journey, and the case studies presented in Section 4 are there to illustrate the principles and to show the direction of travel, not the fully equipped arrival lounge.
A software engineering analogy is pertinent here: we believe that there is benefit from moving from a “parallel” approach, in which several separate models are analysed simultaneously and then the results integrated by model averaging, towards a soft “serial” approach, where input and output components and loose chains of models are considered. In a straightforward serial process, one could use posterior output as input into the next model. However, doing this in a fully Bayesian manner can be as computationally demanding as a full uber-model. Furthermore, as we will illustrate in our first case study (Section 4.2), there are instances where it is beneficial to cut feedback [9]. In other cases, the serial process will be akin to approximate Bayesian melding where posterior outputs are approximated by a suitable parametric distribution [5].
3. The Many Ingredients of Interoperability
Interoperability is driven by a desire to deliver timely and robust statistical inference to answer several related research questions on a common process. As such, interoperability intersects and affects many aspects of the statistical workflow, from model specification and inference to computations and data deployment.
3.1. Shared latent quantities
We consider there to be an important distinction between an underlying model for the scientific process of interest, S say, with parameters θ whose interpretation does not depend on what data are available, and an observation model for data D given S, with parameters ϕ. Dawid [21] calls θ and ϕ the extrinsic and intrinsic parameters respectively. Making this distinction clarifies how a new data-source can be added to an existing model without the need to re-build the model from scratch. In the current context, our inferential focus is on extrinsic latent quantities such as incidence, prevalence or the growth rate. We note, however, that care is needed in defining precisely the inferential target to answer any particular question; for example, an unqualified reference to “prevalence” as a latent quantity is open to multiple interpretations. In the case studies in Section 4, we use point prevalence defined as the number of individuals in the population who would be found to be PCR-positive if tested, averaged over a specified time interval (e.g. over a week for the debiasing model described in Section 4.2.1).
3.2. Modularity
Once latent quantities and scenarios of interest are specified, a common modelling framework is desirable for building each model, to facilitate principled propagation of uncertainty. We have chosen to formulate our models within the flexible framework of Bayesian hierarchical models (BHM) as it brings to the foreground conditional independence assumptions between the quantities of interest (whether observables or not) and encodes the probabilistic relationships between them. BHMs clarify information flows through the use of Directed Acyclic Graphs (DAGs), key assumptions made on exchangeability and ways of borrowing information. They also enable inclusion of new data sources in the DAGs in a coherent and computationally efficient manner.
It is often helpful to decompose a complicated model into smaller modules. For example, modules could represent different parts of the prior, the evolving dynamics of the latent epidemic, and the likelihood model for different data sources. Modularity creates a spectrum of choices between the full joint model approach and the interoperability approach.
Working within a Bayesian inference framework enables the possibility of coherent propagation of uncertainty without resorting to the direct specification of a full joint model. We wish to be able to freely specify each module separately, and then subsequently join them into a single full joint model via their common parameters. This can be accomplished via Markov melding [5, 22], which builds upon the ideas of Markov combination [23, 24] and Bayesian melding [25]. Markov melding can be used to join several Bayesian models that involve a common parameter, with the prior combined using a “pooling function”. The joint Markov melded model is the product of the conditional distributions of each module (given the common parameter) and the pooled prior for the common parameter [5].
We apply Markov melding at various points in our case studies in Section 4. In Section 4.2, our core model combines two modules and two sources of data to infer the posterior distribution of debiased prevalence; there we use a form of Markov melding for the model’s bias parameter, creating its prior via product-of-experts pooling, i.e. the combined prior is proportional to the product of module-specific priors.
3.3. Structural robustness
When models are constructed from multiple modules, a desirable property is that misspecification of one module does not adversely affect others. Cut models [7, 8, 9] and semi-modular inference [10] can be deployed to block, or respectively regulate, the information flow from misspecified modules to more trustworthy modules. Cut models have been applied in a broad range of areas, such as pharmacokinetic-pharmacodynamic data modeling [26, 6, 8], complex computer models [7] and epidemiology [27]. Cut and semi-modular models can be computationally challenging to fit, requiring nested MCMC by default [9], though there is currently much active work on developing more effective computationally strategies [8, 28, 29, 30, 31] as well as clarifying such models' technical properties [31, 32, 33].
We provide details of our use of cut posterior distributions in Section 4.2.2, as an example of structural robustness. In this case we are giving more weight to an unbiased-by-design source of evidence within our interoperability framework, relative to a data module that may suffer from misspecification.
As a further point of note on the use of cut posterior distributions, many epidemiological models make use of knowledge of generation intervals, serial intervals, and incubation periods. These are typically estimated from small-scale but direct studies of transmissions, producing broad confidence/credible intervals reflecting the inherent uncertainties (e.g. [34]). If these are used as priors for generation/serial intervals or incubation periods for a large scale epidemiological model such as Epimap ([35]; see Section 4.5), the lower quality yet larger amounts of information in the large scale data (e.g. test counts in case of Epimap, but can also include hospitalisation and death counts) can easily overwhelm the priors. Instead 280 a common approach (besides Epimap, see also [36]) is to draw multiple samples from the priors of these quantities, compute the posterior predictive distribution for each sample, then aggregate across prior samples to capture the uncertainties over the generation/serial interval and incubation period. This can be equivalently viewed as nested Monte Carlo estimation for a cut posterior distribution.
3.4. Dynamic model validation
Adopting a common inference framework for all models (here we choose to use Bayesian inference) allows a unified interpretation of their results. Additionally, it facilitates the adoption of common ways to validate outputs, including the type of metrics to use, e.g. the use of marginal predictive distributions on observables. As an example, in Section 4.2.4 and Figure 2, we are able to identify which model is performing best in terms of prediction by validating the resulting posterior estimates against held-out gold-standard data. More generally, using a modular approach has the benefit to make each modelling component easier to validate using similar criteria on shared parameters.
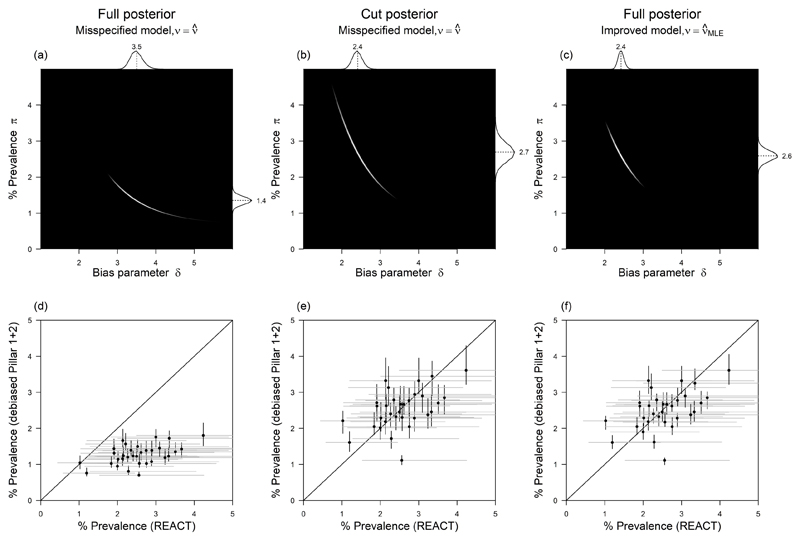
Fig 2. Comparison of full vs cut posterior inference for bias parameter δ under different inference strategies for ν.
(a) Full, misspecified joint log posterior – logarithm of equation (5) with . (b) Cut, misspecified joint log posterior – logarithm of equation (6) with . (c) Full, improved joint log posterior – logarithm of equation (5) with (d) LTLA-level debiased % prevalence based on full, misspecified posterior (vertical) vs gold-standard REACT % prevalence (horizontal), one point per LTLA. (e) LTLA-level debiased % prevalence based on cut, misspecified posterior (vertical) vs gold-standard REACT (horizontal). (f) LTLA-level debiased % prevalence based on full, improved posterior (vertical) vs gold-standard REACT (horizontal). In panels (a-c) the marginal posterior distributions are plotted at the panel top and right edges, with marginal means labelled. Inference is based on REACT and Pillar 1+2 data for London and its constituent LTLAs for W/C 14th Jan 2021. The gold-standard LTLA-level estimates used for validation on the horizontal axes in (d-f) are based on REACT round 8 aggregated data (6th-22nd Jan 2021).
3.5. Composability
Here we are concerned with computational strategy. We use the term “composability” for an approach which is sometimes called “recursive” or “two stage” in a Bayesian framework, [37, 38], and has been advocated as a way to enable computationally-efficient model exploration and cross-validation [39] and integrate different statistical software packages [40]. As examples, in our last two case studies (Sections 4.4 and 4.5), we transfer results between analyses via a Normal approximation, which can also be viewed as an approximation to Markov melding, as discussed in [5]; we discuss this approach in more detail in Section 4.2.5.
From an operational point of view, it is also easier to perform unit testing, debugging and identification of computational bottlenecks within small, self-contained modules. For example, one can perform the prior, posterior or conditional predictive checks for these components 305 independently. Then, using the modules, one can freely choose between building a joint model by assembling these components or treating them as separate models, perform inference, and connect them using a cut or melding mechanism as introduced in Sections 3.2 and 3.3.
Considerations of interoperable modularity suggest there are benefits in targeting the marginal distributions of core quantities that feature within multiple models. This is because 310 inference from these marginal models can then be fed into multiple downstream analyses, providing a common and coherent representation of key parameters.
3.6. Probabilistic programming
One powerful way of performing statistical inference in an automated and timely manner is probabilistic programming, which allows one to write models in a concise, modular, intuitive syntax and automate Bayesian inference by using generic inference strategies (e.g. Gibbs sampling, Hamiltonian Monte Carlo). This significantly speeds up iterating models4 during a preliminary data analysis phase. However, most probabilistic programming languages lack native support for interoperability. We thus based our implementation on the Julia programming language [41], a very fast language, specially designed for numerical computations, together with Turing.jl [17] an independently developed software package5 implemented in Julia.
Julia has the advantage that it contains highly specialized implementations for specific computations, e.g. convolutions, that are essential for our epidemic models, drastically improving computational performance. Turing.jl provides a convenient syntax for defining, for example, a standard Julia function that computes the log-probability of any desired generative model and samples from that model. Moreover, to fully embrace the modularisation principle, we added a new module feature in the Turing.jl language. Each specified module behaves like an independent model and allows us to perform all kinds of operations and diagnostics available to a full model. Moreover, the programming language allows these modules to be combined into more complex models, similarly to assembling elemental probability distributions. Thus, the module feature allows us to break a highly complex model into many composable, reusable modules. Note that the Julia community has extensively tested many of the dependencies of the internal packages, and that we have ourselves tested “under the hood” implementations of numerical computations such as “convolution” to ensure reproducibility.
In principle, any general-purpose programming language can implement the optimisations available in Turing.jl. However, Julia makes such optimisations accessible by providing high-level dynamic language features similar to Python without sacrificing performance. For example, we can implement convolutions in Stan, but the code is not very concise and much 340 less reusable. These issues make Turing.jl more suitable for complex and computationally demanding models. Modularity via high-level language abstraction in these models is required to keep the implementation composable, interoperable, and reusable.
We experimented with the module feature on the Epimap model of the local reproduction number [35]. The module mechanism enables us to implement interoperability between Epimap and the Debiasing model with a minimal amount of extra work (i.e. one author implemented the code for interoperability of Epimap and Debiasing models within a day). It also allowed us to spot and fix a computational bottleneck arising from distributional changes. We discuss more details of this example of interoperability in Section 4.5.
3.7. Data pipelines
The data deployment and its synchronisation is of paramount importance to ensure interoperable modelling, requiring meticulous data synthesis pipelines and high quality data curation and tracking. To ensure that interoperable models provide a coherent and robust set of outputs, consistent, high quality data feeds must be applied. This is challenging when the generation of datasets is evolving rapidly, the data is frequently changing, and the downstream synthesis is continually being updated and modified. The complex datasets generated are typically being made available to a diverse user group resulting in data proliferation and redundancy. Parallel, superficially redundant data feeds may be maintained to increase resilience, analogous to the Redundant Arrays of Inexpensive Disks (RAID) storage framework [42]. Note that differing levels of information governance dependant on the proposed data use dictate the granularity of data available to specific users, requiring strict data management to ensure data synchronisation.
Data curation processes may be performed at the source of the data and centrally for both basic data cleaning and sophisticated curation [43]. The tracking of metadata describing the data granularity and data curation are important to assess outputs that are comparable. All of these factors mean that the same core data may be required to be provided to users in several different forms, with varied provision and annotation of metadata. The data selection requirements for our interoperable models may also vary, for example the level of granularity of age or geography may be different, and so the transparency of the data transformation is key to informing interoperability. To reduce data redundancy, “Single-source-of-truth” or “Master Data Management principles” could be applied to the provision of datasets. These principles suggest that only a single, master copy of each dataset is maintained, and that datasets are combined into for example a data warehouse by linking rather than duplication. The deployment of resilient ETL (Extract-Transform-Load) processes that implement the differing business logic (e.g. data transformations) to capture and integrate data from multiple feeds into a single data repository facilitates downstream consistent data feeds, data synchronisation and reduces redundancy. In this manner, the ETL facilitates the definition of the data transformation and processes required to manage rapidly evolving data and its underlying structure. The data warehouse is then a stable research-ready dataset that facilitates data releases and snapshots of the primary data, e.g. COVID-19 test results, to specified users.
3.8. Reproducibility
Reproducibility is the principle that all policy decisions or publication should be based on analysis outputs that can be generated exactly, by other researchers in their own computing environments, given the same data inputs and hyperparameter settings. Reproducible, reliable, and transparent results comprise one of the key ingredients of the data life science framework for veridical data science, that is, “principled inquiry to extract reliable and reproducible information from data, with an enriched technical language to communicate and evaluate empirical evidence in the context of human decisions and domain knowledge”, as proposed in [43]. To achieve reproducibility, both input data and software code must be versioned, and each version must be retrievable at a later date. Code versioning is easily achieved using a source code management tool such as Git [44]. Data versioning can be achieved through a variety of methods, depending on the stability of the data structures. For static data structures, temporal tables (or manually timestamped records) provide the ability to query data as of a specific time. The normalised data structures described above promote static data structures; when new fields are required, a new table is used instead of adding fields to existing tables. When changes in schemas are unavoidable, regular data dumps with named versions may be more appropriate.
4. Case Studies
Our case studies are chosen to illustrate some of the benefits and issues relating to interoperability that the Lab has encountered in its work. The concept of interoperability first crystallised through our work on debiased prevalence [45]. In Section 4.2 we describe this work and demonstrate how careful information synthesis (in this case cutting feedback) between data modules improved prevalence estimation. In Section 4.3 we demonstrate how we can coherently integrate and propagate the uncertainty of resulting estimates of debiased prevalence into a compartmental epidemic model.
In the final two case studies in Sections 4.4 and 4.5, we provide additional examples of model interoperability, showing different methods of inputting debiased prevalence into other models to answer new questions. In each case study, we outline some additional advantages (e.g. computational ease) but also new questions that arise in the process (e.g. appropriate handling of uncertainty in the prevalence estimates or how to link models built for different time scales).
Overall, the case studies demonstrate how analyses in a demanding, fast-moving, public health context can be operationalised within a framework that flexibly combines a set of independent analysis modules.
4.1. Data
We first describe the data used across the case studies. All scripts and data to reproduce the results of our case studies are available online.6
4.1.1. Randomized surveillance data
These record u positive tests out of U total subjects tested. The REal-time Assessment of Community Transmission (REACT) study is a nationally representative prevalence survey of SARS-COV-2 based on repeated polymerase chain reaction (PCR) tests of cross-sectional samples from a representative subpopulation defined through stratified random sampling from England’s National Health Service patient register [46].
4.1.2. Targeted surveillance data
These record n positive tests of N total subjects tested. Pillar 1 tests comprise “all swab tests performed in Public Health England (PHE) labs and National Health Service (NHS) hospitals for those with a clinical need, and health and care workers”, and Pillar 2 is defined as "swab testing for the wider population" [47]. Pillar 1+2 testing has more capacity than REACT, but the protocol incurs ascertainment bias as those at higher risk of being infected are more likely to be tested, such as front-line workers, contacts traced to a COVID-19 case, or the sub population presenting with COVID-19 symptoms, such as loss of taste and smell [47]. The ascertainment bias potentially varies over the course of the pandemic as the testing strategy and capacity changes. We exclude lateral flow tests and use exclusively test data from Pillar 1+2 PCR tests.
4.1.3. Population metadata
We enrich the testing data by population characteristics related to the following measures of ethnic diversity and socio-economic deprivation in each local area:
Ethnic diversity. The proportion of BAME (Black, Asian and Minority Ethnic) population is retrieved from the 2011 Census.
Socio-economic deprivation. The 2019 Index of Multiple Deprivation (IMD) score is retrieved from the Department of Communities and Local Governments [48]. IMD is a composite index calculated at Lower Super Output Area level (LSOA) and based on several domains representing deprivation in income, employment, education, crime, housing, health and environment. For other geographies, e.g. Lower Tier Local Authority (LTLA) which we use in the case studies, the IMD is obtained as the population weighted average of the corresponding LSOAs, using the 2019 mid-year population counts.
4.1.4. Commuter flow data
As one of its data inputs, the Epimap model [35] uses commuting flow data from the 2011 Census [49]. After preprocessing, these data are used to create a flux matrix F that determines how transmission events occur within and between lower tier local authoritys (LTLAs); see [35] for full details. In Section 4.5.4 we will discuss the relationship between flux matrix F and estimates of .
4.2. Estimating and adjusting for ascertainment bias in Pillar 1+2 data
We now summarise our debiasing model, which combines targeted surveillance data with randomized surveillance data to obtain local estimates of prevalence. A useful way of motivating the debiasing model is to compare the properties of the randomised and targeted surveillance datasets. REACT provides unbiased information on prevalence, though with limited sample size and publicly accessible only at a coarse spatiotemporal scale. In contrast, Pillar 1+2 has a large sample size providing strong and biased information about fine-scale spatiotemporal variation in prevalence, but which can be useful for prevalence estimation when the bias is smooth and estimable. In other words, our model is aimed at using Pillar 1+2 to extend REACT to a finer spatiotemporal scale. Full details can be found in [45] along with accompanying R code.7
4.2.1. Debiasing model
The REACT data provide accurate but relatively imprecise estimates of prevalence at the PHE region level (i.e. coarse scale). Note that REACT total test counts U tend to be much smaller than Pillar 1+2 test counts N, with U/N of order 10−2. The REACT data likelihood for the PCR-positive prevalence proportion π is
| (1) |
based on observing u positive tests out of a total of U randomly allocated in a population of known size M; our inference under (1) and (2) is based on a latent integer number of infected πM (see [45] for details). Note that, for simplicity, we are ignoring the stratified sampling design in likelihood (1). We also assume here for simplicity that the PCR-tests have perfect specificity and sensitivity; it is straightforward to incorporate known type I and II error rates within the test debiasing framework (see [45] for further details).
In contrast, test positivity rates in Pillar 1+2 data are strongly biased upwards relative to the population prevalence proportion, as the testing is directed at the higher risk population (e.g. symptomatics, frontline workers). We show how careful modelling of the ascertainment process allows us to estimate prevalence accurately, and with good precision, even at a fine-scale level such as LTLA.
We introduce the following causal model for the observation of n of N positive targeted (e.g. Pillar 1+2) tests:
| (2) |
where δ and ν parameterise (on log odds scale) the binomial success probabilities ℙ(Tested | Infected) and ℙ(Tested | Not Infected):
| (3) |
| (4) |
By causal, we mean that we explicitly take into account the way the Pillar 1+2 data was generated by inferring, and conditioning in (2), on the probability of individuals in the population being tested. We provide a detailed description of the model in [45]. The parameter requiring most careful treatment is δ, i.e. the log odds ratio of being tested in the infected versus the non-infected subpopulations.
Our default approach for the other parameter, ν, is to use the plug-in estimator in likelihood (2), because it allows fast and tractable computation, and is precise with little bias when prevalence is low. While this allows for efficient computation, heuristically using the sub-optimal plug-in estimator can lead to model misspecification because of its bias when prevalence is high, a point we return to in Section 4.2.3.
4.2.2. Structurally robust estimation of ascertainment bias δ
In Figure 1(a), the joint posterior distribution (without cutting any information flow) is:
| (5) |
and we use the plug-in estimator for computational convenience, as introduced in Section 4.2.1. This provides effective inference when the model space contains the true data generating mechanism and is not too biased. However, if the Pillar 1+2 likelihood (2) is misspecified for any reason, then inference on π, and hence on δ, can be adversely affected. In the current context, the consequences of misspecification are particularly severe because, conditional on δ, the relative sample sizes lead to the Pillar 1+2 likelihood (2) typically containing far more information on π than the REACT likelihood (1).
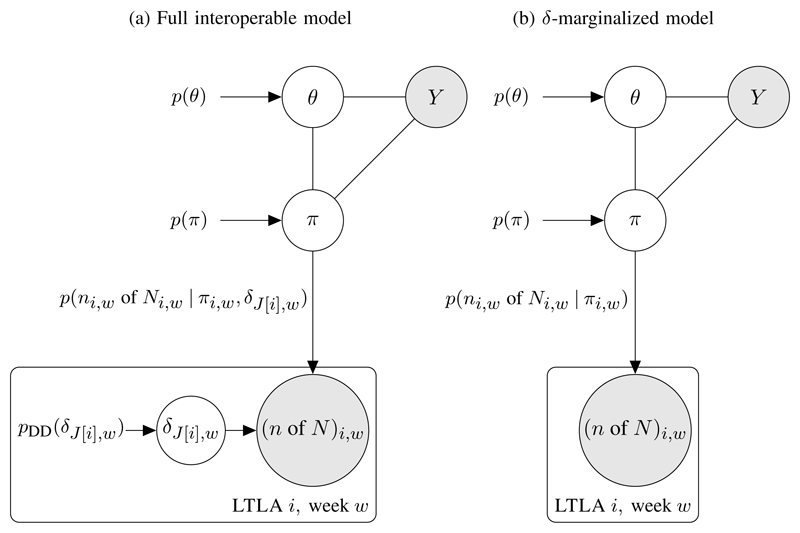
Fig 1. Models for debiasing.
(a) Cut model where the dashed line represents cutting feedback from Pillar 1+2 to π. (b) Data-dependent prior pDD(δ) has been created from cut posterior for δ from stage (a), and now only Pillar 1+2 data are used to infer π at the local (LTLA) level.
With this in mind, we use a cut posterior distribution, as described in [9]:
| (6) |
again with plug-in estimator . where the first distribution on the RHS of (6) is no longer conditioning on the n of N from Pillar 1+2. Switching from model (5) to (6) “cuts feedback” from Pillar 1+2 to π in inference on (π, δ). Figure 2(a-b) compares the joint full posterior (5) with the joint cut posterior (6) for Pillar 1+2 and REACT data gathered in London during the week commencing (W/C) 14th Jan 2021. In this week the Pillar 1+2 data were n of N = 60,749 of 326,986 and the REACT data were u of U = 101 of 3,778, i.e. the Pillar 1+2 data have 87 times as many tests as REACT that week.
The joint posteriors in Figure 2(a-b) have clearly quite different support. The mean (95% CI) for δ under the full posterior is 3.5 (3.2-3.9) whilst under the cut posterior it is 2.4 (2.2-2.7). Which model, full or cut, is estimating δ more accurately? Note that in the cut posterior (6) the marginal distribution of the prevalence proportion π depends only on the REACT data,
| (7) |
and that the maximum likelihood estimator for π based on model ℙ(u of U | π) at (1) is approximately unbiased, since REACT is a designed, randomised study. We say that the estimator is approximately unbiased as, for simplicity, we do not account for the stratified sampling design nor for the non-response (> 75%), which we assume is non-informative. Thus, under a weakly informative prior pflat(π), the cut-posterior π-marginal mean (95% CI) of 2.7 (2.2-3.2) estimates π reasonably accurately. However, the full-posterior π-marginal mean of 1.4 (1.1-1.6) is quite different, suggesting that the Pillar 1+2 causal testing model at (2) is misspecified and, having a relatively large amount of data, swamps the accurate information in the REACT data.
4.2.3. Exploring model misspecification
We initially posit two explanations for the model misspecification identified in Figure 2(a-b):
-
(E1)
Violation of the Binomial distributional assumption in (2) through over-dispersion caused by systematic variation of δ, ν and π across subpopulations within an LTLA having different COVID-19 beliefs and behaviors;
-
(E2)
Bias in the plug-in estimator introduced in Section 4.2.1.
Upon further investigation, we conjecture that explanation (E2) is the main source of misspecification because, while it allows efficient computation, using the sub-optimal plug-in estimator can lead to model misspecification because of its bias when prevalence is high. To illustrate this, we note that a better plug-in approach would instead use the unbiased MLE estimator However, estimator is more computationally expensive as it requires the unknown prevalence π as an input (and this is why we do not apply as our default).8 To target we implement Algorithm 1, which estimates ν according to its π-conditioned maximum likelihood estimator alternately with estimating π. For the current example, this leads to the estimate = -3.460 which is to be contrasted with the biased, computationally convenient estimate = -3.486.
The joint (π, δ) full posterior downstream of this improved estimator is shown in Figure 2(c), and has π-marginal mean (95% CI) of 2.6 (2.3-2.9), which is now compatible with the cut-posterior's estimate of 2.7 (2.2-3.2) shown in in Figure 2(b). It is interesting to compare the width of these intervals, noting that the posterior distribution in Figure 2(c) is relatively concentrated compared to the one in Figure 2(b). This reflects the extra information on π provided by the Pillar 1+2 data in the full model, relative to the cut model in which information flow from Pillar 1+2 to π is blocked, as illustrated in Figure 1(a).
Algorithm 1. Fixed point algorithm targeting .
Input: REACT u of U, Pillar 1+2 n of N, and population size M
repeat
where p(π | ⋅) here is (5) marginalized wrt δ
until convergence
Output:
It is a matter of taste and expediency whether one chooses to fit the full joint model, or to use the unbiased plug-in , or to use the biased plug-in repaired by cut modelling. In our case, the heuristic estimator applied with a cut model is far more computationally efficient, and we are able to validate the overall method to be unbiased. It is an interesting philosophical debate, deliberately to choose a misspecified module, which is then repaired using cut modelling techniques, to make up the overall model. Our choice reflected our priority on computationally tractability.
Note that the bias of relative to tends to be larger for high prevalence and will have a greater impact when the Pillar 1+2 sample size is large (both of which apply to the illustrative example of London w/c 14th Jan 2021, where prevalence is estimated at 2.7% and N = 326,986). We further compare and contrast inference under the full and cut posteriors after having applied them to estimate local prevalence in Section 4.2.4.
4.2.4. Inferring cross-sectional local prevalence
We specify a data-dependent prior pDD(δJ,w) for each week w in each region J, based on the posterior distribution at (6). We begin by approximating the marginal posterior distribution for δJ,w with a moment-matched Gaussian based on the cut posterior:
| (8) |
| (9) |
For example, in the case of the marginal density at the top of Figure 2(b), we specify pDD(δJ,w) by setting and for London W/C 14th Jan 2021. Each of the three inferential approaches shown column-wise in Figure 2 will yield its own data-dependent prior in the form of (8) which approximates the δ-marginal posteriors at the top of panels Figure 2(a-c), and which then feeds forward into the cross-sectional debiased % prevalence estimates on the vertical axes of Figure 2(d-f) respectively.
While this approach provides a prior for weeks at which both Pillar 1+2 and REACT data are available (since we are able to estimate δ), we also wish to interpolate and/or extrapolate information on δ to weeks at which REACT data are unavailable (e.g. between sampling rounds). We achieve this by introducing a smoothing component into a product-of-experts prior ([50]; details in Appendix A), thereby allowing us to specify independent priors pDD(δJ,w) of the form (8) for all weeks, including those without REACT data.
Having specified a prior at the coarse-scale regions J, we proceed to perform full Bayesian inference at a fine-scale LTLA i using the prior from its corresponding region, pDD(δJ[i],w). We plot cross-sectional % prevalence posterior medians (with 95% posterior CIs) on the vertical axes of Figure 2(d-f), with each point corresponding to the estimated % prevalence for one LTLA in London for W/C 14th Jan 2021. Observe in Figure 2(d-f) that the horizontal REACT CIs are relatively broad, compared to the vertical debiased Pillar 1+2 CIs, exemplifying the relatively large amount of information in the Pillar 1+2 data if δ can be inferred.
The results in Figure 2(d-f) are also informative for our discussion of inference under the various models, because we are able to validate against “gold-standard” LTLA-level randomised surveillance data aggregated across round 8 of the REACT study (6th-22nd Jan 2021). On the horizontal axis, we plot the REACT unbiased prevalence estimates (with 95% exact binomial CIs). Compared to the accurate REACT estimates, the debiased prevalence estimates based upon the full posterior in Figure 2(d) are biased downwards – the estimated bias across the LTLAs plotted is % (SE = %). In contrast, the debiased prevalence estimates based on the cut posterior in Figure 2(e) appear to be accurate, having estimated bias of -0.01% (SE = 0.11%). The full posterior estimates based on improved plug-in estimator in Figure 2(f) also appear accurate, having estimated bias of % (SE = %).
4.2.5. General interoperability between models
The graph in Figure 3(a) relates the debiasing model (in the i,w plate) to another arbitrary model with parameters (π, θ) and data/covariates Y (with Y not containing Pillar 1+2). One approach to fitting Figure 3(a)’s model would be to perform full Bayesian inference directly, i.e. sampling from (θ, π, δ). However, as will be illustrated with the SIR model in Section 4.3, we can reduce the computational complexity by first marginalising with respect to δJ[i],w yielding the marginal likelihood:
| (10) |
which is an unnormalized function of πJ,w encapsulating all information on πJ,w that results from observing ni,w of Ni,w positive Pillar 1+2 tests. As illustrated in Figure 3(b), we then need sample only (θ, π) in the δ-marginalised interoperable model.
Fig 3. Interoperable interface of debiasing output with a model parameterised by θ and with other data Y.
(a) Full interoperable model. (b) Collapsed representation, in which the full model has been marginalized wrt δ. We use π to denote the entire spatiotemporal collection of prevalence proportions π1:I,1:W.
While the marginal likelihood p(ni,w of Ni,w | πi,w) at (10) can easily be evaluated pointwise, it does not have a closed parametric form. We can further simplify inference at the interface between models by approximating (up to a multiplicative constant) the marginal likelihood with a parametric distribution. A Gaussian moment-matched approximation on log odds scale (Figure 3(b)),
| (11) |
is a natural choice here because it provides an empirically good fit and also integrates conveniently with methods and software for hierarchical generalised linear models with logit link function, as we shall see in Section 4.4. This approach of summarising a module with a moment-matched Gaussian distribution for use as an approximate likelihood term in subsequent modules has been previously widely used in simpler contexts, including evidence syntheses [51] and more general hierarchical models [52, 38].
Depending on the context, either one of (10) or (11) may be preferred. Using the exact marginal likelihood at (10) avoids making a Gaussian approximation, but (10) can be computationally unwieldy as it is a mass function on integer prevalence πM. The Gaussian approximated marginal likelihood at (11) is often more computationally convenient to integrate with other models. We use (10) in Section 4.3 and we use (11) in Sections 4.4 and 4.5.
4.3. Interoperability with an SIR model
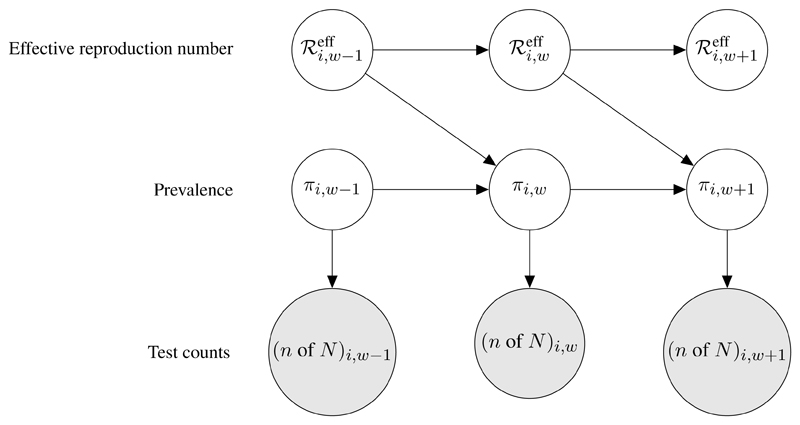
The marginal likelihood p(ni,w of Ni,w | πi,w) from (10) can be used to link the Pillar 1+2 data directly to latent prevalence nodes in a graphical model. As a concrete example, we implemented a full Bayesian version of the standard stochastic SIR model [53, 45, 54]. Figure 4 illustrates the SIR model DAG, relating prevalence proportion πi,w, effective reproduction number , and test data (n of N)i w ≡ ni,w of Ni,w. Note that Figure 4 is a special case of Figure 3(b) with data node Y empty and . In Figure 4 each πi,w is linked to its corresponding test data (n of N)i,w via the marginal likelihood p(ni,w of Ni,w | πi,w). Consecutive πi,w and nodes are related by a discrete time Markov chain, in which the stochastic change in the number infected at week w, relative to week w−1, is modelled as the difference between a Poisson-distributed number of new infections and a Binomial-distributed number of new recoveries:
| (12) |
| (13) |
| (14) |
γ is the (pre-specified) probability of recovery from one week to the next; and the are modelled sequentially by an AR1 process. We sample from the full Bayesian posterior for this SIR model using MCMC methods (see [45] for details).
Fig 4.
Directed acyclic graph showing interoperability of the debiasing model output with a stochastic SIR epidemic model. Latent nodes for LTLA i’s prevalence and effective reproduction number in week w, πi,w and respectively, are shown, along with weekly Pillar 1+2 test counts, integrated via the debiasing model-outputted marginal likelihood at (10). Details of the discrete time Markov chains on the latent nodes are given in equations (12)-(14).
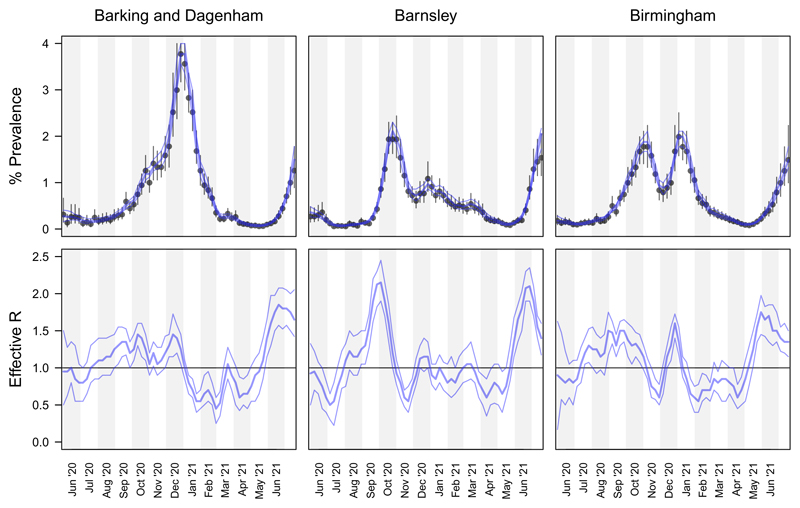
Figure 5 compares, for three example LTLAs, the cross-sectional posteriors for π with the SIR-model MCMC-sampled longitudinal posteriors for π and ℛeff. The width of the SIR posterior 95% credible intervals are often much narrower than the cross-sectional posterior CI width, illustrating the benefit of sharing prevalence information across time points within the framework of an epidemiological model. Fitting the full Bayesian SIR model provides posterior credible intervals on the effective reproduction number ℛeff (Figure 5 bottom panels), which is an important measure of spatiotemporally local rates of transmission. In Section 4.5, we compare these estimates of local ℛeff (based on Pillar 1+2 from a single LTLA only) with spatially smoothed estimates of local ℛeff from Epimap [35].
Fig 5.
SIR longitudinal posterior (% prevalence and effective reproduction number) compared with cross-sectional posterior for % prevalence. Top panels: cross-sectional % prevalence posterior median and 95% CIs (black points and whiskers), and SIR modelled % prevalence posterior median and 95% CIs (blue curves). Bottom panels: SIR modelled longitudinal posterior median and 95% CIs.
4.4. Interoperability between debiasing and space-time equality analysis
There is extensive evidence to suggest that ethnically diverse and deprived communities have been differentially affected by the COVID-19 pandemic in the UK [55, 56, 57]. It is thus very important to be able to relate unbiased prevalence estimates such as those introduced in Section 4.2 to area level covariates, in order to assess associations between the spread of the virus and particular population characteristics. Given the infectious nature of the disease, residual heterogeneity is likely to have a spatio-temporal structure, which needs to be accounted for in the model. Failing to account for autocorrelation may result in narrower credible intervals for parameters of interest and may inflate covariates effects [58]. One option to incorporate sources of spatial autocorrelation in estimates of disease surveillance metrics such as prevalence, would be to run the debiasing model presented in Section 4.2.4 augmented by a spatio-temporal prior structure both on the πi,w and on the ascertainment bias δi, while simultaneously adding the population characteristics as covariates to assess their impact on the spread of the disease. However, such a strategy would entail a prohibitive computational cost, not only due to the large number of latent variables typically involved in the specification of even a relatively simple spatio-temporal model, but also because of implementing a cut model in such a high-dimensional setting. As an alternative, in this section we illustrate two interoperable models which differ in how they treat the uncertainty of prevalence estimates.
We focus on ethnic composition and socio-economic deprivation as covariates of interest, to assess the impact of socio-economic factors on the evolution of the pandemic. As our aim is to assess a link between prevalence proportion and these two factors, first we specify a probability distribution for the outcome, πi,w as:
| (15) |
where ηi,w is a linear predictor containing the area level variables of interest as well as space and time structured random effects defined at (18) below, while σ2 is the variance of the error term.
Since πi,w is unknown, it is not possible to fit this model directly. A first interoperable approach, which we call the naive model, simply consists of plugging-in the debiased prevalence proportion point estimates (e.g. median) outputted by the debiasing model of Section 4.2:
| (16) |
This model considers the prevalence estimates as fixed quantities, neglecting their uncertainty.
A second interoperable approach accounts for the posterior uncertainty from the debiased prevalence model via (11), similarly to [59, 60]. In practice, for the i-th LTLA and w-th week this heteroscedastic model reformulates (16) to include the variance component
| (17) |
In both models, we use the following specification for the linear predictor ηi,w, in order to assess the effect of the area level variables of interest (proportion of BAME and IMD score) on the prevalence estimates:
| (18) |
where β0 is the global intercept {β1, β2} quantify the effects of the covariates of interest, λi denotes the area specific random effect accounting for spatial autocorrelation, and ϵw represents the temporal random effect. Details on the model specification can be found in Appendix B.
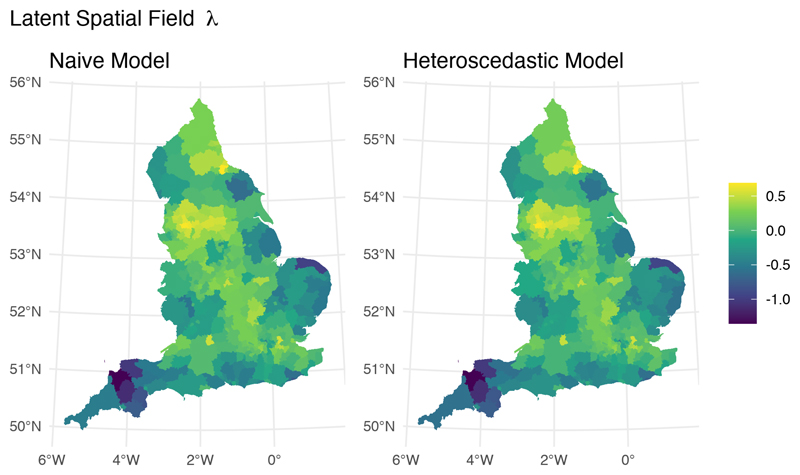
Output from the two interoperable modelling approaches presented above is used to examine the effects of socio-economic factors (i.e. ethnic diversity and socio-economic deprivation) on COVID-19 unbiased prevalence.9 Additionally, the models allow us to characterise the baseline spatial distribution of prevalence across LTLAs in England, after accounting for their socio-economic and ethnic profiles. This enables us, for example, to identify LTLAs that have been particularly badly affected by COVID-19 relative to their level of deprivation and size of BAME population and as a result may require further consideration by policy-makers.
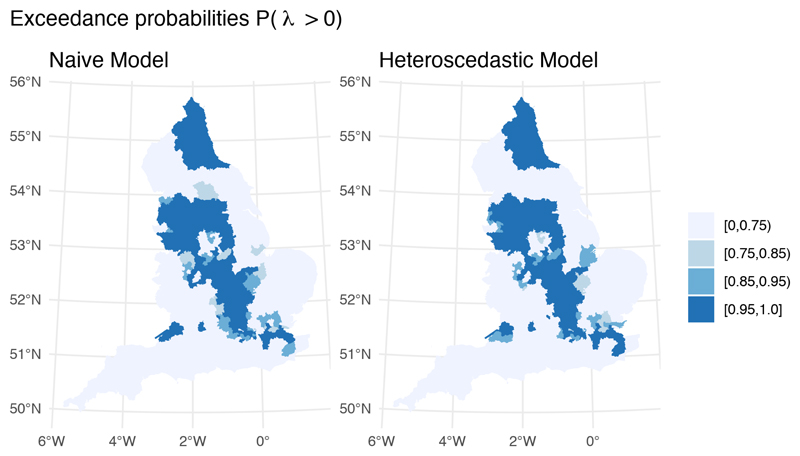
While both models are examples of interoperability, they differ in how they handle uncertainty in the debiased prevalence proportion outcome measure; the naive model treats the prevalence estimates as fixed quantities, while the heteroscedastic model propagates their uncertainty through an additional variance term. This difference is predominantly reflected in the uncertainty of parameter estimates. Although the posterior median point estimates for the effects of IMD and BAME (Table 1) and the underlying spatial fields (Figure 6) are largely indistinguishable, the precision for the global error term (i.e., 1/σ2) is almost twice as large in the heteroscedastic model. Precision for the spatial component is also larger in the heteroscedastic model compared to the naive model, suggesting that the global error and the spatial random effect in the naive model were capturing part of the spatial variability present in the prevalence proportion estimates. It is also interesting to note that the exceedance probability map corresponding to the heteroscedastic model is sharper, showing that the ranking of areas deviating from the national average is influenced by the inclusion of uncertainty on the debiased prevalence estimates (Figure 7).
Table 1.
Posterior mean and corresponding 95% Credible Interval for the parameter estimates of the Naive (left) and Heteroscedastic (right) space-time equality analyses. Estimates for the fixed effect coefficients are on the Odds Ratio scale. The precision of the time and spatial random effects, and τ are defined in Appendix B.
| Median | 95% CI | Median | 95% CI | |
|---|---|---|---|---|
| BAME effect (β1) | 1.22 | (1.17, 1.28) | 1.20 | (1.15, 1.25) |
| IMD effect (β2) | 1.11 | (1.07, 1.16) | 1.11 | (1.07, 1.15) |
| Precision of the Gaussian residuals () | 2.67 | (2.59, 2.73) | 4.05 | (3.95, 4.15) |
| Precision of time random effect () | 30.41 | (13.72, 48.51) | 31.37 | (19.38, 52.29) |
| Precision of spatial random effect (τ) | 10.89 | (9.03, 13.28) | 12.26 | (10.00, 14.56) |
Fig 6. Posterior median of the spatial random effect λ.
Fig 7. Posterior probability of having a positive spatial residual.
4.5. Interoperability between the debiasing and Epimap models
Epimap is a hierarchical Bayesian method for estimating the local instantaneous reproduction number that models both temporal and spatial dependence in transmission rates [35]. Epimap incorporates information on population flows to model transmission between local regions, and performs spatiotemporal smoothing on the . The data inputted to Epimap are daily positive Pillar 1+2 test counts at LTLA level, the ni,t in our notation.
4.5.1. Epimap model overview
The observation model for ni,t is an overdispersed negative binomial model with mean Ei,t given by a convolution of a testing delay distribution with the past incidences Xi,1:t [12], i.e.
| (19) |
| (20) |
where ϕi ~ 𝒩+(0, 5).
LTLA i’s incidence Xi,t is probabilistically modelled conditional on past incidences X1:n,1:t–1 via local and cross-coupled infection loads, denoted Zi,t and respectively. Specifically, the local infection load Zi,t is given by a convolution of Ws with the past incidences Xi,1:t, where the generation distribution Ws is the probability that a given transmission event occurs s days after the primary infection. The local infection loads contribute transmission events not only locally but also to other regions, giving the cross-coupled infection load , with inter-regional transmission defined via a flux matrix F, built on the commuter flow data introduced in Section 4.1.4, in which Fji denotes the probability that a primary case based in area j infects a secondary case based in area i. In summary, the local and cross-coupled infection loads are defined as
| (21) |
The incidence Xi,t follows an overdispersed negative binomial distribution with mean given by the product of the reproduction number with the cross-coupled infection load :
| (22) |
Note that the are our primary inferential target, and are estimated via the posterior distribution of the ratio In Figures 8 and 9 below we present the posterior distribution of the weekly averaged ratio, A final aspect of the Epimap model is the smoothing on , whereby information is shared across time and space through specification of various Gaussian processes on log (see [35] for details).
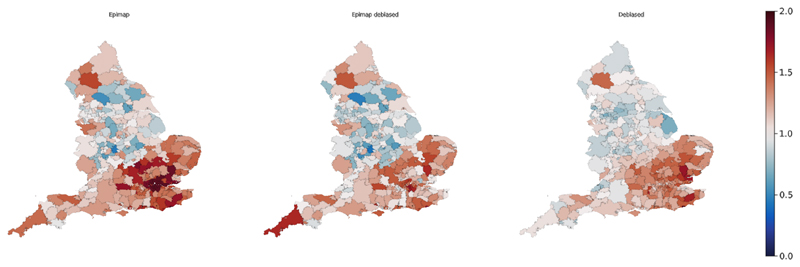
Fig 8. Maps of estimated for three different models across all LTLAs in England W/C 4th December 2020.
(a) Epimap (ℳE). (b) Epimap debiased interoperable model (ℳED). (c) Debiased SIR model (ℳD).
Fig 9.
Longitudinal trajectories superimposed above corresponding Pillar 1+2 test data. Top: posterior median and 95% CIs of for three models (see upper legend). Bottom: weekly test counts, positive ni,w and total Ni,w, as well as test positivity ni,w/Ni,w (see lower legend). Vertical dashed lines in panels (b-c) indicate instances of model discordance in estimates, preceding or coinciding with local surges in testing capacity.
4.5.2. Probabilistic interface between Epimap ℳE and debiasing model ℳD
There are three immediate and important differences between Epimap and the debiasing model that require attention at the model interface. First, Epimap's measure of infection burden is incidence (i.e. the number of new infections contracted in a time interval), whilst the debiasing model is based on point prevalence, as we defined in Section 3.1. Second, Epimap is at daily frequency, indexed t, while the debiasing model is at weekly frequency, indexed w. Third, some LTLAs were recently merged to create a more coarse-scale local geography, and the debiased model works with the newer coarser LTLA geography, while Epimap still works with the older finer-scale LTLA geography.
To map from incidence to prevalence, we draw from the existing COVID-19 literature on the probability of testing PCR positive when swabbed s days post infection [62]; we denote this as
| (23) |
To address the daily-to-weekly mapping, we average the daily prevalence proportion (mapped from daily incidence) across the days of each week. To address the models' differences in LTLA geography, we are able straightforwardly to preserve the geographies of both models by deterministically aggregating Epimap's latent incidences as part of the mapping between models described below in (24) (details omitted for simplicity), thereby creating a seamless interface between models. In summary, the mapping from daily incidence Xi,t to weekly prevalence proportion πi,w is:
| (24) |
with Mi denoting local population size. Finally, the latent weekly prevalence proportions πi,w in the interoperable Epimap model are related to the debiasing model outputs via the approximate π-marginal likelihood of (11) (see also Figure 3(b)):
| (25) |
where t[w] denotes the final day in week w.
In summary, the interface between Epimap and debiasing models is created by removing Epimap's observation model of (19) and (20), and replacing it with the debiasing-model outputted marginal likelihood defined at (24) and (25).
4.5.3. Comparing and contrasting estimated across models
We estimated under each of the three models: Epimap (ℳE) described in Section 4.5.1; the debiased SIR model (ℳD) output as described in Section 4.3; and the interoperable combination of Epimap and debiased models (ℳED) described in Section 4.5.2. Movie 1 in Supplementary Information provides a global perspective on the results, showing the longitudinal changes via maps evolving through time. Figure 8 shows one snapshot of this movie, for all LTLAs in England W/C 4th December 2020. The general theme is one of consistency in estimates across models, but there are points in space and time at which results differ. We will discuss these differences, demonstrating that they can help us to characterise and understand model performance.
4.5.4. Interpreting model outputs via data synchronisation
We turn first to the maps in Figure 8, visually comparing and contrasting the three models across all LTLAs in W/C 4th December 2020. One interesting feature here is the presence of a few LTLAs with low in both ℳE and ℳED, but with relatively high in ℳD. The two most prominent, coloured blue in Figure 8(a-b), are (North Warwickshire, Craven), which have estimated to be (0.37, 0.47) by ℳE and (0.33, 0.42) by ℳED, but estimated to be higher at (0.80, 0.90) by ℳD. When we compare two models that differ in both data inputs and in probabilistic structure (as do ℳE and ℳD) any difference in results cannot immediately be attributed solely to either data or model structure. However, by constraining the two models to have the same data inputs – as we have here by using the prevalence outputs of ℳD as inputs to ℳED – we can potentially learn more. Observing that ℳED agrees with its “model twin” ℳE, but disagrees with its “data twin” ℳD, leads us to conclude that differing results in (North Warwickshire, Craven) between ℳD and ℳE arise because of differences in model structure rather than because of differences in data inputs.
We examine the hypothesis that the differences in (North Warwickshire, Craven) between ℳE and ℳD are attributable to Epimap's cross-coupled infection load, in (21), which allows transmission across regional boundaries; in contrast, the debiased SIR model has only within-LTLA transmission. Note from (22) that Epimap's expected number of new infections is represented as the product so that low estimates of will arise when the cross-coupled infection load is large relative to the latent incidence Xi,t. For 4th December 2020 in (North Warwickshire, Craven) ℳED outputs a posterior median for Xi,t of (42.7, 24.8) and for of (114.5, 81.1), consistent with the low estimates of (0.33, 0.42). We can further decompose the cross-coupled infection load into infection load Zi,t originating from within LTLA i (27.5, 31.1), and Z−i,t originating from other LTLAs (86.7, 49.9). See Figure 10 in Appendix C for a map of the proportion of infection load arising external to each LTLA. It is clear that for (North Warwickshire, Craven) the majority of the infection load in the ℳE (and ℳED) models is external, and that these are among only a handful of LTLAs having external load at > 50% of the infection burden. Through data synchronisation, theorizing on salient differences between models, and examining confirmatory diagnostic plots, we have increased our understanding of the operational differences between the ℳE and ℳD models.
4.5.5. Illustrating synergy between models
The top panels in Figure 9 present longitudinal curves for three selected LTLAs for each of the three models; the bottom panels display the corresponding Pillar 1+2 weekly test counts and positivity rate. First note that the plot for Birmingham in Figure 9(a) exhibits reassuring similarity between models; indeed this is what we observe for the majority of LTLAs that are not shown in Figure 9. But the LTLAs in Figure 9(b-c) display some interesting and contrasting behaviour between models.
The vertical dashed line in each panel 9(b-c) coincides with, or immediately precedes, a surge in community testing capacity - see the sharp increase in total test counts in the bottom panels at or after each dashed line. Figure 9(b) includes a mass testing pilot study in Liverpool beginning 6th November 2020 which led test positivity to drop sharply from 11.9% in W/C 29th October 2020 to 3.6% the following week. Such an abrupt and localized change in testing ascertainment is at odds with the spatiotemporally smooth parameterization of the debiasing model, leading to artefactual deflation of in ℳD in W/C 5th November (marked with a dashed line). The deflation is not however evident in ℳE or ℳED.
Turning to Figure 9(c) we note that, in mid-December 2020, parts of Essex and London, including the illustrated example of Havering, were moved into Tier 3 - the very high alert level – and earmarked for extra community testing. This led to a large spike in testing capacity and uptake, but test positivity rates remained relatively constant in the two weeks following the dashed line (in contrast to the mass testing pilot in Liverpool a month earlier: see bottom panels of Figure 9(b-c)). This caused artefactual inflation of in ℳE, since positive cases surged in line with testing capacity, and ℳE takes as input only the positive cases ni,t (but not the total tests Ni,t). The other two models, ℳED and ℳD, are not obviously affected by the December 2020 testing surge in Figure 9(c).
The steady performance of the interoperable model ℳED across Figure 9 points to a desirable synergistic form of structural robustness – we aspire to synthesise models in such a way that they support one another, with the strengths of one model stabilising inference if and when the other model shows any weakness with respect to the data generating mechanism. The suboptimal estimation observed in 9(b-c) occurred when there were sudden changes in the ascertainment mechanism; it is reassuring that both adversely affected models (ℳD in Figure 9(b) and ℳE in 9(c)) apparently return to agreement with the other models just one week after these extreme shifts in ascertainment bias.
5. Discussion
Based on our experience, we believe that striving for interoperability across all facets of the delivery of statistical projects will provide:
Agility: the ability to rapidly interlink and recycle statistical modelling outputs across analyses, with components transferable across health security problems;
Robustness: the structural assembly of modules that can be tested independently and connected in such a way as to mitigate any widespread impact of model misspecification;
Sustainability: a shareable, high-quality, reusable, open-source analytic code base of modules that grows over time;
Transferability: a way to facilitate co-ownership of projects with public health and health policy teams, allowing rapid impact from academia and industry to be delivered against relevant, time-sensitive problems;
Preparedness: solutions built for a specific health emergency, such as the COVID-19 pandemic, can be re-purposed to meet future public health challenges. In particular, the necessary generic structural links between the data engineering architecture and the analytic and modelling side will have already been built.
Many challenges lie ahead on the path towards an effective, interoperable, and comprehensive disease surveillance system. From a statistical point of view, it is most relevant to focus our attention on issues that are generic and likely to recur when addressing a range of questions. For brevity we will only mention three particularly challenging ones.
A major hurdle that interoperability will face is the need to integrate evidence from data collected at different time steps and spatial scales. For example, the time granularity of the randomised survey data used in our debiased prevalence model is a week, yet most epidemic models have been built on the basis of daily case numbers, thus necessitating an additional time-alignment interface. Similarly, it will be common to have to integrate different geographies into a single model, constrained by the data sources. Misaligned geographies is a recurrent statistical issue that has been much discussed in environmental sciences [63], and for which pragmatic but robust solutions need to be investigated.
A second challenge is situations when moment-matched Gaussian distributions, as used here, do not provide adequate approximations; alternatives include particle-based approaches, in which posterior samples from a module are used as a proposal within an MCMC scheme [38, 5] or for importance sampling [64] or within a sequential Monte Carlo scheme [65].
A final challenging issue that we have already encountered, and dealt with in Section 4.2.2 by using a cut posterior, is how best to balance or weight different sources of evidence, to take into account prior knowledge; see [66] for a discussion of evidence weighting from an epidemiological perspective. Rather than completely preventing feedback, as per a cut posterior, it may be desirable to only partially down-weight, as proposed by [10]. For example, in the case of diagnostic tests, weights might take into consideration their modus operandi and context of use.
Although the analyses presented here were motivated by the specific example of the COVID-19 pandemic, the overarching principle of interoperability is pertinent in a variety of contexts with complex modelling requirements in a dynamic environment, such as climate change or natural disaster management.
Supplementary Material
Funding
MB acknowledges partial support from the MRC Centre for Environment and Health, which is currently funded by the Medical Research Council (MR/S019669/1). RJBG was funded by the UKRI Medical Research Council (MRC) [programme code MC_UU_00002/2] and supported by the NIHR Cambridge Biomedical Research Centre [BRC-1215-20014]. BCLL was supported by the UK Engineering and Physical Sciences Research Council through the Bayes4Health programme [Grant number EP/R018561/1] and gratefully acknowledges funding from Jesus College, Oxford. GN and CH acknowledge support from the Medical Research Council Programme Leaders award MC_UP_A390_1107. CH acknowledges support from The Alan Turing Institute, Health Data Research, U.K., and the U.K. Engineering and Physical Sciences Research Council through the Bayes4Health programme grant. SR is supported by MRC programme grant MC_UU_00002/10; The Alan Turing Institute grant: TU/B/000092; EPSRC Bayes4Health programme grant: EP/R018561/1. HG and TF acknowledge partial support from Huawei Research UK. Infrastructure support for the Department of Epidemiology and Biostatistics is also provided by the NIHR Imperial BRC. Authors in The Alan Turing Institute and Royal Statistical Society Statistical Modelling and Machine Learning Laboratory gratefully acknowledge funding from the Joint Biosecurity Centre, a part of NHS Test and Trace within the Department for Health and Social Care. This work was funded by The Department for Health and Social Care with in-kind support from The Alan Turing Institute and The Royal Statistical Society. The computational aspects of this research were supported by the Wellcome Trust Core Award Grant Number 203141/Z/16/Z and the NIHR Oxford BRC. The views expressed are those of the authors and not necessarily those of the National Health Service, NIHR, Department of Health, Joint Biosecurity Centre, or PHE.
Footnotes
We stress at the outset that when we refer simply to “interoperability”, we always mean statistical interoperability. The concept of interoperability referred to in engineering or for computer hardware is not the subject of this paper.
We distinguish structural robustness from the more general statistical notion of robustness, namely good performance across of wide class of possible true data generating mechanisms.
We use the term composability by analogy with its definition in system design as a principle that deals with the inter-relationships of components.
The process of specifying and estimating models, making it practicable to explore a range of models.
The name Turing given to this software package has nothing to do with The Alan Turing Institute.
The most principled approach would be jointly to infer (π, δ, ν), though again at a greater computational cost (we do not fit the joint model here).
For a detailed analysis of the effect of time varying association between deprivation, ethnicity and SARS-CoV-2 infections in England, please see [61].
Contributor Information
George Nicholson, Email: george.nicholson@stats.ox.ac.uk.
Sylvia Richardson, Email: sylvia.richardson@mrc-bsu.cam.ac.uk.
References
- [1].Covid-19 Task Force. URL https://rss.org.uk/policy-campaigns/policy-groups/covid-19-task-force/
- [2].Davison AC. Statistical Models. Cambridge University Press; Cambridge: 2003. (Cambridge Series in Statistical and Probabilistic Mathematics). URL https://www.cambridge.org/core/books/statistical-models/8EC19F80551F52D4C58FAA2022048FC7. [Google Scholar]
- [3].Ades AE, Sutton AJ. Multiparameter evidence synthesis in epidemiology and medical decision-making: current approaches. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2006;169:5–35. doi: 10.1111/j.1467-985X.2005.00377.x. [DOI] [Google Scholar]
- [4].Green PJ, Hjort NL, Richardson S. Highly Structured Stochastic Systems. Oxford University Press; Oxford, New York: 2003. (Oxford Statistical Science Series). [Google Scholar]
- [5].Goudie RJB, Presanis AM, Lunn D, Angelis DD, Wernisch L. Bayesian Analysis. Vol. 14. International Society for Bayesian Analysis; 2019. Joining and Spliting Models with Markov Melding; pp. 81–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Lunn D, Best N, Spiegelhalter D, Graham G, Neuenschwander B. Combining MCMC with 'sequential' PKPD modelling. Journal of Pharmacokinetics and Pharmacodynamics. 2009;36:19–38. doi: 10.1007/s10928-008-9109-1. [DOI] [PubMed] [Google Scholar]
- [7].Bayarri MJ, Berger JO, Liu F. Bayesian Analysis. Vol. 4. International Society for Bayesian Analysis; 2009. Modularization in Bayesian analysis, with emphasis on analysis of computer models; pp. 119–150. [DOI] [Google Scholar]
- [8].Plummer M. Cuts in Bayesian graphical models. Statistics and Computing. 2015;25:37–43. doi: 10.1007/s11222-014-9503-z. [DOI] [Google Scholar]
- [9].Jacob PE, Murray LM, Holmes CC, Robert CP. Better together? Statistical learning in models made of modules. arXiv: 1708.08719 [stat] 2017:ArXiv: 1708.08719. URL http://arxiv.org/abs/1708.08719. [Google Scholar]
- [10].Carmona CU, Nicholls GK. Semi-Modular Inference: enhanced learning in multi-modular models by tempering the influence of components. arXiv:2003.06804 [math, stat] 2020:ArXiv: 2003.06804. URL http://arxiv.org/abs/2003.06804. [Google Scholar]
- [11].Anderson R, et al. Reproduction number (R) and growth rate (r) of the COVID-19 epidemic in the UK: methods of estimation, data sources, causes of heterogeneity, and use as a guide in policy formulation. Tech Rep. London, UK: Royal Society; 2020. [Google Scholar]
- [12].Flaxman S, et al. Estimating the effects of non-pharmaceutical interventions on covid-19 in europe. Nature. 2020;584:257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- [13].Department of Health and Social Care Guidance. Reproduction number (R) and growth rate: methodology. URL https://www.gov.uk/government/publications/reproduction-number-r-and-growth-rate-methodology.
- [14].Maishman T, et al. Statistical methods used to combine the effective reproduction number, R(t), and other related measures of COVID-19 in the UK. arXiv:2103.01742 [physics, q-bio, stat] 2021:ArXiv: 2103.01742. doi: 10.1177/09622802221109506. URL http://arxiv.org/abs/2103.01742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Bracher J, Ray EL, Gneiting T, Reich NG. PLOS Computational Biology. Vol. 17. Public Library of Science; 2021. Evaluating epidemic forecasts in an interval format; e1008618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Presanis AM, Ohlssen D, Spiegelhalter DJ, Angelis DD. Statistical Science. Vol. 28. Institute of Mathematical Statistics; 2013. Conflict Diagnostics in Directed Acyclic Graphs, with Applications in Bayesian Evidence Synthesis; pp. 376–397. [DOI] [Google Scholar]
- [17].Ge H, Xu K, Ghahramani Z. In: Storkey A, Perez-Cruz F, editors. Turing: A Language for Flexible Probabilistic Inference; Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics; Playa Blanca, Lanzarote, Canary Islands. 2018. pp. 1682–1690. Proceedings of Machine Learning Research. [Google Scholar]
- [18].Birrell P, Blake J, van Leeuwen E, Gent N, De Angelis D. Philosophical Transactions of the Royal Society: B Biological Sciences. Vol. 376. Royal Society; 2021. Real-time nowcasting and forecasting of COVID-19 dynamics in England: the first wave; 20200279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Pouwels KB, et al. Community prevalence of SARS-CoV-2 in England from April to November, 2020: results from the ONS Coronavirus Infection Survey. The Lancet Public Health. 2021;6:e30–e38. doi: 10.1016/S2468-2667(20)30282-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].COVID-19 Infection Survey - Office for National Statistics. URL https://www.ons.gov.uk/surveys/informationforhouseholdsandindividuals/householdandindividualsurveys/covid19infectionsurvey.
- [21].Dawid AP. Probability, symmetry and frequency. The British journal for the philosophy of science. 1985;36:107–128. [Google Scholar]
- [22].Manderson AA, Goudie RJB. Combining chains of Bayesian models with Markov melding. arXiv:2111.11566 [stat] 2021:ArXiv: 2111.11566. doi: 10.1214/22-BA1327. URL http://arxiv.org/abs/2111.11566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Dawid AP, Lauritzen SL. Hyper Markov laws in the statistical analysis of decomposable graphical models. Annals of Statistics. 1993;21:1272–1317. [Google Scholar]
- [24].Massa MS, Lauritzen SL. In: Contemporary Mathematics: Algebraic Methods in Statistics and Probability: II. Viana MAG, Wynn HP, editors. 2010. Combining statistical models; pp. 239–260. [Google Scholar]
- [25].Poole D, Raftery AE. Inference for deterministic simulation models: The Bayesian melding approach. Journal of the American Statistical Association. 2000;95:1244–1255. [Google Scholar]
- [26].Zhang L, Beal SL, Sheiner LB. Simultaneous vs. sequential analysis for population PK/PD data I: best-case performance. Journal of Pharmacokinetics and Pharmacodynamics. 2003;30:387–404. doi: 10.1023/b:jopa.0000012998.04442.1f. [DOI] [PubMed] [Google Scholar]
- [27].Maucort-Boulch D, Franceschi S, Plummer M, IARC HPV Prevalence Surveys Study Group International correlation between human papillomavirus prevalence and cervical cancer incidence. Cancer Epidemiology, Biomarkers & Prevention: A Publication of the American Association for Cancer Research, Cosponsored by the American Society of Preventive Oncology. 2008;17:717–720. doi: 10.1158/1055-9965.EPI-07-2691. [DOI] [PubMed] [Google Scholar]
- [28].Jacob PE, O’Leary J, Atchadé YF. Unbiased Markov chain Monte Carlo methods with couplings. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2020;82:543–910. doi: 10.1111/rssb.12336. [DOI] [Google Scholar]
- [29].Liu Y, Goudie RJB. Stochastic approximation cut algorithm for inference in modularized Bayesian models. Statistics and Computing. 2021;32:7. doi: 10.1007/s11222-021-10070-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Yu X, Nott DJ, Smith MS. Variational inference for cutting feedback in misspecified models. arXiv:2108.11066 [stat] 2021:ArXiv: 2108.11066. URL http://arxiv.org/abs/2108.11066. [Google Scholar]
- [31].Pompe E, Jacob PE. Asymptotics of cut distributions and robust modular inference using Posterior Bootstrap. arXiv:2110.11149 [math, stat] 2021:ArXiv: 2110.11149. http://arxiv.org/abs/2110.11149 . [Google Scholar]
- [32].Liu Y, Goudie RJB. Generalized Geographically Weighted Regression Model within a Modularized Bayesian Framework. arXiv: 2106.00996 [stat] 2021:ArXiv: 2106.00996. doi: 10.1214/22-BA1357. http://arxiv.org/abs/2106.00996 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Nicholls GK, Lee JE, Wu C-H, Carmona CU. Valid belief updates for prequentially additive loss functions arising in Semi-Modular Inference. arXiv: 2201.09706 [stat] 2022:ArXiv: 2201.09706. http://arxiv.org/abs/2201.09706 . [Google Scholar]
- [34].Bi Q, et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. The Lancet Infectious Diseases. 2020;20:911–919. doi: 10.1016/S1473-3099(20)30287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Teh YW, et al. Efficient bayesian inference of instantaneous re-production numbers at fine spatial scales, with an application to mapping and nowcasting the covid-19 epidemic in british local authorities. Tech Rep. 2021 doi: 10.1111/rssa.12971. https://localcovid.info/assets/docs/localcovid-writeup.pdf . [DOI] [PMC free article] [PubMed]
- [36].Brauner JM, et al. Science. Vol. 371. American Association for the Advancement of Science Section: Research Article; 2021. Inferring the effectiveness of government interventions against COVID-19. URL https://science.sciencemag.org/content/371/6531/eabd9338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Hooten MB, Johnson DS, Brost BM. Making Recursive Bayesian Inference Accessible. The American Statistician. 2019;186:1–10. [Google Scholar]
- [38].Lunn D, Barrett J, Sweeting MJ, Thompson S. Fully Bayesian hierarchical modelling in two stages, with application to meta-analysis. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2013;62:551–572. doi: 10.1111/rssc.12007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Goudie RJB, Hovorka R, Murphy HR, Lunn D. Rapid model exploration for complex hierarchical data: application to pharmacokinetics of insulin aspart. Statistics in Medicine. 2015;34:3144–3158. doi: 10.1002/sim.6536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Johnson DS, Brost BM, Hooten MB. Greater Than the Sum of its Parts: Computationally Flexible Bayesian Hierarchical Modeling. arXiv: 2010.12568 [stat] 2020:ArXiv: 2010.12568. URL http://arxiv.org/abs/2010.12568. [Google Scholar]
- [41].The Julia Programming Language. URL https://julialang.org/
- [42].Chen PM, Lee EK, Gibson GA, Katz RH, Patterson DA. RAID: high-performance, reliable secondary storage. ACM Computing Surveys. 1994;26:145–185. doi: 10.1145/176979.176981. [DOI] [Google Scholar]
- [43].Yu B, Kumbier K. Proceedings of the National Academy of Sciences. Vol. 117. National Academy of Sciences Section: Physical Sciences; 2020. Veridical data science; pp. 3920–3929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Git. https://git-scm.com/
- [45].Nicholson G, et al. Improving local prevalence estimates of SARS-CoV-2 infections using a causal debiasing framework. Nature Microbiology. 2022;7:97–107. doi: 10.1038/s41564-021-01029-0. Bandiera_abtest: a Cc_license_type: cc_by Cg_type: Nature Research Journals Number: 1 Primary_atype: Research Publisher: Nature Publishing Group Subject_term: Epidemiology;Viral infection Subject_term_id: epidemiology;viral-infection; URL https://www.nature.com/articles/s41564-021-01029-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Riley S, et al. Community prevalence of sars-cov-2 virus in england during may 2020: React study. medRxiv. 2020 [Google Scholar]
- [47].Department of Health and Social Care (UK) COVID-19 testing data: methodology note. https://www.gov.uk/government/publications/coronavirus-covid-19-testing-data-methodology/covid-19-testing-data-methodology-note .
- [48].Ministry of Housing, Communities & Local Government. National Statistics: English indices of deprivation 2019. URL https://www.gov.uk/government/statistics/english-indices-of-deprivation-2019.
- [49].Service UD Census. URL https://ukdataservice.ac.uk/learning-hub/census/
- [50].Hinton GE. Training Products of Experts by Minimizing Contrastive Divergence. Neural Computation. 2002;14:1771–1800. doi: 10.1162/089976602760128018. Conference Name: Neural Computation. [DOI] [PubMed] [Google Scholar]
- [51].Welton NJ, Sutton AJ, Cooper NJ, Abrams KR, Ades A. Evidence Synthesis for Decision Making in Healthcare. John Wiley & Sons; Chichester: 2012. [Google Scholar]
- [52].Daniels MJ, Kass R. A note on first-stage approximation in two-stage hierarchical models. Sankhya: The Indian Journal of Statistics. 1998;60:19–30. [Google Scholar]
- [53].Brauer Fred, van den Driessche Pauline, Wu J. Mathematical Biosciences Subseries. Springer-Verlag; Berlin Heidelberg: 2008. Mathematical Epidemiology. [Google Scholar]
- [54].Scott SL. Bayesian methods for hidden Markov models: Recursive computing in the 21st century. Journal of the American Statistical Association. 2002;97:337–351. doi: 10.1198/016214502753479464. [DOI] [Google Scholar]
- [55].Morales D, Ali S. Covid-19 and disparities affecting ethnic minorities. Lancet. 2021;397:1684–1685. doi: 10.1016/S0140-6736(21)00949-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Mathur R, et al. Ethnic differences in sars-cov-2 infection and covid-19-related hospitalisation, intensive care unit admission, and death in 17 million adults in england: an observational cohort study using the opensafely platform. Lancet. 2021;397:1711–1724. doi: 10.1016/S0140-6736(21)00634-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Rose TC, et al. Inequalities in covid19 mortality related to ethnicity and socioeconomic deprivation. MedRxiv. 2020 [Google Scholar]
- [58].Lee D, Sarran C. Controlling for unmeasured confounding and spatial misalignment in long-term air pollution and health studies. Environmetrics. 2015;26:477–487. doi: 10.1002/env.2348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Pirani M, Mason A, Hansell A, Richardson S, Blangiardo M. A flexible hierarchical framework for improving inference in area-referenced environmental health studies. Biometrical Journal: journal of mathematical methods in biosciences. 2020;62:1650–1669. doi: 10.1002/bimj.201900241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Dominici F, Samet JM, Zeger SL. Combining evidence on air pollution and daily mortality from the 20 largest us cities: a hierarchical modelling strategy. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2000;163:263–302. [Google Scholar]
- [61].Padellini T, et al. The Lancet Regional Health - Europe. Elsevier; 2022. Time varying association between deprivation, ethnicity and SARS-CoV-2 infections in England: A population-based ecological study. 0 URL https://www.thelancet.com/journals/lanepe/article/PIIS2666-7762(22)00015-1/fulltext. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Hellewell J, et al. medRxiv. Cold Spring HarborLaboratory Press; 2020. Estimating the effectiveness of routine asymptomatic PCR testing at different frequencies for the detection of SARS-CoV-2 infections; 2020.11.24.20229948. URL https://www.medrxiv.org/content/10.1101/2020.11.24.20229948v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Mugglin AS, Carlin BP, Gelfand AE. Journal of the American Statistical Association. Vol. 95. Taylor & Francis; 2000. Fully Model-Based Approaches for Spatially Misaligned Data; pp. 877–887. [DOI] [Google Scholar]
- [64].Mauff K, Steyerberg E, Kardys I, Boersma E, Rizopoulos D. Joint models with multiple longitudinal outcomes and a time-to-event outcome: a corrected two-stage approach. Statistics and Computing. 2020;30:999–1014. [Google Scholar]
- [65].Lindsten F, et al. Divide-and-Conquer With Sequential Monte Carlo. Journal of Computational and Graphical Statistics. 2016;26:445–458. [Google Scholar]
- [66].De Angelis D, Presanis AM, Birrell PJ, Tomba GS, House T. Four key challenges in infectious disease modelling using data from multiple sources. Epidemics. 2015;10:83–87. doi: 10.1016/j.epidem.2014.09.004. URL https://www.sciencedirect.com/science/article/pii/S175543651400053X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Simpson D, et al. Penalising model component complexity: A principled, practical approach to constructing priors. Statistical science. 2017;32:1–28. [Google Scholar]
- [68].Riebler A, Sørbye SH, Simpson D, Rue H. An intuitive bayesian spatial model for disease mapping that accounts for scaling. Statistical methods in medical research. 2016;25:1145–1165. doi: 10.1177/0962280216660421. [DOI] [PubMed] [Google Scholar]
- [69].Sørbye SH, Rue H. Scaling intrinsic gaussian markov random field priors in spatial modelling. Spatial Statistics. 2014;8:39–51. [Google Scholar]
- [70].Rue H, Martino S, Chopin N. Approximate bayesian inference for latent gaussian models by using integrated nested laplace approximations. Journal of the royal statistical society: Series b (statistical methodology) 2009;71:319–392. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.