A computational study on how structure influences the optical properties in model crystal structures of amyloid fibrils

Abstract

Amyloid fibrils have been shown to have peculiar optical properties since they can exhibit fluorescence in the absence of aromatic residues. In a recent study, we have shown that proton transfer (PT) events along hydrogen bonds (HBs) are coupled to absorption in the near UV range. Here, we gain more insights into the different types of hydrogen bonding interactions that occur in our model systems and the molecular factors that control the susceptibility of the protons to undergo PT and how this couples to the optical properties. In the case of the strong N–C termini interactions, a nearby methionine residue stabilizes the non-zwitterionic NH₂–COOH pair, while zwitterionic NH₃⁺–COO– is stabilized by the proximity of nearby crystallographic water molecules. Proton motion along the hydrogen bonds in the fibril is intimately coupled to the compression of the heavier atoms, similar to what is observed in bulk water. Small changes in the compression of the hydrogen bonds in the protein can lead to significant changes in both the ground and excited state potential energy surfaces associated with PT. Finally, we also reinforce the importance of nuclear quantum fluctuations of protons in the HBs of the amyloid proteins.

1. Introduction

Amyloid proteins have been the subject of intense study due to their importance in understanding the origins of neurodegenerative diseases like Alzheimer’s and Parkinson’s.^2–4 Under particular conditions, amyloid proteins can convert from soluble free monomers into hierarchically aggregated fibrils. The structure of this aggregated form of amyloid protein consists of elongated protofibrils, rich in beta-sheet domains which are interconnected by a dense network of hydrogen bonds. There is an ongoing effort to provide deeper insights into the structural and kinetic factors that lead to aggregation and the formation of these networks of hydrogen bonds.⁵

One of the other growing areas in amyloid research is the study of the optical properties of the amyloid fibrils.^1,6–14 Recently, we reported a combined experimental and theoretical study on the molecular origins of the optical properties of amyloid proteins.¹ On the experimental side, we showed that two amyloid-β (Aβ) variants (either with or without aromatic amino acids) show fluorescence in the visible range, with a measured excitation peak at around 365 nm.¹ This behavior is very intriguing since most, if not all empirical evidence for fluorescence in molecular organic systems like proteins, is attributed to the presence of aromatic residues like tryptophan¹⁵ and more rarely to tyrosine¹⁶ and phenylalanine. More generally, fluorescence is associated with the existence of π-conjugation, a feature that is not required in these systems. We also found that the fluorescence is sensitive to isotope effects, pH and the polarity of the surrounding solvent. Such experimental findings support the significance of a role played by hydrogen bonding interactions, and in particular of proton transfer. The importance of these effects was confirmed using first principles ab initio molecular dynamics (AIMD) simulations on model amyloid fibrils. In particular, we showed that protons along strong hydrogen bonds between the N and C termini are labile leading to the formation of both zwitterionic NH₃⁺–COO– and non-zwitterionic NH₂–COOH pairs in the fibril. Using excited state calculations, we have shown that optical absorption is quite sensitive to the motion of protons along hydrogen bonds and we have further proposed a qualitative model suggesting that proton delocalization along hydrogen bonds provides a mechanism for preventing non-radiative transitions thereby facilitating fluorescence.

It is clear that the dense network of hydrogen bonds in amyloid fibrils plays an important role in tuning their optical properties, although the exact mechanisms behind these phenomena remain unknown. At this point, due to the sheer complexity of the system, performing explicit non-adiabatic dynamics on the excited states of the protein fibrils is not computationally feasible. There are, however, many interesting and fundamental issues that can still be addressed with ground-state calculations. For example, are backbone and N–C termini hydrogen bonds the same with respect to their propensity to allow proton transfer (PT)? What are the molecular origins controlling the formation of zwitterionic vs. non-zwitterionic N–C termini pairs? How do different hydrogen bonds and the corresponding PT along them couple to optical absorption? These are a few of the type of questions that we wish to address in this work. Besides laying the foundation for understanding the optical properties of these systems, there is a plethora of molecular dynamics simulations using classical empirical potentials to study amyloid aggregation.⁴ In these types of models, the electronic degrees of freedom are not treated and hence processes such as PT are not accounted for. The insights we gain from this work are highly relevant for understanding the quality of hydrogen bonding interactions using empirical potentials in the ground state.

In this work we build on the findings of our previous work and further characterize the properties of hydrogen bonds in our model systems. The structural patterns of backbone hydrogen bonds in both parallel and anti-parallel beta sheets reveal the presence of two candidate hydrogen bonds with subtle differences in their geometry. Proton transfer along these hydrogen bonds and in particular the stronger N–C termini is facilitated by the compression and expansion of the heavy nitrogen and oxygen atoms similar to what is observed in bulk water as well as in other hydrogen bonded systems.^17–19 By examining the optical absorption, we show that both the ground and excited state potential energy surfaces (PESs) as a function of PT are quite sensitive to the geometrical properties of the hydrogen bonds such as the extent to which they are compressed. As indicated earlier, our AIMD simulations show the presence of the non-zwitterionic state of the N–C termini being stabilized in some regions of the fibril. Here we show that the origin of this feature points to the presence of a methionine amino acid being in close proximity to the C-terminus. For the zwitterionic salt-bridge pairs, we find that a trapped water molecule in close proximity leads to the proton being stabilized on the N-terminus. These features will likely be very important for creating different initial conditions and for the subsequent evolution on the excited state.

In most AIMD simulations of organic systems, the nuclei are treated classically. It is well appreciated, however, that for systems consisting of light atoms such as hydrogen, nuclear quantum effects (NQEs) alter the structural, dynamic and even the optical properties of the organic molecular systems.^1,2–23 Here we expand on that analysis and show that NQEs significantly alter the fluctuations of covalent bonds forming the peptide backbone including the carbonyl–oxygen, amide carbon–nitrogen and carboN–Carbon bonds. This in turn provides a molecular rationale for the roles that NQEs play in the optical spectra.

The paper is organized as follows. In Section 2 we briefly describe and discuss the important computational protocols used in this work. In Section 3, we discuss the hydrogen bond patterns involving the backbone peptide bonds and the N–C termini and on the role of the compression of the hydrogen bonds in PT. Section 4 examines how the curvature of the potential energy landscape on both the ground and excited state surfaces is sensitive to the type of hydrogen bond in the protein. In Section 5 we discuss the role of NQEs in both the structural and optical properties of the amyloids. Finally Section 6 ends the paper with some concluding remarks.

2. Computational details

The computational methods employed in this work were described in detail in our previous study.¹ Here we recall some of the important details relevant for this study. We focus on the structural and optical properties of two model amyloid fibril systems, namely 2Y2A and 2Y3J,²⁴ consisting of about 400 and 700 atoms respectively. Born–Oppenheimer molecular dynamics (BOMD) simulations were conducted for both systems at 300 K using the CP2K package²⁵ where the electronic degrees of freedom are treated using both a Gaussian basis set and plane-wave representation. The BLYP functional²⁶ with Grimmes D3²⁷ empirical dispersion corrections together with the DZVP basis set was used in all the simulations. We have already shown that one of the essential results, namely the transfer of protons along the N–C termini hydrogen bonds, was observed using both BLYP and also using the more expensive accurate hybrid functional B3LYP.²⁸ The simulation time of the BOMD calculations was 23 ps and 18 ps for 2Y3J and 2Y2A respectively. The PIGLET simulations for the quantum nuclei in 2Y2A were run for about 6 ps. The probability distributions we show later in the manuscript involve motions on fast timescales (~ 10² fs) in a tightly packed crystal environment. Longer timescales associated with large conformational changes of the amino acids have not been sampled by our simulations. More details on the convergence of various properties extracted from our simulations are shown in the ESI.†

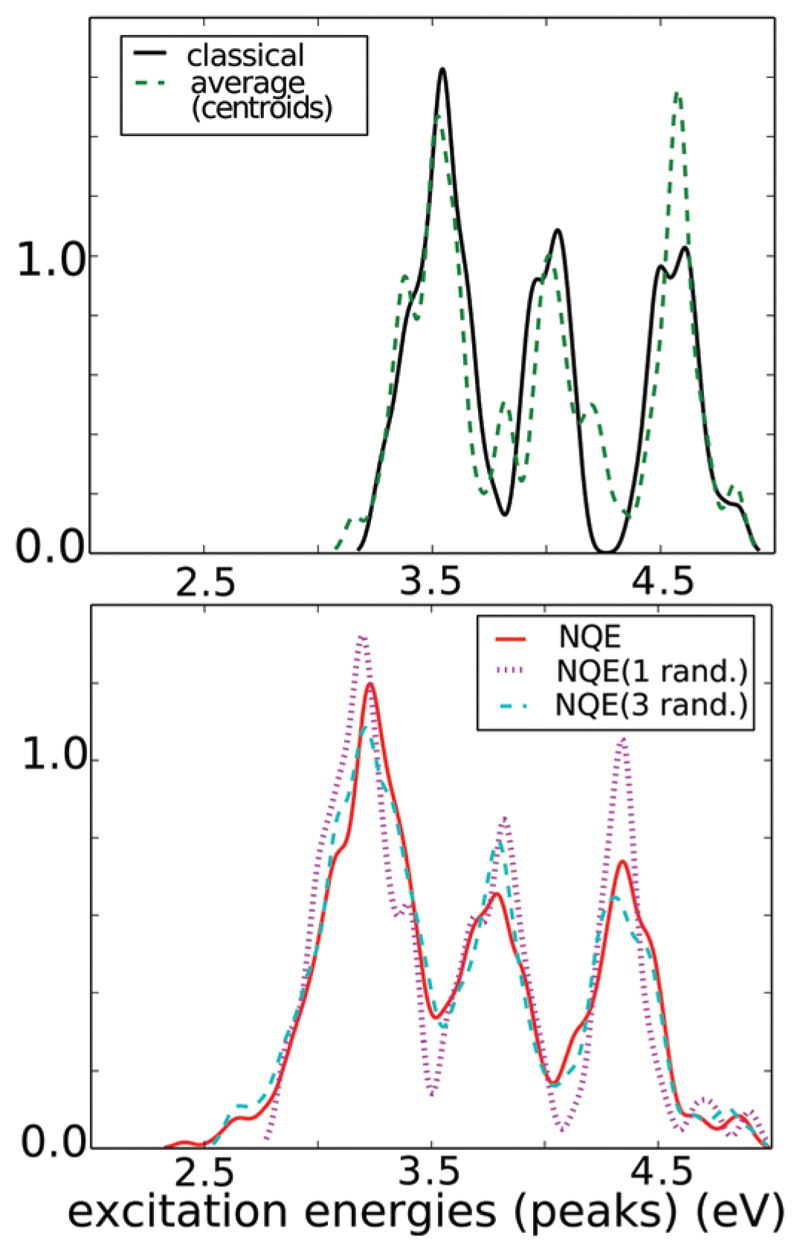
In order to examine how the optical properties of the system change along specific selected coordinates, we perform excited state calculations with time-dependent density functional theory (time-dependent DFT or TDDFT). These coordinates include the proton transfer coordinate along both N–C termini and backbone hydrogen bonds, as well as the C═O stretch. TDDFT calculations were performed with BLYP functional, using quantum-Espresso²⁹ and TDDFT linear response densities were computed using the Lanzcos method.³⁰ TDDFT is one of the most popular tools in computational chemistry for computing excited states since it provides a computationally tractable way to perform excited state calculations on relatively large molecular systems. Usually in TDDFT, a few low-lying excitation energies are calculated individually as eigenvalues of a linear-response equation (Casida formalism). This approach becomes unfeasible as the system size and its spectral density increase. For the very large fibril systems considered here, we therefore employ a Lanczos-based approach to TDDFT where the optical spectrum is computed directly, without addressing the individual excited states. We use here such an implementation of TDDFT which is available in the quantum-ESPRESSO software that can also handle the periodic boundary conditions necessary in our system.¹ We are acutely aware that TDDFT can often be sensitive to the choice of density functional. For this reason, on a smaller model system, we performed some benchmark simulations comparing the GGA functional, BLYP, with a hybrid long range corrected functional (CAM-B3LYP).³¹ Although there are differences in the absolute potential energies, the qualitative trends of how the excitation energies evolve with PT are robust (see the ESI† in ref. 1). For the results discussed in Section 5 (Fig. 9; classical distributions), a total of 41 configurations were uniformly sampled from the ground-state 2Y2A trajectory choosing frames every ~ 0.3 ps. For the PIGLET simulations, 21 configurations uniformly sampled from the trajectory were chosen (every ~240 MD steps). In each of the configurations, we use a different number of beads to construct the spectra: all 6, 3 randomly selected beads and then 1 randomly selected bead (see below and in the ESI†). Thus in total, for the 6-bead spectra, 126 configurations were used.

Fig. 9.

Distribution of excitation energies in 2Y2A for simulations with classical treatment of nuclei (black cont. line) and NQE/PIGLET (all other lines). All beads sampling with NQE correspond to red cont. line see text.

3. Hydrogen bonding patterns in fibrils

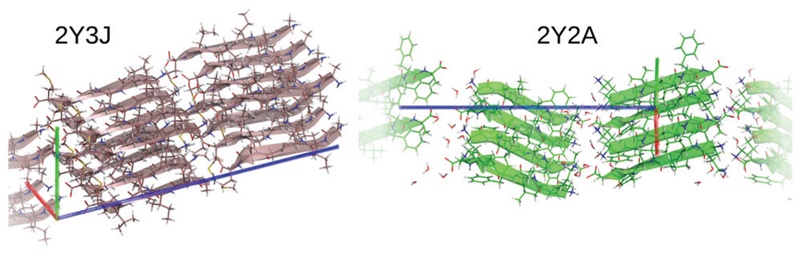
In the following, we focus on the hydrogen bonding patterns observed in the beta sheet structures of two model amyloid fibril crystal structures, 2Y2A and 2Y3J referring to two previously solved model amyloid crystals by Eisenberg and co-workers.²⁴ 2Y2A consists of anti-parallel beta strands while 2Y3J consists of parallel beta strands. Fig. 1 sketches the two packing configurations of the model fibrils. Note that the unit cells of 2Y2A and 2Y3J consist of short polypeptide chains forming a periodic crystal.²⁴ Very recently, two experimental groups have characterized the structure of Aβ_1–42 by solid state NMR.^32,33 Due to the pronounced presence of hydrophobic amino acids in Ab_1–42, a dense packing of interdigitated side alkylic chains is observed in the plane perpendicular to fibril axes. Despite this wealth of structures, amino acid composition, protofibril arrangement, protofibril number, number of N–C pairs, the observed fluorescence is a common phenomenon, with very similar spectral characteristics.¹² Thus the systems we study here provide excellent model systems to study the coupling between the structural and optical properties.^5,34

Fig. 1.

Packing in the two model systems: in 2Y3J (left), the beta sheets are arranged in a parallel fashion around the fibril axes whereas in 2Y2A (right) they are arranged in an anti-parallel fashion. The number of chains per unit cell is 8 and 4 respectively, in both cases two unit cells are shown. Unit cell axes are shown and colored in red, green, blue for a, b, c respectively.

Besides the N–C termini hydrogen bonds, the beta-sheet fibrils also include various possible intra-strand backbone hydrogen bonds between the amide bonds. In order to probe the various hydrogen bond patterns involving the beta-sheet backbone, we searched for all candidate oxygen atoms (O) which are potential hydrogen bond acceptors from each nitrogen atom (N). In order to do this, we focused on distances that were less than 3.5 Å. We then examined two coordinates, namely the oxygen–nitrogen distance (d_O–N) as well as the proton transfer coordinate (PTC) along that candidate hydrogen bond. This was determined by the difference between the N–H and H–O distances. Here, H refers to the hydrogen atom for which the N–H–O angle is maximized. Since our BOMD simulations are relatively short, we have included a section in the ESI† on the convergence of various properties that we illustrate below, such as PT coordinate distributions and H-bonding patterns.

2Y2A

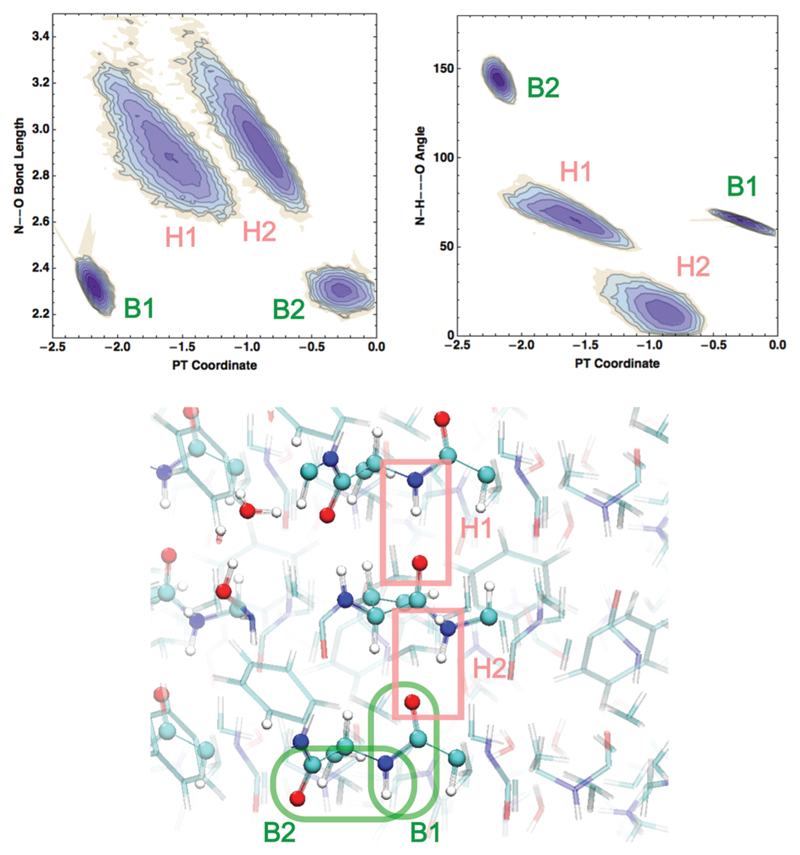
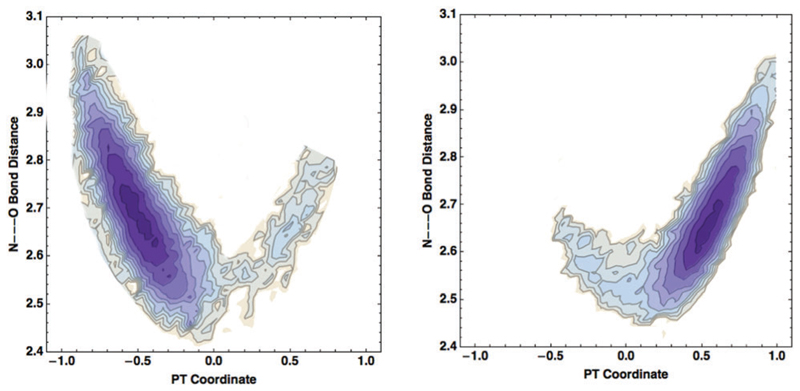
We begin by illustrating the 2-dimensional probability distributions of the PTC and d_O–N coordinates in Fig. 2. We observe 4 peaks (labeled B1, B2, H1, H2) which correspond to 4 different candidate interactions involving the amide backbone nitrogen and carbonyl oxygen. The two peaks at shorter d_O–N distances of ~2.3 Å (B1, B2) are not hydrogen bonds and involve the amide backbone interactions that are covalently linked to each other. In the bottom panel of Fig. 2 a snapshot of the fibril is shown – the solid and dashed enclosed regions illustrate these interactions more clearly with corresponding labels B1, B2.

Fig. 2.

2D distributions of the PT coordinate with respect to N–O distances (left) and N–H–O angles (right), resulting from AIMD simulations on 2Y2A at 300 K. Bonded pairs are labeled in green as B1 and B2, while H-bonded pairs are labeled in light red as H1, H2. Here and in all following figures atoms are colored as red, white, blue, light green and yellow for O, H, N, C and S respectively.

More interesting are the two peaks at around d_O–N ~ 2.8 Å but with two distinct PTCs (H1, H2). The physical origin of this can be understood by examining the distribution of the N–H–O angles – the peak associated with the larger PTC has a larger hydrogen bond angle of about 60 degrees while the shorter one has an angle close to 10 degrees. Thus, the intra-strand back-bone interactions of the fibrils include two different types of hydrogen bonds – one that is more distorted and hence weaker than the other. The average hydrogen bond length is about 2.9 Å in both these cases and can take on a rather broad range of values due to thermal fluctuations of the beta-sheet chains. In the bottom panel of Fig. 2, examples of these different types of hydrogen bonds are illustrated: H1 corresponds to the more linear hydrogen bond while H2 is more distorted – in one case, we see that the C═O group accepts a hydrogen bond from the amide N–H as well as a nearby crystallographic water molecule. Below we will see that the PTC along these different types of hydrogen bonds can cause subtle changes in the manner in which the ground and excited state potential energy surfaces are coupled.

2Y3J

Similar features of the backbone hydrogen bonds are also observed in 2Y3J (see Fig. S1 in the ESI†). In our earlier study, it was found that in 2Y3J at both 0 and 300 K, the protons forming strong hydrogen bonds between the N and C termini were quite labile. More specifically, we found that there were strong hydrogen bonds where the proton is thermodynamically stabilized on the N terminus forming a zwitterionic NH₃⁺–COO– pair as one would expect based on known pK_a estimates.¹ On the other hand, there are also situations where the proton spends most of its time on the C terminus forming a non-zwitterionic NH₂–COOH pair. These results suggested that in the environment of the amyloid fibrils, the pK_a values of both the N and C termini can be shifted, although the exact origin of this was not addressed.

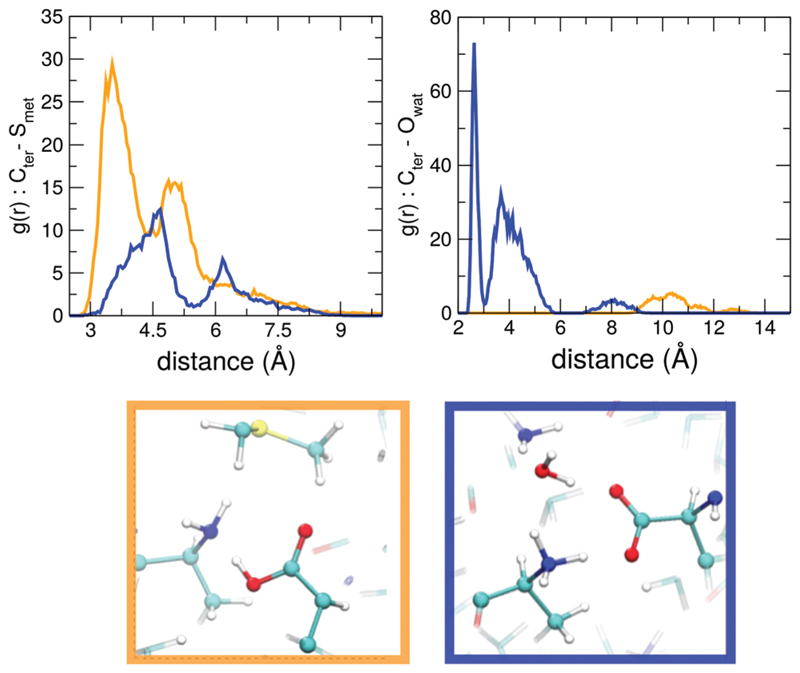
We have traced the molecular origins of the stabilization of the proton on the N or C terminus to specific interactions in the fibril. For the salt-bridges where the proton is stabilized on the C terminus forming the NH₂–COOH pair, we observe a thiol group of a methionine residue that is in close proximity to the pair. This feature is quantified in the left panel of Fig. 3 where we show the radial distribution function (RDF) of the carbon atom of the putative COO–/COOH group with respect to the sulphur atom of the methionine. The green and blue curves show the RDF for situations where the proton is stabilized on the C and N termini respectively. Clearly, the green curve is characterized by a peak at a shorter distance which corresponds to a very different orientation of the methionine residue relative to the N–C termini salt bridge. Snapshots from the simulations illustrating these features are shown in the bottom panels of Fig. 3.

Fig. 3.

RDFs of carbon from C-termini oxygen groups at the termini with respect to the sulfur atom from methionine in the nearby chains (left) and of the C-termini oxygen groups with respect to the water oxygen (right). Orange and blue curves distinguishes cases where proton is stabilized on the C- or on the N-termini, respectively.

For situations where the zwitterionic pair was thermodynamically stable, we found the presence of a single trapped water molecule in close proximity to the N terminus. This is seen in the right panel of Fig. 3 showing the radial distribution functions (RDFs) of the C-termini oxygens with respect to the water oxygens. The blue curve corresponds to the carbonyl oxygens where the proton resides on the N-terminus – there is a high probability of finding a water molecule near these sites.

The proton stabilized in either the zwitterionic or non-zwitterionic state is not static – we showed that at room temperature the proton-transfer potentials (see Fig. 2(c) of ref. 1) feature a double well character. This implies that the proton is labile and can undergo many successful proton transfer events back and forth between the nitrogen and oxygen atoms. This ability of the proton to make large fluctuations along the hydrogen bonds suggests that there might also be some dynamic coupling of high and lower frequency modes in the system. In particular, it has been shown in numerous protonated hydrogen bonded systems^18,35–38 that proton transfer along a hydrogen bond is strongly coupled to a shortening of the distance between the heavy atoms that sandwich the proton. Interestingly, a similar type of phenomenon also occurs for proton transfer in our model systems for the amyloids. The left and right panels of Fig. 4 illustrate the distribution of the compression coordinate vs. the PT coordinate for the proton that spends most of its time on the N and C terminus, respectively (see the bottom panels of Fig. 3). In both cases, we see features of a banana-shape like distribution as has been seen previously in other systems, implying that successful proton transfer events are strongly coupled to the shrinking of the hydrogen bond. Fig. 4 shows that when the distance between the heavy atoms decreases from 2.8 Å to 2.5 Å, the proton transfer barrier is lowered. This mechanism appears to be rather generic for proton transfer processes. It is also interesting to note that the average hydrogen bond length associated with the N–C termini is about 2.65 Å which is 0.25 Å shorter than those associated with the backbone. This is one of the important differences that essentially determines how labile the protons are along the hydrogen bonds.

Fig. 4.

Distribution of the hydrogen bond compression coordinate (N–O distance) and of the PT coordinate for the proton that spends most of its time on the N terminus (left) or on the C terminus (right).

The preceding results showing that both the zwitterionic and non-zwitterionic states can be stabilized in the model-amyloid fibrils suggest that both the N and C termini undergo large perturbations in their pK_as. Large pK_a shifts in charged groups like lysine, aspartate and glutamate have been observed in several proteins when these amino acids are buried in the interior of a protein.^39,40 This behavior is typically rationalized in terms of the difference in the dielectric constant of the solvent environment compared to that of a protein. The electrostatic landscape created at the microscopic level due to the specific arrangement and the proximity of polar and non-polar groups likely plays a role in inducing pK_a shifts. It would be interesting in the future to theoretically determine pK_as of amino acids in model fibrils. At the same time, our results should also motivate the experiments performing site-mutagenesis studies on the amino-acids near the N–C termini and also on the termini itself, such as introducing methylated capped termini, to understand how exactly the optical properties are affected by the termini hydrogen bonding interactions.

4. Potential energy surface scans

Up to this point in the manuscript, we have shown that the hydrogen bonds in the fibrils involving both the backbone and N–C termini interactions are characterized by the interesting structural and dynamical properties. Motivated by the recent experiments showing the importance of a structural chromophore in the amyloid fibrils, we move on to understand how the ground and excited state surfaces can couple along vibrational coordinates connected to hydrogen bonds. Upon excitation, the relative shape and the evolution of the potential energy surface (PES) on both the ground and excited state affect the efficiency of non-radiative transitions which may either facilitate or hinder fluorescence.

Here, we thus expand our analysis of how the ground- and lowest excited-state potential energies evolve as a function of proton transfer along different hydrogen bonds in the fibril. In particular, by performing scans along coordinates that involve changes in the PT coordinate, we build 0 K potential energy surfaces by evaluating ground and excited state energies using DFT and TDDFT calculations respectively (see Section 2 for more details). This provides indirect clues into how different types of hydrogen bonds in the fibril may couple to optical absorption. This type of analysis where proton transfer scans along specific hydrogen bonds are performed has proven to be very useful in a wide variety of systems.^41,42 More specifically, in light of the preceding results, we examine how hydrogen bonds of varying degrees of compression along both backbone and N–C termini hydrogen bonds alter both the ground and excited state potential energy surfaces.

4.1. N–C termini hydrogen bonds

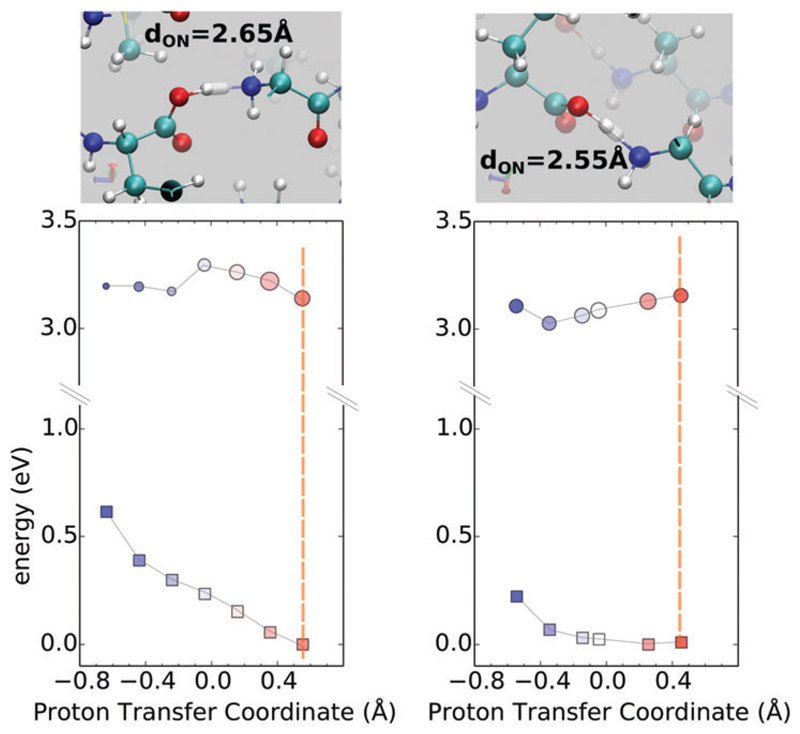
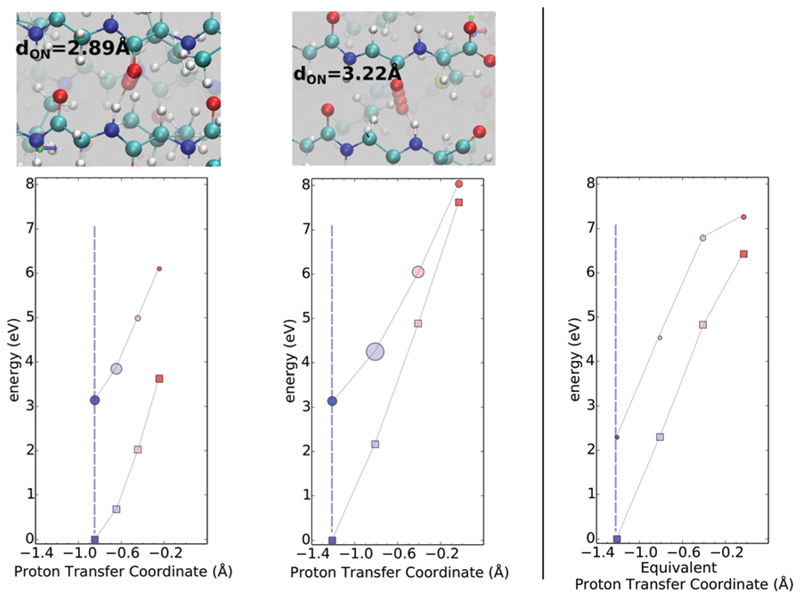
Fig. 5 shows the ground and excited state surfaces computed for 2Y3J for two PTCs where the proton is stabilized on the C terminus – the minima in the ground state are located at a positive PTC. The left and right panels illustrate how a small change in the distance between the heavy atoms can lead to rather significant changes in both the ground and excited state PES. In both cases, proton transfer in the ground state from the C to the N terminus faces a repulsive wall with very different curvatures. In fact, in the right panel, the PES along the proton transfer in the ground-state is primarily flat which originates from the more compressed nature of the HB. Since the two surfaces are not equally coupled to the PT coordinate, the corresponding excitation energies show a rather monotonic trend along the PTC displaying a red-shift when moving towards the N-terminus (see the ESI† for corresponding spectra). These are typical examples of cases where the two electronic states would probably never intersect, and the motion of the proton is mainly effective for a red shift of the excitation energies. It is interesting to observe that the role of the compression is manifested in the steepness of the ground-state potential energy surface – in the right panel, the shorter hydrogen bond is characterized by a much softer repulsive potential when the proton moves from the C to the N terminus. For the excited state, we see that in the less compressed hydrogen bond (left panel), there is a barrier for proton transfer in the excited state. Thus, the compression of the hydrogen bond has important effects on the optical properties like the excitation energies.

Fig. 5.

Ground and first excited-state PES is shown in squares and circles respectively using the zero-K equilibrium structure along the PTC at the N–C termini. In both these situations, the proton is stabilized on the C terminus. The size of circles is proportional to the oscillator strength of the transition. Colors from red to blue qualitatively match the displacement from oxygen to nitrogen. The vertical dashed bar serves as a guide for the equilibrium position. Figures on the top of each graph show the relevant steps along the PT coordinate.

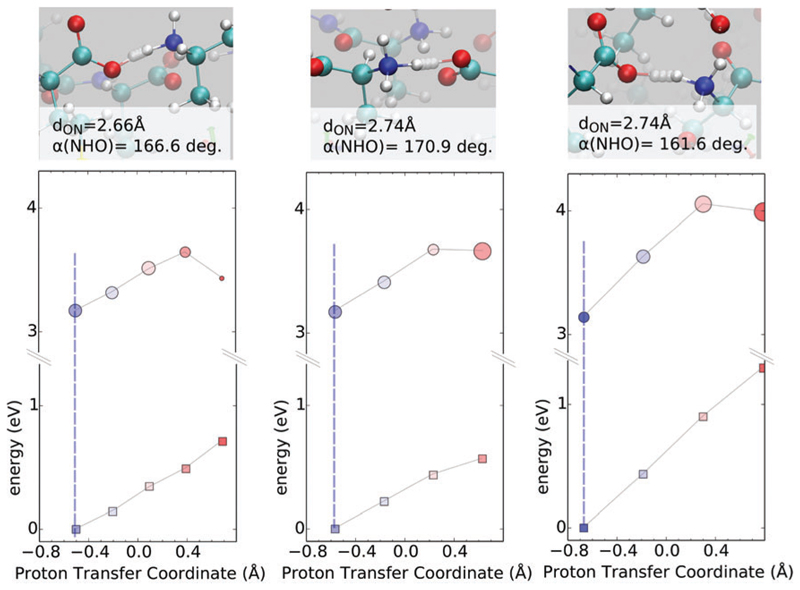
As shown earlier, our finite temperature simulations show that the proton can be stabilized either on the N or C terminus. Fig. 6 (bottom) shows how the excitation energies change for proton motions in which the NH₃⁺…COO^– state is stabilized. In all cases, we see that proton transfer from the N to the C terminus in the ground state encounters a repulsive wall. This feature is also present for the excited state although there does seem to be some partial stabilization when the proton localizes on the C terminus on the excited state. In these hydrogen bonds there is an apparent competition between the extent of compression and the linearity of the HB. The left and middle panels have very similar ground and excited state potential energy surfaces along the PTC despite having different compression lengths of the HB. This is because the longer HB (middle panel) is slightly more linear as indicated by the N–H…O angle. In one case (right panel) we observe a much larger change in the ground state as the proton moves from the N to C terminus (approximately 1 eV). This is due to the fact that for this specific PT, the hydrogen bond between the donor and acceptor groups is both long and distorted as seen in the N–H…O angle at the top of Fig. 6. For the excited state, the repulsive potentials along the PTC almost mirror those in the ground-state and proton transfer could lead to either a blue or a red shift. It is clear when comparing Fig. 5 and 6 that the way in which the ground and excited state PES couple to proton transfer depends on where the proton is stabilized, as well as on subtle variations in the geometrical properties of the hydrogen bonds.

Fig. 6.

Ground (squares) and first excited-state (circles) PESs on 0 K equilibrium structure, along PTC at N–C termini, in three cases where the proton is stabilized on the N. The size of circles is proportional to the oscillator strengths of the transition. Colors from red to blue match the moving from oxygen to nitrogen, respectively. The vertical dashed line sets the position at the equilibrium coordinates. Figures on the top of each graph show the relevant steps along the PT coordinate, starting from equilibrium (solid atom sphere).

4.2. Backbone hydrogen bonds

Besides the N–C termini hydrogen bonds, there is also an extensive network of hydrogen bonds formed between the backbone strands as shown earlier in Fig. 1. Our interest in understanding the role of backbone proton transfer stems from theoretical studies that show how these modes can provide non-radiative transition pathways in model peptide systems allowing for quick deactivation to the ground-state.^43–46 Fig. 7 shows that the proton transfer along the backbone hydrogen bonds is significantly more unfavorable compared to the N–C termini. For backbone PT from the amide N to the oxygen of the adjacent chain, the repulsive potential for PT is significantly steeper undergoing energetic changes larger than 2 eV for both ground and excited states. These results suggest that on the excited state, backbone proton transfer is unlikely to be a dominant de-activation mechanism via a non-radiative transition. However, we do find that at large values of the PT coordinate corresponding to the proton being localized on the carbonyl oxygen, there is a substantial stabilization of the excited state as seen in the dip in excited state energies for positive values of the PTC coordinate.

Fig. 7.

Ground and first excited state surfaces are shown in squares and circles respectively in the fibril. Left and middle panels correspond to two different backbone hydrogen bonds. Size of the circle is proportional to the oscillator strength. Colors from red to blue match the displacement of the proton from oxygen to nitrogen, respectively. Central figures top and bottom (corresponding to left, mid-right panels respectively) sketches the structure and the relevant steps along the PT coordinate, starting from equilibrium (solid atom sphere). The vertical dashed line sets the position at the equilibrium coordinates. Plot on the extreme right is the corresponding scan obtained for a single chain in vacuum (see text), to be compared with the centre one.

Besides the protons moving along hydrogen bonds, there are numerous other coordinates that could potentially couple to deactivate the excited state. In carbonyl-based isolated molecular systems, it has been observed that the elongation of the carbonyl oxygen bond often coupled to a pyramidalization of the carbonyl C serves as a deactivation mode on the excited state leading to a conical intersection with the ground state^47,48 and hence hindering fluorescence. As alluded to earlier, rigorously quantifying these processes requires the use of non-adiabatic dynamics on the excited state. In order to gain some qualitative insights into the role of this deactivation mechanism, we have tested the behavior of the ground and excited state PES along the elongation of the C═O bond length (and consequently changes in the PT coordinate of H–N of the nearby chains). The involved atoms are the same as in Fig. 7, but in this case we moved the oxygen atom. These results are shown in Fig. 8, which show both the ground and excited state feature repulsive potentials along this coordinate. In this case, the steepness of the repulsive potential is more sensitive to the length of the hydrogen bond compared to what was observed when the proton was moved in Fig. 7. When the hydrogen bond is the longest (right panel) we observe a possible conical intersection between ground and excited states. However, this intersection point occurs very high up in energy on the excited state and is unlikely to be a deactivation mechanism that can occur on short nanosecond timescales. We have also performed a similar analysis on 2Y2A and we obtained similar results. The corresponding figures for the PESs are shown in the ESI.†

Fig. 8.

Ground and first excited state surfaces are shown in squares and circles respectively in the fibril. Left and middle panels correspond to two different backbone hydrogen bonds. Note that in this case, the changes in the PTC involve the same atoms as in Fig. 7. Size of the circle is proportional to the oscillator strength of the transition. Colors from red to blue match the moving from oxygen to nitrogen, respectively. Central figures top and bottom (corresponding to left, right panels respectively) sketch the structure and the relevant steps along the PT coordinate, starting from equilibrium (solid atom sphere). The vertical dashed set the position at the equilibrium coordinates. The rightmost panel is the corresponding scan obtained for a single chain in vacuum (see text), to be compared with the one in the middle panel.

4.3. Environmental effects on PESs

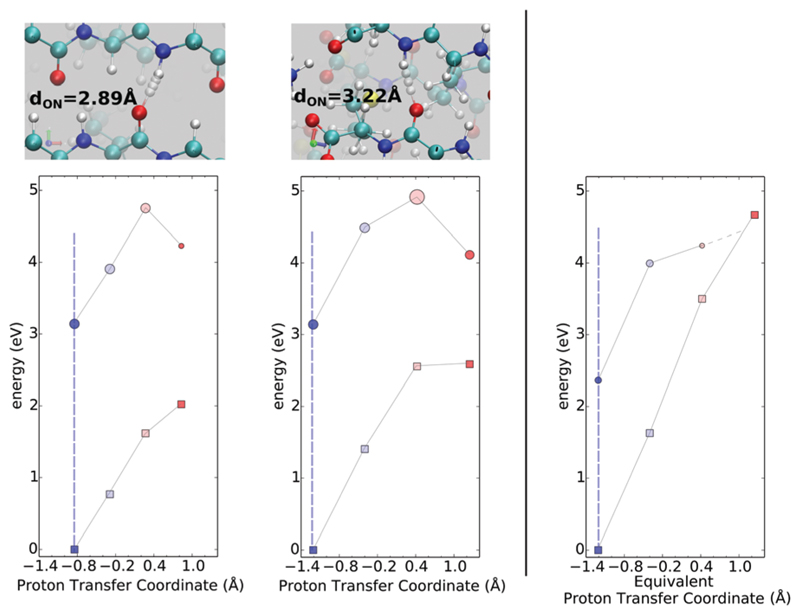
The PES scans explored earlier include effects of the environment on the respective coordinate that is being adjusted. In order to establish the role of the fibril environment in the coupling between ground and excited state surfaces, we repeated the PTC and C═O stretch scans for some of the cases shown earlier using an isolated 2Y3J chain with vacuum buffer surrounding it in all the directions.

For the N–H stretch along the PTC, we observe a steeper PES for the ground state compared to what is observed with the fibril environment included as can be seen in the rightmost panel of Fig. 7. This produces eventually a crossing between ground and excited states at large values of N–H bond elongation confirming the effect of destabilization of the ground state and potentially the occurrence of a conical intersection in isolated chains. The effect of the environment on the curvature of the potentials is seen in the rightmost panel of Fig. 8 compared to what is observed in the middle panel. Besides the changes in the curvature of the potentials due to the environment, it is also clear that for both the N–H and C═O stretch, the oscillator strengths associated with absorption are also stronger in the presence of the full protein environment.

5. Importance of nuclear quantum effects

In the preceding analysis, the hydrogen bond and proton fluctuations along them are examined through the lens of treating the nuclei classically. In our earlier study, we showed that nuclear quantum effects (NQEs) have a significant effect on the delocalization of protons along hydrogen bonds in the model system 2Y2A. Since the zero-point energy (ZPE) of covalent interactions like the O–H and N–H bonds can be about a factor of 5–10 larger than thermal energy at room temperature, these effects are somewhat expected. Besides changes in the structural properties, NQEs also have an effect on the electronic and optical properties.^1,37,49,50

5.1. Optical spectra

Our results provide interesting ground to understand how the fluctuations of protons and more specifically, their quantum fluctuations along hydrogen bonds, couple to the electronic properties such as the optical spectra. In order to disentangle the importance of NQEs on the optical spectra, we previously computed the spectra from PIGLET simulations using all the 6 beads of each imaginary time slice and found that NQEs cause a significant broadening as well as a red shift in the absorption spectra.

In order to assess whether these observations were biased by the correlations that exist between the beads, we compared the spectra coming from different sampling protocols: (a) averaging over all six beads, (b) averaging over a single random bead, or (c) averaging over three random from each imaginary time slice and finally (d) where we compute the spectra over only the centroid of all the beads. Interestingly, all the procedures (a) through (c) produce spectra that are essentially the same as seen in Fig. 9. Furthermore, in all cases the spectra are red shifted relative to the classical simulations. Protocol (d) which averages over the centroid is instead very similar to the classical absorption spectra (e). This is rather interesting because it really demonstrates the role of quantum fluctuations of nuclei in the spectra. Furthermore, from a methodological point of view, these results show that using a single-bead would be sufficient for reproducing the effects of NQEs on the spectra and is also more computationally tractable.

5.2. Structural origins

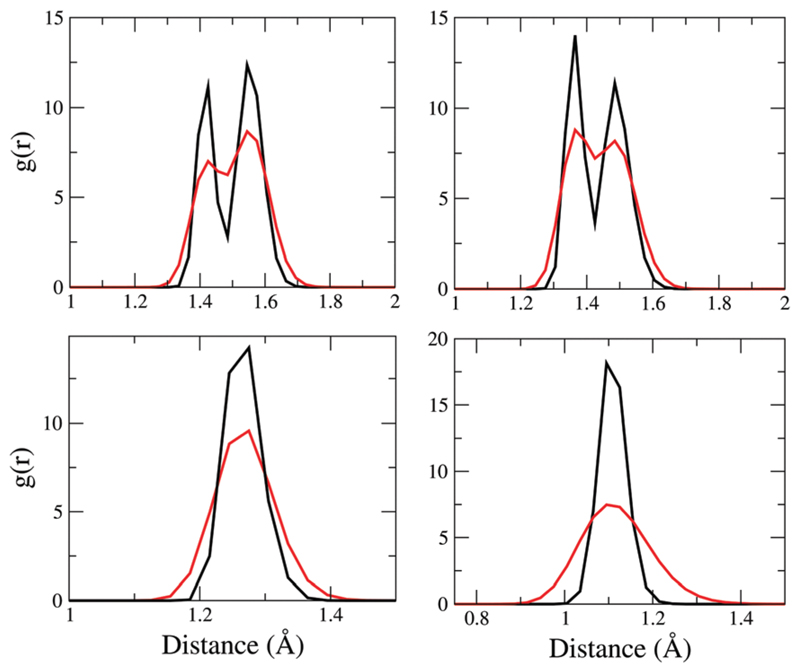
Pinpointing the exact molecular origins of the effect of NQEs on the spectra is quite challenging. This is because the effect of NQEs is actually rather collective - not only does it affect the fluctuations of the protons along the hydrogen bonds, but it also affects the fluctuations and hence underlying distributions of many different covalent bonds in the protein. Indeed in the simulations of our model fibrils, NQEs significantly alter the structural fluctuations of the entire peptide backbone. These effects are encoded in Fig. 10 that shows the C–C, C–N, C═O, and C–H RDFs for the classical and quantum simulations. We only show the first peaks of the distributions since these correspond to covalently linked atoms. The C–C RDF features two distinct peaks – one at ~1.42 Å and another at ~1.55 Å which correspond to covalent bonds with aromatic and single bond character respectively. NQEs significantly affect these distributions by not only broadening them overall, but also blurring out the distinction between the two types of bonds with different chemistry – comparing NQE and classical runs, we see an enhanced propensity for a C–C bond length of 1.5 Å. The C–N distributions also exhibit similar features and trends as a function of including NQE – in this case, the two peaks correspond to the single amine vs. peptide (amide) bond, the latter of which has a partial double bond character.

Fig. 10.

Distribution of bond length CC (top left), CN (top right), CO (bottom left) and CH (bottom right) in 2Y2A. Black lines correspond to simulations with classical treatment of nuclei, red lines includes NQE/ PIGLET (see the text).

6. Discussion and conclusions

In a recent work, we have shown that amyloid proteins are capable of fluorescing in the absence of aromatic residues.¹ Using both experiments and computation, we found that the anomalous optical properties appear to be tied to proton transfer events in the hydrogen bond network. In this work, we have expanded our analysis of the structural and electronic properties of the amyloid proteins, examining in more detail the features of the hydrogen bond from the point of view of both structure and dynamics.

The proximity of the electron rich sulphur group to the C-terminus shifts its pK_a making it a better acceptor of a proton leading to situations where the non-zwitterionic NH₂–COOH groups are favored. Beyond structural facts, sulfur, like other electron-rich atoms or groups, might also play a role by providing electronic levels lying close to the frontier orbitals, possibly giving rise to smaller optical gaps: this was suggested in our former works (see the ESI† in ref. 1). However, according to our evidence, the presence of such groups or atoms is not a prerequisite for observing intrinsic fluorescence.^6–9,14 We also find that water molecules that get trapped into the fibril can result in cases where the zwitterionic NH3⁺–COO– state is stabilized. Although these observations remain purely theoretical at this point, it could motivate further experiment in the future. Besides the heterogeneity in the electrostatic potential of the fibrils leading to the zwitterionic vs. non-zwitterionic pairs along different hydrogen bonds, we also demonstrated that the mechanism of proton hopping is very similar to what is seen for the Grotthuss mechanism of PT in bulk water. Successful PT involves the compression of the hydrogen bond by about ~0.3 Å as this lowers the barrier for PT significantly. Experimentally it has been shown that extreme pH conditions reduce the fluorescence intensity, although the mechanism by which this happens is not understood.¹ Furthermore, there are also some subtle isotope effects on the emission. The effect of extreme pH and isotopes on the compression coordinate is something that should be explored in more detail both in the ground and the excited state. We are currently performing IR experiments on the fibrils formed under several pH conditions, in order to understand the role played by both the hydrogen bond networks and salt bridges. These experiments are being complimented by ab initio calculations in an effort to disentangle the IR spectra of the fibrils.

Besides having an expected effect on the fluctuations of the light atoms, NQEs significantly impact the chemistry of single and double bond characters in the fibrils which is associated with heavy atoms. In the classical simulations, there is a clear distinction between two types of C–C and C–N bonds reflecting double-bond vs. single bond. In the quantum simulations, this distinction is much less pronounced implying that quantum fluctuations cause some important changes in the underlying electronic structure. Similar to our observations made on a smaller system, quantum effects significantly enhance the delocalization of the protons along the strong hydrogen bonds formed between the salt-bridges.

In this work, we also extended our earlier analysis of the coupling between ground and excited state energies as a function of the motion of protons along various different hydrogen bonds. An important finding of this analysis is that not all hydrogen bonds in the model fibrils are the same in terms of the energetic profiles leading to subtle differences in the curvature of the potential energy landscape on both ground and excited state. This will likely have important implications for the mechanism by which energy is dissipated on the excited state. In particular, if proton transfer is coupled to the fluorescence, then its role becomes a question about how easy or difficult it is to access conical intersections between the excited and the ground state potential energy surfaces. For the proton transfer potential energy surfaces in the ground-state that are softer, or in other words have a smaller curvature, an intersection with the excited state surface is likely to occur much higher in energy and thus less likely to be accessed. This may encourage radiative vs. non-radiative transitions (see Fig. 10 of ref. 1). It should be stressed again that these types of analyses only permit indirect and qualitative insights into the origins of fluorescence in the amyloids. Future work will deal with explicitly modeling the dynamics of excited states on smaller model systems to gain insights into the possible origins of this intriguing phenomenon.

The phenomenon of the fluorescence observed in these fibrils is distinct from that associated with luminescence observed in marine or terrestrial organisms in that in the latter, the origin of the emission of light typically comes from a chemical reaction involving specific molecules like luciferin.⁵¹ While amyloid fibrils themselves do not serve any evolutionary advantage and thus their intrinsic fluorescence is unlikely to be a physical process that was exploited in a similar manner to that in chemiluminescent systems, it would be interesting to understand how generic the intrinsic fluorescence mechanism is to other protein aggregates made up of different types of amino acids.

Supplementary Material

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp07564a