Association between the high levels of gynoid fat and the increase of bone mineral density in women

Abstract

Introduction

In women, bone mineral density it is related to age, estrogenic action and appendicular skeletal muscle mass (ASMM). The gynoid fat distribution is linked to estrogenic action.

Objective

Assess if increase of gynoid fat be associated to high bone mineral density (BMD) independent to age and appendicular skeletal muscle mass.

Methods

Observational study performed on women of age between 20 to 79 years. Fat mass, ASMM and BMD were measured with Dual-energy x ray absorptiometry. The binned scatterplots and multivariate linear regression models were used to study the relationship between hip BMD and age, height, android fat, gynoid fat, and ASMM.

Results

For 673 women invited, 596 accepted to participate. The mean age was 55.4 ± 12.8 years, weight 63.4 ± 9.4 Kg, height 1.61 ± 0.06 m, body mass index 24.54 ± 3.59 Kg/m2, average hip BMD 0.914 ± 0.122 gr/cm², android fat 2.12 ± 0.83 kg, gynoid fat 4.54 ± 1.07 kg and ASMM 15.15 ± 1.97 kg. The final regression model included age (linear coefficient -0.004; 95% CI: -0.005 to -0.003; p <0.001), ASMM (linear coefficient 0.013; 95% CI: 0.009 to 0.018; p <0.001) and gynoid fat (linear coefficient 0.013; 95% CI: 0.005 to 0.022; p <0.002).

Conclusion

Gynoid fat is associated with BMD in the hip independently of age and ASMM.

Introduction

On women, bone mineral density it is related to age, estrogenic action and appendicular skeletal muscle mass (1-5). Also, women, compared to men, have higher percent body fat and deposit it in a different pattern, with relatively more adipose tissue in the hips and thighs. This, ‘female’ fat distribution, seems at least in part due to oestradiol-induced increase of anti-lipolytic α2-adrenergic receptors in gluteofemoral subcutaneous depots (6). In this way, the gynoid fat distribution is linked to estrogenic action and therefore an increase of gynoid fat should be associated with a high bone mineral density independent to age and appendicular skeletal muscle mass. Of fact, on postmenopausal Korean women gynoid fat was positively associated with better trabecular bone (7). In another study, conducted in postmenopausal Caucasian women, the gynoid fat showed correlated positive to bone mineral density (8). Shao et al, on Chinese women pointed out that the reduction of android-to-gynoid fat ratio during menopause may have vital clinical significance in decreasing postmenopausal osteoporosis (9). Healthy Postmenopausal Thai Women study showed that higher gynoid adiposity was associated with higher bone mineral density (10).

Notwithstanding the foregoing and given the cross between gynoid and android fat, there is no consensus on the effect of the distribution of body fat on bone mineral density (1). This leaves room to the complement available evidence with new studies from different ethnic and socio-demographic backgrounds; that distinguish between android and gynoid fat.

The aim of this study is Assess if increase of gynoid fat be associated to high bone mineral density (BMD) independent to age and appendicular skeletal muscle mass in women.

Methods and Subjects

Study participants

This is a retrospective observational study that included women aged 20 to 79 years old. Participants, who attended a preventive health control in Santiago de Chile between January 2015 and October 2016, were randomly selected.

Exclusion criteria included: i) women who used medications likely to have an effect on muscle mass or bone (e.g., Levothyroxine, corticosteroids, hormone replacement therapy and oral contraceptives); ii) women who were on dedicated dietary or exercise programs; iii) women with non-communicable diseases: polycystic ovarian syndrome, and chronic pulmonary, cardiac, hepatic, or renal diseases. Furthermore, women with limb deformities and disorders of the nervous and musculoskeletal systems were excluded too.

Instruments

Questionnaires and clinical examination were conducted following standardized procedures and by trained clinicians: age (years), weight (kg), height (m), average hip bone mineral density (this includes the average bone mineral density between right and left hip; it was measured on gr/cm²), android fat (kg), gynoid fat (kg) and appendicular skeletal muscle mass (kg).

Dual-energy x ray absorptiometry (DXA) was performed on all study participants. DXA (Lunar Corporation, Madison, WI, USA) was used to measure whole and regional body composition. Percentage of fat mass, lean mass and bone mineral content were measured. In addition, the bone mineral density in both femoral necks were recorded. The determination of the bone mineral density in vertebral spine, not were used to avoid the interference caused by osteoarthritis in the spine. The information retrieved included bone mineral content, mineral density, T-score and Z-score, and was analysed with the software provided by the manufacturer (version 4.7e). We calculated appendicular lean mass (aLM) as the sum of lean mass in arms and legs (11). The calibration for the measurement of bone mineral density were performed using a spine phantom made of calcium hydroxyapatite and embedded in a lucite block. Scans of the phantom spine occurred every other day according to the manufacturer’s guidelines. The bone mineral density values obtained from calibration were stable over the entire study period (mean 0.991 g/cm² ; coefficient of variation of 0.08%).

The “android” and “gynoid” regions were defined using the software provided by the manufacture. The “android region” has a lower boundary at the pelvis cut and the upper boundary above the pelvis cut by 20% of the distance between the pelvis and the neck cuts. The lateral boundaries are the arm cuts. The “gynoid region” has an upper boundary between the upper part of the greater trochanters and a lower boundary defined at a distance equal to twice the height of the android region. The lateral boundaries are outer leg cuts (12). All scans were performed by the same operator while the subjects were wearing light indoor clothing and no removable metal objects.

Statistical analysis

The analysis was conducted with Stata (Stata/SE 15.0 for Windows, Copyright 1985-2017 Stata Corp LLC). Quantitative variables were described according to their distribution and the corresponding central tendency and dispersion estimates were computed (13).

Binned scatterplots are a non-parametric method of plotting the conditional expectation function (which describes the average dependent value for each independent value) (14). Therefore, binned scatterplots inform about the functional form of variables and their standards errors. The binned scatterplots were used to study de la relationship between average hip bone mineral density and the following variables: age, height, weight, android fat, gynoid fat, appendicular skeletal muscle mass, and; the corresponding Pearson’s correlation coefficients were computed as well (15).

A preliminary linear regression model including age, height, android fat, gynoid fat, and appendicular skeletal muscle mass as predictors, was fitted (14); the dependent variable (predicted or outcome) was average hip bone mineral density. A stepwise backward selection approach was followed to select the final predictors in the regression model. The final model included predictors which linear coefficients had a p <0.05 (16).

The following information was estimated from the final model: log likelihood (LL), Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), adjust R-squared (Adj-R²). Also, for each predictor in the final model, their linear coefficients and standardized linear coefficients were computed. In addition, the adequate compliance of the following assumptions for ordinary least squares (OLS) regressions were assessed: normality of residuals, homoscedasticity, multicollinearity, functional form (linearity), and model specification, independence (15,16). The normality of residuals was evaluated with graphic methods (p-norm, q-norm and kernel density estimation on histogram) and tests for normality of a random variable based on the quantile-mean covariance (17,18,19). The error variance constant (homoscedasticity) was assessed plotting the residuals versus fitted (predicted) values and the Breusch-Pagan test (null hypothesis: variance of the residuals is homogenous) (20). The variance inflation factor (VIF) for each predictor in the final model was studied to avoid multicollinearity (16). When we estimate linear regressions, we assume that the relationship between the response variable and the predictors is linear. The linearity assumption of the regression between the response and the predictors was established through the augmented component-plus-residual plot (21). A model specification error can occur when one or more relevant variables are omitted from the model or one or more irrelevant variables are included in the model. The linktest (22, 23) and Ramsey (24) reset test were using to assess specification error. Finally, the assumption of independent errors was evaluated with the Durbin-Watson test and Durbin’s alternative test (25,26).

Ethical considerations

The study was approved by the CEGEP (Centro de Estudios Ginecológicos y Preventivos, Santiago, Chile) and in complete agreement with the Declaration of Helsinki. All patients provided written informed consent.

Results

For this study, 673 women were invited, and 596 (88.5%) accepted to participate. All variables were symmetrically distributed. The mean ± standard deviation of variables of interest was: age 55.36 ± 12.77 years, weight 63.36 ± 9.41 kg, height 1.61 ± 0.06 m, body mass index 24.54 ± 3.59 Kg/m2, average hip bone mineral density 0.914 ± 0.122 gr/cm², android fat 2.12 ± 0.83 kg, gynoid fat 4.54 ± 1.07 Kg and appendicular skeletal muscle mass 15.15 ± 1.97 kg.

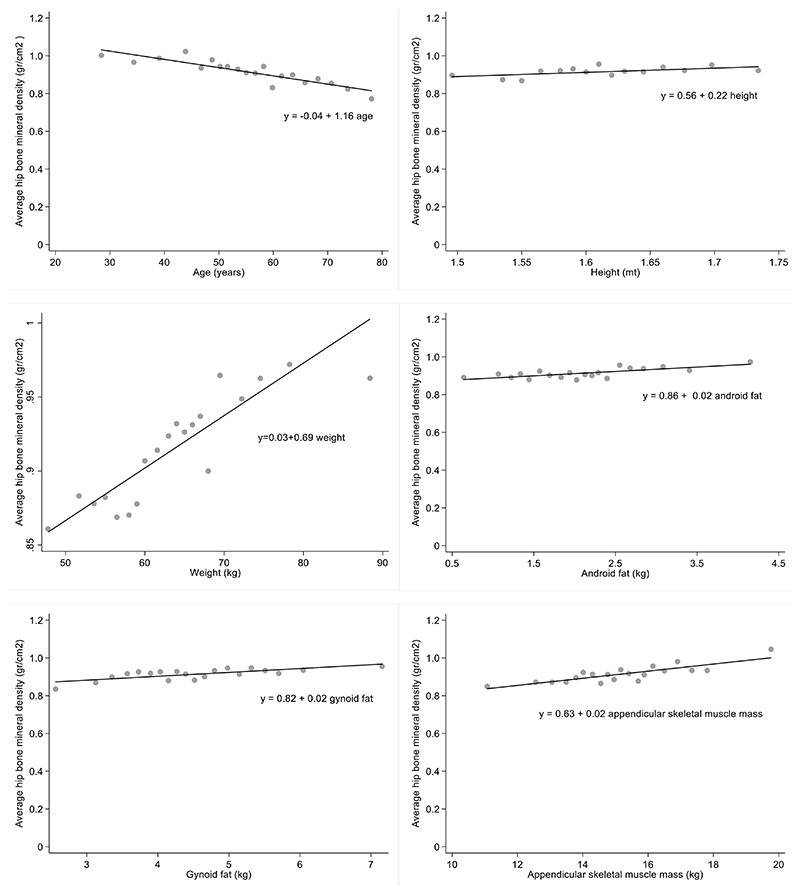
The Binned scatterplots between average hip bone mineral density and the following variables: age, height, weight, android fat, gynecoid fat, and appendicular skeletal muscle mass, suggested there is a linear relationship among these variables (figure 1). The Pearson’s correlation coefficients are shown on Table 1. Of note, the correlation between average hip bone mineral density and age, height, weight, android fat, gynoid fat and appendicular skeletal muscle mass, and was highly significant (p <0.01).

Figure 1.

Binned scatterplots between average hip bone mineral density and following variables: age, height, android fat, gynecoid fat, appendicular skeletal muscle mass on 596 who attended a preventive health control on city Santiago of Chile, during the period January 2015 and October 2016. (y= simple linear regression using method ordinary least squares for predictor according plot).

Table 1.

The Pearson’s correlation coefficient between the pairs: average hip bone mineral density, age, height, android fat, gynecoid fat, appendicular skeletal muscle mass on 596 women who attended a preventive health control on city Santiago of Chile, during the period January 2015 and October 2016.

Variables		Pearson’s correlation coefficient
Average hip bone mineral density	Age	-0.46*
	Height	0.11*
	Android fat	0.16*
	Gynoid fat	0.18*
	Appendicular skeletal muscle mass	0.30*
	Weight	0.27*
Age	Height	-0.11*
	Android fat	0.17*
	Gynoid fat	0.01
	Appendicular skeletal muscle mass	-0.12*
	Weight	0.07
Height	Android fat	0.03
	Gynoid fat	0.19*
	Appendicular skeletal muscle mass	0.55*
	Weight	0.30*
Android fat	Gynoid fat	0.74*
	Appendicular skeletal muscle mass	0.28*
	Weight	0.85*
Gynoid fat	Appendicular skeletal muscle mass	0.32*
	Weight	0.82*

^*indicate p value less than 0.01

The weight is not suitable to be incorporated in linear regression model (15,16) because gynoid fat and android fat are linear combination for the weight (Pearson coefficient greater to 0,8).

The stepwise backward selection approach yielded a final linear regression model including age (linear coefficient of -0.004; 95% CI: -0.005 to -0.003; p <0.001), appendicular skeletal muscle mass (linear coefficient of 0.013; 95% CI: 0.009 to 0.018; p <0.001), and gynoid fat (linear coefficient of 0.013; 95% CI: 0.005 to 0.022; p =0.002). The android fat showed a very close positive correlation with the gynoid fat and was automatically excluded from the final model. The linear coefficient of the intercept in the final model was 0.880 (95% CI: 0.800 to 0.959; p <0.01). The final model had these characteristics: LL was 506.82, AIC was -1005.64 and BIC was -988.08, Adj-R² was 0.28. The standardized linear coefficients for the final model were as follow: age: -0.43, appendicular skeletal muscle mass: 0.22 and gynoid fat: 0.12.

The final regression model residuals showed normal distribution on plots: p-norm, q-norm and kernel density estimation on histogram. Tests for normality of a random variable based on the quantile-mean covariance showed (epsilon 0.05 and T3) a p value of 0.1. Plots of the final model residuals versus fitted values did not show any patterns. The Breusch-Pagan test yielded a p value of 0.13. The VIF for each predictor in the final model were, age: 1.02, appendicular skeletal muscle mass: 1.14 and gynoid fat: 1.12.

The condition number for all the predictors on the final model was 23.76. On final model, for each predictor, the augmented component-plus-residual plot showed a linear fit. The link test showed a correct specification for the final model. The Ramsey reset test showed a p value of 0.59. The Durbin-Watson test showed a value of 2.0002. Durbin’s alternative test showed p value of 0.81.

Discussion

The result of univariate analysis (binned scatter plots and Pearson’s correlation coefficients) supports that bone mineral density it is related to age, gynoid fat and appendicular skeletal muscle mass. However, the significant correlation between bone mineral density of the hip and height and android fat It could be a product of confounding factor, among which highlight: gynoid fat, appendicular skeletal muscle mass and other not considered but mentioned in the study limitations.

The final regression model indicates indicate that appendicular skeletal muscle mass is associated with better bone density which could be explained by the cross-talking between muscle and bone. Numerous studies support the concept of a bone-muscle unit, where constant cross-talking between the two tissues takes place, involving molecules released by the skeletal muscle secretome, which affects bone, and osteokines secreted by the osteoblasts and osteocytes, which, in turn, impact muscle cells (2). Also, the association between bone mineral density and muscle can be influenced by estrogen, since the muscle has estrogen receptors that seem to play a significant role in the apoptosis of muscle cells (3).

Another result is the negative effect of age on bone mineral density. Aging progressively triggers greater cellular senescence, a process that is expressed in bone as osteoporosis (4). The oestradiol attenuates this process by increasing osteogenic differentiation by promoting increased expression of SATB2, a protein that regulates cellular transcription and which is crucial for osteogenic differentiation of bone stem cells and therefore for bone quality (5).

On the absence of detailed information about menopause status, some epidemiologic studies consider age alone as a crude proxy for menopause status (28). On this study the age incorporated: the aging and the menopausal status linked to hypoestrogenism. Although several of the factors associated with low bone mass in women are linked to hypoestrogenism, we cannot consider it to be the most relevant factor in bone metabolism and in the risk of osteoporosis, since many other conditions can modify bone mass. Proof of this is the broad list of diseases that can cause secondary osteoporosis (29). However, hypoestrogenism is another factor to consider when assessing the risks of osteoporosis in a woman and the important thing is that it is a modifiable factor and that there is solid evidence that shows the positive results of menopausal hormone therapy in the prevention of osteoporotic fractures (30).

The principal result indicates that gynoid fat independent of age and appendicular skeletal muscle mass predict bone mineral density of the hip. This result support that the gynoid fat is associated with better bone mineral density; being consistent with evidence observed (7-9). The bone mineral density has been describe associated inter alia, to ethnicity, sex, age, body phenotype, oestrogen, calcium and lifestyle factors (31). The positive association between gynoid fat and bone mineral density can not only be explained by the positive relationship between gynoid fat and estrogenic effect; but also, for other factors related to greater gynoid fat such as: lifestyle and physical exercise.

The results of this study has limitations due to the lack of incorporation the variables that could have influenced bone mass, such as: physical activity, menopause status, age at menopause, smoking, alcohol consumption, parity, lifetime duration of lactation, level of physical activity, personal history of fracture, family history of fracture osteoporosis, vitamin D status and intake of supplements. This study is an initial contribution to a causal model of the factors that affect bone mineral density in women and therefore new studies should performed for establishing causal relations.

Conclusion

Greater gynoid fat is associated with better bone mineral density in the hip; therefore, there could be lower risk of osteoporosis. It would be interesting to study whether this association could be due to some action of the gynoid fat on the bone, or an effect on hypoestrogenism, or indirect effect of lifestyle and physical exercise.