Colocalization for super-resolution microscopy via optimal transport

Abstract

Super-resolution fluorescence microscopy is a widely used technique in cell biology. Stimulated emission depletion (STED) microscopy enables the recording of multiple-color images with subdiffraction resolution. The enhanced resolution leads to new challenges regarding colocalization analysis of macromolecule distributions. We demonstrate that well-established methods for the analysis of colocalization in diffraction-limited datasets and for coordinate-stochastic nanoscopy are not equally well suited for the analysis of high-resolution STED images. We propose optimal transport colocalization, which measures the minimal transporting cost below a given spatial scale to match two protein intensity distributions. Its validity on simulated data as well as on dual-color STED recordings of yeast and mammalian cells is demonstrated. We also extend the optimal transport colocalization methodology to coordinate-stochastic nanoscopy.

Many cellular processes depend on spatial arrangements of proteins and their interactions. Therefore, the analysis of spatial proximity, or colocalization, is an important tool to investigate these interaction networks. The distributions of such proteins in cells or cellular compartments are commonly visualized by fluorescence light microscopy. In conventional microscopy, the attainable optical resolution is diffraction limited. On the contrary, in diffraction-unlimited super-resolution microscopy, or nanos-copy, this resolution limit is fundamentally overcome, enabling a resolution down to the molecular scale. The quantitative colocalization analysis of such high-resolution datasets comes with new challenges. All nanoscopies rely on the molecular transitions (switching) between two (or more) fluorophore states, typically a fluorescent on’ and a dark, non-fluorescent ‘off’ state^1,2 and can be categorized into the following two types. Coordinate-stochastic nanoscopy methods such as (fluorescence) photo-activated localization microscopy (PALM) and stochastic optical reconstruction microscopy (STORM) establish the on-state at the single-molecule level, so that a sparse collection of emitters, each farther apart from the others than the diffraction limit, is able to fluoresce^3–5. The fluorophores are separately localized using a camera. Coordinate-targeted nanoscopy methods such as stimulated emission depletion (STED) and reversible saturable/switchable optical linear fluorescence transitions rely on the targeted reversible light-induced off-switching at defined spatial coordinates that are scanned over the sample^1,6–8. In coordinate-stochastic nanoscopy, the obtained data represent a collection of molecule coordinates, which are estimated from the recorded intensity distributions of single molecules. In contrast, as STED nanoscopy is scanning based, the obtained raw image data represent fluorescence distributions that are stored as matrices containing the corresponding intensities. All of these super-resolution methods can be performed in multicolor mode.

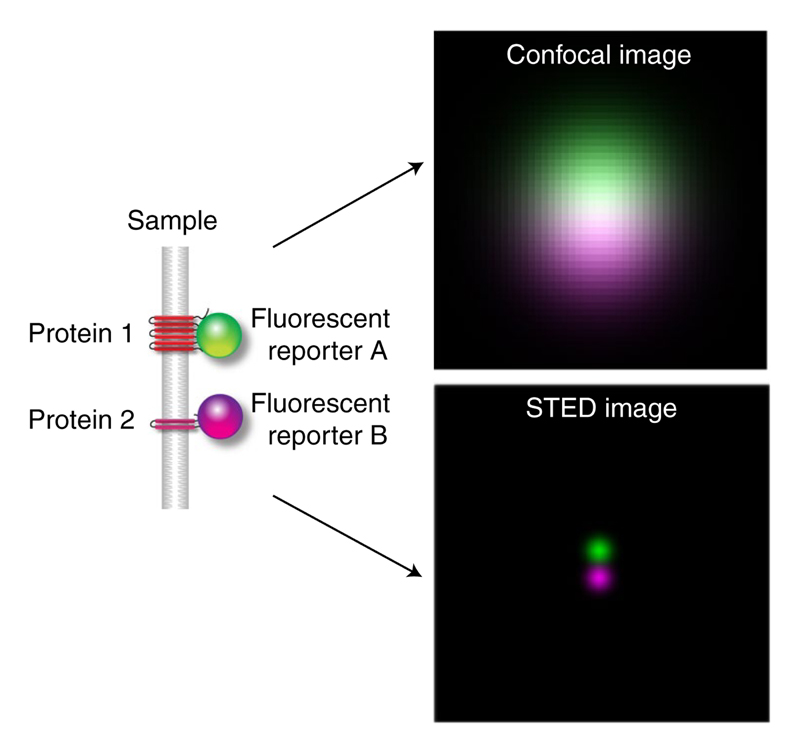
Colocalization analysis of conventional microscopy images is based on the (correlative) comparison of the pixel intensities, therefore denoted as pixel-based methods^9–12. Among the most widely used methods are those based on the correlation principle including Pearson’s correlation, a thresholded version of Pearson’s correlation^13–15 and image cross-correlation spectroscopy (ICCS)16. Manders’ colocalization coefficient^17,18 and the thresholded overlap coefficient¹⁹ are based on the direct overlap of the two intensity distributions. These methods offer a global analysis of the whole image. Developing techniques for detecting areas where colocalization occurs²⁰ and the development of spatial adaptation of the pixel-based methods²¹ are an active field of research. However, it has been noticed that the pixel-based methods are very sensitive to the resolution of the images to be compared. In fact, with increasing resolution, the correlative nature of colocalization decreases (Fig. 1 and Supplementary Video 1) as it is more likely that two neighboring proteins are imaged in two different pixels.

Fig. 1 |. Illustration of confocal and STED images obtained by Gaussian convolution of two point sources that are located at a distance of 45 nm.

The resolution of the confocal image is 244 nm and for the STED image it is 40 nm.

On the scale of a true single-molecule resolution, all these coefficients would be close to zero and hence would indicate no colocalization at all although the proteins are in close proximity at a subcellular scale. This fact leads to the need of new methods for colocalization analysis of super-resolution images and also to a new definition of colocalization. In the course of conventional light microscopy, colocalization was defined as the actual overlap of signals from two different proteins. In the era of nanoscopy, we redefine colocalization as spatial proximity between two types of molecules.

As explained above, the datasets that are generated by the two types of super-resolution microscopy methods are fundamentally different. For datasets recorded with coordinate-stochastic nanoscopy, colocalization methods based on distances or on concepts from spatial statistics are often used to overcome the above-mentioned issue^22–25. This includes a coefficient that measures the relative frequency of how often the first protein lies inside the mask of the second protein¹⁴ and colocalization methods based on Ripley’s K^26–28. Ripley’s K²⁹ measures spatial homogeneity between two point patterns. Further approaches are based on the nearest-neighbor distribution based on spatial Gibbs statistics^30,31. All these methods are known as object-based methods as they operate on the estimated coordinates of the fluorophores. On the contrary, STED raw data provide pixel images representing an intensity profile of the fluorophores. Hence, the object-based methods are not directly applicable per se. One could estimate the coordinates from the images using mathematical approaches³², as detailed in ‘Colocalization analysis of 2D and 3D STED datasets’, but this potentially comes along with the introduction of a statistical error and some loss of the pixel intensity information. The other way around, to compute normalized pair densities from overlapping Voronoi diagrams and applying afterwards Spearman’s correlation and the Manders’ method offers a way to transfer the well-established pixel-based methods to data from coordinate-stochastic nanoscopy³³. In summary, there is further demand for a direct pixel-based method that is able to quantify colocalization in coordinate-targeted nanoscopy. In this Article, we derive such a method based on optimal transport, called optimal transport colocalization (OTC) curve analysis. Moreover, we will argue that the suggested methodology can also be successfully applied to coordinate-stochastic nanoscopy. Hence, the method provides a unifying approach to measure colocalization in super-resolution images. Recently, optimal transport was used to compare the recorded intensity distributions to the uniform distribution³⁴. However, reducing the two-dimensional (2D) image data to a one-dimensional (1D) intensity distribution leads to a loss of spatial information, which is pertinent for understanding of colocalization. In contrast, our approach makes explicit use of this information, leading to a substantially different analysis. This difference will be highlighted in numerical Monte Carlo experiments and on real data. Conceptually closer to the suggested approach is entropy regularized optimal transport³⁵ for measuring spatial colocalization³⁶. This is computationally simpler, but requires the specification of a regularization parameter, which hinders a valid interpretation as a measure of colocalization from the present bio-logical perspective.

Results

Optimal transport colocalization

Optimal transport has a long history^37,38 and is nowadays a highly active area in mathematics, computer science and related disciplines³⁹. It found its way into many areas of applications and aspects of data analysis⁴⁰.

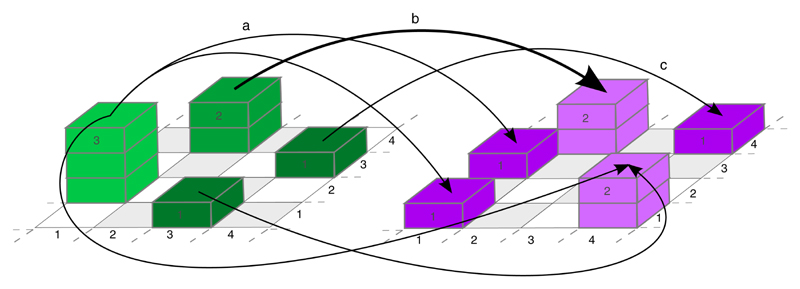
Optimal transport in general deals with the problem of transporting goods from one destination to another while archiving the smallest possible cost. In our context, this corresponds to the matching of an initial structure and a target structure on a spatial domain. As an example consider two 4 × 4 grids on which some particles (proteins of type A and B) are located (Fig. 2). In the left part of Fig. 2, the green stacks indicate how many particles of protein A are located in which pixel; the particles of protein B are visualized by the magenta stacks in the right part. Optimal transport matches these different particle distributions in the most efficient way, for example, in terms of minimal total spatial distance (cost function). The optimal transport plan (here a 16 × 16 matrix) describes the pixel location and amount of particles that are matched to achieve this minimum.

Fig. 2 |. Illustration of optimal transport based on two protein distributions.

The thickness of the arrows indicates how many particles from protein distribution A (left, green) are matched to corresponding particles in protein distribution B (right, magenta). Examples: arrow a indicates that one particle from the green stack of size three located at (1, 2) is matched with the magenta particle located at (1, 3) (mass splitting). Arrow b shows that the green stack of size two at (2, 4) is matched with the magenta stack of size two at the same location (no transport). Arrow c shows that the green stack of size 1 at (4, 3) is matched with the magenta stack of size one located at (4, 4) (shift).

Based on optimal transport, we introduce curves (OTC) as a measure for colocalization. Intuitively, OTC(t) describes the amount of mass that will be transported on distances not larger than t in the most efficient way to match two structures (two spatial intensity distributions on an image). By definition, OTC is a value in [0, 1] for any t. OTCs are monotone increasing, starting at zero and approaching one. General technical details are given in ‘OTC curves’ in Methods and how this is applied to images in ‘Protocol for OTC’ in Methods. In contrast to methods that provide a fixed colocalization value, OTC is able to quantify colocalization on different scales and even across scales, simultaneously, as demonstrated in Fig. 3 and ‘OTC curves’ in Methods. A further feature of OTC is that it is able to detect colocalization even if there is no linear relation between the two intensity distributions41 unlike Pearson’s correlation, which is not able to show nonlinear relationships. We stress that the optimal transport plan and hence the OTC curve is not unique, in general. However, uniqueness will be achieved if the same computational protocol is used, as detailed in ‘Uniqueness of OTC’ in Methods.

Fig. 3 |. OTC analysis.

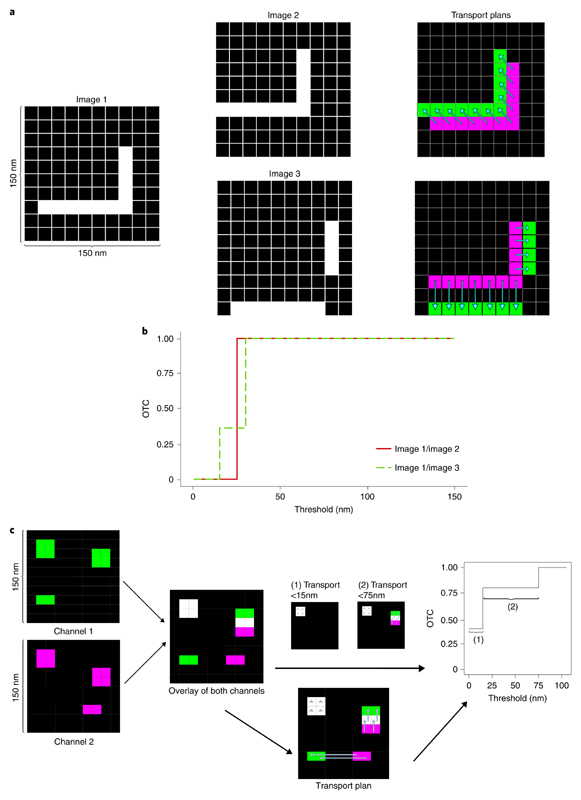
a, Pixel images with structures that are colocalized on different scales. In the right column, the transport plans of image 1 with image 2 and image 1 with image 3 are displayed via the light blue arrows. b, OTC analysis of image 1/image 2 and image 1/image 3 in a. c, Schematic for protocol to calculate OTC curves from data through the optimal transport plan. Arrows in the middle part represent the transport plan. In the case that the arrow is only a triangle, the mass stays at that pixel.

To perform the subsequent OTC date analyses on large images, a resampling scheme is introduced in ‘Computational aspects of OTC’ in Methods and mathematical evidence for its validity (confidence bands) is provided in ‘Resampling and confidence bands for OTC’ in Methods.

Evaluation of simulated images

We conducted a detailed simulation study to investigate the pixel- and the object-based methods on synthetic STED data. Four different types (sparse structures, dense structures, random points and ring-type structure, the later not shown here, see ‘Simulation setup and methods’ in Methods) of simulated image were evaluated with OTC (equation (3)) and compared with all methods listed in Supplementary Table 1.

This includes the DeBias method³⁴. A potential drawback of this method is that it does not generate a value in a fixed range, so it is hard to compare different protein combinations and furthermore they dismiss the spatial distribution of the proteins. Further details on this method, the simulation setup and the implementation of the methods to be compared are given in ‘Simulation setup and methods’ in Methods.

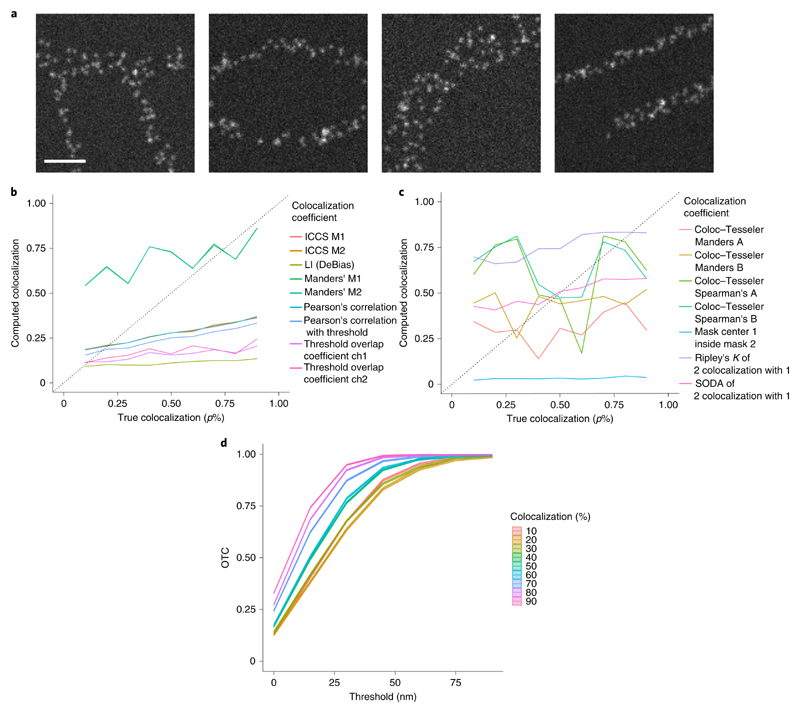
First, we investigate the case of simulated sparse structures that are similar to the true STED images evaluated in ‘Evaluation of real STED data’ (Fig. 4). Figure 4a shows exemplary images of all simulated structures. We find that none of the methods listed in Supplementary Table 1 is able to detect the right amount of colocalization (Fig. 4b,c). Here, the M1 and the M2 value of image cross-correlation spectrocsopy (ICCS M1/M2)¹⁶ give almost the same results as Pearson’s correlation. Furthermore, as there is no asymmetry in the distribution of the proteins in the two images, Manders’ M1 and M2 yield the same results. Almost all pixel-based methods (except Manders’ M1/M2) underestimate the predefined amount of colocalization (p%) in this setting (Fig. 4b). Although, the local index (LI) coefficient of the DeBias method is monotonically increasing it has a slope that is almost zero (0.05) and hence it appears difficult to discriminate between different degrees of colocalization. Furthermore, the object-based methods based on Ripley’s and Mask center inside Mask method show only very little sensitivity to the level of colocalization (Fig. 4c). The two methods based on Ripley’s K overestimate the colocalization for small percentages of colocalization and underestimate it for the high values (change points at 50% for Statistical Object Distance Analysis (SODA)27 and 70% for Ripley’s K). The coefficients calculated with Coloc−Tesseler are not even monotonically increasing. In contrast to all these methods, OTC (equation (3)) gives the right ordering of the predefined amounts of colocalization (Fig. 4). Note, that the 95% confidence intervals are so tight that they are almost not visible in the figure. They reveal significant differences for all predefined amounts of colocalization. There are two settings for which the discrimination seems to be harder than for others. For the settings 40% and 50% as well as 60% and 70% a significant discrimination is not possible over the whole range of scales, but for t = 30 nm. For an evaluation of the setting with random points, dense structures and the ring formation based on ref. ⁴², see Supplementary Section D.2 as well as Supplementary Figs. 1-3.

Fig. 4 |. Evaluation of simulated images with sparse structures.

a, Exemplary images of the simulated structures. Scale bar, 500 nm. b, Evaluation of n = 5 image sections per structure and per true colocalization (p%) with pixel-based methods. ICCS M1/M2 yield the same results as Pearson’s correlation with threshold. Furthermore, Manders’ M1 and M2 calculate the same amount of colocalization. For the threshold overlap coefficient ‘ch’ abbreviates channel. c, Evaluation of n = 5 image sections per structure and per true colocalization (p%) with object-based methods. d, OTC analysis including 95% confidence bands of n = 5 image sections per structure and per true colocalization (p%).

To sum up, we found that similar to the sparse regime, neither the pixel-based nor the object-based methods are able to detect the right amount of colocalization in simulated STED images, whereas OTC detects the right ordering in all settings.

Evaluation of real STED data

In this section, we investigate several properties of OTC on real STED datasets and compare this with other methods as well.

Comparison methods on real STED and confocal data

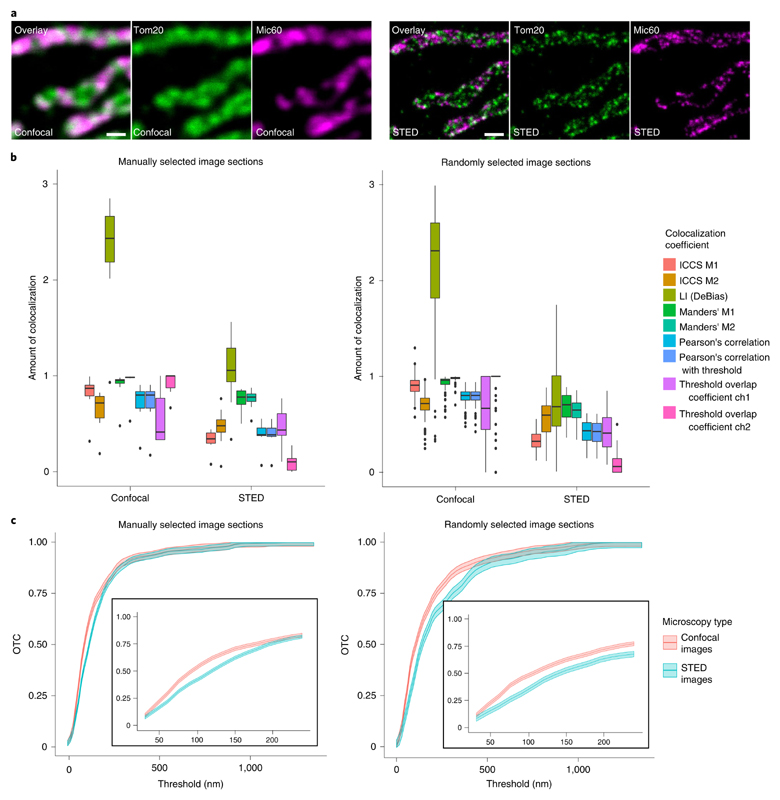
To compare the performance of OTC with the pixel-based colocalization coefficient, we utilized confocal and STED images recorded on immunolabeled human cells. We labeled the cells for a protein in the mitochondrial outer membrane (Tom20) and Mic60 in the mitochondrial inner membrane (Fig. 5a)⁴³. A simple overlay of the two confocal images reveals many white areas, that is, areas where both signals are superimposed, suggesting that the labeled mitochondrial proteins are colocalized at this level of resolution. As expected, in the overlay of the STED images, however, only a few white dots remain, due to the higher resolution of around 40 nm. This dependence of resolution and colocalization as seen by visual inspection of the images renders a quantitative determination of colocalization of STED image data challenging and is in line with our findings from the simulation study. We manually selected sections from the image datasets as well as based on the described random selection mechanism (see ‘Protocol for OTC’ and ‘Computational aspects of OTC’ in Methods). The manually selected sections contained mitochondria and were chosen based on structural preservation and signal-to-noise ratio. As the random selection mechanism singles out image regions containing fluorescence signals, the manually selected sections have a large overlap with the randomly selected sections (Supplementary Figs. 9 and 10). Both datasets were analyzed with all pixel-based methods listed in Supplementary Table 1 (Fig. 5b). Furthermore, we evaluated the manually picked sections also with all object-based methods listed in Supplementary Table 1. For the thresholded Pearson’s correlation coefficient, the background of the images is removed by iteratively setting all intensities above a given threshold to zero until the remaining pixel intensities are no longer correlated. We first determined on the manually selected sections the amount of colocalization with the pixel-based colocalization methods and compared the findings for the confocal and STED datasets recorded on corresponding regions. Overall, we find a significant decrease of the determined amount of colocalization comparing the results of the confocal and the STED image sections (see Supplementary Table 2 for precise values). Big differences can be found for Pearson’s methods, ICCS as well as on channel of the thresholded overlap. The most drastic difference is found for the LI of DeBias. This coefficient is in general hard to interpret as is can be arbitrarily large. In addition, the standard errors of the LI are about one magnitude larger than for all other methods. This shows a very high variability in the results of the LI. Hence, compared with the confocal images, we moved from the highly colocalized regime to a regime with almost no colocalization as the coefficients based on pixel intensity correlation can only detect the actual signal overlap (Supplementary Video 1). However, the two proteins are still in close proximity compared with the subcellular scale. The considerably smaller values in the analysis of the STED data illustrate that the pixel-based colocalization methods that are based on pixel-intensity correlation and are well-suited for the colocalization analysis of diffraction-limited datasets are not equally well-suited for colocalization analysis of nanoscopy datasets. The analysis of the randomly chosen datasets yields comparable results (an average over 100 different randomly selected sections was analyzed). Together, the analysis reveals that the conventional colocalization methods report very different amounts of colocalization when applied on diffraction-limited or super-resolved datasets.

Fig. 5 |. Comparison of pixel-based methods and OTC for confocal and STED images.

a, Exemplary confocal (left) and STED (right) nanoscopy images of Tom20 and Mic60 in HDFa. Tom20 and Mic60 were labeled via antisera specific for Tom20 and Mic60 respectively. Detection was facilitated through secondary antibodies custom labeled with the dyes Alexa Fluor 594 or Abberior STAR RED. Scale bar, 500 nm. b, Colocalization analysis of Tom20/Mic60 in HDFa cells with pixel-based methods. Left: analysis of n = 10 manually picked image sections per protein. Numeric values of the boxplot elements are provided in Supplementary Table 2. Right: analysis of n = 102 randomly selected image sections. Numeric values of the boxplot elements are provided in Supplementary Table 3. For the threshold overlap coefficient ‘ch’ abbreviates channel. c, OTC analysis of Tom20/Mic60 including 95% confidence bands in HDFa cells. Left: analysis of n = 10 manually picked image sections. Right: analysis of n = 102 randomly selected image sections. The inserted graphs show magnifications of the treshold region [30 nm, 250 nm].

The analysis ofboth datasets with the object-based methods shows a contrary behavior (Supplementary Fig. 6a and Supplementary Table 4). In contrast to the methods based on Ripley’s K leading to a slight decrease in the colocalization level, we find an increase for most of the coefficients calculated with Coloc−Tesseler (Manders’ B, Spearman’s A and B). For Manders’ A as well as for the Mask center inside Mask method there is almost no difference between the confocal and STED images. The observed sensitivity of object-based coefficients to resolution might be explained by the inaccuracy caused in the spot detection step due to convolution. Next, we analyzed the datasets with OTC (Fig. 5c). As described in the ‘Optimal transport colocalization’ section, OTC is a curve that increases from zero to one. Over the range of thresholds t in the interval [0, 2,000], we find a maximal difference between the average OTC curves over 10 manually selected sections of 0.12 at a threshold of 105 nm. The 95% confidence bands show that this is a significant difference. For the OTC analysis of 100 randomly selected sections, we find a difference of 0.11 at a threshold of 90 nm. In contrast to the manually picked sections, there is no significant difference at a level of 95%. Hence, as with the pixel intensity correlation-based methods, the OTC analysis also reveals only a slight difference between the manually and the randomly selected sections. In the zoomed region (Fig. 5c, inset), the OTC curves are displayed for thresholds t between 30 nm and 250 nm, which represents the characteristic range between the obtained resolution in the STED images and the resolution of the confocal images and hence is the most interesting regime. Therefore, we will restrict the evaluation of the OTC curves to the range between 30 nm and 250 nm in all following analyses. Over this entire regime, we find a slightly higher amount of colocalization in the confocal recordings than in the STED images. The higher value in the confocal images is due to the blurring caused by diffraction as there are more pixels that contain mass and hence the transport takes place on smaller scales. Interestingly, the close proximity and similar shape of the two curves over the entire spatial range shows that OTC is little sensitive to differences in resolution. In contrast to the established colocalization methods, OTC can quantify spatial proximity even if fluorophores are detected in different pixels.

Proof of concept on real STED data

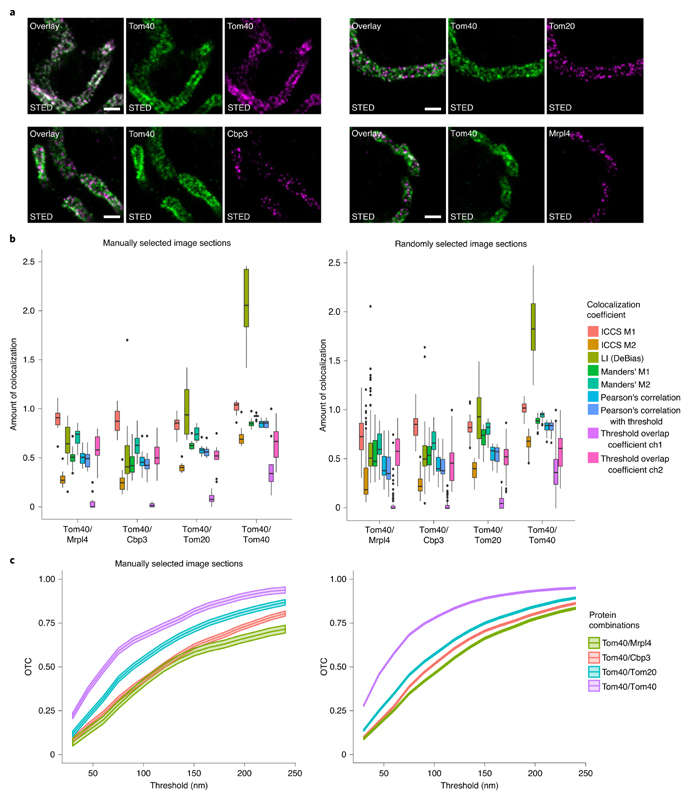
To evaluate the OTC analysis for the quantification of colocalization in STED data, we recorded dual-color STED images from yeast mitochondria labeled for the mitochondrial protein Tom40 paired with the mitochondrial proteins Tom20, Cbp3 and Mrpl4 (Fig. 6a) whose sub-mitochondrial distributions were previously investigated by cryo-immunogold electron microscopy, generating a ground truth dataset^44,45. From this dataset, it is known that Tom40 and Tom20 have the highest spatial proximity, whereas Tom40 and Mrpl4 have the least proximity and Tom40 and Cbp3 are at an intermediate proximity range. In addition, as a control experiment, we labeled Tom40 with a specific antiserum that was subsequently detected by two differently labeled secondary antibodies to generate a sample with the highest experimentally possible colocalization. An analysis with the pixel-based methods was performed on manually and randomly selected image sections of the STED data. As we found again comparable results for the manually selected and the randomly selected sections, we will only describe the findings for the manually selected image sections. We found that the conventional colocalization coefficients report that Tom40/Tom40 have a higher degree of colocalization than the other three pairs (Fig. 6b). However, these colocalization coefficients failed to find differences between the other pairs. It seems to be especially difficult to distinguish the proximity difference between the pairs Tom40/Cbp3 and Tom40/Mrpl4. Using Manders’ colocalization coefficient, we would deduce the wrong ordering of the proximity behavior. The two versions of Pearson’s correlation as well as ICCS and the thresholded overlap coefficient are also not able to distinguish between the proximity of these two protein pairs; neither is the LI of DeBias (see Supplementary Tables 5 and 6 for precise values). All pixel-based methods besides ICCS find a slightly higher amount of colocalization of Tom40/Tom20 compared with Tom40/Cbp3 and Tom40/Mrpl4, which corresponds to the ground truth derived from electron microscopy data⁴⁴. ICCS obtains the wrong ordering even for this protein combination.

Fig. 6 |. Proof of concept for OTC analysis on proteins with known proximity.

a, Exemplary STED nanoscopy images of protein pairs with a known decrease of colocalization. Top-left triple, Tom40/Tom40; top-right triple, Tom40/Tom20; bottom-left triple, Tom40/Cbp3; bottom-right triple, Tom40/Mrpl4. Labeling was achieved via antisera specific to Tom40 or GFP respectively. Detection was facilitated through secondary antibodies custom labeled with the dyes Alexa Fluor 594 or Abberior STAR RED. Scale bar, 500 nm. b, Colocalization analysis of the data represented in a with pixel-based methods. For the Coloc-Tesseler methods, one gets only a summary value for the whole dataset. Left: analysis of n = 10 manually picked image slices per protein combination. Numeric values of the boxplots are provided in Supplementary Tables 5 and 6. Right: analysis of randomly selected image slices (Tom40/Cbp3 n = 105, Tom40/Mrpl4 n = 100, Tom40/Tom20 n = 100, Tom40/Tom40 n = 100). Numeric values of the boxplots are provided in Supplementary Tables 7 and 8. For the threshold overlap coefficient ‘ch’ abbreviates channel. c, OTC analysis including 95% confidence bands of the datasets represented in a. Left: analysis of n = 10 manually picked image sections per protein combination. Right: analysis of randomly selected image sections (Tom40/Cbp3 n = 105, Tom40/Mrpl4 n = 100, Tom40/Tom20 n = 100, Tom40/Tom40 n = 100). See Supplementary Videos 2 and 3 for an illustration of the optimal transport.

Furthermore, we analyzed the manually selected image sections with all object-based methods (Supplementary Fig. 6b and Supplementary Table 9). None of the object-based methods is able to detect the right ordering of the protein combinations. In contrast, the OTC analysis on the same datasets reveals a difference between all four labeled pairs; the order of spatial proximity is fully in line with the known distribution of the proteins (Fig. 6c). However, according to the OTC analysis the difference between Tom40/Mrpl4 and Tom40/Cbp3 is only marginal (in a range between 0.01 and 0.09). The difference gets bigger for thresholds larger than 150 nm. These findings are supported by the confidence bands. Comparing the OTC analysis of the manually selected and the randomly selected image sections, we find that the randomly selected sections give a better representation over the whole regime. We can deduce from this OTC curves that the difference in the degree of colocalization for the pair Tom40/Tom40 compared with the three other pairs is much larger (difference to OTC curve of Tom40/Tom20 in range between 0.06 and 0.23). The differences between the OTC curves of Tom40/Tom20 and Tom40/Cbp3 are between 0.03 and 0.07 and for Tom40/Cbp3 and Tom40/Mrpl4 between 0.007 and 0.055. Especially for the small scales between 30 nm and 75 nm, the degree of colocalization of Tom40/Mrpl4 is almost not distinguishable from the degree of colocalization of Tom40/Cbp3. Nevertheless, the uniform 95% confidence bands show a significant difference between Tom40/Mrpl4 and Tom40/Cbp3. The Supplementary Information contains videos that illustrate the transport from Tom40 to Mrpl4 and from Tom40 to Tom40 (Supplementary Videos 2 and 3).

OTC is robust against background

A common challenge of immunofluorescence microscopy is an unspecific background signal, which often complicates the analysis of the images. We labeled adult human dermal fibroblasts (HDFa) with antibodies against the mitochondrial proteins Tom20 and Mic60 or with antibodies against Tom20, Mic60 and Mic27. The antibody against Mic27 binds to the Mic60 interacting protein Mic27, and, in addition to unspecific structures in the cells. As a result, the cells labeled with the Mic27 antibody show a stronger background signal (Supplementary Fig. 7a). We asked the question whether OTC can be used also to analyze such noisy datasets. Manually as well as randomly selected sections from the noisy datasets and the datasets that have a low background were analyzed with OTC (Supplementary Fig. 7b). For the manually selected section, we found that the colocalization in the recordings with high background is a little higher than in the recordings with low background (maximal difference 0.12). The 95% confidence bands indicate that this difference is significant. In contrast, for the randomly selected sections, there is even a smaller difference (maximal difference 0.02). The confidence bands prove this findings. Where Fig. 6b already indicated a slightly better performance of OTC with randomly selected sections, we found evidence that the random selection mechanism performs better in the case of noisy data. The robustness of OTC against background is in line with the robustness of the pixel-based methods (Supplementary Fig. 11).

Colocalization analysis of 2D and 3D STED datasets

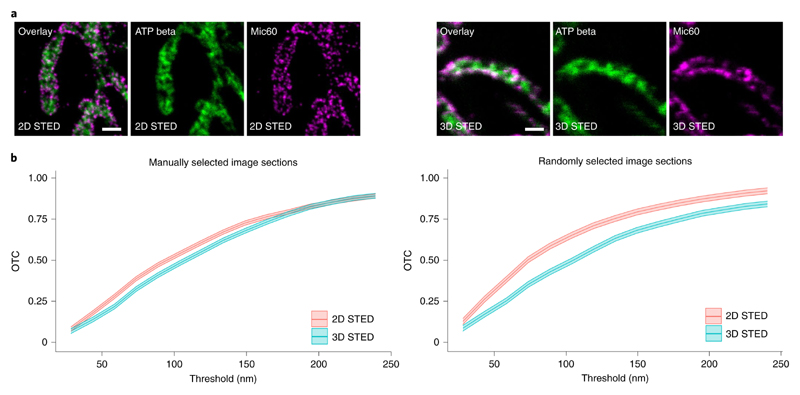
So far, we have analyzed STED images that were recorded in the 2D mode. Here we compare OTC analysis of datasets recorded in the 2D and 3D modes. In the case of the 3D mode, the STED microscope provides an almost uniform 3D resolution of <100 nm in all directions in space and in the 2D mode it provides ~40 nm lateral resolution and ~500 nm axial resolution. We imaged human osteosarcoma cells (U2OS) labeled for the inner membrane proteins Mic60 and a beta subunit of the F₁F_O ATP synthase (ATP beta) in the 2D and 3D modes (Fig. 7a). Mic60 is enriched at the crista junctions, whereas the ATP beta is primarily localized in the crista membrane. Therefore, Mic60 is localized at the rim of the tubular mitochondria, whereas the ATP beta is preferentially distributed in the organelle’s interior. As 2D STED inherently makes a 2D projection of the mitochondrion, we expect that the detected colocalization between the images recorded in the 2D mode is higher than the colocalization in the 3D mode. Contrary to this expectation, the visual impression of the 2D and 3D STED images (Fig. 7a) suggest that the colocalization between the 3D STED images is higher than between the 2D STED images. To analyze this counterintuitive observation, we evaluate manually and randomly selected sections from both datasets with OTC (Fig. 7b). For the manually selected sections, we find a small difference (~0.05) between the colocalization in the 2D and the 3D images for thresholds smaller than 175 nm. For thresholds between 175 nm and 250 nm, we cannot deduce a difference. Here the OTC analysis with randomly selected sections shows the difference in the colocalization between the 2D and 3D STED images more clearly. To be more precise, the difference between the curves of the randomly selected sections ranges over the whole range of thresholds from 0.04 to 0.15. The 95% uniform confidence bands reveal that these differences are significant. Altogether, OTC analysis of STED data recorded in the 3D mode provides better results in this setting where proteins in a relatively thick organelle are imaged. Such a benefit was not observed in the analysis of the same data with the pixel-based methods (Supplementary Fig. 12). For the LI of DeBias, it gets even worse for the 3D point-spread function (PSF) instead of the 2D PSF.

Fig. 7 |. The application of a 3D STED PSF enhances colocalization analysis.

a, Exemplary STED nanoscopy images of ATP beta and Mic60 in human osteosarcoma cells (U2OS). A 2D STED PSF (superior resolution along the x and y axes but no improvement along the z axis) was utilized to generate the images shown on the left side. A 3D STED PSF (isotropic resolution improvement) was applied to generate the images shown on the right side. ATP beta and Mic60 were labeled using antisera specific for ATP beta and Mic60 respectively. Detection was facilitated through secondary antibodies custom labeled with the dyes Alexa Fluor 594 or Abberior STAR RED. Scale bar, 500 nm. b, OTC analysis including 95% confidence bands of the datasets represented in a. Left: analysis of n = 10 manually picked image sections per 2D/3D PSF. Right: analysis of n = 102 randomly selected image sections per 2D/3D PSF.

OTC on data from coordinate-stochastic nanoscopy

To investigate the performance of OTC on data from coordinate-stochastic nanoscopy, we imitate such datasets by estimating the location of the fluorophores with the wavelet spot detector implemented in ICY⁴⁶ for all real data STED images. This results in datasets containing lists with molecule coordinates. The evaluation of the yeast dataset (the dataset with known spatial proximity) also reveals that Tom40/Tom40 has the highest colocalization. However, compared with the analysis without estimating the coordinates, OTC did not order the other three pairs correctly. For thresholds t greater than 250 nm, OTC detects that Tom40/Cbp3 is the pair that shows the farthest distance (Supplementary Fig. 8a). Also in the cases with high and low background, the outcome of the OTC analysis is not as good as for the STED data. The colocalization in the high-background setting is estimated lower than in the low-background setting. Surprisingly, the high background does not lead to a larger number of estimated locations in this channel, but it leads to the fact that there are more locations estimated in the background and hence the transport has to take place on larger scales (Supplementary Fig. 8b). The evaluation of the locations of the data from the comparison between 2D and 3D STED PSF is in line with the findings on the STED images (Supplementary Fig. 8c). Contrary to the visual impression, OTC also reveals here that the colocalization between the 3D STED datasets is less than for the 2D STED datasets. Altogether, our computer experiments suggest that OTC is also applicable on data from coordinate-stochastic nanoscopy. In this evaluation, we found that some results are biased by the wrong detection of spots.

Discussion

Bearing in mind the challenges of colocalization analysis in super-resolution light microscopy, it seems to be prudent to reassess the concept of colocalization for nanoscopy in general. It seems to be appropriate to overcome the terminology of correlation and to speak of relative spatial proximities of protein distributions at a certain spatial scale when it comes to nanoscopy datasets. This is reflected in OTC curves, which also reflect the fact that two protein clusters will never be physically perfectly colocalized as they cannot be at the same location at the same time. Our analysis suggests that OTC also will be a valid tool for other scanning-based nanoscopy methods, for example, reversible saturable/switchable optical linear fluorescence transitions. This, however, has to be investigated carefully in future work. Our computer experiments further suggest that OTC analysis performs quite well on data from coordinate-stochastic nanoscopy but evidence on real OTC data has not been given. OTC takes care of the intensities as it matches intensity distributions in an optimal way. This has been achieved by rescaling these intensities to total mass one and can become critical when the total intensities differ too much or when a protein matching in a many to one correspondence is the biological target. Adaptations to such situations, for example, based on partial transport, have to be investigated carefully in future research. It also would be of interest to extend the current OTC method to distance thresholds and geometric constraints depending on a priori biological knowledge from object-based methods^26,30,31 to a pixel-based method.

In contrast to pixel-based methods (Supplementary Fig. 12), the performance of OTC analysis is enhanced by the application of a 3D STED PSF (Fig. 7) and therefore enables users to utilize the full potential of modern 3D STED nanoscopy. It would be important to investigate this for other 3D nanoscopy devices, including MINFLUX⁴⁷.

Methods

OTC curves

To reformulate the colocalization problem in terms of optimal transport, we consider the set of N pixels as a ground space χ = {x₁,…, x_N} The (non-negative) intensities on the images are standardized, such that they sum up to one and hence can be considered as discrete probability distributions on these N pixels (see ‘Protocol for OTC’ for a detailed description of the protocol). The set of probability measures on χ is denoted as

$${\Delta }_N=\left\{r\in {ℝ}^N:r_i\ge 0,1\le i\le N\text{and}{\displaystyle \sum _{i=1}^N{r}_i=1}\right\}.$$

The optimal transport distance of order 2 for the Euclidean cost function ||·|| between two such probability measures r, s ∈ Δ_N is now given by

$$W_2\left(r,s\right)={\left(\underset{\pi \in \Pi \left(r,s\right)}{\min }{\displaystyle \sum _{i,j=1}^N{\Vert x_i-x_j\Vert }^2{\pi }_{ij}}\right)}^{1/2},$$ (1)

where

$$\Pi \left(r,s\right)=\left\{\pi \in {ℝ}^{N\times N}:{\displaystyle \sum _{i=1}^N{\pi }_{ij}=r_j,{\displaystyle {\sum }_{j=1}^N{\pi }_{ij}=s_i}}\right\}$$ (2)

is the set of matrices such that their columns sum up to r and their rows to s. The matrix π* for which the minimum in equation (1) is attained is called optimal transport plan and each entry ${\pi }_{ij}^{*}$ describes the amount of mass that is transported from pixel i in the first image to pixel j in the second one in the most efficient way. Basic properties and computation of these optimal transport plans are summarized in ‘Computational aspects of OTC’. We introduce the OTC curve at spatial size t (scale) between two probability measures r and s as

$$\text{OTC}\left(t\right):={\displaystyle \sum _{i,j=1}^{N}1\left\{\Vert x_i-x_j\Vert \le t\right\}{\pi }_{ij}^{*},}$$ (3)

where 1 is the indicator function, that is

$$1\left\{\Vert x_i-x_j\Vert \le t\right\}=\{\begin{array}{ll}1,\hfill & \text{if}\Vert x_i-x_j\Vert \le t\hfill \\ 0,\hfill & \text{else}\text{.}\hfill \end{array}$$

Figure 3a illustrates the case of colocalized structures that require only a relatively small spatial adjustment to be matched, that is, they are highly colocalized at a small spatial scale. For image 1 and image 2 in Fig. 3a, we observe that these structures are perfectly colocalized at a distance of one pixel in the diagonal direction. This is displayed by the optimal transport plan, which is indicated as light blue arrows in the right column of Fig. 3a. The structures in image 1 and image 3 are colocalized on different scales, that is, the vertical part is shifted by one pixel and the horizontal part by two pixels, see the respective optimal transport plan shown as light blue arrows in the right column of Fig. 3a. The size of the pixels in the three images is set to 15 nm as in the following real datasets. Hence, the whole image is contained in [0 nm, 150 nm]². The OTC curve captures these different scales, see Fig. 3b. The red curve indicates that the structures in image 1 and image 2 are perfectly colocalized at a scale of 25 nm. The green dashed curve shows that roughly 37% of the objects in images 1 and 3 (that is, the vertical part) are colocalized at a scale of 15 nm and the whole structures are colocalized at a scale of 30 nm.

Protocol for OTC

We consider an N_x × N_y = N pixel image with intensities as generated by STED nanoscopy as a probability measure in two dimensions by rescaling the intensities such that they sum up to one. This can be done for a given image by dividing each pixel intensity with its total intensity (which is measured). More precisely, for a pixel size of l nm, we consider the image as a probability measure supported on an equidistant grid in [0, N_x·l] × [0, N_y · l]. The equidistant grid represents the pixels, that is, x_{(j−1)Ny + i} = P_ij, where P_ij for i = 1, …, N_y and j = 1,…,N_x denotes pixel i, j which is represented by its midpoint. OTC is calculated for these two probability distributions, which represent the pixel intensities according to equation (3). For a given threshold of t nm, the OTC is given by equation (3) as the proportion of mass that is matched at distances less than t nm. See Fig. 3c for a schematic representation.

Uniqueness of OTC

The optimal transport plan and hence the OTC curve in equation (3) is not unique, in general, that is, the vertex in the simplex of possible (optimal) solutions that is selected may depend on the specific algorithm used (Supplementary Fig. 5). Although empirically we found the differences to be small, we suggest to compare OTC curves over different samples when generated with the same algorithm. The algorithm used in this paper to solve the optimal transport plan is based on the shielding method⁴⁸ in combination with a CPLEX solver (‘Computational aspects of OTC’). The shielding algorithm is particularly suited for our purposes as this method solves the problem in an iterative manner by refining the grid in each step and using the solution from the previous step as the starting value. Hence, our method converges to a unique solution. Another way to overcome the non-uniqueness is to regularize the optimal transport problem such that a strictly convex optimization problem results. Applying this regularization technique leads to an entropy-regularized version of OTC³⁶. However, despite computational advantages, conceptual issues occur. Intuitively, regularization leads to spreading the transport plan smoothly in many directions. The amount will depend on the regularization parameter that has to be chosen by the data analyst. In contrast, the exact plan provided by optimal transport is genuinely sparse as its number of support points is always less than 2N + 1. Further, the interpretation of colocalization as minimizing a total transport cost (in the sense of a distance) is not valid anymore for such penalized surrogates. This typically results in a blurred colocalization curve, which can lead to a wrong specification of the colocalization level. See Supplementary Fig. 4 for the comparison of a regularized and an exact transport plan where the (regularized) transport plan between image 1 and image 2 of Fig. 3 is displayed.

Computational aspects of OTC

For all computational tasks we use R⁴⁹ version 4.0.2. The optimal transport plan is calculated with the R package transport (v0.12-2)⁵⁰ which uses the shielding algorithm⁴⁸. To deal with images of large size outside the scope of computational feasibility, we propose a uniform random sampling scheme (statistically justified and described in ‘Resampling and confidence bands for OTC’) that selects image sections of size 128 × 128 pixels from bigger images to gain computational speed. Further, we analyze the colocalization only in image sections that are not only background. To this end, we select sections such that the proportion of the pixels that are non-zero is at least as large as the proportion in the whole image. The OTC is robust to a varying size of randomly selected image sections (Supplementary Fig. 13). For smaller image sections, the OTC curves have a larger slope as the maximal distance on which mass can be transported is smaller for smaller image sections.

Resampling and confidence bands for OTC

For many computations, we have used the resampling protocol in the previous section to decrease the size of image pairs that are used to compute the OTC. In general, we evaluate n image pairs of protein combinations. To estimate the true colocalization of the two proteins under investigation, we define the empirical OTC as

$$\widehat{{\text{OTC}}_n}\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\text{OTC}}_i\left(t\right).}$$ (4)

If the OTC curve can be computed on the entire image of size N, n = 1. However, as for large-scale images of size N it is not feasible to compute the full OTC, we restrict to OTCs computed on subimages (sections). In our application, we have chosen sections of size 128 × 128. Accordingly, we denote by OTC_128×128)(t) the true (population) colocalization averaged over all possible (squared) sections of 128 × 128 pixels, which are (up to boundary effects) of the order ${\left(\sqrt{N}-128\right)}^2=O\left(N\right)$. This average is still too large to compute explicitly in many applications (as N can be easily of the magnitude of several million pixels) and we specify the following randomized computational scheme. Consider each patch indexed by its left upper corner x_i, say, and choose randomly n < < N of such sections, that is, its index is independently chosen and uniformly distributed over the full grid of N pixels (up to boundary values), which gives, as n grows⁵¹

$$\sqrt{n}\left(\widehat{{\text{OTC}}_n}-{\text{OTC}}_{128\times 128}\right)\left(t\right)\stackrel{𝒟}{\to }𝒢\left(t\right),$$

where $𝒢$ denotes a mean zero Gaussian process. Here, $\stackrel{𝒟}{\to }$ indicates convergence in distribution. Then, the continuous mapping theorem yields

$$\sqrt{n}{\Vert \widehat{{\text{OTC}}_n}-{\text{OTC}}_{128\times 128}\Vert }_{\infty }\stackrel{𝒟}{\to }{\Vert 𝒢\Vert }_{\infty }.$$ (5)

With equation (5), we can provide approximate confidence bands for OTC. Let α ∈ [0, 1] and u_1−α the 1 − α quantile of ${\Vert 𝒢\Vert }_{\infty }$. Then, the approximate uniform confidence band is given by

$$\left[\widehat{{\text{OTC}}_n}-\frac{u_{1-\alpha }}{\sqrt{n}},{\widehat{\text{OTC}}}_n+\frac{u_{1-\alpha }}{\sqrt{n}}\right].$$ (6)

For given data, it is sufficient to compute the OTC curves for finitely many ts, that is t₁…,t_m. To simulate the u_1−α quantile of ${\Vert 𝒢\Vert }_{\infty }$, we estimate the covariance matrix of $𝒢$ by the multivariate samples (OTC₁(t₁),…, OTC₁(t_m)),…, (OTC_n(t₁),…, OTC_n(t_m)) and compute in each simulation step the value of ${\Vert 𝒢\Vert }_{\infty }$. For the confidence bands in all figures, we choose α=0.05.

Simulation setup and methods

We simulated pairs of images. The first STED image was simulated as follows:

• (1)n points are uniformly drawn in a pre-specified area.
• (2)The points are matched to an equidistant grid in [0, N_x · l] × [0, N_y · l] with pixel size of l nm.
• (3)The images (number of counted photons per pixel) are generated by a realization of a Poisson distribution with Poisson noise, that is, as Pois(t · g) + Pois(t · λ). Here, t denotes the number of pulses, g the fluorescence intensity and λ the noise intensity which equals half the response probability of a fluorophore, which is given by a uniformly drawn value in the interval [0.7α, 1.3α]. Furthermore, α denotes the average activation probability of the fluorophores.

The fluorescence intensity is given by a convolution of the pixel image on which we mapped the points in the second step scaled with the response probability with a simulated PSF. We choose to model the STED PSF with a Gaussian kernel, which is approximated by $2^{-\frac{{\Vert x\Vert }^2}{{\sigma }^2}}$ with ${\sigma }^2=\frac{\text{FWHM}}{2}$ (ref. 52). Full-width at half-maximum (FWHM) is approximately the resolution of the microscope. Note, that the kernels are normalized in such a way that their maximum is 1.

For the second STED image with colocalized points, we draw uniformly a pre-defined percentage p% of the points²⁷. In the analysis of the simulation results, we will refer to p% as true colocalization. To determine the colocalized partner, we locate the second spot on a circle around the spot from the first image. The radius r of this circle is distributed according to the absolute value of a normal variate $\mathcal{N}\left({\mu }_r,{\sigma }_r^2\right)$ and the angle is chosen uniformly. Here, μ_r is the expected scale on which the points colocalize. The remaining 1 − p% points are chosen uniformly in the pre-specified structure. Step two and three are performed as described above.

With this set up, we consider two different scenarios. First, random points in the square [0, N_x · l] × [0, N_y · l] with pixel size of l nm and N_x=N_y. Second, we restricted the sampling points to the four different structures..An exemplary image from the random points setting (Supplementary Fig. 1a) as well as exemplary images for the different structures (Fig. 4 and Supplementary Fig. 2) are displayed. In the second set up, we study two different settings. First, sparse structures with the same number (n₁ = n₂ = 100) of points in both channels (Fig. 4a) and second, dense structures with the same number (n₁ = n₂ = 1000) of points in both channels (Supplementary Fig. 2a).

For our simulations, we choose images of size 128 × 128 pixels with a pixel size of 15 nm. These are the same parameters as in the real data from the next subsections. The number of pulses is chosen to be t = 2,000, an activation probability of α = 0.01 and a resolution of 40 nm (this is also approximately the resolution of the real datasets considered in this paper). Furthermore, we choose the parameters μ_r = 30 nm and ${\sigma }_r^2=0.5$ for the distance of the colocalized points and varied the amount of colocalized points for all p% ∈ {10, 20,..90}. For the random points setting, we simulated 100 pairs of images for each p% and for the different structures five pairs per structure, that is, 20 images in total for each channel and each p%.

Methods included in the study

For the DeBias method, we used the original implementation in MATLAB (MATLAB version 2018a). As it is rather complex and relates to our approach as it compares intensity histograms using optimal transport, we summarize the main steps here. The first step of the DeBias method is to normalize the recorded intensities (x_i)_i, (y_i)_i such that they are in the interval [0, 1]. The next step is to subtract the two protein distributions pixel-wise, that is x_i − y_i. From this point on, one needs to gather all intensity differences in a 1D histogram with K bins and find an optimal K³⁴. The obtained histogram is resampled to calculate the global index (GI). The GI is defined as the optimal transport distance of order one between the resampled histogram and the histogram of the uniform distribution with K bins on the range of the intensity differences. The LI is given by the difference between the optimal transport distance of order one of the observed histogram and the uniform histogram and GI. For Pearson’s correlation, ICCS and Manders’ M1/M2 we used an own implementation to calculate these values. Pearson’s correlation with threshold and Manders’ M1/M2 are sensitive to the threshold, so we use the optimal threshold¹³. For the thresholded overlap coefficient, we used the original implementation in Squassh (as part of ImageJ 2.0.0)¹⁹ as it is based on an image segmentation method. The object-based methods all rely on a spot detection; therefore, we used the wavelet spot detector in ICY (version 2.0.3.0)⁴⁶ and also the colocalization studio53 for the evaluation of the object-based methods besides Coloc−Tesseler³³. The methods based on Ripley’s K are strongly dependent on input parameters. One needs to choose a maximal radius for these methods and if it is chosen too small, the methods will not detect any colocalization at all. Hence, one needs to have some a priori information about the scale on which the investigated proteins colocalize. We chose the preset value of five pixels as this maximal radius. This corresponds to 75 nm, which is double the mean predefined colocalization distance. For Coloc−Tesseler (version 1.0)³³ we used the GUI available on GitHub.

Statistics and reproducibility

The staining of the proteins was done with a standard technique and repeated more than three times for all images shown in Figs. 5–7 and Supplementary Figs. 7, 9 and 10.

Yeast strains

For colocalization analysis of mitochondrial proteins in the yeast Saccharomyces cerevisiae wild-type or newly tagged strains isogenic to the wild type strain W303 were used. The generation of GFP (green fluorescent protein) fusions of the proteins of interest was achieved by genomic tagging (Supplementary Table 18) via a HIS3 cassette for positive selection as described previously^44,54. Cultivation of yeast cells was done, using standard protocols, in liquid media containing 2% (w/v) galactose as the sole carbon source.

To verify the expression of full-length fusion proteins, logarithmically growing yeast cells, with galactose as their only carbon source, were collected by centrifugation and incubated on ice for 20 min in lysis buffer (2 M NaOH; 5% (v/v) β-mercaptoethanol, 20 mM EDTA; 20 mM PMSF; protease inhibitors (Complete protease inhibitor cocktail, Roche)). Proteins were precipitated by TCA (trichloroacetic acid) and separated from soluble components by centrifugation (16,000 × g). The ensuing protein pellets were neutralized using TBE buffer (100 mM tris(hydroxymethyl)aminomethane; 100 mM boric acid; 2 mM EDTA; pH 8.3) resuspended in PAGE sample buffer and denaturized by incubation at 95 °C for 5 min. Subsequently, the samples were analyzed by immunoblotting using a GFP-specific antiserum (Clontech; diluted 1/3,000 in blocking buffer). As a loading control, porin-specific antiserum (abcam; diluted 1/3,000 in blocking buffer) was utilized. Viability analysis of the newly generated strains on fermentable and non-fermentable carbon sources was done by spotting tenfold serial dilutions of logarithmically growing cells onto plates containing the carbon sources for fermentable (glucose) or non-fermentable (glycerol) growth. Viability was analyzed after 4 d of incubation at 30 °C. Only strains expressing full-length fusion proteins (Supplementary Fig. 14) and showing wild-type-like growth rates on a non-fermentable carbon source were used for this study (Supplementary Fig. 15).

Immunofluorescence labeling of yeast cells

Cultivation, preparation and immunolabeling was done as described previously⁴⁴. Essentially S. cerevisiae cells were grown to the early logarithmical phase (OD_600nm = 0.4−0.7) and fixed with 3.7% formaldehyde in growth medium. Subsequently cell walls were partially removed via zymolyase treatment and the cells were attached to the surface of cover slips coated with poly-L-ysine. Cells were blocked (2% (w/v) bovine serum albumine; 0.4% (w/v) SDS; 0.1% (v/v) Tween20 in PBS/sorbitol) and decorated with antisera specific to GFP (anti-GFP [3E6] mouse, Thermo Fisher Scientific, A11120, lot 1859591) or Tom40 (anti-Tom40, rabbit, Peter Rehling, Georg-August-University Göttingen, Germany⁵⁵) respectively. Primary antibodies were detected via incubation with secondary antibodies custom-labeled with Abberior STAR RED (Abberior) or Alexa Fluor 594 (Thermo Fisher Scientific). Finally the samples were mounted using Mowiol containing 1,4-diazabicyclo[2.2.2] octan (DABCO).

Cultivation and immunofluorecence labeling of human cells

Cultivation of HDFa and human osteosarcoma cells (U2OS) was done in compliance with standard protocols. Cells were grown in DMEM containing 4.5 g l⁻¹ glucose and GlutaMAX additive (Thermo Fisher Scientific) supplemented with 100 U ml⁻¹ penicillin and 100 μg ml⁻¹ streptomycin (Merck Millipore), 1 mM sodium pyruvate (Sigma Aldrich) and 10% (v/v) fetal bovine serum (Merck Millipore). Cells were cultivated on glass coverslips for 1−3 d at 37°C and 5% CO₂. Fixation and immunolabeling was done as described previously⁵⁶. In brief, cells were fixed using a 4% formaldehyde solution (pre-warmed to 37°C), permeabilized by treatment with 0.5% (v/v) Triton X-100 and blocked with 5% (w/v) bovine serum albumin. The proteins of interest were labeled by specific antisera against Tom20 (anti-Tom20, mouse, BD Biosciences, Clone 29/Tom20, 612278, lot 6210812), Mic60 (anti-Mic60/IMMT, rabbit, Proteintech, 10179-1-AP, lot 2), Mic27 (anti-APOOL/Mic27, rabbit, ATLAS Antibodies, HPA000612, lot A96569) and ATPB (anti-ATPB, mouse, abcam, [4.3E8.D10], ab5432, lot GR3177231-2), respectively. Detection was facilitated via secondary antibodies custom-labeled with Abberior STAR RED (Abberior) or Alexa Fluor 594 (Thermo Fisher Scientific), respectively. Finally, the samples were mounted using Mowiol containing DABCO.

STED nanoscopy

Super-resolution light microscopy was performed using a 775 nm quad scanning STED microscope (Abberior Instruments) equipped with a UPlanSApo 100x/1,40 Oil [infinity]/0,17/FN26,5 objective (Olympus) and a Katana-08 HP laser (Onefive) utilizing a pixel size of 15 nm (2D PSF) or 40 nm (3D PSF). Fluorophore excitation was facilitated at 594 nm or 640 nm, respectively, whereas STED was achieved using a wavelength of 775 nm. Besides contrast stretching, no other image processing technique was applied. The STED microspcope was controlled by Imspector 0.14.13919.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

All data⁵⁷ used to create the figures in the main text as well as in the supplement can be found in the Zenodo archive at https://doi.org/10.5281/zenodo.4553856 as well as in the GitHub repository. The data for all figures and Extended Data figures are available in Source Data.

Code availability

The code⁵⁸ is available on GitHub. The specific version of the OTC package and the scripts generating all figures in this paper can be found at https://doi.org/10.5281/zenodo.4553632. To speed up computation we used the solver CPLEX (v12.6.3.0)⁵⁹. This IBM product is free for academic use. To download the solver sign up for the IBM academic initiative and download the solver afterwards. To use the solver, download the transport package⁵⁰ from CRAN as a tar.gz file and change the settings in the makevars file before installing the package. To reproduce any results from the paper please just run the respective script. Without the CPLEX solver, the runtime may take much longer or will not terminate on a standard laptop. With the CPLEX solver, the script for Fig. 5 requires less than 10 min runtime on a standard laptop. If you want to use the OTC package with your own data please see the read me on GitHub.