Pitch perception at very high frequencies: On psychometric functions and integration of frequency information

Abstract

Lau et al. [Lau, Mehta, and Oxenham (2017), J. Neuroscience, 37, 9013-9021] showed that discrimination of the fundamental frequency (F0) of complex tones with components in a high frequency region was better than predicted from the optimal combination of information from the individual harmonics. The predictions depend on the assumption that psychometric functions for frequency discrimination have a slope of 1 at high frequencies. This was tested by measuring psychometric functions for F0 discrimination and frequency discrimination. Difference limens for F0 (F0DLs) and difference limens for frequency (FDLs) for each frequency component were also measured. Complex tones contained harmonics 6-10 and had F0s of 280 or 1400 Hz. Thresholds were measured using 210-ms tones presented diotically in diotic threshold-equalizing noise (TEN) and 1000-ms tones presented diotically in dichotic TEN. The slopes of the psychometric functions were close to 1 for all frequencies and F0s. The ratio of predicted to observed F0DLs was around 1 or smaller for both F0s, i.e. not super-optimal, and was significantly smaller for the low than for the high F0. The results are consistent with the idea that place information alone can convey pitch, but pitch is more salient when phase locking-information is available.

I. Introduction

Pitch is important for the perception of music, the perception of speech intonation, and the segregation of sounds in complex auditory scenes (see e.g. Brokx and Nooteboom, 1982; Scheffers, 1983; Hartmann, 1996; Vliegen and Oxenham, 1999). Popular models of pitch perception depend at least partly on the use of information derived from the pattern of phase locking in the auditory nerve (Cariani and Delgutte, 1996; Meddis and O'Mard, 1997; de Cheveigné, 1998), and phase locking has generally been assumed to be weak or absent for frequencies above about 4-5 kHz (Johnson, 1980; Palmer and Russell, 1986), although the exact upper limit of phase locking in the auditory nerve in humans is unknown (Verschooten et al., 2019). The importance of phase locking cues for pitch perception has been challenged recently by studies showing good melody discrimination for complex tones consisting only of high-frequency components (all audible components above 6 kHz) but with a “missing” fundamental frequency (F0) that is much lower (Carcagno et al., 2019; Oxenham et al., 2011). The present paper re-examines the differences in pitch perception for complex tones with medium-frequency components and tones with very high-frequency components, and tests one of the assumptions underlying a recent claim that discrimination of the fundamental frequency (F0) of complex tones with components in a high frequency region was better than predicted from the optimal combination of information from the individual harmonics (Lau et al., 2017).

Lau et al. (2017) used complex tones containing harmonics 6-10 with an F0 of either 1400 Hz, with the lowest harmonic at 8.4 kHz, where phase locking is assumed to be weak or absent, or an F0 of 280 Hz, with the lowest harmonic at 1680 Hz, where phase locking would occur. The tones were presented at a low sensation level in threshold-equalizing noise (TEN; Moore et al., 2000), to mask possible distortion products, and individual component levels were randomized by ±3 dB to reduce level cues. Lau et al. (2017) measured difference limens for fundamental frequency (F0DLs) and difference limens for frequency (FDLs) for the individual harmonics presented in isolation. For the high F0, the FDLs were very large (around 20-30%), but the F0DLs were much smaller (around 5%), although still larger than the F0DLs for the low F0 (around 1%). In contrast, and in agreement with previous results, for the low F0, the F0DLs were not smaller than the FDLs of the individual harmonics (Henning and Grosberg, 1968; Fastl and Weinberger, 1981).

Lau et al. (2017) compared the observed F0DLs with F0DLs predicted from the observed FDLs using a model based on signal detection theory (Green and Swets, 1966), assuming optimal combination of frequency information from the individual components. According to signal detection theory, the detectability of a change in a stimulus parameter depends on the perceived change in the decision variable and the variability of the decision variable:

$$d^{\prime }=\frac{{\text{P}}_1-{\text{P}}_0}{\sigma }$$ (Eq. 1)

where d´ is a measure of sensitivity to the change, P₀ and P₁ are the magnitudes of the internal decision variable without and with the change, respectively, and σ is the standard deviation of the decision variable. The decision variable is assumed to follow a Gaussian distribution. Dai and Micheyl (2011) reported that sensitivity to a change in frequency of a pure tone was proportional to the frequency difference, ΔF in Hz, over a wide range of frequencies and levels. Assuming this holds for all frequencies, the difference between the decision variables P₁ and P₀ in equation 1 can be substituted with ΔF, and a plot of d´ as a function of ΔF/F on a log-log plot should be a straight line with a slope of 1. To predict F0 discrimination performance, Lau et al. (2017) assumed that this unity slope held for all frequencies tested, and that independent frequency information from all of the components is combined optimally.

Assuming independent noise across peripheral channels, i.e. that performance is limited by noise before information is combined across frequency channels, the sensitivity (d´_c) to changes in F0 can be expressed as:

$$d_c^{\prime }=\sqrt{{{{\displaystyle \sum }}^{\text{}}}_{k=1}^N{d}_k^{\prime 2}}$$ (Eq. 2)

where d´_k is the sensitivity to a change in the frequency for component k. With the assumption of a linear relationship between d´ and ΔF, and between d´ and ΔF0, the relationship between thresholds can be expressed as:

$${\left(\frac{1}{F0D{L}_{pred}}\right)}^2=\underset{k=1}{\overset{N}{{{\displaystyle \sum }}^{\text{}}}}{\left(\frac{1}{FD{L}_k}\right)}^2$$ (Eq. 3)

where F0DL_pred is the predicted F0DL (expressed as a percentage of F0) and FDL_k is the FDL for the kth harmonic (expressed as a percentage of the frequency of that harmonic). Eq. 3, with k = 6, …, 10, is equivalent to Eq. 4 of Lau et al. (2017).

This type of model for predicting F0DLs for complex tones with peripherally resolved components from the FDLs of the individual components has been tested before (see e.g. Goldstein, 1973; Moore et al., 1984; Gockel et al., 2007), and it has been argued that the appropriate estimates of FDL_k are not the FDLs for the harmonics measured in isolation, but rather the FDLs measured when each component is presented within the complex (Moore et al., 1984). The latter FDLs are higher, probably due to partial masking between components, and thus the estimated values of FDL_k are larger. As a consequence the value of F0DL_pred is larger. For complex tones with resolved components in a low to mid-frequency range, this gave more accurate predictions of the F0DL than when using FDLs for the harmonics presented in isolation (Moore et al., 1984).

In contrast, for the high-frequency tones in the study of Lau et al. (2017), the observed F0DLs were actually smaller (by about a factor of 2) than predicted from the FDLs for the harmonics presented in isolation, based on the assumption that performance is limited by peripheral independent noises. Lau et al. (2017) described this as super-optimal integration and argued that it can be explained by the existence of central harmonic template neurons that receive rate-place information; this explanation is considered in more detail in section IV. Gockel and Carlyon (2018) reported even smaller F0DLs (around 2%) for the same complex tones as those used by Lau et al. (2017), but, in that study, did not measure FDLs.

The present study had two objectives. Firstly, we wished to measure psychometric functions for the discrimination of frequency of very high-frequency pure tones and complex tones, in the same noise background as used by Lau et al. (2017) and as used in the second part of our study. Psychometric functions are of general theoretical and practical interest, but, to the best of our knowledge have not been measured before for very high frequencies. The combination of very high frequencies and a noise background in the study of Lau et al. led to very high FDLs, of 20% or more, which correspond to frequency differences much higher than are typically used for the measurement of psychometric functions. The pure-tone psychometric functions measured by Dai and Micheyl (2011) were limited to tones in quiet and with frequencies up to 8 kHz. Plack and Carlyon (1995) reported that sensitivity to a change in F0 was proportional to the difference in F0, but their data were also restricted to lower frequencies. Therefore, it is not clear whether the psychometric function has a slope of 1 for pure and complex tones with much higher frequencies, where phase locking is likely to be absent. As outlined above, the assumption that d´ is linearly related to the change in frequency and in F0 is crucial for the predicted relationship between F0DLs and FDLs (within the framework of the model) and for making meaningful comparisons across conditions. For example, if the psychometric functions for discrimination of very high-frequency tones as used by Lau et al. (2017) were shallower than those for low-frequency tones, i.e. with a slope < 1 on a log-log plot of d´ as a function of ΔF/F or of ΔF0/F0, then the true value of F0DL_pred would be smaller and thus closer to the measured F0DLs. In other words, basing the prediction of the F0DL incorrectly on a slope of 1, when it is actually less than 1, could give the appearance of super-optimal frequency integration when in fact integration was not super-optimal. This is illustrated schematically in Fig. 1.

Fig. 1.

(Color online) Schematic illustration of how the slopes of the psychometric functions for pure-tone and complex-tone frequency discrimination can influence the predicted value of the F0DL. Solid lines and dashed lines show hypothetical psychometric functions for pure tones and complex tones, respectively. In this example, all thresholds are determined at d´ = 1. The measured FDL is 1%. The goal is to predict the F0DL for a complex tone that consists of four harmonics where, for simplicity, the psychometric functions for all components are assumed to be identical. The value of d´ for ΔF0 = 1%, would be a factor of √4 = 2 larger than the d´ of 1 for ΔF = 1% (see Eq. 2), so the psychometric function for F0 discrimination passes through d´ = 2 at ΔF0 = 1%. If the slope of the psychometric functions is assumed to be 1 (black lines), then the predicted F0DL for d´ = 1 is a factor of 2 smaller than the FDL, i.e. it is 0.5%. If the slope of the psychometric functions is assumed to be 0.5 (red lines), then the predicted F0DL is a factor of 4 smaller than the FDL, i.e. it is 0.25%.

The second objective of this study was to try to replicate the finding of Lau et al. (2017) of super-optimal frequency integration, using very similar stimuli together with an additional condition that was designed to increase the salience of the pure tones in the background noise in which they were presented. Observed and predicted F0DLs were compared for low and high frequency regions.

II. Methods

A. Subjects and screening procedure

Ten young normal-hearing musically trained subjects (7 females) between 16 and 28 years of age (mean age of 22 years) participated in the main experiments. To ensure audibility of the high-frequency tones and basic frequency discrimination ability, subjects had to pass a three-stage screening, as in Lau et al. (2017) and Gockel and Carlyon (2018), to be eligible for the main part of the study. The screening comprised:

• (1)Pure-tone audiometric thresholds in quiet were measured at octave frequencies from 0.25 to 8 kHz and at 6 kHz, using a Midimate 602 audiometer (Madsen Electronics, Minnesota, Minneapolis, USA). Thresholds had to be ≤ 15 dB HL at all frequencies for subjects to pass this stage.
• (2)Thresholds were measured for detecting 210-ms sinusoidal tones (including 10-ms onset and offset hanning-shaped ramps) at 10, 12, 14 and 16 kHz in a continuous TEN (Moore et al., 2000) extending from 0.02 - 22 kHz. This was done separately for each ear. At 1 kHz, the TEN had a level of 45 dB SPL/ERB_N, the same as used in the experiment (see below), where ERB_N stands for the average value of the equivalent rectangular bandwidth of the auditory filter for young normal-hearing listeners tested at low sound levels (Glasberg and Moore, 1990). A two-interval two-alternative forced-choice task (2I-2AFC) with a 3-down 1-up adaptive procedure estimating the 79.4% correct point on the psychometric function (Levitt, 1971) was used. The step size was 5 dB until two reversals occurred and 1 dB thereafter. The adaptive track terminated after 10 reversals, and the threshold was determined as the mean of the levels at the last six reversals. Three thresholds (three adaptive tracks) were obtained for each frequency and ear. The final threshold was the mean of these three thresholds. Masked thresholds had to be ≤ 45 dB SPL up to 14 kHz, and ≤ 50 dB SPL at 16 kHz.
• (3)F0DLs were measured in quiet for diotically presented complex tones containing harmonics 6-10 with an F0 of 280 or 1400 Hz (the same tones as used in the main experiment, except for the absence of level randomization; see below), and FDLs were measured for the components of the complex tones presented in isolation. A 2I-2AFC task with a 3-down 1-up adaptive procedure was used. Subjects had to indicate the tone with the higher pitch, and received correct-answer feedback after each trial. The signal duration was 210 ms (including 10-ms onset and offset hanning-shaped ramps) and the inter-stimulus interval was 500 ms. Initially, the difference in F0 (or frequency) was 20%. This was reduced (or increased) by a factor of two for the first two reversals, by √2 for the next two reversals, and by 1.2 thereafter. The adaptive track terminated after 12 reversals, and the threshold was determined as the geometric mean of the frequency differences at the last 8 reversals. The final threshold was the geometric mean of the thresholds from three adaptive tracks. F0DLs and FDLs had to be < 6% and < 20% in the low and high frequency regions, respectively.

Initially 30 musically trained subjects between 16-28 years old were tested, ten of whom passed all screening stages. Three dropped out at the first stage, 14 at the second stage, and three at the last stage. Most of the subjects took part in some other experiment(s) involving high-frequency tones before data collection for the present study commenced. Informed consent was obtained from all subjects. This study was carried out in accordance with the UK regulations governing biomedical research and was approved by the Cambridge Psychology Research Ethics Committee.

B. Psychometric functions

The goal was to determine the slopes of the psychometric functions for F0 discrimination of complex tones containing harmonics 6-10, with F0 of either 1400 Hz (“High”) or 280 Hz (“Low”), and for frequency discrimination of pure tones at 11200 Hz (the 8^th harmonic of a 1400-Hz F0) and at 2240 Hz (the 8^th harmonic of a 280-Hz F0). For each presentation, the starting phases of all components were randomized and individual component levels were randomized, following a uniform distribution, by ±3 dB about the mean component level, which was 55 dB SPL for harmonics 7-9 and 49 dB SPL for harmonics 6 and 10. The level of the edge components was reduced to minimize edge pitches. The level randomization was done to weaken envelope cues for complex tones and level cues for pure tones. The tones had a duration of 210 ms (including 10-ms onset and offset hanning-shaped ramps) and were presented diotically in a background of a continuous diotic TEN, extending from 0.02 - 22 kHz and with a level of 45 dB SPL/ERB_N at 1 kHz, to mask possible distortion products for the complex tones. These stimuli were the same as used by Lau et al. (2017), except that they used gated rather than continuous TEN.

For each of the four conditions (2 F0s and 2 pure tone frequencies) a five-point psychometric function was measured using the method of constant stimuli. In each trial, the subject heard two tones with F0s or frequencies geometrically centered on the mean F0 or frequency (depending on the condition); in one randomly chosen interval the F0 or frequency was a factor r above the mean and in the other interval it was a factor r below the mean. The two tones were separated by an inter-stimulus interval of 500 ms. Subjects indicated which of the two was higher in pitch. Feedback was provided as to whether the answer was correct. To obtain a wide range of d´ values, for each subject and condition the largest frequency difference used was a factor of 4 larger than the smallest frequency difference used; the five values of ΔF (or ΔF0) were equal to (1/2)x, 1/√2(x), x, √2(x) and 2x. The value of x was chosen for each subject individually so as to give a d´ value in the range 1.0 - 1.2. This usually required several runs to set the final value of x. For some subjects and conditions, psychometric functions were determined for multiple values of x.

First, the psychometric functions for frequency discrimination of the pure tones were measured. Blocks consisted of 50 trials using a fixed condition (for example the high pure-tone condition or the low pure-tone condition). Within a block of 50 trials, the order of ΔF values cycled 10 times from the largest to the smallest value. The order of the conditions across blocks followed an ABBA design, followed by a short break and then a BAAB design, followed by a break and an ABBA design, until at least 500 trials were collected for each value of ΔF in each condition. The measurement of psychometric functions for F0 discrimination followed the same design.

Five subjects participated in the measurement of psychometric functions. All of them had participated in other experiments on high-frequency pitch perception, one of which was the attempted replication of the super-optimal integration of frequency information reported below. On average it took about 11 sessions of 2 hours each (including breaks) to obtain one set of psychometric functions for each subject for all four conditions.

C. Determination of F0DLs and FDLs

F0DLs were measured for complex tones containing harmonics 6-10, with F0s of 1400 Hz (“High”) or 280 Hz (“Low”). FDLs were measured for each of the components presented in isolation. For each presentation, the starting phases of all components were randomized and individual component levels were randomized by ±3 dB, following a uniform distribution, about the mean component level, which was 55 dB SPL for harmonics 7-9 and 49 dB SPL for harmonics 6 and 10. In condition “short, diotic”, the tones had a duration of 210 ms (including 10-ms onset and offset hanning-shaped ramps) and were presented diotically in a background of a continuous diotic TEN, extending from 0.02 - 22 kHz and with a level of 45 dB SPL/ERB_N at 1 kHz. These stimuli were the same as used by Lau et al. (2017), except that they used gated rather than continuous TEN.

In condition “long, dichotic”, the tone duration was increased to 1 s and the tones were presented diotically in dichotic TEN (an independent TEN at each ear), keeping all other parameters constant. Both the longer duration and the independent noise across the two ears were expected to increase the salience of the pure tones in the background noise via a multiple-looks process (Viemeister and Wakefield, 1991; Jackson and Moore, 2014).

Thresholds were measured using a 2I-2AFC task and the same adaptive procedure as used to determine FDLs and F0DLs during subject screening (Section II.A). The final threshold was the geometric mean of the thresholds from four adaptive tracks. Each adaptive track measured the threshold for one of the 24 conditions [2 frequency regions × 2 durations/noise modes × 6 stimuli (i.e. complex tone plus 5 pure-tone stimuli with frequencies corresponding to harmonic ranks 6, 7, 8, 9, and 10)]. The presentation order of the 24 conditions was randomized. One threshold was obtained for each condition in turn before any measurement was repeated. For each subject and each repetition cycle, a new random presentation order for the 24 conditions was employed. Ten subjects participated. Data collection took on average about five sessions of 2 hours each (including breaks) for each subject.

D. Equipment

All stimuli were generated digitally in MATLAB (The Mathworks, Natick, MA) with a sampling rate of 48 kHz. They were played out through four channels (two for the continuous noise and two for the signals) of a Fireface UCX (RME, Germany) soundcard using 24-bit digital-to-analog conversion, and were attenuated independently with four Tucker-Davis Technologies (Alachua, FL) PA4 attenuators. They were mixed with two Tucker-Davis Technologies SM5 signal mixers, and fed into a Tucker-Davis HB7 headphone driver, which also applied some attenuation. Stimuli were presented via Sennheiser HD 650 headphones (Wedemark, Germany), which have an approximately diffuse-field response. The specified sound levels are approximate equivalent diffuse-field levels. Subjects were seated individually in a double-walled, sound-insulated booth (IAC, Winchester, UK).

E. Analysis

For statistical analysis, repeated-measures analyses of variance (RM-ANOVA) were calculated using SPSS (Chicago, IL). Throughout the paper, if appropriate, the Huynh-Feldt correction was applied to the degrees of freedom (Howell, 2009). In such cases, the original degrees of freedom and the corrected significance values are reported.

III. Results and Discussion

A. Psychometric functions

Figures 2 and 3 show psychometric functions for F0 discrimination of the complex tones and frequency discrimination of the 8^th harmonic, respectively. In Panels A-E, d´ is plotted as a function of the F0 (or frequency) difference (in %) for each of the five subjects. All functions appear to be linear on the log-log plots.

Fig. 2.

Psychometric functions for F0 discrimination of complex tones containing harmonics 6-10 for F0s of 280 Hz and 1400 Hz. Panels A-E show data for individual subjects. Panel F shows the average of the straight-line fits to the individual psychometric functions. The dashed line indicates a slope of 1 with arbitrary offset.

Fig. 3.

Psychometric functions for frequency discrimination of pure tones with frequencies of 2240 Hz and 11200 Hz. Otherwise as Fig. 2.

To estimate the slopes of the psychometric functions, a straight line was fitted separately to each function for each subject. The line was described by

$$\text{log}(d^{´})=s^{\ast }\text{log}(\text{ΔF}0/\text{F}0)+b$$ (Eq. 4)

and

$$\text{log}(d^{´})=s^{\ast }\text{log}(\text{ΔF}/\text{F})+b,$$ (Eq. 5)

for F0 discrimination and frequency discrimination, respectively, where the free parameters s and b were adjusted so that the sum of the squared deviations between the log-transformed measured d´ values and those predicted by the line was minimized. Table I gives the values of s and b, and R², a measure of the goodness of fit known as the coefficient of determination (Howell, 2009).

Table I.

Estimated values of parameters s and b in Eq. 4 and 5, fitted to the psychometric functions for frequency discrimination of pure tones at 2240 Hz and 11200 Hz, and for F0 discrimination of complex tones containing harmonics 6-10 with F0s of 280 Hz and 1400 Hz. Goodness of fit (R²) values are also given. Values are for each of the five subjects, the average (Av.) and the standard deviation (in brackets) across all subjects.

Subj.	F = 2240 Hz			F = 11200 Hz			F0 = 280 Hz			F0 = 1400 Hz
	s	b	R2	s	b	R2	s	b	R2	s	b	R2
02	0.89	0.46	1.0	0.99	–0.46	0.97	0.97	0.42	1.0	0.72	–0.17	0.99
04	0.96	0.79	0.98	1.08	0.07	0.98	0.90	0.67	0.97	0.97	–0.01	0.96
06	0.98	0.72	0.98	1.09	0.12	0.99	0.96	0.60	0.99	0.86	0.15	0.96
08	0.97	0.55	0.98	1.33	–1.32	0.98	1.19	0.43	0.98	1.29	–0.67	0.99
10	1.02	0.70	1.0	0.85	–0.13	0.96	0.97	0.42	0.98	0.91	–0.26	0.99
Av.	0.97	0.64	0.99	1.07	–0.34	0.98	1.0	0.51	0.98	0.95	–0.19	0.98
	(0.05)	(0.14)	(0.01)	(0.18)	(0.59)	(0.01)	(0.11)	(0.12)	(0.01)	(0.21)	(0.31)	(0.02)

For some subjects and conditions, multiple functions were measured with different center values of ΔF0 (or ΔF). Because the resulting functions were similar, Table I shows the average of the s, b, and R² values for these “repeated” functions. The values of b are greater for the 2240-Hz than for the 1120-Hz pure tone, and greater for the 280-Hz than for the 1400-Hz F0, reflecting greater sensitivity to changes in low than in high frequencies and F0s. Importantly, all slopes were close to 1, for both the high- and the low-frequency conditions. In addition, the R² values were high, ranging from 0.96 to 1.0, with a mean of 0.98. Panels F in Figs. 2 and 3 show the average of the estimated slopes and offsets (b) across subjects. The dashed line indicates a slope of 1 with arbitrary offset. It is clear that, for both frequency regions, the slopes of the psychometric functions for F0 discrimination and frequency discrimination were very close to 1 (slopes averaged across subjects ranged from 0.95 to 1.07). A two-way RM-ANOVA (with factors tone type and frequency region) was calculated on the s values. There was no significant main effect or interaction. The 95% confidence intervals for the mean slopes included the value 1 in all conditions.

Overall, the data are consistent with previous reports of psychometric functions for frequency discrimination and F0 discrimination with a slope of 1 in the low- to mid-frequency regions and extend this finding to very high frequency regions, where phase locking is presumed to be absent. The data show that a major assumption underlying the use of Eq. 3 to predict F0DLs from FDLs is satisfied, and thus rule out one possible explanation for the apparent super-optimal frequency integration in the high frequency region reported by Lau et al. (2017).

B. F0DLs and FDLs

Figure 4 shows the geometric mean FDLs and F0DLs (open symbols). Error bars show ± one standard error of the mean (SE). As expected, thresholds were overall higher in the high-frequency region (red symbols; ranging from about 1.4% for F0DLs to 8% for the FDLs at the highest harmonic ranks) than in the low-frequency region (blue symbols; ranging from about 0.2% to 0.5%). Thresholds were lower in condition “long, dichotic” (upward and downward pointing triangles) than in condition “short, diotic” (circles and squares), especially for the pure-tone conditions. This is consistent with the idea that the salience of the longer tones in dichotic TEN was increased and that this affected thresholds. In addition, in condition “short, diotic”, thresholds were lower than observed by Lau et al. (2017), by at least a factor of 2, especially for the FDLs for the high-frequency region. Lau et al. (2017) reported FDLs and F0DLs that were both about 1% in the low region; in the high region their FDLs and F0DLs were about 20-30% and 5%, respectively.

Fig. 4.

(Color online) Geometric mean FDLs (symbols connected by lines) and F0DLs (left side), and standard errors of the mean for 10 subjects. In condition short, diotic (circles and squares), 210-ms tones were presented in diotic TEN. In condition long, dichotic (triangles), 1-s tones were presented in dichotic TEN. Solid symbols show F0DLs predicted using Eq. 3.

Two RM-ANOVAs were conducted on the log-transformed thresholds, one for the F0DLs and one for the FDLs. The ANOVA for the F0DLs (with factors F0 and type of presentation) showed significant effects of F0 [F(1,9)=42.13, p<0.001] and type of presentation [F(1,9)=15.67, p=0.003]. The interaction was not significant [F(1,9)=0.01, p=0.925]. Thus, increasing the salience of the complex tones in the TEN by increasing their duration and presenting them in a dichotic rather than a diotic TEN decreased F0DLs for both F0s by a small but similar amount.

The ANOVA for the FDLs (with factors frequency region, type of presentation and harmonic rank) showed significant effects of frequency region [F(1,9)=143.60, p<0.001], type of presentation [F(1,9)=139.0, p<0.001], and harmonic rank [F(4,36)=10.53, p<0.001]. There was a significant interaction between frequency region and harmonic rank [F(4,36)=10.73, p<0.001], reflecting the fact that FDLs increased with increasing harmonic rank in the high-frequency region but not in the low-frequency region. The interaction between type of presentation and harmonic rank was also significant [F(4,36)=3.39, p=0.019]. The interaction between type of presentation and frequency region was not significant [F(1,9)=1.50, p=0.252], indicating that the effect of increasing the salience of the individual harmonics in the TEN was on average similar for the low and the high frequency regions. Finally, there was a significant three-way interaction [F(4,36)=4.63, p=0.004].

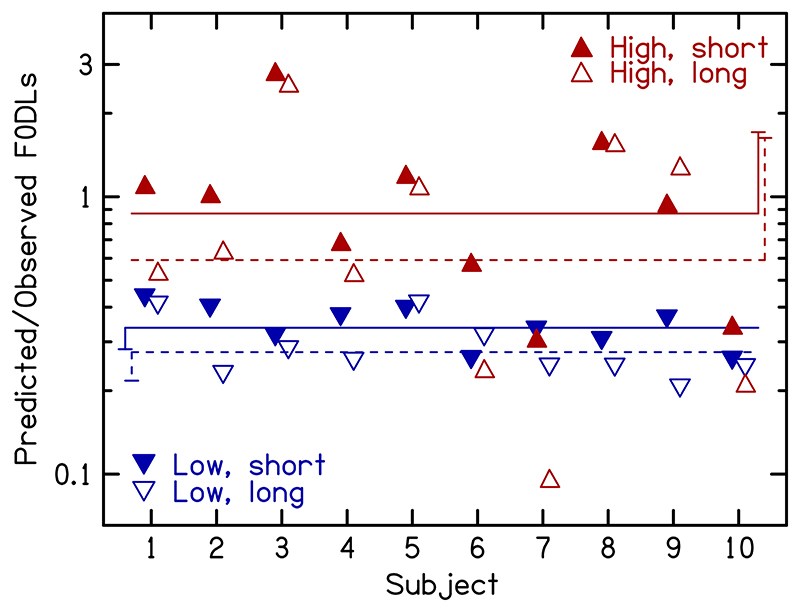
The predicted F0DLs (filled symbols) were derived from the observed FDLs using Eq. 3, with k = 6,…,10. The differences in predicted F0DLs between conditions “short, diotic” and “long, dichotic” reflect the differences in the observed FDLs across the two conditions. The solid and open symbols in Fig. 5 show the ratios of predicted/observed F0DLs for each of the ten subjects in the short-diotic and long-dichotic conditions, respectively; the geometric mean ratios across subjects are shown by the solid and dashed horizontal lines. Data for the high and the low F0s/frequencies are shown by the red upright and blue inverted triangles, respectively. For the low F0, the predicted F0DLs were smaller than the observed F0DLs, leading to ratios less than one. This is in agreement with previous studies (Goldstein, 1973; Fastl and Weinberger, 1981; Moore et al., 1984; Gockel et al., 2007; Lau et al., 2017). For the high F0, the ratio of predicted F0DLs to observed F0DLs was about 1 or perhaps smaller, in contrast to the finding of Lau et al. (2017) who show an arithmetic mean ratio of about 3 in their Figure 1C (geometric mean of about 2.2; data read from their figure). Thus, the present data did not replicate the super-optimal integration in the high frequency region reported by Lau et al. (2017), using very similar methods. In addition, for both F0s, the ratio between predicted and observed F0DLs was smaller in condition “long, dichotic” than in condition “short, diotic”. This reflects the finding that the FDLs decreased more than the measured F0DLs when the tone duration was increased and the TEN was presented dichotically.

Fig. 5.

(Color online) Individual ratios of predicted F0DLs (assuming optimal combination of frequency information and assuming that peripheral independent noise limits performance) to measured F0DLs for 10 subjects. The top two (red) and bottom two (blue) horizontal lines show the geometric means across subjects for F0s of 1400 Hz and 280 Hz, respectively. The solid and dashed lines are for conditions “short, diotic” and “long, dichotic” respectively. The vertical error bars show one standard deviation of the corresponding mean; to avoid clutter they are plotted downwards for the 280 Hz F0 and upwards for the 1400 Hz F0.

A two-way RM-ANOVA (with factors F0 and type of presentation) on the log-transformed ratios showed significant effects of F0 [F(1,9)=11.25, p=0.008] and type of presentation [F(1,9)=18.59, p=0.002]. The interaction was not significant [F(1,9)=1.02, p=0.338], reflecting the fact that the decrease in the ratio due to the longer tone duration and the use of dichotic TEN was similar for the high and the low frequency regions. An independent samples t-test was used to assess whether the ratios of predicted and observed F0DLs for the high F0 observed here differed significantly from those observed by Lau et al. (2017). Input data were the log-transformed ratios for condition “short, diotic” of the present study (n=10) and those of Lau et al. (2017) (n=16, data read from their Figure 1B). The difference was significant [t(24)=–2.88, p=0.008, 2-tailed].

As described earlier, psychometric functions with slopes less than 1 could lead to apparently super-optimal integration and hence to predicted/observed ratios greater than 1. Psychometric functions were determined here for subjects s02, s04, s06, s08, and s10. For subjects s02 and s10, the slopes of the psychometric functions for discrimination of high frequency tones were shallower than for all other listeners (see Table I), but the ratio of predicted to observed F0DLs was equal to or below 1. On the other hand, for s08 the ratio of predicted to observed F0DLs was above 1, but the slopes of the psychometric functions for the high tones were the steepest. This further strengthens the conclusion that a shallower slope of the psychometric functions for discrimination of very high frequencies can be ruled out as an explanation of the large integration of frequency information across harmonics at very high frequencies.

IV. General Discussion

The first experiment showed that psychometric functions for frequency discrimination and F0 discrimination for the very high frequency region have a slope of 1, the same as observed for low- to mid-frequency regions. This rules out one possible explanation for the larger amount of across-frequency integration observed at high than at low frequencies, both here and by Lau et al. (2017). Note, however, that the FDLs obtained by Lau et al. were much larger than observed here, and so we do not have measures of the psychometric function for the range of very large frequency differences that encompass their FDLs. Nevertheless, experiment 1 shows that the main findings of our second experiment, which was a replication and extension of the study of Lau et al., cannot be attributed to differences in the slopes of the psychometric functions across conditions.

In the second experiment FDLs and F0DLs were measured. In both experiments the level of each component was varied randomly over a 6-dB range to reduce the usefulness of level cues, as was also done by Lau et al. (2017). For this rove range, a level difference of 2.1 dB would be needed for an ideal observer to achieve “threshold” (79% correct) based on the use of level alone (Green, 1988). Given this, the rove range may have been insufficient to prevent the use of level cues at high frequencies, at which the frequency response of the Sennheiser HD650 headphones, used here and by Lau et al., contains distinct peaks and dips whose pattern depends on the headphone placement and the individual ear.

To quantify the typical magnitude of potential level cues, use was made of measurements on the HD650 headphones obtained using a HEAD Acoustics (Herzogenrath, Germany) Head Measurement System (HMS) with ear simulator (Rtings.com, 2020). The “uncompensated” response from five different placements of the headphones on the HMS was used. For each harmonic, the two frequencies corresponding to the upper and lower boundaries of the mean FDL were determined. For example, for the harmonic centered at 8400 Hz, for the short duration the mean FDL was 231 Hz and the two boundary frequencies were 8285 and 8517 Hz. The response of the headphone at each of these two frequencies was estimated for each placement. The difference in response for the two frequencies gives an estimate of the level cue associated with that FDL. The magnitude of the level cue varied markedly across placements. Also, the direction of the level cue varied across harmonics and sometimes across placements for a given harmonic. For condition “short, diotic” the mean absolute value of the level cue (with SD in parentheses) was 0.8 (0.4), 2.2 (1.0), 2.3 (1.0), 3.8 (3.6), and 5.1 (3.4) dB at 8.4, 9.8, 11.2, 12.6, and 14 kHz, respectively, corresponding to the 6^th, 7^th, 8^th, 9^th and 10^th harmonics of the 1400-Hz F0. For condition “long, dichotic” the corresponding values were 0.4 (0.2), 1.3 (0.6), 2.1 (0.9), 2.0 (2.1), and 3.0 (2.4). Thus, in principle, changes in level could have provided usable cues for the higher-frequency individual harmonics in the high region, especially for the short, diotic condition, where the FDLs were larger.

So far, the level changes have been described as “cues”. However, it should be noted that the direction of the level changes was not consistent; an increase in frequency could result in an increase or a decrease in level, depending on the specific harmonic being tested and on the placement of the headphones for that specific run. The direction might also vary within an adaptive run, as the frequency difference changed. This might make it difficult for subjects to use level as a cue. It seems likely that, because level did not provide a useful cue in the majority of conditions that were tested (in random order), and because the musically trained subjects were instructed to judge the pitch of the stimuli, the subjects tried to ignore the level changes for all conditions. In that case, rather than providing a cue, the level changes probably had a distracting effect, similar to the effect that occurs when the level of each tone in a frequency-discrimination task is roved (Henning, 1966; Emmerich et al., 1989). The distracting effect would increase with increasing magnitude of the level changes, and this could contribute to the increase in FDLs with increasing frequency. Consistent with this interpretation, Moore and Ernst (2012) used insert earphones with a reasonably flat response at the eardrum and found that FDLs were roughly constant for frequencies above 8-10 kHz. In any case, for the three lowest harmonics the level changes caused by the frequency response of the headphones at threshold were probably too small to explain the FDLs based solely on use of a level cue and too small to add a marked distracting effect. The predictions of F0DLs based on the optimal combination of the information from different harmonics depend mainly on the FDLs for the harmonics with the lowest FDLs, and these were the three lowest harmonics. Thus, level changes probably did not affect the validity of the predictions of the F0DLs.

For the complex tones, both the level randomization and the changes in level introduced by the frequency response of the headphones would have resulted in the prominence of individual harmonics varying from stimulus to stimulus, especially for the high region. In principle, this might have reduced the perceptual integration of the harmonics. However, the perceptual integration of harmonics is promoted by the use of background noise (Houtgast, 1976; Hall and Peters, 1981) and in the high region the F0DLs were mostly lower than the individual FDLs in condition “short,diotic”, suggesting that subjects did integrate across harmonics.

The results of experiment 2 showed that subjects achieved F0DLs of less than 2% when all the harmonics had frequencies at or above 8 kHz. This suggests that a reasonably salient pitch can be heard when presumably only place information is available. However, the F0DLs were a factor of about 3.5 larger in the high than in the low frequency region, indicating a less salient pitch in the high frequency region.

The results of the second experiment differed from those of Lau et al. (2017) in two ways. One was that the FDLs and F0DLs found here were lower than those reported by Lau et al. (2017) by at least a factor of 2. Possible reasons for this include the use of continuous TEN here in contrast to gated TEN in their study, and greater experience of the present subjects with both the low- and the high-frequency complex tones. Additionally, it is conceivable that our inclusion of the “long, dichotic” condition, which was expected to increase the salience of the tones in the TEN, also improved performance in the “short, diotic” condition, by helping subjects to “home in” on the appropriate cues. The second difference was that the present data did not replicate the super-optimal integration of frequency information reported by Lau et al. (2017) for the high frequency region. However, importantly, and in agreement with their findings, the ratio of predicted to observed F0DLs was significantly smaller for the low than for the high frequency region.

The super-optimality of integration of frequency information in the high frequency region was interpreted by Lau et al. (2017) in terms of central, possibly cortical, pitch-sensitive neurons that respond most strongly to combinations of harmonically related tones but not to a single harmonic at high frequencies. It was assumed that there are no pitch-sensitive neurons tuned to F0s above about 5 kHz. Physiological studies have identified two classes of neurons that respond to harmonic structure. Bendor and Wang (2005) found neurons in the auditory cortex of marmosets that respond both to pure tones (each with a preferred frequency, f_p) and to missing-fundamental harmonic complex sounds with F0 = f_p. These were referred to as “pitch-selective neurons”. The F0s to which these neurons were tuned were below about 0.8 kHz and the input frequency range was below about 5 kHz. Feng and Wang (2017) found a different class of neurons in the auditory cortex of marmosets, which they called “harmonic-template neurons”. These responded somewhat to pure tones and were tuned to frequency, having a best frequency (BF). They responded more strongly to harmonic complex tones with low-numbered harmonics, which were presumably resolved, and each neuron also had a best F0. The best F0 was mostly below the BF. These neurons responded across a wide range of F0s, including F0s above 0.8 kHz, and they responded to multiple harmonically related components even when all had frequencies above the limits of phase locking. Lau et al. (2017) did not explicitly state which of the two above classes of neurons were involved in producing super-optimality of frequency integration. They also did not state what types of neurons were involved in the frequency discrimination of high-frequency pure tones, but it was implicitly assumed that, whatever neurons are involved, these give relatively imprecise information about frequency. Why this should be the case was not stated. It is known that there are neurons tuned to audio frequency throughout the auditory system (Palmer, 1995), and it has been shown that the rate-place responses of cortical neurons tuned to audio frequency would allow relatively fine frequency discrimination (Micheyl et al., 2013). The explanation of Lau et al. (2017) therefore rests on the assumption that, whatever neurons are involved in the frequency discrimination of pure tones, the coding of frequency is much less precise at high than at low frequencies.

The fact that we did not replicate the super-optimality found by Lau et al. (2017) potentially reduces the need for an interpretation based on pitch-sensitive neurons. However, conclusions about the existence or not of super-optimality depend on an appropriate measure of the accuracy with which the frequency of each harmonic is encoded. In the present study, and that of Lau et al. (2017), this accuracy was estimated from the FDL for each harmonic presented in isolation (FDL_k in Eq. 3). Doing so led to predicted F0DLs for the 280-Hz F0 that were lower than actually obtained. This can be attributed to the FDLs for isolated harmonics over-estimating the accuracy with which those harmonics are encoded when part of the complex (Gockel et al., 2007; Moore et al., 1984). In the studies of Gockel et al. and Moore et al., FDLs were measured for each harmonic when presented within the complex tone, by mistuning a given harmonic upwards in one interval of a trial and downwards in the other interval. The F0DL for the complex closely matched that predicted by optimal integration (Eq. 3) based on those within-complex FDLs. In principle, it would be useful to perform similar measurements with the harmonics of the 1400-Hz-F0 complex tone used here, so as to compare the F0DL to that predicted from the FDLs for each component presented within the complex. Unfortunately, this may be difficult or impossible in practice. Subjects have great difficulty in detecting mistuning of a single component in a high-frequency complex tone, like the one used here, when beating cues are minimised, because they have difficulty in hearing out the mistuned high-frequency component (Gockel and Carlyon, 2018). This finding was attributed to the absence of phase locking to the mistuned component (Gockel and Carlyon, 2018). If subjects cannot hear out a mistuned component, frequency discrimination of that component is likely to be very poor.

Despite not having a measure of the FDLs of the components when presented within the complex tones, two conclusions seem justified. First, it is highly likely that the FDLs for isolated harmonics, measured here and by Lau et al. (2017), over-estimate the accuracy with which the frequencies of those harmonics are encoded when part of the complex. Given that the ratio of predicted to obtained F0DLs obtained using the FDLs for isolated harmonics was close to one here, it can be concluded that the integration of the high harmonics was “really” super-optimal. This line of argument suggests that super-optimal integration also occurred in experiment 5 of Lau et al. (2017), which used a version of the 1400-Hz-F0 condition, in which all components were shifted by 0.5F0, so as to produce a complex with a weak, ambiguous pitch. They argued that, because the predicted/observed ratio did not differ significantly from 1 for the shifted complex, the super-optimality observed in their original experiment with the un-shifted complex was specific to harmonic tones. However, the predicted/observed ratio that they observed for the shifted high-frequency complex was slightly above one, and if the isolated FDLs over-estimate the accuracy of encoding of each harmonic, then the “true” ratio of predicted to observed F0DLs would have been greater than one. It is also worth noting that Lau et al. (2017) did not test whether the predicted/observed ratio was significantly smaller for the shifted than for the un-shifted complex, which is what would be required to conclude that across-frequency integration is affected by harmonicity.

Overall, it is likely that F0DLs at very high frequencies are smaller than would be predicted by optimal integration of information about the individual harmonics and that the “true” ratio between predicted and obtained F0DLs is higher for the 1400-Hz than for the 280-Hz F0. Possible explanations for these two findings, and for the fact that F0DLs and FDLs are greater for the 1400-Hz F0 and its harmonics than for the 240-Hz F0 and its harmonics, are considered next.

The large FDLs at very high frequencies may have occurred because human listeners have little experience listening to high-frequency pure tones (Verschooten et al., 2019). Another possibility is to do with the likelihood that only excitation-pattern cues were available for the high-frequency pure tones. The peak in the excitation pattern evoked by the pure tone in each observation interval may be highly confusable with peaks produced by random fluctuations in the short-term spectrum of the TEN (Jackson and Moore, 2014). To perform well, the subject has to compare the positions of the “correct” peaks in the excitation pattern (those corresponding to the signal frequency in each interval) and this may not always be done, leading to large FDLs. We refer to this as the excitation-pattern (EP) confusion hypothesis. When all of the harmonic components are presented together, this creates a regular pattern of peaks in the excitation pattern, and all of those peaks shift in the same way when the F0 is changed. This might improve F0 discrimination for three reasons: (1) Because sensitivity to spectral regularity helps to perceptually group the excitation-pattern peaks that correspond to the signal components (Roberts, 2005); (2) Because the coherent change in the position of multiple excitation-pattern peaks activates multiple frequency-shift detectors that are sensitive to the direction of a frequency change, providing a cue as to the direction of the F0 shift (Demany and Ramos, 2005); (3) Because the presence of multiple excitation-pattern peaks improves performance via a multiple-looks process (Viemeister and Wakefield, 1991). These factors could account for the super-optimality at high frequencies, although an explanation based on multiple-looks alone would give predictions similar to those based on Eq. 3.

For the low frequency region, the frequency of an isolated component may be coded in the pattern of phase locking to that component. The pattern of phase locking could potentially be confused with phase locking to random peaks in the short-term spectrum of the TEN, but the confusion may be less than when only excitation-pattern information is available for two reasons. Firstly, phase locking in principle provides much more precise information about the frequency of a tone in noise than place information (Heinz et al., 2001; Hienz et al., 1993). Secondly, when a stimulus evokes an excitation pattern with multiple peaks, the phase locking is dominated by the largest peaks, an effect called synchrony suppression (Hind et al., 1967; Young and Sachs, 1979). For our stimuli, the peak in the excitation pattern produced by the tone signal would usually have been larger than the peaks produced by random fluctuations in the TEN, and so synchrony suppression would have emphasized phase locking to the signal.

The long, dichotic condition was intended to reduce EP confusion. For the longer duration, the random peaks in the EP produced by fluctuations in the TEN would vary over the duration of each stimulus, while the peak produced by the tone would remain stable. Also, the dichotic TEN would have led to random EP peaks that differed across the two ears, while the peak produced by the tone would have been the same across the two ears. Consistent with the EP confusion hypothesis, the improvement for the long, dichotic condition relative to the short, diotic condition was greater for the FDLs than for the F0DLs. Based on the EP confusion hypothesis, one might expect that the improvement in the FDLs would be greater for the high than for the low frequency region. The FDLs were improved by a geometric mean factor of 1.7 for the high-frequency region and 1.48 for the low-frequency region, but the interaction between type of presentation and frequency region was not significant (p = 0.252). At first sight, this appears to be inconsistent with the EP confusion hypothesis. However, it should be remembered that the long, dichotic condition corresponds to a stimulus configuration, S0Nπ, that gives rise to a binaural masking level difference (MLD), and the MLD for this condition is essentially zero at high frequencies, but is 2-8 dB for the frequency range 1-2 kHz when a broadband noise background is used (van de Par and Kohlrausch, 1999). The existence of an MLD for the low but not for the high region may have contributed to the improvement in FDLs for the low region for the long, dichotic condition. Thus, the results do not rule out the EP confusion hypothesis.

The EP confusion hypothesis also leads to the prediction that the ratio of high-frequency to low-frequency FDLs should be greater for tones presented in noise than for tones presented in quiet. Unfortunately, the authors are not aware of any studies that have directly compared FDLs for tones in quiet and in noise at very high frequencies. Existing data on FDLs in quiet or in noise show considerable variability in the way that FDLs vary with frequency for frequencies up to 8 kHz, both across studies and for individuals within studies (Dai et al., 1995; Rose and Moore, 2005; Micheyl et al., 2012; Moore and Ernst, 2012). Hence, the available data do not clearly support or refute the EP confusion hypothesis. Direct comparisons of FDLs in quiet and in noise at very high and at low frequencies, using the same methods and participants, are needed so as to provide a stronger test of the hypothesis.

The fact that F0DLs were markedly higher for F0 = 1400 Hz than for F0 = 280 Hz could be explained in several ways. Firstly, the inputs to the cortical pitch-selective or harmonic-template neurons may be more precise at low than at high frequencies. This is unlikely to be based on differences in sharpness of tuning at high and low frequencies (Glasberg and Moore, 1990), but could occur because the component frequencies are coded by phase locking at low but not at very high frequencies. Secondly, the input pathways to pitch-selective neurons may be less well formed when those inputs are tuned to very high frequencies because the formation of the template requires phase locking, as has been proposed in neural models of central harmonic templates (Shamma and Klein, 2000; Shamma and Dutta, 2019). Both of these explanations are consistent with the idea that accurate pitch perception depends on phase locking, but do not preclude the possibility that rate-place information can produce a pitch, albeit a weaker one. Indeed, Shamma and Dutta (2019) argued that a template using place information alone could emerge by association with a template that was initially formed using phase-locking information, following exposure to high-F0 tones containing both low and high harmonics. According to this view, phase locking is essential for the formation of the templates, but not for the discrimination of F0 once those templates have been formed.

A third possibility, not requiring a role for phase locking, is that pitch-selective or harmonic-template neurons at very high frequencies are poorly formed due to a lack of exposure to high-frequency resolved harmonics. Lack of exposure has also been proposed as an explanation for the worsening of pure-tone frequency discrimination at high frequencies (Verschooten et al., 2019), as noted earlier. However, lack of experience in hearing high-frequency tones does not explain why FDLs for pure tones increase with increasing frequency up to about 8-10 kHz and then reach a plateau, when large distracting level changes are avoided (Moore and Ernst, 2012).

A fourth explanation is that, although there are harmonic-template neurons that respond to harmonic components spaced by 1400 Hz or more, those neurons might be fewer in number or less sharply tuned than those tuned to harmonics spaced at 280 Hz. The data of Feng and Wang (2017) indicate that, for the marmoset, the percentage of harmonic-template neurons is actually greater for BFs around 8 kHz than for BFs around 2 kHz (their Figure 5). However, the numbers of neurons as a function of BF for humans are unknown. In any case, the hypothetical poorer tuning of the harmonic-template neurons tuned to high F0s is inconsistent with the accurate pitch perception observed for high F0s when lower-numbered harmonics are present. For example, Mehta and Oxenham (2020) found that F0DLs for complex tones with high F0s (>800 Hz) only exceeded 3% once the frequency of the lowest audible harmonic increased above about 7-8 kHz; note that their Fig. 4 shows F0DLs as a function of the harmonic rank (or lowest component frequency) of the lowest full amplitude harmonic, rather than for the lowest audible component that was present in the harmonic complex. Hence, it appears that, for the present stimuli, the accuracy of pitch coding depends more on the frequencies of the harmonics of a complex tone than on the F0 of the complex tone. It is plausible that the worsening of F0 discrimination for very high F0s reflects the reduced or absent phase locking to the individual components, but in the absence of electrophysiological recordings from the auditory nerve and higher levels of the auditory system in humans one cannot be certain that this is the case.

V. Summary and Conclusions

Psychometric functions were measured for F0 discrimination of complex tones containing harmonics 6-10 with F0s of 1400 and 280 Hz, and for frequency discrimination of pure tones with frequencies of 11200 Hz (8×1400 Hz) and 2240 Hz (8×280 Hz). The slopes of the psychometric functions were close to 1 on log-log coordinates for both the low and the high frequencies, showing that d´ is linearly related to the change in frequency and in F0 even at very high frequencies where phase locking is probably absent. Thus, a major requirement for allowing meaningful comparisons across different conditions, including those with very high frequencies, is fulfilled.

F0DLs were measured for diotically presented complex tones containing harmonics 6-10 with F0s of 1400 and 280 Hz, and FDLs were determined for all component frequencies presented in isolation. Difference limens for all tones were significantly lower when the tone duration was increased from 210 ms to 1000 ms and the tones were presented in dichotic rather than diotic TEN. Thresholds were at least a factor of 2 lower (better) than reported by Lau et al. (2017). Predictions of the F0DLs were derived from the observed FDLs assuming optimal combination of frequency information and that performance is limited by peripheral noise that is independent for each harmonic. The ratio of predicted to observed to F0DLs was around 1 or below for both F0s, and was significantly smaller for the low than the high F0. The results are consistent with a role of phase locking in the perception of a salient pitch, but also with the idea of a template mechanism that can operate, albeit less effectively, on the basis of rate-place information alone.