Priming Effects on Subsequent Episodic Memory: Testing Attentional Accounts

Abstract

Prior work has shown that priming improves subsequent episodic memory, i.e., memory for the context in which an item is presented is improved if that item has been seen previously. We previously attributed this effect of “Priming on Subsequent Episodic Memory” (PSEM) to a sharpening of the perceptual/conceptual representation of an item, which improves its associability with an (arbitrary) background context, by virtue of increasing prediction error (Greve et al, 2017). However, an alternative explanation is that priming reduces the attentional resources needed to process an item, leaving more residual resources to encode its context. We report four experiments that tested this alternative, resource-based hypothesis, based on the assumption that reducing the available attentional resources by a concurrent load would reduce the size of the PSEM. In no experiment was there an interaction between attentional load and priming on mean memory performance, nor a consistent correlation across participants between priming and PSEM, failing to support the resource account. However, formal modelling revealed that a resource account is not, in fact, inconsistent with our data, by confirming that nonlinear (sigmoidal) resource-performance functions can reproduce any interaction with load, and, more strikingly, any pattern of correlation between priming and PSEM. This work reinforces not only the difficulty of refuting attentional resource accounts of memory encoding, but also questions the value of load manipulations more generally.

Introduction

It is not surprising that recognition memory for an item (e.g, word or picture) – i.e, a judgment of whether it was seen recently – is generally improved the more times that item is repeated (Kinoshita, 1997; Jacoby, 1999, although c.f. Gardiner et al., 1996; Dewhurst & Anderson, 1998), since repetitions can be assumed to increase the “strength” with which that item is represented in memory (or increase its “familiarity”, Yonelinas, 2002). Measures of priming, such as the speed of making a decision about an item, also generally increase with the number of item repetitions (Ostergaard, 1998). Perhaps more surprising is the finding of a number of recent studies (Gagnepain, Lebreton, Desgranges, & Eustache, 2008; Gagnepain et al., 2011; Greve, Cooper, Kaula, Anderson, & Henson, 2017) that repeating an item (producing greater priming) can also improve subsequent episodic memory for the context in which that repetition occurred, i.e, improve subsequent “recollection” (Yonelinas et al, 2002). We call this the effect of Priming on Subsequent Episodic Memory (PSEM).

For example, Gagnepain et al. (2008) asked participants to make a lexical decision about auditory words and pseudowords, where one half of the words had been presented on the previous day (Day 1) in a different task (phoneme monitoring). To make the lexical decision task harder, the words and pseudowords were presented simultaneously with one of two background sounds. Those words that had been seen on the previous day had faster lexical decision times, i.e, showed priming. More importantly, words from the lexical decision task were then presented again, together with new words, in a surprise recognition memory test, where participants were asked to indicate which words occurred on Day 2. Primed words not only received a higher probability of “remember” responses (a subjective measure of recollection; Tulving, 1985), but also had higher accuracy for remembering which sound they had been presented with during the lexical decision task (an objective measure of “source”memory; Mitchell & Johnson, 2000). This PSEM effect was subsequently replicated by Gagnepain et al (2011) using similar stimuli, and then by Greve et al. (2017) using different (visual) stimuli, in which images of unfamiliar faces were primed and memory tested for their pairing with arbitrary and unique background scenes. A related finding was reported by Poppenk et al. (2011), using primed versus unprimed proverbs and source memory for the task in which they were studied (though priming was not measured directly). Note however that another study by Kim, Yi, Raye & Johnson (2012) found the apparent opposite effect – whereby source memory decreased with the number of times an item had been seen previously – which we discuss in more detail in the General Discussion

The PSEM effect reported in Greve et al. (2017, Experiment 3) was one of three empirical effects predicted by the PIMMS framework (“Predictive Interactive Multiple Memory Signals”, Henson & Gagnepain, 2010). According to this framework, associative memory is proportional to prediction error (PE), which reflects the divergence between the prior probability of an item (given a context) and the likelihood of that item (based on, e.g., sensory evidence). When the prior probability is flat (because the context scenes in Greve et al, 2017, did not predict a particular face), then sharpening the sensory evidence by priming increases the PE, and therefore improves the encoding of the context-item (scene-face) pairing.

However, while PSEM is just one example of a memory effect consistent with PIMMS, it also has an alternative explanation in terms of attentional resources. According to this account, priming reduces the resources needed to process an item, and therefore the remaining resources are available for encoding the context in which the item occurred. This resembles the “item-context trade-off” account of Jurica & Shimamura (1999), who observed that several factors that affect item memory tend to have opposite effects on context (source) memory, and the ‘stimulus learning/predifferentiation’ account considered by Kim et al. (2012), which proposes that resource demands are reduced for pre-exposed items.

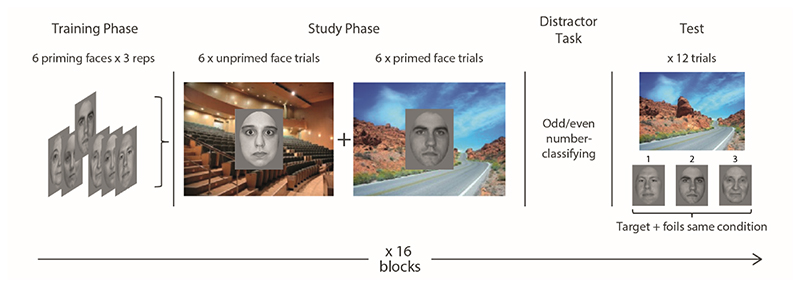
We conducted four experiments to test the resource account of the PSEM effect, using the same basic scene-face associative memory paradigm of Greve et al. (2017). This paradigm consists of three phases. In the first “Training” phase, one half of the face stimuli (the primed ones) are presented on their own for an arbitrary pleasantness rating task (see Methods). In the second “Study” phase, these primed faces, together with faces not seen in the training phase (unprimed), are presented on a background scene. The primary task again requires pleasant/unpleasant decisions about on the faces (for which response speed provides a measure of priming), but participants also have to detect (rare occasions) when the scene contained the moon (so the scenes could not be ignored). In the final “Test” phase, each scene is presented together with three faces from the same (primed/unprimed) condition (three-alternative-forced-choice, 3AFC), all of which had appeared in the study phase, and participants have to indicate with which face had been paired with the scene (see Figure 1).

Figure 1.

The basic design of Experiments 1-3. One of the 16 blocks shown, with each block testing memory for 12 scene-face pairs. In the initial Training phase, 6 faces were shown three times, serving to “prime” those faces. These faces were then repeated again in the Study phase, intermixed with 6 faces that were not shown in the Training phase, and each face was presented in front of a unique scene. In both Training and Study phases of a block, the primary task was to judge pleasantness of the faces. During the Study Phase, an additional task was to detect the occasional target scenes that contained the moon (not shown), to ensure all scenes were attended. The Distractor task involved 10 s of odd/even number classification, to disrupt immediate memory. The Test phase required 3-alternative forced choice (3AFC) for which face occurred with a given scene (foils were faces that were seen in the Study phase with different scenes). The main manipulations in each experiment occurred during the Study phase, as described in the text.

The simplest form of resource account is the “time-on-task”. It is possible that the reduced time taken to perform a task on a primed stimulus in the study phase (as evident by faster responses) means that more time remains (before the next trial starts) to encode aspects of its context. Experiment 1 tested this “temporal resource” account by fixing the “free time” between the response on one trial and the start of the next trial. One way to conceive of this manipulation is that it places a load on temporal resources, such that it reduces any additional resource that would otherwise be freed by priming. Two other types of resource that have been distinguished in the attention literature are “perceptual resources”, which are directed to the sensorium, and “central resources”, which operate on representations independent of current sensory input (see e.g. Yi, Woodman, Widders, Marois, & Chun, 2004; Chun & Johnson, 2011; Lavie, Beck, & Konstantinou, 2014). Experiment 2 used a typical operationalisation of perceptual load, in which one half of the face stimuli were made harder to see in the study phase, while Experiments 3a and 3b used a typical operationalisation of central load, in which an additional demanding secondary (auditory) task was imposed during the Study phase.

Using the same intuition used in many prior “dual task” studies, the resources account predicts an interaction between load and priming, whereby PSEM (a difference score of primed minus unprimed) is reduced under higher load. The resources account would also seem to predict a positive correlation between the amount of behavioural priming (the effect of Priming on response speed, or PRS) in the study phase and associative memory in the test phase (i.e, size of PSEM), and that this relationship should also be modulated by load. In short, we found no evidence for these predictions, with Bayes Factors preferring the null hypothesis of no effect. One might be tempted to conclude that the absence of such interactions with load questions the resources account, and thereby favours alternative accounts (like the PIMMS account). However, we go on to show that relatively simple computational models, based on a limited resource, can reproduce the complete set of qualitative patterns in our data, including the lack of effect of load on PSEM and lack of PRS-PSEM correlations (despite significant main effects of load), and therefore our data are not, in fact, inconsistent with a resources account. Indeed, we conclude that such resource models are impossible to reject with the type of experimental manipulations performed here, which has implications for any experiment that uses load manipulations.

Experiment 1: Temporal Resources

Experiment 1 tested the simple possibility that the PSEM effect arises because priming speeds response to an item, leaving more time to encode its context (before the next item appears).

Methods

16 participants (6 male) were recruited aged 18-35 (M = 25, SD = 4.1), and paid £6 for their time, according to ethics protocol CPREC 2005.08. For this first, exploratory experiment, sample size was based on similar sample sizes in the literature, in combination with counterbalancing constraints. Two participants were replaced because they did not perform significantly above chance at test (see Statistical Analysis section below). All were right handed and had normal or corrected-to-normal vision.

The experiment consisted of 4 phases, repeated across 16 blocks. Participants sat at a computer and used a keyboard to respond. After a brief summary of the tasks given by the experimenter, instructions were presented onscreen. A short (approx. 2 minute) practice session consisting of shortened versions of each task was completed prior to the beginning of the experiment proper, and thus participants were aware of the task requirements from the outset.

Task 1: Training Phase

This phase consisted of 18 evenly-spaced trials in which 6 faces were presented three times in a pseudorandom order (with all faces being presented, in a random order, before being repeated). A trial began with a white fixation cross in the centre of the screen for 500 ms, after which a face image appeared, with the fixation cross remaining visible over the face, always sitting approximately halfway down the nose. Participants indicated with a speeded response whether they found the face to be a ‘more pleasant’ or ‘less pleasant’ (than some subjective average) face, a judgement which could be neither correct nor incorrect. When a response was made, feedback that a response had been logged was given by the white crosshair changing to black. Each face image was presented for 1750ms, after which the next trial began, giving an SOA of 2250ms. After 18 trials which took ~45s, the software presented a brief reminder of the instructions for the next task, with participants indicating with a key press when they were ready to continue.

Task 2: Study Phase

This phase consisted of 12 study trials plus 2 (+/- 1) target trials interspersed randomly. Study stimuli in each trial were pairings of scenes with either primed or unprimed faces. The Load parameter alternated in each block, counterbalanced with respect to whether participants started with a Load or No Load block. Trial sequences were pseudo-randomly generated such that neither Primed nor Unprimed trials occurred for more than 3 successive trials. Each study trial began with a scene presented in the centre of the screen for 1000 ms. Target trials were scenes that included a moon, to which participants responded with a speeded key-press (spacebar). All other non-target scenes were followed by a face image, overlaid centrally on the scene image, with a white fixation cross appearing in the centre of the face image, as in the Training Phase. After a further 400ms, the images disappeared from the screen, leaving only the fixation cross. As in the Training Phase, participants indicated their speeded judgement about whether the face was ‘more pleasant’ or ‘less pleasant’, with feedback given in the form of the fixation cross turning to black. In Low Load blocks, the response window was fixed at 1200 ms from face onset (800 ms from stimulus offset), regardless of when a response key was pressed (i.e, a variable response-stimulus interval, vRSI). Thus, no RTs greater than 1200 ms were possible, which piloting suggested would capture more than 95% of responses. In High Load blocks, the trial ended a fixed 485 ms after a response was made (fixed response-stimulus interval, fRSI), such that the average response window was approximately matched with the Low Load condition (based on mean response times in pilot experiments). Note that, for all remaining experiments (2-3b), Study trial length was response-linked, as in the fRSI condition, and due to load manipulations expected to lengthen response times at study, faces were onscreen for 800 ms rather than 400 ms, which had the effect of lengthening the available response window to allow responses up to 1600 ms from stimulus onset (previously 1200 ms) for these later experiments.

Task 3: Distraction Phase

In order to prevent contributions from working memory, and to minimise recency effects, whereby the later-presented face-scene pairings would be better remembered, a short distractor task followed the Study Phase. This consisted of five trials of an odd/even number-categorisation task with a fixed SOA of 2000 ms. At the start of each trial, a white fixation cross appeared in the centre of the screen, replaced after 250 ms with a randomly selected number between 10 and 100. When the participant responded, feedback was given via replacement of the number with either a green (correct response) or red (incorrect) fixation cross, which remained onscreen until the end of the fixed trial time. At the end of the task, reminder instructions were presented for the next task.

Task 4: Test Phase

The Test Phase consisted of a 3AFC task, where all pairings encountered in the study phase were tested, yielding 12 trials. Trials ended when a response was given. In each trial, a scene was presented from the study phase, together with 3 face images presented at 75% scale and arrayed below the scene image, numbered 1-3. The position of the target and the 2 foils was pseudo-randomised such that the target could not appear in the same position for more than 3 consecutive trials, and appeared in each position an equal number of times. Target and foils were always chosen from the same condition (i.e. primed/unprimed) and were always of the same sex. At the end of this task, participants were informed that the block had ended and given reminder instructions for Task 1 of the following block, or informed at the end that the experiment had ended.

Statistical Analysis

Linear mixed effects (LME) modelling was used to model each trial, using the “lmer” and “glmer” functions in R (see /https://osf.io/rh5sc/ for all data and analysis code). Study phase RT data were transformed by taking the natural log of the reciprocal of the response time in seconds, yielding a measure of speed (and rendering the distribution over trials more Gaussian). For Test phase accuracy data, each trial was coded as 1 or 0, and logistic LME was implemented via a binomial linking function, yielding a Z-statistic for each fixed effect. All LME models assumed factorial fixed effects of load and priming, with random effects for participants and participant-by-effect interactions. A random effect of each face stimulus was also added to model stimulus-related variance (except in Experiment 3b, where convergence was only possible without this random effect). For the accuracy data, we additionally ran a Bayesian LME using the “brm” function in R, with unit normal shrinkage priors on all fixed effects, with mean of zero and standard deviation of 1, and 4 chains of 50,000 iterations. This enabled us to report a Bayes Factor (BF) in favour of either the alternative hypothesis (BF₁₀) or null hypothesis that the effect was zero (BF₀₁). Parameter estimates are reported in terms of their mean (M) and standard error (SE); for Study RS, their units are log(s^-1); for Test Accuracy, they are probabilities on the logit scale. For the figures, data are shown as trial-averaged means for each participant, plus additional across-participant statistics for simple effects on these trialaveraged data.

Correlations between priming of RS at Study and accuracy at Test were tested with Pearson’s correlation coefficient, and the effect of Load on these correlations was tested with Pearson and Filon's Z-statistic (1898), as implemented in the “cocor” package in R. All p-values are two-tailed.

Some participants found the memory task so difficult that they appeared to give up. We therefore replaced participants who performed at chance: overall Test performance (averaged across conditions) was tested with a permutation test, where answers to the 16 blocks x 12 trials (192 in total) were randomly shuffled and compared with the correct responses 10,000 times, to give a null distribution of Test scores. The actual test score was then ranked in this distribution of scores, and accepted as significantly different from chance if it was greater than the 95^th percentile score, otherwise the participant was replaced.

Results

Study

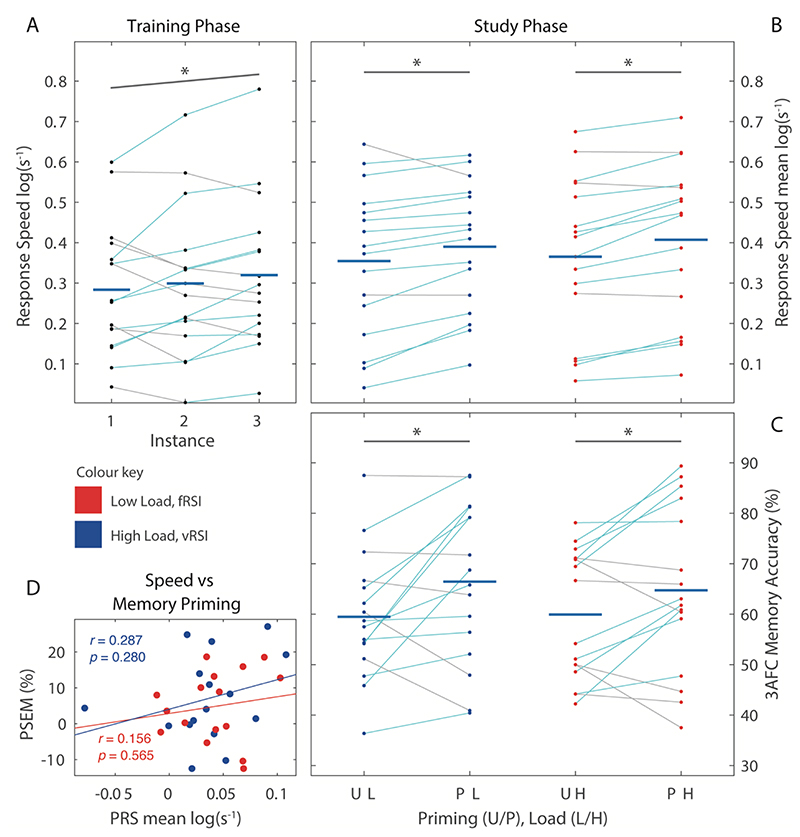
The linear mixed effects (LME) model of Study Phase response speed showed a significant main effect of Priming (M = 0.036, SE = 0.013), T(26.9) = 2.86, p = .008, with faster responses to primed trials, as expected (Figure 2B). There was no significant effect of Load, (M = 0.010, SE = 0.011), T(14.9) = 0.93, p = .354 (as expected, because the manipulation only affected the time after a response), nor interaction, T(41.1) = 4.04, p = .688.

Figure 2.

Panels A-C show mean scores (N = 16) during 3 phases of Experiment 1. Priming of face pleasantness responses was found during Training (A, using a linear trend analysis across the three presentations) and during Study (B). Panel C shows effect of priming on memory during final 3AFC Test phase (chance = 33%), revealing no effect of restricting temporal resources during Study, nor interaction. Panel D shows relationship between priming effects at study (PRS) and test (PSEM) with no overall correlation, no correlation under either load condition, nor any difference in slopes. Cyan (expected, priming direction) and grey (no-priming) lines link individual subject data points across conditions. Abbreviations fRSI and vRSI: fixed (f), variable (v) response-stimulus interval. Bars with asterisks indicate significant linear trend (Training phase), or significant simple effect as analysed using a paired-sample T-test, p <.05.

Test

The logistic LME of Test accuracy showed a significant main effect of Priming (M = 0.35, SE = 0.15), Z = 2.41, p = .016, with greater associative memory for primed trials i.e., a significant PSEM effect. Fixing the time after a response did not produce a significant change in Test performance (M = 0.01, SE = 0.11), Z=0.055, p = .956, nor did it moderate the size of the PSEM effect, with no significant interaction between Study Load and Priming (M = -0.02, SE = 0.14), Z=-0.596, p = .551. Indeed, priming was significant in the predicted direction when analysing Low and High load conditions separately (see Figure 2C). Bayes Factors did not provide evidence for or against priming, BF₀₁ = 1.32, but did provide decisive evidence against any effect of load or interaction with priming, BF₀₁ > 18.4.

PRS-PSEM correlations

After averaging over trials in order to create a mean priming score for each participant, there was no significant correlation across participants between the effects of priming on response speed (PRS) at Study and its effects on subsequent memory (PSEM) at Test, averaged across Load, R = 0.288, p = .279, nor was there any significant difference in the correlations for high versus low Load, Z = 0.387, p = .700 (Figure 2D).

Discussion

Experiment 1 replicated the PSEM effect of Gagnepain et al. (2008, 2011) and Greve et al (2017; Experiment 3). However, it did not find any evidence to support the hypothesis that PSEM occurs because priming increases the time available for episodic encoding after a response has been made to primed stimuli, i.e, no evidence for priming increasing the availability of temporal resources. Despite significant priming of response speed (PRS) to faces during the Study phase, the PSEM effect was not reduced when the interval between a participant’s response on one Study trial and the start of the next was fixed (High Load condition), relative to variable (Low Load condition), i.e, removing the potential extra time released by priming a face did not reduce the size of the priming advantage on subsequent memory for a scene-face association.

The general resource account would seem to predict a positive correlation between the PRS and PSEM effects when collapsing across conditions, i.e, the greater speed-up a participant showed from priming, the greater the PSEM effect for that participant. We did not find this correlation. Moreover, the strength of any relationship between priming effects at Study and Test did not differ between high and low temporal loads, contrary to the reduced correlation that might be expected if a fixed response-stimulus interval removed additional temporal resources available for primed trials. Thus, we concluded that while PSEM may be explained by the freeing-up of resources, these are not temporal resources, and so explored other types of attentional resource in Experiments 2-3.

Experiment 2: Perceptual Resources

The manipulation of perceptual load has been shown to affect processing of surrounding stimuli (see Lavie, 2005 for review). According to Burgess et al., (2007), stressing perceptual attention requires: i) the immediate availability of information to be processed, ii) that the processing requires target perceptual features of the present stimulus, and iii) that the responses and rules governing them are relatively well-learned. Experiment 2 fulfilled these criteria for increasing perceptual load by degrading one half of the face images through the addition of pixelwise noise (as also used successfully by Yi et al., 2004).

To show that our perceptual load manipulation affected face processing, it is important to demonstrate a main effect of degradation on memory. However, if faces were only degraded at Study (and presented intact at Test), then any effect of perceptual degradation on memory performance could simply reflect a reduced perceptual overlap between Study and Test stimuli. In other words, degrading faces at Study would induce a Study-Test mismatch in the face images (and in the extreme case, participants might not recognise the same face at Test when the visual noise is removed). This is a potential confound in Experiment 3 of Greve et al (2017), and the present experiment controlled for this by adding a second (within-participant) factorial manipulation of perceptual degradation at Test, as well as Study. In order to retain power while including this additional factor, the sample size from Experiment 1 was doubled to 32. If Study-Test match is an important determinant of memory, then there would be a main effect of matching versus mismatching conditions. If the freeing of perceptual resources by priming is the cause of PSEM effects, then there should be an interaction between priming and image-clarity (perceptual load), regardless of study-test match.

Method

32 participants (10 male), age 18-35 (M = 25, SD = 4.5) years were included, none of whom had participated in previous PSEM experiments. Four participants were replaced: 1 because of extremely rapid responses, faster than 3SD from mean response speed, and 3 because they did not perform significantly above chance during test (see Methods of Experiment 1).

Degradation of faces during the Study phase alternated between Low Load ‘clear’ blocks and High Load ‘degraded’ blocks. In half of both Low and High Load blocks, the Test face stimuli were also degraded, so that face stimuli either were a match or a nonmatch between Study and Test phases, with this ‘Match’ factor rotating over blocks. Piloting suggested that that making a random 57% of pixels gray was sufficient to make the face harder to identify. Face images remained onscreen during Study Phase trials for an increased period of 800 ms (from 400 ms previously). Otherwise, the procedure was identical to the fRSI condition of Experiment 1.

Results

Study

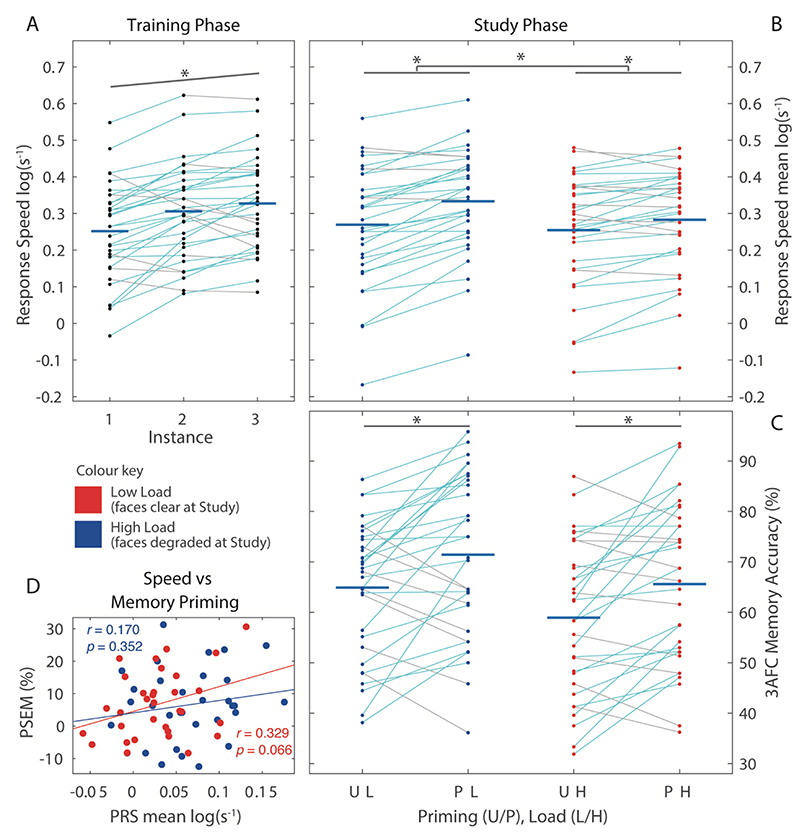
The LME on response speed at Study showed a significant main effect of Priming (M = 0.065, SE = 0.009), T(43.5) = 7.24, p < .001, with faster responses to primed trials as expected (Figure 3B). The main effect of Load was not significant, (M = -0.014), SE = 0.009), T(48.0) = -1.62, p = .112, but there was a significant interaction between Load and Priming (M = -0.038, SE = 0.011), T(149)=-3.51, p < .001. Separating trials by Load revealed that priming was significant for both Low load trials (M = 0.065, SE = 0.009), T(70.7) = 7.78, p < .001, and High load trials, (M = 0.028, SE = 0.008), T(30.7) = 3.63, p = .001, but was greater for clear faces (Low load) than degraded faces (High load), most likely because of the perceptual match with the faces at Training, which were always clear.

Figure 3.

Panels A-C show mean scores (N = 32) during 3 phases of Experiment 2. Priming of face pleasantness responses was found during Training (A, using a linear trend analysis across the three presentations) and Study (B), in addition to a main effect (longer bar) of degradation during Study. Panel C shows effect of priming on memory accuracy during final 3AFC Test phase (chance = 33%) and effect (longer bar) of degrading face images during Study Phase, but no interaction. Data collapsed over Match factor, which did not show significant effects (see text). Panel D shows relationship between priming effects at study (PRS) and test (PSEM) with a positive correlation for the Perceptual Load condition.

Test

The logistic LME of Test accuracy included an additional fixed effect of Study-Test Match (whether a face was clear at Study and at Test, degraded at both, or switched), in case memory was improved when perceptual format matched. There was a significant main effect of Priming (M = 0.479, SE = 0.145), Z = 3.30, p < .001, i.e, significant PSEM, as in Experiment 1. There was also a significant main effect of Load (M = -0.271, SE = 0.125), Z=- 2.18, p = .029, with worse associative memory for degraded trials, demonstrating that the manipulation had an effect. There were no more significant effects, i.e, no main effect or interaction with Study-Test Match, |Z| < 0.891, p > .373, and importantly, no interaction between Priming and Load (M = -0.052, SE = 0.176), Z = -0.071, p = .944 (see Figure 3C, where data averaged over Test degradation; for full data, see Supplementary Table 1). Bayes Factors provided decisive evidence for priming, BF₁₀ = 79.0, and for a load effect, BF₁₀ > 1e15, but also decisive evidence against any interaction, BF₀₁ = 31.5.

PRS-PSEM correlations

There was a borderline positive correlation across participants between PRS at Study and PSEM at Test, averaged across Load (and Study-Test Match), R = 0.348, p = .051. This did not appear to differ according to Load, Z = -0.703, p = .482 (Figure 3D).

Discussion

Experiment 2 found no evidence to support the perceptual load account of the PSEM effect. Perceptual load was increased by adding pixel noise to one half of the faces. This manipulation was clearly successful in affecting face (item) processing, because Study responses overall were slower, and memory at Test was worse, for faces that were degraded at Study (when collapsing over primed and unprimed conditions). However, there was no evidence that this perceptual load reduced the PSEM, i.e, no evidence at Test for an interaction between Load and Priming, with the PSEM effect significant under both low and high perceptual loads, and numerically similar.

There was some suggestion that the perceptual match between Study and Test phases also affected memory (which would have confounded any effect of perceptual load if we had only presented clear faces at Test), in that there was a borderline interaction between Study-Test match and priming on memory performance at Test, with a bigger PSEM effect for non-matching faces. Nonetheless, the PSEM was significant for matching and non-matching conditions separately, and most importantly, this potential effect of matching did not interact with the perceptual load at Study, which was the main manipulation of interest.

There was a significant interaction between Load and Priming on response speed in the Study phase, in that the priming effect was greater for clear than degraded faces. This can be explained by greater perceptual overlap for the clear faces in the Low load condition with the clear faces presented in the Training phase. However, the mean positive correlation between effects of priming at Study (PRS) and at Test (PSEM) showed no evidence of being moderated by perceptual load, i.e, whether faces were clear or degraded at study. In other words, while the positive average correlation is consistent with a resource account in general, the lack of moderation of PSEM by perceptual load suggested an alternative type of resource is critical.

Experiment 3a: Central Attentional Resources I

Experiments 3a and 3b attempted to manipulate central rather than perceptual load, by using a concurrent secondary task on auditory stimuli. Central load is assumed to affect cognitive processes like maintenance, refreshment, rehearsal, and manipulation of offline, internal representations (Baddeley, 2003; Chun & Johnson, 2011). The primary difference between Experiments 3a and 3b concerned the difficulty of this secondary task.

The procedure for Experiment 3a was identical to Experiment 2, except that only clear faces were used, all trials were accompanied by occasional auditory tones, and on alternating blocks there was a secondary task to be performed on the tones. This secondary task (High load condition) required participants to maintain a 2-digit number, and update it each time a tone was heard. This satisfies the criteria of Burgess et al., (2007) for central, stimulus-independent processing, in that the number being attended is not present in the environment and the responses referring to these internal representations. In baseline (Low Load) blocks, participants were asked to ignore the tones.

Method

Maintaining the sample size of Experiment 2, 32 participants (12 males) aged 18-35 (M = 23, SD = 3.2) years were recruited, none of whom had participated in previous PSEM experiments. One participant was replaced due to outlying (slow) Study Phase responses, three were replaced who did not perform significantly above chance overall in the Test Phase, while one was replaced due to an extremely outlying Test data.

The experiment was identical to Experiment 2 apart from the use of clear faces only, and the following changes. During the Study Phase, participants wore headphones through which they heard occasional tones. Tones were timed to appear with a probability of .6 during the period immediately before onset of a scene stimulus, with their precise occurrence during this 500 ms period sampled from a normal distribution with μ = 250 ms, σ = 125 ms. Prior to the Study Phase, instructions presented onscreen indicated whether tones should be attended to (High Load blocks), or ignored (Low Load blocks); 8 blocks of each. High Load block instructions showed a ‘starting number’, between 10 and 87, and participants were instructed to begin maintaining this number in their head while they performed the primary face task, adding one each time they heard a tone. At the end of a High Load block, participants were prompted to report the final tally, which they input via the keyboard.

Results

Study

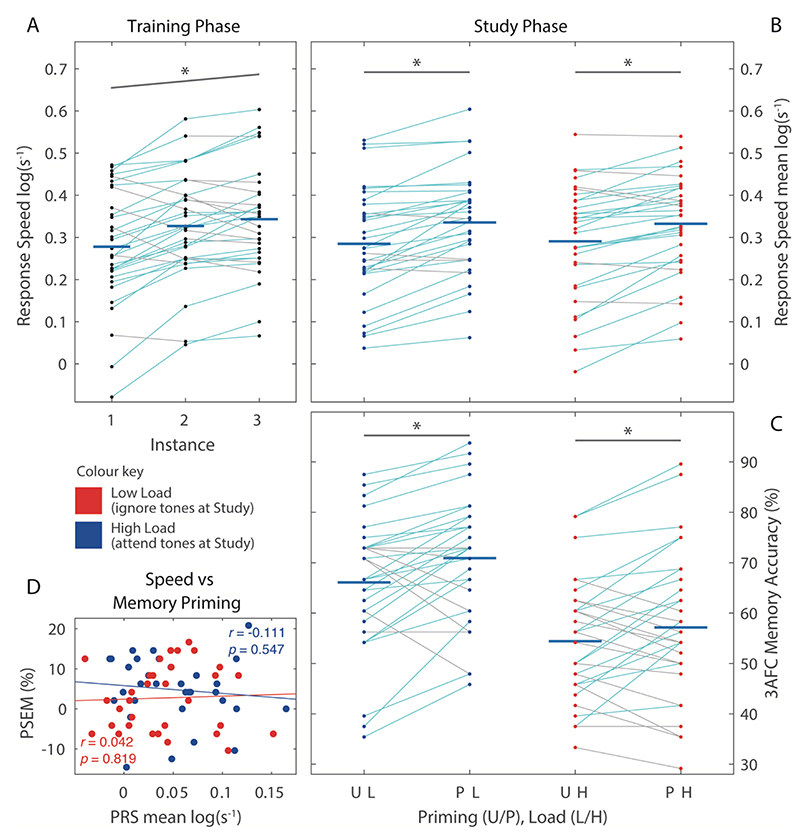
The LME on response speed at Study showed a significant effect of Priming, (M = 0.050, SE = 0.009), T(45.4) = 5.69, p <. 001, with faster responses to primed trials as expected (Figure 4B). Interestingly, the presence of a secondary task did not affect primary (face) task performance, with no significant effect of Load, (M = 0.006, SE = 0.011), T(35.6) = 0.503, p = .618, nor interaction, T(834) = -0.772, p = .440.

Figure 4.

Panels A-C show mean scores (N = 32) during 3 phases. Priming of face pleasantness response speed was found during Training (A) and Study (B), but not affected by secondary task during Study. Panel C shows effect of priming on memory accuracy during final 3AFC Test phase and main effect of secondary task during Study Phase, but no interaction. See Figure 2 legend for more details. Panel D shows no observed relation between priming effects on RS and subsequent memory.

Secondary task performance was close to ceiling, with a median 7 correct out of 8 responses (range = 4 to 8).

Test

The logistic LME of Test accuracy showed a significant main effect of priming, (M = 0.241, SE = 0.083), Z = 2.89, p = .004, again replicating the PSEM effect. A main effect of secondary task showed that attending to tones in the Study phase resulted in worse memory (M = -0.526, SE = 0.091), Z = -5.79, p <.001, also as expected (Figure 4C). However, though PSEM was numerically smaller under High than Low Load, the interaction did not approach significance (M = -0.113, SE = 0.117), Z = -0.961, p = .337. Bayes Factors showed some evidence for priming, BF₁₀ = 3.72, decisive evidence for an effect of Load, BF₁₀ > 1e19, and decisive evidence against any interaction with priming, BF₀₁ = 20.4.

PRS-PSEM correlations

The mean correlation between PRS and PSEM (averaged across Load) was not significant, R = 0.019, p = .915, and there was no significant difference between Load conditions, Z =-0.616, p = .538 (Figure 4D).

Discussion

Even though it did not seem to adversely affect Study response speed, the secondary task used to increase central load was successful in reducing memory accuracy at Test. Nonetheless, even though the PSEM effect was numerically smaller in the High than Low (central) Load condition, the interaction did not reach significance, and the PSEM effect remained significant in the High Load condition. Again, any correlation between PRS and PSEM was not significant, and did not differ between conditions.

One possible limitation is that the secondary task was not demanding enough to abolish the PSEM effect in the High Load condition. A second potential limitation is that the tones in the Low Load condition still made some demand on central resources, even though they were supposed to be ignored (particularly given the frequent switching across blocks in the taskrelevance of the tones). This might have reduced the effective difference in central load between the two conditions (reducing the size of the predicted interaction, despite there still being a main effect of central load). A final limitation of Experiment 3a is that the measure of secondary task performance in the High Load condition was coarse and at ceiling. This meant we could not test whether there was any effect of priming on secondary task performance, which might arise if participants prioritised resources for the primary (face) task, such that differences in the central resources remaining affected the secondary (tone) task instead. These limitations were addressed in Experiment 3b.

Experiment 3b: Central Attentional Resources II

Experiment 3a addressed the limitations of Experiment 3a by using: 1) a more difficult task on the tones in the High Load condition, which required incrementing a number in working memory by either 1 or 2, depending on whether the tone was of low or high pitch, 2) no tones or task in the Low Load condition, thereby maximising the difference in central load between conditions, and 3) a secondary task that provided a more continuous, trial-by-trial measure of performance. This measure was a judgment, at the end of a trial, of the duration of the last tone presented (see Methods for details), based on pilot data showing that we could detect an effect of a primary task on this measure.

Method

Participants

32 participants (9 males) aged 18-35 (M = 23, SD = 4.4) years were included in the analysis, none of whom had participated in previous PSEM experiments. Because of the extremely challenging nature of the High Load condition, a total of 21 participants had to be replaced, after failing to achieve above-chance performance across Load conditions in either the primary memory task (N=6) or the secondary task (in the High Load condition), as measured by absence of a significant correlation between duration of the tones heard and their judged duration (N = 17, 2 of whom were also below chance on the primary task).

Procedure

The procedure was identical to Experiment 3a apart from the following changes. Tones only occurred in the High Load blocks. They were equiprobably high (1000 Hz) or low (500 Hz) pitched, with onset at either 200 ms or 700 ms after trial onset, and durations sampled from a normal distribution, μ = 500 ms, σ = 175 ms, matched within blocks so that tone pitches, onsets and durations were equated between primed and unprimed trials. In High Load blocks, participants had to increment a starting number between 10 and 87 by adding 1 when they heard a low tone or by 2 when they heard a high tone. Due this added complexity, the interval after a response was extended by 1250 ms, after which the text ‘Now!’ appeared onscreen. This cued participants to reproduce as accurately as possible, using a sustained keypress, the duration of the tone they had heard at the beginning of the trial. They then entered the number that their internal tally had reached at the end of each High Load block.

Statistical analysis

Analyses were identical to previous experiments, except for the additional exclusion of trials where no duration report was recorded (median = 6, range of 0 to 23 trials lost). Furthermore, performance of the secondary task in the High Load condition was analysed by measuring the correlation, over trials, between actual and reported tone duration (therefore ignoring individual differences in offsets of temporal perception). The correlations for primed and unprimed trials were compared using a paired T-test after Fisher-transforming the Pearson correlation coefficient.

Results

Study

The LME on response speed at Study showed a significant showed a main effect of priming, (M = 0.058, SE = 0.008), T(82.1) = 6.81, p < .001, with faster responses to primed faces (Figure 5B). Unlike Experiment 3a, there was also a significant main effect of Load, (M = -0.097, SE = 0.015), T(32.3) = -6.29, p < .001, such that the concurrent task slowed responses, as expected. Furthermore, there was an interaction between Priming and Load, (M = -0.028, SE = 0.013), T(122) = -2.23, p = .028, where Priming under Low Load was greater than under High Load.

Figure 5.

Panels A-C show mean scores (N = 32) during 3 phases. Priming of face pleasantness responses was found during Training (A) and Study (B), but not affected by secondary task during Study. Panel C shows effect of priming on memory accuracy during final 3AFC Test phase and main effect of secondary task during Study Phase, but no interaction. See Figure 2 legend for more details.

Test

The logistic LME of Test accuracy showed a significant main effect of priming (M = 0.210, SE = 0.094), Z = 2.22, p = .026, again replicating the PSEM. A main effect of Load (M = -0.550, SE = 0.089), confirmed that the concurrent task in the Study phase impaired subsequent memory Z = -6.12, p < .001 (Figure 5C). However, as in previous experiments, any evidence for an interaction between Priming and Load (M = -0.146, SE = 0.124) did not reach significance, Z = -1.18, p = .238.

Bayes Factors did not support evidence for a main effect of priming, BF₁₀ = 0.194, but did provide decisive evidence for a main effect of load, BF₁₀ > 1e19, and, most importantly,decisive evidence against any interaction between priming and load, BF₀₁ = 21.6, suggesting that it was not the case that the data were simply too noisy to detect an interaction.

PRS-PSEM correlations

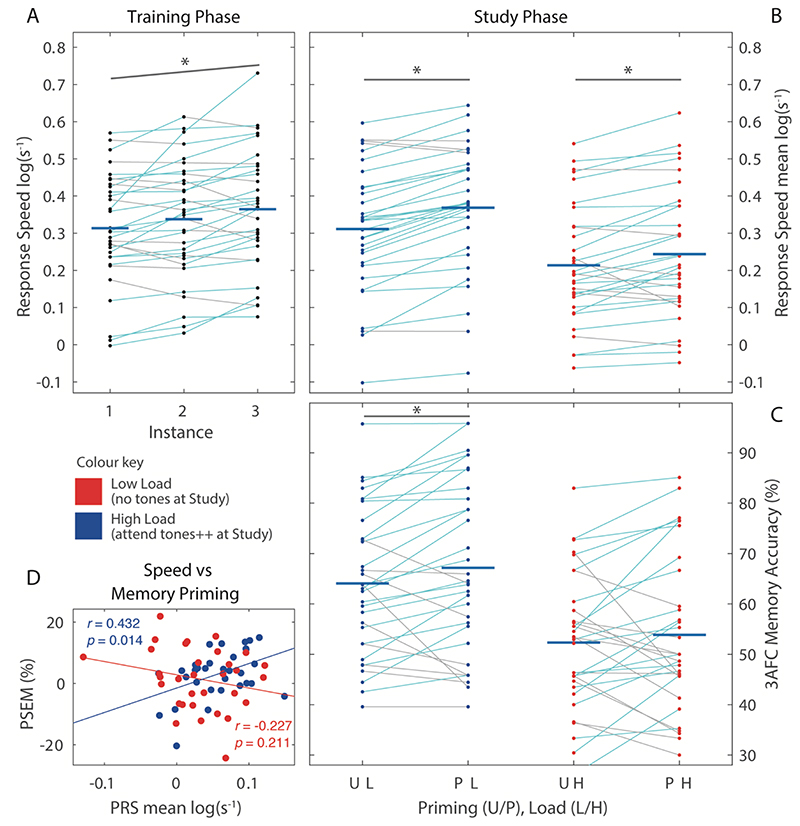
PRS and PSEM were not significantly correlated across Load conditions, R = .208, p = .251. However, the correlations did differ significantly by Load, Z = 3.07, p = .002, being significantly positive in the Low load condition, but not differing significantly from zero in the High load condition (Figure 5D).

Secondary Duration Report Task and Number Maintenance Task

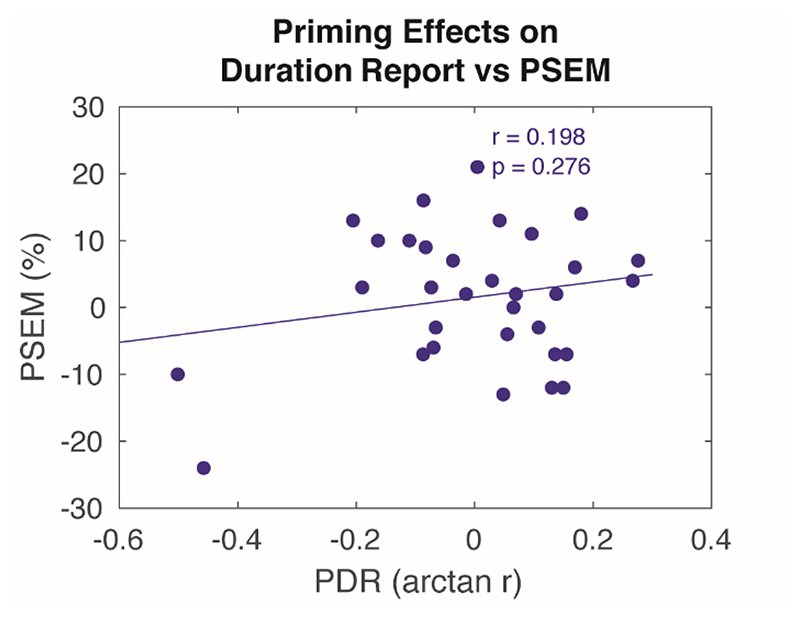
After Fisher transform, the correlation coefficients between heard and reported duration for the secondary duration report task in the High Load condition did not differ between Primed (M = .431, SE = .025) and Unprimed (M = .437, SE = .036) trials, T(31) = 0.51, p = .610. In other words, participants did not differ in their ability to maintain tone durations depending on whether faces were primed or unprimed. The scatter plot in Figure 6 shows that PSEM did not appear related to any effect of priming on the secondary, ‘duration report’ task. The median number of correct responses in the mental number-maintaining-and-incrementing task was 5 out of a possible 8 (range = 8).

Figure 6.

Scatter plot shows no relationship between PSEM and priming effects on duration report (PDR) in the High Load condition, where latter measured as Fisher-transformed correlation between actual and reported tone duration.

Discussion

Despite increasing the difficulty of the secondary task in the High (central) Load condition, and minimising the load in the Low Load condition (by removing any tones), Experiment 3b, like Experiment 3a, still failed to find evidence of a significant interaction between central load and PSEM. The increased difficulty was confirmed by the significant slowing of Study responses (unlike Experiment 3a), in addition to their impaired Test performance. Nor did any effect of priming appear in the new measure of secondary task performance, as might happen if participants allocated a greater proportion of their resources to the primary task (maintaining the PSEM effect), such that resources freed by priming facilitated secondary task performance instead. Indeed, there was no evidence of a significant correlation between priming effects on primary and secondary tasks in the High Load condition. (Although it might have been helpful to have a baseline measure of secondary task performance under Low Load, this would compromise the effort to maximise the difference in central load between High and Low Load conditions.)

Though the interaction between Load and Priming on subsequent memory did not reach significance, the PSEM effect was numerically smaller in the High Load condition, and the simple effect of Priming under High Load no longer reached significance. This lack of evidence for the interaction is unlikely to owe simply to noise in the data, because the Bayes Factor still provided decisive evidence for no interaction (if the data had been noisy, then the Bayes Factor would not favour either the null or the alternative hypothesis). Nonetheless, it remains logically possible that, despite our efforts and the difficulties experienced by participants, we were unable to sufficiently impact the resources available, and therefore simply failed to find a true effect of load on PSEM. Rather than leaving this investigation with the possibility of insufficient load manipulations, we created a formal model of how a resource account might apply to the present experiments. This turned out to be important in appreciating the limitations of dual-task logic, and particularly illuminating about the elusive nature of correlations between priming effects on our various measures.

Modelling of Experiments

The above experiments tested the idea that some form of resource is “freed up” by the prior processing of primed stimuli, and these freed resources are used to improve subsequent memory (the PSEM effect). However, any interaction between Load and the PSEM effect failed to reach significance in all four experiments. We now address the question from a computational perspective.¹

Relating resources to performance

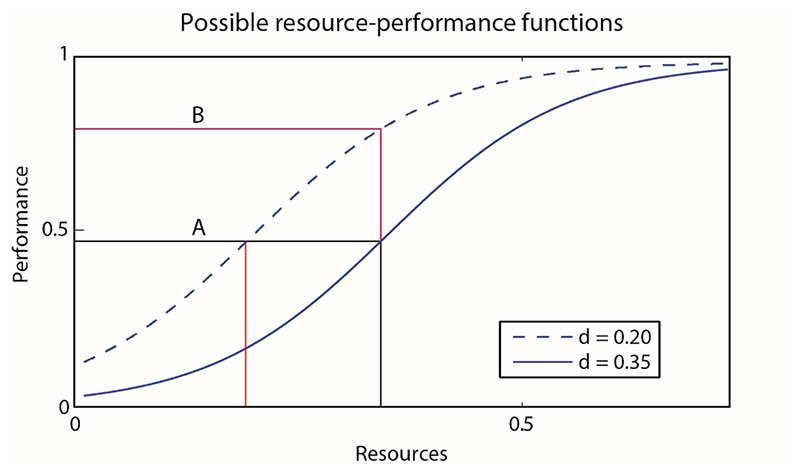
Norman and Bobrow (1975) describe a function that relates task performance to attentional resource in its most general terms as monotonically non-decreasing. In theory, a wide variety of such functions are plausible, but a reasonable case is a sigmoid: at low levels of resource allocation, task performance is impossible, and after this threshold there is an improvement in performance as more resources are applied, followed by a tailing-off as additional resources no longer improve performance due to other limits, e.g., sensory or response limits:

$$P=\frac{1}{(1+e^{-(r-d)/s})}$$

where P is performance, r is resources, s is the sharpness of the sigmoid and d is the “difficulty” of the task.² If r ranges between 0 and 1, and s = 0.1, then Figure 7 shows two different difficulties: d = 0.35 (harder) and d = 0.20 (easier). As can be seen from comparing Line B with Line A, a lower difficulty (for example, in processing a face because of prior exposure to that face) means a higher performance (P) results from the same level resources (r).

Figure 7.

Schematic illustration shows how changing difficulty parameter, d, allows improved performance with reduced resources. Line A shows normal performance. Line B shows that when difficulty parameter d is reduced, performance for the same amount of resources is increased. Red vertical line between x-axis and Line A indicates resources required for maintenance of performance when change in d makes the task easier.

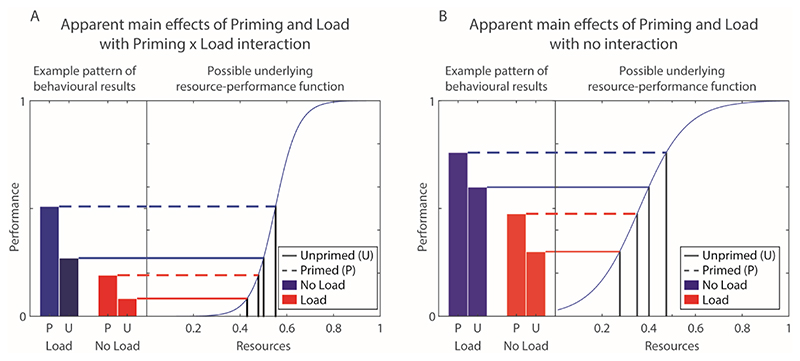
A well-established (e.g., Dunn & Kirsner, 1988) feature is clear even before any further modelling takes place: given we do not know the form of the function, and cannot directly measure the hypothesised resources, it is possible to produce several qualitatively different data patterns from a single underlying resource. Figure 8 shows two such patterns. Panel A shows an interaction pattern, which is often used to argue for a single underlying resource. However, Panel B shows that the same single resource can also produce two main effects in the absence of an interaction, which is often used to argue for separate resources. Whether or not an interaction pattern is found (on subsequent memory) depends only on whether there is a difference in the gradient of the resource-performance function between primed and unprimed data points under high and low load, and thus in the absence of further information, one cannot predict the outcome in a 2x2 design.³ In other words, without any further assumptions, it is apparent that there exists a set of parameters that can reproduce the lack of interaction between Load and Priming.

Figure 8.

Schematic shows how distinct data patterns can arise from sampling different points on a single (nonlinear) performance-resource function. Panel A shows a priming-by-load interaction, while Panel B shows main effects of both priming and load, but no interaction.

However, performance on the final associative memory task is not the only measure in our experiments: there are also measures of performance (response speed) for the primary study task in the Study Phase (which is when resources are assumed to impact), as well as for the secondary task in Experiment 3b, and according to a limited-resources account, one might expect a positive correlation between the effects of priming on response speed and subsequent memory (if PRS indexes the amount of resources freed), and a negative correlation between the effects of priming on subsequent memory and performance of the secondary task (if more of the resources freed by priming are devoted to secondary task rather than to memory encoding). To model these, we need to consider performance-resource functions for the face-processing task at Study (as well that for subsequent memory at Test), specify how resources are allocated to each task, and add variability across participants to estimate correlations.

Simulation 1: Modelling basic PRS and PESM, e.g, in Experiment 1

Participant Resources and Resource Allocation

In the model, each participant, s, is assumed to possess some total amount of resource, R_s, sampled from a normal distribution, with the proportion allocated to each of i = 1 …M simultaneous tasks being defined as 0 < a_i < 1, such that ${\displaystyle {\sum }_{i=1}^M{a}_i=1}$ and r_is = a_iR_s. For the basic paradigm without any concurrent load, M = 2, such that r_1s = a₁R_s represents the resources allocated (by participant s) to the primary Study task of making face pleasantness judgments (hereafter, “Face Task”) and r_2s = a₂R_s or r_2s = (1 − a₁)R_s represents the resources remaining for the other “task” of encoding the scene-face associations into memory (hereafter, “Memory Task”). Finally, to introduce some random variability, measurement noise was added, u~N(0, σ), to the final performance values.

Effect of Prior Exposure

As alluded to earlier, prior exposure/training can be modelled as decreasing the difficulty, d_j, of the jth task. Priming reduces the difficulty of the primary (face) task, such that d_1p < d₁, where p indicates a primed (trained) trial (and unprimed trials correspond to the baseline case, i.e, d_1u = d₁). Changing parameter d has the effect of translating the resource-performance function in question along the x–axis, as seen already in Figure 7. This means that the participant can reduce the proportion of resources allocated to this primary task by as much as allowed by the change in difficulty, d₁ − d_1p produced by training, and still maintain performance of that task. This in turn releases more resources for the “other task” of memory encoding, i.e. r_2sp = a_2pR_s > (1−a₁)R_s = r_2s. More resources released means that memory encoding is better for primed-face trials, explaining the basic PSEM effect. Note that in the simulations that follow, we assume that the resource-performance functions for the Study task and the Memory task are identical (i.e., difficulty parameters d₁ and d₂, as well as the sharpness parameter s, are equal). Of course, this is unrealistic in practice, but rather than trying to fit the data, we are interested in the simplest model possible that can accommodate our results, i.e, the model with the fewest assumptions and fewest degrees of freedom.

In reality, we know that performance on the primary task also improves, suggesting that participants (on average) do not release all the resources that are saved by priming. Instead, it is assumed that participants maintain a proportion, 0 <x_p < 1, of the resources freed by priming, i.e, r_1ps = a₁R_s − x_p(d₁ − d_1p) and hence r_2ps = (1−a₁)R_s + x_p(d₁−d_1p).

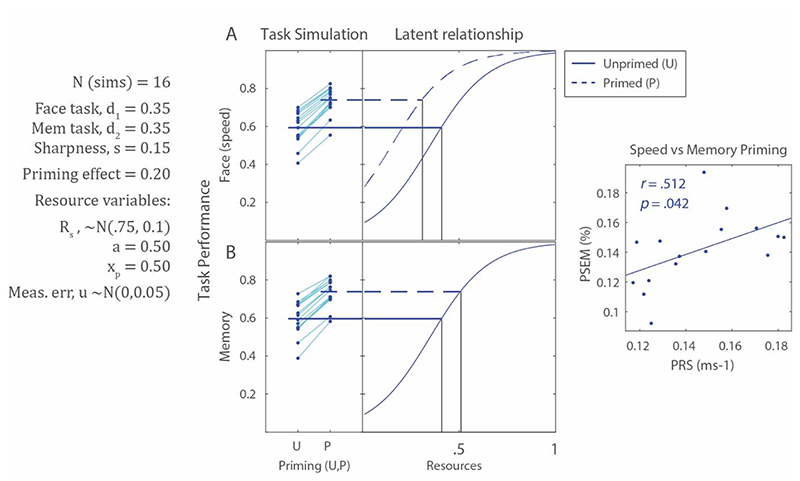
Figure 9 shows the results of a simulation of Experiment 1. Here, our load manipulation is not modelled, since it had no effect on performance of either the Face or Memory Task. This simulation instead offers a simple demonstration of how we can model the basic PSEM effect. Performance on the Face Task improves following priming (Panel A), concurrent with improved performance on the Memory Task (Panel B). With additive measurement noise included, a weak correlation is seen between PRS and PSEM effects. The reason for the weakness and sometimes lack of correlation is explored in the next section.

Figure 9.

Basic simulation (N=16) of PRS and PSEM, illustrating how priming can be modelled as freeing up resources from Face Task for Memory Task. Lines between boxplot markers show individual simulations. Note this simulation shows an exaggerated effect for illustration purposes. Variation in simulated performance comes from randomly sampling values of simulated-subject overall resources, R_s, and by addition of measurement error for each data point.

Correlations Between PRS and PSEM

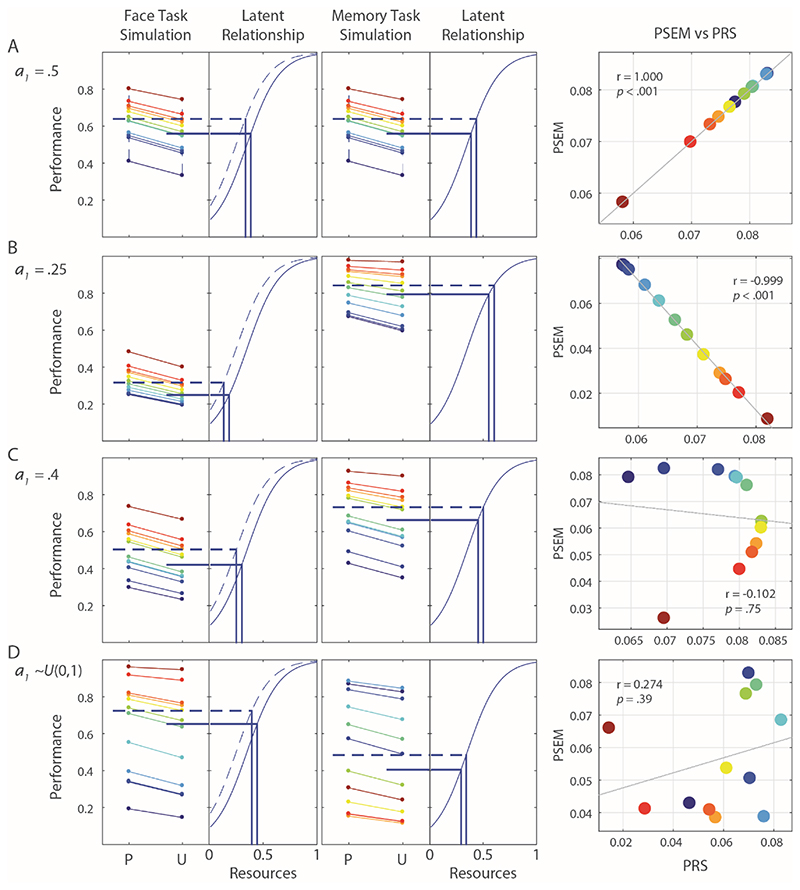
In the experiments above, we did not always find significant correlations between priming effects at Study and Test, and this seemed puzzling if they depend on the same resource, since we might assume that the more resources that have been freed by priming, the more priming effect would be seen in both tasks. Moreover, another reason for a positive correlation is that participants with a higher R_s should show larger priming effects on both measures. However, simulation of the simplest version of the experiment (i.e. Face Task and Memory Task, with no perceptual or central load, as in the model of Experiment 1) shows that simply by varying only the allocation parameter, a₁, a range of positive, zero or negative correlations can be produced (see Figure 10).

Figure 10.

Panels A-D show 4 (N=12) simulations of primed (P) and unprimed (U) performance in Face and Memory tasks. Overall resources, R_s, were randomly sampled from N(0.75, 0.15) each with a different value for allocation paramater, a₁, with all other settings equated and measurement error, u, set to zero. Horizontal lines show mean task performance, solid (U), dotted (P). Colours used are consistent for individual simulations across panels, for ease of comparing performance across tasks and with scatter plots.

To understand the reasons for this, first, measurement error, u, is removed from the simulation. Performance of the two primary (Face and Memory) tasks is then simulated, randomly sampling R_s while keeping the s and d sigmoid parameters equated for both tasks, and keeping a₁ and x_p both fixed at .5, equivalent to participants allocating resources evenly between the tasks (Panel A of Figure 10). In this case, PRS and PSEM are almost perfectly positively correlated. As can be seen from the illustration, this positive correlation arises because, under these assumptions about allocation, priming effects on both RS and Memory are produced from the same regions of the sigmoids underpinning task performance.

However, as a₁ is allowed to vary towards either 0 or 1 (entailing asymmetries of R_s allocation), correlations become negative (Panel B). Again, the illustration helps understand this feature of the model: for higher-than-average-value samples of R_s, higher performance in the task allocated more of the resources places a participant at the lowest-gradient part of a decreasing-gradient part of the sigmoid, thus producing limited priming effect. Meanwhile, in the other task, task performance for the same participant will be produced from the highest-gradient part of an increasing-gradient part of the sigmoid, producing a relatively large priming effect, and thus we see the negative correlation between PRS and PSEM.

If a₁ is set between values producing strong positive and negative correlations, then sampling R_s produces a complex relationship between PSEM and PRS (Panel C). Under this situation, the pattern (which could be described as divergent values of PSEM produced for similar values of PRS) may be explained by the fact that both PRS and PSEM are difference scores, so higher and lower R_s values may place simulated participants in similar-gradient regions of one sigmoid and differing-gradient regions of the other.

The relationships shown in the simulations are delicate: small differences in a₁ tip the balance from positive, to ‘complex’, to negative. However, it seems unrealistic to assume that every participant uses the same re-allocation of their resources between the two tasks. If random sampling of a₁ from a uniform distribution U(0,1) is now added, then, as shown in Panel D, any apparent relationship between PRS and PSEM is no longer seen. Note that in all other simulations shown and discussed in this chapter, the parameter a₁ is kept fixed at .5, and measurement error, u~N(0,0.05) is sufficient to obscure what would otherwise be positive corellations between PSEM and PRS.⁴

Simulation 2: Effects of Perceptual Load

A simple way to model the effect of adding perceptual load is to assume that it increases the difficulty of the face task, meaning more resources are required to maintain performance, i.e. d_1h > d₁, where h stands for high load (again we assume that the low load condition, l, corresponds to the baseline case, i.e, d_1l = d₁). In the high load condition, the participant must either redirect resources from the memory task, or perform the face task less well, or both. Since in the experiment we observed that on average participants did perform both tasks less well, we can assume that some proportion, 0 < x_h < 1, of the additional resources that would have been required to maintain performance in the face task are redirected from the memory task, i.e., for unprimed trials:

$$\begin{array}{l}{r}_{1hs}=a_1{R}_s+x_l\left(d_{1h}-d_1\right)\hfill \\ r_{2hs}=\left(1-a_1\right)R_s-x_h\left(d_{1h}-d_1\right)\hfill \end{array}$$

whereas for primed trials:

$$\begin{array}{l}{r}_{1phs}=a_1{R}_s-x_p\left(d_1-d_{1p}\right)+x_h\left(d_{1h}-d_1\right)\hfill \\ r_{2phs}=\left(1-a_1\right)R_s+x_p\left(d_1-d_{1p}\right)-x_h\left(d_{1h}-d_1\right)\hfill \end{array}$$

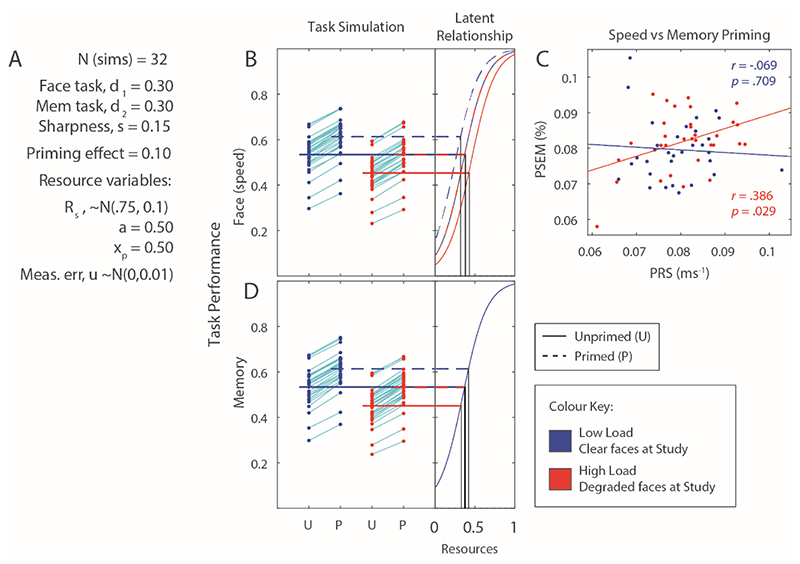
This model can easily produce the qualitative pattern of results in Experiment 2, with main effects on RS and subsequent memory of both priming and load, as shown in Figure 11, and a significant positive correlation in the High Load condition (like the trend in Experiment 2, though as above, this can easily be made nonsignificant by changing parameters).

Figure 11.

Qualitative reproduction of the results of Experiment 2. Panel B shows PRS in the Face Task, and also an effect of perceptual load. Panel D shows effects of both priming and load on subsequent memory performance, with no apparent interaction. Lines plotted between points panels A and D, connect single subject performance in Primed and Unprimed conditions of No Load and Perceptual Load. Heavier lines linking line plots with sigmoid curves show mean performance in each of the 4 conditions, and how that performance maps to the sigmoid functions that underlie performance.

Simulation 3: Effects of Central Load in Experiment 3

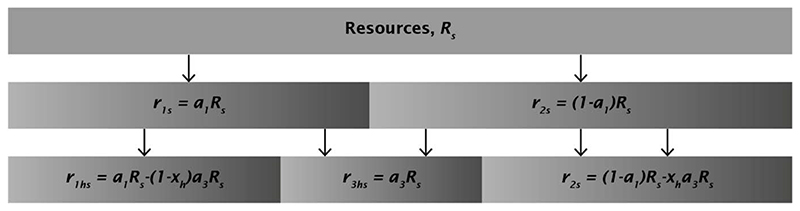
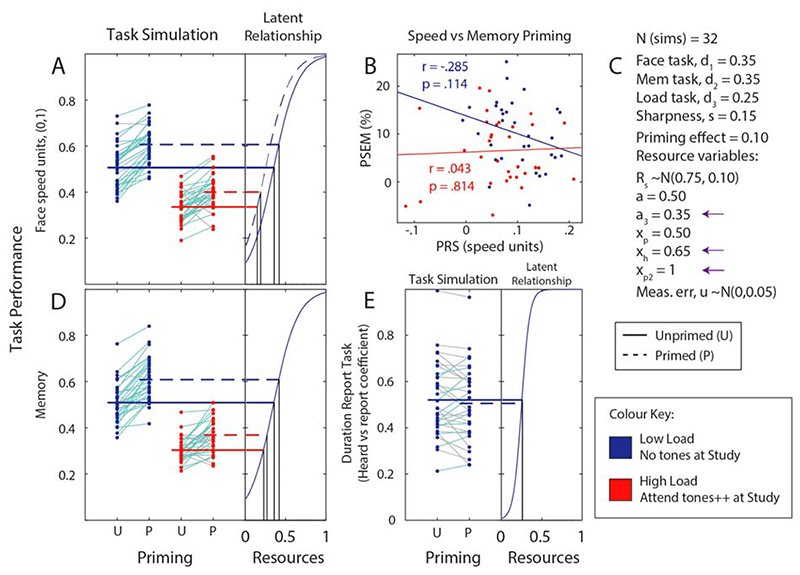
In Experiment 3, a secondary central load task was added to the study phase. It is possible to model both of these experiments by introducing a third task with its own (independent) resource-performance curve, and with some amount, r_3s, of a participant’s overall resources being directed to Task 3 performance, as determined by the task’s allocation parameter, a₃. The most obvious difference between how Experiments 2 and 3 are modelled is that, instead of resources being transferred from Memory Task to Face Task, they are instead transferred away from both tasks in some proportion (see Figure 12 for illustration).

Figure 12.

Initial resource allocation (1^st row), resource allocation in No Load condition (2^nd row), with resources split between Face and Memory tasks, and in High (central) Load condition (3^rd row), where a secondary task is added to Face and Memory tasks.

The parameter x_h can continue to be used, but in this case, it will determine the proportion of the resources required for the central load task to be taken from the Memory Task, x_ha₃R_s, and from the Face Task, (1 − x_h)a₃R_s. Thus in unprimed trials under high load, resources for the three tasks will be:

$$\begin{array}{l}{r}_{1hs}=a_1{R}_S-\left(1-x_h\right)a_3{R}_S\hfill \\ r_{2hs}=\left(1-a_1\right)R_s-x_h{a}_3{R}_S\hfill \\ r_{3hs}=a_3{R}_S\hfill \end{array}$$

In Experiment 3a, there was not a trial-by-trial measure of performance, so it was not possible to address whether performance was improved in primed trials. In Experiment 3b however, a measure was found that was sensitive to changes in central attentional resources (The Duration Task). This can be modelled by adding a further parameter, x_p2, which is the proportion of the resources freed from the Face Task by priming which go toward Memory Task performance, the remainder of which (i.e. 1 − x_p2) will be added to secondary (Duration Task) resources, so in primed trials under high load, resources are distributed thus:

$$\begin{array}{l}{r}_{1phs}=a_1{R}_s-\left(1-x_h\right)a_3{R}_s-x_p\left(d_1-d_{1p}\right)\hfill \\ r_{2phs}=\left(1-a_1\right)R_s-x_h{a}_3{R}_s+x_{p2}{x}_p\left(d_1-d_{1p}\right)\hfill \\ r_{3phs}=a_3{R}_s+\left(1-x_{p2}\right)x_p\left(d_1-d_{1p}\right)\hfill \end{array}$$

In practice, there was no advantage of priming for Duration Task trials, so x_p2 = 1, and all resources freed from the Face Task by priming go towards performance of the Memory Task.

In Experiment 3a, performance of the secondary load task was at ceiling. Furthermore, we observed a main effect of load on memory performance, but no such effect on response speed in the study phase, so we can assume that performance of that task was accomplished using resources redirected away from the Memory Task, not Face Task, and thus set the proportion of load demand to be met by Memory Task resources, x_h, to 1. With x_h set to 1, no load effect is seen on performance of the Face Task: the demands of the secondary task are met wholly by resources redirected from the memory task, and so there is a large main effect of load on subsequent memory (see Supplementary Figure 1). In line with the experimental data, in which performance of the secondary load task was at ceiling in Experiment 3a and in which Memory Task performance was not reduced to the same extent as in Experiment 3b, it is simply assumed that resource allocation to the load task, a₃, is smaller than in Experiment 3b. Performance of the secondary task is not simulated, but it is assumed that r_3hs is always sufficient for maximum performance (the underlying difficulty parameter, d₃, simply being low enough to accommodate this).

In contrast to the results of Experiment 3a, Experiment 3b produced a main effect of load on response speed and also on memory performance. In addition, the design afforded a secondary-task performance measure during each trial, in which it was hypothesised an effect of priming may be seen, although none was found. Experiment 3 was therefore simulated (Figure 13) by adjusting 2 parameters (see small arrows, Panel C) of the Experiment 3a model and adding another parameter. The secondary task load allocation parameter, a₃, was increased from 0.20 to 0.35, reflecting the increased load of the secondary task, and the load distribution parameter, x_h, was reduced from 1 (all resources redirected from Memory Task) to 0.65, reflecting load’s effect on Face Task performance in Experiment 3b. As with previous simulations, and consistent with behavioural results, no obvious relationship was found between PRS and PSM (Panel B). A new parameter, x_p2, was included, which was the proportion of resources freed from the Face Task by priming which would go towards Memory Task performance, and the remainder of which would go towards secondary (Duration) task performance. Since no significant effects of priming on Duration Task performance were seen, this new parameter, x_p2 was set to 1, and the simulation does not produce any priming effect on Duration Task performance (Panel E).

Figure 13.

Qualitative reproduction of the results of Experiment 3b, in which we further increased Central Load by including a more difficult dual task during the study phase in half of the blocks. Panel A shows PRS and effect of load in the Face Task. Panel D shows effects of both priming and load on subsequent memory performance, with the suggestion of an interaction between load and PSEM. Consistent with behavioural results, panel B does not show any clear relationship between PRS and PSEM. Panel E shows simulated performance on the secondary load task, with no effect of priming. Panel C shows the settings used in this simulation, and small arrows highlight the two parameters which were changed from the simulation of Experiment 3, and the addition of parameter x_p2 (see text).

General Discussion

The present experiments and modelling were designed to test an intuitive, resourcebased account of the effect of priming on subsequent episodic memory (PSEM), as demonstrated here when the pairing of a scene which a face was better remembered if the face had been primed. Despite replicating the PSEM effect four times, in no experiment did we find that a manipulation of resources, whether temporal, perceptual or central resources, reduced the size of the PSEM effect. Nor did these load manipulations affect the correlation between the amount of priming and size of the PSEM effect. We then developed a computational model, which demonstrated that our results are not, in fact, inconsistent with a resource-based account. With only minimal assumptions about sigmoidal resource-performance functions for each task, our model was able to simulate any pattern of interaction between load and PSEM, and, more counter-intuitively, any correlation between amount of priming and PSEM.

Experiment 1 tested the simple idea that the faster responses enabled by priming faces increase the time available post-response for the encoding of the scene-face association. However, constraining this time by ensuring that the next trial always started a fixed interval after the response had no effect on PSEM, ruling out this ‘temporal resources’ account (nonetheless, this ‘self-paced’ procedure was used in all subsequent experiments). Experiment 2 tested the idea that the PSEM effect can be explained by a “freeing up” of perceptual resources. Visually degrading faces, while successfully slowing responses to faces during Study and reducing overall memory performance at Test, did not moderate the PSEM effect. Experiments 3a and 3b tested instead the role of central resources by adding a secondary task involving auditory stimuli. Again, though this task (load) reduced overall memory performance, any interaction with PSEM did not reach significance in either experiment, nor did any priming effects emerge in performance of the secondary task instead (Experiment 3b). Experiments 2 and 3 relied on a different logic from Experiment 1, because they addressed types of resources that cannot be directly measured or controlled. In Experiment 1, temporal resources (time-on-task) were in fact matched between primed and unprimed trials in the variable Response-Stimulus Interval conditions, without impacting PSEM: thus, time-on-task could be ruled out as an explanation for the PSEM effect. In Experiments 2 and 3, however, the availability of resources in primed and unprimed conditions could not be controlled in the same way, and although an interaction would have been positive evidence for involvement of the hypothesised resources, the modelling reinforced the point that (unlike in Experiment 1), the absence of such an interaction cannot be used to reject the involvement of the particular resources placed under load in Experiments 2 and 3.

Formal modelling

Rather than simply conclude that we had found no evidence for a resource-based account of the PSEM effect, we formalised various resource accounts in computational models. Starting with the common and reasonable assumption that performance of any task is a sigmoidal function of resources, we simulated priming as reducing the difficulty of the task (shifting the sigmoid to the left, such that similar performance can be achieved with fewer resources). If the resources that are released by this reduced difficulty of the primary (face judgment) task at Study are put towards encoding the scene-face pairing instead, then this explains the basic PSEM effect. The memory encoding processes facilitated by these “freed” resources could act simultaneously with the processes required for the primary face judgment task, such that there is no added effect of curtailing the time after a response to the face has been made, thereby explaining the lack of any moderation of the PSEM effect in Experiment 1.

The increased perceptual load in Experiment 2 was simulated by making the primary face task more difficult, i.e, shifting the sigmoid for the primary task to the right instead. This affects the amount of resources that are left for the other task of memory encoding, for which performance is also a (separate) sigmoidal function of those resources. It then becomes apparent that the presence and nature of an interaction between priming and perceptual resources (load) on subsequent memory depends on where each of the four conditions (primed/unprimed under low/high load) lies on the sigmoid for memory encoding. Given that the resource requirement of each condition is not known a priori, the nonlinear aspect of the sigmoid effectively allows any pattern of single dissociation between priming and load, including no interaction when close to the central (more linear) part of the sigmoid (see Figure 8). Moreover, because the conditions can lie on different points on the primary task sigmoid relative to the memory task sigmoid, one can obtain an interaction on priming (RS) measures of the Study task, but no (or the opposite) interaction on memory in the Test phase, or vice versa. Therefore the lack of interactions in Experiment 2 cannot be used to refute a perceptual resources account.

If the amount of resources freed by priming differs across participants (e.g, owing to different effects of priming on the task difficulty, or even differences in the total resources available to each participant), one might expect a positive correlation between the effect of priming on primary task speed (i.e, PRS) and its effect on subsequent memory (i.e, PSEM), since participants for whom priming frees more resources, or who have greater resources in total, should show greater effects of priming on memory. However, our simulations showed this intuition to be incorrect. The correlation between PRS and PSEM can vary from positive through zero to negative, again depending on where the four conditions lie on the sigmoidal performance functions for each task (see Figure 10).⁵ This can explain why we sometimes found a significant positive correlation (when averaging over condition) between PRS and PSEM, but mostly failed to find significant correlations. This flexibility, counter to initial intuitions, reinforces the value of formal modelling.

A different way to model attentional load was adopted for Experiments 3a and 3b, where a third task was added to the model (namely, the auditory task performed during Study, in order to reduce central resources available for the primary face task). Depending on parametrisation of how the total resources are divided among the three tasks, the model could again simultaneously fit performance on all three tasks (face RS, face-scene memory and tone duration judgments) in both experiments, including the critical lack of interaction between (central) load and PSEM. Moreover, it could reproduce the lack of load effects on various correlations between performance on the different tasks. Again, this prevents us from ruling out resource accounts of the PSEM effect.

More generally, the flexibility of this relatively simple modelling reinforces the difficulty of interpreting the results of experiments that manipulate attentional load (resources). Indeed, we constrained the models as much as we could (e.g, identical parameters for the resource-performance curves for each task; allocations of resources to tasks that were fixed across participants, but in reality could vary across people, etc). Future studies could explore the consequences of relaxing some of these constraints. As well as being educational, the models raise further conceptual questions, in particular how to model load manipulations. Perceptual load was modelled by changing task difficulty (i.e, parameters of the sigmoid), whereas central load was modelled by changing the allocation of resources. This seemed justifiable because degrading the faces (in high perceptual load condition) affected the same performance measure as priming, i.e, speed in the primary (face judgment) task, rather than create a new task with a new performance measure. The central load manipulations in Experiments 3a and 3b, on the other hand, introduced a new measure of performance on the distractor task, so required an additional resource allocation. Nonetheless, the effects of these two model parameters – task difficulty vs resource allocation – is largely equivalent, particularly on the primary outcome of interest (PSEM), so these conceptual differences in modelling would seem difficult to test by behavioural data alone.⁶ It is possible that these two choices for modelling load correspond to different brain mechanisms, as supported by neuroimaging studies reporting separable systems subserving perceptual- and central-attentional tasks (e.g. Burgess et al., 2007).

Relation to previous studies

Regardless of the precise explanation of the PSEM effect, the present findings should be related to previous empirical studies. Our experiments replicate the PSEM effect originally reported by Gagnepain et al. (2008; 2011) using auditory stimuli, and by Greve et al. (2017; Experiment 3) using visual stimuli (the latter paradigm identical to that used here; for fuller description of these studies, see Introduction). The PSEM effect would therefore seem robust.

Although effects of priming on subsequent item recognition memory have been reported (both apparent adverse effects, e.g., Rosner, López-Benítez, D’Angelo, Thomson, & Milliken, 2018; Wagner, Maril, & Schacter, 2000, and positive effects, e.g., Turk-Browne, Yi, & Chun, 2006), these are not directly relevant to the present source/episodic memory effects we report here. However, there is one prior study by Kim, Yi, Raye, & Johnson (2012), which reported what would seem to be the opposite pattern to the present one, whereby priming impaired episodic memory (i.e, a negative PSEM effect). This study reported 6 experiments with a similar design to here: There was an initial pre-exposure/training (Phase 1), in which participants made animacy judgements to standardised line drawings of common objects (Snodgrass and Vanderwart, 1980). Each drawing was presented one, four, or sixteen times in this phase (what they called “exposure frequency”). Then in Phase 2 (the critical study phase), these items were shown once, in one of 4 quadrants of the screen, while participants performed the same animacy task. In Phase 3, the final test phase, participants were required to indicate whether items had been seen previously in the experiment (‘Old’), or not (‘New’), and if ‘Old’, required to indicate in which quadrant the item was thought to have appeared (a source memory test of episodic memory). In all their experiments, they found a convincing detrimental effect of exposure frequency on recall for the study phase context, i.e, greater “priming” was associated with worse, rather than better, episodic memory (though Kim et al. do not report a measure of priming, such as RS, for the animacy judgement, nor correlate with the effect on subsequent memory).

The authors explained their results in terms of a ‘recursive reminding’ hypothesis: encountering a stimulus brings to mind previous encounters with that stimulus (including potentially the experience of being reminded of that stimulus), and this directs attention away from perceptual aspects of the encounter (such as the stimulus location on the screen), towards an internally-generated representation instead. This is a converse of the perceptual resource account we attempted to test here, arguing that availability of perceptual resources is diminished because these resources are involuntarily directed to another process (memory retrieval).

Regardless of the explanation of their findings, this empirical result is prima facie at odds with the present findings and those of Gagnepain et al. (2008; 2011) and Greve et al. (2017). There are a number of procedural differences that might explain this. One possibility is that the present findings (and those of Greve et al, 2017, Experiment 3) could be confounded by intentional encoding strategies, since even though participants were not instructed to memorise the scene-face pairing in the Study phase, the benefit of doing so would soon be apparent after one study-test cycle (given that multiple study-test cycles were run within each participant). However, this intentional vs incident explanation would not account for the positive PSEM effect reported in the two Gagnepain et al. studies, which also used incidental study, like Kim et al. (i.e, the memory test came as a surprise), and, in one experiment, Kim et al. continued to find their negative effect of prior exposure frequency despite explicitly instructing participants to attempt memorisation during critical study. Another difference is that each context (source) used here was a unique scene, whereas the four locations used by Kim et al. repeated over trials both during pre-exposure and at study, raising the possibility that interference could account for the negative frequency effect they report. This also seems unlikely however because Gagnepain et al. used only recurring sources (two concurrent sounds), like Kim et al. (Kim et al. also aimed to mitigate interference effects in another experiment.)

Another potentially important difference in results is that Kim et al. only included new items at study (i.e, not presented during pre-exposure/training phase, equivalent to the present “Unprimed” condition) in one experiment, and source memory for these items did not differ significantly from once-exposed items. In other words, Kim et al. only found worse source memory for items that had all been pre-exposed, but some less often pre-exposed than others, whereas the present paradigm and those of Gagnepain et al found better memory for items pre-exposed 1-3 times relative to items never pre-exposed. With more statistical power (comparable perhaps to that in the present experiments), the numerical advantage of once preexposed relative to non-exposed items that Kim et al reported in their one experiment might have become significant, in which case it would match the present findings, and suggest something important about experimental novelty during the Study phase.

However, we think the most likely explanation of the apparent discrepancy across studies relates to the complexity of the visual stimuli and their contexts (sources), with the line-drawings and quadrants of Kim et al. potentially requiring fewer (perceptual) resources than the more complex faces and scenes used here, or possibly the more complex sounds and words used by Gagnepain (if one can compare complexity across modalities). For example, the scenes in the present paradigm (and sounds in the Gagnepain et al paradigm), could have competed with processing of the target faces (or words in the Gagnepain et al paradigm), whereas the spatial location of the line-drawings in Kim et al’s study is unlikely to affect their processing. In other words, there may have been minimal demands on resources in Kim et al’s paradigm, leaving an opportunity for other factors to play a role, such as like recursive reminding. Whereas in the present paradigm, and that of Gagnepain et al, the greater overall demands meant that resources play a more important role, overcoming any encoding disadvantage for primed items in terms of recursive reminding, and producing instead an encoding advantage for primed items.

Prediction Error and PIMMS

Our claim that we cannot refute resource-based accounts does not of course rule out the account based on prediction error (PE) in Greve et al. (2017), whereby priming increases the divergence between minimal prior expectations (of a face given a scene/context) and sensory evidence (for a face), owing to priming sharpening the sensory evidence, and this increased PE leads to a stronger scene-face association. Indeed, a generalised theory based on PE (e.g, in the PIMMS framework of Henson & Gagnepain, 2010) might also explain the Kim et al. results. If one assumes that predictions derive not only from concurrent stimuli, but also from the general experimental context (including history of recent experiences), then the different exposure frequencies during the pre-exposure (training) phase of Kim et al’s study could establish predictions of the probability of certain items re-occurring in the critical study phase, such that the presentation of a low-frequency item during Phase 2 is less expected (more surprising) than the presentation of a high-frequency item. If so, PE would be higher for low-frequency items, potentially resulting in them becoming better associated with their (spatial) context in the critical study phase, and producing a negative PSEM. In the present and Gagnepain et al. paradigms, on the other hand, there is less likely to be greater general expectancy for the primed than unprimed stimuli in the Study phase, particularly given that the training-study-test cycle is repeated multiple times, so that participants are likely to realise the the probability of a primed versus unprimed item appearing in the study phase is approximately equal (since there were half of each type). If this difference in prior expectation were the only factor at work, then no PSEM would be expected. To explain the positive PSEM effect that was found, one could appeal to the sharpening of sensory evidence by priming proposed by Greve et al. (2017), which does predict a higher PE (greater divergence between prior and evidence) for primed stimuli. Because the stimuli were more complex in the present and Gagnepain paradigms, compared to the Kim et al paradigm, this second factor would also have less effect in the Kim et al. study, explaining how the PSEM effect can be positive or negative as a function of the trade-off between priming(exposure)-related changes in prior expectation and priming-related changes in sensory evidence. This could be easily tested by simultaneously manipulating the prior probability of stimulus occurrence and the complexity of the stimulus, and testing for opposite effects on subsequent episodic memory.

Conclusions and future directions

Whereas the experimental work presented here provides no support for a resources account of the PSEM effect, the modelling work shows that the lack of any effect of manipulating current resources (via load) on the PSEM effect does not rule out a resources account. In more general terms, the modelling highlights the difficulty of inferring relationships between performance on different tasks when an experimenter does not have control of, a model of, or a way to measure, resource allocation. In light of the different PSEM effects reviewed above, an interesting future direction would be to manipulate a factor like stimulus probability, which might produce a pattern of episodic memory performance that cannot be so easily explained by a resources account.