Abstract
Field spectroscopy is an accurate, rapid and nondestructive technique for monitoring of agricultural plant characteristics. Among these, identification of grapevine varieties is one of the most important factors in viticulture and wine industry. This study evaluated the discriminatory ability of field hyperspectral data and statistical techniques in case of five common grapevine varieties in the western of Iran. A total of 3000 spectral samples were acquired at leaf and canopy levels. Then, in order to identify the best approach, two types of hyperspectral data (wavelengths from 350 to 2500 nm and 32 spectral indices), two data reduction methods (PLSR and ANOVA-PCA) and two classification algorithms (LDA and SVM) were applied in a total of 16 scenarios. Results showed that the grapevine varieties were discriminated with overall accuracy of 89.88%–100% in test sets. Among the data reduction methods, the combination of ANOVA and PCA yielded higher performance as opposed to PLSR. Accordingly, optimal wavelengths in discrimination of studied grapevine varieties were located in vicinity of 695, 752, 1148, 1606 nm and 582, 687, 1154, 1927 nm at leaf and canopy levels, respectively. Optimal spectral indices were R680, WI, SGB and RATIO975_2, DattA, Greenness at leaf and canopy levels, respectively. Also, the importance of spectral regions in discriminating studied grapevine varieties was ranked as near-infrared > mid-infrared and red edge region > visible. As a general conclusion, the canopyspectral indices-ANOVA-PCA-SVM scenario discriminated the studied species most accurately.
Keywords: Grapevine varieties, Field spectroradiometry, Optimal wavelength, Spectral indices, Varieties discrimination, Support vector machine, Linear discriminant analysis
1. Introduction
Thousands of grapevine varieties (Vitis Vinefera L.) are known worldwide (Galet, 1979; Cervera et al., 1998), and each variety serves multiple applications such as fresh consumption or converting to secondary products: grape seed oil, jelly, jam, juice, raisins, vinegar and wine (Mirzaie et al., 2018). Identifying grapevine varieties is an important step in viticulture and wine industry due to the high economic and social impact of these businesses (Gutiérrez et al., 2016). Also, correct identification can help to determine the cultivated area of each variety (Galvão et al., 2009) and support the supply and demand estimates.
When it comes to identifying plant varieties, a diversity of destructive methods exists, such as those relying on morphological-physiological features (Galet, 1979), isoenzymes chemistry and DNA analysis (Cervera et al., 1998). However, due to the physical and biological similarity of plant varieties, ground-based distinguishing surveys of varieties is time consuming (Lacar et al., 2001). These methods also imply some disadvantages, including: (1) morphological-physiological methods require an expert with extensive training, or isoenzymes chemistry, and (2) DNA analysis approaches are time consuming and tedious (Gutiérrez et al., 2016; Diago et al., 2013). Alternatively, in-field, airborne and satellite spectral data are recommended to discriminate plant varieties as eco-friendly (solvent-free), nondestructive, rapid, and high-precision methods (Galvão et al., 2009; Zhang et al., 2012; Diago et al., 2013; Fassnacht et al., 2015; Gutiérrez et al., 2016). By applying in-field hyperspectral analysis and expanding obtained relationships to airborne and satellite remote sensing data, it becomes possible to measure plant characteristics for discriminating different plant varieties in a fast way over vast areas (Gutiérrez et al., 2016; Diago et al., 2013). In field spectrometry, reflectance of electromagnetic waves from various plant species are recorded as contiguous spectral wavelengths, so that the collected spectral curve of any plant species is like a special fingerprint (He et al., 2007). Consequently, it can be expected that each plant variety leads to a distinct reflectance spectrum due to heterogeneity in intracellular and extracellular physicochemical components (Xu et al., 2009; Zhang et al., 2012; da Silva Junior et al., 2018).
By using in-field spectroscopy a large amount of data can be obtained in the form of spectral curves, which in turn can be analyzed with statistical techniques to reveal desirable plant properties (Adam and Mutanga, 2009; Aneece and Epstein, 2017). For instance, linear and nonlinear multivariate statistical methods such as ANOVA test (Adam and Mutanga, 2009), principal component analysis-PCA (Li and He, 2008), linear discriminant analysis-LDA (Belton et al., 1998), artificial neural network-ANN (Li and He, 2008) and support vector machine-SVM (Prospere et al., 2014) have been applied to address questions related to plant species discrimination from hyperspectral data. Some studies took specific advantage of applying multivariate statistical analyses to field spectroradiometry data to enable discriminating plant species/varieties. For instance, Manevski et al. (2011) used parametric statistical tests in discrimination of common Mediterranean species, Aneece and Epstein (2017) applied SVM in identifying invasive plant species, and Xu et al. (2009); Diago et al. (2013); Lehmann et al. (2015) and Abbasi et al. (2012) employed partial least squares regression (PLSR) to discriminate plant species/varieties. According to Diago et al. (2013), PLSR is among the most common statistical method in the processing of high dimension spectroscopic data for introducing optimal wavelengths in discrimination of plant species and varieties.
However, more often than not additional processing steps are required to reach an adequate discrimination accuracy. The spectral reflectance curve can be influenced by environmental disturbances, such as light propagation of adjacent phenomena, water vapor, leaf moisture, air temperature, biochemical parameters, and other variables (Abbasi et al., 2012). In part to overcome these confounding factors, the usage of spectral indices enables to eliminate atmospheric and background disturbance (Darvishsefat et al., 2011). Spectral indices are mathematical transformations of reflectance to improve vegetation signals (Prospere et al., 2014). As such, they can reveal biochemical and physiological properties of intact leaves or canopies, which may provide facilities for discriminating the characteristics of plant species or varieties (Cho et al., 2008; Prospere et al., 2014).
Grapes and related products play an important role in the human food basket, and Iran is among the top ten grape producers in the world (FAO, 2016). So far in-field spectroscopy studies have not yet been conducted on grapevines varieties cultivated in the country. Nevertheless, conducting spectroscopy studies can play a valuable role in managing vineyards, and collecting a spectral library for each grapevine variety can provide a basis for variety discrimination. Also, the identification of optimal wavelengths in discrimination of common grapevine varieties can create a great leap in vineyard airborne and satellite monitoring, which is an effective step forward in precision agriculture (Zhang et al., 2003; Ferreiro-Arman et al., 2006; Mazzetto et al., 2010; Liu et al., 2011; Gutiérrez et al., 2015, 2016). Therefore, this study attempted to develop hyperspectral libraries from the most common grapevine varieties in Chaharmahal-va-Bakhtiari province in the western of Iran. To do so, full range in situ spectroscopy (350–2500 nm) was conducted at leaf and canopy levels for each variety, with the aim of examining which level has more potential for differentiation of the varieties. In addition, the ability of two types of hyperspectral data (wavelengths and spectral indices) was also compared in an attempt to discriminate studied varieties. Since statistical methods play a significant role in hyperspectral data reduction (Prospere et al., 2014), the performance of PLSR as the most common method in reduction of spectroradiometry data, and a two-step approach (ANOVA-PCA) was also evaluated in discrimination of native Iranian grapevine varieties. Finally, the LDA and SVM algorithms were applied to classify grapevine varieties and to identify optimal discrimination scenario(s).
2. Materials and methods
2.1. Study area
Iran is among the top ten countries in grapevine (Vitis vinifera) production, and Chaharmahal-va-Bakhtiari province is one of the main centers of grapefruits and its secondary products such as grape seed oil, jelly, jam, juice, raisins and vinegar. The province is located in western of Iran (39° 10′ 00″ to 32° 50′ 00″N latitude and 49° 30′ 00″ to 52° 25′ 00″E longitude) and has a wet cold climate with warm and dry summers (Fig. 1). The cultivated area of grapevine consists of 4,800 ha, which Yaqooti, Perllet, Rishbaba, Black Seedless, and Askari are the common (make up 98%) varieties in this province.
Fig. 1. Location of the study site (Chaharmahal-va-Bakhtiari) in Iran.
2.2. Field spectral acquisition
2.2.1. Samples collection
In order to analysis the ability of in-field hyperspectral data to discriminate native Iranian grapevine varieties, samples were collected from leaf and canopy levels in June, July and August 2017. Five common grapevine varieties, including V. vinifera cv. Askari (AS), V. vinifera cv. Hologhi (HG), V. vinifera cv. Mehre (MH), V. vinifera cv. Siyah (SI) and V. vinifera cv. Yaghooti (YG) were selected, all originating from the Chaharmahal-va-Bakhtiari province of Iran.
To form a comprehensive spectral library of a plant variety or species, multiple samples of various status and distribution should be collected (Clevers et al., 2010). Therefore, we attempted to take samples from a wide range of situations to support community variance. So, for each variety 20 vineyards from different situations and local positions were selected as sampling sites. Then, leaf and canopy samples were collected from the studied vineyards during a vegetative season (Van Til et al., 2004). The samples were collected with five replications and their average was calculated to enter the next analysis. At the leaf level, 100 healthy leaves in sunlight position were collected from 20 individual vine trunks per variety in three times series (beginning, middle and late of vegetative season). It led to a total collection of 1500 leaf samples. Because of differences in the amount and properties of photosynthesis, leaves have unique spectral behavior at different ages and different positions in the canopy (shadow-Light or top-middle-down) (Prospere et al., 2014), therefore all samples were collected from mature leaves located at top of canopy. At the canopy level, samples in sunlight position of healthy vine were collected for all of the studied varieties. The canopy samples were collected with five replications from 20 vineyards and their average for studied varieties was calculated to perform the next analysis. So, a total of 500 canopy samples were prepared for spectroscopy measurements (3 (time series) × 5 (variety) × 5 (replication) × 20 (vineyard) = 1500 (sample)).
2.2.2. Spectra acquisition
Reflectance spectra of grapevine varieties at leaf and canopy levels were collected with the ASD FieldSpec®3 spectroradiometer. The ASD has three separate spectrometers, which ranged from 350 to 975, 976–1770 and 1771–2500 nm, with spectral resolution of 3 and 10 nm and a sampling interval of 1.4 nm and 2 nm, for the spectral regions of 350–1000 nm and 1000–2500 nm, respectively (ASD, Analytical Spectral Devices, Inc., 2005). The wavelength configuration of the spectroradiometer are organized as the Near-ultraviolet (NUV: 350~400 nm) the visible (VIS: 400~700 nm), Red Edge Region (RDE: 680~750 nm), Near-Infrared (NIR: 700~1300 nm) and Mid-Infrared (MIR: 1300–2500 nm) wavelengths (Kumar et al., 2001). To eliminate the effect of water vapor, temperature, wind and other environmental interferences errors, the spectroscopy operation was carried out in a completely dark room laboratory with a special bulb light (Abbasi et al., 2012). It should be noted that the spectral curve of each sample was taken in 100 replicates. The obtained cures were initially reviewed and in cases where the obtained curves were inconsistent with the typical plant curve they were discarded. The raw data recordings were converted to reflectance (between 0–1) by ViewSpect version 6.0, and the reflectance curves were exported as text file in order to transfer them into the statistical software.
2.3. Extraction of hyperspectral indices
This study aims to exploit the capabilities of hyperspectral indices for the separation of grapevine varieties. To do so, a total of 32 spectral indices were selected and described in Table 1. These indices had been used in previous studies, and have proven to be sensitive to tiny differences in plant characteristics (Prospere et al., 2014; Devadas et al., 2009; Cho et al., 2008).
Table 1.
Characteristics of hyperspectral indices which had been used by Prospere et al. (2014) and Cho et al. (2008) in discrimination of plant species.
| Index Name | Formula | Comments / Biophysical significance |
|---|---|---|
| Normalized Difference Vegetation Index, NDVI | )R831 — R667) /(R831 + R667( | among the most widely used plant indices which is sensitive to chlorophyll content |
| Carter index (CI) | (R760 / R695) | sensitive to chlorophyll content |
| Vogelman index (VOG) | (R740 / R720) | sensitive to chlorophyll content |
| Carotenoid reflectance index (CRI) | R800 (1/ R520 - 1/ R550) | sensitive to plant stress and the content of carotenoids |
| Photochemical Reflectance Index, PRI | PRI1 = (R531 — R570) /(R531 + R570) PRI2 =1.5 (R830- R660) / (R830 — R660 + 0.5) PRI3 = (R539 — R570) /(R539 + R570) | sensitive to vegetation type, water stress condition, efficiency of radiation and photosynthetic capacity |
| Gitelson and Merzlyak chlorophyll, GM 1 and 2, | GM1 = (R750) /(R550) GM2 = (R750) /(R700) |
estimating of chlorophyll content in plant leaves / chlorophyll index |
| Lichtenthaler Indices 1 to 3 | Lic1 = (R800 — R680) /(R800 + R 680) Lic2 = (R440)/(R690) Lic3 = (R440)/(R740) |
used to detect stress in green leaves |
| Simple Ratio Pigment Index, SRPI | (R430) /(R680) | sensitive to carotenoids and chlorophyll a content |
| Normalized Phaepophytiniz Index, NPQI | (R415 — R435) /(R415+ R435) | |
| Normalized Pigment Chlorophyll Ratio Index, NPCI | (R680 — R430)/(R680 + R430) | sensitive to pigments and chlorophyll content |
| Greenness Index, G | (R554) /(R677) | long-term plant stress index due to changes in the structure of the canopy, but not due to biochemical components |
| Structure Intensive Pigment Index, SIPI | (R445— R800) /(R680 — R800) | estimation of the carotenoids: chlorophyll a ratio |
| Simple Ratio, SR | (R774) /(R677) | long-term plant stress index due to changes in the canopy structure |
| Reflectance at 550 nm, R550 | (R550) | sensitive to chlorophyll content |
| Reflectance at 680 nm, R680 | (R680) | sensitive to chlorophyll content |
| Water Index, WI | (R900) /(R970) | related to water status |
| Cellulose Absorption Index, CAI | 0.5 (R2000+ R2200) — R2100 | indicates the cellulosic absorption values |
| Moisture Stress Index, MSI | (R1600) /(R820) | related to water status |
| Normalized Difference Water Index, NDWI | (R860 — R1240) /(R860 + R1240) | related to water status |
| Disease Water Stress Index, DWSI | (R802 +R547) /(R1657 + R 682) | related to plant disease and water status |
| Band ratio at 975 nm, RATIO975 | 2×R960— 990/(R920-940 + R1090—1110) | related to water status |
| Band ratio at 1200 nm, RATIO975-2 | 2×R1180— 1220 /(R1090 —1110+ R1265-1285) | related to water status |
| Leaf Chlorophyll Index, LCI | (R850—R710) /(R850 + R680) | an indicator of chlorophyll content that is not affected by the scatter variation and represents the pigments absorption |
| DattA | (R780—R710) /(R780-R680) | sensitive to chlorophyll content |
| Chlorophyll Index, SGA | (R750 + R705) /(R750 + R705 — 2×R445) | sensitive to chlorophyll content |
| Chlorophyll Index, SGB | (R750 — ρ445) /(R705— R445) | sensitive to chlorophyll content |
| Water Index at 1180nm, WI1180 | (R900) /(R1180) | related to water status |
R: Reflectance.
2.4. Feature selection / data reduction
In situ spectrometry produces a large amount of contiguous data in the form of spectral curves, which were converted to non-derivative reflectance. A reflectance spectrum comprised 2151 wavelengths from 350 to 2500 nm. From these wavelengths, the 32 spectral indices were extracted to analyze their ability in discriminating grapevine varieties at leaf and canopy levels. To achieve this, a feature selection process for spectral indices and wavelengths should be performed in order to identify the most suitable wavelengths and indices in discriminating of grapevine varieties. Multivariate statistical analysis is an appropriate method for removing redundant data. Two statistical methods were applied to introduce the optimal wavelengths and spectral indices for separating of grapevine varieties at leaf and canopy levels. The first method was PLSR, which is widely used in discrimination studies of varieties and species. The second method was a two-step method including ANOVA and PCA. Based on these methods, the optimal wavelengths and indices were derived. In order to evaluate the accuracy of derived results from these methods, optimal wavelengths and spectral indices were considered as inputs variables for re-testing and selecting the higher-performance approach. Therefore, the performances of PLSR and ANOVA-PCA were subsequently evaluated by SVM (as a non-Linear classifier) and Linear Discrimination Analysis (as a linear classifier) based on overall accuracy (OA).
In this regard, the grapevine variety classes were considered as dependent variables and the wavelengths and spectral indices were assumed as independent variables. All data of wavelengths and spectral indices were divided into two categories, 70% as training and 30% as testing data, randomly.
2.4.1. Partial least squares regression (PLSR)
PLSR was employed as a classification method to reduce the dimension of hyperspectral data and select the optimal feature for classifying the studied grapevine varieties. This method is based on linear least squares regression that performs some new components, instead of on the original inputs data. The main advantage of PLSR as opposed to PCA, is that the response variables are also considered in PLSR in parallel with the dimensionality reduction and the overlapping elimination are done (Xu et al., 2009). Other capabilities of PLSR are the ability to analyze highly collinear and high-volume spectroscopy data, providing a regression model between independent and dependent variables and also the acceptable processing speed (Peerbhay et al., 2013). After running PLSR, some components are formed, which each of them explained a part of community variance. The degree of correlation between independent variables and components is represented by factor load. Therefore, the basis for selecting of optimal wavelengths or spectral indices to discriminating of grapevine varieties had been the factor load of wavelengths and indices in each component. So that any wavelength or index that had more factor load in the component was chosen as the representative of that component. It is worth noting that wavelength and spectral indices were considered as independent variables and the grapevine varieties were assumed as dependent/target variables. More information about the theory and the structure of PLSR is given by Wold et al. (2001).
2.4.2. ANOVA-PCA method
The second method for reducing input data and identifying optimal wavelengths or spectral indices was a two-step method including ANOVA-PCA. One-Way ANOVA was used to test which of the wavelengths or spectral indices had been able to separate five grapevine varieties into five distinct subsets. In this regard, ANOVA was performed at a significant level of 95% (i.e. p < 0.05) with a post-hoc of Scheffé test (Adam and Mutanga, 2009). So at the end of this step, all the wavelengths or spectral indices that were able to separate the grapevine varieties were introduced. But there was a high probability that the number of introduced wavelengths or spectral indices would be high and there would be a severe overlap between them. So, in the next step, the ANOVA-selected wavelengths or spectral indices were entered to PCA. PCA is able to reduce the dimensions of the data into the components that these components can well explain the variance of society. The Varimax rotation method was used in order to better separation inputs (ANOVA selected wavelengths or spectral indices) in the principal component (PC) (Jolliffe, 1986; Mirzayi et al., 2014). The basis for selecting optimal wavelengths or spectral indices to discriminate five grapevine varieties had been the factor load in each PC. So that any wavelength or index that had more factor load in the PC was chosen as the representative of that component (Prospere et al., 2014).
2.5. Support vector machine (SVM)
Considering that each of the feature selection methods identified different multiple wavelengths or spectral indices for separating of studied grapevine varieties, it was therefore necessary to evaluate the performance of the applied feature selection methods (PLSR and ANOVA-PCA) in the same circumstances. Two algorithms were used to evaluate the PLSR and ANOVA-PCA performances, being SVM and LDA. SVM is a nonparametric statistical learning algorithm for regression and classification purposes, which are used in classification of hyperspectral and situ spectroradiometry data with acceptable performance (Prospere et al., 2014; Laurin et al., 2016; Ferreira et al., 2016). Transferring the n-dimensional input vector into a high-dimensional feature space and developing the optimal separating hyper-plane are the main presses in the SVM algorithm (Stitson et al., 1996). Here SVM was applied in different scenarios and architectures to achieve the best performance of the model in the classification of grapevine varieties at leaf and canopy levels. The selected wavelengths or spectral indices by PLSR and ANOVA-PCA were considered as independent variables and the grapevine varieties assumed as categorical dependent variables. In SVM, a kernel function relates input vectors with linear and nonlinear functions to output vectors. So when using SVM, one of the most important issues is to select the type of kernel function and its related parameters (Mirzaei et al., 2018). Therefore, regression SVM-type 1 was used with linear, polynomials, radial basis function (RBF) and sigmoid kernel functions. The training constants were optimized by V-fold cross validation (V value: 10 and seed: 1000) and the kernel parameters were changed (0 ≤ coefficient ≤ 3, 0 ≤ gamma ≤ 1, 1 ≤ degree ≤ 3) to gain the maximum classification performance. More details about the theory of SVM algorithm is given by Stitson et al. (1996).
2.6. Linear discriminant analysis (LDA)
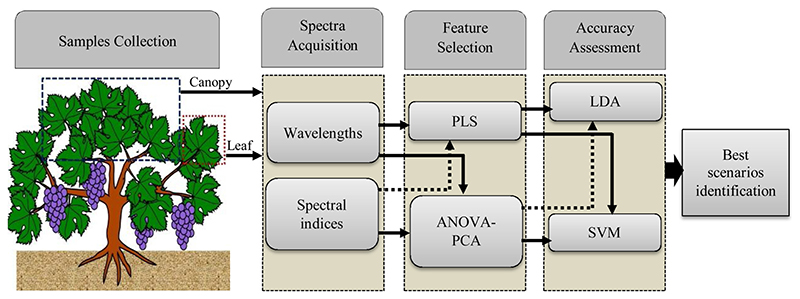
LDA is a parametric statistical method applied to classify inputs data into two or more groups. The usage of LDA in species or varieties separation studies is very common because the response variable in this method is categorical (Belton et al., 1998 and Prospere et al., 2014). LDA can also be used as a discriminant analysis to investigate how variables contribute to group separation and to place objects or individuals into defined groups. In the training set, LDA was carried out at leaf and canopy levels with 70% of the data and the structure of the model was saved for testing set, then in the testing set, performance evaluation was performed with remaining data. An outline of the steps applied in this study is shown in Fig. 2.
Fig. 2. Flowchart of processes described for identifying best scenarios in the grape varieties discrimination.
3. Results and discussion
3.1. Reflectance spectra of grapevine varieties
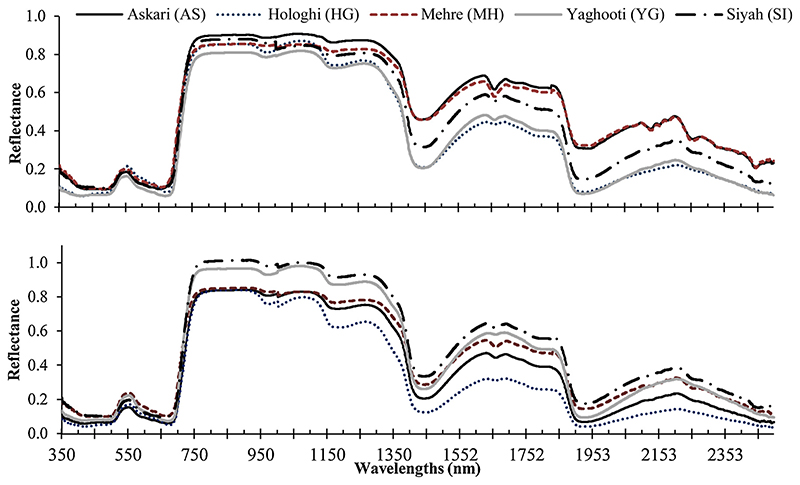
The acquisition of spectral reflectance measurements at full range wavelength (350–2500 nm) and calculated 30 spectral indices was assessed in order to discriminate five grapevine varieties (AS, HG, MH, SI and YG) in the western of Iran. Fig. 3 shows the mean reflectance spectrum of the grapevine varieties at leaf and canopy levels. The spectral curves obtained from five grapevine varieties were similar to that recorded by Strever (2012); Diago et al. (2013); Cao et al. (2010); Páscoa et al. (2016) and da Silva Junior et al. (2018), which indicate their compliance with the typical spectral pattern of healthy green plants. Also, all the obtained spectra were error-free (Fig. 3) represents the high accuracy of the spectroradiometer device (ASD Field spect) and the stable conditions of the laboratory environment (Wang et al., 2018; Abbasi et al., 2012).
Fig. 3. Average of reflectance spectrum of the five studied grapevine varieties at leaf (top) and canopy (down) levels from 350 to 2500 nm.
The difference between grapevine varieties was hardly detectable in the VIS region, but sharp reflectance peaks were observed in the NIR region. Also, the greatest differences for both leaf and canopy levels were observed in the MIR region (Fig. 3). Due to the presence of foliar pigments (mainly chlorophylls and carotenoids) a strong absorption was detected in the VIS region, whereas, in the NIR and MIR regions, the adsorption rate was significantly reduced, because pigments do not absorb in these regions, and the spectral behavior were affected by structural/morphology and water content in the plant organs, respectively (Penuelas et al., 1993; Xu et al., 2009; Strever, 2012). At the leaf level, AS vs. MH vs. SI and HG vs. YG varieties showed similar reflectance trends in the NUV and VIS regions (Fig. 3). In the NIR and MIR regions, the spectral reflectance similarity was also observed for AS vs. MH and HG vs. YG varieties (Fig. 3). AS vs. MH vs. SI and HG vs. YG varieties exhibited similar trends, but at the canopy level the similarities between the spectral behaviors of the varieties were less obvious in the NUV and VIS regions.
It does not come as a surprise to find that the studied grapevine varieties expressed a distinct spectral behavior, since similarly Li and He (2008); Xu et al. (2009); da Silva Junior et al. (2018) also obtained a different spectral behavior in the tea, tomato and soybean varieties, respectively. Although the plants’ morphological and biochemical parameters are not measured in this study, but as mentioned in many related studies (Adam and Mutanga, 2009; Mutanga and Skidmore, 2007; Prospere et al., 2014; Aneece and Epstein, 2017; Damm et al., 2018), it can be concluded that the differences in the spectral behavior of studied grapevine varieties result from chlorophyll, carotenoid, nitrogen, water contents and intracellular and extracellular structure of leaf and canopy samples.
In all studied spectral regions, visual interpretation of spectral curves suggests that the spectral similarities between grapevine varieties at the canopy level are less prominent than the leaf level: at the canopy level the varieties are more aptly spectrally distinguishable (Fig. 3).
3.2. Feature selection
Varieties discrimination based on hyperspectral data can be achieved with various statistical methods. These methods can be either applied individually, or several methods can be combined to identify most appropriate features among hyperspectral data (Prospere et al., 2014; Große-Stoltenberg et al., 2016; Adam and Mutanga, 2009; Shang and Chisholm, 2014). Here, two data reduction methods i.e., PLSR and ANOVA-PCA were applied to select the optimal wavelengths and spectral indices in discrimination of grapevine varieties at leaf and canopy levels. The PLSR is considered as a common method in this field; it had been used in many similar studies aiming for data reduction or feature selection of hyperspectral data (Xu et al., 2009; Diago et al., 2013; Lehmann et al., 2015; Abbasi et al., 2012). The second was a two-step proposed method, which combines ANOVA with PCA, subsequently. As Adam and Mutanga (2009) and Manevski et al. (2011) mentioned, ANOVA can select all wavelengths or spectral indices that have the primary potential to separate the studied varieties. Then, PCA can reduce the dimensions of the selected data and identify the most important ones (Prospere et al., 2014). In the following, the results of both methods are described.
3.2.1. ANOVA
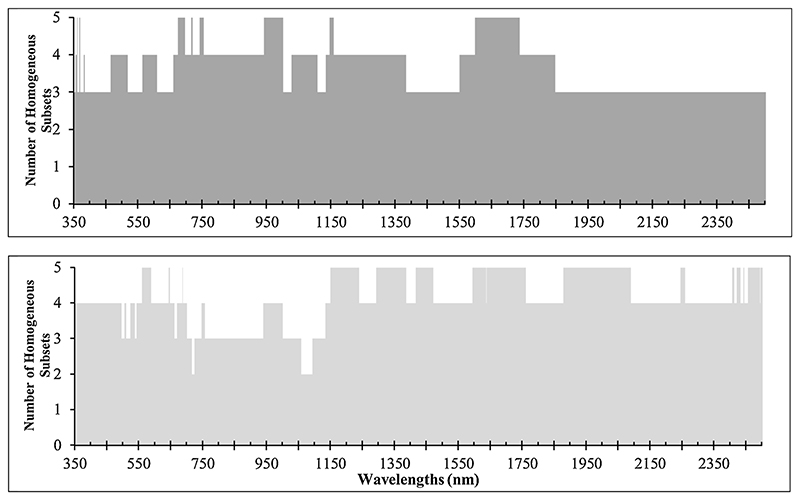
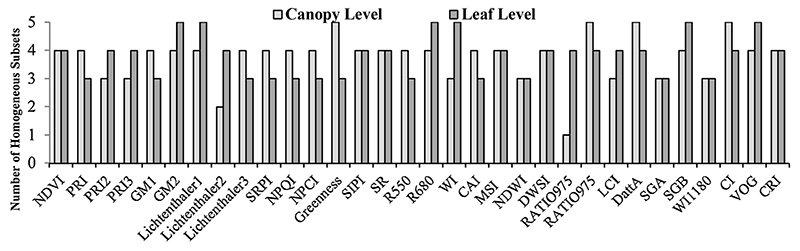
The ANOVA test was conducted to identify the wavelengths or spectral indices that had the potential to discriminate grapevine varieties (AS, MH, SI, HG and YG) at leaf and canopy levels. The results are shown in Fig. 4. According to this Fig, the variance of the spectral curves of grapevine varieties in all wavelengths (350–2500 nm) was significantly different at both leaf and canopy levels. For further investigation of these spectra, the means comparison analysis was conducted with Scheffé test. The results of Scheffé test revealed the existence of at least three and two subsets for the leaf and canopy levels, respectively.
Fig. 4.
ANOVA results in representing the potential of each wavelength at leaf (top) and canopy (down) levels in the grouping of five grapevine varieties at 95% confidence level with a post-hoc of Scheffé test.
At the leaf level, 50.10% (n = 1077) and 38.23% (n = 822) of the total wavelengths were able to separate three and four subsets, respectively, which the highest frequency of these wavelengths located in the MIR region (Fig. 4). Thus, 11.67% of the wavelengths (n = 251) were able to separate five grapevine varieties into five distinct subsets such that 3, 9, 30, 74 and 138 of these wavelengths were located in the NUV, VIS, RDE, NIR and MIR regions (Fig. 4). This suggests that these significant wavelengths have the potential to discriminate five grapevine varieties from each other, and are subsequently introduced as PCA-inputs at leaf level.
At the canopy level, 2% (n = 43), 16.46% (n = 354) and 47.76% (n = 1027) of the total studied wavelengths were able to separate two, three and four subsets, respectively (Fig. 4). Because we are only interested at identifying wavelengths that can separate the five varieties into five distinct groups, the wavelengths separating less than five groups were excluded from further analysis. Therefore, 33.81% (n = 727) of studied wavelengths were potentially separated of five grapevine varieties in five distinct subsets and selected as PCA inputs at canopy level (Fig. 4). Frequency analysis of these selected wavelengths demonstrated that 32, 2, 96 and 597 wavelengths were located in VIS, RDE, NIR and MID regions, respectively (Fig. 4).
The ANOVA was subsequently applied to test for significance differences between 32 spectral indices versus grapevine varieties at leaf and canopy levels. According Fig. 5, six indices at leaf level i.e., GM2, Lichtenthaler1, VOG, R680, WI and SGB, and four indices at the canopy level i.e., RATIO975_2, DattA, Greenness and CI were able to divide the studied grapevine varieties into five separate subsets. Therefore, these indices were introduced as inputs of the next step (i.e., PCA) and other indices were excluded.
Fig. 5.
ANOVA results in representing the potential of each spectral index in the grouping of five grapevine varieties at 95% confidence level with a post-hoc of Scheffé test.
Finally, the ANOVA results showed that 251 and 727 wavelengths, and on the other hand, 6 and 4 spectral indices had the primary potential for separating five grapevine varieties into five distinct subsets at leaf and canopy level, respectively (Fig. 4). The wavelength-ANOVA results confirmed the visually observed trends of the grapevine varieties spectra curves, such that ANOVA results reveal a higher potential for varieties discrimination at canopy level as opposed to leaf level. This is promising, given that the canopy is directly sensed with aerial and satellite sensors, and the canopy level thus provides a better matching between field spectrometry and satellite remote sensing data (Clevers et al., 2010). From the application perspective, this finding supports the use of remote sensing into agricultural or viticulture monitoring i.e. grapevine varieties (Gitelson and Merzlyak, 1996; Goswami and Matharasi, 2015; Jiménez and Díaz-Delgado, 2015).
Nevertheless, we encountered two challenges in choosing the optimal wavelengths or indices. Firstly, the introduced wavelengths and spectral indices had a significant overlap with each other and express the same information. Secondly, the introduced wavelengths were numerous, and it was necessary to select an optimal number. Therefore, the PCA was used to resolve the above two problems.
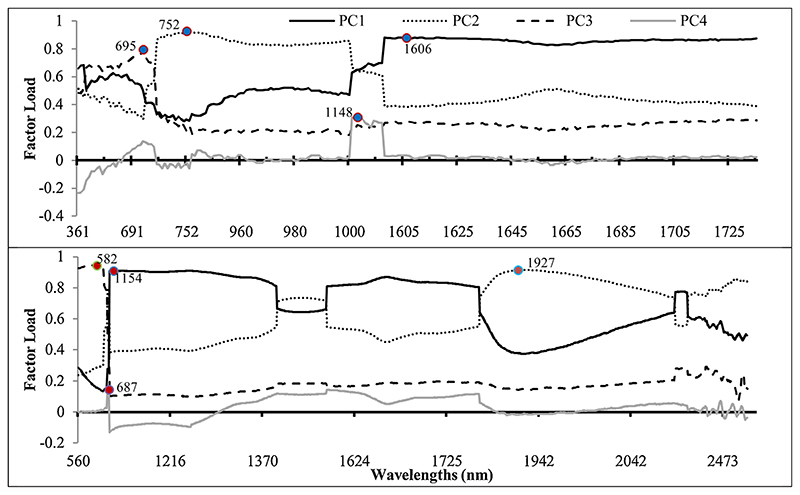
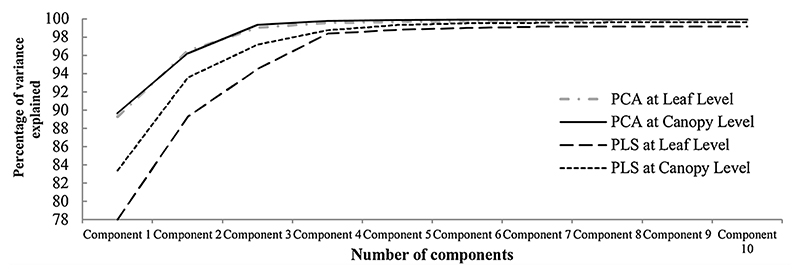
3.2.2. PCA
A summary of the PCA results for wavelengths are presented in Figs. 6 and 7 at leaf and canopy levels. The first four principal components (PC) were able to explain a total of 99.57% of the wavelength variance at the leaf level (Fig. 7). So that, PC1, PC2, PC3 and PC4 explained 52.43%, 35.69%, 10.87% and 0.58% of the variance, respectively (Fig. 7). The wavelengths with the most factor load in a PC (which indicates the correlation between wavelength and PC) were selected as the representative of that PC (Mirzayi et al., 2014 and Mirzaei et al., 2018). Therefore, the wavelengths in the vicinity of 1606, 752, 695 and 1148 (nm) were selected as optimal ones for discrimination of studied grapevine varieties at leaf level, which had the highest correlation with PC1, PC2, PC3 and PC4, respectively (Fig. 6). The PCA results at the canopy level indicated that the first four PCs can explain 99.78% of the variance of the wavelengths which introduced by ANOVA, cumulatively (Fig. 7). In this regard, each of the PC1, PC2, PC3 and PC4 can explain 89.64%, 6.62%, 3.10% and 0.42% of variance, individually (Fig. 7). The factor loads of wavelength for each of the PCs is shown in Fig. 6. According to this Fig, the wavelength in the vicinity of 1154 nm had the most factor loads in PC1 and was selected as the representative of this PC. The wavelengths in the vicinity of 1927, 582 and 687 nm also had the highest factor loads in PC2, PC3 and PC4, respectively, and were selected as representatives of these PCs.
Fig. 6. The factor load of wavelengths at leaf (top) and canopy (down) levels in each principal component with Varimax rotation method.
Fig. 7. Cumulative variance explained (%) for wavelengths in the first ten components extracted by PCA and PLS R at leaf and canopy levels.
PCA was also used to select the optimal spectral indices for discrimination of studied grapevine varieties. A summary result of this analysis is presented in Table 2. At the leaf level, the first three PCs were able to explain a total of 90.64% of the variance. SGB, WI and R680 indices had the most factor loads in PC1, PC2 and PC3, respectively. Therefore, these indices were preferred for discrimination of studied grapevine varieties at the leaf level. At the canopy level, the first three PCs were able to explain 98.92% of variance, accumulatively. So, in PC1, PC2 and PC3, the indices of DattA, Greenness and RATIO975_2 had the highest factor loads and were preferred for discrimination grapevine varieties at canopy level.
Table 2. The factor loads of spectral indices at leaf and canopy levels with Varimax rotation method and cumulative variance explained by each principal component.
| Spectral Indices | PC1 | PC2 | PC3 | |
|---|---|---|---|---|
| Leaf level | GM2 | 0.879 | 0.221 | 0.420 |
| Lichtenthaler1 | 0.606 | 0.478 | 0.634 | |
| R680 | −0.584 | −0.475 | −0.657 | |
| WI | 0.150 | 0.965 | 0.215 | |
| SGB | 0.967 | 0.140 | 0.201 | |
| VOG | 0.892 | 0.231 | 0.373 | |
| Cumulative Variance Explained | 53.94 | 79.07 | 99.64 | |
| Canopy level | RATIO975_2 | −0.114 | −0.272 | 0.955 |
| DattA | 0.988 | 0.012 | −0.088 | |
| CI | 0.892 | 0.409 | −0.123 | |
| Greenness | 0.181 | 0.932 | −0.306 | |
| Cumulative Variance Explained | 45.43 | 73.19 | 98.92 |
3.2.3. PLSR
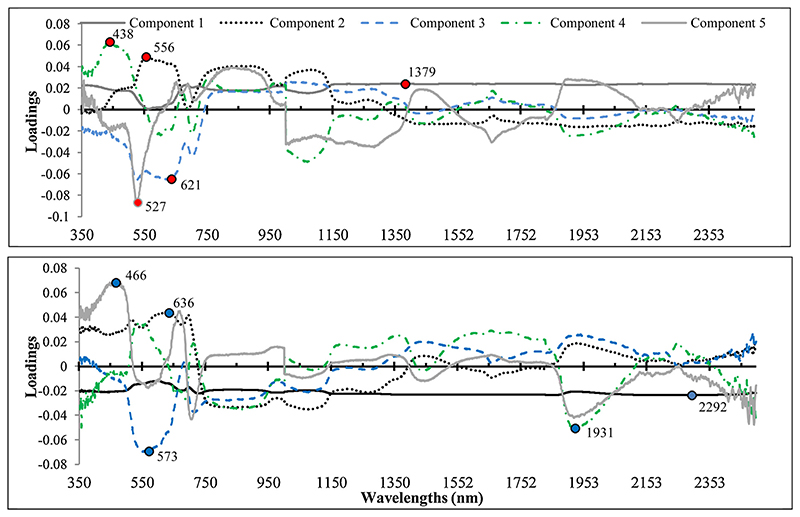
PLSR was used as another data reduction method for selecting optimal wavelengths and spectral indices to discriminate of grapevine varieties. Therefore, 2151 wavelengths (350–2500 nm) were entered into PLSR at leaf and canopy levels and grapevine varieties considered as dependent variables. One of the most important aspects in using of PLSR is to select the optimal component number (Diago et al., 2013). The high number of components leads to an increase in the overlap risk between the components, and the low number of components leads to the loss of the variance description (Mirzayi et al., 2014). According to Fig. 7, if the first five components are selected, 99.02% and 98.35% of the variance of wavelengths is described at the leaf and canopy levels. After the fifth component, the gradient of the graph is very low and it seems that there is no need to enter another component and the first five components are optimal. In Fig. 8, the loads of the first five components are shown. According to this Fig, in components 1, 2, 3, 4, and 5, the wavelengths in the vicinity of 1379, 556, 621, 438, and 527 nm had the highest absolute loads, respectively. Therefore, these five wavelengths can be considered as representing the PLSR components, and are considered as most suitable in the separation of grapevine varieties at the leaf level.
Fig. 8. The loadings of wavelengths at leaf (top) and canopy (down) levels in the first five extracted components by PLSR.
At the canopy level, the components of 1, 2, 3, 4 and 5 had the highest absolute loads in the wavelengths in vicinity of 2292, 636, 573, 1931, and 466 nm. Therefore, these wavelengths can be selected as representatives of these components in the discrimination of grapevine varieties at the canopy level.
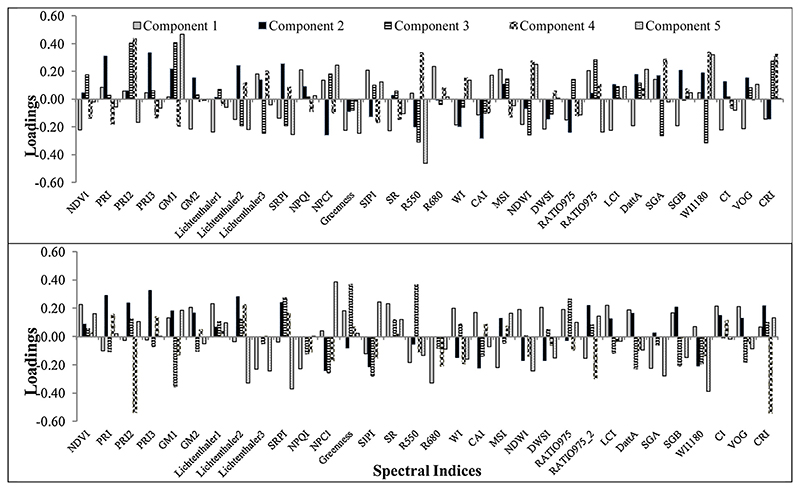
In order to identify the optimal spectral indices in discriminating of grapevine varieties, 32 calculated indices were entered into PLSR. The results of PLSR for this section indicate that the first five components were able to explain a total of 99.81% and 99.35% of the spectral indices variance at leaf and canopy levels, respectively. At the leaf level, R680, PRI3, GM1, PRI2 and R550 indices had the highest absolute loads in components 1, 2, 3, 4 and 5, respectively (Fig. 9). Therefore, these indices can be selected as optimal for discriminating grapevine varieties at the leaf level.
Fig. 9. The loadings of spectral indices at leaf (top) and canopy (down) levels in the first five extracted components by PLSR.
At the canopy level, R680, PRI3, Greenness, CRI and NPCI indices had the highest absolute loads in components 1, 2, 3, 4 and 5, respectively (Fig. 9). Therefore, it is possible to select these indices as the best indices of PLSR method for discriminating of grapevine varieties at canopy level.
3.3. Spectral region importance
One of the most important matters in the hyperspectral in situ spectroscopy studies is identifying the location of optimal wavelengths in the electromagnetic spectrum (Li and He, 2008). A small set of wavelengths must be selected to provide in-depth information about the study targets while at the same time missing data must be minimized (Prospere et al., 2014; Adam et al., 2010). Therefore, both PLSR and ANOVA-PCA were exploited to determine the optimal number and location of wavelengths for discrimination of grapevine varieties. The ANOVA-PCA results demonstrated that PC1, PC2, PC3 and PC4 were affected by the MIR, NIR, RDE and NIR regions at the leaf level, respectively (Fig. 6). Hence, the highest frequency of separation wavelengths of grapevine varieties at the leaf level was located in the NIR region. Also, at the canopy level, PC1, PC2, PC3 and PC4 were affected by NIR, MIR, VIS and RDE regions, respectively (Fig. 6). As a general summary of the ANOVA-PCA method, the importance of spectral regions was ranked as NIR > MIR and RDE > VIS. However, in the PLSR method, component 1 was affected by MIR region and the components 2, 3, 4, and 5 were affected by the VIS region, at the leaf level (Fig. 8). Also, at the canopy level the greatest influence of components 1 and 4 was on the MIR region, and the most effective of components 2, 3 and 5 were formed by VIS region (Fig. 8). Generally, according to PLSR results, the highest frequency of optimal wavelengths for grapevine discrimination was located in the VIS and MIR regions (ranking order: VIS > MIR > NIR and RDE).
According to these results, two remark s are worth addressingFirst, changing the data reduction method led to the selection of different wavelengths from different spectral regions. So that, in the ANOVA-PCA method the NIR and in the PLSR method the VIS were the most important regions, respectively. Manevski et al. (2011) also observed different results from ANOVA and U test methods in data reduction process. They discussed that the reasons for these differences was due to the two types of statistical analyzes (parametric and nonparametric). Here both methods belong to parametric statistical analysis. It can therefore be admitted that the choice of data reduction methods plays a significant role in introducing optimal wavelengths, which was also confirmed by Prospere et al. (2014). Second, the selected wavelengths by the ANOVA-PCA method yielded the highest frequency in the NIR region, which was confirmed by the findings of Adam and Mutanga (2009), Schmidt and Skidmore (2003) and Aneece and Epstein (2017). However, in Vaiphasa et al. (2005) and Abbasi et al. (2012) the RDE was considered as a most sensitive region for discrimination of plants, which in this study had medium and no effect on the discrimination of grapevine varieties by ANOVA-PCA and PLSR, respectively.
According to Vogelmann, (1993); Slaton et al. (2001); Xu et al. (2009) and Strever (2012), the NIR region is mostly indicative of plant structural characteristics. On the other hand, the PLSR method selected most wavelengths in the VIS region, which is mostly driven by plant pigments (Boyer et al., 1988; Penuelas et al., 1993). This suggests that the studied grapevine varieties were likely different in terms of structural characteristics and foliar pigment concentrations, although these parameters were not measured.
3.4. Accuracy assessment results
After the selection of optimal wavelengths or indices for discriminating grapevine varieties by ANOVA-PCA and PLSR, it was necessary to settle a benchmark to evaluate the performance of different scenarios. In this regard, the LDA and SVM algorithms were used to evaluate the performance of different data collection level (canopy and leaf levels), hyperspectral data type (wavelength and spectral indices) and feature selection methods (ANOVA-PCA and PLSR). So, a total of 16 models were developed to support all existing scenarios. A summary of the results obtained by LDA in discriminating grapevine varieties is shown in Table 3. At the leaf level, the overall accuracy (OA) of discriminating grapevine varieties was 100% at both training and testing sets in wavelength-ANOVA-PCA, indices-ANOVA-PCA and indices-PLSR scenarios (Table 3). Similarly, at the canopy level, the overall accuracy was 100% at the training and testing sets in wavelength-PLS, indices-ANOVA-PCA and indices-PLSR scenarios (Table 3). It should be noted that the wavelength-PLSR scenario performed poorer in discriminating the studied grapevine varieties at the leaf level, whereby the overall accuracy of this scenario at the training and testing sets was 91.85% and 89.88%, respectively (Table 3). At the canopy level, the weakest performance was related to the wavelength-ANOVA-PCA approach. This method was able to discriminate grapevine varieties in the training and testing sets with overall accuracy of 97.14% and 96.66% (Table 3).
Table 3. A summary result of LDA in discriminating grapevine varieties at leaf and canopy levels based on wavelengths and spectral indices.
| Hyperspectral Data Type | Feature selection Method | Selected Inputs | Train OA % | Test OA % | |
|---|---|---|---|---|---|
| Leaf Level | Wavelengths | ANOVA-PCA | w695, w752, w1148, w1606 | 100 | 100 |
| PLSR | w1379, w556, w621, w438, w527 | 91.85 | 89.88 | ||
| Indices | ANOVA-PCA | R680, WI, SGB | 100 | 100 | |
| PLSR | R680, PRI3, GM1, PRI2, R550 | 100 | 100 | ||
| Canopy Level | Wavelengths | ANOVA-PCA | w582, w687, w1154, w1927 | 97.14 | 96.66 |
| PLSR | w2292, w636, w573, w1931, w466 | 100 | 100 | ||
| Indices | ANOVA-PCA | RATIO975_2, DattA, Greenness | 100 | 100 | |
| PLSR | R680, PRI3, Greenness, CRI, NPCI | 100 | 100 |
w: wavelength.
The SVM algorithm was applied by varying the kernel function (linear, polynomials, RBF, and sigmoid) and its related parameters (coefficient, gamma, degree) in order to achieve the highest performance (Gutiérrez et al., 2016; Mirzaei et al., 2018). Table 4, shows the structure and the best results obtained from SVM for each of the studied scenarios. According to the table, SVM was able to discriminate all leaves and canopies samples into their related variety names with accuracy of 100% in both training and testing sets. In many cases, SVM with the linear kernel function led to the best performance (Table 4).
Table 4. A summary results and properties of the best SVM models in discriminating grapevine varieties at leaf and canopy levels based on wavelengths and spectral indices.
| Hyperspectral Data Type | Feature selection Method | Selected Inputs | Kernel type | Number of support vectors | Kernel Parameters | Train | Test | |||
|---|---|---|---|---|---|---|---|---|---|---|
| coefficient | degree | gamma | OA % | OA % | ||||||
| Leaf Level | Wavelengths | ANOVA-PCA | w695, w752, w1148, w1606 | Linear | 28 | – | – | – | 100 | 100 |
| PLSR | w1379, w556, w621, w438, w527 | RBF | 43 | – | – | 0.20 | 100 | 100 | ||
| Indices | ANOVA-PCA | R680, WI, SGB | Linear | 25 | – | – | – | 100 | 100 | |
| PLSR | R680, PRI3, GM1, PRI2, R550 | Linear | 27 | – | – | – | 100 | 100 | ||
| Canopy Level | Wavelengths | ANOVA-PCA | w582, w687, w1154, w1927 | RBF | 32 | – | – | 0.25 | 100 | 100 |
| PLSR | w2292, w636, w573, w1931, B466 | Linear | 28 | – | – | – | 100 | 100 | ||
| Indices | ANOVA-PCA | RATIO975_2, DattA, Greenness | Linear | 24 | – | – | – | 100 | 100 | |
| PLSR | R680, PRI3, Greenness, CRI, NPCI | Linear | 26 | – | – | – | 100 | 100 | ||
Only in the leaf-wavelength-PLSR and canopy- wavelength- ANOVA-PCA scenarios outperformed the RBF kernel the other kernel functions (Table 4). The superiority of the linear function over other kernel functions (polynomials, RBF, and sigmoid) can be due to the linear nature of the inputs data to the SVM model. Similarly, the data reduction methods (PLSR and ANOVA-PCA) are based on parametric statistics and linear relationships.
According to the results, in all scenarios the SVM performance was 100%, while the LDA was lower (OA < 100%) in two scenarios (Tables 3 and 4). Similar results in comparing of SVM and LDA were obtained in Große-Stoltenberg et al. (2016) and Yang et al. (2015) studies. The reason for such findings can be attributed to the benefits of machine learning techniques (i.e. SVM) as opposed to parametric methods (e.g. LDA) (Verrelst et al., 2018). These techniques have proven flexibility, generalization capability and accuracy in discrimination topics (Gutiérrez et al., 2016). So, the strength of the SVM can lie in the use of linear and nonlinear functions in the SVM kernel as well as confirming the high suitability and adaptability of machine learning approaches in classification studies (Gutiérrez et al., 2015, 2016; Verrelst et al., 2018).
Since SVM yielded a similar performance in all scenarios (OA = 100%), the decision for introducing the most suitable scenarios was possible only based on the LDA results. Accordingly, the OA of test sets were 89.88% and 96.66% in the leaf-wavelength- PLSR and canopy-wavelength-ANOVA-PCA scenarios, respectively (Table 3). So, despite the fact that the results were alike, on the whole, the ANOVA-PCA method selected input features for discriminating of studied grapevine varieties with a higher performance. This result suggests that, although the PLSR is most common method in reduction of in situ spectroradiometry data (Xu et al., 2009; Diago et al., 2013; Lehmann et al., 2015; Abbasi et al., 2012), the ANOVA-PCA can also be considered as an excellent alternative in this regard.
In accordance with Table 3, it is possible to calculate that averages OA in test sets were 97.47% and 99.17% for leaf and canopy levels, respectively. Therefore, it can be deduced that the canopy level is more suitable for discriminating grapevine varieties. In confirming these results, Fig. 3 also displayed a distinct average foliar and canopy reflectance spectrum of studied varieties. As in the visual interpretation, the discrimination of varieties was more successful at the canopy level. This difference in scale can be attributed to the addition of some plant organs such as petioles, cords and branches to the spectroscopy process. So, when these plant organs were added to the spectroscopy process, the potential for the separation of grapevine varieties was higher than with individual leaves. Therefore, as a general finding, it can be admitted that the canopy level has a higher potential for separating grapevine varieties than the leaf level. The difference in spectral reflectance at the leaf and canopy levels is due to various factors such as canopy architecture, leaf orientation, leaf area index, non-photosynthetic elements and etc., which drive the spectral reflectance of the canopy level (Asner, 1998; Kalacska et al., 2007). Also Cho et al. (2008) found that the canopy level had a higher performance in plant species discriminating.
As a final remark, two types of hyperspectral data were applied, i.e. wavelengths and indices. According to Table 3, the OA was 100% in all indices-based scenarios, whereas in two wavelength-based scenarios (leaf-wavelength-PLSR and canopy-wavelength-ANOVA-PCA) the OA was less than 100%. The success of spectral indices lies in their ability to improve vegetation signals (Prospere et al., 2014) while mitigating atmospheric or background disturbances (Darvishsefat et al., 2011) and thus provides more facilities for discriminating the characteristics of plant species or varieties (Cho et al., 2008; Prospere et al., 2014). Similarly, also Prospere et al. (2014) reported a preference of spectral indices in comparison to original spectral reflectance data to discriminate tropical wetland species.
4. Conclusions
The capability of in-field spectroscopy and multivariate statistical techniques was investigated to identify optimal features in discriminating common grapevine varieties in the western of Iran. In this regard, two types of hyperspectral data (wavelengths from 350 to 2500 nm and 32 spectral indices), two data reduction methods (PLSR and ANOVA-PCA) and two classifier algorithms (LDA and SVM) at leaf and canopy levels were applied in a total of 16 scenarios to consolidate the best approach. According to the obtained results, it can be concluded that: 1) Data reduction methods play a very important role in the application of in-field spectroscopy data. In this regard the combination of ANOVA with PCA outperformed PLSR. 2) Optimal wavelengths in discrimination of studied grapevine varieties were located in vicinity of 695, 752, 1148, 1606 nm and 582, 687, 1154, 1927 nm at leaf and canopy levels, respectively. On the other hand, optimal spectral indices were R680, WI, SGB and RATIO975_2, DattA, Greenness at leaf and canopy levels, respectively. 3) both in the visual interpretation and on the basis of statistical analyzes, the canopy level was more able to discriminate the grapevine varieties as opposed to the leaf level. 4) The spectral indices outperformed wavelengths in discrimination of grapevine varieties. 5) According to ANOVA-PCA method, the importance of spectral regions in discriminating studied grapevine varieties was ranked as NIR > MIR and RDE > VIS. 6) in all scenarios, the SVM performance was 100%, while the LDA had lower (OA < 100%) in some scenarios. Therefore, SVM was concluded as best classification algorithm. 7) The grapevine varieties were discriminated with OA: 89.88%-100%, which supports the acceptable performance of the applied techniques. These results support the use of in-field spectroscopy as a nondestructive, rapid, and highly accurate method in plant varieties discrimination.
Altogether, the canopy-spectral indices-ANOVA-PCA-SVM scenario discriminated grapevine varieties most accurately. This scenario is related to in-field data acquisition level, hyperspectral data type, data reduction method and classification algorithm, respectively. We encourage similar studies to complete the spectral library of grapevine or other orchards varieties and to use such data for the purpose of precision agriculture. A next step would be working on upscaling by coupling in-field spectroscopy data with hyperspectral-satellite imagery.
Acknowledgements
This research was supported by the Research Institute for Grapes and Raisin (RIGR), Malayer University, Iran and Jochem Verrelst was supported by the European Research Council (ERC) under the ERC-2017-STG SENTIFLEX project (grant agreement 755617).
References
- Abbasi M, Darvishsefat AA, Schaepman ME, Sobhani H, Shirvany N, Shabestan S. Spectral reflectance differences of Alnus subcordata, Quercus castaneifolia and Parrotia persica leaves based on nitrogen content using PLS regression. J For, Wood Prod. 2012;64(4):399–417. [Google Scholar]
- Adam E, Mutanga O. Spectral discrimination of papyrus vegetation (Cyperus papyrus L.) in swamp wetlands using field spectroscopy. ISPRS J Photogramm Remote Sens. 2009;64(6):612–620. [Google Scholar]
- Adam E, Mutanga O, Rugege D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: a review. Wetlands Ecology and Management. 2010;18(3):281–296. [Google Scholar]
- Aneece I, Epstein H. Identifying invasive plant species using field spectroscopy in the VNIR region in successional systems of north-central Virginia. Int J Remote Sens. 2017;38(1):100–122. [Google Scholar]
- ASD, Analytical Spectral Devices, Inc. Handheld Spectroradiometer: User’s Guide, Version 405. Boulder, USA: 2005. [Google Scholar]
- Asner GP. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens Environ. 1998;64(2):234–253. [Google Scholar]
- Belton PS, Colquhoun IJ, Kemsley EK, Delgadillo I, Roma P, Dennis MJ, Sharman M, Holmes E, Nicholson JK, Spraul M. Application of chemometrics to the 1H NMR spectra of apple juices: discrimination between apple varieties. Food Chem. 1998;61(1-2):207–213. [Google Scholar]
- Boyer M, Miller J, Belanger M, Hare E. Senescence and spectral reflectance in leaves of northern pin oak (Quercus palustds muenchh.) Remote Sens Environ. 1988;25:71–87. [Google Scholar]
- Cao F, Wu D, He Y. Soluble solids content and pH prediction and varieties discrimination of grapes based on visible–near infrared spectroscopy. Comput Electron Agric. 2010;71:S15–S18. [Google Scholar]
- Cervera MT, Cabezas JA, Sancha JC, De Toda FM, Martinez-Zapater JM. Application of AFLPs to the characterization of grapevine Vitis vinifera L. genetic resources. A case study with accessions from Rioja (Spain) Theor Appl Genet. 1998;97(1-2):51–59. [Google Scholar]
- Cho MA, Sobhan I, Skidmore AK, De Leeuw J. Discriminating species using hyperspectral indices at leaf and canopy scales. Int Archives Photogr Remote Sens Spatial Inf Sci. 2008;37(B7) [Google Scholar]
- Clevers JG, Kooistra L, Schaepman ME. Estimating canopy water content using hyperspectral remote sensing data. Int J Appl Earth Obs Geoinf. 2010;12(2):119–125. [Google Scholar]
- da Silva Junior CA, Nanni MR, Shakir M, Teodoro PE, de Oliveira-Júnior JF, Cezar E, Shiratsuchi LS. Soybean varieties discrimination using non-imaging hyperspectral sensor. Infrared Phys Technol. 2018;89:338–350. [Google Scholar]
- Damm A, Paul-Limoges E, Haghighi E, Simmer C, Morsdorf F, Schneider FD, van der Tol C, Migliavacca M, Rascher U. Remote sensing of plant-water relations: an overview and future perspectives. J Plant Physiol. 2018 doi: 10.1016/j.jplph.2018.04.012. [DOI] [PubMed] [Google Scholar]
- Darvishsefat AA, Abbasi M, Schaepman M. Evaluation of spectral reflectance of seven Iranian rice varieties canopies. J Agric Sci Technol. 2011;13:1091–1104. [Google Scholar]
- Devadas R, Lamb DW, Simpfendorfer S, Backhouse D. Evaluating ten spectral vegetation indices for identifying rust infection in individual wheat leaves. Precis Agric. 2009;10(6):459–470. [Google Scholar]
- Diago MP, Fernandes AM, Millan B, Tardaguila J, Melo-Pinto P. Identification of grapevine varieties using leaf spectroscopy and partial least squares. Comput Electron Agric. 2013;99:7–13. [Google Scholar]
- FAO. 2016. http://www.fao.org/faostat/en/#rankings/countries_by_commodity .
- Fassnacht FE, Stenzel S, Gitelson AA. Non-destructive estimation of foliar carotenoid content of tree species using merged vegetation indices. J Plant Physiol. 2015;176:210–217. doi: 10.1016/j.jplph.2014.11.003. [DOI] [PubMed] [Google Scholar]
- Ferreira MP, Zortea M, Zanotta DC, Shimabukuro YE, de Souza Filho CR. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens Environ. 2016;179:66–78. [Google Scholar]
- Ferreiro-Arman M, Da Costa JP, Homayouni S, Martin-Herrero J. Hyperspectral image analysis for precision viticulture; International Conference Image Analysis and Recognition; Berlin, Heidelberg. Springer; 2006. pp. 730–741. [Google Scholar]
- Galet P. A Practical Ampelography. Cornell University Press; 1979. [Google Scholar]
- Galvão LS, Roberts DA, Formaggio AR, Numata I, Breunig FM. View angle effects on the discrimination of soybean varieties and on the relationships between vegetation indices and yield using off-nadir Hyperion data. Remote Sens Environ. 2009;113(4):846–856. [Google Scholar]
- Gitelson AA, Merzlyak MN. Signature analysis of leaf reflectance spectra: algorithm development for remote sensing of chlorophyll. J Plant Physiol. 1996;148(3-4):494–500. [Google Scholar]
- Goswami S, Matharasi K. Development of a web-based vegetation spectral library (VSL) for remote sensing research and applications (No. e1129) Peer J Pre Prints. 2015 [Google Scholar]
- Große-Stoltenberg A, Hellmann C, Werner C, Oldeland J, Thiele J. Evaluation of continuous VNIR-SWIR spectra versus narrowband hyperspectral indices to discriminate the invasive Acacia longifolia within a Mediterranean dune ecosystem. Remote Sens. 2016;8(4):334. [Google Scholar]
- Gutiérrez S, Tardaguila J, Fernández-Novales J, Diago MP. Support vector machine and artificial neural network models for the classification of grapevine varieties using a portable NIR spectrophotometer. PLoS One. 2015;10(11):e0143197. doi: 10.1371/journal.pone.0143197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutiérrez S, Tardaguila J, Fernández-Novales J, Diago MP. Data mining and NIR spectroscopy in Viticulture: applications for plant phenotyping under field conditions. Sensors. 2016;16(2):236. doi: 10.3390/s16020236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Li X, Deng X. Discrimination of varieties of tea using near infrared spectroscopy by principal component analysis and BP model. J Food Eng. 2007;79(4):1238–1242. [Google Scholar]
- Jiménez M, Díaz-Delgado R. Towards a standard plant species spectral library protocol for vegetation mapping: a case study in the Shrubland of Doñana National Park. ISPRS Int J Geoinf. 2015;4(4):2472–2495. [Google Scholar]
- Jolliffe IT. Principal component analysis and factor analysis Principal Component Analysis. Springer; New York: 1986. pp. 115–128. [Google Scholar]
- Kalacska M, Bohlman S, Sanchez-Azofeifa GA, Castro-Esau K, Caelli T. Hyperspectral discrimination of tropical dry forest lianas and trees: comparative data reduction approaches at the leaf and canopy levels. Remote Sens Environ. 2007;109(4):406–415. [Google Scholar]
- Kumar L, Schmidt KS, Dury S, Skidmore AK. In: Imaging Spectrometry: Basic Principles and Prospective Applications. Van Der Meer FD, De Jong SM, editors. Kluwer Academic Press; Dordrecht, the Netherlands: 2001. Review of hyperspectral remote sensing and vegetation science. [Google Scholar]
- Lacar FM, Lewis MM, Grierson IT. Use of hyperspectral reflectance for discrimination between grape varieties; Geoscience and Remote Sensing Symposium, 2001. IGARSS’01; 2001. pp. 2878–2880. [Google Scholar]
- Laurin GV, Puletti N, Hawthorne W, Liesenberg V, Corona P, Papale D, Chen Q, Valentini R. Discrimination of tropical forest types, dominant species, and mapping of functional guilds by hyperspectral and simulated multispectral Sentinel-2 data. Remote Sens Environ. 2016;176:163–176. [Google Scholar]
- Lehmann JRK, Große-Stoltenberg A, Römer M, Oldeland J. Field spectroscopy in the VNIR-SWIR region to discriminate between Mediterranean native plants and exotic-invasive shrubs based on leaf tannin content. Remote Sens. 2015;7(2):1225–1241. [Google Scholar]
- Li X, He Y. Discriminating varieties of tea plant based on Vis/NIR spectral characteristics and using artificial neural networks. Biosyst Eng. 2008;99(3):313–321. [Google Scholar]
- Liu M, Liu X, Ding W, Wu L. Monitoring stress levels on rice with heavy metal pollution from hyperspectral reflectance data using wavelet-fractal analysis. Int J Appl Earth Obs Geoinf. 2011;13(2):246–255. [Google Scholar]
- Manevski K, Manakos I, Petropoulos GP, Kalaitzidis C. Discrimination of common Mediterranean plant species using field spectroradiometry. Int J Appl Earth Obs Geoinf. 2011;13(6):922–933. [Google Scholar]
- Mazzetto F, Calcante A, Mena A, Vercesi A. Integration of optical and analogue sensors for monitoring canopy health and vigour in precision viticulture. Precis Agric. 2010;11(6):636–649. [Google Scholar]
- Mirzaei M, Jafari A, Gholamalifard M, Azadi H, Joorabian Sh, Movahhed S. Mitigating environmental risks: modeling the interaction of water quality parameters and land use cover. Land use Policy Accepted. 2018 [Google Scholar]
- Mirzaie M, Abbasi M, Marofi S, Solgi E, Karimi R. Spectral discrimination of important orchard species using hyperspectral indices and artificial intelligence approaches. RS GIS Nat Res. 2018;9(2):76–92. [Google Scholar]
- Mirzayi M, Riyahi Bakhtiyari A, Salman Mahini A, Gholamali fard M. Analysis of the physical and chemical quality of Mazandaran province (Iran) rivers using multivariate statistical methods. J Mazandaran Univ Med Sci. 2014;23(108):41–52. [Google Scholar]
- Mutanga O, Skidmore AK. Red edge shift and biochemical content in grass canopies. ISPRS J Photogramm Remote Sens. 2007;62(1):34–42. [Google Scholar]
- Páscoa RNMJ, Lopo M, dos Santos CT, Graça AR, Lopes JA. Exploratory study on vineyards soil mapping by visible/near-infrared spectroscopy of grapevine leaves. Comput Electron Agric. 2016;127:15–25. [Google Scholar]
- Peerbhay KY, Mutanga O, Ismail R. Commercial tree species discrimination using airborne AISA Eagle hyperspectral imagery and partial least squares discriminant analysis (PLS-DA) in KwaZulu–Natal, South Africa. ISPRS J Photogramm Remote Sens. 2013;79:19–28. [Google Scholar]
- Penuelas J, Gamon JA, Griffin KL, Field CB. Assessing community type, plant biomass, pigment composition, and photosynthetic efficiency of aquatic vegetation from spectral reflectance. Remote Sens Environ. 1993;46(2):110–118. [Google Scholar]
- Prospere K, McLaren K, Wilson B. Plant species discrimination in a tropical wetland using in situ hyperspectral data. Remote Sens. 2014;6(9):8494–8523. [Google Scholar]
- Schmidt KS, Skidmore AK. Spectral discrimination of vegetation types in a coastal wetland. Remote Sensing of Environment. 2003;85(1):92–108. [Google Scholar]
- Shang X, Chisholm LA. Classification of Australian native forest species using hyperspectral remote sensing and machine-learning classification algorithms. IEEE J Sel Top Appl Earth Obs Remote Sens. 2014;7:2481–2489. [Google Scholar]
- Slaton MR, Raymond Hunt E, Jr, Smith WK. Estimating near-infrared leaf reflectance from leaf structural characteristic cs. Am J Bot. 2001;88(2):278–284. [PubMed] [Google Scholar]
- Stitson MO, Weston JAE, Gammerman A, Vovk V, Vapnik V. Theory of Support Vector Machines. University of London; 1996. [Google Scholar]
- Strever AAE. Non-destructive Assessment of Leaf Composition as Related to Growth of the Grapevine (Vitis Vinifera L Cv Shiraz) (Doctoral Dissertation. Stellenbosch University, Stellenbosch. 2012. [Google Scholar]
- Vaiphasa C, Ongsomwang S, Vaiphasa T, Skidmore AK. Tropical mangrove species discrimination using hyperspectral data: a laboratory study. Estuarine, Coast Shelf Sci. 2005;65(1):371–379. [Google Scholar]
- Van Til M, Bijlmer A, de Lange R. Seasonal variability in spectral reflectance of coastal dune vegetation. EARSel eProceedings. 2004;3(2):154–165. [Google Scholar]
- Verrelst J, Malenovský Z, Van der Tol C, Camps-Valls G, Gastellu-Etchegorry JP, Lewis P, North P, Moreno J. Quantifying vegetation biophysical variables from imaging spectroscopy data: a review on retrieval methods. Surv Geophys. 2018:1–41. doi: 10.1007/s10712-018-9478-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogelmann TC. Plant tissue optics. Annu Rev Plant Biol. 1993;44(1):231–251. [Google Scholar]
- Wang F, Gao J, Zha Y. Hyperspectral sensing of heavy metals in soil and vegetation: feasibility and challenges. ISPRS J Photogramm Remote Sens. 2018;136:73–84. [Google Scholar]
- Wold S, Sjöström M, Eriksson L. PLS-regression: a basic tool of chemometrics. Chemometr Intell Lab Syst. 2001;58(2):109–130. [Google Scholar]
- Xu HR, Yu P, Fu XP, Ying YB. On-site variety discrimination of tomato plant using visible-near infrared reflectance spectroscopy. J Zhejiang Univ Sci B. 2009;10(2):126–132. doi: 10.1631/jzus.B0820200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Hong H, You Z, Cheng F. Spectral and image integrated analysis of hyperspectral data for waxy corn seed variety classification. Sensors. 2015;15:15578–15594. doi: 10.3390/s150715578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M, Qin Z, Liu X, Ustin SL. Detection of stress in tomatoes induced by late blight disease in California, USA, using hyperspectral remote sensing. Int J Appl Earth Obs Geoinf. 2003;4(4):295–310. [Google Scholar]
- Zhang X, Liu F, He Y, Li X. Application of hyperspectral imaging and chemometric calibrations for variety discrimination of maize seeds. Sensors. 2012;12(12):17234–17246. doi: 10.3390/s121217234. [DOI] [PMC free article] [PubMed] [Google Scholar]