Evolutionary Refinement of DNA Nanostructures Using Coarse-Grained Molecular Dynamics Simulations

Abstract

In the last decade, DNA nanostructures have made the leap from small assemblies of a handful of oligonucleotides to megadalton objects assembled from hundreds or thousands of component DNA strands. Most DNA designs today are either lattice based with simple and reliable design tools or lattice free with a larger shape space but more challenging design and lower rigidity. In parallel with the development of DNA nanostructures, software packages for the simulation of nucleic acids have seen rapid development allowing for the simulation of the dynamics of full DNA nanostructure assemblies. Here, we implement an unsupervised software based on the coarse-grained molecular dynamics package oxDNA to simulate DNA origami structures and evaluate their rigidity. From this, the software autonomously produces mutant structures by adding or removing base pairs or modifying the positions of internal supports. These mutant structures are iteratively generated and evaluated by simulation to create an in-silico evolution towards more rigid DNA nanostructures.

Constructing nanoscale assemblies from nucleic acids was first proposed in the early 1980’s¹ and in the following two decades several theoretical, and experimental demonstrations showed that the concept was feasible. These early demonstrations typically used a handful of synthetic oligonucleotides to construct discrete^2,3 or polymeric⁴ 2D and 3D structures. The field of DNA nanotechnology was revolutionized in 2006 by the introduction of DNA origami⁵. In DNA origami a long strand called scaffold strand is folded by hybridizing with many shorter synthetic oligonucleotides called staple strands. By using scaffold strands close to 10 000 bases long and hundreds of staple strands, discrete megadalton assemblies with sizes in the order of 100 nm can be assembled with close to perfect yield.

The geometry of DNA is a fundamental factor in the design of DNA nanostructures, most notably its helical twist, making a full turn in roughly 10.5 base-pairs.⁶ Most 3D DNA origami design consists of parallel DNA strands packed in a square⁷ or honeycomb⁸ lattice. The structures are held together by four-arm junctions formed by crossovers of the scaffold or staples strands between adjacent helices. The positioning of these crossovers should follow the twist of the DNA in the connected helices to minimize strain in the structure, and this essentially creates simple design rules for DNA structures based on parallel packed helices. The first DNA origami structures were designed by hand or with limited computer assistance. This was quickly overcome by the introduction of dedicated design software, most notably caDNAno,⁹ where the design rules form an integral part allowing for the quick design of lattice-based DNA origami structures. DNA origami structures based on parallel packing have been successfully assembled in diverse shapes, and the addition of functional groups have yielded structures with promising applications in drug delivery,^10,11 nano-fabrication,^12,13 plasmonics¹⁴ and as tools for biophysical and life-science studies.^15–17

We recently introduced a method for automatically generating wireframe DNA origami designs from polyhedral meshes.¹⁸ Other tools have been demonstrated for the production of lattice free DNA origami structures,^19,20 including with edges composed of two²¹ or more²² DNA double helices.

Wireframe designs are routinely used in macroscopic engineering as it offers superior strength to weight ratio compared with solid beams. One of the goals of wireframe design of DNA nanostructures is to harness this effect on the nanoscale. Although wireframe DNA origami can fold with high yield to its designed shape, it is evident from experiments that their rigidity is below that of designs relying on the parallel packing of DNA.²³

During the last decades, molecular dynamics simulations have evolved as a powerful tool for studying molecular systems.²⁴ In all-atom molecular dynamics, every atom of the system of interest is simulated as separate particles including solvent molecules. As the number of simulated atoms increases so does the computational cost, limiting this approach to small systems for short simulated time. This approach has been demonstrated on DNA origami structures with simulated times on the order of hundreds of nanoseconds, requiring supercomputers.²⁵

In parallel with the computationally heavy all-atom molecular dynamics simulations, alternative models have been developed where the systems are simplified to reduce computational complexity. One of the most widely used systems for simulating DNA origami structures is CanDo where DNA is modeled as deformable cylinders in a finite element solver.^26,27 The simulations are performed rapidly through a web interface, but the model lacks a description of electrostatics and DNA base pairing. Another popular tool is coarse-grained molecular dynamics, here the studied biomolecules are represented by few-body models with simplified interactions, and the solvent is only modeled implicitly, one such approach is the oxDNA model. In the oxDNA system, every DNA base is modeled as two bodies, representing the backbone and a base.^28,29 These bodies can interact through base pairing, stacking and electrostatic interactions. This simplification dramatically reduces computational cost, and it is now possible to simulate large DNA origami systems for up to 1 μs per day on a single GPU,³⁰ and the model can reproduce the geometry of DNA origami with high precision.³¹

With the increase of computational power over the last decades it has become possible to predict the properties of designs made from diverse materials through simulation. This has revealed that human intuition cannot always predict the properties of a design, and as a result may be incapable of predicting designs with optimal performance. From this realization, the concept of shape optimization has emerged where desired properties and constraints for a design is specified by a user together with initial designs. The design is then evaluated by simulation and compared to its specifications after which it is automatically modified; this cycle is repeated iteratively to find designs that perform better according to the specifications. This approach has been applied from the microscopic scale to produce photonic cavities,³² to the macroscopic scale for the optimization of the internal structures of airliner wings.³³

In the field of rational protein design, significant computational resources are now routinely used to algorithmically develop proteins with novel structures and properties.³⁴ In DNA nanotechnology, simulations are regularly used to evaluate individual designs, but autonomous evaluation and algorithmic improvement of DNA structures have not yet been demonstrated.³⁵ In this paper, we use the oxDNA package to estimate the flexibility of wireframe DNA origami structures. We then modify our DNA origami design pipeline to allow for automatic modification of the DNA nanostructure design, we combine these two to create a system for iteratively generating mutant DNA nanostructures that we evaluate by oxDNA simulations. The system automatically retains structural modifications that yield lower flexibility leading to an in-silico evolution of structural rigidity.

Results And Discussion

Even when using GPU acceleration, the computational time of oxDNA simulations is considerable and grows with the number of nucleotides. We started by optimizing a relatively small structure with 60 helices and around 2200 base-pairs. Simulating this structure on a modern GPU (Nvidia GTX 1080) for 10⁸ time steps (corresponding to approximately 1.5 μs) takes about 20 hours. We can control the size of the explored search space by altering the number of iterations in combination with the number of mutant structures we simulate in each iteration. It is most practical to run one simulation per GPU, and we implement our simulations on two compute nodes with four GPU’s each meaning that we typically use eight mutant structures in each iteration. We created a server software that we run on the compute nodes that configures and runs the oxDNA simulations as well as performs pre-processing on the output data. In addition to this we use a master node that runs a modified version of vHelix¹⁸ that is capable of generating mutant structures, converting these to the oxDNA simulation format, and sending them over network to the compute nodes. When the compute nodes finish their simulations, they return the pre-processed data to the master node over network and the master node software evaluates the simulations and uses this information to generate the next generation of mutant structures. This software is capable of running completely autonomously and send a progress log over email after each finished iteration.

The primary metric of flexibility used in this study is the time-series of the end-to-end distances of the helices that compose the wireframe DNA origami structure. In an ideal wireframe DNA structure, the helices representing the edges should be rigid and thus have small fluctuations in end to end distances during the simulation. These time-series can be extracted from simulation trajectories and be tracked in a plot, or the standard deviation of the time-series can be used as a single metric for the performance of a helix. Supplementary figure 1 shows the extracted end-to-end distances of each helix of a small wireframe DNA origami structure. The dynamic behavior of two adjacent helices can be drastically different, many helices behave rigidly with lengths close to the design, while some are on average considerably shorter than designed and show large standard deviations in their end-to-end distance fluctuations. Deformations of the structure can also be caused by the junctions transitioning between stacked and unstacked conformations during the simulation. It should be noted that helices could take stable bent states in the simulations, and this would yield a lower average length but a low standard deviation.

The standard deviation in end-to-end distance can be used to rank the helices of a structure from most to least rigid. The least rigid helices should be the most significant contributors to the flexibility of a structure. In our first approach (Figure 1) to increase rigidity, we individually modify the four least rigid helices by adding or removing base-pairs to create eight mutant structures. Adding or removing a base-pair from a helix will have two effects: It will increase or decrease the length of the helix causing an additional push or pull on the two vertices that the helix connects to. Secondly, due to the helical twist of DNA, it will alter the preferred angle between the ends of the helix, leading to increased or decreased strain in the connected vertices. These effects can change the behaviour of the helix (Supplementary figure 2), and could conceivably propagate through the structure and have non-local effects on rigidity.

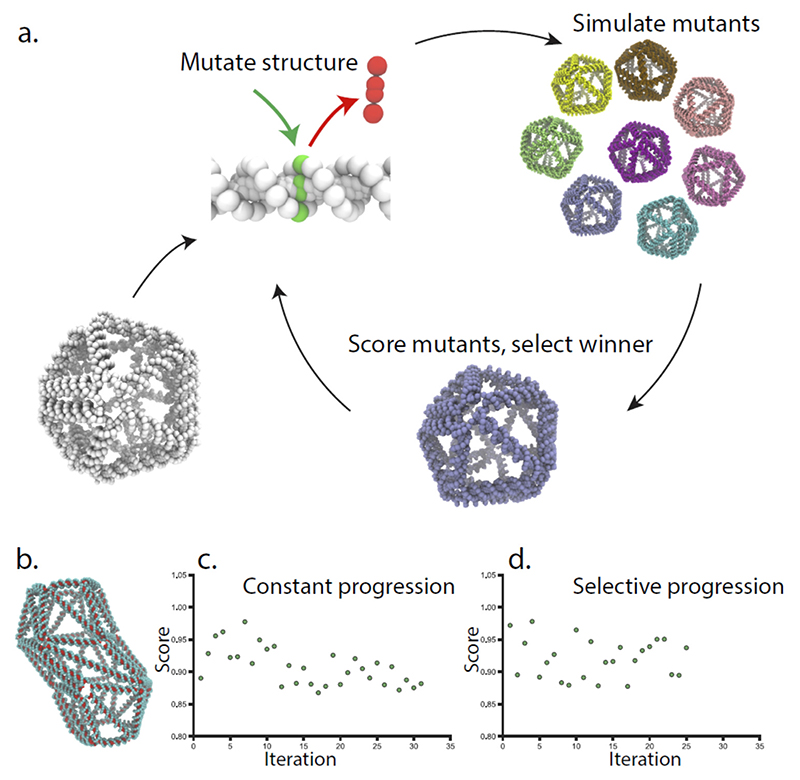
Figure 1. Overview of the iterative evolution through simulation.

a. A wireframe DNA origami is used as template for the first iteration, the structure is modified by introducing or removing base pairs from individual edges, creating a new generation of mutant structures that are all simulated. The simulated structure with the highest performance is selected as the template for the next generation of mutations. b. A barrel-like wireframe origami was used as the starting point, and optimized with “constant progression” (c.), and “selective progression” (d.) Here the score is the average standard deviation of the fluctuation in all helices of the best structure in the iteration compared to the initial structure, for the selective progression the best structure will not be retained if it does not perform better than the previous best.

We then simulate these structures and use the average standard deviation of all helices of the structures as a metric of rigidity. If this metric is reduced, we conclude that the modification was positive and include it in the structure.

We use two iteration schemes to select how to proceed. In the simplest scheme called “constant progression” the mutant structure with the lowest average standard deviation was used as a template structure for the next iteration. This is done regardless of the modification makes the structure more rigid than the previous iteration. If the modified helix is again one of the least rigid edges of the structure, it will be again modified in the next generation of mutant structures, and the modification may revert. The second iteration scheme is called “selective progression”, here the best mutant structure is compared with the previous best structure score. The modification made in the mutant structure is only retained if it generates a lower overall score. If the new structure score is not better than the previous best, the mutation will be discarded and the software will try to modify the second to worst set of helixes of the best structure. One crucial difference between the iteration schemes is that the “selective progression” scheme may run out of edges to modify in the best structure and thus terminate, in what may be a local minimum. The “constant progression” scheme will continue modifying the helices of the structure indefinitely.

After running the two iterations schemes on the small barrel-shaped DNA origami structure for 31 and 25 Iterations respectively, we could see a gradual decrease in mean standard deviation (Figure 1c-d). The “constant progression” scheme showed a decreasing trend throughout, but the lowest value of the simulation constant was found already at iteration 17. The “selective progression” scheme did not show the same type of trend but rapidly found modifications leading to a lower average standard deviation. To test the effect of simulation time we evolved a smaller structure with five times longer simulations, using the “constant progression” scheme (Supplementary figure 3). For this small structure, the iterative evolution initially showed a positive trend, but then appeared to get caught in a minima where the same edges were consistently mutated.

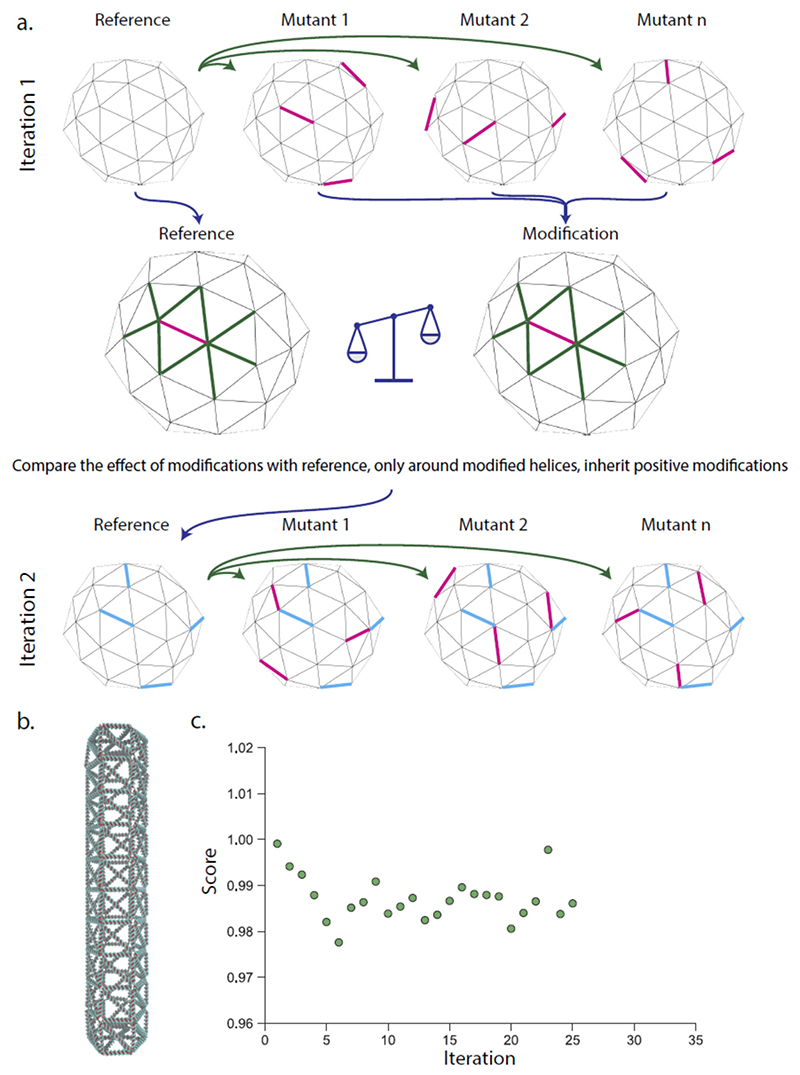
An iterative scheme that makes only one modification per simulated structure is intrinsically slow, and the effect of single base pair modifications on a full structure could be minimal for larger origami structures. To overcome this, we implement a multiplexed modification scheme where several modifications are introduced in the same mutant structure at random (Figure 2) but with a constraint that they are spatially separated. After simulation, the modifications are evaluated individually by scoring the modified edge and the edges that share a vertex with it and comparing these with the score for the same edges on a reference simulation without this mutation. All positive modifications that yield an improvement larger than a threshold is then incorporated in the structure used in the next iteration. We tested this iterations scheme with a full-size DNA origami structure (around 8 000 base-pairs) with up to 10 modifications in each structure for a total of up to 70 modifications in each iteration. For the large structure, the initial iterations showed a decreasing trend in the flexibility, but after six iterations a single modification was incorporated that increased the flexibility. These mutations led to very modest effects on the rigidity of the structure, and it is possible that scoring the effect only locally around the mutation is inadequate as mutations may have long-range effects on the structures. In our evaluation of the multiplexed strategy, we performed over 500 independent simulations of variants of a hexagonal rod and implemented and evaluated over 4 000 mutations. These mutations were introduced at random, and in the tested structure, only a fraction (389) were beneficial. This fraction could be increased if it was possible to predict what edges could benefit from a mutation.

Figure 2. Multiplexed iterative evolution of DNA nanostructures.

a. The original structure is simulated together with mutant structures with several random modifications (magenta edges). The modifications are evaluated individually by scoring the change in the length fluctuations of the modified edge and its neighbors (green) and comparing this with the same edges on the reference. All modifications that improve the edge more than a threshold is then incorporated in the next iteration (blue edges). b. A full-size DNA origami rod was used as a template with up to 70 modifications per iteration. C) The progression of the fluctuations in the structure compare to the initial structure over 26 iterations. Here the score is the average standard deviation of the fluctuation in all edges of the structure compared to the initial structure. Additional analysis in supplementary figure 4.

We took a machine learning approach and used this data to train a convolutional neural network on predicting if an edge could benefit from a mutation (Supplementary figure 5). After training the network we simulated a spherical wireframe structure and evaluated the simulation data of the individual edges with the neural network, yielding a prediction of what edges where most likely to benefit from adding or removing a base pair. We modified the 10, 20 or 30 edges that where most strongly predicted to benefit from modification, compared to 10, 20 or 30 random modification. Interestingly, when we evaluated the local effect of these mutations, we found that the neural network was better at predicting edges that benefited from modifications compared to random modifications, but the overall score of the structure did not improve by these modifications, again indicating that modifications can have long range effects, and that local evaluation may not be adequate. Machine learning approaches are used in many other design problems, including protein structure prediction,³⁶ and could be implemented in multiple ways in DNA nanostructure design. Additional simulations would also yield a larger training data set, potentially improving the accuracy of a machine learning model.

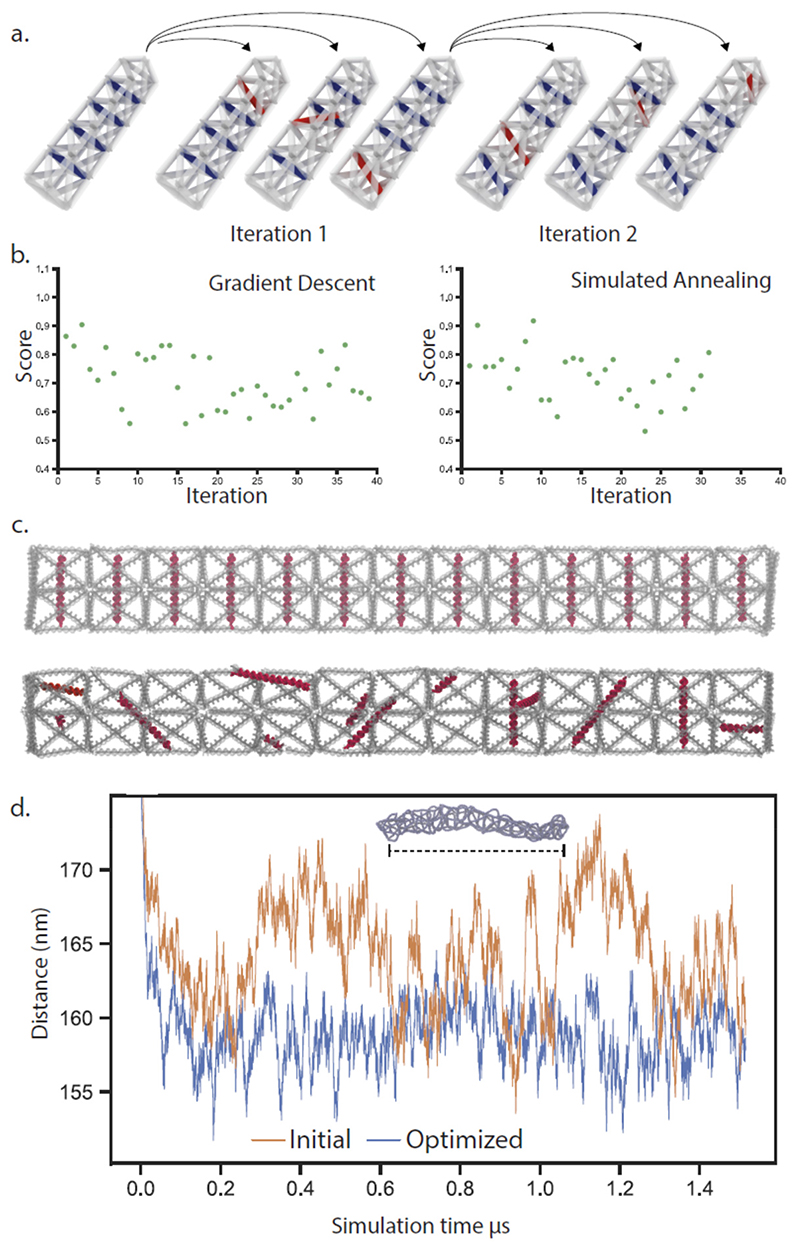
Addition or removal of individual base pairs represent modest modifications and appears to give modest improvements to structure performance, but iterative strategies can also be based on more significant modifications of the designs. We created a scheme where a hollow DNA structure is internally supported by edges connecting two helices of the original mesh. This was achieved by designing staple-staple protrusions that connect internally by hybridization. In each iteration, eight separate mutant structures are generated by disconnecting one end of one internal support and reconnecting it randomly to another helix (within a maximum permitted distance). These mutant structures are simulated, evaluated, and a top performing structure is selected as template for the next iterations of mutations. This allows internal supports to “walk” inside the structure and find positions in the structure where they contribute the most to the performance of the structure. We tested this concept by designing a prismatic wireframe rod with a square cross-section and 13 subunits, initially designed to have one internal support running through each subunit. The global performance of this structure was evaluated by tracking the distance between the top and bottom subunits of the structure, in a rigid rod, this distance should be constant. We implemented two algorithms: gradient descent, where in each iteration the mutant structure with the best performance is chosen, and simulated annealing, where a decreasing probability of choosing suboptimal mutant structures in each iteration should lower the risk of getting caught in local minima. The optimization using gradient descent showed a rapid reduction in end-to-end fluctuations of the structure in the first ten iterations and then appeared to level off with a decrease of fluctuations of almost 50 %. The simulated annealing showed a slower decrease in fluctuations and was also able to reach a state of almost 50% less fluctuation after 23 iterations. After optimization with simulated annealing, the position and orientations of the internal edges have gone from an ordered pattern to a seemingly random configuration (Figure 3c). A plot of the end to end distance of the rod (Fig 3d) shows that the fluctuations are smaller in the optimized structure compared to the initial state. We attempted to validate these results by assembling the initial and optimized structures experimentally. The initial structure assembled, but did not appear rod-like in electron microscopy, while the optimized structures did appear rod-like (supplementary figure 6).

Figure 3. Iterative refinement of DNA origami structures through placement of internal supports.

a. A structure is designed with internal supports, mutant structures are then generating by reconnecting one end of an internal support. These mutant structures are then individually simulated and scored and mutations are incorporated to the next generation either through gradient descent or simulated annealing. b. The performance of a rod structure is evaluated by the amount of fluctuation in the overall end-to-end distance. c.) Renderings of a 13-unit rod before (top) and after (bottom) 23 iterations of simulate annealing-based refinement, internal supports are highlighted in red. d. End-to-end fluctuations of the rod structure in a simulation, before and after refinement.

Wireframe DNA origami structures may be of use in biomedical applications but are less rigid than structures based on the parallel packing of helices. Here we demonstrate a method to evaluate the rigidity of wireframe DNA nanostructure in silico using coarse-grained molecular dynamics simulations. We use this to create an iterative evolution of the nanostructures where mutant structures are generated by the addition or removal of base pairs from selected helices, or by moving the position of internal supports. These mutant structures are simulated in oxDNA, and the effect of their modification is evaluated on the entire structure or in the region around the modification. Modifications that are beneficial to the rigidity of the structure are incorporated in the next generation that serves as the base for new mutant structures. We tested this on DNA origami structures of varying sizes and saw moderate improvements with single base modification and improvements on the order of 50 % for modification of internal supports. We also used the large dataset generated from these simulations to train a neural network to predict what edges could benefit from insertions or deletion. This neural network was capable of identifying mutations that where locally, but not globally beneficial to the structure.

The iterative evolution of structures by simulations is not limited to the simple scoring metric used here but could be modified depending on the desired application of the structure. If a moving part is being designed, the dynamics of the structure can be used as metric, if a high degree of similarity to the initial design is needed, the root-mean-square deviation (RMSD) between the simulated structure and the initial model could be used as a metric. The long simulation time on current hardware makes this refinement slow, but we believe that this approach still has merit as the modularity of DNA origami means that a single well optimized design can find many applications through addition of different functional groups. Additionally, the computing power of GPU’s is increasing with every hardware generation, meaning that what we do on clusters today may be done on a laptop in the future.

Methods

DNA nanostructure design

Wireframe meshes was designed in Autodesk Maya, exported in the STL format and then converted to the PLY format using the software Meshlab. The software package BSCOR (available from www.vhelix.net) was used to automatically find a scaffold route through the mesh and then construct a DNA nanostructure geometry based on the mesh. The resulting DNA geometry is output to a file in the RPOLY file format that describes the length, position, orientation and connectivity of the DNA helices.

Iterative simulation and evaluation of DNA origami structures in oxDNA

A software package consisting of three components, capable of running without supervision was designed. A standard workstation running Windows was used as a master node. On it, a main script running inside the python interpreter of Autodesk Maya copied and modified the RPOLY file to include the desired modifications to helices of the structure. The script then sequentially imported the modified DNA nanostructure to vHelix, assigned a scaffold sequence and saved the structure to the MA file format. The script then executed a converter to the oxDNA input format (TOP and CONF), this converter had been modified to also extract the ID of a nucleotide on the second to first and second to last base pair of each helix and save these to a file. This script was set up to generate 8 mutant structures for each iteration. In parallel with this script, a server script was running in a separate python interpreter on the master node, when it detected that all mutant structures had been generated and converted it sent the simulation files over network to the compute nodes, after sending these files, the server script sent an email to a determined address with a logfile of the modifications and the progress of iterative evolution and then waited for the compute nodes to perform the simulations.

The compute nodes were based on dell T630 servers with double Intel Xeon e5-2620 v4 CPUs, 64 GB of RAM and four consumer GPUs (Nvidia GeForce 1080 or 1080Ti) and ran Ubuntu Linux. On the compute nodes, a server script waited for the simulation files to be sent over network and then started running one oxDNA simulation per GPU for 10⁸ simulation time steps. After the simulations finished, the server script extracted the coordinates of the nucleotide ID’s as specified for the end of the helices from the simulation trajectory frames and saved these to a reduced size simulation trajectory. This reduced size trajectory was sent back over network to the master node server script.

When the data from all simulations had been sent to the master node it would trigger the main script to begin evaluating the results of the simulations by calculating the end to end distance of each helix through the simulation from the reduced size trajectory. The standard deviation of these datapoints was used to estimate the flexibility of each helix, and the average standard deviation of all helices was used to estimate the flexibility of the entire structures. The script then used this information to determine what mutant structure to proceed with and what helices to modify in it.

Simulations were run in molecular dynamics mode on oxDNA version 2.2.2 (new-relax branch) with CUDA acceleration, mixed back-end precision and the oxDNA2 interaction type. Simulation parameters were temperature: 30 C, salt concentration: 0.15 M or 0.5 M, and an Anderson-like thermostat. Simulation frames were saved every 20 000 timesteps to the trajectory file.

Supplementary Material

The Supporting Information is available free of charge on the ACS publication website

Additional analysis of wireframe DNA origami, and the effects of mutations using oxDNA; evolving DNA origami with longer individual simulations; additional evaluation of multiplexed evolution of wireframe origami; prediction of the effect of edge mutations using a neural network; experimental study of the effect of evolution (PDF)

Python software package for starting and running an iterative oxDNA server (ZIP)