Simulating polarizable molecular ionic liquids with Drude oscillators

Abstract

The Drude oscillator model is applied to the molecular ionic liquid 1-ethyl-3-methyl-imidazolium triflate. The range of manageable Drude charges is tested. The strength of the polarizability is systematically varied from 0% to 100%. The influence on the structure, single particle dynamics and collective dielectric properties is investigated.

The generalised dielectric constant can be decomposed into a dielectric permittivity, a dielectric conductivity and an optical dielectric constant ϵ_∞. The major part of the static generalized di-electric constant comes from the collective rotation of the ions, i.e. the dielectric permittivity. The translational contribution from the dielectric conductivity is about 58% of the dielectric permittivity. For the evaluation of the optical dielectric contribution the computational dielectric theory was adapted to the case of heterogeneous polarizabilities. In case of 100% polarizability, it reaches a value of approximately two.

I. Introduction

Molecular ionic liquids [MIL] offer the interesting possibility to investigate systems composed of charged, dipolar species at room temperature. Although representing an ensemble of molecular ions, MILs are liquid without an addition of a solvent. The fluidity comes from the competition of steric anisotropy and electrostatic forces. Tuning this rather different types of molecular topology and charge distribution by choosing specific cations and anions can generate a wide range of physical properties.^1–3 The most common cations are imida-zolium based. Anions are usually smaller and more symmetrical but cover the whole regime from hydrophobicity to hydrophilicity.³ For the present study we have selected 1-ethyl-3-methyl-imidazolium [EMIM⁺] triflate [CF₃SO₃^–] because the cationic anisotropy contrasts with the pronounced anionic dipole moment. Within each EMIM⁺ the imidazolium ring is the center of polarity leaving the side chains almost apolar. The cationic dipole moment computed with respect to the center of mass does not coincide with the plane of the ring because of the different side chains attached to the nitrogens. Moreover, EMIM⁺ is one of the most frequently used cations in MILs. The direction of the anionic dipole with respect to the center of mass coincides with the molecular axis. Its molecular volume of roughly 100 ų is approximately 50% of that of EMIM⁺.

Although there exists now a considerable set of experimental data a full atomistic interpretation can only be achieved with the aid of computer simulations, e.g. radial distribution functions, diffusion coefficients and time correlation functions.^4–10 So far, almost all molecular dynamics simulations of MILs were conducted with a classical force field built on pairwise additive forces with fixed atomic partial charges. The most obvious drawback of this type of simulations is the retardation of dynamics as compared to experiment.^5,11–15 Alternatively, one could perform quantum mechanical Car-Parinello simulations or ab initio MD.^16–20 However, this limits the system size to less than 50 ion pairs and the length of the simulation period to 25 ps.^17,20,21 Often experimental data, however, refer to time scales of several nanoseconds or even more and their collectivity requires larger ensembles. Therefore, remedies have been developed to accelerate dynamics within the framework of classical simulation: First, one may reparametrize the set of atomic partial charges but keeping the principal features of the molecular electrostatic potential.^14,22,23 Second, one may rescale the charge set thus reducing the system’s total Coulomb energy.²⁴ Finally, the Lennard-Jones parameters modelling the steric forces may be adjusted.^22,23,25

All this remedies aim at the reorganisation of the charge distribution in an effective or mean way to model the average induction, but they cannot account for instantaneous changes of the nuclei geometry. The electron density of real molecules responds to fluctuating electric fields arising from the changing local environment. Polarization models offer the possibility to mimic the spontaneous induction arising from a perturbation of the molecular electronic structure due to its environment.^26,27 In the literature three different methods have established to model instantaneous charge reorganization: The fluctuating charge model fixes the position of the charges but changes their strength as a reaction to a changing environment. Amongst others these models have been applied to liquid water,²⁸ and hydrated ionic melts.^29,30 To our knowledge, MILs have not been considered so far.

A frequently used method is the point-polarized dipole model which augments the set of permanent charges by inducible atomic dipoles.^11,31–33 In this way the charge distribution can be altered as a reaction to the changed molecular electric fields but the net charge of the system remains unchanged because the set of induced dipoles represents an additional neutral charge distribution. Nevertheless, these point-polarized dipoles have to be handled with special care in the traditional electrostatics algorithms, e.g. Particle-Mesh-Ewald [PME].^34,35 The extension of PME to point-dipoles can only be found in the molecular dynamics packages AMBER³⁶ and Lucretius. ³⁷

A method to retain the point-charge PME and at the same time model induced dipoles is the concept of Drude oscillators also known as “charge on a spring”.^26,38–42 It represents electronic induction by introducing a pair of charges, attached to each polarizable atom by a harmonic spring. GROMOS and CHARMM have incorporated Drude oscillators.^43,44 This method has been applied successfully to a diversity of molecular systems but not to MILs so far.^45–50 Therefore, the following study is the first one modelling charge reorganization in MILs by Drude oscillators. The aim of this study is the analysis of the behaviour of the Drude oscillator model under the severe conditions of strong electrostatic forces as typical for MILs. In this sense, we want to investigate how additional Drude oscillators change the structure and dynamics of MILs. Since we want to study the systematic increase of polarizability from 0% to 100% in steps of 10% a reparametrization of the force field is not intended. Of course, this might be a second step in order to better reproduce experimental data.

II. Theory And Methods

The inclusion of polarizable forces does not only affects the translational and rotational behaviour of the molecules but it also has an impact on the computation of dielectric properties. On the one hand, the dipoles induced by the polarizable forces changes the total collective dipole moment of the sample. Thus, they alter the shape and position of peaks in the dielectric loss spectrum. Consequently, our dielectric theory has to be adopted.^51,52 On the other hand, the induced dipoles affects the electronic contribution ϵ_∞ in the high frequency regime. In classical nonpolarizable molecular dynamics simulation this contribution is neglected making ϵ_∞ unity. In a former study we have evaluated ϵ_∞ in case of uniform molecular polarizabilities.⁵³ This work extend the computation of ϵ_∞ to heterogeneous atomic polarizabilities.

A. Collective dipole moments and collective polarizability

Applying a weak, spatially homogeneous, external electric field E₀(ω) of harmonic frequency ω to an overall neutral sample of charged species induces a dielectric polarization P(ω)

$$P\left(\omega \right)=\frac{{\langle {\text{M}}_{tot}\rangle }_{E0}}{V}$$ (1)

$$=\left\{\frac{1}{k_{B}T}{\displaystyle \underset{0}{\overset{\infty }{\int }}-\frac{d}{dt}\langle M_{tot}\left(0\right)\cdot M_{tot}\left(t\right)\rangle e^{i\omega t}dt+\text{tr}\langle \mathcal{A}\rangle }\right\}\frac{E_0\left(\omega \right)}{3V}$$ (2)

which equals the average of the total collective dipole moment M_tot per volume V. Thereby, we have already used Linear Response theory being valid for not too strong fields.^51,53–55 Here the electronic degrees of freedom are represented by the macroscopic polarizability tensor $\mathcal{A}$ of the complete sample. In other words, $\mathcal{A}$ · E₀(ω) is the collective electronic dipole moment induced by the external field E₀(ω). On contrast, the nuclear degrees of freedom show up in the time correlation function of the total collective dipole moment M_tot(t). For its computation, we decompose M_tot(t) into a translational part M_J(t), a rotational part [including vibrations] $M_D^0\left(t\right)$ and an inductive component $M_D^{ind}\left(t\right)$

$$M_{tot}\left(t\right)=M_J\left(t\right)+M_D^0\left(t\right)+M_D^{ind}\left(t\right).$$ (3)

$$=M_J\left(t\right)+M_D\left(t\right)$$ (4)

$M_D^{ind}\left(t\right)$ is the collective dipole moment induced by the local field E(ω). It is still present in the absence of an external field E₀(ω) and completely different from $\mathcal{A}$ · E₀(ω). Both induced dipoles occur in addition to those dipoles which originate from the permanent charge distribution which may change in space either by molecular rotation leading to $M_D^0\left(t\right)$ or translation of charged species leading to M_J(t). Classical molecular dynamics simulation exclusively consider $M_D^0\left(t\right)$ and M_J(t) ignoring $M_D^{ind}\left(t\right)$.^{5,14,51,52,56–58} This study, however, realizes the induced collective dipole moment $M_D^{ind}\left(t\right)$ by explicitly including polarization forces in the force field [details are given below]. In order to simplify the following expressions, we combine the rotational $M_D^0\left(t\right)$ and the induced $M_D^{ind}\left(t\right)$ to the non-translational collective dipole moment $M_D\left(t\right)=M_D^0\left(t\right)+M_D^{ind}\left(t\right)$.

So far, we have concentrated on the collective dipole moments inferred from Linear Response theory. The link of these quantities to experimental data is provided by the constitutive relation

$$P\left(\omega \right)=\left\{{\displaystyle \sum \left(\omega \right)+\left({ϵ}_{\infty }-1\right)}\right\}\frac{E\left(\omega \right)}{4\pi }$$ (5)

relating the macroscopic polarization to the internal local field E(ω) and not to the external field E₀(ω). Only in case of conducting boundary conditions, e.g. perfect Ewald summation, these two fields are equal.^59,60 Under this condition Eq. (2) and (5) result in

$${\displaystyle \sum \left(\omega \right)}=\frac{4\pi }{3V{k}_{B}T}{\displaystyle \underset{0}{\overset{\infty }{\int }}-\frac{d}{dt}\langle M_{tot}\left(0\right)\cdot M_{tot}\left(t\right)\rangle e^{i\omega t}dt}$$ (6)

$$\left({ϵ}_{\infty }-1\right)=\frac{4\pi }{3V}\text{tr}\langle \mathcal{A}\rangle .$$ (7)

The quantity in Eq. (6) is called generalized dielectric constant (GDC) and may be decomposed into the dielectric permittivity ϵ(ω), and the dielectric conductivity ϑ(ω).^52,55,61

$${\displaystyle \sum \left(\omega \right)=\left(ϵ\left(\omega \right)-{ϵ}_{\infty }\right)+\vartheta }\left(\omega \right)$$ (8)

This relation refers to the full frequency range. In this work, however, we focus on the static values of the GDC. The zero-frequency value of the dielectric conductivity ϑ(0) is determined by the collective translational dipole moment M_J(t):

$$\vartheta (0)=\underset{\omega \to 0}{\lim }\vartheta (\omega )=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_J^2\rangle +\langle M_D\cdot M_J\rangle \right)$$ (9)

$\langle M_J^2\rangle$ can be evaluated from the axis intercept of the mean squared displacement of M_J(t)

$$\underset{t\to \infty }{\lim }\langle |M_J(0)-M_J(t){|}^2\rangle =6V{k}_{B}T\sigma (0)t+2\langle M_J^2\rangle .$$ (10)

The slope of $\langle |M_J(0)-M_J(t){|}^2\rangle$ yields the static conductivity σ(0).

The static limit of the dielectric permittivity ϵ(0) can be analogously to Eq. (9) written as

$$ϵ(0)-{ϵ}_{\infty }=\underset{\omega \to 0}{\lim }ϵ(\omega )-{ϵ}_{\infty }=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle +\langle M_D\cdot M_J\rangle \right)$$ (11)

Since the cross-contribution $\langle M_D\cdot M_J\rangle$ is normally quite small, we will neglect it in this present work. $\langle M_D^2\rangle$ can be directly computed from the trajectory of the molecular dynamics simulation. However, in case of insufficient sampling the average of the collective rotational dipole moment is non-zero, i.e. $\langle M_D\ne 0\rangle$. Taking this into account, the static dielectric permittivity is

$$ϵ\left(0\right)-{ϵ}_{\infty }=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle -{\langle M_D\rangle }^2\right)$$ (12)

Altogether, the static GDC Σ(0) reads

$${\displaystyle \sum \left(0\right)=\frac{4\pi }{3V{k}_{B}T}\langle M_{tot}^2\rangle .}$$ (13)

As experiments measure the total static GDC ϵ_stat, one has to increase Σ(0) by ϵ_∞. All dielectric properties are in units of 4πϵ₀ with ϵ₀ being the vacuum permittivity.

B. Atomic dipoles and atomic polarizabilities

In molecular dynamics simulations $M_D^{ind}\left(t\right)$ has to be realized by appropriate terms in the force field. In principle, there exists three methods to describe the reorganization of the charge distribution: First, the fluctuating charge model changes the atomic charges q_iβ(t) of the atoms β of molecule i according to the local environment.²⁸ Second, induced point dipole method augments the set of permanent charges q_iβ by atomic dipoles ${\mu }_{i\beta }^{ind}$.^31,32 These dipoles are parallel to the local field acting on atom iβ:

$${\mu }_{i\beta }^{ind}={\alpha }_{i\beta }.E_{i\beta }$$ (14)

The strength of the induced dipole moment depends on the atomic polarizability α_iβ which is specific for each atom type. Third, the Drude oscillator model emulates ${\mu }_{i\beta }^{ind}$ with an additional Drude pair. The first Drude particle has a charge of -q^δ and is located at the atom iβ. The second mobile Drude particle has the opposite charge q^δ and is attached to the first Drude particle by a harmonic spring with a force constant $k_{i\beta }^{\delta }$ of

$$k_{i\beta }^{\delta }=\frac{1}{4\pi {ϵ}_0}\cdot \frac{{\left(q^{\delta }\right)}^2}{2{\alpha }_{i\beta }}.$$ (15)

Thus, the induced, atomic dipoles ${\mu }_{i\beta }^{ind}$ points from the central atom to the mobile Drude particle. Please note that in our case q^δ is a global property, i.e. all Drude particles have the same charge and are therefore independent of the atom iβ to which the Drude pair is attached. Thus, the force constants $k_{i\beta }^{\delta }$ is only a function of the atomic polarizability α_iβ. A high polarizability α_iβ corresponds to a low force constants $k_{i\beta }^{\delta }$ and results in larger displacement d_iβ of the Drude pair and larger induced dipoles ${\mu }_{i\beta }^{ind}$

$$\begin{array}{lll}{\mu }_{i\beta }^{ind}\hfill & =\hfill & q^{\delta }\left(r_{i\beta }+d_{i\beta }\right)-q^{\delta }{r}_{i\beta }\hfill \\ \hfill & =\hfill & q^{\delta }{d}_{i\beta }\hfill \end{array}$$ (16)

Usually, one tries to keep d_iβ as small as possible by increasing q^δ. The last equation may, therefore, be seen as a test for a proper choice of the Drude charge. Changing the Drude charge should result in very similar induced dipole ${\mu }_{i\beta }^{ind}$. One goal of this work is to show the lower limit of q^δ.

The major advantage of the Drude oscillator model is that the Drude particles can be handled more or less like normal atoms. Instead of intramolecular potentials describing bond vibrations, angle bending and torsions, Drude pairs possess only a harmonic bond potential U^self

$$U^{self}={\displaystyle \sum _{i\beta }\frac{1}{2}{k}_{i\beta }^{\delta }{\left(d_{i\beta }\right)}^2}$$ (17)

For the total electrostatic potential two types arises from the interaction of the Drude pairs.

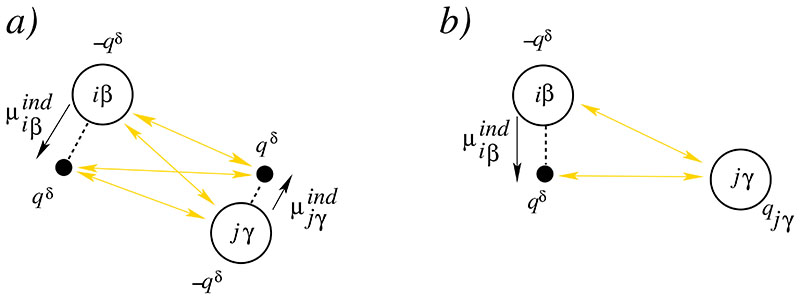
The first concerns the interaction between Drude charges q^δ depicted in Fig. 1a:

$$\begin{array}{ccc}{U}^{\delta \delta }& =& \frac{1}{4\pi {ϵ}_0}{\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma \ne i\beta }(\frac{q^{\delta }\cdot q^{\delta }}{\left|\left(r_{i\beta }-r_{j\gamma }\right)+\left(d_{i\beta }-d_{j\gamma }\right)\right|}}}\\ & & -\frac{q^{\delta }\cdot q^{\delta }}{\left|\left(r_{i\beta }-r_{j\gamma }\right)+d_{i\beta }\right|}-\frac{q^{\delta }\cdot q^{\delta }}{\left|\left(r_{i\beta }-r_{j\gamma }\right)-d_{j\gamma }\right|}+\frac{q^{\delta }\cdot q^{\delta }}{\left|r_{i\beta }-r_{j\gamma }\right|})\end{array}$$ (18)

Fig. 1.

a) Interaction between two Drude pairs iβ and jγ. The mobile Drude particles [carrying the charge q^δ] are represented by black filled circles whereas the Drude particle located at the corresponding atom are shown as open circles. The induced dipoles ${\mu }_{i\beta }^{ind}$ and ${\mu }_{j\gamma }^{ind}$ point from the central Drude particle to the mobile Drude particle. b) Interaction between a Drude pair iβ and a permanent charge of an atom jγ.

Since $\left|d_{i\beta }-d_{j\gamma }\right|$ is very small compared to the distance $r=\left|r_{i\beta }-r_{j\gamma }\right|$, the last equation may be expanded in a Taylor series in (d_iβ – d_jγ). Fortunately, many terms from the four summands in Eq. (18) cancel each other, so that after some simplification, e.g. using Eq. (16),

the interaction of Drude charges may be approximated by

$$U^{\delta \delta }=-\frac{1}{4\pi {ϵ}_0}{\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma \ne i\beta }{\mu }_{i\beta }^{ind}\overleftrightarrow{T}\left(r_{i\beta }-r_{j\gamma }\right){\mu }_{j\gamma }^{ind}+\dots }}$$ (19)

with the dipole-dipole tensor $\overleftrightarrow{T}\left(r_{i\beta }-r_{j\gamma }\right)=\nabla \nabla r^{-1}$. Eq. (19) shows that the interaction between two Drude pairs mainly corresponds to the interaction of two induced Drude dipoles located at atomic positions.

The second contribution of Drude pairs to the overall electrostatic potential is their interaction with the permanent charges q_jγ shown in Fig. 1b

$$U^{\delta q}=-\frac{1}{4\pi {ϵ}_0}{\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma }\frac{q^{\delta }\cdot q_{j\gamma }}{\left|\left(r_{i\beta }-r_{j\gamma }\right)+d_{i\beta }\right|}}}+\frac{-q\cdot q_{j\gamma }}{\left|r_{i\beta }-r_{j\gamma }\right|}$$ (20)

Expanding the last equation in a Taylor series yields

$$U^{\delta q}=-\frac{1}{4\pi {ϵ}_0}{\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma }{q}_{j\gamma }\left(\nabla r^{-1}\right){\mu }_{j\gamma }^{ind}+\dots }}$$ (21)

and shows that the permanent charges interact with the induced dipole moment made up by the Drude pair.

The Drude oscillators can be applied in the simulation in two different ways: First, it can be implemented with the self-consistent field condition corresponding to the Born-Oppenheimer scheme of quantum mechanics. The forces acting on the atoms iβ must be computed after the Drude particles have relaxed to minimize the total potential energy.^45,62,63

Nonetheless, the self-consistent field procedure is computationally expensive, because the energy has to be converged at a minimum. Otherwise, systematic drag forces on physical atoms considerably affect energy conservation and the stability of the temperature. A simple alternative to the self-consistent field method is to consider Drude dipoles as additional dynamical degrees of freedom extending the Lagrangian of the system in analogy to the Car-Parinello method of quantum mechanics.^27,39,50 The mobile Drude particles are attributed a small mass m^δ taken from the masses of the corresponding atoms iβ.^39,50 Both, the atom and the mobile Drude particle are integrated by equations of motion:

$$\left(m_{i\beta }-m^{\delta }\right){\ddot{r}}_{i\beta }=-{\nabla }_{r_{i\beta }}U$$ (22)

$$m^{\delta }{\ddot{r}}_{i\beta }=-{\nabla }_{r_{{}_{i\beta }}^{\delta }}U$$ (23)

with $r_{i\beta }^{\delta }=r_{i\beta }+d_{i\beta }$. The total potential energy U of the system includes intramolecular potentials, e.g. bonds, angles and dihedrals, Lennard-Jones and Coulomb interactions as well as U^self, U^δδ and U^δq. The motion of Drude particles is expected to be decoupled from the atomic motion if m^δ is sufficiently small,³⁸ in particular, much smaller than that of the hydrogen atoms. Thus, the electrostatics of the permanent charges and that of the induced dipoles should be separated in their dynamic behaviour. However, an obvious drawback of small m^δ is a small integration time step.⁴⁶ In order to ensure that the mobile Drude particles do not accumulate kinetic energy, they are coupled to an additional thermostat at very low temperature.^38,46

C. From the atomic to the collective level

So far, we described how to the embed the computation of the induced atomic dipoles ${\mu }_{i\beta }^{ind}$ into the force field on the basis of atomic polarizabilities α_iβ using the Drude charge pairs. The simulation is intrinsically performed within the framework of point charge electrostatics, i.e. the mobile Drude particle are recognized as additional point charges. For the analysis, however, we switch to a description in terms of dipoles:

$${\mu }_{i\beta }={\mu }_{i\beta }^0+{\alpha }_{i\beta }{\displaystyle \sum _{j\gamma }{\overleftrightarrow{T}}^{EW}}\left(r_{i\beta }-r_{j\gamma }\right){\mu }_{j\gamma }$$ (24)

$$={\mu }_{i\beta }^0+{\mu }_{i\beta }^{ind}$$ (25)

with ${\mu }_{i\beta }^0$ being the non-induced “atomic” dipole originating from the permanent charge distribution. Summing Eq. (25) over all atoms iβ yields the collective non-translational dipole moment

$$M_D={\displaystyle \sum _{i\beta }{\mu }_{i\beta }}={\displaystyle \sum _{i\beta }{\mu }_{i\beta }^0}+{\displaystyle \sum _{i\beta }{\mu }_{i\beta }^{ind}}$$ (26)

$$=M_D^0+M_D^{ind}$$ (27)

which determines the dielectric permittivity ϵ(ω).

The interpretation of dielectric experiments, however, also requires the macroscopic polarizability $\mathcal{A}$ of the whole sample. The link between the macroscopic and the atomic level of the polarizability is given by

$$\begin{array}{lll}{\mathcal{A}}_{xy}\hfill & =\hfill & {\displaystyle \sum _{i\beta }{\alpha }_{i\beta }{\displaystyle \sum _{j\gamma }{\delta }_{i\beta ,j\gamma }{\delta }_{xy}}}\hfill \\ \hfill & +\hfill & {\displaystyle \sum _{i\beta }{\alpha }_{i\beta }^2{\displaystyle \sum _{j\gamma }{\overleftrightarrow{T}}_{xy}^{EW}\left(r_{i\beta }-r_{j\gamma }\right)}}\hfill \\ \hfill & +\hfill & {\displaystyle \sum _{i\beta }{\alpha }_{i\beta }^3{\displaystyle \sum _z{\displaystyle \sum _{j\gamma }{\overleftrightarrow{T}}_{xy}^{EW}\left(r_{i\beta }-r_{j\gamma }\right){\displaystyle \sum _{k\lambda }{\overleftrightarrow{T}}_{zy}^{EW}\left(r_{j\gamma }-r_{k\lambda }\right)}}}}\hfill \end{array}$$ (28)

with {x, y, z} being the component in one dimension of the respective Ewald tensors.⁵³

${\overleftrightarrow{T}}^{EW}$ is not the double gradient of the bare Coulomb-potential ∇∇r⁻¹ but of the Ewald-potential

$${\overleftrightarrow{T}}^{EW}(r)=\nabla \nabla \left\{\frac{\text{erfc}(\kappa r)}{r}+{\displaystyle \sum _k\frac{4\pi }{k^2}{e}^{-k^2/4{\kappa }^2}{e}^{ikr}}\right\}$$ (29)

Under toroidal boundary conditions the averaging of the Ewald-tensor over all pairs of atoms iβ and jγ is equivalent to an integral of the simulation volume V

$$\langle {\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma }{\overleftrightarrow{T}}^{EW}\left(r_{i\beta }-r_{j\gamma }\right)}}\rangle =\frac{N\left(N-1\right)}{V}{\displaystyle \underset{V}{\int }{\overleftrightarrow{T}}^{EW}\left(\text{r}\right)dr}$$ (30)

$$=\frac{4\pi N\left(N-1\right)}{3V}I$$ (31)

with the unity matrix I and N equals the number of inducible dipoles. The last equation is only valid for perfect Ewald conditions and an isotropic sample volume.

For the computation of the electronic contribution ϵ_∞ we need the trace of the average of the macroscopic polarizability tensor $\mathcal{A}$.

$${ϵ}_{\infty }-1=\frac{4\pi }{3V}\text{tr}\langle \mathcal{A}\rangle$$ (32)

$$=\frac{4\pi }{V}{\displaystyle \sum _{i\beta }{\alpha }_{i\beta }+\frac{4\pi }{3V}{\alpha }^2\text{tr}\left(\frac{4\pi N\left(N-1\right)}{3V}I\right)}+\mathcal{O}\left({\alpha }^3\right)$$ (33)

with the average atomic polarizability $\alpha =1/N{\displaystyle {\sum }_{i\beta }{\alpha }_{i\beta }}$. As the second term in Eq. (28) is of second order in the atomic polarizability α_iβ we are using the approximation of a uniform ${\alpha }_{i\beta }^2={\alpha }^2$ such that the double sum over the Ewald tensor can be replaced by Eq. (31). From Eq. (33) a Clausius-Mossotti type equation⁶⁴ can be derived

$$\frac{{ϵ}_{\infty }-1}{{ϵ}_{\infty }+2}=\frac{4\pi }{3V}{\displaystyle \sum _{i\beta }{\alpha }_{i\beta }+\mathcal{O}\left({\alpha }^3\right)}$$ (34)

being accurate up to an order of $\mathcal{O}\left({\alpha }^3\right)$.

D. Computational setup

The force field parameters of EMIM⁺ stems from Ref. 65 and 66 with Lennard-Jones parameter from the AMBER force field.⁶⁷ The classical partial charges q_iβ, are changed to the values reported in Ref. 68 as done previously in our works.^14,61,69 The anionic force field parameters are taken from Ref. 70 without any further modification. All these parameters were left unchanged in case of the “Drude” simulations in order to compare both types of simulation. All carbon-hydrogen bonds are kept fixed by the SHAKE algorithm,⁷¹ whereas all other bonds, bond angles and torsions are left flexible.

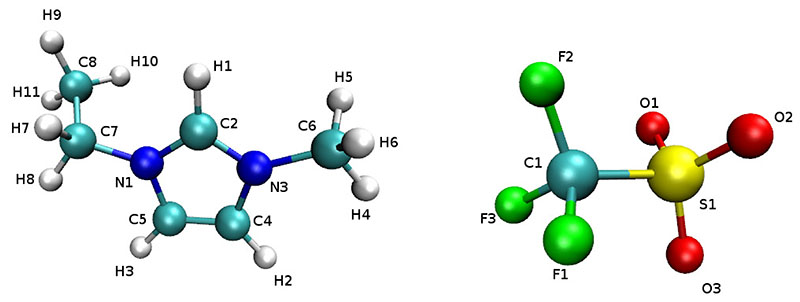
The polarization of the atoms was mimicked by the so-called “Drude oscillator” model which has been implemented in the molecular dynamics program package CHARMM since 2007.⁴⁴ The polarizability a of each atom type can be defined in the topology file. Our α’s are taken from Ref. 72 and are tabulated in Table I. The nomenclature of the atoms is illustrated in Fig. 2. The mobile Drude particles have a mass of 0.1 amu which is subtracted of the mass of the corresponding “polarizable” atom.^39,50 The total mass of the molecules is constant regardless of the polarization. In CHARMM it is also possible to mix polarizable and nonpolarizable atoms within a molecule. In this work only non-hydrogen atoms were made polarizable although the small Drude mass would allow for polarizable hydrogens, too. In practice, however, this led to instable system in some cases. This may be explained by the exposure of the hydrogen dipoles on the surface of the cations making them more sensitive to environmental effects.

Table I. Polarizability α_i of atom type i according to Ref. 72. The hydrogens were made nonpolarizable.

			$\langle \left|{\mu }_{i\beta }^{ind}\right|\rangle /D$
atom	αi / Å3	qδ=-0.5 e	-1.0 e	-2.0 e	-4.0 e
H
C6	1.28860	0.171	0.162	0.163	0.164
N1	0.97157	0.147	0.136	0.121	0.120
C2	1.28860	0.242	0.236	0.221	0.222
N3	0.97157	0.143	0.125	0.110	0.110
C4	1.28860	0.182	0.164	0.149	0.147
C5	1.28860	0.181	0.167	0.153	0.151
C7	1.28860	0.175	0.163	0.158	0.156
C8	1.28860	0.292	0.271	0.267	0.265
C1	1.28860	0.267	0.311	0.342	0.359
F1	0.44475	0.269	0.278	0.286	0.291
F2	0.44475	0.269	0.278	0.287	0.291
F3	0.44475	0.269	0.279	0.286	0.291
S1	2.47445	0.222	0.203	0.207	0.209
01	0.85197	0.212	0.215	0.220	0.220
02	0.85197	0.212	0.216	0.219	0.220
03	0.85197	0.212	0.215	0.220	0.221

Fig. 2.

Nomenclature of EMIM⁺CF₃SO₃^– in the present force field. Drude pairs were attached to all non-hydrogens.

The Drude charge q^δ of each atom is defined indirectly by specifying the force constant $k_{i\beta }^{\delta }$ of the Drude oscillator pair iβ in the parameter file of CHARMM. These force constants are typically in the range of several hundreds kcal/mole Å^-2 depending on the grade of polarization and the desired q^δ. In order to test the influence of q^δ on the properties under investigation, completely independent simulations of 1000 EMIM⁺CF₃SO₃^– with q^δ = –0.5e, -1.0e, -2.0e and -4.0e were performed. These Drude charges are in the range typically used by Roux et al.^38,40,49 but lower than those of van Gunsteren et al.⁴¹ Even with the lowest q^δ = –0.5e and the highest polarization α_S=2.47445 ų the maximal displacement of the Drude particle was less than 0.095 Å.

The electrostatic forces of both, Drude particles and the attached atoms, are treated by the PME technique.^34,35 The “cutoff” for the real-space part interactions is r^EW =12 Å and the damping constant for the reciprocal-space interactions is κ =0.410 Å⁻¹. The grid spacing equals 1.05 Å and a sixth-order interpolation of the charge to the grid is used. The interactions between permanent charges q_iβ and Drude pairs are excluded between atoms which share a bond or an angle.⁴⁰ The interaction between the corresponding Drude pairs are screened by a Thole function according to Ref. 40. All non-Drude particles were thermostatted at T = 300 K by a Nosé-Hoover thermostat with a relaxation time of ${\mathcal{T}}_{therm}=0.1\text{ps}$. The Drude particles were thermostatted at 1 K with a ${\mathcal{T}}_{therm}=5\text{fs}$.³⁸ Nonbonded and image lists were updated heuristically using a 16 Å neighbour list distance. Lennard-Jones energies and forces were smoothly switched off between 11 and 12 Å.

The impact of the polarizability α was studied by simulating 1000 EMIM⁺CF₃SO₃^– with 0 to 100% of the α’s in Table I in steps of 10%. Since the trajectories with 10% and 20% of the α’s were unstable, the corresponding results are omitted in the further discussion. Each trajectory was computed separately for more than 20 ns with CHARMM⁴⁴ under constant volume [V = (67.195 Å)³] with a time step of Δt =0.5 fs. In case of a Drude charge q^δ of – 2.0e and –4.0e the time step Δt has to be reduced to 0.1 fs since the strong electrostatic forces destabilized the Verlet integration. The inclusion of polarizability prolongates the computational simulation period by a factor of three to five in case of Δt =0.5 fs compared to a nonpolarized system. In case of Δt =0.1 fs this factor is increased, of course, by an additional factor of five.

III. Results And Discussion

All simulations were performed in full atomistic detail at the level of point charges comprising permanent and Drude particles as described in Section II B. The final link to dielectric experiments is based on the computation of collective dipole moments, i.e. the whole sample. The following interpretation of the simulations, however, is given at the molecular level although the force field lacks any molecular potentials. This is an attribute to the traditional way of analysing the structure and dynamics of liquids. For example, the electrostatic interactions are always computed between point charges, i.e. permanent q_iβ and Drude charges q^δ, but interpreted in terms of a truncated multipole expansion involving molecular charges q_i and dipoles μ_i.

Concerning the interpretation of the Drude method our simulations of molecular ionic liquids have to be seen under two aspects: On the one hand, there is the methodical aspect concerning the variation of the strength of the Drude charges. On the other hand, the effect of an increasing polarizability on the structure and dynamics of molecular ionic liquids is analysed. Prior to these two principal aspects we will check our simulated trajectories for their proximity to self-consistency.

A. Proximity to self-consistency

As stated in the Theory section the Drude method may be applied in two different ways: The simulation of the trajectory can be conducted self-consistently, i.e. the position of the Drude particles is optimized by energy minimization at every time step. Due to the strong electrostatic forces in ionic liquids this optimization is very expensive and may extend up to hundred iteration steps. Alternatively, the positions of the mobile Drude particles may be included as additional degrees of freedom in an extended Lagrangian of the system. Consequently, they follow from time evolution of the system as the solution of a appropriate equations of motion. In our simulations the Drude mass m^δ was set to very small value of 0.1 amu. As can be seen from Eq. (23) the smaller m^δ the closer is the gradient of potential energy to zero, i.e. to self-consistency. Equivalently, a small Drude mass enables a quick response of the Drude system to changes in the electric field. The analogue to energy minimization is a Drude thermostat of typically 1 K and a response time of ${\mathcal{T}}_{therm}=5\text{fs}$. As a result, the Drude system is systematically annealed and thus kept in proximity to self-consistency.

In order to quantify this proximity we have analysed our trajectories is the following way: For selected frames of the polarizable system the potential energy was minimized by Newton-Raphson method. Since the atomic positions where the permanent charges are located were kept fixed, the position of the Drude charges was optimized exclusively. As a result of this minimization we observed for q^δ =-0.5 e that the binding energy ofthe Drude pairs decrease by less than 3% of the total Drude binding energy. This decrease is accompanied by an increase of the electrostatic energy of the system by more or less the same amount. Due to this compensation the change in the total potential energy is less than 0.1% for all strengths of the Drude charges q^δ. Increasing q^δ further reduces the shift in Drude binding, electrostatic and total potential energy. This is a clear evidence of the close proximity of our simulations to self-consistency.

In fact, a recalculation of the distribution of the induced atomic dipoles for the optimized structures and the original structures shows an almost perfect coincidence (data not shown). Only in case of the imidazolium atom N1, the distribution is a little bit sharpened.

B. The influence of the Drude charge

The Drude charges were varied from -0.5 e up to -4.0 e with 100% of the polarizabilities of Table I. According to Eq. (15) this variation corresponds to a change of the Drude force constant $k_{i\beta }^{\delta }$ by a factor of 64 and reminds one to be very careful with the choice of the simulation time step Δt. One could compensate the necessary reduction of the time step by an enhancement of the Drude mass m^δ. But this would lead to a stronger coupling between the Drude dipoles and the electrostatics of the permanent charges of the atoms. Therefore, we kept the Drude mass at the small value of 0.1 amu and rather used very small time steps as well. Ideally, there should be a range of Drude charges for which the the strength of the induced dipoles $\left|{\mu }_{i\beta }^{ind}\right|$ is constant according to Eq. (16). Table I shows the averaged strength of atomic Drude dipoles for each atom type as a function of the four Drude charges under investigation. One sees that the lowest value q^δ of -0.5 e is somewhat problematic while the other values of $\left|{\mu }_{i\beta }^{ind}\right|$ are almost constant.

Another point to mention is that the strongest induced dipoles of the cations are found for the C2 of the imidazolium ring and the terminal carbon C8 of the ethyl chain. By the way, this effect is visible for all Drude charges. As we have used identical polarizabilities α_iβ for all carbons, this effect must be due to the local environment of the respective atoms. This offers a natural explanation of the often discussed “acidity” of the hydrogen attached to C2. In case of C8 the induced effect is of comparable size but has to be shared with three hydrogens [H9, H10 and H11] instead of one [H1].

1. Molecular dipoles

Dielectric experiments measure macroscopic properties and are therefore connected with collective dipole moments, e.g. M_tot, M_J and M_D. Computational force field works permanent atomic charges q_iβ and induced, atomic dipoles ${\mu }_{i\beta }^{ind}$. Chemical interpretation, however, operates at the molecular level which is intermediate between macroscopic and the atomic level. It is intuitively appealing, but has no implications for the computation of the primary data along the trajectory. Rather, it is a practical tool for interpretation.

It can be easily shown that the sum of all induced, atomic dipoles ${\mu }_{i\beta }^{ind}$ within a molecule i is the molecular induced dipole moment ${\mu }_i^{ind}$

$${\mu }_i^{ind}={\displaystyle \sum _{\beta }{\mu }_{i\beta }^{ind}}={\displaystyle \sum _{\beta }{q}^{\delta }{d}_{i\beta }}$$ (35)

which does not change if it is calculated with respect to the center of mass of the molecule i due to the charge neutrality of the Drude pair. Consequently, the overall molecular dipole moment μ_i equals the sum of the classical dipole moment ${\mu }_i^0$ with respect to the center of mass $r_i^{cm}$ and the induced dipole moment ${\mu }_i^{ind}$.^51,56

$${\mu }_i={\mu }_i^0+{\mu }_i^{ind}$$ (36)

$$={\displaystyle \sum _{\beta }{q}_{i\beta }\left(r_{i\beta }-r_i^{cm}\right)+{\mu }_i^{ind}}$$ (37)

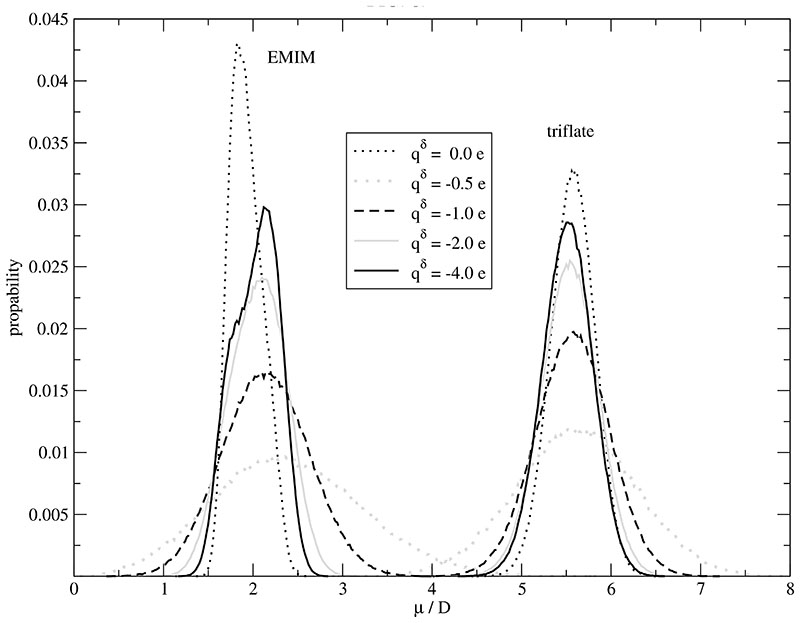
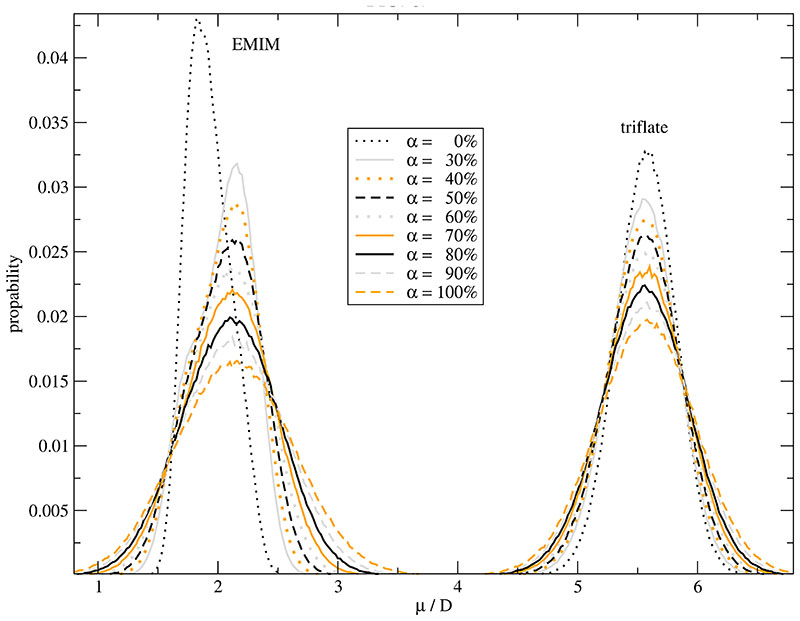
The distribution of the total molecular dipole |μ_i| of the cations and the anions is displayed in Fig. 3. The spread of the distribution is smallest for the non-polarized system. Quite generally, inclusion of the polarizability considerably changes the distribution of |μ_i| with respect to height and position. With decreasing Drude charge q^δ the spread of |μ_i| increases for both, cations and anions. The Full Width at Half Maximum between the non-polarizable system and that with a Drude charge of q^δ =-1.0 e differs by a factor of 2.4 and 1.5 for the cations and anions, respectively. This goes along with the higher anisotropy and charge delocalization of the cations. The stronger influence on the cation is also observed for the shift in position. A remarkable shift to higher values is found for the cations whereas a marginal reduction is visible for the anions. This is surprising since the absolute values of the induced, atomic dipoles in EMIM⁺ are smaller than those in CF₃SO₃^–. As the number of polarizable atoms is equal there has to be a considerable compensation in case of the anion. In other words, the induced dipoles of the cation are correlated in same way.

Fig. 3.

Distribution of the molecular dipole μ of the cations and anions as a function of the Drude charge q^δ. In these simulations the polarizability is 100% of the values given in Table I.

2. Charge ordering

Having discussed the influence of the Drude charges on the intramolecular level, we now turn to the intermolecular spatial correlation. Instead of analysing the individual radial distribution functions $g_{++}^{000}\left(r\right),g_{--}^{000}\left(r\right)$ and $g_{+-}^{000}\left(r\right)$ we present the charge ordering function

$$\Delta g^{000}\left(r\right)=g_{++}^{000}\left(r\right)+g_{--}^{000}\left(r\right)-2\cdot g_{+-}^{000}\left(r\right)$$ (38)

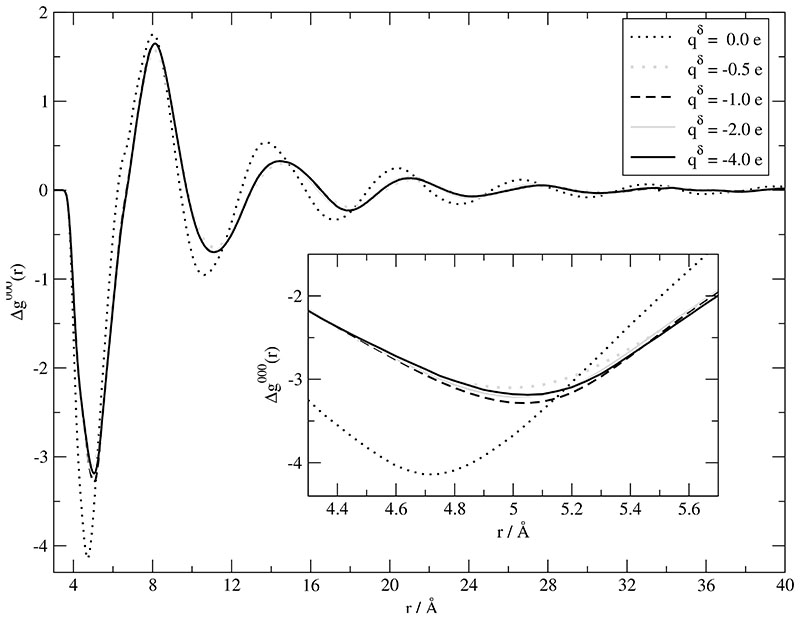
in Fig. 4. Negative values of Δg⁰⁰⁰(r) are indicative of preferred correlations between unlike ions whereas positive values correspond to enhanced correlations between like ions. The obvious first, negative peak located at 4.7 Å is reduced and shifted to 5.1 Å by the polarization forces. This phenomenon is observed for the following maxima and minima as well. Δg⁰⁰⁰(r) for the non-polarized and the polarized systems seem to run out of phase. Overall, the repulsion of like charges and the attraction of unlike charges is weakened by the polarization forces. The resulting damping of structural oscillations can be interpreted as a reduction of the correlation length of the charge ordering. The variation of the Drude charges q^δ does not affect the charge ordering function: Once there is a Drude dipole, its influence on the charge ordering is independent of the actually used Drude charge.

Fig. 4.

Charge order function $\Delta g^{000}\left(r\right)=g_{++}^{000}\left(r\right)+g_{--}^{000}\left(r\right)-2g_{+-}^{000}\left(r\right)$ as a function of the Drude charge q^δ. In these simulations the polarizability is 100% of the values given in Table I.

The dynamics of the systems with different Drude charges can be characterized by the translational diffusion coefficients and the rotational time constant. It turns out that in case of q^δ =-0.5 e the diffusion coefficients are D⁺ = 4.0 o 10⁻⁷cm²/s and D^– = 2.5 · 10⁻⁷cm²/s whereas in all other cases D⁺ and D^– are approximately 0.61 and 0.34.·^-7cm²/s. This shows once more that the exceptional behaviour of the lowest Drude charge under investigation. This exceptional behaviour is also found for the rotational relaxation times. For the static dielectric permittivity ϵ(0) and the static dielectric conductivity ϑ(0) given in Table II the same trend for the various Drude charges shows up again. Nevertheless, the static GDC ϵ_stat in case of q^δ ≠-0.5e yields a value of approximately 15.4 which seems independent from the actual strength of the Drude charge.

Table II.

Dielectric properties of EMIM⁺CF₃SO₃^– as a function of the grade of polarizability and Drude charge q^δ. The static GDC ϵ_stat can be measured by experiments. S is a hypothetical scale factor of the permanent charges q_iβ to reproduce the effective Coulomb energy.

α [%]	qδ [e]	ϵ (0) – ϵ∞	ϵ∞	ϑ(0)	ϵstat	S
0	0.0	7.73	1.00	4.19	12.92	1.00
30	1.0	7.99	1.23	4.75	13.97	0.92
40	1.0	9.07	1.32	3.79	14.18	0.90
50	1.0	8.81	1.41	3.86	14.08	0.88
60	1.0	8.23	1.50	4.23	13.96	0.85
70	1.0	8.73	1.60	5.03	15.36	0.82
80	1.0	9.61	1.71	5.16	16.48	0.79
90	1.0	9.59	1.82	4.61	16.02	0.77
100	0.5	10.90	1.94	6.76	19.60	0.75
100	1.0	8.57	1.94	4.97	15.48	0.74
100	2.0	8.06	1.94	5.47	15.47	0.72
100	4.0	9.59	1.94	3.69	15.22	0.71

3. Comparison to experiment

The computational values found in this work can be compared to experimental data. Experimentally, there exists two values for the static GDC: ϵ_stat ≃14 (see Ref. 73) and ϵ_stat ≃16 (Ref. 74). Our value for 100% polarizability for q^δ =-1.0 e,-2.0 e and -4.0 e is around 15.4. Furthermore, the agreement between the computational ϵ_∞ of 1.94 and the experimental value of 2.31 is very good.^73,74

A preliminary decomposition of our computed ϵ_stat is enabled by a comparison with the study of Taylor et al. . They found two dominating Debye processes with time constants of ${\mathcal{T}}_1=2.6\text{ps}$ and ${\mathcal{T}}_2=0.24\text{ps}$. The latter one can be easily addressed to the regime of the dielectric conductivity ϑ(ω). Therefore, the experimental value of ϵ₂ =3.89 should be part of ϑ(0) in the corresponding computer simulation. Our computational value of ϑ(0) =4.97 is higher, but may contain parts of the experimental ϵ₁ because the time constant ${\mathcal{T}}_1$ of 2.6 ps is still in the range of the time constants of processes contributing to the dielectric conductivity.⁶⁹ The experimental GDC contribution ϵ₁ =8.03 characterized by ${\mathcal{T}}_1=2.6\text{ps}$ looks similar to our computational ϵ(0) –ϵ_∞> of 8.57 [see Table I], but this may be accidentally. On the one hand, ϵ₁ may be the sum of processes contributing to the dielectric permittivity and dielectric conductivity as mentioned above. On the other hand the experimental method is restricted to frequencies above 0.2 THz. Thus, not all collective rotational dynamics can be tracked in the cited work.⁷³ Unfortunately, time correlation functions of the collective non-translational dipole moment are not available for our polarized system at the moment but on the way. With this information a more detailed assignment of ϵ₁ and ϵ₂ will be possible.

C. The influence of the polarizability

The analysis of the previous section has shown that the Drude charge q^δ of -0.5 e is too small for an adequate representation of the induced dipoles. On the other hand, Drude charges of q^δ of -2.0 and -4.0 e would require a reduction of the simulation time step Δt to 0.1 fs, an order of magnitude smaller than that used for the nonpolarizable systems. Consequently, the choice q^δ =-1.0 e with the time step Δt =0.5 fs is the best compromise achievable. With this time step we have systematically varied the degree of polarizabilityfrom 0% to 100% in increments of 10%. Thus, various properties can be analysed as a function of the strength of polarizability.

1. Perturbation model and effective Coulomb energy

In order to get the first impression of the influence of polarizability on the Coulomb energy energy, we have performed an analysis based on a perturbation model. We have used snapshots of the trajectory of the nonpolarized system and added Drude pairs afterwards.

Initially, the positions of all Drude particle coincide with the corresponding atomic positions and the Coulomb interactions U^elec are exclusively between permanent charges

$$U^{elec}=U^{qq}$$ (39)

$$U^{qq}=\frac{1}{4\pi {ϵ}_0}{\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma }\frac{q_{i\beta }\cdot q_{j\gamma }}{\left|r_{i\beta }-r_{j\gamma }\right|}}}.$$ (40)

The final position of the mobile Drude particles is computed by energy minimization keeping all atomic positions fixed. For these optimized positions the total electrostatic energy $U_{eff}^{elec}$ changes to

$$U_{eff}^{elec}=U^{qq}+U^{\delta q}+U^{\delta \delta }$$ (41)

Of course, U^qq is the very same in both expressions since the atoms did not move.

Following traditional concepts $U_{eff}^{elec}$ may be reformulated in terms of effective, permanent charges $q_{i\beta }^{eff}$. The simplest way to introduce effective charges is a uniform scaling of the primary charges:

$$q_{i\beta }^{eff}=\mathcal{S}\cdot q_{i\beta }$$ (42)

Consequently, the effective Coulomb energy now reads

$$U_{eff}^{elec}\simeq \frac{1}{4\pi {ϵ}_0}{\displaystyle \sum _{i\beta }{\displaystyle \sum _{j\gamma }\frac{\left(\mathcal{S}\cdot q_{i\beta }\right)\cdot \left(\mathcal{S}\cdot q_{j\gamma }\right)}{\left|r_{i\beta }-r_{j\gamma }\right|}}}$$ (43)

Table II gives the scaling factor $\mathcal{S}$ as a function of the polarizability. For 100% polarizability a typical value of $\mathcal{S}$ = 0.74 is found which seems to correspond to those proposed in Ref. 20 and 75. A rescaling of the atomic charges inevitably reduces the net charge q_i of the molecular ions i by the factor $\mathcal{S}$. Furthermore, Kato et al. showed for water that the reduction of atomic charges may reduce U^qq to $U_{eff}^{qq}$, but further distance dependent scaling, e.g. with Thole-like screening function, has to be done to reproduce the local structure.⁷⁶ In this study we showed that polarizable force fields reproduce local structure effects, in particular subtle effects like the C2-acidity, without any further reparametrization, additional potentials or screening functions. Furthermore, the Coulomb energy is reduced to $U_{eff}^{elec}$ avoiding a rescaling of the net charge q_i of the molecular ions.

2. Molecular structural and dielectric properties

While we have used snapshots from a nonpolarizable system in the perturbation model above, we now turn to analysis of trajectories of intrinsically polarizable systems. As already indicated at the beginning of the result section, the interpretation at the molecular level are often done in terms of the net charge q_i and net dipole moment μ_i of molecules i. In terms of the electrostatic energy, this change in interpretation results in

$$4\pi {ϵ}_0{U}_{eff}^{elec}={\displaystyle \sum _i{\displaystyle \sum _j\frac{q_i\cdot q_j}{r_{ij}}}}+{\displaystyle \sum _i{\displaystyle \sum _j{q}_i}\nabla r_{ij}^{-1}{\mu }_j}-{\displaystyle \sum _i{\displaystyle \sum _j{\mu }_i\overleftrightarrow{T}\left(r_{ij}\right){\mu }_j+\dots }}$$ (44)

with the total molecular dipole moment μ_i defined in Eq. (37). Thereby, we have implicitly replaced the atomistic terms of U^δδ and U^δq in Eq. (19) and Eq. (21) by their molecular analogues. The last two terms of the last equation are responsible for the reduction of the electrostatic energy. They depend on both, the position of the molecular centers r_i and r_j as well as on the orientation of the molecules represented by their dipole moments μ_i and μ_j.

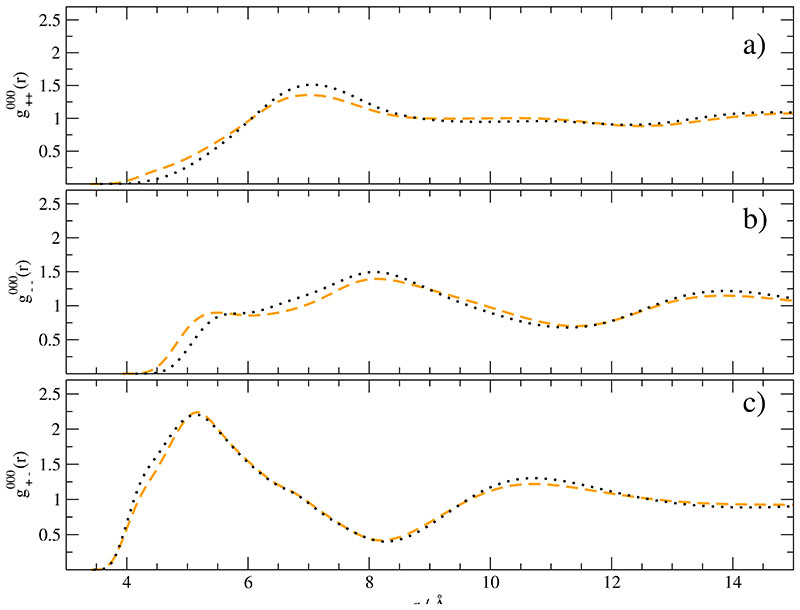
We discuss the dependence on r_i, i.e. the structure of molecular centers, first. Fig. 5 shows the radial distribution functions for EMIM⁺–EMIM⁺ [Fig. 5a], CF₃SO--CF₃SO-[Fig. 5b] and EMIM⁺-CF₃SO-[Fig. 5c] in case of a nonpolarized simulation [black dotted line] and with 100% polarizability [orange line]. In accordance with previous studies the radial distribution functions $g_{++}^{000}\left(r\right),g_{+-}^{000}\left(r\right)$ and $g_{--}^{000}\left(r\right)$ do not change significantly.^11,45,77,78

Fig. 5.

Radial distribution function with respect to a) EMIM⁺ and EMIM⁺, b) CF₃SO₃^– and CF₃SO₃^– as well as c) EMIM⁺ and CF₃SO₃^–. The black dotted line corresponds to the simulation of non-polarized ions whereas the orange dashed line stems from the simulation with 100% polarizability.

Only a slight shift to shorter distances is observed for like charge pairs. The polarizability seems to slightly damp the mutual repulsion. $g_{--}^{000}\left(r\right)$ is also insensitive. It peaks at the shortest distances and thus dominates the electrostatic interaction between molecular centers

$$\langle {\displaystyle \sum _i{\displaystyle \sum _j\frac{q_i\cdot q_j}{4\pi {ϵ}_0{r}_{ij}}}}\rangle =4\pi \rho q^2{\displaystyle \int \frac{\Delta g^{000}\left(r\right)}{r}}\cdot r^{2}dr$$ (45)

with the charge-ordering function Δg⁰⁰⁰(r) defined in Eq. (38). The last integral yields very similar values for the polarized and nonpolarized systems. Hence, this energy term is insensitive and justifies the application of perturbation theory mentioned above. This also refers the gradient $\nabla r_{ij}^{-1}$ and the dipole-dipole tensor $\overleftrightarrow{T}\left(r_{ij}\right)$ entering Eq. (43). As a consequence the change in electrostatic energy has to come from changes of the size and orientation of the molecular dipoles μ_i.

Analogously to Fig. 3 the distribution of the total molecular dipole moment μ_i of the cation and the anion as a function of polarizability is displayed in Fig. 6. The inclusion of polarizability shifts the cationic dipole moment to a higher value. The amount of this shift, however, seems to be independent of the strength of the polarizability which broadens the dipole’s distribution. The broadening is also visible for the anion. A shift, if visible at all, occurs to smaller values. In both cases, the broadening is a monotonously increasing function of the degree of polarizability.

Fig. 6.

Distribution of the molecular dipole μ of the cations and anions as a function of the amount of polarizability. In these simulations the Drude charge q^δ is -1.0 e.

As a caveat we note that an enhancement of the scalar value of the cationic dipoles does not automatically imply a dielectric increment, because it ignores collectivity, i.e. the orientational correlation of cationic dipole vectors. According to Eq. (12) thestaticdielectric permittivity is essentially determined by $\langle M_D^2\rangle /V$. In terms of molecular dipole moments this ratio reads

$$\frac{\langle {\text{M}}_D^2\rangle }{V}=\frac{1}{V}\left({\displaystyle \sum _{ij}\langle {\mu }_i^{+}\cdot {\mu }_j^{+}\rangle }+{\displaystyle \sum _{ij}\langle {\mu }_i^{-}\cdot {\mu }_j^{-}\rangle }+2{\displaystyle \sum _{ij}\langle {\mu }_i^{-}\cdot {\mu }_j^{-}\rangle }\right)$$ (46)

All the scalar products appearing in this expression do not only contain the strength of the molecular dipoles but also depends on the mutual orientation characterized by

$$g^{110}\left(r\right)=\frac{{\displaystyle \sum _j\cos \left({\mu }_i,{\mu }_j\right)}\delta \left(r-\left|r_{ij}\right|\right)}{4\pi r^{2}drN/V}.$$ (47)

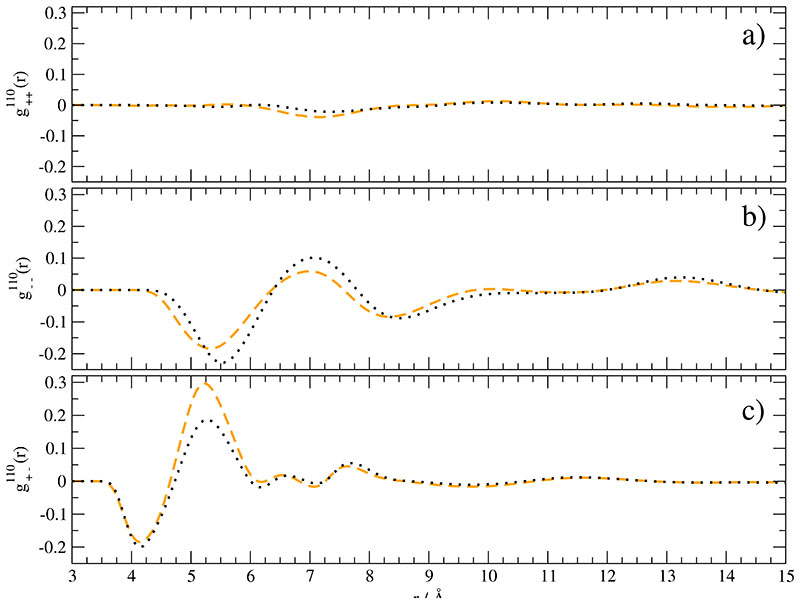
This differs from the traditional radial distribution function by the additional orientational co-factor cos(μ_i, μ_j) and thus measures the cosine between molecular dipoles on a radial scale r.⁷⁹ The summation in Eq. (46) corresponds to an integration ofEq. (47) over spherical shells. The corresponding $g_{++}^{000}\left(r\right),g_{+-}^{000}\left(r\right)$ and $g_{--}^{000}\left(r\right)$ are shown in Fig. 7a-c. Obviously, $g_{++}^{110}\left(r\right)$ in Fig. 7a shows no preferred orientational correlations between cations. Consequently, the first term on the right hand side of Eq. (46) can be neglected. Therefore, the shift in dipolar strength created by the polarization cannot play a dominant role for $\langle M_D^2\rangle /V$. The mutual orientation of the anions, however, is much stronger. A first negative peak of $g_{--}^{110}\left(r\right)$ in Fig. 7b located at 5.5 Å is followed by a positive peak at 7.0Å. Polarization synchronously reduces these two peaks. As a result the second term in Eq. (46) remains almost unchanged. Therefore, the slight increase of static dielectric permittivity ϵ(0) – ϵ_∞ in Fig. 8 and Table II has to be attributed to the third term in Eq. (46) representing the correlation between cations and anions. In fact, Fig. 7c shows an increased correlation at 5.3 Å. Moreover, this contribution is multiplied by a factor of two. In summary, this analysis shows that the behaviour of ϵ(0) – ϵ_∞ as a function of polarizability cannot be explained on the basis of a molecular dipole histogram as in Fig. 6 because neither the cationic nor the anionic self-contribution is responsible for the slight increase of ϵ(0) – ϵ_∞ [grey circles in Fig. 8]. In other words, the neglect of the cross-term between cations and anions, i.e. of the third term in Eq. (46), as done in the traditional Fröhlich formula Eq. (7.43) of Ref. 80 is not justified. Even more it plays the dominant role.

Fig. 7.

Mutual orientation between a) EMIM⁺ and EMIM⁺, b) CF₃SO₃^– and CF₃SO₃^– as well as c) EMIM⁺ and CF₃SO₃^–. The black dotted line corresponds to the simulation of non-polarized ions whereas the orange dashed line stems from the simulation with 100% polarizability.

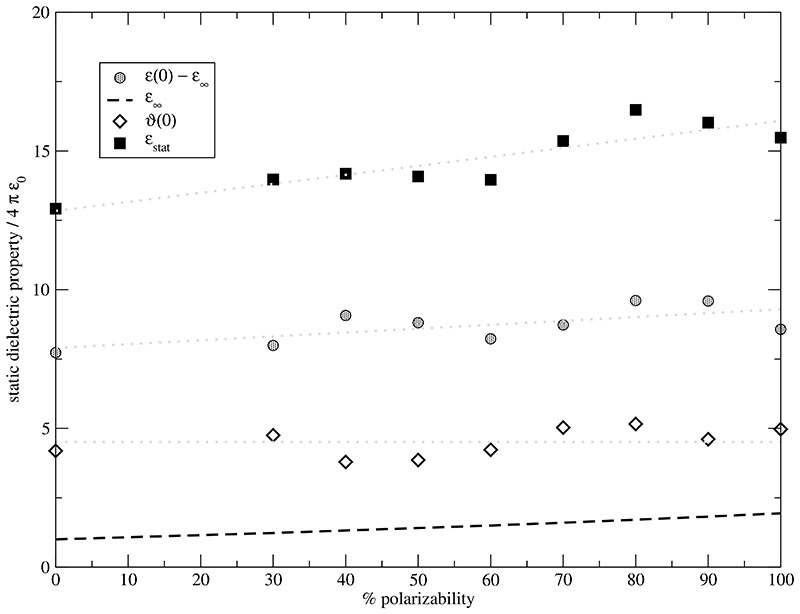
Fig. 8.

Static dielectric constant ϵ_stat [filled squares] as function of the polarizability α. It may be decomposed into the static dielectric permittivity ϵ(0) [grey circles], the static dielectric conductivity ϑ(0) [open diamonds] and the electronic contribution ϵ_∞ [black dashed line].

In addition to this implications for the static dielectric constant the comparative analysis of the three orientational correlation functions in Fig. 7 leads to a quite general result concerning correlation length scales in molecular ionic liquids. At very short distances up to approximately 4.5 Å the steric forces modelled by Lennard-Jones interactions dominate the structural behaviour. For example, they force molecular dipoles to align roughly anti parallel as indicated by the negative sign of g¹¹⁰(r) at these distances. Between 4.5 Å and circa 8.0 Å dipolar interactions play a significant role because the discrepancies between the orange line [100% polarizability] and the black dotted line [0% polarizability] is there strongest. The almost coincidence of the curves beyond 8 Å indicates the regime of the molecular charges q_i made up by the non-Drude charges because they are not affected by polarizability. In fact, long range oscillations of the radial distribution function g⁰⁰⁰(r) extend to over 20 Å.^5,22,81 These three regimes ofinteraction correlate with the r-dependence of the respective potentials: The Lennard-Jones potential falls off with r⁻⁶, dipole-dipole interaction with r⁻³ and charge-charge interaction with r⁻¹.

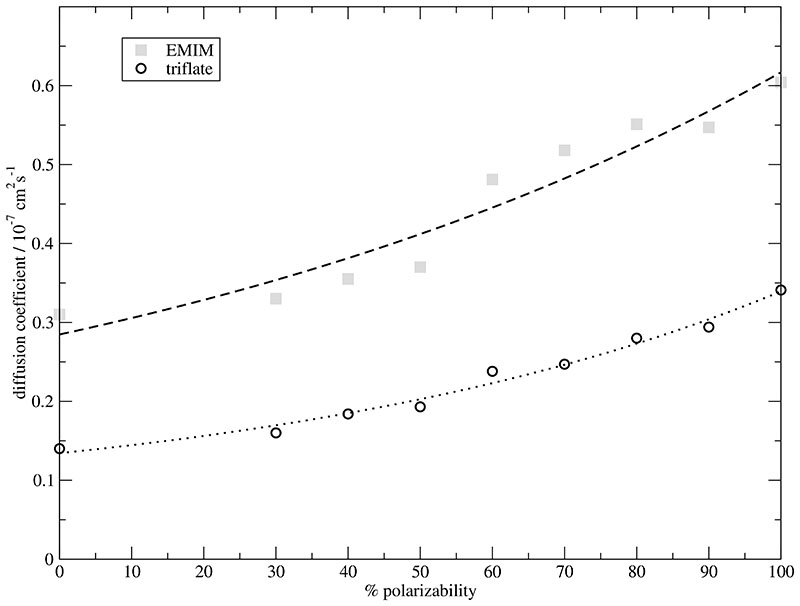
This slight increase caused by the enhanced cation-anion orientational correlation as a function of polarizability is accompanied by an increased electronic contribution ϵ_∞ [dashed line in Fig. 8]. The electronic contribution ϵ_∞ is related to the polarizability by Eq. (33) and Eq. (34). The last missing contribution to static GDC ϵ_stat is the static dielectric conductivity ϑ(0) [open diamonds in Fig. 8]. As opposed to all other contributions ϑ(0) is almost unaffected by changes in polarizability. This can also be only understood on a collective level since the diffusion coefficients of all ions increase with increasing polarizability as shown in Fig. 9. This situation is analogous to the molecular dipole distributions. Again, a collective property cannot be predicted from the behaviour of single molecules. Crosscorrelations between cations and anions can compensate an increase at the single molecular level.

Fig. 9.

Diffusion coefficients of the cations EMIM⁺ [grey squares] and anions CF₃SO₃^–[open circles] as function of the degree of polarizability.

3. Rotational and translational dynamics

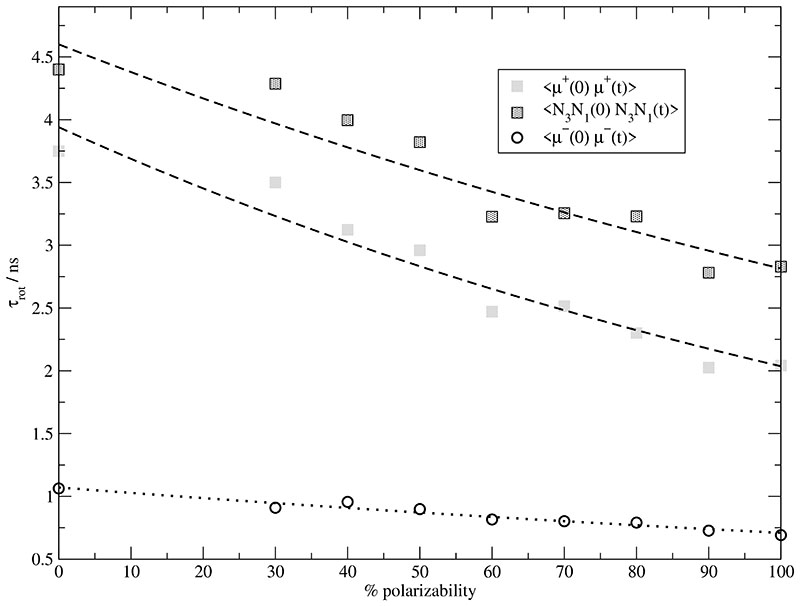
So far, we have discussed the impact of the induced dipoles on the energy and structure of the molecular ionic liquids. The rotation of the molecules can be characterized by the reorientation of their molecular dipoles, i.e. by the time correlation function $\langle \mu \left(0\right)\cdot \mu \left(t\right)\rangle$. Thereby, we have used the total molecular dipole moment [refer Eq. (36)] comprising the sum of the permanent ${\mu }_i^0$ and induced component ${\mu }_i^{ind}$. The mean rotational time constant ${\mathcal{T}}_{rot}$ for the cations [light grey squares] and the anions [open circles] are depicted in Fig. 10. In order to show that the time decay of $\langle \mu \left(0\right)\cdot \mu \left(t\right)\rangle$ is primarily caused by reorientation and not by fluctuations of the induced dipole’s magnitude we have also computed ${\mathcal{T}}_{rot}$ for the N3–N1 vector which points in a similar direction as the cationic dipole vector. As visible in Fig. 10 the relaxation of the vector N₃–N₁ follows that derived from $\langle {\mu }^{+}\left(0\right)\cdot {\mu }^{+}\left(t\right)\rangle$. With increasing polarizability ${\mathcal{T}}_{rot}^{+}$ decreases non linearly. This decrease is also found for the anionic rotational time constant ${\mathcal{T}}_{rot}^{-}$ but at a much faster level. Although the decrease seems to be smaller in Fig. 10 in case ofthe anion, the time constant ${\mathcal{T}}_{rot}^{-}$ is more than halfed from 0% to 100% polarizability.

Fig. 10.

Rotational time constants of the cations EMIM⁺ [grey squares] and anions CF₃SO₃^–[open circles] as function of the degree of polarizability. Additionally, the rotational time constant of the N₃-N₁-vector is shown.

This factor of two is also visible from the cationic and anionic diffusion coefficients in Fig. 9. Quite generally, the diffusion coefficients are rather low, but polarizability brings them closer to experimental data.^11,82 Interestingly, the cations are faster than the anions although their volume is twice that of the anions. Consequently, it cannot be a single molecule effect but has to do with the environment: the cations are surrounded by a cage of anions and vice versa. Within this cage the anion may rotate faster because of its smaller volume. Leaving the cage, however, is determined by the cage of its counterions. Obviously, the cage made up by the cations is stronger and thus releases the anions at a lower rate. This would explain the smaller anionic diffusion coefficient. Due to larger volume of the cation their cage is larger too and consists of more molecules preferably anions which rotate faster. This offers more possibilities for EMIM⁺ to escape.

IV. Conclusion

To our best knowledge the method of Drude oscillators to describe polarizability has been applied directly to a molecular ionic liquid for the first time in this study. Since the electrostatic forces acting on nuclei are much stronger in ionic liquids as compared to molecular liquids, the limits of applicability of the Drude model have been tested. For a fictitious Drude mass m^δ of 0.1 amu the strength of the Drude charges is practical limited to q^δ =-1.0 e in order to keep the time step at Δt =0.5 fs. Higher Drude charges require a considerable reduction of the time step.

In addition the computer adapted dielectric theory of polarizable systems has been generalized from uniform molecular polarizabilities⁵³ to a set of diverse atomic polarizabilities. Furthermore, the sum of the induced dipole moments can be covered by the collective, non-translational dipole moment.

As a general principle the inclusion of polarization forces does not change the structure of molecular centers significantly but accelerates translational and rotational motion of molecular ions. This trend is highly welcomed since simulations based on classical pairwise additive forces usually yield a retarded dynamics as compared to experiment. As a remedy some authors have tried to rescale permanent charges in order to cope with this retardation effect. An analysis of the effective Coulomb energy in polarizable systems, however, shows that the induced dipoles decrease the original Coulomb energy in the desired way without reduction of molecular net charges. In fact, the interaction between permanent and/or induced dipoles comes into action in a distance range from 4.5 up to 8 Å. This is clearly visible in the orientational structure, in particular in the mutual orientation of cations and anions. For shorter distances the steric forces modelled by Lennard-Jones potentials dominate and prohibit any substantial structural changes. At longer distances charge-charge interactions create the typical long-ranged oscillations of the charge-ordering function. In other words, the molecular ions exhibiting typical effects at short and medium distances behave like simple ions in the asymptotic regime. This renders a rescaling of the molecular net charge impracticable. The extension of the three regions correlates with the r-dependence of the respective interactions: Lennard-Jones r⁻⁶, dipole-dipole r⁻³ and charge-charge r⁻¹.

For the special system EMIM⁺CF₃SO₃^– the inclusion of polarization affects the cationic and anionic dipole in a different way: Both dipole distributions are broadened but the mean value of the molecular dipole is almost unchanged in case of CF₃SO₃^– and shifted to higher values for EMIM⁺. From this single dipole behaviour no conclusions can be drawn for the dielectric constant which is intrinsically characterized by collective effects. Even more, one cannot restrict the interpretation to collective effects among the set of cations or anions as done in the traditional Froohlich formula. Rather, it is the collective coupling between cations and anions that determines the dielectric increment.

As a function of increasing polarizability the following changes are observed: First, the molecular dipole distribution is monotonously broadened with increasing polarizability for EMIM⁺ and CF₃SO₃^–. Second, the rotation and diffusion of cations and anions is accelerated by a factor of roughly two from 0% to 100% polarizability. Third, the generalized dielectric constant ϵ_stat increases as a result of a slight increase of the dielectric permittivity ϵ₀ – ϵ_∞ and a systematic increase of the electronic contribution ϵ_∞. The contribution of the dielectric conductivity remains unchanged despite the acceleration of dynamics. At the highest polarizability the conductivity contribution ϑ(0) and the electronic contribution are of equal size.