On the collective network of ionic liquid/water mixtures: II. Decomposition and Interpretation of dielectric spectra

Abstract

This study deals with the dielectric spectra of mixtures of the ionic liquid 1-butyl-3-methyl-imidazolium (BMIM⁺) tetrafluoroborate with water at three selected mole fractions 0.767≤ x_H2O ≤0.967. The focus lies on the comparison of experimental and computational data. On the one hand, a computational analysis permits a complete decomposition of spectra, both with respect to dynamical behavior (translation and rotation) as well as to composition of the mixture (cation, anion and water). Thereby, not only the peak assignment in experimental spectra is enabled but one can also learn more about solvation properties. Of particular importance is the interplay of the dielectric constant and the conductivity representing a measure of collective rotational and translational motion. On the other hand, the comparison with experimental spectra is essential for the validation of the force fields used in simulation. The satisfying agreement between corresponding peaks in the dielectric spectra confirms computed dielectric relaxation times but also other collective dynamical properties such as the viscosity. Nevertheless, the detailed fine structure of the conductivity regime reveals specific ion pair effects not covered by the simulation. A possible confinement of dynamical heterogeneity as a consequence of a system size effect is also indicated.

I. Introduction

Ionic liquids (ILs) are non-volatile, non-flammable and possess only a marginal vapor pressure as well as high thermal and electrochemical stability,^1–5 which makes them promising replacements for conventional organic solvents. Their properties permit a range of separation techniques such as distillation or sublimation of products and co-products which are less possible using traditional low-boiling organic solvents.⁶ Ionic liquids can act as solvent in three different ways: First, pure ionic liquids are nonaqueous but polar solvents^7–9 and dissolve a wide range of inorganic and organic compounds.¹⁰ Furthermore, an increased enzyme stability and activity in ionic liquids has been reported.¹¹ Second, the immiscibility of ILs with several organic compounds, e.g. linear hydrocarbons, is used in biphasic catalysis.^12–14 The miscibility, however, of the ionic liquid with water depends on the choice of the cation and anion.^15,16 In some reactions ionic liquid/water systems are used as biphasic system.¹⁷ This enables, for example, the suppression of product hydrolysis in galactosylation reactions¹⁸ Alternatively, in other reactions the IL was used as miscible co-solvent to water. On the one hand, the solubility of hydrophobic compounds may be increased in aqueous systems.¹⁸ On the other hand, the yield of enzyme reactions may be enhanced.^19–21

Computational studies are an excellent tool to analyze and interpret the plethora of experimental data. In fact, some simulation studies concerning ionic liquid/water mixtures have been reported.^22–25 All these studies have focused mainly on thermodynamic and structural properties and single particle dynamics. Our pilot study also dealt with structural properties, but with an emphasize on orientational correlation functions and the static dielectric constant.²⁶ From the perspective of IL/water mixtures as solvents dielectric properties are the most interesting class of collective dynamics. On a mesoscopic level, this enables an evaluation of the solvation capabilities of a particular combination of ions. For such a procedure, however, three prerequisites are necessary: First, statistical averaging of the desired quantities is only possible over the simulation time and can not be performed over residues or particles. This requires long-term simulations over tens of nanoseconds. Second, one needs a computer adapted dielectric theory in order to extract correctly dielectric properties from computational trajectory data. The correct and consistent treatment of long-range electrostatic forces is a conditio sine qua non.^27,28 Furthermore, the balance of dielectric constant ϵ(ω) and the conductivity σ(ω) plays a crucial role as shown in a recent study.²⁹ The third and most important point is the validation of computational data by experimental measurements.

Dielectric spectroscopy of mixtures of ionic liquids with polar solvents is experimentally challenging. The spectrum of the pure IL is already complicated with slow dipolar modes partly swamped by DC conductivity.^30,31 Additionally, the contribution of the added component strongly overlaps with IL modes^32,33 and often peaks at rather high (linear) frequencies, ν (ω = 2πν), in the case of water at ν ≈ 18 GHz, so that solvent modes are not properly covered with commercial instrumentation restricted to ν ≤ 20 GHz. For this reason the only investigation into the dielectric properties of IL/water mixtures published so far provides only limited information on the structure and dynamics of these mixtures.³⁴ With the spectral range accessible to us, 0.2 ≤ ν/GHz ≤ 89, the situation is considerably improved.³³ However, the interpretation of the experimental spectra remains problematic. This mainly arises from the necessity to find an appropriate mathematical description for the experimentally accessible total dielectric spectrum, ∑(ω). Generally, the spectrum is decomposed into a sum of n individual relaxation processes j of amplitudes S_j, relaxation frequencies ${\omega }_j^p$ and associated band-shape parameters.^35,36 Such a formal description can almost always be found. However, the experimenter is then faced with the problem to assign a physical meaning to the individual contributions, which is not always straightforward.^33,35–37 Especially in the case of ILs and their mixtures the link between the modes resolved in the formal fit and the molecular motions of the sample is still problematic. Obviously, the proper assignment of resolved modes to physical processes is prerequisite for the quantitative discussion of the experimentally derived S_j and ${\omega }_j^p$. Here the accurate simulation of ∑(ω) and its decompo-sition into dielectric, ϵ(ω), and conductivity, σ(ω), contributions should be able to provide valuable input.

II. Theory And Computational Setup

A. Computational setup

A detailed description of the simulation setup is given in Ref. 26. Therefore, we will only give a brief summary here: Three different mixtures of 1-butyl-3-methyl-imidazolium tetrafluoroborate $\left({\text{BMIM}}^{+}{\text{BF}}_4^{-}\right)$ and TIP3P-water were simulated and their compositions are tabulated in Table I. The force field parameters of the cation, anion and water were taken from Ref. 38,39, Ref. 40 and Ref. 41, respectively. The electrostatic interactions were calculated by the Particle-Mesh Ewald method,^42,43 using a 10 Å cutoff and a k of 0.41 Å⁻¹ for the real-space part interactions. All bond lengths were kept fixed by the SHAKE algorithm,⁴⁴ whereas bond angles and dihedrals were left flexible. Trajectories were generated under constant volume with a boxlength of 41.8 Å and an average temperature of T = 300 K with a time step of ∆t =2 fs, up to a total simulation length of 62 ns.

Table I. Composition and diffusion coefficients of the simulated systems.

x H2O,sim	${\text{BMIM}}^{+}{\text{BF}}_4^{-}$	H2O	D+ [10−5cm2s−1]	D− [10−5cm2s−1]	D0 [10−5cm2s−1]	figure code
0.768	166	548	0.201	0.266	0.887	solid
0.912	111	1147	0.622	0.876	2.24	dashed
0.967	55	1592	1.33	2.01	4.14	dotted

B. Total collective dipole moment M_tot

Each molecular ion i is composed of a set of atomic charges q_i,α positioned at r_i,α. The complete sample of all ions can be characterized by the total collective dipole moment

$${\mathbf{\text{M}}}_{tot}\left(t\right)={\displaystyle \sum _i{\displaystyle \sum _{\alpha }{q}_{i,\alpha }\cdot {\mathbf{\text{r}}}_{i,\alpha }\left(t\right)}}$$ (1)

Of course, the time evolution of this total collective dipole moment is governed by the motion of the individual atoms α as shown in Section IIA and IIB of Ref. 45. In terms of molecular entities this motion may be described as a translation of the molecular center-of-mass r_i,cm, a rotation about this center and additional internal motions. The collectivity of translational motion is manifested in the charge-weighted sum over all molecular centers:

$${\mathbf{\text{M}}}_J\left(t\right)={\displaystyle \sum _i{\displaystyle \sum _{\alpha }{q}_{i,\alpha }\cdot {\mathbf{\text{r}}}_{i,cm}\left(t\right)={\displaystyle \sum _i{q}_i\cdot {\mathbf{\text{r}}}_{i,cm}\left(t\right)}}}$$ (2)

We will use the term rotation as a synonym for all non-translational contributions to M_tot(t) throughout this work. Consequently, the respective collective dipole moment M_D(t) represents the complement of M_J(t):

$${\mathbf{\text{M}}}_D\left(t\right)={\mathbf{\text{M}}}_{tot}\left(t\right)-{\mathbf{\text{M}}}_J\left(t\right),$$ (3)

Since the net charge of the complete sample is zero, M_tot(t) and M_J(t) are uniquely defined, i.e. they can be evaluated invariantly with respect to the origin of any coordinate system. Consequently, their difference M_D(t) is invariant, too.

In equilibrium the average value 〈M_tot〉_eq is zero. Practically, this criterion can be used to judge the statistical quality of a simulation. If the simulation period is too short, remarkable non-zero values are observed, in particular for highly viscous systems. For ionic liquids this requires a simulation period covering several tens of nanoseconds.

Exposing the sample to a spatially homogeneous external field E₀ increases the average value 〈M_tot〉_E0. Generally, this external field is counteracted by the internal molecular fields. It has been shown, however, that for perfect Ewald conditions (tinfoil boundaries) this net Maxwell field E equals the applied external field E₀.⁴⁶ Therefore, both fields may be used synonymously in this particular case. For not too strong electric fields, the dependence of 〈M_tot〉_E on E is linear:

$$\frac{{\langle {\mathbf{\text{M}}}_{tot}\rangle }_E}{V}=\frac{{\displaystyle \sum {}^{*}\left(\omega \right)}}{4\pi }\cdot \mathbf{\text{E}}\left(\omega \right)$$ (4)

The susceptibility ∑*(ω) is called “generalized dielectric constant” being the central quantity measured in microwave spectroscopy.^{32,35,36,47,48} In order to have an intensive property, traditionally called “dielectric polarization”, M_tot is divided by the volume, V.

Computationally, one may follow two roots: First, the external field may be directly applied in the molecular equations of motions and the average value of M_tot monitored. However, such a procedure has to be carried out carefully. On one hand, strong external fields lead to a non-linear relationship between the dielectric polarization and the field. On the other hand, weak external fields are plagued by high statistical noise. Second, one performs a long equilibrium simulation and uses “Linear Response Theory” which relates the susceptibility ∑(ω) to the Fourier-Laplace transform of the derivative of the time correlation function of M_tot.

$${\displaystyle \sum \left(\omega \right)={\displaystyle \sum {}^{*}\left(\omega \right)-{ϵ}_{\infty }=\frac{4\pi }{3V{k}_{B}T}ℒ\left[-\frac{d}{dt}{\langle {\mathbf{\text{M}}}_{tot}\left(0\right)\cdot {\mathbf{\text{M}}}_{tot}\left(t\right)\rangle }_{eq}\right]}}$$ (5)

In the following all time correlation functions are evaluated at equilibrium conditions. Please note that the substraction of ϵ_∞ removes the offset of ∑*(ω) at infinite frequency, a feature necessary for Fourier-Laplace transformation. When comparing with experimental spectra, however, the electronic contribution ϵ_∞ is essential.

The response of a system to an applied external field depends on the character of its constituting species: Neutral molecular liquids are characterized by a frequency-dependent dielectric constant ϵ(ω) arising from dipole reorientation. The translational motions induced by the external field in ionic melts consisting of atomic ions are reflected by the conductivity spectrum, σ(ω). Molecular ions as the building blocks of ionic liquids unite both features within the very same molecule. Therefore, their response is a combination of ϵ(ω) and σ(ω):^49,50

$${\displaystyle \sum \left(\omega \right)=ϵ\left(\omega \right)-{ϵ}_{\infty }+4\pi }i\frac{\sigma \left(\omega \right)}{\omega }$$ (6)

$$=ϵ\left(\omega \right)-{ϵ}_{\infty }+\vartheta \left(\omega \right)$$ (7)

Here, ϵ_∞ stands for the high frequency limit of ∑(ω) resulting from intramolecular polarizability. In the second step, we have introduced the quantity ϑ(ω) in order to emphasize the 1/ω scaling of the conductivity σ(ω). Furthermore, ϑ(ω) represents the translational part of the dielectric spectrum and is caused by the translational part M_J of the collective total dipole moment M_tot.

C. Translational part of M_tot

The translation of the covalently bound charge set {q_i,α} may be viewed as the movement of the net charge q_i located at the center-of-mass. On the macroscopic level, this net charge movement is characterized by the electric current

$$\mathbf{\text{J}}\left(t\right)={\displaystyle \sum _i{q}_i\cdot {\mathbf{\text{v}}}_{i,cm}\left(t\right)=\frac{d}{dt}{\mathbf{\text{M}}}_J\left(t\right),}$$ (8)

which may be also obtained as the time derivative of a translational collective dipole moment M_J(t). Linear response theory relates the time correlation function, 〈J(0) · J(t)〉, to the electrical conductivity, σ(ω), by

$$\sigma \left(\omega \right)=\frac{1}{3V{k}_{B}T}\left[ℒ\left[\langle \mathbf{\text{J}}\left(0\right)\cdot \mathbf{\text{J}}\left(t\right)\rangle \right]+i\omega ℒ\left[\langle {\mathbf{\text{M}}}_D\left(0\right)\cdot \mathbf{\text{J}}\left(t\right)\rangle \right]\right]$$ (9)

$$\simeq \frac{1}{3V{k}_{B}T}\left[ℒ\left[\langle \mathbf{\text{J}}\left(0\right)\cdot \mathbf{\text{J}}\left(t\right)\rangle \right]\right]$$ (10)

The second Fourier-Laplace transform involves the rotational collective dipole moment M_D. Recent simulations have shown that the contribution of this second Fourier-Laplace transform representing translation-rotation cross correlations is rather small and will thus be omitted in the following.^45,51

An alternative to the Green-Kubo like computation of σ(ω) according to Eq. (9) is the so-called “Einstein-Helfand” approach. The latter uses the mean-squared displacement $\langle \Delta {\mathbf{\text{M}}}_J^2\left(t\right)\rangle =\langle {\left[{\mathbf{\text{M}}}_J\left(t\right)-{\mathbf{\text{M}}}_J\left(0\right)\right]}^2\rangle$ and thus restricted to static values. In Ref. 29 we showed that from the limiting behavior of $\langle \Delta {\mathbf{\text{M}}}_J^2\left(t\right)\rangle$ one gets the static conductivity according to:

$$\underset{t\gg t_c}{\lim }\langle \Delta {\mathbf{\text{M}}}_J^2\left(t\right)\rangle =\left[6V{k}_{B}T\sigma \left(0\right)\right]t+2\langle {\mathbf{\text{M}}}_J^2\rangle .$$ (11)

This last equation does not only provide the static (DC) conductivity, σ(0), but its axis intercept, $\langle {\mathbf{\text{M}}}_J^2\rangle ,$ is of special importance for the low-frequency limit of the dielectric spectrum.²⁹ This may be shown in the following way: The translational part of the general-ized dielectric constant ∑(ω),

$$\vartheta \left(\omega \right)=\frac{4\pi i}{\omega }\cdot \sigma \left(\omega \right)$$ (12)

can be obtained by reformulation of Eq. (9) in terms of M_J:

$$\vartheta \left(\omega \right)=\frac{4\pi }{3V{k}_{B}T}[\langle {\mathbf{\text{M}}}_J^2\rangle +\langle {\mathbf{\text{M}}}_D\cdot {\mathbf{\text{M}}}_J\rangle +i\omega ℒ\left[\langle {\mathbf{\text{M}}}_J\left(0\right)\cdot {\mathbf{\text{M}}}_J\left(t\right)\rangle +\langle {\mathbf{\text{M}}}_D\left(0\right)\cdot {\mathbf{\text{M}}}_J\left(t\right)\rangle \right]]$$ (13)

$$\simeq \frac{4\pi }{3V{k}_{B}T}[\langle {\mathbf{\text{M}}}_J^2\rangle +i\omega ℒ\left[\langle {\mathbf{\text{M}}}_J\left(0\right)\cdot {\mathbf{\text{M}}}_J\left(t\right)\rangle \right]]$$ (14)

Now, one can see that in the zero frequency limit ϑ(0) is proportional to the axis intercept $\langle {\mathbf{\text{M}}}_J^2\rangle$.

D. Rotational part of M_tot

The major part of dipolar relaxation results from overall and internal rotation. Formally, each species in the system contributes to the collective rotational dipole moment M_D. In our case, three species (BMIM⁺, ${\text{BF}}_4^{-}$ and water) had to be considered. However, due to the high symmetry of the anion its contribution is practically negligible. Therefore, M_D can be decomposed into its cationic (+) and aqueous component (0) :

$${\mathbf{\text{M}}}_D={\mathbf{\text{M}}}_D^{+}+{\mathbf{\text{M}}}_D^0$$ (15)

In analogy to Eq. (3) the dielectric constant ϵ(ω) is given by:

$$ϵ\left(\omega \right)-{ϵ}_{\infty }={\displaystyle \sum \left(\omega \right)-\vartheta \left(\omega \right)}$$ (16)

$$=\frac{4\pi }{3V{k}_{B}T}ℒ\left[-\frac{d}{dt}\left\{\langle {\mathbf{\text{M}}}_D\left(0\right)\cdot {\mathbf{\text{M}}}_D\left(t\right)\rangle +\langle {\mathbf{\text{M}}}_D\left(0\right)\cdot {\mathbf{\text{M}}}_J\left(t\right)\rangle \right\}\right]$$ (17)

As already said for the conductivity the second term of the Fourier-Laplace transform is marginal and can again be omitted. Inserting Eq. (15) into (17) and exploiting the linearity of the Fourier-Laplace transform one gets:

$$ϵ\left(\omega \right)-{ϵ}_{\infty }={ϵ}^{+}\left(\omega \right)+{ϵ}^0\left(\omega \right)$$ (18)

$${ϵ}^{+}\left(\omega \right)=\frac{4\pi }{3V{k}_{B}T}ℒ\left[-\frac{d}{dt}\left\{\langle {\mathbf{\text{M}}}_D^{+}\left(0\right)\cdot {\mathbf{\text{M}}}_D^{+}\left(t\right)\rangle +\langle {\mathbf{\text{M}}}_D^{+}\left(0\right)\cdot {\mathbf{\text{M}}}_D^0\left(t\right)\rangle \right\}\right]$$ (19)

$${ϵ}^0\left(\omega \right)=\frac{4\pi }{3V{k}_{B}T}ℒ\left[-\frac{d}{dt}\left\{\langle {\mathbf{\text{M}}}_D^0\left(0\right)\cdot {\mathbf{\text{M}}}_D^0\left(t\right)\rangle +\langle {\mathbf{\text{M}}}_D^{+}\left(0\right)\cdot {\mathbf{\text{M}}}_D^0\left(t\right)\rangle \right\}\right]$$ (20)

These equations enable the assignment of characteristic peaks in the dielectric spectrum to specific species.

E. Link to experiment

As already stated above, both frequency-dependent quantities σ(ω) and ϵ(ω) cannot be determined separately by experiment. Only the overall dielectric response of the system, the so-called generalized dielectric constant ∑*(ω), can be extracted from the measurements. Because of their conducting nature, i.e. its non-zero static conductivity σ(0), dielectric measurements in ionic solutions and ionic liquids are carried out a finite frequencies to avoid short-circuiting.³⁵ In the literature the low-frequency branch of the imaginary part of ∑*(ω) is often fitted to the hyperbola σ(0)/ω which is subsequently subtracted from ∑*(ω):

$${\displaystyle {\sum }_0\left(\omega \right)+{ϵ}_{\infty }={\displaystyle \sum *\left(\omega \right)-4\pi i\frac{\sigma \left(0\right)}{\omega }}}$$ (21)

$$=ϵ\left(\omega \right)+\vartheta \left(\omega \right)-4\pi i\frac{\sigma \left(0\right)}{\omega }.$$ (22)

In our laboratory σ(0) is determined in a separate experiment.^30,52 Since σ(0) is a real but not a complex number, this correction only affects the imaginary part of ∑₀(ω). Especially, the last term of this equation does not equal to ϑ(0) but cancels the imaginary part of ϑ(0), removing thus the singularity of the imaginary part of ∑*(ω)

$$\underset{\omega \to 0}{\lim }Im\left[{\displaystyle {\sum }_0\left(\omega \right)}\right]=0.$$ (23)

The real part remains unchanged by the above correction and its zero frequency limit is given by

$$\underset{\omega \to 0}{\lim }Re\left[{\displaystyle {\sum }_0\left(\omega \right)}\right]=ϵ\left(0\right)-{ϵ}_{\infty }+\vartheta \left(0\right)={ϵ}_{stat}-{ϵ}_{\infty }$$ (24)

Furthermore, we note that the concept of ϵ_stat is the generalization of the “apparent dielectric constant” ϵ_sol of an ionic solution to an ionic liquid.⁴⁹ In ionic solutions the ϵ(ω) and σ(ω) contributions to ∑₀(ω) in Eq. (22) come from different species, namely solvent and ions. Note, that this equation and all subsequent formulae containing a dielectric constant (ϵ(ω), ϑ(ω), ∑(ω) or ∑₀(ω)) are in units of 4π ϵ₀ with ϵ₀ being the vacuum permittivity.

In principle, ∑₀(ω) covers the complete frequency range from quasi-static conditions to the optical regime. The contributions at optical frequencies arising from intramolecular polarizability are summarized by ϵ_∞ ≃ n², where n is the optical refraction index. Because standard molecular dynamics simulations use non-polarizable force fields, ϵ_∞ becomes unity in those cases.⁵³ On the other hand, the standard methods for microwave dielectric relaxation experiments dictate a high-frequency cut-off of the spectra in the GHz regime, in our case at ω ≃ 560 GHz (ν = 89 GHz). This implies that relaxation processes can only be observed on the timescale longer than ~2 ps. Consequently, ϵ_∞ has to be treated as an adjustable parameter in the formal fit of the experimental spectra, subsuming thus the missing portion of the spectrum between 2 ps and the optical femtosecond regime, e.g. libration processes, as well as inter- and intramolecular vibrations in the far-infrared regime. Since bond lengths are fixed, intramolecular vibrations are also not covered by our simulations, which extend to ν ≃ 10 THz (300 cm⁻¹). However, the present simulations monitor fast intermolecular processes and it turns out (see below) that the dielectric spectrum in the far-infrared region is essentially determined by fast components of σ(ω).

III. Experiment

Binary water + ${\text{BMIM}}^{+}{\text{BF}}_4^{-}$ mixtures of water mole fractions x_H2O = 0.967, 0.926 and 0.801 were made up on an analytical balance without buoyancy corrections. Water was deionized and purified with a Millipore Milli-Q system equipped with a 0.22 μm filter. ${\text{BMIM}}^{+}{\text{BF}}_4^{-}$ was prepared from purified reactants as described elsewhere,⁵² yielding material with <150ppm halide impurities (potentiometric titration against Ag⁺). After drying under vacuum (p < 10^–8 bar) at ~40 °C for at least 7 days the water content was < 40 ppm (coulometric Karl Fischer titration). The dried compound was stored in a nitrogen-filled glove box and all measurements were conducted under a N₂ atmosphere. To minimize errors associated with the hydrolysis of BF₄⁻ the samples were measured immediately after preparation. All experiments were performed at (298.15 ± 0.05) K.

For all solutions total complex permittivity spectra, ∑*(ω) = ∑(ω) + ϵ_∞, were measured as a function of frequency in the range 0.2 ≤ ν/GHz ≤ 89 (1.26 ≤ ω/GHz ≤ 560) by com-bining data obtained with a frequency-domain reflectometer (0.2 ≤ ν/GHz ≤ 20)⁵⁴ and with two waveguide interferometers (27 ≤ ν/GHz ≤ 89).⁵⁵ Raw data of the frequency-domain reflectometer, obtained by using air, mercury and water as the primary calibration standards, were corrected for calibration errors with a Padé approximation using pure propylene carbonate, dimethylacetamide, benzonitrile and 1-butanol as secondary standards.⁵⁶ The interferometers do not require calibration. To account for the Ohmic loss of the samples the static conductivities of the mixtures, σ(0), were determined to ±0.2% using an AC bridge and capillary cells described in detail elsewhere.⁵²

After correcting ∑*(ω) for σ(0) [c.f. Eq. (21)] the experimental spectra of all investigated mixtures could be well fitted with a sum of four Debye equations:

$${\displaystyle \sum *\left(\omega \right)-4\pi i\frac{\sigma \left(0\right)}{\omega }={\displaystyle {\sum }_0\left(\omega \right)+{ϵ}_{\infty }={\displaystyle \sum _{j=1}^4\frac{S_j}{1+i\omega /{\omega }_j^p}+{ϵ}_{\infty }}}}$$ (25)

Details of the fitting procedure will be given in a subsequent paper covering the entire miscibility range of water + ${\text{BMIM}}^{+}{\text{BF}}_4^{-}$.⁵⁷ The obtained amplitudes, S_j, relaxation frequencies, ${\omega }_j^p$ and associated ϵ_∞ are summarized in Table II; an example for such a fit is shown in Fig. 1. Note that due to the experimental limitation to ν ≤ 89 GHz intra-molecular vibra-tions in the THz region associated with σ(ω) contribute to the ϵ_∞ values of Table II.^30,33 The experimental value of the generalized static dielectric constant, ϵ_stat, of the mixtures is given by

$${ϵ}_{stat}={\displaystyle \sum _{j=1}^4{S}_j+{ϵ}_{\infty }}$$ (26)

TABLE II.

Static dielectric constants, ϵ_stat, of water + ${\text{BMIM}}^{+}{\text{BF}}_4^{-}$ mixtures at 298 K together with the fit parameters of Eq. (25) (amplitudes, S_j, and relaxation frequencies, ${\omega }_j^p$ of relaxations j = 1… 4; ϵ_∞) derived from the experimental dielectric spectra.

xH2O	ϵstat	S 1	${\omega }_1^p$ [THz]	S 2	${\omega }_2^p$ [THz]	S 3	${\omega }_3^p$ [THz]	S 4	${\omega }_4^p$ [THz]	ϵ ∞
0.801	26.58	3.99	0.0046	10.83	0.0302	5.73	0.116	1.58	0.735	4.46
0.926	49.09	5.47	0.0069	12.33	0.0270	24.29	0.0870	3.23	0.990	3.77
0.967	64.25	5.57	0.0081	10.07	0.0276	41.72	0.0952	3.54	1.150	3.35

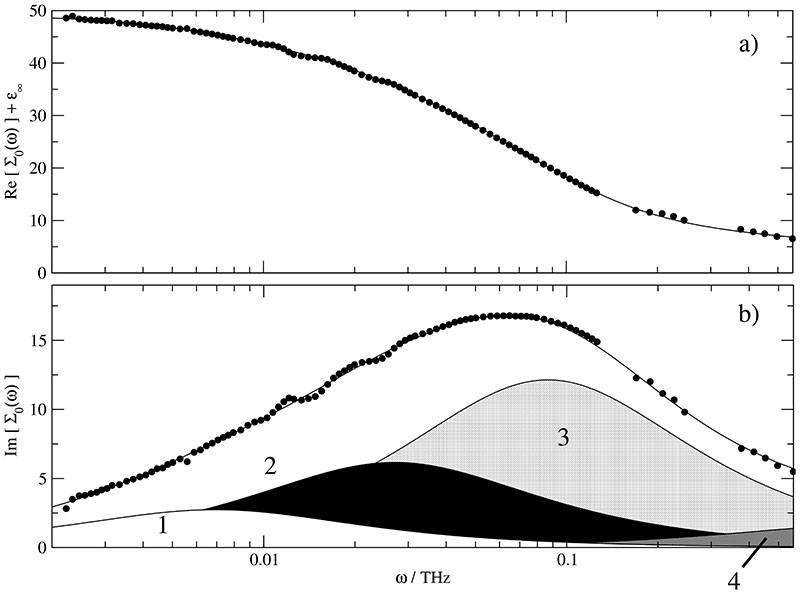
Fig. 1.

Experimental spectra (symbols) at x_H2O=0.926 of (a) the total permittivity, Re[∑₀(ω)] + ϵ_∞ and (b) the total loss corrected for DC conductivity, Im[∑₀(ω)], together with the spectra calculated with Eq. (25) from the parameters of Table II (lines). In (b) the contributions of the resolved Debye relaxations j = 1 … 4 are indicated.

IV. Results And Discussion

A. Decomposition of ∑₀(ω)

A major goal of this study is the presentation and interpretation of dielectric spectra of ionic liquid/water mixtures at various mole fractions x_H2O. The central link between simulation and experiment is the generalized dielectric constant ∑₀(ω) which is corrected for the singularity at zero frequency in Eq. (22). In principle, the computational spectrum may be decomposed into a rotational and a translational contribution. The rotational part is represented by the dielectric constant ϵ(ω) to be interpreted in detail first. Later on, the translational part ϑ(ω) will be discussed.

The rotational part of ∑₀(ω) can be computed by Eq. (17). ϵ(ω) itself may be further subdivided into contributions of each species. In our ternary system ${\text{BMIM}}^{+}{\text{BF}}_4^{-}/{\text{H}}_2\text{O,}$ however, the contribution of the highly symmetric anion can be neglected. As a result, ϵ(ω) is made up by the cationic ϵ⁺(ω) and the aqueous ϵ⁰(ω) components as shown in Eqs. (18) to (20). Strictly speaking, each contribution contains a cross-term with the other species. But in this study we have found that this cross-contribution is rather small. Therefore, ϵ⁺(ω) and ϵ⁰(ω) stand directly for the dielectric properties of the cations and the water molecules. The marginal influence of the cross-term, however, does not automatically reduce the diversity of dynamical behavior in different hydration shells. Indeed, relaxation times contributing to ϵ⁰(ω) differ by an order of magnitude.

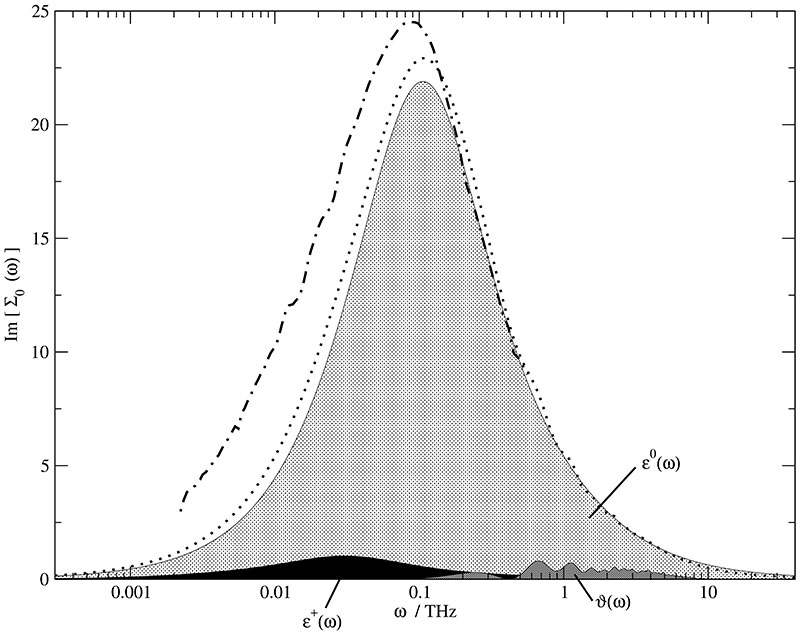
Fig. 2 shows the dielectric absorption Im[∑₀(ω)] for the mole fraction x_H2O = 0.967. Since the water content in this mixture is rather high, ϵ⁰(ω) (light grey shaded area) dominates the spectrum and ϵ⁺(ω) (black area) makes only a small contribution. The maxima of ϵ⁺(ω) and ϵ⁰(ω) are located at ω^p = 0.03 THz and 0.1 THz. The ratio of the corresponding peak heights is approximately 22, but the water concentration is 29 times higher than the cation concentration. Taking into account the molecular dipole moments of TIP3P water (μ⁰ = 2.35 D) and BMIM⁺ (μ⁺ = 5.7 D) the observed peak height ratio should be smaller by a factor of 4. The deviation cannot be explained from single molecule properties but must be a collective phenomenon. The extent of collectivity, however, is quite different between the two molecular species as visible in g¹¹⁰(r) of water–water and BMIM⁺ –BMIM⁺ (see Fig. 4 and Fig. 6 in Ref. 26). While the coupling of distant molecular dipoles is already strong in pure water and even enhanced in IL/water mixtures due to some directing influence of the ions, the dipole orientations of the cations are only weakly correlated among each other. As a result, the water contribution to the dielectric constant arises not only from the bare water dipole moments but also from their intermolecular coupling through hydrogen bonds which leads to a preferentially parallel alignment. In case of the cations, this coupling is rather weak. Consequently, their part is essentially given by the molecular self contributions.

Fig. 2.

Experimental (dashed dotted line) and computational (dotted line) dielectric spectra at x_H2O = 0.967 and their decomposition into ϵ⁺(ω) (black area), ϵ⁰(ω) (light grey area) and ϑ(ω) (dark grey area).

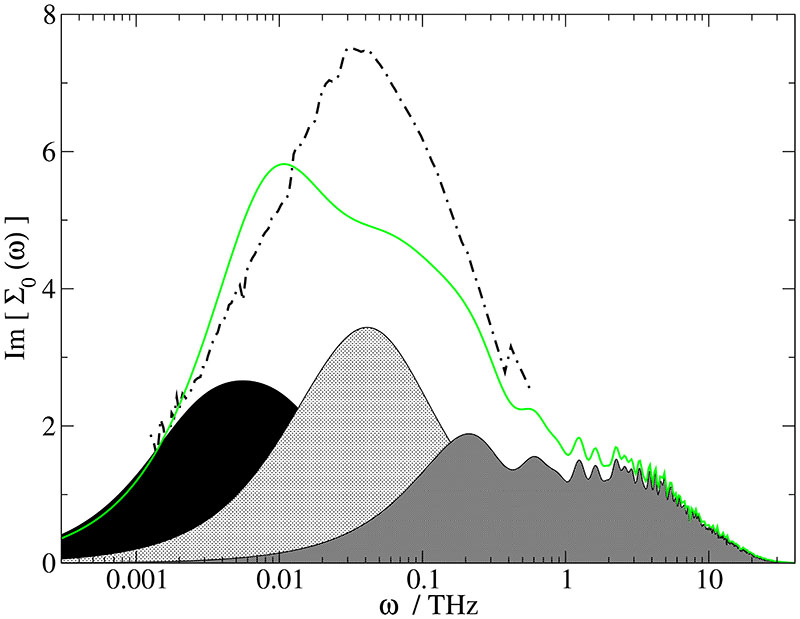
Fig. 4.

Experimental (dashed dotted line) and computational (solid line) dielectric spectra at x_H2O,exp = 0.801 [x_H2O,sim = 0.768] and their decomposition into ϵ⁺(ω) (black area), ϵ⁰(ω) (light grey area) and ϑ(ω) (dark grey area).

Fig. 6.

Real and imaginary part of the frequency-dependent conductivity σ(ω) at various mole fractions: x_H2O,sim = 0.768 (solid line), x_H2O,sim = 0.912 (dashed line) and x_H2O,sim = 0.967 (dotted line).

When the water content of the mixture decreases to a mole fraction of x_H2O,sim = 0.912 (Fig. 3) the cationic contribution is still under-represented. Although the intermolecular coupling of the water dipoles decreases because of the reduced connectivity of their hydrogenbond network and the increasing influence of ion-water interactions, this contribution still overrules the weak and almost stagnating effect of cation-cation coupling. Only due to their increased number density the cations now contribute with a larger relative weight. The peak positions are now ω^p = 0.02 THz and 0.06 THz, respectively. In Fig. 4 at a mole fraction of x_H2O,sim = 0.768 the cationic and aqueous peak are already playing at similar strength. This leads to a peak-shoulder structure of ϵ(ω). The peak maxima occur at ω^p = 0.005 THz and 0.04 THz. A combined analysis of all three mixtures reveals a twofold influence of the viscosity: First, peak maxima are down-shifted monotonously with increasing viscosity. Second, the increasing viscosity enhances the dipolar correlations between the cations. Consequently, the under representation of the cations decreases with decreasing water mole fraction.

Fig. 3.

Experimental (dashed dotted line) and computational (dashed line) dielectric spectra at x_H2O,exp = 0.926 [x_H2O,sim = 0.912] and their decomposition into ϵ⁺(ω) (black area), ϵ⁰(ω) (light grey area) and ϑ(ω) (dark grey area).

Figures 2 to 4 show the increasing influence of ϑ(ω) (dark grey shaded area) which is much more than a redefinition of the conductivity σ(ω). This shows up most prominently in the zero-frequency limit of both quantities. While σ(ω) tends to zero, ϑ(ω) reaches a constant but non-zero value:²⁹

$$\vartheta \left(0\right)=\underset{\omega \to 0}{\lim }\vartheta \left(\omega \right)\simeq \frac{4\pi }{3V{k}_{B}T}\underset{\omega \to 0}{\lim }{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{\text{sin}\left(\omega t\right)}{\omega t}t}\langle \mathbf{\text{J}}\left(0\right)\cdot \mathbf{\text{J}}\left(t\right)\rangle dt=\frac{4\pi }{3V{k}_{B}T}\langle {\mathbf{\text{M}}}_J^2\rangle$$ (27)

Therefore, the transition from σ(ω) to ϑ(ω) is more than a simple 1/ω-scaling but essentially determined by the limiting behavior $\underset{\omega \to 0}{\lim }\text{sin}\left(\omega t\right)/\omega t=1.$ The actual zero-frequency limit of ϑ(ω), i.e. the last part of Eq. (27), can be also obtained from Eq.(14) and contributes to ϵ_stat at ω = 0. At higher frequencies the most obvious difference of σ(ω) and ϑ(ω) is the 1/ω downscaling visibile in Fig. 6 compared to Figs. 2–4. As a result, the ϑ(ω) spectrum spreads over several orders of magnitude in the frequency range. Therefore, it does not only dominate the high frequency regime where ϵ(ω) is almost zero, but also contributes in the typical frequency regime of ϵ(ω).

B. Conjunction of experiment and simulation

The previous section dealt with the computational decomposition of the ∑₀(ω) spectrum. In this way, the complete spectrum can be synthesized from the individual contributions of each species. In principle, this synthesis allows the assignment of each peak to the dominant species. A specific peak may be further resolved into its rotational [ϵ(ω)] and translational [ϑ(ω)] components. In order to validate this decomposition analysis the conjunction to the experiment is essential. Consequently, the experimental spectra of ionic liquid/water mixtures at close mole fractions are given in Figs. 2 - 4 as black dashed lines.

Fig. 1 shows the experimental spectra of permittivity, Re[∑₀(ω)] + ϵ_∞ (a), and loss, Im[∑₀(ω)] (b), for x_H2O = 0.926 together with the decomposition of Im[∑₀(ω)] into four Debye relaxation processes according to Eq. (25). The modes resolved in the formal fit peak at ${\omega }_1^p$ = 0.0069THz (white area), ${\omega }_2^p$ = 0.027THz (black area), ${\omega }_3^p$ = 0.087THz (light grey shaded), and, ${\omega }_4^p$ = 0.99 THz (dark grey shaded). For the water-rich mixtures of this study processes 2 & 3 dominate the spectra. From the evolution of the corresponding amplitudes, S_j, and relaxation frequencies, ${\omega }_j^p$, with x_H2O it can be concluded that relaxation j = 3 is essentially associated with water whereas mode j = 2 mainly results from the reorientation of free cations.⁵⁷ The correspondence with the simulated contributions ϵ⁺(ω) and ϵ⁰(ω) is evident. The fastest mode, (S₄, ${\omega }_4^p$), just extends its low-frequency wing into the covered frequency range. However, it cannot be neglected and the present simulations offer the explanation: Figs. 2-4 indicate significant translational contributions, ϑ(ω), in this area which increase in relative magnitude with increasing IL content. This is in line with the increase of the experimental S₄/(ϵ_stat – ϵ_∞). The nature of the low-frequency mode, (S₁, ${\omega }_1^p$), is not so clear because it does not show up in simulated spectra. In principle, there may be three reasons for this behavior:

First, our simulated spectra are based entirely on the dominant autocorrelation functions comprising altogether more than 95% of the total dielectric response. Cross terms, for example the coupling between cations and water, are highly demanding in terms of statistical quality. Nevertheless, no trend to slow motions can be extracted on first inspection. This is in accordance with the general rule that the slower partner dictates the time regime for the cross term. As an alternative to the coupling between different species a cross term between different modes of motion, i.e. translation and rotation, may be imagined. However, it turns out that the amplitudes of such inter-mode coupling are much smaller than those due to inter-species coupling.

Second, there might be an intrinsic process not covered by simulation. Indeed, there are experimental indications for the formation of ${\text{BMIM}}^{+}{\text{BF}}_4^{-}$ contact ion pairs at very low IL contents but already at x_H2O ≈ 0.9 their concentration appears to be rather low again and at x_H2O = 0.8 they are definitely negligible.⁵⁷ Whilst the reorientation of contact ion pairs might explain the observed low-frequency mode for x_H2O,exp = 0.967 & 0.926, this is clearly not the case for x_H2O,_exp = 0.801.

Third, the experimental observation of a significant amplitude, S₁, not only at all three water contents discussed in this paper but down to x_H2O ≈ 0.1⁵⁷ suggests the existence of a slow, possibly collective, motion in IL-rich mixtures. Eventually, this points to the existence of microheterogeneities governed by different dynamics, which may not be well reproduced in the present simulations because of small box sizes. Therefore, we are currently investigating IL/water systems which are four times larger in box size. Indeed, recent simulation of pure ILs^58,59 and their IL-rich mixtures with polar compounds⁶⁰ suggest a unique spatial heterogeneity in these systems with a polar network formed by the anions, the charged groups of the cations and the added solute, which is permeated by non-polar regions formed by the sidechains of the cations. One may speculate that such nanometersized heterogeneities are sufficient to support a slow relaxation process similar to those arising from interfacial polarization effects⁶¹ which were detected for charged micelles.⁶² Ongoing experimental studies explore this hypothesis.⁵⁷ In this context, it is also interesting to note that at x_H2O ≃0.925 a transition in the mixing state of ${\text{BMIM}}^{+}{\text{BF}}_4^{-}/{\text{H}}_2\text{O}$ is suggested by recent small angle neutron scattering experiments.⁶³

Compared with the simulation, the experimental peak is slightly shifted to lower frequencies for the highest water concentration x_H2O = 0.967 in Fig. 2. This is in accordance with the higher experimental viscosity tabulated in Table III. Additionally, a broadening of the experimental spectrum on the low-frequency side is observed, which at this IL concentration is most likely due to contact ion pairs. In Fig. 3 the experimental spectrum for x_H2O,exp = 0.926 is compared to the computational one at x_H2O,sim = 0.912. Now, the peak maxima coincide which goes along with the close proximity of experimental and computational viscosities. Again, the experimental peak is much broader than the computational one affecting low- and high-frequency side. But note, that the amplitude-weighted geometrical average of ${\omega }_1^p$ and ${\omega }_2^p$ ~0.018 THz, coincides with the simulated peak frequency (0.02 THz) for ϵ⁺(ω). For the lowest water concentration, i.e. x_H2O,exp = 0.801 and x_H2O,sim = 0.768 (Fig. 4), both peaks cover the very same frequency range, but the computational spectrum is more structured: The cation contribution is slightly down-shifted. This may be explained by the higher computational viscosity in Table III. As a consequence, a peak shoulder structure emerges from the interplay of the cationic and the aqueous contribution.

Table III. Juxtaposition of the experimental and computational static transport properties. The experimental viscosity are extracted from the data set of Ref. 66.

experiment				simulation
xH2O	η [mPa s]	σ(0) [S m−1]	ϵstat – ϵ∞	xH2O	η [mPa s]	σ(0) [S m−1]	σNE [S m−1]	ϵstat − 1
0.801	5.8	4.2	22.1	0.768	6.4	5.8	6.6	20.6
0.926	2.2	5.2	45.3	0.912	2.0	11.0	14.1	35.1
0.967	1.4	4.4	60.9	0.967	0.9	13.2	15.6	50.4

Overall, the agreement of experimental and computational spectra is very satisfying. Therefore, the computational decomposition discussed in detail in the previous section can be transferred with high confidence to the experimental spectra. For a perfect agreement, the height of the computational peak had to be increased. In other words, the mean value of collective rotational dipole moment M_D had to be raised which in its turn would demand higher molecular dipole moments. Since the water dipoles in our simulation are already adapted to the liquid state, it is left to the cationic dipoles to be increased. This is not surprising since their charge distribution was derived from quantum-mechanical calculations of isolated ions.³⁸ From the ratio of experimental and computational peak heights one would infer a 10% increase of computational cationic dipole moments as an educated guess. These too low cationic dipoles also show up in the static dielectric constant ϵ_stat in Table III. However, the trend of ϵ_stat as a function of the mole fraction is fairly reproduced. Of course, the inclusion of polarizability would be the next step of improvement since the charge distribution of the individual cations becomes flexible and can thus react to the inhomogeneous field exerted by its neighboring anions and water molecules. However, the use of polarizable force fields reduces the elapsed simulation time and thus deteriorates the statistical quality of the correlation functions from which the final spectra are calculated.

C. On the role of conductivity

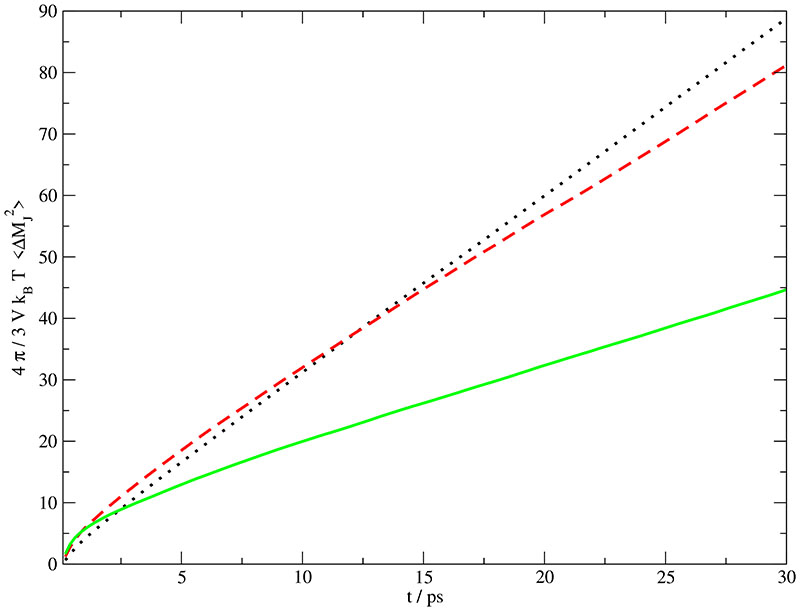
A direct comparison between simulation and experiment is possible on the low-frequency end of the spectrum, i.e. for the static conductivity. The computed static values of σ(0) have been derived from a linear asymptotic fit of the collective dipolar displacement defined in Eq. (11) and shown in Fig. 5 and are given in Table III. Alternatively, these values can be evaluated from an extrapolation of the real part of σ(ω) given in Fig. 6a. Both methods result in the very same σ(0). This agreement points out that the statistical quality of our data is sufficient. Overall, the computational σ(0) increases with increasing water content. In other words, the decreasing number of charge carriers is overcompensated by their increasing mobility due to the decreasing viscosity. This higher fluidity stems from the very low viscosity of pure TIP3P water.⁶⁴ In contrasts, the experimental data exhibit the typical maximum for plots of σ(0) vs. salt concentration at x_H2O,exp = 0.900,⁵² As a result experiment and simulation deviate most at the highest water concentration, see Table III.

Fig. 5.

Einstein-Helfand plot of the mean squared displacement of the total translational dipole moment at various mole fractions: x_H2O,sim = 0.768 (solid line), x_H2O,sim = 0.912 (dashed line) and x_H2O,sim = 0.967 (dotted line). ¿From the slopes of these curves the static conductivity σ(0) given in Table III is derived.

In addition to the dominating effect of balancing ion concentration and ion mobility, the experimental conductivities also reflect the formation of ion-pairs at very low IL content and their subsequent redissociation⁶⁵ with decreasing x_H2O that is evident from the experimental dielectric spectra.⁵⁷ Some indirect evidence for ion-pair formation can also be inferred from the present simulations: if one computes the static conductivity σ_NE from the Nernst-Einstein relation

$${\sigma }_{NE}=\frac{N\cdot q^2}{V{k}_{B}T}\left(D^{+}+D^{-}\right)$$ (28)

inserting the computational values for the ionic diffusion coefficients given Table I, the σ_NE-values tabulated in Table III are obtained. Usually, conductivity values calculated with Eq. (28) deviate substantially from those derived from collective correlation functions as discussed above. The small deviation of roughly 15% in our case points to a small degree of collectivity, i.e. a weak interaction between cation and anion in the simulation. In a previous study we have already found a strong anion–water network which competes with the ionic network.²⁶

At present the frequency range of experimental spectra is limited to ≃0.5 THz so that a full comparison of with simulation in not yet possible. However, the high-frequency excess contribution extracted as the (S₄, ${\omega }_4^p$) mode in the formal fit of the experimental spectra (Fig. 1, Table II) is almost certainly a direct reflection of the translational contribution, ϑ(ω), to the simulated spectra.

Figs. 6a and b show the simulated conductivity spectrum, σ(ω). The interesting region of σ(ω) starts at 0.1 THz and ends at 40 THz. Here, the amplitude increases with decreasing mole fraction x_H2O and the maximum is shifted from 4 THz to approximately 8 THz. This points to collective oscillations of the ionic network: First, with increasing viscosity structural relaxation is slowed down. Second, with increasing number of ions the network is strengthened. Both facts together narrow the dynamical regime as represented by the conductivity peak.

As mentioned at the end of Section A, the imaginary part of the σ(ω) in Fig. 6b approaches zero in the zero frequency limit, but with a finite slope

$$-4\pi \underset{\omega \to 0}{\lim }\frac{Im\left[\sigma \left(\omega \right)\right]}{\omega }=\vartheta \left(0\right)$$ (29)

making an important contribution to the dielectric spectrum. According to Eq. (27) this limit υ(0) is proportional to $\langle {\mathbf{\text{M}}}_J^2\rangle$. Alternative to the slope, these values $\langle {\mathbf{\text{M}}}_J^2\rangle$ may be also evaluated by means of Eq. (11) using the axis intercept of the linear fit. The corresponding values are 6.2, 5.5 and 2.1 for x_H2O,sim = 0.768, 0.912 and 0.967, respectively. Eq. (24) shows the importance of this contribution υ(0) to ϵ_stat. The respective values of ϵ_stat given in Table III decrease with increasing mole fraction (decreasing viscosity) from 29% to 4%. Intuitively, one would expect the opposite behavior: Enhanced translational motion should make a larger contribution. But, higher mobility averages out the fluctuations of the ionic network leaving only its remnant static features.

V. Conclusion

The combined analysis of experimental and computational dielectric spectra reveals two dominating processes that can be associated with ϵ⁺(ω) and ϵ⁰(ω), i.e. with the rotational part of the dielectric constant ∑*(ω) originated from the cations and the water molecules, respectively. In addition, the experimental spectra indicate a slow mode which seems to be missing in the simulation. At $x_{H_{2}O}\underset{˜}{<}0.9$ this mode is probably dominated by contact ion pairs but its origin at higher IL content is not clear. The (S₁, ${\omega }_1^p$) relaxation does not explicitly show up in the present simulations, but for x_H2O = 0.926, where the agreement between simulation and experiment is best, the loss peak frequency of ϵ⁺(ω) coincides with the amplitude-weighted average of ${\omega }_1^p$ and ${\omega }_2^p$. This might suggest some “fine structure” in ϵ⁺(ω).

The significant excess contribution to the experimental spectra observed at high frequencies $\left(\omega \underset{˜}{<}0.3\text{THz}\right)$ is almost certainly associated with ϑ(ω), i.e. the translational component of ∑*(ω) brought about by the cations and anions. Therefore, this second process is inherently connected to the conductivity σ(ω). Another item concerning the conductivity is the zero-frequency limit. While in simulation the static value σ(0) increases with increasing water content, the experimental data show the typical maximum for plots of σ(0) vs. salt concentration at x_H2O,exp = 0.900.⁵²

The qualitative agreement of experiment and simulation already puts the assignment of the modes resolved in the formal fit of the experimental spectra on solid physical grounds. This is particular remarkable in view of the different strategy of analysis: bottom-up in simulation and top-down in experiment. In this context, the determination of corresponding peak frequencies was completely independent. Therefore, it might occur that a low frequency peak is splitted up in experiment or simulation. This is, however, more a question of interpretation than a shortcoming of one of the two methods. The important next step will be to achieve quantitative agreement with respect to relative amplitudes. To this end the electrostatic part of the IL force field as reflected by the distribution of charges has to be adjusted when going from the gas phase to the bulk.