Retroviruses integrate into a shared, non-palindromic DNA motif

Abstract

Many DNA-binding factors, such as transcription factors, form oligomeric complexes with structural symmetry that bind to palindromic DNA sequences¹. Palindromic consensus nucleotide sequences are also found at the genomic integration sites of retroviruses^2–6 and other transposable elements^7–9, and it has been suggested that this palindromic consensus arises as a consequence of the structural symmetry in the integrase complex^2,3. However, we show here that the palindromic consensus sequence is not present in individual integration sites of human T-cell lymphotropic virus type 1 (HTLV-1) and human immunodeficiency virus type 1 (HIV-1), but arises in the population average as a consequence of the existence of a non-palindromic nucleotide motif that occurs in approximately equal proportions on the plus strand and the minus strand of the host genome. We develop a generally applicable algorithm to sort the individual integration site sequences into plus-strand and minus-strand subpopulations, and use this to identify the integration site nucleotide motifs of five retroviruses of different genera: HTLV-1, HIV-1, murine leukaemia virus (MLV), avian sarcoma leucosis virus (ASLV) and prototype foamy virus (PFV). The results reveal a non-palindromic motif that is shared between these retroviruses.

Integration of a cDNA copy of the viral RNA genome is essential to establish infection by retroviruses. This process (see, for example, ref. 10 for a review) is catalysed by the virus-encoded enzyme integrase (IN) and is composed of two steps: (1) the 3’ processing reaction and (2) strand transfer. During the 3’ processing reaction, a di- or tri-nucleotide is removed from the 3’ ends of the viral long terminal repeats (LTRs) to expose the nucleophilic 3’OH groups, which consequently attack the phosphodiester backbone of the target DNA during strand transfer. Strand transfer results in single-stranded DNA gaps that are filled in and repaired by host cellular enzymes. Depending on the retrovirus, the strand transfer reaction takes place with a four (for example, murine leukaemia virus (MLV) and prototype foamy virus (PFV)), five (for example, human immunodeficiency virus type 1 (HIV-1)) or six (for example, human T-cell lymphotropic virus (HTLV-1 and 2)) base pair stagger, giving rise to a duplication of the respective number of nucleotides at the integration site.

Integration is not random. Each retrovirus has characteristic preferences for the genomic integration site (InS) (for example, refs 11–15). These preferences are evident on at least three scales: chromatin conformation and intranuclear location; proximity to specific genomic features such as transcription start sites or transcription factor binding sites; and the primary DNA sequence at the InS itself. Certain host factors also play an active part, the best characterized of which is lens epithelium-derived growth factor^16,17, which biases HIV-1 integration into genes in preference to intergenic regions¹⁸, and bromodomain and extraterminal proteins, which direct MLV integration into the 5’ end of genes¹⁰.

A nucleotide sequence is said to be palindromic if it is equal to its reverse complement (for example, GAATTC and its complement, CTTAAG). Previous studies have revealed a weak palindromic consensus sequence at the InS in several retroviral infections, including HTLV-1, avian sarcoma leucosis virus (ASLV), PFV, MLV, simian immunodeficiency virus (SIV) and HIV-1 (refs 2,3,19–23). The reason for the presence of a palindromic consensus sequence remains unknown, but authors have speculated that it reflects the binding to the DNA of the pre-integration complex (PIC) in symmetrical dimers or tetramers, so that each half-complex has a similar DNA target (that is, potential integration site) preference². However, the consensus sequence is a population average, defined by taking the modal nucleotide at each position in a population of InS sequences. The question arises whether or not the consensus is truly representative of the population. It may be a poor representation of the population if, for example, the population is highly variable or is composed of two or more distinct subpopulations (and hence is bi- or multimodal). Retroviral InS sequences are known to be highly diverse, which immediately indicates the need for caution when interpreting the consensus. Here, we perform statistical analyses to determine whether or not the palindromic consensus sequences efficiently represent the populations of InS sequences from which they are calculated. We find strong evidence that this is not the case and investigate the possibility that these palindromic consensus sequences arise from the presence of motif sequences that appear in both ‘forward’ and ‘reverse complement’ orientations in the genome.

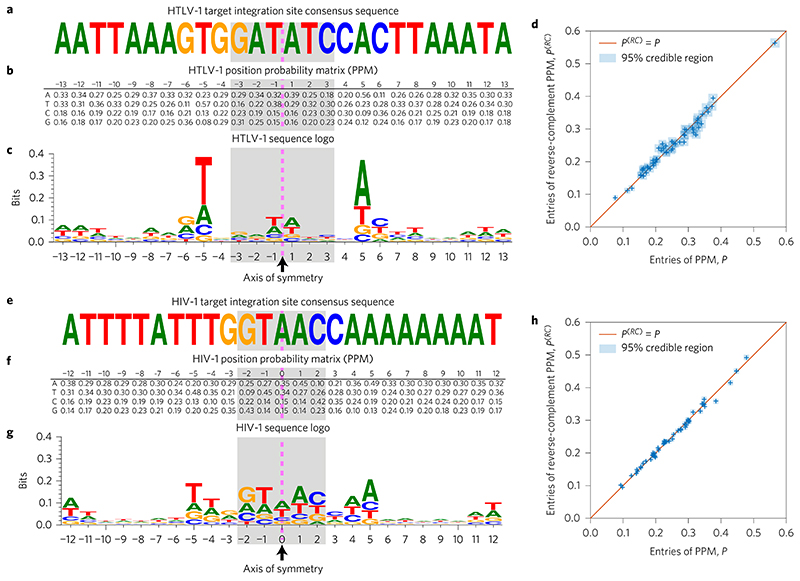
To depict the sequence of the consensus integration site motif, we calculated the frequency of each nucleotide at each respective position in the motif. The result, shown as a sequence logo (Fig. 1), shows a clear palindrome for each virus, as previously described^2,3,19. However, on close inspection an anomaly becomes evident: the sequence is palindromic not only in the most frequent nucleotide, but also at the second, third and (therefore) fourth nucleotide at every position. Although it is plausible that the symmetry of the integrase complex should favour a palindromic motif in the nucleotides that make contacts with the integrase protein, it is not clear why the less frequent nucleotides across all positions in the motif should also be perfectly palindromic.

Figure 1. Palindromic HTLV-1 and HIV-1 target integration site consensus sequences and position probability matrices (PPMs), calculated from 4,521 HTLV-1 and 13,442 HIV-1 InS sequences.

a, In agreement with previous studies, we find the HTLV-1 consensus sequence to be a distinctive weak palindrome. The dashed pink line indicates the palindrome’s axis of symmetry, while the shaded area indicates the duplicated region. b, The PPM, P, for the target integration sites is also palindromic; that is, P₁,–j ≈ P₂,j, P₂,–j ≈ P₁,j, P₃,–j ≈ P₄,j and P₄-j≈ P₃J for j = 1,…,13. Sequence positions to the left of the symmetry line are labelled as negative, and those to the right as positive. c, The symmetry in the PPM may be conveniently visualized using a sequence logo, which also highlights that the palindrome is only weak (has low information content). d, We plot the entries in the first 13 columns of the PPM, P, against the corresponding entries in the reverse-complement PPM, P^(RC) (that is, the PPM obtained after first taking the reverse complement of all of the sequences). Uncertainty in the PPM entries is indicated using blue squares showing the 95% credible interval (highest posterior density) range (see Methods). A perfectly palindromic PPM would be one for which P^(RC = P, the entries of which would lie along the diagonal shown in the plot. e-h, As in a-d, but using the HIV-1 integration sites.

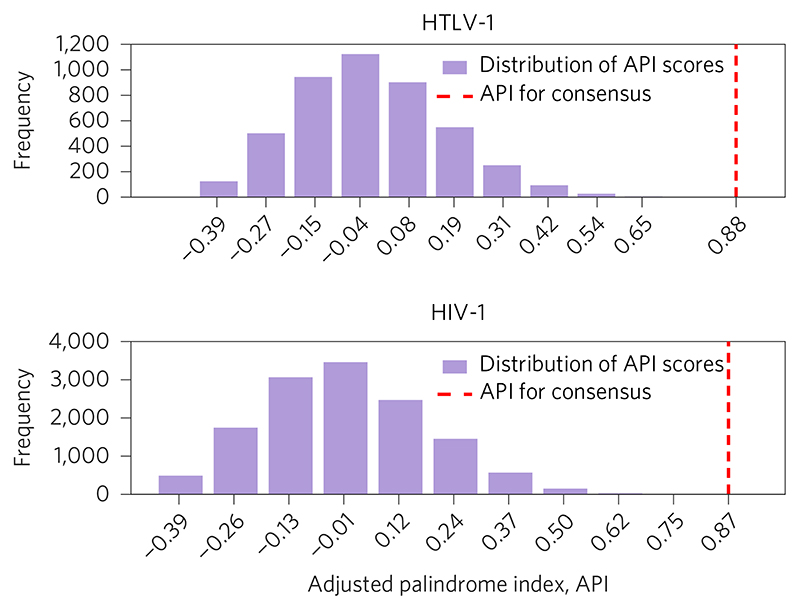
To quantify whether or not an individual sequence is palindromic, we defined the adjusted palindrome index (API), as described further in the Methods. The API is 1 if the sequence is perfectly palindromic, 0 if the sequence is as palindromic as expected by chance, and negative if the sequence is less palindromic than expected by chance. The APIs of the HTLV-1 and HIV-1 motifs confirmed the very high palindromicity of the consensus sequence in each case (Fig. 2). However, examination of the APIs of individual observed integration site sequences reveals a second anomaly: the mean values of the API across the populations of InS sequences are significantly less than zero, for both the HTLV-1 (Table 1) and HIV-1 (Table 2) InS sequences. Although the effect size is small (as might be expected given that the sequences are highly diverse), the key point is that, on average, the InS sequences are less palindromic than we would expect by random chance.

Figure 2. Distribution of adjusted palindrome index (API) scores.

Scores over all 4,521 HTLV-1 integration site sequences (top, taking the sequence length to be 2n = 26, where n is the number of positions each side of the line of palindromic symmetry) and over all 13,442 HIV-1 integration sequences (bottom, with 2n +1 = 25). In both cases, the API for the corresponding consensus sequence (indicated by the red dashed line) is in the extreme positive tail of the distribution.

Table 1. API scores for HTLV-1 integration site sequences.

Sequence length	API for consensus	Mean API, $\overline{{\rho }_A}$	p value (𝓗0)
26	0.79	–0.01	2.12 ×10–6
24	0.89	–0.01	2.99 ×10–7
22	0.87	–0.01	5.31 × 10–7
20	0.86	–0.02	1.58 × 10–7
18	0.85	–0.02	1.08 × 10–7
16	1	–0.02	2.41 × 10–11
14	1	–0.03	5.00 × 10–15
12	1	–0.03	1.08 × 10–14
10	1	–0.04	1.58 × 10–18
8	1	–0.03	1.15 ×10–14
6	1	–0.04	5.04 × 10–18
4	1	–0.05	1.28 ×10–15
2	1	–0.08	2.83 ×10–21

We consider a variety of possible sequence lengths, ranging from 2n = 26 to 2n = 2, where n is the number of positions each side of the line of palindromic symmetry. The mean API values were calculated by finding the API for each of the 4,521 individual InS sequences, and then taking the mean. The final column contains p values resulting from one-sample ř-tests assessing the null hypothesis (H0) that the population mean value is equal to zero.

Table 2. Adjusted palindrome index (API) scores for HIV-1 integration site sequences.

Sequence length	API for consensus	Mean API, $\overline{{\rho }_A}$	p value (𝓗0)
25	0.88	–0.01	8.21 × 10–9
23	0.87	–0.01	1.60 ×10–8
21	0.86	–0.01	4.29 ×10–9
19	0.85	–0.01	1.29 × 10–11
17	0.83	–0.01	1.08 ×10–12
15	0.8	–0.02	1.04 ×10–13
13	1	–0.02	3.16 ×10–18
11	1	–0.03	1.69 × 10–26
9	1	–0.03	1.02 ×10–27
7	1	–0.03	8.57 × 10–25
5	1	–0.04	1.09 ×10–24
3	1	–0.07	1.95 × 10–35

How can a population of individually non-palindromic sequences generate a palindromic consensus motif? We hypothesized that the retroviral integrase complex recognizes a non-palindromic motif present either on the plus strand (‘forward’ orientation) or the minus strand (‘reverse’ orientation) of the host genome: the reverse complement of the minus-strand motif appears as the mirror image of the plus-strand motif, so that when the two are combined in a population of sequences, the consensus appears as a palindrome.

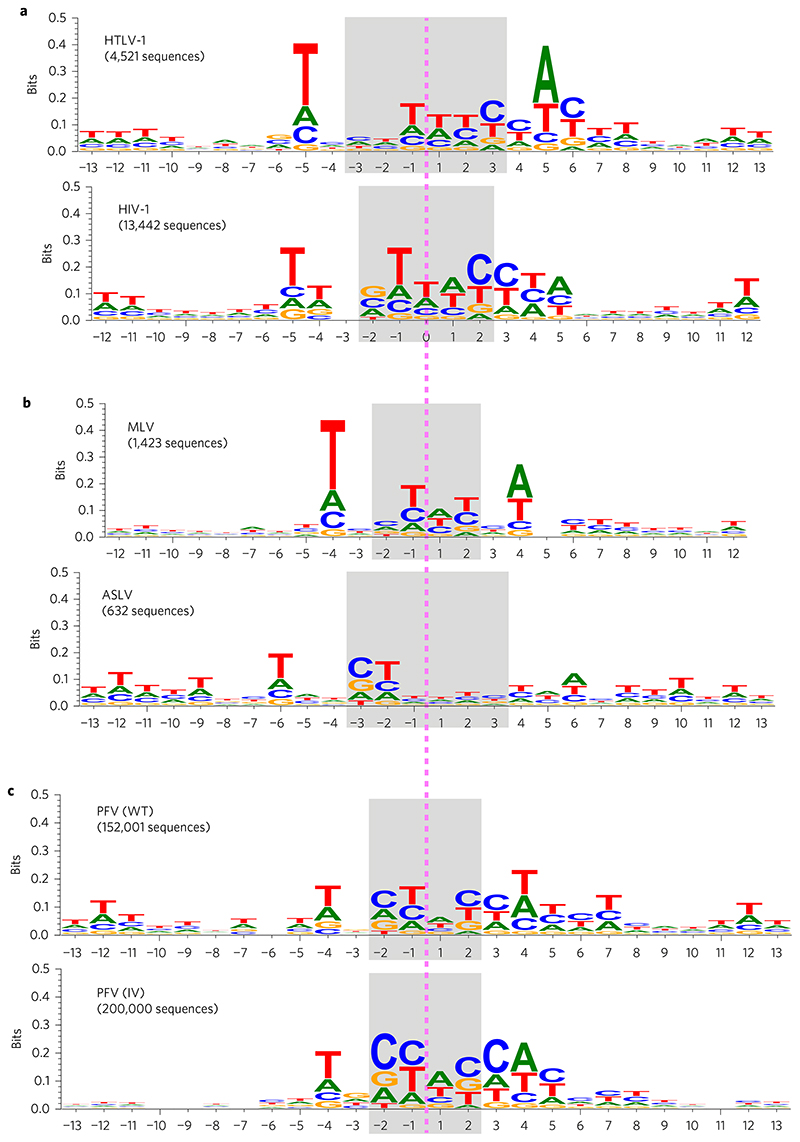
To test this hypothesis, we fitted a model to resolve the population of observed integration sites into two components, one component corresponding to the subpopulation of sequences in the forward orientation and the other corresponding to those in the reverse orientation. We fitted the model by maximum likelihood (see Methods for details of the model and fitting procedure, and the ‘Code availability’ section for an implementation). We additionally considered a number of alternative algorithms for fitting the models (maximum profile likelihood and Gibbs sampling approaches), which provided qualitatively identical results (Supplementary Fig. 1). For both HTLV-1 and HIV-1, the algorithms identified complementary subpopulations within the collections of InS sequences (Fig. 3a), with the subpopulations appearing in approximately equal proportions (λ_HTLV = 0.47 and λ_HIV = 0.49, where λ denotes the proportion of sequences in the ‘forward orientation’). As a further check, we also considered an unconstrained clustering of the sequences, which also identified complementary clusters among the InS sequences (Supplementary Figs 2 and 3).

Figure 3. Summary of results from fitting the two-component mixture model by maximum likelihood.

a, Sequence logo summaries of one of the two subpopulations of integration site sequences in the HTLV-1 and HIV-1 data sets (in each case, the other subpopulation is characterized by the reverse complement of the sequence logo shown). b, As in a, but for the MLV and ASLV data sets. c, As in a, but for the PFV (WT) and PFV (IV) data sets.

We next assessed whether the hypothesis of two complementary subpopulations provided a significantly better description of the data than the hypothesis of a single population characterized by a palindromic motif. A likelihood ratio test (see Methods) decisively rejected the single-population hypothesis (p < 0.001). We also calculated for each model the Bayesian information criterion²⁴ (BIC), which provides a measure of the ability of a model to explain the observed data. The results again showed that for both HIV-1 and HTLV-1 there was very strong evidence against the one-population (palindromic) model (ΔBIC_HIV = 2.86 × 10³ and ΔBIC_HTLV = 1.48 × 10³).

We fitted our two-component mixture model to smaller data sets on HTLV-1, HIV-1, MLV and ASLV taken from the literature¹⁹. The results on MLV and ASLV are given in Fig. 3b. The results for HTLV-1 and HIV-1 are qualitatively identical to those obtained from the larger data sets and are given in Supplementary Fig. 4. We also considered two large PFV data sets from Maskell et al.²⁵: (1) the PFV (WT) data set, which comprises integration sites for 153,447 unique integration events in HT1080 cells and (2) the PFV (IV) data set, comprising ~2 × 10⁶ integration sites determined using purified PFV intasomes and deproteinized human DNA.

After pre-processing to remove duplicates and sequences containing indeterminate nucleotides (Ns), 152,001 integration sites remained in the PFV (WT) data set and 2,197,613 in the PFV (IV) data set. To reduce computation time, we randomly sampled 200,000 integration site sequences from the PFV (IV) data set to use for analysis. The results on PFV (WT) and PFV (IV) are given in Fig. 3c. The results obtained for all retroviruses reveal similarities between the non-palindromic motifs.

The factors that influence the pattern of integration of retroviruses and transposable elements operate at different physical scales. The strength of association between specific genomic features and retroviral integration frequency depends on the genomic scale on which the data are analysed^20,26. Broadly, three scales have been studied: chromosome domains and euchromatin/heterochromatin; genomic features such as histone modifications and transcription factor binding sites; and primary DNA sequence.

The primary DNA sequence of the host genome is thought to influence the site of retroviral integration by determining both the binding affinity of the intasome and the physical characteristics of the target DNA, especially the ability of the double helix to bend^7,27, which depends in turn on the presence of specific dinucleotides and trinucleotides. Müller and Varmus²⁸ concluded that the bendability of DNA could explain the preferential integration of certain retroviruses in DNA associated with nucleosomes. The requirement for DNA bending during retroviral integration has been explained by the discovery of the crystal structure of the foamy viral intasome complexed with target DNA^29,30. Complete unstacking of the central dinucleotide at the site of integration allows the scissile phosphodiester backbone to reach the active sites of the IN protomers. Although the bending of the tDNA observed in the crystal structure does not correspond with the bend described in nucleosomal DNA³¹, the cryo-electron microscopy structure of the foamy viral intasome in complex with mononucleosomes²⁵ showed that the nucleosomal DNA is lifted from the histone octamer to allow proper accommodation within the active sites of the IN protomers. Given that integration catalysed by different retroviral INs gives rise to a different target duplication size, it is expected that DNA bending at the site of integration will be more severe for integrations with a 4 bp target duplication compared to those with a 6 bp target duplication²⁹.

Whereas some retroviruses preferentially integrate into regions of dense nucleosome packing (for example, PFV and MLV)²⁵, others prefer regions of sparse nucleosome packing (for example, HIV and ASV³²). However, even in cases where nucleosome sparseness is preferred, a nucleosome at the integration site itself contributes to efficient integration.

In addition to the impact of specific dinucleotides and trinucleotides on DNA bendability, the other chief impact of primary DNA sequence on retroviral integration is the presence of a primary DNA motif, that is, preferred nucleotides at specific positions in relation to the integration site. Palindromic DNA sequences have been reported at the insertion site of transposable elements in Drosophila⁷, yeast^8,9 and retroviruses^2–6,19. The presence of the palindrome has been attributed by several workers to the symmetry of the multimeric viral pre-integration complex^2,3. However, Liao et al.⁷ noted that, although the palindromic pattern that they observed at the insertion site of a P transposable element in Drosophila could be discerned when as few as fifty insertion sites were aligned and averaged, the palindrome was not evident at the level of a single insertion site.

It was previously assumed that the non-appearance of the palindromic nucleotide sequence in individual retroviral integration sites was due to the fact that the palindrome was weak, that is, poorly conserved. However, in the present study we found evidence that the palindrome was statistically significantly disfavoured at the level of individual sites: the palindrome is evident only as an average—a consensus—of the population of integration sites. We propose that the most likely explanation is that the palindrome results from a mixture of sequences that contain a non-palindromic nucleotide motif in approximately equal proportions on the plus strand and minus strand of the genome. In fact, while the integrase components of the in vitro purified intasome form a highly symmetrical structure, within the in vivo pre-integration complex, which also includes other viral and host proteins, a degree of asymmetry is imposed by the presence of the retroviral DNA. This asymmetry may be sufficient to favour a non-palindromic sequence at the integration site.

On the hypothesis of a non-palindromic nucleotide motif in approximately equal proportions on the plus strand and minus strand of the genome, we sorted the populations of sequences of several different retroviral integration sites into those with a conserved motif respectively on the plus and minus strand of the genome. The resulting alignment revealed the putative true nucleotide motif that is recognized by the intasome in each case. Comparison of these motifs among the respective viruses showed certain similarities between the sequences (Fig. 3), including two T residues upstream of the integration site and an A residue two or three nucleotides downstream. There is a shared motif 5’-T(N1/2) [C(N0/1)T|(W1/2)C]CW-3’, where the square brackets ([and]) represent the start and end of the duplicated region, W denotes A or T, and | represents the axis of symmetry. The preference for an A (T) two or three nucleotides downstream (upstream) of the integration site was previously observed and was explained by a direct contact between A and the residue at the PFV IN Ala188 equivalent position^29,30,33. Indeed, the recent X-ray structure of the poststrand-transfer complex of the alpharetrovirus Rous sarcoma virus (RSV) IN illustrates a direct contact with an A (T) three nucleotides downstream (upstream) of the integration site and the homologous Ser124 residue site³⁴. Using the same algorithm on InS sequences generated with HIV-1 IN Ser119Thr (equivalent to PFV IN Ala188)³³ the shared motif is preserved (Supplementary Fig. 5), with a stronger preference for an A(T) three nucleotides downstream (upstream) of the InS. It remains to be seen whether the nucleotide composition of the remainder of the shared motif, in particular the central T-rich region, is preferred because of the flexibility of the DNA at such sequences, or is due to direct contact between IN and the bases. Further structural information on lenti-, gamma- and delta-retroviral synaptic complexes is needed to answer this question.

To summarize, we conclude that, in contrast to the palindromic sequence motifs that are bound by many transcription factors, the primary DNA motif recognized by the retroviral intasome is non-palindromic.

Methods

Mapped integration sites

To focus on the initial integration targeting profile of HTLV-1 and HIV-1, integration sites were identified in DNA purified from cells infected experimentally in vitro. Jurkat T cells were infected either by short co-culture with HTLV-1-producing cell line MT2 (ref. 35) or by VSV-G pseudotyped HIV-1 (gift from A. Fassati, UCL). The identification of4,521 HTLV-1 integration sites from in vitro infected Jurkat T cells has been described before^15,36. The identification of 13,442 HIV-1 integration sites was carried out using a similar approach, using the following HIV-specific PCR forward primers: HIVB3 5’-GCTTGCCTTGAGTGCTTCAAGTAGTGTG-3’, HIVP5B5 5’-AATGATACGGCGACCACCGAGATCTACACGTGCCCGTCTGTTGTGTGAC TCTGG-3’ and HIV-specific sequencing primer 5’-ATCCCTCAGACCCTTTT AGTCAGTGTGGAAAATCTC-3’.

Credible intervals for entries of the position probability matrices (PPMs)

To obtain the credible intervals given in Fig. 1d,h, we regard the elements of the PPM as parameters, which we then infer using Bayesian methods. Let p_X,k denote the probability that nucleotide X ∈ {A, T, C, G} is observed in position k, and define n_x,k to be the number of times X was observed in position k. For column k of the PPM, which we denote p_k = [p_A,k p_T,k P_C,k p_G,k], we know that each p_X,k ≥ 0 and that Σ_{x∈{A,T,C,G}pXk} = 1, so a Dirichlet prior is appropriate. We take a symmetric Dirichlet prior with a = 1 (which is equivalent to a uniform prior). Assuming [n_A,k n_T,k n_C,k n_G,k] are jointly distributed according to a multinomial distribution with n_TOTAL = Σ_{X∈ {A,T,C,G}} ⁿX,k trials and probabilities [p_A,k p_T,k p_C,k p_G,k], it can be shown that the marginal posterior distributions for the entries of column k of the PPM are p_X,k ~ Beta(1 + n_X,k, 4 + n_TOTAL – (1 + n_X,k)). Using these, we find 95% highest posterior density (HPD) regions using the betaHPD function from the pscl package³⁷ in the R statistical programming language³⁸.

API

We define the palindrome index (PI) for a sequence to be the proportion of positions at which it is equal to its reverse complement. For example, the PI for the sequence s = ATCCGGTT is 0.75, because the reverse complement sequence is s’ = AACCGGAT, and s and s’ are identical at six of the eight positions (6/8 = 0.75). For sequences of odd length, we first remove the central letter. Hence sequences may be assumed to be of even length. The API is a ‘corrected for chance’ version of the PI, which controls for the fact that the expected value of the PI depends on the length of the sequence. Such adjusted indexes are common (for example, ref. 39) and are calculated as Adjusted Index = (Observed Index – Expected Index)/(Maximum Index – Expected Index). For the PI, the maximum value is 1 (when a sequence is perfectly palindromic). Given sequence s = σ_-n...σ_-1σ₊₁...σ_+n, the expected value for the PI is the expectation when σ₊j and σ- are independent, which is given by

$$\frac{1}{n}{\displaystyle \sum _{j=1}^n\left(\underset{x\in |A,T,CG|}{{{\displaystyle \sum }}^{\text{}}}p\left({\sigma }_{-j}=X\right)p\left({\sigma }_{+j}=c(X)\right)\right)}$$

Here c(X) denotes the complement of X and p(σ_±j = X) are the empirical marginal probabilities, which may be taken from the entries of the PPM.

Two-component mixture model

We model the InS sequences as being drawn from a two-component mixture model, p(s|P,λ) = λf(s|P) + (1 – λ)f(s|P^(RC)), where f(s|P) is the likelihood of sequence s given PPM P, and P^(RC) denotes the reverse complement of PPM P (which follows automatically from P by reversing the order of the columns, and swapping the A and T rows with one another and the C and G rows with one another). We define the likelihood straightforwardly as the product of probabilities of each of the elements of s, where the individual probabilities are given by the entries of the PPM. To fit the model, we must estimate parameters λ and P. We find the maximum likelihood estimates of these parameters using the expectation maximization algorithm.

Expectation-maximization (EM) algorithm for our model

We refer the reader to ref. 40 for general information about the EM algorithm, and here provide the update equations for the model parameters, λ and P. Suppose we have a collection of N InS sequences, s⁽¹⁾,...,s^(N). At iteration t, define $w_t^{(i)}$ to be the posterior probability of sequence s⁽ⁱ⁾ belonging to the subpopulation with PPM P, given λ_t–1 and P_t–1 (the parameter estimates at iteration t–1). That is, $w_t^{(i)}=\left({\lambda }_{t-1}f\left(s^{(i)}\mid P_{t-1}\right)\right)/\left({\lambda }_{t-1}f\left(s^{(i)}\mid P_{t-1}\right)+{\lambda }_{t-1}f\left(s^{(i)}\mid P_{t-1}^{(RC)}\right)\right)$. Also, for X ∈ {A, T, C, G} and k = 1,.,.,n (or k = 0,.,.,n in the odd palindrome case), we define $Q_{t(k,X)}={\displaystyle {\sum }_{i=1}^N\left(w_t^{(i)}]\text{}]\left({\sigma }_{-k}^{(i)}=X\right)+\left(1-w_t^{(i)}\right)\right]\left({\sigma }_{+k}^{(i)}=c(X)\right)})$. Then ${\lambda }_t={\displaystyle \sum _{i=1}^N\left(w_t^{(i)}/N\right)}$, and defining the element of P_t in column k and row labelled by nucleotide X to be P_t,(k,X), we have P_t(k, X) = (Q_t(k, X))/(Σ_x∈ {ATCG} Q_t(k, X)).

Initialization and stopping criteria for the EM algorithm

We initialize the EM algorithm by setting the initial PPM, P₀, to be the original (palindromic) PPM and setting the initial mixture weight, λ₀, to be 0.5. At iteration t, we calculate the loglikelihood associated with the full data set using the current parameter estimates, ${\ell }_{\text{t}}={\displaystyle \sum _{i=1}^N\log \left(p\left({\text{s}}_i\mid {\lambda }_t,P_t\right)\right)}$. We terminate the algorithm when l_t+1 – l_t < τ, for some preset threshold value τ. To obtain the results shown in Fig. 3, we set τ = 1 × 10^–10. To reduce run times when finding the null distribution of the likelihood ratio test (LRT) statistic, we set τ = 0.1, because it was necessary to run the algorithm a large number of times.

Likelihood ratio tests for quality of fit

Although it is tempting to apply a simple LRT to determine if the unconstrained two-component mixture model provides a significantly better fit to the data than the constrained, single-component palindromic model (in which P = P^(RC), it is well known that for mixture models the LRT statistic does not in general follow standard χ² distributions⁴¹. We therefore adopted McLachlan’s approach⁴² to construct an empirical null distribution for the LRT statistic, D. Note that the null model here is a single component with PPM equal to the empirical PPM (given in Fig. 1b for HTLV-1 and Fig. 1f for HIV-1), while the alternative is the fitted two-component mixture model. Briefly, we simulated 1,000 new data sets using the null model, fitted both the null and alternative models to each simulated data set and calculated the LRT statistic each time. In this way, we obtained empirical null distributions for the LRT statistic, which we then used to assess the significance of the observed LRT statistic. For the HTLV-1 InS sequences, the 1,000 values sampled from the null distribution of the LRT statistic all fell between –28.64 and 18.79, while the observed LRT statistic was 1.49 × 10³. For the HIV-1 InS sequences, the sampled LRT statistics all fell between –32.37 and 29.24, while the observed LRT statistic was 2.86 × 10³. For both the HTLV-1 and HIV-1 data sets we may clearly reject the null model in favour of the alternative model (p <0.001).

Data availability

The data used to reproduce the results on HTLV-1 presented in this study are included with the code (see section ‘Code availability’). All other data that support the findings of this study are available from the corresponding author upon request.

Code availability

Code is available from http://www.mrc-bsu.cam.ac.uk/software/bioinformatics-and-statistical-genomics/.