Tension at intercellular junctions is necessary for accurate orientation of cell division in the epithelium plane

Significance

In growing epithelia, divisions are typically oriented in the epithelial plane to drive tissue expansion. In some organs, divisions are then reoriented to occur perpendicular to the epithelium plane to drive tissue stratification and cell differentiation. When uncontrolled, this switch in orientation can lead to defects in tissue organization and has been suggested to contribute to cancer metastasis. While much is known about the molecular machinery guiding mitotic spindle orientation, less is known about the role of mechanical factors. Here, we show that mechanics plays a role in controlling the plane of division. Overall, our data suggest that the orientation of spindles in the epithelium plane requires a threshold level of mechanical tension at intercellular junctions.

Abstract

The direction in which a cell divides is set by the orientation of its mitotic spindle and is important for determining cell fate, controlling tissue shape, and maintaining tissue architecture. Divisions parallel to the epithelial plane sustain tissue expansion. By contrast, divisions perpendicular to the plane promote tissue stratification and lead to the loss of epithelial cells from the tissue—an event that has been suggested to promote metastasis. Much is known about the molecular machinery involved in orienting the spindle, but less is known about the contribution of mechanical factors, such as tissue tension, in ensuring spindle orientation in the plane of the epithelium. This is important as epithelia are continuously subjected to mechanical stresses. To explore this further, we subjected suspended epithelial monolayers devoid of extracellular matrix to varying levels of tissue tension to study the orientation of cell divisions relative to the tissue plane. This analysis revealed that lowering tissue tension by compressing epithelial monolayers or by inhibiting myosin contractility increased the frequency of out-of-plane divisions. Reciprocally, increasing tissue tension by elevating cell contractility or by tissue stretching restored accurate in-plane cell divisions. Moreover, a characterization of the geometry of cells within these epithelia suggested that spindles can sense tissue tension through its impact on tension at subcellular surfaces, independently of their shape. Overall, these data suggest that accurate spindle orientation in the plane of the epithelium relies on a threshold level of tension at intercellular junctions.

Orientation of cell division plays a key role in the regulation of tissue growth, cell fate, and differentiation during development as well as in adult tissue homeostasis (1–3). In monolayered epithelia, divisions typically occur in the plane of the epithelium (XY plane)—driving tissue expansion. In some tissues, divisions can then be reoriented such that they occur perpendicular to the epithelium plane to drive stratification and cell differentiation. This has been studied in detail in the epidermis, where the division of stem cells perpendicular to the plane of the basal layer gives rise to one basal daughter, that retains its stem cell identity, and one suprabasal daughter, that goes on to differentiate and contributes to stratification of the tissue (4, 5). However, in other contexts, aberrant out-of-plane divisions can lead to failures in morphogenesis (6) and may contribute to cancer metastasis (reviewed in refs. 7 and 8).

The molecular and mechanical cues controlling the orientation of cell division within the plane of epithelia have been the focus of much attention. The axis of cell division is set by the orientation of the mitotic spindle, whose position is controlled by the balance of pulling and pushing forces exerted on astral microtubules. Pulling forces are mediated by a conserved protein complex composed of Gαi, LGN, and NuMA located at the cell periphery. In epithelia, Gαi and LGN are localized to intercellular junctions by interactions with E-cadherins during interphase and, when NuMA is released into the cytoplasm after nuclear envelope breakdown, it is recruited to intercellular junctions by LGN (9). During mitosis, the Gαi–LGN–NuMA complex recruits dynein motors, which exert pulling forces on the astral microtubules. Pushing forces that arise from microtubules polymerizing against their site of interaction with the cell cortex also participate in spindle centring both in vitro and in vivo (10–12). The combination of pulling and pushing forces on astral microtubules results in a torque on the centrosomes, which orients the spindle.

During normal development and throughout adult life, tissues are continuously subjected to mechanical stress. As a result, mechanical stresses also participate in regulating the orientation of in-plane cell division (13–19). In many cases, a complex interplay between molecular, geometrical, and mechanical cues appears to control orientation within the plane of the tissue. Thus, in mammalian epithelia, the recruitment of LGN to intercellular contacts was shown to be promoted by high junctional tension, leading to alignment of cell divisions with tissue tension (14). Computational studies indicate that cellular aspect ratio and cortical pulling forces can work together to control the orientation of the spindle (19). Recently, the presence of isotropic tissue tension generated by myosin was shown to be necessary to enable spindles to orient toward the long cell axis in cells within the Drosophila notum (16). Consequently, factors that affect astral microtubule dynamics and stability, classic polarity pathways, cell shape, and external forces can all contribute to the regulation of spindle orientation and division (reviewed in refs. 20 and 21).

The factors controlling and constraining out-of-plane divisions are comparatively less well understood. This is especially the case when considering the impact of mechanical forces on spindle orientation. In some tissues, the localization of the Gαi, LGN, and NuMA complex to intercellular junctions and its exclusion from the apical domain by aPKC phosphorylation appear to effectively constrain divisions to the plane of the epithelium (13, 22, 23). Conversely, in later stages of mouse epidermis morphogenesis or in Drosophila neuroblasts, the relocalization of LGN to the apical cell surface orients spindles along the apicobasal axis (4, 24–26). Interestingly, however, out-of-plane cell division can take place in the absence of the Gαi, LGN, and NuMA complex, for example during early development of the mouse epidermis, when these proteins have yet to be expressed (24). This has led to the exploration of geometrical cues (such as cell shape and local cell density) as additional factors modulating the early switch from in-plane to out-of-plane divisions. The mouse epidermis starts as a single layer of cells which divide within the plane of the tissue, until an increase in cell density promotes a switch in division orientation that leads to tissue stratification (27). Although it has been suggested that this is because of a decrease in tissue stress that accompanies the increase in cell density, direct measurements of cell- and tissue-scale stresses are challenging, making this hypothesis hard to test. Furthermore, teasing out the relative importance of stress, deformation, and molecular cues is complex because mechanical cues affect cell density, cell shape, and protein localization. As examples of this, reductions in tissue tension have been reported to reduce LGN and E-cadherin signals at cell–cell contacts 14, 27; while, in the midline of the developing fly, cell crowding is accompanied by a reduction in junctional tension (28). In summary, the exact stimulus or a combination of stimuli influencing the plane of cell division remains unclear.

Here, to investigate the relative contribution of geometrical and mechanical cues in regulating out-of-plane spindle orientation, we image cell divisions in suspended epithelial monolayers. We show that, when cells are exposed to a moderate level of tissue tension, divisions are robustly oriented within the plane of the monolayer. Strikingly, however, a decrease in tissue tension induced by chemical treatment or by compression increased the frequency of out-of-plane divisions. These data suggest that tension at intercellular junctions is required to efficiently orient division in the plane of the epithelium – revealing a role for mechanical tension at subcellular surfaces in this process.

Results

Application of Uniaxial Compressive Strain Promotes Division Out-of-Plane.

Our first goal was to image the orientation of divisions relative to the plane of epithelial monolayers. In our experiments, we used Madin-Darby Canine Kidney (MDCK) epithelial monolayers devoid of a substrate and suspended between test rods [Fig. 1 A and B, Methods, (29, 30)]. This experimental system allows the accurate control of tissue-scale stress and strain, while simultaneously allowing for imaging of the subcellular localization of proteins and cell shape.

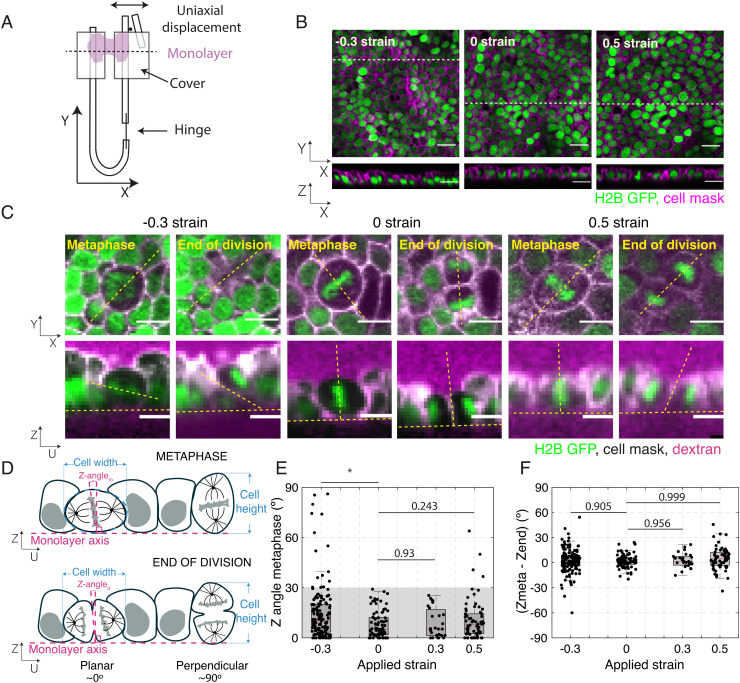
Fig. 1.

Application of uniaxial compressive strain to epithelial monolayers promotes division out-of-plane. (A) Diagram of the device for mechanical manipulation of suspended MDCK monolayers. The U-shaped device consists of a rigid arm and a flexible arm. Small cover glasses (gray) are glued to the extremities of each arm creating a gap of ~500 μm. A drop of collagen is then polymerized in this gap, and cells are seeded on top of it. Once the cells form a monolayer spanning the gap (magenta), the collagen is removed by enzymatic digestion leaving the monolayer suspended between the two plates. Uniaxial strain can be applied to the monolayer by displacing the flexible arm with a motorized manipulator. (B) Representative images of suspended MDCK cell monolayers subjected to different strains along the X-axis viewed in the XY (Top) and XZ (Bottom) planes. The strain to which the monolayer was subjected is indicated in the Top Left corner. Nuclei are marked with H2B GFP (green) and cell membrane with CellMask (magenta). Dashed white lines indicate the planes at which the XZ profiles were taken. (Scale bar: 10 μm.) (C) Examples of cell divisions in MDCK monolayers subjected to different strains viewed in the XY (Top) and UZ (Bottom) planes. Each cell is shown at metaphase and at the end of cytokinesis. Nuclei are marked with H2B GFP (green), cell membranes are visualized with CellMask (white), and Alexa Fluor 647 dextran (magenta) is added to the medium to allow visualization of the cell outlines. For each cell, the orientation of the spindle defines a UV referential with the U-axis oriented along the pole-to-pole axis (dashed yellow lines) and the V-axis along the metaphase plate (SI Appendix, Fig. S1A). Profile views were taken along the UZ axis. In the profile views, the horizontal yellow dashed lines indicate the plane of the monolayer, while the slanted and vertical dashed lines indicate the orientation of the metaphase plate or the division furrow. (Scale bar: 10 μm.) (D) Diagram of the spindle and division orientation measurements in the UZ plane. The spindle Z-angle at metaphase (Z-angle_m) was calculated as the angle between the line passing through the metaphase plate and the line perpendicular to the monolayer plane. Similarly, the spindle Z-angle at the end of division (Z-angle_d) was calculated as the angle between the line passing through the closed cytokinetic furrow and the line perpendicular to the monolayer plane. (E) Distribution of spindle Z-angles at metaphase (Z-angle_m) for different applied strains. Gray shaded area highlights Z-angles <30°. The number of mitotic cells examined for each condition was N = 147 for −30% strain, N = 81 for 0% strain, N = 27 for 30% strain, and N = 68 for 50% strain. Experiments were performed on n = 14 independent days for −30% strain, n = 8 independent days for 0% strain, n = 4 independent days for 30% strain, and n = 8 independent days for 50% strain. The P-value compared with 0% strain was P = 0.003 for −30% strain, P = 0.93 for 30% strain, and P = 0.243 for 50% strain. (F) Difference between spindle Z-angles at the beginning of metaphase and the end of division for each applied strain. The data correspond to the same experiments as in (E). Distributions were compared with 0 with a Z-test. The P value was P = 0.965 for −30% strain, P = 0.992 for 0% strain, P = 0.956 for 30% strain, and P = 0.999 for 50% strain. (E and F) Box plots indicate the 25th and 75th percentiles, the red line indicates the median, and the whiskers extend to the most extreme data points that are not outliers. Individual data points are indicated by black dots.

To characterize the orientation of division in suspended epithelia, we acquired confocal stacks of the monolayers every minute for 1 h. To allow visualization, we imaged cells expressing the nuclear marker H2B-GFP with their cell membranes fluorescently labeled. We define the X-axis as the direction of tissue stretch, the Y-axis as the axis perpendicular to X in the plane of the monolayer, and the Z-axis as the apicalbasal axis (Fig. 1 A and B). For each division, we also define a UV referential centered on the cell of interest with the V-axis taken along the midline of the metaphase plate, and a perpendicular U-axis, which corresponds to the pole-to-pole axis. The UV plane is coplanar with the XY plane but is rotated by an angle, which defines the orientation of the spindle in the plane with respect to the direction of stretch (or the “X-angle”, SI Appendix, Fig. S1A). To quantify the orientation of division with respect to the plane, we generated a UZ profile and measured the orientation of the mitotic spindle relative to the plane of the tissue (or “Z-angle”, Fig. 1 C and D and SI Appendix, Fig. S1A). For metaphase cells, the Z-angle was defined as the angle between the line going through the metaphase plate and a line perpendicular to the monolayer plane (see Methods, Fig. 1 C and D, Top row and SI Appendix, Fig. S1A). After anaphase, as cells underwent cytokinesis, the Z-angle was defined as the angle between the line going through the furrow and the normal to the monolayer plane (see Methods and Fig. 1 C and D, Bottom row). We found that in nonperturbed monolayers (exposed to 0% strain), divisions are oriented so that all cells divide within 28° of the monolayer plane (median = 5.1°, N = 81 cells, Fig. 1E and SI Appendix, Fig. S1B). Although some cells experienced large transient changes in the spindle Z-angle between metaphase and the end of division, the difference in orientation between these two time-points was not significantly different from 0 (median = −1.5°, z-test compared with 0: P = 0.99, Fig. 1F and SI Appendix, Table S1). Therefore, under control conditions, cell divisions in suspended MDCK epithelia lie within the epithelial plane, consistent with previous reports examining tissues growing on a substrate (31, 32).

Out-of-plane division in epithelia has been observed when cell density increases in physiological and pathological conditions. To mimic this situation, we subjected epithelial monolayers to a −30% compressive strain that significantly increases cell density (see Methods, Fig. 1 B and C and SI Appendix, Fig. S1C). In these experiments, the magnitude of compressive strain and strain rate were chosen based on our previous work (32), such that the tissues stayed planar at all times. When we examined the impact on division orientation, we found that compressive strain significantly changed the spindle Z-angle distribution resulting in a doubling of the median spindle tilt (median = 10.1°, P = 0.003, Wilcoxon rank sum test (WRST), based on a threshold for significance of P = 0.01, Fig. 1E and SI Appendix Fig. S1B). By contrast, the application of tensile strains of 30% and 50% did not significantly change the Z-angle distribution (median = 5.3°, P = 0.93 and median = 8.2°, P = 0.24, respectively, WRST, Fig. 1E) and did not significantly alter the orientation of spindles as they transitioned from metaphase to anaphase (Fig. 1F and SI Appendix, Fig. S1B and Table S1). Based on the distribution of spindle orientations at 0% strain, we defined out-of-plane divisions as occurring for Z-angles ≥ 30°, which would be considered as outliers in the 0% strain data. To compare the prevalence of out-of-plane divisions in each condition, we categorized our data into spindles dividing in the plane (Z-angle < 30°) and out-of-plane (Z-angle ≥ 30°), and compared conditions using Fischer’s exact test (FET), using a threshold for significance of P = 0.01. Whereas no mitotic cell had a Z-angle larger than 30° at metaphase at 0% strain (0/81 divisions), 11% were misoriented when the monolayer was subjected to −30% compressive strain (16/147 divisions). A significant increase in the prevalence of out-of-plane divisions was only seen following compressive strain, although we did observe occasional out-of-plane divisions for 50% strain (SI Appendix, Fig. S1D). Taken together, these data show that the application of compressive strain leads to an increase in the frequency of out-of-plane divisions.

Cell Shape, Dimensions, and Density Do Not Correlate with More Frequent Out-of-Plane Division.

As previous work has highlighted roles for cell shape, cell height, and cell density in regulating the orientation of divisions, we examined the relevance of these parameters to the increased out-of-plane division observed in compressed monolayers. For division in the plane of the tissue to be possible, the dimensions of the cell must be larger than the spindle length, and the cell height must be larger than the height of chromosomes congregating at the metaphase plate (Fig. 2A). Compression of epithelial monolayers shortens cells along the axis of compression (X-axis) and lengthens them along the out-of-plane axis (Z-axis) (33). Conversely, stretch elongates cells along the X-axis and thins them along the Z-axis. Importantly, in this system, neither manipulation changes the cell size along the Y-axis (33).

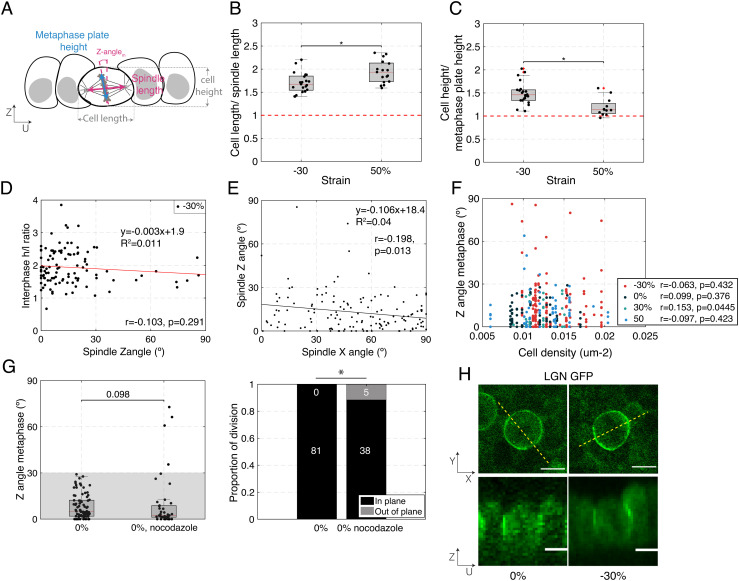
Fig. 2.

Cell shape, cell density, or localization of the spindle positioning machinery do not correlate with increased out-of-plane division induced by mechanical manipulation. (B–D, F) Box plots indicate the 25th and 75th percentiles, the red line indicates the median, and the whiskers extend to the most extreme data points that are not outliers. Individual data points are indicated by black dots. (A) Diagram indicating cell and spindle measurements in the UZ plane. Cell width is measured along the U-axis and cell height along the Z-axis. The bounds of the cell were determined from the CellMask fluorescence signal. The metaphase plate height was determined as the extent of the H2B GFP signal, and the spindle length was determined as the pole to pole distance visualized using SiR-tubulin fluorescence signal. (B) Ratio of cell width to spindle length for dividing cells in compressed (−30%) and stretched monolayers (50%). N = 21 cells for −30% strain and N = 17 cells for 50% strain. Data from n = 2 and n = 1 independent days, respectively. (C) Ratio of cell height to metaphase plate height for dividing cells in compressed (−30%) and stretched monolayers (50%). N = 22 cells for −30% strain and N = 12 cells for 50% strain. Data from n = 2 and n = 1 independent days, respectively. (D) Ratio of cell height h to length l at interphase as a function of spindle Z-angle for dividing cells in compressed monolayers (−30%). N = 102 cells from n = 14 independent days. Correlation coefficient, r = −0.103, P-value (two-tailed Student's t-distribution) = 0.291. (E) Spindle Z-angle as a function of spindle X-angle for cells in monolayers subjected to −30% strain. The solid line shows the linear regression. The slope of the regression and the coefficient of determination R² are indicated on the graph. N = 142 cell divisions. Correlation coefficient, r = −0.198, P-value (two-tailed Student's t-distribution) = 0.013. (F) Spindle Z-angle as a function of cell density for monolayers subjected to different amplitudes of uniaxial strain. N = 147 cells for −30% (red dots), 81 cells for 0% (black dots), 27 cells for 30% (light blue dots), and 68 cells for 50% strain (dark blue dots). Experiments were performed on n = 14, n = 8, n = 4, and n = 8 independent days. −30%: Correlation coefficient, r = −0.063, P-value (two-tailed Student's t-distribution) = 0.432. 0%: Correlation coefficient, r = 0.099, P-value (two-tailed Student's t-distribution) = 0.376. 30%: Correlation coefficient, r = 0.153, P-value (two-tailed Student's t-distribution) = 0.445. 50%: Correlation coefficient, r = −0.097, P-value (two-tailed Student's t-distribution) = 0.423. (G) Left – Distribution of spindle Z-angles at metaphase for untreated monolayers and monolayers treated with 20 nM nocodazole. WRST (P = 0.098). Gray box highlights Z-angles <30°. N = 81 mitotic cells for 0% strain, N = 39 for nocodazole treatment. Experiments were performed on n = 8 and n = 2 independent days, respectively. The data shown for 0% strain are from Fig. 1E. Right – Proportion of spindles dividing in-plane and out-of-plane as a function of strain. Out-of-plane divisions are shown in gray and in-plane divisions in black. The number of divisions in each category is indicated in the corresponding region of the bar. Comparison of nocodazole treated cells with untreated cells with a FET: P = 0.004. (H) Representative localization of LGN in dividing cells in a monolayer subjected to 0% and −30% compressive strains viewed in XY (Top) and UZ (Bottom) planes. Dashed yellow lines indicate the locations at which UZ profiles were taken. (Scale bars: 10 μm.)

To compare the cell dimensions to the spindle length, we measured the cell length along the U-axis using a fluorescent membrane marker and the pole-to-pole length using fluorescently labeled metaphase spindles. The height of the metaphase plate measured from the H2B GFP signal in the UZ plane was compared with the cell height measured from the membrane marker (see Methods and Fig. 2A). With these measurements, it became clear that neither metaphase plate height nor spindle length changed with compression (SI Appendix, Fig S2 A and B). Metaphase cell height h did not change with compression but decreased with stretch (SI Appendix, Fig. S3E). Conversely, metaphase cell length l decreased with compression but did not change with stretch (SI Appendix, Fig. S3D). These changes in shape were more limited than in interphase cells (SI Appendix, Fig. S3 A and B), perhaps because of mechanical differences between metaphase and interphase cells (34). As a consequence, the ratio of cell length to spindle length decreased with compression, while the ratio of cell height to metaphase plate height increased (Fig. 2 B and C). However, since both ratios remained above one, it is unlikely that the spindle is physically constrained by the cell dimensions under these conditions.

Next, we investigated if the cell shape after deformation might be responsible for the increased incidence of out-of-plane division in compressed monolayers. For each cell that went on to divide after deformation, we measured the length l along the U-axis and height h and characterized cell shape by computing the height/length (h/l) ratio. We could not find any correlation between the spindle Z-angle and h/l ratio for cells that were in interphase (Fig. 2D and SI Appendix, Fig. S4F) or metaphase (SI Appendix, Fig S4C) at the time of deformation. Similarly, we were unable to observe a correlation between Z-angle and h or l in cells that were in metaphase when the mechanical deformation was applied (SI Appendix, Fig. S4 A and B) or in cells that entered metaphase after mechanical deformation (SI Appendix, Fig. S4 D and E). To further investigate potential differences between in-plane and out-of-plane divisions, we categorized metaphase cells in compressed monolayers as either in-plane (Z-angle < 30°) or out-of-plane (Z-angle ≥ 30°). We compared h, l, and h/l ratios for cells from each category but could find no difference (SI Appendix, Fig. S5). Overall, our data suggest that the higher frequency of out-of-plane spindle orientation observed in compressed monolayers does not correlate with the shape or dimensions of cells after compression.

Compression induces a change in cell height, cell length, and cell shape (SI Appendix, Fig. S3) alongside a change in the Z-angle distribution and an increase in the frequency of out-of-plane division. Therefore, we asked if spindle Z-angle correlated with changes in cell dimensions $\delta l$, $\delta h$, and $\delta (\frac{h}{l})$ induced by compression (see Methods). However, no correlation was apparent for cells that were in metaphase when the mechanical deformation was applied or cells that entered metaphase after mechanical compression (SI Appendix, Fig. S6).

Cells within nondeformed monolayers show a quasiuniform distribution of their long axis orientation in the XY plane (30). When the monolayer is uniaxially deformed, the strain along a cell’s long axis will depend on its orientation with respect to the direction of stretch. For example, in response to monolayer compression, cells oriented along the X-axis will be subjected to a decrease in their long axis length, while those oriented along the Y-axis will not feel any change because the cell dimensions in the Y-axis are not affected by compression (33). Therefore, one might expect spindles oriented along the X-axis to divide out-of-plane in response to shortening of the cell long axis, while those oriented along the Y-axis might not. This was not borne out by the data, since there was no observable correlation between a spindle’s Z-angle and its orientation in the XY plane (X-angle, Fig. 2E).

Finally, since previous work has demonstrated that epithelia possess a well-defined homeostatic density that they return to following a perturbation (35, 36), we considered the possibility that out-of-plane divisions might be regulated by cell density or a change in density (SI Appendix, Fig. S1C). In suspended MDCK monolayers, density can only be varied between 0.005 and 0.02 cells.μm⁻² because less dense monolayers rupture, while denser seeding leads to “lumpy” monolayers with regions of multilayering. Within this experimentally attainable range of cell densities, our results show no correlation between cell density and the metaphase spindle Z-angle (Fig. 2F) nor between the change in density and the spindle Z-angle (SI Appendix, Fig. S7A).

Overall, neither cell shape, cell dimensions, cell density, nor orientation correlated with an increased frequency of division out-of-plane or spindle Z-angle. Compression led to changes in cell shape, cell dimensions [$\delta l$, $\delta h$, and $\delta (\frac{h}{l})$], and density alongside changes in the frequency of out-of-plane division, but none of these parameters were correlated with spindle Z-angle. Therefore, there did not appear to be a deterministic link between Z-angle and any parameter we examined, although we could not exclude the existence of stochastic links.

Interaction of Astral Microtubules with the Cortex Is Necessary for Orientation of Division in the Plane.

In isolated MDCK cells grown on an adhesive substrate, spindle orientation results from the interactions of astral microtubules with the actin cortex, such that loss of astral microtubules results in an increase in spindle Z-angle (32). To test whether this is also the case in our system, we treated mechanically unperturbed suspended monolayers with a concentration of nocodazole sufficiently low to affect astral microtubules without preventing division (13) (SI Appendix, Fig. S7B). This treatment resulted in an increase in the incidence of metaphase spindle Z-angles larger or equal to 30° (5/43 divisions, P = 0.004, FET, Fig. 2G). This was the case even though the orientation of the whole population of spindles was not significantly changed (P = 0.098, WRST, Fig. 2G). Intriguingly, when outliers were not included, spindles displayed a narrower distribution in orientations than in control conditions. Overall, these data suggested that interaction between astral microtubules and the cortex remains essential for correct metaphase spindle orientation despite the lack of a substrate.

Interactions between astral microtubules and the cell cortex are usually mediated by a complex formed by Gαi, LGN and NuMA. Moreover, previous work has shown that LGN recruitment to intercellular junctions in adherent epithelia depends strongly on E-cadherin adhesions (9) and is promoted by tension across these complexes (14). These data suggested that changes in the localization of this machinery might promote spindle reorientation in response to tissue strain. To better test this idea, as a measure of the local activity of Gαi, LGN, and NuMA, we examined LGN–GFP localization in epithelial monolayers in the presence and absence of a 30% compressive strain. In both cases, LGN localized to the cell periphery in the XY plane at metaphase, with a weaker localization at the cell equator in the vicinity of the metaphase plate, and stronger localization at the poles. In the UZ plane, LGN localized homogenously along the entire height of the intercellular junction, consistent with previous reports examining MDCK cysts (14, 23) (Fig. 2H). Our experimental approach did not allow us to determine whether the amount of LGN at junctions changed in response to compression, but levels of LGN remained sufficiently high to be detectable. Although we could not exclude the possibility that the localization of LGN or its associated proteins is specifically lost or perturbed in cells that divide out-of-plane, changes in the localization of the spindle positioning machinery appear unlikely to explain the increased occurrence of out-of-plane division in response to a compressive strain.

Reduction in Tissue Tension Increases the Frequency of Out-of-Plane Division.

Previous work has shown that increases in cell density precede reorientation of division out-of-plane (27) and that density increase is accompanied by a decrease in tissue tension (28). For example, in the Drosophila notum, cell density is the highest in the midline, and tissue tension is the lowest in that region (28). Therefore, given the lack of correlation between cell density and spindle Z-angle (Fig. 2F), we hypothesized that the orientation of division with respect to the tissue plane may be sensitive to tissue tension rather than cell density. In support of this, tissue tension affects spindle orientation in the XY plane of the monolayer (2, 15–18) and other work hypothesized that it may influence spindle positioning in the XZ plane in the mouse epidermis (24, 27). However, an accurate characterization of tissue stresses and how they influence spindle orientation is missing because of the difficulty of measuring stress in vivo. Further complexity arises because, in living tissues, tension can emerge from either active or passive processes. Active stress originates from the action of myosin motors on the cytoskeleton that is transmitted to other cells through adhesion complexes to generate tissue tension, whereas passive stresses arise from deformation of cytoskeletal networks in response to external forces applied on the tissue. Previous work has shown that both types of stress are present in epithelial monolayers subjected to deformation (37). Therefore, we examined the influence of a reduction in active and passive stresses on cell division orientation.

We first characterized resting tissue tension in suspended monolayers (see Methods, Fig. 3A, and ref. 32). At 0% strain, the tissue tension was 238 ± 148 Pa (Fig. 3 C and D). The application of −30% compressive strain significantly reduced tissue tension to 52 ± 51 Pa (P = 0.004, WRST compared with 0% strain), suggesting that the frequency of out-of-plane division may increase when tissue tension is low.

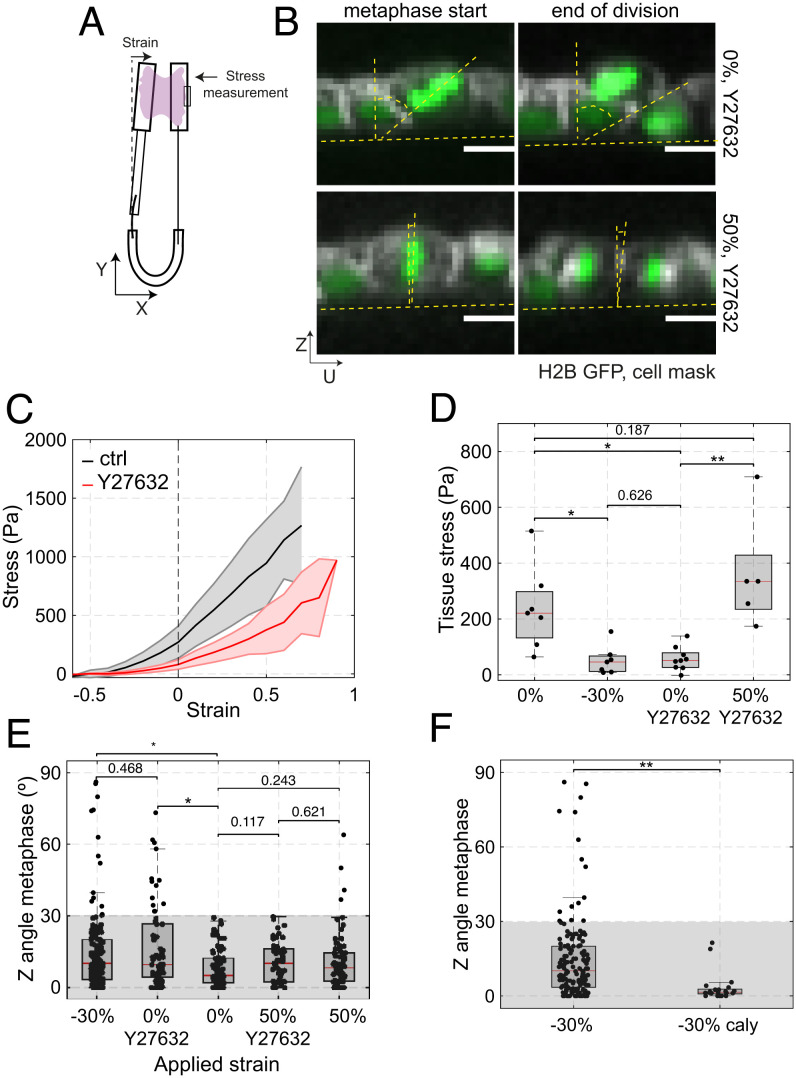
Fig. 3.

The accuracy of in-plane cell division is controlled by tissue tension. (D–F) Box plots indicate the 25th and 75th percentiles, the red line indicates the median, and the whiskers extend to the most extreme data points that are not outliers. Individual data points are indicated by black dots. (A) Diagram of the device used for measurement of stress during application of uniaxial strain. Monolayers are cultured between a reference rod and a flexible rod. Measurement of the deflection of the flexible rod allows determination of the stress applied to the epithelium (see Methods). (B) Example of cell division in a monolayer treated with 50 μM Y27632 at 0% (Top row) and 50% strain (Bottom row). Spindle Z-angle is measured at the beginning of metaphase (Left) and at the end of division (Right). Nucleic acids are visualized with H2B GFP (green), the cell membrane is labeled with CellMask 568 dye (white). In the profile views, the horizontal yellow dashed lines indicate the plane of the monolayer, while the angle between the slanted and vertical dashed lines indicate the orientation of the metaphase plate or the division furrow. (Scale bars: 10 μm.) (C) Tissue stress as a function of strain in response to a ramp in deformation applied at low strain rate (0.5%.s⁻¹) for control (black) and Y27632-treated (red) monolayers. Solid lines indicate the mean and the shaded area shows the SD. N = 7 monolayers for control and N = 8 monolayers for Y27632 treatment. n = 4 and n = 5 independent days, respectively. (D) Tissue stress in MDCK monolayers as a function of strain in control conditions and in monolayers treated with 50 μM Y27632. WRST, P = 0.0041 (−30%, 0%), P = 0.626 (−30%; 0% + Y27632), P = 0.0009 (0% + Y27632, 50% + Y27632), P = 0.187 (0%, 50% + Y27632). (E) Distribution of spindle Z-angles at metaphase for nontreated monolayers at −30%, 0%, and 50% strain, and monolayers treated with 50 μM Y27632 at 0% and 50% strains. Gray box highlights Z-angles <30°. The number of mitotic cells examined for each condition was N = 147 for −30% strain, N = 66 for 0% strain with Y27632, N = 81 for 0% strain, N = 53 for 50% strain with Y27632, and N = 68 for 50% strain. Data from n = 14, n = 8, n = 8, n = 11, and n = 8 independent days, respectively. The data shown for −30% strain, 0% strain, and 50% is from Fig. 1E. Comparisons are as follows: P(0%, −30%) = 0.003, P(0%, 0% + Y27632) = 0.002, P(0%, 50% + Y27632) = 0.117, P(0%, 50%) = 0.243, P(−30%, 0% + Y27632) = 0.468, P(50%, 50% + Y27632) = 0.621. (F) Distribution of the spindle Z-angles at metaphase for monolayers subjected to −30% strain in control conditions or treated with 35 nM calyculin. WRST, P = 1.945 10⁻⁵. Gray box highlights Z-angles <30°. N = 147 mitotic cells for −30% strain and N = 21 for −30% strain with calyculin treatment. Data from n = 14 and n = 2 independent days, respectively. The data shown for −30% strain is from Fig. 1E.

Our previous work has shown that, at 0% strain, most of the tension in the tissue originates from active stresses due to myosin contractility in the submembranous actin cortex (33, 37). Furthermore, in dividing cells, cortical actomyosin plays a crucial role in enabling proper orientation and centring of the mitotic spindle (16, 38, 39). This led us to investigate whether a reduction in tissue stress induced through the treatment of monolayers with an inhibitor of rho-kinase would also increase the frequency of out-of-plane divisions in the absence of tissue compression. Treatment with Y27632 significantly decreased tissue tension to 57 ± 42 Pa at 0% strain, similar to the effect of a −30% compression (Fig. 3 C and D, P = 0.12 compared with −30% compression, WRST).

Importantly, in Y27632-treated monolayers, reduction in tension was accompanied by an increase in out-of-plane divisions (Fig. 3 B and E and SI Appendix, Fig. S8A, 14/66 divisions, P = 0.001, FET), as was the case for compressed monolayers. Again, spindle orientation was not correlated with cell dimensions or cell shape (h/l ratio) (SI Appendix, Figs. S9 A and B and S10). Thus, we observed an increased frequency of out-of-plane division in both compressed and Y27632-treated monolayers despite cell shape being different between these two conditions (SI Appendix, Fig. S9 C and D). As no deformation was applied to Y27632-treated monolayers, these experiments further indicate that the frequency of out-of-plane division does not correlate with changes in cell dimensions, shape, or density. Finally, the localization of LGN did not appear qualitatively changed by the Y27632 treatment (SI Appendix, Fig. S9G). Overall, these data further suggest that changes in shape, density, or localization of LGN cannot account for the observed increase in the frequency of out-of-plane division but that a decrease in tissue tension might.

Increasing Active or Passive Stress Reduces Out-of-Plane Divisions in Monolayers with Low Tension.

Since decreasing tissue tension through either chemical treatment or compression increased the occurrence of out-of-plane divisions, we asked if the accuracy of in-plane orientation of division could be restored by treatments that increased tissue tension by orthogonal means.

To do so, we first examined if the increased frequency of out-of-plane division induced by chemical inhibition of contractility could be rescued by stretching the monolayer such that the original tissue tension was restored. For this, we characterized the stress response of Y27632-treated monolayers and compared their stress–strain curves with those of control monolayers (Fig. 3C). Our measurements showed that application of a 50% stretch to a Y27632-treated monolayer results in a tissue tension comparable to that in control monolayers at 0% strain (Fig. 3 C and D). We then examined the orientation of cell division in monolayers treated with Y27632 subjected to a 50% stretch. In these conditions, spindle Z-angles returned to a distribution similar to that in nonstretched control monolayers (Fig. 3E, P = 0.12, WRST) and the frequency of out-of-plane division returned to control values (1/53 divisions, P = 0.002 FET compared with Y27632 alone, SI Appendix, Fig. S8A). This was the case despite differences in interphase and mitotic cell shape between nonstretched control monolayers and stretched, Y27632-treated monolayers (SI Appendix, Fig S9 E and F). Together these data further reinforce the idea that cell shape does not influence the frequency of out-of-plane divisions.

Next, we determined if more frequent out-of-plane division orientation induced by a decrease in tension due to compression could be rescued by increasing cell contractility by treating monolayers with calyculin, a phosphatase inhibitor that increases tissue tension (33). We performed experiments in which we compressed monolayers to −30% strain before adding calyculin. Our previous work indicates that, for strains of −30%, calyculin treatment increases monolayer tension to 115 ± 74 Pa (33), roughly doubling the tension of compressed tissues. Although cytokinesis was perturbed in a fraction of cells, the cells that did undergo cytokinesis divided within the plane of the monolayer as they do in control nonstretched monolayers (0/21 divisions, P = 1 FET compared with 0% strain, SI Appendix, Fig. S8B). In this case, the distribution of Z-angles was restored and was significantly different to that observed in nontreated, compressed monolayers (Fig. 3F, P = 2 × 10⁻⁵, WRST). Importantly, this rescue could be achieved without a significant change in cell shape (SI Appendix, Fig. S9 H and I).

Together, these experiments show that an increase in tissue tension is sufficient to reduce the frequency of out-of-plane divisions induced by compression or inhibition of contractility. Remarkably, active and passive tissue stresses appear interchangeable in this regard, which suggests that they are sensed in the same way by dividing cells.

Mechanical and Chemical Manipulations of the Tissue Have Similar Effects on the Mechanical Environment of Interphase and Mitotic Cells.

So far, our experiments indicate that more frequent out-of-plane division is associated with low tissue tension but, at the cellular-scale, we do not know if treatments have similar effects on cortical tension in interphase and mitotic cells. Indeed, as suspended MDCK monolayers are primarily composed of cells in interphase with only about 1–2% mitotic cells at any given time, the mechanics of monolayers largely reflects the mechanics of interphase cells, which is controlled by the submembranous actin cortex (37). When examined in isolation in vitro, mitotic cells are stiffer than interphase cells (34, 39–41), signifying that they are likely to deform less when the tissue is subjected to stretch. Since we hypothesize that the accuracy of division orientation is sensitive to tissue tension, we sought to determine if changes in the tissue tension differentially affect mitotic cells and their interphase neighbors.

We first confirmed that the previously reported differences in mechanics between mitotic and interphase cells are also observed in suspended epithelia. To do so, we subjected epithelia to cyclic uniaxial deformation with a 50% amplitude (see Methods) and imaged the change in length of interphase cells and mitotic cells along the direction of stretch. Under these conditions, interphase cells were ~2.5-fold more deformed than mitotic cells (Fig. 4 A and B), indicating that mitotic cells are ~2.5-fold stiffer than their interphase neighbors – comparable to the increase in cortical tension noted in isolated mitotic cells (34). The larger stiffness of mitotic cells and their smaller deformations during tissue manipulations suggest that stress may be unevenly distributed around the dividing cell and that they may experience mechanical stress that differs significantly from the tissue tension. To gain a conceptual understanding of how the tension in mitotic cells evolves relative to the tension in interphase cells and in the tissue, we devised a simple computational model of the monolayer to reproduce the range of experimental conditions studied above and characterize the distribution of stress in the vicinity of a mitotic cell.

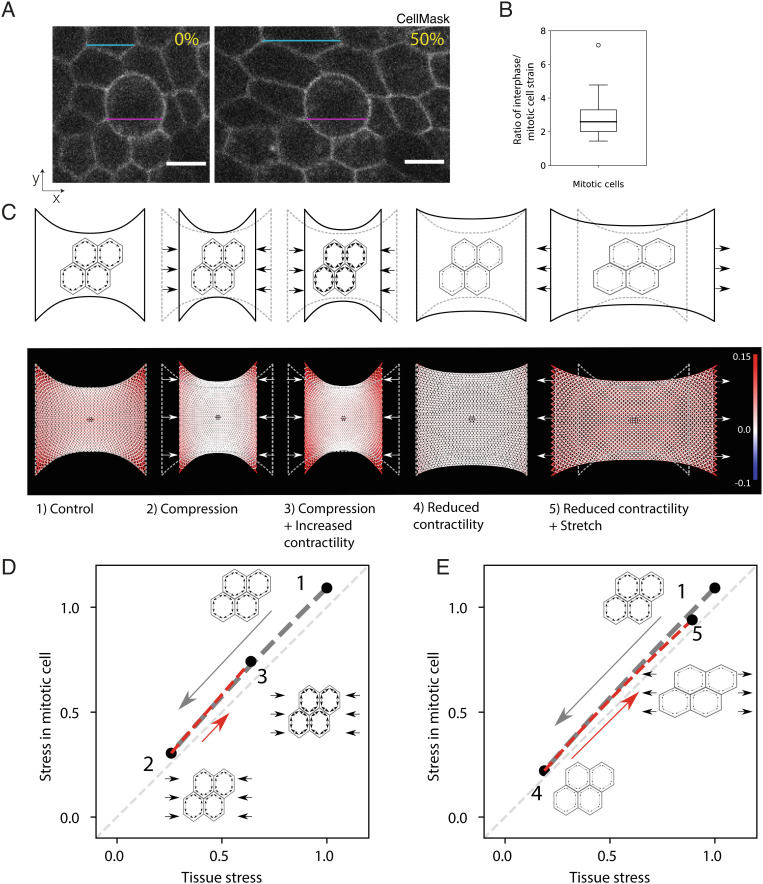
Fig. 4.

Mechanical stress at the tissue-scale reflects the mechanical environment of interphase and mitotic cells in response to chemical and mechanical manipulations. (A) Representative images of mitotic cells in a monolayer subjected to 0% strain and 50% strain. The magenta lines denote the length of the mitotic cell in both images, while the blue lines show the length of an interphase cell in both conditions. Cells are labeled with CellMask membrane stain. (Scale bars: 10 μm.) (B) Ratio of interphase cell strain to mitotic cell strain, calculated from the cyclical stretching experiments with an amplitude of ~50% shown in panel A. Strain calculated from measurements of the bounding box of the respective cell before and after a stretch is applied to the monolayer. Eleven mitotic cells were measured from 11 different monolayers. Mean strain in interphase cells is calculated from the strain in three interphase neighboring cells that do not have any junction in common with the mitotic cell of interest. The distribution’s median, first and third quartiles, and range are represented by the central bar, bounding box, and whiskers, respectively. An outlier is represented by a dot. (C) Finite element model predictions of the stress distributions in monolayers subjected to mechanical and chemical manipulations. Top: schematic representation of the experimental conditions: 1) a monolayer in its initial configuration clamped at both ends (0% strain) and subjected to a tensile stress arising due to cell contractility; 2) a monolayer subjected to a −30% compressive strain applied by displacing the test rods; 3) a monolayer subjected to a −30% compressive strain and treated with a drug increasing cell contractility (calyculin); 4) a monolayer at 0% strain treated with a drug decreasing cell contractility (Y27632); 5) a monolayer treated with a drug decreasing cell contractility and subjected to a 50% tensile strain. Bottom: Stress distribution within the monolayer. The mesh representing the monolayer is color coded to display the stress in each element with red colors representing tensile stress, blue colors compressive stress, and white colors regions of low stress. A mitotic cell simulated as a stiffer inclusion is present in the center of the monolayer (dark region). Stress distributions are presented for the experimental conditions depicted above. (D) Stress in a mitotic cell in the center of a monolayer as a function of the stress in the tissue in response to compressive strain followed by a chemical treatment to increase contractility. In the monolayer’s initial configuration, the stress on the mitotic cell is approximately equal to the tissue stress (state 1, corresponding to condition 1 in panel C). When a compressive strain is applied to the monolayer, the stress in the mitotic cell decreases in proportion to the decrease in the tissue stress (gray dashed line, transition from state 1 to 2 in panel C – gray arrow). Increasing prestress in the cells by increasing myosin contractility by calyculin treatment leads to a partial recovery of the tensile stress in the tissue and the mitotic cell (red dashed line, transition from state 2 to 3 in panel C – red arrow). All stresses are normalized to the tissue stress in state 1. (E) Stress in a mitotic cell in the center of a monolayer as a function of the stress in the tissue in response to a chemical treatment to decrease contractility followed by application of a tensile strain. In the monolayer’s initial configuration, the stress on the mitotic cell is approximately equal to the tissue stress (state 1, corresponding to condition 1 in panel C). When a chemical treatment that decreases cellular prestress is applied, the stress in the tissue and the cell drops to values close to 0 (gray dashed line, transition to state 4 in panel C – gray arrow). To recover a stress similar to condition 1, a 50% stretch is applied to the monolayer (red dashed line, transition from state 4 to 5 in panel C – red arrow). All stresses are normalized to the tissue stress in state 1.

In the model, the monolayer is a 2D elastic material discretized into a triangular mesh in which cells are represented as hexagons (42) (SI Appendix, Fig. S11). Because most of the tension is borne by the basal surface of the monolayer (43), all springs corresponding to interphase cells have the same spring constant k. Active tension γ is imposed by introducing a difference between the reference length l_init of the junction and its rest length l₀ (see Materials and Methods). First, we adjusted the parameters of the model to obtain a stress–strain relationship for the virtual tissue similar to that measured experimentally in suspended monolayers at low strain rates (37) (Fig. 3C). Then, we modeled the mitotic cell as an inclusion in the center of the sheet of cells (blue cell, SI Appendix, Fig. S11) with different values for the spring constant k and rest length l₀ such that their active tension is 2.5 times larger than in interphase cells (34) and their stiffness is increased by a factor 2.5 to fit the lower deformation of mitotic cells observed in response to stretch (Fig. 4 A and B).

Using the model, we can compare the tension in a mitotic cell, with the tension in neighboring interphase cells and with the overall tissue tension. To simulate mechanical manipulations, we apply a compressive or tensile strain to the network. To simulate chemical treatments affecting contractility, we change junctional tension γ (Fig. 4 C–E). For all experimental conditions, our simulation data show that the tension in the mitotic cells remains close to tension in the neighboring interphase cells and in the tissue as a whole (Fig. 4 D and E). However, the model shows that the increased rigidity of the mitotic cells amplifies the mechanical stress they experience, despite them being less deformed (Fig. 4 D and E). The model also illustrates the mechanical interplay between contractility and extrinsic deformations in controlling the stress to which mitotic cells are subjected. Thus, when monolayers are compressed, tissue tension decreases, and as a consequence the stress that the mitotic cells experience also decreases (transition from 1 to 2, Fig. 4D). With the addition of calyculin to increase contractility, there is an increase in tissue tension as well as in the tension experienced by mitotic cells (transition from 2 to 3, Fig. 4D). Further, our analysis reveals that the interplay between the increased contractility at the cell periphery and the tissue boundary conditions restores a cell stress tensor very close to that observed in control conditions (SI Appendix, Figs. S12 and S13). Similarly, when contractility was inhibited (transition from 1 to 4, Fig. 4E), the stress experienced by mitotic cells decreased in proportion to the tissue stress and the stress tensor in mitotic cells became similar to that in compressed monolayers (SI Appendix, Fig. S13). The application of stretch restored the stress experienced by mitotic cells in the model to a level and tensor similar to that in control conditions (transition from 4 to 5, Fig. 4E and SI Appendix, Fig. S13). Thus, the model suggests that the tissue tension measured in our experiments is likely a good proxy for the tension experienced by the mitotic cells.

Chemical Treatments that Modulate Tissue Tension Have Identical Effects on the Surface Tensions of Interphase and Mitotic Cells.

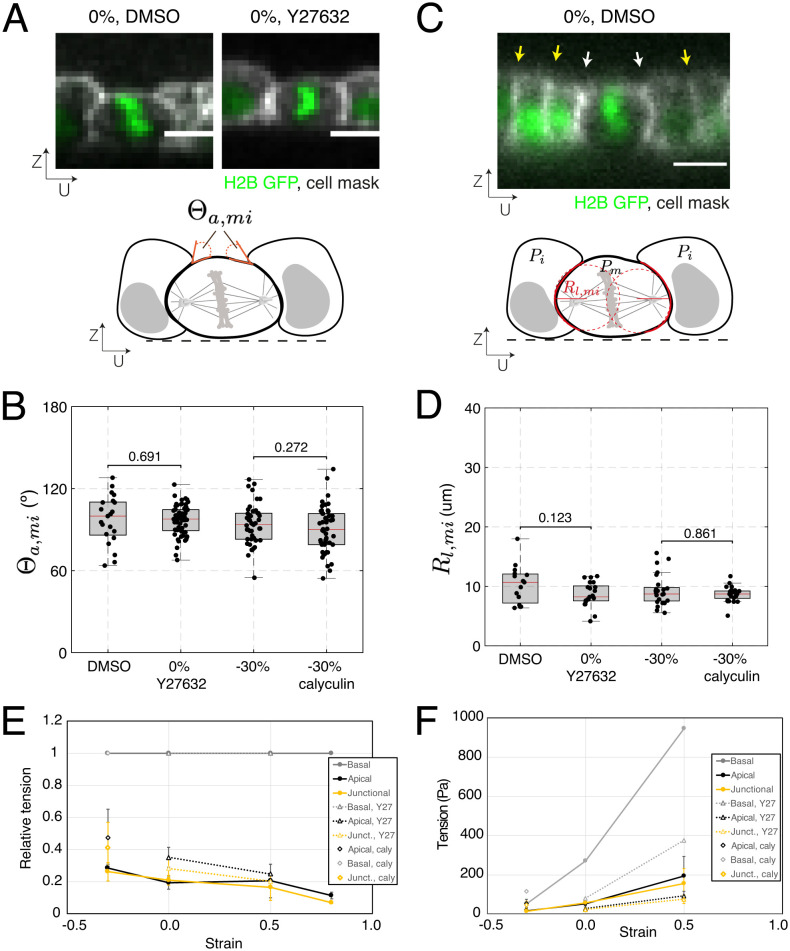
Because cortical mechanics likely play an important role in the mechanical response of cells within the monolayer, we characterized the interaction of mitotic cells with their interphase neighbors by measuring their apical angle of contact Θ_a,mi (Fig. 5A). This angle is determined by the balance of tensions in the apical cortices of the mitotic cell and its interphase neighbors, together with the tension at the intercellular junction through the Young-Dupré relationship (44) (see Methods). A change in the apical angle of contact Θ_a,mi in response to a treatment would indicate that the cortical tension in mitotic cells and interphase cells respond differently to treatment. We compared Θ_a,mi in monolayers treated with Dimethyl sulfoxide (DMSO) and Y27632, since rho-kinase inhibition leads to more frequent out-of-plane divisions without any detectable change in mitotic cell shape. Θ_a,mi did not change in response to treatment (P = 0.691, WRST, Fig. 5B). As treatment of compressed monolayers with calyculin reduces out-of-plane divisions without changes in cell shape, we examined its effect on Θ_a,mi but found no effect (P = 0.162, WRST, Fig. 5B). These data suggest that both drug treatments affect cortical tension in a similar way in mitotic and interphase cells, in line with the conclusions of our simulations.

Fig. 5.

Treatments that modulate tissue tension have identical effects on the surface tension of interphase and mitotic cells. (B, D) Box plots indicate the 25th and 75th percentiles, the red line indicates the median, and the whiskers extend to the most extreme data points that are not outliers. Individual data points are indicated by black dots. (A, C) (Scale bars: 10 µm.) (A) Top: Representative profile of a dividing cell surrounded by interphase neighboring cells within a monolayer at 0% strain, treated with DMSO or Y27632. Nucleic acids are visualized by H2B GFP (green), the cell membrane is labeled with CellMask 568 dye (white). Bottom: Diagram indicating the apical angle of contact between the mitotic cell and its interphase neighboring cells, Θ_a,mi. (B) Distribution of apical angles of contact between dividing cells and their interphase neighbors at 0% strain, measured in monolayers treated with DMSO or Y27632, and at −30% compression, measured in control monolayers or monolayers treated with calyculin. DMSO vs. Y27632: WRST, P = 0.691; N = 19 cells, DMSO; N = 60 cells, Y27632; n = 4 independent days, DMSO; n = 8 independent days, Y27632. −30% compression vs. −30% compression with calyculin: WRST, P = 0.272; N = 30 cells, −30% compression; N = 22 cells, −30% compression with calyculin; n = 14 independent days, −30% compression; n = 2 independent days, −30% compression with calyculin. (C) Top: Representative profile of a dividing cell surrounded by its interphase neighboring cells within a monolayer at 0% strain, treated with DMSO. Yellow arrows indicate intercellular junctions between interphase cells, and white arrows indicate intercellular junctions between the mitotic and interphase cells. Nucleic acids are visualized by H2B GFP (green), the cell membrane is labeled with CellMask 568 dye (white). Bottom: Diagram indicating measurement of the lateral radii of curvature of mitotic cells (red dashed lines). (D) Distribution of lateral radii of curvature for dividing cells in monolayers at 0% strain, treated with DMSO or Y27632, and at −30% compression, measured in control monolayers or monolayers treated with calyculin. DMSO vs. Y27632: WRST, P = 0.123; N = 15 cells, DMSO; N = 21 cells, Y27632; n = 4 independent days, DMSO; n = 8 independent days, Y27632. −30% compression vs. −30% compression with calyculin: WRST, P = 0.861; N = 21 cells, −30% compression; N = 21 cells, −30% compression with calyculin; n = 14 independent days, −30% compression; n = 2 independent days, −30% compression with calyculin. (E) Relative surface tension in the apical, basal, and junctional surfaces as a function of strain for control monolayers, monolayers treated with Y27632, and monolayers treated with calyculin. Surface tensions are normalized to the basal tension for each strain magnitude. The error bar is the SD of the surface tension (calculated as the mean of 10 cells per monolayer). (F) Absolute surface tension as a function of strain for apical, basal, and junctional surfaces for control, monolayers treated with Y27632, and monolayers treated with calyculin. Basal tension is taken equal to the monolayer tension (Fig. 3C), and apical and junctional tensions are calculated using panel E. The error bar is the SD of the surface tension (calculated as mean of 10 cells per monolayer).

As a complement to this analysis, we also measured the curvature of lateral junctions R_l between mitotic cells and their interphase neighbors using UZ profiles. This curvature reports on the difference in pressure between adjacent cells through Laplace’s law: $R_l=2\frac{{\gamma }_l}{(P_2-P_1)}$, where γ_l is the tension in the junction between two cells, and P₂ and P₁ are the pressures in each of the cells (Fig. 5C). When intracellular pressure in adjacent cells is equal, their junction will appear straight (i.e., they have an infinitely large radius of curvature). Conversely, if the pressure is larger in one of the cells, the junction will curve away from the more pressurized cell. In suspended monolayers, junctions between interphase cells always appeared straight, whereas junctions between mitotic cells and interphase cells were always curved away from the mitotic cell (Fig. 5C). Changes in R_l in response to a treatment would indicate that the pressure in mitotic and interphase cells is affected differentially. However, our experiments showed no change in curvature of lateral junctions, R_l, when unstretched monolayers were treated with Y27632 (P = 0.123, WRST, Fig. 5D) or when compressed monolayers were treated with calyculin (P = 0.172, WRST, Fig. 5D), again suggesting that interphase cells and mitotic cells are identically affected by rho-kinase inhibition or calyculin treatment.

Overall, measurements of the apical angle of contact, Θ_a,mi, and curvature of lateral junctions, R_l, indicate that, although mitotic cells are more contractile than interphase cells, the pharmacological treatments used to modulate tissue tension do not change the relative values of cortical tension and internal pressure between mitotic and interphase cells, nor do they dramatically change the morphology of the cells.

Changes in Tissue Tension Are Reflected by Changes in Tension at Cellular Surfaces.

Our experiments could not identify morphological attributes associated with the alignment of cell division within the plane of the monolayer. However, tissue tension provided a more reliable predictor (Fig. 3 C and D), but how spindles sense this is unclear. As astral microtubules and cortical contractility were both necessary to ensure accurate division in-plane, we hypothesized that spindles may sense tissue tension through its impact on tension in the cell cortex relayed through astral microtubules. When they are integrated into epithelia, cells present clear differences in molecular composition, cytoskeletal organization, adhesion, and signalling at their apical, lateral, and basal surfaces as a result of the pathways that establish apicobasal polarity (45, 46). In consequence, apical, basal, and junctional surfaces likely differ in their mechanics as well as their response to drug treatments and deformation. In turn, changes in tension at cellular surfaces will affect the forces exerted on astral microtubules and the balance of torques acting on centrosomes to orient spindles. However, little is known about the relative magnitude of tension in each cellular surface or how tissue-scale deformation and drug treatments affect tension in these domains.

Assuming that cellular surfaces can be approximated to portions of sphere (see Methods and SI Appendix, Fig. S14D), the tension γ in a cellular surface is linked to its curvature r and internal cellular pressure P through Laplace’s law. Therefore, measuring the apical and basal radii of curvature of interphase cells allows to determine relative changes in tensions in those surfaces as a function of strain (SI Appendix, Fig S14A, see Methods). Indeed, Laplace’s law indicates that: $\frac{r_{\mathit{apical}}}{r_{\mathit{basal}}}=\frac{{\gamma }_{\mathit{apical}}}{{\gamma }_{\mathit{basal}}}$. In addition, the ratio of junctional to apical tension can be inferred from geometrical and physical considerations as: $\frac{{\gamma }_{\mathit{junctional}}}{{\gamma }_{\mathit{apical}}}=\frac{a}{r_{\mathit{apical}}}$ with $a$ being the cell length (see Methods). Therefore, measuring a, r_apical , and r_basal as a function of applied strain allows to characterize the relative evolution of surface tensions in the different subcellular domains in response to mechanical or chemical perturbations. We examined changes in radii of curvature in interphase cells because our modeling and experiments indicated that the mechanical changes in mitotic cells are proportional to those occurring in interphase cells and because this allows to gather sufficient data for statistical comparison between conditions.

At 0% strain, the radius of curvature of the basal side was approximately fivefold larger than on the apical side (SI Appendix, Fig. S14 B and C), indicating a larger tension on the basal surface that was consistent with the greater enrichment in myosin observed on the basal side of suspended monolayers (43). Both the apical and basal radii of curvature increased nonlinearly with increasing strain, with the basal radius of curvature remaining systematically larger (SI Appendix, Fig. S14 B and C). When we computed the relative tension at subcellular surfaces (normalizing basal tension to one), we found that basal tension was higher than apical and junctional tensions – whose magnitudes were very similar (Fig. 5E). With increasing strain, both junctional and apical tensions decreased relative to basal tension from ~0.3 at −30% strain to ~0.1 at 80% strain. As basal tension appeared several fold larger than apical tension, we approximated cellular basal tension to tissue tension (Fig. 3C) to estimate absolute tensions in cellular surfaces. Using this approximation, basal tension grew linearly with strain from approximately 50 Pa at −30% strain to 950 Pa at 50% (Figs. 3 C and 5 F). Apical and junctional tensions increased from ~15 Pa at −30% strain to ~150–200 Pa at 50% (Fig. 5F and SI Appendix, Fig. S14 E and F).

Tension at the apical surface and at junctions was significantly lower at 0% strain in Y27632-treated monolayers than it was in controls (P = 3.8 × 10⁻⁵, apical; P = 0.002, junctional; WRST), with magnitudes similar to those in control monolayers subjected to −30% strain (Fig. 5 E and F and SI Appendix, Fig. S14E). The application of a 50% strain to Y27632-treated monolayers increased apical and basal tensions to levels comparable to controls at 0% strain (Fig. 5 E and F and SI Appendix, Fig. S14F). Treatment of compressed monolayers with calyculin increased the junctional and apical tensions significantly compared with control compressed monolayers (P = 0.002, apical; P = 0.008 junctional; WRST), with the absolute tensions increasing to magnitudes similar to those in control monolayers at 0% strain (Fig. 5 E and F and SI Appendix, Fig. S14G).

These measurements together with our characterization of the orientation of division for different applied tissue strains and pharmacological treatments indicate that out-of-plane divisions are more frequent under conditions where tension at cellular surfaces is low.

Discussion

By mechanically manipulating suspended epithelial monolayers, we have demonstrated that the increased frequency of out-of-plane divisions correlates with low tissue tension rather than with cell shape, cell dimensions, or cell density. The impact of decreasing tissue tension was similar whether tension reduction was induced through the application of compressive strain or through chemical inhibition of myosin contractility. Furthermore, the accuracy of division orientations could be restored by orthogonal means of returning tissue tension to levels similar to those in control monolayers. Thus, the accuracy of in-plane divisions in monolayers subjected to compressive strain could be rescued by increasing cell contractility; while in monolayers in which contractility was inhibited, the frequency of out-of-plane divisions could be reduced by application of mechanical stretch. As our experiments and modeling indicate that tissue tension and cell surface tension evolve in similar ways, these data indicate that the molecular mechanism ensuring accurate in-plane division is sensitive to cellular surface tension in mitotic cells but not the exact manner in which this tension is generated. Interestingly, our data are consistent with recent work showing that a sufficiently large cortical tension is necessary for spindles to orient along the cellular long axis in the Drosophila notum midline (16). While it is not clear precisely how surface tensions in the different subcellular domains are read out by the spindle, it seems likely that junctional tensions are critical.

How cell surface tension influences the accuracy of spindle positioning in the plane is unclear. In our experiments, we rarely observed significant repositioning of the spindle between metaphase and anaphase. This suggests that the spindle position is decided as cells enter mitosis and that this is less accurate under conditions of low tension. In mitosis, spindle and centrosome positioning arise from interactions of astral microtubules with the cell cortex that generate pushing forces and pulling forces (12, 47, 48). Pushing forces arise due to growth of microtubules against the cortex; while pulling forces rely on a complex formed by Gαi, LGN, and NuMA at the plasma membrane that recruits dynein. Dynein motor activity together with microtubule shrinkage generate pulling forces (23, 49, 50). In mitotic cells within epithelia, the localization of the Gαi, LGN, and NuMA complex is restricted to intercellular junctions (23). The balance of all of the interaction forces between astral microtubules and the cortex results in a torque that acts on the centrosomes to orient spindles. In principle, both pulling and pushing forces could be sensitive to cortical tension, and as a result perturbing either could lead to changes in spindle orientation.

Pulling forces could be altered either by changes in localization of cortical regulators, changes in their enrichment, or by changes in the pulling efficiency of dynein. Our data showed that LGN was localized to cell-cell contacts in suspended monolayers, consistent with its reported localization and signifying that pulling forces are restricted to these interfaces. Qualitatively, LGN appeared to maintain its localization when tissue tension was low. Previous work has shown that high tension promotes LGN recruitment to intercellular junctions in MDCK cells (14) and therefore, we would expect that, when tissue tension is low and out-of-plane divisions are more frequent, less LGN is recruited to junctions resulting in lower pulling forces. However, whether this is the case here was not something we could determine. In addition, recent work has shown that spindles in the Drosophila notum cannot orient along the long axis of cells in the midline, where tissue tension is low (16, 28). In this system, where spindles align in mitosis, it was proposed that a less-tensed junctional cortex provides a less stable substrate for dynein motors to generate the pulling forces required to align spindles in the plane of the epithelium. Consistent with this, in C. elegans embryos whose F-actin cortex has been depolymerized, microtubules contacting the cell periphery extract membrane tethers rather than generate spindle centering forces (51). Thus, low tissue tension may decrease pulling forces emanating from intercellular junctions through a combination of lower recruitment of dynein to junctions due to lower LGN accumulation and less efficient force generation by dynein.

Pushing forces are thought to arise from the microtubule plus-end polymerizing against the cortex. When the cortex is very stiff (or tensed), new GTP-bound tubulin heterodimers cannot be added to microtubules leading to hydrolysis of the GTP cap, catastrophes, and depolymerization of the astral microtubules (52). Conversely, when the cortex is softer (or less tensed), microtubule growth can continue by deforming the cortex, leading to an increase in pushing forces. Thus, surfaces under high tension give rise to short-lived pushing forces and catastrophes, whereas surfaces with low tension give rise to longer lasting pushing forces. In MDCK cells, astral microtubules emanate from the spindle poles with a large opening angle in the UZ plane such that they likely contact each of the apical, basal, and junctional cellular surfaces (32). With these assumptions, because basal tension is several fold larger than apical tension, we would expect larger pushing forces to be generated by astral microtubules contacting the apical surface than those contacting the basal surface. Therefore, if pushing forces dominate, we would expect that the larger pushing forces against the apical surface would displace spindles toward the basal side of cells. Since we did not observe such displacement, we speculate that pulling forces dominate and that the most likely cause of spindle misalignment is a decrease in pulling forces induced by low junctional tension. Future work will be necessary to test this hypothesis directly.

Out-of-plane cell divisions are observed in physiological contexts during stratification of multi-layered epithelia such as the skin and pathologically during hyperplasia and cancer. In monolayered epithelia, out-of-plane division orientation may act as a mechanism to maintain density homeostasis by retaining a single daughter cell. In both cases, out-of-plane division is preceded by an increase in cell density, which may decrease tissue tension. Our data show that a decrease in tissue tension leads to increased out-of-plane division and a reduction in surface tension at the cellular scale. We speculate that lower surface tension at junctions decreases pulling forces on astral microtubules, preventing the generation of torques that can efficiently position spindles in the plane of the epithelium. Thus, the initiation of multilayering may stem from a tissue-scale mechanical change that induces a cellular-scale mechanical cue, which leads to out-of-plane division as a consequence of the feedback between the spindle positioning machinery and a less-tensed cell cortex.

Materials and Methods

MDCK Cell Culture.

MDCK cells were grown in Dulbecco's Modified Eagle Medium (DEMIM) (Thermo Fisher Scientific) supplemented with 10% fetal bovine serum (Sigma-Aldrich), 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) buffer (Sigma-Aldrich), and 1% penicillin/streptomycin in a humidified incubator at 37 °C with 5% CO2.

Generation of Suspended MDCK monolayers.

Suspended MDCK monolayers were made as described in ref. 29. Briefly, a drop of collagen was placed between two test rods and left to dry at 37 °C to form a solid scaffold. The dry collagen was then rehydrated, and cells were seeded on top of it and cultured for 48–72 h until cells covered the whole of the collagen and part of each test rod. Immediately before each experiment, the collagen scaffold was removed via collagenase enzymatic digestion, leaving the monolayer of cells suspended between the two test rods (Fig. 1A).

Supplementary Materials and Methods.

Additional materials and methods can be found in SI Appendix.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All reagents are available from the corresponding author upon request. Code and primary data are available from the UCL data repository (https://rdr.ucl.ac.uk/) with a unique doi (https://doi.org/10.5522/04/16930864) (53).