The perception of octave pitch affinity and harmonic fusion have a common origin

Abstract

Musicians say that the pitches of tones with a frequency ratio of 2:1 (one octave) have a distinctive affinity, even if the tones do not have common spectral components. It has been suggested, however, that this affinity judgment has no biological basis and originates instead from an acculturation process ‒ the learning of musical rules unrelated to auditory physiology. We measured, in young amateur musicians, the perceptual detectability of octave mistunings for tones presented alternately (melodic condition) or simultaneously (harmonic condition). In the melodic condition, mistuning was detectable only by means of explicit pitch comparisons. In the harmonic condition, listeners could use a different and more efficient perceptual cue: in the absence of mistuning, the tones fused into a single sound percept; mistunings decreased fusion. Performance was globally better in the harmonic condition, in line with the hypothesis that listeners used a fusion cue in this condition; this hypothesis was also supported by results showing that an illusory simultaneity of the tones was much less advantageous than a real simultaneity. In the two conditions, mistuning detection was generally better for octave compressions than for octave stretchings. This asymmetry varied across listeners, but crucially the listener-specific asymmetries observed in the two conditions were highly correlated. Thus, the perception of the melodic octave appeared to be closely linked to the phenomenon of harmonic fusion. As harmonic fusion is thought to be determined by biological factors rather than factors related to musical culture or training, we argue that octave pitch affinity also has, at least in part, a biological basis.

1. Introduction

Humans enjoy melody, "the essential basis of music" in the words of Helmholtz (1863/1954). A melody is a sequence of periodic sounds with specific frequency ratios, forming musical intervals that are perceived as pitch relations. The precision with which these intervals are perceived is of course limited; it depends on the listener's musical training, the intervals themselves, and other factors (Burns and Ward, 1978; Rakowski, 1990; Perlman and Krumhansl, 1996; McDermott et al., 2010; McClaskey, 2017; Graves and Oxenham, 2017). However, in the Western world at least, even people with no substantial musical education readily detect an error of only one semitone (corresponding to a frequency change of about 6 %) in the production of one note of a familiar melody (Dowling and Fujitani, 1971; Trainor and Trehub, 1994).

Throughout the human auditory system, up to the cortical level, frequency is represented tonotopically, along unidimensional neural maps (Romani et al., 1982; Talavage et al., 2004). A straightforward hypothesis, therefore, is that the representation of a melodic interval in the auditory system is simply a distance between neural excitations along an axis representing pitch as a logarithmic function of frequency. This would suggest that there is no "physiologically special" melodic interval (apart from the unison). Psychophysical results in line with this hypothesis were obtained by Kallman (1982, experiment 1), who required ordinary Western students to rate the similarity of successive pure tones as a function of their frequency ratio. The ratings smoothly decreased as the frequency ratio varied in small logarithmic steps from 1:1 to about 5:1. Remarkably, no local peak was observed for the simple frequency ratio 2:1, i.e., one octave, even though in the Western musical system two notes forming an octave interval bear the same name and are treated as equivalent sounds (Krumhansl and Shepard, 1979). Analogous findings were reported by Hoeschele et al. (2012, experiment 1).

However, at odds with these results, a number of other experiments have suggested that for a substantial proportion of human listeners, two tones forming a small-integer frequency ratio have a distinctive affinity (or similarity) in pitch. Ratios such as 3:2, 4:3, or 5:4 have been used in some of these experiments (Cohen et al., 1987; Schellenberg and Trehub, 1994, 1996), but the ratio most often used was 2:1, one octave. The demonstrations of octave pitch affinity (OPA) have been based on a variety of methodologies (Deutsch, 1973; Idson and Massaro, 1978; Kallman and Massaro, 1979; Massaro et al., 1980; Demany and Armand, 1984; Hoeschele et al., 2012; Borra et al., 2013; Jacoby et al., 2019).¹ In the eight studies that we just cited, OPA was observed using pure-tone stimuli. This is an important detail since the peripheral auditory system behaves as a spectrum analyzer (Schnupp et al., 2012). Ordinary periodic sounds are instead complex tones, and thus consist of a sum of harmonics with frequencies equal to integer multiples of a given fundamental frequency. Consequently, two complex tones one octave apart typically have common spectral components. In addition, the pitch of certain complex tones is subject to octave ambiguities (Terhardt et al., 1982, 1986), which could explain the perception of an affinity between such tones when their fundamental frequencies are one octave apart (Regev et al., 2019). The phenomenon of OPA is more intriguing when it is observed for sounds with no common spectral component and an unambiguous pitch, such as pure tones.

The origin of OPA, for sounds such as pure tones, is the subject of a basic controversy. On one side of the debate, it is contended that OPA is essentially the consequence of an acculturation process (Burns and Ward, 1982; Sergeant, 1983, Jacoby et al., 2019). According to this culturalist hypothesis, Western listeners exhibit OPA because they have learned, consciously or unconsciously, a musical grammar in which tones one octave apart are functionally equivalent. Arbitrary musical grammars can be learned quite rapidly, by mere passive exposure to sound sequences constructed from these grammars (Loui et al., 2010; Rohrmeier et al., 2011). The musical rule of octave equivalence is certainly not arbitrary, because this rule is culturally widespread (Dowling and Harwood, 1986; Brown and Jordania, 2011). However, its main origin might be unrelated to the perception of pitch relations (Burns and Ward, 1982; McPherson et al., 2020). The rule might originate from the mere fact that the sum of two complex tones one octave apart is a single complex tone, with the same period as one of the two added tones. The culturalist explanation of OPA is consistent with the fact that, within the Western adult population, sensitivity to OPA appears to be stronger in musicians than in non-musicians (Allen, 1967; Demany and Armand, 1984; Jacoby et al., 2019), although this could of course be due to an influence of sensitivity to OPA on the willingness to become a a musician. Jacoby et al. (2019) suggested in addition that the Tsimane', an Amazonian population living in isolation from Western culture, are completely insensitive to OPA. Western children tested by Sergeant (1983) showed a similar insensitivity and this led the author to assert that OPA was a "concept" rather than a percept. In line with such a view, Regev et al. (2019) found that musically educated listeners who were able to identify an octave interval as such did not manifest a sensitivity to OPA when their brain response to pitch changes was assessed via the "mismatch negativity" evoked potential.

On the other side of the debate, it is contended that OPA originates from physiological processes that are essentially independent of the cultural environment. The experimental evidence supporting this general hypothesis is currently very limited. Sensitivity to OPA has been found in two studies on non-human animals (Blackwell and Schlosberg, 1943; Wright et al., 2000); but the stimuli used by Wright et al. were spectrally rich periodic sounds. Using instead pure tones, Demany and Armand (1984) obtained results suggesting that OPA exists, and is even strong, in 3-month-old human infants. Another argument was put forth by Terhardt (1971, 1974, 1987). In his view, OPA originates from a learning process, but not from musical acculturation: what is learned is the harmonic structure of natural periodic sounds, such as human vocalizations. Due to this learning process, the pitch interval corresponding to a subjectively perfect melodic octave is the pitch interval of harmonics with a frequency ratio of 2:1 in natural periodic sounds. A well-established fact is that when musically educated listeners are requested to set two successive pure tones exactly one octave apart by adjusting their frequency ratio, the obtained ratio is generally slightly larger than 2:1 (Ward, 1954; Ohgushi, 1983; Demany and Semal, 1990; Hartmann, 1993; Rosner, 1999). Terhardt argued that this apparent anomaly ‒ often called the "octave enlargement" effect ‒ can be explained by small repulsive interactions between the representations of simultaneous pure tones in the periphery of the auditory system. He found confirmation of this hypothesis in precise measurements of the pitch of individual spectral components of complex tones. However, Peters et al. (1983) and Hartmann and Doty (1996) failed to replicate Terhardt's observations: they found that the pitch of a complex tone component is not significantly affected by the other components. Their work thus cast serious doubts on the validity of Terhardt's ideas about OPA.

Here, we report new evidence that OPA has a natural basis. More precisely, our study indicates that even for musically educated Western listeners, the pitch interval defining a subjectively perfect melodic octave is largely determined by universal auditory processes rather than by cultural factors. Our essential finding is that the perception of OPA is closely linked to the auditory phenomenon of harmonic fusion. A periodic complex tone is normally heard as a single sound, with a single pitch (related to the fundamental frequency). Yet, it is initially represented in the auditory system as a set of harmonics that, in isolation, evoke different pitches. Their subsequent fusion involves a detection of small-integer frequency ratios ("harmonicity"). When, for example, a 800-Hz harmonic is mistuned by 5 % in a complex tone with a 400-Hz fundamental frequency, adult Western listeners perceive two sounds rather than one: the mistuned harmonic is heard as a pure tone standing out of a complex tone (Moore et al., 1986; Hartmann et al., 1990). Harmonic fusion is thought to be helpful in everyday life because real-world acoustic scenes often include simultaneous periodic sounds, produced by separate sources and differing in fundamental frequency; the perceptual segregation of such sounds requires a grouping of their respective spectral components (Bregman, 1990; de Cheveigné, 1997; Kidd et al., 2003; Carlyon and Gockel, 2008; Micheyl and Oxenham, 2010; Popham et al., 2018). Harmonic fusion is apparently operative in newborn infants (Bendixen et al., 2015), in Amazonian listeners isolated from Western culture (McDermott et al., 2016; McPherson et al., 2020), and in at least some non-human mammals (Tomlinson and Schwarz, 1988; Kalluri et al., 2008; Song et al., 2016). Moreover, neural correlates of this perceptual phenomenon have been found in the auditory cortex of monkeys (Fishman and Steinschneider, 2010; Fishman et al., 2014; Feng and Wang, 2017). Thus, harmonic fusion clearly has a natural basis. This should also be the case for OPA if OPA is closely linked to harmonic fusion.

In all but three of the past studies concerning OPA and harmonic fusion, these two phenomena have been investigated in isolation. Interestingly, a similar asymmetry was observed in both cases. First, the "octave enlargement" effect mentioned above indicates that OPA is generally stronger slightly above the physical octave (2:1) than slightly below it. Second, when the listeners' task was to detect small octave mistunings in stimuli consisting of simultaneous pure tones, performance was found to be generally poorer when the octave was stretched than when it was compressed, thus suggesting that harmonic fusion is more tolerant to stretchings than to compressions (Demany et al., 1991; Borchert et al., 2011; Bonnard et al., 2013, 2017). From this resemblance, one could suspect the existence of a link between OPA and harmonic fusion. However, the three studies in which the two phenomena were examined jointly, in the same listeners, did not provide evidence for such a link (Demany and Semal, 1990; Bonnard et al., 2013, 2016). In the present study, OPA and harmonic fusion were again investigated in the same listeners, but with a new methodology. We provide evidence that the two phenomena are linked by showing that the perception of OPA by a given listener is highly correlated with the perception of harmonic fusion by the same listener.

2. Experiment 1: Detection of octave mistunings in quiet

2.1. Method

2.1.1. Conditions and stimuli

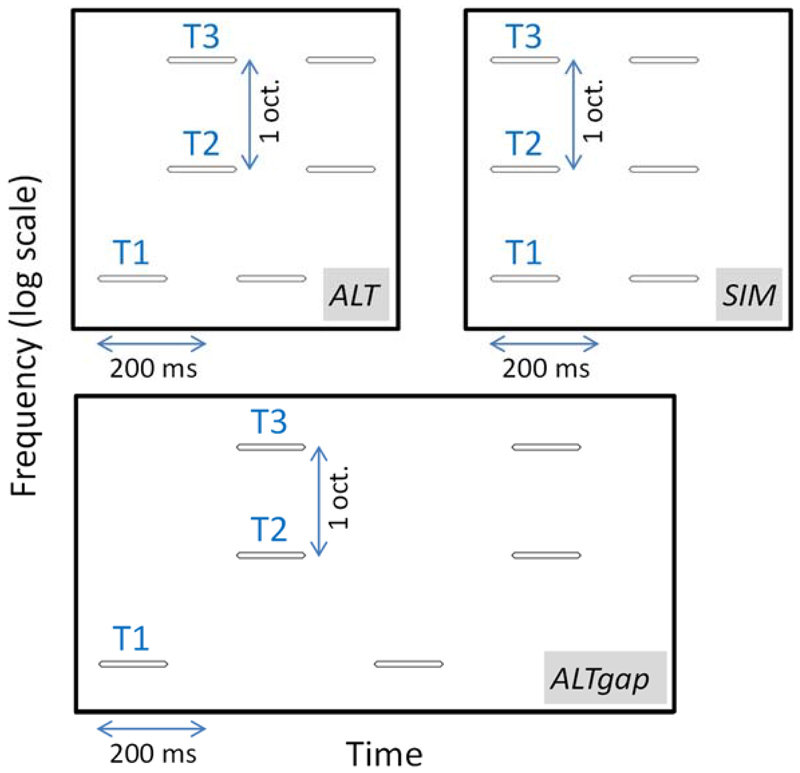
In this experiment, as well as experiments 2, 5, and 6, we measured the perceptual detectability of octave mistunings, i.e., deviations from a frequency ratio of 2:1, in cyclical sound sequences. Each sequence was built from two short stimuli: (1) a pure tone (T1); (2) a sum of two simultaneous pure tones with higher frequencies that were always exactly one octave apart (T2+T3). Each stimulus had a total duration of 130 ms and was gated on and off with 5-ms raised-cosine amplitude ramps. There were three experimental conditions in experiment 1 (ALT, ALTgap, and SIM); they are depicted in Fig. 1.² In two conditions (ALT and ALTgap), T1 and T2+T3 were presented in alternation; they were temporally contiguous in ALT whereas in ALTgap they were separated by 130-ms intervals of silence. In the third condition (SIM), T1, T2 and T3 were simultaneous and the successive presentations of the resulting complex were separated by 130-ms intervals of silence. The sequences were composed of 6 cycles in the ALT and SIM conditions, and 3 cycles in the ALTgap condition; thus, the duration of a sequence was the same (1560 ms) in the three conditions.

Figure 1.

(color). Two cycles of the sound sequences used in the ALT, ALTgap, and SIM conditions of experiment 1. T1, T2, and T3 were 130-ms pure tones.T2 and T3 were always one octave apart. T1 and T2 were exactly one octave apart in some sequences and formed a mistuned (either stretched or compressed) octave in other sequences.

On each trial, in each condition, two sequences were presented, one after the other; they were separated by a silent pause of 500 ms. In one sequence (the first or the second sequence, equiprobably), T1 and T2 were exactly one octave apart. In the other sequence, T1 and T2 formed either a stretched octave (positive mistuning) or a compressed octave (negative mistuning); mistuning magnitude, denoted Δ, was defined in cents (1 cent = 1/100 semitone = 1/1200 octave). The listener had to indicate if the mistuned sequence was the first or the second one. This could not be determined from pitch comparisons across sequences, because mistuning sign (positive or negative) was not known in advance (more details below) and because the absolute frequencies of the tones varied at random from sequence to sequence: in every sequence presentation, the frequency of T1 was drawn at random between 300 and 600 Hz; the probability distribution was rectangular, frequency being scaled logarithmically. Listeners knew how the sequences were constructed. They were instructed to detect the octave mistunings by any means, but they were also told that an efficient subjective cue should be "consonance", defined as either pitch affinity or perceptual fusion.

The ALT and ALTgap conditions were intended to gauge sensitivity to OPA while the SIM condition was intended to gauge sensitivity to harmonic fusion. The stimuli were such that the ALT and ALTgap conditions could clearly gauge "genuine" OPA, i.e., OPA in the absence of spectral overlap and pitch ambiguity. In the SIM condition, on the other hand, it was conceivable that the task would be performed using a subjective cue other than fusion. One possibility was that listeners would detect mistunings via roughness sensations produced by low-frequency beats resulting from a cochlear interaction of T1 and T2 (Plomp, 1967; Moore et al., 1985; Viemeister et al., 2001). We minimized this possibility by presenting all tones at low sensation levels: the sound pressure level (SPL) of the tones was 45 dB for T1, and 39 dB for T2 as well as T3. Another possibility was that listeners would always be able to segregate T1 from T2+T3, and would then perform the task by comparing explicitly, as in the ALT and ALTgap conditions, the pitch of T1 to the pitch of T2+T3 (or T2 alone). This "analytic strategy" was hindered by the fact that the sum of T1 and T2+T3 consisted of more than two pure tones. Sums of only two pure tones can be easily heard as such by some listeners, even if the tone frequencies are in a small-integer ratio (Smoorenburg, 1970; Demany and Semal, 1990; Houtsma and Fleuren, 1991; Rousseau et al., 1998), but the addition of a third tone makes analytic listening more difficult (Laguitton et al., 1998; Schneider et al., 2005).

2.1.2. Procedure

Listeners were tested individually in a sound-attenuating booth. The sound sequences were generated in MATLAB, at a sampling rate of 44.1 kHz, via 24-bit digital-to-analog converters. They were presented diotically by means of headphones (Sennheiser HD 650). Responses were given by mouse clicks on one of two virtual buttons, labeled "1" and "2". Response time was unlimited. Importantly, listeners were not given feedback about response accuracy.

In the experiment proper, trials were organized in blocks of 40, during which the condition and Δ (mistuning magnitude) were fixed. Within each block, mistuning sign was positive in half of the trials and negative in the other half; these two sets of 20 trials were randomly shuffled. An equal number of blocks were run for each condition within each session; two successive blocks were always run in different conditions. The experiment consisted of 600 trials in each condition, and was run in five sessions of about 1 h each.

Δ was varied across listeners and conditions. For each listener, however, it was identical in conditions ALT and ALTgap. Its values were chosen so as to obtain, for each listener, a similar proportion of correct responses (P_c), about 0.75, in conditions SIM and ALT. The appropriate Δ values were estimated informally before the experiment proper. The length of this adjustment phase, also serving as a practice phase, was listener-dependent. In a few cases, Δ was modified during the experiment proper, between two sessions.

2.1.3. Listeners

The experiments reported here were all performed at Université de Bordeaux. The tested listeners were mostly students who had responded to an announcement. They gave written informed consent before testing and were paid an hourly wage for their participation. Overall, 47 listeners were preselected based on the following criteria: (1) age < 30 y; (2) at least 3 y of formal musical education and of significant (> 1 h / week) musical practice; (3) subjectively normal hearing; (4) absolute hearing threshold ≤ 20 dB HL for each ear at octave frequencies from 125 to 8000 Hz. For each experiment, an additional inclusion criterion was defined by performance in a pretest (generally omitted for those who had previously completed another experiment). 13 of the 47 preselected listeners were pretested for a single experiment and failed to meet the inclusion criterion for that experiment. The 34 remaining listeners completed a variable number of experiments. Table I provides information on each of these listeners. None of them were unsuccessful in a pretest, except for L31. Only one listener, L24, was a professional musician, and about one listener out of three was no longer making music regularly. Table I indicates that "experiment 1" was completed by 10 listeners (mean age: 21.5 y; range: 19-25), but that 9 of them had previously completed one or more other experiments. In the pretest, listeners were required to perform with P_c ≥ 0.70 for Δ = 100 cents in each of the three conditions. Three of the preselected listeners were unsuccessful.

Table 1. Information on the listeners who completed at least one experiment. Only three listeners (L3, L4, and L9) completed all experiments. Experiments 2, 3, and 4 were performed on the same listeners. Numbers in parentheses indicate the order in which the experiments were completed.

Listener	Gender	Instrument(s)	Age (y) in expt 1	Age (y) in expts 2-4	Age (y) in expt 5	Age (y) in expt 6
L1	F	piano		22
L2	M	voice	20(2)			19(1)
L3	F	piano, flute	24(4)	23(1)	23(2)	23(3)
L4	F	violin	24(4)	23(1)	23(2)	24(3)
L5	F	piano, voice				23
L6	M	violin, trumpet	21
L7	M	piano, guitar		21(1)	21(2)
L8	F	violin, voice				21
L9	M	voice	20(4)	19(1)	19(2)	20(3)
L10	M	guitar		25(1)	25(2)
L11	M	piano, accordion				19
L12	F	organ, voice	19(2)			19(1)
L13	F	piano, guitar		24
L14	F	viola	22(2)			22(1)
L15	F	voice, guitar				20
L16	F	piano				19
L17	F	flute		23
L18	F	clarinet				24
L19	F	cello	25(2)			24(1)
L20	F	piano, voice				20
L21	F	piano		20(1)	20(2)
L22	F	violin	21(2)			21(1)
L23	F	piano		25
L24	M	percussion, guitar	19(2)			19(1)
L25	F	celtic harp				21
L26	F	piano			25
L27	M	piano		24
L28	M	piano, voice		23
L29	M	bass guitar, voice			22
L30	M	percussion			23
L31	F	piano			25
L32	F	violin, voice				22
L33	M	guitar, clarinet				21
L34	M	piano				19

Table 2. Performance of the group of listeners tested in experiment 4. Overall, each of the four sequence categories (SIM, ALT, SIMnoise, and ALTnoise) was used on 300 trials (25 trials per listener).

PRESENTED
SIM	298	2	0	0
ALT	4	296	0	0
SIMnoise	0	0	253	47
ALTnoise	0	0	123	177
	SIM	ALT	SIMnoise	ALTnoise
		RESPONSE

2.2. Results and discussion

The mean value of Δ was 40 cents (range across listeners: 28-70) in the SIM condition, and 59 cents (range: 37-100) in the ALT and ALTgap conditions. This indicates that the task was easiest in the SIM condition.

P_c was converted to d' (Green and Swets, 1974) by the formula:

$$d^{\prime }=\sqrt{2}nor\mathit{min}v\left(P_c\right)$$

in which norminv is the inverse of the standard normal cumulative distribution function.

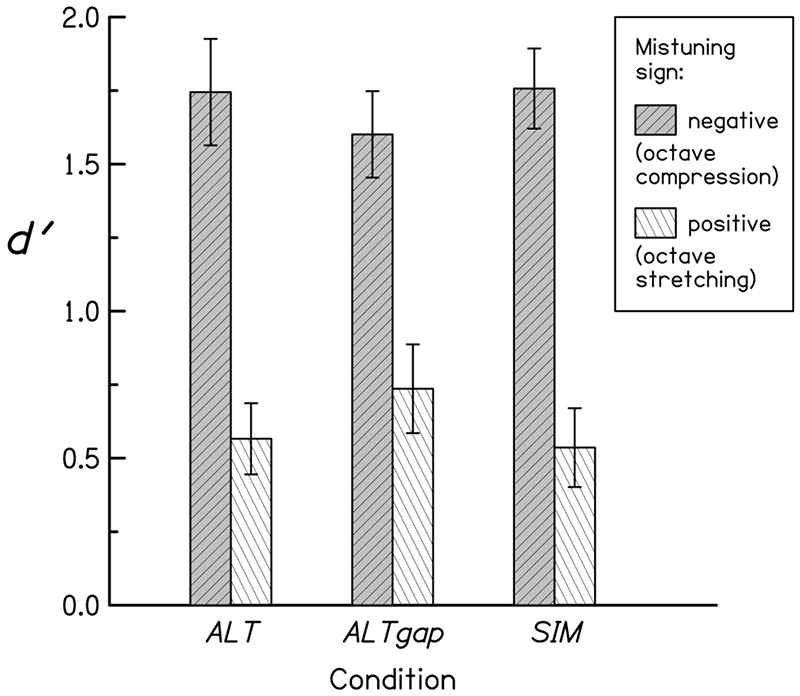
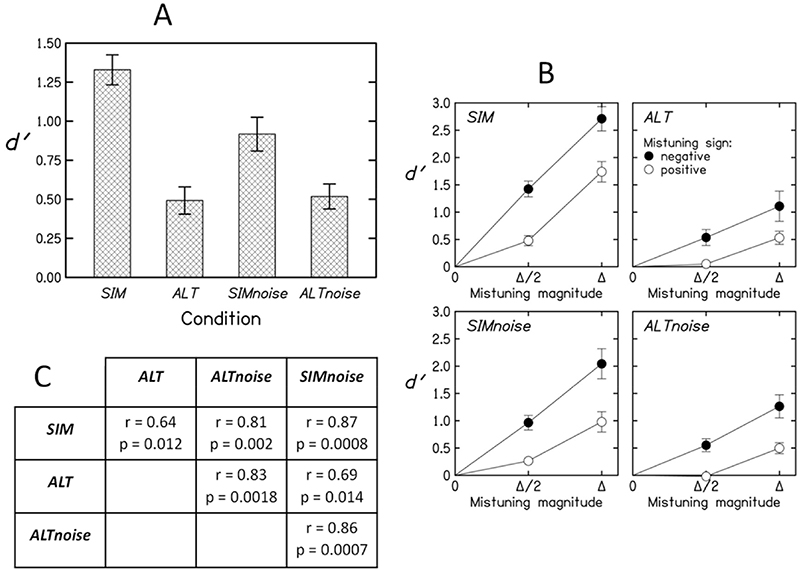
Fig. 2 displays the group performance as a function of condition and mistuning sign. In each condition, negative mistunings (octave compressions) were markedly better detected than positive mistunings (octave stretchings). The main effect of mistuning sign was confirmed by a repeated-measures ANOVA (F(1, 18) = 18.9; p = 0.002; η² = 0.60), which also indicated that condition had no main effect (F(2, 18) = 0.04; p = 0.96; η² < 0.01) and did not interact significantly with mistuning sign (F(2, 18) = 3.6; p = 0.076; η² = 0.01). The effect of mistuning sign in ALT and ALTgap is qualitatively consistent with the so-called "octave enlargement" phenomenon. In SIM, the results are at odds with the beat detection hypothesis: given that Δ was only a small fraction of 1 octave, this hypothesis predicted, wrongly, that positive and negative mistunings would be detected with a very similar efficiency.

Figure 2. Results of experiment 1: mean of d' across listeners as a function of condition and mistuning sign (negative for octave compressions, positive for octave stretchings); the error bars represent ± 1 standard error of the means.

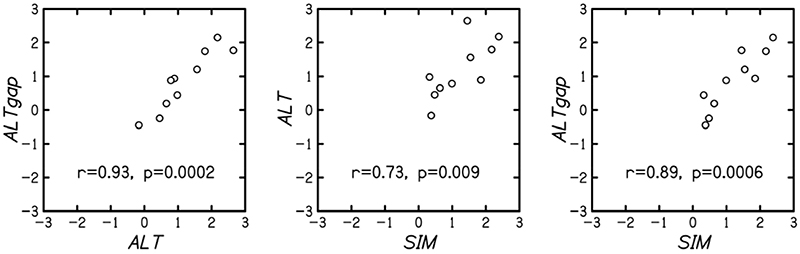
For each listener and condition, we quantified the asymmetry of mistuning detection (AMD) by simply subtracting the d' obtained for positive mistunings (d'_pos) from the d' obtained for negative mistunings (d'neg). Fig. 3 displays, for each possible pairing of conditions, the individual values of AMD and the correlation (Pearson's r) of the conditions with respect to this variable; the p value corresponding to r (one-tailed test, with the correction of Holm (1979) for multiple testing) is also indicated. As could be expected, a high correlation (0.93) was found between ALT and ALTgap. The crucial finding is that the correlations of SIM with ALT and ALTgap (0.73 and 0.89) were also high. It is noteworthy that if the AMD is computed not as d'_neg ‒ d'_pos but as (d'_neg ‒ d'_pos) / (d'_neg + d'_pos), very similar results are obtained (r = 0.93 between ALT and ALTgap; r = 0.75 between SIM and ALT; r = 0.85 between SIM and ALTgap). The high correlations of SIM with ALT and ALTgap provide further evidence that performance in SIM was not determined by the detection of beats, as this cue was certainly not available in ALT and ALTgap. Most importantly, under the hypothesis that listeners' performance in SIM was based on a fusion cue, the correlations of SIM with ALT and ALTgap strongly suggest that OPA is linked to harmonic fusion. Experiments 2-5 provided confirmatory evidence for the use of a fusion cue in the SIM condition.

Figure 3.

Scatter plots of the individual AMD (asymmetry of mistuning detection) values obtained in the three conditions of experiment 1 (ALT, ALTgap and SIM). Each dot represents an individual listener. The r values are Pearson's correlations. The p values (one-tailed) are adjusted using the Holm correction for multiple testing (3 tests).

3. Experiment 2: Real simultaneity versus illusory simultaneity

3.1. Method

In experiment 1, mistuning detection was easier in SIM than in ALT, as revealed by the fact that Δ had to be larger in ALT than in SIM to get a similar level of performance. Experiment 2 confirmed that the SIM condition was easier than the ALT condition, and determined whether the perceptual advantage provided by a simultaneous presentation of T1 and T2+T3 could be obtained if the simultaneity was illusory rather than real.

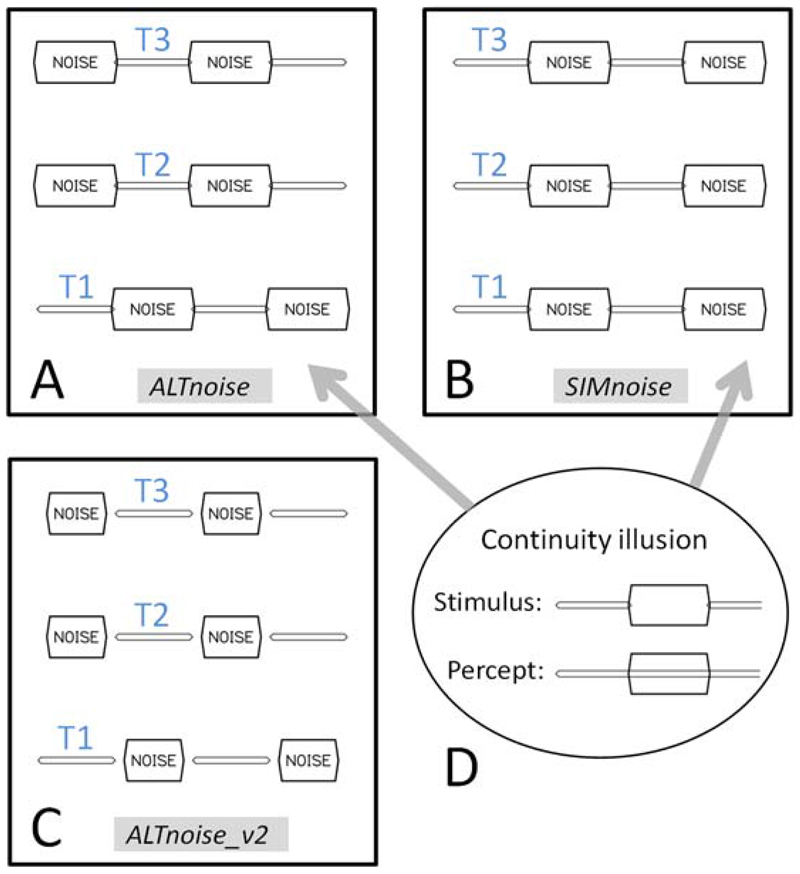
Four conditions were employed. In two of them, the sound sequences were constructed exactly as in the ALT and SIM conditions of experiment 1, except for two minor differences: (1) the number of cycles in a sequence was 4 instead of 6; (2) the onset and offset of every sequence were smoothed by 50-ms raised-cosine amplitude ramps. The other two conditions, ALTnoise and SIMnoise, are depicted in Fig. 4 (A and B). Whereas, in ALT and SIM, successive presentations of a given tone (T1, T2, or T3) were separated by an interval of silence, this interval was filled with a noise band in ALTnoise and SIMnoise. This noise band, with spectral edges positioned 200 cents above and below the tone frequency, was more intense than the tone by 8 dB. It was gated on and off with 5-ms raised-cosine amplitude ramps, like the tone. Onset ramps of the tone were synchronous with offset ramps of the noise, and vice versa, so that the total duration of a noise presentation was 140 ms. Each noise band resulted from the addition of 81 sinusoids with equal amplitudes, random initial phases, and a frequency spacing of 5 cents.

Figure 4.

(color). A, B, C: Two cycles of the sound sequences used in the ALTnoise, SIMnoise, and ALTnoise_v2 conditions. D: Schematic of the continuity illusion, which was elicited in the ALTnoise and SIMnoise conditions, but not the ALTnoise_v2 condition.

The expected effect of the noise bands was to elicit a continuity illusion in the perception of the tones (Houtgast, 1972; see Fig. 4D). Making the tones perceptually continuous was intended to create, in ALTnoise, an illusory simultaneity of T1 and T2+T3. Carlyon et al. (2002) and Heinrich et al. (2011) produced a similar illusion with two-formant vowels in which the formants alternated in time; they showed that the simultaneity illusion could improve vowel identification. We verified by three different experiments, reported in section 4, that T1 and T2+T3 were perceived as continuous and simultaneous in ALTnoise as well as SIMnoise.³ This being admitted, suppose that in both of these conditions mistuning was detected using an analytic strategy and explicit pitch comparisons between the illusory percepts evoked by T1 and T2+T3. Performance was then expected to be the same in the two conditions. By contrast, if in the SIMnoise condition mistuning was detected using a fusion cue, more efficient than explicit pitch comparisons, then it was expected from previous research by Darwin (2005) that performance would be poorer in ALTnoise than in SIMnoise. Darwin (2005) demonstrated that, in the auditory system, the continuity illusion is generated at a higher (more central) level than that at which harmonic fusion takes place; this implies that the illusory simultaneity perceived in ALTnoise is not sufficient for harmonic fusion; the real simultaneity occurring in SIMnoise (or SIM) is necessary.

In experiment 2, unlike in experiment 1, mistuning magnitude did not depend on condition. For a given listener, this parameter took two different values, Δ and Δ/2. In every block of trials, each of these mistuning magnitudes was used on 10 trials for each mistuning sign, and the four corresponding sets of trials were randomly shuffled. Δ was varied across listeners in order to minimize floor and ceiling effects. It had a mean value of 85 cents and ranged from 48 to 160 cents. For each listener, its value was chosen after a preliminary experimental session including the pretest and about 120 practice trials in each of the four conditions. The experiment proper consisted of 800 trials in each condition, and was run in five sessions of about 75 min each. Every session consisted of four series of four blocks of trials (one block in each condition); within each series, the four conditions were randomly ordered.

Table I indicates that 12 listeners (mean age: 22.7 y; range: 19-25) completed the experiment and that none of them had been previously tested in another experiment. In the pretest, listeners had to perform with P_c ≥ 0.70 for Δ = 100 cents in condition SIM. Only one of the preselected listeners was unsuccessful.

3.2. Results and discussion

Fig. 5A shows the global effect of condition on d', and Fig. 5B shows the effect of mistuning sign and relative magnitude in each condition. A repeated-measures ANOVA using as factors condition type (SIM/SIMnoise vs. ALT/ALTnoise), noise (present vs. absent), and mistuning sign (positive vs. negative) indicated that each of these factors had a significant effect (condition type: F(1, 11) = 131.4; p < 10^-6; η² = 0.25; noise: F(1, 11) = 9.36; p = 0.011; η² = 0.03; mistuning sign: F(1, 11) = 29.0; p = 0.0002; η² = 0.27). There was also a significant interaction between condition type and noise (F(1, 11) = 10.0; p = 0.009; η² = 0.03) and between condition type and mistuning sign (F(1, 11) = 8.9; p = 0.013; η² = 0.01). In contrast, there was no significant interaction of noise and mistuning sign (F(1, 11) < 1) and the three-way interaction was also not significant (F(1, 11) = 3.3; p = 0.096; η² < 0.01).

Figure 5.

Results of experiment 2. A: Mean of d' across listeners as a function of condition; the error bars represent ± 1 standard error of the means. B: Same data as A, but we show here the effects of mistuning sign (positive or negative) and mistuning magnitude (Δ or Δ/2) in each condition; Δ varied across listeners. C: Pearson's correlations between the four conditions with respect to the individual AMD values; the p values (one-tailed) are adjusted using the Holm correction for multiple testing (6 tests).

Although the interaction of condition type and mistuning sign was significant, Fig. 5B indicates that mistuning sign (as well as mistuning relative magnitude) had a similar effect in the four conditions. As in experiment 1, negative mistunings were better detected than positive mistunings in each condition (t(11) ≥ 2.8; p ≤ 0.017; Cohen's d^z ≥ 0.8). More importantly, an examination of the individual AMD values (d'neg ‒ d'pos) revealed, as in experiment 1, high correlations between all conditions with respect to this variable (r ≥ 0.64; p ≤ 0.014; see Fig. 5C).

Mistuning detection was markedly better in SIM than in ALT (t(11) = 7.4; p < 10^-4; Cohen's d_z = 2.1). Crucially, performance was also definitely better in SIMnoise than in ALTnoise (t(11) = 8.1; p = 10^-5; Cohen's d_z = 2.3), despite the fact that T1 and T2+T3 were perceived as continuous and simultaneous in both of these conditions. The latter result indicates that the real simultaneity occurring in SIMnoise allowed listeners to use an efficient subjective cue which was unavailable when simultaneity was illusory. The cue in question is presumably fusion. This conjecture is supported by the findings of Darwin (2005), demonstrating as mentioned above that the continuity illusion is generated more centrally than harmonic fusion in the auditory system. The superiority of performance in SIMnoise shows that in this condition listeners did not use an analytic strategy and explicit pitch comparisons between T1 and T2+T3. If so, this strategy was very unlikely to be used in SIM, because in SIM the common onsets and offsets of T1 and T2+T3 discouraged analytic listening.

The accuracy of mistuning detection was not significantly different in ALTnoise and ALT (t(11) = 0.5; p = 0.60). This supports the idea that in ALTnoise, as in ALT, listeners made explicit pitch comparisons. However, d' was significantly smaller in SIMnoise than in SIM (t(11) = 3.2; p = 0.008; Cohen's d_z = 0.9). In SIMnoise, therefore, the noise had a deleterious effect, which can be understood as a distraction effect or a partial forward masking effect. It is reasonable to think that in ALTnoise as well, performance was adversely affected by a distracting and/or masking effect of the noise. Yet, d' was not smaller in ALTnoise than in ALT; moreover, the difference in d' between ALT and ALTnoise was reliably smaller than the difference between SIM and SIMnoise, as indicated by the significant interaction of factors condition type and noise in the outcome of the ANOVA. It thus seems that, in ALTnoise, the negative impact of the noise was compensated by a benefit of the continuity/simultaneity illusion. This hypothesis was tested in experiment 5.

4. Experiments 3-5: Confirmations of the simultaneity illusion

4.1. Experiment 3

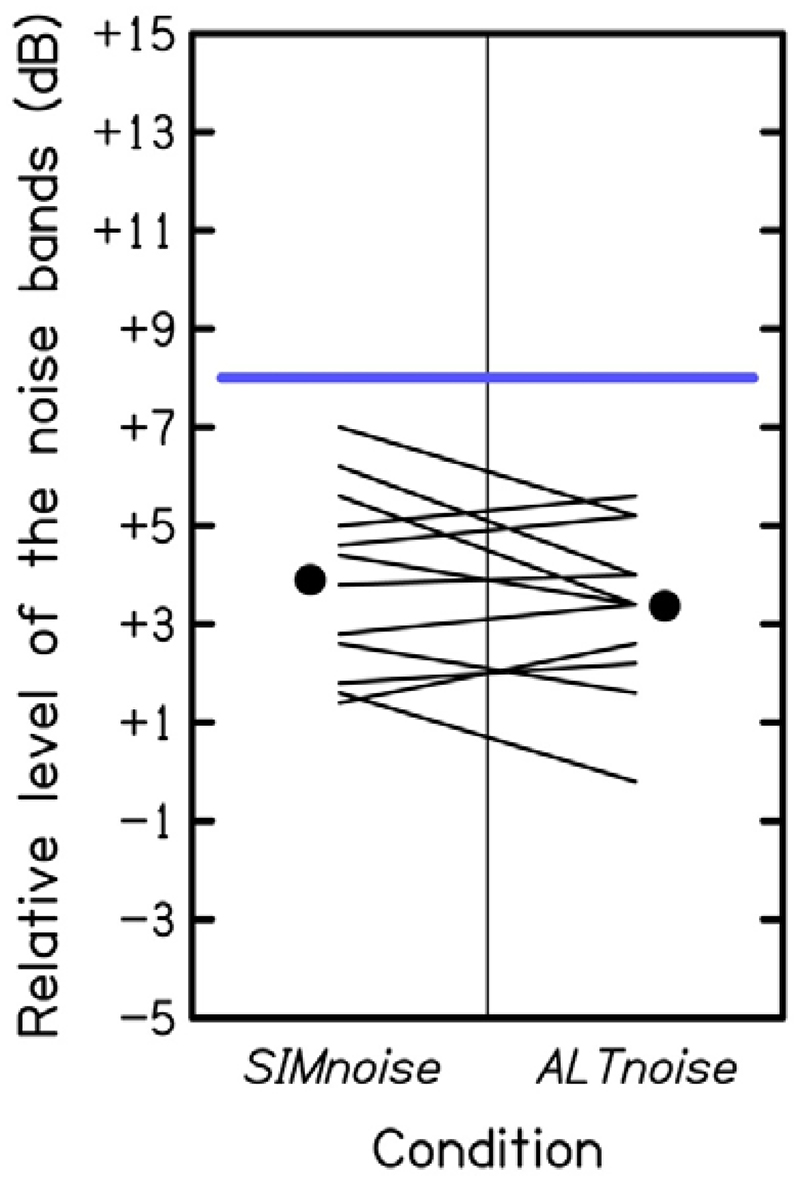
To check that T1 and T2+T3 were perceived as simultaneous in ALTnoise, we firstly verified that the noise bands were of a sufficiently high level to elicit a continuity illusion. In experiment 3, the 12 listeners who had completed experiment 2 were presented with ALTnoise and SIMnoise sequences in which the level difference between the noise bands and the tones (+8 dB in experiment 2) was now adjustable. The task was to set the noise bands (as a whole) to the level just sufficient for the continuity illusion. In the sequences used during a given adjustment, T1 and T2 were exactly 1 octave apart and T1 had a fixed frequency, randomly drawn between 300 and 600 Hz. T1, T2 and T3 had the same SPL as in experiment 2, i.e., 45 dB for T1 and 39 dB for T2 and T3. The relative level of the noise bands could be varied from ‒5 to +15 dB, by steps of ± 1 or 3 dB. After the presentation of a sequence, the listener could replay it without any change or with a one-step change in the noise relative level; this was done ad libitum, by mouse clicks on five virtual buttons. The initial relative level of the noise was selected at random within the range of the possible adjustments. Five adjustments were made by each listener in each of the two conditions (SIMnoise and ALTnoise).

Fig. 6 shows each listener's mean adjustment in each condition. There was no significant effect of condition (t(11) = 1.5, p = 0.17). The highest of the listeners' mean adjustments was +7.0 dB. This was 1 dB below the relative level used in experiment 2, which was therefore sufficient to elicit the continuity illusion.

Figure 6.

(color). Results of experiment 3. Each oblique line segment indicates the mean of the relative level adjustments made by a given listener in each of the two conditions. Dots represent means of the individual results. The horizontal blue segment indicates the relative level actually used in experiment 2.

4.2. Experiment 4

Experiment 4 stemmed from the reasoning that if, in ALTnoise and SIMnoise, the tones were heard as similarly continuous and simultaneous, an ALTnoise sequence might easily be mistaken for a SIMnoise sequence, whereas an ALT sequence should not be mistaken for a SIM sequence. The 12 listeners who had completed experiment 2 were therefore requested, soon after this experiment, to perform a test in which, on each trial, they were presented with a single sequence belonging, pseudo-randomly, to the SIM, ALT, SIMnoise, or ALTnoise category, and the task was to identify the sequence category. Listeners were given an instruction sheet on which the sequences of each category were schematized and the categories were numbered from 1 to 4; these numbers served as responses. In each presented sequence, T1 and T2 were exactly 1 octave apart and the frequency of T1 was randomly drawn between 300 and 600 Hz. For each listener, 100 trials were run, in which each of the four categories was selected 25 times; these four sets of 25 trials were randomly shuffled. No feedback about response accuracy was provided.

The obtained confusion matrix is displayed in Table II. SIM and ALT sequences were almost always correctly identified. However, SIMnoise sequences were assigned to the ALTnoise category on 16 % of trials, and ALTnoise sequences were assigned to the SIMnoise category on 41 % of trials. Remarkably, these confusions occurred even though the SIMnoise and ALTnoise sequences differed from each other with respect to the timing of the noise bursts and could thus be identified on this basis alone. We cannot estimate the contribution of the latter cue to listeners' performance, but the experimental results provide clear evidence that listeners perceived continuous and simultaneous tones in both SIMnoise and ALTnoise sequences.

4.3. Experiment 5

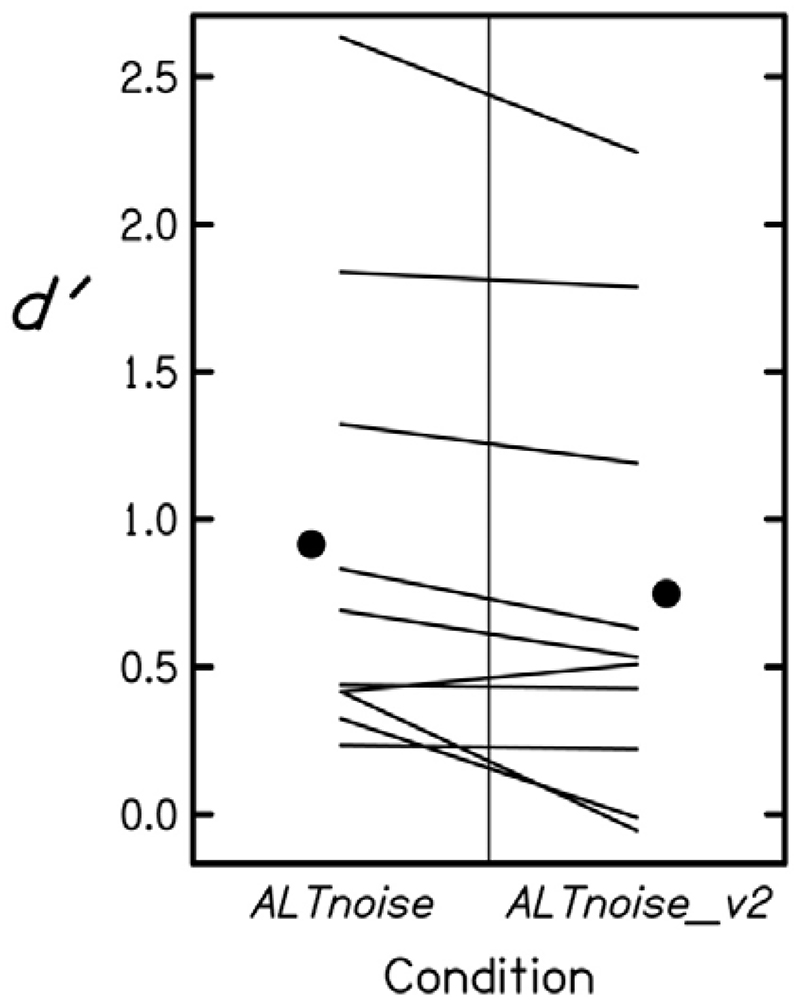
In experiment 5, mistuning detection was measured in two conditions: the ALTnoise condition of experiment 2 (Fig. 4A) and a modified version of this condition, called ALTnoise_v2 (Fig. 4C). The only difference between the two conditions was that in ALTnoise_v2 the noise bursts had a shorter duration and no longer filled the intervals separating successive tone presentations: each noise burst (still gated on and off with 5-ms ramps) had a total duration of 100 ms, instead of the 140-ms duration used in ALTnoise; the noise bursts were therefore separated from the tones by 15-ms silent intervals; this destroyed the continuity/simultaneity illusion.

Δ was fixed at 100 cents. The experiment consisted of 320 trials (8 blocks of 40 trials) in each of the two conditions. It was run in a single session of about 1 h, during which the two conditions alternated from block to block. It was completed by 10 listeners (mean age: 22.6 y; range: 19-25; see Table I). The pretest required listeners to perform with P_c ≥ 0.70 for Δ = 100 cents in the SIMnoise condition of experiment 2. Five of the preselected listeners were unsuccessful.

Fig. 7 shows the global performance of each listener in each condition. Mistuning detection was significantly poorer in ALTnoise_v2 than in ALTnoise (t(9) = 2.9; p = 0.018; Cohen's d_z = 0.9). Since the distracting and/or masking effect of noise was unlikely to be larger in ALTnoise_v2 than in ALTnoise, the advantage of ALTnoise can reasonably be interpreted as a benefit of the simultaneity illusion. However, this advantage was small (a 22 % difference in d', on average). Its small size, together with the much larger size of the advantage of SIMnoise over ALTnoise in experiment 2 (Fig. 5A), suggests that the simultaneity illusion had at most a minor positive effect on performance in experiment 2.

Figure 7. Results of experiment 5. Line segments indicate the performance of each listener in each condtion. Dots represent means of the individual results.

5. Experiment 6: The effect of frequency register on mistuning detection

5.1. Rationale and method

In the experiments described above, mistuning detection was investigated in a limited frequency register: the frequency of T1 varied between 300 and 600 Hz. Experiment 6 essentially replicated the ALTnoise and SIMnoise conditions of experiment 2 with two new ranges of T1 frequency: a "low" register, 200-300 Hz, and a "high" register, 1200-1800 Hz. In the low register, there was no a priori reason to expect results very different from those of experiment 2. However, previous research suggested that very different results could be obtained in the high register. Sensitivity to mistunings of one harmonic in a complex tone has been found to strongly deteriorate when the harmonic exceeds about 1000 Hz (Demany and Semal, 1988, 1990; Hartmann et al., 1990; Demany et al., 1991; Gockel and Carlyon, 2018). In contrast, the precision of melodic octave adjustments by musicians remains approximately constant as long as the higher tone does not exceed about 4000 Hz (Ward, 1954; Demany and Semal, 1990). In our high register, therefore, it could be expected that sensitivity to OPA would be keener than sensitivity to harmonicity, and would no longer be linked to the phenomenon of harmonic fusion. Instead, OPA might be the outcome of a musical acculturation process, imprinting in memory a melodic octave template determined by factors unrelated to auditory physiology.

The ALTnoise and SIMnoise sequences of experiment 6 differed from those of experiment 2 mainly with respect to frequency register. However, other modifications were made.⁴ First, whereas in experiment 2 the sequences always began as shown in Fig. 4, with T1 before T2+T3 for an ALTnoise sequence and tones before noise for a SIMnoise sequence, this was no longer true in experiment 6. On each trial, instead, a random choice was made between the two possible orderings of T1 and T2+T3 (for ALTnoise sequences) or tones and noise (for SIMnoise sequences); the same ordering was used for the two sequences of a given trial. We also increased the number of cycles in each sequence, from 4 to 6. Unlike in experiment 2, the SPL of the tones was now 60 dB for T1 and 57 dB for T2 and T3. The level of the noise bands associated with each tone was still higher than the tone level by 8 dB. Each sequence was mixed with continuous and wideband (100 Hz-10 kHz) threshold-equalizing noise (TEN; Moore et al., 2000). The TEN was set at 59 dB SPL. As a result, the sensation level of the tones in each frequency register was nominally 19 dB for T1 and 16 dB for T2 and T3. This was established by preliminary measurements (in 13 listeners) of the detection threshold of a 1-kHz and 130-ms tone in the TEN. In these preliminary measurements, the detection threshold was defined as the SPL giving P_c = 0.75 in a two-interval forced-choice procedure.

Trials were organized as in experiment 2, except that here the two sequences presented on a given trial were separated by a silent pause of 800 ms. In every block of trials, mistuning magnitude took again two different values, Δ and Δ/2; each of these mistuning magnitudes was used on 10 trials for each mistuning sign, and the four corresponding sets of trials were randomly shuffled. Δ did not depend on condition or frequency register, but was varied across listeners in order to minimize floor and ceiling effects. Δ was kept unchanged in the course of the experiment proper, except for three listeners for whom Δ was modified once, between two sessions. Overall, Δ had a mean value of 74 cents and ranged from 36 to 130 cents across listeners. The experiment proper consisted of 480 trials in each of the four combinations of condition and register. It was run in six sessions of about 1 h each. Half of the sessions were devoted to the SIMnoise condition and the other half to the ALTnoise condition; the SIMnoise sessions were the odd-numbered sessions for half of the listeners, and the even-numbered sessions for the other half. Within each session, the two frequency registers alternated from block to block.

As indicated by Table I, the experiment was completed by 20 listeners (mean age: 21.0 y; range: 19―24). Only three of them had been previously tested in another experiment reported here, but 10 other listeners had previous experience with the detection of octave mistunings. Before the experiment proper, a listener-dependent number of sessions were run to provide practice and to determine the experimental Δ. For the novice listeners, there were generally four preliminary sessions, including overall more than 1000 trials. The pretest required listeners to perform with P_c ≥ 0.70 for Δ = 130 cents in at least one frequency register for the SIMnoise condition. Five of the preselected listeners were unsuccessful.

5.2. Results and discussion

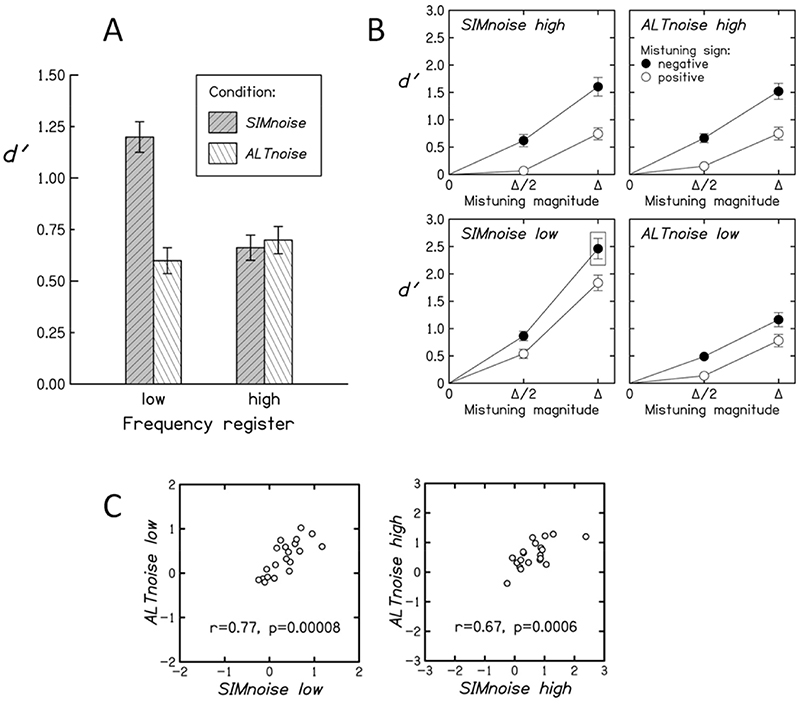
Fig. 8A shows the global effects of condition and register on mistuning detection performance, and Fig. 8B shows how performance depended on mistuning sign and relative magnitude. The data were submitted to a repeated-measures ANOVA using as factors condition, register, and mistuning sign. Each of these factors had a significant main effect (condition: F(1, 19) = 39.1; p < 10^-5; η² = 0.08; register: F(1, 19) = 10.6; p = 0.004; η² = 0.04; mistuning sign: F(1, 19) = 39.5; p < 10^-5; η² = 0.22). The ANOVA also revealed, more importantly, a highly significant interaction between condition and register (F(1, 19) = 59.8; p < 10^-6; η² = 0.10) and a reliable interaction between register and mistuning sign (F(1, 19) = 6.7; p = 0.018; η² = 0.02. In contrast, there was no significant interaction between condition and mistuning sign (F(1, 19) < 0.1) and no significant three-way interaction (F(1, 19) = 0.4; p = 0.56; η² < 0.01).

Figure 8.

Results of experiment 6. A: Mean of d' across listeners as a function of condition (SIMnoise or ALTnoise) and frequency register; in the "low" and "high" registers, the frequency ranges of tone T1 were 200-300 Hz and 1200-1800 Hz, respectively; the error bars represent ± 1 standard error of the means. B: Same data as A, but we show here the effects of mistuning sign (positive or negative) and mistuning magnitude (Δ or Δ/2) in each condition and register; Δ varied across listeners; regarding the framed data point in SIMnoise low, see Footnote 5. C: Scatter plot of the individual AMD values obtained in the two conditions, for each register; the r values are Pearson's correlations; the p values (one-tailed) are adjusted using the Holm correction for multiple testing (2 tests).

Fig. 8A indicates that, in the low register, performance was markedly better in SIMnoise than in ALTnoise (t(19) = 8.4; p < 10^-6; Cohen's d_z = 1.9), as was found in experiment 2. In the high register, by contrast, there was no significant effect of condition (t(19) = 0.76; p = 0.46). ALTnoise performance was similar in the two registers (t(19) = 1.9; p = 0.067), whereas SIMnoise performance was markedly better in the low register (t(19) = 6.3; p = 10^-4; Cohen's d_z = 1.4). These results strongly suggest that listeners used a fusion cue in SIMnoise when the register was low, and made explicit pitch comparisons in ALTnoise regardless of register. The cue used in SIMnoise when the register was high is more uncertain. A plausible possibility is that listeners used a fusion cue, as in the low register, but less efficiently because sensitivity to harmonicity was poorer. Alternatively, in spite of the real simultaneity of T1 and T2+T3, it may be that explicit pitch comparisons were feasible and more efficient than the (impoverished) fusion cue in this register.

Once more, negative mistunings were better detected than positive mistunings (see Fig. 8B).⁵ This was true in each condition for each register (t(19) ≥ 4.0; p ≤ 0.0007; Cohen's d_z ≥ 0.9). However, the AMD was more pronounced in the high than in the low register. This is reminiscent of the fact that the "octave enlargement" observed in experiments requiring listeners to adjust melodic octaves was generally stronger at high than at low frequencies (Ward, 1954). As in experiment 2, a significant correlation was found between the individual AMD values in SIMnoise and ALTnoise. Fig. 8C indicates that this was true in the high register (r = 0.67; p = 0.0006) as well as the low one (r = 0.77; p < 10^-4).

Overall, the results of this experiment are consistent with the idea that OPA was intimately linked to harmonic fusion in both frequency registers. For the higher register, where performance level was similar in the two conditions, we cannot exclude the possibility that listeners based their responses on explicit pitch comparisons in both conditions, rather than in ALTnoise only. However, it is important to note that the data displayed in the ALTnoise high panel of Fig. 8B are strikingly similar to those displayed in the ALT and ALTnoise panels of Fig. 5B, concerning experiment 2. The similarity of the data obtained in the two ALTnoise conditions can be quantified in terms of Pearson's correlation: r = 0.9946. This almost perfect correlation strongly suggests that OPA had the same origin in the two registers.

6. General discussion

In the present study, we investigated the perceptual detectability of octave mistunings via two subjectively quite different cues: OPA (for tones presented sequentially) and harmonic fusion (for tones presented simultaneously). Our results demonstrate, in a population of musically educated Western listeners, the existence of an intimate link between OPA and harmonic fusion. Since harmonic fusion undoubtedly originates from physiological processes taking place in every human auditory system, we are led to the conclusion that OPA is also based, at least in part, on biology. Even for listeners who have explicitly learned the rules of Western music, in which tones one octave apart are treated as equivalent sounds, it appears that the melodic octave, as a perceptual entity, is largely defined by basic auditory mechanisms, involved in the perception of any periodic sound, rather than by a cultural norm. This finding clearly disqualifies a purely culturalist conception of OPA. Previous evidence against that conception was provided by the observation of OPA in 3-month-old infants (Demany and Armand, 1984). However, as pointed out in the Introduction, there is also evidence that in adult listeners sensitivity to OPA depends on the musical environment and musical practice (Allen, 1967; Demany and Armand, 1984; Jacoby et al., 2019). It thus seems that sensitivity to OPA can be largely promoted, or preserved, by appropriate cultural factors, even though these factors do not generate OPA ex nihilo. Demany and Armand (1984) suggested that sensitivity to OPA is strong in infancy but, like some other perceptual abilities, decreases with age in the absence of appropriate cultural factors. The results reported here provide no information about the salience of OPA in the general population.

At odds with the present work, three previous studies in which OPA and harmonic fusion were examined in the same listeners suggested at first sight that these two phenomena are not directly related. In one of these studies (Bonnard et al., 2016), the perception of 11 frequency ratios, ranging from 0.96 to 1.04 octave, was investigated using stimuli consisting of simultaneous or successive pure tones. On each trial, two stimuli, representing two different frequency ratios, had to be compared; the task was to indicate which stimulus evoked the stronger sensation of fusion (for simultaneous tones) or pitch affinity (for successive tones). Unlike in the present study, both stimuli generally consisted of mistuned octaves because, from trial to trial, the 55 possible combinations of two different frequency ratios were used equally often. For simultaneous tones, maximum fusion was found to occur for a ratio very close to exactly 1 octave and fusion appeared to decrease less steeply above this peak than below it. For successive tones, the obtained pattern also had an inverted-V shape, but it was different: its peak occurred for a ratio significantly larger than 1 octave, and its upper flank was steeper than the lower flank. One possible explanation of this difference is that when the tones were successive, the fact that both of the stimuli presented on a trial were generally mistuned led the listeners to base their responses not on pitch affinity per se but rather on an aesthetic preference. In the range of frequency ratios producing a subjectively acceptable melodic octave, the aesthetically optimal octave may well be the upper limit of the range rather than its central value (Rakowski, 1990).

In another study (Bonnard et al., 2013), the listeners' task was to discriminate a frequency ratio of 0.97 octave from larger "target" ratios. For simultaneous pure tones, the obtained psychometric functions were non-monotonic: as the target ratio varied from 0.98 to 1.04 octave, discrimination performance initially increased, then decreased, and finally increased again; performance was better when the target was exactly 1 octave than when the target was slightly larger. These results indicated that detectable octave mistunings with opposite signs were perceptually difficult to distinguish from each other. For successive pure tones, in contrast, the psychometric functions were monotonic; this was consistent with previous research indicating that it must be possible to identify the sign of a melodic octave mistuning as long as this mistuning is detectable (Dobbins and Cuddy, 1982). The non-monotonicity observed with simultaneous tones could not be explained by the detection of beats resulting from peripheral interactions of the tones. It was instead due, presumably, to the use of a fusion cue by the listeners. Bonnard et al. (2013) thus suggested that the perception of the melodic octave is not directly linked to the phenomenon of harmonic fusion. We will show below that a different interpretation of their results is possible.

The third previous study in which OPA and harmonic fusion were investigated jointly (Demany and Semal, 1990) required listeners to perform repeated octave adjustments for pairs of simultaneous or alternating pure tones. Demany and Semal measured, in each condition, the precision of each listener's adjustments by computing the adjustments' standard deviation within each experimental session. The frequency of the lower tone (fL) was varied from 270 to 2000 Hz. When the tones were alternating, listeners' precision was not strongly dependent on fL. However, when the tones were simultaneous, precision was markedly poorer for high than for low fL values. Above 1 kHz, precision was much poorer for simultaneous tones than for alternating tones. The data thus suggested that increasing fL disrupted sensitivity to harmonicity without affecting sensitivity to OPA. Demany and Semal considered this as evidence that OPA is not directly related to harmonic fusion. Here, in experiment 6, we obtained results which are in important respects consistent with those of Demany and Semal, but performance was never significantly poorer in SIMnoise than in ALTnoise. We argued above that even in the high frequency register of experiment 6, OPA may be linked to harmonic fusion. If that is true, however, it remains to be explained why sensitivity to OPA and sensitivity to harmonicity are not affected similarly by frequency register, as suggested by both the present results and those of Demany and Semal (1990). We come back to this issue below.

How could OPA and harmonic fusion be linked? The physiological basis of perceptual sensitivity to harmonicity is still a topic of speculation. A currently popular scenario is the "autocorrelation" model (Licklider, 1951; Meddis and Hewitt, 1991; Cariani, 2001, 2019; de Cheveigné and Pressnitzer, 2006; Balaguer-Ballester et al., 2007; see also Patterson, 1986). This model is based on the fact that the spikes elicited by a pure tone in an auditory nerve fiber are precisely phase-locked to the tone waveform, as long as the tone frequency does not exceed some limit (Rose et al., 1967). Due to this phase-locking, consecutive spikes are separated by time intervals nearly equal to the period of the tone and integer multiples of the period. This temporal encoding of frequency deteriorates at higher levels of the auditory system, and no longer exists at the cortical level beyond about 250 Hz (Wallace et al., 2002). However, the precise spike sequences observable peripherally could in theory be subjected to a neural autocorrelation, recoding the temporal information into place information at a more central site (hereafter called "C"). For a pure tone with frequency f, the expected outcome of autocorrelation in site C is a set of excitations at places characterizing f and subharmonics of that frequency (f/2, f/3, f/4, etc.). If the stimulus consists of two simultaneous pure tones with a simple frequency ratio such as 2:1 or 3:2, these two tones will elicit sequences of spikes in separate groups of auditory nerve fibers, due to cochlear spectral analysis, but their respective autocorrelations should result in excitations at common places in site C. Such spatial coincidences are a potential explanation of sensitivity to harmonicity.

In the autocorrelation model, sensitivity to harmonicity does not require any learning process. By contrast, Terhardt (1974) and Schwartz et al. (2003) supposed that exposure to spectrally rich periodic sounds is a prerequisite. Shamma and Klein (2000) proposed a model in which it is also supposed that a learning process is involved, but exposure to noise is sufficient; the learning phase, therefore, could in principle occur entirely before birth. The assumed learning process is based on temporal coincidences beween spikes elicited in separate cochlear channels. As these temporal coincidences require neural phase-locking, the model implies, exactly like the autocorrelation model, that sensitivity to harmonicity is limited by the strength of neural phase-locking. The outputs of the two models in response to a tonal stimulus are in fact essentially the same, and therefore both models explain sensitivity to harmonicity in fundamentally the same way.

All the subharmonics of frequency f are also subharmonics of 2f. Thus, a sum of two pure tones one octave apart should excite site C at a set of places which is identical to the set excited by the higher tone alone. This can account for the perceptual fusion of the tones. If the tones are presented sequentially rather than simultaneously, the detection of commonality between their representations in C will be possible if activations of C can be memorized. We hypothesize that the required memory exists and leads to the perception of OPA. Importantly, our study shows that the memory in question must be distinct from conscious memory for pitch. In the ALTnoise conditions of our experiments, the listeners perceived, during each noise burst, an illusory tone which was consciously undistinguishable from the real tone presented just before the noise burst. The tones were perceived as simultaneous, exactly as in the SIMnoise conditions. Nevertheless, performance in ALTnoise was markedly worse than in SIMnoise (except at high frequencies). This suggests that the illusory tones were unable to activate site C, in contrast with the real tones.

Consider a pair of simultaneous pure tones forming a slightly mistuned octave. In site C, the slight mistuning should result in imperfect superpositions of excitations, broader than the perfect superpositions obtained in the absence of mistuning. This broadening is plausibly the physiological cue permitting mistuning detection. If so, one can understand why the sign (positive or negative) of a mistuning is not identifiable as soon as this mistuning is detectable (Bonnard et al., 2013). In contrast, if the tones are presented sequentially rather than simultaneously, a slight octave mistuning is expected to be detectable in C as a set of small local shifts of excitation, and the direction of these shifts should be identifiable as soon as they are detectable.

If, as implied by the autocorrelation model and the model of Shamma and Klein (2000), sensitivity to harmonicity is limited by the strength of neural phase-locking, it should disappear at high frequencies. We did observe this decay in the SIMnoise condition of experiment 6. However, performance in ALTnoise was not poorer in the high register than in the low one. This might be explained as follows. In the high register, the average frequencies of tones T1 and T2 were about 1.5 and 3 kHz, respectively. It can be reasonably assumed that, in humans, neural phase-locking is weaker at 3 kHz than at 1.5 kHz (Verschooten et al., 2019). If so, a local excitation of site C by a 3-kHz tone is expected to be weaker than the excitation produced at the same place by a 1.5-kHz tone. Thus, the former excitation is likely to be "swamped" by the latter excitation if the two tones are presented simultaneously. This should hinder the detection of octave mistunings. By contrast, the swamping effect cannot occur if the tones are presented successively. In that case, therefore, the limitation of mistuning detection at high frequencies by neural phase-locking may be less severe.

Our study was focused on the asymmetry of the detection of octave mistunings in various conditions. We paid special attention to individual differences regarding the asymmetry, and it appeared that these individual differences were large. At the group level, however, we found in every condition that octave compressions were more detectable than octave stretchings. This systematic asymmetry remains to be explained. The "octave enlargement" previously observed in adjustments of melodic octaves is likely to stem from the same source (in addition to purely aesthetic factors). As mentioned in the Introduction, Terhardt (1971, 1974, 1987) proposed an explanation for the enlargement effect but objections were raised against this explanation. McKinney and Delgutte (1999) searched for a correlate of the enlargement in a fine-grained analysis of auditory-nerve fibers' responses to pure tones, but they met with limited success (see especially, in this regard, section IV.B.3 of their paper).

The present work has been concerned with the perception of a single melodic interval, namely the octave. Is this melodic interval perceptually unique? The scenario that we put forth to explain OPA implies that other melodic intervals defined by a small-integer frequency ratio (e.g., the melodic fifth, 3:2) could also be perceptually special due to physiological processes independent of the cultural environment. However, this set of perceptually special intervals cannot be large. It is unlikely to include an interval such as the major second (nominally 9:8, or 2^1/6), which is very frequently used in music throughout the world (Vos and Troost, 1989; Kuroyanagi et al., 2019; Mehr et al., 2019). Thus, the impact of sensitivity to harmonicity on the production and perception of typical musical melodies is certainly limited. Neverthess, our findings compellingly suggest that the universality of the octave in the construction of musical scales is at least partly due to the biological underpinnings of harmonic fusion and pitch perception.

Abbreviations

AMD

asymmetry of mistuning detection

OPA

octave pitch affinity