The road towards understanding embodied decisions

Abstract

Most current decision-making research focuses on classical economic scenarios, where choice offers are prespecified and where action dynamics play no role in the decision. However, our brains evolved to deal with different choice situations: “embodied decisions”. As examples of embodied decisions, consider a lion that has to decide which gazelle to chase in the savannah or a person who has to select the next stone to jump on when crossing a river. Embodied decision settings raise novel questions, such as how people select from time-varying choice options and how they track the most relevant choice attributes; but they have long remained challenging to study empirically. Here, we summarize recent progress in the study of embodied decisions in sports analytics and experimental psychology. Furthermore, we introduce a formal methodology to identify the relevant dimensions of embodied choices (present and future affordances) and to map them into the attributes of classical economic decisions (probabilities and utilities), hence aligning them. Studying embodied decisions will greatly expand our understanding of what decision-making is.

Introduction

The ability to make effective value-based decisions is crucial for the survival of living organisms. Despite its popularity in psychology and neuroscience (Gold and Shadlen, 2007), value-based decision-making is often studied in restricted laboratory settings, using simple tasks that are inspired by economic theory, such as binary choices between lotteries (e.g., do you prefer 50 dollars with 20% probability or 20 dollars with 50% probability) or intertemporal offers (e.g., do you prefer 20 dollars now or 50 dollars in a month?). In this “classical” setting, there are a limited number of choices to be selected (often two) that are prespecified by the experimenter and presented simultaneously. Furthermore, the relevant choice dimensions (e.g., rewards and probabilities) are usually fixed throughout the experiment and unambiguous. In human studies, choice dimensions are usually labeled with symbols and easy to identify. Similarly, in animal studies, choice dimensions become stereotyped and unambiguous as an effect of long learning periods. Finally, the action component is often trivialized, not just because the action itself is simple (e.g., a button press) but also because there is no effect of the action on subsequent perception - i.e., there is no action-perception loop. The experiments conducted in this classical setting have crystallized a serial view of decision-making, which identifies three distinct sequential stages (Fodor, 1983; Pylyshyn, 1984): the perception of the attributes of the predefined alternatives, the decision between the alternatives, and the reporting of the decision by action (i.e., decide-then-act).

While using the classical setting permits methodological rigor, this comes at the expense of an excessive focus on just one kind of choice - economic choices that can be most easily studied in the lab - while disregarding the fact that there are other kinds of choices that are equally (or even more) frequent in our lives and important from an evolutionary perspective. The classical setting is relatively well suited to certain types of choices, such as choosing between a fixed number of dishes from a restaurant menu. However, these are just a small subset of the choices that we make in our everyday lives. For example, on the way to the restaurant one made countless choices about actions, such as whether to stop or try to pass through an intersection, how to get around other people walking on the sidewalk, which chair to sit in, etc. In many of these situations, the choices themselves as well as their costs and benefits are always in flux, and they are difficult to model using classical concepts from economic choice settings.

Furthermore, classical economic choices are not the kinds of scenarios that drove the evolution of the brain’s neural mechanisms. Instead, throughout its long history the brain adapted to deal with very different choice situations, such as deciding whether to approach or avoid an object, how to navigate to feeding sites, and how to move among obstacles (some of which might themselves be in motion). These kinds of “embodied decisions” dominated animal behavior long before humans existed, and are accomplished by neural mechanisms that have been conserved for hundreds of millions of years (Rodríguez et al., 2002; Saitoh et al., 2007; Striedter and Northcutt, 2019). Furthermore, the innovations of neural circuitry introduced in mammals and more recently, primates, were all made within the constraints of that ancestral context (Cisek, 2019; Passingham and Wise, 2012). Even now, in our daily lives, humans continue to perform many similar embodied decisions every day, such as when we play a sport, drive on a busy road, prepare a meal or play hide-and-seek with children, and it has often been suggested that our cognitive abilities are constructed upon a scaffolding provided by the sensorimotor strategies of such embodied behavior (Hendriks-Jansen, 1996; Piaget, 1952). Thus, one could argue that understanding embodied decisions is of primary importance for understanding many aspects of human cognition and behavior.

Embodied decisions − and how they differ from standard decision settings

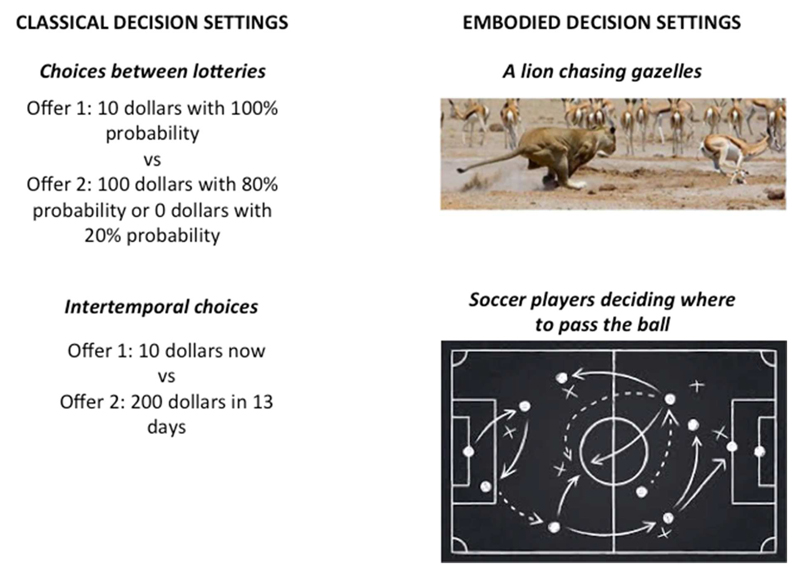
Embodied decision settings are very different from classical settings for a number of reasons (Cisek and Pastor-Bernier, 2014) (Figure 1). First, the number of offers that enter the deliberation is not predefined and can vary on a moment-by-moment basis. For example, it is likely that a lioness in front of hundreds of gazelles does not consider each as a separate offer, but instead clusters them into “patches” of potential food sources. Second, choice offers and their dimensions are rarely discretized or labeled with symbols and units (e.g., “option 1”, “option 2”, “dollars”, “percentages”). Rather, the decision-maker has to identify the options perceptually (under uncertainty) and to select the relevant choice dimensions; these choice dimensions often include geometric dimensions and affordances, such as the relative lion-gazelle distance, which are disregarded in classical settings.

Figure 1. Examples of classical decision settings (left) versus embodied decision settings (right).

Finally, and most importantly, perception, decision and action dynamics are intertwined. The action component is not simply a way to report a choice but an essential component to secure the reward (i.e., the lion has to actually chase the gazelle). Furthermore, action dynamics change the perceptual landscape (e.g., one or more gazelles can go out of sight when the animal starts moving) and the decision landscape (e.g., some gazelles can go out of reach and hence cease to be valid offers, or conversely become more available and extend the offer menu). Action and decision dynamics cannot be fully separated in time and are instead “continuous” (Yoo et al., 2021). The decision-maker can start acting before completing the decision, to buy time (Barca and Pezzulo, 2012; Pezzulo and Ognibene, 2011) or to exploit an option that would otherwise disappear; for example, a lion can start running toward a group of gazelles before deciding which one to chase, otherwise the gazelles will simply run away (i.e., act while deciding). Furthermore, the decision-maker can change their mind while acting, due to reconsidering a previous decision (Resulaj et al., 2009), gathering novel evidence, or the appearance of novel opportunities, e.g., previously ignored gazelles may come within reach (i.e., decide while acting).

These examples illustrate that there are crucial differences between the classical laboratory settings in which decisions are usually studied and the embodied settings in which real life decisions are deployed. While it is intuitively clear that studying decisions in restricted laboratory settings is methodologically simpler than studying them “in the wild”, it worth asking whether certain aspects of lab settings, such as the focus on stable, predefined alternatives and the trivialization of action, have contributed to a distorted (or at least incomplete) view of how we solve decision tasks. For example, one may ask to what extent the serial view of decision-making (decide-then-act) applies beyond simple binary decisions in the lab, or whether capturing the richness of real life decisions (act while deciding and decide while acting) requires a different class of (embodied) models, which acknowledge the fact that decision and action dynamics deploy in parallel and influence each other bidirectionally (Lepora and Pezzulo, 2015).

For example, a classic model of decision-making posits that one deliberates by accumulating sensory evidence until it reaches a threshold, and initiates movements at that time (Gold and Shadlen, 2007; Ratcliff, 1978). But how does that model generalize to situations, common during real-time behavior, in which one must already be acting (and thus “above threshold”) while still deliberating? Must the very concept of a threshold be abandoned when considering embodied settings, and if so, then where does that leave current models? Recent studies are starting to examine how humans make decisions during ongoing actions (Grießbach et al., 2021; Michalski et al., 2020) but models of the underlying mechanisms will need to go beyond traditional ideas of initiation thresholds, possibly toward ideas of task-specific subspaces in high-dimensional neural populations (Kaufman et al., 2014).

We argue that to broaden our understanding of decision-making, it is necessary to go beyond restricted laboratory settings and design novel experimental paradigms bringing embodied dynamics tasks under controlled conditions. To this end, it is necessary to remove some conceptual and methodological barriers that make embodied decisions challenging to address.

Towards a deeper understanding embodied decisions

This paper has three goals. The first goal is clarifying what are the key characteristics of embodied decisions and the novel questions they raise. The second goal is identifying a novel methodology for the study of embodied decisions, by distilling key insights from recent studies in sports analytics, experimental psychology and other fields. The third goal is discussing to what extent the study of embodied decisions requires novel theories − or will change our understanding of what decisions are.

Specifically, the remainder of this paper addresses the following three points:

• (1)Novel questions. What are the key differences between classical and embodied decision settings? What are the novel experimental questions that only arise when studying embodied settings and are instead ignored in classical settings? What can we learn from embodied settings that we cannot learn in the “classical” way?
• (2)Novel methodologies. How can we experimentally address the above empirical questions? Given that studying embodied decisions poses additional challenges compared to restricted laboratory settings, is it possible to develop a methodology that does not sacrifice rigor? Can we identify success cases? Can we borrow methodologies from other fields that address similar problems?
• (3)Novel theories. Would a widespread use of embodied settings change the way we understand decision-making? Is it possible that by studying decision-making in the classical way we have mischaracterized its mechanisms? Will the study of embodied decisions require novel conceptual frameworks and how would they differ from standard decision models? What will be the impact of novel studies of embodied decision making for cognitive science, neuroscience, robotics and other fields?

What are the novel questions that we can ask by studying embodied decisions?

In the introduction, we argued that embodied decision settings include a number of dimensions that are missing from classical settings. Here, we reconsider these unique dimensions of embodied settings and highlight that they prompt novel research questions that are impossible or difficult to study in classical settings. Below we focus on three novel questions that, despite being not exhaustive, exemplify well the heuristic potential of embodied settings. To illustrate the novel questions, we will use the example of a soccer player who decides where (or to which teammate) to pass the ball.

Question 1. How are offers and their attributes identified?

In classical settings, the offers are clearly identifiable by the decision-maker and their number is fixed and known in advance. The situation is different for the soccer player, because (despite an awareness that she has 10 teammates) she might not know exactly where they are and would hardly consider all of them as good choices. This situation prompts the novel question of how many (and which) choice alternatives she considers in the first place.

A closely related question is what are the dimensions that the soccer player considers during the decision. The choice can clearly benefit from considering multiple possible dimensions, such as the distance from the player, whether the positioning of the receiving player is appropriate or advantageous to score a goal, etc. We will argue in the next Section that it is advantageous to group these dimensions into the two classes of probabilities and utilities, because this permits establishing a mapping with the two usual dimensions of expected value in economics.

Crucially, however, the soccer player is not provided a priori with a list of the dimensions to consider and of the values of these dimensions, but has to figure them out as part of the decision-making task. This prompts a number of additional questions: which dimensions are considered? To what extent are these dimensions context-sensitive and time-varying? What are the contextual factors (e.g., situated aspects of the choice) and individual differences (e.g. personality or cognitive factors) that influence the selection of relevant dimensions?

Another set of questions regards the way the values of these dimensions are estimated under uncertainty and how this influences dimension selection (e.g., it would be ineffective to select a choice dimension for which one has no access to reliable values). In classical studies of value-based decision-making, the perceptual phase is often trivial. Under the rubric of perceptual decision-making or attention selection, perceptual dynamics are studied in isolation from value-based computations. In contrast, in the domain of embodied decisions, the different (e.g., perceptual, attentional, value-based) aspects of the decision process are tightly intertwined. While studying each in isolation may be fruitful as a first approximation, embodied settings may offer a unique window into how they interact.

Finally, the classical setup suggests that the identification of offers and evaluation of their attributes are largely sequential processes. Conversely, embodied decision settings allow us to study their interactions. For example, as you identify the offers, you may discover what are the attributes that differentiate them, which then helps to eliminate some offers from consideration (e.g. some players may be just too far to be considered, or too close to an opponent), leaving a new set of offers with a new set of attributes to consider (e.g. some players may be moving too fast). These examples suggest that, first, the consideration of some attributes comes before and influences the identification of offers; and second, the identification of offers could be considered as the first stage of a decision process, which filters out irrelevant choice alternatives. These are all problems that hardly arise in classical settings.

Question 2. How is the deliberation between choice offers performed?

Classical settings start from the premise that choice offers are predefined and presented in parallel; and the offer-attribute mapping is fixed throughout the decision. These assumptions are directly incorporated into decision-making models, like drift-diffusion models (Ratcliff et al., 2016), accumulator models (Usher and McClelland, 2001), or attractor-based models (Wang, 2008). For example, the drift diffusion model requires fixing two thresholds (one for each offer) and the decision variable (that reflects the value of the first offer minus the value of the second offer) for all the computation. The attractor-based model requires fixing the synaptic connections between populations that encode attribute values and populations that encode offer values. Without these fixed mappings, the mathematical guarantees of these models break down. However, as we have discussed above, in embodied decisions neither offers nor their mapping with attributes are predefined or fixed, nor can we assume they are presented simultaneously. It is unclear whether the most popular decision-making models can deal with these complexities in embodied situations, both mathematically and conceptually (e.g., embodied choices would require a rapid reconfiguration of the neural architecture supporting attractor-based decisions, but it is unclear to what extent this is plausible).

One may therefore argue that we need a different conceptualization of the deliberative process that leads to embodied decisions. At minimum, we should consider that the mathematical guarantees of models that deal with fixed data streams are not appropriate for embodied decisions, where the choice conditions change over time and hence the most recent data streams are more relevant (Cisek et al., 2009). A more drastic change of perspective comes from studies of foraging (Charnov, 1976) (which have strong decide-while-act components), where the standard assumption is that the deliberation is between “select the current offer” (exploit) vs. “search for other offers” (explore), not “decide between two fixed choices” as in classical decision settings. A series of studies suggest that birds (and other animals) use by default strategies for dealing with sequential choices and these lead them to make irrational decisions when faced with simultaneous choices (Kacelnik et al., 2011). However, it remains an open question whether this or other perspectives offer a broader and more appropriate conceptualization of situated decision-making in real life situations (we will return to this point later).

Question 3. How do perception, decision and action processes influence each other?

In embodied settings, perception, decision and action processes are deeply intertwined. Leaving aside perceptual processes (which we briefly discussed above), the interplay of decision and action - and the “continuity” of the decision (Yoo et al., 2021) - is evidenced by the fact that decision-makers can start acting before completing a decision (act-whiledeciding) and can change their mind along the way, perhaps to consider new offers that were not initially present (decide-while-acting). These situations create novel opportunities that are rarely (if ever) addressed in classical settings.

As an example of a novel question, it is unclear at what point of the decision a commitment emerges for one of the alternatives and under which conditions a person can change their mind (Cos et al., 2021). Additionally, what is the range of novel strategies that embodied settings afford? For example, a common observation in studies that ask people to answer by clicking one of two response buttons with a computer mouse is that participants sometimes move rapidly in between the two buttons, perhaps as a strategy to “buy time” and avoid committing until necessary (Pezzulo and Ognibene, 2011). These strategies are not normally available in classical settings but are very important in real life, where decision commitment dynamics are less constrained and postponing is often an option.

Finally, while decisions are normally treated as independent from the context and from one another, sequential dynamics are ever-present in embodied settings. As each decision and action influences subsequent decisions, actions and perception dynamics, the “dynamical affordance landscape” of decisions (Pezzulo and Cisek, 2016) cannot be easily disregarded. For example, if the soccer player has the ball and goes to the left, he will open some affordances (a left attack) but also close others (an attack to the right).

What novel methodologies do we need to address these new questions?

Embodied decision settings prompt several novel research questions. Some studies are already meeting these challenges. For example, studies that track continuous (eye, hand or mouse) movement dynamics during the choice are revealing how decision and action processes influence each other; for example, how decision uncertainty provokes changes of movement trajectories during a continuous decision; and how motor costs influence the initial decision and the subsequent changes of mind (Barca and Pezzulo, 2015; Burk et al., 2014, 2014; Cos et al., 2021; Marcos et al., 2015; Resulaj et al., 2009; Spivey, 2007; Spivey and Dale, 2006)(Spivey et al., 2005). Other studies are addressing how we make decisions while we are already engaged in performing an action are revealing the importance of geometric and situated aspects, such as the relative distances between currently pursued and another available target, influence the choice of changing target (Michalski et al., 2020).

Studies of embodied decision-making sometimes target interactive situations too, such as joint decisions (Pezzulo et al., 2021b) and joint actions, either collaborative, as in grasping something together, or competitive, as in martial arts (Candidi et al., 2015; Pezzulo et al., 2013; Pezzulo and Dindo, 2011; Sebanz et al., 2006; Yamamoto et al., 2013). These studies reveal how the decision and action processes of two (or more) co-actors are interdependent and how they can become aligned over time, especially when the two can engage in a reciprocal sensorimotor (nonverbal) communication (Pezzulo et al., 2018).

Another example is a promising trend in systems neuroscience toward studies of more naturalistic settings. This includes neural recordings in animals that are freely moving (Chestek et al., 2009; Schwarz et al., 2014; Sodagar et al., 2007) or navigating through controlled environments (Etienne et al., 2014; Krumin et al., 2018), as well as studies in humans using portable magnetoencephalography or encephalography equipment (Boto et al., 2018; Djebbara et al., 2021) (Djebbara et al., 2019) (Topalovic et al., 2020).

Towards a methodology that connects classical and embodied domains of decision

Despite these promising developments, most aspects of embodied decisions remain unaddressed − in part because embodied decisions are more challenging to study compared to classical settings. A key question is whether it is possible to develop a sound methodology for the study of embodied decisions in their full complexity, without sacrificing rigor. One aspect that makes the study of embodied decisions challenging is that most of the choice dimensions reflect spatial and geometric aspects of the situation, such as “passability” affordances for a soccer player. Unlike choice dimensions usually considered in classical settings, such as dollars and seconds, affordances are more difficult to formalize − but they are exactly the dimensions that our situated brains evolved for.

The methodology we propose here involves mapping the choice dimensions of embodied problems into the two factors − probabilities and utilities − that are often used in classical problems to define expected value. Establishing a formal correspondence between classical and embodied settings will permit addressing classical questions about (for example) utility maximization, risk-avoidance and sunk costs in embodied settings.

Example 1: The case of soccer

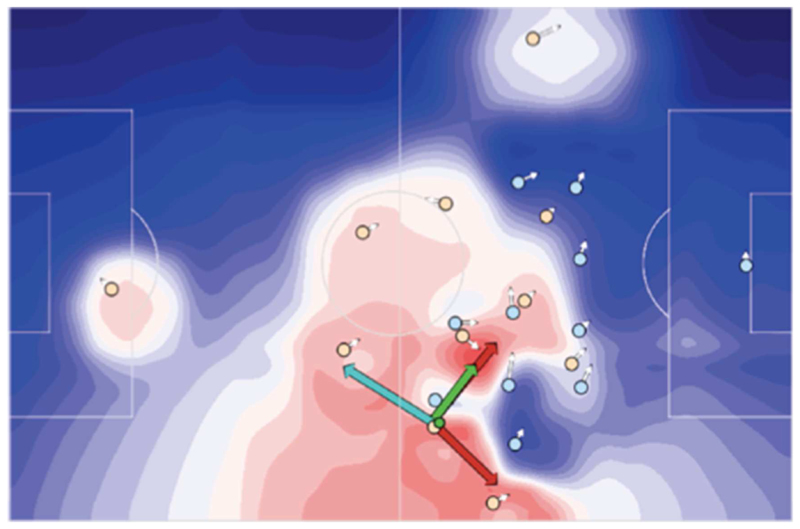
Fortunately, there are some success cases that exemplify this methodology, especially in sports analytics, as in the case of statistical studies of basketball (Cervone et al., 2016) and soccer (Fernández et al., 2019). For example, Figure 2 shows an example of a soccer player (yellow circle) who has to decide to whom he wants to pass the ball (small green circle) − or more precisely, where to pass it, since the passage can be to any location of the field, not just to his teammates’ current positions. The figure shows the “expected pass value (EPV)” surface for the soccer player (zones in red and blue have high and low EPVs, respectively). The notion of EPV is exactly the same notion of expected value used in economic studies and it is calculated by combining the usual two factors of probabilities and utilities. In this setting, the probability that a pass will succeed is itself modeled as a function of several subfactors, such as the distance from teammates and whether the passage zone is “under control” by a teammate or opponent. The utility of a pass is modeled as spanning both positive and negative dimensions, in consideration of the fact that passing to a certain zone can change the chances of scoring a goal (positive dimension) or receiving a counterattack (negative dimension). The positive and negative dimensions of utility are thus calculated separately by considering several subfactors, such as where the target of the pass is located within a precomputed “zone value surface” that spans the whole playing field (and is higher in the opponent’s field), and how many times a successful pass to the target zone resulted in a goal or a counterattack in the model’s training data. The values of each of the subfactors that contribute to probabilities or utilities are in part derived analytically (e.g., by calculating the zones that each player “controls”) and in part learned from data (e.g., how many times a goal was scored from each zone of the playing field, in a large database of recent matches).

Figure 2.

Expected pass value (EPV) surface in soccer, from (Fernández et al., 2019), permission pending. Warm (red) colors represent higher EPV whereas cool (blue) colors represent lower EPV. Yellow circles represent the location of the player holding the ball (green circle) and his teammates. Blue circles represent the locations of the opponents. The colored arrows identify potential passes having the highest EPV on the surface (green arrow), the highest utility (red arrow) or the lower turnover expected value (cyan arrow), which (roughly) corresponds to the lowest probability of a counterattack in this setup. This visualization illustrates that a continuous decision process can be described in terms of classical concepts and analyzed with established techniques. For example, this formalism permits assessing whether soccer players chose “risky” (i.e., higher utility, lower probability) or “safe” (i.e., higher probability, lower utility) passes.

While the ways probabilities and utilities are calculated is context dependent (e.g., depends on specific game models that differ for soccer, basketball and other games), the methodology is general and it permits establishing a strong formal connection between embodied and classical settings. In other words, regardless of the difficulties of establishing how probabilities and utilities should be modeled for each embodied setting, and how to estimate their values, once these two factors have been estimated they can be combined to form an expected value surface, in the same way they are combined in classical settings and economics. This is evident if one considers that in Figure 2, it is possible to identify the choices (passes) that provide the highest rewards, defined here as moving the ball into an area from which it is possible to shoot at the goal (red arrows), those that provide the best expected value (green arrow) and those that provide the lowest risk of a counterattack (cyan arrow). This makes it possible to ask (for example) whether the soccer player selected the pass that maximizes utility or whether he is risk-seeking or risk-averse.

Interestingly, despite the EPV being continuous, in most cases it is possible to enumerate a discrete (and small) number of choice offers, by focusing on the “peaks” of EPV on the field. This exemplifies a possible approach to map continuous aspects of embodied decisions (e.g., physical space) to discrete choice dimensions, which are most commonly used in standard decision-making models. However, while standard decision-making models specify a-priori a discrete set of options, it is possible that these emerge from continuous surfaces. This phenomenon can be formalized using various computational models that show decision surfaces developing peaks and troughs (Amari, 1977; Cisek, 2006; Furman and Wang, 2008; Sandamirskaya et al., 2013; Schneegans and Schöner, 2008) and transitioning from representing multiple options to choosing a single winner (Grossberg, 1973; Standage et al., 2011).

Example 2: The case of crossing the river

We illustrate how to use the same methodology used in the soccer study to derive “expected value surfaces” to deal with other embodied decision settings; for example, the case of a person who has to cross a river by jumping between stones having different sizes and placed at different distances, see Figure 3.

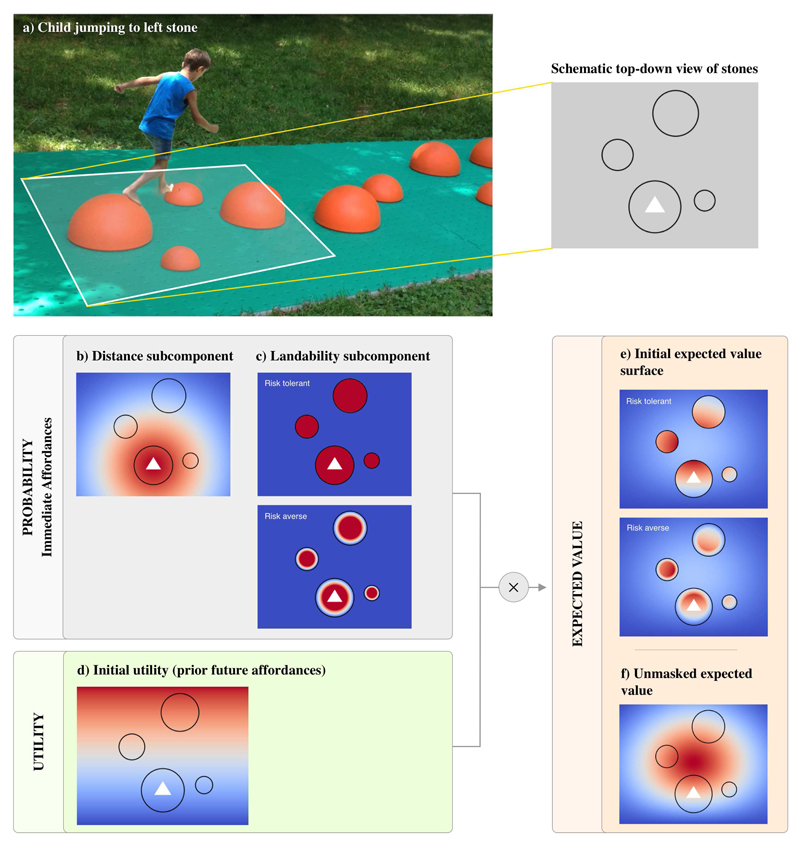
Figure 3. Cross the river setup.

This figure illustrates the two components of the affordance landscape for the situation shown in the photo in a), where a child must decide between three candidate stones for their next jump. In (b-f) we show a schematic view of an affordance landscape summarizing the child’s decision, with black circles representing the stones, and the white triangle at the child’s present location. The figure shows both probability surfaces and utility surfaces and how they are integrated to form an expected value surface for jumping. See the main text for explanation.

As in the soccer example, this situation can be addressed by deriving various “surfaces” that consider spatial and geometric elements of the task, such as child-stone distance and stone sizes (as examples of probability surfaces) and distance between stones and the end of the river (as an example of a utility surface).

Before analyzing the task of crossing the river, it is useful to mention explicitly the guiding principle that we use to distinguish probability and utility factors. In our analysis, the former (probability) factor relates to “present affordances” and the latter (utility) factor relates to “future affordances”, respectively (Gibson, 1977; Pezzulo and Cisek, 2016). Probabilities (and present affordances) only depend on the current situation (e.g., current position of the jumper, distance from the stones and their size), not the intended destination. As a result, computing the probability (or “present affordance”) surface amounts to asking: “which stones are most ‘jumpable’ given my current situation”? This question can be asked irrespective of the intended destination. On the contrary, the notion of utility depends on the future, up until the goal destination (in our example, the end of the river). Hence, computing the utility (or “future affordance”) surface amounts to asking: “Will this jump increase the chances of reaching the goal destination (and by how much)? What affordances will I create (or destroy) by doing a certain jump?”

A concrete example may help. Let’s consider the jumper shown in Figure 3. He has the choice between three options: the small stone to the right, the small stone to the left and the big stone to the center. The right stone is much closer and hence has the greatest present affordance, but it has lesser utility, as it does not allow progress towards the goal. The center stone has the greatest utility as it is closer to the destination, but (despite its size) it may have a lower present affordance, given it is farther from the jumper. The jumper actually selects the left stone, which seems a good compromise despite having neither the greatest present affordance nor the greatest utility. Yet, its utility is noteworthy as it “opens up” novel affordances: it permits reaching the next, bigger stone with small effort - and eventually the goal destination.

Figure 3b-f shows a schematic view of an affordance landscape summarizing the child’s decision (Figure 3a), with black circles representing the stones, and the white triangle representing the child’s present location and orientation. In this example, we formalize the “probability” (or “immediate affordance”) component in terms of two subcomponents. The first subcomponent of probability, A_d, takes into consideration the child-stone distance and prioritizes shorter jumps. It is calculated as:

$$A_d(x,y)=-\sqrt{{\left(x-x_{child}\right)}^2+{\left(y-y_{child}\right)}^2}$$

Note that the units in which x and y can be expressed relative to the subject’s size, to account for the fact that distance depends on bodily parameters (Warren, 1984).

The second subcomponent of probability takes into consideration “landability” and assigns positive values to locations with stones and zero value to locations without stones (as it is impossible to land on water). For illustrative purposes, we show two landability affordances,which cover the whole stone or only its center, respectively; see Figure 3c. The former may be perceived by very accurate (or risk-seeking) jumpers, whereas the latter may be perceived by less accurate (or risk-averse) jumper, who may not perceive the outer edge of the stone being landable, knowing that their jumps have some variance and hence aiming at the outer edge poses a risk of falling (Trommershäuser et al., 2008).

Furthermore, we formalize the “utility” component as the forward progress towards the end of the river, see Figure 3d. This is approximated as

$$A_{u,0}(x,y)=y-y_{child}$$

This naive method does not correspond to the optimal utility surface (see below) but it is sufficient in this simple example to provide some directionality.

By combining the two (probability and utility) components it is possible to calculate an “expected value (EV) surface”, see Figure 3e. This can be calculated simply as the product of the scaled probability and utility surfaces discussed above:

$$E{V}_0=\left(A_d\cdot A_l\right)\cdot A_{u,0}$$

We use min-max scaling, where $X_{\text{scaled}}=\frac{X-X_{\min }}{X_{\max }-X_{\min }}$

Note that the EV surface is shown in two versions, each integrating one of the two landability surfaces shown in Figure 3c. It can be informative, as well, to visualize the EV surface with subsets of its subcomponents. For example, Figure 3f shows only the distance subcomponent of probability and utility (Figures 3b & 3d), which expresses the preferred location of stones irrespective of their true position, which may provide a useful guide during visual search - or if the task is to place stones optimally.

While useful, the EV value surface is myopic as it only considers the immediate utility of each jump derived from a naive notion of “direction to goal”, not long-term utility. Given that we are dealing with a sequential decision problem that involves multiple jumps, long-term utilities should consider not just the utility of the next jump but also of the successive ones that may become available or unavailable as a function of the next jump; for example, using a look-ahead planning algorithm such as REINFORCE (Sutton and Barto, 1998).

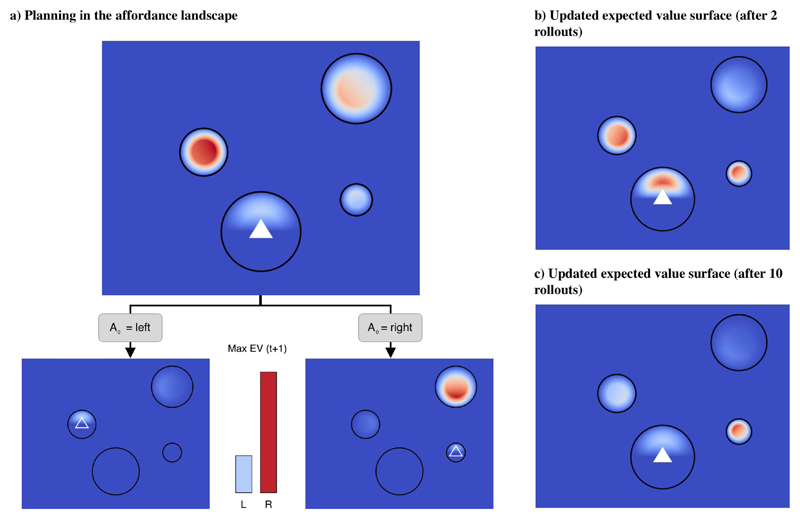
Look-ahead planning permits addressing cases in which the myopic strategy is maladaptive and leads to dead ends. One such case is illustrated in Figure 4. This is a variant of the situation shown in Figure 3, in which we moved the final stone from the left to the right. A myopic strategy would still assign the highest EV to the left stone, even if this is a dead end (Figure 4a). However, using a one-step look-ahead planning algorithm such as REINFORCE (Sutton and Barto, 1998), will permit predicting how the value surface will change after jumping to the left or right, respectively. In turn, considering this future utility instead of the immediate utility would change the EV surface at the start position − and assign the highest utility to the right stone (Figure 4b). This simple example illustrates the benefits of planning in situations where naive notions of utility (such as direction to goal) are misleading.

Figure 4. An example of planning while crossing the river.

(a) Expected value surface without planning, and below, the expected result of each available action (left, right). (b-c) Expected value surfaces updated based on 1-step planning. The cost of computing these updated expected value surface is a function of various parameters specific to both the planner (e.g. learning rate, planning depth) and problem context (e.g. number and differentiation of offers available, branching factor, etc). Here, we show two updated utility surfaces, calculated using 2 rollouts (b) or 10 rollouts (c) of the REINFORCE algorithm with the same parameterization (Sutton and Barto, 1998). Please note that these are just examples of updated utility surfaces, as the updating depends on the specific parameterization of the algorithm (e.g., its learning rate).

From an empirical perspective, people may be quite effective in avoiding dead ends while crossing the river (in person or in a videogame-like setting), but at the expense of investing some (cognitive) cost − which may reflect the process of planning ahead, while overriding current affordances. Interestingly, such cognitive costs can be modeled as the computational costs required to update the expected value surface, from the “immediate” utility of Figure 4a to the “future” utility of Figure 4b-c. By using REINFORCE or a similar Monte Carlo algorithm, we can generate predictions for this cost as the number of rollout steps required to disambiguate between competing immediate affordances.

In general, the greater the differences between the “immediate” utility surface of Figure 4a and the “future” utility surface of Figure 4b, the greater the computational cost to compute the latter (Ortega and Braun, 2013; Todorov, 2009; Zénon et al., 2019). If these computational costs correspond to mental effort, they could plausibly become apparent when comparing the RT distributions of peoples’ choices before a jump, when the “immediate” and “future” utility surfaces are more or less similar.

Note that calculating the most accurate expected value surface may have a high computational cost. If people optimize a trade-off between the accuracy of the expected value surface and the computational costs of obtaining it, they could select adaptively the amount of resources to invest (e.g., number of rollouts; compare the two updated expected utility surfaces of Figure 4b-c which are obtained using 2 rollouts (Figure 4b) or 10 rollouts (Figure 4c) of the REINFORCE algorithm). In tasks that involve multiple choices, people might also select the strategy to plan ahead (and invest cognitive resources) only during the most critical decisions; for example, when they need to choose between two sequences of stones in opposite directions, but not in simpler situations, such as the one shown in Figure 3, where the benefits of planning might not be worth its cost. By looking at subjects’ choices during the task, it would be possible to infer the expected value surface that they actually computed, which could provide an indication their (cognitive) effort investment – and whether and how often they look ahead during embodied choices.

Example 3: The case ofclimbing

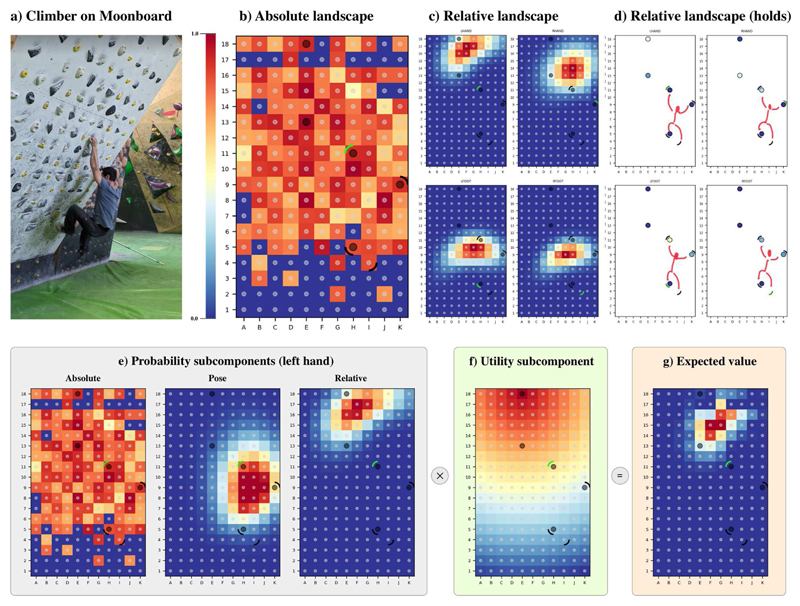
We consider one final application of “expected value surfaces”: the case of a rock climber who has to plan the best way to climb a wall − and more specifically, the best sequence of holds to traverse with their hands and feet, until reaching the “top” hold that marks the end of a climbing problem. Figure 5a shows a climber solving an example problem on a bouldering wall (called MoonBoard). The MoonBoard wall implies a standard configuration of all possible holds, and a problem is defined as a subset of these holds that are allowed. The goal is to start with each hand touching two predefined holds, then executing a sequence of movements until reaching a predefined “top” hold with both hands. Figure 5a shows a climber on an example bouldering problem on the MoonBoard, whereas Figures 5b-g show various probability and utility surfaces for the same problem (the holds that belong to the problem are marked with circles Figures 5b-g; and the current positions of the climber’s hands and foot are marked with short arcs around the holds; the green arc around marks the position of the climber’s left hand). As in the case of crossing the river, the value surfaces combine the two factors of “probabilities” (or current affordance, e.g., which holds are reachable given the current situation?) and “utilities” (or future affordance, e.g., which holds are more useful to open up future affordances that permit progress towards the top of the wall?).

Figure 5. The present affordance landscape of a bouldering wall (the MoonBoard).

(a) A climber attempts an example problem on the MoonBoard. (b-d) Example subcomponents of the probability surface: absolute landscape, relative landscape (unfiltered) and relative landscape (filtered to show only the available holds for this problem, with a sketch of a climber superimposed to show the posture). The black circles show the positions of the climbing holds in the example problem. The curved lines show the current positions of the hands and feet of the climber in Figure 1a, with the green curved line highlighting the limb whose landscape is shown. (e) The three subcomponents that are combined to form the probability surface of the climber’s left hand, which is the next to move; these are the absolute landscape (which is the same as figure 1b), the pose subcomponent, and the relative landscape of the left hand (which is the same as the top-left panel of figure 1c). (f) This is a naïve utility component: a distance gradient starting from the final hold of this MoonBoard problem. (g) The final Expected Value for the left hand, which is obtained by combining probability subcomponents of Figure 1e and the utility subcomponent of Figure 1f. See the main text for explanation.

However, there is an important difference in the way we calculated “probabilities” in the two cases of crossing the river and climbing. In the case of crossing the river, we calculated them analytically, by only considering geometric aspects of the situation: agent-stone distance (for the distance subcomponent) and stone sizes (for the landability subcomponent). However, this analytical approach is much more challenging in the case of climbing, as a climber’s current affordances plausibly depend on a much larger set of factors (e.g., climbing hold types, posture, distance) that are challenging to model. For this, to model probability surfaces, we first identified a small set of subcomponents and then used a data-driven approach to learn their associated probabilities from a large dataset of climbing data, much like the soccer example described above (Fernández et al., 2019). This implies that the probability surfaces considered here reflect the average climbing patterns of multiple climbers.

Figure 5b-e show the subcomponents of the probability surface that we consider in this example (which are provided as examples, but may not fully capture the full complexity of climbing). Figure 5b shows the first subcomponent, called “absolute landscape”, which depends only on the specific climbing hold (i.e., its type, shape, size) in any given position, not on the climber’s current position, and only depends on the kind and shape of the climbing hold. Here, the holds in the positions marked in red are “good” (or “easy to grasp and hold”) while those in blue are “bad” (or “difficult to grasp and hold”). The absolute landscape subcomponent is calculated empirically, using data freely available from the MoonBoard app (https://www.moonboard.com/moonboard-app), under the assumption that “good” (bad) climbing holds occur more often in easy (difficult) climbing routes.

Figure 5c shows a second subcomponent of probability: the relative landscape. This is the likelihood of moving each limb to a particular region of the board and hence capturing aspects of limb-hold distance. Note that this subcomponent is specific for the current position of the climber; in the figure, the positions of the hands and foot are indicated by the small curved lines (with green indicating the limb whose subcomponent is shown, i.e., the left hand). Furthermore, the relative landscape subcomponent is limb-specific, which means that there is a separate subcomponent for each limb: the two top panels of Figure 5c are for the two arms, while the two bottom panels are for the two feet. The relative landscapes are calculated empirically from sequences chosen by climbers (not based on geometric considerations as in the case of crossing the river), conditioned on the starting pose of each limb. Figure 5d shows the same landscape, but “filtered” to show only holds that exist in the given problem.

Figure 5e shows the aggregate probability surface for the climber’s left hand. This is the combination of the two probability subcomponents introduced earlier (the absolute landscape of Figure 1b and the relative landscape of Figure 1c, here limited to the left arm, i.e., the top-left panel) plus a third subcomponent: the pose. The pose subcomponent favors more common spatial configurations of the hands and feet, and discourages those that are less common. For example, low probability is assigned to moves resulting in configurations that break simple biomechanical constraints such as hands positioned farther apart than a climber’s arm-span would allow (e.g. in our example above, the pose constraint limits movement of the left hand away from the other limbs, which can be seen in the second plot in 5e). Like the relative subcomponent, the pose subcomponent is computed empirically by fitting a set of bivariate Gaussian distributions over the distributions of the Euclidean distance of limb’s pairs as observed in the solutions dataset.

Figure 5f shows a naïve utility surface for this climbing problem. This is a simple gradient that originates from the last climbing hold of the problem, similar to the utility surface for the case of cross the river. Figure 5g shows that the probability surfaces (Figure 1e) and the naïve utility surface (Figure 5f) can be combined, to derive a final expected value (EV) surface for the left hand of the climber (Figure 5g). Obviously, the same can be done for the other three limbs.

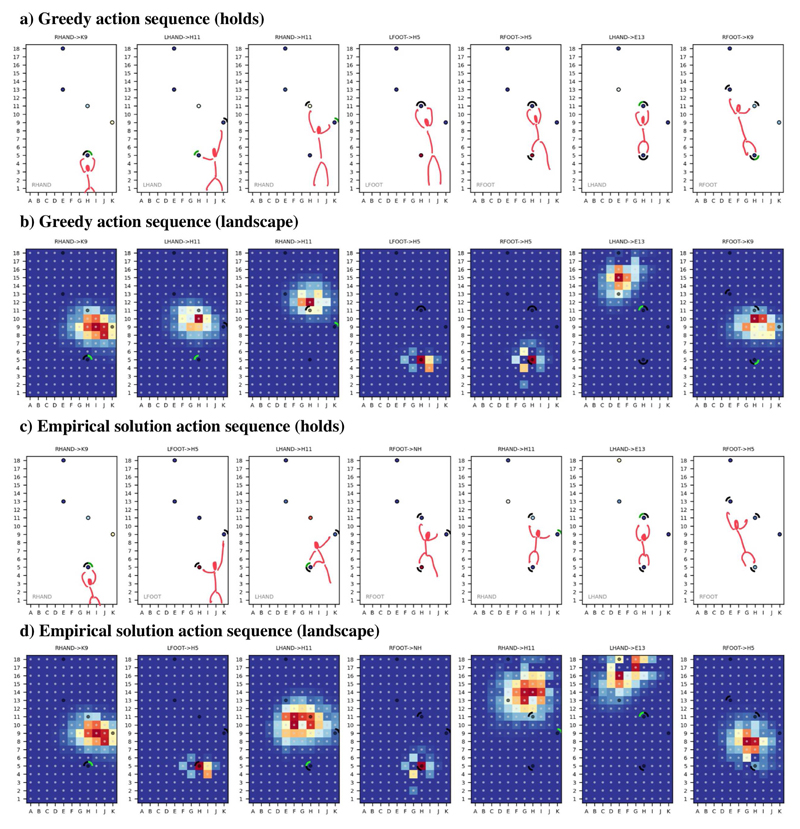
As in the cases of soccer and crossing the river, deriving expected value surfaces permits modeling the embodied choices of a climber who faces the same problem as shown in Figure 5a. Figure 6 illustrates a simulated climber that uses the expected value surfaces described so far to solve the problem of Figure 5a. Note that at each step during the simulated climb, we actually consider four value surfaces, one for the movements of each arm and foot - which means that at each moment in time, the climber has a choice not just between where to move a limb but also which limb to move. Figure 6a-b illustrates the resulting climbing behavior of a “greedy” planner that always selects the climbing hold whose expected value is the highest across the four surfaces (the alternation of hands and feet is an emergent effect of this strategy). This figure shows that some climbing holds (those at the top of the wall) have very low expected value at the beginning but acquire value as the climber progresses to the top of the wall. This exemplifies the concept of an evolving “landscape” of affordances as a function of the changing position and pose of the climber; and the fact that by moving the climber creates some affordances (and destroys others) (Pezzulo and Cisek, 2016).

Figure 6.

Partial action sequences for a selected problem showing the complete underlying affordance landscapes (a & c), and the value of each hold (b & d). The first two plots show a greedy policy in which the maximum hold value (across all four limbs) is selected and the corresponding expected value map shown. The second two plots show a partial sequence from the true solution as annotated by an expert climber.

Figure 6c-d shows an empirical solution of the same problem, i.e., the actual sequence of movements selected by an experienced climber, with an expected utility landscape (generated from the same model) superimposed above. In this particular example, some of the expert’s movements were well-predicted by the greedy planning strategy, but not all. This is not surprising, given that the climbing scenario poses significant modeling challenges. Furthermore, it is worth reminding that the simulated climber of Figure 6a-b uses a naive utility surface, without look-ahead, which can potentially lead to dead ends. A better utility surface can be calculated with model-based planning, e.g., by doing rollouts from the current position up until the goal to be reached (i.e., the top hold); see our previous discussion of planning while crossing the river.

Interestingly, while we considered the four value surfaces as independent so far, they become interdependent during planning; for example, by moving the left arm I can change the value surface of the other limbs. This is very interesting from a planning perspective, because it makes it possible to model the fact that in climbing, foot movements are often instrumental to create future affordances for the hands (e.g., render a distal hold reachable). Given that the goal is reaching the top with the hands, feet have ancillary roles: they are fundamental to change the hand value surfaces.

As our discussion exemplified, modeling climbing is significantly more challenging than modeling the case of crossing the river, as there are many more dimensions that contribute to the notion of “affordance” in this setup; and these are difficult to treat analytically. For this, we used a data-driven methodology, analogous to what done in other sports like basketball (Cervone et al., 2016) and soccer (Fernández et al., 2019). This methodology can be readily adapted to model other domains of embodied choice that resist an analytic treatment. However, it is worth noting that the data driven methodology we used here blurs the distinction between probabilities and utilities that we assumed so far, by endowing probability surfaces with some element of utility. This is evident from the fact that the maxima of the relative landscape are above the current positions of the limbs (this is different from crossing the river, where the distance subcomponent was independent of direction). The fact that the relative probability surface is imbued with some utility results from the fact that we compute the relative landscape from empirical data, from climbers that always go to the top of the wall.

Borrowing methodologies from other fields

Apart for sports analytics, many other disciplines have addressed embodied decision problems and developed methodologies to deal with them.

Robotics

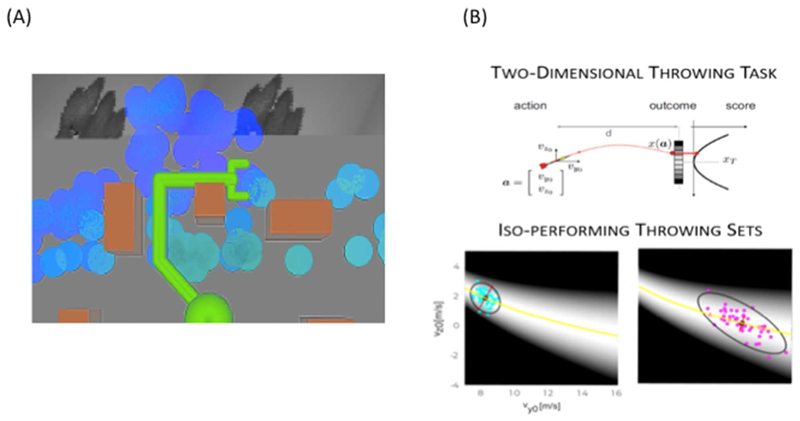
One field where embodied decisions have been object of interest is robotics. For example, when a robot has to make a decision between which objects to grasp, it has to consider situated and embodied aspects of the task, such as biomechanical constraints and the presence of obstacles. Recent work illustrates that deriving good movement policies benefits from learning internal (latent) codes that represent body-scaled “distance” metrics, as illustrated for example in Figure 7A, taken from (Srinivas et al., 2018). In this figure, lighter colors indicate larger latent distance and darker colors indicate smaller latent distance learned by the robot. Crucially, latent distance is body-scaled and sensitive to the robot arm biomechanics and to the presence of obstacles, rather than reflecting Euclidean distance. This line of research shows that it is possible to derive body-scaled perceptions akin to affordance (reachability) surfaces that we considered above for the tasks of crossing the river or climbing, using methods from deep learning and robotics. See also (Roberts et al., 2020; Zech et al., 2017) for recent reviews of other models of affordances in robotics.

Figure 7. Examples from other fields.

(A) A learned distance metric in a robotic setting, from (Srinivas et al., 2018). Lighter (darker) colors indicate smaller (larger) latent body-scaled distances. Please note that the learned distance metric takes obstacles and arm biomechanics into account. (B) Example solution manifold in (Sternad, 2018). The upper panel depicts a two-dimensional throwing task in which the throwing position is fixed and one can modulate the velocity vector on a vertical plane. The gray shaded landscapes in the lower panel show performance (i.e. quadratic distance from the target) as a function of the vertical and horizontal velocities, while the yellow line represent the solution manifold, i.e. the set of actions with perfect performance (zero-error). The super-imposed dots represent the action distributions for two iso-performing throwers, showing how it is possible to trade-off accuracy (compact action distributions) with higher motor cost (larger velocities).

Reinforcement Learning

The Reinforcement Learning (RL) paradigm, which typically presupposes a situated agent interacting with a changing environment, is sufficiently general to take on some of the embodied dynamics of interest. Model-free techniques, such as Q-learning, center on the learning of a value function to score state-action candidates. This value function, however, is typically global and amounts to a reflexive stimulus-action mapping that is not easily extended to the kind of forward planning required by humans in complex environments. One attempt to bridge model-free and more flexible model-based approaches in RL, which exhibits some similarity with the relative landscape used in our climbing example, is the successor representation (SR) (Dayan, 1993; Gershman, 2018; Momennejad et al., 2017). The SR uses a simple store of discounted expected occupancy mapping each origin state to a distribution over destination states. This technique avails a temporally extended local representation from which expected value can be efficiently computed without the use of Monte Carlo sampling. The SR can be combined with online Dyna-like replay to accommodate changes in environment and reward structure that pose challenges for continual learning (Momennejad et al., 2017). Other work in RL has begun to integrate the concept of affordances more explicitly. In one recent effort affordances are defined as action intents in a Markov Decision Process setting in order to reduce the space of state-action pairs evaluated (Khetarpal et al., 2020), though empirical results are so far limited to simple grid-world settings. In another example, a neural network is trained to model contextual affordances in order to predict the consequences of an action using a particular object (identified a priori) and thereby avoid arrival in a failure condition from which the goal cannot be reached (Cruz et al., 2018).

Ecological Psychology

In ecological psychology, Gibson’s work on affordances (Gibson, 1977) has been extended into an approach known as ecological dynamics, which applies methods from dynamical systems theory to understand behavioral interactions between organisms and their environment. Consistent with the conception of decision-making presented in this work, the ecological dynamics literature acknowledges that decisions are temporally extended and not easily separated from their behavioral expression (Beer, 2003; Nolfi, 2009; Nolfi and Floreano, 2001). Araújo et al. further suggest that because decisions are ultimately expressed as actions, an ecological analysis of human movement offers a “grounded” method to understand decision-making (Araújo et al., 2006). In one demonstration of a such an analysis, a study of human locomotion and obstacle avoidance analyzed path data as participants chose either an “inside”, or less direct “outside”, path to a goal location (Warren and Fajen, 2004). The authors modeled behavior as a differential equation where acceleration was a function of both goal distance and the angle between the goal and an intervening obstacle. Their analysis finds “bifurcation points” in the space of initial conditions (e.g. when the obstacle-goal angle exceeds 4 degrees) from which participants consistently shift to the inside path. According to this model, the selection of a path can be seen as an emergent behavior that arises from the dynamics of steering interacting with a particular environmental structure (Araújo et al., 2006). Furthermore, paths could be explained by these on-line dynamics without reference to explicit planning within an internal world model. Another insight that comes from ecological theory of development is Eleanor Gibson’s notion of prospectivity (Gibson, 1997). Prospectivity is one of four fundamental aspects of human behavior and it describes anticipatory, future-oriented behaviors such as an infant who reaches out for an object in anticipation that it will move within catching distance. This is an example of what we might call a future affordance, as the movement of the hand creates a new affordance (catching) that did not exist in the original configuration. This concept, that planning can be seen as the search for useful transformations to the available affordance landscape (Pezzulo et al., 2010; Pezzulo and Cisek, 2016; Rietveld and Kiverstein, 2014), is a central theme for the “affordance calculus” we propose.

Motor control

While the two domains of decision-making and motor control have long remained separated, a more recent trend sees motor control as a form of decision-making - or the problem of maximizing the utility of movement outcomes under various sources of uncertainty (Shadmehr et al., 2016; Wolpert and Landy, 2012). This analogy licenses the cross-fertilization of ideas and formal tools (e.g., statistical theory) across the two domains; and the development of novel computational models that combine objective functions used in economics, such as the maximization of expected utility, and in motor control, such as the minimization of motor costs (Ganesh and Burdet, 2013; Lepora and Pezzulo, 2015; Wispinski et al., 2018) These formulations become relevant when considering complex redundant tasks for which the same outcome can be achieved with different actions, as in a throwing task for which it is possible to hit a target (a fixed locations) with virtually infinite combinations of the release velocity of the projectile (Figure 7B). This redundancy poses the issue of selecting one among a set of actions, or sequences of actions, that guarantee the same level of performance.

Interesting insights on how humans select actions in redundant tasks have been provided by computational (Cohen and Sternad, 2009; Müller and Sternad, 2004) and analytical approaches (Cusumano and Dingwell, 2013; Scholz and Schöner, 1999; Tommasino et al., 2021) based on the characterization of the action-to-performance mapping geometry. Such mappings can be seen as landscapes describing performance in a continuous space of actions, and the way in which executed actions are distributed in relation to the landscape geometry (e.g. gradient and Hessians) can reflect idiosyncratic differences in task execution strategies or learning patterns (Sternad, 2018; Tommasino et al., 2021). A similar approach could be beneficial for modeling embodied decision-making. For example, in the case of soccer, action selection could be further informed by considering the EPV (expected pass value) surface gradients, rather than just the peaks, so to take into account the risk associated with the intrinsic variability of motor execution (i.e. motor noise).

Also, when the overall goal requires the execution of subtasks, while for a given subtask the solution manifold may allow for distant actions, only a part of the manifold could be compatible with concurrent or subsequent tasks. In this case, planning could be formalized as reciprocal constraints on subtasks manifolds. It has been shown empirically that in sequential actions, each action can be executed differently as a function of the preceding and the subsequent actions in the sequence. This coarticulation effect has been observed across various domains, such as speech, fingerspelling, and reaching and grasping actions (Jerde et al., 2003; Rosenbaum et al., 2012). For example, people grasp (and place their fingers on) a bottle differently depending on the next intended movement (Sartori et al., 2011). This and other similar results can be accounted for by a computational model where the solution manifolds of subsequent actions reciprocally constrain each other (Donnarumma et al., 2017).

In general, the close integration between decision-making and motor control is supported by a large body of neurophysiological data showing the neural correlates of decisions throughout cortical and subcortical regions that are clearly implicated in sensorimotor control (for review, see (Cisek and Kalaska, 2010; Gold and Shadlen, 2007). For example, decisions about where to move the eyes take place in oculomotor circuits (Basso and Wurtz, 1998; Ding and Gold, 2010; Platt and Glimcher, 1999; Shadlen and Newsome, 2001), while decisions about reaching or grasping occur in arm or hand areas (Baumann et al., 2009; Cisek and Kalaska, 2005). In particular, when decisions are made about different targets for reaching, neural activity in dorsal premotor cortex reflects the changing probability (Thura and Cisek, 2014) and relative utility of the choices (Pastor-Bernier and Cisek, 2011), the competition between targets is modulated by the geometry of their placement (Pastor-Bernier and Cisek, 2011), and the very same cells continue to reflect online changes-of-mind (Pastor-Bernier et al., 2012). In short, embodied decisions appear to unfold as a continuous competition between neural correlates of potential actions (affordances) biased by all factors relevant to the choice (Cisek, 2007; Shadlen et al., 2008) and modulated by an urgency signal that helps to control the trade-off between the speed and accuracy of decisions (Cisek et al., 2009); see also (Standage et al., 2011; Thura and Cisek, 2017).

Will the study of embodied decisions require the development of novel theories of decision-making and how would they differ from classical theories?

In the introduction, we reviewed the fundamental differences between classical and embodied decision settings. There is not just one but several types of decisions − for example, choosing which class to take is not the same as choosing where to sit in the classroom − and these may require different mechanisms, serial or parallel, dynamic or static, etc. While the study of classical settings has advanced our knowledge in many ways, it is important to ask whether the knowledge we gathered by studying classical choices, and the models we developed to explain them, generalize to other situations, or whether they produced a distorted (or at least incomplete) view of how we solve decision tasks.

The literature on value-based decision-making is currently fragmented into two main classes of models. The first (classical) class of models directly stems from economic theory and target economic-like laboratory tasks − and indeed, the study of the neural underpinnings of decision-making is often called “neuroeconomics” (Glimcher and Rustichini, 2004). In this approach, decision-making is described as the selection between a menu of prespecified offers whose values are putatively coded by the orbitofrontal cortex (Padoa-Schioppa, 2011). In this class of model, decision is therefore a centralized (prefrontal) process that only assigns action and perception systems ancillary roles.

The second (action-based) class of models instead assumes that decision-making is a more distributed process within which the motor system plays an important role. When choices map directly to specific actions, as is the case in many of the choices for which our brains plausibly evolved, the selection can directly involve motor or premotor cortices − hence consisting in a competition between action affordances (Cisek, 2007). The action-based view does not assume that the prefrontal structures highlighted by the “classical” view are irrelevant; but rather that the decision emerges from a “distributed consensus” between several brain areas, each contributing different inputs to the decision (e.g., subjective values versus motor costs) (Cisek, 2012). Indeed, mapping at least some aspects of the choice into the action system is more advantageous than a centralized model for animals that have to decide and act in real time. Since it is implausible that we have developed a completely different decision architecture to deal with economic decision in the lab, it is possible that the ancestral action-based architecture is also in play when choice-action mappings are more arbitrary. We risk, perhaps, only observing parts of this system when we contrive lab-based choice settings, which often remove the situated aspects that motivated its evolution.

Elaborations of action-based models, called “embodied models”, highlight that the distributed consensus architecture does not complete the decision before action initiation but rather continues deliberating afterwards, as the action unfolds in time. This is important for at least two reasons. First, as the deliberation continues, it is possible to change one’s mind or revise an initial plan along the way if novel opportunities arise. Second, action dynamics change the dynamical landscape of choice (e.g., the motor costs required to pursuing the selected plans). To the extent that these changing factors can be incorporated in the deliberative process, action deployment feeds back on the decision process, hence breaking the serial assumption of classical models (Lepora and Pezzulo, 2015).

While these models seem more appropriate than classical models to deal with embodied decisions, current research has just scratched the surface of the possible ways the brain may implement decisions “in the wild” (and perhaps also in the lab). In the same way we are in need of novel methodologies to study embodied decisions, we also need a new theoretical framework to study them. It is important to acknowledge that future models of decisionmaking may radically change some of the core assumptions of current models. For example, embodied choice models are at odds with the classical serial view of decision-making. Decision models used in foraging theory (Charnov, 1976; Hayden and Moreno-Bote, 2018) are at odds with the standard definition of a decision as a competition between two (or more)offers and propose instead that the competition is between “exploit the current offer” and “explore alternatives”. While these decision models were originally developed to deal with offers that are not presented simultaneously (as is common in foraging studies), they can deal equally well with offers presented simultaneously (as common in lab studies) if one assumes that the offers are attended to serially (Hayden and Moreno-Bote, 2018).

Another fundamental limitation of classical decision setups (and corresponding models) is that they keep perceptual aspects of the task extremely simplified (to avoid confounds). However, the situation is completely different in embodied settings, which often require making decisions based on perceived affordances (Gibson, 1979) and body-scaled perceptions (Proffitt, 2006). Similarly, the field of decision-making often assumes that we have ready-to-use representations of utilities (Padoa-Schioppa and Assad, 2006), but instead we showed that utility surfaces for embodied decisions need to be computed in context dependent ways − for example, to reflect future affordances − and in real time. We showed examples of how to quantify present affordances (or probabilities) and future affordances (or utilities) to study embodied decisions in ways that are commensurate to the study of classical neuroeconomic tasks. However, it remains to be assessed whether these formalizations really reflect the ways our brains process affordances or are only convenient ways to study them (Pezzulo and Cisek, 2016).

In sum, the field of embodied decisions offers opportunities not just for conducting novel experiments but also for developing novel theories of decision-making and other cognitive processes. Future models of decision-making may not even answer the questions currently being pursued but instead lead to new types of questions; for example, if one sees the brain as a control system, the most important question is not “how does the brain represent knowledge about the world and subjective values”, but instead becomes “how does the brain learn to control increasingly complex interaction with the world”. In turn, the development of these theories could lead to a novel fundamental understanding of the brain as an organon that evolved for interaction, not for contemplation.

An additional challenge of future theories of embodied decisions is offering a more comprehensive description of “embodied decision-makers,” which considers for example the fact that they feel emotions, remember past experiences, and monitor their ongoing performance. In our literature review, we largely omitted the important influences of arousal, motivation and emotion on decision-making processes and the roles of our neurocognitive capacities for executive functioning, attention and working memory in the solution of embodied decision tasks. While a comprehensive analysis of the above processes is beyond the scope of this article, advancing the field of embodied decision-making will require their systematic analysis and integration. In turn, a systematic study of embodied decision settings might potentially help refine our taxonomies of cognitive, emotional, motivational and executive processes, which we often take for granted, but which might not correspond to separate processes or neuronal substrates (Barrett and Finlay, 2018; Buzsaki, 2019; Cisek, 2019; Passingham and Wise, 2012). One example that we discussed multiple times already is the deep involvement of sensorimotor brain areas in decision-making processes, which is at odds with classical taxonomies (Cisek and Kalaska, 2010; Gold and Shadlen, 2007; Song and Nakayama, 2009); but there are other putative segregations (e.g., between planning and attention processes) that might be less compelling if one considers embodied choice situations.

Potential impact of novel studies and theories of embodied decision-making

The novel insights gathered from embodied decision experiments could have a significant impact on several fields, such as cognitive science, neuroeconomics, cognitive robotics and other disciplines interested in decision-making and sensorimotor control − as well as their deficits. As we discussed, most decision-making studies in cognitive science and neuroeconomics focus on simple choices between fixed menus. Embodied decision studies can shed light on other kinds of decisions − and possibly decision-making circuits in the brain − that are more deeply integrated with sensorimotor processes than traditionally considered. As noted in the introduction, brain evolution has for millions of years been driven by the challenges of embodied decisions during closed-loop interaction with a dynamic environment (Ashby, 1952; Cisek, 1999; Gibson, 1979; Maturana and Varela, 1980; Pezzulo and Cisek, 2016; Powers, 1973), and the neural systems meeting those challenges have been highly conserved (Cisek, 2019; Striedter and Northcutt, 2019). It is likely that even the abstract abilities of modern humans are built atop that sensorimotor architecture (Hendriks-Jansen, 1996; Pezzulo et al., 2021a; Pezzulo and Cisek, 2016; Piaget, 1952) and would be difficult to understand outside of its context (Buzsaki, 2019; Cisek, 2019). Furthermore, clarifying the neuronal and computational processes that living organisms use to make embodied choices would be extremely important for sports psychology and analytics as well as for cognitive robotics. All these fields deal natively with decisions deployed in embodied settings and have developed useful methodologies to study them (see our discussion above of analysis methodologies) that have a great potential for cross-fertilization. From a technological perspective, the realization of effective robots able to operate in unconstrained environments (e.g., homes or hospitals) critically depends on their ability to address embodied decisions, such as the choice between available affordances (including social affordances). Unlike current AI systems that are largely non-embodied, these robots will need to more deeply integrate decision and sensorimotor processes, and this is why the novel paradigms of embodied decision studies (e.g., decide-while-acting as opposed to decide-then-act) could be most beneficial. Finally, the novel insights gathered via embodied decision studies can help shed light on deficits that involve a combination of motor and decision processes. For example, it has been suggested (Mink, 1996) that the inability of Parkinsonian patients to take a step (apparently, a purely motor deficit) might be due to an inability to resolve the competition between actions (hence, a decision deficit) or to endow them with sufficient vigor or urgency. The development of novel theories of how we make embodied decisions in the first place could help us better understand how these processes can break down, as apparent in Parkinson’s or other diseases.

Conclusions

Every day we make countless embodied decisions, when we drive in a busy road, prepare a meal or play hide-and-seek with children. In this paper, we discussed how embodied decisions differ from classical economic decisions and which novel questions they raise that are poorly investigated. We then reviewed recent studies in fields like sports analytics and experimental psychology that start addressing these questions and distilled from them a general methodology to study embodied decisions more rigorously. We provided examples of how to cast key dimensions of embodied choices (namely, present and future affordances) into the attributes of classical economic decisions (namely, probabilities and utilities) - hence helping to align the two decision settings. Our hope is that this contribution will raise interest towards the emerging field of embodied decisions and pave the way for the realization of novel experiments, novel formal tools and novel theories that capture more appropriately its most distinctive features.