Designing ecologically-optimised pneumococcal vaccines using population genomics

Abstract

Streptococcus pneumoniae (the pneumococcus) is a common nasopharyngeal commensal that can cause invasive pneumococcal disease (IPD). Each component of current protein-polysaccharide conjugate vaccines (PCVs) generally induces immunity specific to one of the approximately 100 pneumococcal serotypes, and typically eliminates it from carriage and IPD through herd immunity. Overall carriage rates remain stable owing to replacement by non-PCV serotypes. Consequently, the net change in IPD incidence is determined by the relative invasiveness of the pre- and post-PCV carried pneumococcal populations. Here, we identified PCVs expected to minimise the post-vaccine IPD burden by applying Bayesian optimisation to an ecological model of serotype replacement that integrated epidemiological and genomic data. We compared optimal formulations for reducing infant-only or population-wide IPD, and identified potential benefits to including non-conserved pneumococcal carrier proteins. Vaccines were also devised to minimise IPD resistant to antibiotic treatment, despite the ecological model assuming resistance levels in the carried population would be preserved. We found expanding infant-administered PCV valency is likely to result in diminishing returns, and that complementary pairs of infant- and adult-administered vaccines could be a superior strategy. PCV performance was highly dependent on the circulating pneumococcal population, further highlighting the advantages of a diversity of anti-pneumococcal vaccination strategies.

The asymptomatic carriage prevalence of S. pneumoniae peaks in the first five years of life, reaching 25-50% in high-income countries, and 20-90% in low- and middle-income countries¹. Hence S. pneumoniae strains frequently encounter one another and compete through multiple mechanisms, either during co-colonisation², or indirectly through immune-mediated interactions³. The polysaccharide conjugate vaccines (PCVs), routinely administered to infants to limit IPD, induce strong mucosal immunity to a limited set of serotypes. This inhibits vaccine serotype carriage, and alleviates some competition for hosts between the remaining broad diversity of circulating serotypes^4,5. The resulting serotype replacement process typically eliminates vaccine types without any reduction in the overall S. pneumoniae carriage prevalence^6,7. Nevertheless, PCVs have substantially reduced infant disease just through altering the carried bacterial population, because serotypes differ in their invasiveness: the rate at which they progress from carriage to cause IPD.

Transmission dynamic modelling of the serotype replacement process has made it possible to quantify the competition between vaccine and non-vaccine serotypes^8,9. However, understanding which S. pneumoniae serotypes will succeed following alterations to the web of competitive interactions is difficult. Recent population genomic studies have enabled analyses to move beyond serotypes to consider all variable, including accessory, genetic loci^10,11. Corander et al observed that accessory loci were present at “equilibrium frequencies” both in separate locations with different strain compositions, and in pre- and post-vaccination populations within a location¹². They hypothesised that multi-locus negative frequency-dependent selection (NFDS) explained these observations, based on functional annotation of the accessory genome and the significantly improved predictive ability of an NFDS model compared with other ecological models¹². Similar multi-locus NFDS models have also proved informative when applied to trends in Escherichia coli epidemiology¹³, and when reformulated to identify strains likely to invade a vaccine-disrupted population¹⁴.

The first pneumococcal PCV contained seven serotypes (4, 6B, 9V, 14, 18C, 19F, and 23F) selected to minimise the infant IPD burden, based on epidemiological data primarily from North America and Europe¹⁵. It was also hoped that PCV7 would reduce the proportion of IPD that was antibiotic resistant, a phenotype strongly associated with some of these vaccine serotypes¹⁶. Prior to PCV introduction it was not known whether vaccination would protect against colonisation by vaccine types^1,15, hence serotype replacement was not a major consideration in its design. Following substantial post-vaccine alterations to the carried pneumococcal population, PCV7 substantially decreased the burden of infant IPD in many countries^4,17,18. In response to increases in some non-vaccine serotypes’ contribution to IPD post-PCV7, the vaccine was replaced by PCV10 (which expands PCV7 to include serotypes 1, 5 and 7F) and PCV13 (which adds 3, 6A and 19A to those in PCV10)¹. These updated formulations are now administered to millions of children across hundreds of countries¹, and recent modelling predicted global use of PCV13 would avert almost 400,000 infant deaths annually¹⁹. Nevertheless, there are some continuing instances of problematic serotype replacement in infant disease, such as penicillin-resistant meningitis rising in France post-PCV13²⁰. More generally, the PCVs’ effects on the proportion of IPD caused by anti-microbial resistant (AMR) pneumococci have been variable, with the long-term impact sometimes not evident for some years after vaccine introduction^21–24. The complexity and high costs²⁵ of PCV manufacture limits the capacity to address these problems through substantial expansion of their valency, with a full course of PCV13 immunisations costing over $540 per child in the USA²⁶.

Older adults also suffer elevated incidences of IPD, but do not usually carry S. pneumoniae at the high levels observed in children¹. Hence infant PCV immunisation programmes remove vaccine serotypes from adult disease through herd immunity^1,17,27,28. Yet adult and infant IPD differ in their serotype composition, which appears to reflect their invasiveness varying with host age^17,29. Hence post-vaccine trends in infant and adult IPD can diverge. In the UK, for instance, there has been a 4% increase in adult IPD as infant IPD has declined post-PCV13²⁸. This highlights the risks attendant to reshaping the bacterial population through PCV-associated strain replacement, as the post-vaccine population can have an increased propensity to cause IPD relative to that preceding the immunisation campaign¹⁸.

Thus there is a tremendous opportunity to design improved PCVs: vaccination is highly effective at shifting the serotype composition of pneumococcal populations, but is expensive²⁵ and sometimes undermined by serotype replacement¹⁷. Here, we use the multi-locus NFDS ecological model¹² and genomic data describing the carried pneumococcal population^10,11 to predict the carried serotype distributions resulting from hypothetical vaccines, and identify formulations that minimise IPD.

Results

Incorporating ecology into vaccine design

The two datasets to which the modelling approach was applied had distinct circulating serotypes and genotypes (Extended Data 1). The first was from Massachusetts, consisting of 616 genomes sampled from nasopharyngeal carriage in children over three winters following the introduction of PCV7, representing a typical Western S. pneumoniae population^10,12. The second was from the Maela refugee camp on the Thailand-Myanmar border, comprising 2,336 genomes carried by an unvaccinated population^11,12. Based on the number of detected serotypes, approximately 3.47x10⁹ and 1.05x10¹³ 13-valent PCVs were possible in each, respectively. To enable computationally efficient simulation of these populations’ changes in response to arbitrary vaccine designs, the multi-locus NFDS model of S. pneumoniae ecology was reimplemented in a deterministic form using ordinary differential equations¹² (Methods). Each genotype’s behaviour in the model was determined by its serotype, antibiotic resistance profile, and the subset of accessory loci it encoded. The simulated dynamics are initially driven by vaccination perturbing the population through imposing a fitness cost on those serotypes included in the proposed formulation, followed by a return to an equilibrium under NFDS. The vaccine-driven changes in population composition typically stabilised after a decade in the model (Extended Data 3, Supplementary Figure 1), in agreement with epidemiological data³⁰. Simulations successfully replicated the restructuring of the Massachusetts pneumococcal population following vaccination, reproducing the post-PCV7 serotype frequency data more accurately than a previously-described neutral model¹⁸ (Extended Data 2). Any specified vaccine formulation drives different post-vaccine outcomes in the two populations, due to the different bacterial genotypes present in each. Therefore we employed Bayesian optimisation and genetic algorithms to generate hypothetical vaccine formulations separately in the two populations, and evaluated their impact on IPD 10 years post-vaccination.

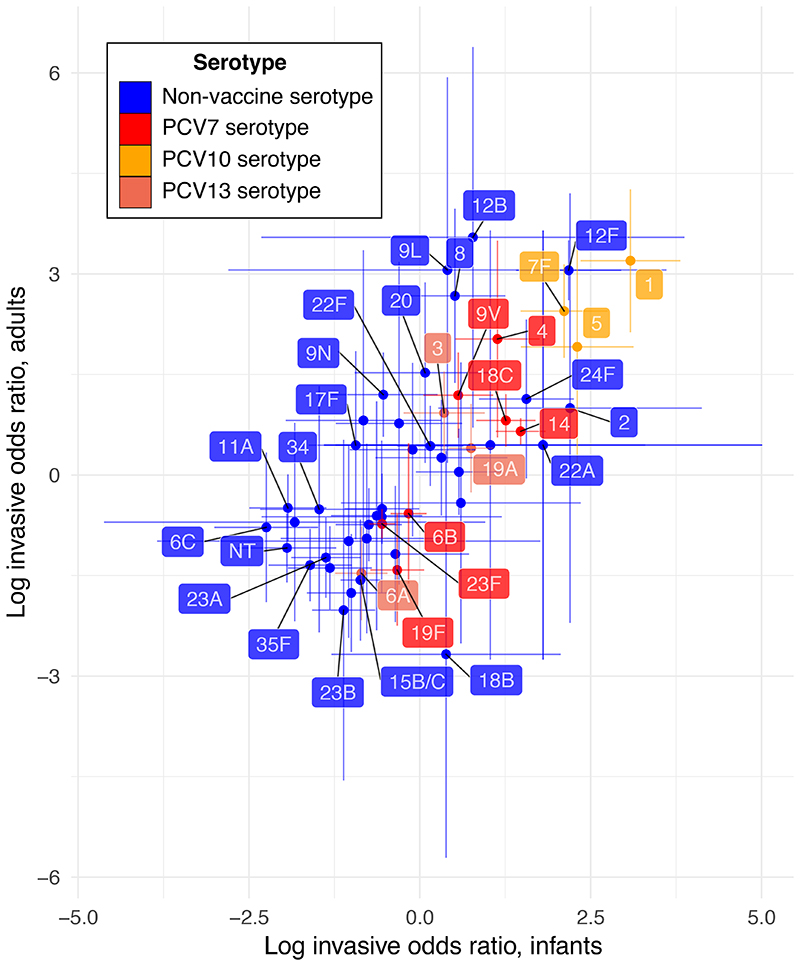
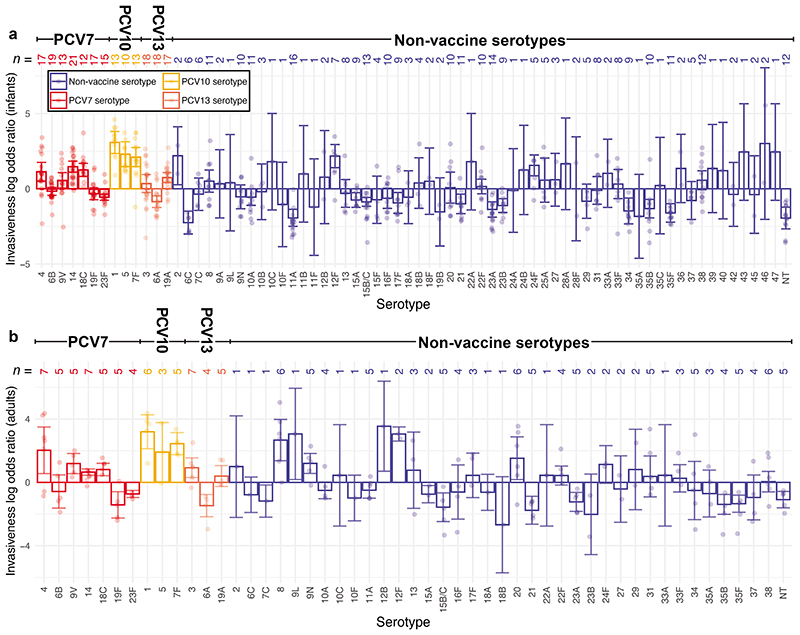
NFDS modelling only simulates the carried population dynamics. Therefore calculating the IPD burdens used for optimisation required estimating serotypes’ invasiveness. A meta-analysis of matched carriage and IPD serotype surveys was used to calculate the odds ratios for a serotype being isolated from IPD (either in infants or adults) rather than infant carriage, relative to all other serotypes detected in the population (Supplementary Tables 1-3). This found the ‘epidemic’ serotypes (1, 5, 7F and 12F) to be more invasive than some of the PCV7 ‘paediatric’ serotypes (6A, 6B, 19F and 23F; Figure 1)¹⁶. Most invasiveness odds ratios were broadly similar in adults and infants, with some other serotypes (8, 12B, 13, 9L, 9N, 20 and 29) having a relatively elevated propensity to cause disease in adults (Extended Data 4, Supplementary Figure 2).

Figure 1. Variation in the invasiveness of pneumococcal serotypes.

Invasiveness logarithmic odds ratios were calculated for pneumococcal serotypes in infants and adults through meta-analaysis of epidemiological datasets with random effects models (Supplementary Tables 1–3). Each point shows the estimated value of a serotype’s invasiveness logarithmic odds ratio in each age group, and the error bars show the corresponding 95% confidence intervals. Only serotypes for which estimates in each age group were possible (n = 51) are included. Points are coloured according to the licensed vaccine in which they are found, if any.

Minimising infant IPD

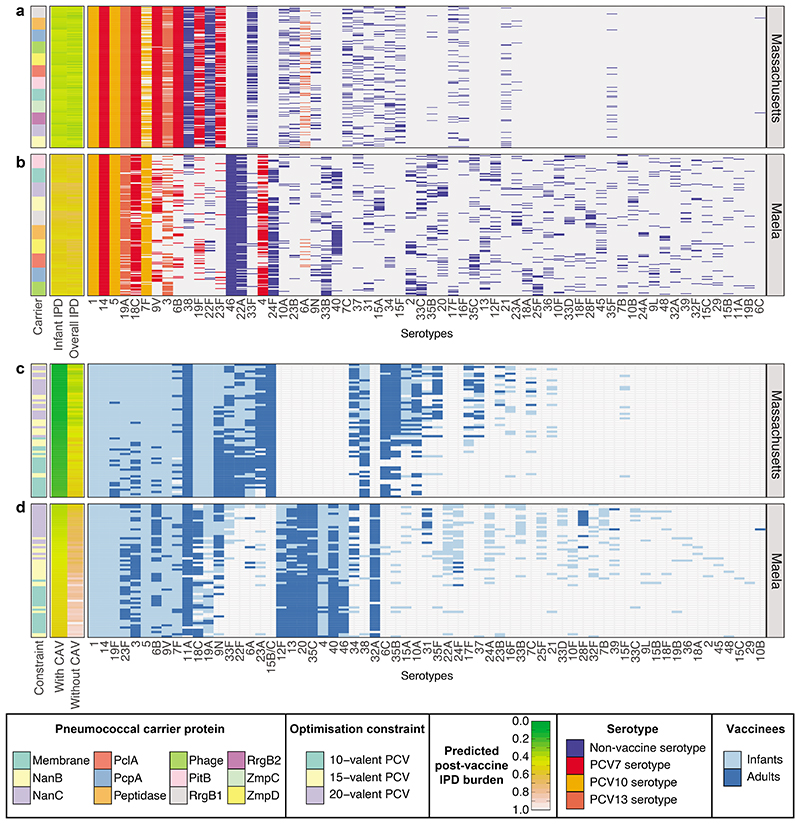
We first designed PCV formulations to minimise infant IPD. Optimisation was run with one of three different constraints: maximum valency of 15; maximum valency of 20; or a maximum valency of 10, limited to the components of PCV13. These latter formulations are known to be feasible, as the constituent antigens already feature in vaccines, and their cost would be below that of PCV13. We constrained the formulations to include serotypes 1, 5 and 14, which are rare in carriage but highly invasive, and mandatory antigens for a vaccine to be eligible for subsidised introduction into lower-income countries¹. These optimised formulations were compared to 15-valent formulations selected using serotype invasiveness, serotype virulence (i.e., the most common in IPD), or a previously-published algorithm¹⁸. Of these, only the invasiveness-based approach was predicted to match the performance of the optimised formulations, and only in Massachusetts (Methods; Supplementary Table 4). The optimised formulations were also forecast to generally outperform the current, and next, generations of PCVs (Methods; Supplementary Figure 3, Supplementary Table 4). The exception was PCV15, in Massachusetts only, although the absence of the highly invasive serotypes 8 and 12F from the carriage data in this location hindered the evaluation of PCV20.

In Maela, optimised 15- and 20-valent PCV formulations were predicted to lower infant IPD substantially more than PCV13 (Figure 2). The best-performing vaccines were those containing highly invasive serotypes. Some are found in current PCVs (e.g. 4, 7F, 18C, 19A). Others not included in licensed formulations included 22A, 33B, 24F, 40 and 46, across all formulations; 10B and 12F, enriched in successful 15-valent formulations; and 23A, 33F, 33B and 40, enriched in 20-valent formulations. Some of these have emerged as important cases of IPD following the introduction of expanded-valency PCVs, such as 12F (in the UK²⁸, The Gambia²⁴ and Japan³¹), 10B (in Israel²⁴), and 24F (in Japan³¹, Denmark³² and France²⁰).

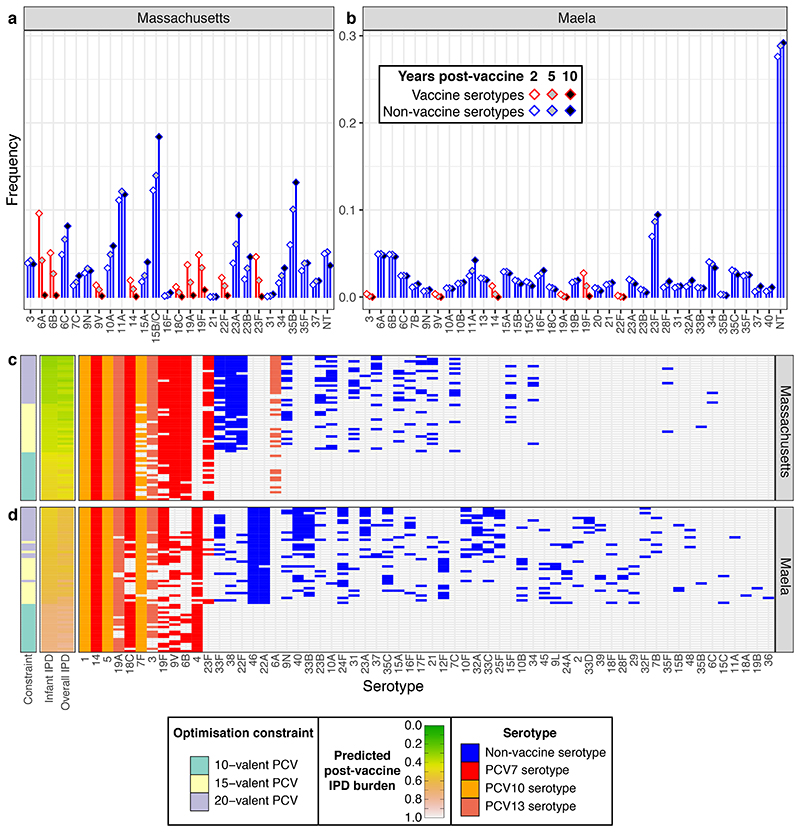
Figure 2. Optimising conjugate vaccines to minimise infant IPD.

a, b Predicted changes in serotype frequencies at different timepoints following introduction of 15-valent vaccine formulations found to be optimal for minimising infant IPD, in a Massachusetts and b Maela. c, d These plots summarise the PCV formulations identified when optimising for minimising infant IPD under different constraints in c, Massachusetts and d, Maela (n = 20 for each combination of optimisation constraint and criterion in each population). The first column shows the constraint on optimisation (10-, 15-, or 20-valent vaccine). The adjacent columns are heatmaps showing the predicted level of IPD in infants 10 years post-vaccine introduction (by which the rows are ordered), and the overall population (equally weighting the burden of infant and adult IPD). The grid shows the composition of the vaccines, with included serotypes indicated by cells coloured according to their presence in licensed vaccines. The columns are ordered by the frequency with which each serotype was included in vaccines across the two populations.

The model also predicted the performance of PCV13 could be improved in Maela by omitting some components. The best-performing ‘subset’ vaccine did not contain the paediatric serotypes 6A, 6B, 19F and 23F, and reduced infant IPD partly by maintaining high levels of these serotypes in the post-vaccine population (Supplementary Figure 4). Were these serotypes to be removed by PCV13, the mixture of serotypes replacing them would include some that are potentially highly invasive (e.g. 40 and 46).

In the Massachusetts dataset, 15-valent formulations could only slightly outperform PCV13 in terms of forecast infant IPD, whereas 20-valent formulations offered more opportunities for reducing disease (Figure 2). The most frequently added non-PCV13 serotypes were the moderately common and invasive 22F, 33F and 38, resulting in populations dominated by low-invasiveness serotypes (Extended Data 5, Supplementary Figure 5). Surveillance of infant IPD after the introduction of higher-valency PCVs has identified 22F as the most common non-PCV13 serotype, with 33F and 38 also problematic³³, although global population genomic analysis suggests these serotypes’ contribution to post-PCV IPD varies between countries²⁴.

Minimising population-wide IPD through infant vaccination

We then used an alternative optimisation criterion to identify vaccines that would minimise overall infant and adult IPD, weighting each equally (Figure 3). The resulting formulations in Massachusetts do not include serotype 6A, unlike the PCVs designed to minimise infant IPD only (Figure 2), likely due to the risk of replacement by serotype 6C, which has a high invasiveness in adults³⁴. Similar reasons likely underlie the omission of 19F from PCVs optimised for reducing overall IPD in Maela, unlike those vaccines optimised for minimising infant IPD (Figure 2). PCVs minimising overall IPD instead commonly feature serotype 9N in both locations, which could have helped avoid the substantial increases in adult IPD with this serotype recorded in the UK and Sweden post-PCV13^28,33. They also include 6C, in Massachusetts, and 13, in Maela, reflecting the elevated invasiveness of these serotypes in adults (Figure 1).

Figure 3. Vaccine strategies for minimising population-wide IPD.

a-b, These plots summarise the infant-administered PCV formulations identified when optimising for minimising both infant and adult IPD under different constraints in a, Massachusetts and b, Maela (n = 20 for each combination of optimisation constraint and criterion in each population). Data are displayed as described in Figure 2c-d, except that the rows are ordered by the predicted post-vaccination overall IPD burden. This assumes herd immunity induced by the infant vaccination campaign would also eliminate the vaccine serotypes from adult IPD. c-d, The plots summarise combined strategies in which complementary adult vaccines (CAVs) were designed for each of the infant vaccinations shown in Figure 2c-d for c, Massachusetts and d, Maela. Pneumococcal population dynamics were assumed to be driven by the carried population in infants, such that elimination of serotypes in infants resulted in population-wide herd immunity. The CAVs were designed to provide protection against the 10 serotypes predicted to cause the most IPD in adults 10 years after the introduction of the infant-administered vaccines. The adult-administered vaccines were assumed not to drive herd immunity themselves. These formulations are represented as in panels a and b, except that the heatmaps show the predicted population-wide IPD burden for infant vaccination without a CAV, or combining infant vaccination with a CAV. The rows are ordered by the overall IPD burden predicted for each combined vaccination strategy, with cells coloured light blue if serotypes were included in the infant-administered formulation, or dark blue if serotypes were included in the adult-administered formulation.

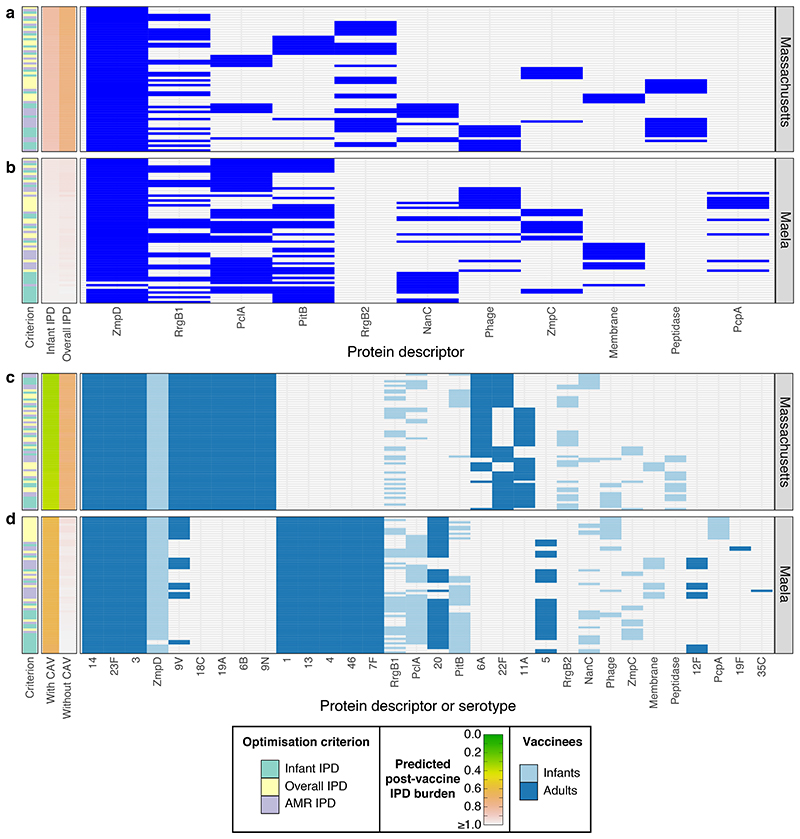
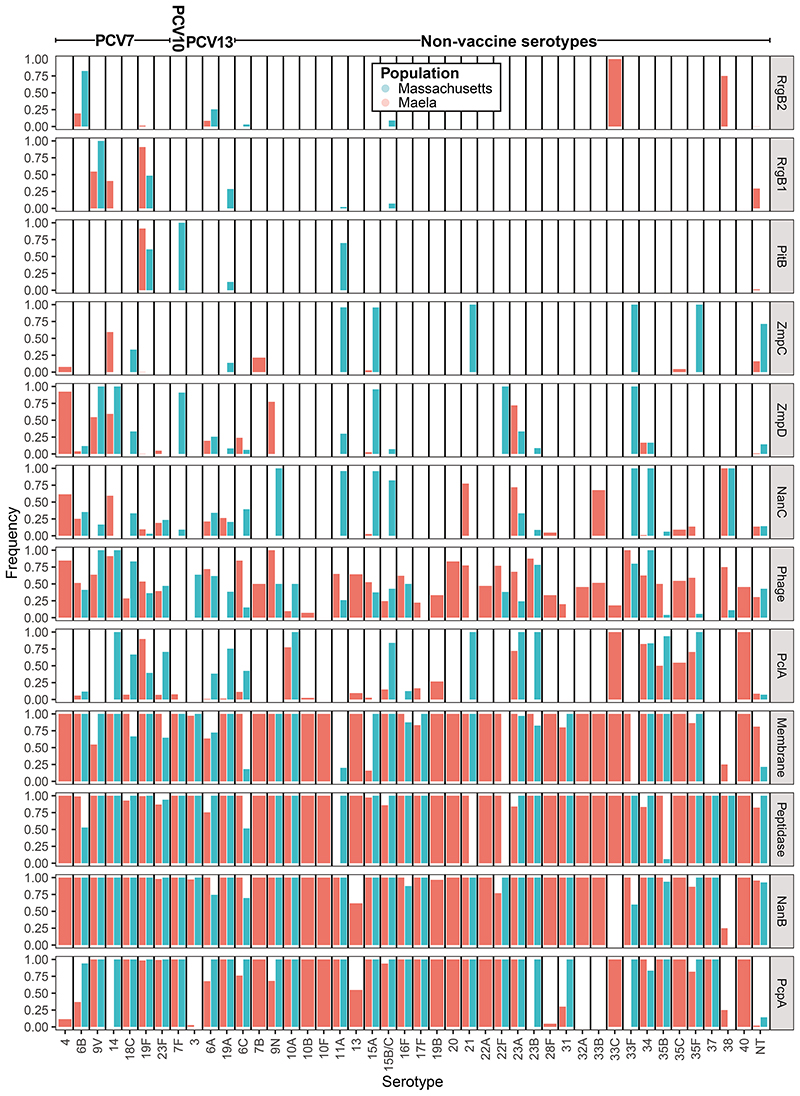
Pneumococci express immunogenic surface proteins, some of which are present at intermediate frequencies in pneumococcal populations^35,36 (Supplementary Figure 6, Supplementary Table 5). These could be used to generate a multivalent protein vaccine, analogous to a PCV but with fewer components, each of which would be cheaper to manufacture. Furthermore, removal of the targeted strains by vaccine-induced anti-protein immunity would still be enhanced by competition between vaccine and non-vaccine types⁸. Assuming vaccine-induced anti-protein immunity to be at most half that induced by PCVs, optimisation was used to select combinations of intermediate-frequency antigenic proteins (Figure 4). This consistently recommended the inclusion of the zinc metalloprotease ZmpD and pilus protein RrgB1, enriched in invasive serotypes such as 9V and 14 in both populations (Extended Data 6). Nevertheless, these multiprotein vaccines were forecast to be much less effective than PCVs.

Figure 4. Optimising multiprotein vaccines to minimise IPD.

a-b, These plots summarise the protein-based formulations identified when optimising to minimise infant, overall or AMR IPD (as indicated by the first column). These were composed of a mixture of immunogenic proteins found at intermediate frequencies (5%-95%) in the pneumococcal populations of a, Massachusetts (12 proteins) and b, Maela (10 proteins), respectively (n = 20 formulations for each combination of optimisation constraint and criterion in each population). Results are otherwise displayed as described for Figure 2c-d, with rows ordered by the formulations’ effectiveness in minimising infant IPD. c-d, These plots summarise combined vaccination strategies in which a capsule-based CAV was devised for each multiprotein infant vaccine. Results are displayed as described in Figure 3c-d.

Formulations assumed to include a pneumococcal protein as a carrier, with 15-valent PCVs generated through optimisation of the added capsular antigens, were more successful (Extended Data 7). Many of these formulations outperformed 15-valent PCVs with unspecified carriers in both populations (Extended Data 8). In Maela, the targeted serotypes varied with the identity of the carrier, suggesting an interaction of different types of vaccine-induced immunity (Extended Data 7; Supplementary Figures 7-8). However, the association of surface proteins and serotypes is inconsistent between populations, making the benefits of pneumococcal carrier proteins difficult to generalise.

Minimising antimicrobial-resistant IPD

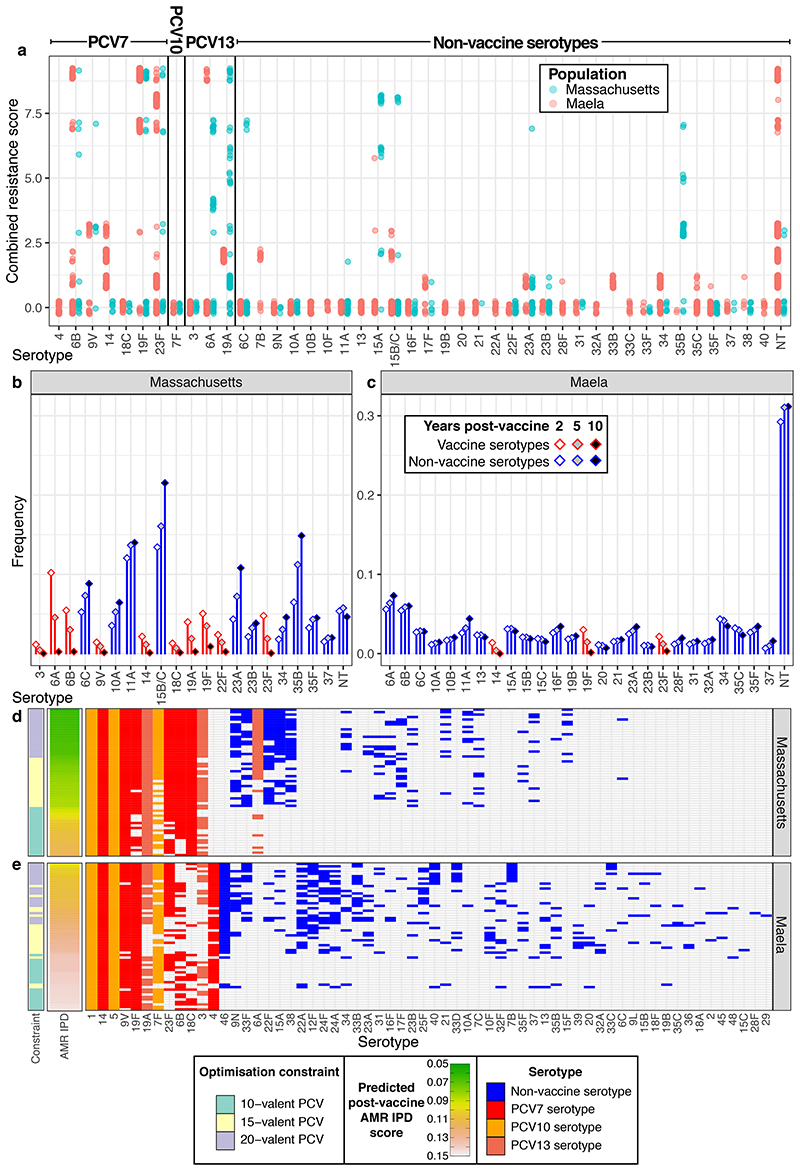
The distribution of antimicrobial-resistant (AMR) genotypes is an important consideration in PCV design, as IPD has a higher mortality rate when the pathogen is resistant to antibiotics^37,38. Rather than employing vaccines to lower antibiotic consumption by limiting bacterial disease³⁹, we optimised PCVs to directly reduce AMR IPD in the absence of any change in antibiotic consumption. Despite moderate changes in antibiotic use during the epidemiological studies, antibiotic resistance phenotypes were maintained at approximately stable levels in the Massachusetts and Maela carriage populations^10,11,40,41. Correspondingly, the model assumed that individual AMR phenotypes have stable frequencies in carriage that are maintained by NFDS^12,13,42, such that elimination of vaccine-type resistant isolates would drive replacement by other non-susceptible genotypes. Given this constraint, we optimised vaccine formulations to minimise multidrug-resistant IPD across infants and adults. Each genotype’s AMR profile was scored according to non-susceptibility to penicillins, macrolides, co-trimoxazole and tetracyclines, with further penalties for particular combinations of AMR phenotypes (Methods). This AMR score’s distribution was highly heterogeneous across both populations, with most serotypes pansusceptible, but a few associated with high levels of multidrug-resistance (Figure 5). Each genotype’s invasiveness was combined with its AMR score to estimate the probability it would cause IPD and be resistant to the administered treatment, which was used as the criterion for optimisation (Methods).

Figure 5. Optimising conjugate vaccines to minimise AMR IPD.

a, Distribution of AMR score by serotype across the two populations. Only serotypes with at least ten representatives across both populations are included in the graph. b-c, Predicted changes in serotype frequency following the introduction of 15-valent vaccine formulations found to be optimal for reducing AMR IPD in b, Massachusetts and c, Maela, displayed as described in Figure 2a-b. d-e, These plots summarise the PCV formulations identified optimising for minimising AMR IPD under different constraints in d, Massachusetts and e, Maela, displayed as described in Figure 2c-d (n = 20 for each combination of optimisation constraint and criterion in each population). The rows of the plot are ordered by the predicted post-vaccine AMR IPD burden, as shown by the heatmap.

The resulting designs (Figure 5) often contained serotypes 9V, 19A, 19F and 23F in both populations, which were the only serotypes consistently associated with resistance across the two locations (Extended Data 1, Supplementary Figure 9). Serotypes 6A and 15A were additionally included in formulations for Massachusetts, where they were associated with AMR¹⁰. These formulations enabled the post-vaccine success of pan-susceptible serotypes (11A in Massachusetts; 6A and 11A in Maela), low-invasiveness AMR serotypes (6C, 23A and 35B in Massachusetts; 6A and unencapsulated non-typeables, or NTs, in Maela) and penicillin-susceptible isolates resistant to non-β-lactam treatments (e.g. some 15B/C in Massachusetts). While the distinct objectives of minimising overall and AMR IPD require an inevitable trade-off, it was small (Extended Data 8).

Age-specific vaccine design

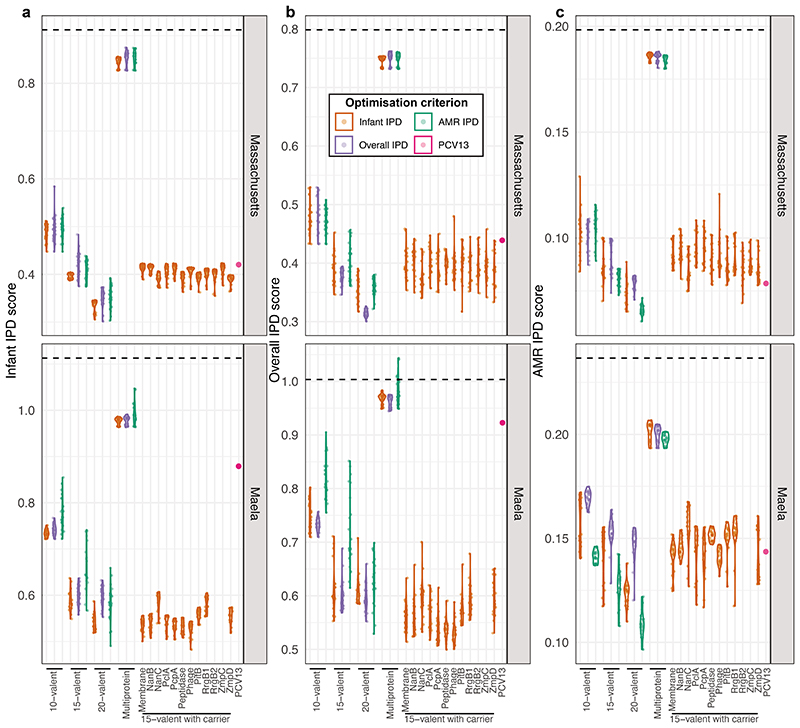
Across all criteria, the benefits of expanding infant-administered PCV valency were predicted to diminish over the analysed range (Extended Data 8). Given serotypes’ differential invasiveness in infants and adults, a more effective strategy may be to develop paired infant-administered and complementary adult-administered vaccines (CAVs). Assuming infant-administered vaccines established herd immunity after 10 years, CAVs were designed to include the 10 serotypes causing the most adult IPD, based on serotypes’ infant carriage prevalence and invasiveness in adults (Figures 3-4; Extended Data 7). We did not consider CAVs to affect infant IPD, as the adult demographics at highest risk of IPD are unlikely to contribute sufficiently to pneumococcal transmission for their vaccination to drive herd immunity.

Assuming CAVs afforded 90% protection against IPD caused by the included serotypes, the combination of a 10-valent infant PCV and CAV was predicted to be more effective at reducing overall IPD than a 20-valent infant PCV (Figure 6). CAVs tended to include both serotypes with elevated invasiveness in adults (6C in Massachusetts; 3, 9N and 12F in Maela), and low-invasiveness serotypes common in the post-infant vaccination population (11A and 34 in both; 15B/C, 22F, 35B in Massachusetts; 13, 20, 23F and 35C in Maela). Many of these (e.g. 6C, 13, 34, 35B, 35C, 35F and 40) do not feature in any currently-available vaccine administered to adults¹.

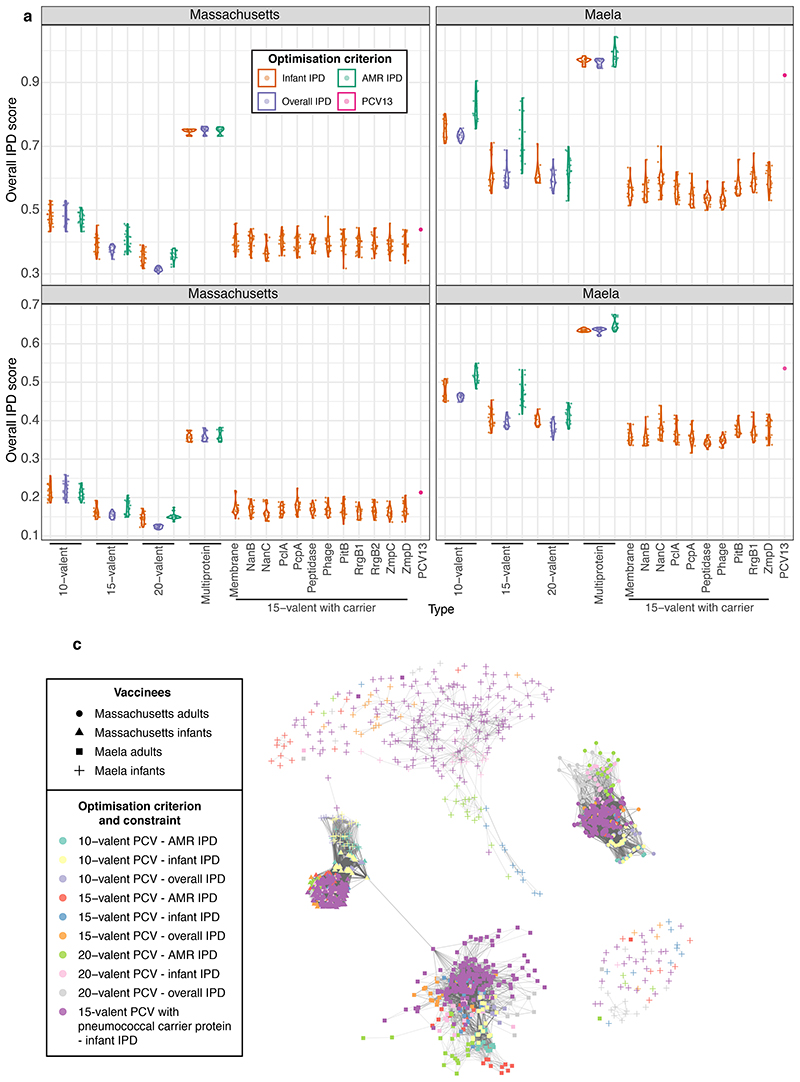
Figure 6. Comparing the design and effectiveness of different vaccination strategies.

a, Violin plots showing the predicted overall IPD burden 10 years post-vaccination in Massachusetts and Maela for all infant-administered vaccine formulations generated by optimisation. Each plot is positioned by, and labelled with, the constraint on formulation design, and coloured according to the criterion optimisation was intended to minimise. The overlaid points show the estimated effects of each individual optimised formulation (n = 20 for each combination of constraint and optimisation criterion in each population). The purple point in each panel shows the corresponding estimates for PCV13. b, Violin plots showing the same estimates with the introduction of CAVs appropriate to each infant-administered vaccine (n = 20 for each combination of constraint and optimisation criterion in each population). c, Network summarising the optimal vaccine formulations identified in this work. Each node (n = 1600) corresponds to a vaccine formulation, with its colour reflecting the optimisation constraint and criterion, and its shape indicating the intended recipient population. Edges link similar vaccine formulations, identified by applying an empirically-determined threshold to the distribution of pairwise Jaccard distances (Supplementary Figure 10).

Discussion

Many interventions against infectious diseases are designed using models that do not exploit population genomic datasets, or consider the ecological forces driving population dynamics. Yet, transmission-blocking vaccines and treatments are continually undermined by pathogen evolution. Our work shows how integrating genomics and modelling could address this deficiency. This analysis identified a set of pneumococcal vaccines, each of which was designed to be optimal for a defined starting population, a design constraint, and an optimisation criterion specifying the type of IPD to be minimised. For each of the infant-administered vaccines expected to alter the carried population, we defined complementary adult-administered vaccines to further reduce the population-wide burden of IPD. These age-specific vaccines therefore maximally benefit the respective vaccinee demographics, assuming that infant vaccination programmes establish herd immunity after ten years. This is consistent with post-PCV surveillance datasets, excepting those locations where high adult carriage may allow infant vaccine serotypes to persist^17,27.

We illustrate the relationships among the high-performing vaccine designs with a network that links formulations with similar compositions (Figure 6, Supplementary Figure 10). There are four main groupings, corresponding to infant- and adult-administered vaccines in the two populations. For each of these four groups, we manually refined the results of logic regression⁴³ to summarize the optimal PCV formulations (Supplementary Table 6). The infant-administered PCVs for Massachusetts-like populations should include 18C and 19A, which were present in high-performing designs optimised for minimising infant or overall IPD; effective formulations also had 6B or 9V, and at least three of 3, 6A, 7F, 19F, 22F, 23F, 33F and 38 (Supplementary Figure 7). Similar definitions of Massachusetts CAVs, and both types of formulation for Maela, are presented in Supplementary Table 6.

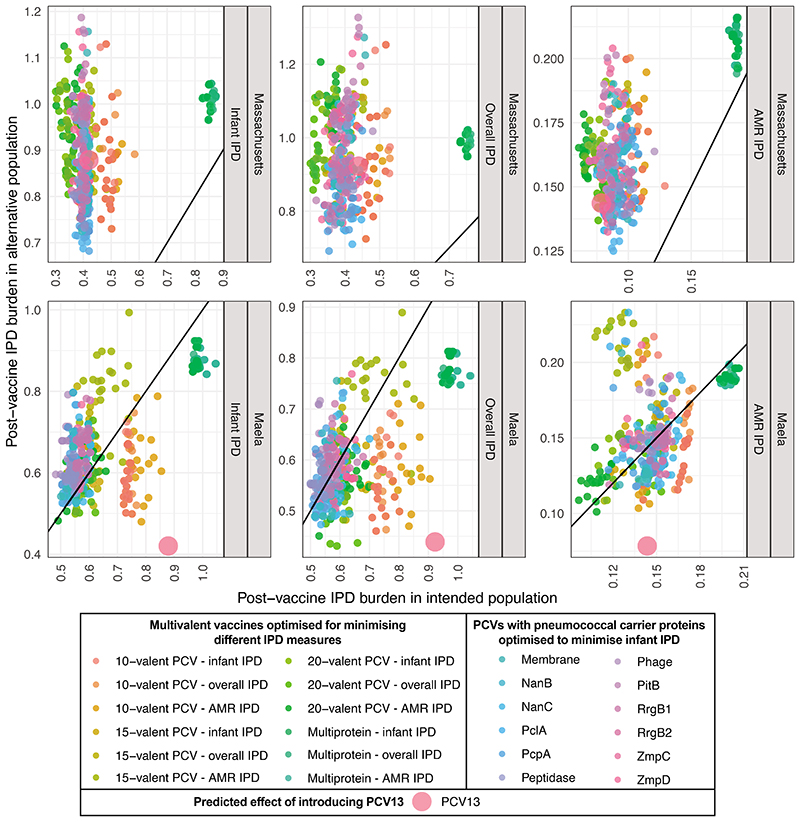
Therefore the optimal formulations were determined by the circulating bacterial population, and whether they were expected to block transmission in infants, or only prevent disease in adults. Consequently there are risks to expanding use of vaccines designed for Western populations in locations like Maela, where the outcomes of introducing PCV13 are predicted to be sub-optimal (Extended Data 9), and could be improved by replacing four of PCV13’s components with six alternative antigens (Supplementary Table 4). Hence it would appear to be beneficial to broaden the portfolio of licensed formulations, rather than globally optimise a single formulation. Although the first country-specific PCVs are currently being implemented in India, the practical difficulties of vaccine manufacture will limit more widespread PCV customisation until new conjugation technologies have proved effective⁴⁴. Regulating a multitude of formulations would also prove challenging, although the standards required for licensing have already changed substantially between generations of PCVs⁴⁵. The network displayed in Figure 6 illustrates that regulating individual antigens, or a mixture spanning all serotypes included in a cluster of highly similar formulations, may prove more feasible than testing each individual combination.

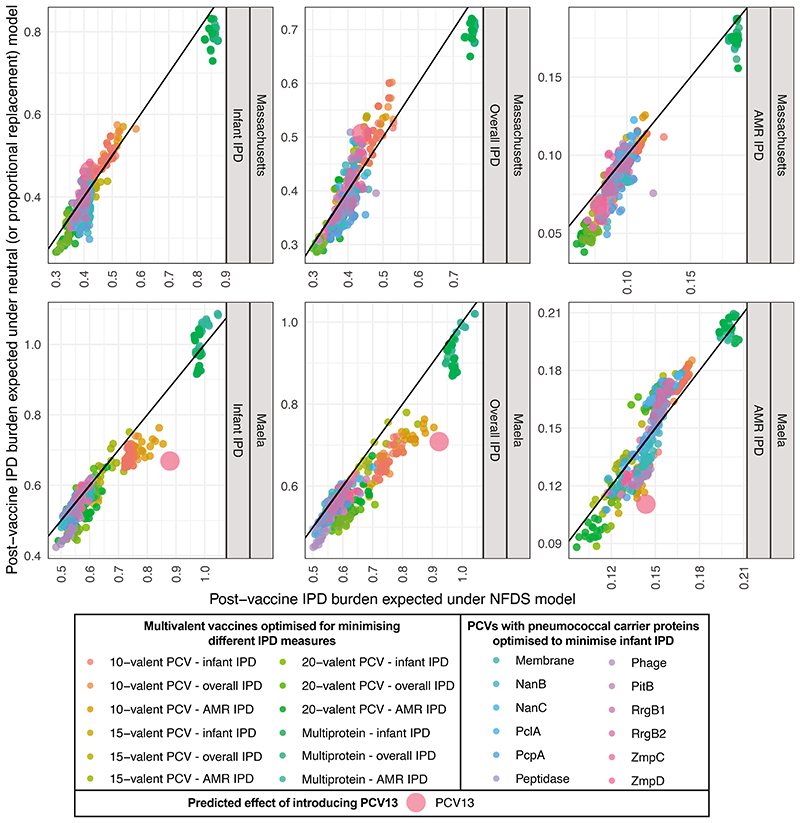
These conclusions are subject to four principal sources of uncertainty. Firstly, bacterial ecology remains incompletely characterised; further evidence of NFDS shaping populations, and more precise characterisation of the selective pressures involved, are necessary to confidently forecast the effects of vaccines. Yet our optimised formulations are similarly effective in the absence of NFDS, suggesting they do not critically depend on this process for their success (Extended Data 10). Instead, simulations featuring NFDS filter out vaccines that might appear effective in a neutral model, but are at risk of causing harmful serotype replacement. Secondly, the unknown genetic basis of strains’ invasiveness, whether entirely serotype-determined or not, makes estimating the IPD burden difficult. This is particularly acute for a location such as Maela, where many detected serotypes are associated with little epidemiological data on their propensity to cause disease (Supplementary Figure 11). These poorly-characterised serotypes may emerge as more global concerns as higher-valency PCVs deplete currently-circulating serotypes. Thirdly, highly invasive strains are omitted from the simulations, if they are not detected in carriage. Adding the serotypes of such strains to formulations should not substantially alter the predicted strain replacement process, owing to the small fraction of the carried population they comprise. However, even small perturbations of invasive serotypes’ frequencies, resulting from the population restructuring induced by the formulations designed in this work, could have substantial impacts on IPD rates²⁸. Fourthly, our modelling of serotype replacement is limited by our understanding of global transmission patterns and strain diversity. International sequencing-focussed research projects^24,46, and routine genomic surveillance⁴⁷, will help address all these lacunae. These advances can be integrated through the framework presented here to aid vaccine design, and inform policy making at a regional level, given sufficient sampling and sequencing of both local, and global, carriage and IPD isolates. Combined with recent advances in manufacturing techniques, there is an emerging opportunity to apply the principles of ‘precision medicine’ to ensure PCVs are maximally effective for everyone.

Methods

Meta-analysis of serotype invasiveness

To identify paired samples of pneumococci from invasive disease in infants or adults, relative to the circulating carriage population in infants, PUBMED was searched with the following terms on 5th October 2017:

(case[All Fields] OR disease[All Fields] OR episode[All Fields] OR patient[All Fields]) AND (carriage[All Fields] OR carrier[All Fields] OR nasopharyngeal[All Fields]) AND (invasiveness[All Fields] OR “attack rate”[All Fields] OR “type distribution”[All Fields] OR “serotype distribution”[All Fields] OR “serogroup distribution”[All Fields] OR “invasive capacity”[All Fields] OR “invasiveness ratio”[All Fields] OR “odds ratio”[All Fields] OR “carrier ratio”[All Fields] OR (“invasive isolates”[All Fields] AND “carriage isolates”[All Fields])) AND (“serogroup”[MeSH Terms] OR “serogroup”[All Fields] OR “serotype”[All Fields]) AND (“streptococcus pneumoniae”[MeSH Terms] OR (“streptococcus”[All Fields] AND “pneumoniae”[All Fields]) OR “streptococcus pneumoniae”[All Fields] OR “pneumococcus”[All Fields])

This returned 136 results, the abstracts of which were reviewed to identify those in which data could be extracted for meta-analysis at a serotype-specific level of precision. Thirty-four abstracts were found likely to be appropriate. After reading the papers, six did not contain matched disease and asymptomatic carriage samples, and seven further individual studies were rejected due to bias towards particular serotypes or lack of serotype-level reporting, very high co-colonisation complicating analysis of the carriage sample, difficulties using data when stratified by age, or inability to access the raw data. This left 21 studies with matched systematically-sampled and thoroughly serotyped asymptomatic carriage and disease samples^29,48–67. Within these, isolates of the rapidly-interconverting serotypes 15B and 15C were combined into a single 15B/C category. Samples were then stratified by age and date of vaccine introduction, generating 23 pairs of infant carriage and infant IPD samples (seven of which were post-PCV introduction), and seven pairs of infant carriage and primarily adult IPD samples (one of which was post-PCV introduction). Logarithmic invasiveness odds ratios were calculated across datasets by fitting random effects models using the metafor package⁶⁸ in R. The studies are listed in Supplementary Table 1, and the data summarised in Supplementary Tables 2 and 3.

When calculating IPD burdens, if an adult invasiveness value was not available for a serotype, its infant invasiveness was used instead. If an infant invasiveness estimate was not available, the lowest invasiveness estimate from within the same serogroup was used, where one was available; otherwise a value associated with a similarly rare serotype with a low invasiveness estimate was selected. The invasiveness of vaccine serotypes was not changed in the post-vaccine period, as vaccine serotypes’ invasiveness odds ratios were not substantially altered between the pre- and post-PCV periods, relative to the variation observed for non-vaccine serotypes (Supplementary Figure 2).

Model specification

We approximate the stochastic model of Corander et al¹² with a deterministic set of ordinary differential equations describing the evolution of the pneumococcal population in response to a vaccine strategy. We model the same negative frequency-dependent selection (NFDS), in which each intermediate-frequency locus l (present at between 5% and 95% prevalence in the initial population) is assumed to have an equilibrium frequency, e_l. This frequency is calculated from the pre-vaccine population. The NFDS assumption is that loci will return to their equilibrium frequencies following a perturbation of the population. Each isolate is defined by its serotype, resistance profile and its genotype, determined by the intermediate-frequency loci it encodes. The genotypes are recorded in a matrix G with G_il = 1 if strain i encodes l, and 0 otherwise. Vaccine-induced immunity perturbs the population through removal of vaccine-type serotypes, meaning the instantaneous frequency of l at time t after the vaccine’s introduction, f_l,t, may deviate from e_l. As NFDS means loci are most advantageous when rare, a genotype will have a high fitness in a population at t if it contains many loci whose instantaneous frequencies are below their corresponding equilibrium frequencies. The model represents this high fitness with an increased reproduction rate, and this acts to return the locus frequencies towards their equilibria, e_l. Conversely, genotypes containing many loci that are currently above their equilibrium frequencies have a reduced reproduction rate.

This model assumes that carriage remains stable post-vaccination, as has typically been observed following PCV introduction^1,18, such that density-dependent competition is constant¹². Per-locus NFDS effects are assumed to be additive. Additionally, the model does not feature recombination, implicitly assuming genotypes are stable over the 10 year interval between vaccine introduction and evaluation. This is consistent with the observed frequency of homologous recombinations occurring once every few years within S. pneumoniae lineages⁶⁹, and the stable non-prophage accessory genomes of S. pneumoniae strains^12,70,71, which are known to be decades or centuries old^10,72–74.

We model the NFDS with a term ${\pi }_{i,t}(G,Y)={\sum }_{l=1}^L{W}_l{G}_{il}(e_l-f_{i,t})$, where L is the total number of intermediate-frequency loci, and Y is a vector whose components y_i, are the prevalences of the genotypes, indexed by i. The w_l values are weights modifying the strength of NFDS for each locus l¹². The index i runs from 1 to M, the number of unique intermediate-frequency locus profiles in the model (M is 603 for the Massachusetts data and 674 for the Maela data). The NFDS term depends on the prevalence of all the genotypes in the model because it depends on the frequency of each locus; this couples the genotypes together. The frequencies are computed from the prevalences:

$$f_{l,t}=\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\sum }_{i=1}^M{y}_i$}\right.\right){\displaystyle {\sum }_{i=1}^M{y}_i{G}_{il}}$$

To derive a deterministic model describing the same average population dynamics as Corander et al¹² we use the standard first-order approach, equating the fractional change in a fixed time frame in the two models. This gives ${\stackrel{.}{y}}_l=\left(K(Y)-r_i+\rho {\pi }_{i,t}(G,Y)\right)y_i+\epsilon$, where $K(Y)=log\left(\frac{\kappa }{N}\right)$ is a term enforcing density-dependent selection with a carrying capacity of ĸ (here taken to be 10⁵) and $N={\sum }_{i=1}^M{y}_i$. The vaccine strategy is embedded in the values r_i, which are either a constant r (if genotype i encodes an antigen included in the vaccine), or 0. The constant ρ is the overall strength of NFDS; for the neutral (or ‘proportional replacement’) simulations exploring the effects of NFDS, we set ρ = 0.

The parameters r and ρ were fitted to the model of Corander et al¹² to obtain the same rates of decline of vaccine strains and rise in non-vaccine strains following the simulated introduction of PCV7 into the Massachusetts population (Extended Data 2), yielding r = 0.063 and ρ = 0.165. Equilibrium locus frequencies e_l and weights w_l are equal to those in Corander et al¹². Such replication of the PCV7-associated population dynamics depended on using the pre-vaccine population frequency of each genotype i, taken as a proportion of the carrying capacity, as the initial frequency y_i(0). To validate that this deterministic model replicated the dynamics of the stochastic version, the frequencies of the pneumococcal ‘sequence clusters’ (analogous to strains) 10 years after PCV7 introduction were compared between simulations run using the ordinary differential equation (ODE) and stochastic models (Extended Data 2). One hundred replicates were run for each of two stochastic model simulation types: one assuming a uniform migration rate per sequence cluster, which was used to facilitate model fitting, and one assuming a uniform migration rate per isolate. These reach slightly different population compositions after ten years. The ODE model necessarily uses a deterministic uniform migration rate per genotype, which is intermediate between the two mechanisms implemented for the stochastic model: each genotype may represent multiple isolates, and each sequence cluster contains multiple genotypes. Appropriately, these simulations arrive at a third equilibrium, in which each sequence cluster’s frequency matches that in at least one, and usually both, of the stochastic model outputs. This is consistent with an accurate replication of the NFDS mechanics, and the uncertainty of the migration process, given the current paucity of well-sampled carriage collections from the wider S. pneumoniae metapopulation.

Currently, there is a lack of evidence for vaccine-induced anti-protein immunity providing similar protection against S. pneumoniae carriage to that induced by PCVs¹. Additionally, pneumococcal proteins vary extensively in their immunogenicity^35,36. Hence the strength of vaccine-induced immunity, r, against protein antigens was modified by a factor a (Supplementary Table 5), whether they featured in a multiprotein formulation or were present as a carrier in a PCV. This factor was calculated as half the median normalised immunoglobulin G binding to the specified protein antigen, measured using a panproteome array, divided by the maximum observed median normalised immunoglobulin G binding in the same study³⁵. Hence a had a range of zero to 0.5.

To reduce the dimensionality in the Maela dataset, we modelled frequencies of clusters of genotypes, rather than each individual genotype. We obtained clusters using a network approach, by creating a graph whose nodes were individual genotypes and whose edges joined two genotypes if they differed at fewer than 20 loci and had the same serotype and resistance loci. Each of the 674 connected components in this graph was modelled as having the properties and gene content of the component’s highest-degree genotype. The Maela samples were collected over a short period in an unvaccinated population, and therefore we modelled each sequence cluster as equally prevalent initially.

Optimisation approach

We optimised for minimising one of three distinct criteria: (1) infant IPD; (2) overall IPD, which equally weighted each serotype’s invasiveness in infants and adults; and (3) AMR IPD, a criterion under which genotypes scored highly if they were both resistant and invasive. For a modelled population with prevalences y_i(t) of genotype i at time t following the introduction of a vaccine, the infant IPD burden was estimated as $\frac{1}{N}{\sum }_{i=1}^M{y}_i\text{exp}\left(K_i\right)$ where K_i, is the infant invasiveness logarithmic odds ratio (log OR) of genotype i, based on its serotype, and N is the total prevalence (which is very close to the carrying capacity). Similarly, the overall IPD burden was calculated as $\frac{1}{N}{\sum }_{i=1}^M{y}_i\text{exp}(\frac{1}{2}(K_i+A_i))$, where A_i, are the serotype-derived log OR of invasive disease in adults for genotype i. We used ORs, rather than log ORs, in the criteria because this will drive the optimisations to suppress highly invasive strains.

To define the optimisation criterion for minimising AMR IPD, we calculated a resistance score for each isolate, and used this to develop a logistic model based on minimising the probability of a pneumococcus causing IPD being non-susceptible to an administered treatment. The score for an isolate was 0 if it was susceptible to penicillin, which corresponded to the isolate having β-lactam-susceptible alleles at each of the three relevant penicillin-binding protein-encoding loci (pbp1a, pbp2b and pbp2x)^10,12. If the strain appeared to exhibit any β-lactam non-susceptibility, this conferred a score equal to the number of loci at which β-lactam resistance alleles were present (n_p). If the genotype was also inferred to be macrolide resistant, then n_m (set equal to one) was added to the score; furthermore, if the macrolide-resistant genotype encoded loci conferring resistance to trimethoprim, sulphamethoxazole (the components of co-trimoxazole, cumulatively quantified as n_c), or tetracycline (quantified as n_t), then the resistance score was incremented by the appropriate number of resistance loci. In summary, if I_p and I_m are indicators for the presence of any β lactam or macrolide resistance loci, respectively; and if n_p, n_m, n_c and n_t are the numbers of loci associated with the four described antibiotic classes, the resistance score of genotype i is:

$$R_i=l_p(n_p+I_m(n_m+n_c+n_t))$$

This is broadly motivated by prescribing practices that first use penicillin and, if that is ineffective, a macrolide, followed by less common use of other antibiotic classes. Based on the score, we model a logistic probability⁷⁵ of resistance to treatment as $P_i=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1+\text{exp}(-a-b{R}_i)$}\right.$ with a = -2 and b = 0.5.

The combined AMR IPD criterion is calculated as $\frac{1}{N}{\sum }_{i=1}^M{y}_i\text{exp}\left(\frac{1}{2}(K_i+A_i)\right)P_i$, which combines infant and adult invasiveness with the probability of resistance to treatment.

The optimisation criteria are uncertain, as they are calculated from the invasiveness estimates. The serotype-based invasiveness in infants and adults (log ORs K_i, and A_i) are point estimates associated with 95% confidence intervals. To assess uncertainty in the criteria, we resampled each serotype’s invasiveness log OR from a Gaussian distribution with mean and standard deviation inferred from the meta-analysis. Each strain was assigned the new log OR corresponding to its serotype, and the criterion was recomputed. Because our criteria feature ORs (not log ORs), the resampled criteria are positively skewed. We illustrate the magnitude of uncertainty in the infant invasiveness estimates in Supplementary Figure 11; other criteria are qualitatively similar in uncertainty. We also explored resampling the invasiveness of a serotype in different individual hosts according to the same distribution, as the same serotype could have different propensities to cause invasive disease in different individuals. This results in less variance in the objective estimates than is shown in Figure 1 because prevalent serotypes’ invasiveness is sampled many times, and the average of these samples is close to the mean (by the central limit theorem); rare serotypes have more variance, but as they are rare, they contribute less to the objective function.

The model was solved in matlab with the ode15s solver. All prevalences were set to be non-negative, the absolute tolerance was 10^-8 and the relative tolerance was 10^-5. Simulating the pneumococcal population over 10 years took approximately 0.5 s for the Maela population, and 0.33 s for the Massachusetts population. We primarily used Bayesian optimisation in matlab to explore the space of possible vaccine strategies; this is implemented in the ‘bayesopt’ function in the statistics and machine learning toolbox. We constrained the number of serotypes to generate a 15- or 20-valent formulation, while enforcing the inclusion of serotypes 1, 5 and 14, which are mandatory for a PCV to be eligible for subsidised introduction into lower-income countries through the GAVI Advance Market Commitment¹. We also ‘downsampled’ PCV13, selecting up to 7 of the serotypes in this vaccine, in addition to 1, 5 and 14. The ‘bayesopt’ function uses its own acquisition function to determine where next to search the space of possible strategies; where this failed due to its chosen strategies not meeting our constraints, we used a genetic algorithm (‘ga’ in matlab’s Global Optimization Toolbox) with customised mutation and crossover functions to sample vaccine strategies that matched our constraints.

Complementary adult vaccine design

To identify complementary adults vaccines (CAVs) to minimise IPD in older age groups, we forecast the carried pneumococcal population 10 years after the introduction of an infant-administered formulation. We computed the contribution of each serotype, n, to the total adult IPD burden, a_n, as a_n = Σ_{i: s(i)=n} y_iA_i, where s(i) is the serotype of genotype i and A_i is the invasiveness log OR in adults for serotype s(i). The complementary vaccine included the 10 serotypes making the greatest contributions to adult IPD. To model the updated adult IPD burden we assumed that inclusion in the complementary vaccine would reduce a serotype’s invasiveness in adults by 90%⁷⁶. Hence the overall IPD burden measure used for comparison with those resulting from infant vaccination strategies was calculated as:

$$IP{D}_{CAV}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^M{y}_i\text{exp}(\frac{1}{2}(K_i+A_i+I_{CAV}log(0.1))}$$

The parameter I_CAV represents a binary indicator of whether the serotype of genotype i was included in the CAV formulation.

Model dynamics

We chose to assess the objective functions at a 10-year time point. While the model has long transient behaviour in the genotype frequencies, this is primarily due to slow drifting amongst very similar genotypes. The objective functions are very similar at the 10, 25 and 50-year time points (Extended Data 3, Supplementary Figure 1).

The equilibria and their stability are not obtainable analytically, even if the logarithmic term were replaced with a polynomial one (e.g. a logistic term, which is a good approximation if the population N is near the carrying capacity K). In a simplified version of the model in which the population is at this carrying capacity, and in which the migration term is 0, the equilibrium condition can be written (a_i − ρ Σ_l w_l Σ_j y_jG_jl)y_i = 0, where a_i = −r_i + ρ Σ_lw_le_l and e_l are the equilibrium locus frequencies. In matrix notation, the term ∑_lw_l ∑_j y_jG_ji is w^TG^Ty, with w the vector of weights w_l and y the vector of prevalences y_i. The matrix w^TG^T has rank 1 (it is a row vector), and a null space of rank M-1. This means that if y* is a solution to the equilibrium equation such that the term in brackets is 0, then y*+y_n is also an equilibrium solution, for any vector y_n in the null space of w^TG^T. On this basis we expect that there are many possible equilibria of the system, including also others where for some i the term in brackets vanishes and for others the strain is eliminated (so the y_i term in the equilibrium equation vanishes instead). With a polynomial term in place of the logarithmic one, it may be possible to characterize the equilibria using techniques from algebraic geometry to describe the solutions to this high-dimensional polynomial equation.

Sensitivity to initial conditions

The possibility of multiple equilibria means that the solutions depend on the initial conditions, potentially even after long periods. We resampled the initial conditions of the model in two ways. First, we added Gaussian random noise to the initial prevalence of each genotype, parameterising the standard deviation of the added noise as 10% of the genotype’s starting prevalence. This models the notion that the dataset is correct with regards to which genotypes are present, but uncertain about their precise prevalence. This perturbed the overall IPD burden by less than 1% on average (e.g., a standard deviation of 0.0027 for an overall IPD burden of 0.41), and a maximum of 2%. We then modelled the notion that the dataset may not correctly reflect which genotypes are initially present in larger numbers, due to sampling effects. We permuted the initial frequencies of 10% of the genotypes, thereby substantially altering the pneumococcal population at the time of vaccine introduction. This resulted in a larger variation than adding 10% noise to all initial conditions (e.g., a standard deviation of 0.01 for an overall IPD burden of 0.41). Overall the invasiveness objectives remained generally robust to changes in the initial conditions.

We also resampled the equilibrium locus frequencies, defined from the initial population, by adding Gaussian random noise with a standard deviation of 10% of the default values. The resulting invasiveness varied more than under perturbed initial conditions, which is not surprising given that the specified locus frequencies shape the long-term population dynamics through the frequency-dependent selection term. The resulting invasiveness values had standard deviations of under 5% of the typical objective for the strategy (e.g. 0.018 for an overall IPD burden of 0.41). Changes to the locus weights had similar effects to perturbations to the equilibrium frequencies.

Comparison with alternative design approaches

To test whether optimisation provided an advantage over alternative approaches to rational vaccine design, we generated 15-valent formulations by applying three different heuristics to the pre-vaccination samples as alternative strategies: selecting the set of serotypes present that were most invasive; the set that were expected to be most common in IPD (i.e. having the highest virulence, defined as the product of prevalence and invasiveness¹), and those identified by a previous algorithm¹⁸. As for the formulations identified by optimisation, the inclusion of 1, 5 and 14 was enforced, regardless of whether or not they were selected by the underlying method. The ‘invasiveness’ approach ordered serotypes present in the pre-vaccine population by their ORs, and selected the most invasive set. The ‘virulence’ approach ordered serotypes by the product of their ORs and pre-vaccine prevalence, and selected the set expected to make the greatest contributions to pre-vaccine IPD. The Nurhonen & Auranen method, described previously¹⁸, was applied assuming complete elimination of vaccine serotypes, and complete replacement by non-vaccine serotypes.

For the Maela population, these heuristics all performed similarly to one another, and were predicted to cause a less substantial reduction in IPD than those formulations identified by the optimization approach (Supplementary Table 4). For the Massachusetts population, the formulations composed of the most invasive serotypes in the pre-vaccine population performed similarly well to those identified by optimisation. By contrast, formulations based on serotype virulence performed poorly. Those generated using the approach of Nurhonen and Auranen¹⁸, which assumes a neutral model of pneumococcal evolution, were forecast to perform suboptimally in the NFDS model, which predicted that the vaccine serotypes they eliminated would be at least partially replaced by more invasive genotypes.

The optimised formulations were also compared to the forecast impact of PCV15 and PCV20, which are in late-stage clinical trials¹, on the pre-PCV7 population. PCV15 adds 22F and 33F to PCV13, and consistent with our results, is expected to perform effectively in Massachusetts (Supplementary Table 4). Correspondingly, a 15-valent design featuring in our formulations optimised for this location differed in only one serotype (17F in place of 3). PCV20 is forecast to substantially disrupt the carried population in Massachusetts through the elimination of the common, low invasiveness vaccine types 10A, 11A and 15B/C; these were replaced by 15A, 15F, 7C and 9N in the simulations, resulting in a worse performance than PCV13 (Supplementary Figure 3). However, our model cannot account for the benefits of PCV20’s inclusion of highly invasive serotypes (e.g. 8 and 12F) that were not detected in the Massachusetts carried population, but have emerged as important causes of IPD post-PCV13^24,28. The rareness of these serotypes in carriage means their elimination should not cause substantial serotype replacement, and therefore it is unlikely this model would forecast any problematic consequences of their removal. In Maela, all the licensed PCVs are predicted to perform similarly sub-optimally, as the elimination of paediatric serotypes risks highly-invasive serotypes entering the population (Supplementary Table 4). Hence, in contrast to its poor predicted performance in Massachuetts, PCV10 is the licensed vaccine predicted to perform best in Maela, assuming it does not eliminate 6A through cross-immunity with its 6B component⁷⁷.

Extended Data

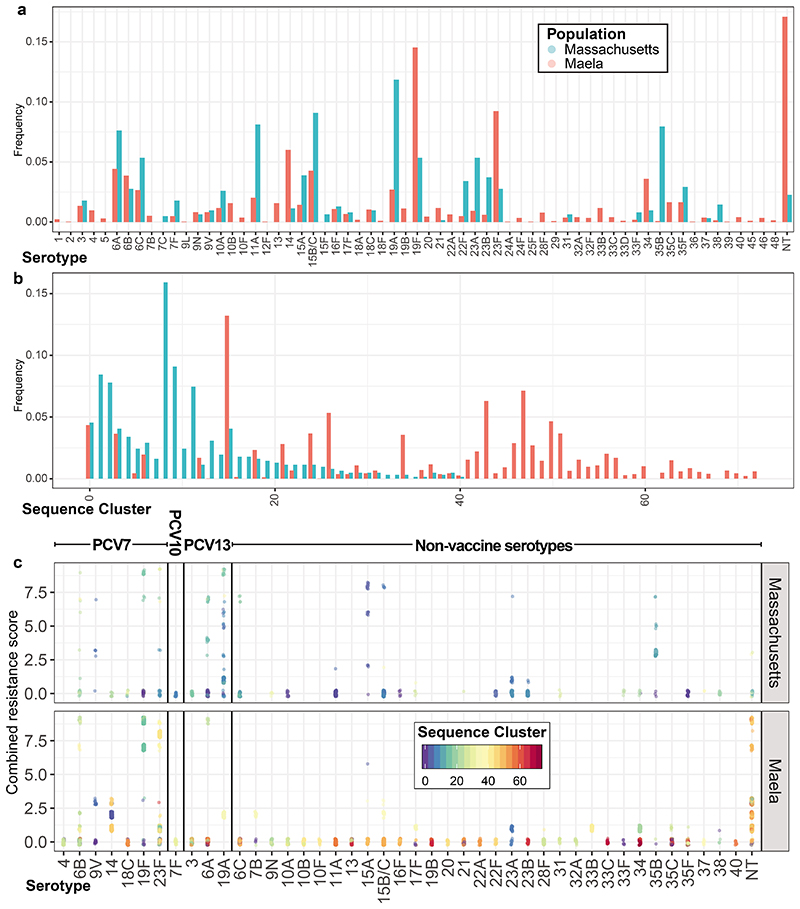
Extended Data Figure. 1. Comparison of the Massachusetts and Maela S. pneumoniae populations.

Comparison of the Massachusetts and Maela populations. a, Frequencies of serotypes across the two studied populations; serotypes 15B and 15C, which rapidly interchange but were resolved separately in the Maela dataset, are merged into 15B/C for comparability in this plot. b, Frequencies of sequence clusters, groupings analogous to strains defined by Corander et al, across the two populations. Both plots demonstrate the dissimilarity of these two S. pneumoniae populations, despite them being isolated from nasopharyngeal carriage almost contemporaneously. c, Distribution of resistance scores relative to the population structure within each serotype across the Massachusetts and Maela populations. Each colour represents a different sequence cluster, such that they can be distinguished within a serotype.

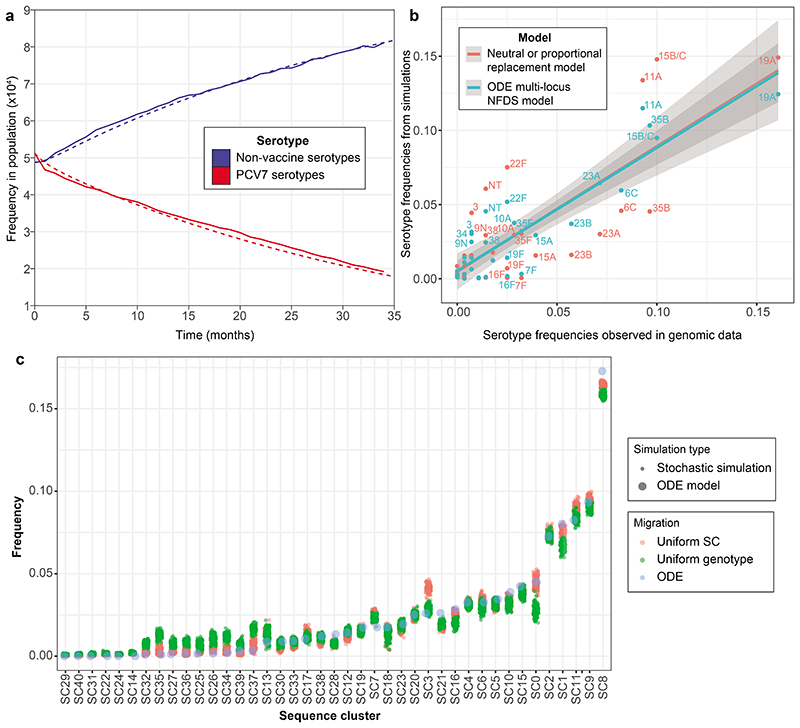
Extended Data Figure. 2. Validation of the ODE negative frequency-dependent selection model.

a, Parameterising the ordinary differential equation (ODE) model. The solid lines (stochastic model output) and dashed lines (ODE model output) show the post-vaccine rate of serotype replacement. They demonstrate the deterministic ODE model is appropriately parameterised to replicate the post-PCV7 temporal dynamics of the stochastic version, which was directly fitted to genomic surveillance data. b, Serotype frequencies observed in the genomic data (horizontal axis) and in simulations (vertical axis). The outputs of the NFDS model (blue) were compared to those from a neutral ‘proportional replacement’ model (red), in which each non-vaccine serotype expanded to replace the eliminated vaccine serotypes in proportion to its original carriage prevalence. The best-fitting linear relationships are shown by the corresponding coloured lines, and the surrounding shaded regions represent the 95% confidence intervals for each. The NFDS model correlates more strongly with the observed data (Pearson correlation, n = 32, R² = 0.90) than the neutral model (Pearson correlation, n = 32, R² = 0.78). c, This plot compares the predicted frequencies of pneumococcal sequence clusters 10 years post-PCV7 when using the ODE and stochastic NFDS models (n = 100 replicates for both versions of the stochastic model). The differences between the ODE and stochastic models are smaller than the differences between alternative mechanisms of strain migration implemented in the stochastic NFDS model (see Methods for details), demonstrating the ODE implementation to accurately replicate the population dynamics of the stochastic implementation.

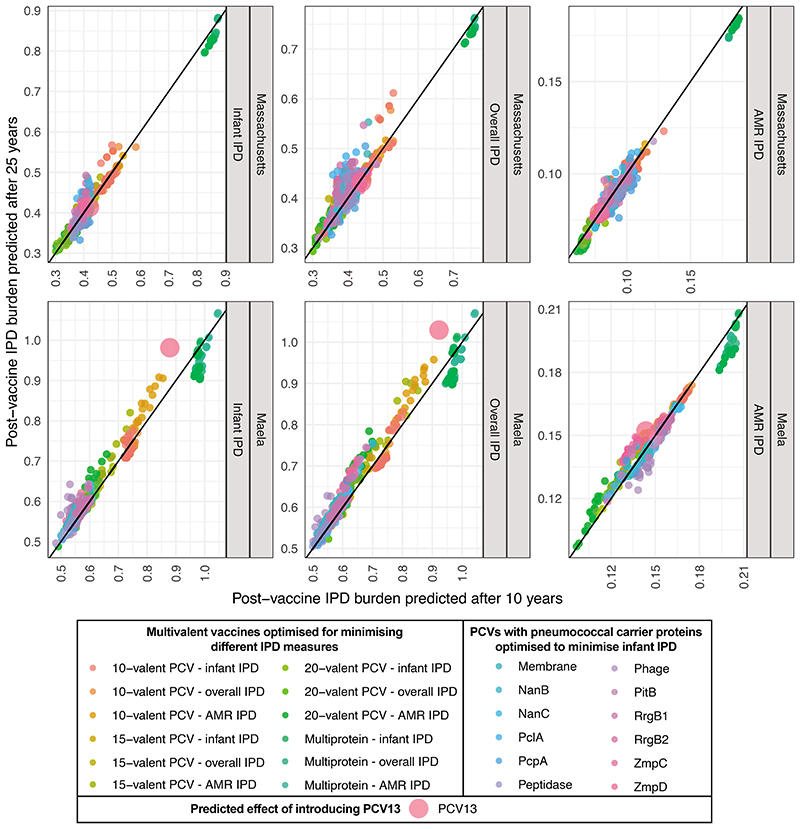
Extended Data Figure. 3. Comparison of optimisation criteria at the 10 and 25 year timepoints.

These scatterplots compare the IPD burden measures used for vaccine optimisation at 10 and 25 years post-vaccination in Massachusetts (n = 480 optimised formulations in each plot) and Maela (n = 440 optimised formulations in each plot). Each plot also displays the simulated effect of introducing PCV13 into a vaccine-naïve population. Plots are separated by population and IPD burden measure. Points are coloured by the constraint on the formulation, and the criterion used for optimisation. The line of identity is marked in black. The IPD measures are very similar at the two timepoints, indicating that while the model dynamics have long transient behaviour driven by drift among similar genotypes, the IPD burden criteria converge towards a feasible-time value relatively early.

Extended Data Figure. 4. Invasiveness of pneumococcal serotypes in infant and adults.

Variation in invasiveness between serotypes in infants and adults. Each bar represents the logarithmic invasiveness odds ratios for a serotype, estimated from the meta-analyses of IPD and carriage isolates (Supplementary Tables 1–3) using a random effects model. The 95% confidence intervals associated with these estimates are shown by the error bars. The number of studies contributing to the estimates for each age group for each serotype are enumerated at the top of the plot, with the individual study estimates overlaid as individual points. Results are coloured according to the currently-available vaccines in which the serotype is found, if any. a, Invasiveness in infants relative to carriage in infants. b, Invasiveness in adults relative to carriage in infants. Fewer serotypes are present in this panel, as there were fewer datasets available to estimate these values.

Extended Data Figure. 5. Post-vaccine populations forecast following optimised 20-valent PCV introductions.

Differences in serotype prevalences, forecast 10 years after vaccine introduction, between the best-performing 20-valent strategies optimised under different criteria in a, Massachusetts, and b, Maela. Bars are coloured according to whether they represent the frequency of a vaccine or non-vaccine serotype in the corresponding formulation. In Massachusetts, serotypes 6C, 11A, 15B/C and 35B are typically prevalent in the post-vaccine population regardless of the optimisation criterion, owing to their low infant invasiveness. Serotypes 15A and 23A are higher when minimising infant IPD, whereas serotypes 6A and 23B are higher when minimising overall IPD, in accordance with their age-specific invasiveness (Extended Data 4). Minimising AMR IPD results in higher prevalence of serotype 10A, which is pansusceptible in Massachusetts. In Maela, all optimal formulations result in high post-vaccine prevalences of serotypes 6A, 6C, 11A, 15F, 19B, as well as non-typeables. Serotypes 19F and 23F remain prevalent when optimising for overall and infant IPD, respectively; both are suppressed when optimising for AMR IPD, owing to their antibiotic resistance profiles (Figure 5). These are partially replaced by serotypes 6A and 6B, which have a weaker association with resistance.

Extended Data Figure. 6. Distribution of protein antigens across serotypes.

The prevalences of the intermediate-frequency protein antigens are shown for those serotypes with at least 10 representatives across the Massachusetts and Maela populations.

Extended Data Figure. 7. Alternative strategies for minimising IPD.

a-b, These plots summarise the formulations of PCVs optimised with pneumococcal carrier proteins in a, Massachusetts and b, Maela. Results are displayed as in Figure 2c-d, except that the first column denotes the carrier protein on which the design was based. Rows are ordered first by the featured pneumococcal carrier protein, and then by the predicted post-vaccine infant IPD burden, which the formulations were designed to minimise. c-d, These plots summarise the compositions of complementary adult vaccines (CAVs) designed to minimise adult IPD following introduction of infant vaccines to minimise AMR IPD (corresponding to the vaccines in Figure 5) in c, Massachusetts and d, Maela. On each row, the light blue cells define the infant formulation, and the dark blue cells define the adult formulation. Rows are ordered by the overall IPD burden estimated following the implementation of the combined vaccination strategy.

Extended Data Figure. 8. Comparing formulations’ effects on IPD using different criteria.

Performance of vaccination strategies judged by different criteria: a, minimising infant IPD; b, minimising overall IPD; c, minimising AMR IPD. Each violin plot is labelled with the constraint on formulation design, and coloured according to the criterion optimisation was intended to minimise. The overlaid points show the estimated effects of each individual optimised formulation (n = 20 for each combination of constraint and optimisation criterion in each population). The purple point in each panel shows the corresponding estimates for PCV13. For the Maela population, no optimisation was performed for two proteins (RrgB2 and ZmpC) that were below the threshold frequency of 0.05 in the starting population (Supplementary Figure 6), and therefore not included in the multi-locus NFDS simulations. The diminishing returns of expanding infant vaccine valency can be inferred from the predicted effects of the 10-, 15- and 20-valent vaccines relative to the horizontal dashed line, which marks the pre-vaccine value of the optimisation criterion.

Extended Data Figure. 9. Comparing formulations’ effects on IPD in different populations.

Performance of vaccine strategies in the alternative population to that for which they were designed. Simulations of each strategy were run in the alternative population, and their performance compared to that in the intended recipient population using different criteria: minimising infant IPD; minimising overall IPD, and minimising AMR IPD. Panels are labelled to indicate the population for which the formulation was designed. For those panels in which the intended target population was Massachusetts, results are shown for 480 optimised formulations. For those panels in which the intended target population was Maela, results are shown for 440 optimised formulations. Each plot also displays the estimated effect of introducing PCV13 into a vaccine-naïve population. Notably, those vaccines designed to reduce infant and overall IPD in Massachusetts are predicted to perform poorly in Maela.

Extended Data Figure. 10. Comparing formulations’ effects on IPD using different ecological models.

These scatterplots compare the simulated effectiveness of vaccine formulations in the original multi-locus NFDS model and an otherwise equivalent ‘proportional replacement’ neutral model (Extended Data 2). Each plot shows the expected post-vaccine IPD burden expected under NFDS and neutral evolution. Points (n = 480 for the Massachusetts population; n = 440 for the Maela population) are coloured by optimisation constraint and criterion, and the line of identity is marked. The results are very similar under each ecological model, with vaccine compositions that we predict to perform better than PCV13 also tending to do so in the neutral model. This indicates the formulations we have identified perform well despite the predicted effects of NFDS, rather than because of them.

Code Availability

The model code is available at https://github.com/carolinecolijn/optimvaccine.

Data Availability

The original sequence datasets underlying this analysis are in the public sequence databases with the accession codes given in Supplementary Dataset 3 of Corander et al¹². The epidemiological and phylogenetic data are also available at https://microreact.org/project/multilocusNFDS. The input matrix G, the serotype for each isolate, the equilibrium frequencies for each locus, and other input data are available from https://github.com/carolinecolijn/optimvaccine.