Abstract
As drugs can be multichannel blockers it is important to assess their cardiac safety taking into account multiple currents. In silico action potential (AP) models have been proposed for being able to integrate drugs effect on ionic currents and generate the resulting AP. However, a mathematical description of drug effects is required, which could be inaccurate.
Dynamic Clamp has been proposed for drug cardiac safety assessment. In the dynamic action potential clamp (dAPC) configuration it creates an hybrid model connecting a real cell with a computer simulation. This way, drugs could be administrated directly to real cells, and effects on currents can be taken into account when generating the AP. Here we design and simulate a parallel multichannel dAPC system. The system includes the real cells overexpressing the currents of interest, the voltage clamp acquisition system, and the AP in silico model.
1. Introduction
Drug cardiac safety assessment is a fundamental step in drug development. In particular, it is essential to detect, in pre-clinical experiments, those drugs which could cause arrhythmias. As drugs can be multi-channels blockers, it is useful to assess their effect on multiple currents, but, given the complex interaction between currents during the action potential (AP), it can be difficult to understand the overall effect on the AP. In silico simulations can be useful, but a mathematical description of a drug’s effect on each ionic current is needed, which may be incorrect or not exhaustive. The dynamic action potential clamp (dAPC) technique [1] could offer a solution as it creates a closed circuit in real-time between the in silico model and in-vitro cells. Currents of interest could be acquired from the cells and given in input to the AP model, which computes the corresponding membrane potential (Vm) value. In this configuration, no drug description is required, as drugs can be administrated directly to the cells and their effects will reflect accordingly in the AP computed by the model. Moreover, as automated patch clamp systems are available, Dynamic clamp experiments can be performed with a high throughput rate [2].
In this project, we recreated a simulator of a multicellular dAPC system, incorporating each system component and the protocols needed, which could serve as a reference for predicting outcomes of future experiments. Moreover, given the presence of some undesirable effects from the acquisition system, it was possible to evaluate how such components and their compensations affect the AP computed by the in silico model. Lastly, we evaluated if it is possible to correctly quantify drug effects in dAPC. We determined those effects by calculating APD90 changes upon drug administration to the cells. Those results were then compared with the one obtained from virtually administrating the same drugs to a ventricular cardiomyocyte simulated with the the O’Hara-Rudy (ORd) model [3].
2. Methods
The main system components to be modelled are: i) the real cells overexpressing the currents of interest, ii) the voltage clamp acquisition system, and iii) the action potential (AP) computational model to be numerically integrated in real time by the dAPC system.
2.1. Computational modelling of currents overexpressed in heterologous cells
We modelled three cells, each one overexpressing a different current: ICaL, IKr and IK1. In particular, we assumed cells to be small chinese hamster ovary (CHO) cells where each current was modeled with its ORd formulation [3] with a typical maximum conductance value for CHO cells. The K+ reversal potential was the same for all cells and equal to the diastolic value in ORd. White noise was added to every current. In cells expressing ICaL, intracellular Ca++ concentration was set equal to the diastolic value in ORd as it is constant given the presence of the pipette and the lack of sarcoplasmic reticulum in non-cardiomyocytes.
2.2. Computational modelling of the Voltage Clamp system
The acquisition system was modelled as in Lei et al. [4]. The system represents a whole-cell patch-clamp voltage-clamp amplifier setup with adequate compensations. Compensations, as written in the ODE system, include a capacitance compensation and a finite series resistance compensation.
2.3. AP computational model
The AP model we used is the ORd model [3]. Some model modifications were needed to perform a dAPC simulation. Firstly, IKr and IK1 equations were deleted as well as the activation gate equation for ICaL and its permeability (PCa) value. On the other hand, equations for the driving force (ΨCa), inactivation gates, and phosphorylation have been left. Then, [K+]i is kept equal to its initial condition, consistently with [K+]i in the CHO cells where it is supposed constant given the presence of the pipette.
Model differential equations were implemented in Simulink (Mathworks Inc., Natick, MA, USA) and solved with a variable order solver (ode15s), based on numerical differentiation formulas.
2.4. Implemented protocols
As the experiment is to be run in real-time, offline leakage current subtraction is not an option, so an online leakage compensation protocol needs to be included. Considering the leakage current as a linear function of the pipette potential (Vp) it is possible to estimate the two parameters needed (Gleak and Eleak) with a linear fitting applying a ramp voltage-clamp protocol, in a range of membrane potentials in which the current of interest is zero, so that the measured current must be a leakage current. Then, during the experiment, the estimated leakage current is subtracted from the measured current in real-time.
As currents are acquired from heterologous systems overexpressing the channel of interest, it is reasonable to expect a greater current amplitude than the one from the in silico model. Therefore, every current must be scaled before giving it in input to the AP model. The major issue with this step is that while we perfectly know the maximum conductance of the current of interest in ORd model, the maximum conductance of the in-vitro cell is unknown. The method we used to overcome this problem was to maximize the similarity between currents, the one from the in-vitro cell, and the one expected from ORd model, which was previously saved. Current from the cell is acquired in AP clamp with an AP saved from the ORd model, then the scaling factor (Gscale) is found by minimizing the mean square error between currents.
A different protocol has to be considered for ICaL. The lack of calcium transient into the CHO cells causes, in turn, lack of calcium-dependent inactivation (CDI). Therefore, it wouldn’t be accurate to include ICaL in the AP model without CDI and with a driving force substantially different from the one in cardiomyocytes. To overcome this problem, we acquired ICaL from the simulated CHO cell and divided the current for the estimated values of the ΨCa and the inactivation gates. This way only is given in input to the AP model. Then, in the ORd model, the rest of the equation is computed according to the [Ca++]ss computed value:
Therefore, not only the scaling factor has to be inferred, but also the [Ca++]ss,CHO estimation, needed for CDI compensation, is required. This time, ICaL is acquired from the cell with an AP clamp and serves as a reference. Then, both the scaling factor and [Ca++]ss are estimated as the values which maximize the similarity between the measured current and the current from the AP model (calculated in AP clamp with a fixed value for [Ca++]ss) minimizing the mean square difference between them.
3. Results
3.1. Simulaton of multichannel Dynamic Clamp with perfect compensations
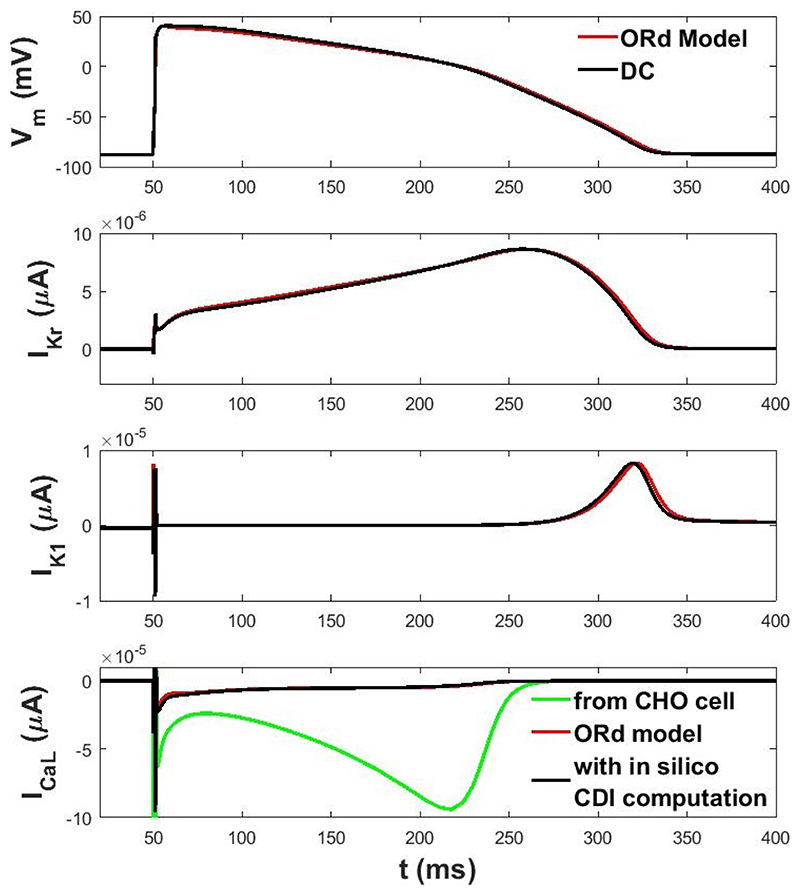
We performed a dAPC simulation with three different cells, each one expressing a different current, in a perfectly compensated acquisition system. Results are shown in Figure 1. The APD90 obtained in dAPC is 268.3 ms, to be compared to 270.6 ms as in the original ORd model.
Figure 1. AP computed in dAPC and currents acquired from cells multiplied by their own scaling factor (in black), compared with AP and currents from ORd (in red).
3.2. Sensitivity to incomplete compensations
In the acquisition system, there are many undesirable effects worsening the quality of the measurement, which are therefore compensated. These compensations will never be perfect, so in the simulation, we observed how a variation in compensations affects the APD90 in dAPC.
Membrane capacitance
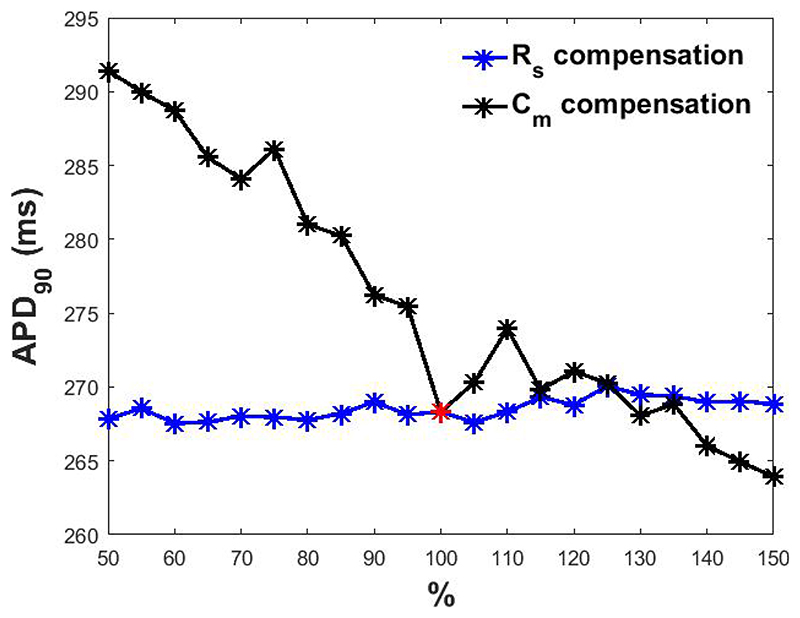
the presence of the membrane capacitance and its incomplete compensation can affect the scaling factor estimation protocol and the APD90 as seen in Figure 2, black line.
Figure 2.
APD90 obtained at different percentage levels of Cm (in black) and Rs (in blue) compensation. In red, APD90 when Cm and Rs are perfectly compensated.
Series resistance
the presence of finite series resistance and its compensation has only milder effects as seen in Figure 2, blue line.
Voltage Offset
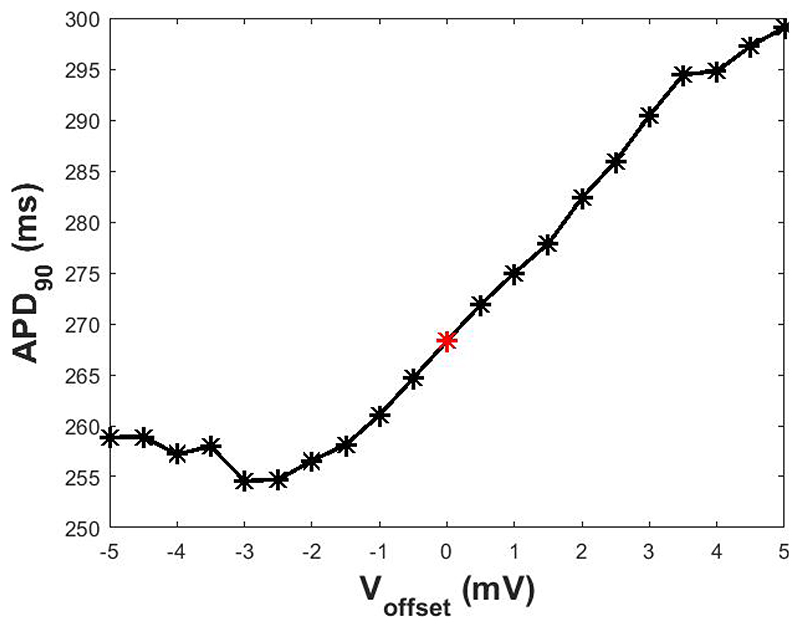
a voltage offset, which remains after the bridge balance compensation performed before every experiment is run, has a significant impact on the APD90 in the simulation (Figure 3). Besides the need to do an optimal compensation before the experiment starts, this result suggests that the scaling factor estimation protocol should be performed considering only currents acquired during the systolic phase of the AP, as their dyastolic value is more sensitive to the presence of an offset voltage.
Figure 3.
APD90 obtained in presence of different levels of Voffset. In red, APD90 when Voffset is zero.
Leak current
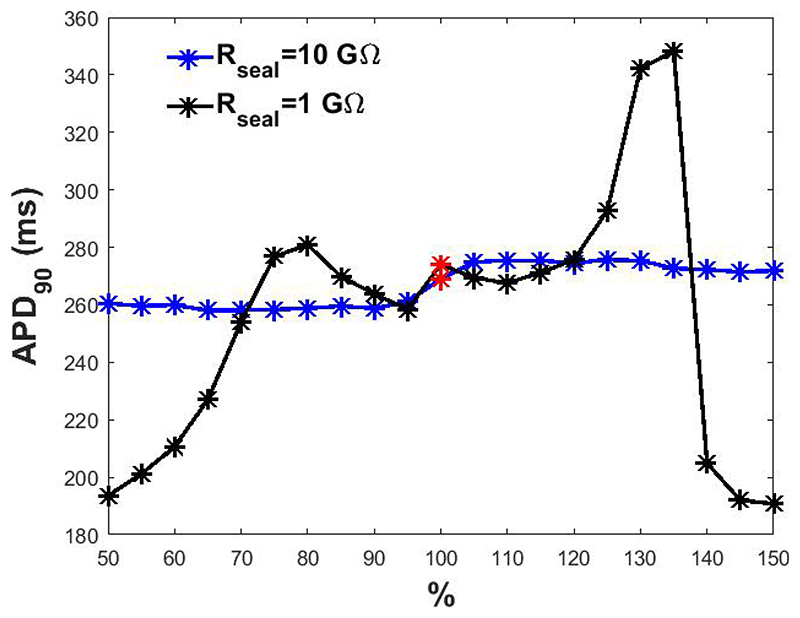
although the seal between the micropipette and the cell membrane must exhibit a resistance value higher than 1 GΩ to meet the quality standard, leakage compensation is still required. This compensation has a mild effect if Rseal has a high value, but it becomes essential for lower values as seen in Figure 4.
Figure 4.
APD90 obtained at different percentage levels of Ileak compensation. In red, APD90 when Ileak is perfectly compensated.
3.3. Virtual drug administration
Drug administration was simulated by decreasing each maximum conductance by the corresponding percentage block (e.g. Verapamil: 6.75% for IKr, 47.76% for ICaL, 0.96% for IK1, at EFTCPmax = 0.088 μM) [5]. The effect was then assessed in terms of APD90 change after drug administration. Virtual administration of Verapamil in the perfectly compensated dAPC system induced ΔAPD90 = -19.5 ms, compared to ΔAPD90 = -14.8 ms in the ORd model. Moreover, to evaluate if it is possible to assess drug effects in an experiment where variability between cells and wells occurs, we simulated 10 different experiments where cells and acquisition system parameters varied according to Table 1. In these experiments, ΔAPD90 = -12.9 ± 8.1 ms.
Table 1. Parameters variation.
| Parameter | mean ±standard deviation |
|---|---|
| Gmax | Gmax ± 20% |
| Voffset | 2 ± 1 mV |
| Rs | 5 ± 0,5 MΩ |
| Cm | 10 ± 0,5 pF |
| Rseal | 8 ± 4 GΩ |
4. Discussion and Conclusions
We have successfully simulated a multicellular dAPC system. When the acquisition system was supposed to be ideal and all the artifact sources perfectly compensated, the APD90 computed dynamically by integrating the results from 3 cells overexpressing 3 different ionic currents was substantially the same of an isolated cell (simulated by the ORd model). The residual small difference (about 2 ms) is likely due to the unavoidable delay introduced in the digital feedback loop.
Importantly, a novel approach to manage the dynamic clamping of ICaL, in which only the relevant (voltage-dependent) information acquired from the cell, lacking proper calcium handling, is integrated into the in silico AP model, in which the calcium-dependent features of the current are simulated, has been designed and implemented.
The main undesired effects that can be anticipated in the real system have been analysed and their effects have been quantified, pointing out that the membrane capacitance, offset voltage and leakage current are the main responsible for changes in APD90. The model dependency of the presented results should be tested by using different models both for the currents in the ”real” cells, and for the ”in silico” AP.
The simulation results fully support the feasibility of such an hybrid system for cardiac safety assessment. The developed simulator might be a useful tool for the design and implementation of the real system by predicting outcomes of future experiments.
Acknowledgements
CLL acknowledges support from the Clarendon Scholarship Fund; and the Engineering and Physical Sciences Research Council, the Medical Research Council and F. Hoffmann-La Roche Ltd. for studentship support [grant number EP/L016044/1]. TdB acknowledges support from the ZonMW MKMD programme [grant number 114022502]. GRM acknowledges support from the Wellcome Trust via a Wellcome Trust Senior Research Fellowship [grant number 212203/Z/18/Z].
References
- [1].Wilders R. Dynamic clamp: a powerful tool in cardiac electrophysiology. J Physiol. 2006;575(2):349–359. doi: 10.1113/jphysiol.2006.115840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Goversen B, Becker N, Stoelzle-Feix S, Obergrussberger A, Vos MA, van Veen TAB, Fertig N, de Boer TP. A hybrid model for safety pharmacology on an automated patch clamp platform: using dynamic clamp to join iPSC-derived cardiomyocytes and simulations of IK1 ion channels in real-time. Front Physiol. 2018;8:1094. doi: 10.3389/fphys.2017.01094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].O’Hara T, Virag L, Varro A, Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput Biol May. 2011;7(5) doi: 10.1371/journal.pcbi.1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Lei CL, Clerx M, Whittaker DG, Gavaghan DJ, de Boer TP, Mirams GR. Accounting for variability in ion current recordings using a mathematical model of artefacts in voltage-clamp experiments. Phil Trans R Soc. 2020;378(2173):20190348. doi: 10.1098/rsta.2019.0348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Passini E, Britton OJ, Lu HR, Rohrbacher J, Hermans AN, Gallacher D, Greig RJH, Bueno-Orovio A, Rodriguez B. Human in silico drug trials demonstrate higher accuracy than animal models in predicting clinical pro-arrhythmic cardiotoxicity. Front Physiol Sep. 2017;8:668. doi: 10.3389/fphys.2017.00668. [DOI] [PMC free article] [PubMed] [Google Scholar]