Abstract
The Coronavirus Disease 2019 (COVID-19) pandemic has changed many social, economic, environmental and healthcare determinants of health. We applied an ensemble of 16 Bayesian models to vital statistics data to estimate the all-cause mortality effect of the pandemic for 21 industrialized countries. From mid-February through May 2020, 206,000 (95% credible interval, 178,100-231,000) more people died in these countries than would have had the pandemic not occurred. The number of excess deaths, excess deaths per 100,000 people and relative increase in deaths were similar between men and women in most countries. England and Wales and Spain experienced the largest effect: ~100 excess deaths per 100,000 people, equivalent to a 37% (30-44%) relative increase in England and Wales and 38% (31-45%) in Spain. Bulgaria, New Zealand, Slovakia, Australia, Czechia, Hungary, Poland, Norway, Denmark and Finland experienced mortality changes that ranged from possible small declines to increases of 5% or less in either sex. The heterogeneous mortality effects of the COVID-19 pandemic reflect differences in how well countries have managed the pandemic and the resilience and preparedness of the health and social care system.
COVID-19, as a result of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection, has been the direct cause of hundreds of thousands of deaths in the world. The indirect effects of the pandemic and responses to it, acting through social, economic, environmental and healthcare pathways, can also be substantial1. Indirect effects include denied or delayed disease prevention and medical procedures for acute and chronic conditions; loss of jobs and income; disruption of social networks; increases in self-harm and crime, especially domestic abuse; changes in quantity and quality of food and the use of tobacco, alcohol and other drugs; and changes in other infectious diseases, road traffic crashes, other injuries and air pollution resulting from changes in social contacts, mobility and transportation1. How these developments affect mortality varies across countries, reflecting the sociodemographic characteristics of the population, the extent and timing of the epidemic and the response, the overall health status of the population, the resilience and agility of the health and social care system and the effectiveness of social and economic safety nets that support those in need. Knowledge of the total effect on mortality is needed to understand the true public health effects of the pandemic and the policy response. Comparative multi-country analyses2 offer insights into how responses can be made more effective and timely and how health and social care systems could be made more resilient. However, some politicians have rejected country benchmarking based on the argument that the data, methodology and timing of the analysis are not comparable across countries3. In this study, we developed and applied a probabilistic model averaging approach, using an ensemble of 16 Bayesian models, for comparable quantification of the weekly mortality effects of the first wave of the COVID-19 pandemic in 19 industrialized countries in central and western Europe, plus Australia and New Zealand. The models accounted for factors that affect death rates, including seasonality, temperature and public holidays, as well as for medium-term and long-term secular trends and the dependency of death rates in each week on those in preceding week(s). A summary of the main findings, limitations and policy implications of our study is shown in Table 1.
Table 1. Policy summary.
| Background | The COVID-19 pandemic and the policy responses to it can affect deaths from different diseases and injuries in adverse as well as beneficial ways, above and beyond deaths in those who are infected with SARS-CoV-2. We used 16 models to make estimates of how many people would have died had the pandemic not occurred and subtracted these from the actual observed number of deaths to measure the all-cause mortality effect of the first wave of the pandemic in 21 industrialized countries in a consistent and comparable manner. |
| Main Findings and Limitations | From mid-February through the end of May 2020, over 200,000 more people died in these 21 countries than would have had the pandemic not occurred. The total number of excess deaths, excess deaths per 100,000 people and relative increase in deaths were similar between men and women in most countries, which contrasts with the widely reported male disadvantage in deaths among those with confirmed SARS-CoV-2 infection. The effect of the pandemic on total mortality was highly variable across countries. Bulgaria, New Zealand, Slovakia, Australia, Czechia, Hungary, Poland, Norway, Denmark and Finland avoided a detectable rise in all-cause mortality, contrasting with England and Wales and Spain, followed by Italy, Scotland and Belgium, where the all-cause death toll was very high. |
| Policy Implications | How the pandemic has affected all-cause mortality arises from the interactions of population and community characteristics, the immediate response to the pandemic and the resilience and preparedness of the public health and health and social care systems. As the pandemic continues, reducing the mortality toll requires both suppressing transmission-putting in place comprehensive and effective testing and contact tracing, timely provision of information to individuals and public health bodies, creating a sense of trust and responsibility and economic and social support to increase participation in testing, contact tracing and adherence to isolation advice—and integrated care pathways at the community and facility levels that manage COVID-19 cases and other acute and chronic conditions. |
Results
We selected countries for our analysis if their total population in 2020 was more than 4 million and if we could access weekly data on all-cause mortality divided by age group and sex that went back at least to 2015 and extended through late-May 2020. The 21 countries in our analysis were Australia, Austria, Belgium, Bulgaria, Czechia, Denmark, England and Wales, Finland, France, Hungary, Italy, Netherlands, New Zealand, Norway, Poland, Portugal, Scotland, Slovakia, Spain, Sweden and Switzerland. We used data on weekly deaths from the start of time series of data through mid-February 2020 to estimate the parameters of each model, which were then used to predict death rates for the subsequent 15 weeks as estimates of how many deaths would have occurred without the pandemic. These were then compared to reported deaths to calculate excess mortality due to the pandemic.
Magnitude of excess deaths
We report the number of excess deaths, excess deaths per 100,000 people and relative (percent) increase in deaths together with their corresponding 95% credible intervals. For the purpose of reporting, we rounded results on number of deaths that are 1,000 or more to the nearest hundred to avoid giving a false sense of precision in the presence of uncertainty; results less than 1,000 were rounded to the nearest ten. We also report posterior probability that the observed change in deaths represents an increase or decrease in deaths compared to what would be expected if the pandemic had not occurred. Posterior probability represents the inherent uncertainty in how many deaths would have occurred in the absence of the pandemic. In a country and week in which the actual number of deaths is the same as the posterior median of the number expected in a no-pandemic counterfactual, an increase in deaths is statistically indistinguishable from a decrease; in such a situation, there is a 50% posterior probability of an increase and a 50% posterior probability of a decrease. Where the entire posterior distribution of the number of deaths expected without the pandemic is smaller than the actual number of deaths, there is a ~100% posterior probability of an increase and a ~0% posterior probability of a decrease and vice versa. For most countries, the posterior distribution of the number of deaths expected without the pandemic covers the observed number, but there is asymmetry in terms of whether much of the distribution is smaller or larger than the observed number. In such cases, there would be uneven posterior probabilities of an increase versus decrease in deaths, with the two summing to 100% (for example, 80% and 20%). Posterior probabilities more distant from 50%, toward either 0% or 100%, indicate more certainty.
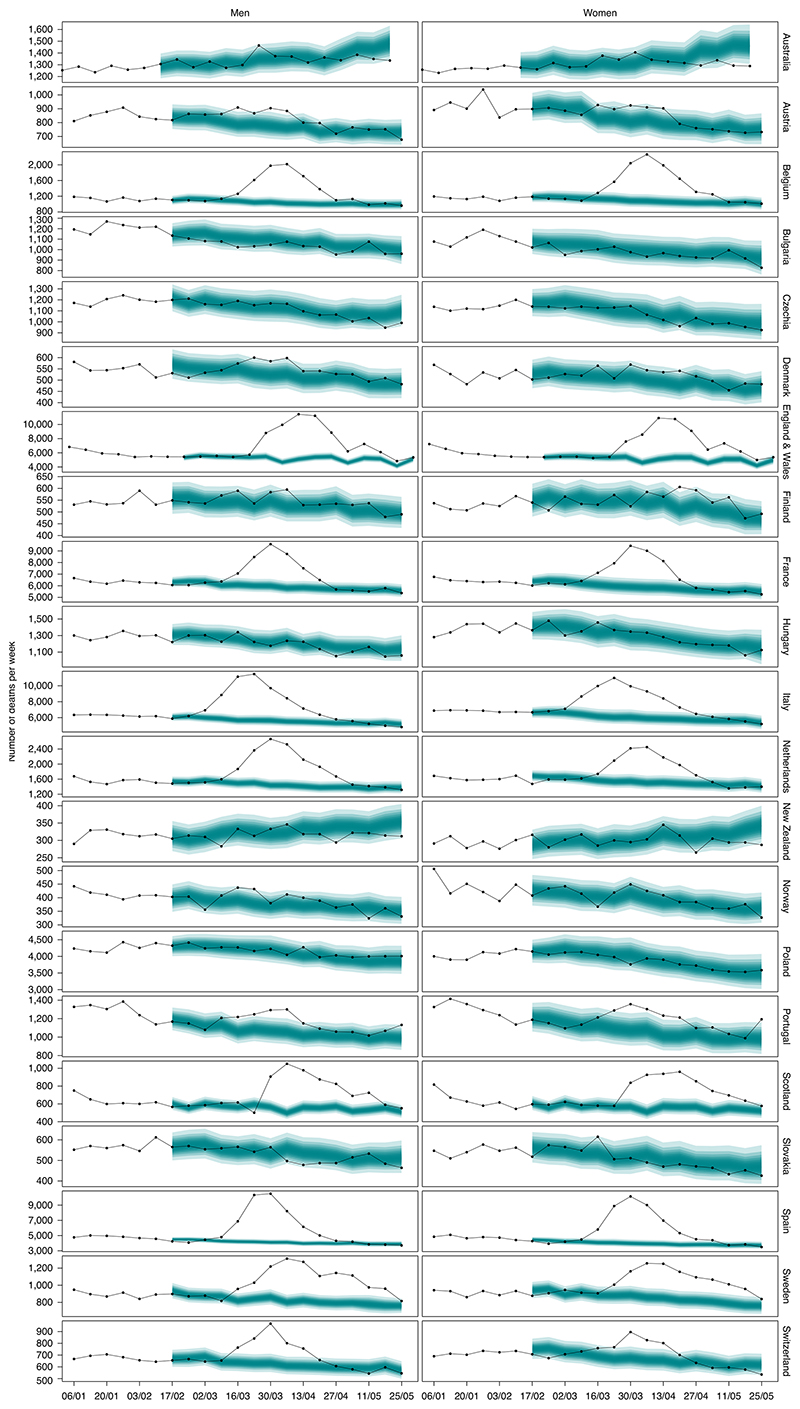
Deaths in all these countries were at the levels that would be expected in the absence of the pandemic through the month of February but started to diverge to higher levels at various times in March in some (Fig. 1). From mid-February through the end of May 2020, an estimated 206,000 (95% credible interval 178,100–231,000) more people died in these 21 countries than would have been expected had the pandemic not occurred. This number is similar to the number of deaths from lung cancer in these countries in an entire year and more than twice the number of deaths from diabetes or breast cancer in an entire year4. Of these deaths, 105,800 (90,400–119,000) were in men and 100,000 (82,000–117,500) were in women (Extended Data Table 1). In relative terms, this amounts to an 18% (15–21%) increase in deaths over this period in these countries combined. Italy, Spain and England and Wales accounted for 24%, 22% and 28% of these excess deaths, respectively.
Fig. 1. Weekly number of deaths from any cause from January 2020 through May 2020.
The points show reported deaths (placed at the start of each week in this graph). The turquoise-shaded areas show the predictions of how many deaths would have been expected from mid-February had the COVID-19 pandemic not ocurred. The shading shows the credible intervals around the median prediction, from 5% (dark) to 95% (light) in 10% increments, obtained from 16,000 posterior draws as described in the Methods. Extended Data Fig. 1 shows results by age group.
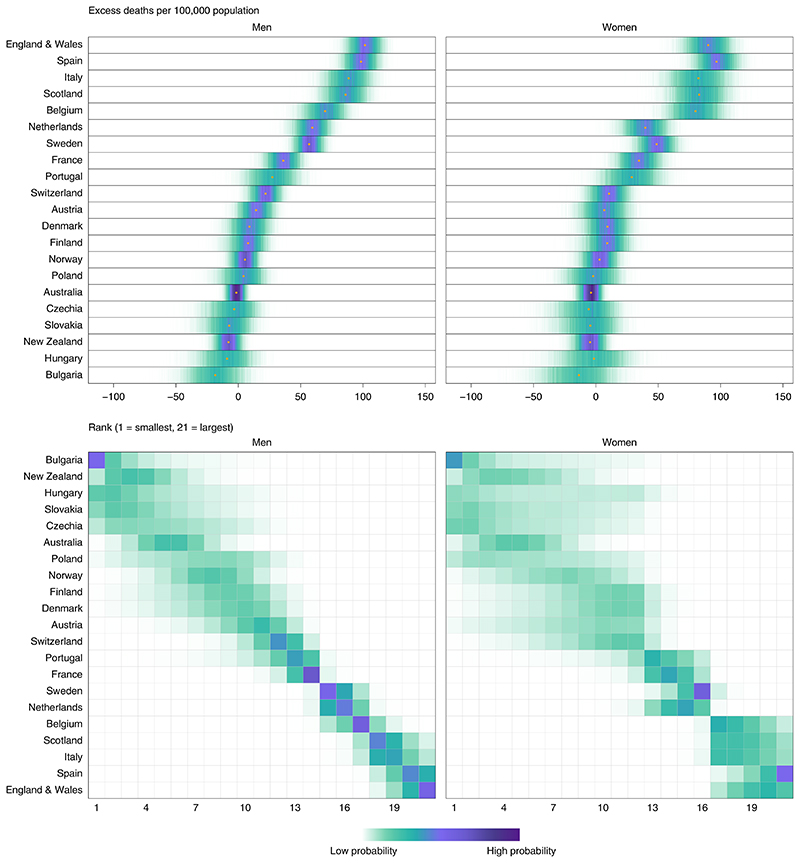
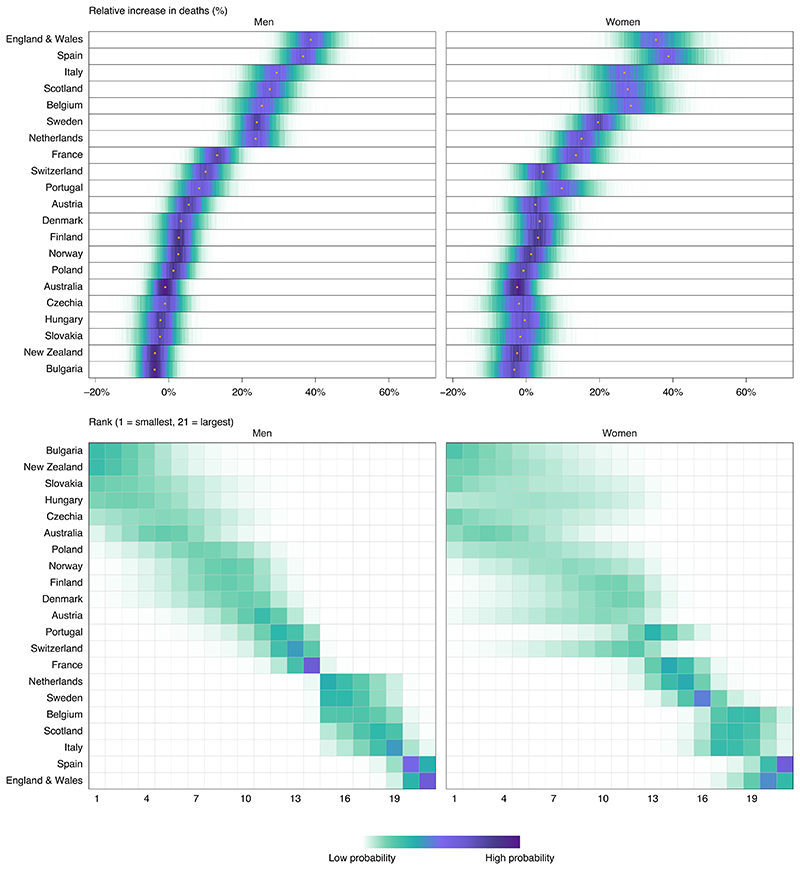
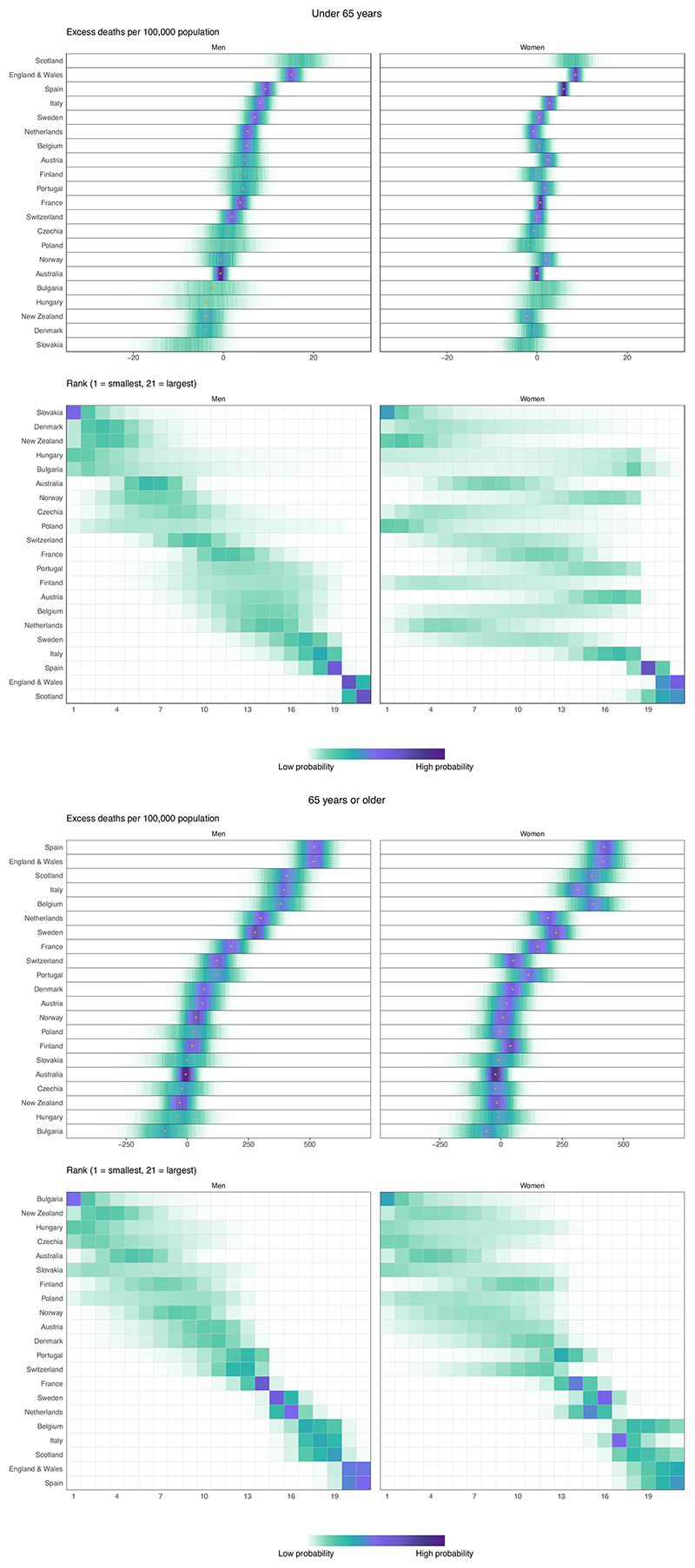
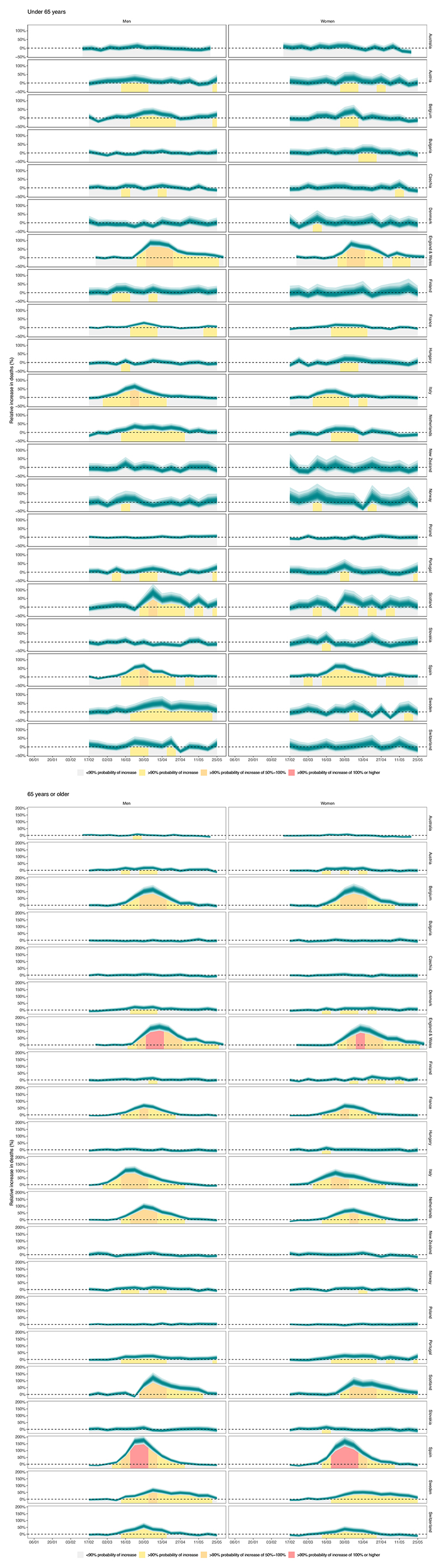
The posterior probability that there was a rise in deaths over the entire first wave of the pandemic was less than 50% (that is, a decline in deaths is more likely than an increase) for both sexes in Bulgaria, New Zealand, Australia, Slovakia, Czechia and Hungary and for women in Poland; 50–75% for women in Norway and Austria and men in Poland; 75–90% for men and women in Denmark and Finland, men in Norway and women in Switzerland; 90–99% for men and women in Portugal and men in Austria; and more than 99% for men in Switzerland and for both sexes in the Netherlands, France, Sweden, Belgium, Italy, Scotland, Spain and England and Wales (Fig. 2). In countries and sexes where mortality increased relative to the no-pandemic counterfactual with a posterior probability of at least 90%, the number of excess deaths per 100,000 people was lowest for men in Austria (14.3, -1.3 to 29.4), Switzerland (21.9, 7.6–34.9) and Portugal (27.4, 3.6–49.6), and for women in Portugal (28.7, 2.1–54.2) (Fig. 2). It was highest in Spain and England and Wales, with posterior median estimates for the two sexes ranging from 90 to 102 per 100,000 population. The posterior median increase was also more than 70 per 100,000 people for both sexes in Belgium, Italy and Scotland. Relative increases in deaths, compared to what would be expected in the absence of the pandemic, ranged from 10% or less in Austrian, Swiss and Portuguese men and Portuguese women to one quarter or more in Belgium, Italy, Scotland, Spain and England and Wales (Fig. 3). The largest rise in mortality for men was most likely to be in England and Wales (63% posterior probability of having the largest percent increase and 55% of having the largest number of deaths per 100,000 people), followed by Spain; for women, Spain was most likely to have experienced the largest rise in mortality (61% posterior probability of having the largest percent increase and 51% of having the largest number of deaths per 100,000 people), followed by England and Wales.
Fig. 2. Posterior distribution of excess deaths from any cause per 100,000 people from mid-February to the end of May 2020 and posterior distribution of each country’s rank.
Gold dots in the top panels show the posterior medians. Countries are ordered vertically by median excess (top panels) and mean rank (bottom panels) in men. Extended Data Fig. 2 shows results by age group. In the top panels, there is a relatively high posterior probability that excess deaths per 100,000 people in each country are in the ranges shaded in dark purple and a low posterior probability that they are in the ranges shaded in light green. In the bottom panels, there is a relatively high posterior probability that each country ranks in the positions shaded in dark purple and a low posterior probability that it ranks in the positions shaded in light green.
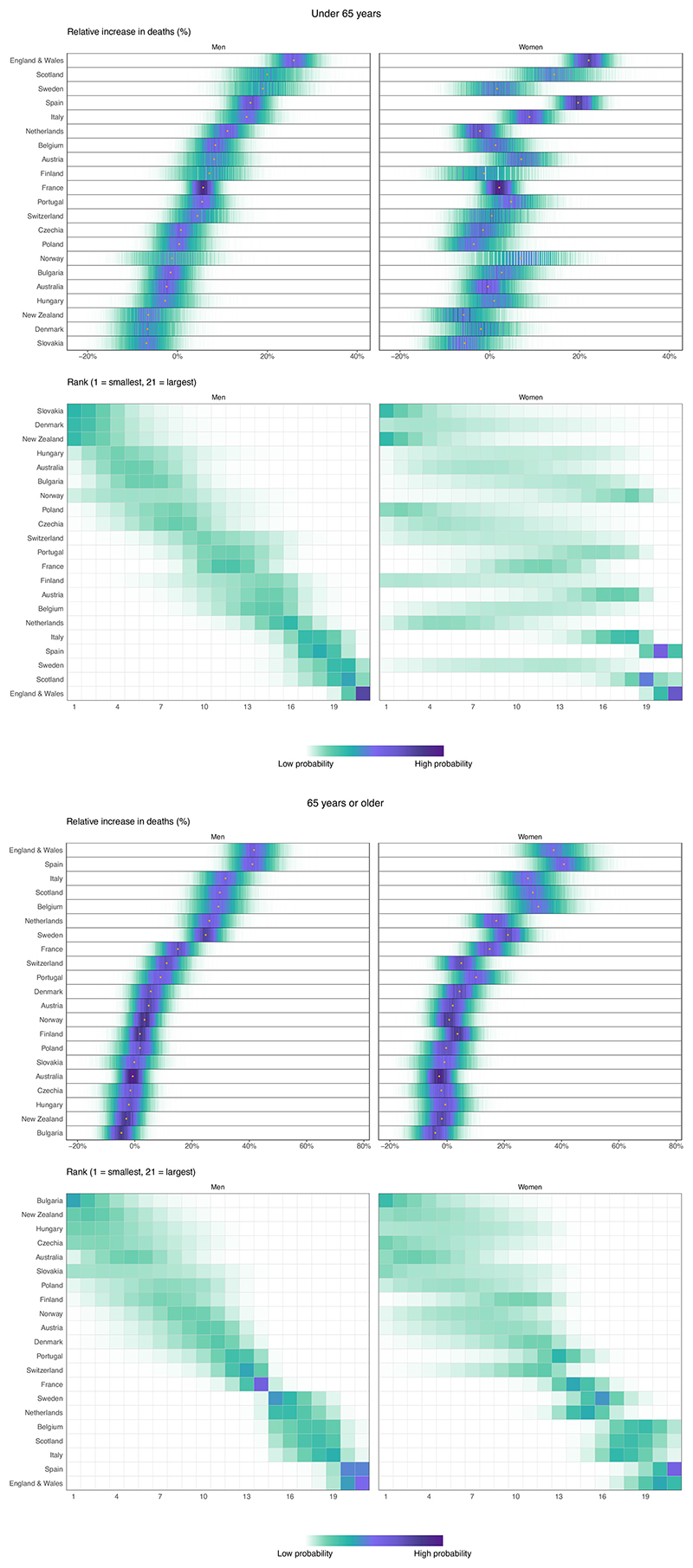
Fig. 3. Posterior distribution of percent increase in deaths from any cause from mid-February to the end of May 2020 and posterior distribution of each country’s rank.
Gold dots in the top panels show the posterior medians. Countries are ordered vertically by median increase (top panels) and mean rank (bottom panels) in men. Extended Data Fig. 3 shows results by age group. The Fig. 2 caption explains how the shadings in the two panels should be interpreted.
Taken across all 21 countries, the number of excess deaths from all causes was 23% (7–38%) higher than the number of deaths assigned to COVID-19 as underlying cause of death (Extended Data Table 1). The difference between all-cause excess and COVID-19 deaths was largest in Spain and Italy, where all-cause excess deaths were 69% (47–90%) and 46% (14–77%), respectively, higher than deaths assigned to COVID-19. This difference might be due to a combination of undetected infections5,6, whether or not deaths from ‘suspected COVID-19’ (based on clinical symptoms) are assigned to COVID-197, and some increase in mortality from other diseases due to reductions in acute and chronic care8–14. In contrast to Italy and Spain, the overall (all-cause) number of excess deaths was smaller than deaths assigned to COVID-19 in France, Belgium and Switzerland. This situation might have arisen because some countries have assigned any death in a person with confirmed or suspect SARS-CoV-2 infection to COVID-19; some of these deaths might have been in patients with multiple existing chronic conditions who already had a high risk of dying7,15–17. Finally, there might have been a reduction in deaths from influenza and other respiratory infections because of reduced contact among people18,19 as well as a decline in traffic injuries, falls and violence as people spent more time at home20. As a result of these differences, although France and Spain have reported similar numbers of deaths assigned to COVID-19, all-cause mortality increased by twice as much in Spain as in France. These variations show the importance of using all-cause mortality to capture the true death toll due to the pandemic.
Timing of excess deaths
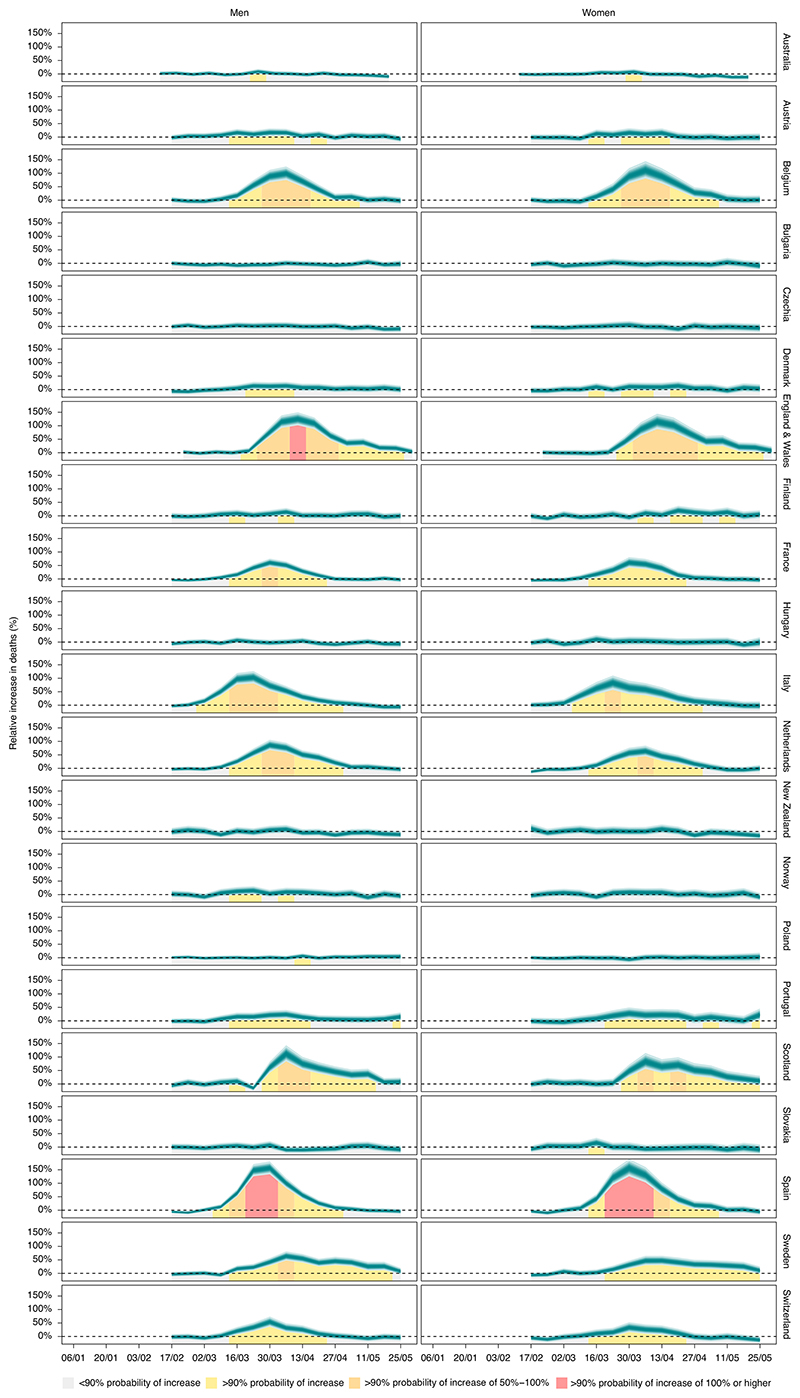
Italian men were the first group to experience a rise in mortality, with the first week of March 2020 as the earliest week in which the posterior probability of an increase in deaths was more than 90%. This was followed by Italian women and Spanish men in the subsequent week (Fig. 4). Deaths in some countries with large early excess mortality returned to levels that would be expected in the absence of the pandemic in April—for example, in France, followed by Spain. Deaths remained above the levels expected in the absence of the pandemic in England and Wales and Sweden throughout the month of May, which resulted in longer periods of adverse effect. As a result, in countries and sexes where the posterior probability of an increase in deaths was more than 90%, the period of time when deaths were higher than would be expected in the absence of the pandemic ranged from 5 weeks in Austrian men to 9–10 weeks in men and women in England and Wales and Sweden, women in Scotland and men in Italy.
Fig. 4. Weekly percent increase in mortality from any cause as a result of the COVID-19 pandemic by country.
The turquoise shading (placed at the start of each week) shows the credible intervals around the median prediction, from 5% (dark) to 95% (light) in 10% increments, obtained from 16,000 posterior draws as described in the Methods. The background shading indicates the magnitude of the weekly increase that was detectable with a posterior probability of at least 90%. Extended Data Fig. 4 shows results by age group.
The large adverse effect of the pandemic in England and Wales and, to some extent, in Spain is a consequence of having both long durations and large weekly rises, with amore than 90% posterior probability that, in some weeks, deaths in men and women in Spain and men in England and Wales more than doubled. In contrast, Portugal, Switzerland and possibly France had smaller weekly rises, and for fewer weeks, and, hence, had overall increases between one quarter and one half of those in England and Wales and Spain. Sweden had the longest duration of excess deaths but had smaller weekly increases in deaths than countries such as England and Wales, Spain, Scotland, Italy and Belgium. As a result, the overall mortality toll in Sweden, in terms of relative increase and deaths per 100,000 people, fell between those of countries with low-to-moderate effects (for example, Portugal and Switzerland) and countries with extreme tolls (for example, Spain and England and Wales).
Demographic distribution of excess deaths
Although it is widely quoted that more men die from COVID-1921–24, the number of excess deaths for all causes, excess deaths per 100,000 people and relative increase in deaths were similar between men and women in most countries (Fig. 5). In all 21 countries together, 105,800 (90,400–119,000) men died from any cause of death as a result of the pandemic compared to 100,000 (82,000–117,500) women. Furthermore, in many countries, the balance of excess deaths changed from male dominated early in the pandemic to being equal (for example, in England and Wales) or female dominated (for example, in Italy, Spain and France) later on.
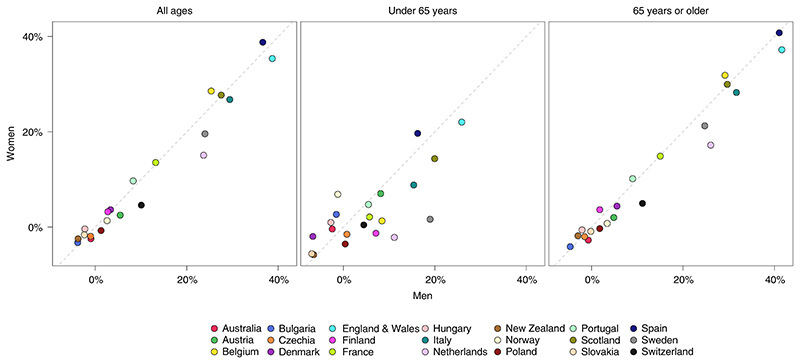
Fig. 5. Comparison of percent increase in deaths from any cause as a result of the COVID-19 pandemic between men and women, for all ages and by age group.
When considered in terms of relative increase in deaths, male disadvantage was largest in the Netherlands (24% (16–31%) increase in male deaths compared to 15% (7–24%) increase in female deaths) and Switzerland (10% (3–17%) increase in male deaths compared to 5% (-3% to 13%) increase in female deaths). In contrast, in Belgium (25% (16–34%) increase in male deaths compared to 29% (18–40%) increase in female deaths) and Spain (37% (29–45%) increase in male deaths compared to 39% (29–50%) increase in female deaths), there was a slight female disadvantage in total mortality effects. A male disadvantage in pandemic-related excess deaths was more pronounced before 65 years of age, whereas, in older ages, the relative effects were similar in men and women (Fig. 5). For example, the pandemic led to an estimated 19% (9–29%) increase in deaths in males younger than 65 years compared to 2% (-7% to 10%) in females of the same age in Sweden; 15% (8–22%) and 9% (3–15%) in Italy; and 11% (5–17%) and -2% (-8% to 4%) in the Netherlands.
In absolute terms, the total mortality toll of the pandemic was overwhelmingly in those aged 65 years and older, who experienced 94% of all excess deaths. In relative terms, older people were also affected more, with mortality in these ages being ~40% higher than it would have been in the absence of the pandemic in Spain and England and Wales and ~30% higher in Belgium, Scotland and Italy. The largest effect on those younger than 65 years was in England and Wales—26% (20–32%) for males and 22% (17–28%) for females—followed by Scotland, Spain, Sweden and Italy. In men and women in New Zealand and men in Denmark and Slovakia, there might have been a slight decline in deaths in men younger than 65 years as a result of the pandemic, with posterior probabilities of the observed declines being true declines above 90%. In these ages, injuries are an important cause of death, especially for men. For example, in men younger than 65 years in New Zealand, Denmark and Slovakia, injuries account for 22%, 11% and 15% of all deaths, respectively4.
Discussion
With our consistent and comparable analysis, we identified four groups of countries in terms of the overall death toll of the first wave of the COVID-19 pandemic. The first group comprises countries that have avoided a detectable rise (with a posterior probability of at least 90%) in all-cause mortality and includes Bulgaria, New Zealand, Slovakia, Australia, Czechia, Hungary, Poland, Norway, Denmark and Finland. The second and third groups of countries experienced a low-to-medium effect of the pandemic on overall deaths and include Austria, Switzerland and Portugal (low effect) and France, the Netherlands and Sweden (medium effect). The fourth group of countries, which experienced the highest mortality toll, consists of Belgium, Italy, Scotland, Spain and England and Wales.
The main strength of our study is the development and application of a method to systematically and consistently use time series data from 2010 to early 2020 to estimate how many deaths would be expected in the absence of the pandemic. The models incorporated important features of mortality, including seasonality of death rates, how mortality in one week might depend on previous week(s) and the seasonally variable role of temperature. This methodology not only allows more robust estimation of the total effects of the pandemic but also enables comparisons of excess deaths across countries on a real-time basis. The use of a modeling framework, as we have done, allowed us to make estimates by age group and sex, which, because of smaller numbers of deaths, might not be possible (or at least stable) otherwise. By modeling death rates rather than simply the number of deaths, as is done in most other analyses, we account for changes in population size and age structure. We used an ensemble of models that typically leads to more robust projections and better accounts for both the uncertainty associated with each individual model and model choice.
A limitation of our study is that we did not have data on underlying cause of death. Having a breakdown of deaths by underlying cause will help develop cause-specific models and understand which causes have exceeded or fallen below the levels expected. We also could not access age-specific and/or sex-specific data for several other countries, nor did we have data on total mortality by socio-demographic status to understand inequalities in the effects of the pandemic beyond deaths assigned to COVID-19 as the underlying cause of death. Releasing these data will allow more granular analysis of the effects of the pandemic, which can, in turn, inform resource allocation and a more targeted approach to mitigating both the direct and indirect effects of the COVID-19 pandemic. Finally, we are not yet in a position to provide an overall unified explanation for the observed quantitative differences among countries, if such a task is ever possible25. Rather, the reasons are likely to lie in complex interactions of the social, economic, environmental and health system features of each country and specific events and responses that promote or suppress transmission. We discuss some of these below together with lessons for subsequent waves of the pandemic.
The total death toll for the first wave of the COVID-19 pandemic in a country is affected by three key groups of determinants and the social and political factors that shape them26: the baseline characteristics of the population and communities they live in; the response policies that affect mortality positively by interrupting transmission and negatively by isolation and denial of essential services; and the preparedness, resilience and agility of the public health and health and social care systems. Information on some relevant characteristics is presented in Extended Data Table 4.
The first group of determinants comprises characteristics of individuals and communities that make them vulnerable or resilient to the spread and adverse health consequences of infection and those of the restrictions. These include baseline demography and health; social networks and inequalities; employment status and occupation; and environmental features, such as transport and housing. The risk of death from COVID-19 increases with age, with social and material deprivation and in the presence of long-term conditions such as obesity, diabetes and vascular and kidney diseases. Most countries in our analysis have an aging population, and none stands out as particularly older or younger than the others. For example, the share of the population that is older than 65 years ranges from 16% in Australia and New Zealand to 23% in Italy, but this share weakly correlated with excess mortality (correlation coefficient, 0.25) (Extended Data Table 4). Obesity and associated morbidities are higher in the United Kingdom, which experienced one of the highest effects, than in other European countries in our analysis27–29. But New Zealand and Australia, which had no detectable excess deaths, have an even higher prevalence of obesity than the United Kingdom, whereas Belgium, Italy and Spain, which have lower prevalence, also experienced large effects. Similarly, although reported multi-morbidity varies across Europe30, it is not correlated with excess mortality: Sweden and Denmark, which had different magnitudes of excess deaths, have low levels of multi-morbidity; Hungary, Spain and Italy, which also span the entire range of excess mortality, have some of the highest. Finally, although the United Kingdom has higher relative poverty than countries such as Norway, Denmark and Finland31, excess deaths were higher in Sweden (similar relative poverty to Denmark and Finland) than in New Zealand (similar relative poverty to the United Kingdom). These findings suggest that these contextual factors, although important, are individually insufficient to lead to the massive cross-country variation in mortality observed here. Other important population characteristics lack consistent data across countries and, hence, remain unexplored. For example, in some countries, regional outbreaks have started among low-wage workers in poor working conditions, such as garment factories and food processing plants. The role of overcrowded social housing complexes and public transportation (and, more generally, frequency, routes and means of mobility) in the extent and geographical distribution of transmission is also unknown32.
The second determinant of mortality toll of the pandemic is the policy and public health response, which has varied vastly across countries in timing, character and extent33. The timing of the lockdown in relation to when initial infections occurred34 affects the peak number of people who are infected, which drives both the number of deaths from COVID-19 and the pressure on the healthcare system that displaces routine care for other diseases. The stringency of the lockdown, together with the extent and effectiveness of testing, contract tracing and isolation, determines how long it takes for the number of cases to return to low levels and can therefore account for some of the variations in the intensity and duration of excess deaths observed here (Extended Data Table 4). Among the countries analyzed here, Bulgaria, New Zealand, Slovakia, Czechia, Hungary, Norway and Finland acted early in terms of putting in place various movement restrictions or lockdowns33,35 and kept the number of cases to such low levels that they could identify and isolate cases and their contacts through their existing public health systems. Austria and Denmark experienced an early rise in the number of cases but enacted lockdowns soon after and used effective testing, contact tracing and isolation to contain the epidemic and its mortality effect. At the other extreme, Italy, which was the initial European epicenter of the pandemic, Spain, the Netherlands, France and the United Kingdom put lockdown measures in place only after the number of cases and deaths had risen to such levels that the epidemic continued for weeks. For example, the United Kingdom, Spain, Italy, France and the Netherlands introduced lockdowns after a larger number of cases had been detected and after a longer period since the first few COVID-19 deaths occurred than New Zealand and other countries in Europe, such as Denmark (Extended Data Table 4)33,34,36. Sweden, the only country that did not put in place a mandatory lockdown and used only voluntary social distancing measures, had one of the longest durations of excess mortality. Extensive (and, at the extreme, universal) testing and effective contact tracing and isolation of cases and their contacts can also minimize transmission even without a lockdown37. Countries also varied in how extensively they conducted community testing, contact tracing and isolation of cases and their contacts at each stage of the pandemic, with Austria, Denmark, Finland, New Zealand and Norway introducing effective systems and Belgium, Spain, France and the United Kingdom being more limited in community testing and/or contact tracing for many months33, with some, like the United Kingdom, Spain and France, still not having a system that is able to respond to the dynamic geographical, demographic and social nature of the epidemic38–40.
Third, the preparedness and resilience of the public health infrastructure not only influence how well the spread of infection is controlled but also influence the choice of policy, as decision-makers assess what they think is possible with existing capacity41. Denmark and Austria (as well as Germany, for which data were not available for our analysis) were able to scale up testing rapidly because they had extensive and well-coordinated laboratory networks and public health infrastructure in place. Some central European countries had existing contact tracing infrastructure, a legacy of their more recent experience with infectious diseases such as tuberculosis. Others had more limited capacity but were able to scale it up rapidly based on the existing public health structures, such as New Zealand’s contact tracing system. In contrast, the United Kingdom and Spain had limited testing capacity (or ability to use capacity in non-governmental labs) and contact tracing systems, early in the pandemic. As above, their testing, contact tracing and ability to persuade and support people to isolate when necessary are still not effective42,38–40. Countries also varied substantially in terms of how their healthcare system continued to provide life-saving services: those countries that had less capacity and were less able to rapidly enhance capacity, partly related to uneven health and social care spending, responded less effectively to healthcare needs. Notably, per capita spending is lower in the United Kingdom, Italy and Spain than in Austria, Norway, Sweden and Denmark43. One effect of financing variation is on the number of hospital beds, which, on a per capita basis in Austria, is nearly three times that of the United Kingdom44. Where hospital beds are more limited—for example, in the United Kingdom, Spain and Hungary45—concerns about breeching capacity might have led to delaying admission of patients with COVID-19 and other patients until their health deteriorated and to early discharge of patients to long-term care facilities (care homes) often without systematic testing. The spread of infection within and between hospitals and care homes, and between them and the community, is itself an important determinant of infections and deaths in both the vulnerable groups and the general population46,47. Where infection rates were high and care homes were not appropriately safeguarded—namely in Spain, the United Kingdom, Belgium, Italy, France and Sweden—a large number of care home residents died from confirmed or probable COVID-1946. The initial seeding through discharge of infected patients to care homes was compounded by lack of testing and protective equipment for staff and residents and, especially in privately run care homes, regular movement of (temporary) staff across facilities48. Finally, some of the variations in excess deaths might be due to variation in community-based and primary care that affected preventive and pre-hospital care for patients with COVID-19 as well as for patients with other conditions.
Although our results demonstrate that countries with timely lockdowns had smaller numbers of excess deaths in the first wave of the epidemic, lockdowns have adverse short- and long-term health, psychosocial and economic effects. They might become needed, as a mechanism of last resort, as the number of cases increases, but they also require effective surveillance and agile operation, with sufficient geographical granularity to limit restrictions to as small an area as possible. Lockdowns, especially nationwide ones, can be avoided or be less stringent if countries can put in place comprehensive (and, in the extreme, universal) and effective testing and contact tracing systems; provide information to individuals and local public health bodies in a timely manner; create a sense of trust and responsibility; and put in place economic and social support that helps to increase participation in testing, contact tracing and adherence to isolation advice. In addition to controlling transmission, there is a need for integrated care pathways at the community and facility level that manage both milder COVID-19 cases and allow other acute and chronic conditions to be rapidly and appropriately triaged and cared for in community facilities as well as in health and long-term care facilities. For some countries, this might involve a re-allocation and re-direction of care resources and, for others, where there has been chronic underinvestment in health and social care, the more challenging task of rebuilding public health and health and social care systems that serve their entire population41.
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41591-020-1112-0.
Methods
Data sources
We included industrialized countries in our analysis if:
We could access weekly data on all-cause mortality divided by age group and sex that extended through May 2020. We selected late-May 2020 to have a consistent period of analysis for all countries and because our results showed that, by this date, the probability that deaths were above the level that would be expected had the pandemic not occurred was within the 90% credible interval in the great majority of countries.
The time series of data went back at least to 2015 so that model parameters could be reliably estimated. For countries with longer time series, we used data starting in 2010.
Their total population in 2020 was more than 4 million. We excluded countries with data but with smaller populations (Estonia, Iceland, Latvia, Liechtenstein, Lithuania, Luxembourg and Montenegro) because, in many weeks, the number of deaths would be small or zero, especially for people younger than 65 years. This would, in turn, lead to either large uncertainty that would make it hard to differentiate between those places with and without an effect or unstable estimates because the model is fitted to many weeks with zero deaths.
The sources of population and mortality data are provided in Extended Data Table 2. We calculated weekly population through interpolation of yearly population, consistent with the approach taken by national statistical offices for intra-annual population calculation49. Population for 2020 was obtained through linear extrapolation from the last 5 years. We obtained data on temperature from ERA550, which uses data from global in situ and satellite measurements to generate a worldwide meteorological data set, with full space and time coverage over our analysis period. We used gridded temperature estimates measured four times daily at a resolution of 30 km to generate weekly temperatures for each first-level administrative region and gridded population data (https://sedac.ciesin.columbia.edu/data/collection/gpw-v4) to generate population estimates by first-level administrative region in each country. We weighted weekly temperature by population of each first-level administrative region to create national-level weekly temperature summaries.
Statistical methods
The total mortality effect of the COVID-19 pandemic is the difference between the observed number of deaths from all causes and the number of deaths had the pandemic not occurred, which is not directly measurable. The most common approach to calculating the number of deaths had the pandemic not occurred has been to use the average number of deaths over previous years—for example, the most recent 5 years—for the corresponding week or month when the comparison is made51. This approach, however, does not take into account changes in population size and age structure, nor long- and short-term trends in mortality, which are particularly pronounced for some age groups52,53. Nor does this approach account for time-varying factors, such as temperature, that are largely external to the pandemic but also affect death rates.
We developed an ensemble of 16 Bayesian mortality projection models that each make an estimate of weekly death rates that would have been expected if the COVID-19 pandemic had not occurred. We used multiple models because there is inherent uncertainty in the choice of model that best predicts death rates in the absence of pandemic. These models were formulated to incorporate features of weekly death rates as follows:
First, death rates might have a medium-term to long-term trend that affects mortality in 2020 compared to earlier years. We developed two sets of models, one with no trend and one with a linear trend term over weekly deaths.
Second, death rates have a seasonal pattern that varies by age group and sex54–57. We included weekly random intercepts for each week of the year. To account for the fact that seasonal patterns ‘repeat’ (that is, late December and early January are seasonally similar), we used a seasonal structure58,59 for the random intercepts. The seasonal structure allows the magnitude of the random intercepts to vary over time and implicitly incorporates time-varying factors, such as annual fluctuations in flu season.
Third, death rates in each week might be related to rates in preceding week(s) due to short-term phenomena, such as severity of the flu season. We formulated four sets of models to account for this relationship. The weekly random intercepts in these models had a first-, second-, fourth- or eighth-order autoregressive structure58,59. The higher-order autoregressive models allow death rates in any given week to be informed by those in a progressively larger number of preceding weeks. Furthermore, trends not picked up by the linear or seasonal terms would be captured by these autoregressive terms.
Fourth, beyond having a seasonal pattern, death rates depend on temperature and, specifically, on whether temperature is higher or lower than its long-term norm during a particular time of year60–65. The effect of temperature on mortality varies throughout the year and might be in opposite directions for different times of the year. We used two sets of models, one without temperature and one with a weekly term for temperature anomaly, defined as deviation of weekly temperature from the local average weekly temperature over the entire analysis period. The coefficients of temperature anomalies were specified as a random effect with a random walk prior of order one, so that temperature effects are more similar in adjacent weeks. The random effect had a circular structure so that late December and early January are treated as adjacent.
Death rates might be different around major holidays, such as Christmas and New Year. We included effects (as fixed intercepts) for the week containing Christmas and New Year in all countries. For England and Wales and Scotland, we also included effects for the weeks containing other public holidays, because reported death rates in weeks that contain a holiday were different from other weeks. This term was tested but not included for other countries because the effect was negligible.
We also tested, but did not include, terms for the weeks that coincided with a change to and from daylight saving time because the effect was negligible.
These choices led to an ensemble of 16 Bayesian models (2 trend options × 4 autoregressive options × 2 temperature options). The ensemble of models is shown in Extended Data Table 5. In each model, the number of weekly deaths follows a Poisson distribution:
Log-transformed death rates were modeled as a sum of components described above:
The term α0 denotes the overall intercept, and αholiday(week) is the holiday intercept, applied to weeks with a holiday. For example, if a week includes the 25 th of December, then αhoiiday(week) = αChristmas. For weeks that did not contain a holiday, this term did not appear in the above expression. All intercepts were assigned 𝓝(0,1000) priors. The term β-week represents the linear time trend. The coefficient β was also assigned a 𝓝(0,1000) prior. As described above, this term appeared in half of our models, whereas, in the other half, trends over time were captured by the remaining terms.
The models used different orders (first, second, fourth or eighth) of the autoregressive term with the superscript i denoting the order. The first-order autoregressive term is defined as where the parameter φ lies between –1 and 1 and captures the degree of association between the number of deaths in each week and the preceding week. Hyperpriors are placed on the parameters and K2 = lθg((1 + φ)/(1 – φ)), which were assigned logGamma(0.001,0.001) and 𝓝(0,1) distributions, respectively. Similarly, an ith order autoregressive term is given by with – < ϕj < 1. The parametrization of these models was based on the partial auto-correlation function of the sequence ϕj66.
The term θweek captures seasonality in mortality trends with a period of 52 weeks. The sums of every 52 consecutive terms θweek + θweek +1 + … + θweek+51 were modeled as independent Gaussian with zero mean and variance .. We used a logGamma(0.001, 0.001) prior on the log-precision . Each week is assigned an index between 1 and 52 depending on which week of the current year it is (the incomplete week 53 is mapped to either index 1 or 52 depending on whether it has greater overlap with week 52 of the current year or week 1 of the next year).
The effect of temperature anomaly on death rates is captured by the two terms γ and νWeek of year. The term γ · temperature anomalyweek is the overall association of temperature anomaly in a week. The term νWeek of year · temperature anomalyweek captures deviations from the overall association for each week of the year. It has a circular first-order random walk with 52 terms so that temperature associations change smoothly throughout the year and so that they are similar in late December and early January65. The first-order random walk prior is defined via and the prior assigned to the log-precision is .
Finally, the term εweek is a zero-mean term that accounts for additional variability. It is assigned an independent and identically distributed prior and a logGamma(0.001, 0.001) prior is placed on the log-precision .
The components α0, αholiday(week), θweek, ≡week and (for each autoregressive order of i = 1, 2, 4 or 8) appear in the expression for log(death rateweek) in all models. The remaining components appear in some models only. Extended Data Table 5 shows the terms included in each of the 16 models in the ensemble.
We used data on weekly deaths from the start of the time series of data through mid-February 2020 to estimate the parameters of each model, which were then used to predict death rates for the subsequent 15 weeks as estimates of the counterfactual death rates (that is, if the pandemic had not occurred). For the projection period, we used recorded temperature so that our projections take into consideration actual temperature in 2020. This choice of training and prediction periods assumes that the number of deaths that are directly or indirectly related to the COVID-19 pandemic was negligible through mid-February 2020 in these countries, but it allows for effects to have appeared in subsequent weeks.
We tested the sensitivity of the results to the choice of prior through the use of penalized complexity priors and found that the results were similar. All models were fitted using integrated nested Laplace approximation (INLA)67, implemented in the R-INLA software (version 20.03). We used a model-averaging approach to combine the predictions from the 16 models in the ensemble68,69. Specifically, we took 1,000 draws from the posterior distribution of sex- and age-specific deaths under each of the 16 models and pooled the 16,000 draws to obtain the posterior distribution of sex- and age-specific deaths if the COVID-19 pandemic had not occurred. This approach generates a distribution of estimates that has equal samples from that of each model in the ensemble and, hence, incorporates both the uncertainty of estimates from each model and the uncertainty in the choice of model. The reported credible intervals represent the 2.5th and 97.5th percentiles of the resultant posterior distribution of the draws from the entire ensemble. We also report the posterior probability that an estimated increase in deaths corresponds to a true increase (or decrease), which is described in the main paper. We also evaluated the sensitivity of our results to how the different models are weighted. Specifically, in the sensitivity analysis, the number of draws from each model was inversely proportional to the absolute error of prediction in the validation analyses described below. The results of the sensitivity analysis were virtually identical to those with equal draws, with median excess deaths estimates differing by 1.6% on average and by 0.5% when summed across all countries.
We did all analyses separately by sex and age group (0–64 years and 65+years) because death rates, and how they are affected by the pandemic, vary by age group and sex. To obtain estimates of excess deaths across age groups and both sexes, we summed draws from age- and sex-specific estimates.
Validation of no-pandemic counterfactual weekly deaths
We tested how well our model ensemble estimates the number of deaths expected had the pandemic not occurred by withholding data for 15 weeks starting from mid-February (that is, the same projection period as done for 2020) for an earlier year and using the preceding time series of data to train the models. In other words, we created a situation akin to 2020 for an earlier year. We then projected death rates for the weeks with withheld data and evaluated how well the model ensemble projections reproduced the known-but-withheld death rates. We repeated this for three different years: 2017 (that is, trained model using data from January 2010 to mid-February 2017 and tested for the subsequent 15 weeks); 2018 (that is, trained model using data from January 2010 to mid-February 2018 and tested for the subsequent 15 weeks); and 2019 (that is, trained model using data from January 2010 to mid-February 2019 and tested for the subsequent 15 weeks). We performed these tests for all sexes and age groups used in the analysis. We report the projection error (that measures systematic bias) and absolute forecast error (that measures any deviation from the withheld data). Additionally, we report coverage of the projection uncertainty; if projected death rates and their uncertainties are well estimated, the estimated 95% credible intervals should cover 95% of the withheld data.
The results of model validation (Extended Data Table 3) show that the estimates of how many deaths would be expected had the pandemic not occurred from the Bayesian model ensemble were unbiased, with mean projection errors of 1% (between –3% and 6% in different age groups, sexes and years). The mean absolute error was between 4% and 9% in different age groups, sexes and years. Ninety-five percent coverage, which measures how well the posterior distributions of projected deaths coincide with withheld data, was 95% on average, which shows that the posterior distribution is well estimated.
Comparison with other estimates
The Financial Times, The Economist and The New York Times have reported the number of weekly deaths for some of the same countries as we have and compared them with either averages of the past 5 years or projections based on a linear model with a seasonal term. These comparisons have been for both sexes combined and, in most cases, for all ages combined and have not accounted for the role of temperature. Countries with small, medium and large numbers of excess deaths are consistent between our analysis and these reports. There are, nonetheless, some differences. For example, we estimated a small number of excess deaths, with low posterior probabilities, for Denmark and Norway, whereas these sources reported a decline in deaths. We also estimated a slightly larger number of excess deaths for Portugal, Italy and Sweden than some of these sources. EuroMoMo fits a sinusoidal seasonal model to death counts but does not report country-specific excess deaths and, hence, could not be compared with our results. The United Kingdom Office for National Statistics (ONS) calculated several age-standardized measures of excess mortality for January to June 2020, for both sexes combined, for European countries70. The analysis did not account for temperature or holidays. Because the analysis began in January, it also covered the period before the pandemic had reached Europe in a widespread manner. The overall grouping of countries into small, medium and large effects was mostly similar to us, but the ONS concluded a better performance (that is, lower excess mortality relative to other countries included) for France than we did. They also estimated a decline in mortality in Portugal and Switzerland, which contrasts with an increase in our analysis. Differences between our results and those of the ONS might be partly related to the fact that the ONS analysis also included the pre-pandemic months of 2020 and did not account for inter-annual variations in temperature. Most weeks during the period of January to March were warmer in 2020 than the average of the past 10 years.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Extended Data
Extended Data Fig. 1. Weekly number of deaths from January 2020 through May 2020, by age group.
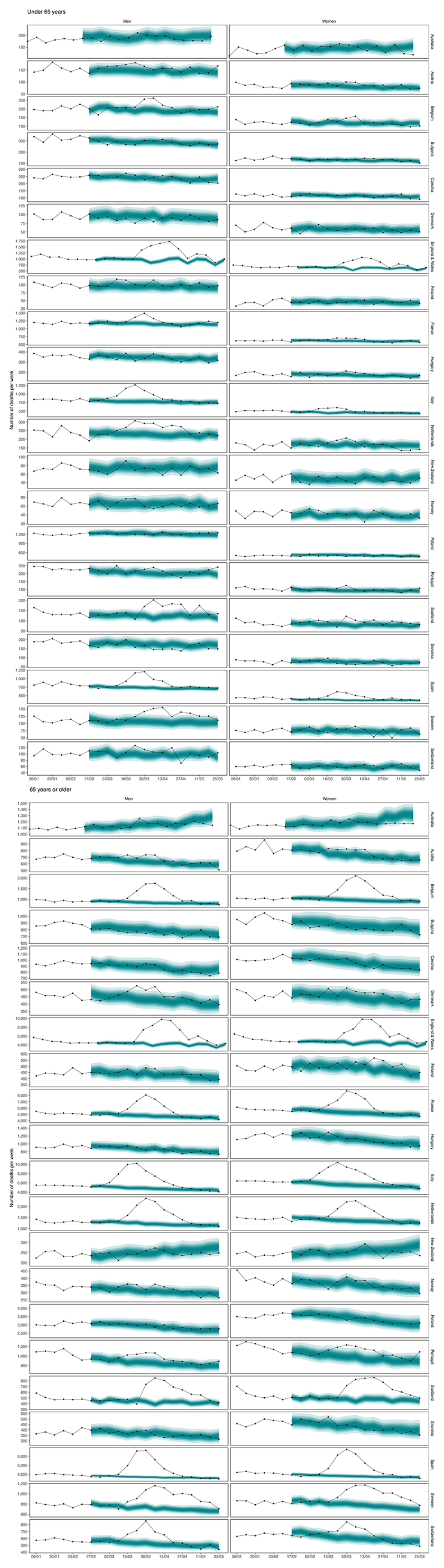
The points show reported deaths. The grey-shaded areas show the predictions of how many deaths would have been expected from mid-February had Covid-19 pandemic not taken place. The turquoise shading shows the credible intervals around the median prediction, from 5% (dark) to 95% (light) in 10% increments, obtained from 16,000 posterior draws as described in Methods.
Extended Data Fig. 2. Posterior distribution of excess deaths from any cause per 100,000 people from mid-February to end of May 2020 and posterior distribution of each country’s rank, by age group.
Gold dots in the top panels show the posterior medians. Countries are ordered vertically by median excess (top panels) and mean rank (bottom panels) in men.
Extended Data Fig. 3. Posterior distribution of percent increase in deaths from any cause from mid-February to end of May 2020 and posterior distribution of each country’s rank, by age group.
Gold dots in the top panels show the posterior medians. Countries are ordered vertically by median increase (top panels) and mean rank (bottom panels) in men.
Extended Data Fig. 4. Weekly percent increase in mortality as a result of the Covid-19 pandemic by country, by age group.
The turquoise shading shows the credible intervals around the median prediction, from 5% (dark) to 95% (light) in 10% increments, obtained from 16,000 posterior draws as described in Methods. The background shading indicates the magnitude of the weekly increase that was detectable with a posterior probability of at least 90%.
Extended Data Table 1.
Number of excess deaths from any cause and deaths assigned to Covid-19 from mid-February to the end of May 2020, by country. Excess deaths ≥1,000 are rounded to the nearest hundred and excess deaths <1,000 to the nearest ten. Deaths assigned to Covid-19 were taken directly from the cited sources and not rounded
| Number of excess deaths (median and 95% credible interval) | Number of deaths assigned to Covid-19 as underlying cause1 | |||
|---|---|---|---|---|
| Men | Women | Both sexes | ||
| Australia | -190 (-1,230 to 770) | -500 (-1,870 to 610) | -700 (-2,500 to 830) | 102 |
| Austria | 630 (-60 to 1,300) | 310 (-690 to 1,200) | 930 (-290 to 2,100) | 668 |
| Belgium | 4,000 (2,800 to 5,000) | 4,700 (3,200 to 6,000) | 8,600 (6,700 to 10,400) | 9,487 |
| Bulgaria | -620 (-1,550 to 250) | -490 (-1,790 to 620) | -1,110 (-2,840 to 340) | 140 |
| Czechia | -170 (-1,560 to 880) | -310 (-2,000-970) | -510 (-2,880 to 1,300) | 319 |
| Denmark | 260 (-280 to 760) | 270 (-320-820) | 530 (-270 to 1,300) | 571 |
| England & Wales | 30,000 (25,400 to 34,400) | 27,200 (20,600 to 33,300) | 57,300 (48,900 to 65,000) | 47,104 |
| Finland | 220 (-320 to 640) | 260 (-340 to 770) | 470 (-360 to 1,100) | 316 |
| France | 11,700 (6,500 to 16,600) | 12,000 (5,400 to 18,600) | 23,700 (14,900 to 32,300) | 28,771 |
| Hungary | -420 (-1,690 to 660) | -80 (-1,770 to 1,500) | -510 (-2,660 to 1,500) | 524 |
| Italy2 | 24,700 (18,700 to 30,200) | 24,100 (15,800 to 31,900) | 48,700 (38,100 to 58,900) | 33,340 |
| Netherlands | 5,100 (3,600 to 6,400) | 3,500 (1,600 to 5,200) | 8,600 (6,100 to 10,800) | 5,951 |
| New Zealand | -180 (-470 to 80) | -110 (-480 to 200) | -300 (-780 to 120) | 22 |
| Norway | 150 (-190 to 440) | 80 (-360 to 480) | 230 (-340 to 720) | 236 |
| Poland | 780 (-3,330 to 4,100) | -430 (-5,190 to 3,800) | 380 (-6,41 Oto 6,000) | 1,061 |
| Portugal | 1,300 (170 to 2,400) | 1,600 (11 Oto 2,900) | 2,900 (1,000 to 4,700) | 1,396 |
| Scotland | 2,300 (1,700 to 2,800) | 2,300 (1,600 to 3,000) | 4,600 (3,700 to 5,500) | 3,914 |
| Slovakia | -190 (-850 to 320) | -120 (-980 to 540) | -330 (-1,440 to 540) | 28 |
| Spain | 22,700 (19,000 to 26,100) | 23,200 (18,500 to 27,700) | 45,800 (39,900 to 51,700) | 27,127 |
| Sweden | 3,000 (2,300 to 3,600) | 2,500 (1,600 to 3,400) | 5,500 (4,400 to 6,500) | 4,395 |
| Switzerland | 940 (320 to 1,500) | 460 (-340 to 1,200) | 1,400 (350 to 2,300) | 1,656 |
Data are from Office for National Statistics for England and Wales (https://www.ons.qov.uk/peoplepopulationandcommunitv/birthsdeathsandmarriaαes/deaths/datasets/weeklvDrovisionalfiαuresondeathsreαisteredinenαlandandwales: accessed on 20 August 2020), National Records of Scotland for Scotland (https://www.nrscotland.αov.uk/covid19stats: accessed on 20 August 2020), and the European Centre for Disease Prevention and Control (ECDC) for other countries (https://www.ecdc.euroDa.eu/en/Dublications-data/download-todavs-data-αeoαraDhic-distribution-covid-19-cases-worldwide: accessed on 20 August 2020). ECDC data were only available for both sexes combined.
Data on all-cause mortality, which is used to estimate excess deaths, for Italy are from municipalities with up-to-date death registration, that ∞ver 95.0% of the population and 98.0% of COVID deaths. Data for deaths assigned to Covid-19 are for the entire country.
Extended Data Table 2. Sources of data on deaths and population.
| Data sources for deaths and population | Start of time series | |
|---|---|---|
| Australia | Australian Bureau of Statistics1, UN2 | 01/01/2015 |
| Austria | Eurostat3,4 | 04/01/2010 |
| Belgium | Eurostat3,4 | 04/01/2010 |
| Bulgaria | Eurostat3,4 | 04/01/2010 |
| Czechia | Eurostat3,4 | 04/01/2010 |
| Denmark | Eurostat3,4 | 04/01/2010 |
| England & Wales | Office for National Statistics5,6 | 02/01/2010 |
| Finland | Eurostat3,4 | 04/01/2010 |
| France | Eurostat3,4 | 31/12/2012 |
| Hungary | Eurostat3,4 | 04/01/2010 |
| Italy | Istat7 | 05/01/2015 |
| Netherlands | Eurostat3,4 | 04/01/2010 |
| New Zealand | Stats NZ8, UN2 | 27/12/2010 |
| Norway | Eurostat3,4 | 04/01/2010 |
| Poland | Eurostat3,4 | 04/01/2010 |
| Portugal | Eurostat3,4 | 04/01/2010 |
| Scotland | National Records of Scotland9, Office for National Statistics5 | 04/01/2010 |
| Slovakia | Eurostat3,4 | 04/01/2010 |
| Spain | Eurostat3,4 | 04/01/2010 |
| Sweden | Eurostat3,4 | 04/01/2010 |
| Switzerland | Eurostat3,4 | 04/01/2010 |
https://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPaqe/3303.0.55.004Jan%2ũ-%20Mav%202020. Data are provided by week-of-year, split into 52 complete weeks and one incomplete week. To form a continuous sequence of complete weeks across all years of the study, we divided deaths in each complete or incomplete week by the corresponding number of days to create daily numbers, and then summed daily deaths over each consecutive 7-day period.
https://ec.europa.eu/eurostat/data/database (table demo_r_mwk_05)
https://ec.europa.eu/eurostat/data/database (table demo_pjangroup)
https://www.istat.it/it/archivio/240401. Data on all-cause mortality, which is used to estimate excess deaths, are from municipalities with up-to-date death registration, that ∞ver 95.0% of the population and 98.0% of COVID deaths.
Extended Data Table 3.
Results of the external predictive validity (out-of-sample validation) of the estimated no-pandemic counterfactual weekly deaths from the ensemble of Bayesian models. Each number represents the total error over the validation period, averaged across countries
| Validation year | Age group (years) | Projection error (relative projection error) | Absolute projection error (relative absolute projection error) | Percent covered by 95% credible interval | |||
|---|---|---|---|---|---|---|---|
| Men | Women | Men | Women | Men | Women | ||
| 2017 | 0-64 | 134 (2%) | 28 (1%) | 265 (7%) | 177(9%) | 96% | 98% |
| 65+ | 878 (5%) | 1201 (6%) | 1036 (7%) | 1343 (7%) | 93% | 91% | |
| 2018 | 0-64 | -92 (-3%) | -49 (-3%) | 278 (8%) | 186(9%) | 95% | 97% |
| 65+ | -223 (-2%) | -370 (-2%) | 1058(7%) | 1420 (8%) | 88% | 87% | |
| 2019 | 0-64 | 112(2%) | 50 (2%) | 261 (8%) | 164(9%) | 96% | 96% |
| 65+ | 430 (2%) | 558 (2%) | 696 (4%) | 898 (5%) | 98% | 100% | |
| All three years | 0-64 | 51 (0%) | 10(0%) | 268 (8%) | 176(9%) | 95% | 97% |
| 65+ | 361 (2%) | 463 (2%) | 930 (6%) | 1220 (7%) | 93% | 93% | |
Australia, France and Italy were not used for validation analysis because they had shorter time series. Hence leaving out the last three years of data would leave a time series that was too short for estimating model parameters.
Extended Data Table 4. Selected population, policy and health systems characteristics of the 21 countries included in the analysis.
| Spain | 38 | 19.4 | 11,491 | 288 | 3.0 | 9.7 | 7.6 | 4.0 | 7.1 | 24.6 | 19.1 | 79.6 | 3.47 | 83.4 | 1.8 | 8.9 | 0.35 | 15.9 |
| England and Wales* | 37 | 18.4 | 10,312 | 364 | 2.7 | 6.6 | 8.5 | 3.0 | 5.8 | 28.8 | 15.2 | 82.6 | 3.48 | 81.3 | 0.9 | 9.6 | 0.36 | 10.4 |
| Italy | 28 | 22.9 | 5,883 | 233 | 3.3 | 12.5 | 3.8 | 4.0 | 5.8 | 20.7 | 21.2 | 69.6 | 3.76 | 83.3 | 1.3 | 8.8 | 0.33 | 13.3 |
| Scotland* | 28 | 19.0 | 10,312 | 364 | 2.7 | 6.6 | 8.5 | 3.0 | 5.8 | 28.8 | 15.2 | 82.6 | 3.48 | 81.3 | 0.9 | 9.6 | 0.36 | 10.4 |
| Belgium | 27 | 18.9 | 2,566 | 42 | 6.2 | 15.9 | 12.3 | 3.1 | 4.6 | 22.9 | 17.5 | 97.9 | 6.39 | 81.6 | 1.4 | 10.3 | 0.27 | 10.0 |
| Sweden | 22 | 19.9 | No lockdown | No lockdown | 2.5 | 5.8 | 13.3 | 4.3 | 4.9 | 21.4 | 19.3 | 86.6 | 4.92 | 82.6 | 1.1 | 11.0 | 0.28 | 8.8 |
| Nethrlands | 19 | 19.2 | 4,204 | 179 | 4.7 | 6.4 | 10.6 | 3.3 | 4.4 | 21.2 | 18.7 | 90.2 | 5.20 | 81.8 | 1.1 | 10.1 | 0.28 | 8.4 |
| France | 13 | 20.1 | 6,633 | 148 | 6.4 | 11.6 | 9.9 | 3.4 | 5.9 | 22.4 | 22.1 | 79.7 | 6.36 | 82.7 | 1.1 | 11.3 | 0.29 | 8.0 |
| Portugal | 9 | 21.8 | 1,280 | 12 | 3.3 | 4.2 | No data | No data | 6.9 | 21.6 | 24.4 | 63.5 | 4.17 | 81.3 | 2.3 | 9.0 | 0.34 | 13.6 |
| Switzerland | 7 | 18.5 | 3,863 | 33 | 4.6 | 11.0 | 11.7 | 4.3 | 4.1 | 20.3 | 18.0 | 73.7 | 6.08 | 83.8 | 1.5 | 12.3 | 0.30 | 8.6 |
| Austria | 4 | 18.8 | 860 | 1 | 7.6 | 21.8 | 7.8 | 5.2 | 4.3 | 20.9 | 21.0 | 57.7 | 5.19 | 81.7 | 1.1 | 10.4 | 0.28 | 9.0 |
| Denmark | 3 | 19.6 | 1,024 | 4 | 2.5 | 6.7 | 8.2 | 4.2 | 4.3 | 20.4 | 20.6 | 87.5 | 3.77 | 81.0 | 1.9 | 10.1 | 0.25 | 5.4 |
| Finland | 3 | 21.8 | 267 | 0 | 4.5 | 6.1 | 11.3 | 3.2 | 5.4 | 23.1 | 19.3 | 85.2 | 5.52 | 81.7 | 1.9 | 9.2 | 0.26 | 6.8 |
| Norway | 2 | 17.3 | 489 | 0 | 3.8 | 8.0 | 8.3 | 4.9 | 5.1 | 24.0 | 19.6 | 81.1 | 5.63 | 82.8 | 1.8 | 10.4 | 0.25 | 7.8 |
| Poland | 0 | 17.7 | 749 | 8 | 6.5 | 6.9 | 2.6 | 2.4 | 7.7 | 23.9 | 28.8 | 60.3 | 4.71 | 77.6 | 1.4 | 6.5 | 0.30 | 10.5 |
| Hungary | -1 | 19.3 | 39 | 1 | 7.0 | 13.8 | 8.4 | 3.4 | 7.8 | 27.4 | 30.0 | 70.5 | 4.40 | 76.1 | 1.9 | 6.9 | 0.29 | 10.1 |
| Czechia | -2 | 19.6 | 298 | 0 | 6.4 | 11.6 | 6.9 | 4.0 | 7.5 | 26.9 | 27.8 | 73.5 | 4.73 | 79.0 | 1.6 | 7.2 | 0.26 | 6.0 |
| Australia | -2 | 15.8 | 3,809 | 14 | 3.8 | No data | No data | 3.8 | 5.9 | 30.0 | 15.2 | 85.7 | 5.92 | 82.7 | 1.1 | 9.2 | 0.34 | 12.8 |
| Slovakia | -2 | 16.1 | 61 | 0 | 5.8 | 9.2 | 7.2 | 3.5 | 7.2 | 21.3 | 28.6 | 53.9 | 5.96 | 77.3 | 2.2 | 6.7 | No data | No data |
| New Zealand | -3 | 15.82 | 189 | 0 | 2.7 | No data | No data | 3.4 | 6.9 | 31.8 | 16.3 | 86.3 | 5.99 | 81.6 | 1.2 | 9.2 | 0.33 | 9.9 |
| Bulgaria | -4 | 21.3 | 23 | 1 | 7.2 | 12.2 | 0.4 | No data | 7.7 | 25.8 | 28.3 | 74.0 | 2.56 | 75.0 | 1.5 | 8.1 | No data | No data |
England and Wales and Scotland assigned UK numbers
WHO European Health Information Gateway (https://gateway.euro.who.lnt/en/lndlcators/hfa_476-5050-hospital-beds-per-100-000/) for European countries and OECD (https://stats.oecd.org/lndex.aspx?DataSetCode=HEALH_REAC) for Australia, New Zealand
Our World In Data (https://ourworldindata.org/grapher/critical-care-beds-per-10001
WHO European Health Information Gateway (https://gatewsy.euro.who.int/en/indicators/hlthres_23-beds-in-nurslng-and-residential-care-facilities-per-100-000/)
NCD-RIsC (http://ncdrts.org/dat3-downloads.html)
World Bank (https://data.wortdbank.org/indicator/SP.DyN.LE00.IN)
World Bank (https://data.worldbank.org/indicator/SH.XPD.CHEX.GD.ZS)
Extended Data Table 5.
Combination of terms used in each of the 16 models for estimating number of weekly deaths that would be expected had the pandemic not occurred. See Methods for an explanation of each term
| Model number | Global intercepts | Time slope | Non-linear (autoregressive) term | Seasonal term | Temperature anomaly terms |
|---|---|---|---|---|---|
| 1 | α0 + αholiday(week) | - | θ week | - | |
| 2 | α0 + αholiday(week) | - | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 3 | α0 + αholiday(week) | - | θ week | - | |
| 4 | α0 + αholiday(week) | - | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 5 | α0 + αholiday(week) | - | θ week | - | |
| 6 | α0 + αholiday(week) | - | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 7 | α0 + αholiday(week) | - | θ week | - | |
| 8 | α0 + αholiday(week) | - | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 9 | α0 + αholiday(week) | β · week | θ week | - | |
| 10 | α0 + αholiday(week) | β · week | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 11 | α0 + αholiday(week) | β · week | θ week | - | |
| 12 | α0 + αholiday(week) | β · week | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 13 | α0 + αholiday(week) | β · week | θ week | - | |
| 14 | α0 + αholiday(week) | β · week | θ week | (γ + νweek of year) · temperature anomalyweek | |
| 15 | α0 + αholiday(week) | β · week | θ week | - | |
| 16 | α0 + αholiday(week) | β · week | θ week | (γ + νweek of year) · temperature anomalyweek |
Supplementary Material
Acknowledgements
We thank L. Clearly and R. Jackson for information about data from New Zealand and G. Mangiameli for help with background materials and references. This study was partially supported by the Abdul Latif Jameel Institute for Disease and Emergency Analytics at Imperial College London. The development of methodology for estimating the effect of the pandemic as an extreme event was supported by the Pathways to Equitable Healthy Cities grant from the Wellcome Trust (209376/Z/17/Z).
Footnotes
Author contributions
M.E., V.K. and J.E.B. designed the study. V.K. and J.E.B. developed and tested statistical methods with input from T.R., R.M.P. and M.E. V.K. wrote computer code, conducted analysis and prepared results. V.K., R.M.P., T.R. and J.E.B. accessed, harmonized and analyzed data with input from M.G., M.B., G.C. and C.D.M.. M.E., V.K., J.E.B., J.P.-S. and M.M. wrote the first draft of the paper, and other authors contributed to the paper.
Competing interests
M.E. reports a charitable grant from the AstraZeneca Young Health Programme and personal fees from Prudential, outside the submitted work. J.P.-S. is vice-chair of the Royal Society for Public Health and reports personal fees from Novo Nordisk A/S and Lane, Clark & Peacock, outside of the submitted work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Additional information
Extended data is available for this paper at https://doi.org/10.1038/s41591-020-1112-0.
Supplementary information is available for this paper at https://doi.org/10.1038/s41591-020-1112-0.
Peer review information Jennifer Sargent was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team
Reprints and permissions information is available at www.nature.com/reprints.
Data availability
Estimates of weekly excess deaths by country are available at http://globalenvhealth.org/code-data-download/. Input data on deaths, population and temperature are available at http://globalenvhealth.org/code-data-download/.
The data sets used in the study are publicly available from the following locations: Data on deaths and population: https://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3303.0.55.004Jan%20-%20May%202020
https://ec.europa.eu/eurostat/data/database (tables demo_r_mwk_05 and demo_pjangroup)
https://www.istat.it/it/archivio/240401
https://www.stats.govt.nz/experimental/covid-19-data-portal
Data on temperature and gridded population: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 https://sedac.ciesin.columbia.edu/data/collection/gpw-v4
Code availability
The computer code for the Bayesian model ensemble used in this study is available at http://globalenvhealth.org/code-data-download/.
References
- 1.Douglas M, Katikireddi SV, Taulbut M, McKee M, McCartney G. Mitigating the wider health effects of COVID-19 pandemic response. BMJ. 2020;369:m1557. doi: 10.1136/bmj.m1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pearce N, Lawlor DA, Brickley EB. Comparisons between countries are essential for the control of COVID-19. Int J Epidemiol. 2020 doi: 10.1093/ije/20.4.1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Merrick R. Coronavirus: Boris Johnson’s claim it is ‘too early’ to draw global death toll comparisons mocked by Keir Starmer. The Independent. 2020. https://www.independent.co.uk/news/uk/politics/coronavirus-daily-briefings-boris-johnson-keir-starmer-cases-deaths-comparison-a9511931.html .
- 4.World Health Organization. Global Health Estimates: Deaths by Cause, Age, Sex and Country, 2000-2016. World Health Organization; 2018. [Google Scholar]
- 5.Fuller T, Baker M. Coronavirus death in California came weeks before first known U.S. death. The New York Times. 2020 https://www.nytimes.com/2020/04/22/us/coronavirus-first-united-states-death.html . [Google Scholar]
- 6.Perraudin F. All care home staff and residents in England to be tested for coronavirus. The Guardian. 2020 https://www.theguardian.com/world/2020/may/15/coronavirus-care-home-residents-deaths-england-wales . [Google Scholar]
- 7.Schultz T. Belgium’s coronavirus (over)counting controversy. DW. 2020. https://www.dw.com/en/belgiums-coronavirus-overcounting-controversy/a-53660975 .
- 8.Campbell D, Bannock C. Coronavirus crisis could lead to 18,000 more cancer deaths, experts warn. The Guardian. 2020 https://www.theguardian.com/society/2020/apr/29/extra-18000-cancer-patients-in-england-could-die-in-next-year-study . [Google Scholar]
- 9.Sample I. More than 2m operations cancelled as NHS fights COVID-19. The Guardian. 2020 https://www.theguardian.com/society/2020/apr/26/more-than-two-million-operations-cancelled-as-nhs-fights-covid-19 . [Google Scholar]
- 10.Hiom S. Science Blog. Cancer Research; UK: 2020. How coronavirus is impacting cancer services in the UK. https://scienceblog.cancerresearchuk.org/2020/04/21/how-coronavirus-is-impacting-cancer-services-in-the-uk/ [Google Scholar]
- 11.Bernstein L, Sellers FS. Patients with heart attacks, strokes and even appendicitis vanish from hospitals. The Washington Post. 2020 https://www.washingtonpost.com/health/patients-with-heart-attacks-strokes-and-even-appendicitis-vanish-from-hospitals/2020/04/19/9ca3ef24-7eb4-11ea-9040-68981f488eed_story.html . [Google Scholar]
- 12.Pell MB, Lesser B. COVID’s other casualties. Reuters Investigates. 2020 https://www.reuters.com/investigates/special-report/health-coronavirus-usa-cost/ [Google Scholar]
- 13.Kansagra AP, Goyal MS, Hamilton S, Albers GW. Collateral effect of COVID-19 on stroke evaluation in the United States. N Engl J Med. 2020;383:400–401. doi: 10.1056/NEJMc2014816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gaudino M, et al. Response of cardiac surgery units to COVID-19: an internationally-based quantitative survey. Circulation. 2020;142:300–302. doi: 10.1161/CIRCULATIONAHA.120.047865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guillot M, Khlat M. Épidémie de Covid-19: quel impact sur lespérance de vie en France? The Conversation. 2020 https://theconversation.com/epidemie-de-covid-19-quel-impact-sur-lesperance-de-vie-en-france-141484 . [Google Scholar]
- 16.Karanikolos M, McKee M. How comparable is COVID-19 mortality across countries? Health System Response Monitor; 2020. https://analysis.covid19healthsystem.org/index.php/2020/06/04/how-comparable-is-covid-19-mortality-across-countries/COVID-19 . [Google Scholar]
- 17.Newton J. Behind the headlines: counting COVID-19 deaths. Public Health Matters. 2020 https://publichealthmatters.blog.gov.uk/2020/08/12/behind-the-headlines-counting-covid-19-deaths/ [Google Scholar]
- 18.Jones N. How coronavirus lockdowns stopped flu in its tracks. Nature. 2020 doi: 10.1038/d41586-020-01538-8. [DOI] [PubMed] [Google Scholar]
- 19.Klein A. Australia sees huge decrease in flu cases due to coronavirus measures. NewScientist. 2020 https://www.newscientist.com/article/2242113-australia-sees-huge-decrease-in-flu-cases-due-to-coronavirus-measures/ [Google Scholar]
- 20.Nuñez JH, et al. Impact of the COVID-19 pandemic on an emergency traumatology service: experience at a tertiary trauma centre in Spain. Injury. 2020;51:1414–1418. doi: 10.1016/j.injury.2020.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cunningham A. COVID-19 kills more men than women. The immune system may be why. ScienceNews. 2020 https://www.sciencenews.org/article/coronavirus-covid-19-kills-more-men-than-women-why-immune-system . [Google Scholar]
- 22.Devlin H. Men are much more likely to die from coronavirus-but why? The Guardian. 2020 https://www.theguardian.com/world/2020/mar/26/men-are-much-more-likely-to-die-from-coronavirus-but-why . [Google Scholar]
- 23.Bhopal SS, Bhopal R. Sex differential in COVID-19 mortality varies markedly by age. Lancet. 2020;396:532–533. doi: 10.1016/S0140-6736(20)31748-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gebhard C, Regitz-Zagrosek V, Neuhauser HK, Morgan R, Klein SL. Impact of sex and gender on COVID-19 outcomes in Europe. Biol Sex Differ. 2020;11:29. doi: 10.1186/s13293-020-00304-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Berlin I. The Hedgehog and the Fox: An Essay on Tolstoy’s View of History. Weidenfeld Nicolson; 1953. [Google Scholar]
- 26.Dahlgren G, Whitehead M. Policies and strategies to promote social equity in health. Institute for Futures Studies; 1991. https://www.iffs.se/en/publications/working-papers/policies-and-strategies-to-promote-social-equity-in-health/ [Google Scholar]
- 27.NCD Risk Factor Collaboration (NCD-RisC) Worldwide trends in diabetes since 1980: a pooled analysis of 751 population-based studies with 4.4 million participants. Lancet. 2016;387:1513–1530. doi: 10.1016/S0140-6736(16)00618-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.NCD Risk Factor Collaboration (NCD-RisC) Worldwide trends in body-mass index, underweight, overweight, and obesity from 1975 to 2016: a pooled analysis of 2416 population-based measurement studies in 128.9 million children, adolescents, and adults. Lancet. 2017;390:2627–2642. doi: 10.1016/S0140-6736(17)32129-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.NCD Risk Factor Collaboration (NCD-RisC) Long-term and recent trends in hypertension awareness, treatment, and control in 12 high-income countries: an analysis of 123 nationally representative surveys. Lancet. 2019;394:639–651. doi: 10.1016/S0140-6736(19)31145-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Palladino R, Tayu Lee J, Ashworth M, Triassi M, Millett C. Associations between multimorbidity, healthcare utilisation and health status: evidence from 16 European countries. Age Ageing. 2016;45:431–435. doi: 10.1093/ageing/afw044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Organisation for Economic Co-operation and Development. OECD Income Distribution Database (IDD) 2020 https://www.oecd.org/social/income-distribution-database.htm . [Google Scholar]
- 32.Bouffanais R, Lim SS. Cities-try to predict superspreading hotspots for COVID-19. Nature. 2020;583:352–355. doi: 10.1038/d41586-020-02072-3. [DOI] [PubMed] [Google Scholar]
- 33.Hale T, et al. Oxford COVID-19 Government Response Tracker. Blavatnik School of Government; 2020. https://www.bsg.ox.ac.uk/research/research-projects/coronavirus-government-response-tracker . [Google Scholar]
- 34.Okell LC, et al. Have deaths from COVID-19 in Europe plateaued due to herd immunity? Lancet. 2020;395:e110–e111. doi: 10.1016/S0140-6736(20)31357-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Baker M, Kvalsvig A, Verrall AJ, Telfar-Barnard L, Wilson N. New Zealand’s elimination strategy for the COVID-19 pandemic and what is required to make it work. N Z Med J. 2020;133:10–14. [PubMed] [Google Scholar]
- 36.Hirsch C. Europe’s coronavirus lockdown measures compared. Politico. 2020 https://www.politico.eu/article/europes-coronavirus-lockdown-measures-compared/ [Google Scholar]
- 37.Peto J, et al. Weekly COVID-19 testing with household quarantine and contact tracing is feasible and would probably end the epidemic. R Soc Open Sci. 2020;7:200915. doi: 10.1098/rsos.200915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Palmer B. Chart of the week: Covid-19 test and trace programme is still a leaky system. Nuffield Trust; 2020. https://www.nuffieldtrust.org.uk/resource/chart-of-the-week-covid-19-test-and-trace-programme-is-still-a-leaky-system . [Google Scholar]
- 39.Briggs A, Jenkins D, Fraser C. NHS Test and Trace: the journey so far. The Health Foundation: 2020. https://www.health.org.uk/publications/long-reads/nhs-test-and-trace-the-journey-so-far . [Google Scholar]
- 40.Moon J, et al. Optimising ‘Test and Trace’ systems: early lessons from a comparative analysis of six countries. 2020. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3694441 .
- 41.Froud J, Haslam C, Johal S, Law J, Williams K. When systems fail: UK acute hospitals and public health after COVID-19. Foundational Economy Collective; 2020. https://foundationaleconomycom.files.wordpress.com/2020/08/when-systems-fail-uk-acute-hospitals-and-public-health-after-covid-19.pdf . [Google Scholar]
- 42.Scally G, Jacobson B, Abbasi K. The UK’s public health response to COVID-19. BMJ. 2020;369:m1932. doi: 10.1136/bmj.m1932. [DOI] [PubMed] [Google Scholar]
- 43.Cooper J. How does UK healthcare spending compare with other countries? Office for National Statistics; 2019. https://www.ons.gov.uk/peoplepopulationandcommunity/healthandsocialcare/healthcaresystem/articles/howdoesukhealthcarespendingcomparewithothercountries/2019-08-29 . [Google Scholar]
- 44.Organisation for Economic Co-operation and Development. Hospital beds. 2020. https://data.oecd.org/healtheqt/hospital-beds.htm .
- 45.McKee M. Learning from success: how has Hungary responded to the COVID pandemic? Gero Science. 2020 doi: 10.1007/s11357-020-00240-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Comas-Herrera A, et al. Mortality associated with COVID-19 outbreaks in care homes: early international evidence. International Long-Term Care Policy Network; 2020. https://ltccovid.org/2020/04/12/mortality-associated-with-covid-19-outbreaks-in-care-homes-early-international-evidence/ [Google Scholar]
- 47.Royal Society DELVE Initiative. Scoping Report on Hospital and Health Care Acquisition of COVID-19 and Its Control. 2020. https://rs-delve.github.io/reports/2020/07/06/nosocomial-scoping-report.html .
- 48.O’Neill D. COVID-19 in care homes: the many determinants of this perfect storm. BMJ. 2020;369:m2096. doi: 10.1136/bmj.m2096. [DOI] [PubMed] [Google Scholar]
- 49.Office for National Statistics. Quarterly mortality report, England: October to December 2019 and year-end review. 2019. https://www.ons.gov.uk/releases/quarterlymortalityreportenglandoctobertodecember2019 .
- 50.European Centre for Medium-Range Weather Forecasts. ERA5: reanalysis datasets. 2019. https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 .
- 51.Giles C. Excess UK deaths in COVID-19 pandemic top 50,000. Financial Times. 2020 https://www.ft.com/content/40fc8904-febf-4a66-8d1c-ea3e48bbc034 . [Google Scholar]
- 52.Wang H, et al. Age-specific and sex-specific mortality in 187 countries, 1970–2010: a systematic analysis for the Global Burden of Disease Study 2010. Lancet. 2012;380:2071–2094. doi: 10.1016/S0140-6736(12)61719-X. [DOI] [PubMed] [Google Scholar]
- 53.Kontis V, et al. Future life expectancy in 35 industrialised countries: projections with a Bayesian model ensemble. Lancet. 2017;389:1323–1335. doi: 10.1016/S0140-6736(16)32381-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Parks RM, Bennett JE, Foreman KJ, Toumi R, Ezzati M. National and regional seasonal dynamics of all-cause and cause-specific mortality in the USA from 1980 to 2016. eLife. 2018;7:e35500. doi: 10.7554/eLife.35500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Feinstein CA. Seasonality of deaths in the U.S. by age and cause. Demogr Res. 2002;6:471–488. [Google Scholar]
- 56.Fowler T, et al. Excess winter deaths in Europe: a multi-country descriptive analysis. Eur J Public Health. 2014;25:339–345. doi: 10.1093/eurpub/cku073. [DOI] [PubMed] [Google Scholar]
- 57.McKee CM. Deaths in winter: can Britain learn from Europe? Eur J Epidemiol. 1989;5:178–182. doi: 10.1007/BF00156826. [DOI] [PubMed] [Google Scholar]
- 58.Hyndman RJ, Athanasopoulos G. Forecasting: Principles and Practice. OTexts; 2018. [Google Scholar]
- 59.Congdon P. Applied Bayesian Modelling. John Wiley Sons; 2003. [Google Scholar]
- 60.Basu R. High ambient temperature and mortality: a review of epidemiologic studies from 2001 to 2008. Environ Health. 2009;8:40. doi: 10.1186/1476-069X-8-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Basu R, Samet JM. Relation between elevated ambient temperature and mortality: a review of the epidemiologic evidence. Epidemiol Rev. 2002;24:190–202. doi: 10.1093/epirev/mxf007. [DOI] [PubMed] [Google Scholar]
- 62.Gasparrini A, et al. Mortality risk attributable to high and low ambient temperature: a multicountry observational study. Lancet. 2015;386:369–375. doi: 10.1016/S0140-6736(14)62114-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Song X, et al. Impact of ambient temperature on morbidity and mortality: an overview of reviews. Sci Total Environ. 2017;586:241–254. doi: 10.1016/j.scitotenv.2017.01.212. [DOI] [PubMed] [Google Scholar]
- 64.Bennett JE, Blangiardo M, Fecht D, Elliott P, Ezzati M. Vulnerability to the mortality effects of warm temperature in the districts of England and Wales. Nature Clim Change. 2014;4:269–273. [Google Scholar]
- 65.Parks RM, et al. Anomalously warm temperatures are associated with increased injury deaths. Nat Med. 2020;26:65–70. doi: 10.1038/s41591-019-0721-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Holbek SS, Rue H. Penalised complexity priors for stationary autoregressive processes. J Time Ser Anal. 2017;38:923–935. [Google Scholar]
- 67.Rue H, Martino S, Chopin N. Approximate Bayesian inference for latent Gaussian models using integrated nested Laplace approximations. (J R Stat Soc Series B).2009;71:319–392. [Google Scholar]
- 68.Timmermann A. In: Handbook of Economic Forecasting. Elliott G, Granger C, Timmermann A, editors. Vol. 1. Elsevier; 2006. Forecast combinations; pp. 135–196. [Google Scholar]
- 69.Graefe A, Küchenhoff H, Stierle V, Riedl B. Limitations of ensemble Bayesian model averaging for forecasting social science problems. Int J Forecast. 2015;31:943–951. [Google Scholar]
- 70.Office for National Statistics. Comparisons of all-cause mortality between European countries and regions: January to June 2020. 2020. https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/articles/comparisonsofallcausemortalitybetweeneuropeancountriesandregions/januarytojune2020 .
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Estimates of weekly excess deaths by country are available at http://globalenvhealth.org/code-data-download/. Input data on deaths, population and temperature are available at http://globalenvhealth.org/code-data-download/.
The data sets used in the study are publicly available from the following locations: Data on deaths and population: https://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3303.0.55.004Jan%20-%20May%202020
https://ec.europa.eu/eurostat/data/database (tables demo_r_mwk_05 and demo_pjangroup)
https://www.istat.it/it/archivio/240401
https://www.stats.govt.nz/experimental/covid-19-data-portal
Data on temperature and gridded population: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 https://sedac.ciesin.columbia.edu/data/collection/gpw-v4
The computer code for the Bayesian model ensemble used in this study is available at http://globalenvhealth.org/code-data-download/.