Abstract
To date, we have scarce information about the relative myelination level of different fiber bundles in the human brain. Indirect evidence comes from postmortem histology data but histological stainings are unable to follow a specific bundle and determine its intrinsic myelination. In this context, quantitative MRI, and diffusion MRI tractography may offer a viable solution by providing, respectively, voxel-wise myelin sensitive maps and the pathways of the major tracts of the brain. Then, “tractometry” can be used to combine these two pieces of information by averaging tissue features (obtained from any voxel-wise map) along the streamlines recovered with diffusion tractography. Although this method has been widely used in the literature, in cases of voxels containing multiple fiber populations (each with different levels of myelination), tractometry provides biased results because the same value will be attributed to any bundle passing through the voxel. To overcome this bias, we propose a new method - named “myelin streamline decomposition” (MySD) - which extends convex optimization modeling for microstructure informed tractography (COMMIT) allowing the actual value measured by a microstructural map to be deconvolved on each individual streamline, thereby recovering unique bundle-specific myelin fractions (BMFs). We demonstrate the advantage of our method with respect to tractometry in well-studied bundles and compare the cortical projection of the obtained bundle-wise myelin values of both methods. We also prove the stability of our approach across different subjects and different MRI sensitive myelin mapping approaches. This work provides a proof-of-concept of in vivo investigations of entire neuronal pathways that, to date, are not possible.
Keywords: Human brain, Myelin streamline decomposition, Diffusion MRI, Tractography, Microstructure, Microstructure informed tractography, Bundle-specific myelin content
1. Introduction
Brain structural connectivity – which is mediated by the intricate network of axonal bundles connecting different brain regions - is a major determinant of brain function (Baum et al., 2020; Chu et al., 2018). Indeed, the morphological characteristics of the axons constituting these bundles (e.g. internal diameter), as well as the thickness of their myelin sheath, influence the conduction velocity and hence the transmission of information (Goldman and Albus, 1968; Rushton, 1951; Waxman, 1980). Thus, methods that permit individual differences in such physical attributes are of pivotal importance in understanding brain physiology and pathology. Through them we can study individual differences in development or degeneration, and detect disruptions caused by disease. Being able to infer this information non-invasively and in vivo would allow longitudinal studies to be performed which may be useful to understand subject-specific development and plasticity, and to monitor treatment efficacy.
Anatomical studies of the brain’s myelo-architecture and of short/long-range fiber systems have yielded remarkable details about the structural properties and organization of brain connectivity (Felleman and Essen, 1991; Mesulam, 1998; Schüz and Braitenberg, 2002). Animal studies also showed that myelination of axonal bundles begins before birth and continues over the life span with a peak during the first 2-years of life. Myelination extends progressively from the caudal brain stem to the rostral forebrain (Kinney and Volpe, 2017) and develops in the central sensory systems before the central motor systems. In addition, myelination in regions involved in higher level associative functions and sensory discriminations (e.g., association areas, intracortical neuropil, and cerebral commissures) occurs well after birth and progresses over decades (Kinney and Volpe, 2017).
To date, there is little evidence of myelination differences among fiber bundles in the human brain. Indirect evidence comes from post-mortem histology data showing that the relative myelination across cortical regions is highly heterogeneous (Nieuwenhuys and Broere, 2017): primary sensory, motor, auditory, and visual regions are densely myelinated (Nieuwenhuys and Broere, 2017), and major fiber tracts originating/projecting from/to primary cortical areas have higher myelin content than tracts developing from neurons in less myelinated areas (Nieuwenhuys and Broere, 2017). Nevertheless, a histological comparison of the myelin content of (i) different fiber bundles projecting/originating to/from primary areas, as well as of (ii) other fiber bundles projecting/originating to/from other cortical areas is lacking. Hence, there is a clear need for methods to decouple the myelination of axons constituting different bundles as, today, this information is not available.
Magnetic resonance imaging (MRI) allows the computation of myelin content estimates from in vivo data (West et al., 2018) from sources of MRI contrast such as transverse relaxation (Kucharczyk et al., 1994) and magnetization transfer (Heath et al., 2018). Unfortunately, diffusion-weighted MRI (dMRI) cannot provide such information. In fact, although it has been shown that myelin contributes to the anisotropy measured via dMRI (Beaulieu, 2002), the signal from myelin water (T2 ∼ 5 - 20 ms) has typically decayed away in dMRI experiments due to the comparatively long echo times employed (Tax et al., 2021). Thus, although some dMRI derived properties might naturally co-vary with myelin content (Jelescu et al., 2016; Mancini et al., 2020), this technique is not myelin-specific and need to be complemented with a more specific one to safely interpret results. Semi-quantitative estimates of magnetization transfer include the magnetization transfer ratio (MTR) (Dousset et al., 1995) or MT saturation (Helms et al., 2008; 2010; Helms et al., 2019; Rowley et al., 2021). The latter biomarker offers increased specificity to myelin concentration and is inherently corrected for bias from the radio-frequency fields. MT saturation maps can be scaled to derive maps of the myelin volume fraction (MVF) in each image voxel (Mohammadi et al., 2015). Alternatively, the water trapped between myelin bilayers and the water inside or outside of axons have different transverse relaxation times T2, and an estimate of the voxel-wise myelin water fraction (MWF, which quantifies the signal fraction of the myelin water over the total water in a voxel), can be obtained by measuring the relative signal contribution from each component (Deoni et al., 2008; Mackay et al., 1994). The acquisition can be achieved using a number of sequences such as multi-echo T2 sequences (MET2) (Stewart et al., 1993; Piredda et al., 2020), the recently proposed fast acquisition with spiral trajectory and T2prep (FAST-T2) (Nguyen et al., 2016) or multicomponent driven equilibrium single pulse observation of T1 and T2 (mcDESPOT) (Deoni et al., 2008).
All contrast mechanisms mentioned above can provide voxel-wise myelin sensitive maps of brain white matter (WM), and, over the past decades, extensive validations against histology have been made to find the most specific and sensitive (Lazari and Lipp, 2021; Mancini et al., 2020). Nevertheless, as each voxel’s value reflects the contribution of thousands of axons belonging to different bundles (at least two in ∼90% of the white matter voxels (Jeurissen et al., 2013)), these maps tend to show little spatial contrast or intensity variations and cannot resolve the bundle-specific myelination. Thus, they are mostly used to study specific regions of pathological tissues or to perform average measures along major tracts (Lipp et al., 2019; Yeatman et al., 2014). In particular, the latter is commonly called ‘tractometry’ and, extending the idea in (Jones and Deoni, 2006), it was introduced by Bells and colleagues in (Bells et al., 2011) to assign a more quantitative meaning to tractograms recovered by analyzing dMRI data (Yeh et al., 2020). This method consists of sampling voxel-wise microstructural metrics at each vertex of the reconstructed tracts and computing the mean of these metrics along specific pathways or studying their variability along the bundle’s profiles. Very recently, Baumeister et al. applied the same method to investigate average myelin values in sections along fiber bundles rather than integrating over the whole tracts (Baumeister et al., 2020). Although such methods provide useful macroscopic information on the quantification of myelin of fiber bundles (Yeatman et al., 2012; Yeatman et al., 2014; Baumeister et al., 2020), we argue that, in cases of voxels containing multiple fiber populations (each possibly with different levels of myelination), projecting the same voxel’s myelin index on different pathways will provide biased results. To mitigate this problem, recently Boshkovski et al. (Boshkovski et al., 2020) suggested to use the median along the path instead of the average, showing promising results at the level of the connectome, but still not solving the bias of considering the same value for each streamline interdigitating in the same voxel.
On the other hand, Convex Optimization Modelling for Microstructure Informed Tractography (COMMIT) (Daducci et al., 2013; 2015) addresses this problem in the case of dMRI data by deconvolving specific dMRI microstructural features on each fiber so that it is possible to recover individual streamline contributions to the measured signal. These values represent the effective signal of intra-axonal cross-sectional area of each streamline (Raffelt et al. 2015) and provide a more ‘biologically-informative’ assessment of brain connectivity (Schiavi et al., 2020). In this work, we propose a novel method called myelin streamline decomposition (MySD) to assess the effective myelin cross-sectional area of each bundle by decoupling the myelin information measured in each voxel with MRI using deconvolution in the fibers’ space. In particular, we modified the COMMIT framework to accommodate maps of MWF derived from FAST-T2 (Nguyen et al., 2016) and maps of MVF derived from MTsat (Helms et al., 2008) data, and compute bundle-specific estimates of myelin fraction (BMF). We show that our method recovers an overall pattern of BMF estimates that is consistent across MRI markers of MWF and MVF. We compare our results with existing histopathological studies on WM myelination. Finally, by projecting the recovered WM myelin content in the cortex, we also show a good agreement with previous in vivo measurements of myelin on the cortex.
2. Materials and methods
2.1. Myelin streamline decomposition
In its original formulation, COMMIT (Daducci et al., 2013; 2015) combines the streamlines estimated with tractography, i.e., a tractogram, with the dMRI signal measured in each voxel to provide enhanced robustness in structural connectivity mapping. Assuming invariance of the dMRI-derived microstructural parameters along a particular streamline, such as the intra-axonal signal fraction (Jelescu and Budde 2017), COMMIT removes streamlines that are not compatible with the measured dMRI signal and estimates the actual contribution of the remaining ones. In a recent study (Schiavi et al., 2020) it was also high-lighted how network measures computed on structural connectivity matrices can benefit from the COMMIT application even in the presence of neurological diseases.
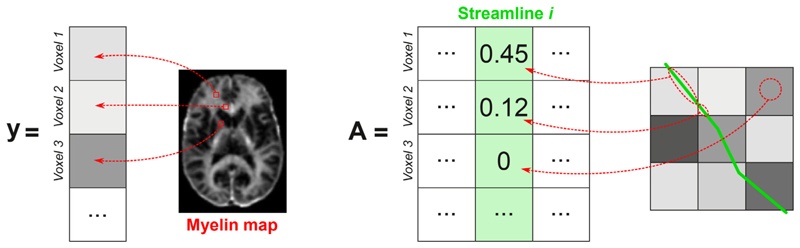
To infer the individual myelin content of each streamline from the total value measured in each voxel with MRI, we extended the original formulation to accommodate input maps other than dMRI as input to the fit. The problem can still be formulated as
where contains the MVF or MWF measures derived from MRI data in the nv voxels, the matrix A ∈ ℝnv×nf encodes the length of the nf streamlines in each image voxel (i.e. the length of the portion of the streamline in that voxel) and η accounts for both acquisition noise and modeling errors (see Fig. 1). The coefficients xi, i = 1, …, nf, of the vector are the myelin contribution per unit of length of each of the nf streamlines (i.e. input MVF or MWF divided by the length of the streamline in the voxel, which gives the effective myelin cross-sectional area) and can be estimated using non-negative least squares (NNLS):
where ‖ ‖2is the Euclidean norm in ℝn. The convex optimization process is then the same as in the original COMMIT framework and the novelty is in how we build the matrix A to adapt it to myelin maps instead of diffusion signal (Fig. 1). Thus, by fitting to the myelin sensitive maps, our model allows us to filter out redundant and implausible streamlines as in the original framework, but at the same time, to decompose the myelin effective cross-sectional area for each of them. We call this approach Myelin Streamline Decomposition (MySD).
Fig. 1.
Description of the input and forward model of the MySD method. The vector y (on the left) contains the values of the myelin map for all the voxels of the image. The matrix A (on the right) is built such that each column is associated with a streamline of the input tractogram and the entries contain the length of the streamline in each voxel.
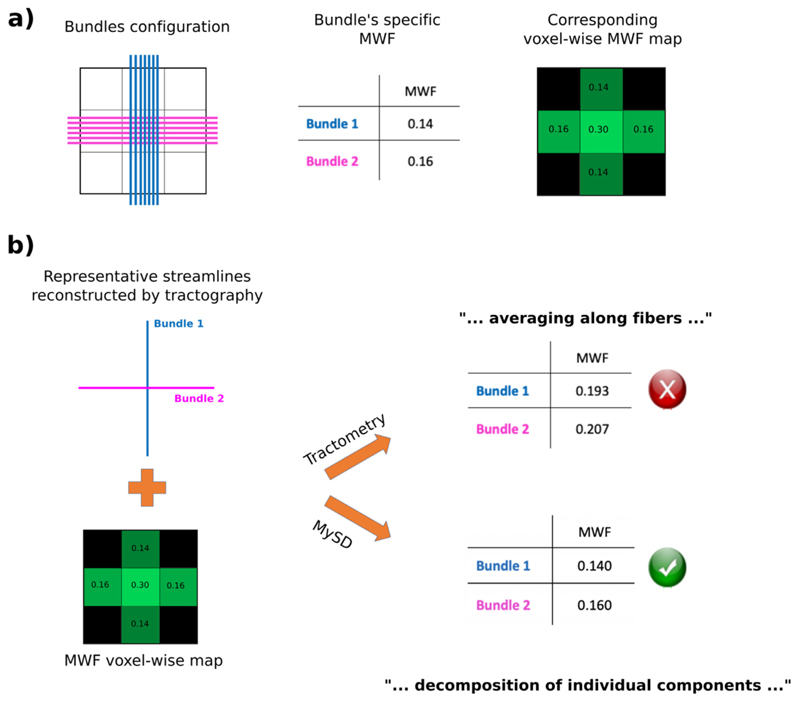
To better explain the underlying idea of our approach, let us consider the example shown in Fig. 2. The ground-truth configuration of the simulated phantom is illustrated in panel (a) and consists of two bundles crossing in the voxel at the center with a 90° angle (Fig. 2a left). Assuming that the myelin content of each bundle is constant and equal to those reported in the table in Fig. 2a center, we have that the corresponding voxel-wise MWF map measured by MRI would be as follows: 0.14 for the voxels crossed only by Bundle 1, 0.16 for those crossed only by Bundle 2 and 0.30 in the central voxel containing both bundles (see Fig. 2a right). In Fig. 2b we show the difference between our proposed approach and the state-of-the-art method called tractometry (Bells et al., 2011). Starting from the same reconstructed streamlines and MWF map (Fig. 2b left) tractometry performs the averaging of such maps along the streamlines, while MySD decomposes the signal on each individual streamline. Tractometry results in a biased over estimation whereas MySD recovers the correct myelin content of each individual bundle (see table in Fig. 2b right). Despite being a very simplistic toy example, we can appreciate the clear bias created by averaging voxel-wise microstructural maps instead of decoupling the contribution to the signal on the actual streamlines. From the values reported in the two tables, we also notice how this bias reduces the contrast between the two bundles (1.07 for tractometry, 1.14 for MySD). This will become also evident on the in vivo results provided below.
Fig. 2.
Synthetic example showing the performance of our proposed method against the state-of-the-art tractometry technique. Starting from the left, in the top row we show the ground-truth bundle configuration, a table with the MWF of the two bundles and the corresponding MWF map. In the bottom row we present the representative streamlines reconstructed by tractography as well as the noiseless MWF map used for both tractometry and MySD approaches. The tables in the last column show that by averaging along the tracts we overestimate the MWF of both bundles, whereas by applying MySD we correctly decompose the MWF on each bundle.
2.2. MRI acquisition
Four healthy volunteers underwent MRI on a Siemens Prisma 3T whole-body scanner (Siemens Healthineers, Erlangen, Germany) with a 64-channel head coil for signal reception. The MRI protocol included the following sequences: sagittal T1-weighted 3D magnetization-prepared rapid gradient echo with two Turbo-FLASH GRE readouts between each inversion pulse (MP2RAGE) (Marques et al., 2010) (TR = 5000 ms, TI1 = 700 ms TI2 = 2500 ms, spatial resolution 1.0 ×1.0 ×1.0 mm3); fast acquisition with spiral trajectory and adiabatic T2prep (FAST-T2) (spiral repetition time/echo time = 7.5/0.5 ms, six T2prep times = 0 (T2prep turned off), 7.5, 17.5, 67.5, 147.5, 307.5 ms, spatial resolution 1.25 ×1.25 ×5 mm3, as described in (Nguyen et al., 2016)); three variants of a 3D FLASH (RF spoiled GRE) sequence were used with 1.33 mm3 isotropic resolution, matrix size 192 ×186 ×120, PPF = 6/8; SPF = 6/8, GRAPPA_R = 2 in each phase encoding direction: T1-weighted (TE = 4.92 ms, TR = 11 ms, alpha = 15°), Proton Density weighted (TE = 4.92 ms, TR = 25 ms, alpha = 5°), MT-weighted (TE = 4.92 ms, TR = 25 ms, alpha = 5°, Gaussian MT pulse Delta_f = 2.2KHz as in (Helms et al., 2008)); B1 maps to correct for effects of radio frequency transmit inhomogeneities on the quantitative maps were acquired employing the steady state free precession based B1-TRAP approach (Ganter et al., 2013); twice-refocused spin echo EPI sequence for dMRI with a total of 137 directions subdivided in 4 shells with 6/20/45/66 measurements for b-value = 700/1000/2000/3000 s/mm2 and 12 for b = 0 s/mm2 (TR/TE:4500/75 ms, spatial resolution 1.8 ×1.8 ×1.8 mm3). In addition, 12 non-diffusion-weighted images corresponding to b = 0 s/mm2 were acquired with reversed phase-encode blips, resulting in pairs of images with distortions in opposite directions. The study was approved by the local Ethics Committee of Basel University Hospital. All subjects gave written consent prior to enrollment.
2.3. MRI processing
dMRI images were pre-processed to remove noise (Veraart and Novikov, 2016; Veraart et al., 2016), eddy currents (Andersson and Sotiropoulos 2016; Andersson et al., 2016), motion and EPI distortion artefacts (Andersson et al., 2003; Smith et al., 2004) using MRtrix3 (Tournier et al., 2019) and FSL (https://fsl.fmrib.ox.ac.uk). Then, we performed B1 field inhomogeneity correction using the N4 bias field correction algorithm in the ANTs software package (Tustison et al., 2010) of MRtrix3 (Tournier et al., 2019).
After the pre-processing steps, dMRI images were upsampled to match the resolution of the MP2RAGE images to improve the ability of the streamlines to reach the cortex. MP2RAGE images were processed using FreeSurfer (http://surfer.nmr.mgh.harvard.edu) to obtain subject specific gray matter parcellations in 84 regions of interest (ROIs) according to the standard Desikan-Killiany atlas (Desikan et al., 2006). To improve the connectome creation and consider also the bundles going down to the spinal column, we also subdivided the brainstem into four subregions using (Iglesias et al., 2015) and we added the medulla to our collection of ROIs defining the connectome’s nodes. We then registered the MP2RAGE images and the corresponding parcellations on dMRIs using FLIRT (Jenkinson et al., 2002) with boundary-based optimization (Greve and Fischl, 2009). Tractography was performed using MRtrix3 (Tournier et al., 2019). We first performed multi-shell multi-tissue constrained spherical deconvolution (Jeurissen et al., 2014) and then, with the recovered fiber orientation distributions, we performed whole brain deterministic tractography using the SD_STREAM algorithm (Tournier et al., 2012) by seeding in the white matter voxels and imposing the maximum length equal to 250 mm, the minimum length 20 mm, the maximum angle between successive steps 60° and the step size 0.25 mm. For each subject, we generated 3-million streamlines and, using the 85 ROIs of the co-registered parcellation, we subsequently filtered out possible streamlines not reaching the gray matter. This is a crucial step to be done when using microstructure informed tractography methods as discussed in (Zalesky et al., 2020). In our data, each tractogram eventually consisted of about 2′825’264 ± 24′471 connecting streamlines.
Myelin water fraction (MWF) maps were reconstructed by fitting the T2 decay of the assumed three water components with the constraint of spatially local smoothness on the six echoes in FAST-T2 as done in (Nguyen et al., 2016). Maps of MTsat were computed according to (Helms et al., 2008) using the hMRI toolbox (Tabelow et al., 2019). Maps of myelin volume fraction (MVF) were then computed by calibrating the MTsat using a scaling factor, as described in (Mohammadi et al., 2015). Both these myelin maps were also co-registered to the up-sampled dM-RIs space using linear registration with boundary-based optimization (Greve and Fischl 2009) and visually inspected to guarantee a good matching also in regions that were highly affected by EPI induced distortions before the dMRI pre-processing.
2.4. Estimation of bundle-specific myelin content
After the application of MySD to decompose the myelin effective cross-sectional area on each streamline, those with zero contribution were discarded and those remaining were grouped in bundles according to the pair of cortical regions they connected. To estimate the resulting total myelin content of a bundle, we summed the contributions assigned by MySD to the streamlines belonging to that bundle. Specifically, to obtain the total myelin water or volume associated with each streamline (using either MWF or MVF as input map in MySD), we multiplied its length by the effective cross-sectional area estimated with MySD, similarly to what was proposed in (Schiavi et al., 2020). Then, to obtain the Bundle Myelin (BM) we summed up the values of all the streamlines connecting the same two ROIs multiplied by the volume of a voxel, i.e., for each bundle
where Nstreamlines is the number of streamlines composing that bundle, xi is the effective cross sectional myelin associated by MySD to streamline i, li is the length of streamline i and Vvoxel is the volume of a voxel (i.e. the resolution of the myelin sensitive map). However, to report values comparable to those of the voxel-wise maps (which represent the amount of water or volume associated to myelin within each voxel), we divided the obtained BM by the volume of voxels crossed by that bundle, obtaining the Bundle Myelin Fraction (BMF):
which simplifies to
where Nvoxels is the number of voxels crossed by that bundle. This measure can be obtained using either MWF or MVF as the input map in MySD and reflects the myelin water or volume fraction associated to the bundle.
We compared our proposed method to the “tractometry” approach (Bells et al., 2011; Yeatman et al., 2012), as it represents the state-of-the-art and is widely used in the field.
2.5. Myelin projection on cortex
To indirectly validate our procedure, and under the assumption that at the available MRI resolution all the axons represented by the streamlines maintain their total myelin fraction also when entering the cortex, we projected both MySD and tractometry derived values on the inflated cortical ribbon both MySD and tractometry values and compared the results with the existing literature. Finally, to compare the results at the level of different cortical ROIs and verify the agreement with anatomy, we used the streamline effective cross-sectional area estimated with MySD and the streamline values assigned by tractometry to compute the total myelin content of the projection fibers of each cortical region as estimated by both methods. Practically, for each of the 85 ROIs of the Desikan-Killany atlas, we summed all the contributions of the afferent and efferent streamlines (whose direction is indistinguishable using only dMRI and myelin data). Moreover, to avoid biases caused by the ROI extension, we normalized by the cortical region volume (i.e., to prevent that bigger regions reached by more bundles get a larger final myelin content than regions reached by fewer bundles). The results obtained by the cortical projections allow us to verify that the values we decompose on the streamlines using only WM voxels are in agreement with what is expected to be measured in the cortex.
2.6. In vivo MySD pipeline
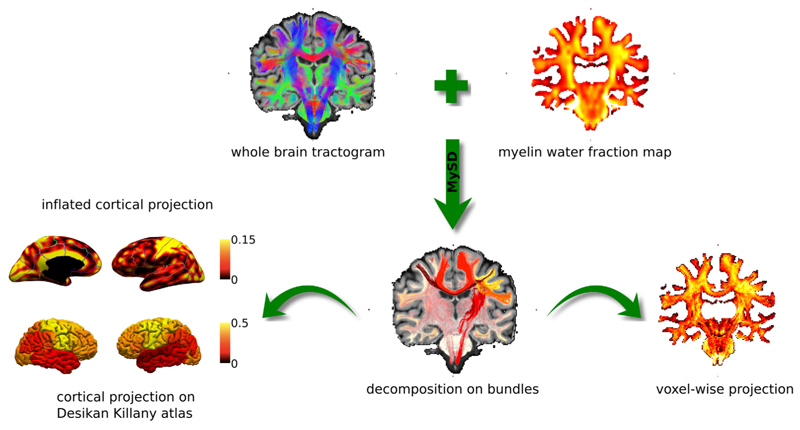
Fig. 3 illustrates the strategy to evaluate the bundle-specific myelin content estimated with our method. Starting from a whole brain tractogram and a voxel-wise myelin-sensitive map, MySD decomposes the actual myelin content on individual streamlines allowing us to estimate the myelination of separate bundles. From this decomposition, as already demonstrated in the original COMMIT framework (Daducci et al., 2015), we can reconstruct the voxel-wise map corresponding to these estimated individual values and compare it to the maps measured with MRI to evaluate the quality of the fit (on the right), as well as project the values of each streamline on the inflated cortex and compute the total amount of myelin reaching distinct cortical regions (on the left).
Fig. 3.
Evaluation of the bundle-specific myelin content estimated with our approach. After performing whole brain tractography and estimating voxel-wise myelin-sensitive maps from MRI, we estimate the bundle-specific myelin content of different bundles using MySD. Using these estimates, we can either compute the inflated cortical projection as well as the cortical projection subdivided according the Desikan-Killany atlas (left) as well as reproject back voxel-wise values and compare with the acquired myelin map. Color bars are without units because they refer to fractions of myelin.
3. Results
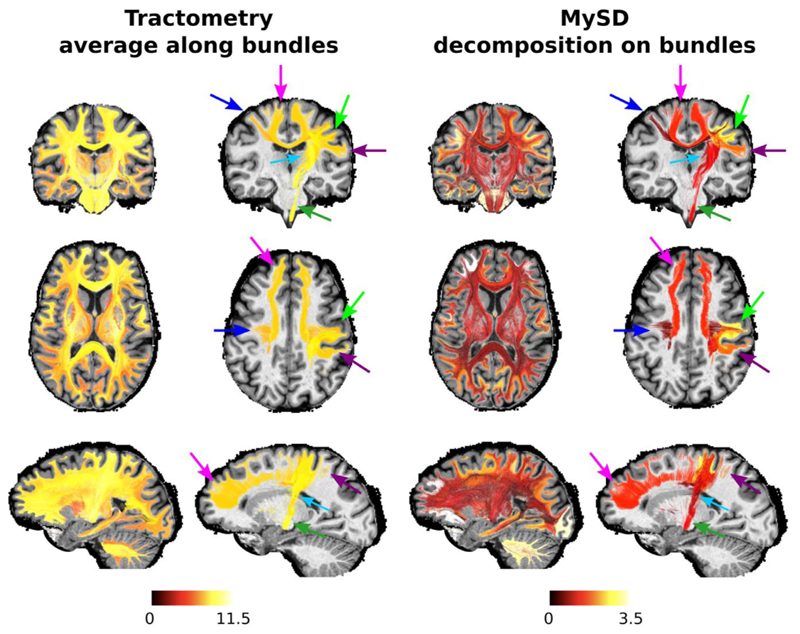
Fig. 4 reports the myelin content of bundles as estimated with tractometry and our approach. As already shown for the toy example in Fig. 2, while tractometry produces estimates with very little contrast between bundles, with our approach we can distinguish bundles with different myelin content. We also show a few selected bundles, which belong to the left motor network, to have a more direct comparison. In agreement with indirect information from the literature, we found that the myelin content associated by MySD results in higher myelination of the bundles connecting the left and right precentral gyri (PrCG) and PrCG with the medulla (blue and dark green arrows in Fig. 4) than those that connect the PrCG with the subcortical nuclei (thalamus, caudate, putamen - light blue arrow in Fig. 4) (Kimura and Itami 2009). We also show that the interhemispheric bundle to which MySD assigned the highest BMF coincides with the anterior frontal bundle (magenta arrow in Fig. 4). Interestingly, this bundle was already reported as one of the more myelinated in (Stikov et al., 2011). The differences in values obtained by tractometry and MySD are clear in the image. As highlighted in the toy example in Fig. 2, whenever tractometry computes an average using the value of a voxel with more than one bundle interdigitating in it, the result will be an overestimation of the actual myelin water fraction of the bundle. In particular, since the values of the MWF map are rather flat while spanning from 0 to ∼20, on average all the bundles get a value between 9 and 11. On the contrary, the BMF assigned by MySD is lower than the values in the voxels, because it comes from the decomposition of those values on each streamline.
Fig. 4.
Comparison of the myelin water fraction of separate bundles as estimated with tractometry (left) and MySD (right) from MWF maps. Results are shown for the whole brain as well as for selected bundles of the left motor network: homologues pre-central gyri (blue arrow), right pre-central gyrus with itself (light green arrow), right pre-central gyrus – right post-central gyrus (purple arrow), right pre-central gyrus – medulla (dark green arrow), right pre-central gyrus – right thalamus (light blue arrow), right pre-central gyrus – right caudate (light blue arrow), right pre-central gyrus – right putamen (light blue arrow) and anterior frontal bundle (magenta arrow). In both cases, MySD results show more contrast between different bundles than tractometry. Moreover, in agreement with the previous works, our decomposition approach found higher myelination of the bundles connecting the left and right precentral gyri and precentral gyrus with the medulla than those that connect the precentral gyrus with the subcortical nuclei. Since MWF maps contained% values, measures on tracts are also reported in%. Color bars are then without units of measure.
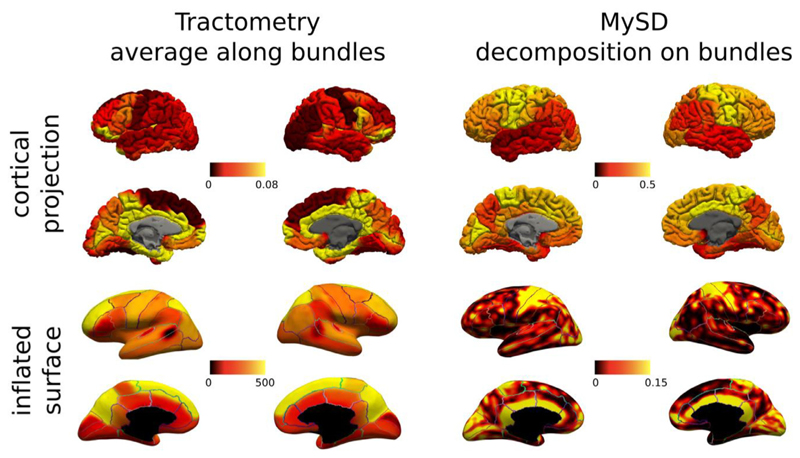
As indirect validation on the anatomy of the same subject, Fig. 5 reports the cortical (subdivided in regions according to the Desikan-Killany atlas) and inflated (smoothed values of each streamline with ending points in the same cortical voxel) projections obtained with MySD and tractometry. We can appreciate that MySD values are in very good agreement with those reported in previous histological (Nieuwenhuys and Broere 2017) and imaging studies (Lutti et al., 2014; Marques et al., 2017; Sereno et al., 2013), which show higher intra-cortical myelin content in primary motor, sensory, visual and auditory areas in comparison to other cortical brain regions (Nieuwenhuys and Broere 2017). On the inflated surfaces, high levels of myelination in the dorsal temporal regions are also evident, as previously reported in myeloarchitectonic studies (Nieuwenhuys and Broere 2017). Thus, based on the fact that the intra-cortical myelination is highly influenced by the myelin content of afferent and efferent axons in that area (Turner 2019), these results show that MySD are in line with the values already measured in literature.
Fig. 5.
Cortical and inflated projections obtained for the same subject using MWF maps coupled with tractometry (left) and MySD (right). To enable the visual comparison between different cortical areas on the inflated surfaces, we overlayed also the boundaries of Desikan-Killiany parcellation. The contrast obtained with MySD is in line with the known pattern of myelin in cortex, while tractometry, because of its assumptions, cannot reproduce the expected behavior. We also note that the color bars of cortical projections and inflated surfaces are different because, while cortical projections were computed by summing up all the contributions of streamlines starting/ending in those ROIs and dividing by the ROI volume (connectivity-like approach), the inflated surfaces were created by summing up all the values of streamlines ending in the same voxel and using 5 mm smoothing (voxel-based approach). Color bars are without units because they refer to fractions of myelin.
In contrast, results obtained with tractometry do not correspond well with the current histological knowledge about cortical myelination characteristics: indeed, this approach recovers higher values in the frontal poles than in the primary motor cortex. The fact that the higher values are located at terminations of fibers passing through the corpus callosum, seems to suggest that this wrong behavior is due to the overestimation of the value of each streamline as the consequence of assigning the same value to streamlines crossing in the same voxel. Thus, termination areas like the frontal lobes that are reached by bundles crossing a lot with others, result in being more myelinated by tractometry.
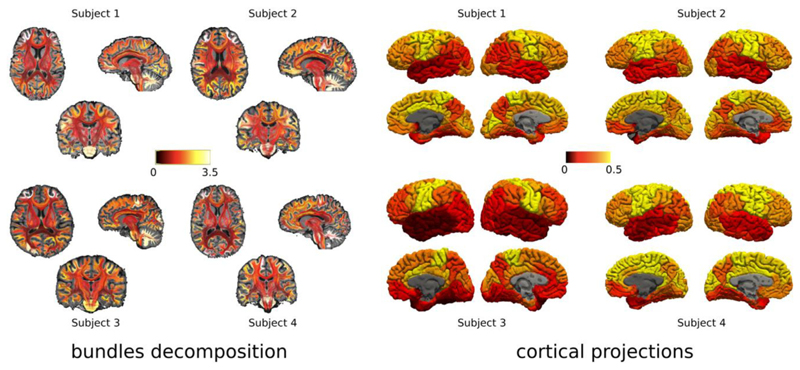
Fig. 6 reports the consistency of the results obtained with our approach across the four volunteer participants using MWF maps. We observe that the contrast between bundles and projections on the cortical regions obtained by using MySD and MWF maps are very similar across all the subjects. Indeed, the overall pattern is the same with the same bundles (on the right) and cortical areas (on the left) appearing to be more highly myelinated than others. However, in both bundles’ decompositions and cortical projections, we can clearly see that the values are not exactly the same across the subjects which is in agreement with the natural inter-subject structural variability. This confirms the stability of the proposed method, and the same results hold also for MVF (not shown here).
Fig. 6.
Consistency of our method across the four different subjects who were scanned with the same acquisition protocol. For each subject, on the left we show the bundles color-coded by the obtained bundle myelin fraction obtained from MySD, while on the right we present the corresponding cortical projection. In both cases the contrast between different bundles and cortical regions obtained using the MySD approach on MWF maps are highly consistent across all the subjects with local differences comparable with intrinsic differences in MWF values in the white matter of each subject. Color bars are without units because they refer to fractions of myelin and we used the same interval of values for all the subjects.
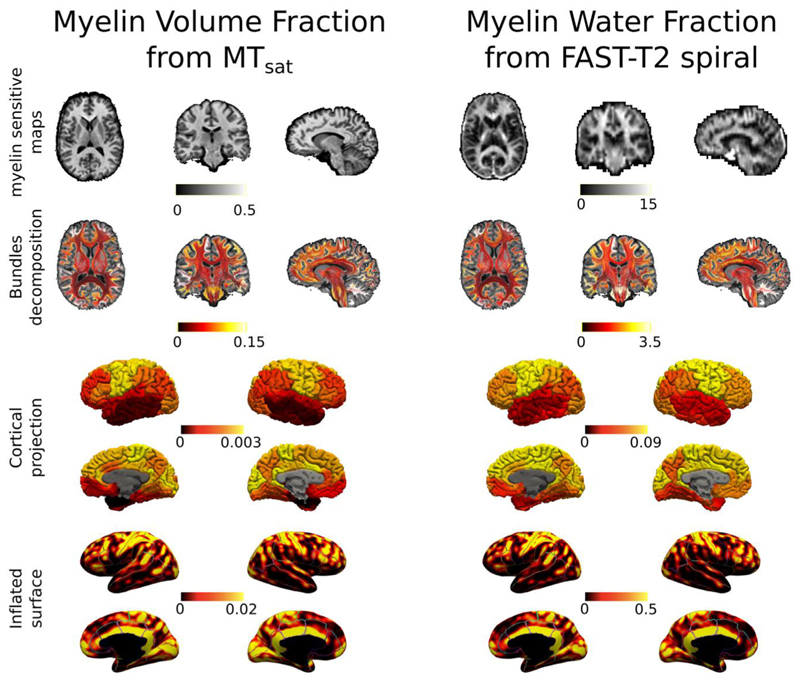
Fig. 7 shows axial, coronal and sagittal views of the streamlines color-coded with the myelin content of the bundle they are in as well as their cortical and inflated projections recovered on the same subject from both MWF and MVF. Although the two microstructural maps are sensitive to different aspects of myelin (Mancini et al., 2020; Lazari and Lipp 2021), we observe similar patterns in myelin related values for bundle specific, cortical and inflated projections found with MySD using the same tractogram but fitting to the two different maps. For the same subject used in Fig. 7, inflated projection maps of the input MVF and MWF are reported in supplementary data.
Fig. 7.
Same subject different myelin maps. On the left, axial, coronal, and sagittal views of myelin-sensitive map, bundles color-coded by their BMF as well as cortical and inflated projections obtained with the proposed method on the tractogram and the MVF map estimated from the MTsat acquisition. On the right, axial, coronal, and sagittal views of myelin-sensitive map, bundles color-coded by their BMF as well as cortical and inflated projections obtained with the proposed method on the tractogram and the MWF map estimated from the FAST-T2 spiral acquisition. To facilitate the visual comparison between different cortical areas on the inflated surfaces, we also overlaid the boundaries of Desikan-Killiany parcellation. Color bars are without units because they refer to fractions of myelin (between 0 and 1 for MVF and between 0 and 100 for MWF).
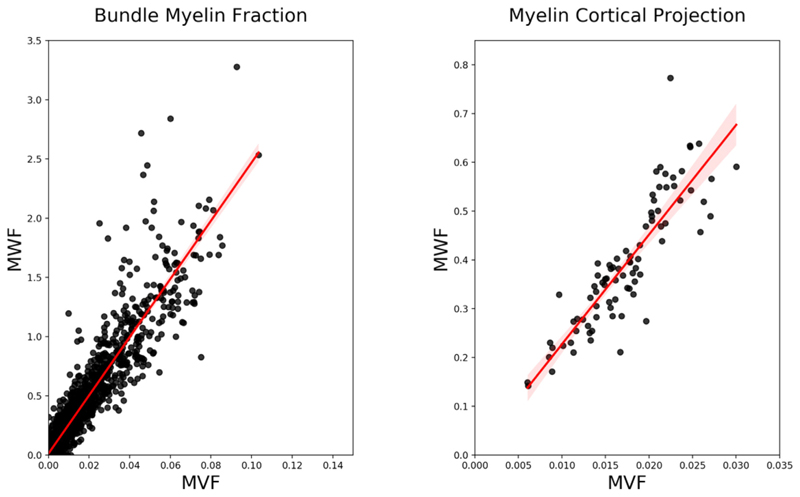
Lastly, in Fig. 8 we show the correlation between the values obtained with MySD applied on MWF and MVF maps. We see very high correlation for both bundle myelin fraction on the left (R2 = 0.94, p<0.001) and streamline cross-sectional areas projected on cortex on the right (R2 =0.87, p <0.001).
Fig. 8.
Correlations between bundles (defined as connections between cortical ROIs thus resulting in (85 × 85–85)/2 points) and cortical projections values (84 points) derived with MySD applied on MWF and MVF maps of one subject in our dataset. The linear fit is showed in red with shadowed 95% confidence interval.
4. Discussion
Over the last decades tractography has been widely used to study the neuronal architecture of healthy and pathological brains. Structural connectomic analyses use tractography results to construct a graph, whose edges (i.e., connections between cortical regions or nodes) are weighted according to some metrics, the most common being the number of streamlines passing between a pair of nodes. Recent works, however, questioned the typical way of weighting white matter connections using the streamlines count (Jones et al., 2013; Yeh et al., 2020; Zhang et al., 2021). To define more quantitative edge-weights for the structural connectome, “tractometry” was introduced in (Bells et al., 2011) and successfully employed to study brain development, anatomy and pathology (Yeh et al., 2020; Zhang et al., 2021; Yeatman et al., 2014). This involves mapping microstructural measures along the tractography-reconstructed pathways and averaging their values for quantitative comparisons between metrics. However, tractometry does not provide the actual myelination of individual bundles. Indeed, when multiple bundles pass through the same voxel, results obtained with tractometry are biased (as shown in Fig. 2) since it is not possible to disentangle the individual contribution of each bundle to the average (Daducci et al., 2016).
In this study, we have introduced myelin streamline decomposition (MySD), a new method extending COMMIT (Daducci et al., 2013; 2015), which allows the decoupling of the individual myelin content of separate bundles. Comparing this method with tractometry, we obtained bundle-specific myelin contents that are consistent with the known underlying connectivity anatomy. Indeed, MySD revealed higher myelination in the bundles connecting the left and right precentral gyri (primary motor cortex) through the corpus callosum and the precentral gyrus with the medulla (projecting fibers of the cortico-spinal tract) when compared to the myelin content of the bundles connecting the precentral gyrus with subcortical gray matter nuclei (Kimura and Itami 2009).
The obtained results not only provide the unique opportunity to understand the structure – and eventually the structural-function relationship (Drakesmith et al., 2019) – of brain connections, but also open new perspectives for the investigation of developmental trajectories in health and disease, aging and pathological processes affecting specific brain bundles or connections. The proposed MySD appeared to be consistent when using different myelin sensitive measures, such as MWF from FAST-T2spiral acquisition and MVF from MTsat, in leading to very similar quantifications of bundle-related myelin content. A deeper investigation to properly characterize discrepancies and similarities between the two maps and which one is the most appropriate to study bundle-wise differences in myelin content will be a subject of future studies (Mancini et al., 2020; Lazari and Lipp 2021). Furthermore, the potential of MySD to generate voxel-wise fiber specific myelin measure by reprojecting back the myelin content to each segment of the streamlines in a voxel might be exploited also to perform fixel-based analysis studies (Raffelt et al., 2015). Indeed, although to date all fixel-based analysis studies have only been limited to the apparent fiber density measure, a recent work has described how this framework can work with any fiber-specific measure and coupling it with MySD estimates might provide interesting insight on clinical studies (Dhollander et al., 2021).
This study has some limitations. First, we decided to employ a deterministic tracking algorithm to avoid the presence of a high number of false positive connections that could bias the results (Sarwar et al., 2019). Although this is a widely accepted option in the field, some bundles might have been underrepresented in our data. A possibility for future studies could be to investigate the performance of the recently proposed COMMIT2 approach (Schiavi et al., 2020; Ocampo-Pineda et al., 2021) coupled with the myelin-specific approach introduced here. COMMIT2 allows introducing the possibility of considering the notion that fibers are naturally organized in bundles, and then performs the fitting by organizing the input streamlines into groups to achieve superior filtering performances. The same method could be also used to merge quantitative measures coming from different modalities (e.g., bundle myelin fraction, bundle-specific axon diameter index (Barakovic et al., 2021a), bundle-specific intra-axonal T2 (Barakovic et al., 2021b), Tax et al., 2021), etc.) and simultaneously recover all the microstructural properties attached to each bundle. We speculate that the bundle estimation of all these quantities might provide a more stable estimation of bundle-wise g-ratio and conduction velocity (Drakesmith et al., 2019; Campbell et al., 2018). Second, we recognized that because there is very little evidence on the differential myelination of different white matter tract, the validation we performed is at the level of agreement with previous literature on cortical rather than white matter myelination. Apart from the biological relevance, this validation procedure might be affected by the well-known technical issue in tractography of gyral bias (Schilling et al., 2018). To mitigate this, an extensive quality check was performed on the reconstructed tractograms. Moreover, because MySD is a fitting procedure, by smoothing the values associated at the end points of the streamlines to project them to the surface, this potential bias is reduced compared to techniques that use only the streamline count at each position on the cortex. However, for applications to clinical studies we suggest that particular care is taken when performing cortical projection and methods like seeding at the gray/white matter interface (Smith et al., 2012), surface-enhanced tractography (St-Onge et al., 2018) or asymmetric fiber orientation distributions (Wu et al., 2020) should be considered. Another key assumption in our formulation is that, at the current resolution of MRI-derived maps and recalling that streamlines do not represent single axons, the myelin content of every streamline remains constant along its path. We highlight that this assumption is not in contradiction with what was recently shown in (Lee et al., 2019, 2020), however this effect happens at a resolution that is not detectable with our acquisitions and this is why we always refer to “a group of axons sharing the same trajectory”, rather than single axons. On the other hand, while this assumption might remain reasonable in the case of pathology that affects more or less the entire trajectory of certain tracts, it might not hold in the case of neurological pathologies localized along the bundles. To account for that it might be beneficial to couple the myelin estimation with dMRI derived properties (which have been proved to be stable in case of multiple sclerosis (Schiavi et al., 2020)). Another possibility might be to add a supplementary term in the streamline forward model to account for possible smooth variations of the myelin content along the tracts. Future work will be dedicated to investigating the behavior of MySD in presence of pathologies.
5. Conclusions
For the first time we were able to assess the intrinsic myelin content of distinct bundles within a voxel by extending the microstructure informed tractography formulation to consider myelin-sensitive maps. This proof of concept opens the possibilities for in vivo investigations of the myelination of neuronal pathways that, to date, were partially possible only partially postmortem.
Supplementary Material
Acknowledgments
This work was supported by the Rita Levi Montalcini Programme for young researchers of the Italian Ministry of Education, University and Research (MIUR). This work was funded by the Swiss National Funds PZ00P3_154508, PZ00P3_131914 and PP00P3_176984, the Stiftung zur Förderung der gastroenterologischen und allgemeinen klinischen Forschung and the EUROSTAR E!113682 HORIZON2020, Wellcome Trust Investigator Award (096646/Z/11/Z) and Wellcome Trust Strategic Award (104943/Z/14/Z). This work was supported by the Swiss National Science Foundation (grant no 320030_184784 (AL)) and the ROGER DE SPOELBERCH Foundation. For the purpose of open access, the author has applied a CC-BY public copyright license to any author accepted manuscript version arising from this submission.
Footnotes
Credit authorship contribution statement
Simona Schiavi: Conceptualization, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. Po-Jui Lu: Formal analysis, Writing – review & editing. Matthias Weigel: Data curation, Writing – review & editing. Antoine Lutti: Project administration, Writing – review & editing. Derek K. Jones: Conceptualization, Validation, Writing – review & editing. Ludwig Kappos: Supervision, Funding acquisition, Writing – review & editing. Cristina Granziera: Conceptualization, Validation, Supervision, Funding acquisition, Writing – original draft, Writing – review & editing. Alessandro Daducci: Conceptualization, Methodology, Software, Validation, Supervision, Funding acquisition, Writing – original draft, Writing – review & editing.
Declarations of Competing Interest
None.
Code and data availability
The in vivo MRI data used were acquired at University Hospital Basel and are available upon reasonable request. The code is open source and freely available at https://github.com/daducci/COMMIT.
Data and code availability statement
The brain MR data was obtained from the University Hospital of Basel and are available from the corresponding author upon reasonable request.
The code is open source and freely-available at https://github.com/daducci/COMMIT.
References
- Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016 January;125:1063–1078. doi: 10.1016/J.NEUROIMAGE.2015.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Graham MS, Zsoldos E, Sotiropoulos SN. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage. 2016;141:556–572. doi: 10.1016/j.neuroimage.2016.06.058. [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20(2):870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- Barakovic M, Girard G, Schiavi S, Romascano D, Descoteaux M, Granziera C, Jones DK, Innocenti GM, Thiran JP, Daducci A. Bundle-specific axon diameter index as a new contrast to differentiate white matter tracts. Front Neurosci. 2021a;15:687. doi: 10.3389/fnins.2021.646034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barakovic M, Tax CMW, Rudrapatna U, Chamberland M, Rafael-Patino J, Granziera C, Thiran JP, Daducci A, Canales-Rodríguez EJ, Jones DK. Resolving bundle-specific intra-axonal T2 values within a voxel using diffusion-relaxation tract-based estimation. NeuroImage. 2021b;227:117617. doi: 10.1016/j.neuroimage.2020.117617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum GL, Cui Z, Roalf DR, Ciric R, Betzel RF, Larsen B, Cieslak M, et al. Development of structure-function coupling in human brain networks during youth. Proceedings of the National Academy of Sciences of the United States of America. 2020 doi: 10.1073/pnas.1912034117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumeister TR, Kolind SH, MacKay AL, McKeown MJ. Inherent spatial structure in myelin water fraction maps. Magn Reson Imaging. 2020;67:33–42. doi: 10.1016/j.mri.2019.09.012. [DOI] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. 2002;15(7-8):435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Bells S, Cercignani M, Deoni S, Assaf Y, Pasternak O, Evans CJ, Leemans A, Jones DK. Tractometry-comprehensive multi-modal quantitative assessment of white matter along specific tracts; Proceedings of the ISMRM; 2011. p. 1. [Google Scholar]
- Boshkovski T, Kocarev L, Cohen-Adad J, Mišić B, Lehéricy S, Stikov N, Mancini M. The R1-weighted connectome: complementing brain networks with a myelin-sensitive measure. Netw Neurosci. 2020:1–34. doi: 10.1101/2020.08.06.237941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell JSW, Leppert IR, Narayanan S, Boudreau M, Duval T, Cohen-Adad J, Bruce Pike G, Stikov N. Promise and pitfalls of G-ratio estimation with MRI. NeuroImage. 2018 November;182:80–96. doi: 10.1016/j.neuroimage.2017.08.038. [DOI] [PubMed] [Google Scholar]
- Chu SH, Parhi KK, Lenglet C. Function-specific and enhanced brain structural connectivity mapping via joint modeling of diffusion and functional MRI. Sci Rep. 2018 doi: 10.1038/s41598-018-23051-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daducci A, Palu AD, Lemkaddem A, Thiran JP. A convex optimization framework for global tractography; Proceedings of the International Symposium on Biomedical Imaging; 2013. [DOI] [Google Scholar]
- Daducci A, Palù AD, Lemkaddem A, Thiran JP. COMMIT: convex optimization modeling for microstructure informed tractography. IEEE Trans Med Imaging. 2015 doi: 10.1109/TMI.2014.2352414. [DOI] [PubMed] [Google Scholar]
- Daducci A, Dal Palú A, Descoteaux M, Thiran JP. Microstructure informed tractography: pitfalls and open challenges. Front Neurosci. 2016 doi: 10.3389/fnins.2016.00247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deoni SCL, Rutt BK, Arun T, Pierpaoli C, Jones DK. Gleaning multicomponent T1 and T2 information from steady-state imaging data. Magn Reson Med. 2008;60(6):1372–1387. doi: 10.1002/mrm.21704. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006;31(3):968–980. doi: 10.1016/J.NEUROIMAGE.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Dhollander T, Clemente A, Singh M, Boonstra F, Civier O, Dominguez Duque J, Egorova N, et al. Fixel-based analysis of diffusion mri: methods, applications, challenges and opportunities. NeuroImage. 2021 doi: 10.1016/j.neuroimage.2021.118417. [DOI] [PubMed] [Google Scholar]
- Dousset V, Brochet B, Vital A, Gross C, Benazzouz A, Boullerne A, Bidabe AM, Gin AM, Caille JM. Lysolecithin-induced demyelination in primates: preliminary in vivo study with MR and magnetization transfer. AJNR Am J Neuroradiol. 1995;16(2):225–231. [PMC free article] [PubMed] [Google Scholar]
- Drakesmith M, Harms R, Rudrapatna SU, Parker GD, John Evans C, Jones DK. Estimating axon conduction velocity in vivo from microstructural MRI. NeuroImage. 2019;203:116–186. doi: 10.1016/j.neuroimage.2019.116186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Essen DCV. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Ganter C, Settles M, Dregely I, Santini F, Scheffler K, Bieri O. B+-Mapping with the transient phase of unbalanced steady-state free precession. Magn Reson Med. 2013;70(6):1515–1523. doi: 10.1002/mrm.24598. [DOI] [PubMed] [Google Scholar]
- Goldman L, Albus JS. Computation of impulse conduction in myelinated fibers; theoretical basis of the velocity-diameter relation. Biophys J. 1968;8(5):596–607. doi: 10.1016/S0006-3495(68)86510-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. NeuroImage. 2009;48(1):63–72. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heath F, Hurley SA, Johansen-Berg H, Sampaio-Baptista C. Advances in non-invasive myelin imaging. Dev Neurobiol. 2018;78(2):136–151. doi: 10.1002/dneu.22552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helms G, Weiskopf N, Lutti A. Correction of FLASH-Based MT Saturation in Human Brain for Residual Bias of B1-Inhomogeneity At 3T. 2019 Submitted to MRM. [Google Scholar]
- Helms G, Dathe H, Kallenberg K, Dechent P. High-resolution maps of magnetization transfer with inherent correction for RF inhomogeneity and T1 relaxation obtained from 3D FLASH MRI. Magn Reson Med. 2008;60(6):1396–1407. doi: 10.1002/mrm.21732. [DOI] [PubMed] [Google Scholar]
- Helms G, Dathe H, Kallenberg K, Dechent P. Erratum: helms, dathe, kallenberg and dechent, high-resolution maps of magnetization transfer with inherent correction for Rf Inhomogeneity and T 1 relaxation obtained from 3D FLASH MRI (Magnetic Resonance in Medicine (2008) 60:6 (1396-1407)) Magn Reson Med. 2010 doi: 10.1002/mrm.22607. [DOI] [PubMed] [Google Scholar]
- Iglesias JE, Leemput KV, Bhatt P, Casillas C, Dutt S, Schuff N, Truran-Sacrey D, Boxer A, Fischl B. Bayesian segmentation of brainstem structures in MRI. NeuroImage. 2015;113:184–195. doi: 10.1016/j.neuroimage.2015.02.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, Zurek M, Winters KV, Veraart J, Rajaratnam A, Kim NS, Babb JS, et al. In vivo quantification of demyelination and recovery using compartment-specific diffusion MRI metrics validated by electron microscopy. NeuroImage. 2016 doi: 10.1016/j.neuroimage.2016.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, Budde MD. Design and validation of diffusion MRI models of white matter. Front Phys. 2017;5:61. doi: 10.3389/fphy.2017.00061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17(2):825–841. doi: 10.1006/nimg.2002.1132. [DOI] [PubMed] [Google Scholar]
- Jeurissen B, Leemans A, Tournier J-D, Jones DK, Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp. 2013;34(11):2747–2766. doi: 10.1002/hbm.22099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeurissen B, Tournier J-D, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage. 2014;103:411–426. doi: 10.1016/j.neuroimage.2014.07.061. [DOI] [PubMed] [Google Scholar]
- Jones DK, Deoni SCL. Visualization of absolute T1 and T2 along specific white matter tracts; Proceedings of the International Society for Magnetic Resonance in Medicine; 2006. p. 2774. [Google Scholar]
- Jones DK, Knösche TR, Turner R. White matter integrity, fiber count, and other fallacies: the do’s and don’ts of diffusion MRI. NeuroImage. 2013 doi: 10.1016/j.neuroimage.2012.06.081. [DOI] [PubMed] [Google Scholar]
- Kimura F, Itami C. Myelination and isochronicity in neural networks. Front Neuroanat. 2009;3:12. doi: 10.3389/neuro.05.012.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinney HC, Volpe JJ. Volpe’s Neurology of the Newborn e-Book. Elsevier Health Sciences; 2017. Myelination Events; pp. 176–188. [Google Scholar]
- Kucharczyk W, Macdonald PM, Stanisz GJ, Henkelman RM. Relaxivity and magnetization transfer of white matter lipids at MR imaging: importance of cerebrosides and PH. Radiology. 1994;192(2):521–529. doi: 10.1148/radiology.192.2.8029426. [DOI] [PubMed] [Google Scholar]
- Lazari A, Lipp I. Can MRI measure myelin? Systematic review, qualitative assessment, and meta-analysis of studies validating microstructural imaging with myelin histology. NeuroImage. 2021;230:117744. doi: 10.1016/j.neuroimage.2021.117744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HH, Jespersen SN, Fieremans E, Novikov DS. The impact of realistic axonal shape on axon diameter estimation using diffusion MRI. NeuroImage. 2020 doi: 10.1016/j.neuroimage.2020.117228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HH, Yaros K, Veraart J, Pathan JL, Liang FX, Kim SG, Novikov DS, Fieremans E. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Struct Funct. 2019 doi: 10.1007/s00429-019-01844-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipp I, Jones DK, Bells S, Sgarlata E, Foster C, Stickland R, Davidson AE, et al. Comparing MRI metrics to quantify white matter microstructural damage in multiple sclerosis. Hum Brain Mapp. 2019;40(10):2917–2932. doi: 10.1002/hbm.24568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lutti A, Dick F, Sereno MI, Weiskopf N. Using high-resolution quantitative mapping of R1 as an index of cortical myelination. NeuroImage. 2014;93:176–188. doi: 10.1016/j.neuroimage.2013.06.005. [DOI] [PubMed] [Google Scholar]
- Mackay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. 1994;31(6):673–677. doi: 10.1002/mrm.1910310614. [DOI] [PubMed] [Google Scholar]
- Mancini M, Karakuzu A, Cohen-Adad J, Cercignani M, Nichols TE, Stikov N, Jbabdi S, Baker CI, Jbabdi S, Does M. An Interactive Meta-Analysis of MRI Biomarkers of Myelin. ELife. 2020:e61523. doi: 10.7554/eLife.61523. Edited by 9 (October) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques JP, Kober T, Krueger G, Zwaag W, Moortele PFV, Gruetter R. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. NeuroImage. 2010 doi: 10.1016/j.neuroimage.2009.10.002. [DOI] [PubMed] [Google Scholar]
- Marques JP, Khabipova D, Gruetter R. Studying Cyto and myeloarchitecture of the human cortex at ultra-high field with quantitative imaging: R1, R2* and magnetic susceptibility. NeuroImage. 2017;147:152–163. doi: 10.1016/j.neuroimage.2016.12.009. [DOI] [PubMed] [Google Scholar]
- Mesulam MM. From sensation to cognition. Brain. 1998;121(6):1013–1052. doi: 10.1093/brain/121.6.1013. [DOI] [PubMed] [Google Scholar]
- Mohammadi S, Carey D, Dick F, Diedrichsen J, Sereno MI, Reisert M, Callaghan MF, Weiskopf N. Whole-brain in-vivo measurements of the axonal G-Ratio in a group of 37 healthy volunteers. Front Neurosci. 2015;9:441. doi: 10.3389/fnins.2015.00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen TD, Deh K, Monohan E, Pandya S, Spincemaille P, Raj A, Wang Yi, Gauthier SA. Feasibility and reproducibility of whole brain myelin water mapping in 4 Min using fast acquisition with spiral trajectory and adiabatic T2prep (FAST-T2) at 3T. Magn Reson Med. 2016;76(2):456–465. doi: 10.1002/mrm.25877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuys R, Broere CAJ. A map of the human Neocortex showing the estimated overall myelin content of the individual architectonic areas based on the studies of Adolf Hopf. Brain Struct Funct. 2017 doi: 10.1007/s00429-016-1228-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ocampo-Pineda M, Schiavi S, Rheault F, Girard G, Petit L, Descoteaux M, Da-ducci A. Hierarchical microstructure informed tractography. Brain Connect. 2021 doi: 10.1089/brain.2020.0907. [DOI] [PubMed] [Google Scholar]
- Piredda GF, Hilbert T, Canales-Rodríguez EJ, Pizzolato M, Deuster C, Meuli R, Pfeuffer J, Daducci A, Thiran J-PP, Kober T. Fast and high-resolution myelin water imaging: accelerating multi-echo GRASE with CAIPIRINHA. Magn Reson Med. 2020 doi: 10.1002/mrm.28427. n/a(n/a) [DOI] [PubMed] [Google Scholar]
- Raffelt DA, Smith RE, Ridgway GR, Tournier JD, Vaughan DN, Rose S, Henderson R, Connelly A. Connectivity-based fixel enhancement: whole-brain statistical analysis of diffusion MRI measures in the presence of crossing fibres. NeuroImage. 2015 doi: 10.1016/j.neuroimage.2015.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowley CD, Campbell JSW, Wu Z, Leppert IR, Rudko DA, Pike GB, Tardif CL. A model-based framework for correcting B1+ inhomogeneity effects in magnetization transfer saturation and inhomogeneous magnetization transfer saturation maps. Magn Reson Med. 2021 doi: 10.1002/mrm.28831. [DOI] [PubMed] [Google Scholar]
- Rushton WAH. A theory of the effects of fibre size in medullated nerve. J Physiol. 1951;115(1):101–122. doi: 10.1113/jphysiol.1951.sp004655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarwar T, Ramamohanarao K, Zalesky A. Mapping connectomes with diffusion MRI: deterministic or probabilistic tractography? Magn. Reson Med. 2019;81(2):1368–1384. doi: 10.1002/mrm.27471. [DOI] [PubMed] [Google Scholar]
- Schiavi S, Ocampo-Pineda M, Barakovic M, Petit L, Descoteaux M, Thiran JP, Da-ducci A. A new method for accurate in vivo mapping of human brain connections using microstructural and anatomical information. Sci Adv. 2020a doi: 10.1126/sci-adv.aba8245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiavi S, Petracca M, Battocchio M, Mendili MMEl, Paduri S, Fleysher L, Inglese M, Daducci A. Sensory-motor network topology in multiple sclerosis: structural connectivity analysis accounting for intrinsic density discrepancy. Hum Brain Mapp. 2020b doi: 10.1002/hbm.24989. n/a(n/a) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling K, Gao Y, Janve V, Stepniewska I, Landman BA, Anderson AW. Confirmation of a gyral bias in diffusion MRI fiber tractography. Hum Brain Mapp. 2018 doi: 10.1002/hbm.23936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schüz A, Braitenberg V. The human cortical white matter: quantitative aspects of cortico-cortical long-range connectivity. Cortical Areas Unity Divers. 2002:377–385. [Google Scholar]
- Smith RE, Tournier J-D, Calamante F, Connelly A. Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information. NeuroImage. 2012;62(3):1924–1938. doi: 10.1016/J.NEUROIMAGE.2012.06.005. [DOI] [PubMed] [Google Scholar]
- Sereno MI, Lutti A, Weiskopf N, Dick F. Mapping the human cortical surface by combining quantitative T(1) with retinotopy. Cerebral Cortex (New York, N.Y) 2013;23(9):2261–2268. doi: 10.1093/cercor/bhs213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004 doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- St-Onge E, Daducci A, Girard G, Descoteaux M. Surface-enhanced tractography (SET) NeuroImage. 2018 doi: 10.1016/j.neuroimage.2017.12.036. [DOI] [PubMed] [Google Scholar]
- Stewart WA, MacKay AL, Whittall KP, Moore GR, Paty DW. Spin-spin relaxation in experimental allergic encephalomyelitis. Analysis of CPMG Data using a non-linear least squares method and linear inverse theory. Magn Reson Med. 1993;29(6):767–775. doi: 10.1002/mrm.1910290608. [DOI] [PubMed] [Google Scholar]
- Stikov N, Perry LM, Mezer A, Rykhlevskaia E, Wandell BA, Pauly JM, Dougherty RF. Bound pool fractions complement diffusion measures to describe white matter micro and macrostructure. NeuroImage. 2011;54(2):1112–1121. doi: 10.1016/j.neuroimage.2010.08.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabelow K, Balteau E, Ashburner J, Callaghan MF, Draganski B, Helms G, Kherif F, et al. HMRI – a toolbox for quantitative MRI in neuroscience and clinical research. NeuroImage. 2019;194:191–210. doi: 10.1016/j.neuroimage.2019.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tax CMW, Kleban E, Chamberland M, Baraković M, Rudrapatna U, Jones DK. Measuring compartmental T2-orientational dependence in human brain white matter using a tiltable RF coil and diffusion-T2 correlation MRI. NeuroImage. 2021 doi: 10.1016/j.neuroimage.2021.117967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A. MRtrix: diffusion tractography in crossing fiber regions. Int J Imaging Syst Technol. 2012;22(1):53–66. doi: 10.1002/ima.22005. [DOI] [Google Scholar]
- Tournier J-D, Smith R, Raffelt D, Tabbara R, Dhollander T, Pietsch M, Christiaens D, Jeurissen B, Yeh C-H, Connelly A. MRtrix3: a fast, flexible and open software framework for medical image processing and visualisation. NeuroImage. 2019;202:116–137. doi: 10.1016/j.neuroimage.2019.116137. [DOI] [PubMed] [Google Scholar]
- Turner R. Myelin and modeling: bootstrapping cortical microcircuits. Front Neural Circuit. 2019;13:34. doi: 10.3389/fncir.2019.00034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC. N4ITK: improved N3 bias correction. IEEE Trans Med Imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med. 2016;76(5):1582–1593. doi: 10.1002/mrm.26059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. NeuroImage. 2016;142:394–406. doi: 10.1016/j.neuroimage.2016.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waxman SG. Determinants of conduction velocity in myelinated nerve fibers. Muscle Nerve. 1980;3(2):141–150. doi: 10.1002/mus.880030207. [DOI] [PubMed] [Google Scholar]
- West KL, Kelm ND, Carson RP, Gochberg DF, Ess KC, Does MD. Myelin volume fraction imaging with MRI. NeuroImage. 2018;182:511–521. doi: 10.1016/j.neuroimage.2016.12.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Ye, Hong Y, Feng Y, Shen D, Yap PT. Mitigating gyral bias in cortical tractography via asymmetric fiber orientation distributions. Med Image Anal. 2020 doi: 10.1016/j.media.2019.101543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeatman JD, Dougherty RF, Myall NJ, Wandell BA, Feldman HM. Tract profiles of white matter properties: automating fiber-tract quantification. PLOS ONE. 2012;7(11):1–15. doi: 10.1371/journal.pone.0049790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeatman JD, Wandell BA, Mezer AA. Lifespan maturation and degeneration of human brain white matter. Nat Commun. 2014;5(1):4932. doi: 10.1038/ncomms5932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh CH, Jones DK, Liang X, Descoteaux M, Connelly A. Mapping structural connectivity using diffusion MRI: challenges and opportunities. J Magn Reson Imaging. 2020 doi: 10.1002/jmri.27188. n/a(n/a) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Sarwar T, Ramamohanarao K. A cautionary note on the use of SIFT in pathological connectomes. Magn Reson Med. 2020;83(3):791–794. doi: 10.1002/mrm.28037. [DOI] [PubMed] [Google Scholar]
- Zhang F, Daducci A, He Y, Schiavi S, Seguin C, Smith R, Yeh CH, Zhao T, JO’Donnell L. Quantitative mapping of the brain’s structural connectivity using diffusion MRI tractography: a review. 2021 doi: 10.1016/j.neuroimage.2021.118870. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The in vivo MRI data used were acquired at University Hospital Basel and are available upon reasonable request. The code is open source and freely available at https://github.com/daducci/COMMIT.
The brain MR data was obtained from the University Hospital of Basel and are available from the corresponding author upon reasonable request.
The code is open source and freely-available at https://github.com/daducci/COMMIT.