Resolving bundle-specific intra-axonal T₂ values within a voxel using diffusion-relaxation tract-based estimation

Abstract

At the typical spatial resolution of MRI in the human brain, approximately 60–90% of voxels contain multiple fiber populations. Quantifying microstructural properties of distinct fiber populations within a voxel is therefore challenging but necessary. While progress has been made for diffusion and T₁-relaxation properties, how to resolve intra-voxel T₂ heterogeneity remains an open question. Here a novel framework, named COMMIT-T₂, is proposed that uses tractography-based spatial regularization with diffusion-relaxometry data to estimate multiple intra-axonal T₂ values within a voxel. Unlike previously-proposed voxel-based T₂ estimation methods, which (when applied in white matter) implicitly assume just one fiber bundle in the voxel or the same T₂ for all bundles in the voxel, COMMIT-T₂ can recover specific T₂ values for each unique fiber population passing through the voxel. In this approach, the number of recovered unique T₂ values is not determined by a number of model parameters set a priori, but rather by the number of tractography-reconstructed streamlines passing through the voxel. Proof-of-concept is provided in silico and in vivo, including a demonstration that distinct tract-specific T₂ profiles can be recovered even in the three-way crossing of the corpus callosum, arcuate fasciculus, and corticospinal tract. We demonstrate the favourable performance of COMMIT-T₂ compared to that of voxelwise approaches for mapping intra-axonal T₂ exploiting diffusion, including a direction-averaged method and AMICO-T₂, a new extension to the previously-proposed Accelerated Microstructure Imaging via Convex Optimization (AMICO) framework.

1. Introduction

Diffusion-weighted magnetic resonance imaging (DW-MRI) (Le Bihan and Breton, 1985) permits the microstructural organization of brain tissue to be studied in vivo. Despite the nominal DW-MRI resolution (i.e., voxel size ~2 × 2 × 2 mm³) being orders of magnitude larger than tissue features at the cellular level, i.e., on the order of a few micrometers, this technique is sensitive to the microscopic environment because cellular dimensions and the distance traveled by water molecules during the measurement time are similar, (Le Bihan, 2003). Several approaches have been proposed in recent years to quantify tissue microstructure, in which the diffusion processes taking place in the intra- and extra-cellular spaces are characterized using distinct models (Stanisz et al., 1997; Behrens et al., 2003; Assaf and Basser, 2005; Jespersen et al., 2007; Zhang et al., 2012; Kaden et al., 2016a). Similarly, T₂ relaxation times appear to be different in sub-components of the white matter, with short T₂ of water trapped in the myelin layers (Mackay et al., 1994), and differences in the T₂ of the extra-axonal and intra-axonal water. Complementing diffusion-based microstructural assessment with T₂ quantification will therefore provide a more complete characterization of tissue.

Indeed, previous studies have proposed the integration of multi-contrast acquisition techniques and multi-compartment models to characterize distinct features of the tissue (Peemoeller et al., 1981; English et al., 1991). More specifically, the acquisition of DW-MRI data using different echo times (TEs) allows the T₂ relaxation times of the different tissue compartments to be disambiguated (Benjamini and Basser, 2016; Kim et al., 2017; Tax et al., 2017; Canales-Rodriguez et al., 2018; De Almeida Martins and Topgaard, 2018; Lemberskiy et al., 2018; Veraart et al., 2018; Pizzolato et al., 2018; Lampinen et al., 2019; McKinnon and Jensen, 2019; Ning et al., 2019; Martins et al., 2020; de Almeida Martins et al., 2020; Reymbaut et al., 2020; Yu et al., 2020). Limitations of clinical scanners, constrain diffusion MRI sequences to have TE>70 ms, at which the short T₂ myelin water signal (Mackay et al., 1994) contribution is negligible, and thus only the intra- and extra-axonal compartments are considered.

Recently, Veraart et al. (2018) developed the TedDI framework to estimate the intra- and extra-axonal diffusion signal fractions and their absolute T₂ values simultaneously. Other studies, by applying diffusion weighting with b >4000 s/mm² with a view to suppressing the extra-axonal signal, aimed to estimate the mean intra-axonal T₂ in each voxel (Veraart et al., 2018; McKinnon and Jensen, 2019). Critically, these works suggested that T₂ values measured within single fiber populations were similar within the tracts and different between tracts (Veraart et al., 2018), suggesting that T₂ relaxation may be bundle-specific. Thus, in voxels containing multiple fiber populations, T₂ heterogeneity exists. However, currently-available methods can only derive an ensemble average of the T₂ values in such a voxel. Our aim, in this work, is to move away from this ensemble-averaging approach to a tract-specific T₂-mapping approach, enhancing the anatomical specificity of white matter microstructural characterization throughout the brain. Here, we focus on a specific sub-compartment of white matter, i.e., the intra-axonal space.

As axonal bundles are structurally homogeneous in their composition, i.e., axons tend to group into fascicles of their type (Bray et al., 1980; Kapfhammer et al., 1986; Kröger and Walter, 1991; Mills et al., 1984; Zipser et al., 1989), and the value of T₂ depends on the tissue microstructure, we assume that each bundle can have a specific T₂ value. Given that 60–90% of brain voxels at typical resolution contain multiple fiber populations (Jeurissen et al., 2013), a more complete characterization of the tissue necessitates new methods that can estimate the T₂ of each constituent bundle within the voxel.

There is a precedent for resolving bundle-specific relaxation properties within a voxel. De Santis et al. (2016) developed a framework that combined inversion recovery with DW-MRI to assign a specific value of the longitudinal relaxation time T₁ to each fiber population within a voxel. It was shown that this method resulted in less inter-subject variability compared to conventional voxel-by-voxel T₁-mapping methods in areas containing two or three crossing fibers, suggesting an increased specificity to distinct fiber populations. Importantly, despite many microstructural models positing 1, 2, or 3 fiber bundles in a voxel, it is not always possible to specify a priori the number of distinct bundles within a voxel, and thus the analytical pipeline needs sufficient flexibility to handle an arbitrary number of bundles.

Here, we propose an extension of the Convex Optimization Modeling for Microstructure Informed Tractography (COMMIT) framework (Daducci et al., 2015b) named COMMIT-T₂, which focuses on T₂ rather than T₁ and yields a number of distinct T₂ estimates that is limited only by the number of tractography streamlines that pass through the voxel. Currently, as with the vast majority of diffusion MRI-modeling frameworks, the original COMMIT framework implicitly assumes that all white matter bundles have the same T₂, contrary to evidence from recent studies (Veraart et al., 2018; McKinnon and Jensen, 2019). In contrast, COMMIT-T₂ estimates the intra-axonal T₂ value of each streamline, independently of the organizational complexity within the voxel. The fitting is based on a global optimization approach that estimates a T₂ for each and every streamline in the whole-brain tractogram.

The framework was evaluated using numerical simulations and a proof of concept was demonstrated with in vivo data. Furthermore, our streamline-based COMMIT-T₂ method was compared with voxel-based methods, including the direction-averaged method proposed in (McKinnon and Jensen, 2019) and AMICO-T₂, a new extension to the Accelerated Microstructure Imaging via Convex Optimization (AMICO) framework (Daducci et al., 2015a) that considers the DW-MRI dependence on T₂.

As a demonstration of the utility of this new framework, we show in vivo that our approach can detect differences in T₂ within two commonly-studied bundles, the Corpus Callosum (CC) and the Posterior Limb of the Internal Capsule (PIC); and can disentangle a three-way crossing area, including the central parts of the CC and Corticospinal Tract (CST), and Arcuate Fasciculus (AF).

2. Methods

2.1. Generative model

The measured signal $S\text{(}TE,b,\overrightarrow{g}\text{)}$ for a given T E, b-value, and diffusion gradient unit vector $\overrightarrow{g}$ is modeled by:

$$S\text{(}TE,b,\overrightarrow{g}\text{)}\text{=}kPD\text{(}{f}_i{e}^{-\frac{TE}{T_{2,i}}}{S}_i(b,\overrightarrow{g})+f_{e}e{}^{-\frac{TE}{T_{2,e}}}{S}_e(b,\overrightarrow{g}))+\eta ,$$ (1)

where P D is the proton density; k is a scalar dependent on the MRI machine and MRI acquisition, including the pulse sequence, image-reconstruction algorithm, and digital converter, etc.; f¡ and f_e denote the intra- and extra-axonal water signal fractions respectively; T_2,¡ and T_2,e are the T₂ values of the intra- and extra-axonal compartments, and S_i and S_e denote the diffusion-weighted signals from the intra- and extra-axonal compartments, respectively; η is the noise superimposed on the acquired signal. An experimental repetition time (TR) larger than 4 s is assumed to suppress T₁ effects. It is important to note that this model is built on the assumption that the intra- and extra-axonal spaces are in slow exchange, due to the relatively small distances travelled by the spins during the experimental time. All the models considered in this work are based on the same assumption.

As in (McKinnon and Jensen, 2019), we assume that S_e ≃ 0 for b = 6000 s/mm² (Fieremans et al., 2011; Jensen et al., 2016; McKinnon et al., 2017; Novikov et al., 2018; McKinnon and Jensen, 2019) and Eq. (1) becomes:

$$S\text{(}TE,b,\overrightarrow{g}\text{)}\text{=}C(e^{-\frac{TE}{T_{2,i}}}{S}_i(b,\overrightarrow{g}))+\eta ,$$ (2)

where C = k P D f_i.

In this work, the estimation of T_2,i was implemented using three different approaches: 1) the direction-averaged technique proposed in (McKinnon and Jensen, 2019); 2) AMICO-T₂; and 3) COMMIT-T₂, as detailed below.

2.2. Direction-averaged technique

Following the approach of (Edén, 2003; Lasič et al., 2014), Eq. (2) can be simplified by computing the direction-averaged (spherical mean) DW-MRI signal $\stackrel{\_}{S}\text{(}TE,b\text{)}=<S(TE,b,\overrightarrow{g})>$ (McKinnon and Jensen, 2019):

$$\stackrel{\_}{S}\text{(}TE,b\text{)}\text{=}Ae{}^{-\frac{TE}{T_{2,i}}}+\stackrel{\_}{\eta },$$ (3)

where $A=C<S_i(b,\overrightarrow{g})>=C{\stackrel{\_}{S}}_i(b)$ and $\stackrel{\_}{\eta }=<\eta >.$ After taking the logarithm on both sides, Eq. (3) reduces to a linear problem from which T_2,ican be estimated straightforwardly (McKinnon and Jensen, 2019).

2.1. 2.3. AMICO-T₂

The conventional AMICO framework (Daducci et al., 2015a) is based on solving the following equation for each voxel:

$$y=Ax+\eta ,$$ (4)

where y is the vector of measurements, A is the dictionary or design matrix, η denotes the vector of experimental noise, and x is the vector of coefficients to be estimated: each element in x contains the weight that quantifies the contribution of the corresponding column/atom in A to explain the measurements.

In this work, the matrix A was built using a generative model that explicitly incorporates the signal dependence on T₂. Specifically, each element of A was obtained by evaluating the model given by Eq. (2): ${\mathbf{\text{A}}}_{j,k}=e^{-\frac{T{E}_j}{T_{2}ik}}{S}_i(b_j,{\overrightarrow{g}}_j),$ where TE_j, b_j, and $\overrightarrow{g_j}$ are the experimental parameters used to acquire the j-th measurement (i.e., y_j), and T₂i_k is the k-th value from a set of predefined T₂i times. Here the dictionary was built using 20 equally-spaced T₂i values in the range 40–135 ms. For the diffusion times used here (Δ = 22 ms, see Section 2.5 ‘Acquisition Protocol), the intra-axonal perpendicular diffusivity D’± is effectively zero (Veraart et al., 2020a) and thus S_i was evaluated by simplifying the axon model to that of a “stick” (Behrens et al., 2003; Kroenke et al., 2004; Jespersen et al., 2007), with a D’i⊥ that is effectively zero. To reduce the number of model parameters and thus improve the stability of the fit, we chose to fix D _i|| = 2 ⋅ 10^-3 mm²/s (Dhital et al., 2019). Before evaluating S_i,, the fiber orientation was estimated by fitting a diffusion tensor representation (Basser et al., 1994) and estimating the principal eigenvector.

The vector of coefficients was estimated using a non-negative least square (NNLS) algorithm:

$$\hat{x}=\underset{x\ge 0}{\arg \min }\parallel Ax-y{\parallel }_2^2,$$ (5)

and the average ${\stackrel{-}{T}}_{2}i$ was calculated for each voxel as the weighted mean:

$${\stackrel{-}{T}}_{2}i=\frac{{\displaystyle {\sum }_{k=1}^{20}\stackrel{}{{\hat{x}}_k{T}_2{i}_k}}}{{\displaystyle {\sum }_{k=1}^{20}{\hat{x}}_k}}.$$ (6)

The implemented method is freely-distributed at https://github.com/daducci/AMICO.

2.4. COMMIT-T₂

The original COMMIT framework (Daducci et al., 2015b, 2013) models the DW-MRI signal in each image voxel as a linear combination of the intra- and extra-axonal signals generated in each location of the brain by using a set of candidate streamlines estimated using standard fibertracking techniques. COMMIT then solves a global convex optimization problem to estimate the effective contribution, or weight, of each streamline, such that they globally fit the measured signal. In practice, COMMIT creates a large system of linear equations by concatenating the vectors of measurements from all brain voxels and corresponding dictionaries. Importantly, each dictionary entry is not associated with a given voxel, but with a specific fiber bundle (i.e., the microstructural properties of the bundle that contribute to the diffusion-weighted signal are invariant along their length).

In the current extension, COMMIT is modified to allow for estimation of tract-specific T_2,i by using the generative slow-exchange model given in Eq. (2). Similar to COMMIT, which assumes that the diffusion properties of a streamline are invariant along its length, COMMIT-T₂ additionally assumes that T_2,i is invariant along a given streamline, but can vary between streamlines within the same voxel. Specifically, the same model parameters used in AMICO-T₂ are employed (i.e., D _i⊥, D _i∥, and predefined set of T_2,i values). After solving the resulting global optimization problem using the large-scale NNLS solver implemented in (Daducci et al., 2015b), a vector of coefficients x for each fiber bundle is obtained, where the k-th element x_k quantifies the signal fraction explained by that fiber bundle with a predefined T_2,i value. Thus, a distribution of T_2,i values is obtained for each streamline, whose mean value is computed using Eq. (6). For more technical details about how all the brain voxels and corresponding dictionaries are concatenated and the optimization algorithm is used to solve the resulting large scale problem, the reader is referred to the original COMMIT articles (Daducci et al., 2015b, 2013).

In order to compare this tract-based estimation method with the voxel-based approaches described in previous sections, the resulting mean T_2,i values from multiple streamlines are averaged and projected at each voxel. To foster reproducible research the open-source code is freely available at https://github.com/daducci/COMMIT.

The starting input set of candidate streamlines was estimated using the constrained spherical deconvolution (CSD) method (Tournier et al., 2019) and the deterministic SD_STREAM fiber tracking algorithm included in the MRTrix3 software (http://www.mrtrix.org). The reconstruction was carried out using default parameters. Approximately 150 K streamlines were obtained, and those ending in the white matter were filtered out.

2.5. Acquisition protocol

The DW-MRI acquisition protocol comprised two parts: one for trac- tography and one dedicated to T₂ relaxometry. For all data, the diffusion times Δ and δ were fixed to 22 ms and 8 ms, respectively. The tractog- raphy protocol used 6 images with b = 0 s/mm², 8 diffusion-encoding directions at b = 750 s/mm² and 30 directions at b = 3000 s/mm² with TE = 45 ms. The T₂ relaxometry protocol comprised four complete sets of 4 images with b = 0 s/mm² and 48 directions at b = 6000 s/mm² for each of the following echo times: TE = 73, 93, 118, and 150 ms. This acquisition protocol was used to generate synthetic data and to acquire real brain data.

2.6. Numerical simulations

An optimization process (Rafael-Patino et al., 2020) was used to generate a fiber crossing phantom with 2867 streamlines saved in ‘.obj’ file format. This file was then converted to ‘.trk’ format to be read by COMMIT (https://github.com/daducci/COMMIT), which was then used to simulate the synthetic DW-MRI data. Specifically, the DW-MRI signals were generated by using the model given by Eq. (2) with the acquisition parameters described in Section 2.5 and the following model parameters: T₂ Bundle1 (T_2,B1) = 78 ms; T₂ Bundle2 (T_2,B2) = 116 ms. The same signal fraction was assumed for all streamlines, which was normalized such that their total sum at each voxel was equal to 1. As motivated above, the diffusivities of all streamlines in both bundles were fixed to D_i⊥ = 0 and D_i∥ = 2 ⋅ 10^-3 mm² /s. However, in some experiments these parameters were changed to study the stability of the fitting, as is detailed below.

In order to study the limits of validity of COMMIT-T₂, four experiments were carried out to study the bias in the T₂ estimates as a function of 1) the noise level, 2) intra-axonal T₂ values, 3) discrepancy between the assumed and actual diffusivity, and 4) the impact of using an imperfect tractogram with missing true-positives and false-positive streamlines, respectively.

The same parallel diffusivity and set of fibers that were used to simulate the data were employed to generate the dictionary in the first experiment. Eleven synthetic datasets were generated by corrupting the noise-free data with 11 different noise levels, equally-spaced within a predefined noise range. The highest noise level was determined from the raw human brain data, and the lowest noise level was estimated from the same data after denoising. Both were computed by using the noise estimation algorithm developed in MRtrix3 software (Veraart et al., 2016). For more details see Figures S1 and S2 in the Supplementary Material. The fitting was conducted for each independent dataset, allowing us to quantify the estimation error as a function of the noise.

The second experiment was performed to evaluate the sensitivity of the studied algorithms to differences in the T₂ values of the two bundles. As in the first experiment, the same parallel diffusivity and set of fibers were employed to simulate the data and generate the dictionary. In contrast, forty-one different datasets were created by fixing the T₂ of the first bundle to T_2,B1 = 78 ms, while changing the T₂ of the second bundle in the range T_2,B = 40–135 ms with 41 equally-spaced values. In this case, the data was corrupted with the lowest noise level estimated in the first experiment.

In the third experiment, the same set of fibers that were used to simulate the data were employed to generate 21 different dictionaries. However, this time each dictionary was created by using a different parallel diffusivity, which was chosen to vary from 1 ⋅ 10⁻³ mm²/s to 3 ⋅ 10⁻³mm² /s with 21 equally-spaced values. The fitting was repeated for each dictionary and the corresponding intra-axonal T₂s were estimated for each case. This allowed us to evaluate the bias induced in the estimated T₂s as a function of the assumed diffusivity.

The fourth experiment tested the algorithm’s robustness against fiber tracking errors. Various dictionaries were created by randomly removing a certain percentage of the ground-truth streamlines, which varied from 10% to 90%. The streamlines removed were replaced by the same number of false-positive streamlines obtained by running CSD and then SD_STREAM, as implemented in MRtrix3 (Tournier et al., 2019). The tractography generated 10 K streamlines, from which around 50% are false positives connections. False-positives were identified as those tracts arriving at the wrong bundle, e.g., streamlines which seed points were located in the first bundle but arrived at the endpoints of the second bundle, and vice-versa. The same diffusivity used to create the signal was used to generate the dictionaries. For more details see Figure S3 in the Supplementary Material.

2.7. In-vivo data acquisition and preprocessing

DW-MRI data were acquired using a Siemens Connectom 3T MRI scanner with 300 mT/m gradients. A healthy human volunteer was scanned using the acquisition parameters described in Section 2.5. The Cardiff University School of Psychology ethics committee approved the study, written informed consent was obtained. Other imaging parameters were: repetition time (TR) = 4100 ms, voxel size = 2.5 mm isotropic, number of slices = 46. For each TE dataset, one additional image with b = 0 s/mm² and opposite phase encoding direction was also acquired to correct for susceptibility distortions (Andersson et al., 2003). Additionally, a structural T₁–weighted image was collected using a 3D magnetization-prepared rapid acquisition with gradient echo (MPRAGE) sequence with the following parameters: TR = 2300 ms, TE = 2 ms, inversion time (TI)=857 ms, voxel size = 1 mm isotropic, flip angle =9°

Preprocessing steps were applied in the following order: 1) noise level estimation and removal (Veraart et al., 2016); 2) Rician unbiasing (Kaden et al., 2016b); 3) removal of Gibbs ringing artifacts (Kellner et al., 2016); and 4) motion and geometric distortion corrections using the ‘topup’ and ‘eddy’ tools included in FSL (Andersson et al., 2003; Andersson and Sotiropoulos, 2016). To compensate for motion between the different scan-sets, all data with different TE were preprocessed separately and co-registered using a rigid registration (Klein et al., 2010). The registration was based on the images without diffusion weighting, i.e., b = 0 s/mm². Finally, the T₁-weighted image was parcellated with FreeSurfer (Dale et al., 1999; Destrieux et al., 2010), the resulting white matter mask was used for tractography (see tractography details above in Section 2.4), while the white matter parcellation was used for the extraction of the different bundles using the White Matter Query Language (WMQL) (Wassermann et al., 2016).

The experiment was conducted on the CUBRIC cluster computing system on a node equipped with 192 GB of RAM and 12 cores. The computational time of the experiment took about 12 h using parallel computing.

3. Results

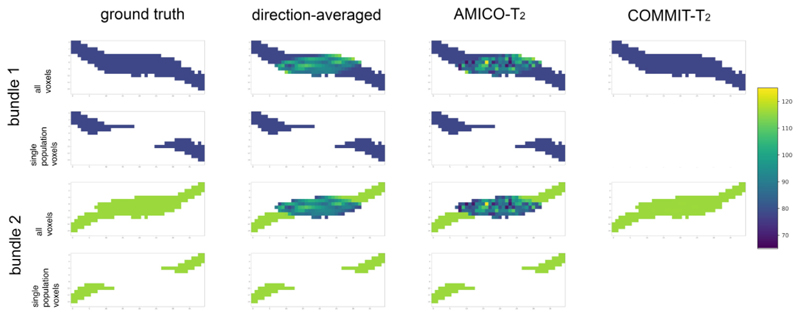
Results from the first numerical experiment described in Section 2.6 are shown in Figs. 1 and 2, and Figure S4 in the Supplementary Material. Fig. 1 depicts the T₂ estimated by each evaluated method: the direction-averaged, AMICO-T₂, and COMMIT-T₂. This result was obtained using noise-free data. The first column depicts the two bundles with ground-truth values of T_2,B1 = 78 ms and T_2,B2 = 116 ms, respectively. The analysis was performed separately on all voxels and those voxels containing a single fiber population. In voxels containing a single fiber population, the three methods seem to perform equally-well in correctly recovering the ground-truth values (although see Fig. 2). Conversely, in regions with fiber crossings, the T₂i values estimated by the voxel-based methods (i.e., both the direction-averaged and AMICO-T₂ techniques) lie between the two ground truth T_2,B1and T_2,B2 values. In contrast, COMMIT-T₂ correctly estimated the T₂i values in both bundles in the fiber crossing region.

Fig. 1. A cross-section of the synthetic phantom.

The phantom simulates a crossing of two fiber bundles with different T₂ values: T_2,B1 = 78 ms (in blue color) and T_2,B2 = 116 ms (in green color). Voxels with a single fiber were differentiated to test the performance of the three methods: the direction-averaged technique, AMICO-T₂, and COMMIT-T₂.

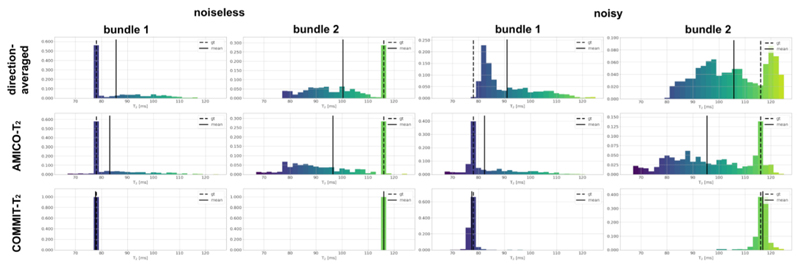
Fig. 2.

Histograms of the T₂i values estimated in the phantom using the three evaluated methods: the direction-averaged technique, AMICO-T₂, and COMMIT-T₂. The solid black line indicates the mean value of the histogram. The ground-truth (dashed line) values are T_2,B1 = 78 ms and T_2,B2 116 ms respectively. For more details, see Fig. 1. Results from both the noise-free and noisy datasets are reported. Bundle 1 represents the analysis performed on all the voxels passed by the streamlines defined in bundle 1 (see ground truth Fig. 1). Similarly, Bundle 2 represents the analysis performed on all the voxels passed by the streamlines defined in bundle 2.

The voxel-wise histograms for the three methods of the T₂ i values obtained from both the noise-free and noisy datasets are shown in Fig. 2. This result corresponds to the data corrupted with the lowest noise level. The direction-averaged technique and AMICO-T₂ tend to overestimate the mean T_2,B1 value by 7.60 ms and 5.11 ms, respectively, and to underestimate the mean T_2,B2 by 17.70 ms and 21.55 ms, even in the noise-free case. In the noisy case, the mean T₂ values estimated by AMICO-T₂ were T_2,B1= 83.12 ms and T_2,B2= 96.45 ms, while those estimated by the direction-averaged method were T_2,B1 = 90.96 ms and T_2,B2 = 105.70 ms. Neither method addresses the crossing fiber problem directly. COMMIT-T_2,B1 =77.72 ms and T_2,B2 =116.04 ms in the noiseless case and T_2,B1 =77.40 ms and T_2,B2 =116.83 ms in the noisy experiment.

The stability of COMMIT-T₂ for 11 different noise levels is depicted in Figure S4 of the Supplementary Material. As can be seen, COMMIT-T₂ is stable across these SNR levels, including the lowest SNR found in the raw data. At this noise level, we found an error lower than 5 ms, which decreased to less than 2 ms for the highest SNR.

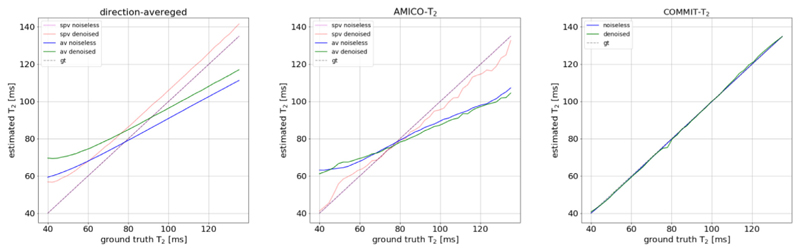
Results from the second numerical experiment are shown in Fig. 3, which plots the estimated mean T₂ value of Bundle 2 vs the ground-truth value. In single bundle population voxels, estimates derived from the direction-averaged and AMICO-T₂ methods using the noise-free data are close to the ground-truth value. The error among the 41 numerical phantoms is 3.94e-7 ms +/- 4.75e-7 and −0.03 ms +/- 0.04 for the direction-averaged and AMICO-T₂, respectively. The estimates from the direction-averaged method were biased by the noise. Specifically, the mean T₂ overestimation is 7.42 ms + /- 2.45 and the bias is more pronounced at the lower T₂ values. In AMICO-T₂ T₂, the overall error (i.e., −1.64 ms +/ 4.01) is much smaller across the range of T_2,B2, being positive up to about T_2,B2 = 65 ms (i.e., 3.36 ms +/- 1.96), and negative beyond T_2,B2 = 80 ms (i.e., −4.59 ms + /- 2.12).

Fig. 3.

Comparison of the T₂i estimation per bundle in the numerical phantom which varies T_2,B2 and keeps a constant T_2,B2 =78 ms as described in Section 2.6, against ground-truth for the direction-averaged, AMICO-T₂, and COMMIT-T₂ methods. The comparison for the direction-averaged and AMICO-T₂ methods is performed in a single population voxels (spv) and all voxels (av), which includes a single and multiple populations. The comparison was done on the noiseless data and on noisy data with the same amount of noise estimated after denoising the in-vivo data.

In the whole phantom, including all voxels with a single bundle and two bundles, both voxel-based estimation methods failed at recovering the ground- truth values, even in the noise-free case. The direction-averaged and AMICO-T₂ methods overestimated the actual values for T₂ values lower than 78 ms (i.e., 8.91 ms +/- 5.83, and 9.69 ms +/- 6.93, respectively), and underestimated for T₂ values higher than 78 ms (i.e., −12.30 ms +/- 6.81 and −14.96 ms +/- 8.76, respectively). In contrast, COMMIT-T₂ recovered T₂ values close to the ground truth over the range of T_2,B2, with a mean error of −0.23 ms +/- 0.22 in the noiseless case and −0.11 ms +/- 0.77 in the noisy experiment.

Results from the third experiment are depicted in Figure S5 in the Supplementary Material. COMMIT-T₂ recovered the closest T₂ values to ground-truth when the correct diffusivity value was set (i.e., 0.0002 mm²/s). When the diffusivity was fixed to a much higher value (i.e., 0.0003 mm²/s) or a much lower value (i.e., 0.0001 mm²/s) the error in T₂ was up to 8 ms (for Bundle 1). However, this bias was reduced by half when the diffusivities were set within a more realistic range, i.e., 0.0017–0.0023 mm²/s.

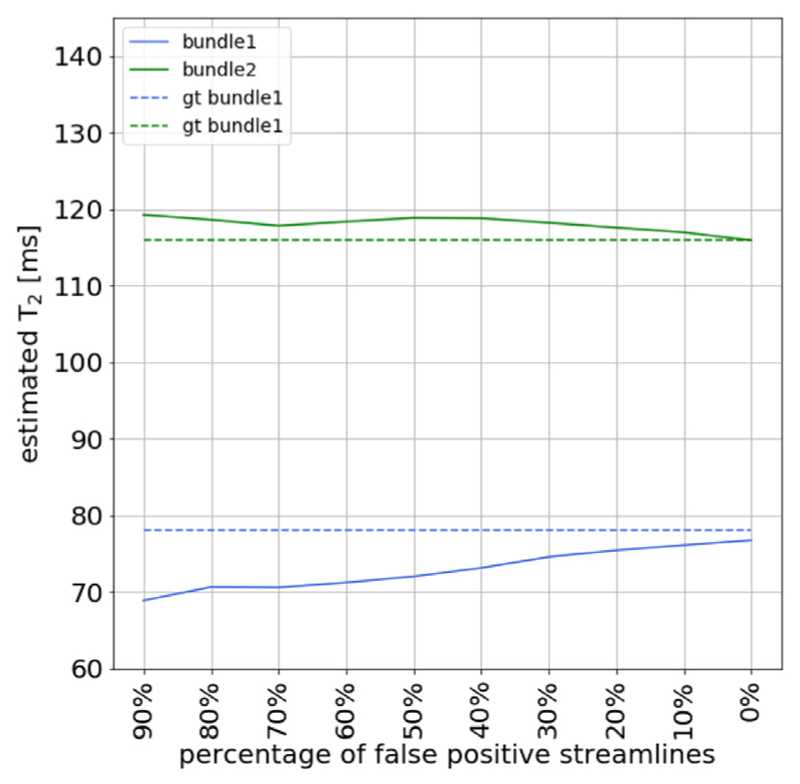
Finally, results from the fourth experiment are displayed in Fig. 4, which tested the influence of fiber tracking errors on the estimates simulated by gradually replacing true-positive by false-positive streamlines. This analysis shows that with 90% false-positive streamlines, an under-estimation of 10 ms for bundle 1 and an overestimation of 4 ms for bundle 2 is found. As expected, when the number of false-positive streamlines is reduced, the estimated T₂s are closer to the ground truth values. For 40% false-positives, the bias is less than 5 ms.

Fig. 4.

Effect of introducing false positive streamlines in the simulated phantom with two fiber bundles with different T₂ values: T_2,B1 = 78 ms (in red color) and T_2,B2 = 116 ms (in green color), respectively. The figure shows the effect of the COMMIT-T₂ estimation when a different percent of false positives is introduced and the same numbers of true-positives are removed, while keeping constant the number of streamlines in the dictionary. The ground-truth T₂ values are displayed in dashed lines as a reference.

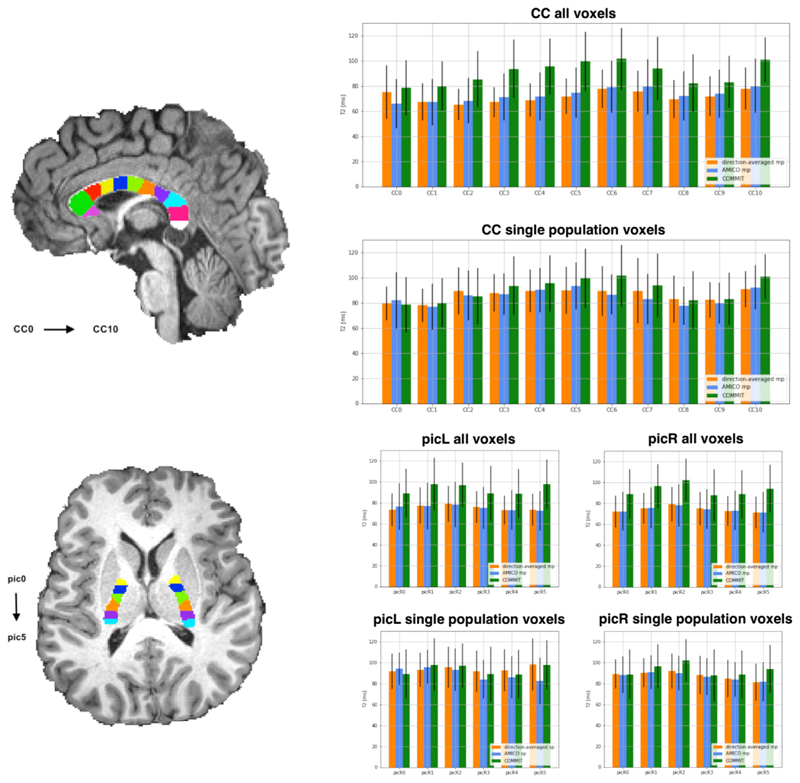
As a proof of concept of the application of COMMIT-T₂ in vivo, we first analyzed two commonly-studied white matter bundles: the Corpus Callosum (CC) and the Posterior Limb of the Internal Capsule (PIC). The CC was divided into 11 sub-bundles and the PICs into 6 sub-bundles, using equally separated ROIs created, and analysis of T₂ bundle-specific estimates were performed, see Fig. 5.

Fig. 5.

T₂ estimations using the direction-averaged, AMICO-T₂, and COMMIT-T₂. The analysis is performed on two commonly-studied white matter fasciculus: the Corpus Callosum (CC) and the Posterior limb Internal Capsule (PIC). The CC was subdivided into 11 ROIs while the PIC was subdivided into 6 ROIs. The ROIs shown in the figure are used to separate the bundles passing through them, i.e. they are not the ROIs from which the measurements are extracted. A comparison is performed for the three methods considering the mean and standard deviation of the voxels appertaining to a bundle. Furthermore, we compared all the voxels of the bundles, multiple populations, and voxels in which only one fiber population is present (defined as having a voxel-based fractional anisotropy (FA) greater than 0.7). Bar height corresponds to mean value and whiskers represent the standard deviation across voxels.

The performance of the three algorithms was compared for all voxels, using the entire extent of the sub-bundles (i.e. irrespective of whether they contained a single fiber population or more), and voxels deemed to contain a single fiber population (by virtue of having fractional anisotropy (FA) higher than an arbitrary threshold of 0.7). When considering all voxels, the results show that the voxel-based methods recover T₂ values around 20 ms lower compared to those obtained by COMMIT-T₂, both in the CC and the PIC. In single bundle population voxels, however, the voxel-wise methods yielded similar T₂ estimates to COMMIT-T₂. This demonstrates that in vivo, unlike COMMIT-T₂, existing voxel-based methods cannot adequately handle complex configurations. When voxels containing different bundle populations are included in the estimation, the overall T₂ estimation of each distinct bundle is weighted by the different T₂ bundle components and cannot be disentangled.

We explored the variation of T₂ throughout the CC and PIC with the COMMIT-T₂ framework in Fig. 5. Values of bundle-specific T₂ recovered in the CC ranged from 80 to 100 ms. More specifically, we find that the CC5, CC6, and CC10 areas of the CC, which correspond to regions of bundles ending in motor, somatosensory cortex, and visual area, have considerably higher T₂.

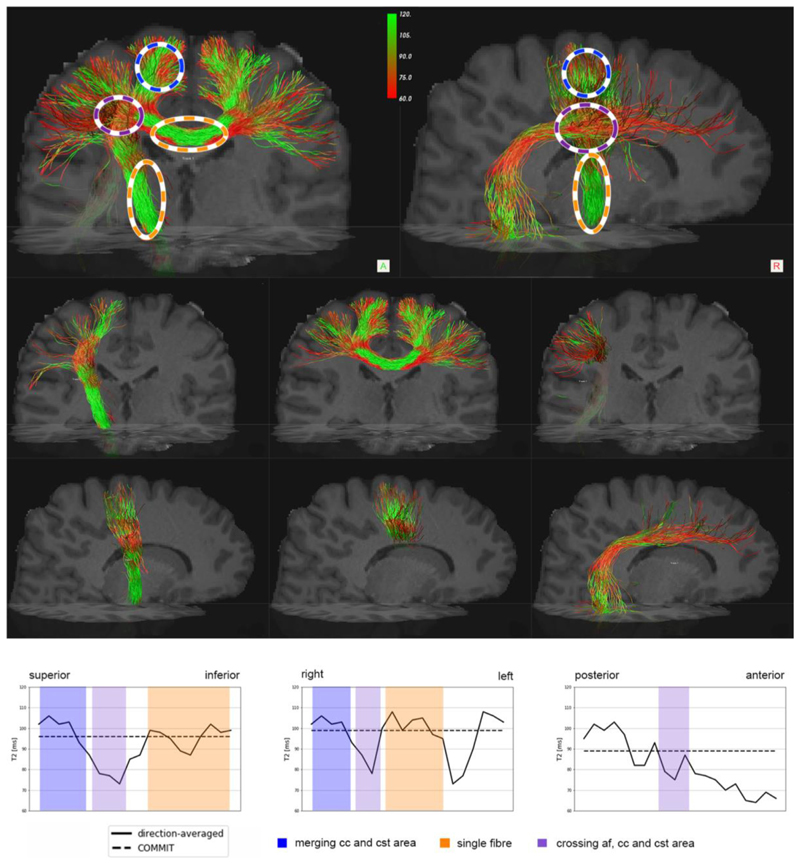
In Fig. 6 we show an example of the direction-averaged voxelwise T₂ estimation projected onto the CC, Corticospinal Tract (CST), and Arcuate Fasciculus (AF). We report that in the voxels where the three bundles are crossing, highlighted in purple, there is a significant decrease in T₂ values for the CC and CST bundles. This decrease seems to be related to the apparently lower T₂ values of the AF bundle, which overall has a lower T₂ values within the bundle. Single bundle population voxels, highlighted in orange, for CC and CST have a higher T₂, and when they merge (region highlighted in blue), tend to preserve high T₂ values. In the dashed line we report the estimated COMMIT-T₂ values that are constant within the bundle.

Fig. 6.

Profiles of T₂ estimates by using the direction-averaged approach for three well-known bundles: the central parts of the Corticospinal Tract (CST) and the Corpus Callosum (CC), and Arcuate Fasciculus (AF). In the top row of the figure, the three bundles are merged. The orange ovals highlight regions containing a single bundle population, the blue ovals highlight two-bundle populations, and the purple ovals highlight the crossing of all three bundles. The bottom part of the figure shows the profile of the estimated T₂s along the CST, CC, and AF bundles, respectively. The profile has been calculated based on the centroid of the bundle; we numbered each voxel of the centroid, then we calculate the distance from each voxel of the bundle mask to the centroid; finally, we calculate the mean of all the voxels associated with each voxel of the centroid. The estimates of intra-axonal T₂ from COMMIT-T₂ are shown by the dashed line as a reference.

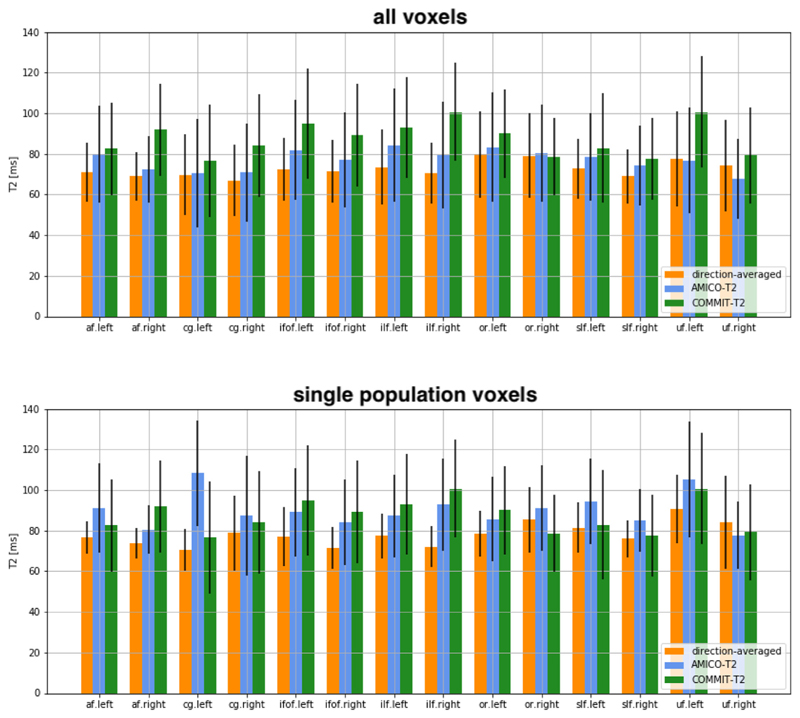
In Fig. 7 we compare the T₂ values obtained with the three methods in other commonly-studied white matter fasciculi: the cingulum bundle (CG), inferior fronto-occipital fasciculus (IFOF), inferior longitudinal fasciculus (ILF), optic radiation (OR), superior longitudinal fasciculus (SLF), uncinate fasciculus (UF) and AF. The analysis was performed on both hemispheres. Similarly, to the analysis in the CC and PICs, we see that for the voxel-based methods, larger T₂ values are estimated in voxels containing a single fiber population compared to voxels containing multiple fiber populations.

Fig. 7.

T₂ values estimated by using the direction-averaged method, AMICO-T₂ and COMMIT-T₂. The analysis is performed on the arcuate fasciculus (AF), cingulum (CG), inferior fronto-occipital fasciculus (IFOF), inferior longitudinal fasciculus (SLF), optic radiation (OR), superior longitudinal fasciculus (SLF), and uncinate fasciculus (UF). Comparison is performed considering the average along all voxels where the bundle is defined, where multiple populations occurred, and in voxels where only one population is present (by defining a fractional anisotropy (FA) threshold = 0.7, computed by fitting a diffusion tensor model). Bar height indicates the mean value and whiskers represent the standard deviation across voxels.

4. Discussion

In this work, we explored the feasibility of estimating intra-axonal T₂ in tissue with complex tract geometry, i.e., crossing, fanning, and merging within a voxel using the COMMIT-T₂ framework, and assigning a distinct T₂ to each fiber population within a voxel. We adopted high b-value diffusion-weighting as a means of suppressing the extra-axonal signal and TE>70 ms which suppresses the myelin signal (Kiselev and Novikov, 2018; McKinnon and Jensen, 2019).

In the human brain, the origin of differences in T₂ is not completely understood. However, the main factors known to change T₂ in relation to free water (Brownstein and Tarr, 1977, 1979; Kaden and Alexander, 2013) are the macromolecular content, the surface relaxivity, and the surface-to-volume ratio of the confining geometry. Thus, the intra- axonal T₂ is closely related to the inner axon diameter and the intra axonal composition. Notably, in Fig. 5, we notice that the T₂ pattern of the CC follows the histologically well-known low-high-low diameter pattern (Aboitiz et al., 1992). For smaller axons, we expect more surface-relaxation effects, hence quicker T₂-relaxation and therefore shorter T₂, and the opposite for larger axons. The diffusion MRI protocol used here, with a fixed diffusion time of Δ= 22 ms precluded the direct estimation of axon diameter in this work, but we have previously exploited the ultra-strong gradients of the Connectom scanner to obtain in vivo estimates of axon diameter, both on a voxel-level (Veraart et al., 2020b) and in a COMMIT-style framework (Barakovic et al., 2018). In future work, such approaches could be combined with the framework proposed here to gain more insights into the relation between axon diameter and T₂. For instance, if the dominant relaxation mechanism is the surface relaxation, the intra-axonal T₂ would be highly correlated with the inner axon diameter. Conversely, if it is the intra-axonal composition, (i.e., the density of microtubules and neurofilaments), then T₂ would be only partially correlated with the estimated diameters.

Moreover, it is known that different tissue microstructural environments experience different T₂. Previous work mainly focused on disentangling intra-axonal and extra-axonal components (Tax et al., 2017; Canales-Rodriguez et al., 2018; Pizzolato et al., 2018; Veraart et al., 2018) or focusing on the quantification of the water trapped in the myelin layers (Mackay et al., 1994). Previous works have explored this further proposing a possible subdivision of intra-axonal T₂ components in different bundles (McKinnon and Jensen, 2019; Veraart et al., 2018). However, all these previous works used a model that implicitly assumed a single fiber population or an assumption that all fibers have the same properties (i.e., diffusivities and T₂).

COMMIT-T₂ is the first framework designed to disentangle T₂ estimates of different bundles utilizing fiber spatial organization revealed by tractography. This novel approach was compared to two voxel-based methods, the previously-reported direction-averaged method proposed by (McKinnon and Jensen, 2019) and another novel approach named AMICO-T₂.

AMICO-T₂ and COMMIT-T₂, respectively, are extensions of AMICO (Daducci et al., 2015a) and COMMIT (Daducci et al., 2015b, 2013). The original implementations of AMICO and COMMIT used two different computational solvers (i.e., active set and gradient descent, respectively) to perform the non-negative least square (NNLS) optimization. In this work, to avoid differences in performance arising from different solvers, AMICO-T₂ was implemented using the same NNLS solver included in COMMIT, which is more efficient for large-scale applications. In a preliminary evaluation, we verified that for the relative tolerance error used in this study (i.e.,10⁻⁶) the two solvers converge to the same solution. It is important to note that AMICO assumes a single fiber orientation per voxel, which is estimated from the diffusion tensor. In this study, we extended AMICO by integrating the T₂ component, while keeping the original single-fiber assumption. Further works should be done to generalize AMICO-T₂ to multiple fibers, which may also bring improvements in estimating T₂ in complex fiber configurations.

Comparing the two voxel-based approaches, from a theoretical perspective, the main difference is that the direction-averaged method accounts for bundle dispersion, while AMICO-T₂ does not. Despite this, there were no major differences in results obtained by these two methods when applied in vivo. In numerical simulations, our findings suggest that the dictionary-based methods are more robust to noise compared to the direction-averaged method, in which we found constant overestimation of the T₂ estimates. Although we cannot provide a definite answer to explain the observed overestimation, we hypothesize it may be related to how the different models treat the noise. Even though a Gaussian noise model is implicitly assumed for all the evaluated models, the optimization in the direction-averaged technique requires a logarithmic transformation of the raw data for estimating the T₂ value, thus changing the assumed noise distribution. Consequently, the variance of the signal becomes scaled by the inverse of the signal itself, (i.e., if y = In(I), then $\frac{dy}{dI}=\frac{1}{I},$ and ${\sigma }_{lnI}=\frac{{\sigma }_I}{I}$). In a previous diffusion MRI study, an underestimation of the exponent exp(-bD) was found when the noisy data were log-transformed (Jones and Basser, 2004). Our results are consistent with that study because in T₂ relaxation the exponent appears in the denominator, i.e., exp(-TE/T₂). Thus, if the term 1/ T₂is underestimated more with log-transformed data, the T₂ is overestimated. On the other hand, this step is not required in AMICO-T₂ and COMMIT-T₂.

In the first three tractography numerical simulations, one possible reason for COMMIT-T₂ outperforming the other methods is that the tracking algorithm used in the signal fitting was the same as that used to generate the phantom data, warranting the investigation of performance with different tracking algorithms, which we addressed in the fourth tractography experiment introducing false-positive streamlines from a second algorithm. Overall, we found that the estimates from COMMIT-T₂ were robust against various noise levels, intra-axonal T₂values, discrepancies between the assumed and actual diffusivities, as well as potential errors in the fiber tracking algorithm.

There are several interesting avenues to be pursued in future work. Firstly, it will be of interest to extend the analysis of COMMIT-T₂ beyond the analysis of selected tracts to the whole brain T₂ connectivity matrix (Boshkovski et al., 2020). Secondly, it would be informative to explore the ability of the COMMIT-T₂ framework to remove false positive streamline reconstructions and therefore to improve tractography (Schurr et al., 2018; Rheault et al., 2019; Schiavi et al., 2020). Thirdly, it should be possible to extend the COMMIT-T₂ framework to include extra-cellular T₂ estimation and perhaps even myelin water (Tax et al., 2019), exploiting ultra-strong gradients and non-EPI read-outs to minimize the echo-time for a given b-value (Mueller et al., 2019).

One of the main limitations of COMMIT-T₂ is the fact that the model assumes constant properties along a given trajectory. Changes in axonal properties have been reported at the microscale level. However, for long scale connections and for the image resolution achievable with practical acquisition times, this assumption of uniformity is not a strong one, as shown by other methods making similar assumptions (Pestilli et al., 2014; Sherbondy et al., 2010, 2009; Smith et al., 2015, 2013).

Furthermore, the assumption of constant properties along a given trajectory may be limited in studying pathological brain, especially in the presence of focal axonal degeneration. However, there are various brain pathologies where the abnormalities are widespread across the whole brain, or individual fiber bundles, e.g., in psychiatric and neurodevelopmental disorders (Canales-Rodríguez et al., 2014; Kelly et al., 2018; Favre et al., 2019). In those cases, the assumptions behind COMMIT-T₂ are not violated and hence it can be applied. Moreover, we believe there are also valuable applications for studying individual differences in normal, healthy brains (e.g., linking microstructural differences in specific pathways to individual differences in cognition).

Another significant limitation relates to the limits of tractography in general (Maier-Hein et al., 2017; Schilling et al., 2019), and the limits of the fiber orientation distributions (FOD) estimated per voxel (Canales-Rodríguez et al., 2019) which have a direct impact on the quality of tract reconstructions. To address this issue, as a proof-of-concept, we mainly focused on well-characterized fasciculi where we assume false positives are minimal. However, results from synthetic data show that COMMIT-T₂ is robust to the presence of false positives. Another aspect warranting further research is the contribution of other cells in the white matter to the obtained results. Although the signal arising from the extra-axonal space is canceled by using high b-values. It is not known to which extend the signal coming from other cells, e.g., glial cells, is attenuated. Thus, our results may be potentially affected by non-axonal cells. Finally, this work did not try to optimize the MRI acquisition protocol in terms of minimizing acquisition time, which will be addressed along the line of recent parallel studies (Hutter et al., 2018).

5. Conclusion

This work has introduced a novel framework for quantifying intra- axonal T₂ properties of distinct fiber populations within a voxel and presents clear advantages in disentangling different bundles based on T₂ relaxation. In particular, the COMMIT-T₂ framework addresses some limitations of current voxel-wise techniques and enables the recovery of bundle-specific T₂ within a voxel, thanks to the regularization of T₂ estimates derived from the tractography-based reconstruction of white matter pathways. Our new framework may help improve the characterization, and therefore understanding, of the underlying characteristics of complex bundles and could potentially be used to improve fiber-tracking reconstructions.

In summary, we believe that COMMIT-T₂ represents a powerful addition to the microstructural imaging arsenal that should improve the uptake of quantitative relaxometry and diffusion measurements both in research and in the clinic. The ability to disambiguate measurements to a particular white matter pathway will be invaluable in improving our understanding of microstructure-function relationships in development, in understanding individual differences in cognition, and in detecting and monitoring pathology.