Blood flow and transport in the human placenta

Abstract

The placenta is a multi-functional organ that exchanges blood gases and nutrients between a mother and her developing fetus. In humans, fetal blood flows through intricate networks of vessels confined within villous trees, the branches of which are bathed in pools of maternal blood. Fluid mechanics and transport processes play a central role in understanding how these elaborate structures contribute to the function of the placenta, and how their disorganization may lead to disease. Recent advances in imaging and computation have spurred significant advances in simulations of fetal and maternal flows within the placenta, across a range of lengthscales. Models describe jets of maternal blood emerging from spiral arteries into a disordered and deformable porous medium, and solute uptake by fetal blood flowing through elaborate three-dimensional capillary networks. We survey recent developments and emerging challenges in modeling flow and transport in this complex organ.

1. Introduction

The placenta is the life-support system of a growing fetus. It is a versatile exchange organ that delivers oxygen and removes carbon dioxide while also providing essential nutrients and removing waste products. These multiple functions are achieved by bringing fetal and maternal blood into close proximity, while avoiding direct contact. Fluid mechanics and related transport processes are critical to understanding the relationship between the intricate structure of the placenta and its function, and therefore offer important insights into diseases such as preeclampsia and diabetes, in which the architecture and performance of the placenta are disrupted (Rainey & Mayhew 2010). These and other conditions that lead to poor fetal nutrition place the fetus at risk and can have a lifelong impact on health (Barker 2012).

A number of features distinguish the human placenta from other organs. It grows rapidly, invading and remodeling the wall of the mother’s uterus, with fetal blood vessels developing under low-oxygen conditions in a manner that mirrors some features of vascular tumors (Burton et al. 2017). In vivo investigations are hampered by obvious safety and ethical restrictions, and a high degree of variation across species severely restricts the availability of useful animal (non-primate) models (Carter 2007). However, because the placenta is available after birth, there is a short window in which ex vivo flow and transport experiments can safely be undertaken on living human tissue.

A highly ramified epithelial interface (the syncytiotrophoblast or SCT) separates maternal and fetal tissues within the human placenta (Figure 1; see Box 1 for a definition of some key terms). It has an area of up to 15m² (Burton & Jauniaux 1995) and allows maternal and fetal blood within 2-3µm of each other. On one side of this interface, maternal blood emerges from spiral arteries in the uterine wall and passes through the intervillous space (or IVS, which is effectively a porous medium) before draining into decidual veins. On the other side of the SCT, fetal blood flows through networks of vessels confined within branches of villous trees; in total, the fetal vessels are estimated to be up to 550km in length (Burton & Jauniaux 1995). Most of the gas and nutrient exchange takes place in terminal villi, which are peripheral branches of the trees containing networks of fetal capillaries. As reflected by its name in many languages, the placenta as a whole resembles a flat cake, of diameter approximately 22cm and thickness 2.5cm at full term. On the fetal-facing face, blood vessels branch from the umbilicus into a surface (chorionic) network that feeds dozens of separate villous trees. These penetrate through to the basal face of the placenta that is in contact with maternal decidua. Each tree is typically associated with a single spiral artery on the underlying uterine wall in a functional unit known as a placentone.

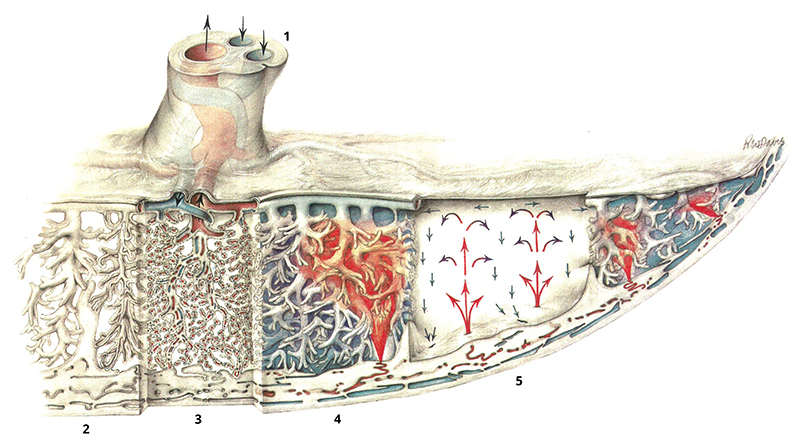
Figure 1. An overview of placental blood flow, from Ramsey & Harris (1966).

The umbilical cord at the top of the image (1) contains two umbilical arteries (blue) and the umbilical vein (red). These connect to the chorionic network that crosses the upper face of the placenta, supplying villous trees beneath. These extend down to the uterine wall (the decidua) at the base of the image. The segments of the illustration show (2) larger ‘stem’ villi of a villous tree, (3) capillaries within villous branches, (4) spiral arteries in the uterine wall supplying a jet of maternal blood that penetrates the intervillous space (IVS) before draining in decidual veins, and (5) the fountain-like recirculation of maternal blood in the IVS within a placentone. The syncytiotrophoblast (SCT) coats the exterior of the villous trees and is in contact with maternal blood.

The placenta offers a diverse fluid-mechanical environment, ranging from the motion of a complex suspension in a deformable and disordered porous medium to flows in jets and through elaborate networks. The past decade has seen imaging techniques (such as X-ray microCT and confocal microscopy) reveal the organ’s intricate three-dimensional (3D) structure in unprecedented detail, driving an upsurge in modeling activity. New images raise challenging questions about how to develop multiscale simulations with potential clinical utility, which are complicated by incomplete data and strong variability. This review provides an overview of recent developments relating to flow and transport in the human placenta in the final trimester of pregnancy, and is intended to complement related reviews on the cardiovascular and reproductive systems in this series (Popel & Johnson 2005; Fauci & Dillon 2006; Van de Vosse & Stergiopulos 2011; Koumoutsakos et al. 2013; Freund 2014; Secomb 2017) and elsewhere (Serov et al. 2016; Clark & Kruger 2017; James et al. 2017).

1. Placental terminology.

• chorion: a layer of fetal tissue, the outer part of which is trophoblast, forming branching villi; the inner part of the chorion faces the amniotic fluid surrounding the fetus

• decidua: the surface of the uterine wall, interfacing with fetal tissue and maternal blood

• endothelium: the tightly packed layer of cells lining tubular blood vessels

• ex vivo (in vivo): relating to conditions involving living tissues outside (inside) the body

• fetal growth restriction (FGR): a set of conditions in which the fetus fails to thrive, often associated with placental pathology

• fetoplacental: relating to the fetal side of the placenta

• hematocrit: the volume fraction of red blood cells in whole blood

• hemochorial: describing placentas (such as in humans) for which maternal blood is in direct contact with chorion

• intervillous space (IVS): the space occupied by maternal blood, exterior to villous trees

• uteroplacental: relating to the maternal side of the placenta

• terminal villus: a peripheral branch of a villous tree, containing fetal capillaries and bounded on its exterior with syncytiotrophoblast

• syncytiotrophoblast (SCT): fetal tissue in contact with maternal blood, comprising a continuous multi-nuclear epithelium that covers villous trees

• vasculosyncytial barrier: the composite barrier separating maternal and fetal blood formed by syncytiotrophoblast, villous tissue and capillary endothelium

2. Flows Across Different Compartments Of The Placenta

2.1. Placental organization

The journey of a molecule delivered from mother to fetus begins with the molecule dissolved in maternal blood leaving a spiral artery to enter the IVS (Figure 1). Diffusing within a parcel of fluid, the molecule is advected along a tortuous path between terminal branches of a villous tree before finally crossing the SCT. For small lipophilic molecules (such as oxygen), diffusion is sufficient to carry the molecule quickly across the SCT; for larger lipid-insoluble molecules (such as amino acids), transport must be facilitated by proteins within both plasma membranes of the SCT. The molecule then diffuses further down concentration gradients into fetal tissue. If it is not taken up by the tissue (in the case of oxygen, for example), it eventually crosses the endothelium of a fetal capillary to enter fetal blood. Thereafter it is swept through the venous side of the chorionic network directly to the umbilical vein and onwards to the fetus. It is evident from this description that for the wide range of molecular species crossing the placenta, different steps in this sequence may be rate-limiting (Burton & Fowden 2015). For dissolved gases that diffuse quickly, transport is more likely to be ‘flow-limited’, i.e. regulated by the rate at which the gases are delivered to, or removed from, a terminal villus by maternal or fetal flow. Thickened fetal tissues in terminal villi may instead make the transport predominantly ‘diffusion-limited,’ while slow active pumping of more complex molecules across the SCT may make the transport ‘membrane-limited.’

A parcel of maternal blood flows past multiple terminal villi on its journey through the IVS, losing a fragment of its nutrient cargo at each encounter. In contrast, the parcel of fetal blood passing through a terminal villus is one of many delivered in massively parallel fashion via the diverging network of fetal arteries, prior to immediate collection by the converging venous network. This arrangement promotes large concentration differences between fetal blood arriving in a terminal villus and the external maternal flow. The price to be paid is potentially large viscous resistance in driving fetal blood through numerous microscopic vessels, and the need to reorganize the maternal circulation in the uterine wall to avoid mechanical damage to fetal tissues.

2.2. Models of blood flow and solute transport

The placenta encompasses a range of flow regimes, with flow speeds (and lengthscales) falling and rising dramatically as blood enters and leaves the organ. Correspondingly, the models of blood flow that we discuss below range from full 3D Navier–Stokes simulations in larger vessels to Stokes-flow simulations in the smallest capillaries, with Darcy’s equation being used to model maternal flow in the IVS. Arterial flows are unsteady at the largest scales (driven by the pumping of maternal and fetal hearts), leading to wave-propagation effects in distensible blood vessels, although unsteadiness is attenuated in smaller vessels where viscous effects dominate.

While it is reasonable to treat blood as Newtonian in larger vessels, the particulate nature of blood has a significant impact on its rheology at lengthscales below a few hundred microns (Secomb 2017). The flexibility of red blood cells drives them away from vessel walls, leading to important non-Newtonian features: the Fårhæus effect describes how red blood cells occupy faster-flowing locations toward the center of a capillary cross-section; the Fårhæus–Lindqvist effect describes the lubricating effect of the peripheral cell-free layer in reducing the effective viscosity of blood in vessels of around 10µm diameter; and the phase separation (plasma-skimming) effect describes how red blood cells and plasma (in which they are suspended) partition at divergent bifurcations. One popular modeling approach is to exploit empirical relationships between hematocrit (red blood cell volume fraction) and effective viscosity derived from careful experiments (Pries et al. 1996). This ‘Pries–Secomb’ model is amenable to a 1D description of network flow in cylindrical vessels, but has yet to be adapted to more complex geometries.

A hierarchy of models are used to describe solute transport in blood, derived from the 3D transport equation for the concentration field C(x, t) of a passive solute in a homogeneous fluid with velocity field u and molecular diffusivity D,

$$C_t+u\cdot \nabla C=D{\nabla }^{2}C.$$ 1

An important modification is necessary to describe oxygen transport in blood, to account for the fact that oxygen binds preferentially to hemoglobin in red blood cells. The equilibrium between oxygen dissolved in plasma and oxygen bound to hemoglobin can be described by a Hill equation (the oxygen–hemoglobin dissociation curve). Accounting for the fact that diffusion of oxygen dissolved in plasma (with concentration C) dominates diffusion of bound oxygen in red blood cells, the transport equations for the two species can be combined to give

$$\left(\frac{\partial }{\partial t}+u\cdot \nabla \right)\left(C+C_{\max }\frac{{\left(C/C_0\right)}^{\alpha }}{1+{\left(C/C_0\right)}^{\alpha }}\right)=D_p{\nabla }^{2}C$$ 2

where C₀ ≈ 0.033mol/m³, C_max ≈ 7.3mol/m³ for maternal blood at a physiological hematocrit (or C_max ≈ 9.8mol/m³ for fetal blood) and α ≈ 2.65 (Serov et al. 2015b; Pearce et al. 2016). D_p denotes oxygen diffusivity in plasma. Linearization of the nonlinear Hill function in (2) leads to the approximation (1) but with the left-hand-side multiplied by a factor B ≈ 94 for maternal blood (or B ≈ 140 for fetal blood), boosting the effective Péclet number of oxygen (measuring the relative strength of advection to diffusion) by two orders of magnitude. We discuss further modifications of (1) below that have been proposed for intervillous transport, incorporating solute uptake terms.

We now address recent studies of different compartments, moving from the fetal to the maternal side of the placenta. We focus on flow in the conducting regions (Secs 2.3 and 2.7), and flow plus solute transport in the exchange regions (Secs 2.4 and 2.6); we briefly touch on subcellular transport processes in Sec. 2.5. A recurrent theme is identifying the transitions between flow-limited and diffusion-limited transport in the exchange units, for each of which an appropriate effective Damköhler number

$${\text{Da}}_{\text{eff}}=\frac{\text{uptake}\text{rate}\times \text{lengthscale}}{\text{flow}\text{speed}}=\frac{\text{transit}\text{time}}{\text{uptake}\text{time}}$$ 3

is of order unity: when Da_eff » 1, flow speed can be increased to enhance uptake; when Da_eff « 1, flow speed can be reduced without loss of uptake. We will see how the parameters appearing in (3) vary between compartments and across scales.

2.3. Umbilical vessels and the chorionic villous network

Two umbilical arteries and the umbilical vein, wrapped in a deformable porous matrix known as Wharton’s jelly, together form the umbilical cord (Ferguson & Dodson 2009). Typically, the vessels coil around each other in a helical fashion. While the pitch of the helix has been shown to influence flow resistance and wall shear stress distributions (at least in steady flow (Kaplan et al. 2010)), the coiled structure may also play a role in the mechanical stability of the cord, for example under compression or bending (de Laat et al. 2005). Flow simulations by Saw et al. (2017) in helical tubes having shapes and flow speeds representative of umbilical arteries from weeks 32 and 33 of gestation show the development of a pair of asymmetric Dean vortices and a distorted axial velocity profile. The latter is significant because errors may be incurred by assuming a Poiseuille profile when inferring flow rates and wall shear stresses from Doppler ultrasound measurements of the maximum axial velocity (Saw et al. 2017).

A bifurcating network of vessels emerges from the base of the umbilical cord, spreading over the chorionic plate before penetrating downwards into the body of the placenta (Figure 2a). The venous and arterial networks follow similar patterns (Benirschke et al. 2012).

Figure 2.

(a) A 3D reconstructed image of an arterial cast of a fetoplacental network following microCT scanning, from Junaid et al. (2017). (b) A 3D reconstruction of a terminal villus, obtained from confocal microscopy showing capillaries (green) and SCT (brown); from Plitman Mayo et al. (2016a). (c) A segmented image from a 2D cross-section through villous tissue, showing fetal capillaries (black) confined in villous branches bounded by SCT (brown lines); from Gill et al. (2011). The vasculosyncytial barrier is very thin where capillaries almost touch the SCT.

A variety of geometric models have been proposed to mimic the network shape, relating the distribution of vessels on the chorionic plate to the location of the cord insertion. Models have been based on diffusion-limited aggregation (Yampolsky et al. 2008; Kato et al. 2014), stochastic growth in response to a chemoattractant (Cotter et al. 2014) and a volume-filling algorithm that generates a random asymmetric network with well-defined statistical properties (Clark et al. 2015). Cord insertion near the periphery of the chorionic plate promotes so-called monopodial branching of chorionic vessels (small lateral bifurcations from a primary vessel), in comparison to more symmetric dichotomous branching when the cord inserts centrally; steady Navier–Stokes simulations by Gordon et al. (2007) suggest that the monopodial structure is energetically more efficient for long-distance transport. Clark et al. (2015) used a Poiseuille-resistance model in a volume-filling network to demonstrate that marginal cord insertion (which has been associated with adverse pregnancy outcomes (Ismail et al. 2017)) promotes more heterogeneous transport across the villous network.

Among models that exploit anatomical data more directly, Franke et al. (2003) simulated pulse-wave propagation across a 25-vessel arterial network obtained from a cast of a single placenta that supported twin fetuses. They solved coupled spatially-1D hyperbolic equations for inviscid flow in flexible tubes, imposing a reflection condition at the periphery of the network to mimic the terminal resistance. This approach is valuable in predicting the waveform imaged by Doppler ultrasound, superseding simpler models in which individual vessels are represented by resistance and compliance elements (Thompson & Trudinger 1990; Guiot et al. 1992). Franke et al. (2003) showed how wave reflection at the periphery of their network could generate reverse flow at the umbilicus, and they explored the impact of different anastomoses (shunts) connecting the two fetal circulations. Viscous attenuation was incorporated in a model of pulsatile flow in the umbilical artery by Kleiner-Assaf et al. (1999), adapting results of Atabek & Lew (1966) for propagation of small-amplitude long-wavelength disturbances in a flexible tube, demonstrating the impact of some material and geometric properties on flow indices commonly recorded in Doppler ultrasound measurements; however they did not account directly for the effect of wave reflections at the junction with the chorionic network. Some of the limitations of Doppler ultrasound in detecting mild occlusions in the chorionic network were demonstrated experimentally using an ex vivo perfusion model by Gordon et al. (2016).

MicroCT imaging of chorionic vascular casts has recently revealed the 3D network structure in the human placenta of vessels down to around 80µm in diameter (Figure 2a, Junaid et al. (2017)). Similar imaging techniques have been used to compute flows in villous networks taken from rodents, which also have a hemochorial placenta, albeit with more labyrinthine networks than humans (Carter 2007). Resolving vessels down to 35 µm diameter, Rennie et al. (2017) showed that the mouse has between 8 and 9 generations in its arterial and venous villous networks (using the ordering system of Strahler (1957)), with almost half of the estimated vascular resistance (evaluated using the Pries–Secomb model, see Sec. 2.2) arising in the villous arteries, and around a quarter in the umbilical vessels. Bappoo et al. (2017) computed steady 3D flow through an 89-vessel sub-network model from a rat (including vessels down to 30µm) using three constitutive models, showing heterogeneous patterns of wall shear stress. Shear stress is significant in this context because it can influence vascular resistance, as revealed by ex vivo perfusion experiments on human placenta (Jones et al. 2015). Vascular resistance can be actively regulated by the smooth muscle lining small fetoplacental vessels. In the absence of neural regulation, vasodilation in the placenta must be mediated by chemical or mechanical signals, with shear-stress-induced release of nitric oxide by endothelial cells being an important mechanism; disruption of this pathway may explain the poor vasodilatory response and high vascular resistance in the condition known as fetal growth restriction (FGR) (Jones et al. 2015). In addition to regulating flow, variable vascular resistance will determine the pressure distribution in fetal vessels: this is potentially important in ensuring that fetal vessels remain patent under exposure to the pressure of maternal blood (which fluctuates as the mother changes posture) and in regulating water transport between maternal and fetal blood (Sebire & Talbert 2002).

2.4. Fetoplacental capillary networks in terminal villi

Capillaries in the terminal branches of the villous tree form elaborate and irregular networks characterized by loops and, in the mature placenta, sinusoids (localized dilations, Figure 2b,c). The exchange capacity of these networks is regulated by numerous factors, including the total capillary surface area within a villous branch (often measured with respect to the outer surface area of the SCT confining the branch), the mean diffusion distance across villous tissue (between the capillary endothelium and the SCT), the flow resistance offered by the capillary network and the metabolic demands of the villous tissue itself. The looping structure of the networks suggests that countercurrent and shielding effects may have an impact on solute exchange. The networks develop in a matter of weeks, show considerable variability in their spatial organization, serve as exchange units for numerous solutes and are ultimately discarded, suggesting that a degree of robustness in their structure may be more important than optimization to fulfil one specific objective.

Confocal laser microscopy has recently revealed the 3D structure of a handful of capillary networks (Jirkovská et al. 2008; Plitman Mayo et al. 2016a; Perazzolo et al. 2017b), enabling transport simulations to be performed on realistic geometries. In addition to establishing the dominant physical processes, quantitative characterization of the performance of each capillary network is important in developing multiscale simulations of placental function. Key features of the networks can then be encapsulated as boundary conditions at the terminal ends of fetal villous trees (Clark et al. 2015), and as volumetric sources or sinks of solute in simulations of maternal flow in the IVS. However, the number of samples currently imaged is too small to provide reliable statistics describing the geometric properties of the network population as a whole.

An upper bound (N_max, say) on a network’s exchange capacity arises when transport is ‘diffusion-limited’: if fetal flow in the capillaries and maternal flow external to the villous surface are both sufficiently rapid to maintain fixed concentrations of a solute at the interfaces between each solid-fluid phase, then the rate of solute exchange is determined solely by the diffusive flux through villous tissue (ignoring for now additional transport barriers at the capillary endothelium or SCT). N_max is determined primarily by the 3D arrangement of capillary vessels within the terminal villus and can be expressed as D_tΔC ℒ, where D_t is the solute diffusivity in fetal tissue and ΔC is the solute concentration difference between the external interface of the villous branch and fetal blood entering the capillary network. The length ℒ is derived purely from the size and shape of the villous branch and is a measure of exchange area over exchange distance. (More precisely, N_max describes the diffusive flux over the internal boundary of villous tissue and the identical flux across the external boundary, both of which are area integrals of D_t times the normal derivative of the concentration field.) As a simple example, an axisymmetric annular cylinder of length L and inner and outer radii a and b respectively supports a diffusive flux proportional to ℒ = 2πL/log(b/a), implying a relatively weak dependence on the inner radius a unless it is very close in magnitude to b. If the inner cylinder is offset (Figure 3a), coming within a small minimum distance δ of the outer boundary (with 0 < δ « b − a), the flux grows significantly, with

$$ℒ\approx \pi L{\left(\frac{2ab}{(b-a)\delta }\right)}^{1/2}$$ 4

(a limiting case of a result obtained by conformal mapping by Gill et al. (2011)). This expression demonstrates the beneficial impact on diffusive transport of the very thin vasculosyncytial barrier bounding capillary sinusoids; numerous examples are evident in the cross-section shown in Figure 2c.

Figure 3.

(a) For an eccentric annulus, of inner radius a, external radius b, minimum thickness δ(≪ b − a) and length L, with fixed concentrations on each circular interface, the diffusive flux between interior and exterior is proportional to the geometric factor as ℒ approximated by (4). (b) Colors show the magnitude of the diffusive flux (in mol/m²s) in a planar cross section across the 3D terminal villus shown in Figure 2b, from a computation by Plitman Mayo et al. (2016a). (c) Solute uptake N versus pressure difference ΔP in three small villous networks, computed by Pearce et al. (2016). These relationships can be approximated in terms of the effective Damköhler number Da_f by (5).

To assess the diffusive capacity of realistic tissue geometries, Gill et al. (2011) evaluated steady diffusive fluxes across planar cross-sections of a population of villous branches, capturing the effects of diffusional screening that takes place between neighboring capillaries within a branch. Likewise, image-based computations in 3D of purely diffusive transport in four capillary networks by Plitman Mayo et al. (2016a) (Figures 2b and 3b) showed how solute gradients are largest where the interfaces confining fetal and maternal blood are closest (for example at sinusoids, consistent with (4)), making fluxes heterogeneous across the external villous surface. In practice, transport can be limited by fetal flow, as Plitman Mayo et al. (2016b) demonstrated by computing flow and transport within the fetal vessels of their imaged networks. Treating fetal blood as Newtonian and coupling (1) for oxygen transport in the capillary lumen to diffusive transport in the villous tissue (assuming a fixed concentration at the SCT), they showed how oxygen flux rises as the flow increases in strength. Their calculations highlighted a common difficulty in computations on microvascular networks, namely in reliably identifying inlets and outlets of capillary flow from an image of an incomplete network.

Strongly flow-limited transport occurs when the fetal flow is so slow that the fetal blood entering the capillary network rapidly comes into equilibrium with its surroundings (via transverse diffusion within capillaries, combined with equilibration of solute concentration within villous tissue), so that the rate at which (for example) fully oxygenated fetal blood leaves the network is directly proportional to the speed of flow leaving the network. If the flow speed increases, axial advection starts to dominate transverse diffusion in the capillaries, so that, at high flow speeds, diffusion may be confined to thin boundary layers close to the vessel walls throughout the network. This regime resembles the classical solution for heat transfer into a shear flow from a flat plate at high Péclet number (Lév ê que 1928). A sufficient increase in flow speed will always bring the system into the regime in which diffusive transport through villous tissue is rate-limiting. Combining scaling arguments based on these physical principles with computations in three villous networks (Figure 3c), Pearce et al. (2016) developed an approximation for the exchange capacity of a given capillary network through a relationship between solute flux N and flow strength taking the form

$$N\approx \frac{N_{\max }}{1+{\text{Da}}_f+{\text{Da}}_F^{1/3}}\text{where}{\text{Da}}_f=\frac{D_tℒR}{B\Delta P},{\text{Da}}_F={\left(\frac{D_tℒ}{D_p{L}_c}\right)}^2\frac{{\text{Da}}_f}{{\alpha }_c^3}.$$ 5

Here ΔP is the pressure drop across the network (between a single inlet and a single outlet), the factor B accounts for oxygen–hemoglobin binding kinetics (from linearizing (2)), R is the viscous resistance of the network (which ideally can be computed directly by CFD), α_c ≈ 5.5 (from the Lévêque solution) and L_c is the total centerline length of the vessels in the network. For sufficiently small ΔP (and large Da_f, the strongly flow-limited regime), N ≈ N_max/Da_f ≡ ΔC BΔP/R, showing how N rises with ΔP ; in contrast, for sufficiently large ΔP (the diffusion-limited regime with Da_f ≪ 1, Da_F ≪ 1), uptake saturates at N ≈ N_max (see Box 2). The approximation (5) was validated for three small networks by Pearce et al. (2016) but it requires further assessment, for example in regard to potential countercurrent effects in more complex networks. It is important to recognize that parameters such as D_t and B vary for different solutes, and that these estimates take no account of additional transport limitations at the membrane level (Sec. 2.5) or in the IVS (Sec. 2.6), nor factors such as metabolic uptake by villous tissue.

Models describing microvascular rheology (such as the Pries–Secomb description of the

2. Two transitions between flow-limited and diffusion-limited states.

Two distinct transitions can be identified in (5) and the uptake/flow-rate relations in Figure 3c. If the exchange areas across the villous tissue are small, exchange distances are large or diffusion in tissue is slow relative to plasma (i.e. D_tℒ ≪ D_pL_c), the strongly flow-limited regime saturates directly at N_max as ΔP increases: the relevant effective Damköhler number (see (3)) is Da_f and N ≈ N_max/(1 +Da_f); the effective Péclet number Pe = BΔP/(RD_pL_c) is low in this case. For capillary networks with much greater capacity for diffusive transport (with D _t ℒ ≫ D_p L_c), an intermediate ‘weakly flow-limited’ regime emerges with N ∝ ΔP^1/3 before saturation occurs at very high flow speeds (the Da_eff describing this transition is Da_F and $N\approx N_{\max }/\left(1+{\text{Da}}_F^{1/3}\right))$ Pe is high in this case. Most networks will likely sit between these two limits.

Fårhæus, Fårhæus–Lindqvist and phase separation effects which allow simulation of flow in 1D representations of vascular networks, e.g. Kiani et al. (1994); Pop et al. (2007)) can be adapted to fetoplacental capillary networks, although their accuracy in describing more irregular features (such as sinusoids) will need careful assessment. Fortunately, simulations capable of resolving suspensions of red blood cells are now able to address such questions and are offering important new insights to capillary network flows (Fedosov et al. 2010; Krüger et al. 2013). Notably, Balogh & Bagchi (2017) demonstrated how spatial and temporal fluctuations in hematocrit distributions are generated by ‘lingering’ groups of red blood cells at bifurcations. Randomness therefore impacts transport both through stochastic fluctuations in the flow and the highly variable network geometry.

2.5. The vasculosyncytial barrier

The vasculosyncytial barrier is the composite interface between maternal and fetal blood, bounded by the SCT and capillary endothelium. Passive diffusion is sufficient to transport small lipophilic solutes, such as respiratory gases (O₂, CO₂) and urea, across the barrier. Some small hydrophilic pharmaceutical compounds, such as mannitol, do not dissolve in the plasma membrane but are believed to cross the barrier passively via water-filled paracellular channels or denuded regions of the SCT (Desforges & Sibley 2010). However, the diffusion of such molecules across the membrane is much slower than that in plasma, rendering them diffusion-limited. Similarly, water transfer between the maternal and fetal circulations occurs over the semi-permeable membrane, regulated by hydrostatic and osmotic pressure differences (Wilbur et al. 1978; Brownbill & Sibley 2006).

A very broad class of hydrophilic substances, including glucose (Hay et al. 1990; Barta & Drugan 2010), amino-acids (Sengers et al. 2010; Panitchob et al. 2015; Widdows et al. 2015), ions and larger hydrophobic molecules, such as fatty acids (Perazzolo et al. 2017a), are predominantly transported across the SCT membrane via specialized membrane transporters, which typically require a supply of energy at the cellular level to operate. The nonlinear transporter-mediated kinetics is typically described by compartmental models that assume fixed solute concentrations in maternal and fetal blood. Although transport of these substances is classed as strongly diffusion-limited, there is preliminary evidence of an indirect effect of inhomogeneous IVS flow, reflected by a non-uniform distribution of membrane transporters over the outer surface of the SCT membrane (Rohan M. Lewis, personal communication).

In addition, some very large proteins, e.g. immunoglobulins, are transported by endo- or exocytosis involving subcellular vehicles shuttling across the villous SCT and endothelial cells (Sibley et al. 2018). Transport of many polar molecules and ions is likely affected by an electrostatic potential difference across the placental barrier, although this has not been identified conclusively in humans and may vary at different stages of pregnancy (Sibley et al. 2018). Future models will need to account for subcellular transport via cytosis and electrokinetics.

2.6. The intervillous space

Models of maternal blood flow in the IVS currently fall into two categories: pore-scale models that resolve features at the level of individual villous branches (at an approximately 50µm scale); and models addressing features on the cm scale of a complete villous tree that adopt a homogenized description of pore-scale processes. Most researchers model blood as Newtonian, using the Stokes equations at the pore scale and Darcy’s equation at the tree scale (each description being modified to account for inertial effects in some circumstances). Solute transport is generally described by (1) or (2) at the pore scale, supplemented with an uptake boundary condition on the SCT, or a homogenized advection-diffusion-uptake equation at the tree scale. Existing macroscopic models have relied on semi-empirical parametrizations of pore-scale effects, and are yet to take systematic advantage of advances in 3D imaging that have provided a significant boost to microscopic models. Questions relating to spatial variability intersect both levels of description, such as how well a simulation of an individual pore flow represents a population of such flows, and how well a relatively simple continuum description at the macroscale captures transport in, and the properties of, a strongly disordered medium.

2.6.1. Tree-scale models

In physical terms, the functional unit at the scale of a single villous tree (the placentone, Figure 1) consists of a porous medium in a box that has openings in one wall, representing a single spiral artery in the uterine wall and nearby decidual veins. Maternal blood enters and leaves the domain through these vessels, passing in the interim through the IVS external to the branches of a villous tree. Models treating the tree as a continuum are helpful in addressing how this spatial arrangement of vessels, and the homogenized properties of the tree, influence the delivery of nutrients to the fetal circulation within the tree. Ultrasound evidence indicates that blood can emerge from the spiral artery either as a continuous diffuse stream (reported in a primate study by Ragavendra & Tarantal (2001)) or as a jet entering a cavity in the tree, suggesting a significant role for inertia (Collins et al. 2012). There is evidence from historical X-ray imaging that the villous branches are sufficiently deformable to be displaced by flow (reported by Erian et al. (1977)), although their spatial arrangement under in vivo conditions remains to be fully characterized.

In a pioneering contribution, Erian et al. (1977) treated the placentone as a rectangular box fully occupied by porous material. They solved a 2D Darcy problem computationally, using a permeability field that depends on position (to mimic the central cavity) and that increases monotonically with flow speed (capturing some aspects of deformability of the villous tree but without encompassing poroelasticity). Chernyavsky et al. (2010) extended this description to 3D by representing the placentone as a hemispherical domain, with maternal vessels in the planar wall represented as a point source (a spiral artery) and two sinks (decidual veins), deriving an analytic expression for the streamfunction using the method of images. In its simplest form, Darcy’s equation implies that the pressure field in a porous-medium flow is harmonic (∇²p = 0), implying that the depth to which the flow penetrates the porous medium is comparable to the distance between the sources and sinks: thus a decidual vein lying too close to a spiral artery offers a ‘short-circuit’ for the flow that degrades nutrient transfer. This feature is offset by the presence of a cavity adjacent to the opening of the spiral artery, as illustrated in simulations by Lecarpentier et al. (2016) (using a Brinkman/Forchheimer model of the porous domain in 2D) and Saghian et al. (2017) (using a Darcy model); in both studies the 2D Navier–Stokes equations were used to describe the jet emerging from the spiral artery into the neighboring cavity. The strength of the jet is regulated by the size and shape of the spiral artery, discussed in Sec. 2.7 below.

With the flow determined, patterns of nutrient concentration across the tree can be evaluated. Assuming a dominant balance between advection and uptake, Chernyavsky et al. (2010) highlighted the influence of the volume fraction ϕ_v of villous material on the overall performance of the placentone. ϕ_v influences two macroscopic parameters: the permeability of the porous medium (taken to be proportional to ${\left(1-{\varphi }_v\right)}^3/{\varphi }_v^2$ according to the Carman–Kozeny equation); and the solute uptake rate (assumed proportional to ${\varphi }_v^{2/3}$). Increasing ϕ_v increases the flow resistance, reducing perfusion (assuming maternal flow is driven by a fixed pressure drop), but also increases the surface area available for uptake. Such parametrizations of pore-scale behavior, so critical to a multiscale description, need refinement in future studies. A step in this direction has been taken by Lin et al. (2016), who coarse-grained a model of a villous tree in a 2D finite-element framework to provide a map of permeability and uptake parameters that are spatially heterogeneous, informing simulations of flow and oxygen transfer. This approach provides a mechanistic link between the tree’s branching structure and its exchange efficiency, which may be disrupted in FGR.

2.6.2. Pore-scale models

Until relatively recently, the complex 3D shape of the IVS had been accessible only from 2D images such as Figure 2c, assessed by random sampling using stereology (Mayhew 2006), which (for example) estimates average volumes from area measurements. Here a central question is how best to identify geometric measures that provide useful insights into transport processes. Simple measures include the villous area fraction in a 2D image, ϕ_a, and the effective villi radius, r_e (defined as twice the villous area intersecting a cross section divided by the total villous perimeter in the cross section). Cross-sectional images such as Figure 2c have recently been exploited by considering 2D flow in the plane of a cross-section, and unidirectional flow in the direction normal to a cross-section.

Lecarpentier et al. (2016) used a planar histological cross section (from the chorionic plate to the decidua) as the basis of a steady 2D Navier–Stokes flow. Using a Carreau model to represent shear thinning of maternal blood, they predicted values of shear stress on the SCT below typical values in other blood vessels (under 5 dyn/cm²). Significantly, their computation illustrates the strongly heterogeneous nature of flow patterns in a highly disordered porous medium (Figure 4a), revealing sparsely distributed high-speed channels. Such heterogeneous perfusion appears to be a generic feature of transport in disordered porous media (De Anna et al. 2013; Alim et al. 2017), challenging the relevance of the Darcy model and traditional reactive transport equations in describing flow at the scale of the placentone.

Figure 4.

(a) A subdomain of a 2D computation of flow in the IVS, from Lecarpentier et al. (2016), showing heterogeneous flow patterns characteristic of strongly disordered media. Colors show flow speed; villi are white inclusions. (b) A ‘stream-tube’ representation of flow parallel to villous branches (white disks), showing relative oxygen concentration; from Serov et al. (2015a) (c) Solute flux over the surface of terminal villi, from a 3D computation by Perazzolo et al. (2017b) (flow is from the bottom right to the top left face of the box; box size 0.78 × 0.78 × 0.25mm). (d) Flow streamlines emerging from a spiral artery at peak systole into the IVS (block size 3 × 2.5 × 2mm; from Roth et al. (2017)). This example mimics FGR, when the spiral artery fails to widen at its mouth, creating a more pronounced jet in the IVS (artery outlet diameter 0.39mm, maximum flow speed (red contours) of 80 cm/s).

The ‘stream-tube’ model of Serov et al. (2015a,b) addresses instead the passage of maternal blood parallel to an array of villous branches, modeled as a set of non-overlapping parallel cylinders randomly arranged within a larger cylindrical domain (Figure 4b). Oxygen is advected axially in the fluid phase and diffuses transversely, being taken up along the wall of each cylinder at a rate determined by a membrane permeability w. A linearized model is adopted for oxygen–hemoglobin dissociation kinetics in maternal blood (see Sec. 2.2). For simplicity, the axial flow in the IVS is assumed uniform with magnitude u. The advection-diffusion transport equation for oxygen then has constant coefficients and is solvable using an eigenfunction expansion (the problem reduces to a 2D Helmoltz equation in a domain containing multiple inclusions). Serov et al. show that for solute at initial concentration ΔC being swept across a region of area S, the oxygen uptake over an axial distance L_m can be approximated by

$$\frac{f_{\max }}{{\text{Da}}_m}\left[1-e^{-{\text{Da}}_m}\right],\text{where}{\text{Da}}_m\equiv \frac{2w\kappa L_m}{r_{e}Bu}\frac{{\varphi }_a}{1-{\varphi }_a}$$ 6

and f_max = 2ΔCwκL_mϕ_aS/r_e Here, κ is an order-unity parameter that depends on the arrangement of villous branches in the plane and arises from an eigenvalue calculation. The factor (1 − ϕ_a) multiplying u in (6) modifies the interstitial flow speed to give the speed averaged over the cross-section; B represents enhanced transport by binding of oxygen to hemoglobin (see (2)). The function (6) has a maximum with respect to ϕ_a for fixed effective villi radius r_e and fixed interstitial flow speed u, because increasing villous area fraction decreases the advective flux while increasing the interface available for uptake. While this offers a credible prediction for the optimal volume fraction ϕ_a, the model does not account for the increased viscous resistance to flow as ϕ_a increases towards unity, which is likely to influence u.

Figure 3c and (5) show how fetal uptake N transitions from strongly flow-limited transport when advection is very weak (with uptake linear in flow speed and independent of vessel length) to a diffusion-limited state when advection is very strong. Likewise, the expression for maternal transport (6) rises from the flow-limited value c₀Bu(1 − ϕ_a)S ≡ f_max/Da_m when Da_m ≫ 1 to the diffusion-limited value f_max as Da_m becomes very small. When Da_m (the effective Damköhler number in this case, see (3)) is of order unity, the maternal solute is fully absorbed using the entire domain.

Analogous transitions appear in models of steady unidirectional advection and diffusion past an array of sinks. Chernyavsky et al. (2011) and Russell et al. (2016) showed how solute transport past an array of point sinks (representing terminal villi) of strength w distributed periodically or uniformly randomly with mean spacing r_e along a line of length L_m (where r_e ≪ L_m) can be approximated by the homogenized model uC_x = D_pC_xx − (w/r_e)C in 0 ≤ x ≤ L_m. For large Péclet number (uL_m ≫D_p), the transition between flow-limited and diffusion-limited uptake at the sinks arises when the effective Damköhler number wL_m/(ur_e) is of order unity; at even larger Péclet number (ur_e » D_p), diffusive boundary layers appear upstream of each sink and the net uptake rate is given by (6) with f_max = ΔCwL_m/r_e and Da_m = wL_m/(ur_e), illustrating the generic nature of this approximation. In practice, shear-flow effects across concentration boundary layers around terminal villi can be expected to lead to uptake dependent on (ur_e/D_p)^1/3, as described for example by Wang & Sangani (1997) for high-Péclet number flow past an array of cylinders.

Initial steps in exploiting recent 3D imaging data at the pore scale have been taken by Lecarpentier et al. (2016), who computed Navier–Stokes flow past a terminal villus in a cylindrical domain. Their model predicts large shear stresses on the tips of terminal villi, although this may be an artefact of neglecting the crowded nature of the flow in the IVS. Perazzolo et al. (2017b) imaged placental tissue with confocal microscopy, staining the SCT and fetal endothelium in order to identify the villous surface and the internal capillaries. Using segmented images, Perazzolo et al. (2017b) computed 3D Stokes flow in the IVS and coupled (1), describing solute transport in the IVS, to purely diffusive transport across the villous barrier; fetal vessels were treated as solute sinks. The solute flux is predicted to be heterogeneous across the trophoblast (Figure 4c); further studies are required to relate the distribution of such ‘hot-spots’ to factors such as the variable thicknesses of the villous tissue (see (4)) and the arrangement of concentration boundary layers as maternal blood sweeps over protrusions of the villous branch.

2.7. Utero-placental flow

Radial arteries carry maternal blood through the muscular wall of the uterus (the myometrium) towards the decidua (the endometrium), where they supply a network of tortuous vessels known as spiral arteries. Early in pregnancy, trophoblast cells invade the decidua and remodel the spiral arteries, generating openings in the decidua that allow maternal blood to enter the IVS. Remodeling involves the disruption of the muscular lining of the spiral arteries, replacement of endothelium by trophoblast cells and dilation of these vessels (which normally have a radius of approximately 0.25mm) over a 2-3mm distance near each opening (Burton et al. 2009). In vivo imaging using Doppler ultrasound reveals the existence of jets of maternal blood at it enters the IVS (Collins et al. 2012). Recent theoretical studies have addressed the relationship between spiral artery remodeling and jet formation. This is significant because abnormal remodeling can be associated with FGR and preeclampsia, conditions in which nutrition and oxygenation of the fetus are impaired.

The Reynolds number Re of spiral artery flow has been estimated to be in the range 20 to 80 (Burton et al. 2009). A funnel-shaped dilation near the mouth of the spiral artery will reduce the cross-sectionally averaged flow speed and reduce the net pressure drop along the vessel. Burton et al. (2009) computed the viscous pressure recovery associated with the dilation by (essentially) a lubrication theory argument, assuming a Poiseuille velocity profile. If flow separation within the dilation is avoided, an inertial contribution to the pressure recovery via the Bernoulli effect can also be anticipated (of magnitude Re times the slope of the dilation, relative to the viscous component), although this was not included in their analysis. The momentum of fluid entering the IVS favors the formation of a jet with the potential to penetrate deep into the compliant villous tree. This can be mediated by the presence of a cavity in the villous branches adjacent to the opening of the spiral artery, ensuring that delicate villous tissues are not exposed to high stresses. Simulations of flow into such a cavity reveal the potential for flow separation within the dilated section of the spiral artery, and the impact of cavity size on jet length (Saghian et al. 2017).

The structure of the jet was investigated by Roth et al. (2017), who built a 3D geometric reconstruction of a spiral artery opening into the IVS (Figure 4d). Modeling blood using the Navier–Stokes equations, and using Doppler ultrasound measurements to inform a pulsatile inlet condition, they simulated the emergence of a jet into the IVS and its interaction with villous tissues. Their computations demonstrate how the absence of a dilation at the spiral artery outlet (mimicking FGR) promotes the formation of vortices at the base of the jet, leading to a less uniform distribution of blood to the IVS and locally elevated shear stresses on the villous surface. This was supported by histological evidence of elevated trophoblast shedding in FGR and preeclampsia. Simulations also revealed an increase of pressure along streamlines as they enter the IVS, not present with spiral artery dilation; this is potentially significant because high pressures may compress villous tissue, impairing fetal blood flow (Karimu & Burton 1994).

The striking morphology of spiral arteries has generated considerable debate (Pijnenborg et al. 2006), including suggestions of providing reserve length during uterine growth, and increasing viscous resistance to, and damping the pulsatility of, maternal blood flow; disruption of the elastic and muscular components of the arterial wall may also contribute to the latter feature. Upstream of the spiral arteries, ultrasound imaging of flows in the uterine arteries provides clinicians with a potential window of placental function (Pennati et al. 2008; Rigano et al. 2010). Models coupling uterine flows to those passing through the spiral arteries and into the IVS will be important in fully exploiting this imaging technique.

3. Challenges

Having surveyed existing models, we now discuss a few areas where there are significant open questions.

3.1. Coupling maternal and fetal placental transport

Studies of transport in individual compartments of the placenta, described above, must be coupled in order to describe solute exchange across the organ as a whole. Early approaches to this problem were influenced by models of co- and counter-current heat exchangers. Faber (1995) for example used this approach to explain how the level of flow limitation of oxygen transfer provides a safety window should either the maternal or fetal circulation be compromised. An estimate emerging from the studies reported in Section 2 is given in Box 4. There is clearly significant potential for refining and generalizing expressions such as (7) to account for realistic pore geometries and transport mechanisms. Multiscale approximations, exploiting large-scale computation, model reduction or homogenization approaches, are promising avenues (Chernyavsky et al. 2011; Clark et al. 2015). The variability of spatial

4. Quantifying solute exchange between mother and fetus.

We can connect fetal and maternal transport by identifying w in (6) with N/(AΔC) from (5), where A measures the area of a terminal villus exposed to maternal flow. This suggests that overall exchange between maternal and fetal circulations in a single placentone can be approximated by an expression of the form

$$\underset{geometry}{\underbrace{N𝓛A}}\underset{diffusion}{\underbrace{D_t\Delta C}}\underset{flow}{\underbrace{F\left({\mathrm{Da}}_f,{\mathrm{Da}}_m;\dots \right)}}.$$ 7

Here ΔC represents the concentration difference between incoming maternal and fetal blood, N is a measure of the number of terminal villi in the placentone and A measures the proportion of available area for exchange that is accessible by maternal flow. (In (6), N appears as L_m/r_e, estimating the number of villi encountered by a parcel of maternal blood as it travels from spiral artery to decidual vein and A is represented by κϕ_aS/A.) D_t can be modified if necessary to account for membrane-barrier effects described in Sec. 2.5. F is a dimensionless function that falls from F (0, 0, …) = 1 (the completely diffusion-limited state) to zero as the effective Damköhler numbers for fetal and maternal flow, Da_f and Da_m, increase. (Candidate expressions for F, Da_f and Da_m are provided by the estimates in (5) and (6), suggesting $F={\text{Da}}_m^{-1}\left(1-e^{-{\text{Da}}_m}\right)/\left(1+{\text{Da}}_f+{\text{Da}}_F^{1/3}\right)$.) The dots in (7) emphasize additional dependence in F on dimensionless quantities such as D_t ℒ/D_pL_c on the fetal side and D_t ℒL_m/D_pA on the maternal side, to allow dependence on local Péclet numbers.

structures, within terminal villi and across the IVS, requires statistical characterization and careful integration. Perturbative methods can be used to describe the effects of weak disorder (Russell et al. 2016; Russell & Jensen 2018) but fully stochastic techniques will likely be essential. The computational cost of quantifying variability in complex computational models remains a major challenge.

3.2. Blood rheology in irregular geometries

Empirical characterization of blood rheology in small tubes (Pries et al. 1990) has proved a successful and accessible low-dimensional model for flow in capillary networks. However simulations resolving individual deformable red blood cells have revealed important features not captured by this approach, such as temporal fluctuations associated with cells negotiating bifurcations in capillary networks (Freund 2014; Balogh & Bagchi 2017). Such effects are not accessible via non-Newtonian constitutive models of the kind used so far to model placental flows (Lecarpentier et al. 2016; Bappoo et al. 2017). Little is known at present about the impact of the highly irregular shape of the fetoplacental capillaries and IVS on blood rheology in the placenta. This could be addressed, for example, by combining image-based simulations of a blood suspension and ex vivo tissue perfusion experiments (Nye et al. 2018). Likewise, there are many intriguing questions regarding the physical processes by which spiral arteries in the uterine wall are plugged with trophoblast cells in early pregnancy before opening to the IVS in the second trimester (Burton et al. 1999).

3.3. Uterine biomechanics, placental poroelasticity and blood flow regulation

The placenta is a soft composite material that is subjected to complex transient mechanical loads. On the maternal side, these may arise from peristaltic contractions of the uterine wall, postural changes of the mother (associated with daily living or sporting activity) and possibly from more extreme situations such as emergency deceleration in a vehicle, which could result in a catastrophic placental abruption (Hu et al. 2009). Fetal movements induce stresses indirectly via the umbilical cord and directly by an occasional impact with fetal limbs. Shear-wave elastography provides a non-invasive method to estimate the stiffness of placental tissue (Habibi et al. 2017) but more complex constitutive features have yet to be characterized. As placental tissue lacks stiff supporting inner structures, a poroelastic description may be appropriate. However, with a few exceptions (Erian et al. 1977), most organ-scale models and all micro-scale models have assumed a ‘frozen’ tissue geometry. Future models will have to relax this assumption.

The villous tissue constituting the ‘solid’ phase of the placenta is capable of altering its dimensions both passively (due to changes in transmural pressure and water transfer between the maternal and fetal compartments) and actively (via biochemically-induced constriction or dilation of smooth muscle in the fetoplacental vasculature (Jones et al. 2015), or even via contraction of an entire villous tree (Lecarpentier et al. 2014)). Such changes may have a profound influence on fetal perfusion and hence solute exchange. Additional factors that merit attention include the amniotic fluid that surrounds the chorionic plate of the placenta (which may compress chorionic vessels and, possibly, contribute to the transport of solutes or even infections between the mother and the fetus) and interactions between neighboring placentones within the human placenta. Although partially separated by septal elevations, placentones can exchange flows and solutes in the subchorionic space on the uteroplacental side and are also coupled as a part of the fetoplacental vascular network.

3.4. Capturing evolving placental structure over gestation

Virtually all existing models of human placental blood flow and transport focus on the full-term placenta, primarily due to the sparsity of microstructural data from earlier stages of gestation (Clark & Kruger 2017). Owing to the unique anatomy of the human placenta (Carter 2007; Benirschke et al. 2012), animal data from all but the higher primates do not help to bridge the gap.

The initial stages of invasive human placental development resemble tumor growth; accordingly, oxygen is low and its supply is diffusion-limited. For oxygen diffusivity of D ≈ 10⁻⁹ m²/s and taking the upper limit of the metabolic timescale to be τ_m ≈ 10² s, the maximum diffusive distance is $\sqrt{D{\tau }_m}\lesssim 1\text{mm}$. The placenta reaches this size about two weeks post-conception (Benirschke et al. 2012). The fetal circulation develops first and maternal blood does not enter the IVS until about week 10 (Schneider 2011). Before this, maternal oxygen and nutrients must therefore be delivered via flow of blood plasma that leaks from spiral arteries (Jauniaux et al. 2000), supported by secretions from uterine glands (Burton et al. 2002). The development of utero-placental flow and the transition from maternal flow-limited to membrane-limited transport may be significant for understanding miscarriages occurring at the end of the first trimester.

The fetoplacental vasculature that forms during the first month of gestation has a very different topology from that of the full-term placenta, with thin extensively branched capillary networks. At about week 25 (the end of the second trimester), the terminal villi switch to predominantly non-branching blood-vessel growth, producing elongated branches with characteristic terminal capillary loops (Figure 2b) (Kaufmann et al. 2004). This legacy of placental development, in combination with possible vascular regression, results in a strongly heterogeneous fetoplacental structure that varies markedly within and between placentones. Future models need to explore this variability in capillary network topology and geometry and its implication for solute transfer.

3.5. Multi-modal data assimilation and model validation

Theoretical or computational models of systems as complex as the human placenta are not practically useful until validated against experimental and clinical data. Modeling approaches have evolved from ‘black box’ algebraic models for equilibrium exchangers and compartmental reaction-kinetics models in the 1960s and 70s (surveyed by Chernyavsky et al. (2010) and Serov et al. (2016)), via idealized porous-medium flow and advection-diffusion-uptake models, to the image-based CFD simulations described in Sec. 2. The latest generation of models thus require rich datasets both structurally, as modeling inputs, and functionally, as spatial fields to test model predictions.

A number of challenges arise even before a mathematical model can be tested. The enormous complexity of placental structure makes functional and shape analysis very difficult. Multiple imaging modalities still suffer from insufficient spatial resolution, low accuracy or poor consistency (see Nye et al. (2018) for a recent overview of oxygen measurement techniques). Even given structural data of sufficient quality, there is a paucity of efficient segmentation tools, since the strong variability of placental micro-geometry requires bespoke image analysis. The development of operator-unbiased (semi-)automated segmentation algorithms optimized for human placenta is critical to build up sufficient statistical understanding of its 3D structure. This has direct relevance to pregnancy pathologies. For instance, the vasculosyncytial barrier thickness is increased and IVS pores are larger in FGR-compromised preeclamptic pregnancies compared to controls (Rainey & Mayhew 2010), and villous branching is more extensive and the IVS packing is denser in diabetic placentas (Leach 2011).

Exploiting approaches developed in geophysics, a consistent assimilation of data into mathematical models will require a statistical approach and careful sampling, such as identifying the optimal size of regions of interest and Latin hypercube designs, to avoid unrepresentative data and over-fitting. Concurrent and iterative model refinement and experimental design should also ensure optimal model development, requiring an appropriate framework for quantifying variability and uncertainty in model predictions (Chernyavsky et al. 2012). The early models of placental blood flow and transport were designed by physiologists for physiologists. Despite being simple, they were transparent and focused on specific research questions. In the context of complex placental structure, the abundance of computational power poses the challenge of responsibly identifying a model’s relevance and limitations. To gain new fundamental insights and develop models useful for the clinic, future studies need to generate and validate a new generation of reduced models, effectively revisiting original low-dimensional descriptions with a new understanding of dominant physical processes and geometrical features.

4. Summary

Solute exchange between mother and fetus in the placenta is regulated by processes occurring at diverse lengthscales, from the thin vasculosyncytial barrier to the macroscopic arrangement of blood vessels across the whole organ. An upper bound on the exchange capacity for a given solute emerges when fetal and maternal flow are sufficient to maintain fixed concentration gradients on either side of the vasculosyncitial barrier: transport in this instance is promoted by small diffusion distances and large exchange areas accessible by both flows, which are being increasingly well quantified using 3D imaging studies. This bound is relevant for solutes that diffuse slowly across the barrier, having low effective Damköhler numbers. For solutes that cross this barrier more rapidly, transport is flow-limited on the fetal or maternal sides of the barrier. In this instance, preliminary estimates of the exchange capacity have emerged from computations of some specific representations of fetal and maternal flow domains. Much work lies ahead in assembling these findings within a coherent framework at the whole-organ level, accounting for variability both within and between individuals, in validating models against experimental data, and ultimately in developing simulation tools having genuine clinical utility.

Summary Points.

1. The exchange capacity of the placenta is strongly influenced by the elaborate shape of the tissue barrier that separates fetal blood flowing through capillary networks on one side and maternal blood flowing through a porous medium on the other.

2. For solutes that diffuse rapidly in tissue, exchange is limited by the rate at which solutes are delivered to, and removed from, the exchange interface by maternal flow emerging from spiral arteries, and fetal flow within the chorionic network.

3. Active processes at the subcellular level in the tissue barrier regulate transport of more complex molecules.

4. Modeling and simulation, exploiting 3D imaging of placental tissues, is advancing quantification of the interactions between flow and diffusive exchange.

Future Issues.

1. Features such as flow-induced deformability of villous tissues, blood rheology in complex flow domains, active regulation of fetoplacental vessels and the impact of the external mechanical environment on placental function (due to factors such as fetal movement, maternal posture, trauma and microgravity) require further exploration.

2. There is a need to characterize 3D placental morphology at a statistical level, in healthy and diseased placentas, and to account for geometric variability and parameter uncertainty in future models.

3. New models are required to describe the growth and development of the human placenta in early pregnancy.

4. Models can be used to address the conflicting demands on the placenta in transporting multiple substances, and to understand structural variations across placental mammalian species.